Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2019 Oct 3;2(11):8010–8021. doi: 10.1021/acsaem.9b01490

Interplay between Charge Carrier Mobility, Exciton Diffusion, Crystal Packing, and Charge Separation in Perylene Diimide-Based Heterojunctions

Kevin M Felter 1, Valentina M Caselli 1, D Deniz Günbaş 1, Tom J Savenije 1, Ferdinand C Grozema 1,*
PMCID: PMC6880777  PMID: 31788664

Abstract

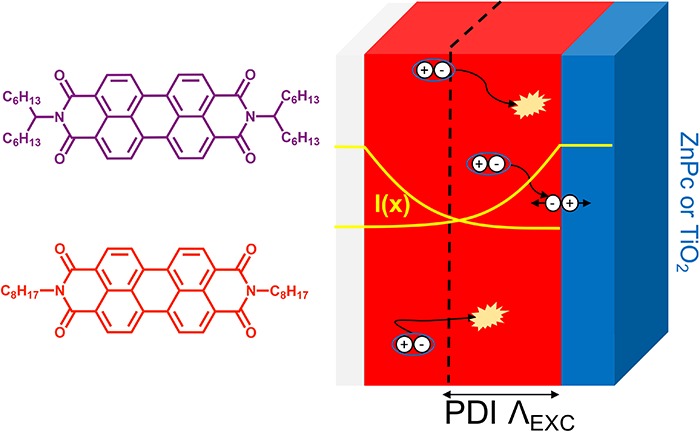
graphic file with name ae9b01490_0010.jpg

Two of the key parameters that characterize the usefulness of organic semiconductors for organic or hybrid organic/inorganic solar cells are the mobility of charges and the diffusion length of excitons. Both parameters are strongly related to the supramolecular organization in the material. In this work we have investigated the relation between the solid-state molecular packing and the exciton diffusion length, charge carrier mobility, and charge carrier separation yield using two perylene diimide (PDI) derivatives which differ in their substitution. We have used the time-resolved microwave photoconductivity technique and measured charge carrier mobilities of 0.32 and 0.02 cm2/(Vs) and determined exciton diffusion lengths of 60 and 18 nm for octyl- and bulky hexylheptyl-imide substituted PDIs, respectively. This diffusion length is independent of substrate type and aggregate domain size. The differences in charge carrier mobility and exciton diffusion length clearly reflect the effect of solid-state packing of PDIs on their optoelectronic properties and show that significant improvements can be obtained by effectively controlling the solid-state packing.

Keywords: exciton diffusion length, PDI, crystal packing, microwave conductivity, charge separation

1. Introduction

Perylene diimides (PDIs) are attractive organic semiconductors for optoelectronic studies and organic photovoltaic technologies owing to their high optical absorption and fluorescence yield, high photochemical stability,1 and strong electron-accepting properties. Among the most appealing characteristics of PDIs is the possibility to control the electronic structure and molecular packing by chemically functionalizing the molecule with a large variety of side groups. As such, they are often used to study energetic and molecular packing effects in connection to organic semiconductor device performance.2 These electron acceptor molecules also offer an attractive alternative to fullerene acceptor molecules that are predominantly used in organic photovoltaic devices.3 An additional aspect of this is that PDIs display unconventional processes such as singlet exciton fission with high efficiency and rate that can ultimately lead to device efficiencies surpassing the Shockley–Queisser limit.4−6 The reverse process, triplet–triplet annihilation up-conversion has also been demonstrated in PDIs.7,8 Both processes can be used to boost organic photovoltaic device efficiencies.

Two key parameters that determine the performance of organic semiconductors in optoelectronic applications are the charge carrier mobility and the exciton diffusion length. However, only a few reports exist on experimentally determined PDI diffusion characteristics. To our knowledge, there are only three previously published studies on the PDI exciton diffusion length ΛEXC. The ΛEXC values in solid-state thin films of phenylethyl imide-substituted PDI vary from 50 to 500 nm (with a 50 nm resolution)9 to 2.5 ± 0.5 μm.10 In addition, two studies on J-aggregates of PDIs in solution reported values of ΛEXC = 70 nm11 and ΛEXC = 96 nm.12 These values are in agreement with that of a related perylene compound, perylene tetracarboxyl dianhydride.13 In a study on this material it was shown how the grain diameter strongly affects the nonradiative decay rate. In turn, the exciton diffusion length that has been determined via photoluminescence quenching was ΛEXC = 6.5 ± 1.0 nm for a grain diameter of ±5 nm to ΛEXC = 21.5 ± 2.5 nm for ±400 nm grain sizes. Some of these singlet exciton diffusion lengths are unusually long, considering that for most organic semiconductors singlet exciton diffusion lengths are in the range of 2–15 nm.14 Therefore, the electronic and structural origins of the large singlet exciton diffusion lengths are interesting to study in PDIs. The second important electronic characteristic of organic semiconductors is the charge carrier mobility. There are several theoretical15−18 and experimental17−21 studies on PDIs reporting electron mobilities μe– ranging from 0.1 to 2 cm2/(V s). Some of these studies indicate that intermolecular orientation and distance strongly influence charge carrier mobility. This was explained by differences in molecular orbital overlap that affect the effective charge transfer integral between neighboring molecules.

The aim of this study is to investigate the interplay between morphology and optoelectronic properties, which is highly relevant considering the aforementioned renewed interest in PDI molecules as electron acceptors and the possible exploitation of singlet fission6,22 and up-conversion in organic photovoltaic devices.23,24 However, while the optical and charge carrier properties have been reported separately,10,17,25−27 no integrated study has been performed reporting on exciton diffusion and charge carrier dynamics using the same experimental technique, that is, time-resolved microwave conductivity. In fact, simultaneous knowledge on all these properties is essential for designing better chromophore systems for organics based optoelectronic devices.

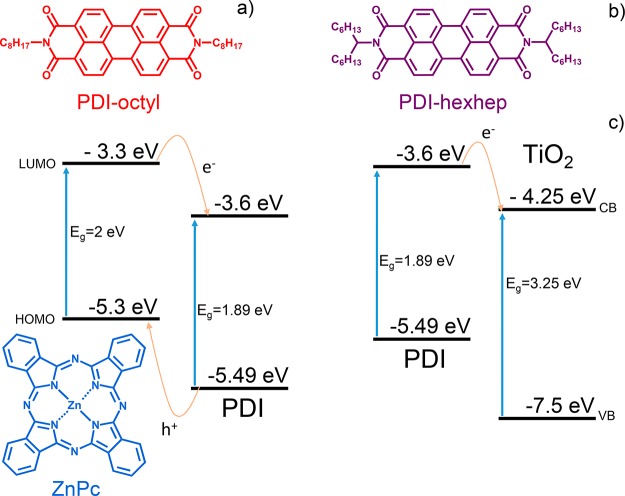
To this end, we examine thin films of octyl (PDI-octyl) and hexylheptyl (PDI-hexhep) imide-substituted PDIs shown in Figure 1. PDI-octyl is a commonly used PDI for organic electronics related studies and has been shown to form large crystalline aggregates.28−31 PDI-hexhep is substituted with a branched alkyl chain that is commonly used to improve solubility by decreasing intermolecular π–π stacking between PDI cores.28 The decreased electronic interaction between the π systems should provide clear differences in optoelectronic behavior between PDI-hexhep and PDI-octyl. Using electron and laser pulsed time-resolved microwave conductivity (TRMC) measurements we determined charge carrier mobilities of 0.32 and 0.02 cm2/(Vs) and corresponding exciton diffusion lengths of 60 and 20 nm for PDI-octyl and PDI-hexhep, respectively. These studies were performed on planar heterojunction systems of PDIs with zinc phthalocyanine (ZnPc) and polycrystalline titanium dioxide (TiO2) of which the electronic diagram is depicted in Figure 1.

Figure 1.

Figure 1

Open in a new tab

Chemical structure of (a) PDI-octyl and (b) PDI-hexhep and ZnPc and (c) energy diagrams for the fully organic PDI/ZnPc and TiO2/PDI planar heterojunction used in this study to investigate charge carrier kinetics and exciton diffusion.

2. Experimental Section

2.1. Sample Preparation and Characterization

PDI-octyl (N,N′-dioctyl-3,4,9,10-perylenedicarboximide) and PDI-hexhep (N′-hexylheptyl-3,4,9,10-perylenedicarboximide) were synthesized from perylene-3,4,9,10 tetracarboxylic acid dianhydride as purchased from Sigma-Aldrich according to procedures published elsewhere.32 The ZnPc powder was purchased from TCP and used without further modification. The polycrystalline TiO2-coated fused silica substrates (∼90 nm thickness) were purchased from Everest Coatings, Inc. and treated at 450 °C for 2 h in a furnace. Pulse radiolysis time-resolved microwave conductivity (PR-TRMC) measurements were performed on PDI powders and flash photolysis TRMC measurements were carried out on thin films. Thin films of PDI and ZnPc powders were deposited on fused silica substrates by thermal evaporation in an AJA ATC Orion evaporator. Prior to deposition, the substrates (ESCO, 12 × 25 × 1 mm) underwent an air plasma treatment (2 min, 1000 mTorr) to clean and charge the substrate surface. During deposition, the powders were heated to their sublimation temperature (180–230 °C) under high vacuum conditions (10–7–10–6 mbar) and heated further until the desired evaporation rate was reached (0.3 Å/s). The deposition rate was monitored using a quartz microcrystal balance. The fused silica substrates were heated to 150 °C during PDI deposition to promote crystallization and were brought back to room temperature prior to ZnPc evaporation in order to prevent blending of the organic layers. TiO2 thin films on fused silica underwent the same processing to fabricate the TiO2/PDI planar heterojunctions except for the substrates heating step. During deposition the substrate holder rotated the substrates at 25 rpm to ensure film homogeneity.

The thin film surface morphology was imaged using an Extreme-Resolution Analytical Field Emission SEM JEOL-7800F Prime Extreme. The images were recorded under high vacuum with an upper electron detector (UED) and a lower electron detector (LED) to measure secondary and backscattered electrons. The resolution of the images was enhanced by occasionally sputtering the organic films with a 5 nm thick Pt layer (sputter coater Leica EM ACE600). The film thickness was determined using a step-profilometer (Veeco Dektak 8 Stylus step-profilometer) and are listed in Table S1. X-ray diffractograms were acquired using a Brüker D8 X-ray diffractometer (Co Kα1 radiation, λ = 1.79 Å) and analyzed with the Brüker program EVA. Steady-state absorption spectra were obtained using a PerkinElmer Lambda 1050 spectrometer with the sample placed inside and in front of an integrating sphere to measure attenuation and transmission, respectively. Emission and excitation spectra of solutions and thin films were recorded with a FLS980 Edinburgh Instruments spectrometer. Time-resolved photoluminescence experiments were performed with a Hamamatsu C5680 streak camera coupled with a Princeton Instruments spectrograph. The excitation wavelength was created via frequency doubling using a Coherent Chameleon oscillator operating at a repetition rate of 80 MHz.

2.2. Pulse Radiolysis Microwave Conductivity

The PDI charge carrier mobilities were measured in pulse radiolysis TRMC measurements. An extensive description of the PR-TRMC technique and its capabilities can be found elsewhere.33,34 In this technique, the powder sample is irradiated with a 1–50 ns duration pulse of high-energy electrons (3 MeV) generated by a Van de Graaff accelerator that creates low concentration (micromolar) but uniformly distributed positive and negative carrier densities. Subsequently, the time-resolved conductivity of the sample is probed by monitoring the attenuation of reflected microwave power (frequency 28–38 GHz, maximum electric field strength in the sample is 10 V/m). The fractional change in microwave power reflected by the cell (ΔP(t)/P) relates to the change in conductivity Δσ(t) as

2.2. 1

The initial concentration of charge carrier pairs, that is, electrons and holes nP can be estimated using dosimetry measurements combined with a charge-scavenging model. From this estimate of the carrier concentration, a summed charge carrier mobility ΣμTRMC can be calculated according to

2.2. 2

where ΣμTRMC is the sum of electron and hole mobility that both contribute to the conductivity and are indistinguishable in the experiment. Almost all known crystal structures show that PDIs preferentially stack in a one-dimensional columnar geometry. Therefore, we derive an intracolumnar mobility that equals three times the isotropic value obtained from the TRMC conductivity measurements

2.2. 3

The measured mobility values in PR-TRMC are related to the charge transfer rate between PDI molecules in the ordered crystallite. An expression for the charge transfer rate ν, between PDI molecules is provided by Marcus theory35,36

2.2. 4

where Jeff is the effective charge transfer integral between neighboring molecules that depends on the mutual orientation and distance, λ is the reorganization energy, T is the temperature, and kB is Boltzmann’s constant. Provided that the PDIs self-assemble in columnar crystalline stacks without structural fluctuations, the charge transfer integrals for PDI molecules in such a stack are identical and the charge carrier mobility in the direction along the stack μ1D can be calculated according to the relation involving an expression for the charge carrier diffusion coefficient DCHARGE = νd2(37)

2.2. 5

In eq 5, d is the intermolecular distance in a PDI stack. Note that for a given value of the charge transfer rate, ν, the charge carrier mobility scales with the square of d, however, for large values of d the charge transfer integral, Jeff, and hence, ν, will be smaller, see eq 4. The charge carrier mobility can be used to provide an estimate of the charge carrier diffusion coefficient DCHARGE according to the Einstein–Smoluchowski relation

2.2. 6

where q is the elementary charge.

2.3. Flash Photolysis Microwave Conductivity

The diffusion length of the PDIs were studied with the laser pulsed TRMC technique. These TRMC measurements were performed on a home-built setup of which the operating principles are described elsewhere.38 In this technique, optical excitation of the sample occurs via 3 ns full width half-maximum (fwhm) laser pulses (λ = 240–2200 nm). The sample is probed by continuous X-band microwaves (∼8.4 GHz) in a microwave resonant cavity cell, that defines the instrument response function to 18 ns. The fractional change in microwave power reflected (ΔP/P) is related to a change in photoconductance, ΔG(t), as

2.3. 7

In eq 7, K is the microwave frequency dependent sensitivity factor that has a predetermined value of 40 × 103 S1– for the current experimental conditions.39 ΔG(t) is directly proportional to the product of the charge carrier density ni and mobility μi according to

2.3. 8

In eq 8, e is the elementary charge, L the film thickness, and β the ratio between the inner width and length dimensions of the microwave waveguide. The index “i” runs over all charged species present, that is, electrons and holes both contribute to the photoconductance. The photoconductance transients can be deconvoluted for the instrumental response function using the cavity response function profile (LP(t)):

2.3. 9

In eq 9, ΔG0 is the initial photoconductance prior to charge carrier decay and ⊗ indicates the convolution between LP(t) and ΔG0. ci and τi are the exponent and decay time characteristic of the i-th transient decay component. The sum of all decay components account for all recombination processes occurring in the sample. ΔG0 can be used to obtain a value for the product of the incident photon to charge carrier generation yield, η0, and the sum of electron and hole mobility, Σμ, as40

2.3. 10

In eq 10, I0 is the measured incident photon fluence, and FR is the fraction of reflected incident photons as deduced from attenuation and transmission measurements.

The applied fitting function to determine the exciton diffusion length ΛEXC was described by Kroeze et al. for steady state illumination and has since been applied to study singlet and triplet exciton diffusion for organic semiconductors in various heterojunction systems.41−44 Such function is used to fit the experimentally measured η0Σμ and has the following general form:

2.3. 11

In eq 11, φCS is the interfacial charge separation yield that is a function of S, the fraction of charges that reaches the interface. S is a function of the absorption coefficient α, L, and ΛEXC. It should be noted that φCS can only be disentangled from the product η0Σμ if the mobility of the generated charge carriers is known. For the bilayers with TiO2, this approach is discussed below. However, for the PDI-ZnPc bilayers this is not possible. Nevertheless, since ΛEXC is independent of the mobility, it can be directly obtained from the thickness dependence, as discussed below. The expression for S is provided in the SI and depends on the illumination side (front side (FS) and back side (BS)) and whether exciton reflection or quenching occurs at the nonheterojunction interface of the system. To determine ΛEXC, planar heterojunction systems were measured by front side and back side illumination and by varying the PDI film thickness L. The measured values for η0Σμ are fitted with eqs 11 and S2 using a predetermined value for α to obtain the indistinguishable product term φCSΣμ and ΛEXC. Similar fitting functions, that is, eqs 11 and S3, were applied to TiO2/PDI heterojunctions. However, instead of varying the PDI layer thickness, an action spectrum was measured acting to vary α. The singlet exciton diffusion coefficient DEXC can be calculated using the relation

2.3. 12

where τEXC is the singlet exciton lifetime obtained from photoluminescence measurements.

3. Results and Discussion

3.1. Crystallinity and Charge Carrier Transport in PDI Powders

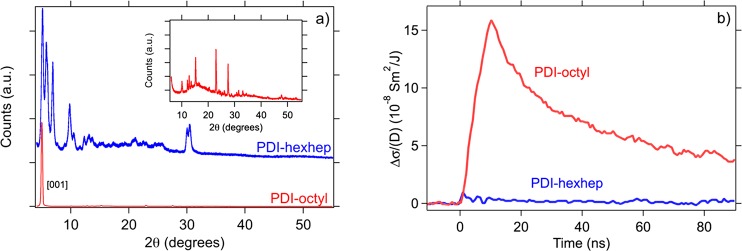
We first investigate the effect of the PDI imid substitution on molecular packing using X-ray powder diffraction and the resulting charge carrier mobility using pulse radiolysis conductivity experiments. The X-ray diffractograms of PDI-octyl and PDI-hexhep powders in Figure 2a display strong differences in reflection intensity. PDI-octyl has a pronounced [001] reflections that is consistent with the known crystal structure,30,31 contrary to the less-well resolved PDI-hexhep diffractogram that indicates rather poor crystallinity. This is consistent with the expected effect of the branched side chains that disrupt the solid-state packing. The radiation induced conductivity transients obtained from PR-TRMC measurement for PDI-octyl and PDI-hexhep powders are shown in Figure 2b. During the 10 ns electron pulse, the conductivity increases linearly with time due to the formation of mobile charge carriers. Subsequently, recombination of electrons and holes or trapping of charges at impurities cause the conductivity to decay. The conductivity of PDI-octyl is an order of magnitude higher than that of PDI-hexhep. The sum of the electron and hole mobility Σμ derived from these transients are Σμ1D = 0.32 for PDI-octyl and 0.02 cm2/(V s) for PDI-hexhep. According to estimates based on Marcus theory made by Delgado et al. for PDI-pentyl, which has a similar crystal packing as PDI-octyl, the values of the electron and hole mobility of PDI-octyl are μe– = 0.1 cm2/(V s) and μh+ = 2.1 cm2/(V s), respectively. These values are larger than what we experimentally find for PDI-octyl, but this can easily be understood by realizing that the calculated values do not account for any static or dynamic structural disorder.15,16 For PDI-hexhep such calculations are not possible since no crystal structure is known. The mobility of PDI-octyl is among the highest values obtained for perylene diimides45 and is attributed to columnar packed PDI units. Such columnar structures are also observed in XRD and SEM measurements of the thin films shown later. The more ordered structure of PDI-octyl, as shown in Figure S1, compared to PDI-hexhep leads to a larger effective orbital overlap and thus higher mobility values.15

Figure 2.

Figure 2

Open in a new tab

(a) Powder X-ray diffractograms of PDI-octyl and PDI-hexhep with the pronounced [001] reflection of PDI-octyl and a 4500x zoomed-in view in the inset. (b) Dose normalized radiation induced conductivity transients for PDI-octyl and PDI-hexhep at room temperature using a 10 ns electron pulse.

3.2. Solid-State Packing and Thin Film Morphology

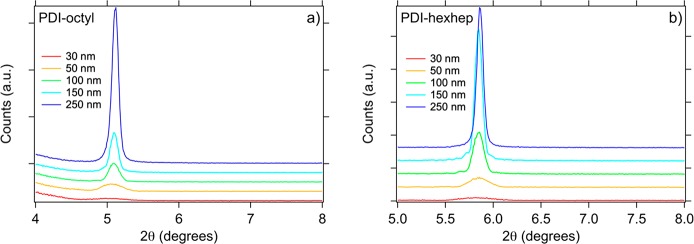
The X-ray diffractograms of PDI films in Figure 3 reveal one reflection for PDI-octyl at 5.1° and PDI-hexhep at 5.86°. This corresponds to intercolumnar spacings of 20.1 and 17.5 Å, respectively. The preferential crystal orientation of PDI-octyl and -hexhep are in accordance with literature.19,30,45 Comparison of the powder with the thin film diffractograms shows the preferred crystal orientation in the thin film since it only has one reflection, in contrast to the powder spectrum. The extent of crystallization of PDI-octyl does not seem to be larger than in PDI-hexhep. This observation is supported by an estimation of the crystalline domain size (provided in Table S2) using the Scherrer equation. The estimate shows that PDI-hexhep has similar crystalline domains ranging from 29 to 131 nm, while in PDI-octyl it ranges from 28 to 97 nm.

Figure 3.

Figure 3

Open in a new tab

X-ray diffractograms for annealed (150 °C) single layer thin films on fused silica of (a) PDI-octyl and (b) PDI-hexhep with thicknesses ranging from 15 to 500 nm.

Previous studies have shown that the formation of organic thin films depends on the substrate properties.20,31,46 We use fused silica and TiO2 as a substrate to investigate a possible relation between substrate type and the solid-state packing of the PDIs. In Figure 4, SEM images are displayed of the PDI film surface morphology on both fused silica and TiO2. The films are not annealed and are carefully coated with a Pt layer (3 nm) to allow better imaging. The PDI-octyl layer on fused silica is composed of rod like domains with lengths up to 500 nm. Similar but rougher structures exist on TiO2 owing to the rougher TiO2 surface (Figure S3). The PDI-hexhep layer on fused silica lacks structure, while on TiO2, we do observe irregular shaped features with diameters up to hundreds of nanometers. The similarity between PDI surface morphology on fused silica and TiO2 is substantiated by an identical position and width of the reflection in the XRD diffractogram of PDI-octyl and PDI-hexhep on fused silica and TiO2 (Figure S5). Upon annealing the film, PDI-octyl and -hexhep both form large rod-like filaments of lengths exceeding a micrometer, as displayed in Figure S2. As mentioned, the annealed films were used in the PDI/ZnPc heterojunctions, while the unannealed variants in Figure 4 were used in the TiO2/PDI heterojunctions. We observe similar sizes of filamental structures in all film thicknesses although the film surface roughens (Figure S2).

Figure 4.

Figure 4

Open in a new tab

Scanning electron microscope images for 100 nm thick films of PDI-octyl (left) and PDI-hexhep (right) on fused silica and TiO2 substrates. Scale bars indicate the size of the features at 10 000× magnification.

3.3. Optical Properties of Thin Films

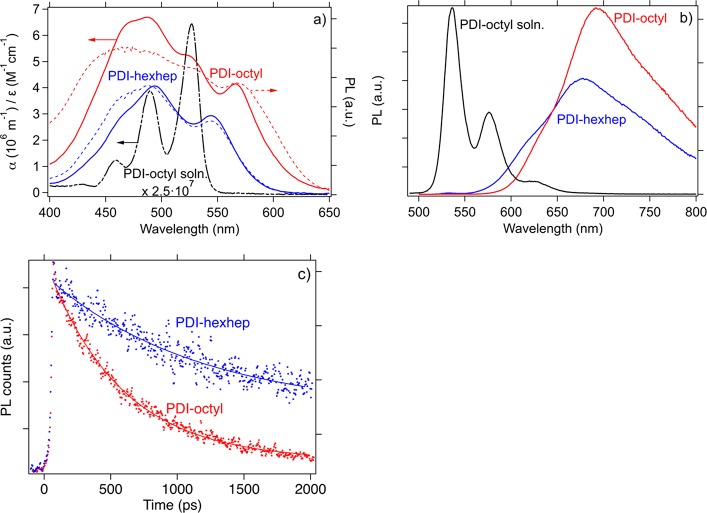
In Figure 5a, we display the absorption spectra of films of PDI-octyl and PDI-hexhep on fused silica and PDI-octyl in solution. In solution, the absorption spectrum of both PDIs is identical (Figure S4) and shows the characteristic PDI absorption in the 450–550 nm region with three bands centered at 460, 490, and 530 nm that belong to the π–π* transition of the PDI aromatic core involved in the vibronic progression of the S0–S1 conversion.26,27 In the solid-state, PDI-octyl and PDI-hexhep show aggregate formation and more particular, H-type structures (visible from the 550 nm absorption shoulder).26,47,48 The stronger red shift in the absorption onset of PDI-octyl (570 nm) than -hexhep (540 nm) indicates stronger excitonic interaction in PDI-octyl.27 The shape of the absorption spectrum of PDI-octyl and PDI-hexhep resembles that of their excitation spectrum. However, the emission intensity of PDI-octyl is less at lower wavelength, which points to the presence of a nonradiative decay pathway. The effect of solid-state packing is also visible in the emission spectra shown in Figure 5b. The PDI emission spectrum in solution has three distinct emission features, while in the thin films, these features broadened strongly and an overall emission redshift is observed. This redshift in the emission in PDIs is commonly attributed to the presence of emissive excimer states that form upon aggregation.49,50 We recently carried out a study in which we showed that bromination in the bay area prevents the formation of excimer states that are a competing decay channel for singlets, next to singlet fission.51 The thin film photoluminescence lifetime of PDI-octyl and PDI-hexhep are τEXC = 0.55 ns and τEXC = 1.13 ns, respectively, as determined from a monoexponential decay fit on fluorescence decays as shown in Figure 5c. In our previous study, we estimated an τEXC = 890 ps for PDI-octyl, which was longer than in the present study, as we presently used a streak camera setup that has a faster detection limit. The shorter fluorescence lifetime of excitons in PDI-octyl may be another indication of its improved packing as PDI-hexhep has a fluorescence lifetime that is more similar to that in solution (τEXC = 4.5 ns).4

Figure 5.

Figure 5

Open in a new tab

(a) Absorption spectra (α on left axis) and fluorescence excitation spectra (right axis) of PDI-octyl and PDI-hexhep films and (b) emission spectra thin films. The absorption (ε on left axis) and emission spectra of PDI-octyl in 1 × 10–5 M CHCl3 solution has also been added in blue. (c) Fluorescence decays of annealed thin films of PDI-octyl (emission at 687 nm) and PDI-hexhep (emission at 630 nm) (dots) upon 460 nm photoexcitation (300 μW) and their monoexponential fit (solid lines).

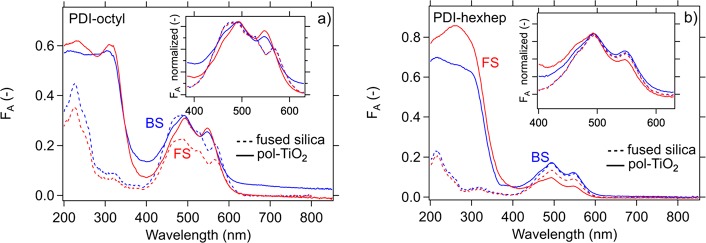
In Figure 6, we show the effect of the substrate on the PDI absorption. For unannealed PDI-octyl on TiO2, we observe absorption features that are more similar to those in solution. In contrast, the optical absorption of PDI-hexhep lacks a strong substrate dependence shown in Figure 6b. The effect on PDI-octyl may be explained by the rougher TiO2 topology or different interfacial tension that negatively affects close packing, although no strong differences are observed in domain sizes. Since PDI-hexhep did not display strong aggregation on fused silica, the difference with TiO2 may be expected to be smaller. XRD measurements confirm that aggregates of PDI-octyl and PDI-hexhep are formed to the same extent on both substrate types with identical crystal phase (Figure S5). We therefore expect little effect of the substrate on the charge carrier and exciton transport properties.

Figure 6.

Figure 6

Open in a new tab

(a) Absorptance spectra of unannealed 50 nm PDI-octyl thin film on uncoated fused silica and TiO2 and (b) a similar plot for a 50 nm PDI-hexhep thin film upon front side (FS) and back side excitation (BS). The insets show the absorptance spectra normalized to the absorption maximum at around 490 nm. They show the difference and spectral similarity for PDI-octyl and PDI-hexhep, respectively.

3.4. Exciton Diffusion in PDI/ZnPc Planar Heterojunctions

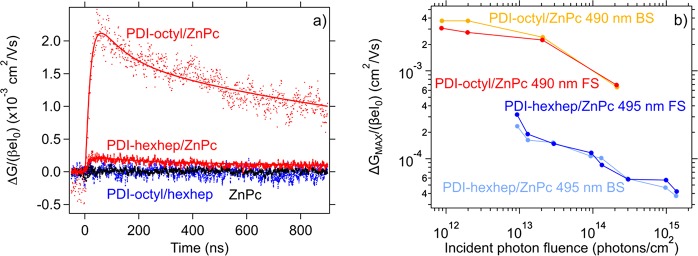
In order to gain insight in the diffusion of excitons in PDI-octyl and PDI-hexhep we have performed TRMC photoconductivity measurements as shown in Figure 7a. In Figure 7a, the photoconductance transients obtained upon photoexciting bilayers of PDI-octyl/ZnPc and PDI-hexhep/ZnPc (50/30 nm) are compared with the photoconductance of the PDI-octyl and ZnPc layers. There is negligible photoconductivity in these single layers. However, the photoconductance maximum increases by a factor 40 and four upon forming the PDI-octyl/ZnPc and PDI-hexhep/ZnPc bilayers, respectively.

Figure 7.

Figure 7

Open in a new tab

(a) Photoconductance transients are shown for a 50 nm PDI and 30 nm ZnPc single film and 50/30 nm bilayer at an incident photon fluence of 1 × 1013–1 × 1014 photons/cm2 upon 490/495 nm excitation for both PDI-octyl and PDI-hexhep (dots). The solid lines represent the triexponential function of eq 9 that is applied to fit the transients. (b) The photon fluence dependence of η0Σμ is represented for a 50/30 nm PDI-octyl/ZnPc (490 nm) and PDI-hexhep/ZnPc bilayer (495 nm) upon FS and BS excitation.

This can be explained by considering the energy diagram shown in Figure 1. The energy difference between the LUMO of ZnPc and PDI is 0.3 eV and that between the HOMO of ZnPc and PDI is 0.19 eV. The LUMO offset is significantly larger than the typical binding energy of singlet excitons in organic solids (0.06 eV).52,53 Therefore, all singlet excitons reaching the interface will dissociate, which cannot happen in a single layer structure. However, the 0.3 eV offset is likely not enough for triplet excitons to charge separate as their binding energy is higher than that of singlets due to the exchange energy.14,53

The charge carrier lifetime exceeds a microsecond. We fit the bilayer transients using the triexponential decay function described in eq 9 represented by the solid lines in Figure 7a. The photoconductance prior to electron–hole recombination ΔG0 and carrier kinetics obtained from the fitting are provided in Table S3 and are comparable to values found in an earlier TRMC study on thin film bulk heterojunction systems of soluble PDIs and copper phthalocyanine.25 Using eq 10, ΔG0 is converted to η0Σμ and shown in Figure 7b as a function of the incident photon fluence Io. We observe a fluence independent photoconductance regime below an Io of 2 × 1012 photons/cm2 for PDI-octyl, while due to the low signal-to-noise ratio in the PDI-hexhep/ZnPc bilayer it was not possible to measure photoconductivity below 1 × 1013 photons/cm2. The low photoconductivity of the PDI-hexhep/ZnPc bilayer may be due to a low charge carrier mobility and/or charge separation yield. We observe a decrease in photoconductance for both bilayers at fluences that are higher than 2 × 1012 photons/cm2 that we attribute to second-order charge recombination,40 which we kept to a minimum during our measurements. The low photoconductivity in the single layers is caused by negligible exciton dissociation and, therefore, a low yield of free and mobile charge carriers. However, in the bilayer heterojunction the charges can separate at the ZnPc-PDI interface between ZnPc and PDI. In this situation, the hole localizes in the ZnPc and the electron in the PDI. Possible reasons for the higher photoconductivity of the PDI-octyl bilayer than the PDI-hexhep bilayer are a higher PDI-octyl electron mobility and a higher yield of free and mobile charge carriers upon photon absorption. The 10-fold higher charge carrier mobility of PDI-octyl found in the pulse radiolysis measurements described above is in agreement with this difference in the photoconductivity.

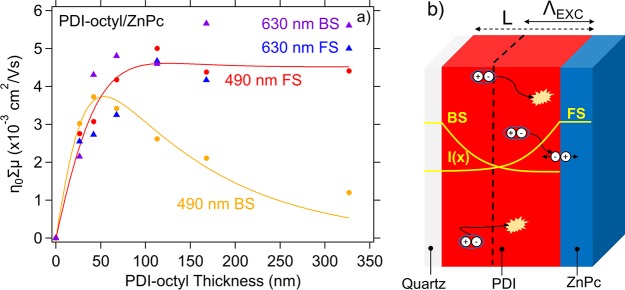
In Figure 8a, we show η0Σμ in the fluence independent photoconductance regime of the PDI-octyl/ZnPc bilayers as a function of PDI film thickness. Upon front side illumination at 490 nm, we observe an increasing η0Σμ that saturates at 100 nm. In contrast, upon back side bilayer illumination η0Σμ reaches a maximum at 50 nm and decreases at higher PDI thicknesses. We explain these trends as follows using the schematic representation shown in Figure 8b. Upon front side (FS) illumination, light is absorbed by both the ZnPc (30 nm thickness) and the PDI where excitons are generated in both materials thus contributing to the photoconductance. These excitons form charge transfer excitons that dissociate at the interface by transferring electrons to the PDI (LUMO offset 0.3 eV) and holes to the ZnPc (HOMO offset 0.19 eV) that are responsible for the photoconductance.54 As the PDI thickness increases, more excitons are created and η0Σμ increases. At a PDI thickness of 50 nm, the linear trend in photoconductance as a function of PDI thickness becomes sublinear as only a fraction of the excitons created beyond 50 nm is capable of diffusing toward the interface and charge separate, while the rest of these excitons undergo recombination. Therefore, the gain in free charge carriers diminishes upon increasing the PDI thickness and the photoconductance trend saturates. Consequently, the exciton diffusion length plays a pivotal role in the observed photoconductive behavior. Moreover, when the PDI excitons are primarily generated near the PDI/substrate interface, most excitons need to diffuse to the heterojunction interface in order to charge separate. Indeed, upon back side (BS) illumination the photoconductance follows a similar trend as in FS illumination up until 50 nm, where exciton diffusion is no limitation to the charge carrier yield. Beyond this length a decreasing amount of PDI excitons reach the PDI/ZnPc interface and less excitons are generated within the ZnPc such that η0Σμ decreases beyond 50 nm and eventually reduces to zero. We fit the data points in Figure 8 with the exciton model described by eqs 11 and S2 and find φCSΣμ = 0.0152 cm2/(V s) and ΛEXC = 59.91 nm for PDI-octyl using α = 7.96 × 106 m2 (at 490 nm). If we assume a unity yield of charge separation, φCS, then the charge carrier mobility Σμ in the thin film would be a factor 50 lower than in the powder as determined from PR-TRMC. However, a unity φCS is unlikely since exciton recombination and geminate interfacial charge recombination are likely to happen. Selective excitation of ZnPc in the PDI-octyl/ZnPc show similar η0Σμ trends and values as PDI excitation close to the interface. The similarity in η0Σμ values points to equal charge separation efficiency when exciting either ZnPc or PDI. We did not carry out the diffusion length determination for PDI-hexhep because the low signal-to-noise ratio in the PDI-hexhep bilayers.

Figure 8.

Figure 8

Open in a new tab

(a) η0Σμ values as a function of PDI thickness of PDI-octyl/ZnPc bilayers (fixed ZnPc thickness of 30 nm). The data are shown for all excitation conditions together with a fit obtained after applying the exciton diffusion model. (b) Schematic representation of the planar heterojunction samples on fused silica. The samples are photo excited with laser pulses from the front side (FS) or back side (BS). The yellow profile represents the PDI excitation profile I(x) in the sample and depends on the absorption coefficient. Excitons created further away from the heterojunction interface have to diffuse to the interface via exciton hopping. During diffusion they can recombine, process that limits their lifetime and diffusion length Λexc.

3.5. Exciton Diffusion in TiO2/PDI Planar Heterojunctions

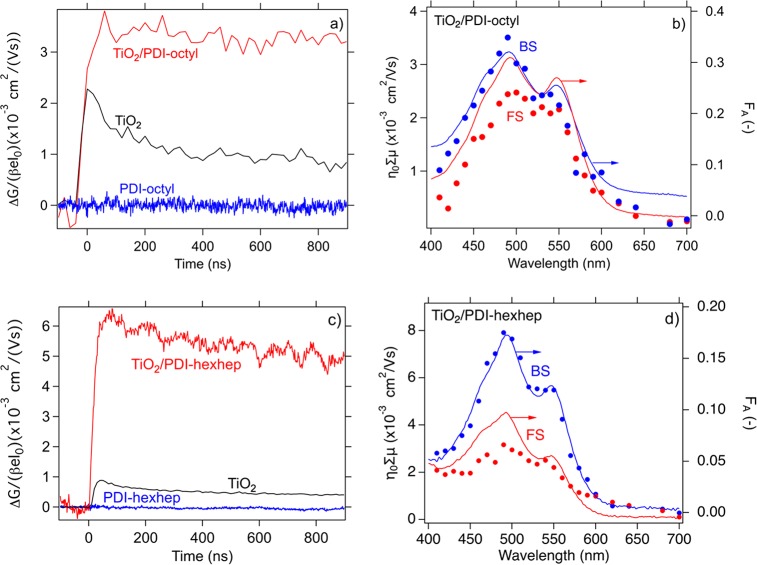
To examine a possible relationship between substrate and PDI supramolecular packing and exciton diffusion length, we deposit the PDIs on polycrystalline TiO2 coated fused silica. TiO2 forms a functional inorganic/organic heterojunction with PDI, where PDI acts as electron donor and injects electrons into the TiO2 conduction band upon photoexcitation and is used to study the exciton diffusion length in the same manner as in the PDI/ZnPc bilayers. However, the added benefit of using TiO2 over ZnPc is the higher TiO2 electron mobility (μe– = 1 cm2/(V s)) and long charge carrier lifetime (μs–ms)55 that is beneficial for the photoconductivity. In Figure 9a–d, we show the photoconductance transients for single layered films of TiO2, PDI-octyl (-hexhep) and a TiO2/PDI-octyl (-hexhep) bilayer, respectively, upon selectively photoexciting the PDI. We observe a 10-fold and 6-fold increase in peak photoconductivity upon combining TiO2 and PDI-octyl and PDI-hexhep when compared to that of the single layer films. In Figure 9b and 9d, we show the action spectrum for the TiO2/PDI-octyl and TiO2/PDI-hexhep bilayer, respectively. The action spectrum contains values for ηΣμ as a function of excitation wavelength and is plotted together with the bilayer absorptance spectrum. Since TiO2 is a wide bandgap semiconductor, its absorption in the visible part of the spectrum is negligible such that PDI is the primary absorbing species. A minor absorption by TiO2 intrabandgap states occurs in the visible. The photoconductivity of TiO2 due to intrabandgap state absorption can be measured and it is subtracted from that of the bilayer response as detailed elsewhere.55 The bilayer photoconductivity is higher when light incites the sample at the heterojunction interface (BS) compared to when it enters the sample at the PDI–air interface (FS). Furthermore, the trend displayed ηΣμ as a function of excitation wavelength matches that of the absorption spectrum when the bilayer is excited near the heterojunction interface. We attribute this agreement to selective PDI excitation and subsequent charge separation and electron injection at the TiO2/PDI interface. The mismatch in trend between ηΣμ and absorptance can be explained by a relatively lower number of injected electrons in TiO2 since the majority of the excitons have decayed due to the limited exciton diffusion length as we described for the PDI/ZnPc bilayers. We apply the same exciton diffusion model used to model the PDI/ZnPc bilayers described by eqs 11 and S2 to estimate an exciton diffusion length for PDI-octyl and PDI-hexhep of which we outline the procedure in the Supporting Information. For PDI-octyl, we obtain φCSΣμ = 0.04 cm2/(V s) and ΛEXC = 48.05 nm, and for PDI-hexhep, a φCSΣμ = 0.064 cm2/(V s) and ΛEXC = 19.6 nm. In the model, we fixed L (L = 100 nm for PDI-octyl and L = 30 nm for PDI-hexhep). The fit parameters together with the charge carrier mobilities and exciton diffusion length from the PDI-octyl/ZnPc bilayer are listed in Table 1.

Figure 9.

Figure 9

Open in a new tab

(a) Photoconductivity transients of a single layer film of pol-TiO2, PDI-octyl (50 nm) and a TiO2/PDI-octyl (50 nm) bilayer at I0 = 2.3 × 1012 photons/cm2 upon BS excitation. (b) Action spectrum of η0Σμ and attenuation spectrum versus excitation wavelength for the TiO2/PDI-octyl (50 nm) bilayer. (c) Photoconductivity transients for a single layer film of pol-TiO2 and PDI-hexhep (38 nm) and a TiO2/PDI-hexhep (38 nm) bilayer at I0 = 2.3 × 1012 photons/cm2 upon BS excitation. Similar to panel b, panel d contains the action spectrum for the TiO2/PDI-hexhep (38 nm) bilayer.

Table 1. Charge Carrier and Exciton Diffusion Parameters for PDI-octyl and -hexhep as Obtained from Analysis of PR- and FP-TRMC Experimentsa.

 
 PDI/ZnPc
 TiO2/PDI
  Σμ1D (cm2/(V s)) α (m–2) φCSΣμ (cm2/(V s)) ΛEXC (nm) φCSΣμ (cm2/(V s)) φCSb (%) ΛEXC(nm)
PDI-octyl 0.32 7.96 × 106 1.5 × 10–2 59.90 FS 1.3 × 10–2 FS 0.55 FS 64
BS 1.5 × 10–2 BS 0.73 BS 61
avg. 1.4 × 10–2 avg. 0.64 avg. 62.5
PDI-hexhep 0.02 4.40 × 106     FS 6.6 × 10–2 FS 3.1 FS 18
    BS 8.3 × 10–2 BS 3.9 BS 18
    avg. 7.4 × 10–2 avg. 3.5 avg. 18
Open in a new tab
a

φCSΣμ and ΛEXC were obtained upon application of the exciton diffusion model described by eqs 11, S2, and S3.

b

μe– = 2.24 and 2.14 cm2/(V s) for TiO2/PDI-octyl and TiO2/PDI-hexhep, respectively.

We use the TiO2 film specific electron mobility to calculate an incident photon to charge separation efficiency φCS of 0.64% and 3.5% for PDI-octyl and PDI-hexhep, respectively, averaged over front- and backside excitation. These efficiencies are similar to those found for electron injection from porphyrins into TiO2 using the same experimental setup. The relatively low φCS values can be due to various loss mechanisms.43,44 The first is inefficient coupling between the organic materials and the TiO2 layer because of strong crystallization of PDI, possibly resulting in a barrier of alkyl chains at the interface.56 This small resulting injection rate gives dominance to alternative decay processes in the PDI. Additionally, if charge injection is followed by fast recombination at the interface, this results in a reduced observed φCS. The mobility of charge in TiO2 is not affected by these processes and has been independently determined as discussed in the Supporting Information. The magnitude of ΛEXC of PDI-octyl that we find for the PDI-octyl/ZnPc and TiO2/PDI-octyl heterojunction is very similar (<10% difference), indicating that the intrinsic ΛEXC is specific for the material and not affected by the interface. This observation is notable considering the difference in aggregate size in the two systems. One would expect a larger diffusion length for larger domain size as the limiting step in the transport is likely to be the interdomain hopping. If the distance between interdomain hops decreases, a larger overall diffusion length would be expected. Interestingly, in this case, such a difference is not observed, indicating that interdomain transport is not limiting transport in this case.57,58

One estimate for the singlet exciton diffusion coefficient DEXC can be obtained using eq 12 and assuming pure singlet character transport of our excitons. In this calculation, we use our estimate of the exciton diffusion length and exciton lifetime (τEXC = 550 ps and 1.13 ns for PDI-octyl and PDI-hexhep, see Figure 5c) of the thin film, resulting in DEXC = 6.47 × 10–2–7.04 × 10–2 cm2/s and DEXC = 2.87 × 10–3 cm2/s for PDI-octyl and PDI-hexhep, respectively. Using the Einstein–Smoluchowski relation (eq 6) and mobility values from the TRMC measurements on PDI powders, we estimate a charge carrier diffusion coefficient DCHARGE = 8.23 × 10–3 cm2/s and DCHARGE = 5.14 × 10–4 cm2/s for PDI-octyl and PDI-hexhep, respectively. The ratio of these two charge carrier diffusion coefficients is 16, which is similar to the ratio of the exciton diffusion coefficients discussed above (22.6). If the exciton diffusion is governed by the Förster mechanism a smaller dependence on distance would be expected. A relevant aspect here is the partial triplet character of the excitons as shown by transient absorption studies that confirm the presence of singlet fission in PDI-octyl.4,6 The triplet character results in much longer exciton lifetimes than for pure singlet species, and the Dexter transfer mechanism for triplets can be considered as a double electron transfer process, making it similar to electron and hole transfer. However, this particular study did not involve in the discrimination of these contributions and conclude that the studied excitons are singlets with possibly a certain amount triplet contribution.

4. Conclusion

In this study, we investigated the effect of imide substitution in PDIs on their solid-state packing and optoelectronic properties. We found a strong influence of the imide substituent on the intermolecular packing of the molecules in the solid-state. The variation in side-chain substitution affected the extent of crystallization in the powder but is less significant in vacuum deposited thin films. In these films, macromolecular organization forming fibrous structures occurred for both PDIs. However, an order of magnitude difference in charge carrier mobility was found that can be related to differences in electronic coupling values. We measured an order of magnitude difference in maximum photoconductance ΔGMAX/βeIo in bilayer heterojunctions of PDI-octyl/ZnPc and PDI-hexhep/ZnPc, owing to the difference in intrinsic charge carrier mobility and lower exciton diffusion length. Using TRMC measurements on PDI/ZnPc heterojunctions with different PDI-octyl thicknesses, we could determine an exciton diffusion length of 60 nm that agrees with earlier found values for related PDIs and structures. Using TiO2 as underlayer for the PDI film instead of fused silica did not strongly affect solid-state packing for the PDIs. Using TiO2, we determined a singlet exciton diffusion length of 18 nm for PDI-hexhep, which is a factor three lower than observed for PDI-octyl and confirmed the same exciton diffusion length for PDI-octyl found from the study on the PDI/ZnPc bilayer. The charge separation efficiencies for PDI-octyl and PDI-hexhep are 0.64 and 3.5%. This study serves to show how different molecular packings of electronically similar molecules can lead to strong differences in charge carrier mobilities, while having a surprisingly small effect on the exciton diffusion length. These results offer a complete view of intrinsic organic chromophore properties relevant to optoelectronic devices.

Acknowledgments

The research leading to these results has received funding from the European Research Council Horizon 2020 ERC Grant Agreement no. 648433. We further thank W. Smaal at the ELORPrintTec at Université de Bordeaux for performing the SEM measurements.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsaem.9b01490.

  • Target and measured PDI film thicknesses, thin film crystallite domain size estimation using the Scherrer equation, SEM images of 30 and 100 nm thick annealed PDI layers on fused silica, SEM images of uncoated fused silica and TiO2 layers on fused silica, optical properties of PDI-octyl, PDI-hexhep and ZnPc, XRD of TiO2/PDI heterojunctions, TRMC photon fluence dependence charge carrier kinetics for PDI-octyl, table with kinetic parameters obtained from fitting of PDI-octyl TRMC transients, TRMC charge carrier kinetics for PDI-hexhep thin films of variable thickness, methodology for exciton diffusion length determination, and determination of the TiO2 electron mobility (PDF)

Author Present Address

† D.D.G.: SABIC Netherlands, Bergen op Zoom, The Netherlands.

The authors declare no competing financial interest.

Supplementary Material

ae9b01490_si_001.pdf (2.2MB, pdf)

References

  1. Herbst W.; Hunger K.. Industrial Organic Pigments: Production, Properties, Applications; John Wiley & Sons, 2006. [Google Scholar]
  2. Würthner F.; Saha-Möller C. R.; Fimmel B.; Ogi S.; Leowanawat P.; Schmidt D. Perylene bisimide dye assemblies as archetype functional supramolecular materials. Chem. Rev. 2016, 116 (3), 962–1052. 10.1021/acs.chemrev.5b00188. [DOI] [PubMed] [Google Scholar]
  3. Zhang G.; Zhao J.; Chow P. C. Y.; Jiang K.; Zhang J.; Zhu Z.; Zhang J.; Huang F.; Yan H. Nonfullerene Acceptor Molecules for Bulk Heterojunction Organic Solar Cells. Chem. Rev. 2018, 118 (7), 3447–3507. 10.1021/acs.chemrev.7b00535. [DOI] [PubMed] [Google Scholar]
  4. Aulin Y. V.; Felter K. M.; Günbas D. D.; Dubey R. K.; Jager W. F.; Grozema F. C. Morphology-Independent Efficient Singlet Exciton Fission in Perylene Diimide Thin Films. ChemPlusChem 2018, 83 (4), 230–238. 10.1002/cplu.201700449. [DOI] [PubMed] [Google Scholar]
  5. Eaton S. W.; Shoer L. E.; Karlen S. D.; Dyar S. M.; Margulies E. A.; Veldkamp B. S.; Ramanan C.; Hartzler D. A.; Savikhin S.; Marks T. J.; Wasielewski M. R. Singlet exciton fission in polycrystalline thin films of a slip-stacked perylenediimide. J. Am. Chem. Soc. 2013, 135 (39), 14701–12. 10.1021/ja4053174. [DOI] [PubMed] [Google Scholar]
  6. Le A. K.; Bender J. A.; Arias D. H.; Cotton D. E.; Johnson J. C.; Roberts S. T. Singlet fission involves an interplay between energetic driving force and electronic coupling in perylenediimide films. J. Am. Chem. Soc. 2018, 140 (2), 814–826. 10.1021/jacs.7b11888. [DOI] [PubMed] [Google Scholar]
  7. Singh-Rachford T. N.; Nayak A.; Muro-Small M. L.; Goeb S.; Therien M. J.; Castellano F. N. Supermolecular-chromophore-sensitized near-infrared-to-visible photon upconversion. J. Am. Chem. Soc. 2010, 132 (40), 14203–11. 10.1021/ja105510k. [DOI] [PubMed] [Google Scholar]
  8. Deng F.; Sommer J. R.; Myahkostupov M.; Schanze K. S.; Castellano F. N. Near-IR phosphorescent metalloporphyrin as a photochemical upconversion sensitizer. Chem. Commun. 2013, 49 (67), 7406–7408. 10.1039/c3cc44479a. [DOI] [PubMed] [Google Scholar]
  9. Adams D. M.; Kerimo J.; O’Connor D. B.; Barbara P. F. Spatial imaging of singlet energy migration in perylene bis(phenethylimide) thin films. J. Phys. Chem. A 1999, 103 (49), 10138–10143. 10.1021/jp992143h. [DOI] [Google Scholar]
  10. Gregg B. A.; Sprague J.; Peterson M. W. Long-range singlet energy transfer in perylene bis(phenethylimide) films. J. Phys. Chem. B 1997, 101 (27), 5362–5369. 10.1021/jp9703263. [DOI] [Google Scholar]
  11. Lin H.; Camacho R.; Tian Y.; Kaiser T. E.; Wurthner F.; Scheblykin I. G. Collective fluorescence blinking in linear J-aggregates assisted by long-distance exciton migration. Nano Lett. 2010, 10 (2), 620–626. 10.1021/nl9036559. [DOI] [PubMed] [Google Scholar]
  12. Marciniak H.; Li X. Q.; Wurthner F.; Lochbrunner S. One-dimensional exciton diffusion in perylene bisimide aggregates. J. Phys. Chem. A 2011, 115 (5), 648–54. 10.1021/jp107407p. [DOI] [PubMed] [Google Scholar]
  13. Lunt R. R.; Benziger J. B.; Forrest S. R. Relationship between crystalline order and exciton diffusion length in molecular organic semiconductors. Adv. Mater. 2010, 22 (11), 1233–1236. 10.1002/adma.200902827. [DOI] [PubMed] [Google Scholar]
  14. Mikhnenko O. V.; Blom P. W.; Nguyen T.-Q. Exciton diffusion in organic semiconductors. Energy Environ. Sci. 2015, 8 (7), 1867–1888. 10.1039/C5EE00925A. [DOI] [Google Scholar]
  15. Delgado M. C. R.; Kim E.-G.; Filho D. t. A. d. S.; Bredas J.-L. Tuning the charge-transport parameters of perylene diimide single crystals via end and/or core functionalization: a density functional theory investigation. J. Am. Chem. Soc. 2010, 132 (10), 3375–3387. 10.1021/ja908173x. [DOI] [PubMed] [Google Scholar]
  16. Vura-Weis J.; Ratner M. A.; Wasielewski M. R. Geometry and electronic coupling in perylenediimide stacks: mapping structure-charge transport relationships. J. Am. Chem. Soc. 2010, 132 (6), 1738–9. 10.1021/ja907761e. [DOI] [PubMed] [Google Scholar]
  17. Marcon V.; Breiby D. W.; Pisula W.; Dahl J.; Kirkpatrick J.; Patwardhan S.; Grozema F.; Andrienko D. Understanding structure-mobility relations for perylene tetracarboxydiimide derivatives. J. Am. Chem. Soc. 2009, 131 (32), 11426–32. 10.1021/ja900963v. [DOI] [PubMed] [Google Scholar]
  18. May F.; Marcon V.; Hansen M. R.; Grozema F.; Andrienko D. Relationship between supramolecular assembly and charge-carrier mobility in perylenediimide derivatives: The impact of side chains. J. Mater. Chem. 2011, 21 (26), 9538–9545. 10.1039/c1jm10500k. [DOI] [Google Scholar]
  19. Tatemichi S.; Ichikawa M.; Koyama T.; Taniguchi Y. High mobility n-type thin-film transistors based on N,N ‘-ditridecyl perylene diimide with thermal treatments. Appl. Phys. Lett. 2006, 89 (11), 112108. 10.1063/1.2349290. [DOI] [Google Scholar]
  20. Briseno A. L.; Mannsfeld S. C. B.; Reese C.; Hancock J. M.; Xiong Y.; Jenekhe S. A.; Bao Z.; Xia Y. N. Perylenediimide nanowires and their use in fabricating field-effect transistors and complementary inverters. Nano Lett. 2007, 7 (9), 2847–2853. 10.1021/nl071495u. [DOI] [PubMed] [Google Scholar]
  21. Chesterfield R. J.; McKeen J. C.; Newman C. R.; Frisbie C. D.; Ewbank P. C.; Mann K. R.; Miller L. L. Variable temperature film and contact resistance measurements on operating n-channel organic thin film transistors. J. Appl. Phys. 2004, 95 (11), 6396–6405. 10.1063/1.1710729. [DOI] [Google Scholar]
  22. Mirjani F.; Renaud N.; Gorczak N.; Grozema F. C. Theoretical Investigation of Singlet Fission in Molecular Dimers: The Role of Charge Transfer States and Quantum Interference. J. Phys. Chem. C 2014, 118 (26), 14192–14199. 10.1021/jp503398a. [DOI] [Google Scholar]
  23. Rao A.; Friend R. H. Harnessing singlet exciton fission to break the Shockley-Queisser limit. Nature Reviews Materials 2017, 2 (11), 17063. 10.1038/natrevmats.2017.63. [DOI] [Google Scholar]
  24. Einzinger M.; Wu T.; Kompalla J. F.; Smith H. L.; Perkinson C. F.; Nienhaus L.; Wieghold S.; Congreve D. N.; Kahn A.; Bawendi M. G.; Baldo M. A. Sensitization of silicon by singlet exciton fission in tetracene. Nature 2019, 571 (7763), 90–94. 10.1038/s41586-019-1339-4. [DOI] [PubMed] [Google Scholar]
  25. Gunbas D. D.; Xue C.; Patwardhan S.; Fravventura M. C.; Zhang H.; Jager W. F.; Sudholter E. J.; Siebbeles L. D.; Savenije T. J.; Jin S.; Grozema F. C. High charge carrier mobility and efficient charge separation in highly soluble perylenetetracarboxyl-diimides. Chem. Commun. (Cambridge, U. K.) 2014, 50 (38), 4955–8. 10.1039/C4CC00330F. [DOI] [PubMed] [Google Scholar]
  26. Ghosh S.; Li X. Q.; Stepanenko V.; Wurthner F. Control of H- and J-type pi stacking by peripheral alkyl chains and self-sorting phenomena in perylene bisimide homo- and heteroaggregates. Chem. - Eur. J. 2008, 14 (36), 11343–57. 10.1002/chem.200801454. [DOI] [PubMed] [Google Scholar]
  27. Chen Z.; Stepanenko V.; Dehm V.; Prins P.; Siebbeles L. D.; Seibt J.; Marquetand P.; Engel V.; Wurthner F. Photoluminescence and conductivity of self-assembled pi-pi stacks of perylene bisimide dyes. Chem. - Eur. J. 2007, 13 (2), 436–49. 10.1002/chem.200600889. [DOI] [PubMed] [Google Scholar]
  28. Chen S.; Slattum P.; Wang C. Y.; Zang L. Self-Assembly of Perylene Imide Molecules into 1D Nanostructures: Methods, Morphologies, and Applications. Chem. Rev. 2015, 115 (21), 11967–11998. 10.1021/acs.chemrev.5b00312. [DOI] [PubMed] [Google Scholar]
  29. O’Brien D. B.; Anglin T. C.; Massari A. M. Surface chemistry and annealing-driven interfacial changes in organic semiconducting thin films on silica surfaces. Langmuir 2011, 27 (22), 13940–9. 10.1021/la202958a. [DOI] [PubMed] [Google Scholar]
  30. Kish E. R.; Nahm R. K.; Woll A. R.; Engstrom J. R. When the Sequence of Thin Film Deposition Matters: Examination of Organic-on-Organic Heterostructure Formation Using Molecular Beam Techniques and in Situ Real Time X-ray Synchrotron Radiation. J. Phys. Chem. C 2016, 120 (11), 6165–6179. 10.1021/acs.jpcc.6b01717. [DOI] [Google Scholar]
  31. Krauss T. N.; Barrena E.; de Oteyza D. G.; Zhang X. N.; Major J.; Dehm V.; Würthner F.; Dosch H. X-ray/atomic force microscopy study of the temperature-dependent multilayer structure of PTCDI-C8 films on SiO2. J. Phys. Chem. C 2009, 113 (11), 4502–4506. 10.1021/jp808037w. [DOI] [Google Scholar]
  32. Duff J.; Hor A.-M.; Melnyk A. R.; Teney D. In Spectral response and xerographic electrical characteristics of some perylene bisimide pigments. Proc. SPIE 1990, 183. 10.1117/12.19813. [DOI] [Google Scholar]
  33. Warman J. M.; de Haas M. P.; Dicker G.; Grozema F. C.; Piris J.; Debije M. G. Charge mobilities in organic semiconducting materials determined by pulse-radiolysis time-resolved microwave conductivity: π-bond-conjugated polymers versus π- π-stacked discotics. Chem. Mater. 2004, 16 (23), 4600–4609. 10.1021/cm049577w. [DOI] [Google Scholar]
  34. Warman J. M.; Gelinck G. H.; de Haas M. P. The mobility and relaxation kinetics of charge carriers in molecular materials studied by means of pulse-radiolysis time-resolved microwave conductivity: dialkoxy-substituted phenylene-vinylene polymers. J. Phys.: Condens. Matter 2002, 14 (42), 9935–9954. 10.1088/0953-8984/14/42/308. [DOI] [Google Scholar]
  35. Marcus R. A.; Sutin N. Electron Transfers in Chemistry and Biology. Biochim. Biophys. Acta, Rev. Bioenerg. 1985, 811 (3), 265–322. 10.1016/0304-4173(85)90014-X. [DOI] [Google Scholar]
  36. Mikkelsen K. V.; Ratner M. A. Electron-Tunneling in Solid-State Electron-Transfer Reactions. Chem. Rev. 1987, 87 (1), 113–153. 10.1021/cr00077a007. [DOI] [Google Scholar]
  37. England S. J.; Kathirgamanathan P.; Rosseinsky D. R. Perturbation Calculation from the Charge-Transfer Spectrum Data of Intervalence Site-Transfer Dc Conductivity in Prussian Blue. J. Chem. Soc., Chem. Commun. 1980, (17), 840–841. 10.1039/c39800000840. [DOI] [Google Scholar]
  38. De Haas M. P.; Warman J. M. Photon-induced molecular charge separation studied by nanosecond time-resolved microwave conductivity. Chem. Phys. 1982, 73 (1–2), 35–53. 10.1016/0301-0104(82)85148-3. [DOI] [Google Scholar]
  39. Infelta P. P.; De Haas M. P.; Warman J. M. The study of the transient conductivity of pulse irradiated dielectric liquids on a nanosecond timescale using microwaves. Radiation Physics and Chemistry (1977) 1977, 10 (5–6), 353–365. 10.1016/0146-5724(77)90044-9. [DOI] [Google Scholar]
  40. Savenije T. J.; Ferguson A. J.; Kopidakis N.; Rumbles G. Revealing the Dynamics of Charge Carriers in Polymer:Fullerene Blends Using Photoinduced Time-Resolved Microwave Conductivity. J. Phys. Chem. C 2013, 117 (46), 24085–24103. 10.1021/jp406706u. [DOI] [Google Scholar]
  41. Fravventura M. C.; Hwang J.; Suijkerbuijk J. W.; Erk P.; Siebbeles L. D.; Savenije T. J. Determination of Singlet Exciton Diffusion Length in Thin Evaporated C60 Films for Photovoltaics. J. Phys. Chem. Lett. 2012, 3 (17), 2367–73. 10.1021/jz300820n. [DOI] [PubMed] [Google Scholar]
  42. Kroeze J. E.; Savenije T. J.; Vermeulen M. J. W.; Warman J. M. Contactless determination of the photoconductivity action spectrum, exciton diffusion length, and charge separation efficiency in polythiophene-sensitized TiO2 bilayers. J. Phys. Chem. B 2003, 107 (31), 7696–7705. 10.1021/jp0217738. [DOI] [Google Scholar]
  43. Huijser A.; Savenije T. J.; Kroeze J. E.; Siebbeles L. D. Exciton Diffusion and Interfacial Charge Separation in m eso-Tetraphenylporphyrin/TiO2 Bilayers: Effect of Ethyl Substituents. J. Phys. Chem. B 2005, 109 (43), 20166–20173. 10.1021/jp053265e. [DOI] [PubMed] [Google Scholar]
  44. Huijser A.; Suijkerbuijk B. M.; Klein Gebbink R. J.; Savenije T. J.; Siebbeles L. D. Efficient exciton transport in layers of self-assembled porphyrin derivatives. J. Am. Chem. Soc. 2008, 130 (8), 2485–92. 10.1021/ja075162a. [DOI] [PubMed] [Google Scholar]
  45. Sergeyev S.; Pisula W.; Geerts Y. H. Discotic liquid crystals: a new generation of organic semiconductors. Chem. Soc. Rev. 2007, 36 (12), 1902–29. 10.1039/b417320c. [DOI] [PubMed] [Google Scholar]
  46. Jones B. A.; Facchetti A.; Wasielewski M. R.; Marks T. J. Tuning orbital energetics in arylene diimide semiconductors. materials design for ambient stability of n-type charge transport. J. Am. Chem. Soc. 2007, 129 (49), 15259–78. 10.1021/ja075242e. [DOI] [PubMed] [Google Scholar]
  47. Gregg B. A. Evolution of photophysical and photovoltaic properties of perylene bis(phenethylimide) films upon solvent vapor annealing. J. Phys. Chem. 1996, 100 (2), 852–859. 10.1021/jp952557k. [DOI] [Google Scholar]
  48. Balakrishnan K.; Datar A.; Naddo T.; Huang J.; Oitker R.; Yen M.; Zhao J.; Zang L. Effect of side-chain substituents on self-assembly of perylene diimide molecules: morphology control. J. Am. Chem. Soc. 2006, 128 (22), 7390–8. 10.1021/ja061810z. [DOI] [PubMed] [Google Scholar]
  49. Kaufmann C.; Kim W.; Nowak-Król A.; Hong Y.; Kim D.; Würthner F. Ultrafast exciton delocalization, localization, and excimer formation dynamics in a highly defined perylene bisimide quadruple π-stack. J. Am. Chem. Soc. 2018, 140 (12), 4253–4258. 10.1021/jacs.7b11571. [DOI] [PubMed] [Google Scholar]
  50. Margulies E. A.; Shoer L. E.; Eaton S. W.; Wasielewski M. R. Excimer formation in cofacial and slip-stacked perylene-3, 4:9, 10-bis (dicarboximide) dimers on a redox-inactive triptycene scaffold. Phys. Chem. Chem. Phys. 2014, 16 (43), 23735–23742. 10.1039/C4CP03107E. [DOI] [PubMed] [Google Scholar]
  51. Felter K. M.; Dubey R. K.; Grozema F. C. Relation between molecular packing and singlet fission in thin films of brominated perylenediimides. J. Chem. Phys. 2019, 151 (9), 094301. 10.1063/1.5110306. [DOI] [PubMed] [Google Scholar]
  52. Rita Narayan M.; Singh J. Study of the mechanism and rate of exciton dissociation at the donor-acceptor interface in bulk-heterojunction organic solar cells. J. Appl. Phys. 2013, 114 (7), 073510. 10.1063/1.4818813. [DOI] [Google Scholar]
  53. Singh J.; Narayan M.; Ompong D.; Zhu F. R. Dissociation of charge transfer excitons at the donor-acceptor interface in bulk heterojunction organic solar cells. J. Mater. Sci.: Mater. Electron. 2017, 28 (10), 7095–7099. 10.1007/s10854-017-6443-3. [DOI] [Google Scholar]
  54. Narayan M.; Singh J. Photovoltaic contribution of photo-generated excitons in acceptor material of organic solar cells. J. Mater. Sci.: Mater. Electron. 2017, 28 (10), 7070–7076. 10.1007/s10854-017-6362-3. [DOI] [Google Scholar]
  55. Kroeze J. E.; Savenije T. J.; Warman J. M. Contactless determination of the efficiency of photo-induced charge separation in a porphyrin-TiO2 bilayer. J. Photochem. Photobiol., A 2002, 148 (1–3), 49–55. 10.1016/S1010-6030(02)00038-2. [DOI] [Google Scholar]
  56. Adams D. M.; Kerimo J.; Olson E. J. C.; Zaban A.; Gregg B. A.; Barbara P. F. Spatially-resolving nanoscopic structure and excitonic-charge-transfer quenching in molecular semiconductor heterojunctions. J. Am. Chem. Soc. 1997, 119 (44), 10608–10619. 10.1021/ja9717774. [DOI] [Google Scholar]
  57. Ye T.; Singh R.; Butt H. J.; Floudas G.; Keivanidis P. E. Effect of local and global structural order on the performance of perylene diimide excimeric solar cells. ACS Appl. Mater. Interfaces 2013, 5 (22), 11844–57. 10.1021/am4035416. [DOI] [PubMed] [Google Scholar]
  58. Singh R.; Giussani E.; Mróz M. M.; Di Fonzo F.; Fazzi D.; Cabanillas-Gonzalez J.; Oldridge L.; Vaenas N.; Kontos A. G.; Falaras P.; Grimsdale A. C.; Jacob J.; Müllen K.; Keivanidis P. E. On the role of aggregation effects in the performance of perylene-diimide based solar cells. Org. Electron. 2014, 15 (7), 1347–1361. 10.1016/j.orgel.2014.03.044. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ae9b01490_si_001.pdf (2.2MB, pdf)

Articles from ACS Applied Energy Materials are provided here courtesy of American Chemical Society

RESOURCES