Abstract
This book chapter describes the use of droplet microfluidics to phenotype single cells. The basic process flow includes the encapsulation of single cells with a specific probe into aqueous micro-droplets suspended in a biocompatible oil. The probe is chosen to measure the phenotype of interest. After incubation, the encapsulated cell turns the probe fluorescent and renders the entire droplet fluorescent. Enumerating drops that are fluorescent quantifies the concentration of cells possessing the phenotype of interest. Examining the distribution of fluorescence further allows one to quantify the heterogeneity among the cell population.
1. INTRODUCTION
Establishing relationship among cell phenotype, gene expression and genotype is critical in many fields of biological and clinical research. While cells can share the same genotype, gene expression is stochastic and regulated by many processes, including environmental factors (Cai, Friedman, & Xie, 2006; Elowitz, Levine, Siggia, & Swain, 2002; Yu, Xiao, Ren, Lao, & Xie, 2006). As such, the same genes in different cells often have different expression levels. As a result, cells with identical genotypes may have different phenotypes (Avery, 2006). It is these differences in gene expressions (and subsequent pathways) that make each cell a unique entity, leading to heterogeneity in cellular behavior and other observed phenotypes within a genotypically identical population. The ability to quantify and measure variations in phenotypes, ideally at the single-cell level, is thus critical to the fundamental understanding of cellular mechanisms that govern the link between genotype, gene expression, and phenotype (Barkai & Leibler, 2000; Ozbudak, Thattai, Kurtser, Grossman, & van Oudenaarden, 2002; Silva & Vogel, 2016). Such understanding is in turn important for disease diagnostics and treatment (Heiden, Cantley, & Thompson, 2009; Kawasaki, Fujita, Nagaike, Tomita, & Saito, 2017; Singh & Sivabalakrishnan, 2015).
Nevertheless, phenotypic measurements have been performed in bulk cell populations traditionally. The ensemble averaged results often mask cell-to-cell differences and the presence of different subpopulations (Altschuler & Wu, 2010; Vera, Biswas, Senecal, Singer, & Park, 2016). For example, the developmental states of individual Bacillus subtilis cells were found to be heterogeneous, but such heterogeneity was masked by population-averaged readouts (Kearns & Losick, 2005). Single-cell analysis decomposed the population heterogeneity during the growth of B. subtilis bacteria and revealed two alternative developmental states during the exponential phase of bacterial growth. Here, the inability to identify the heterogeneity in phenotypes can have negative biological and clinical consequences in the diagnosis and treatment of diseases.
In order to fully characterize the heterogeneity within a cell population, there has been increasing recognition that phenotyping with single-cell resolution is needed. Various methods have been developed in recent years that leverage advances in imaging techniques. For example, Yang et al. demonstrated the phenotyping of mammalian tissues with single-cell resolution by observing differences in quantities such as cell protein expression and showed that they could distinguish between normal and cancerous cells (Yang et al., 2014). The key novelty was in making large volumes of tissue optically clear while preserving fluorescent and protein-based signals. This ability allowed them to observe spatial differences in phenotypes between cells. Their method included tissue preservation by crosslinking the tissue to hydrogel monomers, rapid whole-organism optical clearing using a mild detergent, immunolabeling, and cell imaging. In another example, Patsch et al. developed an image acquisition platform to track the dynamic phenotype of single cells in heterogeneous populations over time for measuring phenotypic heterogeneity in protein translocation, proliferation, cell death, and motility (Patsch et al., 2016). By identifying and filtering out unrealistic trajectories, they increased data quality without introducing bias to track cell-to-cell variation. They showed the ability to track the dynamic phenotype of thousands of cancer cells in a heterogeneous population, and to detect subpopulations, including early apoptotic events and pre-mitotic cells.
In recent years, microfluidics has emerged as a powerful technology for single-cell analysis. For example, Toriello et al. were able to distinguish cells with moderate silencing from cells with complete silencing after siRNA knockdown in individual Jurkat cells (Toriello et al., 2008). Single-cell measurements were enabled by a microfluidic device with single-cell capture pads and electrophoresis separation channels for single-cell measurements on the variation of mRNA knockdown as a result of siRNA treatment. Recently, droplet-based microfluidics has shown to be a promising method for single-cell encapsulation and analysis (Zilionis et al., 2017). For example, El Debs et al. demonstrated the screening of hybridoma clones with different levels of secreted antibodies with single-cell resolution. Conventional hybridoma screens require the generation of immortalized hybridoma cell lines and expanding clones in microtiter plates and can take several weeks. In this work, the authors replaced this work flow with a droplet-based microfluidic platform consisting of modules for the generation, incubation, fusion, and sorting of droplets (El Debs, Utharala, Balyasnikova, Griffiths, & Merten, 2012). They were able to reduce the screening time from over several weeks to less than a day. The success of this method relied on the compartmentalization of individual cells inside drops, which increased the effective concentration of cell-secreted molecules inside the drops and thus reduced the time needed to detect the molecules. The downstream sorting module in the platform further enabled the separation of cells with high antibody expression levels from those that had low levels.
In this book chapter, we describe the methods we have developed based on droplet microfluidics to phenotype single cells. We demonstrate the methods via two examples. In both examples, we encapsulate single cells with a reporter or probe (e.g., fluorogenic enzyme substrates, live-dead indicators such as alamarBlue) into aqueous micro-droplets suspended in a continuous phase of a biocompatible oil. After incubation, the encapsulated cell turns the probe fluorescent and renders the entire droplet fluorescent. Enumerating drops that are fluorescent quantifies the concentration of cells possessing the phenotype of interest. Examining the distribution of fluorescence further allows us to quantify the heterogeneity among the cell population. In example 1, the phenotype of interest is the activity of an enzyme. We aim to quantify cells expressing BlaC, a β-lactamase specific to Mycobacterium tuberculosis, with intended application in the rapid diagnosis of tuberculosis (TB). The approach is based on the co-encapsulation of the BlaC-specific fluorogenic probe “CDG-OMe” and a bacteria sample into micro-droplets. Counting drops that are fluorescent allows us to quantify the concentration of cells that express BlaC. Combined with an automated droplet counting scheme, our results demonstrate the detection of BlaC-expressing cells at concentrations ranging from 10 to 107cfu/mL. Furthermore, the encapsulation of single cells in drops maintains the specificity of the detection scheme even when the concentration of bacteria that do not express BlaC exceeds those that do by one million-fold. In example 2, the phenotype of interest is metabolic function and cellular viability. Here we aim to quantify metabolically active Escherichia coli by using alamarBlue, a live-dead redox indicator, as the probe, with potential applications in identifying bacteria contamination in food, water, and other sources. After the incubation step, drops that contain metabolically active cells turn fluorescent. We show that by considering the distribution of fluorescence intensity, we can infer the heterogeneity arising from biological cell-to-cell variations or from non-biological sources.
2. MATERIALS AND METHODS
2.1. FABRICATION AND DESIGN OF MICROFLUIDIC DROPLET GENERATOR
We fabricated microchannels in poly(dimethylsiloxane) (PDMS) using soft lithography (Xia & Whitesides, 1998). The microchannels were rendered hydrophobic by treatment with Aquapel (Pittsburgh, PA) to avoid droplet wetting of the wall. Monodisperse droplets of diameter ~31 to 52 μm (corresponding volume ~16 to 75 pL) were generated using flow-focusing microchannels with a volume dispersity <3% (Anna, Bontoux, & Stone, 2003). As shown in Fig. 1, the continuous phase was introduced into two side channels, and the two dispersed phases were mixed immediately before they were injected into a central channel. We used two separate inlets for the two dispersed phases: one for bacterial sample and one for the probe to measure the phenotype of interest.
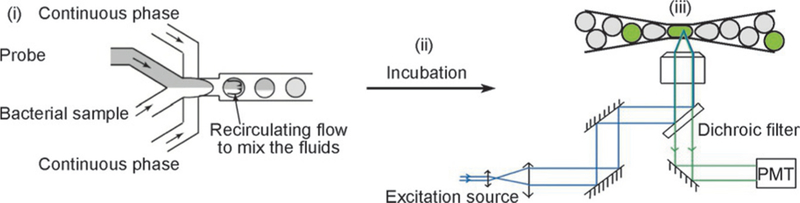
FIG. 1.
Scheme of the microfluidic process flow consisting of three parts: (i) Droplet generation and compartmentalization of the bacterial sample with probe. (ii) Incubation of the drops for sufficient time for fluorescence to turn on. (iii) Detection of fluorescence from the drops.
2.2. CONTINUOUS PHASE
We chose to use a fluorinated solvent as the continuous phase due to their chemical inertness, gas permeability and biocompatibility (Holtze et al., 2008). Common choices of fluorinated solvents for cell-based droplet microfluidics assays include hydrofluoroether HFE-7500 (3M) and Fluorinert FC-40 (3M).
2.3. DROPLET STABILIZER
To stabilize droplets against coalescence, droplet stabilizer was pre-mixed in the continuous phase prior to droplet generation. Two common types of droplet stabilizers are surfactants and amphiphilic nanoparticles. Both adsorb at the liquid-liquid interface and prevent droplet coalescence (Gu, Duits, & Mugele, 2011). Surfactants are most commonly used in current droplet-based assays. In order to stabilize water-in-fluorinated oil emulsions, the surfactant typically contains a fluorinated tail and a PEGylated headgroup. This type of surfactants is shown to be biocompatible and is capable of stabilizing drops against coalescence over a period of at least a few months (Holtze et al., 2008). Nevertheless, this type of surfactant is also found to mediate inter-drop molecular transport of small, hydrophobic molecules such as organic fluorophores. The transport is believed to occur via the reversible adsorption and desorption of surfactant molecules at the water-oil interface, and their association and transport of small molecules from one drop to the other through the continuous phase (Chen, Gani, & Tang, 2012; Gruner et al., 2016). Such transport leads to the cross-contamination of droplet contents and destroys assay accuracy (Chen et al., 2012; Litten, Blackett, Wigglesworth, Goddard, & Fielden, 2015). Recently, our group has shown that amphiphilic nanoparticles, such as partially fluorinated silica nanoparticles, are capable of suppressing the inter-drop transport of small molecules due to the irreversible adsorption of the particles to the liquid interface (Pan, Lyu, & Tang, 2015; Pan et al., 2014). In example 1 (Section 3), we used a biocompatible fluoro-surfactant “EA-surfactant” (RainDance Technologies, Lexington, MA), a PEG-PFPE amphiphilic block copolymer (Holtze et al., 2008), as the droplet stabilizer. The concentration was 2% (wt/wt) in HFE-7500 as the continuous phase. In example 2 (Section 4), we used 60nm fluorinated silica nanoparticles to stabilize the drops, because alamarBlue is known to leak from surfactant-stabilized drops into other drops (Chen et al., 2012). The concentration of silica nanoparticles was 6% (wt/wt) in HFE-7500 as the continuous phase (Pan, Kim, Blauch, & Tang, 2016; Pan et al., 2015, 2014).
2.4. DISPERSED PHASES
Probes.
The probes used to measure the phenotypes of interest are typically fluorogenic to facilitate the use of standard fluorescence microscopy for the readout of the results of the assay. Various fluorogenic probes have been used to indicate the presence and/or activity of target molecules, genes, metabolites, and proteins, and cells (Mehrotra, 2016). In this work, we used two fluorogenic probes as examples. In example 1 (Section 3), we used a BlaC-specific fluorogenic enzyme reporter, CDG-OMe, as our probe (Xie et al., 2012). BlaC is a β-lactamase specific to M. tuberculosis (Hugonnet, Tremblay, Boshoff, Barry, & Blanchard, 2009; Ioerger et al., 2010). Previously, it was shown that CDG-OMe demonstrated a 200-fold increase in fluorescence upon hydrolysis by BlaC (Xie et al., 2012). In example 2 (Section 4), we used alamarBlue as our fluorogenic probe to measure cell viability. AlamarBlue is a cell viability indicator that is converted into a bright fluorescent product by metabolically active cells via cellular redox reactions. The fluorescence evolution of alamarBlue indicates cellular metabolic activity and has been used previously for the detection of a range of live cells including bacteria and mammalian cells (Boedicker, Li, Kline, & Ismagilov, 2008; Churski et al., 2012; Yajko et al., 1995).
Cell sample.
The cell samples used for the two examples were E. coli expressing BlaC in 2-(N-morpholino) ethanesulfonic acid (MES) buffer (0.1M, pH 6.6) and wildtype E. coli (K-12 BW25113) in Luria-Bertani (LB) broth, respectively. In example 1, we also validated some of our results using Bacillus Calmette–Guérin (BCG), a strain of attenuated Mycobacterium bovis.
2.5. ENCAPSULATION OF CELLS INTO DROPS
By using a sufficiently low cell concentration, we were able to encapsulate single cells into droplets as governed by Poisson distribution (Collins, Neild, deMello, Liu, & Ai, 2015). For example, when a bacterial solution with a concentration of 106 cells/mL is compartmentalized into 50-pL droplets, the average number of cells per drop is given by Eq. (1).
| (1) |
Based on Poisson distribution, we obtain a probability of having k (k = 0, 1, 2, …) cells in a single droplet as:
| (2) |
| (2a) |
| (2b) |
| (2c) |
Therefore, among the entire droplet population, 95.12% are empty, 4.76% contain a single cell, and 0.12% drops contain more than one cell. That is, approximately 97.5% of droplets that contain cells have a single cell in the drop. This value is important to note when considering the distribution of the probe intensity (see details in Section 4).
2.6. DROPLET INCUBATION
After droplet generation, incubation of the drops is typically needed to allow sufficient time for the desired biological actions to take place. Droplet incubation can be either on-chip or off-chip. On-chip incubation includes flowing droplets through delay-lines or trapping droplets in microfluidic arrays (Frenz, Blank, Brouzes, & Griffiths, 2009; Shembekar, Chaipan, Utharala, & Merten, 2016). Due to the small length scale of these on-chip incubators, the incubation time is typically on the order of seconds to minutes only. For incubation time on the order of hours to days, off-chip incubation is typically performed by collecting the droplets as an emulsion into conventional test tubes, syringes or capillaries (Mazutis et al., 2009). Compared with on-chip incubation, off-chip droplet incubation allows for the incubation of a larger number of droplets for longer periods of time, but requires the reinjection of droplets into another microfluidic channel for subsequent interrogation or other manipulations (Shembekar et al., 2016). In such reinjection process, care must be taken to avoid the break-up of droplets (Gai, Khor, & Tang, 2016; Gai, Kim, Pan, & Tang, 2017; Khor, Kim, Schutz, Schneider, & Tang, 2017; Pan, Lyu, & Tang, 2017; Rosenfeld, Fan, Chen, Swoboda, & Tang, 2014). In the examples described here, we collected the droplets after their generation into Eppendorf tubes and incubated them off-chip for different time periods depending on the specific cell strains and probes used.
2.7. DROPLET INTERROGATION
To interrogate droplet content, an analytical measurement step is performed after the incubation step, such as bright-field microscopy, fluorescence microscopy, laser induced fluorescence, Raman spectroscopy, mass spectrometry, and nuclear magnetic resonance spectroscopy (Zhu & Fang, 2013). In our examples, we used fluorescence microscopic imaging and photomultiplier tube (PMT) for the interrogation of the fluorogenic probes in the drops.
To image the droplets under the microscope, we reinjected the drops from the incubation tube into a PDMS well with a height of 30 μm. This height was less than the diameter of a drop when spherical and was chosen so that the drops were packed as a monolayer in the well. Fluorescence images were subsequently obtained by a 10× microscope objective in an inverted optical microscope coupled with an Electron Multiplying Charge Coupled Device (EMCCD) camera (Andor Technology, South Windsor, CT). As shown in Fig. 2, we normalized all measured fluorescent intensity (Imeasured) using this equation: Inormalized = (Imeasured–Imin)/(Imax–Imin). The maximum intensity (Imax) was defined as the intensity when the enzymatic reaction was complete (i.e., when the intensity was saturated) at t = 30h. The minimum intensity (Imin) was defined as the average intensity in negative drops at t = 15min. The maximum intensity was the same for all drop sizes, because we used the same channel for intensity measurements and the path length for fluorescence measurement was fixed.
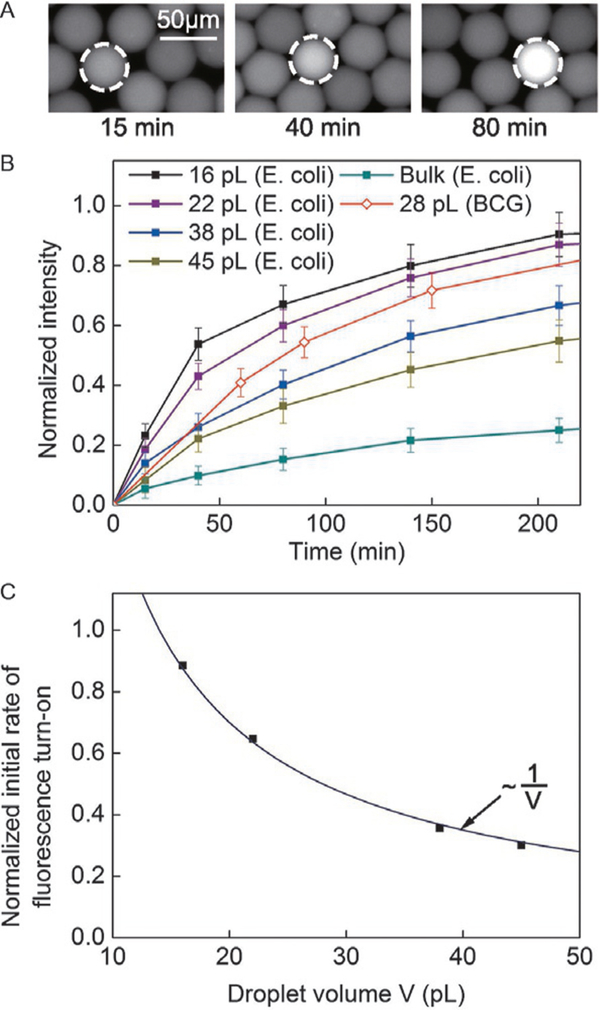
FIG. 2.
(A) Images of selected droplets containing E. coli expressing BlaC with CDG-OMe and B-PER, after an incubation period of 15, 40, and 80min, respectively. (B) Fluorescence signal from drops of various volumes containing a single cell of E. coli expressing BlaC, and drops of 28pL containing BCG. Each data point represents the mean intensity value collected from at least 10 drops. The height of the error bars represents one standard deviation from the mean. The intensities were normalized to the saturating intensity when the enzymatic reactions were complete. (C) Initial rate of fluorescence turn-on as a function of droplet volume for the data presented in (B). The line is a fitted curve to the data.
To count fluorescent drops (Figs. 3–4), we reinjected the drops into a tapered channel consisting of a narrow constriction with a cross section of 30μm × 30μm at a flow rate of 0.6mL/h. The volume fraction of the reinjected drops was about 80%. The width of the constriction (30 μm) was less than one droplet diameter (35–70μm) to ensure that the droplets passed through the constriction one at a time. Excitation light from a UV lamp was focused onto the constriction using a 40 × microscope objective in an inverted microscope (Nikon Eclipse TE2000). The fluorescence from the drops was collected from the same objective through an emission filter into a photomultiplier tube “PMT” (Hamamatsu product number: 56420001). A gain of 13 V was applied to the PMT. We automated the recoding of PMT output voltages with a custom LabView script. A voltage peak above the threshold value was identified as a fluorescent drop. We quantified the number of fluorescent drops by counting the number of voltage peaks above the threshold value. To set the threshold voltage (Vth) to differentiate a fluorescent drop from a non-fluorescent drop, we first measured the mean and the standard deviation (σ) in voltage from drops without bacteria (“negative drops”). A threshold value was then set at. A value of n = 6 was used such that of the negative drops had a value exceeding Vth. Voltage peaks with values V > Vth were counted as a fluorescent drop. Based on the detected number of fluorescent drops, the number of cells can then be estimated from Poisson statistics using Eq. (3).
| (3) |
where N+ is the number of fluorescent drops and N is the total number of drops used.
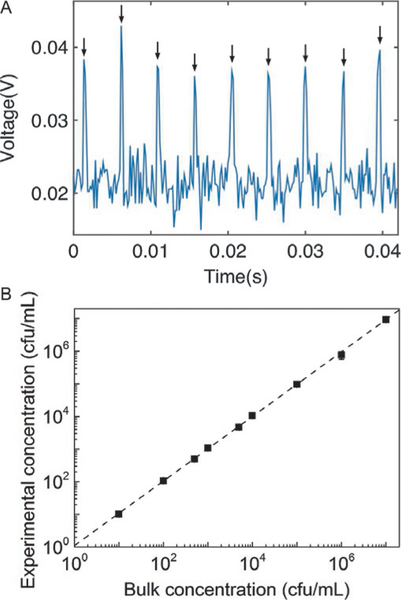
FIG. 3.
(A) Fluorescence signal collected from drops generated from a sample containing E. coli expressing BlaC at a concentration of 106cfu/mL after 3h of incubation. The nine arrows indicate the fluorescent peaks that correspond to nine fluorescent drops detected. The signal was obtained from a photomultiplier tube using the setup outlined in Fig. 1(iii). (B) Linear relationship between the experimentally measured bacteria concentration and the input bacteria concentration. Each data point represents the mean value collected from at least three experiments. The height of the error bars is less than that of the data point markers.
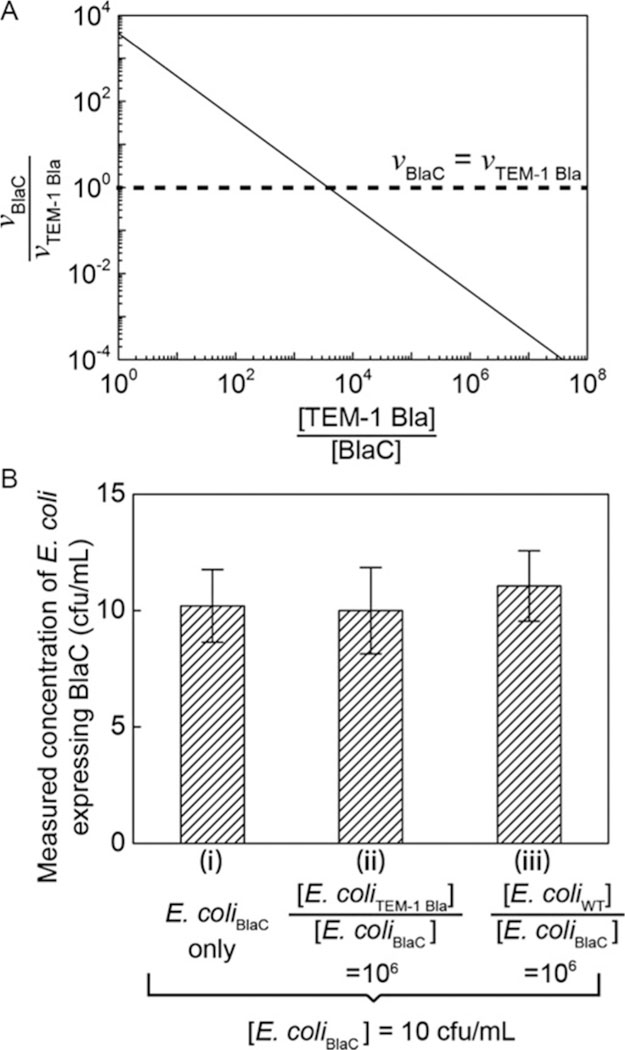
FIG. 4.
(A) The calculated ratio of fluorescence turn-on rate of probe CDG-OMe by BlaC (vBlaC) and by TEM-1 Bla (vTEM-1 Bla), when BlaC and TEM-1 Bla are mixed at different ratios ([TEM-1 Bla]/[BlaC]). When [TEM-1 Bla]/[BlaC] ~ 103, the turn-on rate of CDG-OMe by BlaC equals that by TEM-1 Bla. The graph is calculated based on kinetic parameters of CDG-OMe by BlaC and TEM-1 Bla, respectively. (B) Measured concentration of E. coli expressing BlaC using droplet microfluidics in three separate experiments: (i) 10cfu/mL E. coli expressing BlaC (“E. coliBlaC”) in MES buffer, (ii) 10cfu/mL E. coli expressing BlaC mixed with 107cfu/mL E. coli expressing TEM-1 Bla (“E. coliTEM-1 Bla”), and (iii) 10cfu/mL E. coli expressing BlaC mixed with 107cfu/mL wild-type E. coli (“E. coliWT”). The height of each bar represents the mean concentration collected from at least three experiments. The height of the error bars represents one standard deviation from the mean.
3. EXAMPLE 1. QUANTITATIVE DETECTION OF CELLS EXPRESSING BlaC USING DROPLET-BASED MICROFLUIDICS FOR USE IN THE DIAGNOSIS OF TUBERCULOSIS
Here, we describe the use of our droplet microfluidics platform for detecting cells expressing BlaC, ultimately intended to be used for the detection of TB. To quantify cells expressing BlaC, we encapsulated BlaC-specific fluorogenic probe CDG-OMe and the bacteria sample in a large number (≥108) of picoliter droplets. The bacteria sample was prepared at a limiting dilution such that each drop contained one or no cells (see Section 2.5). We used E. coli expressing BlaC as a surrogate to characterize our method and validate some of our results using BCG cells. If cells expressing BlaC were present inside a drop, the probe was hydrolyzed to render the droplet fluorescent (Fig. 2A).
3.1. FLUORESCENCE DETECTION IN MICRO-DROPLETS
Imaging of drops with the co-encapsulation of B-PER.
The probe CDG-OMe and lysis buffer B-PER (Bacterial-Protein Extraction Reagent, Thermo Scientific) were co-encapsulated with cells into each drop. B-PER enabled the mild extraction of proteins from bacteria and was effective in facilitating the transport of the probe to the enzyme here, even though the probe was already designed to be cell-permeable. Furthermore, the enzyme extracted from bacteria allowed Tokyo Green (the fluorophore of CDG-OMe) to be formed outside the cell and render the entire droplet fluorescent. This ability was important in facilitating the counting of fluorescent drops using a simple optical setup. We thus used B-PER in all subsequent experiments.
3.2. RELATIONSHIP BETWEEN DROPLET SIZE AND FLUORESCENCE TURN-ON RATE
Fig. 2 shows the effect of droplet size on the rate of fluorescence increase. For drops that contained a cell, the rate of increase in fluorescence intensity increased with decreasing droplet size, as expected. We measured the initial rate of fluorescence increase v by finding the slope of the initial linear portion of the curves depicted in Fig. 2B. Fig. 2C shows that v scaled nicely with the inverse of droplet volume V, i.e., v~ V–1 This scaling confirms that the primary effect of drop size was indeed that of increasing the concentration of the cell (and the enzymes) inside the drop. For drops that were 16 pL in volume, the fluorescence intensity reached 80% of its maximum value in about 150min for E. coli expressing BlaC (Fig. 2B). With our current imaging system, the detection of a positive fluorescence signal (defined to be at an intensity level that is three times the standard deviation of the noise level) can be achieved in <60min. We further validated our method using BCG in 28-pL drops and found that the fluorescence turn-on rate was comparable to that of E. coli expressing BlaC (Fig. 2B). The expression level of BlaC in BCG may be different from the endogenous BlaC level in Mtb. The actual detection time for Mtb may be different from that shown here under similar conditions, but is still expected to be significantly shorter than the 4–8 weeks lag time required for the culture-based method.
3.3. HIGH THROUGHPUT DETECTION OF FLUORESCENT DROPS
To detect a small proportion of cells within the bacterial sample, it is necessary to count a large number of drops. To that end, we reinjected the drops into a tapered channel containing a constriction that could fit only one drop at a time. The fluorescence from the drops was collected using a photomultiplier tube (PMT). Fig. 3A shows a representative voltage output from the PMT. The voltage peaks corresponded to a fluorescent drop. Based on the voltage output, the number of BlaC-expressing cells could then be estimated from Eq. (3).
3.4. DYNAMIC RANGE OF OUR METHOD
We counted the number of fluorescent drops using PMT and compared this number with the number of cells as detected by standard methods based on optical density measurement (NanoDrop) and serial dilutions of the bacteria sample. Fig. 3B shows the linear relationship between the measured concentration of cells and the input concentration of cells over the range of 10–107cfu/mL. In deriving the concentration of cells from the counted number of fluorescent drops, we have accounted for Poisson statistics in the encapsulation of cells in drops using Eq. (3). The upper detection limit of our method is bounded by bacteria concentration at which all drops become occupied by cells. For droplet volume of 10pL, the highest concentration of cells we can detect is approximately 108 cfu/mL, a concentration much higher than that needed in practical applications. The lower detection limit of our method is, in theory, one fluorescent drop or one cell. At very low concentrations of cells, the practicality of our method is limited by the speed of the droplet generation and interrogation process (Lyu et al., 2015). For the sample at 10cfu/mL, we used a sample volume of 1 mL. At the flow rates used for a single droplet generator, it took about 6h to generate the drops, much longer than the incubation time needed for the fluorescence signal to turn on. The droplet generation time can be reduced by incorporating parallel droplet generators, which have been described by multiple groups where up to 512 parallel generators have been reported (Blainey, Milla, Cornfield, & Quake, 2012; Li, Greener, Voicu, & Kumacheva, 2009; Nisisako, Ando, & Hatsuzawa, 2012; Nisisako & Torii, 2008; Romanowsky, Abate, Rotem, Holtze, & Weitz, 2012). However, the use of a single droplet generator here did not change the principle of our method. For the serial interrogation of the sample at 10cfu/mL, we counted a total of 1 mL of drops, which took about 1h. Kim et al. showed that it is possible to count drops in a massively parallel format at a rate of ~0.25 million drops/s (Kim et al., 2015). Given this rate, it would require only 2 min to interrogate 1 mL of sample. The assay would then be rate-limited by the kinetics of the probe and the enzyme.
3.5. SENSITIVITY AND SPECIFICITY OF THE DETECTION SCHEME
Contamination of patient samples with non-Mtb or environmental organisms can lead to false positives in the diagnosis. It was recently shown that a healthy lung contains diverse microbial communities (Blainey et al., 2012). In patients with pneumonia caused by the infection of S. pneumonia, the concentration of S. pneumoniae can exceed 107 cfu/mL (Blainey et al., 2012). To differentiate Mtb from other microorganisms and to avoid false positives, it is critical that our method is specific only to Mtb, or BlaC. A previous study has shown the specificity and sensitivity of our probe CDG-OMe for BlaC versus its close class A homologue TEM-1 Bla, as well as versus β-lactamases produced by Pseudomonas, Staphylococcus and the environmental mycobacterium M. smegmatis (Xie et al., 2012). When the concentrations of BlaC and TEM-1 Bla are the same, the probe CDG-OMe has > 1000-fold selectivity of BlaC over its close A homologue TEM-1 Bla. In actual patient samples, the concentration of Mtb (and thus BlaC) can be many times smaller than that of other bacteria. The probe fluorescence intensity for 10cfu of BCG was only 1.2 times higher than that of 105 cfu of other bacteria that expressed β-lactamase, including methicillin-resistant S. aureus (MRSA) (Xie et al., 2012). Based on the enzyme kinetic parameters for the hydrolysis of CDG-OMe by BlaC and TEM-1 Bla (Xie et al., 2012), we used a simple Michaelis-Menten model to estimate the concentration of TEM-1 Bla above which the fluorescence turn-on rate of CDG-OMe by TEM-1 Bla exceeds that by BlaC for a fixed probe concentration. Fig. 4A shows that when BlaC is as equally concentrated as TEM-1 Bla, the probe fluorescence turn-on rate is 3800-fold higher for BlaC than for TEM-1 Bla(, where vBlaC and vTEM–1 Bla are the initial rates of product formation, or the rate of probe fluorescence turn-on, in the presence of BlaC and TEM-1 Bla, respectively). However, this ratio diminishes to 1 when TEM-1 Bla is about 3800-fold more concentrated than BlaC. This limited ratio of turn-on rates is a challenge for the specific detection of BlaC.
This challenge is overcome in droplet microfluidics when individual cells are compartmentalized into droplets. The effective concentration of a single cell in a drop is fixed and is determined only by the volume of the drop, even though the bulk concentration of non-BlaC expressing cells is many times higher than that of BlaC-expressing cells. The use of droplets for single-cell compartmentalization thus allows the original selectivity of the probe to be preserved at. As Fig. 4B shows, when the probe was used with droplet microfluidics, the specificity of probe was indeed maintained in each drop. We were able to measure the concentration of E. coli expressing BlaC accurately at 10cfu/mL, when it was mixed with E. coli expressing TEM-1 Bla or wild-type E. coli present at 106 times higher concentration than E. coli expressing BlaC.
4. EXAMPLE 2. MEASURING VARIABILITY IN METABOLISM WITH SINGLE-CELL RESOLUTION
In this example, we encapsulated single E. coli cells with viability probe alamarBlue into micro-droplets. We show that the examination of the distribution of fluorescence intensity of alamarBlue from the drops gives us information about the heterogeneity arising from both biological and non-biological sources.
4.1. FLUORESCENCE DETECTION OF E. coli IN MICRO-DROPLETS
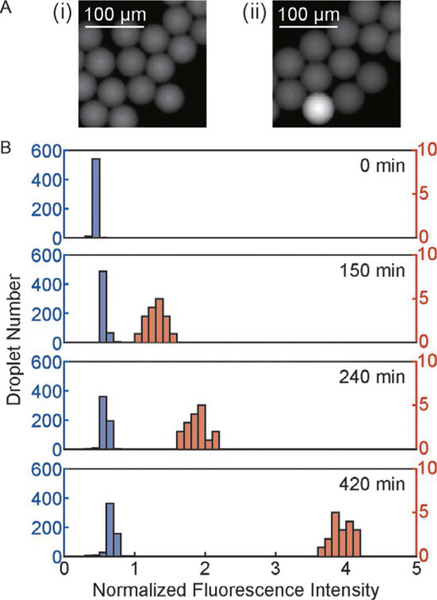
Similar to example 1 in Section 3, in this study, we observed an increase in fluorescence intensity in drops containing E. coli over time (Fig. 5A). Fig. 5B shows the distribution of droplet intensity after 5, 150, 240 and 420 min of droplet generation.
FIG. 5.
Fluorescence of drops containing E. coli overtime. (A) Fluorescence images of droplets generated from a bacterial sample and alamarBlue after an incubation period of (i) 0min and (ii) 150min. The droplet with higher fluorescence intensity than other drops in (ii) contained E. coli. (B) The distribution of alamarBlue fluorescence intensity from droplets after different incubation times. The left axis is for the data represented in blue bars, and the right axis is for the data represented in orange bars.
The detection of a positive signal was achieved in 150min with our imaging system. Because of single-cell encapsulation, the fluorescence signal emitted from the drop can be directly correlated to the viability and metabolic activity of the cell encapsulated in the drop. Similar to example 1, we can enumerate the fluorescent drops and calculate the corresponding measured cell concentration by Eq. (3).
4.2. EFFECT OF BIOLOGICAL AND NON-BIOLOGICAL HETEROGENEITY ON FLUORESCENCE INTENSITY DISTRIBUTION
As Fig. 5B shows, the distribution of fluorescent signals from the droplets was broad. The broad distribution was caused by both biological sources (e.g., cell-to-cell variations and stochasticity in metabolism) and non-biological sources (e.g., variations in droplet sizes, reagent concentrations and other experimental conditions). Here, we model the results of a droplet-based assay that accounts for the effect of biological heterogeneity in cellular metabolism based on the conversion of resazurin, the effective component of alamarBlue, to the fluorescent product resorufin by metabolically viable cells. We also account for the effect of non-biological heterogeneity, such as experimental variations in droplet size and reagent concentration. While we focus on a droplet-based assay here, we note that this analysis can be useful in the analysis of heterogeneity in typical well-plate assays as well.
4.2.1. Reaction model for the conversion of resazurin to resorufin
Viable cells turn resazurin into resorufin, which is more fluorescent than resazurin. The equation for a simplified model of the reaction can be written as Eq. (4).
| (4) |
where A is resazurin and B is resorufin. We model this reaction with three reaction equations Eqs. (5–7).
| (5) |
| (6) |
| (7) |
For simplicity, we assume second-order kinetics for the conversion of resazurin to resorufin. We also assume that cell doubling frequency f is independent of the concentration of resazurin, resorufin, or any other chemical, and that cells are in log phase and do not reach an equilibrium cell concentration.
Our model can be further simplified if we assume a uniform concentration of chemicals within the drop. In drops that are not moving, mixing occurs primarily due to diffusion. If diffusion occurs more quickly than the reaction, we can assume the droplet is well mixed. To test this assumption, we calculate the dimensionless Damkhöler number, Da. We define Da for our system in Eq. (8).
| (8) |
For the reaction time, we used cell concentration instead of resazurin concentration because the cell concentration is typically lower than that of resazurin and is therefore expected to be rate-limiting. For this calculation, we use a typical drop radius of r = 10μm, a diffusion constant of D = 10−10 m2/s, and assume 1 cell per drop. We also estimate k1 from published reaction kinetics plots to be approximately 10−16 m3/(cells/s) (Al-Nasiry, Geusens, Hanssens, Luyten, & Pijnenborg, 2007) Plugging these parameters into Eq. (8) gives Da ~10−2, indicating that the reaction is limiting and that we can assume the drops are well-mixed via diffusion compared with the reaction time scale. This assumption holds for several hours, until 1 cell has divided into many cells such that Da approaches 1. Here, we have not accounted for convection in the drops which always occurs if the drops are in motion (Leong, Gai, & Tang, 2016). Such convection should further decrease Da. On the other hand, for faster reaction conditions, physical mixing of the vessel containing the droplets may be necessary to create the conditions required for well-mixed droplets.
We now solve for the analytical solution to Eqs. (5–7). [A](t) can be immediately solved after plugging in for the initial concentration of cells, [cells]0, and defining to give Eq. (9).
| (9) |
where ,given by the boundary condition [A](t = 0) = [A]0. The solution for [B](t) then follows using the boundary conditions of [B](t=0) = 0 to give Eq. (10).
| (10) |
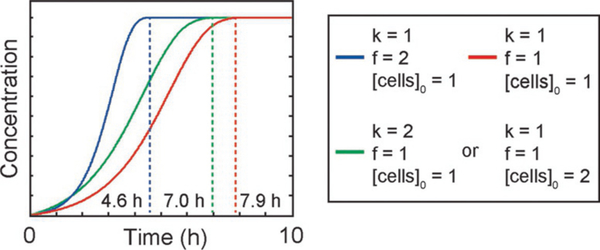
We plot the results of this equation in Fig. 6 for different values of k, f, and [cells]0. From Eq. (10), we can also see that the concentration of B (i.e., resorufin) is most sensitive to f, the cell division frequency. This result is expected because the concentration of one of the reactants—the cells here—is increasing exponentially over time at a rate which depends on f. This increase in cell concentration can then make up for the decrease in reactant and yield a higher reaction rate than a typical second-order reaction with both reactant species decreasing over time.
FIG. 6.
Concentration of resorufin versus time from our reaction model. Dashed lines denote the equilibrium time or end point for the reaction. Both cases plotted on the green curve have the same analytical solution.
The readout for resorufin concentration in our experiments is fluorescence intensity. The concentration of resazurin and resorufin can be related to fluorescence intensity via the Beer-Lambert law in Eq. (11).
| (11) |
where I is the fluorescence intensity, l is the optical path-length, and εi is the wavelength-dependent molar fluorescence coefficient of species i. Because we measure the drop fluorescence in wells with a height smaller than the droplet diameter, the pathlength l is fixed. Using data from the literature Perrot, Dutertre-Catella, Martin, Warnet and Rat (2003), we estimate the ratio between the fluorescent coefficients of resazurin and resorufin to be 1:10.
4.2.2. Biological and non-biological heterogeneity
The broad distribution or the heterogeneity in fluorescence intensity among the drops can be explained by two factors: (1) biological heterogeneity among the cells and/or (2) non-biological heterogeneity among the drops.
Biological heterogeneity can arise from differences in genotype and phenotype among encapsulated cells. This heterogeneity can lead to variations in cellular metabolic rate and division rate. In our reaction model, varying k and f represents cells having different metabolic rates and division rates.
Non-biological heterogeneity can arise from differences in droplet size, the initial number of cells encapsulated in each drop, and/or chemical concentration inside the drop. For our flow-focusing droplet generation system, the variability in drop volume is <3% typically (Pan et al., 2017). The number of cells per drop is determined by Poisson distribution as detailed in Section 2.5. For an initial bacterial concentration of 5 × 105cells/mL compartmentalized into 61 pL drops, approximately 98.48% of the drops that contain cells contain a single cell, whereas 1.52% of the them contain 2 or more cells. In a droplet generation system similar to ours which mixes reactants immediately prior to their encapsulation in droplets, a variability of 0–5% in reactant concentration in droplets was reported (Song & Ismagilov, 2003). This variability likely arises from fluctuations in the flow rates of the two dispersed phases due to mechanical fluctuations from the syringe pumps.
To account for both biological and non-biological heterogeneities, we included the following as input parameters in our model: (1) A cell-to-cell biological variability in k and f from 0% to 10%, assuming a normal distribution. (2) A variability in drop volume from 0% to 3%, and a variability in reactant concentration from 0% to 5%. We assumed a normal distribution for these two variations. (3) The number of cells in each droplet was determined by a Poisson distribution with a mean of 0.05 cells per drop.
4.2.3. Results of model accounting for biological and non-biological heterogeneity
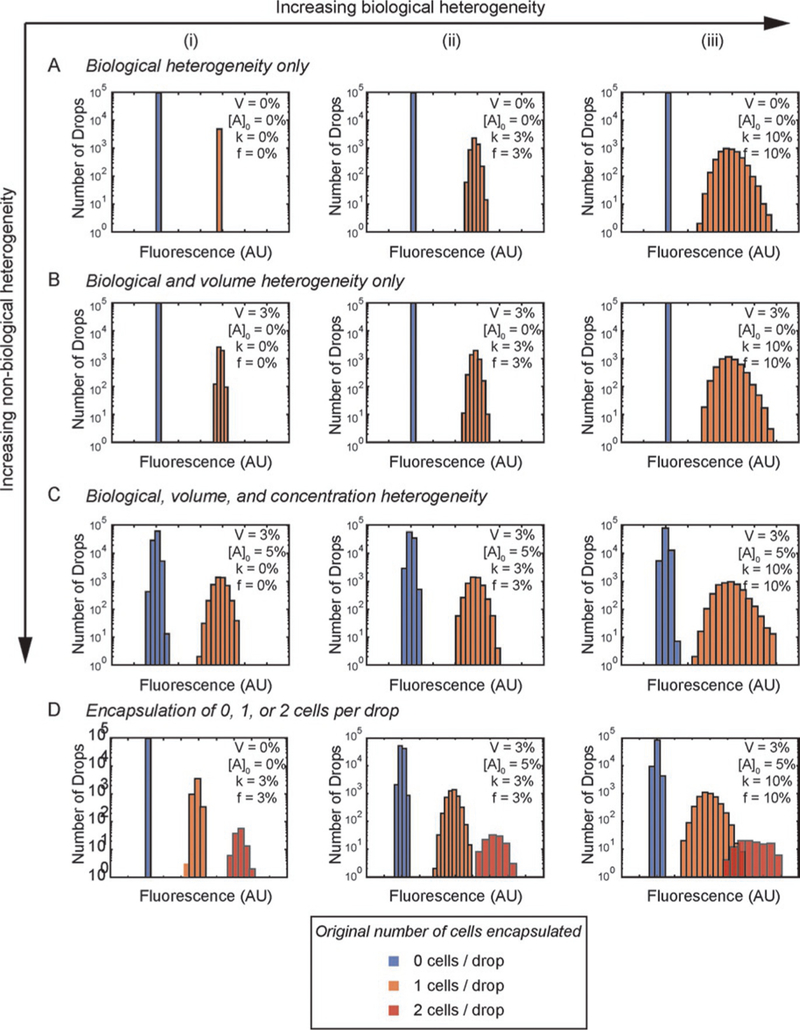
Fig. 7 shows the results of the effects of biological and non-biological heterogeneity on the distribution of droplet fluorescence in our model. We first consider the case when all drops that contain cells have exactly a single cell in them (Fig. 7A–C). This case is useful to illustrate the effect of biological and non-biological heterogeneity, since only a small fraction of drops contain more than one cell, and new methods have been reported to beat Poisson statistics and further decrease the fraction of drops that contain more than one cell (Kamalakshakurup & Lee, 2017).
FIG. 7.
Results of our reaction model in droplets, assuming heterogeneity between drops in cell biology, drop volume, and initial reactant concentration. Percentages in legend refer to heterogeneity normalized to the mean value. (A) Biological heterogeneity only. (B) Biological heterogeneity with 3% heterogeneity in drop volume. (C) Biological heterogeneity with 3% heterogeneity in drop volume and 5% heterogeneity in initial reactant concentration. All cases assume a Poisson distribution of cells in drops with 5% of the drops containing a single cell. Column (i) k=0%, f=0%, Column (ii) k=3%, f=3%, Column (iii) k=10%, f=10%. For (A) through (C), we did not plot drops with >1 cell. (D) Increasing biological and non-biological heterogeneity affect the ability to distinguish between drops containing 1 and 2 cells.
In absence of any heterogeneity (Fig. 7A(i)), each fluorescence peak corresponds to 0 or 1 cells and the number of drops in each peak is determined by Poisson distribution. In the presence of biological heterogeneity only (Fig. 7A), as biological heterogeneity increases (by increasing the variability in metabolic rate k and doubling frequency f from 0% to 10%), the width of the fluorescence peak increases. Measuring the standard deviation in the fluorescence intensity gives a quantitative measure of the biological heterogeneity in the absence of non-biological heterogeneity. In the presence of non-biological heterogeneity only (Fig. 7A(i), B(i), and C(i)), a similar trend is observed. As non-biological heterogeneity increases (by increasing the variability in droplet volume V from 0% to 3% and reactant concentration [A]0 from 0% to 5%), the width of the fluorescence peak increases. In the absence of biological heterogeneity, measuring the standard deviation in the fluorescence intensity gives a quantitative measure of the non-biological heterogeneity.
In most practical applications, both biological and non-biological heterogeneity are present. In these cases, measuring the width of the fluorescence peaks alone is insufficient to differentiate the contribution from biological and non-biological heterogeneity. If we are interested in measuring biological heterogeneity using droplets, it is critical to first characterize or reduce the non-biological heterogeneity. Table 1 shows that when biological heterogeneity is low (i.e., variability in k = 3% and variability in f= 3%), the system is very sensitive to variability in drop size. For this case, increasing the variability in drop volume from 0% to 3% increased the measured variability in fluorescence by 14% (standard deviations of 6.83 ± 0.17 and 7.82± 0.12, respectively). On the other hand, when biological heterogeneity is increased to 10% (i.e., variability in k = 10% and variability in f= 10%), the system is less sensitive to variability in drop size. For this case, increasing the variability in drop volume from 0% to 3% does not increase the measured fluorescence variability (standard deviations of 23.03 ± 0.33 and 22.79 ± 0.11, respectively). If the drop volume variability is further increased to 10%, the measured fluorescence variability is increased significantly (26.98 ± 0.72). Therefore, if the variability in drop size is small compared with biological heterogeneity, variability in drop size is expected to have insignificant effect on the measured fluorescence variability. A similar effect is expected if the non-biological variability arises from variations in reactant concentration.
Table 1.
Standard Deviation of Droplet Fluorescence as a Function of Biological and Drop Volume Heterogeneity
| Biological Heterogeneity |
Drop Volume Heterogeneity |
Standard Deviation of Droplet Fluorescence |
|
|---|---|---|---|
| 3% | 0% | 6.83 ± 0.17 |  |
| 3% | 7.82 ± 0.12 | ||
| 10% | 0% | 23.03 ± 0.33 | |
| 3% | 22.79 ± 0.11 |  |
|
| 10% | 26.98 ± 0.72 |
Increasing biological heterogeneity decreased the effect of drop volume heterogeneity on the distribution of fluorescence in drops. Data averaged from three simulations.
Statistical significance, P<0.01.
Next, we consider the case where the drops that contain cells can have one or more cells in them according to Poisson statistics. Fig. 7D shows that when biological and non-biological heterogeneity are low, drops containing more than one cell are easy to distinguish. However, when biological and non-biological heterogeneities are increased (Fig. 7D(iii)), it becomes increasingly difficult or impossible to distinguish between drops containing one and two cells. In this case, the measured heterogeneity, represented by the standard deviation in the fluorescence distribution, is higher than the actual heterogeneity.
4.2.4. Prediction of biological heterogeneity with known non-biological heterogeneity
In cases where both biological and non-biological heterogeneity exist, it is possible to calculate the contribution from biological heterogeneity using the propagation of uncertainty if all sources of non-biological heterogeneity are known. In general, the overall uncertainty ωR in result R can be calculated using Eq. (12).
| (12) |
where x1 through xn are the set of independent variables and ω1 through ωn are the uncertainties of the independent variables (Holman & Gajda, 2001). Of importance is that the effect of each independent variable on the overall result R must be well-characterized or modeled in order for the derivatives to be obtained. In this equation, the uncertainty is equivalent to the standard deviation of the variable, assuming a normally distributed error.
In our system, the result of interest R is the fluorescence intensity of the drop, I. Eq. (11) can be expanded to give the fluorescence intensity as a function of our independent variables V, [A]0, k, and f, assuming 1 cell per drop in Eq. (13).
| (13) |
The uncertainty in the droplet fluorescence can then be written as:
| (14) |
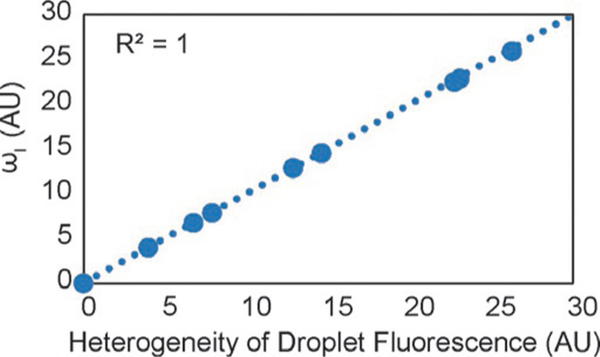
For each case plotted in Fig. 7A–C, the uncertainty ωI was calculated from the uncertainty in V, [A]0, k, and f. Fig. 8 shows that, as expected, the calculated uncertainty and the measured standard deviation in droplet fluorescence (for the drops with 1 cell from Fig. 7A–C) had a perfect correlation (R2 = 1). This result indicates that each droplet is analogous to a separate experimental measurement, and that the distribution in droplet fluorescence can be understood as the uncertainty in the fluorescence due to the combined uncertainty (or heterogeneity) in each independent variable.
FIG. 8.
Uncertainty in fluorescence calculated from Eq. (14), ωI, compared with the heterogeneity of droplet fluorescence measured from Fig. 7A–C.
We then look at whether biological heterogeneity could be predicted from known values of non-biological heterogeneity, ωV and ω[A]0, and overall measured fluorescence heterogeneity ωI. Here, we focus on biological heterogeneity due to the conversion of resazurin to resorufin only, i.e., ωk is finite and unknown, and assume ωf = 0 in Eq. (14), which could occur if the cell is arrested to not divide over the length of the experiment. This gives an equation for ωk,calc in Eq. (15).
| (15) |
Table 2 shows the values for ωk,calc calculated using Eq. (15), the measured standard deviation in fluorescence intensity (ωI) (Fig. 7A–C), and known non-biological heterogeneities (i.e., known ωV and ω[A]0). Table 2 also shows the actual value of ωk, which was the standard deviation we input into the model in Fig. 7. As expected, the calculated ωk,calc matched exactly with ωk for ωf = 0. However, for cases where ωf is finite, the extraction of the contribution from the different sources of biological heterogeneity will be more difficult, unless the sources can be controlled or measured separately.
Table 2.
Calculated Biological Heterogeneity ωk,calc Using Eq. (15), Assuming ωf = 0
| ωk/k (%) | ωV/V (%) | ω[A]0/[A]0 (%) | ωI/I(%) | ωk,calc/k (%) | Error (%) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 0 | 0 | 1.62 | 3 | 0 |
| 10 | 0 | 0 | 5.41 | 10 | 0 |
| 0 | 3 | 5 | 5.26 | 0 | 0 |
| 3 | 3 | 5 | 5.50 | 3 | 0 |
| 10 | 3 | 5 | 7.54 | 10 | 0 |
Error is defined here as the difference between ωk,calc and ωk.
4.2.5. Limitations of our model
A first limitation is that, as long as the drops do not leak (Chen et al., 2012; Pan et al., 2015, 2014), the heterogeneity in fluorescence is expected to vanish at the end point when all resazurin is converted to resorufin. For applications that aim to quantify biological heterogeneity, the fluorescence distribution must be measured before any drops have completely converted resazurin to resorufin. For applications that aim to quantify the number of cells instead of quantifying biological heterogeneity, performing the measurement after the assay has reached the end point will generate a more accurate result than at an earlier time point, but at the expense of increased assay time. A second limitation of our model is that we have not considered any side reactions. Side reactions between cell media and the reactant could increase the non-biological heterogeneity. Complex media containing cell remnants, such as LB, appear to be more likely to cause side reactions. We found that in our system, resazurin reacts with certain components in LB, leading to a small but measurable increase in the heterogeneity as can be seen from the drops which don’t contain cells in Fig. 5B. A third limitation of our model is that we assumed second-order rate kinetics only. To fully capture the reactions, more complex models may be necessary such as those that account for the effect of cell concentration, nutrient density of the media, and the effect of chemicals or antibiotics on division rate. For example, oxygen concentration may vary between drops, which would be expected to affect the metabolic and division rates of the cells. This variation in oxygen concentration could in turn lead to an undesirable increase in biological heterogeneity. Further development of the model should account for these limitations in order to accurately quantify the fluorescence distribution in droplets to elucidate the underlying heterogeneity.
5. CONCLUSIONS
We have described a droplet-based microfluidic method for the quantification of phenotype in single cells. The key advantages of our method are (1) the ability to enumerate cells with a lower detection limit of 10cfu/mL; (2) independence of the results on bacteria growth and low susceptibility to the risk of contamination compared with culture-based methods (Tortoli et al., 1999); (3) preservation of the specificity of the probe regardless of the fraction of target cells present in the sample; and (4) the ability to extract the biological and non-biological heterogeneity by examining the distribution of fluorescence intensity from the drops. Our method is applicable to phenotyping different cells as long as a specific probe is available. For further analysis and mapping between genotypes and phenotypic results, our method can be integrated with droplet sorting and single-cell sequencing (Baret et al., 2009; Cao et al., 2013; Grun & van Oudenaarden, 2015; Lasken, 2012; Zilionis et al., 2017).
REFERENCES
- Al-Nasiry S, Geusens N, Hanssens M, Luyten C, & Pijnenborg R (2007). The use of Alamar blue assay for quantitative analysis of viability, migration and invasion of choriocarcinoma cells. Human Reproduction, 22(5), 1304–1309. [DOI] [PubMed] [Google Scholar]
- Altschuler SJ, & Wu LF (2010). Cellular heterogeneity: Do differences make a difference? Cell, 141(4), 559–563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anna SL, Bontoux N, & Stone HA (2003). Formation of dispersions using “flow focusing” in microchannels. Applied Physics Letters, 82(3), 364–366. [Google Scholar]
- Avery SV (2006). Microbial cell individuality and the underlying sources of heterogeneity. Nature Reviews. Microbiology, 4(8), 577–587. [DOI] [PubMed] [Google Scholar]
- Baret J-C, Miller OJ, Taly V, Ryckelynck M, El-Harrak A, Frenz L, et al. (2009). Fluorescence-activated droplet sorting (FADS): Efficient microfluidic cell sorting based on enzymatic activity. Lab on a Chip, 9(13), 1850–1858. [DOI] [PubMed] [Google Scholar]
- Barkai N, & Leibler S (2000). Biological rhythms—Circadian clocks limited by noise. Nature, 403(6767), 267–268. [DOI] [PubMed] [Google Scholar]
- Blainey PC, Milla CE, Cornfield DN, & Quake SR (2012). Quantitative analysis of the human airway microbial ecology reveals a pervasive signature for cystic fibrosis. Science Translational Medicine, 4(153), 153ra130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boedicker JQ, Li L, Kline TR, & Ismagilov RF (2008). Detecting bacteria and determining their susceptibility to antibiotics by stochastic confinement in nanoliter droplets using plug-based microfluidics. Lab on a Chip, 8(8), 1265–1272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cai L, Friedman N, & Xie XS (2006). Stochastic protein expression in individual cells at the single molecule level. Nature, 440(7082), 358–362. [DOI] [PubMed] [Google Scholar]
- Cao ZN, Chen FY, Bao N, He HC, Xu PS, Jana S, et al. (2013). Droplet sorting based on the number of encapsulated particles using a solenoid valve. Lab on a Chip, 13(1), 171–178. [DOI] [PubMed] [Google Scholar]
- Chen Y, Gani AW, & Tang SKY (2012). Characterization of sensitivity and specificity in leaky droplet-based assays. Lab on a Chip, 12(23), 5093–5103. [DOI] [PubMed] [Google Scholar]
- Churski K, Kaminski TS, Jakiela S, Kamysz W, Baranska-Rybak W, Weibel DB, et al. (2012). Rapid screening of antibiotic toxicity in an automated microdroplet system. Lab on a Chip, 12(9), 1629–1637. [DOI] [PubMed] [Google Scholar]
- Collins DJ, Neild A, deMello A, Liu AQ, & Ai Y (2015). The poisson distribution and beyond: Methods for microfluidic droplet production and single cell encapsulation. Lab on a Chip, 15(17), 3439–3459. [DOI] [PubMed] [Google Scholar]
- El Debs B, Utharala R, Balyasnikova IV, Griffiths AD, & Merten CA (2012). Functional single-cell hybridoma screening using droplet-based microfluidics. Proceedings of the National Academy of Sciences of the United States of America, 109(29), 11570–11575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elowitz MB, Levine AJ, Siggia ED, & Swain PS (2002). Stochastic gene expression in a single cell. Science, 297(5584), 1183–1186. [DOI] [PubMed] [Google Scholar]
- Frenz L, Blank K, Brouzes E, & Griffiths AD (2009). Reliable microfluidic on-chip incubation of droplets in delay-lines. Lab on a Chip, 9(10), 1344–1348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gai Y, Khor JW, & Tang SK (2016). Confinement and viscosity ratio effect on droplet break-up in a concentrated emulsion flowing through a narrow constriction. Lab on a Chip, 16, 3058–3064. [DOI] [PubMed] [Google Scholar]
- Gai Y, Kim M, Pan M, & Tang SKY (2017). Amphiphilic nanoparticles suppress droplet break-up in a concentrated emulsion flowing through a narrow constriction. Biomicrofluidics, 11(3), 034117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grun D, & van Oudenaarden A (2015). Design and analysis of single-cell sequencing experiments. Cell, 163(4), 799–810. [DOI] [PubMed] [Google Scholar]
- Gruner P, Riechers B, Semin B, Lim J, Johnston A, Short K, et al. (2016). Controlling molecular transport in minimal emulsions. Nature Communications, 7, 10392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gu H, Duits MHG, & Mugele F (2011). Droplets formation and merging in two-phase flow microfluidics. International Journal of Molecular Sciences, 12(4), 2572–2597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heiden MGV, Cantley LC, & Thompson CB (2009). Understanding the Warburg effect: The metabolic requirements of cell proliferation. Science, 324(5930), 1029–1033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holman JP, & Gajda WJ (2001). Experimental methods for engineers. Vol. 2 New York: McGraw-Hill. [Google Scholar]
- Holtze C, Rowat AC, Agresti JJ, Hutchison JB, Angile FE, Schmitz CHJ, et al. (2008). Biocompatible surfactants for water-in-fluorocarbon emulsions. Lab on a Chip, 8(10), 1632–1639. [DOI] [PubMed] [Google Scholar]
- Hugonnet J-E, Tremblay LW, Boshoff HI, Barry CE III, & Blanchard JS (2009). Meropenem-Clavulanate is effective against extensively drug-resistant Mycobacterium tuberculosis. Science, 323(5918), 1215–1218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ioerger TR, Feng Y, Chen X, Dobos KM, Victor TC, Streicher EM, et al. (2010). The non-clonality of drug resistance in Beijing-genotype isolates of mycobacterium tuberculosis from the western cape of South Africa. BMC Genomics, 11, 670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kamalakshakurup G, & Lee AP (2017). High-efficiency single cell encapsulation and size selective capture of cells in picoliter droplets based on hydrodynamic micro-vortices. Lab on a Chip, 17(24), 4324–4333. [DOI] [PubMed] [Google Scholar]
- Kawasaki S,Fujita Y,Nagaike T, Tomita K, & Saito H (2017). SyntheticmRNA devices that detect endogenous proteins and distinguish mammalian cells. Nucleic Acids Research, 45(12), e117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kearns DB, & Losick R (2005). Cell population heterogeneity during growth of bacillus subtilis. Genes & Development, 19(24), 3083–3094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khor JW, Kim M, Schutz SS, Schneider TM, & Tang SKY (2017). Time-varying droplet configuration determines break-up probability of drops within a concentrated emulsion. Applied Physics Letters, 111(12), 124102. [Google Scholar]
- Kim M, Pan M, Gai Y, Pang S, Han C, Yang C, et al. (2015). Optofluidic ultrahigh-throughput detection of fluorescent drops. Lab on a Chip, 15(6), 1417–1423. [DOI] [PubMed] [Google Scholar]
- Lasken RS (2012). Genomic sequencing of uncultured microorganisms from single cells. Nature Reviews. Microbiology, 10(9), 631–640. [DOI] [PubMed] [Google Scholar]
- Leong CM, Gai Y, & Tang SKY (2016). Internal flow in droplets within a concentrated emulsion flowing in a microchannel. Physics of Fluids, 28(11), 112001. [Google Scholar]
- Li W, Greener J, Voicu D, & Kumacheva E (2009). Multiple modular microfluidic (M-3) reactors for the synthesis of polymer particles. Lab on a Chip, 9(18), 2715–2721. [DOI] [PubMed] [Google Scholar]
- Litten B, Blackett C, Wigglesworth M, Goddard N, & Fielden P (2015). Artefacts at the liquid interface and their impact in miniaturized biochemical assay. Biomicrofluidics, 9(5), 052607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyu F, Xu M, Cheng Y, Xie J, Rao J, & Tang SKY (2015). Quantitative detection of cells expressing BlaC using droplet-based microfluidics for use in the diagnosis of tuberculosis. Biomicrofluidics, 9(4), 044120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazutis L, Araghi AF, Miller OJ, Baret J-C, Frenz L, Janoshazi A, et al. (2009). Droplet-based microfluidic systems for high-throughput single DNA molecule isothermal amplification and analysis. Analytical Chemistry, 81(12), 4813–4821. [DOI] [PubMed] [Google Scholar]
- Mehrotra P (2016). Biosensors and their applications–A review. Journal of Oral Biology and Craniofacial Research, 6(2), 153–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nisisako T, Ando T, & Hatsuzawa T (2012). High-volume production of single and compound emulsions in a microfluidic parallelization arrangement coupled with coaxial annular world-to-chip interfaces. Lab on a Chip, 12(18), 3426–3435. [DOI] [PubMed] [Google Scholar]
- Nisisako T, & Torii T (2008). Microfluidic large-scale integration on a chip for mass production of monodisperse droplets and particles. Lab on a Chip, 8(2), 287–293. [DOI] [PubMed] [Google Scholar]
- Ozbudak EM, Thattai M, Kurtser I, Grossman AD, & van Oudenaarden A (2002). Regulation of noise in the expression of a single gene. Nature Genetics, 31(1), 69–73. [DOI] [PubMed] [Google Scholar]
- Pan M, Kim M, Blauch L, & Tang SKY (2016). Surface-functionalizable amphiphilic nanoparticles for pickering emulsions with designer fluid-fluid interfaces. RSC Advances, 6(46), 39926–39932. [Google Scholar]
- Pan M, Lyu F, & Tang SKY (2015). Fluorinated pickering emulsions with nonadsorbing interfaces for droplet-based enzymatic assays. Analytical Chemistry, 87(15), 7938–7943. [DOI] [PubMed] [Google Scholar]
- Pan M, Lyu F, & Tang SK (2017). Methods to coalesce fluorinated pickering emulsions. Analytical Methods, 9(31), 4622–4629. [Google Scholar]
- Pan M, Rosenfeld L, Kim M, Xu M, Lin E, Derda R, et al. (2014). Fluorinated pickering emulsions impede interfacial transport and form rigid interface for the growth of anchorage-dependent cells. ACS Applied Materials & Interfaces, 6(23), 21446–21453. [DOI] [PubMed] [Google Scholar]
- Patsch K, Chiu CL, Engeln M, Agus DB, Mallick P, Mumenthaler SM, et al. (2016). Single cell dynamic phenotyping. Scientific Reports, 6, 34785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perrot SB, Dutertre-Catella H, Martin C, Warnet JM, & Rat P (2003). A new nondestructive cytometric assay based on resazurin metabolism and an organ culture model for the assessment of corneal viability. Cytometry. Part A, 55a(1), 7–14. [DOI] [PubMed] [Google Scholar]
- Romanowsky MB, Abate AR, Rotem A, Holtze C, & Weitz DA (2012). High throughput production of single core double emulsions in a parallelized microfluidic device. Lab on a Chip, 12(4), 802–807. [DOI] [PubMed] [Google Scholar]
- Rosenfeld L, Fan L, Chen Y, Swoboda R, & Tang SKY (2014). Break-up of droplets in a concentrated emulsion flowing through a narrow constriction. Soft Matter, 10(3), 421–430. [DOI] [PubMed] [Google Scholar]
- Shembekar N, Chaipan C, Utharala R, & Merten CA (2016). Droplet-based microfluidics in drug discovery, transcriptomics and high-throughput molecular genetics. Lab on a Chip, 16(8), 1314–1331. [DOI] [PubMed] [Google Scholar]
- Silva GM, & Vogel C (2016). Quantifying gene expression: The importance of being subtle. Molecular Systems Biology, 12(10), 885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singh RK, & Sivabalakrishnan M (2015). Feature selection of gene expression data for cancer classification: A review. Procedia Computer Science, 50, 52–57. [Google Scholar]
- Song H, & Ismagilov RF (2003). Millisecond kinetics on a microfluidic chip using nanoliters of reagents. Journal of the American Chemical Society, 125(47), 14613–14619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Toriello NM, Douglas ES, Thaitrong N, Hsiao SC, Francis MB, Bertozzi CR, et al. (2008). Integrated microfluidic bioprocessor for single-cell gene expression analysis. Proceedings of the National Academy of Sciences of the United States of America, 105(51), 20173–20178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tortoli E, Cichero P, Piersimoni C, Simonetti MT, Gesu G, & Nista D (1999). Use of BACTEC MGIT 960 for recovery of mycobacteria from clinical specimens: Multicenter study. Journal of Clinical Microbiology, 37(11), 3578–3582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vera M, Biswas J, Senecal A, Singer RH, & Park HY (2016). Single-cell and single-molecule analysis of gene expression regulation. Annual Review of Genetics, 50, 267–291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xia YN, & Whitesides GM (1998). Soft lithography. Annual Review of Materials Science, 28, 153–184. [Google Scholar]
- Xie H, Mire J, Kong Y, Chang M, Hassounah HA, Thornton CN, et al. (2012). Rapid point-of-care detection of the tuberculosis pathogen using a BlaC-specific fluorogenic probe. Nature Chemistry, 4(10), 802–809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yajko DM, Madej JJ, Lancaster MV, Sanders CA, Cawthon VL, Gee B, et al. (1995). Colorimetric method for determining MICs of antimicrobial agents for mycobacterium-tuberculosis. Journal of Clinical Microbiology, 33(9), 2324–2327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang B, Treweek JB, Kulkarni RP, Deverman BE, Chen CK, Lubeck E, et al. (2014). Single-cell phenotyping within transparent intact tissue through whole-body clearing. Cell, 158(4), 945–958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu J, Xiao J, Ren XJ, Lao KQ, & Xie XS (2006). Probing gene expression in live cells, one protein molecule at a time. Science, 311(5767), 1600–1603. [DOI] [PubMed] [Google Scholar]
- Zhu Y, & Fang Q (2013). Analytical detection techniques for droplet microfluidics—A review. Analytica Chimica Acta, 787, 24–35. [DOI] [PubMed] [Google Scholar]
- Zilionis R, Nainys J, Veres A, Savova V, Zemmour D, Klein AM, et al. (2017). Single-cell barcoding and sequencing using droplet microfluidics. Nature Protocols, 12(1), 44. [DOI] [PubMed] [Google Scholar]