Abstract
Infectious diseases such as Influenza and Ebola pose a serious threat to everyone but certain demographics and cohorts face a higher risk of infection than others. This research provides a computational framework for studying health disparities among cohorts based on individual level features, such as age, gender, income, etc. We apply this framework to find health disparities among subpopulations in an influenza epidemic and evaluate vaccination prioritization strategies to achieve specific objectives. We explore the heterogeneities in individuals’ demographic and socioeconomic attributes as the potential cause of health disparities. An agent-based model is used to simulate an influenza epidemic over a synthetic social contact network of the Montgomery County in Southwest Virginia to identify infected cases which are then labeled with a specific clinical outcome by using a predefined probability distribution based on age and risk level. We divide the population into age and income based cohorts and measure the direct and indirect economic impact of vaccination for each cohort. Simulation-based results find strong health disparities across age and income groups. Various vaccine distribution strategies are considered and outcomes are measured through metrics such as death count, total number of infections, net return per capita, net return per dollar spent and net return per vaccinated person. The results, framework, and methodology developed here can assist public health policy makers in efficiently allocating limited pharmaceutical resources.
Keywords: Agent based, Computational framework, Health disparity, Simulation, Vaccination
1 Introduction
Infectious diseases such as influenza and Ebola pose a serious threat to global public health. In the United States, it is estimated that each year seasonal influenza causes 31.4 million outpatient visits, over 200,000 hospitalizations, 3,300–49,000 deaths, and is responsible for 44.0 million days of lost productivity [20, 34, 39, 41]. Worldwide influenza causes about three to five million cases of severe illness and about 250,000 to 500,000 deaths [45].
To control the spread of influenza, the Advisory Committee on Immunization Practices (ACIP) recommends seasonal influenza vaccination annually for individuals aged 6 months and older without contraindications [15]. However, this recommendation assumes an unlimited supply of vaccine to be available which is not always the case, especially during an influenza pandemic [16, 20, 32].
This work focuses on the study of health disparities and vaccination priorities among different subpopulations. Health disparities can arise due to differences in age, gender, geographic location, income level, and other socioeconomic variables [23] since personal attributes influence behavior, activities, and social interactions, which in turn affect an individual’s vulnerability and infectivity. To effectively control the spread of a disease it is important to understand these differences so scarce public health resources can be distributed efficiently [1, 3, 22, 24, 36, 43].
Health disparity, as measured by case outcome and economic return, varies by the way a population is partitioned. For instance, the disparity may be high among age groups but not so much among income groups, implying that age is a bigger determinant of disparity than income. It is important to understand health disparity with respect to demographic features and identify the most significant ones. This would help identify cohorts that are at a disadvantage in terms of encountering higher infections and may require more resources to achieve herd immunity not only within their own cohorts but among the entire population. Ultimately it will guide the distribution of health care resources so that overall infection rates can be curtailed and economic loss can be minimized. The literature lacks this kind of detailed, individual-based study of health disparities and their consequences on the control of epidemics.
To study cohort level disparities, we use an individual-based model where a synthetic representation of a real population is created at an individual level. The synthetic individuals are statistically equivalent to the Census population when aggregated to a block group level. Each synthetic individual is assigned an activity sequence which is derived from time use surveys. It includes the types of activities performed and the time of day they are performed at [5]. A location for each activity is also assigned and when individuals are co-located at these locations, they are assumed to be in contact with each other, resulting in the creation of a synthetic social contact network. This approach supports fully heterogeneous individuals and does not require assumptions about large-scale regularity of interactions, unlike compartmental models [4, 8].
There have been many articles that study the cost of influenza infections [6, 9, 26]. For example, there are studies focusing on the cost effectiveness of vaccination for children [19, 25, 29, 33, 35, 40], healthy working adults [10, 28], and people of age 65 years and above [37]. Research in [16] compares the cost effectiveness of vaccination using a dynamic model and a static model and prioritizes individuals by age and risk groups. These works focused on the measurement of direct and indirect impacts that take medical cost and productivity loss into account. Meltzer et al. [32] used a Monte Carlo simulation model to analyze the direct economic impact of vaccine-based interventions in pandemic influenza and proposed multiple criteria to generate vaccination priorities for subpopulations. Work by [17] examined herd immunity to further learn the direct and indirect effects of influenza vaccination. However, prior work has not examined health disparities that originate from differences in individual level attributes.
In this work, we build a computational framework to study the impact of heterogeneities in individuals’ demographic and socioeconomic attributes, on health disparities during an influenza epidemic. We also design vaccination prioritization strategies by simulating epidemics where vaccine-based interventions are applied to targeted groups of people in the population to fulfill specific policy objectives. Our contributions include:
-
–
A framework to study health disparities in an influenza epidemic using a synthetic social contact network and an agent-based simulation model. This modular framework is highly generic and can be used to study other disease epidemics and intervention strategies.
-
–
Studied the impact of heterogeneities in individual level attributes on health and economic outcomes. Identified attributes that cause significant health disparities among cohorts.
-
–
Calculated direct and indirect impacts of vaccination-based interventions.
-
–
Designed cohort-based vaccination prioritization strategies using multiple objectives and measured their performance.
The rest of this paper is organized as follows. Section 2 describes the framework and the models used in this research. Section 3 shows simulation results, and discusses health disparities with respect to age and income attributes. Various vaccination strategies are designed and discussed with respect to their case and economic outcomes. Section 4 concludes the paper. Appendix A provides details of the data used in the paper.
2 Framework and Methods
In this section, we present the details of the framework along with the models and the methods used. Although this work focuses on influenza and vaccine based intervention, the framework is generic and can be applied to diseases and be used for other interventions such as antivirals and social distancing.
2.1 Framework
The framework consists of three major components: (1) real/synthesized data, (2) modeling and simulation, and (3) analysis (see Fig. 1). The first component collects data from a variety of sources and synthesizes it [38]. This includes building the social contact network, collecting data on disease model parameters, data on case outcome distributions conditional on demographics, and data on costs conditional on clinical outcomes. The second component consists of a disease spread model which determines the health state (susceptible, exposed, infected or removed) of each synthetic individual at the end of the simulation; and a labeling algorithm for classifying each infected individual into four health outcomes i.e., dead, hospitalized, outpatient, and ill not requiring care. The third component is the analytical engine of the framework that analyzes health disparities based on individual level demographic and health attributes, calculates the impact of interventions, and builds intervention priorities targeting towards specific economic and social objectives.
Fig. 1.
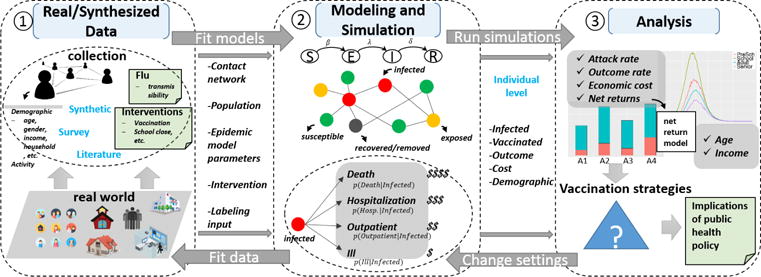
Framework for studying health disparities based on individuals, cohorts, and specific objectives. Real/synthesized data module collects data on costs, disease parameters, interventions etc. and synthesizes data from multiple sources to create the synthetic social contact network. Modeling and simulation module consists of the disease model, net return model which labels health outcomes and associated costs. The inputs are collected by the first module, the outputs generated by the second module are individual level infected cases with a specific outcome (i.e., death, hospitalization, outpatient, ill but not seek medical care), and vaccinated cases. Analysis module performs health disparity analysis and intervention analysis. Health disparity is analyzed with respect to age and household income. Vaccination prioritization strategies are designed and compared to minimize death rate/total death count, or to maximize net returns per dollar spent/total net returns.
The following steps illustrate how the framework processes the data, runs the simulations, and analyzes the results.
-
collect and synthesize data on the population and social contact network → build influenza disease model → run epidemic simulations → label infected cases with clinical outcomes → analyze health disparity with respect to individual level attributes.
To simulate an epidemic, we need individual level data of the population, its contact network on which the transmissions occur, disease model parameters such as transmission rate, i.e., the probability of transmission from an infectious person to a susceptible person per unit of contact time, incubation duration, infectious duration, etc. If vaccination intervention is applied, then vaccine efficacy (reduction on disease transmission probability) and compliance rate (probability that a person will take the vaccine) are also required. The simulation output provides health label (infected or not) and vaccine label (vaccinated or not) for each person. This is joined with the person’s individual level attributes such as age, gender, income etc.
Further, each synthetic individual is assigned with a risk level based on age regardless of health and vaccine label, i.e., whether the person is high-risk or non-high-risk [32]. Then each infected case is labeled with a specific clinical outcome among: death, hospitalization, outpatient, and ill but not seeking medical care, based on age and the risk level of the individual. For each clinical outcome, there is an associated cost of treatment. The clinical outcomes of the infected are decided by age and the risk level as given in [32]; and the data on the treatment costs for each outcome is given in [12]. We have included these data in Appendix A for completeness.
We divide the whole population into subgroups based on a select attribute, e.g. age, and compute the difference between age-groups with respect to cumulative infection rate, health outcome, and economic cost. The statistical significance tests are used to determine whether health disparities exist in terms of the select attribute.
-
design vaccination strategies → change intervention parameter settings → run simulations → analyze the effects of revised vaccination strategies → find public health policy implications.
We consider different vaccine distribution schemes assuming vaccines are in limited supply. A no-priority strategy is defined for comparative analysis where all vaccines are distributed randomly in the population. In other cases, a specific demographic is selected to divide the population into subgroups on which a vaccine prioritization is determined. In this study, vaccination priorities are designed based on a subgroup’s ability to achieve specific objectives such as minimum number of total infections or maximum net return per capita. Different vaccination priorities are considered and compared using simulation results. Our goal is to answer the following kinds of questions through this framework: (1) Can health disparities be explained by the demographics? If yes, what are the causal reasons behind them? (2) Is it possible to design vaccination prioritization strategies assuming vaccines are in limited supply based on this knowledge? (3) What is the level of improvement provided by these vaccination priorities with respect to various measures of performance?
2.2 Method
This section provides details of the data and methods used in the study.
2.2.1 Synthetic Social Contact Network
A synthetic population and its social contact network are used to simulate the spread of the disease. In this study we use the synthetic social contact network of the Montgomery county in Virginia [38]; its basic properties are summarized in Table 1. A methodology for constructing the synthetic population and contact network for any area in the US can be found in [4, 5, 8, 18, 38]. In what follows we briefly describe the procedures; interested readers can find details in the aforementioned references.
Table 1.
Social contact network of Montgomery County, VA
| Nodes | Edges | Avg. degree | Network density |
|---|---|---|---|
| 77820 | 3936774 | 50.7519 | 0.0013 |
The attributes of the synthetic social contact network of Montgomery County, VA. The contact network is represented as an edge-weighted network. Nodes correspond to individuals, edges represent contacts, and edge weights represent contact durations.
First, a statistical representation of the each individual in the population is built using the US Census data. This synthetic population is statistically equivalent to the real population as given in the US census, when aggregated up to a census block group level. Individuals in the synthetic population are endowed with a complete range of demographic attributes as available in the Census [5, 7], including variables such as age and income level. The population synthesis process preserves the confidentiality of the individuals in the original data sets, yet produces realistic attributes and demographics for the synthetic individuals. Joint demographic distributions are reconstructed from the marginal distributions available in typical census data together with joint distributions in Public Use Microdata Samples (PUMS) using an iterative proportional fitting technique. This technique guarantees that a census of our synthetic population is statistically indistinguishable from the input census when aggregated to block groups.
Next, a set of activity templates for households are determined, based on American time-use surveys [11] and National Household Travel Survey. These activity templates provide a daily set of activities for individuals and the time of day they are performed. Each synthetic household is then matched with one of the survey households, using a decision tree based on demographics such as the size of the household, number of workers in the household, number of children, etc. The synthetic household members are then assigned the activity templates of its matching survey household members, giving each synthetic member a daily sequence of activities. The activities can be of type home, work, shop, school and “other”. For each activity, and for each individual, a geographic location is identified based on land-use patterns, transportation network and data from commercially available databases such as Dun and BradStreet.
A social network is formed when individuals are simultaneously present at a location. The co-location based social network is dynamic and changes as people visit different locations and come in contact with individuals at these locations. The contact network G(V, E, w) is an edge-weighted network. Nodes correspond to individuals, edges represent the contact between two end nodes, and edge weights represent contact durations. Edge (u, v) with weight w(u, v) represents that node u is in contact with node v for duration w(u, v), during which the disease may transmit from node u to node v with probability p(w(u, v)) if u is infected and v is susceptible.
2.2.2 Disease Model
In this study, a standard SEIR model is used for modeling the spread of influenza. SEIR models are widely used in mathematical epidemiology literatures [2, 27] and have been extensively developed and applied to model contagious disease outbreaks [30, 31]. Each person is in one of the following four health states at any time: susceptible, exposed, infectious, and removed. A person v is in the susceptible state until he becomes exposed. If v becomes exposed, he remains so for ΔtE(v) days, which is called incubation period, during which he is not infectious. Then he becomes infectious and remains so for ΔtI(v) days, which is called infectious period. Finally he becomes removed (or recovered) and remains so permanently.
The health states of person v during the epidemic period, denoted by (v), can be equivalently represented by τ(v) = (tS→E(v), tE→I(v), tI→R(v)), where tS→E(v) is the day when v becomes exposed, tE→I(v) = tS→E(v) + ΔtE(v) is the day when v becomes infectious, and tI→R(v) = tE→I(v) + ΔtI(v) is the day when v becomes removed. The model of our framework assumes that ΔtE(v) and ΔtI(v) for each person v are known at the beginning of the simulation. It also assumes the health state transitions are not reversible and they are the only possible state transitions [14, 30, 31].
With the SEIR model, the disease spreads in a population in the following way. It can only be transmitted from an infectious node to a susceptible node. On any day, if node u is infectious and v is susceptible, disease transmission from u to v occurs with probability p(w(u, v)) = 1 − (1 − r)w(u, v) where r is the probability of disease transmission for a contact of one unit time. So the disease propagates probabilistically along the edges of the contact network.
To simulate the spread of influenza in the synthetic contact network, we use EpiFast [8], a high-performance agent-based simulation model. It follows the standard SEIR disease model to capture the within-host and between-host disease progressions, and uses a distributed algorithm to compute stochastic disease propagation in the synthetic network. EpiFast provides individual level details while maintaining heterogeneity among individuals.
2.2.3 Label Infected People with Clinical Outcomes
Each infected person can have one of four clinical outcomes attributed to influenza infection: death (D), hospitalization(H), outpatient(O), ill but not seeking medical care(I). These outcomes depend on a person’s underlying risk condition and age. One’s risk condition (high risk/non-high risk) arising from a pre-existing medical condition often depends on age too. Economic cost is assigned to each infected person according to the outcome. The economic cost includes medical costs related to the treatment of infected cases (direct costs) and productivity loss of infected people (indirect costs). Once individual level outcomes and costs are known, we can calculate the total costs for any subgroup in the population.
For an infected individual whose age is known, the risk level and clinical outcomes are determined by the distributions given in [32]; and the treatment costs for each outcome under each age and risk level are determined by the data given in [12]. More details about these distributions are shown in Appendix Table 19, Table 20, and Table 21.
2.2.4 Interventions
Two scenarios regarding interventions are considered in this work: base case, where no intervention is applied to contain the epidemic; and intervention case, where an intervention is applied to a subset of the population. The intervention may be targeted towards a subpopulation chosen by individuals’ specific attributes or completely random where each person is equally likely to be chosen. In our simulation, we focus on mass vaccination, which is applied at the beginning of the epidemic. Each person chosen to be vaccinated complies with a specified probability, called compliance rate. We assume that each person within a cohort follows a same compliance rate. Compliance rate varies across different cohorts.
2.2.5 Net Return Model
The total economic costs under base case include direct and indirect costs. The total costs under intervention case include direct, indirect, and intervention costs. Direct costs are the medical costs associated with the clinical outcome. Indirect costs are measured by the loss of productivity due to illness. Net return (NR) is defined as the reduction in total cost due to intervention. It provides a measure of economic efficiency.
By aggregating individual costs up to a cohort level or population level, and comparing the base case and the intervention case, we can compute the net return of an intervention as:
| (1) |
where Sbase, Sint are sets of infected individuals under base case and intervention case, respectively. Svax is the set of vaccinated individuals. Ci represents the economic cost of individual i who gets infected. is the cost of vaccination for individual k who gets vaccinated. We assume that for any k, is US $30.53 [32]. Ci is a predefined variable that varies based on age, risk factors, and clinical outcomes. The details on cost are provided in the Appendix, Table 21. We can compute total net return, direct net return, and indirect net return by using corresponding Ci of total cost, direct cost, indirect cost, respectively in Table 21. All costs are adjusted to 2016 USD.
To account for difference in group sizes we calculate net return per capita (NRPC), net return per vaccinated person (NRPV), and net return per dollar spent (NRPD) as:
| (2) |
where Nc, Nv, Nd represent the group size, number of vaccinated people within the group, and total dollar spent on vaccinating the group respectively.
Note that our individual based framework allows us to calculate net return for any subpopulation and for any health outcome. More details are shown in Section 3.
2.2.6 Subpopulations
To discover health disparities with respect to various individual level attributes, we split the population into cohorts by the selected attributes. In this work, we use age and household income to build the cohorts. We create: (i) four age groups that are distinct with respect to economic activity and health care related costs: 0–4 year olds (preschool); 5–19 year (school); 20–64 year (adult); and above 65 years (senior); (ii) four quartiles by annual household income: $0–18400 (Q1); $18400–41620 (Q2); $41620–75000 (Q3); and above $75000 (Q4).
2.3 Applications
This framework can be applied to undertake various studies using alternative interventions, disease models, and datasets. Three major tasks become easier within this framework include: (a) study attributes based health disparity; (b) determine which attributes better explain health disparity; (c) design effective intervention strategies and build prioritization for distributing limited health care resources.
3 Simulation Results and Analysis
This section describes simulation settings and results. Vaccination is the only intervention considered here. Firstly, health disparities and economic disparities are discussed separately with respect to age and household income. We assume that vaccines can fully cover the whole population, and the compliance rates of each cohort are the same. Sensitivity of the disparity results are considered with respect to disease transmission rate and compliance rate for vaccination. Secondly, vaccination prioritization strategies are designed assuming vaccines are in limited supply. The compliance to vaccination can be uniform or vary by age.
3.1 Simulation Settings
Table 3 shows list of parameter values and their sources. We seed the epidemic by randomly infecting 10 individuals at the start of the simulation. A base attack rate of 40% is assumed when no interventions are applied. The corresponding disease transmission rate for this network is 0.00007 per minute of contact time. The transmission rate keep the same across base case and intervention case. In intervention case, vaccination is applied randomly with a compliance rate of 50% and the vaccine efficacy is assumed to be 90%. A 90% vaccine efficacy means that the vaccine reduces the probability of disease transmission by 90%. Note that these parameter values do not correspond to any specific epidemic, as they vary from season to season and differ between populations. For each scenario, we run 30 replicates for 300 days and report the average results.
Table 3.
List of parameter values and their sources
| Parameter | Value | Source |
|---|---|---|
| Attack rate (AR) | 40–60% | [30, 32] |
| Transmission rate | calibrated to attack rate | not applicable |
| Proportion of symptomatic | 67% | [13, 21, 42] |
| Avg. incubation period | 1.9 days | [31] |
| Avg. infectious period | 4.1 days | [31] |
| Diagnosis rate | 60% | [21] |
| Compliance to vaccination | 25–70% | [16] |
| Efficacy of vaccine | 50–90% | varies by season |
3.2 Health Disparity
Here we study disparities in attack rate between different age groups (or income groups) when no intervention is applied (base case). The disease model determines the health state of each individual at the end of simulation. We identify all infected cases and split them into age (or income) groups to calculate the attack rates for each group.
Age-based groups
The epidemic curves, which show the number of new infections each day, for each age group are shown in Fig. 2. We find that the epidemic in the school age group starts earlier and peaks higher. To check for significant differences in attack rates (cumulative infection rate) across age groups, the t-tests are performed. Results in Table 4 show p-values of 2-sample t-tests. The average attack rate for each group is reported in their respective rows. The p-values show that there is a significant difference in between any two age groups, and school age group has the greatest attack rate at , making it the most vulnerable group to influenza infection.
Fig. 2.
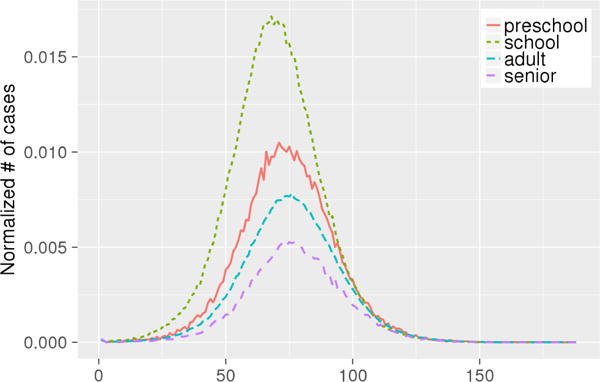
The epidemic curves of age groups along days. X-axis denotes days, Y-axis denotes normalized number of cases (as a fraction of the size of the group).
Table 4.
Disparity in attack rate among age groups: p-value (base-case)
| Attack rate by age group | preschool | school | adult | senior |
|---|---|---|---|---|
| preschool | – | 0.0001*** | 0.0001*** | 0.0001*** |
| school | – | – | 0.0001*** | 0.0001*** |
| adult | – | – | – | 0.0001*** |
| senior | – | – | – | – |
is the average attack rate computed from 30 simulation replicates
p < .05,
p < .01,
p < .001
Table 5 shows that there is also a significant difference in average death rate between any two age groups, and senior age group has the greatest death rate at .
Table 5.
Disparity analysis of death rate among age groups: p-value (base-case)
| Death rate by age group | preschool | school | adult | senior |
|---|---|---|---|---|
| preschool | – | 0.0181* | 0.0001*** | 0.0001*** |
| school | – | – | 0.0001*** | 0.0001*** |
| adult | – | – | – | 0.0001*** |
| senior | – | – | – | – |
is the average death rate computed from 30 simulation replicates
p < .05,
p < .01,
p < .001
We also observe significant difference in average hospitalization rate , average outpatient rate , average ill rate with respect to age. Results are omitted for the sake of brevity.
Income-based groups
Fig. 3 shows the epidemic curves of income groups. We observe that households with high income tend to have an earlier and higher epidemic peak. Table 6 shows p-values of 2-sample t-test where attack rates between any two income groups are tested. Here too, we find a significant difference in between any two income groups, and increases as household income increases. The higher quartile income groups encounter higher infection rates. This is likely due to the fact that higher income households have larger families, as shown in Table 7. In larger families, once one person is infected, the risk of secondary infection can go up by 38% [44].
Fig. 3.
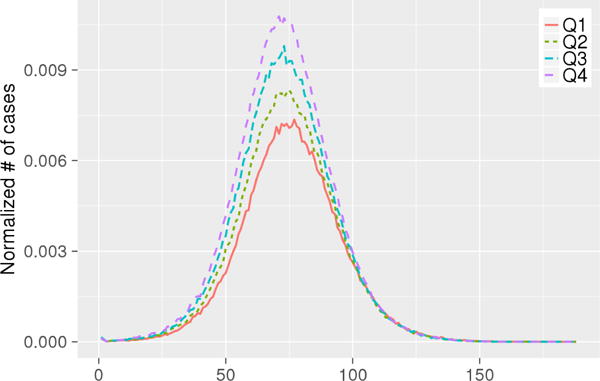
The epidemic curves of income groups along days. X-axis denotes days, Y-axis denotes normalized number of cases.
Table 6.
Disparity analysis of attack rate among income groups: p-value (base-case)
| Income quartiles | Q1 | Q2 | Q3 | Q4 |
|---|---|---|---|---|
| Q1 | – | 0.0001*** | 0.0001*** | 0.0001*** |
| Q2 | – | – | 0.0001*** | 0.0001*** |
| Q3 | – | – | – | 0.0001*** |
| Q4 | – | – | – | – |
is the average attack rate computed from 30 simulation replicates
p < .05,
p < .01,
p < .001
Table 7.
Average household size of income groups
| Income quartiles | Average household size |
|---|---|
| Q1 | 2.00 |
| Q2 | 2.19 |
| Q3 | 2.44 |
| Q4 | 2.85 |
Unlike age groups, we observe no significant difference in among income groups in Table 8. This is because the elderly population which is at a higher risk of death is more evenly distributed among income groups as compared to age groups.
Table 8.
Disparity analysis of death rate among income groups: p-value (base-case)
| Income quartiles | Q1 | Q2 | Q3 | Q4 |
|---|---|---|---|---|
| Q1 | – | 0.1 | 0.02* | 0.4 |
| Q2 | – | – | 0.5 | 0.3 |
| Q3 | – | – | – | 0.1 |
| Q4 | – | – | – | – |
is the average death rate computed from 30 simulation replicates
p < .05,
p < .01,
p < .001
3.3 Economic Disparity
Next we examine the economic impact of intervention by age and income groups. For each group we compute the direct, indirect, and total net returns. To do comparative analysis across groups we measure net return per capita (NRPC), net return per vaccinated person (NRPV), and net return per dollar spent (NRPD) using equation (1) and (2). All returns are measured in 2016 USD.
Age-based groups
We show direct, indirect, and total net return for each age group in Fig. 4. For all age groups the indirect return is the dominant component of total net return. This is because the indirect cost, i.e. loss in wages, from death is much greater than the direct (medical) cost, for all individuals regardless of age and risk level, as shown in Table 21. School-aged and senior groups have significantly higher net return compared to the other two age groups because vaccine intervention reduces the attack rate in school-aged group and the death rate in senior group more. This observation is reflected in all per capita calculations as shown in Table 9. Vaccinations to school-aged and senior groups are economically more beneficial than to preschoolers and adults. However, this does not mean that vaccination based intervention is always more effective in school-aged and senior groups in reducing the attack rate. We will explain this later in the sensitivity analysis section.
Fig. 4.
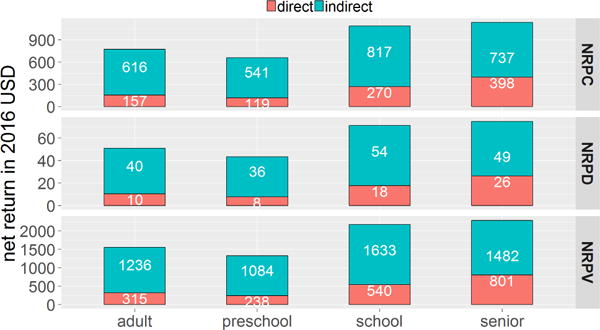
Net return per capita (NRPC), per dollar spent (NRPD), and per vaccinated person (NRPV). The bar height represents value of net return within each one. Each total net return (blue + red) is the sum of indirect net return (upper blue bar) and direct net return (lower red bar). Indirect net returns are significantly larger than direct net returns across all age groups.
Table 9.
Disparity analysis of the net return per dollar spent among age groups: p-value (intervention case)
| NRPD by age group | preschool | school | adult | senior |
|---|---|---|---|---|
| preschool | – | 0.0001*** | 0.14 | 0.0001*** |
| school | – | – | 0.0001*** | 0.44 |
| adult | – | – | – | 0.0001*** |
| senior | – | – | – | – |
p < .05,
p < .01,
p < .001.
is computed over 30 simulation replicates.
Fig. 5 shows distributions of death, hospitalization, outpatient, and ill not seeking medical care among the infected cases, in each age group, and Fig. 6 shows the corresponding cost distributions. Note that for each age group, although the percentage of death count (Fig. 5) is the smallest, the cost of death (in Fig. 6) is the largest. This is because the economic cost of death includes lifetime productivity and hence is higher than the cost for any other clinical outcome (see Table 21).
Fig. 5.
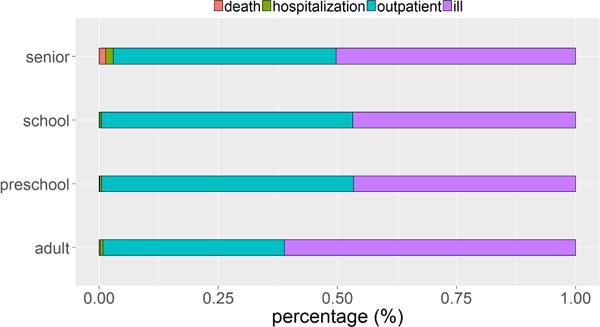
Count distribution of death (first from left in red), hospitalization (second from left in green), outpatient (third from left in blue), and ill but not seeking medical care (forth from left in purple), among the infected cases in each age group. For each age group, the percentage of death count is the smallest.
Fig. 6.
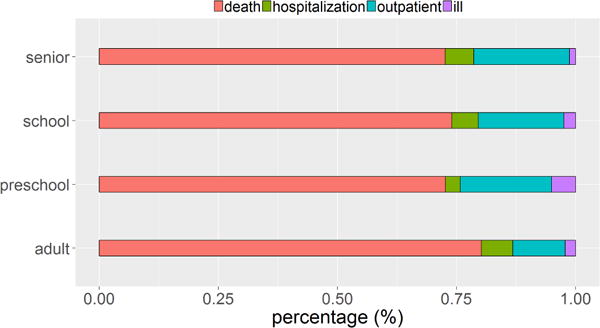
Cost distribution of death (first from left in red), hospitalization (second from left in green), outpatient (third from left in blue), and ill but not seeking medical care (forth from left in purple) in each age group. For each age group, the cost of death is the largest.
Income-based groups
Unlike age groups, the disparity in net return per dollar spent, among income groups is not as significant, see Table 10. The only exceptions are first income quartile versus third and fourth income quartiles.
Table 10.
Disparity analysis of net return per dollar among income groups: p-value (intervention case)
| Income quartiles | Q1 | Q2 | Q3 | Q4 |
|---|---|---|---|---|
| Q1 | – | 0.3 | 0.0051** | 0.0069** |
| Q2 | – | – | 0.0999 | 0.1278 |
| Q3 | – | – | – | 0.8689 |
| Q4 | – | – | – | – |
p < .05,
p < .01,
p < .001.
is computed over 30 simulation replicates.
3.4 Sensitivity Analysis
Next we perform a sensitivity analysis on compliance rate and attack rate (by adjusting the disease transmission rate) to see whether our findings are robust to these changes.
3.4.1 Compliance Rate
The simulation settings remain the same as described in section 3.1 except that compliance to vaccination is reduced from 50% to 25% now. The economic returns of both school-aged group and senior group were significantly higher than for preschoolers and adults at 50% compliance rate, but at lower levels of compliance, the senior group provides the highest benefits, see Table 11. The reason is that the attack rate drops by 66% in senior group and only by 51% among the school-aged children as shown in Table 12. The lower impact on attack rate among school-aged group is probably due to the fact that lower compliance to vaccination prevents this group from gaining herd immunity and the indirect gains from vaccination are disproportionately reduced. The economic returns are not found to be significantly different across preschoolers, schoolers, and adults under 25% compliance.
Table 11.
Disparity analysis of the net return per dollar among age groups: p-value (CMPL=25%)
| NRPD by age group | preschool | school | adult | senior |
|---|---|---|---|---|
| preschool | – | 0.058 | 0.13 | 0.0001*** |
| school | – | – | 0.28 | 0.012* |
| adult | – | – | – | 0.0001*** |
| senior | – | – | – | – |
p < .05,
p < .01,
p < .001.
is computed over 30 simulation replicates.
Table 12.
Reduction in attack rate (%)
| AR (base) | CMPL=50%
|
CMPL=25%
|
|||
|---|---|---|---|---|---|
| AR | Reduction | AR | Reduction | ||
| preschool | 44 | 0.46 | 99 | 17 | 61 |
| school | 70 | 1.09 | 98 | 34 | 51 |
| adult | 34 | 0.29 | 99 | 12 | 64 |
| senior | 22 | 0.18 | 99 | 7 | 66 |
3.4.2 Attack Rate
Next we change the attack rate from 40% to 60%, corresponding to disease transmission rate of 0.00011. All other simulation parameters remain the same as before. We consider both 50% and 25% compliance rate to vaccination. We find the results are qualitatively the same as they are for 40% attack rate and are omitted here to avoid duplication.
The sensitivity analysis results show that the following findings are robust to simulation settings: 1) disparities in health and clinical outcomes exist among age and income groups, but disparities in economic return are only significant with respect to age; 2) school age group is much more vulnerable to influenza infection than other age groups due to their higher contact rates; 3) in random allocation, the vaccination of school-aged group is the most effective in containing the disease except when compliance to intervention is low; 4) deaths have the biggest impact on net return.
3.5 Vaccination Prioritization Strategy
If vaccines are limited it is important to prioritize their use based on specific objectives. Here we consider a simple heuristic for determining priorities based on various objectives, which include: minimizing the total number of deaths, minimizing death rate, maximizing net return per dollar spent, maximizing total net returns, and minimizing attack rate. Our heuristic assigns higher priority to a subpopulation that has a higher (lower) value of the measure we want to minimize (maximize). For example, if the objective is to minimize death rate, then we prioritize age groups according to their death rates, i.e. the age group with a higher death rate is given a higher priority. Given that there is no significant difference in death rate and net return among income-based groups, we only consider age-based groups for deciding vaccination priorities. We use the simulation results based on the setting given in section 3.1 to determine the vaccination priorities for age-based groups. The results are shown in Table 13.
Table 13.
Priorities for age-based groups
| priority | criteria for prioritization
|
||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
|||||
| 1(top) | senior | adult | senior | adult | school | ||||
| 2 | adult | senior | school | school | preschool | ||||
| 3 | school | school | adult | senior | adult | ||||
| 4(bottom) | preschool | preschool | preschool | preschool | senior | ||||
- average death rate; - average death count; - average net return per dollar spent; - average total net return; - average attack rate. , and are normalized values that are comparable across subgroups.
3.5.1 Fixed Compliance Rate Across Age Groups
We first assume the vaccination coverage is 50% and the compliance rate of each cohort is 1. The number of vaccines used is limited to 50% of the population size which is 77, 820 ∗ 50% = 38, 910 for the Montgomery county. Table 14 shows the various prioritization strategies with the actual vaccinated fractions under different objectives. The strategies S4321, S3421, S2134, S4231, and S3241 correspond to minimizing , , , and maximizing , , where subscript numbers of each strategy describe vaccination prioritization of the four age groups. The column values in Table 14 under each strategy represent the actual vaccinated fractions of the corresponding age groups under that strategy. For example S4321 column, which corresponds to minimizing death rate, shows that vaccines are prioritized according to the following ordering: seniors, adults, school-aged children, and preschoolers. Seniors are vaccinated first which uses 7,335 vaccines to cover 100% of the senior group. The remaining 31,575 vaccines are distributed to adults, which cover only 60% of the adults. None of the children receive any vaccines in this case. Strategy with no priority (Snp) is introduced as a baseline in which 50% of each age group is selected uniformly at random for vaccination.
Table 14.
Vaccinated fraction of each age group under different vaccination strategies.
| subgroup (size) | Snp | S4321 | S3421 | S2134 | S4231 | S3241 |
|---|---|---|---|---|---|---|
| preschool (4617) | 0.5 | 0 | 0 | 1 | 0 | 0 |
| school (13310) | 0.5 | 0 | 0 | 1 | 1 | 0 |
| adult (52558) | 0.5 | 0.6 | 0.74 | 0.4 | 0.35 | 0.74 |
| senior (7335) | 0.5 | 1 | 0 | 0 | 1 | 0 |
1-preschool, 2-school, 3-adult, 4-senior; Snp denotes strategy with no priority; S4321 denotes vaccinating seniors first, then adults, then school-aged and then preschoolers. Similarly strategies S3421, S2134, S4231, S3241 follow priorities given by their subscripts. Note that S3421 and S3241 result in the same allocation because adult group has the first priority and it has more people than the size of the vaccine stockpile so no other age groups could be vaccinated.
To compare the performance of strategies, we compute death rate, death count, net return per dollar spent, total net return, and attack rate over the whole population. Note that death rate, net return per dollar spent, and attack rate are normalized values and hence are directly comparable. The results are shown in Table 15. S2134 turns out to be the optimal strategy across all objectives. Followed by S4231 and Snp, whose results are also competitive. These three strategies are significantly better than the other ones. Comparison of S2134, S4231, and Snp with other strategies shows that they have a higher vaccinated fraction of school-aged group.
Table 15.
Performance of different vaccination strategies
| strategy | (%) |
|
(M$) | ($) | (%) | |
|---|---|---|---|---|---|---|
| Snp | 0.000900 | 0.7 | 67.64 | 57.12 | 0.43 | |
| S4321 | 0.015806 | 12 | 47.11 | 38.46 | 14.64 | |
| S3421 | 0.017305 | 13 | 48.44 | 39.13 | 13.20 | |
| S2134 | 0.000600 | 0.47 | 68.15 | 59.69 | 0.29 | |
| S4231 | 0.000643 | 0.50 | 67.88 | 59.54 | 0.42 | |
| S3241 | 0.017305 | 13 | 48.44 | 39.13 | 13.20 |
Low values of (%), , (%) are desirable and high values of ($), (million $) are desirable. Values in bold are optimal.
We conduct the same analysis under other settings to determine optimal vaccination priorities; these include attack rate=40%, compliance=0.25; attack rate=60%, compliance=0.5; attack rate=60%, compliance=0.25. We observe that the optimal strategy always has the highest number of school age people vaccinated.
Snp in Table 15 performs very close to the optimal strategy. Similar observations were made in other settings, except when attack rate=60% and compliance=0.25. Snp performs poorly when the disease transmission rate is high and the compliance rate is low. This indicates that vaccination priority is particularly important when vaccines are in short supply and the virus strain is highly infective.
3.5.2 Age Based Compliance Rates
In previous section, we assume the compliance rate is the same across all age groups. However, this is unlikely to be the case so we estimate compliance rates based on age (showed in Table 16). The compliance rates are extracted from a survey conducted by Gfk.com, under the National Institute of Health grant no. 1R01GM109718. This survey collects data on demographics of the respondents and their preventive health behaviors during a hypothetical influenza outbreak. We categorize survey respondents into four age groups corresponding to the age groups used in this paper and estimate their compliance to vaccination.
Table 16.
Compliance rates based on age
| subgroup | CMPL |
|---|---|
| preschool | 0.65 |
| school | 0.53 |
| adult | 0.54 |
| senior | 0.66 |
The new average compliance rate is 52%. If we still assume the vaccination coverage is 50%, the vaccine supply will be enough to meet the needs of almost everyone, so in order to observe the effect of different vaccine prioritization, we assume the vaccination coverage is 30%, i.e. only 43288 vaccines are available. The vaccinated fraction table (similar to Table 14) is shown in Table 17. It considers both vaccination coverage and compliance rate across each age group. S3421 is exactly the same with S3241.
Table 17.
Vaccinated fraction of each age group under different vaccination strategies (based on age based compliance).
| subgroup (size) | Snp | S4321 | S3421 | S2134 | S4231 | S3241 |
|---|---|---|---|---|---|---|
| preschool (4617) | 0.3 | 0 | 0 | 0.65 | 0 | 0 |
| school (13310) | 0.3 | 0 | 0 | 0.53 | 0.53 | 0 |
| adult (52558) | 0.3 | 0.35 | 0.44 | 0.25 | 0.22 | 0.44 |
| senior (7335) | 0.3 | 0.66 | 0 | 0 | 0.66 | 0 |
1-preschool, 2-school, 3-adult, 4-senior; Snp denotes strategy with no priority; S4321 denotes sequentially vaccinating seniors first, then adults, then school-aged and then preschoolers, according to their priorities. If after vaccines are given to an age group based on its compliance rate, there are vaccines remaining, then the next age group on the priority list is considered. Similarly strategies S3421, S2134, S4231, S3241 follow priorities given by their subscripts. Note that S3421 and S3241 result in the same allocation because adult group has the first priority and it has more people than the size of the vaccine stockpile so no other age group could be vaccinated.
The results are listed in Table 18. The death rate, net return per dollar spent, and attack rate are directly comparable. We can still observe that the optimal strategy is S2134 in terms of all measures and following by S4231 and Snp. The observation is consistent with the former results where the compliance rate is assumed to be uniform.
Table 18.
Performance of different vaccination strategies
| strategy | (%) |
|
(M$) | ($) | (%) | |
|---|---|---|---|---|---|---|
| Snp | 0.020946 | 16.30 | 89.85 | 126.57 | 11.18 | |
| S4321 | 0.029427 | 22.90 | 76.47 | 104.50 | 21.02 | |
| S3421 | 0.032254 | 25.10 | 79.35 | 107.95 | 18.40 | |
| S2134 | 0.009766 | 7.60 | 102.07 | 148.69 | 3.61 | |
| S4231 | 0.013279 | 10.33 | 97.38 | 141.12 | 7.79 | |
| S3241 | 0.032254 | 25.10 | 79.35 | 107.95 | 18.40 |
Low values of (%), , (%) are desirable and high values of ($), (million $) are desirable. Values in bold are optimal.
3.6 Public Health Policy Implications
The public health authorities often publish recommendations of interventions to the population. In case of limited resources, e.g. when vaccines are not enough to satisfy the needs of the whole population, some subpopulations are given higher priorities, to optimize the efficiency of interventions towards specific objectives of containing the epidemic.
Through the simulation results, we observe that school age group is much more critical than other age groups, and a vaccination strategy targeting school age group first can maximize net returns and improve herd immunity. School-aged children tend to have longer contact times with each other and form dense subnetworks at school locations; thus the epidemic spreads faster and more easily within the school age group. If the school age group receives no vaccine or few vaccines, the highly connected subnetworks of students continue to be able to spread the disease among students, impeding the intervention strategy to effectively reduce overall infections and costs. On the other hand, if the school-aged group is well vaccinated, the epidemic is effectively contained not only in this group but across all groups.
3.7 Limitations
This computational framework makes several assumptions about parameter settings. For example, in health and economic disparity study, it assumes that individuals follow the same compliance rate within a cohort and it is forced to be the same across cohorts. In vaccination strategy study, we relax the assumption and make the compliance rate follow a realistic distribution based on age. However, these parameter settings may not correspond to any specific scenario in the real world. Our goal is to provide a framework that can be used to study hypothetical scenarios to support planning, response and decision-making during epidemic outbreaks.
4 Conclusions
In this paper, we build a computational framework that provides a generic methodology for finding health and economic disparities among cohorts based on individual level features. We apply this framework to study disparities with respect to age and income during an influenza epidemic in the Montgomery county of Southwest Virginia. In one scenario, no interventions are applied to control the epidemic and in other scenarios vaccine-based intervention is applied to cohorts that are split by age and income.
We use an agent based disease propagation model to study the transmission dynamics of influenza on the social network. The infected cases are then assigned different clinical outcomes and cost of treatment depending on the severity of clinical outcome. Various vaccine allocation strategies are designed and simulated in this study.
Our results show significant health disparities across age groups and income groups, and economic disparities among age groups. The metrics for measuring the outcome disparities include attack rate, death rate, and death count. The metrics for measuring economic disparities include net return per capita, net return per vaccinated, and net return per dollar spent. We also find that in a severe flu season with a limited vaccination coverage, if vaccines are assigned randomly without priorities, then the intervention is least effective for the school aged cohort. Given the high connectivity of school aged children in the social contact network, they will be at a disadvantage if the vaccine assignment is completely random. After measuring performances of vaccination prioritization strategies under both simulated and realistic scenarios, the strategy that prioritizes the school aged children maximizes the normalized net returns and minimizes attack rate and death rate.
Table 2.
Notations and their meanings
| Notation | Meaning | |
|---|---|---|
| G(V, E, w) | A contact network | |
| V, E | The sets of nodes, edges | |
| w(u, v) | The contact duration of node u with node v on the day | |
| p(w(u, v)) | The probability of disease transmits from node u to node v during w(u, v) | |
| τ (v) | The health states of node v during the epidemic period | |
| tS→E (v) | The day when v becomes exposed | |
| tS→I (v) | The day when v becomes infectious | |
| tI→R(v) | The day when v becomes recovered | |
| ΔtE (v) | Incubation period of node v | |
| ΔtI (v) | Infectious period of node v | |
| NR | Net return | |
| Ci | The cost of an infected individual i | |
|
|
The cost of vaccinating individual k | |
|
|
Net return per capita (average net return per capita) | |
|
|
Net return per dollar spent (average net return per dollar spent) | |
|
|
Net return per vaccinated person (average net return per vaccinated person) | |
|
|
Total net return (average total net return) | |
|
|
Attack rate or cumulative infection rate (average attack rate) | |
|
|
Death rate (average death rate) | |
|
|
Hospitalization rate (average hospitalization rate) | |
|
|
Outpatient rate (average outpatient rate) | |
|
|
Ill but not seeking medical care rate (average ill rate) | |
| CMPL | Compliance rate for vaccination | |
|
|
Death count (average death count) |
Acknowledgments
This work has been partially supported by the National Institutes of Health (NIH) (grant number 1R01GM109718), NSF Research Traineeship (grant number NRT-DESE-154362), Defense Threat Reduction Agency (DTRA) (grant number HDTRA1-11-1-0016), and DTRA Comprehensive National Incident Management System contracts (grant number HDTRA1-11-D-0016-0001, grant number HDTRA1-17-D-0023).
A Supplementary Data
Distribution of risk level
The high risk individuals encounter a different distribution of clinical outcomes than non-high risk individuals. For instance, high-risk individuals have a higher probability of hospitalization or death compared to non-high risk individuals. High-risk can be caused by many factors; it could be due to preexisting conditions; age; occupation e.g. health care worker or emergency worker; immuno-compromised health condition; pregnancy etc. We determine high risk or non-high risk based on the data from Meltzer et al. [32].
Distribution of health outcomes
The clinical outcomes resulting from influenza infection are: death; hospitalization; outpatient; and ill but not seeking medical care. Work by Meltzer et al. [32] provides the distribution of health states per 1,000 people and clinical outcome rates per 1,000 cases. We use our simulation model to determine the health states and case counts but use the clinical outcome rates given by [32] for age groups (0 to 19 years, 20 to 64 years, and 65 years and older) and risk conditions (high risk and non-high risk). Table 20 shows the outcome rates on age groups and risk conditions.
Cost of health outcomes
Data on costs are collected from Carias et al. [12] for different clinical outcomes for cohorts characterized by age and underlying risk condition (Table 21). The population was divided into age categories that are distinct with respect to economic activity and health care-related costs: 6 months–4 year olds; 5–19 year olds; 20–64 year olds; and above 65 years. For each age cohort, costs were calculated for high-risk and non-high risk individuals.
In Table 21, direct costs are the medical costs associated with the clinical outcome as well as the cost of vaccination. Indirect costs are the productivity loss due to illness. The total costs are the sum of direct and indirect costs. All costs are in 2016 USD.
Table 19.
Percentage of population at high/non-high risk level(%)
| Age | High risk | Non–high risk |
|---|---|---|
| 0–19 | 6.4 | 93.6 |
| 20–64 | 14.4 | 85.6 |
| 65+ | 40 | 60 |
Table 20.
Clinical outcome rates for high-risk and non-high risk (%)
| Variable High risk | Death | Hospitalization | Outpatient | Ill |
|---|---|---|---|---|
| High risk | ||||
| 0–19 | 0.76 | 1.37 | 89.15 | 8.72 |
| 20–64 | 1.29 | 1.46 | 61.50 | 35.76 |
| 65+ | 2.63 | 5.09 | 66.90 | 25.39 |
| Non-high risk | ||||
| 0–19 | 0.01 | 0.37 | 50.95 | 48.66 |
| 20–64 | 0.03 | 0.68 | 35.15 | 64.14 |
| 65+ | 0.34 | 1.42 | 38.20 | 60.04 |
Table 21.
Economic cost ($)
| Variable | Direct (medical cost) |
Indirect (productivity losses) |
Total |
|---|---|---|---|
| Death | |||
| High risk | |||
| 0–4 | 51078.87 | 1391426.07 | 1442504.94 |
| 5–19 | 208758.81 | 1651810.98 | 1860569.79 |
| 20–64 | 79726.86 | 862321.26 | 942048.12 |
| 65+ | 49734.66 | 240579.18 | 290313.84 |
| Non-high risk | |||
| 0–4 | 54766.29 | 1391426.07 | 1446192.36 |
| 5–19 | 185465.46 | 1651810.98 | 1837276.44 |
| 20–64 | 73453.14 | 862321.26 | 935774.4 |
| 65+ | 36642.21 | 240579.18 | 277221.39 |
| Hospitalization | |||
| High risk | |||
| 0–4 | 23230.08 | 1165.5 | 24395.58 |
| 5–19 | 44744.1 | 1665 | 46409.1 |
| 20–64 | 32776.08 | 1998 | 34774.08 |
| 65+ | 21199.89 | 1298.7 | 22498.59 |
| Non-high risk | |||
| 0–4 | 10422.9 | 832.5 | 11255.4 |
| 5–19 | 21376.38 | 1165.5 | 22541.88 |
| 20–64 | 25037.16 | 1332 | 26369.16 |
| 65+ | 14084.79 | 909.09 | 14993.88 |
| Outpatient | |||
| High risk | |||
| 0–4 | 669.33 | 166.5 | 835.83 |
| 5–19 | 935.73 | 333 | 1268.73 |
| 20–64 | 738.15 | 166.5 | 904.65 |
| 65+ | 2877.12 | 259.74 | 3136.86 |
| Non-high risk | |||
| 0–4 | 376.29 | 166.5 | 542.79 |
| 5–19 | 307.47 | 166.5 | 473.97 |
| 20–64 | 468.42 | 166.5 | 634.92 |
| 65+ | 1023.42 | 259.74 | 1283.16 |
| Ill (no medical care) | |||
| High risk | |||
| 0–4 | 4.44 | 166.5 | 170.94 |
| 5–19 | 4.44 | 83.25 | 87.69 |
| 20–64 | 4.44 | 83.25 | 87.69 |
| 65+ | 4.44 | 129.87 | 134.31 |
| Non-high risk | |||
| 0–4 | 4.44 | 166.5 | 170.94 |
| 5–19 | 4.44 | 83.25 | 87.69 |
| 20–64 | 4.44 | 83.25 | 87.69 |
| 65+ | 4.44 | 129.87 | 134.31 |
Contributor Information
Lijing Wang, Email: lijingw9@vt.edu, Department of Computer Science, Virginia Tech, Network Dynamics and Simulation Science Laboratory, Biocomplexity Institute of Virginia Tech, Blacksburg, VA 24061 USA.
Jiangzhuo Chen, Email: chenj@vt.edu, Network Dynamics and Simulation Science Laboratory, Biocomplexity Institute of Virginia Tech, Blacksburg, VA 24061, USA.
Achla Marathe, Email: amarathe@vt.edu, Department of Agricultural and Applied Economics, Virginia Tech, Network Dynamics and Simulation Science Laboratory, Biocomplexity Institute of Virginia Tech, Blacksburg, VA 24061 USA.
References
- 1.Badham J, Stocker R. The impact of network clustering and assortativity on epidemic behaviour. Theor Popul Biol. 2010;77(1):71–75. doi: 10.1016/j.tpb.2009.11.003. [DOI] [PubMed] [Google Scholar]
- 2.Bailey NTJ. The Mathematical Theory of Infectious Diseases and Its Applications. 2nd. Griffin; 1975. [Google Scholar]
- 3.Barrett C, Bisset K, Leidig J, Marathe A, Marathe M. Economic and social impact of influenza mitigation strategies by demographic class. Epidemics. 2011;3(1):19–31. doi: 10.1016/j.epidem.2010.11.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Barrett CL, Beckman RJ, Khan M, Kumar VSA, Marathe MV, Stretz PE, Dutta T, Lewis B. Generation and analysis of large synthetic social contact networks. Proceedings of the 2009 Winter Simulation Conference (WSC) 2009:1003–1014. [Google Scholar]
- 5.Beckman RJ, Baggerly KA, McKay MD. Creating synthetic baseline populations. Transportation Research Part A: Policy and Practice. 1996;30(6):415–429. [Google Scholar]
- 6.Biggerstaff M, Reed C, Swerdlow DL, Gambhir M, Graitcer S, Finelli L, Borse RH, Rasmussen SA, Meltzer MI, Bridges CB. Estimating the potential effects of a vaccine program against an emerging influenza pandemic, United States. Clinical infectious diseases. 2015;60:S20–S29. doi: 10.1093/cid/ciu1175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bisset K, Marathe M. A cyber-environment to support pandemic planning and response. DOE SciDAC Magazine. 2009:36–47. [Google Scholar]
- 8.Bisset KR, Chen J, Feng X, Kumar VA, Marathe MV. Proceedings of the 23rd International Conference on Supercomputing. ACM; New York, NY, USA, ICS ’09: 2009. EpiFast: A fast algorithm for large scale realistic epidemic simulations on distributed memory systems; pp. 430–439. [Google Scholar]
- 9.Borse RH, Shrestha SS, Fiore AE, Atkins CY, Singleton JA, Furlow C, Meltzer MI. Effects of vaccine program against pandemic influenza A(H1N1) virus, United States 2009-2010. 2013;19(3):439. doi: 10.3201/eid1903.120394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bridges CB, Thompson WW, Meltzer MI, Reeve GR, Talamonti WJ, Cox NJ, Lilac HA, Hall H, Klimov A, Fukuda K. Effectiveness and cost-benefit of influenza vaccination of healthy working adults: A randomized controlled trial. JAMA. 2000;284(13):1655–1663. doi: 10.1001/jama.284.13.1655. [DOI] [PubMed] [Google Scholar]
- 11.Bureau of Labor Statistics. American time use survey. 2017 https://www.bls.gov/tus/
- 12.Carias C, Reed C, Kim IK, Foppa IM, Biggerstaff M, Meltzer MI, Finelli L, Swerdlow DL. Net costs due to seasonal influenza vaccinationunited states, 2005–2009. PloS one. 2015;10(7):e0132,922. doi: 10.1371/journal.pone.0132922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Carrat F, Vergu E, Ferguson NM, Lemaitre M, Cauchemez S, Leach S, Valleron AJ. Time lines of infection and disease in human influenza: a review of volunteer challenge studies. American Journal of Epidemiology. 2008;167(7):775–85. doi: 10.1093/aje/kwm375. [DOI] [PubMed] [Google Scholar]
- 14.Chen J, Chu S, Chungbaek Y, Khan M, Kuhlman C, Marathe A, Mortveit H, Vullikanti A, Xie D. Effect of modelling slum populations on influenza spread in delhi. BMJ Open. 2016;6(9) doi: 10.1136/bmjopen-2016-011699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Committee NVA. Strategies to achieve the healthy people 2020 annual influenza vaccine coverage goal for health-care personnel: Recommendations from the national vaccine advisory committee. Public Health Reports. 2013;128(1):7–25. [PMC free article] [PubMed] [Google Scholar]
- 16.Dorratoltaj N, Marathe A, Lewis BL, Swarup S, Eubank SG, Abbas KM. Epidemiological and economic impact of pandemic influenza in chicago: Priorities for vaccine interventions. PLoS computational biology. 2017;13(6):e1005,521. doi: 10.1371/journal.pcbi.1005521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Eichner M, Schwehm M, Eichner L, Gerlier L. Direct and indirect effects of influenza vaccination. BMC Infectious Diseases. 2017;17(1):308. doi: 10.1186/s12879-017-2399-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Eubank S, Guclu H, Kumar VA, Marathe MV, Srinivasan A, Toroczkai Z, Wang N. Modelling disease outbreaks in realistic urban social networks. Nature. 2004;429(6988):180–184. doi: 10.1038/nature02541. [DOI] [PubMed] [Google Scholar]
- 19.Glezen WP, Gaglani MJ, Kozinetz CA, Piedra PA. Direct and indirect effectiveness of influenza vaccination delivered to children at school preceding an epidemic caused by 3 new influenza virus variants. J Infect Dis. 2010;202(11):1626–1633. doi: 10.1086/657089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Grohskopf LA, Sokolow LZ, Broder KR, Olsen SJ, Karron RA, Jernigan DB, Bresee JS. Prevention and control of seasonal influenza with vaccines. MMWR Recommendations and Reports. 2016;65(5):1–54. doi: 10.15585/mmwr.rr6505a1. [DOI] [PubMed] [Google Scholar]
- 21.Halloran EM, Ferguson NM, Eubank S, Longini IM, Cummings DA, Lewis B, Xu S, Fraser C, Vullikanti A, Germann TC, et al. Modeling targeted layered containment of an influenza pandemic in the united states. Proceedings of the National Academy of Sciences. 2008;105(12):4639–4644. doi: 10.1073/pnas.0706849105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Halloran ME, Longini IM, Cowart DM, Nizam A. Community interventions and the epidemic prevention potential. Vaccine. 2002;20(27–28):3254–3262. doi: 10.1016/s0264-410x(02)00316-x. [DOI] [PubMed] [Google Scholar]
- 23.Health People. Disparities. 2016 Available at https://www.healthypeople.gov/2020/about/foundation-health-measures/disparities, accessed September 1, 2016.
- 24.Kang GJ, Ewing-Nelson SR, Mackey L, Schlitt JT, Marathe A, Abbas KM, Swarup S. Semantic network analysis of vaccine sentiment in online social media. Vaccine. 2017 doi: 10.1016/j.vaccine.2017.05.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.King JCJ, Beckett D, Snyder J, Cummings GE, King BS, Magder LS. Direct and indirect impact of influenza vaccination of young children on school absenteeism. Vaccine. 2012;30(2):289–293. doi: 10.1016/j.vaccine.2011.10.097. [DOI] [PubMed] [Google Scholar]
- 26.Kostova D, Reed C, Finelli L, Cheng PY, Gargiullo PM, Shay DK, Singleton JA, Meltzer MI, Lu Pj, Bresee JS. Influenza illness and hospitalizations averted by influenza vaccination in the united states, 2005–2011. PLoS ONE. 2013;8(6):1–8. doi: 10.1371/journal.pone.0066312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kuznetsov YA, Piccardi C. Bifurcation analysis of periodic seir and sir epidemic models. Journal of Mathematical Biology. 1994;32(2):109–121. doi: 10.1007/BF00163027. doi: 10.1007/BF00163027. URL . [DOI] [PubMed] [Google Scholar]
- 28.Lee PY, Matchar DB, Clements DA, Huber J, Hamilton JD, Peterson ED. Economic analysis of influenza vaccination and antiviral treatment for healthy working adults. Ann Intern Med. 2002;137(4):225–231. doi: 10.7326/0003-4819-137-4-200208200-00005. [DOI] [PubMed] [Google Scholar]
- 29.Longini IM, Halloran ME, Nizam A, Wolff M, Mendelman PM, Fast PE, Belshe RB. Estimation of the efficacy of live, attenuated influenza vaccine from a two-year, multi-center vaccine trial: implications for influenza epidemic control. Vaccine. 2000;18(18):1902–1909. doi: 10.1016/s0264-410x(99)00419-3. [DOI] [PubMed] [Google Scholar]
- 30.Marathe A, Lewis B, Barrett C, Chen J, Marathe M, Eubank S, Ma Y. Comparing effectiveness of top-down and bottom-up strategies in containing influenza. PLoS ONE. 2011;6:e25,149. doi: 10.1371/journal.pone.0025149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Marathe A, Lewis B, Chen J, Eubank S. Sensitivity of household transmission to household contact structure and size. PLoS ONE. 2011;6 doi: 10.1371/journal.pone.0022461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Meltzer MI, Cox NJ, Fukuda K. The economic impact of pandemic influenza in the united states: priorities for intervention. Emerg Infect Dis. 1999;5(5):659–671. doi: 10.3201/eid0505.990507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Meltzer MI, Neuzil KM, Griffin MR, Fukuda K. An economic analysis of annual influenza vaccination of children. Vaccine. 2005;23(8):1004–1014. doi: 10.1016/j.vaccine.2004.07.040. [DOI] [PubMed] [Google Scholar]
- 34.Molinari NAM, Ortega-Sanchez IR, Messonnier ML, Thompson WW, Wortley PM, Weintraub E, Bridges CB. The annual impact of seasonal influenza in the us: Measuring disease burden and costs. Vaccine. 2007;25(27):5086–5096. doi: 10.1016/j.vaccine.2007.03.046. [DOI] [PubMed] [Google Scholar]
- 35.Monto AS, Davenport FM, Napier JA, Francis TJ. Effect of vaccination of a school-age population upon the course of an A2-Hong Kong influenza epidemic. Bull World Health Organ. 1969;41(3):537–542. [PMC free article] [PubMed] [Google Scholar]
- 36.Moreno Y, Pastor-Satorras R, Vespignani A. Epidemic outbreaks in complex heterogeneous networks. The European Physical Journal B - Condensed Matter and Complex Systems. 2002;26(4):521–529. [Google Scholar]
- 37.Mullooly JP, Bennett MD, Hornbrook MC, Barker WH, Williams WW, Patriarca PA, Rhodes PH. Influenza vaccination programs for elderly persons: cost-effectiveness in a health maintenance organization. Ann Intern Med. 1994;121(12):947–952. doi: 10.7326/0003-4819-121-12-199412150-00008. [DOI] [PubMed] [Google Scholar]
- 38.NDSSL. Synthetic data of Montgomery county. Virginia: 2014. http://ndssl.vbi.vt.edu/synthetic-data/ [Google Scholar]
- 39.Presanis AM, De Angelis D, Hagy A, Reed C, Riley S, Cooper BS, Finelli L, Biedrzycki P, Lipsitch M, The New York City Swine Flu Investigation Team The severity of pandemic H1N1 influenza in the United States, from April to July 2009: A bayesian analysis. PLoS Med. 2009;6(12):1–12. [Google Scholar]
- 40.Prosser LA, Bridges CB, Uyeki TM, Hinrichsen VL, Meltzer MI, Molinari NAM, Schwartz B, Thompson WW, Fukuda K, Lieu TA. Health benefits, risks, and cost-effectiveness of influenza vaccination of children. 2006;12(10):1548. doi: 10.3201/eid1210.051015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Reed C, Chaves SS, Daily Kirley P, Emerson R, Aragon D, Hancock EB, Butler L, Baumbach J, Hollick G, Bennett NM, Laidler MR, Thomas A, Meltzer MI, Finelli L. Estimating influenza disease burden from population-based surveillance data in the united states. PLoS ONE. 2015;10(3):1–13. doi: 10.1371/journal.pone.0118369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Sander B, Nizam A, Garrison LP, Postma MJ, Halloran ME, Longini IM. Economic evaluation of influenza pandemic mitigation strategies in the united states using a stochastic microsimulation transmission model. Value in Health. 2009;12(2):226–233. doi: 10.1111/j.1524-4733.2008.00437.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Sydenstricker E. The incidence of influenza among persons of different economic status during the epidemic of 1918. 1931. Public Health Rep. 2006;121(Suppl 1):191–204. [PubMed] [Google Scholar]
- 44.Tsang TK, Lau LL, Cauchemez S, Cowling BJ. Household transmission of influenza virus. Trends in Microbiology. 2016;24(2):123–133. doi: 10.1016/j.tim.2015.10.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.WHO. Influenza (season) fact sheet. 2016 http://www.who.int/mediacentre/factsheets/fs211/en/, accessed September 1, 2016.


