Multi-modal Image Fusion for Multispectral Super-resolution in Microscopy

Abstract

Spectral imaging is a ubiquitous tool in modern biochemistry. Despite acquiring dozens to thousands of spectral channels, existing technology cannot capture spectral images at the same spatial resolution as structural microscopy. Due to partial voluming and low light exposure, spectral images are often difficult to interpret and analyze. This highlights a need to upsample the low-resolution spectral image by using spatial information contained in the high-resolution image, thereby creating a fused representation with high specificity both spatially and spectrally. In this paper, we propose a framework for the fusion of co-registered structural and spectral microscopy images to create super-resolved representations of spectral images. As a first application, we super-resolve spectral images of retinal tissue imaged with confocal laser scanning microscopy, by using spatial information from structured illumination microscopy. Second, we super-resolve mass spectroscopic images of mouse brain tissue, by using spatial information from high-resolution histology images. We present a systematic validation of model assumptions crucial towards maintaining the original nature of spectra and the applicability of super-resolution. Goodness-of-fit for spectral predictions are evaluated through functional R² values, and the spatial quality of the super-resolved images are evaluated using normalized mutual information.

1. INTRODUCTION

The chemical nature of a biological sample is often investigated through various microscopic spectral imaging modalities such as fluorescence, mass spectroscopy, and others.¹ These methodologies allow for the spatial localization of bio-chemical sources which may be crucial to specific applications. However, they may have poor spatial resolution due to physics-based limitations, such as spreading a relatively small number of photons over multiple spectral channels for example. Conversely, high resolution structural modalities provide unparalleled spatial detail but can lack spectral specificity. This has led to several lines of research attempting to super-resolve the spectral images by leveraging spatial information in a co-registered structural modality.

Image fusion has been studied extensively in the satellite imaging community, ² fusing information from cameras of high spatial resolution and high spectral resolution. The medical image analysis literature focuses largely on transferring details between structural modalities measuring disparate properties. This can be either macroscopic such as with MR and CT,³ or microscopic such as with scanning acoustic microscopy and histology.⁴ However, there has been a recent emergence of work for the fusion of microscopic spectral images and structural images. Van de Plas, et al.⁵ fuse imaging mass spectrometry (IMS) and high-resolution color histology (H&E) images by using multivariate regression and feature engineering. This method uses spectral channels with high SNR only, and cannot accommodate single channel structural images. Vollnhals, et al.⁶ combine electron microscopy with IMS by creating image pyramids and injecting the high-frequency structural image components into the spectral image pyramid. This can cause unwanted artifacts when combining images of different modalities, as reported by the authors.

In this paper, we propose a framework for the super-resolution of multispectral images by using a blind linear degradation model from remote sensing which uses information in a corresponding co-registered structural image. The adopted framework has a secondary denoising effect. We show the potential of the proposed framework to two challenging biomedical applications, where both spatial and spectral information are important. To test the assumptions of the linear degradation model, we validate the predictions of the model using functional R² values and perform a residual analysis, finding a high degree of agreement with observed data. As the parameters of the blind model are unintuitive to tune by hand for disparate imaging modalities, we perform a principled blind parameter search using Bayesian optimization.⁷ The spatial quality of the resulting images is evaluated by using normalized mutual information with respect to the structural image.

2. MATERIALS AND METHODS

2.1. Data Description

In our first dataset, human tissue from the retinal pigment epithelium was imaged by two different fluorescence microscopy modalities excited at 488 nm. The first is Structured Illumination Microscopy (SIM), a form of 3D fluorescence microscopy with twice the resolution of diffraction-limited instruments. The second is confocal Laser Scanning Microscopy (LSM), which in addition to volumetric data, can capture 24 spectral channels over the visible spectrum for each voxel, thus acquiring 4D data. The first and last spectral channels of the LSM data are discarded due to noise. No external fluorescent label was added, and thus these images correspond to autofluorescence measurements. For more details, see Ach, et al.⁸ In this study, we focus on spectral super-resolution at the slice level, leaving a fully 3D treatment as future work.

For the second experiment, we use cropped sample data provided by Van de Plas, et al.⁵ This consists of a high-resolution RGB image of a mouse brain H&E section and a corresponding IMS image. The IMS image is 20 times smaller than the RGB image, with 7945 spectral channels corresponding to mass over charge (m/z) bins.

2.2. Image Registration

For LSM-SIM registration, a reference spectral channel was chosen (600 nm) from the LSM volume, and 3D affine registration with normalized cross correlation as an image matching metric was performed. Corresponding 2D slices out of 4D and 3D data are used in this paper. For IMS-histology registration, scalar images of both modalities are formed via a mean projection and registered with 2D affine registration using normalized cross-correlation. All registrations were computed with the SimpleITK library.⁹ In both cases, non-rigid registration was skipped so as to not affect the estimated blurring kernels.

2.3. Fusion Methodology

We adopt the well-established linear degradation model used in remote sensing for our problem.² Let the multispectral image have p channels and m total pixels in each channel. Let the high-resolution image have c channels and n pixels in each channel. Each channel in both modalities is vectorized, thereby converting an image with two dimensions of space and one of spectra into a matrix. The model is as follows,

$$\begin{gathered} {\mathbf{Y}}_{\mathbf{M}}=\mathbf{Z}\mathrm{B}\mathrm{S}+{\mathbf{N}}_{\mathbf{M}} \\ {\text{y}}_{\text{P}}=\text{rZ}+{\text{n}}_{\text{P}} \end{gathered}$$

where,

$$\begin{gathered} {\mathbf{Y}}_{\text{M}}\in {ℝ}^{p\times m}\text{is the original spectral image,} \\ \mathbf{Z}\in {ℝ}^{p\times n}\text{is the target fused image}, \\ \mathbf{B}\in {ℝ}^{n\times n}\text{is the blurring matrix,} \\ \mathbf{S}\in {ℝ}^{n\times m}\text{is a downsampling matrix,} \\ {\mathbf{\text{y}}}_{\mathbf{\text{P}}}\in {ℝ}^{c\times n}\text{is the original structural image,} \\ \mathbf{r}\in {ℝ}^{c\times p}\text{is the spectral response of the structural image,} \\ {\mathbf{N}}_{\mathbf{\text{M}}}\in {ℝ}^{p\times m}\text{is the reconstruction noise for the spectral image,} \\ {\mathbf{n}}_{\mathbf{\text{P}}}\in {ℝ}^{c\times n}\text{is the reconstruction noise flor the structural image}. \end{gathered}$$

Using the approach of Wei, et al.,¹⁰ we break the problem of estimating B, r and Z for both modalities into two separate stages. First, we estimate B, r by using the method proposed by Simões, et al.¹¹ via the convex minimization of the following objective function,

$$\underset{\mathbf{B},\mathbf{r}}{\min }{\Vert \mathbf{r}{\mathbf{Y}}_M-{\mathbf{y}}_P\mathbf{B}\mathbf{S}\Vert }_2^2+{\lambda }_b{\varphi }_b(\mathbf{B})+{\lambda }_r{\varphi }_r(\mathbf{r}),$$

where ϕ_b and ϕ_r are quadratic regularizers and λ_b and λ_r are their respective weights. S is easily estimated from the dimensions of the co-registered data. We then estimate the target fused image using the method proposed by Wei, et al.¹² for robust fast fusion via solving the following problem,

$$\arg \underset{\mathbf{Z}}{\min }\frac{1}{2}{\Vert {\mathbf{Y}}_{\text{M}}-\mathbf{Z}\mathrm{B}\mathrm{S}\Vert }_F^2+\frac{1}{2}{\Vert {\mathbf{y}}_{\mathbf{P}}-\mathbf{r}\mathrm{Z}\Vert }_2^2+\lambda \Vert \mathbf{Z}-\overline{\mathbf{Z}}{\Vert }_F^2,$$

where the third term acts as a regularizer, corresponding to a Gaussian prior over the target fused image where $\overline{Z}$ is the prior mean. Importantly, these methods rely on the assumption that the target fused image Z lies in a low-dimensional subspace.

2.4. Bayesian Parameter Optimization

As opposed to remote sensing, we do not have any heuristics on parameter tuning in the image fusion optimization for vastly different microscopy modalities. Therefore, we take a principled approach to blind parameter selection. For both sets of images, the three regularization parameters and blurring kernel widths were tuned by using Bayesian optimization for parameter selection,⁷ by maximizing the normalized mutual information (NMI) between the fused image and the high-resolution structural image. NMI is a common measure of image matching when comparing co-registered multi-modal images. By selecting parameters that maximize it, we ensure that our fused image is close to the quality of the high-resolution structural image. All results reported have had their parameters tuned in this manner, with thirty evaluations via Bayesian optimization.

2.5. Validation Methodology

A common goodness-of-fit measure is R². We create prediction and observation pairs by mapping each pixel of the original spectral image to the center of the corresponding patch in the generated image. As each pixel has a spectrum, we consider each pixel as an observation and each spectrum as a functional measurement. Inspired by common practice in functional data analysis,¹³ we report the per-pixel R² measure for an pixel spectrum, defined as,

$$R_i^2=1-\frac{{\sum }_{j=1}^p{\left({\widehat{y}}_i(j)-y_i(j)\right)}^2}{{\sum }_{j=1}^p{\left(y_i(j)-{\overline{y}}_i(j)\right)}^2}$$

where i is the pixel index, j is the spectral channel index, y_i is the observation, ${\widehat{y}}_i$ is the predicted value and ${\overline{y}}_i$ is the mean of the observed values. We also report the per-channel R² as,

$$R^2(j)=1-\frac{{{\sum }_{i=1}^n\left({\widehat{y}}_i(j)-y_i(j)\right)}^2}{{{\sum }_{j=1}^n\left(y_i(j)-{\overline{y}}_i(j)\right)}^2}.$$

To inspect whether the model misses systematic variation, we perform a residual analysis. We finally report a qualitative measure of the super-resolved image by using NMI with respect to the high-resolution image.

3. RESULTS

3.1. LSM and SIM

A 328 × 328 × 22 LSM image stack is upsampled by a co-registered 1312 × 1312 SIM image via the proposed image fusion framework. Using dataset 1 in Fig. 1 as an example, the average per-channel NMI between the original LSM and SIM images is 0.2205, whereas the super-resolved image has an NMI of 0.6874 indicating higher spatial similarity to the high-resolution image. We find a per-channel R² of 0.3853 and a per-pixel R² of 0.4973. While these values are lower than the subsequent experiment, this is easily explained as the original spectra are much noisier (see Fig. 1, Col. 4 for an overlay of raw spectra). Hence, as predictions are denoised, they explain a smaller portion of the total variation which consisted of the noise as well. Importantly, the mean prediction matches the mean observation (Fig. 1, Col. 4).

Figure 1.

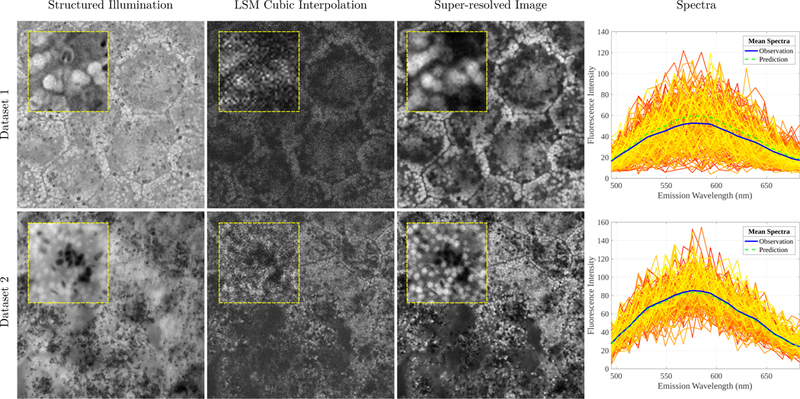
Results from two datasets (rows 1 and 2) of co-registered LSM and SIM images. Column 1: The high-resolution SIM image. Column 2: A reference channel of the LSM image upsampled with cubic interpolation. Column 3: The super-resolved image using the proposed framework. Best case reference channels are shown. Yellow-framed insets show improved resolution using the proposed framework. Column 4: Raw observed spectra from segmented granules showing a high degree of noise. Their mean spectra are reported in blue and the mean prediction of the model is shown in green.

3.2. IMS and H&E

We super-resolve a 20 × 20 × 7945 IMS image stack to a 400 × 400 × 7945 image stack by using spatial information from a 400 × 400 × 3 histology image. We find a pixel-wise average R² of 0.6943 and a channel-wise average R² of 0.8493, indicating excellent agreement with the data overall. The average per-channel residuals have a mean and standard deviation of –5.36 × 10^–4 and 1.7 × 10^–3. The per-channel statistics of the data itself have a mean of 0.1451 and standard deviation of 0.2233, which are orders of magnitude higher than the residual statistics, signifying small error. The average per-channel NMI between the interpolated IMS and histology images is 0.2394, whereas the super-resolved image has an NMI of 0.2401. Instead of using 7945 channels, we can compute NMI on only high SNR channels.⁵ This computes an NMI to the structural image of 0.4072 via cubic interpolation and 0.4322 via super-resolution, indicating higher average structural similarity with the super-resolution.

4. DISCUSSION

The presented model uses a linear approach for estimating spectral responses. It is possible that there may be non-linear models that better fit specific image modality-pairs. Future work will explore and validate the various nonlinear models that might better describe the relationships between the specific modalities presented in this paper. Specific to IMS images, the number of features (m/z bins) exceeds the number of observations (pixels). In this case, more robust super-resolution results may be obtained by incorporating Elastic Net-style regularization¹⁴ into the optimization process. Finally, there has been a recent emergence of deep learning based approaches for spectral image super-resolution via image fusion in remote sensing. Currently, these methods are either supervised,¹⁵ or require a known spectral response,¹⁶ precluding their direct application to this work.

Multispectral super-resolution via image fusion can potentially be used in biomedical research for better spatial localization of chemical signatures, past the resolving ability of spectral imaging systems. Furthermore, it can benefit image analysis pipelines by providing a high-quality reference for segmentation of features which might not be present in the structural image and vice-versa.

Figure 2.

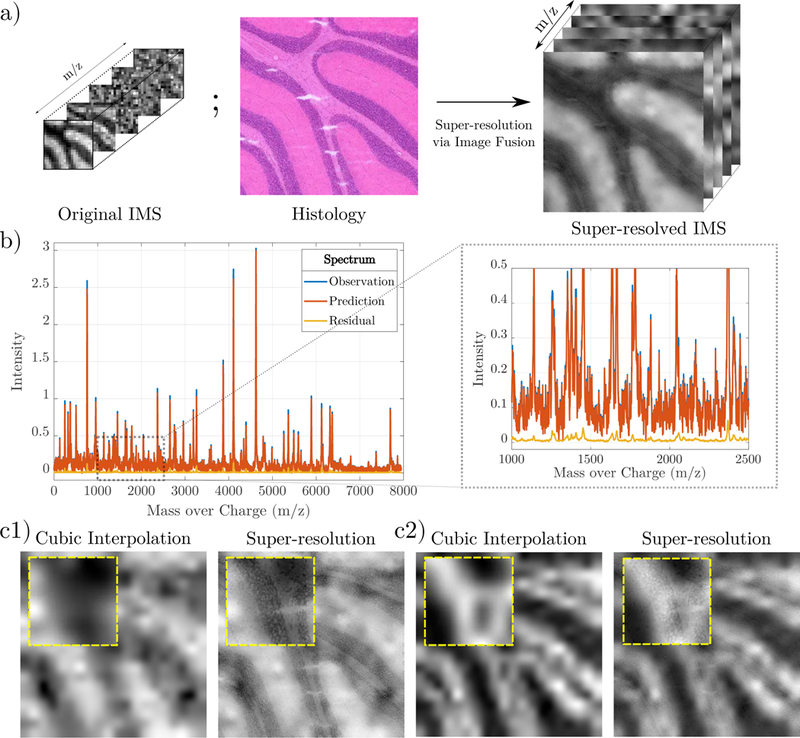
a) An overview of the super-resolution pipeline. Spectral information from IMS and spatial information from H&E is used to create a super-resolved IMS image. b) An overlay of the original, predicted and residual spectrum for an arbitrary pixel. A zoomed section is shown in the adjacent box. Red and blue lines overlap significantly. c1) and c2) Two examples of super-resolved image channels compared to naive cubic interpolation. Zoom-boxes are shown in yellow.