Abstract
It has been suggested that a deep memory of early life is hidden in the architecture of metabolic networks, whose reactions could have been catalyzed by small molecules or minerals prior to genetically encoded enzymes. A major challenge in unraveling these early steps is assessing the plausibility of a connected, thermodynamically consistent proto-metabolism under different geochemical conditions, which are still surrounded by high uncertainty. Here we combine network-based algorithms with physico-chemical constraints on chemical reaction networks to systematically show how different combinations of parameters (temperature, pH, redox potential and availability of molecular precursors) could have affected the evolution of a proto-metabolism. Our analysis of possible trajectories indicates that a subset of boundary conditions converges to an organo-sulfur-based proto-metabolic network fueled by a thioester- and redox-driven variant of the reductive TCA cycle, capable of producing lipids and keto acids. Surprisingly, environmental sources of fixed nitrogen and low-potential electron donors seem not to be necessary for the earliest phases of biochemical evolution. We use one of these networks to build a steady-state dynamical metabolic model of a proto-cell, and find that different combinations of carbon sources and electron donors can support the continuous production of a minimal ancient “biomass” composed of putative early biopolymers and fatty acids.
Keywords: Metabolism, evolution, network expansion, origin of life, constraint-based modeling
The structure of metabolism carries a memory of its evolutionary history that may date back to before the onset of an RNA-based genetic system 1–6. Decoding this ancient evolutionary record could provide important insight into the early stages of life on our planet 2,5–8, but constitutes a challenging problem. This challenge is due both to the difficulty of interrogating complex biochemical networks under different environmental conditions, and to the uncertainty about these conditions on prebiotic Earth. Estimates of plausible Archean environments that led to the emergence and evolution of living systems vary dramatically 9,10, ranging from alkaline hydrothermal vents driven by chemical gradients 11–13 to acidic ocean seawater driven by photochemistry 3,4. Although geochemical data support the availability of mid-potential electron donors (H2) 14,15, sulfur (e.g. H2S) 3,4,16–18 and potentially fixed carbon 19–22 in ancient environments, several key molecules used in living systems may have been severely limiting, including a source of fixed nitrogen 23,24 (e.g. ammonia), low-potential electron donors 25,26 and phosphate 27–29. For example, using network-based algorithms we found evidence that thioesters, rather than phosphate, may have endowed ancient metabolism with key energetic and biosynthetic capacity 30. This raises the broader question of whether other molecules and physico-chemical conditions may not be as crucial as previously thought for the emergence of a proto-metabolism 31.
A computational method that can help address these questions is the network expansion algorithm, which simulates the growth of a biochemical network by iteratively adding to an initial set of compounds the products of reactions enabled by available substrates, until no additional reactions or metabolites can be added 32,33. This algorithm, in its application to the study of ancient life 30,34, relies on three key assumptions. The first assumption is that classes of biochemical reactions essential for the rise of living systems were gradually built upon, but rarely lost throughout early evolution. This would imply that the memory encoded in metabolism about its history is complete enough to allow for inferences of ancient states and their evolutionary expansion.
While this assumption is currently a conjecture, it is strongly supported by the broader evolutionary argument that essential molecules and biological structures tend to be conserved and built upon by subsequent molecules and structures. This layered architecture has been extensively studied and observed in ferredoxins 1, the ribosome 35 and metabolism itself 2,5,36–40. This concept is also consistent with recent evidence that early core biochemical pathways similar to the ones we see today may have arisen readily 19,41,42, and may have become prevalent in the biosphere without further global optimization 43,44. Further support to this conjecture comes from the observation that early innovations in biochemical functions would spread broadly across the biosphere 45–47, suggesting that even upon organismal extinction, the complete loss of fundamental enzymatic capabilities would be very unlikely. It is similarly implausible that whole categories of reactions would have gone extinct in presence of drastic global changes, such as the great oxygenation event, due to the opportunities seized through fast adaptations in specific environmental niches 34. The importance of this conjecture for the current work and possible follow up studies is further examined in the Discussion.
The aforementioned view of metabolism as a biosphere-level phenomenon is an inherent aspect of the network expansion algorithm, and could be viewed as its second key assumption. This assumption allows one to ask questions about the rise of metabolism across organismal boundaries: over long time-scales, horizontal gene transfer produced abundant shuffling of biochemical reactions across different organisms 45–47, supporting the notion that a global ecosystem-level approach to metabolism may be particularly suitable for describing ancient biochemistry. The third assumption is that inorganic or small molecular catalysts could catalyze, in a weaker and less specific manner relative to modern enzymes, a large number of metabolic reactions, as confirmed by an increasing body of experimental evidence 19,41,42,48,49.
In this paper, we systematically explore a combinatorial set of molecules and parameters associated with possible early Earth environments, and use an enhanced network expansion algorithm to determine which proto-metabolic networks are thermodynamically reachable under each of these initial conditions. We further use constraint-based flux balance modeling to demonstrate the capacity of some of these networks to sustain flux, in a way that resembles homeostatic growth of present-day cells. Our results suggest that a thioester-driven organic network may have robustly arisen without phosphate, fixed nitrogen or low-potential electron donors. This network, by supporting the biosynthesis of keto acids and fatty acids may have prompted the rise of complex self-sustaining biochemical pathways, marking a key transition towards the origin of life.
Results
A thermodynamically-constrained network expansion algorithm enables predictions of proto-metabolic networks as a function of environmental boundary conditions
We first sought to systematically characterize the effect of various geochemical scenarios on the possible structure of ancient metabolism. Building on prior work 30,34, we constructed a model of ancient biosphere-level metabolism based on the KEGG database 50. We first modified the network (as described in Methods) to account for previously proposed primitive thioester-coupling and redox reactions30. These modifications include the introduction of reactions whose redox cofactors are substituted by unspecified molecules defined solely by their redox potential. In this sense, many of the reactions in our set truly represent whole classes of reactions, with a multitude of possible specific instances. For each possible set of environmental parameters (including temperature, pH and redox potential) we computed the thermodynamic feasibility of each reaction, and removed infeasible reactions (see Methods). This allowed us to implement a thermodynamically-constrained network expansion algorithm30, which iteratively adds metabolites and thermodynamically-feasible reactions to a network until no additional reactions and metabolites can be added to the network 30,32–34. Importantly, this method ensures that reactions added to the network are locally (rather than globally) thermodynamically feasible (see Fig. 1a and Methods).
Figure 1: Nitrogen is not essential for the initial expansion of metabolism.
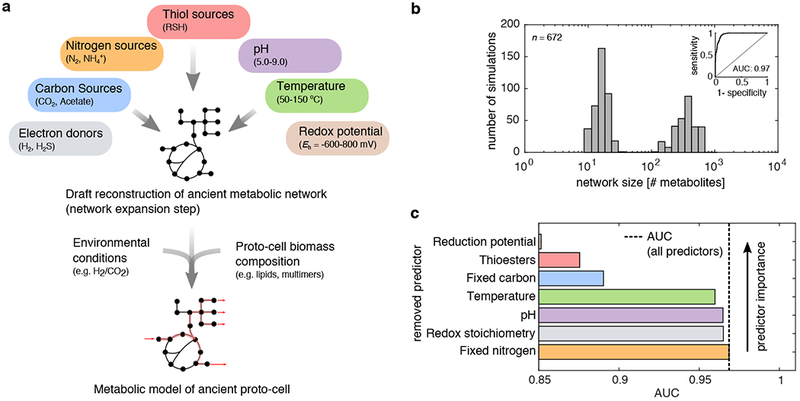
(a) A network expansion algorithm (top) was used to simulate the early expansion of metabolism under 672 scenarios, systematically varying the availability of reductants in the environment, pH, carbon sources, the presence of thiols, temperature and the availability of ammonia. This process is subject to local thermodynamic feasibility constraints, i.e. allows new reactions to occur only if they are individually thermodynamically feasible (see Methods). For a subset of networks obtained from network expansion, we implemented detailed stoichiometric model simulations, using flux balance analysis (bottom), in which we implemented global thermodynamic feasibility constraints (see also Methods and Fig. 4). (b) A histogram of network sizes (x-axis, number of metabolites) revealed that 43 % (288/672) of the scenarios resulted in a bimodal distribution, where expansion occurred beyond 100 metabolites. (inset) A logistic regression classifier was constructed to predict whether a geochemical scenario resulted in a network that exceeded 100 metabolites, and a receiver operating curve (ROC) was plotted. The trained classifier resulted in an area under the curve (AUC) of 0.97 and leave-one out cross-validation accuracy of 0.89. (c) Models were trained without information on specific geochemical variables (y-axis, ranked by predictor importance), and the ensuing AUC was plotted as a bar-chart (x-axis), revealing that knowledge of the availability of fixed nitrogen offers no information on whether networks expanded.
We performed thermodynamically-constrained network expansion (see Methods and Fig. 1a) for n=672 different geochemical scenarios, systematically varying pH, temperature, redox potential of primitive redox systems (analogous to extant NAD/NADP and FAD-coupled reactions), and the availability of key biomolecules including thiols (that subsequently form thioesters), fixed carbon (formate/acetate), fixed nitrogen (ammonia), and various electron donors and acceptors (see Methods, Fig. 1, Supplementary Data 1). Initial seed sets were chosen to be representative of hypothesized prebiotically available sources of carbon, sulfur, oxygen, hydrogen and nitrogen containing biomolecules, spanning a range of relevant redox states11, as also discussed in detail previously 30.
A systematic combinatorial exploration of boundary conditions points to necessary and unnecessary precursors
Of the 672 different simulated geochemical scenarios, we found that 288 (43%) expanded to networks containing over 100 metabolites (Fig. 1b). A logistic regression classifier that uses geochemical parameters as predictors (see Methods and Fig. 1c) allowed us to quantify the importance of each environmental parameter in determining whether the expanded network would reach such a large size. Surprisingly, removing the variable associated with presence/absence of ammonia did not affect the predictive power of the classifier, suggesting that a source of fixed nitrogen is not an important determinant of the expansion. Consistent with the relevance of this result to ancient metabolism, we found that the enzymes that catalyze reactions in the expanded networks before the addition of ammonia were depleted in nitrogen-containing coenzymes (see Extended Data Fig. 1c–d, one-tailed Wilcoxon sign rank test: P < 10−24) and amongst active site amino acids with nitrogenous side chains (see Extended Data Fig. 1e–f and Extended Data Fig. 2, one-tailed Wilcoxon sign rank test: P < 10−24) relative to enzymes added after the addition of ammonia (see Supplemental Text). These results suggest that ammonia may have not been essential for the initial expansion of metabolism, and point to a thioester-coupled organo-sulfur metabolic network (Fig. 1) as a core network that deserves further attention.
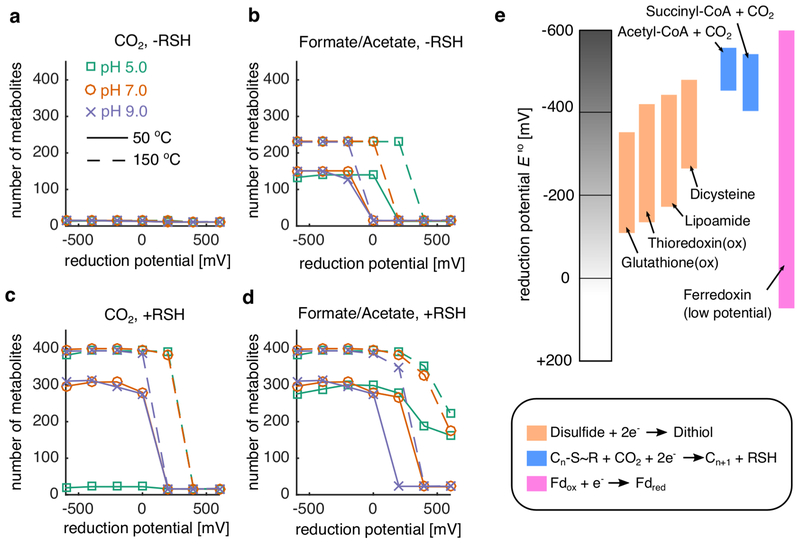
Beyond the dispensability of nitrogen, the simulations described above revealed a number of relationships between plausible geochemical scenarios and the structure and size of our simulated proto-metabolic networks. First, expansion beyond 100 metabolites was feasible in the absence of a source of fixed carbon, but only when thiols were provided in the seed set, highlighting the importance for thioester-coupling for ancient carbon fixation pathways 2,4,22,25,26,30. The presence of thiols enabled the production of key biomolecules, including fatty acids and branched chain keto acids (see Extended Data Fig. 3). Second, we explored the effect of the primitive redox system by systematically varying the reduction potential of the electron donor in the seed set (see Methods, Fig. 2a). Unexpectedly, we found that as we increased the fixed potential of the electron donor, expansion to a large network was feasible over a broad range of reduction potentials (between −150 and 50 mV). Only upon reaching 50mV the expanded network collapsed to a much smaller solution, suggesting that the generation of low-potential electron donors from H2 may not have been a necessary condition for the early expansion of a proto-metabolism (Fig. 3a). We additionally explored conditions with combinations of generic oxidants and reductants (Extended Data Fig. 4) as well as the addition of fixed carbon into the seed sets (Extended Data Fig. 4–5), and found no conditions where expansion was selectively dependent on low-potential electron donors. Thus, less stringent constraints, e.g. the presence of mid-potential redox couples and thioester-forming thiols could have enabled the emergence of a proto-metabolic network capable of producing key biomolecules.
Figure 2: Primitive redox systems and reaction classes constrain network expansion from CO2.
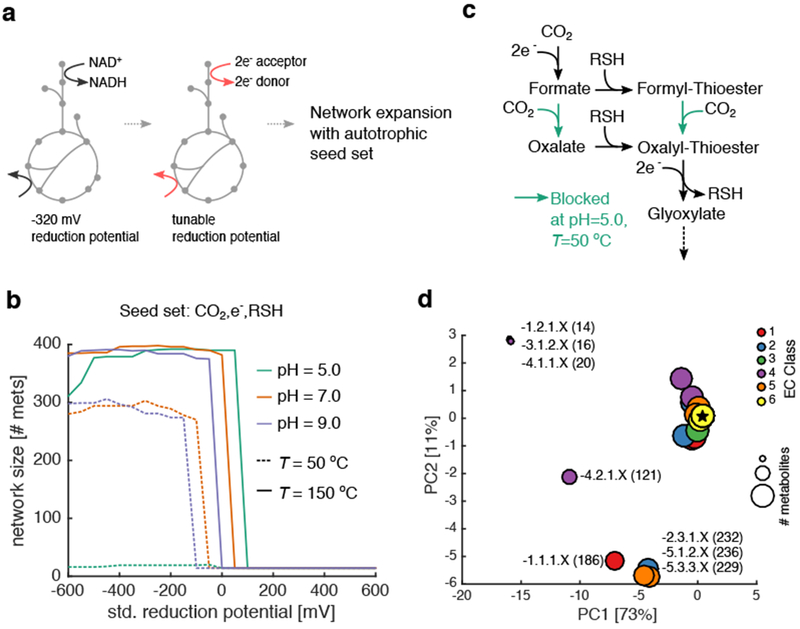
(a) Redox coenzymes (NAD, NADP, and FAD) were substituted with an arbitrary electron donor/acceptor at a fixed reduction potential. (b) We performed thermodynamic network expansion in acidic (pH 5), neutral (pH 7) and alkaline (pH 9) conditions at two temperatures (T =50 and 150 °C), using a two-electron redox couple at a fixed potential (x-axis) as a substitute for NAD(P)/FAD coupling in extant metabolic reactions (see Methods). We plotted the final network size across all pH and temperatures with no fixed carbon sources (e.g. only CO2) and thiols. Notably, for these simulations, we used a base seed set of: H2, H2S, H2O, HCO3−, H+ and CO2. In general, network size is increased at higher temperatures, consistent with Weiss et. al 13. (c) Analysis of the expanding networks revealed a critical set of reactions blocked at pH 5 and T=50 °C, preventing the production of oxalyl-thioesters and subsequently glyoxylate. These reactions belong to Enzyme Commission (EC) class 4.1.1.X (d) We performed network expansion after removing groups of reactions based on EC codes, and performed principal component analysis (PCA) on the ensuing networks. The color represents the EC code removed from the original network, while the size corresponds to the final number of metabolites in the expanded network. Points are labeled by E.C. class, and the number of metabolites in the perturbed networks are provided in parentheses. The star represents the location of the unperturbed network.
Figure 3: Systematic exploration of prebiotic scenarios reveals a core organo-sulfur network.
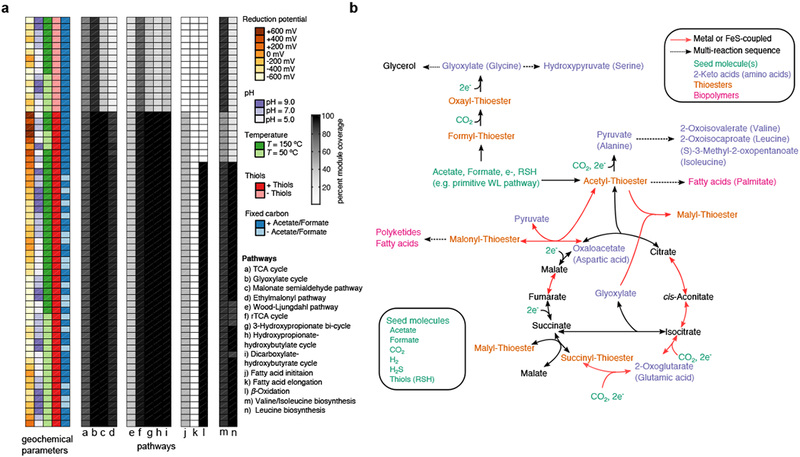
(a) A thermodynamically constrained network expansion algorithm was used to simulate the early expansion of proto-metabolism under various scenarios, including the availability of reductants in the environment, pH, temperature, and the availability of fixed carbon sources and thiols. The proportion of molecules selected KEGG modules involved carbon metabolism are plotted as a heatmap to the right of the parameters. (b) A representation of the core network producible from a prebiotically plausible seed set without nitrogen or phosphate (bottom left box). Acetyl-thioesters are first produced, potentially from a primitive Wood-Ljungdahl pathway8,19 from acetate and thiols provided as seed molecules (green). Acetyl-thioesters enable the production of all intermediates in the reductive tricarboxylic acid (rTCA) cycle, with the exception of phosphoenolpyruvate. ATP-dependent reactions in the rTCA cycle may have been substituted with a primitive malate synthase and transthioesterification of succinate as well as the recently discovered reversible citrate synthase 66,67. The keto acid precursors for 8 common amino acids (A,D,E,G,I,L,S,V) are highlighted in purple, while routes to thioester-mediated polymerization of fatty acids and polyketides are highlighted in pink.
Autotrophic expansion with thioesters was found to be infeasible at pH 5 and T=50 °C (Fig. 2b) due to a blockage in the production of oxalyl-thioesters (Fig. 2c). In our simulations of expansion from autotrophic seed sets, oxalyl-thioester was a critical intermediate in the production of glyoxylate, which was recently proposed to be a key starting material for the production of proto-metabolic networks 42. This observation prompted us to explore more thoroughly the consequences of removing reactions from the set of feasible reactions used during network expansion. To address this, we systematically removed 236 classes of reactions, grouped by E.C. numbers, and performed network expansion using an autotrophic seed set and a mid-potential redox system (−220 mV). Interestingly, we found that three classes of reactions were critical for expansion, including reactions carried out by NAD/NADP-dependent oxidoreductases operating on aldehydes and ketones (1.2.1.X), thioester hydrolases (3.1.2.X) and carboxy-lyases (4.1.1.X). The most perturbed networks were generated by removing reactions catalyzed by enzyme classes involved in fatty acid biosynthesis in (e.g. 3.1.2.X and 5.3.3.X) as well as fatty acid degradation (1.1.1.X, 4.2.1.X and 2.3.1.X).
The emerging organo-sulfur proto-metabolism includes a modified version of the rTCA cycle, and pathways for the production of keto acids and fatty acids
Analysis of the expanded networks without nitrogen revealed that a large number of different initial conditions converged to similar expanded organo-sulfur proto-metabolic networks, spanning variants of key pathways in central carbon metabolism (Fig. 3b). For the majority of simulations, variants of modern heterotrophic carbon assimilation pathways, including the glyoxylate cycle and TCA cycle, were highly represented in the network (Fig. 3b). Several carbon fixation pathways were highly represented in the simulated networks as well: in over half of the networks that expanded beyond 100 metabolites, we found 92 % (12/13) of the compounds (or generalized derivatives) that participate in the reductive tricarboxylic acid (rTCA) cycle, with the exception of phosphoenolpyruvate. We also found that under several geochemical conditions, all intermediates were producible for three carbon fixation pathways, including the 3-hydroxypropionate bi-cycle, the hydroxypropionate-hydroxybutylate cycle, and the dicarboxylate-hydroxybutyrate cycle (Fig. 3a). At-most, only 3 of 9 metabolites used in the Wood-Ljungdahl (WL) pathway were observed, due to the lack of nitrogen-containing pterins in the network. This does not necessarily rule out the primordial importance of the WL-pathway, as its early variants could have been radically different than today’s WL-pathway, relying on native metals to facilitate reduction of CO2 to acetate 19,26. In addition to observing a large number of metabolites used in carbon fixation pathways, we found that a large fraction of the β-oxidation pathway was represented in our networks, which may have supported the production of fatty acids in ancient living systems by operating in the reverse direction. Interestingly, recent metabolic engineering efforts have demonstrated the feasibility of fatty acid synthesis via a reversible β-oxidation pathway51. Lastly, we observed that the majority of intermediates involved in the production of branched-chain amino acids were also producible in the expanded networks. To explore the variability of networks generated by the expansion, we provide an interactive visualization as a supplemental data file (Supplementary Software 1) and website (https://prelude.bu.edu/pmne/).
A more detailed analysis of the convergent organo-sulfur proto-metabolic network reveals new possible ancestral metabolic pathways that involve previously unexplored combinations of reactions and metabolites. Fig. 3b shows a variant of the (r)TCA cycle that is a component of these expanded networks, and that may have served as the core organo-sulfur network fueling ancient living systems. Rather than using ATP-dependent reactions found in extant species (e.g. Succinyl-CoA synthetase and ATP citrate lyase), these reactions are substituted with non-ATP-dependent reaction mechanisms. For instance, the production of a succinyl-thioester in the extant rTCA cycle relies on Succinyl-CoA synthetase, performing the following reaction: ATP + Succinate + CoA → Succinyl-CoA + ADP + Pi. However, in the network presented in Fig. 3b, malyl-thioester, producible through alternative reactions, donates a thiol to succinate, subsequently forming a succinyl-thioester. This (r)TCA cycle analogue is able to produce eight keto acids normally serving as key intermediates and precursors to common amino acids in central carbon metabolism (glyoxylate, pyruvate, oxaloacetate, 2-oxoglutarate and hydroxypyruvate), as well as a few branched-chain keto acids. Additionally, long-chain fatty acids like palmitate are producible in this network, driven by thioester and redox-coupling rather than ATP, like in extant fatty acid biosynthesis. Thus, despite the simplicity of seed compounds, several small molecular weight keto acids and fatty acids may have been producible in an organo-sulfur proto-metabolism.
The sustainability of a proto-metabolic network can be assessed using constraint-based flux balance modeling
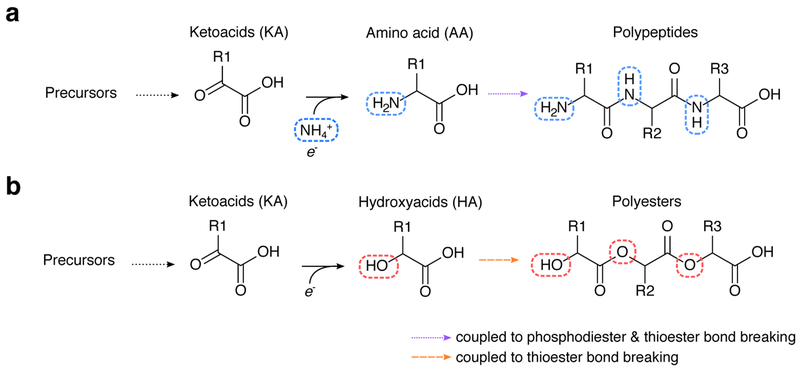
So far, we have focused only on the topology and local thermodynamic feasibility of putative ancient metabolic networks. Inspired by recent studies on the molecular budget of present-day cells 31,52,53, we decided to further explore whether proto-metabolic networks could support thermodynamically-feasible steady state fluxes, and fuel primitive proto-cells with internal energy sources (e.g. thioesters), redox gradients, and primitive biopolymer capable of catalysis and compartmentalization. Flux balance analysis (FBA), originally developed for the study of microbial metabolism, enables the prediction of systems-level properties of metabolic networks at steady-state 52. Fundamentally, FBA computes possible reaction rates in a network constrained by mass and energy balance, usually under the assumption that a specific composition of biomolecules is efficiently produced during a homeostatic growth process. In microbial metabolism, FBA is used to simulate the production of cellular biomass (e.g. protein, lipids, and nucleic acids) at fixed proportions, which are derived from known composition of extant cells. We realized that the same approach could help test the sustainability of a proto-metabolic biochemical system, provided that we could develop a plausible hypothesis for the “biomass composition” of ancient proto-cells. As a starting point, we recalled Christian de Duve’s suggestion that the thioester-driven polymerization of monomers producible from ancient proto-metabolism may have led to “catalytic multimers,” which could have served as catalysts for ancient biochemical reactions 4. Under nitrogen limited conditions, keto acids producible from proto-metabolism (see Fig. 3b) could have been reduced to α-hydroxy acids, and polymerized into polyesters using thioesters as a condensing agent (see Extended Data Fig. 6). Recent work has suggested that polymers of α-hydroxy acids may have been stably produced in geochemical environments 54, and that these molecules could have served as primitive catalysts 55. These results all point to the intriguing possibility that the thioester-driven polymerization of α-hydroxy acids (producible from keto acid precursors of common amino acids) generated the first metabolically sustainable cache of ancient catalysts, leading to a collectively autocatalytic protocellular system. We employed a variant of FBA to specifically test the feasibility of such a system. Using an expanded metabolic network as a scaffold for network reconstruction (Fig. 3b), we constructed a constraint-based model of an ancient proto-cell using a biomass composition consisting of fatty acids (for proto-cellular membranes), “catalytic multimers” derived from eight keto acids (Fig. 4a), and redox and thioester-based free energy sources (Methods, Fig. 4a). We used thermodynamic metabolic flux analysis (TMFA), a variant of FBA that explicitly considers thermodynamic constraints 53 (see Methods), to determine whether homeostatic growth of the whole system was achievable (see Methods). We found that, in order to obtain feasible production of each keto acid and fatty acid precursor, the model required an internal redox system with a fixed potential between −500 and −200 mV, where very low reduction potentials led to an inability to produce 2-oxoisocaprioate (Fig. 4b). We fixed the potential of the internal redox system to −220 mV and determined whether steady-state growth was achievable with a variety of electron donors, electron acceptors and carbon sources (Fig. 4c–d). We found that growth of the proto-cell metabolic model is indeed feasible under a wide variety of assumptions regarding macromolecular compositions, carbon sources, electron donors and acceptors (Fig. 4c–d). Notably, growth is achievable in simple chemoautotrophic conditions with either H2 or glutathione (or a free thiol) as electron donors (Fig. 4c), consistent with recent work suggesting the last universal common ancestor was a thermophilic H2-consuming chemoautotroph 13. In this model, thiols and thioesters are not supplied as food sources, but rather are recycled during steady-state growth of the proto-cell. This reflects the possibility that thiols could have been initially supplied abiotically, followed by the rapid takeover of biotic production of mercaptopyruvate, a keto acid that could have been incorporated into primitive multimers.
Figure 4: Constraint-based modeling of plausible ancient proto-cells.
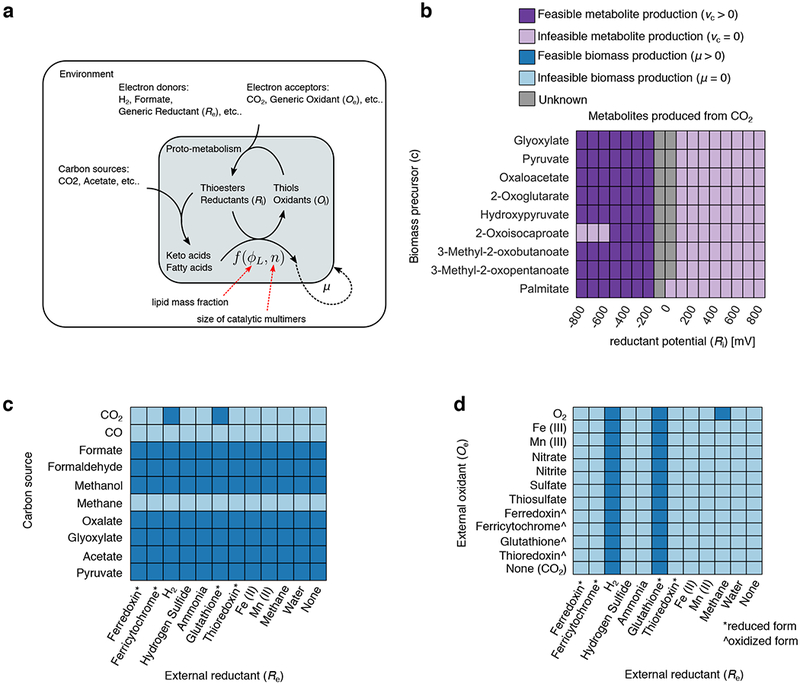
(a) We constructed a metabolic model of a plausible ancient proto-cell and used thermodynamic metabolic flux analysis53 to simulate the feasibility of steady state growth under a variety of environmental conditions. The metabolic model was constructed using internally-generated reductants (Ri) and thioesters that fueled biomass formation. The biomass composition was specified as variable fractions of fatty acids, and polymerized hydroxy-acids from keto-acid precursors (see Methods). In this model, the internal redox coenzyme was assumed to be at a single fixed standard reduction potential, and the production of biomass was fueled by the hydrolysis of acetyl-thioesters. We parameterized the biomass composition using a two-parameter model (see Methods), with the mass fraction of lipids in the proto-cell set to ϕL = 0.1, and the average size of a catalytic multimer, n = 10. (b) We computed fluxes from CO2 to each biomass precursor (y-axis) using a variety of internally generated reductants at various reduction potentials (x-axis), and show the conditions that led to feasible (dark purple) and infeasible (light purple) flux. Note that some cases did not converge to a solution within the allocated maximal CPU time, likely due to numerical issues, and were thus classified as “unknown” (grey). The production of all biomass precursors was feasible if the redox system was between −500 and −200 mV. (c) We next simulated growth on a variety of simple carbon sources (y-axis) and external electron donors (x-axis) and show environments supporting non-zero growth (light blue) or no growth (dark blue). Interestingly, H2 and glutathione were the only reductants capable of supporting fully autotrophic growth on CO2. Furthermore, CO and Methane could not support growth in this model, while the other one-carbon sources like methanol, formate and formaldehyde could support biomass growth. (d) We next simulated autotrophic growth using both an oxidant (y-axis) and reductant (x-axis) and show environments supporting non-zero growth (dark blue) or no growth (light blue). Feasible growth was entirely dependent on the reductant, rather than the oxidant, except for the case with methane as the electron donor and oxygen as the electron acceptor. For models in (c) and (d), the internal redox coenzyme was assumed to be disulfide/dithiol at a standard reduction potential of −220 mV.
Discussion
While most efforts to reconstruct ancient biochemistry have traditionally relied on building qualitative models of small pathways 2,4,5,7,21, we found that quantitative modeling of larger networks can provide substantial new insight into the origin of life. By computationally mapping geochemical scenarios to plausible ancient proto-metabolic structures, we estimated which portions of extant biochemistry may have been very sensitive or very robust to initial geochemical conditions. Our approach reveals that, contrary to expectations 8,11,25,26, environmental sources of fixed nitrogen and low-potential electron donors may have not been necessary for early biochemical evolution, and a substantial degree of complexity may have emerged prior to incorporation of nitrogen into the biosphere 3. The key catalytic role played by nitrogen in the active sites of modern enzymes may have been preceded by positively charged surfaces or metal ions 19,21,41,56, which could have been replaced by amino/keto acids with nitrogen side chains once nitrogen became incorporated into proto-metabolism. Our simulations also cast doubts on the essential role of a low-potential electron donor in early life 8,11,25,26, consistent with the proposal that low-potential electron donors may not be necessary for acetogenesis 57, and with the possibility that energy conservation via electron bifurcation might not have been necessary in primordial metabolism58. The independence of our inferred ancestral networks of low-potential electron donors and ATP, both key substrates for nitrogen fixation 59, suggests that nitrogen fixation may have evolved later throughout the history of life 13,60. A striking feature of our analysis is the convergence of multiple geochemical scenarios towards a core organo-sulfur proto-metabolic network capable of producing various keto acids and fatty acids (Fig. 3b), potentially providing a metabolic flow of molecular substrates for catalysis and self-aggregation 61. In particular, this feature provides a window into how thioester-driven polymerization of α-hydroxy acid monomers (derived from producible keto acids) could have added primitive macromolecular organic catalysts4 to initial inorganic minerals or metal ion catalysts 19,41,42. Further tests of this hypothesis could be pursued by measuring the capacity of these polymers to catalyze key reactions in the network, and by exploring whether these organic compounds are produced in living systems today via mechanisms similar to polyketide or non-ribosomal peptide synthesis. Additionally, the fact that the network expansion is significantly affected by the removal of reactions involved in fatty acid metabolism (Fig. 2d) suggests that future experimental efforts could be directed towards identifying non-enzymatic mechanisms for fatty acid synthesis. Finally, our constraint-based models of this core organo-sulfur proto-metabolism provide an example of how network expansion-based predictions can be translated into dynamical models, whose capacity to estimate sustainable collective growth may drive the search for specific self-reproducing chemical networks and metabolically-driven artificial protocells.
Future models of early metabolic systems could be in principle used to estimate the outcome of evolutionary competitions among different networks, similar to what has been done for stoichiometric models of bacterial metabolism (where the biomass production is used as a proxy for fitness 62,63). In order to enable similar simulations, however, it would be necessary to obtain realistic estimates of the kinetics of nutrient inflow, equivalent to uptake rates in present-day cells. Moreover, in order to perform simulations that are based on thermodynamically feasible metabolic states, one would have to address some of the current challenges we faced with TMFA calculation of protometabolic networks, due to computational complexity of mixed integer optimization problems for large networks (see Methods). Upon addressing these challenges, future stoichiometrically-based eco-evolutionary models of proto-metabolism could help generate specific testable hypotheses about the ancient biosphere.
Future research could also address both specific physico-chemical hypotheses presented in this study, as well as fundamental conjectures implicit in our modeling approach. Our approach assumes that the history of metabolic evolution can be reconstructed by the extant biosphere-level metabolic network, which is primarily catalyzed by genome-encoded enzymes. Future studies could refine this assumption by adding potentially “extinct” reactions to the model reconstructed using alternative computational methods64,65 or removing kinetically-limited reactions using experimental data. While the removal of reactions could dramatically limit the composition of expanded networks (Fig. 2d), the addition of reactions to the model would not change the principal conclusion presented in the study that biomolecules previously assumed to be critical for the emergence of living systems (e.g. phosphate, fixed nitrogen and low-potential electron donors) may have not been essential for the onset of proto-metabolic systems. However, we would expect the stoichiometric modeling results to be sensitive to additions of new reactions, as these could in principle turn currently infeasible states into feasible ones. Overall, the striking concordance between the theory presented in this study and recent experimental models of proto-metabolism42 suggests that extant metabolism might serve as an approximation of abiotic chemical networks, thus providing a window into the earliest phases of biochemical evolution prior to a genetic coding system.
Materials and Methods
Reconstruction of biosphere-level metabolic network
Biosphere-level metabolism was reconstructed from the KEGG database 50 according to protocol described previously 30. We modified the network in several ways to model primitive thioester-based metabolic network without nitrogen or phosphate. First, to simulate the availability of thiols capable of forming thioesters, we included Coenzyme A, Acyl-Carrier Protein and Glutathione into the seed set. However, to enforce the constraint that these metabolites could only be used in reactions as coenzymes (and not products or substrates), we prevented the degradation by removing KEGG reactions R10747, R02973 and R02972.
We next assigned standard molar free energies to reactions using eQuilibriator at a predefined pH 69. Next we substituted NAD, NADP and FAD-coupled reactions with an arbitrary redox couple. For example, if the redox reaction Xox + NADH → Xred + NAD+ was swapped with electron donor with a redox potential of E0+ mV, we would use the following formula to adjust the standard molar free energy for the new reaction r′:
where $n$ are the number of electrons transferred in reaction r and F = 96.485kJ/V. Note that if we assumed that the electron donor/acceptor substitute was a two electron donor/acceptor, we did not change the stoichiometry in the reaction equation. However, in the case where the electron donor/acceptor substitute was a single electron donor/acceptor, we change the stoichiometric coefficients to Scj = 2 for all reactions j, where c represents metabolites NAD(H), NADP(H) and FAD(H2). For this work, we systematically varied the reduction potential E0+ and stoichiometry of the primitive redox coenzyme.
Thermodynamically-constrained network expansion
We performed network expansion using thermodynamic constraints (TNE) in a different way than performed previously30. Previously, we removed reactions above a predefined free energy threshold of τ = 30kJ/mol 30. For this work, we computed the lowest reaction free energy possible using estimates for upper and lower bounds on metabolite concentrations, ui and li, and removed reactions with a positive reaction free energy. For a given biochemical reaction at fixed temperature and pressure, ΔrG′ is defined as:
where the ΔrG°′ is the free energy change of the reaction at standard molar conditions, R is the ideal gas constant, T is temperature, ai is the activity of metabolite i and Sir is the stoichiometric coefficient for metabolite i in reaction r. We fixed ai for each reaction according to the following rules:
We then removed reactions with a ΔrG′ ≥ 0. For all simulations we assumed that ui = 10−1M and li = 10−6 M. Note that because we model each reaction independently, metabolite concentrations could be inconsistent . For instance, if metabolite i is the substrate for reaction p and a product for reaction q, then ai = ui for reaction p and ai = li for reaction q. Additionally, a fundamental assumption of this algorithm is that, over long enough time-scales, network growth is constrained by “local” thermodynamic bottlenecks for each reaction individually, rather than “global” thermodynamic feasibility of the entire network. We also assume that during the expansion, the enthalpic portion of each reaction’s free energy is constant because the primary physico-chemical changes that could change the enthalpy of formations (e.g. pH, ionic strength) are buffered by geochemical boundary conditions.
Using this procedure to systematically remove reactions that were considered to be thermodynamically infeasible, we performed network expansion 32–34 using the computational procedure described in 30.
Parameters for network expansion
We systematically studied the size and composition of networks under precise environmental conditions by varying (a) the reduction potential from the environment, (b) pH, (c) temperature, (d) the presence or absence thiols, (e) the inclusion of fixed carbon into the seed set and (f) the inclusion of fixed nitrogen into the seed set. We now discuss each of these parameters in more detail:
Reduction potential and stoichiometry: A wide range of environmental conditions could have provided electron donors at various potentials: high potential redox pairs, with strong oxidants like Fe(III), may have been present in oceans at high concentrations, while strong reductants like H2, disulfides, proto-ferredoxin, or reductive carboxylation of thioesters have been produced via serpentinization or geochemical analogues of primitive metabolic pathways 25. We substituted reactions coupled to NAD, NADP and FAD with a generic single or double electron donor and acceptor pair at a fixed potential. To prevent unbalanced electron transfer, we removed the following transhydrogenase reactions: R10159, R01195, R00112, R09520, R09748, R05705, R05706, R09662, R09750. We then created a single or double electron donor/acceptor pair with a fixed reduction potential, E0+, ranging from −600 to 600 mV. Note that network expansion was performed by adding either the generic oxidant or reductant for NAD(P)/FAD - coupled reactions into the seed set directly, which assumes that this redox system could be produced abiotically.
pH: We modified the pH by setting reaction free energies at various pH’s (5.0-9.0) using eQuilibriator 69which relies on the component contribution method 70.
Temperature: Temperatures were assumed to have been within a range of 50-150 °C, spanning estimates of ocean seawater temperature in the Archean 71, up to some alkaline hydrothermal vent systems 11.
Thiols: In our model we provided thiols that serve as substitutes for coenzymes that form thioester bonds in extant metabolic networks. To this end, we provided Coenzyme A, acyl-carrier protein and Glutathione in the seed set, but removed key degradation reactions to ensure these compounds only served as coenzymes, rather than material sources, during network expansion 30.
Fixed nitrogen: To study the consequences of adding or removing a source of fixed nitrogen as a seed compounds for network expansion, we either added or removed ammonia from the seed set prior to expansion.
In addition to parameters we varied, we kept constant two additional parameters that could be studied in future work:
Metabolite concentrations: Metabolite concentrations were assumed to be within 1 μM - 100 mM. The upper bound estimate is consistent with recent experimental data showing that key metabolites (formate, methanol, acetate and pyruvate) can be produced near 100 mM 19. Although we do not have empirical evidence to suggest a reasonable lower bound on metabolite concentrations in ancient metabolic networks, we assumed that 1 μM, the estimated lower bound in today’s cells 72, was also the lower bound in our model of ancient metabolism.
Reactions with no free energy estimate: 53% of the biosphere-level metabolic network reactions have no free energy estimate (4851 of 9074). For all simulations presented in this paper, we assumed these reactions were blocked and did not include them in the network.
Generalized linear modeling of network expansion results
To assess the effects of various parameters on the outcome of network expansion, we used generalized linear models to construct logistic regression classifiers to predict whether or not the network expanded beyond 100 metabolites using a combination of predictors, including categorical variables encoding whether or not ammonia, thiols or fixed carbon was provided in the seed set, and continuous variables encoding the reduction potential, pH and temperature used in each simulation. We first define the response variable for simulation k as yk where yk = 1 if the simulation resulted in a network that expanded beyond 100 metabolites, and zero otherwise. For the set of simulations performed in Fig. 1 in the main text, we constructed a design matrix consisting of categorical variables representing the following scenarios:
xN,k ∈ {0,1}: 1 if ammonia was included in the seed set, and 0 otherwise.
xS,k ∈ {0,1}: 1 if thiols were included in the seed set, and 0 otherwise.
xC,k ∈ {0,1}: 1 if fixed carbon was included in the seed set, and 0 otherwise.
:A continuous variable representing the pH. Note for our simulations, we only explored acidic (pH=5), neutral (pH=7) and alkaline (pH=9) regimes.
: A continuous variable representing the reduction potential at standard molar conditions (at the specified pH listed above). For our simulations, we explored a wide range of standard molar reduction potentials (from −600 mV to +600 mV).
: A continuous variable representing the temperature. For our simulations, we explored two temperatures: a high temperature regime (T = 150°C), and a low temperature regime (T = 50°C).
We next constructed the following generalized linear model to model whether the network expanded beyond metabolites:
We fit the parameters (β0, βN, βS, βC, βH, βE, βT) using the fitglm.m function in MATLAB 2015a, and a receiver operating curve (ROC) was generated using the perfcurve.m function. For results presented in Fig. 1c in the main text, individual predictors were removed in the generalized linear model presented above. To assess whether the trained logistic model served as an accurate classifier, we performed leave-one out cross-validation by removing individual samples from the training set and testing the accuracy of the trained classifier on the removed sample. This procedure resulted in a cross-validation accuracy of 0.89.
Constraint-based modeling
We constructed a model of an autocatalytic network at steady state using a variant of constraint-based modeling of cellular metabolism called thermodynamic-based metabolic flux analysis (TMFA) 53. TMFA transforms the non-linear constraints induced by imposing thermodynamic consistency into mixed-integer linear constraints. In this section, we first describe (a) the construction of primitive biomass composition for a model of an ancient proto-cell and (b) the formulation of TMFA used in this analysis.
Prebiotic biomass equation
We constructed a simple model for the macromolecular composition of primitive proto-cells, using empirical knowledge of extant cellular life. Since our metabolic model of proto-metabolism does not include macromolecular production of nucleotides (and thus a nucleic acid based genetic system), we assume that the primary role of proto-cellular metabolism was to initially produce components for a cellular membrane and catalysts. Building off of Christian de Duve’s multimer hypothesis 4, we first propose that the biomass can be constructed using a simple two parameter model consisting of the mass fraction of lipids ϕL and the average length of each catalytic multimer n.
Lipid mass fraction: The lipid content in modern cells is roughly 10% of the total dry mass (Bionumbers ID: 111209) 73, primarily composed of the fatty acid palmitate. For our analysis, we assume that palmitate represents the sole component of lipids. Future models could incorporate glycerol, which enables the production of glycerolipids. While phosphate is used in cellular membranes as a polar head group to produce amphiphilic molecules, primitive processes may have conjugated negatively charged organic acids (e.g. oxalate) to glycerol via a thioester-mediated synthesis mechanism to create amphiphilic lipid molecules resembling modern phospholipids. For our initial model, we simply propose that palmitate was the initial amphiphilic component of primitive membranes, where the negatively charged polar carboxylate ion was sufficient for forming a membrane, and assumed that proto-cells consisted of a lipid mass fraction of ϕL.
Catalytic multimer mass fraction: We propose that ancient catalysts were composed of inorganic molecules (e.g. iron-sulfur clusters, metal ions, mineral surfaces) chelated with multimers of α-hydroxy-acids (see Fig. 4a in main text). For our model, we assume that the eight keto acid precursors producible from our network were the dominant monomers of ancient multimeric catalysts. We assume that the total mass fraction of these catalysts are 1 − ϕL = ϕC = Σk ϕk where ϕk is the mass fraction of polymerized monomer k. For our analysis, we assumed that each monomer is uniformly distributed within the biomass, so that ϕk = constant for all k. Additionally, since each monomer must be reduced to α-hydroxy-acids, there is a linear relationship between the electron demand, Se, and the number of molecules of monomers produced. The stoichiometric equivalents of electron donors are thus: where Mk is the molar mass of monomer k.
Average size of catalytic multimers: The average size of multimeric catalysts sets the number of thioester bonds required for synthesis of catalytic multimers. For each polymer of size n, there are n − 1 thioester bonds required for synthesis. In our model, the total number of monomers are fixed to be: , Mk is the molar mass of monomer k. Thus for a fixed monomer length n, we can compute the number polymers using the following formula: . The thioester demand is thus St(n) = (n − 1)P(n), or: . For our analysis we assumed a fixed polymer length of size n = 10 monomers.
Using these two parameters, we constructed the biomass equation for the proto-cellular model. Note that the electron source and sink was provided by an unspecified internal redox coenzyme system (analogous to NAD(P)/FAD).
Thermodynamic Metabolic Flux Analysis (TMFA)
To simulate a thermodynamically-feasible steady-state of this metabolic network, we used a variant of thermodynamic metabolic flux analysis (TMFA) 53. Briefly, TMFA transforms the non-linear constraints induced by imposing thermodynamic consistency into mixed-integer linear constraints. We first converted the model into an irreversible model by modeling each reaction as both forward and backward half reactions. We then constructed the following mixed-integer linear program (MILP) to find a flux vector, v (with elements vr for each reaction r), log-transformed metabolite concentrations (ln(x)) and binary variables indicating whether a reaction is feasible (z) given a specific objective function was satisfied.
Past implementations of TMFA in microbial metabolism defined the objective function as maximizing biomass yield. However, for our study we simply sought to determine whether non-zero growth was feasible. Therefore, we transformed TMFA into a constraint-satisfaction problem by setting a lower bound on the biomass reaction, vbiomass, such that:
and solving the following MILP:
maximizev,ln(x),z,e 0
subject to
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
where R and M are the sets of all reactions and metabolites, respectively. As discussed in detail elsewhere 53, the first equation in the constraint set ensures that intracellular metabolite concentrations are at steady-state, and are simply mass balance constraints for each metabolite. The second equation sets the bound on individual reaction fluxes, where the maximum flux through reaction r is ubr. Note that when zr = 0, the flux through reaction r is constrained to 0. The third equation sets ensures that zr = 1 if and only if ΔrG′ < 0, and zr = 0otherwise. Note that K is a large number K > maxr{ΔrG′} ensuring that this constraint is not violated with zr = 0. The fourth equation is the free energy of each reaction as a function of log-metabolite concentrations. Note that we also add slack variables, er, to account for the possible error in estimating the standard molar reaction free energies for each reaction (where σr is the standard error for each reaction r), which are bounded by a global error tolerance σm = 0 (set in equation 6). Note that if this global tolerance is greater than zero, thermodynamic infeasible cycles are possible in steady-state solutions. Equation 5 simply constrains the log-metabolite concentrations to be bounded between 1μM and 100 mM. For each simulation we constrained the uptake reactions to be 104 and the lower bound on biomass production to be μmin = 1.
Numerical simulations were performed using the COBRA toolbox 74 and the Gurobi optimizer (Version 7.0.1). All source code is provided in the following github repository: https://github.com/segrelab/BoundaryConditionsForAncientMetabolism
Calculation of coenzyme and sequence-level features within enzymes
To determine which reactions were associated with specific coenzymes (for the results presented in Extended Data Fig. 1) we downloaded information for each Enzyme Commission number (E.C.) in the KEGG ENZYME database: http://www.genome.jp/kegg/annotation/enzyme.html. We downloaded each page and parsed the “comment” field for each E.C. and performed a text-based search to identify coenzymes associated with each E.C. number. We searched for text indicating that the enzyme mechanisms used one of the following coenzymes, cofactors and iron sulfur clusters: biotin, heme, PLP, TPP, pterin, molybdopterin, flavin, Fe, Co, Ni, Cu, Mn, W, Zn, Mo, Mg, FeS, FeFe, Fe2S2, Fe3S4 and Fe4S4, respectively. We also searched E.C. numbers indicating that the reaction mechanisms are non-enzymatic. Text-based searches were pruned manually to remove mis-annotated enzyme-coenzyme relationships.
For Extended Data Fig. 1b, we computed the fraction of reaction E.C. numbers that were associated with one of the following coenzymes: Fe, Co, Ni, Cu, Mn, W, Zn, Mo, Mg, FeS, FeFe, Fe2S2, Fe3S4 and Fe4S, or was marked as non-enzymatic. For results presented in Extended Data Fig. 1d, we computed the fraction of reaction E.C. numbers that were associated with one of the following coenzymes: biotin, heme, PLP, TPP, pterin, molybdopterin, and flavin.
For results presented in Extended Data Fig. 1e, we obtained a database of known enzyme active site residues 68. We first mapped the network reactions to E.C. numbers listed in KEGG, then identified active sites corresponding to E.C. numbers within the the expanded network. We next computed the fraction of active site residues containing nitrogenous side-chains, derived from the following amino acids: Arginine (R), Lysine (K), Glutamine (Q), Asparagine (N), Histidine (H), and Tryptophan (W).
Data availability
All data presented in this paper has been deposited in a public repository and can be accessed at: https://github.com/segrelab/BoundaryConditionsForAncientMetabolism
Code availability
All code presented in this paper has been deposited in a public repository and can be accessed at: https://github.com/segrelab/BoundaryConditionsForAncientMetabolism
Extended Data
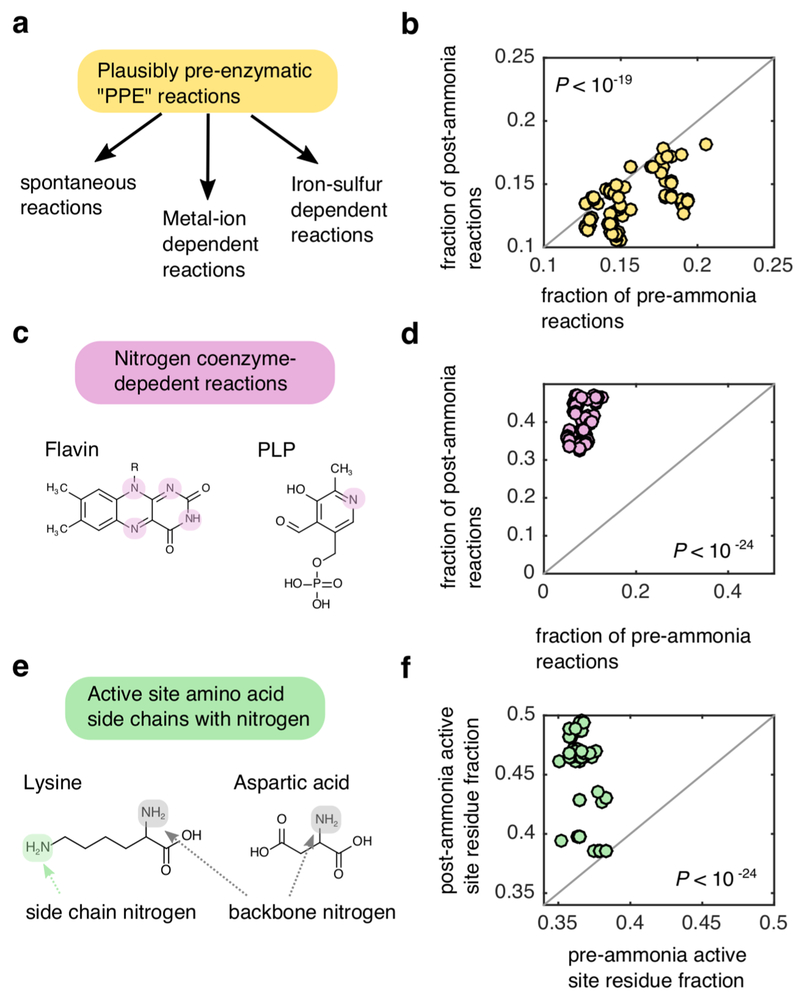
Extended Data Fig 1: Enzymes in thioester-driven protometabolism are depleted in nitrogenous compounds.
(a) We classified reactions in KEGG as being plausibly pre-enzymatic (PPE) reactions if they could (i) proceed spontaneously, (ii) were associated with enzymes that contain at-least one iron-sulfur cluster or (iii) were associated with an enzyme that relied on at-least one metal (Ni, Co, Cu, Mg, Mn, Mo, Zn, Fe, W) cofactor. (b) For all scenarios resulting in expansion of >100 metabolites (n=144) we computed the fraction of PPE-reactions amongst the pre-ammonia reactions (x-axis) and post-ammonia reactions (y-axis). The frequency of PPE-reactions in the pre-ammonia reaction set was on average higher than the frequency of PPE-reactions in the post-ammonia reaction set (one-tailed Wilcoxon sign-rank test: P < 10−19). (c) We identified KEGG reactions that were dependent on at-least one of the following nitrogen-containing coenzymes: flavin, biotin, thiamine pyrophosphate (TPP) pyridoxal phosphate (PLP), heme, pterin or cobalamin. (d) We compute the fraction of pre- and post- ammonia reactions associated with nitrogen containing coenzymes in the KEGG database, and found that a much higher proportion of post-ammonia reactions were dependent on these coenzymes relative to pre-ammonia reactions (one-tailed Wilcoxon sign-rank test: P < 10−24). (e) We parsed the catalytic active site database 68 to find entries associated with pre and post-ammonia reactions, and compute the fraction of entries associated with amino acids with nitrogen-containing side chains (Q,N,W,H,K,R). (f) For each scenario, the fraction of active sites with nitrogen-containing amino acids was significantly higher for post-ammonia reactions relative to pre-ammonia reactions one-tailed Wilcoxon sign-rank test: P < 10−24).
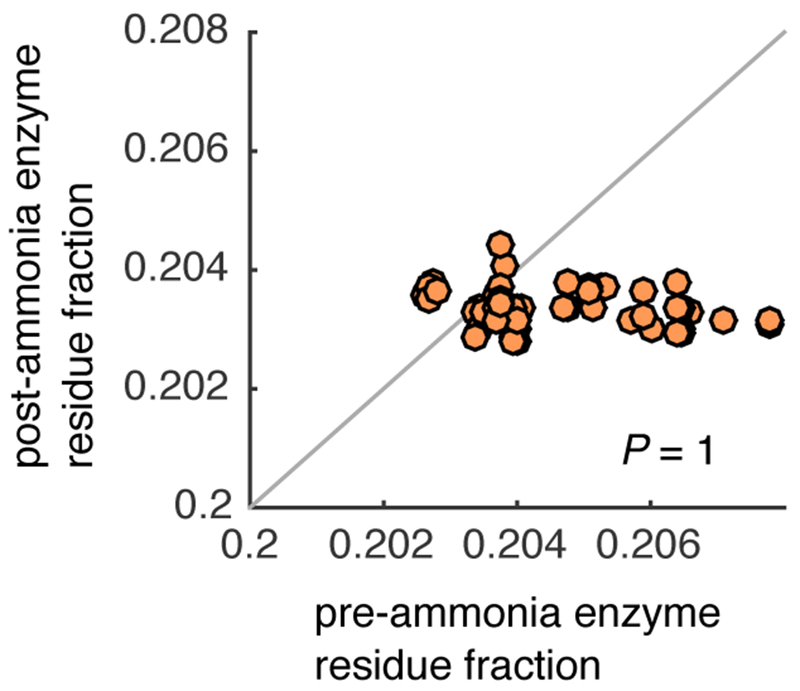
Extended Data Fig. 2: Enzymes catalyzing reactions before the addition of ammonia are not depleted in nitrogen containing amino acids relative to enzymes added after ammonia:
To see if the amino acid biases in active sites of enzymes catalyzing reactions added to the network without ammonia (see Extended Data Fig. 1e–f) is confounded due to evolutionary selection for reduced nitrogen in these enzymes, we computed the fraction of nitrogen side chains in enzymes in pre-ammonia reactions (x-axis) and in enzymes in post-ammonia reactions (y-axis). We found that enzymes in the pre-ammonia networks did not have significantly less nitrogen usage compared to enzymes in post-ammonia reactions (one-tailed Wilcoxon sign-rank test: P = 1).
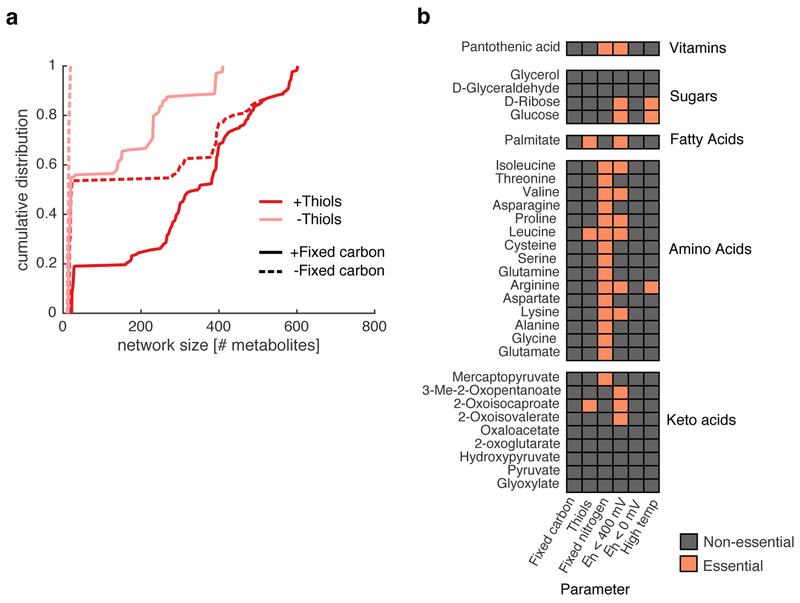
Extended Data Fig. 3: Thiols are required for autotrophic expansion and fatty acid production.
(a) We grouped the n=672 geochemical scenarios into whether a source of fixed carbon and thiols was provided in the seed set. We then plotted the empirical cumulative distributions for each group of scenarios. Notably, when thiols and fixed carbon are not supplied in the seed set, the networks are always below 100 metabolites, indicating that expansion is prohibited without either fixed carbon or thiols in the seed set. (b) We determined what geochemical parameters (x-axis) were essential for the production of important biomolecules (y-axis). For example, palmitate, a long chain fatty acid, is producible only if thiols and reductant below 400 mV is provided in the seed set.
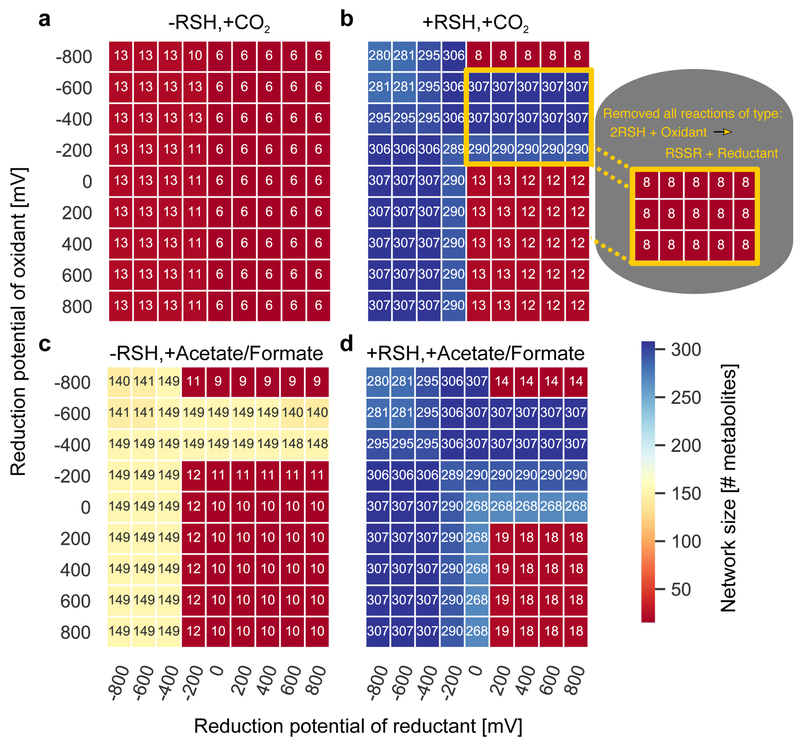
Extended Data Fig. 4: Network expansion with different combinations of carbon sources, thiols, generic reductants and generic oxidants.
We performed network expansion using a seed set with both a generic reductant at a fixed potential (x-axis) and a generic oxidant at a fixed potential (y-axis) with (a) no thiols or fixed carbon, (b) thiols and no fixed carbon, (c) no thiols and fixed carbon, and (d) both thiols and fixed carbon. The color indicates the size (number of metabolites) in the final expanded network. Interestingly, a strong driving force provided by a strong oxidant (>0 mV) never sufficiently compensated for the weak driving force provided by a weak reductant (>0 mV), suggesting that oxidants have little influence on enabling expansion beyond 20 metabolites. The only conditions that led to an expansion that was greater than 20 metabolites with a weak electron donor was when the oxidant was also weak (−200 to −600 mV). We hypothesized that this was due to the ability of thiols or reduced carbon species to reduce the oxidant, enabling the production of a strong reductant. Indeed, when we removed all thiol to disulfide reactions using the generic redox system, expansion was blocked (inset).
Extended Data Fig. 5: Reduction potential of NAD(P)/FAD substitutes influences the size of expanded networks.
We plotted the size (number of metabolites, y-axis) of expanded networks as a function of reduction potential of NAD(P)/FAD substitutes (x-axis) for different physico-chemical conditions with (a) no fixed carbon or thiols, (b) fixed carbon and no thiols, (c) thiols and no fixed carbon, and (d) both fixed carbon and thiols. (e) We plot the range of physiologically-feasible reduction potentials for classes of redox systems potentially relevant for early proto-metabolic systems, showing that dithiol/disulfide redox systems could potentially have enabled expansion under a variety of conditions.
Extended Data Fig. 6: Putative ancient catalysts.
(a) In extant biochemistry, keto acids are converted to amino acids using transamination or reductive amination reaction mechanisms, which are then polymerized using a phosphate or thioester coupled mechanism to make polypeptides. (b) If prebiotic environments did not have a source of fixed nitrogen, then keto acids could have been reduced to -hydroxy acids, which could then be polymerized into polyesters either with 4 or without 55 thioester bond breaking.
Supplementary Material
Cytoscape file containing the data for the interactive visualization of the network expansion and its variability.
Excel tables containing all the network expansion data used to generate Figs. 1–4 and Extended Data Figs. 1–5
Supporting Information Text
Acknowledgements
We thank all members of the Segrè Lab for helpful discussions. We are greatly appreciative of the valuable suggestions and insights provided by anonymous reviewers. We acknowledge support provided by the Directorates for Biological Sciences (BIO) and Geosciences (GEO) at the NSF and NASA under Agreements No. 80NSSC17K0295, 80NSSC17K0296 and 1724150 issued through the Astrobiology Program of the Science Mission Directorate, as well as support by the National Science Foundation (1457695, NSFOCE-BSF 1635070), the Human Frontiers Science Program (RGP0020/2016), and the Boston University Hariri Institute for Computing and Computational Science & Engineering.
Footnotes
Competing Financial Interests
The authors declare no competing financial interests.
References
- 1.Eck RV & Dayhoff MO Evolution of the structure of ferredoxin based on living relics of primitive amino Acid sequences. Science 152, 363–366 (1966). [DOI] [PubMed] [Google Scholar]
- 2.Hartman H Speculations on the origin and evolution of metabolism. J. Mol. Evol 4, 359–370 (1975). [DOI] [PubMed] [Google Scholar]
- 3.Hartman H Conjectures and reveries. Photosynth. Res 33, 171–176 (1992). [DOI] [PubMed] [Google Scholar]
- 4.de Duve C Blueprint for a cell: the nature and origin of life. 275 (Neil Patterson Publishers, Carolina Biological Supply Company, 1991). [Google Scholar]
- 5.Morowitz HJ, Kostelnik JD, Yang J & Cody GD The origin of intermediary metabolism. Proc. Natl. Acad. Sci. U. S. A 97, 7704–7708 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Smith E & Morowitz HJ The Origin and Nature of Life On Earth. 677 (Cambridge University Press, 2016). [Google Scholar]
- 7.Smith E & Morowitz HJ Universality in intermediary metabolism. Proc. Natl. Acad. Sci. U. S. A 101, 13168–13173 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sousa FL et al. Early bioenergetic evolution. Philos. Trans. R. Soc. Lond. B Biol. Sci 368, 20130088 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lazcano A & Miller SL The origin and early evolution of life: prebiotic chemistry, the pre-RNA world, and time. Cell 85, 793–798 (1996). [DOI] [PubMed] [Google Scholar]
- 10.Deamer D & Weber AL Bioenergetics and life’s origins. Cold Spring Harb. Perspect. Biol 2, a004929 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Martin W & Russell MJ On the origin of biochemistry at an alkaline hydrothermal vent. Philos. Trans. R. Soc. Lond. B Biol. Sci 362, 1887–1926 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Martin W, Baross J, Kelley D & Russell MJ Hydrothermal vents and the origin of life. Nat. Rev. Microbiol 6, 805–814 (2008). [DOI] [PubMed] [Google Scholar]
- 13.Weiss MC et al. The physiology and habitat of the last universal common ancestor. Nature Microbiology 1, 16116 (2016). [DOI] [PubMed] [Google Scholar]
- 14.Russell MJ, Hall AJ & Martin W Serpentinization as a source of energy at the origin of life. Geobiology 8, 355–371 (2010). [DOI] [PubMed] [Google Scholar]
- 15.McDermott JM, Seewald JS, German CR & Sylva SP Pathways for abiotic organic synthesis at submarine hydrothermal fields. Proc. Natl. Acad. Sci. U. S. A 112, 7668–7672 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Parker ET et al. Primordial synthesis of amines and amino acids in a 1958 Miller H2S-rich spark discharge experiment. Proc. Natl. Acad. Sci. U. S. A 108, 5526–5531 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Heinen W & Lauwers AM Organic sulfur compounds resulting from the interaction of iron sulfide, hydrogen sulfide and carbon dioxide in an anaerobic aqueous environment. Orig. Life Evol. Biosph 26, 131–150 (1996). [DOI] [PubMed] [Google Scholar]
- 18.Cody GD Primordial Carbonylated Iron-Sulfur Compounds and the Synthesis of Pyruvate. Science 289, 1337–1340 (2000). [DOI] [PubMed] [Google Scholar]
- 19.Varma SJ, Muchowska KB, Chatelain P & Moran J Native iron reduces CO2 to intermediates and end-products of the acetyl-CoA pathway. Nature Ecology & Evolution 2, (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Huber C Activated Acetic Acid by Carbon Fixation on (Fe,Ni)S Under Primordial Conditions. Science 276, 245–247 (1997). [DOI] [PubMed] [Google Scholar]
- 21.Wachtershauser G Evolution of the first metabolic cycles. Proceedings of the National Academy of Sciences 87, 200–204 (1990). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Fuchs G Alternative Pathways of Carbon Dioxide Fixation: Insights into the Early Evolution of Life? Annu. Rev. Microbiol 65, 631–658 (2011). [DOI] [PubMed] [Google Scholar]
- 23.Dörr M et al. A possible prebiotic formation of ammonia from dinitrogen on iron sulfide surfaces. Angew. Chem. Int. Ed Engl 42, 1540–1543 (2003). [DOI] [PubMed] [Google Scholar]
- 24.Navarro-González R, McKay CP & Mvondo DN A possible nitrogen crisis for Archaean life due to reduced nitrogen fixation by lightning. Nature 412, 61–64 (2001). [DOI] [PubMed] [Google Scholar]
- 25.Martin WF & Thauer RK Energy in Ancient Metabolism. Cell 168, 953–955 (2017). [DOI] [PubMed] [Google Scholar]
- 26.Sousa FL, Preiner M & Martin WF Native metals, electron bifurcation, and CO2 reduction in early biochemical evolution. Curr. Opin. Microbiol 43, 77–83 (2018). [DOI] [PubMed] [Google Scholar]
- 27.Halmann M Evolution and Ecology of Phosphorus Metabolism in The Origin of Life and Evolutionary Biochemistry (eds. Dose K, Fox SW, Deborin GA. & Pavlovskaya TE) 169–182 (Springer; US, 1974). [Google Scholar]
- 28.Schwartz AW Phosphorus in prebiotic chemistry. Philos. Trans. R. Soc. Lond. B Biol. Sci 361, 1743–1749 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Keefe AD & Miller SL Are polyphosphates or phosphate esters prebiotic reagents? J. Mol. Evol 41, 693–702 (1995). [DOI] [PubMed] [Google Scholar]
- 30.Goldford JE, Hartman H, Smith TF & Segrè D Remnants of an Ancient Metabolism without Phosphate. Cell 168, 1126–1134.e9 (2017). [DOI] [PubMed] [Google Scholar]
- 31.Goldford JE & Segrè D Modern views of ancient metabolic networks. Current Opinion in Systems Biology (2018). doi: 10.1016/j.coisb.2018.01.004 [DOI] [Google Scholar]
- 32.Ebenhöh O, Handorf T & Heinrich R Structural analysis of expanding metabolic networks. Genome Inform 15, 35–45 (2004). [PubMed] [Google Scholar]
- 33.Handorf T, Ebenhöh O & Heinrich R Expanding metabolic networks: scopes of compounds, robustness, and evolution. J. Mol. Evol 61, 498–512 (2005). [DOI] [PubMed] [Google Scholar]
- 34.Raymond J & Segrè D The effect of oxygen on biochemical networks and the evolution of complex life. Science 311, 1764–1767 (2006). [DOI] [PubMed] [Google Scholar]
- 35.Petrov AS, Gulen B & Norris AM History of the ribosome and the origin of translation. Proceedings of the (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Aziz MF, Caetano-Anollés K & Caetano-Anollés G The early history and emergence of molecular functions and modular scale-free network behavior. Sci. Rep 6, 25058 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Barve A & Wagner A A latent capacity for evolutionary innovation through exaptation in metabolic systems. Nature 500, 203–206 (2013). [DOI] [PubMed] [Google Scholar]
- 38.Szappanos B et al. Adaptive evolution of complex innovations through stepwise metabolic niche expansion. Nat. Commun 7, 11607 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Pál C & Papp B Evolution of complex adaptations in molecular systems. Nature Ecology & Evolution 1, 1084–1092 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Lipmann F Attempts to map a process evolution of peptide biosynthesis. Science 173, 875–884 (1971). [DOI] [PubMed] [Google Scholar]
- 41.Muchowska KB et al. Metals promote sequences of the reverse Krebs cycle. Nature Ecology and Evolution 1, 1716–1721 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Muchowska KB, Varma SJ & Moran J Synthesis and breakdown of universal metabolic precursors promoted by iron. Nature 569, 104–107 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Meringer M & Cleaves HJ Computational exploration of the chemical structure space of possible reverse tricarboxylic acid cycle constituents. Sci. Rep 7, 17540 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Zubarev DY, Rappoport D & Aspuru-Guzik A Uncertainty of prebiotic scenarios: the case of the non-enzymatic reverse tricarboxylic acid cycle. Sci. Rep 5, 8009 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Vetsigian K, Woese C & Goldenfeld N Collective evolution and the genetic code. Proc. Natl. Acad. Sci. U. S. A 103, 10696–10701 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.David L. a. & Alm EJ Rapid evolutionary innovation during an Archaean genetic expansion. Nature 469, 93–96 (2011). [DOI] [PubMed] [Google Scholar]
- 47.Ochman H, Lawrence JG & Groisman EA Lateral gene transfer and the nature of bacterial innovation. Nature 405, 299–304 (2000). [DOI] [PubMed] [Google Scholar]
- 48.Keller MA, Kampjut D, Harrison SA & Ralser M Sulfate radicals enable a non-enzymatic Krebs cycle precursor. Nature Ecology & Evolution 1, 0083 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Keller MA, Turchyn AV & Ralser M Non-enzymatic glycolysis and pentose phosphate pathway-like reactions in a plausible Archean ocean. Mol. Syst. Biol 10, 725 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Kanehisa M & Goto S KEGG: kyoto encyclopedia of genes and genomes. Nucleic Acids Res 28, 27–30 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Dellomonaco C, Clomburg JM, Miller EN & Gonzalez R Engineered reversal of the β-oxidation cycle for the synthesis of fuels and chemicals. Nature 476, 355–359 (2011). [DOI] [PubMed] [Google Scholar]
- 52.Orth JD, Thiele I & Palsson BØ What is flux balance analysis? Nat. Biotechnol 28, 245 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Henry CS, Broadbelt LJ & Hatzimanikatis V Thermodynamics-based metabolic flux analysis. Biophys. J 92, 1792–1805 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Chandru K et al. Simple prebiotic synthesis of high diversity dynamic combinatorial polyester libraries. Communications Chemistry 1, 30 (2018). [Google Scholar]
- 55.Forsythe JG et al. Ester-Mediated Amide Bond Formation Driven by Wet-Dry Cycles: A Possible Path to Polypeptides on the Prebiotic Earth. Angewandte Chemie - International Edition 54, 9871–9875 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Wächtershäuser G Groundworks for an evolutionary biochemistry: the iron-sulphur world. Prog. Biophys. Mol. Biol 58, 85–201 (1992). [DOI] [PubMed] [Google Scholar]
- 57.Bar-Even A Does acetogenesis really require especially low reduction potential? Biochim. Biophys. Acta 1827, 395–400 (2013). [DOI] [PubMed] [Google Scholar]
- 58.Poudel S et al. Origin and evolution of flavin-based electron bifurcating enzymes. Front. Microbiol 9, 1–26 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Duval S et al. Electron transfer precedes ATP hydrolysis during nitrogenase catalysis. Proceedings of the National Academy of Sciences 110, 16414–16419 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Gogarten JP & Deamer D Is LUCA a thermophilic progenote? Nature microbiology 1, 16229 (2016). [DOI] [PubMed] [Google Scholar]
- 61.Segré D, Ben-Eli D, Deamer DW & Lancet D The lipid world. Orig. Life Evol. Biosph 31, 119–145 (2001). [DOI] [PubMed] [Google Scholar]
- 62.Großkopf T et al. Metabolic modelling in a dynamic evolutionary framework predicts adaptive diversification of bacteria in a long-term evolution experiment. BMC Evol. Biol 16, 163 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Ibarra RU, Edwards JS & Palsson BO Escherichia coli K-12 undergoes adaptive evolution to achieve in silico predicted optimal growth. Nature 420, 186–189 (2002). [DOI] [PubMed] [Google Scholar]
- 64.Andersen JL, Flamm C, Merkle D & Stadler PF A Software Package for Chemically Inspired Graph Transformation. in 73–88 (Springer, Cham, 2016). [Google Scholar]
- 65.Banzhaf W & Yamamoto L Artificial Chemistries. (MIT Press, 2015). [Google Scholar]
- 66.Mall A et al. Reversibility of citrate synthase allows autotrophic growth of a thermophilic bacterium. Science 359, 563–567 (2018). [DOI] [PubMed] [Google Scholar]
- 67.Nunoura T et al. A primordial and reversible TCA cycle in a facultatively chemolithoautotrophic thermophile. Science 359, 559–563 (2018). [DOI] [PubMed] [Google Scholar]
- 68.Ribeiro AJM et al. Mechanism and Catalytic Site Atlas (M-CSA): a database of enzyme reaction mechanisms and active sites. Nucleic Acids Res. 46, D618–D623 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Flamholz A, Noor E, Bar-Even A & Milo R EQuilibrator - The biochemical thermodynamics calculator. Nucleic Acids Res. 40, 770–775 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Noor E, Haraldsdóttir HS, Milo R & Fleming RMT Consistent estimation of Gibbs energy using component contributions. PLoS Comput. Biol 9, e1003098 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Halevy I & Bachan A The geologic history of seawater pH. Science 355, 1069–1071 (2017). [DOI] [PubMed] [Google Scholar]
- 72.Bar-Even A, Flamholz A, Noor E & Milo R Thermodynamic constraints shape the structure of carbon fixation pathways. Biochim. Biophys. Acta 1817, 1646–1659 (2012). [DOI] [PubMed] [Google Scholar]
- 73.Milo R, Jorgensen P, Moran U, Weber G & Springer M BioNumbers--the database of key numbers in molecular and cell biology. Nucleic Acids Res. 38, D750–3 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Schellenberger J et al. Quantitative prediction of cellular metabolism with constraint-based models: the COBRA Toolbox v2.0. Nat. Protoc 6, 1290–1307 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Cytoscape file containing the data for the interactive visualization of the network expansion and its variability.
Excel tables containing all the network expansion data used to generate Figs. 1–4 and Extended Data Figs. 1–5
Supporting Information Text
Data Availability Statement
All data presented in this paper has been deposited in a public repository and can be accessed at: https://github.com/segrelab/BoundaryConditionsForAncientMetabolism