2D (2 Dimensional) TEQR design for Determining the optimal Dose for safety and efficacy

Abstract

Designs, such as the Eff-Tox, OBD (optimal biological dose), STEIN (simple efficacy toxicity interval), and TEPI (toxicity efficacy probability interval) designs, have been proposed to determine the optimal dose of a new oncology drug using both efficacy and toxicity. The goal of these designs is to select the optimal drug dose for further phase trials more accurately than dose finding designs that only consider toxicity, such as the 3 + 3, TEQR (toxicity equivalence range), mTPI (modified toxicity probability interval), and EWOC (escalation with overdose control) designs. We propose a new frequentist design for optimal dose selection, the 2D TEQR design, that is easier to understand and simpler to implement than the TEPI, Eff-Tox, STEIN and OBD designs, as it is based on the empirical or observed toxicity and efficacy rates and does not require specialized computations. We compare the performance of this new design with those of the TEPI, STEIN, Eff-Tox and OBD Isotonic designs. Although for the same sample size and cohort size, the frequentist 2D TEQR design is less accurate than the Bayesian TEPI design and also the STEIN design in selecting the optimal dose, the accuracy of optimal dose selection of the 2D TEQR design can be increased, in many cases, with a moderate increase in cohort size. The 2D TEQR design is as accurate as or more accurate than the Eff-Tox design in optimal dose selection, and better than the OBD Isotonic design, unless there is a clear peak in the true response rates, in which case the OBD Isotonic design performs better than the other designs.

1. Introduction

Several oncology dose finding designs, such as the CRM, mTPI, TEQR, EWOC, BOIN, Keyboard and i3+3 designs [[1], [2], [3], [4], [5], [6], [7], [8], [9], [32]], have been proposed to select the maximum tolerated dose (MTD) of the study drug. These designs select the MTD more accurately than the 3 + 3 design, but use only the toxicity of the drug (dose limiting toxicities (DLTs)) in dose selection.

Designs incorporating both safety and efficacy, such as the Eff-Tox, STEIN, OBD and the TEPI designs [[10], [11], [12], [13], [14]] among others [8,[15], [16], [17], [18], [19], [20], [21], [22], [23], [24], [25], [33]], aim to find a better dose than one determined by safety alone. The MTD selected in a Phase 1 oncology trial may not be the best dose for safety and efficacy, and examples demonstrate how critical it is to select the best dose to avoid poor outcomes in later phase trials and clinical use [34]. The drug pegylated liposomal doxorubicin, for treating platinum resistant ovarian cancer, was approved at 50 mg/m² administered every 28 days, but is commonly used at 40 mg/m² due to greater toxicity at the higher dose but equal efficacy at the lower dose [26]. Other examples where the approved dose and the standard clinical dose differ are provided by Schilsky [27]. Furthermore, adverse effects are assumed to increase with dose, but efficacy need not increase with dose, as seen in some immuno-oncology drugs [28,29]. Hence, it is critical to consider both safety and efficacy concurrently in a single reasonably sized trial to determine the best dose.

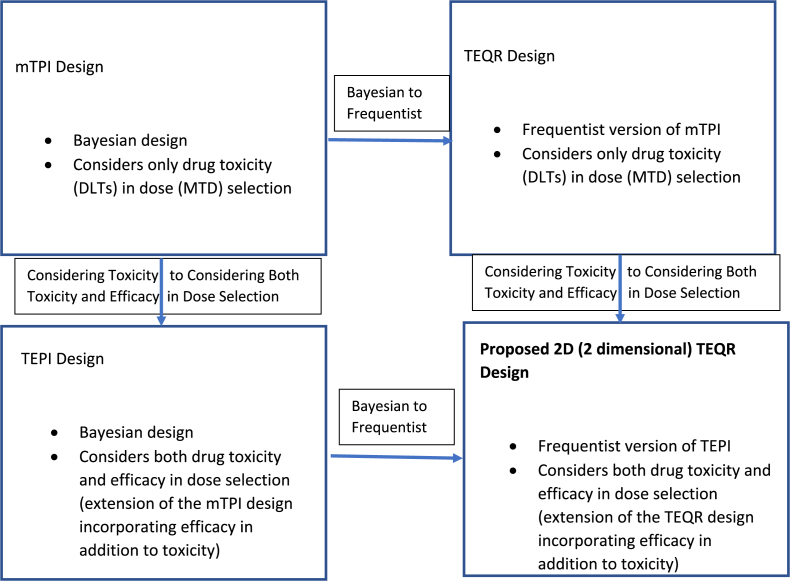
The mTPI is a Bayesian dose finding design that uses the unit probability mass (UPM)s, calculated for underdosing, overdosing and the target intervals from observed DLTs at the current dose level, to make the next dosing decision and determine the MTD. The TEQR design, its frequentist counterpart, uses the DLT rate observed at each dose level for dose finding decisions and determining the MTD. The TEPI is a 2D (2 dimensional) version of the mTPI design, which uses both toxicity and efficacy in determining the optimal drug dose. Here, we propose a non-Bayesian rule-based (frequentist) counterpart of the TEPI design, the 2D TEQR design, which considers toxicity and efficacy to determine the optimal dose (see Fig. 1 for the relationship among the mTPI, TEQR, TEPI and 2D TEQR designs). This design is easier to understand and simpler to implement than the Bayesian TEPI design and requires no complex computation. The Eff-Tox and OBD Isotonic designs are Bayesian designs that consider the efficacy and toxicity outcomes in their dosing algorithm. The Eff-Tox design uses efficacy-toxicity tradeoff contours constructed using three efficacy-toxicity probability pairs considered to be equally desirable as determined by clinical judgement. The contours are used in the dosing decisions (escalate/stay at the same dose/de-escalate) as well as in the final dose selection. The OBD Isotonic design chooses as the optimal dose, the lowest dose with the highest efficacy probability among all the safe doses. The STEIN design, while basing its dosing decisions on the observed DLT and response rates, also incorporates a posterior probability calculation in its dosing algorithm. Isotonic regression is then applied to the observed toxicity rates and model averaging of unimodal isotonic regression(s) is performed on the observed efficacy rates. The final or optimal dose is selected using various utility functions in the STEIN, TEPI and 2D TEQR designs. We compare the operating characteristics of the proposed 2D TEQR design to those of the TEPI, STEIN, Eff-Tox and OBD Isotonic designs and investigate the effect of changing sample and cohort sizes on the accuracy of optimal dose selection of the proposed 2D TEQR design.

Fig. 1.

Relation of mTPI, TEQR, TEPI and Proposed 2D TEQR Designs.

2. Design/methods

2.1. Dosing decisions/dosing algorithm (based on Table 1, Table 2)

Table 1.

Dosing Decision Table for TEQR 2D Design based on the cumulative observed toxicity and efficacy rates at the current dose level subject to acceptable levels at the previous and next dose level(s) (i.e. Table 2 also needs to be considered when Table 1 says Escalate or De-escalate).

	Empirical Efficacy rate low (0, 0.2]	Empirical Efficacy rate moderate (0.2, 0.4]	Empirical Efficacy rate high (0.4, 0.6]	Empirical Efficacy rate superb (0.6, 1]
Empirical Toxicity rate low (0, 0.15]	E	E	E	E
Empirical Toxicity rate moderate (0.15, 0.33]	E	E	E	S
Empirical Toxicity rate high (0.33, 0.4]	D	S	S	S
Empirical Toxicity rate unacceptable (0.4, 1]	D	D	D	D

E, D and S denote “escalate dose”, “de-escalate dose”, and “stay at the same dose” respectively.

Table 2.

Additional Dosing Decisions to Table 1 to be followed for the 2D TEQR design.

Table 1says Escalate
If toxicity rate < toxlim and efficacy rate >= efflim at the next higher dose level, then	Escalate one dose level higher than the current one
If toxicity rate >= toxlim at the next higher dose level, then irrespective of efficacy rate at the next higher dose level	Stay at the same dose level if efficacy rate >= efflim at the same dose level, or if efficacy rate < efflim at the same dose level and the number of patients dosed at this dose level is <= 2*cohort size (this would be 6 patients for cohort size of 3 and 10 patients for cohort size of 5). Otherwise de-escalate one dose level lower than the current one
If toxicity rate < toxlim and efficacy rate < efflim at the next higher dose level, then	Escalate one dose level higher than the current one if the number of patients dosed at the next higher dose level is <= 2*cohort size Stay at the same dose level if the number of patients already dosed at the next higher dose level is >= 3*cohort size and efficacy rate >= efflim at the same dose level, or if efficacy rate < efflim at the same dose level and the number of patients dosed at the same dose level is <= 2*cohort size. Otherwise de-escalate one dose level lower than the current one
Table 1says De-Escalate
If efficacy rate >= efflim at the next lower dose level, then If efficacy rate < efflim at the next lower dose level, then	De-escalate to the next lower dose level than the current one De-escalate to the next lower dose level than the current one if the number of patients at the lower dose is <= 2*cohort size De-escalate one more dose level (i.e. 2 dose levels lower than the current one) if the number of patients at the next lower dose (1 dose level lower than the current one) is >= 3*cohort size
Table 1says Stay	Stay at the same dose

Toxlim and efflim, the upper limit for toxicity and lower limit for efficacy, are parameters chosen by the physician and are respectively 0.51 and 0.1 in this paper.

Our design incorporating toxicity and efficacy in dose selection is a frequentist version of the TEPI design proposed by Li et al. [14]. In the TEQR design, only safety (DLTs) is considered, and the dosing decisions made during the trial are based on the observed DLT rates [4]. In our 2D version of the TEQR design, called the 2D TEQR design, efficacy (response) rates are also used, and the dosing decision table for our proposed 2D TEQR design is given in Table 1. For example, based on Table 1, if the empirical or observed toxicity (DLT) rate is low and the empirical or observed efficacy (response) rate is moderate at the current dose level, then we can escalate to the next higher dose level. However, additional rules are considered in our proposed design when Table 1 recommends escalating or de-escalating a dose level from the current dose, as shown in Table 2. These additional frequentist rules are similar in spirit to the two additional Bayesian rules (safety and futility) proposed and used in the TEPI design. They ensure that we consider dose levels that are neither too toxic nor inefficacious, and that our decision to escalate or de-escalate considers not only the observed cumulative toxicity and efficacy rates at the current dose but also the observed rates at the higher and lower dose(s). In the context of toxicity, note that the underlying toxicity rates are assumed to always increase with an increase in dose, but the underlying efficacy rates need not necessarily increase with an increase in dose. Also, these example rules in Table 2 used in our simulations can be modified for other trials/simulations. The intervals defining low, moderate, high and unacceptable toxicity as well as low, moderate, high and superb efficacy given in Table 1 are example values. They can change for each trial and depend on the maximum accepted toxicity probability and the minimum accepted efficacy probability for that trial and study drug.

Thus, the dosing decisions of a 2D TEQR trial are based on Table 1, Table 2, and these dosing decisions (escalate/stay at the same dose/de-escalate) stop when the maximum sample size is reached or when Table 1 recommends de-escalating from dose level 1. A utility function is then used at the end of the trial to determine the optimal dose based on the toxicity and efficacy data from all the dose levels.

2.2. Selection of optimal dose

In our design, the optimal dose for efficacy and safety is selected at the end of the trial using the following utility function:

$$utilit{y}_i=r_i–c\ast d_i$$

where, i represents the dose level, c is a constant that can vary between 0 and 1, r_i is the fraction of patients having a response and d_i is the fraction of patients with a DLT at dose level i. The dose level i providing the largest value of the utility function is the dose that is selected as optimal at the end of the trial. This kind of utility function was also employed in Ivanova et al. in their adaptive design to find the optimal dose, with application to a crossover dose finding study [30]. Note that c = 1 gives efficacy and toxicity equal weight, while a very small c (say c = 0.1) gives very little weight to toxicity. We also instituted boundary rules such that if the optimal dose selected has a toxicity (DLT) rate ≥ 0.51 or an efficacy (response) rate <0.1, then no dose is considered optimal – the values 0.51 and 0.1 were chosen as limits for toxicity and efficacy for this paper and can be changed for other cases.

3. An example of how the 2D TEQR might work in practice is shown in the appendix

3.1. Simulations

We compared the performance of our proposed 2D TEQR design with that of its Bayesian counterpart, the TEPI design [14], as well as with that of the Eff-Tox design [10,11], that of the STEIN design [12]) and that of the OBD Isotonic design [13], for different scenarios of true efficacy and toxicity rates. The scenarios considered in the main text for true toxicity and efficacy rates are based on those used in Li et al. to evaluate the TEPI design [14]; we also evaluated additional scenarios in the Appendix. For each scenario, we performed 10000 simulations of the 2D TEQR design using SAS. Each simulation stopped when the maximum sample size was reached, or if the design recommended de-escalating from dose level 1. The parameters used in the simulations of the 2D TEQR, TEPI, STEIN, Eff-Tox and OBD Isotonic designs are given in the Appendix.

For each scenario of true toxicity and efficacy rates in the main text, we summarize the average number of patients per dose level, and the percentage of times that each dose level was selected as the optimal dose. For our proposed 2D TEQR design, we selected the optimal dose in each simulation run using the utility function described above – the dose providing the largest value of the utility function in each simulated trial is the dose selected as optimal. If the optimal dose selected in a simulation run, has either a toxicity rate ≥ 0.51 or an efficacy rate <0.1, then no dose level was selected as optimal for that simulation run. The rates of 0.51 and 0.1 are chosen as limits for this paper and can be changed for other cases or trials, and would change the exact value for the accuracy of optimal dose selection from simulations.

We also summarize, for the different scenarios, the average percentages for patients treated at the optimal dose, those that were under-dosed, and those over-dosed. We observed the effect of changing the parameter c in the utility function on the accuracy of optimal dose selection. Finally, we observed the effect of changing the sample size and cohort size used on the accuracy of optimal dose selection.

4. Results

The results in Table 3, Table 4 are obtained by using the parameters shown in Appendix Table 1. In Table 5, the value of c in the utility function is varied, while in Table 6, the sample size and cohort size are varied.

Table 3.

Operating characteristics of the 2D TEQR, TEPI, eff-tox, OBD isotonic and STEIN designs.

Scenario	Dose Level	Toxicity	Efficacy	Percentage Each Dose is Selected as Optimal in Proposed 2D TEQR Design	Percentage Each Dose is Selected as Optimal in TEPI Design	Percentage Each Dose is Selected as Optimal in Eff-Tox Design	Percentage Each Dose is Selected as Optimal in OBD Isotonic Design	Percentage Each Dose is Selected as Optimal in STEIN Design	Average Number of Patients Treated at Each Dose in our TEQR 2D	Average Number of Patients Treated at Each Dose in TEPI Design	Average Number of Patients Treated at Each Dose in Eff-Tox Design	Average Number of Patients Treated at Each Dose in OBD Isotonic Design	Average Number of Patients Treated at Each Dose in STEIN Design
1	1	0.16	0.05	11.8	22.1	0	11.2	23.5	5.1	6.0	3.1	5.4	8.1
	2	0.2	0.1	7.7	17.9	0	20.2	32.8	4.7	5.7	3.1	6.3	8.1
	3	0.25	0.15	6.9	17.2	0	24.7	26.0	3.5	5.1	3.8	6.2	6.4
	4	0.3	0.18	3.4	7.5	8	43.9	9.4	1.9	4.3	5.3	9.2	3.7
2	1	0.15	0.8	66.5	83.9	66	37.9	89.1	9.0	9.1	17.8	9.9	24.4
	2	0.2	0.8	19.7	13.6	30	31.0	8.8	8.2	8.5	8.4	8.0	2.2
	3	0.25	0.8	5.8	2.1	3	18.9	0.8	4.9	5.6	0.7	5.3	0.2
	4	0.3	0.8	1.3	0.3	1	12.3	0.1	2.0	3.8	0.1	3.8	0.0
3	1	0.1	0.1	5.8	7.2	3	0.9	13.4	4.5	4.4	3.7	3.2	5.8
	2	0.2	0.7	65.0	88	42	95.8	84.2	9.9	12.3	11.8	19.1	19.4
	3	0.3	0.2	0.4	0.3	3	3.2	0.7	5.3	7.1	4.3	4.0	1.3
	4	0.7	0.1	0	0.1	2	0.1	0.0	1.1	2.3	2.0	0.6	0.4
4	1	0.15	0.43	49.3	53.9	19	25.1	40.1	6.6	6.1	7.3	8.2	11.6
	2	0.2	0.52	30.8	41.3	49	37.4	51.1	10	9.6	12.4	9.2	11.1
	3	0.4	0.5	4.5	3.6	22	21.9	7.1	5.5	9.0	5.3	5.3	3.6
	4	0.5	0.6	1.1	1.2	5	15.6	0.5	1.2	2.1	1.1	4.4	0.5
5	1	0.1	0.2	16.6	16.4	1	3.6	15.6	5.2	4.7	3.6	3.9	6.2
	2	0.2	0.6	47.5	65.4	48	40.5	66.1	8.6	8.6	12.4	9.4	15.4
	3	0.3	0.6	12.6	13.8	38	34.8	16.4	6.1	7.2	8.5	7.8	4.5
	4	0.4	0.6	2.6	1.0	10	21.1	1.4	2.2	4.9	2.0	5.9	0.7
6	1	0.5	0.4	30.7	33.9	16	45.3	16.9	6.2	14.9	7.9	10.1	13
	2	0.6	0.5	1.5	0.3	13	36.0	1.6	0.9	1.8	6.6	8.3	1
	3	0.7	0.6	0.1	0	2	15.9	0.1	0.05	0.1	1.2	5.3	0
	4	0.8	0.8	0	0	0	2.8	0.0	0	0	0.2	3.3	0

¹The maximum sample size is 27 and the cohort size is 3 for all the designs. The other parameters used for each design are given in the appendix.

²The dose level marked in bold is the optimal dose for each scenario.

No optimal dose is marked for Scenario 6 since even dose level 1 has a high toxicity rate.

No optimal dose is marked for Scenario 1 since dose level 4 has a low response rate.

³The percentages for dose selection for the proposed TEQR 2D design do not always add up to 100, since if the optimal dose selected in a simulation run (using the utility function) has a toxicity rate ≥ 0.51 or an efficacy rate of <0.1, then no dose level is selected as optimal for that simulation run. The percentages for dose selection for TEPI, STEIN, and Eff-Tox need not add to 100, but always do for OBD.

Table 4.

Dosing at optimal dose, under-dosing and over-dosing in the 2D TEQR design and TEPI design.

Scenario	Percentage of Patients Dosed at Optimal Dose in the TEQR 2D Design	Percentage of Patients Under-Dosed in the TEQR 2D Design	Percentage of Patients Over-Dosed in the TEQR 2D Design	Percentage of Patients Dosed at Optimal Dose in the TEPI Design	Percentage of Patients Under-Dosed in the TEPI Design	Percentage of Patients Over-Dosed in the TEPI Design
2	40.6%	0%	59.4%	33.7%	0%	66.3%
3	37.5%	38.5%	24%	47.1%	16.9%	36.0%
4*	37.4% (DL1)	0% (DL1)	62.6% (DL1)	22.8% (DL1)	0% (DL1)	77.2% (DL1)
	37.1% (DL2)	37.4% (DL2)	25.5% (DL2)	35.8% (DL2)	22.8% (DL2)	41.4% (DL2)
5	32.3%	35.1%	32.6%	33.9%	18.5%	47.6%

For Scenario 4, the results are shown for both dose level 1 (DL1) and dose level 2 (DL2), based on Table 3, where dose level 2 is the true optimal dose but dose level 1 is chosen most frequently as the optimal dose by the 2D TEQR and TEPI designs.

Table 5.

Effect of “c” in the utility function on accuracy of optimal dose selection in the 2D TEQR design.

Scenario	Accuracy of Optimal Dose Selection in the 2D TEQR Design when c = 1	Accuracy of Optimal Dose Selection in the 2D TEQR Design when c = 0.5	Accuracy of Optimal Dose Selection in the 2D TEQR Design when c = 0.1
2	66.5%	58.4%	49.9%
3	65.0%	65.9%	65.8%
4*	49.3% (DL1)	39.2% (DL1)	29.5% (DL1)
	30.8% (DL2)	32% (DL2)	27.4% (DL2)
5	47.5%	43.3%	35.6%

*For Scenario 4, the results are shown for both dose level 1 (DL1) and dose level 2 (DL2), based on Table 3, where dose level 2 is the true optimal dose but dose level 1 is chosen most frequently as the optimal dose by the 2D TEQR and TEPI designs.

Table 6.

Effect of sample and cohort size on accuracy of optimal dose selection in the 2D TEQR design.

Scenario	Accuracy of Optimal Dose Selection in the 2D TEQR Design when sample size = 15 and cohort size = 3	Accuracy of Optimal Dose Selection in the 2D TEQR Design when sample size = 27 and cohort size = 3	Accuracy of Optimal Dose Selection in the 2D TEQR Design when sample size = 48 and cohort size = 3	Accuracy of Optimal Dose Selection in the 2D TEQR Design when sample size = 60 and cohort size = 3	Accuracy of Optimal Dose Selection in the 2D TEQR Design when sample size = 25 and cohort size = 5	Accuracy of Optimal Dose Selection in the 2D TEQR Design when sample size = 50 and cohort size = 5	Accuracy of Optimal Dose Selection in the 2D TEQR Design when sample size = 60 and cohort size = 5	Accuracy of Optimal Dose Selection in the 2D TEQR Design when sample size = 80 and cohort size = 5
2	68.6%	66.5%	65.7%	65.1%	66.6%	63.1%	62.5%	63.0%
3	63.7%	65.0%	65.8%	65.9%	82.2%	84.1%	83.7%	84.3%
4*	49.5% (DL1) 30.2% (DL2)	49.3% (DL1) 30.8% (DL2)	49.2% (DL1) 32.3% (DL2)	49.5% (DL1) 33.3% (DL2)	49.5% (DL1) 37.4% (DL2)	49.2% (DL1) 40.3% (DL2)	49.2% (DL1) 41.0% (DL2)	50.3% (DL1) 40.8% (DL2)
5	46.3%	47.5%	48.0%	47.0%	54.1%	54.6%	55.0%	55.8%

*For Scenario 4, the results are shown for both dose level 1 (DL1) and dose level 2 (DL2), based on Table 3, where the true optimal dose is dose level 2 but dose level 1 is chosen most frequently as the optimal dose by the 2D TEQR and TEPI designs.

The proposed frequentist 2D TEQR design is not as accurate as the Bayesian TEPI design in selecting the optimal dose, but is as accurate as or more accurate than the Eff-Tox design in selecting the optimal dose, for the scenarios examined (Table 3). However, the Eff-tox design does treat a larger percentage of patients at the optimal dose compared to the TEPI, 2D TEQR and OBD Isotonic designs in the scenarios presented in Table 3. The STEIN design is very comparable to the TEPI design in terms of accuracy of optimal dose selection and treats a larger percentage of patients at the optimal dose compared to the other designs for the scenarios in Table 3. The OBD Isotonic design does very well compared to the 2D TEQR design and the other designs in terms of optimal dose selection and patient allocation to the optimal dose when there is a clear peak in the true response rates (Scenario 3 of Table 3). Note that the OBD design picks an optimal dose for each simulation run – hence, for Scenario 6, it picks dose level 1 with the lowest toxicity most frequently (Table 3), although the underlying toxicity rate of dose level 1 of 0.5 is higher than the chosen upper bound for the toxicity rate of 0.4. The accuracy of optimal dose selection of the proposed 2D TEQR design can be increased, in many cases, with a moderate increase in cohort size (say cohort size 5; see Table 6 and further examples in the Appendix). The proposed 2D TEQR design puts a comparable percentage of patients at the optimal dose as the Bayesian TEPI design and overdoses a smaller percentage of patients but underdoses a larger percentage of patients, for the scenarios examined (Table 4). For the utility function used here, c = 1 appears to be the best choice in terms of selecting the optimal dose accurately for the proposed 2D TEQR design for the scenarios examined (Table 5 and Appendix scenarios). In each scenario (Table 5), the same dose level is chosen as the optimal dose for c = 1, c = 0.5 and c = 0.1, but is chosen most frequently for c = 1 in most cases (see Scenario 3 of Table 5 where this is not true).

In the scenarios we examined in the main text, where the true optimal dose is a low dose level (dose level 1 or 2), an increase in sample size (say from 27 to 48 for a cohort size of 3, or from 25 to 50 for a cohort size of 5) did not substantially increase the accuracy of optimal dose selection - in fact in Scenario 2 alone, the accuracy of optimal dose selection decreases with an increase in sample size since dose level 2, which has the same efficacy and only a slightly higher toxicity than dose level 1, is chosen more frequently as the sample size is increased (Table 6). However, if the true optimal dose is a higher dose (say dose level 4 or 5), then the accuracy of optimal dose selection is low for a small (inadequate) sample size; in this case, increasing the sample size (from say 25 to 50 for a cohort size of 5) does substantially increase the accuracy of dose selection (see examples in the Appendix).

5. Discussion and conclusion

We propose a new frequentist design for optimal dose selection, the 2D TEQR design, that is easier to understand and simpler to implement than the TEPI, STEIN, Eff-Tox and OBD designs, as it is based on the observed toxicity and efficacy rates and does not require specialized computations. The TEPI, OBD Isotonic and Eff-Tox are Bayesian designs, which require the calculation of posterior probabilities. The STEIN design is model free like the 2D TEQR design and bases its dosing decisions (escalate/stay at the same dose/de-escalate) on the observed DLT and response rates. However, while using the observed DLT and response rates in its dosing algorithm, it also incorporates a posterior probability calculation – the dose level is retained if the observed DLT rate at the dose level is less than the upper critical value for the observed toxicity and the observed efficacy is greater than the critical value for response, but if there is no satisfactory dose, the admissible dose that has the largest posterior probability of efficacy is chosen [12]).

We compare the performance of the proposed 2D TEQR design with those of the TEPI, STEIN, Eff-Tox and OBD Isotonic designs for accuracy of optimal dose selection and patient allocation to the optimal dose. Although the optimal dose selection criterion is not identical for these designs, the same dose level is recognized as the optimal dose level by all the designs for Scenarios 2–5 in Table 3. The frequentist 2D TEQR is not as accurate in selecting the optimal dose as the Bayesian TEPI design for the same sample and cohort size,1 but it is as good as or better than the Eff-Tox design for the scenarios examined. However, the Eff-Tox design treats a larger percentage of patients at the optimal dose compared to the TEPI, 2D TEQR and OBD Isotonic designs for the scenarios examined in Table 3. The 2D TEQR design also selects the optimal dose more accurately than the OBD Isotonic design, unless there is a clear peak in the true response rates, in which case the OBD Isotonic design performs very well compared to the other designs in terms of optimal dose selection and patient allocation to the optimal dose. The STEIN design is very comparable to the TEPI design in terms of accuracy of optimal dose selection and treats a larger percentage of patients at the optimal dose compared to the other designs for the scenarios in Table 3. For many scenarios, the accuracy of optimal dose selection of the proposed 2D TEQR design can be increased for a similar sample size by increasing the cohort size to a moderate cohort size of say 5.

The exact value for the accuracy of optimal dose selection from simulations of the 2D TEQR design would also change with the utility function used. We use a utility function that is very simple to implement and easy to understand - we considered applying isotonic regression to the observed toxicity rates to ensure that they are non-decreasing before applying our simple utility function, but this did not change the accuracy of dose selection substantially in any of the scenarios examined. The accuracy of dose selection would likely be improved with a more complex utility function, similar to the one used in the TEPI design [14]. However, we did not explore other utility functions and systematically evaluate the effect of changing the utility function on the accuracy of optimal dose selection in the 2D TEQR design. For the simple utility function used in this paper, giving equal weight to efficacy and toxicity appears to be the best choice for accuracy of optimal dose selection for the scenarios we examined. Note also that using a utility function at the end of the trial is not the only method to select the final (optimal) dose. As stated in the TEPI paper, the authors could have also proposed to select the dose with the highest probability Pr(p_i<p_T, q_i>q_E+δ|D) as the best dose, where δ is the expected increment over the minimum efficacy rate [14]. The proposed 2D TEQR design puts a comparable percentage of patients at the optimal dose as the TEPI design; it overdoses a smaller percentage of patients, but correspondingly underdoses a larger percentage of patients than the TEPI design.

The accuracy of optimal dose selection of the proposed 2D TEQR design does not increase substantially with an increase in sample size for the scenarios examined in the main text; a sample size of 27 for a cohort size of 3 seems to be adequate to determine the optimal dose in these cases. Note however, that for the scenarios examined in the main text, the true optimal dose is dose level 1 or 2, and in these cases, a large sample size may not be needed. As an example, for a sample size of 27 and cohort size of 3, there are 9 cohorts of patients available, which may be sufficient to determine the optimal dose in these cases where the true optimal dose is a lower dose level. However, if the true optimal dose is dose level 4 or 5 and the sample size is 18 patients with a cohort size of 3, then only 6 cohorts of 3 patients each are available, which may not be sufficient to determine the optimal dose accurately. In such cases, an increase in sample size from 18 to 36 would increase the accuracy of optimal dose selection substantially. The examples shown in the Appendix illustrate the above point - that if the true optimal dose is a higher dose level, then the accuracy of optimal dose selection is low for a small (inadequate) sample size and improves substantially if the sample size is increased. Thus, although in general, the accuracy of optimal dose selection increases with sample size, the percentage of increase in the accuracy of dose selection depends on the true toxicity and efficacy rates, the location of the true optimal dose (i.e. true optimal dose level), the efficacy and toxicity intervals chosen and the upper and lower limits chosen for toxicity and efficacy respectively. We find that this conclusion just described for the 2D TEQR design also holds for the corresponding Bayesian TEPI design regarding the effects of an increase in sample size on the accuracy of optimal dose selection. In the TEPI design too, the accuracy of optimal dose selection increases in many scenarios with a moderate increase in cohort size (simulation results with regard to sample and cohort size are not shown here for the TEPI design).

In conclusion, the proposed 2D TEQR design, a frequentist version of the TEPI design, is a simple design that is easy to understand and implement. Although for the same sample size and cohort size, it is less accurate than the Bayesian TEPI design in selecting the optimal dose, it is simpler to implement and its accuracy of optimal dose selection can be increased, in many cases, with a moderate increase in cohort size.

Appendix A. Supplementary data

The following is the Supplementary data to this article: