Improvement of Signal Inhomogeneity Induced by Radio-frequency Transmit-related Phase Error for Single-step Quantitative Susceptibility Mapping Reconstruction

Abstract

To mitigate the susceptibility inhomogeneity induced by radio-frequency transmit phase error through the whole brain in quantitative susceptibility mapping (QSM) using single-echo gradient echo sequence, we developed a novel single-step QSM reconstruction algorithm and compared it with a previous algorithm in five healthy volunteers. The proposed algorithm had effectively suppressed the susceptibility inhomogeneity through the whole brain and achieved acceptable quality, similar to that of the susceptibility map calculated from a multi-echo gradient echo sequence.

Introduction

Quantitative susceptibility mapping (QSM) is a technique that provides quantification of susceptibility values with high sensitivity of susceptibility changes of the brain, which enables the evaluation of subtle tissue changes underlying neurological pathologies and disorders by directly estimating susceptibility values from phase images. Moreover, susceptibility changes induced by myelin degeneration and abnormal iron overloading mainly influence the concentration and distribution of iron. Previous studies have investigated the usefulness of QSM analysis to clarify the characteristics and underlying mechanisms of various neurological disorders, such as Alzheimer’s and Parkinson’s diseases.^1,2 Scanning for QSM generally uses a multiple spoiled gradient echo sequence (mSPGR) because this sequence can provide the total field map with high signal-to-noise ratio (SNR) from the phase images. However, the scan time is longer for mSPGR sequences because of the requirement of a long TE. The SNR of a phase image shows an interesting behavior in comparison with that of a magnitude image, as the SNR is zero immediately after radio-frequency (RF) irradiation and increases with increasing TE until TE reaches the ${\text{T}}_2^{*}$ value of tissues. Selecting a relatively long TE is required to obtain high-quality images, because the ${\text{T}}_2^{*}$ values are 45, 38, and 80 ms at 3T for the white matter (WM), gray matter (GM), and cerebrospinal fluid (CSF), respectively. Therefore, the scan time of a 1 mm iso-voxel mSPGR sequence with a long TE will be more than 10 min. Earlier studies have proposed the use of a single-echo sequence with a long TE, such as with multi-shot echo-planar imaging (EPI), and the principle of echo shifting with a train of observations sequence (PRESTO)³ for rapid acquisition. However, the B₁ transmit error giving the phase offset (especially at the center of the brain) contributes to the phase of a single-echo sequence.^4,5 This error, which leads to signal inhomogeneity of susceptibility values through the brain, presents a potential problem with QSM reconstruction using a single-echo sequence. A better solution to mitigate the transmit-related phase errors is to perform background field removal techniques with truncated singular value decomposition (TSVD), such as variable kernel size sophisticated harmonic artifact reduction for phase data (VSHARP), because this technique uses the high pass filter approach, which enables the potential mitigation of not only a large phase offset in the boundary but also the phase error induced by B₁ transmit.⁶ However, the optimal TSVD threshold parameters remain unsolved.

A single-step QSM reconstruction technique has been proposed to combine background field removal with dipole inversion as a mean to prevent the error propagation that occurs with each process. On the other hand, total field inversion, as reported by Liu et al.,⁷ is not available for a single-echo sequence, because of the use of an ${\text{R}}_2^{*}$ map calculated from a multi-echo dataset. Conversely, single-step total variation with varying spherical kernel sizes (SS-TVV), as reported by Chatnuntawech et al.,⁸ provides high computational efficiency with a single-echo sequence. However, there is a potential problem regarding the susceptibility inhomogeneity caused by B₁-related phase errors in SS-TVV because SS-TVV cannot eliminate this effect. Here, we introduce a novel single-step QSM reconstruction method to mitigate the effect of B₁ transmit phase errors and compare this technique with SS-TVV in a series of experiments using healthy human brains.

Materials and Methods

Implementation of the SS-TVV-NM

The proposed SS-TVV and norm minimization within the volume of interest (VOI) (SS-TVV-NM) method algorithm has integrated background field removal and dipole inversion to minimize error propagation of each process while mitigating B₁-related transmit errors of single-echo sequences. The integrated background field removal is based on a non-regularized VSHARP (NR-VSHARP) algorithm.⁹ The NR-VSHARP method utilizes kernel sizes with variable spherical mean values (SMVs), which are decreased toward the edge of the VOI, and L2-norm minimization is restricted within the VOI without any regularization. This background field removal technique can accurately distinguish between local and background fields by following the trend in minimization, as described in Eq. [1]:

$${\mathit{argmin}}_{B_L}{\Vert \sum _{i=1}^n{M}_i^{\prime }{F}^{-1}{S}_{i}F\left(B_T-B_L\right)\Vert }_2^2\{\begin{array}{l}i=n,M_i^{\prime }=M_n\hfill \\ i<n,M_i^{\prime }-M_i-M_{i-1}\hfill \end{array}$$ [1]

where n is number of SMV kernels, M_i is the brain binary mask eroded according to the SMV kernel size, S_i is the variable SMV kernel size, and B_T and B_L are the total and local fields, respectively. In this study, the kernel size ranged from 1.5 to 9 mm at 1.5-mm intervals. Moreover, the total variation (TV) is easily combined with the NR-VSHARP as a dipole inversion technique. The TV is solved by the alternative direction method of multiplier (ADMM) algorithm (Eq. [2]), as reported by Bilgic et al. ¹⁰:

$${\mathit{argmin}}_{\chi }{\Vert D_{\chi }-F{B}_L\Vert }_2^2+{\lambda }_{TV}{\Vert G_{\chi }\Vert }_1$$ [2]

where D represents the dipole kernel, χ and B_L are susceptibility and local field maps, respectively, F is the Fourier transform, λ_TV is the L1-regularization parameter, and G is the gradient kernels of the x, y, and z coordinates in the Fourier domain, respectively. We then integrated these background field removal and dipole inversion algorithms as a single-step QSM reconstruction, as expressed by Eq. [3].

$${\mathit{argmin}}_{\chi }\frac{1}{2}{\Vert \sum _{i=1}^n{M}_i^{\prime }{F}^{-1}{S}_{i}F\left(B_T-F^{-1}D\chi \right)\Vert }_2^2+{\lambda }_{TV}{\Vert G\chi \Vert }_1$$ [3]

Equation [3] adopted the ADMM formalism and introduced additional variables z and s.

$$\begin{array}{l}{\mathit{argmin}}_{\chi ,Z}\frac{1}{2}{\Vert \sum _{i=1}^n{M}_i^{\prime }{F}^{-1}{S}_{i}F\left(B_T-F^{-1}D\chi \right)\Vert }_2^2\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\frac{\mu }{2}{\Vert G\chi -z+s\Vert }_2^2+{\lambda }_{TV}{\Vert z\Vert }_1\end{array}$$ [4]

where z is an auxiliary variable and s is the scaled Lagrange multiplier. Equation [4] was solved by two-phase iteration by splitting into the following subproblems, as shown in Eqs. [5] and [6].

$$\begin{array}{l}{\chi }_{t+1}\hspace{0.17em}{\mathit{argmin}}_{\chi }\frac{1}{2}{\Vert \sum _{i=1}^n{M}_i^{\prime }{F}^{-1}{S}_i\left(F{B}_{\text{T}}-D\chi \right)\Vert }_2^2\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\frac{\mu }{2}{\Vert G\chi -z+s\Vert }_2^2\end{array}$$ [5]

$$z_{t+1}={\mathit{argmin}}_z{\lambda }_{TV}{\Vert z\Vert }_1+\frac{\mu }{2}{\Vert G\chi -z+s\Vert }_2^2$$ [6]

This variable splitting allows to effectively minimize L1-norm via L2-minimization and soft-thresholding by iterative optimizations of χ and z separately. The most remarkable quality of SS-TVV-NM is the ability to restrict L1-norm minimization only within VOI. Therefore, the proposed algorithm is solved in Eq. [4] by the addition of a preconditioned gradient method as an iterative calculation. Moreover, Eq. [6] allows to solve with a soft-thresholding operation, as shown in Eq. [7].

$$z_{t+1}=\text{max}{\left(\left|G\chi +s\right|-\frac{{\lambda }_{TV}}{\mu },0\right)}^{*}sign\left(G\chi +s\right)$$ [7]

Here, s was updated, as shown in Eq. [8].

$$s=s+G\chi -z$$ [8]

Here, we chose a stop criterion of 0.001 and the number of maximal iterations for the inner loop for the minimization of 30, as in Eq. [4]. As a result, each B₁-related phase error will be mitigated because of early termination of Eq. [4], which gives the effect of L2-regularization and will slightly compress the resulting value. This phase error introduced the larger susceptibility inhomogeneity, as compared with the intrinsic susceptibility value in brain tissue, so that the early termination of minimization enables suppression of the signal inhomogeneity of the susceptibility map. A stop criterion derived from the optimization of Eq. [3] was determined with the solution change remaining below 1%. Moreover, we chose the fixed L1-regularization parameter of 0.0001. This relatively small regularization parameter introduces severe streaking artifacts because of the zero cone of the dipole kernel. Therefore, the streaking artifact estimation process based on improved sparse linear equation and least-square algorithm (iLSQR)^3,11 was added using Eqs. [9] and [10] after estimation of the initial susceptibility value obtained in Eq. [3] with a relatively small regularization parameter (i.e., 0.0001) to save the details of the edges of brain structures.

$${\mathit{argmin}}_{{\chi }_{SA(k)}}\sum {\Vert W_{G_i}{F}^{-1}{G}_i\left\{{\chi }_{TV}-\left({\chi }_{SA\left(k\right)}{M}_{IC}\right)\right\}\Vert }_2^2$$ [9]

where χ_SA(k) is the streaking artifacts estimated from the initial susceptibility map in the Fourier domain, G is the gradient operator in the Fourier domain, W_Gi is the weight mask calculated from the initial susceptibility given by Eq. [3] based on iLSQR, and M_IC is the binary image representing ill-conditioned k-space points in the dipole kernel, as defined in Eq. [10].

$$M_{IC}=\left|D_{\left(k\right)}\right|<D_{\left(k\right),threshold}$$ [10]

where D_{(k),threshold} is 0.1 for M_IC. The susceptibility map is calculated by subtracting the estimated streaking artifacts from the initial susceptibility, as calculated by Eq. [3] and as expressed in Eq. [11].

$${\chi }_{SS-TVV-NM}=F^{-1}\left({\chi }_{TV}-{\chi }_{SA\left(k\right)}{M}_{IC}\right)$$ [11]

Equation [11] provides a high-quality susceptibility map with minimization of the streaking artifacts and signal inhomogeneity due to the use of a single-echo sequence.

Implementation of the single-step total variation with variable kernel size

The SS-TVV was proposed by Chatnuntawech et al.⁸ to achieve rapid calculation and accurately estimate the susceptibility map. SS-TVV is solved in Eq. [4] by splitting the subproblems into Eqs. [5] and [6]. The difference between SS-TVV-NM and SS-TVV is the use of a simple closed-form solution for greater computational efficiency. Additionally, it is extremely difficult to reconstruct a high-quality susceptibility map with SS-TVV while maintaining the details of brain structures because of the relevant selections of the regularization parameters and the loss of details remain unsolved. Therefore, a relatively small regularization (0.0001) was used to maintain the edge among the structures and all severe streaking artifacts. After the initial susceptibility map was estimated, an estimation of the streaking artifacts was also performed for the susceptibility map obtained from SS-TVV using Eqs [9]–[11], as with SS-TVV-NM. These processes successfully minimized the relevant parameters of both methods and were, therefore, used for unbiased comparisons between SS-TVV-NM and SS-TVV.

Human brain experiments

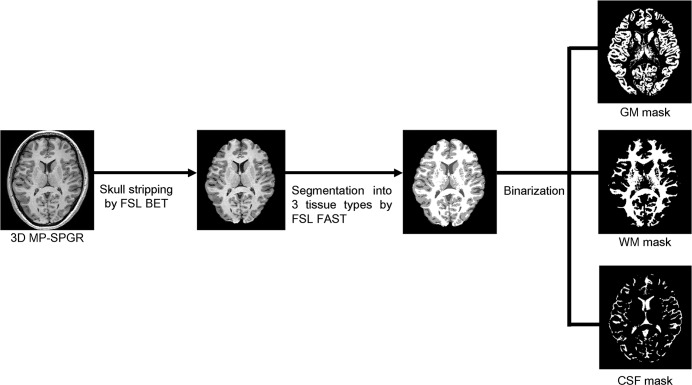
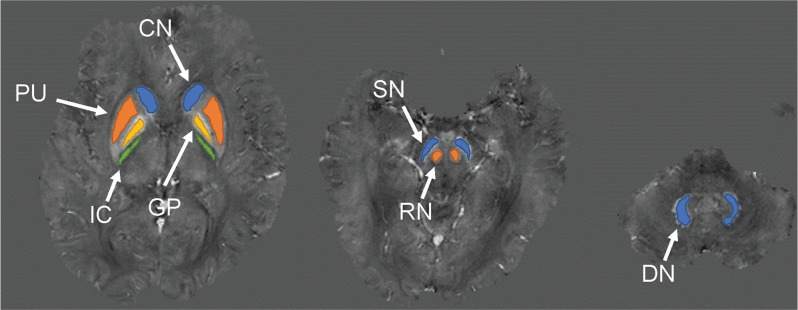
Human brain experiments were performed to validate the superiority of our proposed reconstruction algorithm by comparisons with the existing algorithm. The Institutional Review Board approved the study and informed consent was obtained from all participants. Using a 3T MRI system (Hitachi, Ltd., Tokyo, Japan), single-echo SPGR (sSPGR) sequences of five healthy male volunteers (median age, 28 years; range, 25–37 years) were obtained using a 32-channel head-coil with the following parameters: FOV, 192 × 192 × 140; acquisition matrix size, 192 × 192 × 140 mm³; TR, 35 ms; TE, 30 ms; and flip angle, 15°. Additionally, the mSPGR sequence was set to similar parameters of the sSPGR sequence, except for TE, that is, the TE for mSPGR was set at 6–30 ms at 6-ms intervals. The total field was calculated from multiple phase data in mSPGR. The weighted Laplacian-based phase unwrapping with preconditioned conjugate gradient algorithm was used to extract the phase jumps from both sequences. Subsequently, our SS-TVV-NM algorithm and the previous SS-TVV method were applied to the total field of sSPGR and mSPGR. Note that the binary brain mask extracted by the brain extraction tool was eroded by spherical mean value filtering combined with the dipole inversion process for a robust and accurate susceptibility estimation in the edge of the brain. In this study, the minimal kernel size of spherical mean value filtering was set at 1.5 mm, so that the erosion size of the brain mask was approximately 3 mm. To evaluate the susceptibility inhomogeneity through the whole brain, magnetization-prepared SPGR (MP-SPGR) enhanced T₁ contrast was also acquired. The detailed scan parameters for MP-SPGR were FOV, 192 × 192 × 140; acquisition matrix size, 192 × 192 × 140 mm³; TR, 9.6 ms; TE, 4.8 ms; flip angle, 7°; inversion time, 1000 ms; and shot interval, 2000 ms. The MP-SPGR data were stripped of the head and skull with the brain extraction tool and then segmented into WM, GM, and CSF components using the automated segmentation tool FAST of the Functional Magnetic Resonance Imaging of the Brain Software Library (FMRIB Analysis Group, Oxford, UK). The segmentation results were binarized to generate a mask for each component (Fig. 1). Comparisons of our SS-TVV-NM with SS-TVV were made to identify differences in signal inhomogeneity of each susceptibility map by estimating the standard deviation (SD) of the susceptibility map within the WM, CSF, and GM masks. To investigate the positional dependence of the susceptibility inhomogeneity, the SDs in the slice positions shown in Fig. 2 were measured. Moreover, ROI analysis was performed in iron-rich tissues, such as the basal ganglia (Fig. 3).

Fig. 1.

Flowchart of the generation of the GM, WM, and CSF masks. 3D magnetization-prepared gradient echo sequences, which provide strong T₁ contrast, were obtained. A 3D dataset was constructed with skull-stripping and then segmented into three tissue types (WM, GM, and CSF). The segmented masks were binarized for VOI analyses through the whole brain. WM, white matter; GM, gray matter; CSF, cerebrospinal fluid; VOI, volume of interest; MP-SPGR, magnetization-prepared spoiled gradient echo; FSL BET, brain extraction tool; FSL FAST, FMRIB’s automated segmentation tool.

Fig. 2.

Location of slice position to investigate the effects of slice position-dependent susceptibility inhomogeneity. The standard deviations of the susceptibility value were measured in the centrum semiovale level (Slice 1), basal ganglia level (Slice 2), and cerebellum level (Slice 3).

Fig. 3.

Locations of the ROIs. The ROIs were placed on CN, PU, GP, IC, SN, RN, and DN. ROI, region of interest. CN, caudate nucleus; PU, putamen; GP, globus pallidus; IC, internal capsule; SN, substantia nigra; RN, red nucleus; DN, dentate nucleus.

Furthermore, a multi-shot 3D gradient EPI (SPGR-EPI) sequence was also obtained to determine whether the SS-TVV-NM algorithm was suitable to enable rapid acquisition, as compared with mSPGR and sSPGR, and to evaluate the signal inhomogeneity of the susceptibility map. The scan parameters for SPGR-EPI were FOV, 192 × 192 × 140; acquisition matrix size, 192 × 192 × 140 mm³; TR, 50 ms; TE, 30 ms; flip angle, 15°; EPI factor, 11; and echo spacing, 2.8 ms. The SPGR-EPI sequence did not perform the analysis of the signal inhomogeneity of the susceptibility map because the SPGR-EPIs were slightly distorted because of the high accelerating EPI factor. The shape and position of the brain in SPGR-EPI were not equivalent to those in MP-SPGR; thus, the sequence was evaluated only with the visualization focused on the reconstruction of a uniform susceptibility map.

Results

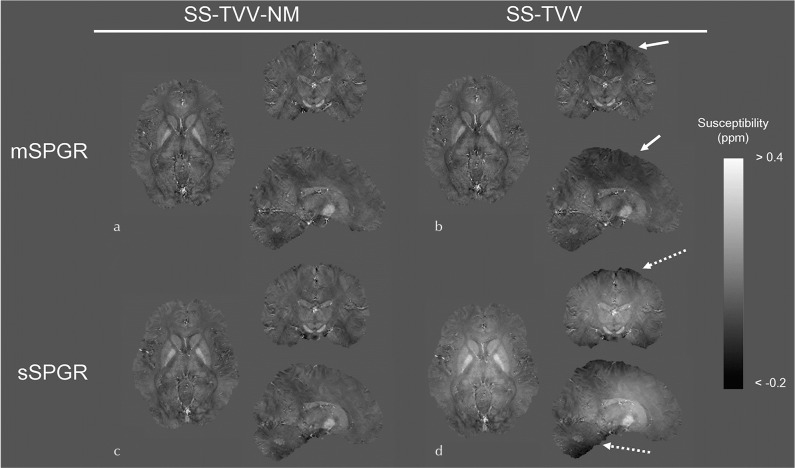
In the human brain experiments, the image quality of the susceptibility maps estimated by SS-TVV-NM were adequate with both mSPGR and sSPGR (Fig. 4a and 4c). A signal inhomogeneity can be slightly observed in the parietal lobe of the susceptibility map estimated from mSPGR and SS-TVV (Fig. 4b, arrows). Additionally, a large shading artifact of susceptibility was found in the map calculated by sSPGR and SS-TVV (Fig. 4d, dashed arrow). The numerical data of ROI analyses through the whole brain using WM, CSF, and GM masks are presented in Table 1. The SDs in the all masks with the combination of sSPGR and SS-TVV were higher than those of other combinations by about 1.5- to 2.0-fold. The SDs in the combination of mSPGR and SS-TVV was slightly higher than the combinations with SS-TVV-NM. The effects of slice position against susceptibility homogeneity are shown in Table 2. In the result of Slice 1, the SDs were high not only in the SS-TVV with sSPGR but also in the SS-TVV with mSPGR slightly, while there were not clear differences in the SDs in the Slices 2 and 3, except for the combination of sSPGR and SS-TVV. The results of ROI analyses based on iron-rich tissues showed that the susceptibility values were equivalent between the two methods using mSPGR and the combination of sSPGR and SS-TVV-NM (Table 3). Conversely, the difference in the susceptibility value, as estimated by sSPGR and SS-TVV, was large in comparison with the other combinations.

Fig. 4.

Susceptibility maps estimated by SS-TVV-NM and SS-TVV from mSPGR and sSPGR, respectively. A slight signal inhomogeneity was observed in the map estimated by SS-TVV from mSPGR (dashed arrow). Moreover, a large shading was observed by the combination of SS-TVV and sSPGR (dashed arrow). mSPGR, multiple spoiled gradient echo sequence; sSPGR, single-echo spoiled gradient echo sequence; SS-TVV-NM, single-step total variation with variable kernel size and norm minimization within the volume of interest.

Table 1.

SD of susceptibility values in the WM, CSF, GM masks through the whole brain

SD of susceptibility value (ppm)	Volunteer	mSPGR		sSPGR
		SS-TVV-NM	SS-TVV	SS-TVV-NM	SS-TVV
WM	1	0.038	0.042	0.029	0.074
	2	0.037	0.045	0.034	0.057
	3	0.040	0.043	0.034	0.060
	4	0.038	0.045	0.035	0.057
	5	0.033	0.038	0.032	0.062
CSF	1	0.067	0.069	0.053	0.077
	2	0.065	0.071	0.054	0.072
	3	0.079	0.082	0.061	0.076
	4	0.062	0.067	0.055	0.072
	5	0.071	0.074	0.058	0.080
GM	1	0.046	0.049	0.034	0.072
	2	0.044	0.049	0.039	0.058
	3	0.051	0.052	0.041	0.061
	4	0.040	0.045	0.035	0.056
	5	0.042	0.045	0.036	0.061

mSPGR, multiple spoiled gradient echo sequence; SS-TVV-NM, single-step total variation with variable kernel size and norm minimization; WM, white matter; CSF, cerebrospinal fluid; GM, gray matter; SD, standard deviation; sSPGR, single-echo spoiled gradient echo sequence.

Table 2.

SD of susceptibility values in the centrum semiovale level (Slice 1), basal ganglia level (Slice 2), and cerebellum level (Slice 3)

SD of susceptibility value (ppm)	Volunteer	mSPGR		sSPGR
		SS-TVV-NM	SS-TVV	SS-TVV-NM	SS-TVV
Slice 1	1	0.021	0.023	0.014	0.040
	2	0.024	0.026	0.020	0.030
	3	0.022	0.025	0.019	0.036
	4	0.021	0.024	0.017	0.025
	5	0.020	0.022	0.019	0.040
Slice 2	1	0.032	0.032	0.026	0.056
	2	0.035	0.037	0.032	0.041
	3	0.039	0.038	0.033	0.047
	4	0.038	0.039	0.035	0.046
	5	0.032	0.032	0.030	0.047
Slice 3	1	0.017	0.015	0.014	0.024
	2	0.016	0.017	0.015	0.026
	3	0.018	0.014	0.015	0.023
	4	0.017	0.016	0.015	0.025
	5	0.014	0.013	0.015	0.022

mSPGR, multiple spoiled gradient echo sequence; SS-TVV-NM, single-step total variation with variable kernel size and norm minimization within the volume of interest; SD, standard deviation; sSPGR, single-echo spoiled gradient echo sequence.

Table 3.

Mean susceptibility values in CN, PU, GP, IC, SN, RN, and DN.

Mean susceptibility value (ppm)	Volunteer	mSPGR		sSPGR
		SS-TVV-NM	SS-TVV	SS-TVV-NM	SS-TVV
CN	1	0.0975	0.092	0.075	0.209
	2	0.0995	0.104	0.076	0.126
	3	0.103	0.084	0.090	0.171
	4	0.0815	0.095	0.082	0.133
	5	0.0645	0.066	0.065	0.144
GP	1	0.147	0.163	0.138	0.273
	2	0.122	0.135	0.132	0.193
	3	0.158	0.140	0.147	0.233
	4	0.227	0.236	0.229	0.287
	5	0.167	0.162	0.173	0.260
PU	1	0.073	0.095	0.064	0.189
	2	0.078	0.098	0.082	0.135
	3	0.083	0.077	0.072	0.154
	4	0.079	0.094	0.092	0.155
	5	0.064	0.066	0.070	0.149
IC	1	−0.016	−0.015	−0.022	0.091
	2	−0.034	−0.020	−0.012	0.043
	3	−0.012	−0.026	−0.035	0.042
	4	−0.032	−0.028	−0.029	0.031
	5	−0.019	−0.030	−0.005	0.090
SN	1	0.106	0.099	0.098	0.180
	2	0.143	0.163	0.1395	0.171
	3	0.131	0.131	0.0905	0.147
	4	0.150	0.165	0.1375	0.158
	5	0.137	0.126	0.141	0.191
RN	1	0.120	0.111	0.128	0.199
	2	0.068	0.111	0.064	0.094
	3	0.099	0.094	0.096	0.140
	4	0.094	0.111	0.099	0.128
	5	0.047	0.038	0.060	0.113
DN	1	0.078	0.084	0.079	0.023
	2	0.062	0.059	0.056	−0.001
	3	0.058	0.053	0.044	−0.012
	4	0.116	0.117	0.107	0.047
	5	0.050	0.049	0.040	0.007

mSPGR, multiple spoiled gradient echo sequence; SS-TVV-NM, single-step total variation with variable kernel size and norm minimization within the volume of interest; CN, caudate nucleus; PU, putamen; GP, globus pallidus; IC, internal capsule; SN, substantia nigra; RN, red nucleus; DN, dentate nucleus; sSPGR, single-echo spoiled gradient echo sequence.

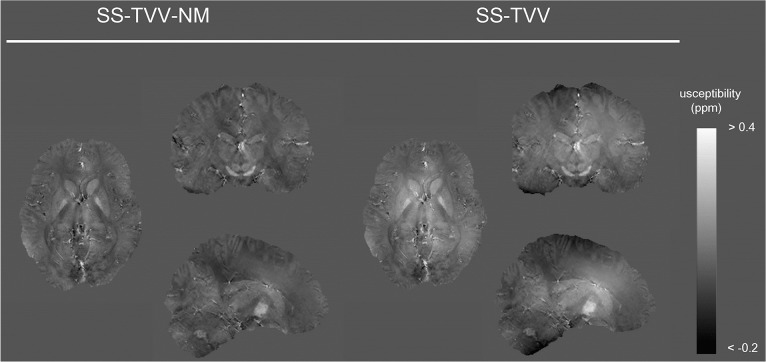
A susceptibility map using SPGR-EPI was successfully estimated by SS-TVV-NM while maintaining image quality, and the sequence enabled a reduction in scan time by 6.7-fold. The susceptibility map obtained with SPGR-EPI and SS-TVV-NM was similar to that obtained with the combination of sSPGR and SS-TVV-NM (Fig. 5).

Fig. 5.

Susceptibility maps estimated from multi-shot gradient EPI (SPGR-EPI) sequence by SS-TVV-NM and SS-TVV. The obtained susceptibility maps had similar tendencies in terms of signal inhomogeneity of the results of sSPGR. SS-TVV-NM, single-step total variation with variable kernel size and norm minimization within the volume of interest.

Discussion

We developed a novel single-step QSM reconstruction algorithm combined with background field removal and dipole inversion processes to correctly estimate a susceptibility map so that the B₁-related phase error was less contaminated by the intrinsic total field induced by the interactions between the tissues and background field. An advantage of SS-TVV-NM is the ability to accurately estimate a susceptibility map even from a single-echo sequence, similar to that with a multi-echo sequence. In particular, the phase of single-echo sequences, such as PRESTO and SPGR-EPI, include the spatial phase offset related to RF transmit.^4,5 Eventually, the previous algorithm cannot be easily adopted to this sequence. The SS-TVV-NM is combined with the L1-norm minimization restricted inside of the brain mask, newly background field removal, and a process to remove severe streaking artifacts. The B₁-related phase offset included in the single-echo sequence was effectively suppressed by restriction of L1-norm minimization within the brain with a relatively small stop criterion and a small number of maximal iterations in the inner loop. Moreover, the use of varying SMV kernel sizes works well to suppress the background field and save the cortical information to achieve a lower phase error.^6,9 Additionally, the small stop criterion and a maximal iteration number work like L2-regularization and, as a result, the susceptibility value is compressed. The summation of the background field and B₁-related offset was higher than the intrinsic tissue field by more than 10-fold. Therefore, SS-TVV-NM can effectively mitigate only the background and B₁-related fields. Even with the application of SS-TVV-NM to a total field without B₁ phase errors, SS-TVV-NM correctly estimated the susceptibility map, as shown by the results obtained with mSPGR. This might be due to the use of small stop criterion and a maximal number of iterations, which mitigated only the redundant field (i.e., the background field).

In the human study, the SS-TVV-NM algorithm had homogeneously estimated the susceptibility map because of its robustness against the redundant errors, including the B₁-related phase error. The results of the map estimated by SS-TVV from sSPGR can be explained by the B₁-related phase error. The B₁-related phase error induces the large phase signal offset. Therefore, the combination of SS-TVV and sSPGR had a greater susceptibility inhomogeneity through the whole brain in comparison with SS-TVV-NM. The SDs through the whole brain shown in Table 1 revealed the presence of a signal inhomogeneity in the map estimated by SS-TVV from sSPGR because the SD was clearly higher than with other methods. This signal inhomogeneity and offset can also be verified in Table 3. The SS-TVV-NM was successfully reconstructed the susceptibility map while minimizing the B₁-related phase error, because the SDs when using SS-TVV-NM and sSPGR were low in comparison with cases using SS-TVV. Moreover, the SD in the combination of sSPGR and SS-TVV-NM was similar to those of mSPGR with SS-TVV and SS-TVV-NM, and the susceptibility values in the iron-rich tissues were equivalent. These results indicated that SS-TVV-NM is suitable for reconstruction of susceptibility map from single-echo sequence. On the other hand, the fact that the susceptibility map generated by mSPGR with SS-TVV was slightly inhomogeneous shown in Fig. 4b and Tables 1 and 2 can be explained by that the mSPGR sequence cannot utilize a full flow compensation for all echoes.¹² This caused a phase error at each echo. Eventually, the total field estimation for mSPGR was inaccurate. The SS-TVV algorithm utilized a simple closed-form solution and soft-thresholding process, which achieved high computational efficiency. However, the SS-TVV had accurately computed the susceptibility value from the field without any extra redundant fields caused by errors of the total field estimation and the limitations of pulse sequences, whereas the SS-TVV-NM algorithm has flexibility against these errors occurring in a clinical situation.

The susceptibility maps estimated by both algorithms with the SPGR-EPI sequence, which is a single-echo sequence, was similar to that of the sSPGR results because the map using SS-TVV had a large signal offset and inhomogeneity, as compared with the map obtained with SS-TVV-NM. A clear merit is that SPGR-EPI successfully aids to reduce the scan time while maintaining image quality, although multi-shot EPI leads to subtle image distortion because of the accelerating EPI factor. In the clinical setting, the rapid acquisition is important for diseases characterized by a decline in cognitive function because of the common association with regional abnormal iron metabolism.

In this study, the statistical analysis was not performed for the data obtained from the human brain experiments, because the sample size was not enough to make the statistical test. However, the purpose of this paper was to report the development of a robust QSM algorithm for single-echo sequences. The results of visualization obtained from the susceptibility maps clearly revealed the superiority of the proposed SS-TVV-NM algorithm. Moreover, optimization of the pulse sequences could not be performed in terms of full flow compensation, because the clinical MRI system requires a specific sequence. The full flow compensation, which rendered the quality of the resulting susceptibility map superior, may enable minimization of the flow-induced phase error and the error of the total field estimation. We could not evaluate the quantitative accuracy of SS-TVV-NM, since it is impossible to reconstruct the gold standard susceptibility map in this study. Because the imperfection of background field removal, RF transmit error for single-echo sequence, and the flow compensation-related phase error for multi-echo sequence cannot be eliminated by any dipole inversion algorithms, such as calculation of susceptibility through multiple orientation sampling (COSMOS) method. However, the results of ROI analysis in iron-rich tissues, which demonstrated that the susceptibility values in sSPGR and mSPGR with SS-TVV-NM were almost equivalent to that in mSPGR with SS-TVV, might indicate the validity of SS-TVV-NM. Despite these limitations, the human experiment results revealed the robustness of the SS-TVV-NM algorithm against the extra phase errors generated by the clinical scanner and the superiority of the proposed algorithm.

Conclusion

The proposed SS-TVV-NM QSM algorithm provides susceptibility maps with acceptable quality without image inhomogeneity and allows for correct estimation of the generated susceptibility map.