An evolutionary stable strategy to colonize spatially extended habitats

Abstract

The ability of a species to colonize newly available habitas is crucial to its overall fitness. Generally, motility and fast expansion is expected to be beneficial to the colonization process and hence to organismal fitness. Here we apply a unique evolution protocol to investigate phenotypical requirements for colonizing habitats of different sizes during range expansion of chemotaxing bacteria. Contrary to the intuitive expectation that faster is better, we show the existence of an optimal expansion speed associated with a given habitat size. Our analysis showed this effect to arise from interactions among pioneering cells at the front of the expanding population, and revealed a simple, evolutionary stable strategy for colonizing a habitat of a specific size: to expand at a speed given by the product of the growth rate and habitat size. These results illustrates stability-to-invasion as a powerful principle for the selection of phenotypes in complex ecological processes.

Evolution in bacterial range expansion

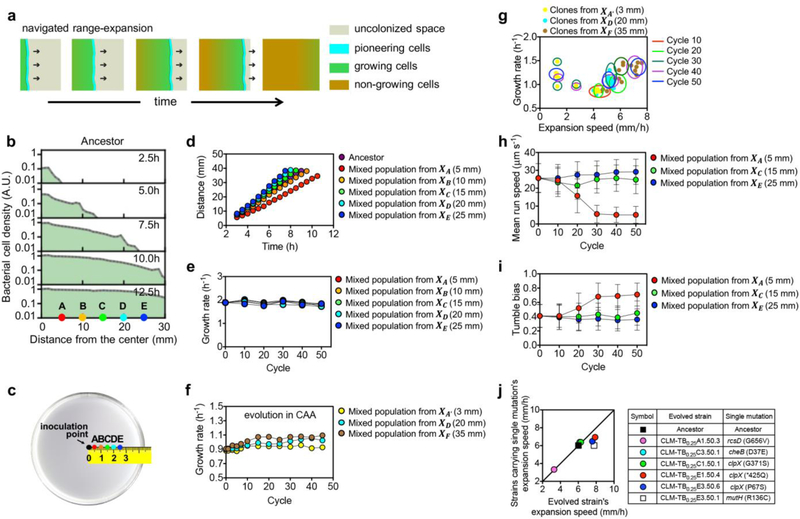
When an organism encounters an unoccupied habitat, it colonizes the habitat by the process of growth and expansion^1–8. In a recent quantitative study of chemotaxis-mediated bacterial range expansion⁹, it has been elucidated that the characteristics of the expanding population is dominated by a group of pioneering cells at the population front; these pioneerers move outward, replicate, and leave behind offsprings (settlers) to grow and occupy the territories traversed; see Extended Data Fig. 1a,b; Supplementary Video 1. To understand the determinants of colonization behind the front, we modified common experimental evolution protocols^10–15 to select for cells at various distances from the point of the initial invasion, well after the passage of the front: Motile E. coli cells inoculated at the center of a semi-solid Tryptone Broth (TB) agar plate were given time to expand outward and colonize the entire plate^2,9,16. 24 hours after inoculation, after the entire plate was full of bacteria, a small volume of agar (containing ~7.4 × 10⁶ cells) was taken at a specific radius and directly transferred to the center of a fresh plate (Fig. 1a). The process was repeated for 50 cycles (~600 generations), with the transferred samples always taken at the same distance. Five such series were generated at 5 different distances from the origin (marked by positions A-E in Extended Data Fig. 1c).

Figure 1. Experimental evolution with position-dependent selection.

a, Schematic illustration of the evolution experiment. Exponentially growing E. coli CLM cells²⁷ (the ‘ancestor’) were inoculated at the center of 0.25 % TB agar plate; after 24h incubation at 37°C, after the bacteria have colonized the entire plate, a 2μl cell-agar mixture was taken at a distance X away from the plate center and inoculated at the center of a fresh plate; see Methods for details. The cycle was repeated with the samples always taken after 24 hours at the same distance X as in previous cycles. b, Expansion speeds of population samples from each of the 5 selection series are shown from Lineage 1 at various evolution cycles. Experiments were repeated 3 times obtaining similar results (see text and Extended Data Fig. 2). c, The expansion speed of 300 individual clones (60 for each selection series) isolated from the population samples at the 50^th cycle. Histogram for each series is shown with the corresponding colors. The average expansion speed of the mixed population of each selection series at 50^th cycle (shown in Extended Data Fig. 1d) are shown as the dashed lines for comparison. The expansion speeds of the ancestor and 6 mutant strains isolated at the 50^th cycle (strain A, B, B’, C, D, E) are indicated on the top of the panel, which resembled the averge expansion speed of the corresponding mixed population of lineage 1.

We first evaluated the growth and expansion characteristics of samples collected at various cycles. When inoculated on fresh TB plates, the evolved populations still expanded steadily outward (Extended Data Fig. 1d), but characterized by expansion speeds with distinct dependences on the selection distance (Fig. 1b): Populations collected at outer radii exhibited a steady increase in expansion speeds while those collected at inner radii exhibited a steady decrease, leaving an intermediate selection distance (position C, with distance X_C= 15 mm) at which the expansion speed of the evolved populations fluctuated around that of the ancestor (~6 mm/h) throughout the evolution process. These results are highly reproducible across different replicates and in different growth media containing generic amino acid supplements (Extended Data Fig. 2a–c). The divergent pattern of the evolved expansion speeds obtained (Fig. 1b) is not the result of a simple trade-off with the rate of cell growth^11,13,17: The batch culture growth rates changed very little for strains evolved in TB (Extended Data Fig. 1e). Strains evolved in casamino acids (CAA) generally showed growth rate improvements (Extended Data Fig. 1f,g); yet, changes in their expansion speeds still followed the divergent pattern in accordance to their selection positions (Extended Data Fig. 2c). On the other hand, expansion speeds increased regardless of selection positions for strains evolved in medium with glycerol and no chemotractants (Extended Data Fig. 2d), suggesting the importance of chemotaxis underlying the divergent evolution phenomenon shown in Fig. 1.

An examination of 300 strains sampled from the 50^th cycle of the 5 evolved series across 3 replicates found the distributions of expansion speeds of individual strains to be well reflected by the previous measurements of samples containing mixed populations (Fig. 1c). Furthermore, changes in expansion speeds are consistent with changes in motility characteristics of the evolved cells obtained from single-cell analysis (Extended Data Fig. 1h,i), and with mutations identified from genomic sequence analysis: Sequencing of population samples at the 50^th cycle of each evolved series yielded a multitude of mutations as enumerated in Supplementary Table 1. Several dominant mutations were introduced individually into the ancestral strain; they were found to change the expansion speeds of the ancestral strain towards those of the evolved strains from which the mutations were derived; see Extended Data Fig. 1j.

Two-strain competition in space

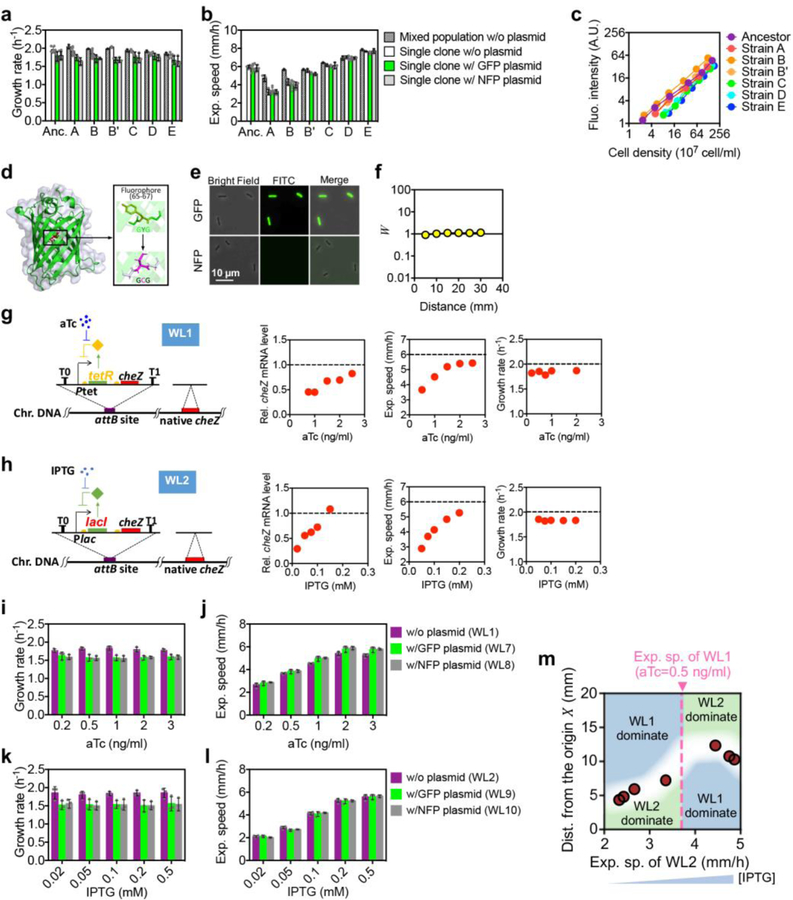
To understand the underlying evolutionary process, we first compared the expansion dynamics of clonal populations that were grown individually. We chose several mutant strains isolated at the 50^th cycle which exhibited a range of expansion speeds but with similar growth rates (marked as A, B, B’, C, D, E in Fig. 1c; see Supplementary Table 2). We transformed each strain with GFP and calibrated their fluorescence intensities by direct cell counting (Extended Data Fig. 3a–c). This allowed direct observations of the spatiotemporal dynamics of density profiles of each strain, shown in Extended Data Fig. 4a–c for the ancestor, mutant B, and mutant D. Clearly, faster strains showed higher abundance at all position and all time.

Next, we competed each mutant strain with the ancestor. We transformed these strains with a non-fluoresent variant of GFP and ensured that each had similar growth rate and expansion speed as the respective strains with fluorescent GFP (Extended Data Fig. 3a–f). Equal mixtures of various strain pairs were inoculated at the center of agar plates and their spatiaotemporal abundance patterns were characterized; see Methods. Fig. 2a shows the outcome of competition between mutant D and the ancestor 12 hours after inoculation. Notably, the two strains dominated different spatial regions: The ancestor (pseudo-colored as purple) dominated the interior while mutant D (pseudo-colored as cyan) dominated the exterior. Repeating the competition process between mutant B and the ancestor (Fig. 2b), we found the opposite, with strain B dominating the interior and the ancestor dominating the exterior. The ratio of the calibrated fluorescence intensities, shown as the colored solid lines in Fig. 2c,d, are in good agreement with the ratio W of the densities of evolved cells over the ancestor (circles in Fig. 2c,d) as obtained from cell counting (Extended Data Fig. 4f), a direct measure of the relative fitness of the mutant¹⁸ at each location. This relative fitness profile is stable through much of the 24-hour course of competition (Extended Data Fig. 4g–j).

Figure 2. Competitive expansion in space.

a, Expansion speeds and growth rates (upper row), the merged pseudo-color images (middle row) and cell density profiles (lower row) of representative two-strain competitions between the fluorescent derivatives (Extended Data Fig. 3) of the ancestor (purple) and mutant strain D (cyan). b, Same competitive expansion as a, but between the ancestor and strain B (orange). See Extended Data Fig. 4d,e for raw images and fluorescence intensity profiles before merging, and Methods for details of the competition assay. Strain details are given in Supplementary Table 2. Scale bar, 10 mm. The data were taken 12 h after co-inoculation of equal initial mixture of the two competing strains at the center of 0.25 % TB agar plates. Data in the tables show the mean of 3 biological replicates. c,d, The relative fitness W_i of strain i (relative to the ancestor), defined here as the ratio of cell densities at different positions. The colored solid lines are obtained as the ratio of the fluorescence density profiles shown in Extended Data Fig. 4d,e (lower panels). The open circles indicate ratios of direct cell counts (see Extended Data Fig. 4f). The colored dashed lines indicate the ratio of fluorescence between the mutant and ancestor, when each is grown individually in the same agar plate 12 h after inoculation at the center; results are derived from the data shown in Extended Data Fig. 4b. e, The circles indicate the crossover distances for the competition of the ancestor with the 5 evolved strains (Extended Data Fig. 4k–m), plotted against their respective expansion speeds (Extended Data Fig. 3b). The dashed vertical line indicates the expansion speed of the ancestor. [For the competition of strain C with the ancestor, their expansion speeds were very close and the relative fitness was difficult to resolve (Extended Data Fig. 3b, 4k–m).] The background color for regions above and below the crossover distances indicate distances where the ancestor (blue) or the mutant (green) dominates. f, The white line gives the crossover distance according to the competitive expansion model (Supplementary Model), for two strains with expansion speeds u and u′, with u (speed of the “ancestor”) fixed (dashed vertical line) and u′ (speed of the competing “mutant”) varied. The background colors again indicate the regions of dominance by one or the other strain. The regions of strain dominance are assigned according to the simple rule that the faster strain dominates for X > d_× and the slower strain dominates for X < d_×. Experiments in a,b were repeated independently 3 times, obtaining similar results. For c-e, mean±s.d. for n=3 biological replicates is shown.

Since strain B expanded slower than the ancestor while strain D expanded faster (Fig. 1c), the competition results suggest a trend with the slower strain dominating inside and the faster strain dominating outside. This is in stark contrast to the ratio of cell densities from single-strain expansion dynamics (colored dashed lines in Fig. 2c,d, derived from Extended Data Fig. 4b), which shows an advantage for the faster strain everywhere. Thus, the faster strain became disadvantaged in the interior only when grown in the presence of the slower strain, manifestating the “game-like” nature of the underlying evolutionary process^19,20, i.e., the fitness of a strain at a location depends on the presence and motility of competing strains.

Repeating the competition assay between the ancestor and each of the 6 mutants, we found the slower strain to dominate inside and the faster strain outside in each case (Extended Data Fig. 4k–m). The competition results can be concisely summarized by defining a “crossover distance” d_× at which the ancestor and the mutant have the same fitness, i.e., W (d_×) = 0. This is indicated as the vertical dashed line in Fig. 2c,d and Extended Data Fig. 4m. This crossover distance is plotted against the expansion speed of the corresponding mutant in Fig. 2e, with various regions shaded according to strain dominance: faster strain for X > d_× and slower strain for X < d_×. To see whether the competition results represented by this ‘phase diagram’ is specific to the evolved strains, we repeated these studies using two synthetic strains, WL1 and WL2 (Supplementary Table 2), which allows titration of swimming speed and expansion speed by using specific inducers without affecting cell growth (Extended Data Fig. 3g–l). When competing the fluorescent versions of these strains with each other, we obtained a phase diagram (Extended Data Fig. 3m) which is very similar to that between the ancestor and evolved strains (Fig. 2e), indicating the latter to be a generic outcome of competition between strains with different motility characteristics, regardless of how the latter are changed.

Modelling competitive expansion dynamics

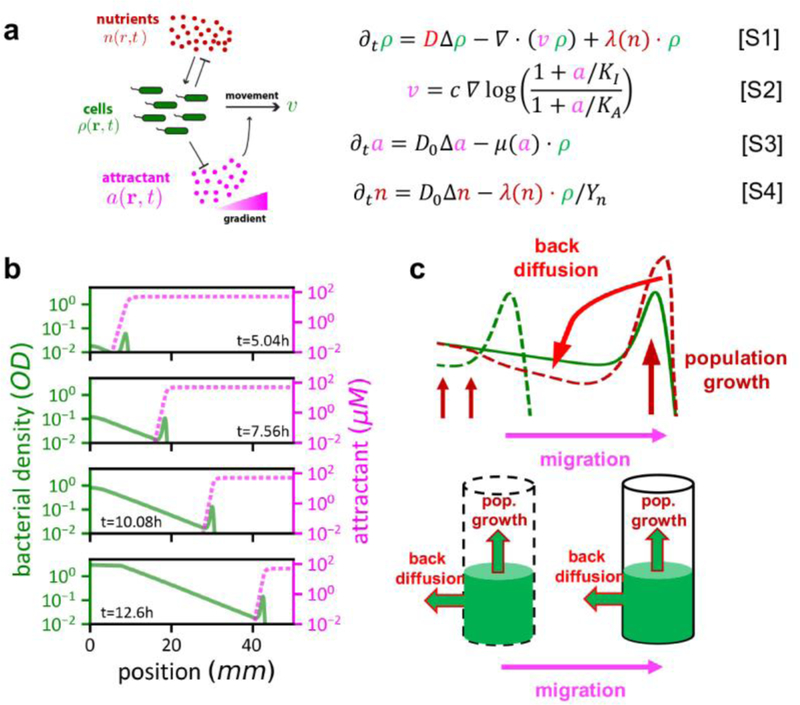
To gain more insight into the competition dynamics, we turn to a recently developed mathematical model of bacterial population expansion⁹, which includes the effect of cell growth along with the random and directed components of cell motion, based on well-characterized molecular interactions^9,21–26 (Extended Data Fig. 5a). Such a model has been established to provide a quantitatively accurate description of the expansion dynamics for a single bacterial strain in soft agar (Extended Data Fig. 5b,c and Ref. 9). We extended this model to describe competition between two strains assumed to respond to the same chemoattractant and grow at the same rate (Extended Data Fig. 6a), with different expansion speeds modeled by different parameters characterizing chemotaxis; see Supplementary Model for details and Supplementary Video 2 for an example of the dynamics. This model captured the spatial dominance pattern of the slow/fast strains observed after a long time (Extended Data Fig. 6b), as well as the time dependence of the crossover distance d_× (Extended Data Fig. 6c). Factors favoring the dominance of slower strains at smaller distances are attributed to shifts in balance among cell growth, forward movement, and back-propagation of pioneering cells⁹ from the population front as explained in detail in Extended Data Fig. 7 and Supplementary Analysis 1. Using this competitive expansion model, we systematically computed the outcome of competition between an equal initial mixture of two strains, varying the expansion speed of one strain (“the mutant”, with speed u′) while holding that of the other (“ancestor strain”, with speed u) at a fixed value. Fig. 2f shows the crossover distances d_×(u, u′) and the resulting phase diagram obtained for these competitions, which are similar to the ones experimentally observed (Fig. 2e, Extended Data Fig. 3m).

The competitive expansion model was further used to probe the dependence of spatial dominance for three strains. Consider three strains (a,b,c) with single-strain expansion speeds u_a, u_b, u_c, such that u_a< u_b< u_c. Let us find the region of dominance by strain b during 3-strain competition. From the two-strain crossover distances d_a= d_×(u_b, u_a) and d_c= d_×(u_b, u_c) between strains a-b and b-c, respectively, the illustration in Fig. 3a clearly suggests that strain b will dominate in the region d_a< d< d_c. This is verified experimentally by directly competiting 3 strains with different expansion speeds (i.e., strains A, C, E in Fig. 3b). Thus the outcome of 3-strain competition can be correctly predicted based on the results of two pairwise 2-strain competitons, particularly, the form of the crossover distance. We next show that this simple result can be generalized to predict the outcomes of evolution experiments described in Fig. 1.

Figure 3. Three-strain competition and the stability distance.

a, The crossover distance d_×(u, u′) for two competing strains with speeds u and u′ encode important information regarding the competitive expansion dynamics. We illustrate this by considering 3 strains (a,b,c) with single-strain expansion speeds u_a, u_b, u_c. To see the region of dominance by strain b, we sketch the crossover distance $d_{\times }(u,u\prime )$ vs u′ for u = u_b. The red point indicates the crossover distance d_a between strains a and b, with d_a = d_×(u_b, u′ = u_a). Similarly, the blue point indicates the crossover distance d_c= d_×(u_b, u′ = u_c) between strains b and c. By the definition of the crossover distance, strain a (which is slower than b) would dominate at distances d < d_a and strain c (which is faster than b) would dominate at distances d > d_c. Hence there is a region d_a < d < d_c where strain b dominates. In the limit $u_a\to u_{\overline{b}}$ and $u_c\to u_b^{+}$, the regime of dominance by strain b becomes narrowly distributed around $d_b={\lim }_{u\prime \to u_b}{d}_{\times }(u_b,u\prime )$; the green point. The analysis described here can be performed more rigorously to formulate a evolutionary stability criterion; see Extended Data Fig. 8. b, Expansion speeds (ES) and growth rates (GR) (left), the merged pseudo-color images (middle) and cell density profiles (right) of representative three-strain competitions between the fluorescent derivatives of strains A (red), C (green), and E (blue). Strain details are given in Supplementary Table 2. Scale bar, 10 The data were taken 12 h after co-inoculation of equal initial mixture of the three competing strains at the center of 0.25 % TB agar plates. Experiment in b was repeated independently 3 times obtaining similar results.

An evolutionary stable strategy

To connect to these evolution experiments, which involve potentially many strains with a continuum of expansion speeds, let us first consider the theoretical limit $u_a\to u_b$ and $u_c\to u_b$ (blue arrows in Fig. 3a). In this case, the region where strain b dominates will be pinched, distributed narrowly around a special distance, $d_b={\lim }_{u\prime \to u_b}{d}_{\times }(u_b,u\prime )$, the distance at which the strain with speed u_b is dominant over other strains even if their speeds are infinitesimally different. As there is nothing special about strain b and its speed, this consideration suggests a much more general result, that for a strain with a single-strain expansion speed u, there is a special distance

$$d^{\ast }(u)\equiv {\lim }_{u\prime \to u}{d}_{\times }(u,u\prime ),$$ (1)

at which no other strain with different speed can dominate.

Given the form of the crossover distance shown in Fig. 4a, the diagonal d^∗(u) (pink dashed line) as defined by Eq. (1) turns out to depend linearly on u as shown in Fig. 4b. This simple result is reinforced by a more detailed mathematical analysis (Supplementary Analysis 1, 2), which further predicts the slope of d^∗ vs u to be inversely proportional to the growth rate λ, i.e.,

$$d^{\ast }(u)\propto u/\lambda .$$ (2)

This form is confirmed by numerical simulation of the competitive expansion model performed at different growth rates; see Extended Data Fig. 6d,e.

Figure 4. Stability line of the competition dynamics.

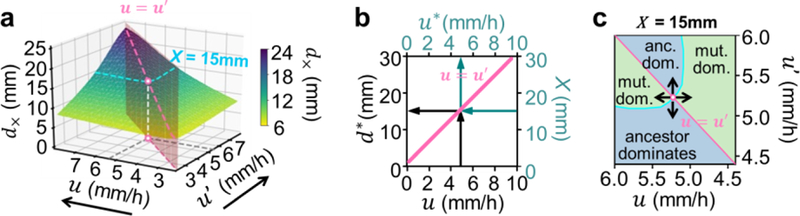
Competition results for pairwise combinations of expansion speeds (u, u′) following the growth-expansion model (Ref. 9, Extended Data Figs. 5,6). The crossover distances $d_{\times }(u,u\prime )$ where both strains are equally abundant (green surface) is shown in (a). The considerations in Fig. 3a indicate that the diagonal (pinked dashed line where u = u′) gives the stability distance d^∗ of a strain with ancestral speed u This relation, d^∗(u) is drawn in panel b and shown to be linear; it is called the “stability line”. This line has an orthogonal interpretation: Following the teal arrows, it gives the expansion speed u^∗ that would be selected at a position X. To verify this orthogonal view, we note that at a given distance, e.g. X = 15mm, there is a set of expansion speed combinations whose crossover distances corresponds to this distance (d_× = X, cyan line in (a)). A distinct speed u^∗ among this set is the one indicated in white, corresponding to the limiting value of d_× when the expansion speeds of the two competing strains approach each other, defined mathematically from $X=\underset{u,u\prime \to u^{\ast }}{\lim }{d}_{\times }(u,u\prime )$. A strain with this special expansion speed u^∗(X) is stable against mutants with different speeds at distance X, according to the strain dominance pattern shown in (c): Different regions in this panel are assigned in the same way as in Fig. 2f. For u > u′, the “ancestor strain” dominates where the green surface in panel a is below X, and the “mutant” dominates where the green surface is above X; vice versa for u′ < u. The expansion speed u^∗(X) is located at where the phase boundary (cyan line) intersects the diagonal. Here, if the speed of one strain is increased or decreased (indicated by arrows), then it is selected against as the other strain dominates.

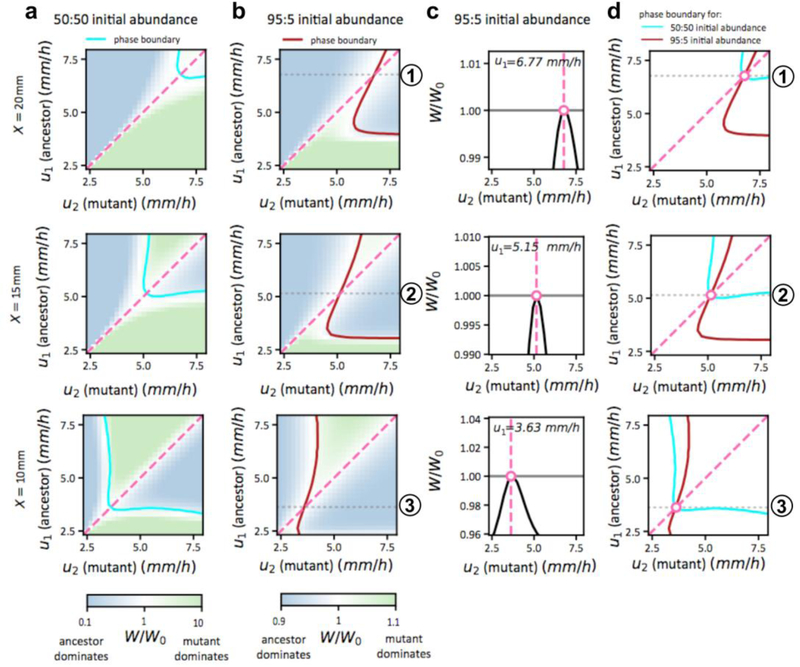
So far, Eqs. (1) and (2) refer to the dominance of a strain to a 50:50 initial mixture of it with a competing strain. To apply these results on multi-strain competition to evolutionary dynamics where mutants may be generated at very low frequencies, it is necessary to recalculate the crossover distance $d_{\times }(u,u\prime )$ for a low frequency of the competing strain. However as we show in Extended Data Fig. 8, for two strains with comparable expansion speeds, their crossover distance is independent of the frequency of the competitor. Thus, Eq. (2) can be applied to competitions involving strains of arbitrarily small frequencies, including spontaneously generated mutants. Eqs. (1) and (2) therefore describe an evolutionary stability criterion, that a strain with expansion speed u is stable against invasion by mutants with different expansion speeds at position d^∗(u) as given by Eq. (2). We therefore refer to d^∗ as the “stability distance” and d^∗(u) as the “stability line”.

The actual selection experiments performed (Fig. 1) poses a slightly different question from the evolutionary stability criterion just described: At a given selection distance X, what speed u^∗(X) is most fit? The answer turns out to be just the mathematical inversion of Eq. (2), i.e.,

$$u^{\ast }(X)\propto X\cdot \lambda .$$ (3)

This result can be appreciated by examining a slice of the crossover landscape of Fig. 4a, for $d_{\times }(u,u\prime )=X$ as shown in Fig. 4c. The stable speed selected is at the intersection of $d_{\times }(u,u\prime )=X$ (the cyan line) and the diagonal (u =u′, the pink line), indicated by the circle, since a strain with speed deviating from the intersection (black arrows) is selected against; see caption for details. In the plot of the stability line (Fig 4b), we added the teal-colored secondary axes: At a given distance X, the selected speed u^∗(X) is obtained by following the teal arrows, whereas for a strain with a given speed u, its stability distance is obtained by following the black arrows.

Validation of the stability criterion

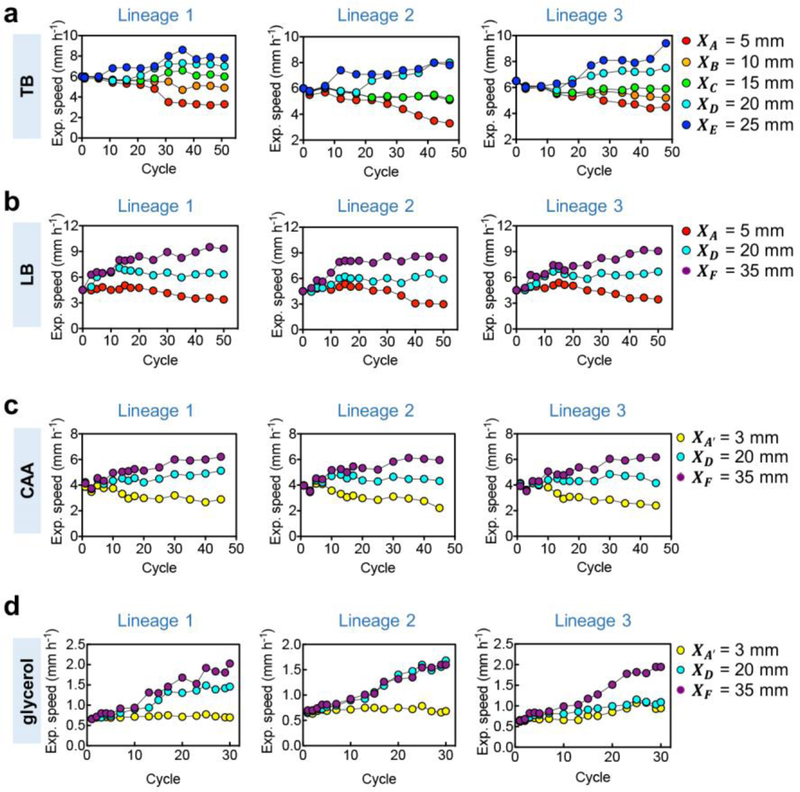
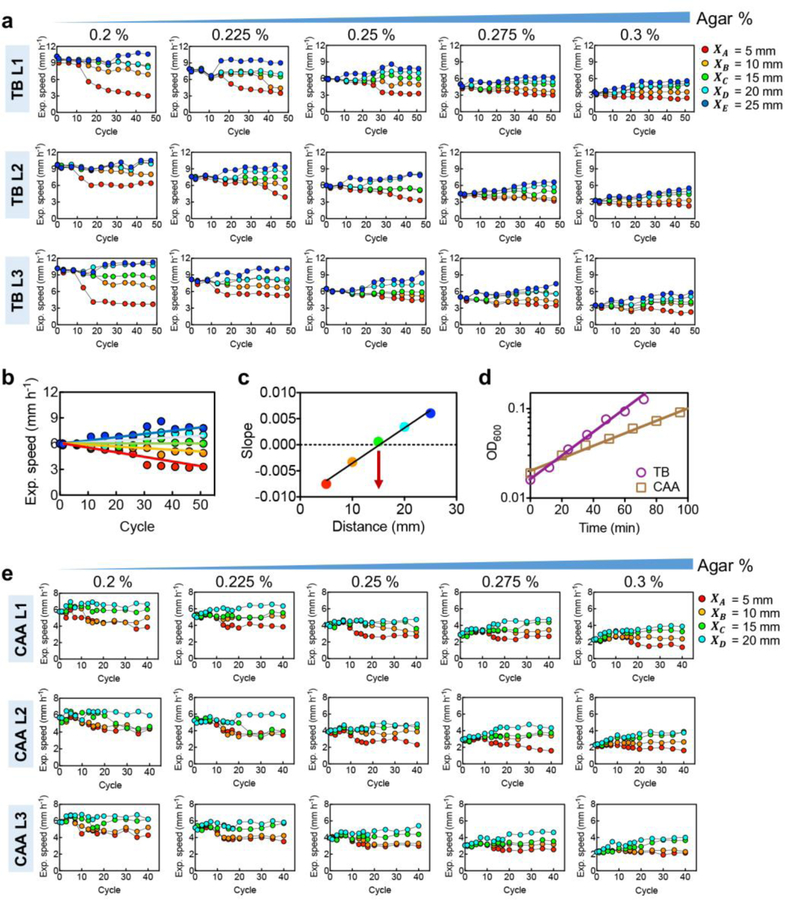
To test the predicted stability line (2) or (3), we designed two additional sets of evolution experiments for growth conditions that provided altered ancestral expansion speed and growth rate. First, we repeated the evolution protocol of Fig. 1a using the same growth medium (TB) but different agar densities. This changed the effective cell diffusion constant²⁷, resulting in a range of expansion speeds (purple squares, Fig. 5a) without affecting the growth rate⁹. The evolution results obtained for 5 agar densities, each for 5 selection distances and different replicates, are highly reproducible (Extended Data Fig. 9a). From the evolved expansion speeds, we determined the stable selection distance for each agar density (Extended Data Fig. 9b,c). The stability distances obtained exhibit a linear relation with the ancestral expansion speeds as predicted (Fig. 5b).

Figure 5. Validation of the evolutionary stability line.

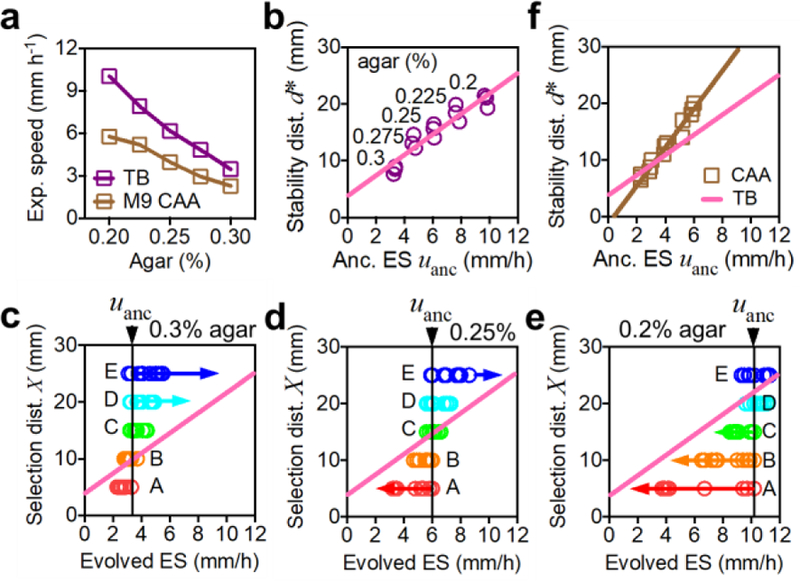
a, Expansion speed of the ancestral strain can be modified by changing the agar density in the range 0.2% to 0.3%. Results are shown for both TB and casamino acid (CAA) as the nutrient source. b, Estimated stability distance d^∗ obtained according to the method of Extended Data Fig. 9b,c at different agar densities; result for each of the 3 replicates is shown. Pink line is a linear fit. c,d,e, Expansion speeds from every 5 cycles of evolution (as shown in Fig. 1b) are plotted at each selection distance (X_A,…, X_E) for agar density of 0.3% (panel c), 0.25% (panel d), 0.2% (panel e). The pink line is the expected stable attractor of evolution dynamics obtained in panel b. f, Stability distances estimated for each agar density in CAA, for each of the 3 replicates. Brown line is the linear fit of the data. The slope increased compared to the pink line (from panel b for TB), as predicted for the slower growth rate in CAA. In a, means for n=3 biologically independent repeats are shown (s.d. error bars are smaller than the size of the symbols). Experiments in c-e were repeated independently 3 times obtaining similar results, see Extended Data Fig. 9.

Next we plotted the expansion speeds obtained from different cycles of evolution (the data in Extended Data Fig. 9a) together with the stability line in Fig. 5c–e, for data from 3 different agar concentrations. Interpreting the stability line as the stable expansion speed u^∗(X) at the corresponding selection distance X (see Fig. 4b), the data from each evolution series (symbols of same color) are seen to approach the predicted final stable values.

Then we repeated all of the evolution experiments yet again, at various selection distances and agar densities, in a medium supporting ~50% slower growth (CAA, brown squares in Extended Data Fig. 9d). Expansion speeds of the evolved strains (Extended Data Fig. 9e) exhibited a similar pattern of changes as those obtained in TB (Extended Data Fig. 9a). The stability distances obtained for different ancestral expansion speeds (Fig. 5f) again followed a linear relation as predicted, with a ~70% increase in the slope, consistent with the dependence on cell growth rate given in (2).

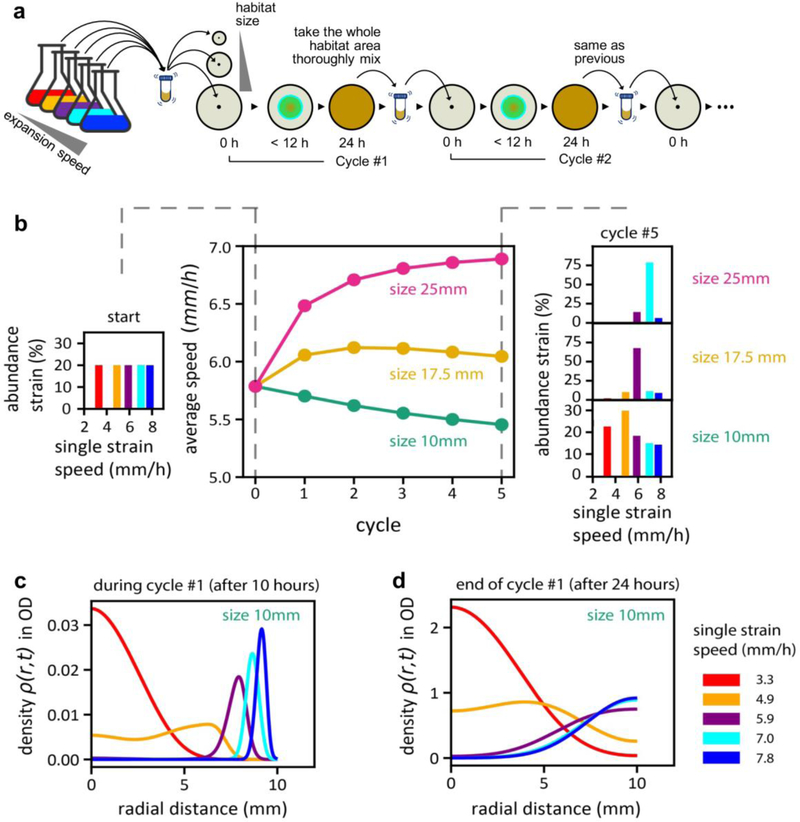
To probe the generality of a stable expansion speed and its linear size-dependence, we investigated another mode of selection in silico using the multi-strain generalization of the competitive expansion model (Supplementary Analysis 5). In this mode of selection, a fraction of all cells contained within a “habitat” of a certain size were repeatedly propagated to the next cycle; see Extended Data Fig. 10a. After just a few cycles of simulations, the average expansion speeds of the populations were seen to diverge according to habitat sizes, with smaller/larger habitats dominated by species with slower/faster expansion speeds (Extended Data Fig. 10b). This follows the trend seen in our evolution experiment with selection at a fixed distance (Fig. 1), despite 2d weighting and edge effects which made the slower species take more cycles to dominate in the smaller habitat (Extended Data Fig. 10c,d). Thus, the results of the spatial competition/evolution scenario studied here are robust to specific implementation of the selection process, and may be applicable to populations confined to environments with finite resource patches, e.g., nutrient hotspot or restricted physical terrains.

Fitness effects depending on the composition of the population are prevalent in natural evolution^28–30. The complex dynamics resulting from these effects were investigated theoretically early on in forms of simple evolutionary games^31,32; recent experimental studies have also considered the consequences of composition-dependent reproduction in synthetic microbial populations^7,33. Here we encounter a natural example where the dominance of one strain at a location depends not only on its own expansion speed but also on the expansion speed of the other (Fig. 2c,d, Extended Data Fig. 3m, and Fig. 3b), as well as on the initial abundance of the other (Extended Data Fig. 8). Dominance patterns such as that in Fig. 4c are analogous to the “payoff matrix” of a “game”, with the expansion speed being a “strategy” taken by a player^{7,19,20,32,33}; the cyan stability line can be viewed as the set of coexistence points of this game. Remarkably, such a highly complex game involving spatial selection and the composition dependence of fitness can be elucidated in quantitative details, with quantitative predictions of the selected phenotypes in different environments, by simply identifying the stable equilibria of the complex dynamics. As there is no fixed fitness landscape to ‘climb’, winners of this evolutionary process are not the ‘fittest’ in an absolute sense, but simply those that are stable against invasion by mutants. This provides a fresh perspective for approaching other complex evolutionary problems in nature, where composition dependent effects are ubiquitous.

METHODS

Media and growth conditions

The tryptone-broth (TB) medium contains 10 g Tryptone and 5 g NaCl per liter. The M9 supplemented medium is based on Knight lab’s recipe: 1× M9 salts, 0.2 % casamino acids, 2 mM MgSO₄, 0.1 mM CaCl₂, and the carbon source is 0.4 % (v/v) glycerol. M9 salts were prepared to be 5 × M9 salts stock solution (in 1 liter): Na₂HPO₄ 30 g, KH₂PO₄ 15 g, NH₄Cl 5.0 g, NaCl 2.5 g. The Luria-Bertani (LB) medium used in this study contains 2.5 g yeast extract, 5 g Bacto Tryptone, and 5 g NaCl per liter. For all the expansion experiments, the bacto-agar (BD, 214010) was added to the growth medium, the agar concentration varies from 0.2 % to 0.3 % (w/v). To prepare semi-solid agar, the above growth medium was buffered to pH 8.0 with 0.1 M HEPES (pH 8.0), the pH variation was less than 0.3. 10-ml of the above medium supplemented with different agar concentration was poured into a 90-mm petri dish, and allowed to harden at room temperature for 90 min. Unless otherwise stated, all other reagents were from Sigma. All experiments were carried out at 37 °C. Plasmids were maintained with 100 μg/ml Ampicillin, 50 μg/ml Kanamycin, 25 μg/ml Chloramphenicol, or 50 μg/ml Spectinomycin.

Strains and plasmid construction

The ancestor, E. coli CLM strain, used in this study was kindly provided by Prof. Antonin Danchin (AMAbiotics, France). All strains used in this study are listed in Supplementary Table 2. Strains are available upon request. Oligonucleotides used are listed in Supplementary Table 4.

The cheZ-titratable strain WL1 (ΔcheZ, Δlac, bla:P_tet-tetR-cheZ at attB site) was constructed as described previously⁴². Briefly, the bla:P_tet-tetR-cheZ feedback loop was amplified from the pMD19-T₀-Amp-T₁-P_tet-tetR-cheZ with primers PR29 and PR30 and inserted into the CL1 (ΔcheZ, Δlac)’s chromosomal attB site by recombineering with the aid of pSIM5⁴³. To construct the cheZ titratable strain WL2 (ΔcheZ, Δlac, bla:P_lac-lacI-cheZ at attB site) the plasmid pMD19-T₀-Amp-T₁-P_lac-lacI-cheZ was firstly constructed. Briefly, the plasmid was constructed by inserting PCR-amplified P_lac-lacI with XhoI and HindIII restriction sites from QL5 into the corresponding restriction sites of the pMD19-T₀-Amp-T₁-P_tet-tetR-cheZ, finally the P_tet-tetR was replaced with the P_lac-lacI. Then the bla:P_lac-lacI-cheZ feedback loop was amplified from the plasmid and inserted into the attB site by recombineering.

The derived clpX (G371S, *425Q, P67S), rcsD (G656V), cheB (D37E), mutH (R136C) alleles were moved into the ancestor strain using the two-plasmid-based CRISPR-Cas9 system described by Jiang et al⁴⁴ with minor modifications. Briefly, the targeted locus was firstly replaced with bla gene by λ-Red, the evolved alleles were then introduced by CRISPR-Cas9 targeting the bla gene. Procedures used for the allelic exchange are as follows. Firstly, the pCASsac plasmid containing the cas9, λ-Red and sacB was electroporated into the ancestor, strains with the kanamycin resistance were selected. Later, PCR products containing ~ 50-bp sequence homologous to the targeted locus on each side of the T0-P_EM7-bla-T1 cassette was amplified from PMD19-T₀-bla-T₁-P_tet-tetR plasmid. The purified DNA fragments were then electroporated into the ancestor strain with pCASsac. The T₀-P_EM7-bla-T₁ cassette was integrated into the targeted locus with the aid of the λ-Red from pCASsac and the ampicillin-resistant clones were selected. These cells were identified by colony PCR. Subsequently, the pTargetF-AmpR plasmid carrying the N20 (20-bp region complementary to the target region) which was targeted to the bla region was obtained by inverse PCR with the primers PCC35 and PCC36 from the pTargetF and followed by self-ligation. PCR products containing the evolved alleles were amplified from the evolved strains with appropriated primers listed in the Supplementary Table 4. The pTargetF-AmpR plasmid carrying the sgRNA, lacIq-P_trc promoter guiding the PMB1 replication of pTarget and the PCR fragments with the evolved allele were co-electroporated into the ancestor with T₀-P_EM7-bla-T₁ cassette at the targeted locus and pCASsac plasmid. Cells grown on the LB agar containing kanamycin and spectinomycin were identified by colony PCR and DNA sequencing. Finally, the constructed strains both contained the pTarget-AmpR and the pCASsac plasmids. The pTarget-AmpR was firstly cured by a second round of genome editing. Cells grown on the LB agar with kanamycin and didn’t grow on the LB agar with spectinomycin were selected. These selected cells were picked into 2ml of LB medium with 5g/L glucose for overnight culture, cells grown on the LB agar containing 5g/L glucose and 10g/L sucrose were selected as the final strains. The fluorescence plasmid PZA31-Ptet-M2-GFP was from the Hwa Lab. To construct a loss of function non-fluorescence GFP mutant NFP⁴⁵, the 66^th amino acid Y was mutated into C by overlapping PCR. Briefly, the PZA31-Ptet-M2-GFP was reversely amplified with a pair of complementary primers GFP-Y66C-f and GFP-Y66C-r. The PCR product was purified and treated with DpnI, gel purified, ligated, and then transformed into the DH5α competent cell. The plasmid was verified by sequencing.

Evolution experiment procedures

Firstly, the ancestor strain from the-80 °C stock was streaked onto an agar plate and cultured at 37 °C overnight. Three to five single colonies were picked into 2-ml of the corresponding growth medium and cultured at 37 °C overnight. Secondly, the overnight culture was diluted into 2-ml pre-warmed fresh growth medium with a ratio of 1:100 the next morning. Bacteria were then cultured to the mid-log phase (OD₆₀₀ was around 0.2~0.3), 2 μl of the ancestor strain was inoculated at the center of a semi-solid agar plate, incubated at 37°C for 24 h. Cells grew and migrated, occupying the whole semi-solid agar plate (marked as cycle 0). 2 μl of the agar-cell mixture was picked from the site A, B, C, D, or E of this master plate (with the radius of 5, 10, 15, 20, or 25 mm away from the inoculum, respectively), and directly inoculated onto fresh semi-solid agar plates (marked as A, B, C, D or E series correspondingly), incubated at 37 °C for another 24 h, marked as the cycle 1. 2 μl of the agar-cell mixture was picked at site A from plate A, site B from plate B, site C from plate C, site D from plate D, and site E from plate E, respectively, and inoculated onto the center of the fresh semi-solid agar plates, incubated at 37°C for 24 h, marked as cycle 2. This process was repeated for 50 cycles, with selection always kept at the same radius. Site A’, A, B, C, D, or F (with the radius of 3, 5, 10, 15, 20, or 35 mm away from the inoculum, respectively)’s bacteria were passaged for 40–50 cycles follwing the above process in the M9 minimal medium supplemented with glycerol and casamino acid medium (M9+glycerol+CAA). For the evolution experiment carried out in the semi-solid LB agar plate, 2 μl of cell-agar mixtures picked from site A, D, or F (with the radius of 5, 20, or 35 mm away from the center of the semi-solid agar plate, respectively) were transferred onto fresh semi-solid agar plates. Considering the fast growth rate and expansion speed in this medium, the cycle of the culture was shortened to 12 h. For the evolution experiment carried out in the M9 minimal medium supplemented with glycerol, A’, D, or F (with the radius of 3, 20, or 35 mm away from the center of the semi-solid agar plate, respectively) were tansfered every 72 h, and this process was repeated for 30 cycles. The samples of the evolving populations were stored at-80°C right after well mixing the agar-cell mixture from indicated sites with the equal volume of 40 % (v/v) glycerol. All the evolution experiments were performed for at least 3 replicates. The 5×10³ folds daily growth corresponds to ~12.3 (log₂5×10³) generations of doubling (The number of doubling during each cycle was estimated as follows, cell density was about 3.54×10⁹/ml in TB medium and 1.93×10⁹/ml in M9+glycerol+CAA after migrating in the semi-solid agar for 24 h. The initial inoculum cell density was about 7.43×10⁵ /ml for TB and 4.94×10⁵/ml for M9+glycerol+CAA, respectively). These numbers were counted by using flow cytometry (see below).

Expansion speed measurement

The semi-solid agar plate was illuminated from below by a circular white LED array with a light box as described before²⁷ imaged at 30 min or 1 h intervals using a Canon EOS 600D digital camera. Images were analyzed with the ImageJ and a custom-written image analysis script using MATLAB. A circle was fitted to the intensity maximum in each image and the area (A) of the fitted circle was determined. The radius (r) of the colony was calculated as $\text{r}=\sqrt{\text{A}/\pi }$. The maximum expansion speed was calculated using a linear fit over a sliding window of at least four time points, with the requirement that the fit has an r² greater than 0.99.

Growth rate measurement

Growth rates of the evolved strains were measured in 100 ml flask with 20 ml corresponding growth medium at 37 °C, 150 rpm. The procedure was as follows. Firstly, the isolated bacteria from-80°C stock was streaked onto the agar plate, and cultured at 37 °C overnight. Secondly, three to five single colonies were picked and inoculated into 2 ml corresponding growth medium and cultured overnight. The overnight culture was diluted into 2 ml pre-warmed medium with a ratio of 1:100 in the next morning, cultured to log phase. The log phase culture was successively diluted into 20 ml pre-warmed growth medium, the final OD₆₀₀ was about 0.02~0.05. OD₆₀₀ was measured by a spectrophotometer reader every 12 min (for TB) or 15 min (for M9). At least 3 doubling times were recorded. Maximum growth rates were calculated using an exponential fit over a sliding window of at least five time points, with the requirement that the fit has an r² greater than 0.99.

Competition assay

Head-to-head chemotactic competition was observed using a pair of strains with competition either between the ancestor strain and one evolved strain, or between the two cheZ-titratable strains (Extended Data Fig. 3) induced with aTc or IPTG. To allow for observation by fluorescence microcopy, strains carrying either GFP or NFP expressing plasmids were prepared (Extended Data Fig. 3). Each competition was repeated for both combinations of plasmids (for example in the competition run ancestor vs A, the growth and expansion of the ancestor strain was observed for the run with Anc_G vs A_N as well as for the run Anc_N vs A_G. Both the fluorescence intensity and the cell number of each pair of competing strains at different positions and different time points were measured to characterize the competitiveness of them in semi-solid agar. Initiation of the competition experiments for ancestor vs an evolved strain was carried out as follows: three to five single colonies of the isolated evolved strain and the ancestor with the GFP/NFP were cultured to log phase (OD₆₀₀ was around 0.20) separately. Two types of the combined mixed strains were prepared, the evolved strain with GFP was mixed with the Anc_N while the evolved strain with NFP was mixed with the Anc_G in a 1:1 ratio. Later, 2 μl of the two types of the combined mixture were inoculated onto the center of pre-prepared semi-solid agar plates separately and allowed to expand at 37 °C. The fluorescence intensity of the evolved strains/ancestor with the GFP reporter from these two plates after the expansion were scanned by a Nikon Ti-E microscope equipped with a 10 × phase-contrast objective (NA=0.30) and a Andor Zyla 4.2 s CMOS camera. The fluorescence intensity was used to represent the bacterial density in semi-solid agar. Samples were also collected before and after the expansion. Images were collected from the Z-axis position at the fixed plane where the bacteria’s fluorescence was constant in the semi-solid agar. Each image was collected at a height of 1 mm horizontally across the plate, 100 images were collected finally. The fluorescence intensity was calculated by the NIS-Elements AR 4.50 software. The competition between different cheZ titratable strains was performed following the same protocol with different concentrations of the aTc and IPTG added to the growth medium and semi-solid agar in addition.

Fluorescence intensity as a function of cell density was calibrated as follows. The Anc_G, A_G, B’ _G, B _G, C _G, D _G and E_G strains were cultured in TB medium to mid-log phase, OD₆₀₀ was around 0.20 for each strain. A total of 200ml culture was collected and concentrated to 1.6×10¹⁰ cells/ml in the TB medium with 2mg/ml kanamycin for each strain. Then, a serial dilution of the above concentrated sample into TB medium with 2mg/ml kanamycin was carried out. Subsequently, the diluted sample were mixed with 0.277% (w/v) TB agar containing 2mg/ml kanamycin in a ratio of 1:9, 10ml of the cell-agar mixture was poured into a 9cm Petri dish and allowed to solidify at room temperature for 90min, and 100 μl of the cell-agar mixture was used for the cell counting with a flow cytometer. The fluorescence intensity of the above cell-agar mixture plate was scanned using a fluorescence microscope, equal to the two-strain competition assay. Then the relationship between the fluorescence intensity of the cell in semi-solid agar and the cell density was plotted.

The initial and final ratio of the two competitors were measured by cell counting with a flow cytometer (Beckman, Cyto-FLEX). Briefly, samples were firstly fixed with pre-cooled cell counting buffer (0.9 % NaCl with 0.12 % formaldehyde). Later, the fixed samples were diluted as necessary with straining buffer (cell count buffer with 0.1 μg/ml DAPI) prior to the flow cytometer analysis. Finally, the strained samples were counted with the flow cytometer. The flow rate was 30 μl/min and at least 50,000 cells were collected. The DAPI-stained particles were deemed as the bacterial cells, and the DAPI positive cells were separated into two groups (GFP and NFP) through the FITC channel. The fitness W_iof strain i (relative to the ancestor) is defined as the ratio of density at distance d (and a sufficient long time t) over the initial inoculent density, ρ_x(d,t)/ρ_x(0,0), relative to the same ratio for the ancestor, i.e., $W_i(d)=[{\rho }_x(d,t)/{\rho }_x(0,0)]/[{\rho }_{anc}(d,t)/{\rho }_{anc}(0,0)]$.

Quantitative Real-Time RT-PCR

A volume of 1ml of the log phase bacteria (OD₆₀₀ ∼0.2) from each condition were immediately mixed with 2 ml RNA protect Bacteria Reagent (Qiagen). Total RNA was extracted using the RNeasy Mini kit (Qiagen) according to the manufacturer’s protocol. The RNA yield and purity were checked by a NanoDrop 2000c spectrophotometer (Thermo Scientific), and the absence of genomic DNA contamination was confirmed by PCR. About 500 ng RNA was reverse transcribed, using a PrimeScript RT reagent kit with gDNA Eraser (Takara) according to the manufacturer’s protocol. Reactions without reverse transcriptase were conducted as controls for the following qPCR reactions. Then the cDNA samples were diluted 1:25 with PCR grade water and stored at-20 °C until use. SYBR Premix Ex Taq (Tli RNaseH plus) (Takara) was used for qPCR amplification of the amplified cDNA. 5 µL diluted cDNA sample, 200 nM forward and reverse qPCR primers, 10 µL SYBR Premix Ex Taq, and up to 20 µL PCR grade water were mixed in a well of a Hard-Shell 96 well PCR plates (BIO-RAD). The non-template control (NTC), containing sterile water instead of cDNA template, was included during each qPCR experiment to check the purity of the reagents. Each reaction was performed in triplicate. The qPCR reactions were performed using a Bio-rad CFX connect Real-Time system with the following program: 30 s at 95 °C and 40 cycles of denaturation (5 s at 95 °C), annealing, and elongation (30 s at 60 °C). Data were acquired at the end of the elongation step. And a melting curve was run at the end of the 40 cycles to check the specificities of the accumulated products. To calculate the PCR efficiency, standard curves were made for the target gene by using serially diluted cDNA samples as the templates. The 16S rRNA was used as the reference gene to normalize the expression level.

Single-cell tracking

Single cell tracking was performed as described by Waite, A.J.⁴⁶ with minor modifications. A custom MATLAB script was used to control the automated stage of the microscope (Nikon Ti-E) via the MicroManager interface⁴⁷. Movies were sequentially acquired using an Andor Zyla 4.2 s CMOS camera at 10 frames/s through a 10× phase-contrast objective (NA=0.30), 1,024 pixel by 1,024 pixel for 1 min. All movies were analyzed using a custom-written MATLAB code as described before^46,48. The single-cell tracking was carried out as follows: Firstly, three to five single colonies of the isolated evolved strain or five microliters of the evolved cell-agar mixture stored in the-80°C were cultured in 2 ml growth medium at 37°C, 150 rpm overnight. Secondly, the overnight culture was diluted into 2 ml pre-warmed growth medium at a 1:100 ratio, cultured at 37°C till the OD₆₀₀ reached 0.2~0.3. This step was then repeated, and cells were diluted into 15 ml pre-warmed growth medium. Bacteria were harvested till the OD₆₀₀ reached 0.2. Thirdly, the harvested sample was diluted with pre-warmed growth medium to a final cellular density of OD₆₀₀= 0.05. Five microliters of the diluted sample were pipetted onto a microscope glass slide (25 mm × 75 mm), a coverslip (18 mm × 18 mm) was placed onto the top of the sample (slolwly and with caution to avoid the formation of air bubbles). Subsequently, sides of the coverslip were sealed with heated wax in order to avoid evaporation. The growth medium used for single cell tracking was supplemented with 0.05 % (w/v) PVP 40,000 to protect the flagella. Two to three slides were prepared for each strain, and five 1-min-long movies were acquired. Temperature was kept at 37°C during the movie aquisitions.

Whole genome sequencing and analysis

Whole genome sequencing was performed using the Illumina platform, obtaining an average > 100 × coverage. Samples directly collected from the TB evolution experiment in 0.25 % agar were used for sequencing. Briefly, the isolated clones were grown in the growth medium as described before and harvested at stationary phase. For the population samples, 100 μl of the frozen cell-agar mixture from the 50^th cycle was grown in 3 ml growth medium and harvested at the 10^th hour. Cellular DNA was extracted by using a genomic DNA purification kit (Tiangen) according to the manufacturer’s protocol. Whole genome libraries were prepared and sequenced on the Illumina HiSeq X10 by BGI. The genome sequence of Escherichia coli str. K-12 substr. MG1655 (NCBI: NC_000913.3) was used as the reference sequence. All sequencing data were analyzed with the BRESEQ pipeline⁴⁹ supported with Python. A subset of the identified mutations was re-sequenced using Sanger sequencing for confirmation.

Numerical simulations of competition dynamics and evolution

The Growth-Expansion model⁹ (Extended Data Fig. 5) was extended to analyze competition and evolutionary dynamics during expansion, see Extended Data Fig. 6 for introduction and defining partial differential equations (PDE), and Supplementary Model for mathematical details. Numerical solution of the partial differential equations was done employing an implicit scheme using Python 2.7 and the PDE solver module FiPy⁵⁰. Integration over time was typically performed with time steps dt = 0.25s, and a grid resolution with spacing dx = 10μm. Simulations were performed using a custom-made Python code which is available via GitHub at https://github.com/jonascremer/chemotaxis_simulation. Used parameter sets are provided in Supplementary File simulationparameters.txt, see Supplementary Model 5 for usage.

Extended Data

Extended Data Figure 1. Characteristics of cell motility and expansion speed for the ancestor and for mixed populations of evolved cells.

a, Navigated range expansion by bacteria⁹ on a soft agar plate involves a group of pioneering cells (cyan) situated at the population front, which move outward towards uncolonized space (grey) in response to a signaling cue. During the outward migration, they replicate and leave offsprings behind the front. The offsprings do not move outward, but settle at wherever they are deposited and grow exponentially (green) until reaching carrying capacity (brown). b, Density profile of a population of ancestor cells containing GFP (Anc_G) at various time after inoculation at the center of a semi-solid TB plate with 0.25 % agar incubated at 37 °C. The population expanded at a defined expansion speed, covering the positions A-E well before selection at 24 h. The density profiles were obtained using confocal microscopy as described in Ref. 9 [Cellular characteristics were not significantly affected by the expression of GFP as shown below in Extended Data Fig. 3.] c, The experiment described in Fig. 1a was carried out independently for 5 distinct selection positions, at distances X_A, X_B, X_C, X_D, X_E, ranging from 5 to 25 mm. Three independent lineages of this experiment were propagated in parallel (Extended Data Fig. 2a). Selected samples at cycle n of series S in Lineage l are referred to as Sl. n in Supplementary Table 2. d, Front position vs time for the ancestral strain CLM (purple) and population of evolved cells obtained at the 50^th cycle of each of the 5 evolution series from Lineage 1. For each mixed population, collected cells were grown to mid-exponential phase (OD₆₀₀=0.20), 2 μl of the batch culture was inoculated at the center of the same TB plate as in panel b and incubated in the same way. The agar plates were photographed at different time after inoculation and the radius of each expanding population was deduced from the area measured using ImageJ. Expansion speed of each population (shown in Fig. 1b) was obtained as the slope of the linear fit of the data after t=3 h. e, Growth rates of population samples from each of the 5 selection series are shown from Lineage 1 at various evolution cycles. f, Growth rates of population samples from each of the 3 selection series (Lineage 1) at various cycles of evolution experiments carried out in CAA medium. g, Scatter plot of growth rates and expansion speeds for single strains isolated from fossil samples at various cycles of CAA evolution experiments. The evolution cycles are indicated by circles. Mean run speed (h), and tumble bias (i) of population samples from each of the 3 selection series from Lineage 1 of evolution experiments carried out in TB medium are shown at various evolution cycles. At least 10,000 cells were subjected to single-cell tracking analysis for each experiment; see Methods for details. Error bars represent the SD of single-cell tracking results. j, Expansion speeds of several strains each carrying an identified mutation plotted against the corresponding evolved strains from which the mutations were identified. The mutations are indicated in the legend; see Supplementary Table 1 for details. mutH does not affect motility and serves as a control. Experiments were repeated independently 3 times for (b, d) and 2 times for (e, f), obtaining similar results. In (h,I) mean±s.d. for a single biological replicate and n=10,000 cells analyzed is shown. In (j) mean for n=3 biological replicates is shown (s.d. error bars are smaller than the size of the symbols).

Extended Data Figure 2. Experimental evolution of expansion speed in different growth media.

Expansion speeds of population samples from each selection series are shown at various cycles of evolution experiments carried in TB (a), LB (b), CAA (c), glycerol containing minimal media (d), respectively. The agar density was 0.25 % (w/v). All three lineages of each medium showed similar trajectories. The absence of a chemoattractant in the glycerol minimal media leads to a very different outcome compared to the experiments carried out for the complex media (a-c). In the absence of a chemoattractant, cells follow the simple Fisher-Kolmogorov dynamics^9,34,35. In line with the absence of a growing population trailing the front, no decrease in swimming behavior was observed over time. However, as previously investigated, slower swimming behavior might get selected for when density dependent growth effects or strong tradeoffs between swimming and cell growth exist^17,36. Experiments in a, b, d were carried out once with three biologically independent repeats obtaining similar results. Experiment in b was repeated independently twice obtaining similar results.

Extended Data Figure 3. Fitness effects for cells expression GFP and its non-fluorescent variant, NFP.

Growth rates (a) and expansion speeds (b) of the ancestor and 6 mutant clones harboring GFP, NFP, or no plasmid, along with the corresponding mixed populations from which the 6 mutant clones were isolated. Plasmid harboring constitutive GFP or NFP expression (PZA31-Ptet-M2-GFP and PZA31-Ptet-M2-NFP) were transformed to the 6 evolved strains A, B, B’, C, D, E, to form A_G, A_N, etc. (see Supplementary Table 2). c, Fluorescence intensity as a function of cell density. The cell growth of cells expressing GFP was arrested by adding 2 mg/ml kanamycin, and concentrated to 1.6×10¹⁰ cells/ml. Subsequently, serial dilutions were carried out. For each cell density, cells were vigorously mixed with the pre-warmed 0.277% (w/v) TB agar containing 2mg/ml kanamycin in a ratio of 1:9 and poured into 3 Petri dishes with 10 ml each. All dishes were allowed to harden at room temperature for 90 min. The cell-agar mixture was subject to cell counting by FACS and the fluorescence intensity of the agar plate was scanned using a fluorescence microscope. d, 3D structure of GFP predicted position of the loss-of-function mutation introduced, Y66C. The shown crystal structure is based on the NFP protein sequence aligned to PDB ID: 1GFL³⁷. The rectangle in the crystal structure corresponds to the mutation position. e, Ancestor cells harboring constitutive GFP or NFP expression (Anc_G and Anc_N cells) as viewed by fluorescence microscopy; the images verify the loss-of-function mutation of GFP. f, The relative fitness W of Anc_G and Anc_N cells at different distances from the agar plate center. Cells harboring GFP or NFP plasmid were equally mixed and inoculated at the center of 0.25 % TB plate. Cell-agar mixtures picked at various distances were subject to cell counting by FACS 24 h after inoculation and the ratio was reported as W; see Methods. g,h, The genetic circuit and characteristics of the cheZ-titratable strains WL1 (g) and WL2 (h). The expression of cheZ is under the control of a P_tet-tetR (WL1) or P_lac-lacI (WL2) feedback loop and the native cheZ was seamlessly removed; see Methods. Relative cheZ mRNA levels are shown to change by ~2-fold under different concentrations of inducers, aTc for WL1 and IPTG for WL2. Relative cheZ mRNA expression level, expansion speed, and growth rates of WL1 (g) and WL2 (h) under various concentration of the respective inducer are shown next to the circuits. Horizontal dashed lines show the corresponding values of the ancestor. The growth rates (i, k) and expansion speeds (j, l) of the aTc-titratable cheZ strain, WL1 (panel g), and its derivatives expressing GFP (WL7) or NFP (WL8), and the IPTG-titratable cheZ strain, WL2 (panel h), and its derivatives expressing GFP (WL9) or NFP (WL10). m, The circles indicate the crossover distance between fluorescent derivatives of two cheZ-titratable strains (WL1 and WL2), with WL1 strains induced at a fixed concentration of its inducer (0.5 ng/ml aTc), and WL2 strains induced at various IPTG concentrations, whose corresponding expansion speeds (h, l) are shown on the x-axis. The background colors again indicate the regions of dominance by WL1 (purple) or WL2 (green). In a,b, g-l, mean±s.d. for n=3 biologically independent repeats is shown (individual data points shown as circles. Eerror bars in g-h were smaller than the size of the symbols. Experiments shown in c, e-f, m were repeated independently 3 times, obtaining similar results.

Extended Data Figure 4. Results of two-strain competitions.

a, Expansion speeds and growth rates of ancestor, strain B, and strain D (see Supplementary Table 2). b, Calibrated fluorescence intensity profiles of singly grown strains 12 h after inoculation at the center of 0.25 % TB agar plates. Unless noted otherwise, the fluorescence intensity in this study is normalized according to the calibration curve shown in Extended Data Fig. 3c; the relative value 1 refers to 5×10⁷ cells/ml. c, Relative fluorescence intensities obtained at various times for the fluorescent mutant strains B_G (orange) and D_G (cyan) and the ancestor Anc_G (purple), each grown singly on TB plate. As can be seen, the faster strain has higher fitness everywhere. d, Raw photographs (upper row) and fluorescence intensity profiles (lower row) before and after merging of a representative two-strain-competition between the fluorescent derivatives of the ancestor and strain D 12 h after initial equal inoculation. We used plasmids GFP and NFP in this study to distinguish the two strains from each other in the head-to-head competition, since there is no systematic influence caused by the expression of GFP or NFP (see Extended Data Fig. 3). Upper row (from left to right): the competition between D_G and Anc_N, the competition between D_N and Anc_G, and the merged photograph in pseudocolor (D_G, cyan; Anc_G, purple). Lower row: the corresponding relative fluorescence intensity profiles. e, The same as panel d, only that strain D was replaced by strain B. Evolved strains and the ancestor with the GFP/NFP were cultured to log phase separately. Two types of the combined mixed strains were prepared, the evolved strain with GFP was mixed with the Anc_N while the evolved strain with NFP was mixed with the Anc_G in a 1:1 ratio. Later, 2 μl of the two types of the combined mixture were inoculated onto the center of pre-warmed semi-solid agar plates separately and allowed to expand at 37°C for up to 24 h. The photograph and fluorescent intensity of the evolved strains/ancestor with the GFP reporter from these two plates after the expansion were taken at various times and merged. See Methods for details. f, The relative fitness W_B obtained as a ratio of direct cell count of the fluorescent derivatives of the ancestor and strain B, inoculated at the center of agar plate. From left to right: the competition between B_G and Anc_N, the competition between B_N and Anc_G, and the averaged curve of the left two ones, giving W_B (shown as panel m). The competition experiments are the same as those shown in panel e. The initial and final ratio of the two competitors were measured by cell counting with a flow cytometer, see Methods for details. The spatiotemporal development of the bacterial density profiles, indicated by fluorescence intensities, are shown for the competition between the ancestor (purple) and strain D (cyan) (g) and between the ancestor and strain B (orange) (i) at various times during the 24h course of their competition. Beyond the initial period (~6 h), the crossover distance could be clearly defined (vertical dashed line) and was practically time-independent, with the ancestor gaining advantage in the interior and strain D gaining advantage in the exterior. The relative fitness values, W_D and W_B, taken as the ratio of the fluorescence intensities (mutant:ancestor) at various distances, are shown for the two competition runs in panels h and j, respectively, for time = 6 h and beyond. The vertical dashed lines indicate the crossover distance d_× where the densities of the two competing strains are equal, i.e., W_i = 1. Thus, the crossover distance was frozen in shortly after the initial period. Fluorescence intensity profiles (k, l), and relative fitness W (m) of representative two-strain competitions between the ancestor and evolution isolates. The black solid line indicates the ancestor. The data were taken 12 h (k, m) or 24 h (l) after co-inoculation of equal initial mixture of the two competing strains at the center of 0.25% TB agar plates, showing that the slower strain spatially outcompetes the faster strain within the crossover distance d_× (dashed lines). From left to right, the evolution isolates are A (red), B (orange), C (green), D (cyan), and E (blue), respectively. See Supplementary Table 2 for strain information. Experiments in a-l were repeated independently 3 times, obtaining similar results. In m, mean±s.d. of n=3 biologically independent repeats is shown.

Extended Data Figure 5: The growth-expansion dynamics of a single strain.

a, We review here the growth-expansion model (GE model) established in Ref. 9 to describe the dynamics of a single strain of E. coli colonizing a soft agar plate. The GE model considers three different variables and their dynamics in space x and time t: (i) cell density ρ(x, t), (ii) the concentration of a signaling molecule (the “attractant”) a(x, t) that cells can sense and move towards, and (iii) the concentration of nutrient n(x, t) cells consume to grow. Following the spirit of the classical model introduced by Keller and Segel³⁸ (KS model), cells can move in a random, undirected manner (effective diffusion constant D and diffusion term in Eq. [S1]) and along the gradient of the signaling molecule (the “attractant gradients”, represented by the convection term in Eq. [S1] and Eq. [S2]), which is generated by the cellular consumption (Eq. [S3]). To account for observed density profiles and their evolution over time, 3 additional aspects are important to consider beyond the KS model. First, cells can only detect and respond to attractant gradient in a scale-free manner within a limited range between K_I and K_A^25,39 as specified in Eq. [S2]. D₀ denotes the molecular diffusion of attractant and nutrient within the agar. The chemotactic parameter c denotes how cells translate the detected attractant gradient into directed movement. Second, cells grow throughout the expansion process, as described by the growth term in Eq. [S1] with growth rate λ. Third, growth does not rely on the presence of the attractant but the presence of nutrients. We model the latter dependence by the nutrient field n(x, t) and a yield factor Y; see Eq. [S4]. The distinct treatment of the role of nutrient and attractant is designed to model the dynamics of bacterial cells in complex media, where non-chemotactic components in the complex media are designated as the “nutrient”, while the (minor) chemotactic components of the complex media are reflected by a low concentration of a single attractant; see Ref. 9 for a detailed discussion and validation of the model, including comparison to other models of chemotactic migration. b, Emerging density profile (green solid line) and attractant concentration (magenta dashed line) in the GE model. At the front is a density “bulge” or peak, within which the attractant profile drops steeply, guiding cells to do chemotaxis. Directed movement of cells in the front bulge is coupled to an exponentially rising trailing region. In this region, cells grow and swim randomly, but there is no directed cell movement there due to the low attractant concentration (a < K_I). [Note that in cases where multiple attractants are present in the medium, the population typically exhibit multiple rings, one corresponding to the exhaustion of each attractant. For these cases, the trailing region involving cell growth but no chemotaxis would correspond to the region interior to the inner-most ring, after the exhaustion of the last attractant. Thus, our model which contains a single attractant, does not attempt to describe the movement of the outer-rings, but models the transition of the density profile from the inner-most ring to the exponential trailing region. As we describe in Supplementary Analysis 1–2, it is the dynamics in this transition region that determines strain dominance in multi-strain competition processes.] c, Stable expansion of the population can be explained by a balance between growth of cells in the front bulge and “leakage” of cells out of the front due to random movement (cell diffusion): For illustration, consider the green dashed line indicating the density profile at a given earlier time. With only directed movement (along attractant gradient) and cell growth, the front peak would be higher at a later time, as illustrated by the brown dashed line. Instead, growth in the front bulge is compensated by back-diffusion of cells away from the front (green solid line indicating a later time). This compensation mechanism is further shown in the cylinder plots below, illustrating that the observed stable expansion dynamics (constant expansion speed, constant peak density), is a consequence of a dynamic balance between growth at the front and back-diffusion. The exponential density profile in the trailing region results from a combination of the steady outward movement of the front and a steady exponential growth of cells leaked out of the front; see Ref. 9.

Extended Data Figure 6: Model of two-strain competitive expansion dynamics.

a, The growth-expansion model of bacterial range expansion developed in Ref. 9 and outlined in Extended Data Fig. 5 is extended to several strains of bacteria, whose densities are denoted by ρ_i(x, t), with i ∈ {1,2} for two strains. The different bacterial strains are assumed to consume the same nutrient (n) and grow at the same rate λ(n), in accordance to Monod’s law. They also sense and consume the same signaling molecule, the attractant (a), at the same rate μ(a). The random motion of each bacterial strain is described by a diffusion term, with effective diffusion coefficients D_i for strain i; see Eqs. [S5], [S6]. The spatial attractant profile a(x, t) (resulting from bacterial consumption, Eq. [S8]) leads to directed motion which is modeled by a drift term in Eqs. [S5] and [S6]. The dependence of the drift velocities, v_i, on the attractant profile is given by Eq. [S7], which describes a range of proportional sensing, v ∝ ∂_xa/a for K_I < a < K_A. The magnitude of the chemotactic response is parametrized by the chemotactic coefficient c_i for strain i. Finally, the dynamics of the nutrient and attractant are described by Eqs. [S8] and [S9], with D₀ characterizing molecular diffusion. b, Outcome of the competitive expansion dynamics, showing the density profiles of two strains, 24 hours after inoculating with equal mixture at the origin. Competition is run for one strain resembling the ancestor (black line, with expansion speed $u_{anc}=6mm/h$) and the other strain resembling a mutant, with expansion speed, u_mut, increasing from left to right as indicated above the plots. The experimental data is taken from Extended Data Fig. 4l. c, Increase and the abrupt freezing of the crossover distance over time as observed in simulations (line) and experiments (circles). The expansion speeds of the competing pair are u_anc vs u_mut = 6mm/ℎ vs 7mm/ℎ, with the latter mimicking the expansion speed of strain D; see Extended Data Fig. 3b. Full temporal evolution of the density profiles is shown in Supplementary Video 2. The experimental data is from Extended Data Fig. 4g. d, The chemotactic competition model of panel a is repeated to determine the stability distance d^∗ for various u and several smaller growth rate values, λ (indicated in legend). The results confirm that the linear relation (2) between the stability distance and expansion speed shown in the main text holds for each growth rate simulated. e, The slope u/d^∗(u) in panel d is plotted against the growth rate λ. A linear dependence on λ is seen as predicted by Supplementary Analysis 2. f, Effect of differing growth-rate (x-axis) on the outcome of competition and cross-over distance, for two strains with different chemotactic coefficients (c₁,c₂). Legend shows the ratio c₂/c₁. The main result that the interior is dominated by the slower strain and exterior dominated by the faster strain still holds. The crossover distance separating the different regions of dominance is found to vary smoothly with growth rate differences, but in opposite ways depending on whether the faster growing strain moves faster (red) or slower (green). The observed change of the crossover distances are minimal when growth-rate differences are minimal (e.g., <1% as we observed experimentally for TB, see Extended Data Fig. 1e) but become substantial when growth-rate differences become large. See Supplementary Analysis 3 for details. g, The stability distance d^∗ as shown in panel d, but for an alternative model formulation of chemotactic movement following Taylor & Stocker⁴⁰ with different functions describing sensing and the directed movement along gradients. See Supplementary Analysis 4 for more details. Despite the model changes, a linear relation with growth-rate dependent slopes were still observed. In b-g, the chemotactic coefficient c was varied to modify expansion speeds. The cellular diffusion coefficient, D, was varied accordingly, with D = c/6.25 remaining constant. Simulations with a fixed diffusion coefficient gave similar results. Experiments in b, c were repeated independently three times, obtaining similar results.

Extended Data Figure 7: Two-strain competition and crossover dynamics.

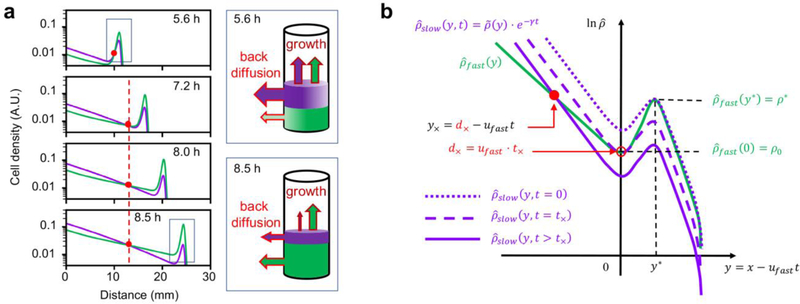
The results in Fig. 2 show clearly that competition between two strains with the same growth rate and different single-strain expansion speeds generically gives rise to a distinct spatial structure where the slower strain dominates inside and the faster strain dominates outside, separated by a “crossover” distance that depends on the two speeds. Here we explain how this feature arises from the underlying growth-expansion dynamics. a, Dynamics simulation using Eqs. [S5]-[S9], for two strains differing only in their chemotactic coefficients, c_slow = 652 μm²/s and c_fast = 727μm²/s, with corresponding single-strain expansion speeds u_slow = 4.95 mm/h and u_fast = 5.17 mm/ℎ; other parameters, equal for both strains, are provided in Supplementary Table 3. The density profile of the strain with faster single-strain expansion speed is shown in green, the other is shown in purple. The red circles indicate the position of the crossover distance, which quickly freezes at a fixed position in the lab frame (dashed red line) after the troughs of the two density bulges cross each other. This important feature, manifested also in the experimental data in Extended Data Fig. 4g,i, allows us to define a simple crossover distance, d_×, that is time invariant. To understand the crossover dynamics in (a), we first provide a qualitative explanation: We note that the competition dynamics involves a single co-migrating even though the two strains would individually expand at different speeds. This is due to the fact that the two strains chase after the same attractant profile which can recede only at a single speed. This has been studied in detail down to the cellular level by Fu et al⁴¹. Because the front is moving at speed faster than the speed the slower strain can stably propagate at, the slower strain gradually gets depleted from the front. As shown by the cylinders in the cartoon, at early times (before the front has reached the crossover distance and where the abundances of the two strains in the front bulge are comparable), the leakage flux of slower cells (in purple) at the back exceeds that of the faster cells (in green). Since the two strains grow at the same rate behind the front, the slower strain dominates there. The faster leakage of the slower strain makes it preferentially depleted from the front bulge. At a later point, the leakage flux of the slower strain drops below that of the faster strain. (This happens despite the faster leakage rate of the slower strain, due to its reduced abundance.) From there on, the back is dominated by the faster strain. The position where the two leakage fluxes are the same marks the crossover distance. b, Next, we describe elements of a simple analysis which captures key features of the crossover dynamics and leads to a time-invariant crossover distance $d_{\times }(u_{fast},u_{alow})$ for two strains with single-strain expansion speeds u_fast and u_slow, and how this crossover distance in turn leads to a special evolutionary stable “selection distance” d^∗ defined in the limit $u_{slow}\to u_{fast}$ (Fig. 3 and 4). The two density profiles shown in panel a, denoted here as ρ_fast(x, t) and ρ_slow(x, t) in the “lab frame” coordinate x, are shown in panel b in the frame moving with speed u_fast. In this moving frame where the spatial coordinate is y = x − u_fastt, the density profile of the faster strain (indicated by the green line) is approximately stationary, i.e.., ${\rho }_{fast}(x,t)={\widehat{\rho }}_{fast}(y)$, where ${\widehat{\rho }}_{fast}(y)$ is the stationary solution of the single-strain dynamics in the reference frame moving at speed u_fast. Defining the position of the trough to be y = 0 in the moving frame, ${\widehat{\rho }}_{fast}(y)$ has a bulge for y > 0, and a trailing exponential for y < 0. In this frame, the density profile of the slower strain is generally not stationary, and is written as. As described in detail in Supplementary Analysis 1, the consequence that the slower strain expands at a speed faster than its single-strain expansion speed is that its density bulge, while preserving the spatial structure, is “depleted” exponentially over time. This is expressed mathematically as ${\widehat{\rho }}_{slow}(y,t)={\tilde{\rho }}_{slow}(y)e^{-\gamma t}$, where ${\tilde{\rho }}_{slow}(y)$ also has a bulge for y > 0, and a trailing exponential for y < 0. Since the density bulges of the two strains are aligned spatially by the common attractant gradient, we denote the position of the bulge peak by y^∗ for both strains. However, in general the peak height would not be the same between the two strains, nor would the slope of the trailing exponentials. In panel b, the density profile of the slower strain, ${\tilde{\rho }}_{slow}(y)e^{-\gamma t}$, is illustrated at 3 different time t by the different purple lines: The dotted purple line indicates the initial time (t = 0) where the density bulge of the slower strain has the same peak value ρ^∗ as the faster strain (green line), i.e., ${\tilde{\rho }}_{slow}(y^{\ast })={\rho }^{\ast }$. The dashed purple line indicates the density profile of the slower strain at time t_× where the two density troughs cross, i.e., ${\tilde{\rho }}_{slow}(y)e^{-\gamma t_{\times }}={\rho }_0$. The spatial location at which the troughs cross (open red circle) is the crossover distance d_× = u_fast ∙ t_× (obtained from y(t_×) = 0). For t > t_×, the density bulge of the slower strain sinks steadily below that of the faster strain, and its density profile (solid purple line) crosses that of the faster strain (green line) at position y_× < 0 which is behind the front and falls steadily backward in the moving frame (filled red circle). Strikingly, detailed analysis in Supplementary Analysis 1 shows that for a steady sinking rate γ ∝ (u_fast − u_slow), the corresponding crossover position in the lab frame remains at d_× for all t > t_×, as illustrated by the fixed position of the red circles in panel b. This important feature of the crossover dynamics can be understood intuitively: Since chemotaxis occurs only within the bulge region, cells at the crossover point (and to its left) experience no net drift. As the two strains grow at the same rate, their densities at this position therefore remain equal to each other for all t > t_×, implying that the density crossover is frozen in at position d_×. What the mathematical analysis provides is an expression (Eq. E14) of how the crossover distance d_× = u_fast ⋅ t_× depends on the two speeds, u_fast and u_slow, and static properties of the two density profiles, ${\widehat{\rho }}_{fast}(y)$ and ${\tilde{\rho }}_{slow}(y)$. From this, we can obtain an expression for the stability distance, defined in the limit the two speeds approach each other, i.e., $d^{\ast }(u)=u\cdot t_{\times }(u_{slow}\to u)$. Importantly, it is shown in Supplementary Analysis 2 that $t_{\times }(u_{slow}\to u)$ approaches a finite limit that is proportional to 1/λ, the doubling time. The proportionality of d^∗ and u is verified in Extended Data Fig. 6d, and the growth rate dependence of the slope is shown in Extended Data Fig. 6e.

Extended Data Figure 8: Fitness landscapes for the competitive expansion process at different positions.

The position-dependent fitness landscapes for the competition between two strains (strain 1 and 2, e.g., an ancestor and a mutant), with expansion speeds u₁ and u₂ respectively, computed according to the competitive expansion model described in Extended Data Fig. 6a. The fitness of the mutant (strain 2) relative to the ancestor (strain 1) is defined as the ratio of its density with respect to the ancestor, i.e., $W(X)\equiv {\lim }_{t\to \infty }\left[\frac{{\rho }_2(X,t)}{{\rho }_1(X,t)}\right]$. In practice, we take t= 24 ℎ, which is well after the dynamics have halted. We further normalize this fitness by the ratio of the initial inoculant, $W_0\equiv \frac{{\rho }_2(X,0)}{{\rho }_1(X,0)}$, to obtain the “relative fitness gain”, W/W₀, which is plotted in various plots above. As indicated by the color bar at the bottom of the figure, green indicates a gain in the fitness of the mutant (W/W₀ > 1), while blue indicates loss of mutant fitness (W/W₀ < 1). The top, middle, and bottom rows refer to results at distances X = 20 mm, 15 mm,10 mm, respectively. a, The plots in the first column show the landscape W/W₀ for equal abundance (50:50) of the two strains at equal inoculation, i.e., W₀ = 1. The cyan and dashed lines are the two special lines, W/W₀ = 1 and u₁ = u₂, respectively. For W₀ = 1, the cyan line is the crossover distance, i.e., X = d_×(u, u′) (corresponding to W = 1) as explained in Fig. 4. The middle row (X = 15mm) is a zoomed out view of Fig. 4c, with a difference that the phase diagram in Fig. 4c only shows qualitative information on which strain dominates, whereas the fitness landscape here also provides quantitative information on the fitness gain. The top and bottom panel shows the corresponding fitness landscapes for X = 20 mm and X = 10 mm. b, The fitness landscape calculations are repeated for a mutant:ancestor inoculant ratio of 5:95 (i.e., W₀ ≡ ρ₂(X, 0): ρ₁(X, 0) = 5: 95). The solid brown line still indicates the phase boundary W/W₀ = 1, but it is no longer directly related to the crossover distance; see below. We see that the topological features of the landscapes in columns 1 and 2 are similar, but the details are different, reflecting the frequency-dependent nature of this competition process. c, In the 3^rd column, we plot the landscape profiles for 3 special ancestor expansion speeds, one at each position X, as indicated by the dotted grey lines marked by circled ① ② ③ in panel b, each obtained as the intersection of the phase boundary and the diagonal (solid brown line and the dashed pink line, respectively). Let us focus on the middle row (X = 15mm): For ancestral speed $u_1^{\ast }=5.15\hspace{0.17em}\hspace{0.17em}mm/h$ marked by grey line ②, the fitness landscape has a maximum at $u_2=u_1^{\ast }$ as marked by the white circle. This indicates that the ancestral expansion speed $u_1^{\ast }$ is stable to invasion by mutants with smaller or larger expansion speeds. Similarly, for X = 20 mm (top row), the ancestral speed $u_1^{\ast }=6.77\hspace{0.17em}\hspace{0.17em}mm/h$ marked by ① is the stable expansion speed, whereas for X = 10 mm (bottom row), the ancestral speed $u_1^{\ast }=3.63\hspace{0.17em}\hspace{0.17em}mm/h$ marked by ③ is the stable expansion speed. d, The phase boundaries shown as the solid cyan and brown lines in panels a,b turn out to intersect the diagonal at the same speed u^∗ for each X. Thus, the stable expansion speeds can be obtained from the crossover distance (cyan line) based on 50:50 inoculant, i.e., the relation (3) in the main text, despite the frequency dependence of the competition process. In other words, even though the overall fitness W depends on the initial frequency W₀ in a complex way, in the vicinity of the diagonal (u₁ ≈ u₂), W is independent of W₀ so that the simple illustration in Fig. 3a on the stability of a strain of speed u at distance d_×(u, u) is verified explicitly in panel c and d. To vary expansion speeds in each panel, the chemotactic coefficients c_i were varied within the range 180‥1500μm²/s. Diffusion coefficients were changed accordingly, D_i= c_i/6.25; see Supplementary Model and Supplementary Table 3.

Extended Data Figure 9: Experimental evolution of expanding bacterial populations in various agar concentrations.

a, Three lineages of evolution trajectories in semi-solid TB plates with different agar concentrations. b,c, Illustration of how the stability distance is determined for each ancestral ES based on the data shown in panel a. Using linear regression of the mean evolution trajectories obtained (here for 0.25 % agar, ancestral ES=6 mm/h, n=3 biological replicates as shown in panel a), we obtained a ‘slope’ for each series, A-E, as shown in panel b. Then in panel c, we plotted the slope obtained in b against the corresponding selection position to obtain another line. The stability distance is estimated as the x-intercept of the line. d, Batch culture growth curve of the ancestor cells grown in TB (purple) or CAA (brown) medium, the growth rate in CAA is almost 50% slower. 2 replicates show similar results. e, The evolution experiment in CAA medium for 5 different agar densities (same as thos shown for TB in panel a). Three independent lineages were run in parallel as for TB.

Extended Data Figure 10: Stable expansion speeds in spatial habitats of different sizes.

a, Illustration of a recurring ecological scenario. A mixed community of species with different motility characteristics expand into an enclosed habitat of a certain size. All cells within the habitat have an equal chance to be passaged on to occupy a new habitat of the same size. The competitive expansion model (Extended Data Fig. 6a) was extended to model the co-expansion of 5 distinct species, chemotaxing on the same attractant gradient (Supplementary Analysis 5). Each species has a distinct expansion speed when expanding alone (between 2mm/h and 8mm/h), due solely to different motility characteristics which are modeled by different chemotactic coefficients c_i in the range {34… 274} μm²/s. A closed (zero-flux) boundary condition is applied so that when cells reach the edge of the habitat, they cannot propagate forward but they can propagate backward by diffusion (backward propagation via chemotaxis along reversed chemoattractant gradients is possible in principle but very limited since the chemoattractant is mostly consumed when the population expands forward throughout the habitat). b, The average expansion speed of the population changes over different cycles of the simulated expansion/selection process. We observe that the average expansion speed increases as the selection proceeds for the larger habitat size (25mm, pink), whereas it decreases for the smaller habitat size (10mm, green). The relative abundance of the species with different single-strain expansion speeds is changed after each round of selection. The result after the 5^th round is shown on the right for the 3 habitat sizes shown. Enrichment of the faster species is seen for selection in the larger habitat (top histogram), and enrichment of the slower species is seen for selection in the smaller habitat (bottom histogram). The slower species takes more cycles to emerge as the winner since they occupy the habitat interior and receive lower weights due to 2d geometry. (c,d) To understand why the faster species were selected against in the smaller habitat, we plotted the radial density function ρ_i(r, t) for each species i attained at t=10 hr and 24hr after expansion during the first selection cycle (i.e., before any selection took place). The density profiles show that after the faster species reach the edge of the habitat, they move backward towards the interior. However, the speed of this backward movement is seen to be quite limited compared to the outward movement. This is attributed to the fact that the chemoattractant behind the front is depleted, so the backward movement cannot rely on chemotaxis but is a result of cell diffusion (via Komolgorov-Fisher dynamics). In d, the cyan and blue lines (expansion speed = 7 and 7.8 mm/h) almost overlap and are hard to distinguish visually.