Quantifying the reliability and replicability of psychopathology network characteristics

Abstract

Pairwise Markov random field networks—including Gaussian graphical models (GGMs) and Ising models—have become the “state-of-the-art” method for psychopathology network analyses. Recent research has focused on the reliability and replicability of these networks. In the present study, we compared the existing suite of methods for maximizing and quantifying the stability and consistency of PMRF networks (i.e., lasso regularisation, plus the bootnet and NetworkComparisonTest packages in R) with a set of metrics for directly comparing the detailed network characteristics interpreted in the literature (e.g., the presence, absence, sign, and strength of each individual edge). We compared GGMs of depression and anxiety symptoms in two waves of data from an observational study (n = 403) and reanalyzed four posttraumatic stress disorder GGMs from a recent study of network replicability. Taken on face value, the existing suite of methods indicated that overall the network edges were stable, interpretable, and consistent between networks, but the direct metrics of replication indicated that this was not the case (e.g., 39–49% of the edges in each network were unreplicated across the pairwise comparisons). We discuss reasons for these apparently contradictory results (e.g., relying on global summary statistics versus examining the detailed characteristics interpreted in the literature), and conclude that the limited reliability of the detailed characteristics of networks observed here is likely to be common in practice, but overlooked by current methods. Poor replicability underpins our concern surrounding the use of these methods, given that generalizable conclusions are fundamental to the utility of their results.

The central tenet of the network theory of mental disorders is that psychopathology is due to dynamic causal interactions among symptoms (Borsboom, 2017). This theory encourages the quantification of the symptom-level structure of psychopathology using network analysis—a method with rapidly growing popularity in psychopathology research. Network analysis of psychopathology symptoms is promoted to improve clinical prevention and intervention strategies by indicating which symptoms are more strongly connected to other symptoms in a network (i.e., more central), as well as which symptoms act as bridges between disorders in comorbidity networks (Fried et al., 2017). In formative papers on the utility of symptom networks, it has been proposed that targeting “central” symptoms and the causal chains among them may be the most effective route to symptom reduction and blocking the pathways to the development of comorbidity between disorders (e.g., Borsboom & Cramer, 2013; Fried et al., 2017; see also Bringmann, Elmer, Epskamp, & Snippe, 2018; Fried et al., 2018 for alternative perspectives).

Recently, there has been an emphasis on the potential limitations of the methods that dominate the psychopathology network literature (Bos et al., 2017; Bringmann & Eronen, 2018; Bulteel, Tuerlinckx, Brose & Ceulemans, 2016; Epskamp, Borsboom & Fried, 2017; Forbes, Wright, Markon & Krueger, 2017a; Forbes, Wright, Markon & Krueger, 2017b; Fried & Cramer, 2017; Guloksuz, Pries & van Os, 2017; Steinley, Hoffman, Brusco & Sher, 2017; Terluin, de Boer & de Vet, 2016; Wichers, Wigman, Bringmann & de Jonge, 2017). Correspondingly, methods have been evolving rapidly with the aim of addressing the reliability and replicability of parameter estimates (e.g., Epskamp et al., 2017; van Borkulo et al., under review). Psychopathology network models are exploratory and often highly parameterized, making them prone to overfitting the data by capitalising on chance. Further, the focus on conditionally dependent relationships (e.g., partial correlations) between symptoms assessed by single self-report or interview items make the network edge estimates vulnerable to measurement error.

The pitfalls of interpreting conditionally dependent relationships have long been known in the contexts of interpreting partial correlations and multiple regression coefficients (e.g., Cohen & Cohen, 1983; Gordon, 1968). For example, the presence of shared variance among symptoms of psychopathology is well-established (e.g., Kotov et al., 2017), and the systematic patterns of overlap among symptoms and syndromes are often modelled using factor analytic methods that summarise these patterns as latent variables. When modelled in this way, the symptom-level structure of psychopathology is often robust (e.g., Anderson & Hope, 2008; Clark & Watson, 1991; Lambert, McCreary, Joiner, Schmidt & Ialongo, 2004; Teachman, Siedlecki & Magee, 2007). It is the reliable variance shared among multiple symptoms that underpins the robustness of these models (Allen & Yen, 2002). However, this shared variance is largely excluded in the estimation of psychopathology networks; each edge is based on the variance shared by each pair of symptoms after removing the variance they share with all other symptoms in the network. In other words, as soon as more than two symptoms in the network measure the same construct, this reliable shared variance is removed from the model. Modelling the remaining variance captured in the conditionally dependent relationships thus increases the likelihood of unreliability in estimates of network edges and node centrality, particularly when the symptoms of interest are substantially correlated.

Unreliability is a significant problem for psychopathology networks because both the reliability of parameter estimates within networks and replicability between networks are fundamental to their generalizability, as well as a prerequisite for making inferences regarding differences in network structure between groups, or regarding changes in network structure over time (e.g., Beard et al., 2016; Fried, Epskamp, Nesse, Tuerlinckx & Borsboom, 2016; van Borkulo et al., 2015). Because network theory depends on direct causal associations between symptoms, the utility of these methods relies on the generalizability of specific network features as they are interpreted in the literature: the presence, absence, sign, and strength of each individual edge, and correspondingly which specific and individual symptoms are most/least central (Epskamp et al., 2017). Recent developments in the literature have consequently focused on implementing methods to maximize and quantify the accuracy, stability, and consistency of psychopathology network characteristics.

Current Psychopathology Network Methods

Edges in pairwise Markov random field (PMRF) networks represent the relationship between each pair of symptoms after controlling for their shared variance with all other symptoms in the network (i.e., conditionally dependent relationships). They are currently considered the “state-of-the-art” in psychopathology network modelling and have become the “default network model”, representing 62% of psychopathology network studies and growing (Borsboom et al., 2017, p. 990). Consequently, much of the recent development in methods has aimed to maximize and quantify the accuracy, stability, and consistency of parameters within and between PMRF networks specifically.

There are three primary tools used to this end, including regularisation as well as bootstrap and permutation tests (using the bootnet and NetworkComparisonTest (NCT) packages in R, respectively). First, regularisation-based model selection uses a least absolute shrinkage and selection operator (LASSO; Tibshirani, 1996) with a tuning parameter to minimize the Extended Bayesian Information Criterion (EBIC; Chen & Chen, 2008). This technique limits the total sum of absolute edge weights, thus shrinking many estimates to zero (i.e., excluding them from the network), resulting in a sparse network that is described as having high specificity for excluding spurious edges and identifying only “true” symptom-to-symptom relationships (Epskamp et al., 2017; Epskamp & Fried, in press; Fried & Cramer, 2017). In small sample sizes, using LASSO regularisation with EBIC for model selection is a conservative approach to network estimation because even moderately large edge weights may be set to zero, which may increase false negatives (i.e., “true” edges may not be estimated), but is intended to maximize specificity for avoiding any false positives (Epskamp et al., 2017; Epskamp & Fried, in press).

Second, the bootnet package (Epskamp et al., 2017) in R (R Core Team, 2013) uses three bootstrapping routines to examine the stability of edge weight and node centrality estimates within networks. (1) A non-parametric bootstrap draws many (e.g., 1000; Fried et al., 2018) different subsamples with replacement from the observed data. The network edges estimated in these subsamples are pooled to generate a sampling distribution for each edge. A bootstrapped 95% confidence interval (CI) for each edge is constructed from its sampling distribution. Narrower bootstrapped CIs indicate greater stability of edge weight estimates, but the authors of the package emphasise that the CIs do not represent significance tests; model selection is performed by LASSO regularisation with EBIC (as described above), so if an edge is present it is expected to be part of the true network and the presence, absence, and sign of the edge are interpretable (Epskamp et al., 2017; Epskamp & Fried, in press). (2) A case-dropping bootstrap (without replacement) can also be used to examine centrality stability—that is, stability of the order of centrality estimates as increasing proportions of participants are excluded from the analyses. These results are usually summarised using a CS-coefficient that quantifies the proportion of participants that can be dropped while retaining a 95% likelihood that the estimated centrality indices correlate at least 0.7 with the original centrality coefficients. Epskamp et al. (2017) recommended this proportion should be at least 25% (ideally 50%) to interpret centrality estimates. (3) Bootstrapped difference tests can also be performed for the estimated weights for each pair of non-zero edges, and for the centrality estimates for each pair of the symptoms: A bootstrapped CI of the difference between each pair of edges (and each pair of centrality estimates) is generated in the same non-parametric bootstrap routine described in (1) above. The null-hypothesis test of whether each pair of edge weights (and each pair of centrality estimates) differ from one another is conducted by checking if zero is in the uncorrected 95% bootstrapped CI. Plots are generated based on these three bootstrap routines to inspect sampling variation in the estimates of edge weights and centrality indices, and to summarize the results of the significance tests. These results are used to indicate which edges are the strongest and most stable, which nodes are the most and/or least central in the network, and more broadly whether edge weights and centrality estimates are interpretable within a given network.

Finally, the NCT package (van Borkulo et al., under review) uses permutation testing to quantify differences between pairs of networks with, ideally, similar sample sizes. This test works by pooling the data from the two networks that are being compared, and then repeatedly randomly re-assigning the data into two groups to estimate many (e.g., 5000; Fried et al., 2018) new pairs of networks. This process results in a reference distribution of differences between the two networks, representing the null hypothesis that the networks are drawn from the same population. These reference distributions are used to test three hypotheses regarding the invariance of the original pairs of networks. (1) The first test is for the null hypothesis that the structures of the two networks (i.e., the matrices of all edge weights) being compared are identical. This omnibus test of network structure invariance is conducted by finding the maximum absolute difference in edge weight between the two observed networks (i.e., the difference corresponding to the edge that changes most from one network to the other) and comparing it to a reference distribution comprised of the maximum absolute differences in each of the permuted networks. If the observed difference is larger than 95% of the distribution of permuted differences (i.e., p < .05), the null hypothesis is rejected, suggesting the network structures are different, in aggregate. (2) The second test quantifies how many of the individual edges differ between the two networks, based on the null hypothesis that each edge is identical between networks (i.e., the individual edge invariance test). This test is conducted by comparing the observed (absolute) difference in each edge to the reference distribution of differences for that edge. If the observed difference is at or beyond the upper extremity of the reference distribution (i.e., p < .05, typically after a Holm-Bonferroni correction for multiple testing), the edge is deemed significantly different between the networks. (3) The third test is for the null hypothesis that global strength (i.e., the sum of the absolute values of all edges in the network) is the same in each network (i.e., the global strength invariance test). As above, this is based on comparing the difference in the observed global strength values for each network to the reference distribution of differences from the permuted networks. In addition to these three tests, networks are often also compared using a “coefficient of similarity” (i.e., a Spearman rank correlation of the edges lists from a pair of networks; e.g., Borsboom et al., 2017; Fried et al., 2018; Rhemtulla et al., 2016).

Borsboom et al. (2017) described the methods in the bootnet and NCT packages as “powerful tools” for assessing the stability and consistency of PMRF networks (p. 990), and together with LASSO regularization they have become the default suite of methods for research on PMRF psychopathology networks. Most of the latest studies use these methods to interpret cross-sectional networks, to examine change in networks over time, and to conduct replication studies (e.g., Beard et al., 2016; Fried et al., 2018; Fried et al., 2016; van Loo et al., 2018). These studies have largely concluded that network characteristics (i.e., estimated edges and symptom centrality estimates) are accurate, sufficiently stable to interpret, consistent over time, and largely generalizable.

However, recent work on the replicability of parameters in networks of major depression and generalized anxiety symptoms has highlighted that different methods for quantifying similarities and differences between networks can lead to vastly different conclusions (Borsboom et al., 2017; Forbes et al., 2017a; Forbes et al., 2017b; Steinley et al., 2017). Forbes et al. (2017a) examined the replicability of four different types of psychopathology networks—including PMRFs in binary data¹ (i.e., Ising models; van Borkulo et al., 2014)—in two nationally representative population surveys. Inconsistencies were evident in the edge estimation and node centrality rank-orders of PMRFs that were obscured in a reanalysis of the same data using the suite of methods described above (Borsboom et al., 2017). For example, 13–14% of the edges failed to replicate between the two samples, including 47% of the bridging edges. In contrast, bootnet results suggested that most of the edge weights were stable and interpretable; the edge lists correlated at r > .95; and—despite being well-powered—the NCT omnibus test failed to reject the null hypothesis that the network structures were identical. Forbes et al. (2017a) concluded that that there were notable differences between the estimated networks. Borsboom et al. (2017) concluded that these networks were “nearly identical” (pp. 990 and 995). Forbes et al. (2017b) subsequently suggested that these contradictory conclusions may be because the bootnet methods, NCT tests, and coefficients of similarity do not focus on the detailed characteristics of networks that are interpreted in the literature (i.e., the presence, absence, sign, and strength of each individual edge; and correspondingly which symptoms are most/least central; Epskamp et al., 2017). The data that were used in that work were drawn from two large (n > 8,000) population surveys, and the symptom data had substantial systematic patterns of missingness due to the structured interview format of the surveys. Psychopathology network studies tend to be based on self-report data in clinical and/or community samples, so the very large samples and patterns of missingness were not typical of the literature, and may have inflated the stability and consistency of the networks.

The Present Study

The aim of this study was to compare (1) the conclusions based on the existing suite of methods for maximizing and quantifying the accuracy, stability, and consistency of PMRF networks to (2) the conclusions based on direct metrics of consistency in the detailed characteristics of networks that are interpreted in the literature (i.e., the presence, absence, sign, and strength of each individual edge; and correspondingly which symptoms are most/least central; Epskamp et al., 2017). To achieve this aim, we selected data that are typical of the extant psychopathology network literature. The primary analyses were based on examining symptom networks of depression and generalized anxiety symptoms in two waves of data from a community sample (n = 403) measured one week apart. We hypothesized that depression and anxiety symptoms would have substantial shared variance that would be consistent over time, but that the detailed characteristics of the networks would be less consistent.

To ensure the results were not solely due to key methodological features of the primary analyses (e.g., a focus on depression and generalized anxiety symptom networks, the use of a community sample, a moderate sample size, or subjectivity in interpreting bootnet results), we also did secondary analyses of the networks estimated in Fried et al.’s (2018) recent study of the replicability of four posttraumatic stress disorder (PTSD) symptom networks. Fried et al. (2018) shared their correlation matrices, model output, and code in the Supplementary Materials and encouraged reanalysis of the data for further replicability research. A summary of the relevant results and corresponding conclusions reported in Fried et al. (2018) is presented in Table 1. Using the existing suite of methods described above, Fried et al. concluded that “Despite differences in culture, trauma type, and severity of the samples, considerable similarities emerged, with moderate to high correlations between symptom profiles (0.43[sic]-0.82), network structures (0.62–0.74), and centrality estimates (0.63–0.75).”² (p. 1). We hypothesized that direct metrics of consistency in the detailed characteristics of the four networks would highlight substantial differences between them that were obscured by the existing suite of methods.

Table 1.

Summary of the results reported in Fried et al. (2018)

Network characteristic	Parameter estimate	Interpretation in Fried et al. (2018)
t-tests between samples for average symptom endorsement	Except for Sample 1 compared to Sample 2, all samples differed significantly in mean symptom severity (ps < 2.2.×10−16)	“Samples differed in average symptom endorsement” (p. 6)
Spearman rank correlations among mean symptom profiles	Range from rs = [.34] to rs = .82 (median rs = .63).	“There were considerable similarities across data sets in their mean symptom profiles” (p. 6)
Visual comparison of the networks1	N/A	“The four networks featured many consistent edges…There were also specific edges that differed considerably…” (p. 8).
Symptom strength centrality order (Pearson correlations between each pair of networks)1	Range from r = .63 to r = .75 (median r = .69)	“centrality order was substantially related across the four networks” (p. 8)
bootnet results2
Correlation-stability coefficients	Range from CS(0.7) = .52 to CS(0.7) = .75 (median CS(0.7) = .60)	“The correlation-stability coefficient[s] for strength centrality…exceeded the recommended threshold for stable estimation of 0.50” (p. 8)
Edge weight 95% confidence intervals	Plot of CIs (see Fig S3 in Fried et al.)	“Stability analyses indicated that all four networks were accurately estimated, with small to moderate confidence intervals around the edge weights” (p. 8).
Coefficient of similarity (Spearman rank correlations of edge lists)1	Range from rs = .62 to rs = .74 (median rs = .71)	“indicating strong similarities” (p. 8).
NetworkComparisonTest results3
Omnibus test of network structure invariance	all ps < .005	“implying that no pair of networks featured exactly the same 120 edge weights” (p. 8)
Individual edge invariance test	Range of 2 (1.7%) to 8 (6.7%) edges differed significantly across the six comparisons (median of 3 [2.5%])	“Overall, networks were moderately to strongly correlated and only a few significantly different edges emerged, which implies considerable similarities.” (p. 9)
Global strength invariance test	Four of the six pairwise comparisons were significantly different (p < .05)	“Global strength values were fairly similar” (p. 9)
Cross-sample variability network4	Three edges were described as “the most variable”, with standard deviations of.15, .15, and .14	“For the remaining edges, standard deviations were small to negligible” (p. 10)
Summary of the results	N/A	“First, whereas data sets differed in overall PTSD severity, the patterns of symptom endorsement were correlated across the four samples… Second, whereas the structures of the four networks were not statistically identical (i.e., not all edges were exactly the same), the networks showed moderate to high intercorrelations, as did strength centrality coefficients. Third, we highlighted the most pronounced differences among networks by estimating a variability network: [Three edges] differed considerably across the four samples, whereas other edges were similar or identical across networks.” (p. 10)

Note.

¹Based on jointly estimated Gaussian graphical models (GGMs) derived from polychoric correlations using fused graphical lasso selecting tuning parameters using k-fold cross-validation.

²Based on individually estimated GGMs derived from polychoric correlations.

³Based on individually estimated GGMs derived from Pearson correlations, excluding the 0.3–3.8% of cases with missing data.

⁴Based on jointly estimated Gaussian graphical models (GGMs) derived from polychoric correlations using fused graphical lasso selecting tuning parameters using information criteria.

Method

Analytic Samples

The primary analyses were based on a subset of community participants from a larger longitudinal study. The methods have been described in detail elsewhere (Forbes, Baillie & Schniering, 2016). Analyses included 403 participants who completed questions online regarding depression and anxiety symptoms two times one week apart. The participants lived in Australia, had an average age of 32 (standard deviation [SD] = 12.0) and were largely female (n = 315, 78.2%), married or living with a partner (n = 212, 52.6%), had at least some university education (n = 253, 62.8%), and were in paid employment (n = 261, 64.8%).

Secondary analyses were conducted based on the networks estimated in Fried et al. (2018), where the methods of the study are described in detail. Briefly, the study included four samples of traumatized patients receiving treatment, including: patients from a Dutch mental health center (n = 526, average age = 47.0, 35.9% female; Sample 1); patients from a Dutch outpatient clinic (n = 365, average age = 35.6, 72.1% female; Sample 2); previously deployed Danish soldiers (n = 926, average age = 36.2, 5.2% female; Sample 3); and refugees with a permanent residence in Denmark (n = 965, modal age category = 40–49, 42.0% female; Sample 4).

Measures

Analyses of the community sample were based on self-report measures of symptoms of depression and generalized anxiety. The Patient Health Questionnaire (PHQ-9; Kroenke, Spitzer & Williams, 2001) is a 9-item measure of depression symptoms with cut-off scores that indicate clinically significant levels of major depression (Lowe, Kroenke, Herzog & Grafe, 2004). At wave one, 29.8% of participants had clinically significant (moderate or stronger) depression, and 23.3% at wave two. In the present study, the PHQ-9 had good internal consistency at both time points (α = .90) and good test-retest reliability (r = .78). The Brief Measure for Assessing Generalized Anxiety Disorder (GAD-7; Spitzer, Kroenke, Williams & Lowe, 2006) is a 7-item measure of anxiety symptoms with cut-off scores that indicate clinically significant levels of generalized anxiety (Spitzer et al., 2006). At wave one, 23.1% of participants had clinically significant anxiety, and 18.6% at wave two. In the present study, the GAD-7 had good internal consistency at both time points (α = .90), and good test-retest reliability (r = .75). The PHQ-9 and GAD-7 have the same stem (“Over the last 2 weeks, how often have you been bothered by any of the following problems?”) and response options (0 “Not at all”, 1 “Several days”, 2 “More than half the days”, 3 “Nearly every day”).

The symptom networks in Fried et al. (2018) were based on PTSD symptoms assessed by the 16-item Harvard Trauma Questionnaire (HTQ; Mollica et al., 1992), the 17-item Posttraumatic Stress Symptom Scale Self-report (PSS-SR; Foa, Cashman, Jaycox, & Perry, 1997), and the 17-item Civilian version of the PTSD Checklist (PCL-C; Weathers, Litz, Herman, Huska, & Keane, 1993). Fried et al. (2018) combined the physiological and emotional reactivity items in the PSS-SR and PCL-C to allow for comparison with the HTC, and rescaled the five-point Likert response scale of the PCL-C to a four-point Likert scale for comparison with the other measures. Fried et al. (2018) indicated that 59.3–100% of the patients in each sample had (probable) PTSD diagnoses, and reported good internal consistency for the measures in each sample (α = .85 to α = .94).

Data Analysis

The raw data for the primary analyses and the analytic code for all analyses are available at https://osf.io/6fk3v/. The correlation matrices, model output, and code used in Fried et al. (2018) are available in the online Supplementary Material for that article.

To start, we quantified the mean level, variability, and bivariate relationships of depression and anxiety symptoms in the community sample within and between waves. To establish whether there was a consistent pattern of shared variance underlying depression and anxiety symptoms at each wave (i.e., whether it was reasonable to expect consistency in the symptom networks), we estimated a two-factor exploratory structural equation model (ESEM). We examined longitudinal measurement invariance, as well as consistency over time in the unconstrained ESEM described below. Longitudinal measurement invariance was tested treating the data as ordinal using delta parameterisation and the means and variances adjusted weighted least squares (WLSMV) estimation. An unconstrained model was estimated first with free factor loadings and indicator thresholds, identifying the model by fixing factor means to 0 and scale factors to 1. This model was compared to a constrained model with factor loadings and indicator thresholds fixed to equality between waves, and with factor means and scale factors freed at wave two (Muthén & Muthén, 1998–2015). Model comparisons were based on fit indices and chi-square difference tests in MPlus. We also compared the pattern of factor loadings across the two waves in the unconstrained model using Tucker’s factor congruence coefficient, which is an index of factor similarity based on deviations of the factor loadings from zero.

Psychopathology Networks

Existing suite of methods

The depression and anxiety symptom networks in the primary analyses were estimated as Gaussian graphical models (GGMs; i.e., PMRFs for ordinal or continuous data) separately at each wave using graphical LASSO regularisation with EBIC, as described above. The four PTSD symptom networks in Fried et al. (2018) were also estimated using this method, as well as several others (see Table 1, and Fried et al., 2018, for more information on these methods). For internal consistency in the results as well as continuity with the methods in the present study and methods currently applied in the literature, we report Fried at al.’s (2018) original results below, but also re-estimated coefficients of similarity, centrality estimates, and calculated all direct metrics of consistency based on the individually estimated GGMs using graphical LASSO regularisation with EBIC (i.e., in line with the bootnet and NCT results). In GGMs based on ordinal data, the edges connecting symptoms represent regularized and fully partialled polychoric correlations.

In line with Fried et al. (2018), we examined only strength symptom centrality (i.e., the sum of the edge weights connected to a node) because estimates of betweenness and closeness centrality are often unreliable (e.g., Epskamp et al., 2017). Cross-sectional network stability was investigated using the methods in the R package bootnet, as described above. Consistency between pairs of networks was evaluated using the tests in the NCT package³ as well as coefficients of similarity (i.e., Spearman rank correlations of edge lists), as described above.

Direct metrics of consistency

Additional metrics used to compare the detailed characteristics of the networks included (1) examining whether individual edges were consistently estimated (present or absent, and with the same sign) between networks, (2) measuring change in the strengths of the strongest and most stable edges in each network, (3) quantifying the relative similarity in the rank-order of symptom strength centrality using Kendall’s tau-b (based on concordant and discordant pairs) and Spearman rank correlations (based on deviations in rank-order), and (4) quantifying the number and proportion of symptoms with the same rank-order⁴ for strength centrality between networks.

We present the primary analyses of the depression and generalized anxiety symptom networks below before briefly summarizing the results in Fried et al. (2018) based on the current suite of methods and comparing them to the results using the direct metrics of consistency.

Results

Major Depression and GAD: Community Sample Characteristics and Change Over Time

Participants in the community sample varied in levels of depression and generalized anxiety symptom endorsement and severity, with 96.8% of the sample endorsing at least one symptom at wave one, and 92.6% of the sample at wave two. While symptom levels were lower at the second wave (see Table 2), the profile of symptom means were highly similar between waves (r_s = .98). The polychoric correlation matrices were also similar: The patterns of the two correlation matrices could be constrained to equality without affecting model fit (CFI = 1.00, TLI = 1.00, RMSEA = .00; χ²_diff(120) = 112.84, p = .666); a model constraining both the correlations and thresholds to equality also had excellent fit (CFI = 1.00, TLI = 1.00, RMSEA = .02), although there was a small but significant increase in chi-square (χ²_diff(168) = 205.82, p = .025). The full unconstrained correlation matrices are included in the supplementary materials (Table S1).

Table 2.

Symptom means (standard deviations) and strength centrality at each wave of data in the community sample (n = 403).

Node Label	Symptom	Wave 1		Wave 2
		Mean (SD)	Strength	Mean (SD)	Strength
PHQ1	Little interest or pleasure in doing things	0.9 (.90)	1.04	0.7 (.80)	1.40
PHQ2	Feeling down, depressed, or hopeless	0.9 (.88)	1.31	0.7 (.84)	1.11
PHQ3	Trouble falling or staying asleep, or sleeping too much	1.2 (.98)	1.00	1.0 (.96)	0.92
PHQ4	Feeling tired or having little energy	1.3 (.95)	1.60	1.2 (.98)	1.28
PHQ5	Poor appetite or overeating	1.0 (1.00)	1.16	0.9 (.98)	1.19
PHQ6	Feeling bad about yourself — or that you are a failure or have let yourself or your family down	0.9 (.99)	1.02	0.7 (.83)	1.50
PHQ7	Trouble concentrating on things, such as reading the newspaper or watching television	0.7 (.90)	0.95	0.7 (.89)	0.97
PHQ8	Moving or speaking so slowly that other people could have noticed? Or the opposite — being so fidgety or restless that you have been moving around a lot more than usual	0.3 (.67)	1.06	0.3 (.67)	1.11
PHQ9	Thoughts that you would be better off dead or of hurting yourself in some way	0.3 (.68)	1.31	0.2 (.61)	1.13
GAD1	Feeling nervous, anxious, or on edge	1.1 (.88)	0.93	0.9 (.87)	1.27
GAD2	Not being able to stop or control worrying	0.9 (.95)	1.36	0.7 (.90)	1.37
GAD3	Worrying too much about different things	1.0 (.96)	1.19	0.9 (.92)	1.15
GAD4	Trouble relaxing	1.0 (.92)	1.22	0.9 (.88)	1.03
GAD5	Being so restless that it’s hard to sit still	0.5 (.77)	1.45	0.5 (.73)	1.34
GAD6	Becoming easily annoyed or irritable	1.1 (.91)	0.96	0.9 (.87)	0.77
GAD7	Feeling afraid as if something awful might happen	0.6 (.88)	0.95	0.5 (.74)	0.84

Note. Bolded values indicate significant (α = .05) differences between waves based on paired t-tests and Wicoxon signed rank tests.

ESEM

At both waves depression—including irritability from the GAD-7—and anxiety factors each accounted for 23.7–41.5% of the variance in the symptoms (see Table 3). Together the factors accounted for an average of 67.7% (SD = 11.0%, range 51–90%) of the variance in each symptom. These factors were consistent over time, with factor congruence coefficients > .99, indicating the depression and anxiety factors were virtually identical at each wave. Correspondingly, the ESEM met criteria for longitudinal measurement invariance: The unconstrained model had adequate fit (CFI = .95, TLI = .94, RMSEA = .08), and fit indices tended to improve in the constrained model (CFI = .96, TLI = .95, RMSEA = .08) without a significant difference in chi-square (χ²_diff(58) = 65.96, p =.221).

Table 3.

Standardised factor loadings of a two-factor exploratory structural equation model in the community sample (n = 403) with free thresholds and loadings between waves

	Factor loadings				Estimated R2
	Depression Wave 1	Depression Wave 2	Anxiety Wave 1	Anxiety Wave 2	Wave 1	Wave 2
PHQ1	0.82	0.88	0.01	−0.00	68.5%	77.5%
PHQ2	0.79	0.76	0.12	0.13	77.8%	74.7%
PHQ3	0.68	0.63	0.12	0.13	60.3%	53.7%
PHQ4	0.78	0.81	0.02	0.04	63.7%	71.4%
PHQ5	0.92	0.92	−0.24	−0.19	56.3%	62.1%
PHQ6	0.66	0.77	0.19	0.07	65.9%	68.5%
PHQ7	0.73	0.73	0.06	0.05	60.3%	59.9%
PHQ8	0.76	0.70	−0.01	0.10	55.8%	60.5%
PHQ9	1.08	1.16	−0.30	−0.36	76.2%	82.8%
GAD1	0.01	0.00	0.81	0.86	67.7%	75.0%
GAD2	−0.03	−0.03	0.97	0.96	89.8%	88.4%
GAD3	0.01	0.06	0.94	0.84	89.4%	79.2%
GAD4	0.22	0.26	0.65	0.63	68.2%	72.0%
GAD5	0.30	0.28	0.50	0.49	56.3%	53.1%
GAD6	0.56	0.52	0.19	0.28	50.7%	56.4%
GAD7	0.19	0.12	0.62	0.71	59.1%	65.0%
Proportion of variance explained by the factor	39.9%	41.5%	23.7%	23.9%	-	-

Note. Bolded loadings are significant at p < .05, All factors were allowed to correlate within and between waves, per standard parameterisation.

Psychopathology Networks

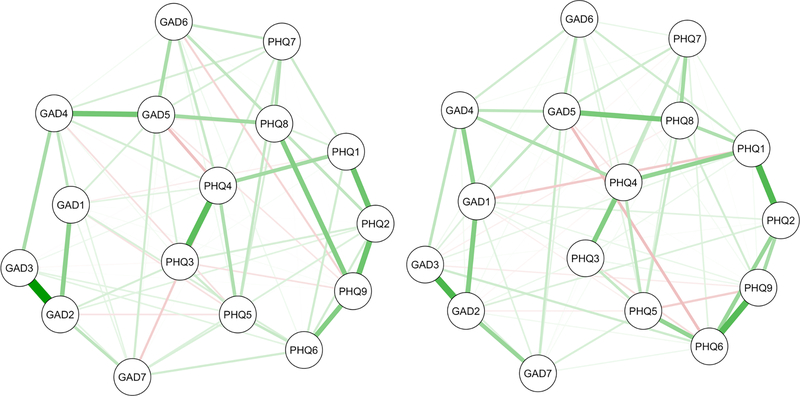
The full depression and generalized anxiety symptom networks are plotted in Figure 1. Table 4 describes the characteristics of the two networks. These networks had different most central nodes, but global characteristics of the networks tended to be similar: Both had the same connectivity, similar proportions of positive and negative edges, a substantial proportion of bridging edges between depression and anxiety symptoms, and similar global strength.

Figure 1.

Regularized GGM networks (ns = 403) at wave one (left) and wave two (right) plotted using the average of the two Fruchterman-Reingold (or “spring”) algorithm layouts in qgraph (Epskamp, Cramer, Waldorp, Schmittmann & Borsboom, 2012). Green edges are positive and red edges are negative. Node abbreviations are shown in Table 2.

Note. We use the averaged layout of the full networks to plot all figures in this study because it is becoming common to plot multiple networks in this way to facilitate comparison (e.g., Fried et al., 2018; Rhemtulla et al., 2016). It is noteworthy that this practice overrides the differences between networks and suggests that the original layouts did not convey important information.

Table 4.

Descriptive overview of each network.

Network characteristic	Community Sample (n = 403)		Posttraumatic Stress Disorder Networks from Fried et al. (2018)
	Wave 1	Wave 2	Sample 1 (n = 526)	Sample 2 (n = 365)	Sample 3 (n = 926)	Sample 4 (n = 965)
Global strength (sum absolute edge weights)	7.28	7.38	7.05	6.59	7.37	6.02
Number of non-zero edges (% possible)	78 (65%)	78 (65%)	77 (64.2%)	73 (60.8%)	77 (64.2%)	77 (64.2%)
Number of zero edges (% possible)	42 (35%)	42 (35%)	43 (35.8%)	47 (39.2%)	43 (35.8%)	43 (35.8%)
Number of positive edges (% total)	64 (82.1%)	66 (84.6%)	76 (98.7%)	69 (94.5%)	74 (96.1%)	77 (100%)
Number of negative edges (% total)	14 (17.9%)	12 (15.4%)	1 (1.3%)	4 (5.5%)	3 (3.9%)	0 (0%)
Number of bridging edges (% total)	41 (52.6%)	34 (43.6%)	–	–	–	–
Number of estimated edges with bootnet CIs that did not span zero (% total)	19 (24.4%)	17 (21.8%)	26 (33.7%)	17 (23.3%)	34 (44.2%)	27 (35.1%)
Most central node (strength)
Depression	Tired/little energy	Guilt/self-esteem	–	–	–	–
Anxiety	Restless	Uncontrollable worry	–	–	–	–
Posttraumatic Stress	–	–	Startle response	Physio/ psychological reactivity	Feeling detached	Feeling detached

Bootstrap and NCT Results

The edges in each network had moderate bootstrapped CIs (see Figure S1)—for example, 22–24% of the estimated edges had CIs that did not include zero—and 23–26% of the bootstrapped difference tests were significant (see Figure S2). It is noteworthy that there are no objective criteria for interpreting these bootnet results, but the examples in the bootnet and GGM tutorial papers had the same proportion (22%) of estimated edges with CIs that did not include zero and fewer significant bootstrapped difference tests (12% and 15%, respectively). These bootnet results were indicated as interpretable “with some care” in both instances (Epskamp et al., 2017, p. 204; Epskamp & Fried, 2018, p. 12). Given the indication of similar stability in the present networks, we inferred that a reasonable conclusion from the present bootnet results would be that these estimated network structures are similarly interpretable “with some care”.

In contrast to this apparent stability, the strength centrality index was not reliable in either network: The plot of centrality stability showed that strength estimates varied substantially as increasing proportions of the sample were dropped (see Figure S3), very few of the bootstrapped difference tests were significant (see Figure S4), and the CS-coefficient was below the minimum recommended cut-off at both waves (CS(0.7) = .13), which notably represents the only clear guideline available for interpreting bootnet output. This implies that the apparent differences among symptoms in their standardized strength centrality (see Figure S5) are not interpretable.

The NCT omnibus test of network structure invariance was not significant (p = .657)—failing to reject the null hypothesis that all edges in the two networks were exactly identical. The individual edge invariance tests found that zero of the 120 possible edges were significantly different between the two waves. Further, the global strength invariance test was not significant (p = .437), indicating that global strength (i.e., the sum of the absolute values of all edges in the network) did not vary significantly over time; and the coefficient of similarity was r_s = .71, which was interpreted as indicating strong similarities between networks in Fried et al. (2018).

Direct Metrics of Consistency

The existing suite of methods did not highlight the evident differences between the networks’ estimated edges (see Figure 2): Each network had 78 non-zero edges, with a total of 97 different edges between the two networks; only 55 were estimated in the same direction at both waves (70.5% of the 78 edges in each network; 56.7% of the 97 total edges). Thirty-eight of the remaining edges were unique to only one of the networks (19 (24.4%) of the edges in each network; 39.2% of the total estimated edges); and four edges were estimated in both networks but reversed direction (e.g., from positive to negative) between waves (5.1% of the edges in each network; 4.1% of the total estimated edges). The bridging edges showed even lower consistency: There were 41 bridging edges at wave one, and 34 at wave two, with a total of 49 different edges between the two networks. Only 23 were estimated in the same direction in both networks (56.1% at wave one; 67.6% at wave two; 46.9% of the total). The edges that were shrunk to zero had the lowest consistency: There were 42 in each network, with a total of 61 between the two networks, and only 23 were consistent between waves (i.e., 54.8% at each wave; 37.7% of the total zeroed edges).

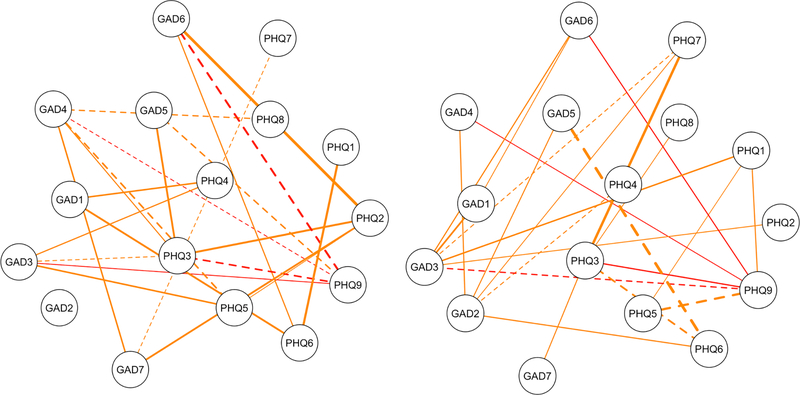
Figure 2.

The edges at wave one (left) and wave two (right) that did not replicate. Each network has nineteen orange edges that were estimated as zero in the other network, and four red edges that were estimated with the opposite sign (e.g., positive at wave one, negative at wave two). Dashed lines are negative edges. Node abbreviations are shown in Table 2.

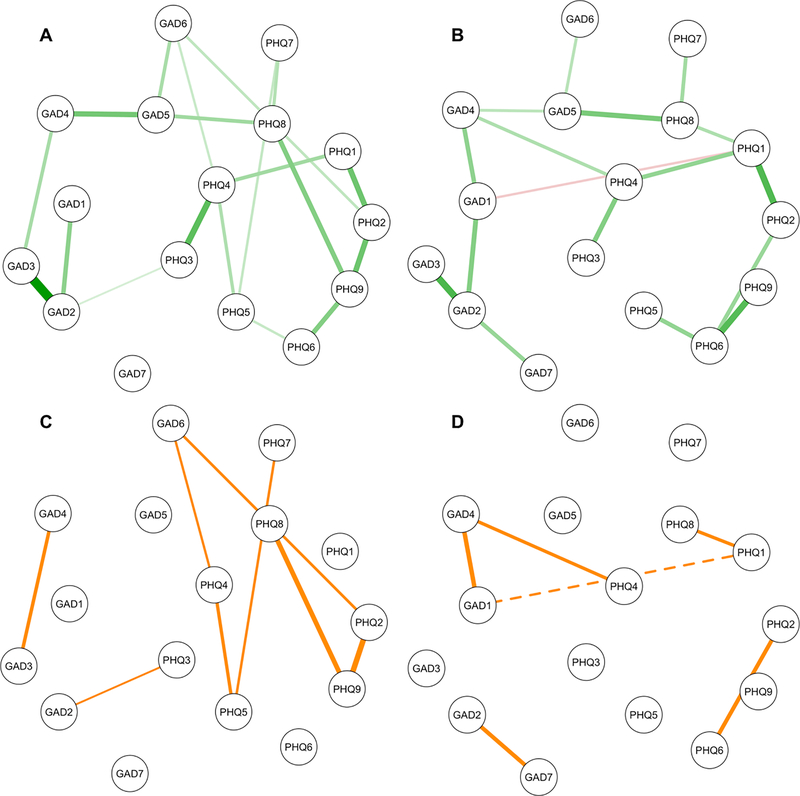
Narrowing the focus to the strongest and most stable edges in each network, we made these same comparisons among the edges with bootstrapped CIs that did not include zero (“bootnet-accurate” edges⁵; see Figure 3A). The large majority of these edges (94.7% from wave one, 100% from wave two) were estimated in the same direction in the other network. However, there was relatively little consistency regarding which edges were bootnet-accurate in each network (see Figure 3B). There were 18 of these edges at wave one, and 17 at wave two, with a total of 25 between the two networks. Only 11 of the edges were in both networks (57.9% at wave one; 64.7% at wave two; 44% of the total). There were six bridging edges in total, and only one (16.7%) was consistent. In line with these differences over time, there was substantial variation in the strength of the edge weights between waves: The consistent bootnet-accurate edges at wave one changed by 36.6% on average to wave two, and the consistent bootnet-accurate edges at wave two changed by 39.7% on average from wave one.⁶

Figure 3.

Top: Subsets of the full networks in Figure 1 showing edges with 95% bootstrapped confidence intervals that did not include zero at wave one (A) and wave two (B); green edges are positive and the red edge is negative. Bottom: The inconsistent edges between the networks at wave one (C) and wave two (D); the dashed line is a negative edge. Node abbreviations are shown in Table 2.

In line with the poor reliability of strength centrality within waves, it also had low consistency between waves on all metrics; τ = .27, r_s = .42, and only one symptom (6.25%) could have the same rank-order at both waves.

PTSD Symptom Networks: Fried et al. (2018)

The key results⁷ reported in Fried et al. are summarised in Table 1, the four individually estimated networks are presented in Figure S6, and a summary of the network characteristics is presented in Table 4. In short, the networks were deemed accurately estimated, stable, interpretable, and considerably similar, albeit not statistically identical; three edges were highlighted as differing considerably between networks, while other edges were “similar or identical across networks” (Fried et al., 2018, p. 10). As before, these results based on the current suite of methods did not capture important differences between the networks. We used the direct metrics of consistency described above to compare the networks pairwise and overall (see Table S2 for the full results). A median of 70.1% of the edges in each network were estimated in the same direction within each pair—corresponding to 56.0% of the total edges estimated between each pair—and a median of 1 (1.3%) of the edges reversed in sign between each pair of networks. Looking at the four networks all together, a total of 114 edges were estimated (95% of the 120 possible edges) and only 39 (34.2%) were estimated consistently in all four networks. Further, 5 (4.4%) edges reversed in sign and 26 (22.8%) edges were estimated in only a single network. Figure S7 depicts the inconsistently estimated edges.

Narrowing the focus to the bootnet-accurate edges in each network (see Figure S8), there was even lower consistency in the edges between these networks (see Figure S9 and Table S2 for the full results): There was a median of 26.5 of these edges in each network (and 36.5 between each pair of networks). A median of 58.8% of these edges in each network were consistently estimated within each pair—corresponding to a median of 39.9% of the total bootnet-accurate edges estimated in each pair. The median of the average change in the strength of the consistent edges in each pair was 45.0%. As above, looking at all four networks together indicated marked inconsistency, with a total of 49 bootnet-accurate edges estimated, but only 6 (12.2%) of the edges were bootnet-accurate in all four networks, and 21 (42.9%) were in only a single network. Further, 23.5–38.2% of the bootnet-accurate edges in each network were absent altogether (i.e., unreplicated) in at least one of the other three full individually estimated networks in Figure S6.

Finally, the median consistency in strength centrality between each pair of networks was low, as above: τ = .33, r_s = .44, and only two symptoms (12.5%) could have the same rank-order in each pair. Comparing the four networks, no symptoms had the same rank-order in all networks.

Discussion

We used the existing suite of methods for maximizing and quantifying the accuracy, stability, and consistency of the “state-of-the-art” psychopathology networks (i.e., LASSO regularization, bootnet, and NCT in PMRF networks; Borsboom et al., 2017, p. 990). We compared these findings to the results of direct metrics of consistency in the detailed network characteristics that are interpreted in the literature (i.e., the presence, absence, sign, and strength of each individual edge; and correspondingly which symptoms are most/least central). We used data from two waves of an observational longitudinal study collected one week apart—so there was no reason to expect substantive differences between the waves a priori—and also reanalyzed four PTSD symptom networks from a recent study of network replicability (Fried et al., 2018). As hypothesized, depression and anxiety symptoms had substantial shared variance that was consistent over time. The existing suite of methods tended to suggest that the networks were accurately estimated, stable, interpretable, and considerably similar, per the standards of interpretation in Fried et al. (2018). In contrast, the methods focused on the network properties that are interpreted in the literature highlighted key differences that indicated limited reliability and replicability in the networks that was not elucidated by the current popular suite of methods. We discuss the key results in more detail below, as well as implications for the psychopathology network literature.

The Importance of Shared Variance

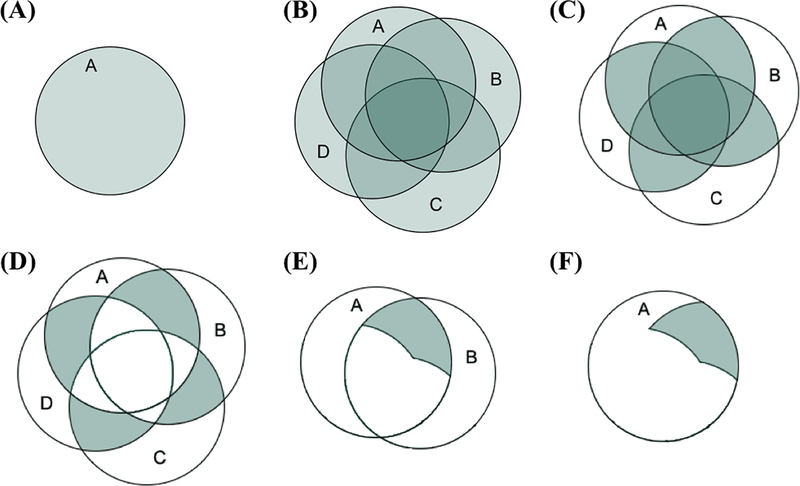
A two-factor ESEM of the pattern of shared variance among the depression and generalized anxiety symptoms displayed longitudinal measurement invariance, showing that the core features of the data were consistent over time. Together the factors accounted for the majority of the variance in all symptoms at each wave, and this pattern of shared variance is key to understanding why we expect the detailed characteristics of networks to be unreliable. Both the factor models and the networks are estimated from the same polychoric correlation matrix at each wave, and this has led to a recent hypothesis that “generalizability problems for one type of model imply generalizability problems for the other” (Borsboom et al., 2017; Fried et al., 2018, p. 13). However, factor models are estimated and interpreted based on the reliable shared variance among the symptoms (see Figure 4C). In contrast, networks are based on the inversion of the correlation matrix (i.e., the partial correlation matrix), which excludes most of the reliable shared variance because each edge is based on the variance shared by each pair of symptoms after removing the variance they share with all other symptoms in the network (see Figures 4D and 4E).

Figure 4.

(A) The green circle represents all of the variance in observed variable A. (B) Four correlated variables A, B, C, and D. (C) The shared variance or correlations among the four variables. (D) The conditionally dependent relationships among the four variables (i.e., the variance shared by each pair of variables after removing the variance they share with other variables). (E) The variance used to estimate the edge A—B in a psychological network. (F) The variance used from A in the edge A—B. Adapted from Forbes et al. (2017a) with permission from the American Psychological Association.

As mentioned in the introduction, the pitfalls of interpreting these conditionally dependent relationships that comprise psychopathology networks have long been known in the contexts of interpreting partial correlations and multiple regression coefficients (e.g., Cohen & Cohen, 1983; Gordon, 1968). Two are particularly pertinent here. (1) By removing much of the variance in each symptom, the essence of the construct is altered (Miller & Chapman, 2001). For example, compare the variance in the observed variable A (Figure 4A) to the variance used from A to estimate the edge A—B (Figure 4F). This makes it difficult to interpret what network edges mean, as they no longer refer to the original “real-world” construct that was measured. The ambiguity of edge interpretation is most clear when there is evidence of suppression: For example, all depression and anxiety symptoms were positively correlated with one another before removing their overlapping shared variance, but 15–18% of the edges in each network were negative. These negative relationships do not exist at the zero-order level, so it is clear they cannot be attributed to the original constructs (Lynam, Hoyle & Newman, 2006). (2) The variance that is shared by multiple overlapping symptoms is the most reliable variance in the measurement of each symptom construct. Removing it means that the remaining construct is less reliable, and that random and systematic error make up a larger proportion of the relationship estimated in the network. Together, these two features of conditionally dependent relationships would suggest that network edges lack validity (i.e., do not measure what they are purported to measure per network theory), and that network edge and symptom centrality estimates are likely to have limited reliability that we would expect to manifest as both instability within networks and inconsistency between networks. In line with this expectation, the depression and generalized anxiety symptom networks were largely unstable and inconsistent over time, but a factor model of the same data demonstrated longitudinal measurement invariance with nearly identical factors at each wave and substantially less variability in unconstrained parameter estimates over time.

Contradictions in Quantifying Network Stability and Consistency Over Time

The results from the existing suite of LASSO regularization, bootnet, and NCT for assessing the stability and consistency of networks were at odds with the unreliability of the edges as reflected in direct metrics of replicability. For example, the current methods led to three broadly consistent conclusions across the six networks examined: (1) The edge weights were interpretable with some care in the two depression and anxiety networks, and “accurately estimated” in the four PTSD networks (Fried et al., 2018, p. 8). (2) None of the edges in the depression and anxiety networks differed significantly over time, and a median of 3 (2.5%) of the edges differed significantly between each pair of PTSD networks. (3) The presence and sign (i.e., positive or negative) of all estimated edges was interpretable, due to the use of LASSO regularization with EBIC (Epskamp et al., 2017). In contrast, the results reported here indicated that: (1) The edge weights of the strongest and most stable edges (i.e., with bootstrapped 95% confidence intervals that did not include zero) changed on average by 21–82% within each pair of networks. (2) A quarter to a third of the estimated edges within each network were unreplicated in the pairwise comparisons. (3) There was marked inconsistency in the presence and sign of the estimated edge weights: A substantial proportion (43.4%) of the edges estimated in the depression and generalized anxiety networks were unreplicated (i.e., either present in one network and absent in the other, or reversed in sign), and nearly two-thirds (63.8%) of the estimated edges among the four PTSD networks were inconsistently estimated. These levels of inconsistency were even higher for the theoretically important bridging edges in the depression and anxiety symptom networks, and among the strongest and most stable edges identified by bootnet in all of the networks.

Looking more closely at the three key methods in the existing suite can help us understand these contradictory conclusions regarding consistency in the symptom networks. First, the limited reliability of edge estimates discussed above inherently limits the specificity of LASSO regularisation for identifying “true” or consistent edges. The intercorrelated nature of psychopathology symptom data not only means that much of the reliable shared variance is removed from the network, but also that psychopathology symptom network structures are likely to be dense (i.e., most of the symptoms are interrelated)—reflecting the factor analytic methods used to generate most self-report measures (cf. Epskamp, Kruis, & Marsman, 2017b). While the specificity of LASSO regularisation is emphasized as a strength in the literature, it will also result in many false negatives when the true model is dense (Epskamp et al., 2017b), which may account for some of the inconsistencies in the networks compared here (e.g., the absent edges in the networks had particularly low replicability). Further, the likelihood that many symptom networks are dense is in marked contrast to the sparsity of the network generating structures that have been used in the key simulation studies to date, as discussed below. Taken together, the intercorrelated nature of psychopathology data along with the low reliability of partial correlations and high rates of false negatives related to LASSO regularisation in such data suggest that the current “state-of-the-art” methods in the psychopathology network literature (Borsboom et al., 2017, p. 990) are not well-suited to analyzing the structure of the relationships between individual symptoms of mental illness.

Second, the guidelines for interpreting bootnet results encourage a false sense of confidence in the stability and interpretability of network characteristics. For example, even with large bootstrapped edge CIs the estimated network structure is described as interpretable “with some care” (e.g., Epskamp et al., 2017, p. 204; Epskamp & Fried, 2018, p. 12) when in fact they should be a red flag of unreliability: Edge CIs that spanned zero indicated that the corresponding edge was variably estimated as positive, absent, and negative between the bootstrapped networks based on subsamples of the data. In the six networks examined here, 14–60% (median 23%) of the 120 possible edges in each network performed in this way (19–59% [45%] were variably estimated as positive or absent; 4–12% [6%] were variably negative or absent; and 0% were consistently absent across bootstraps), indicating marked differences in the interpretations of the networks even within subsamples of each data set. The bootstrapped difference tests for edges—used to determine whether some edges are stronger than others—are also described as “slightly conservative” for smaller sample sizes (Epskamp et al., 2017, p. 7) despite the fact that they are uncorrected for multiple comparisons; our difference tests made comparisons between 3003 pairs of edges in each network, but the significance level remained uncorrected at .05 making false positives a near certainty. Further, researchers are encouraged to interpret significant centrality difference tests—used to determine whether some symptoms are more central than others—but to ignore non-significant results (Epskamp et al., 2017a). In each case, these guidelines err towards emphasizing stability and interpretability in the network characteristics.

Third, the NCT methods focus on the difference scores between networks, which amplifies unreliability in the edge estimates and may result in poorly defined distributions that are underpowered to identify meaningful differences. For example, all NCT results indicated that the depression and anxiety symptom networks had no significant differences when in fact they had a multitude of differences that fundamentally affected the interpretation of the networks: Edges varied substantially in weight over time, were often absent altogether in one of the networks, and even occasionally reversed in sign between waves. The NCT omnibus test of network structure is purported to be sensitive enough to pick up the difference of a single edge between two networks (Fried et al., 2018; van Borkulo et al., under review), but it did not identify any of these differences in the depression and anxiety symptom networks. The simulations in van Borkulo et al. (under review) indicated that the NCT omnibus test should be adequately powered to compare these networks, so the failure to reject the null hypothesis likely correctly indicates that there are no reliable differences between the networks, but rather that the substantial observable differences between the networks reflect the noise in the parameter estimates due to their limited reliability. Similarly, the NCT individual edge invariance tests indicated that 93–100% of the edges were invariant in the pairwise comparisons among all six networks despite the fact that 39–49% of the estimated edges and 59–70% of the absent edges were unreplicated within each pair. The sensitivity of the individual edge invariance tests to identify these differences is limited by the focus on difference scores, as above, but is further reduced by the use of a Holm-Bonferroni correction for multiple testing. In much the same way the interpretation guidelines for bootnet results err towards indicating stability and interpretability in networks, the NCT package errs towards indicating consistency between networks, likely in part because the simulations do not reflect the complexities of real-world data analyzed here.

In short, the existing suite of methods for assessing “state-of-the-art” psychopathology networks are largely based on global summary statistics (e.g., CS coefficients, coefficients of similarity for edge lists, and the global strength invariance test) and distributions of unreliable parameter estimates (e.g., the NCT omnibus test of network structure invariance, and individual edge invariance tests). These methods do not examine and compare the key structural features that undergird network theory and its purported clinical utility (i.e., the presence, absence, sign, and weight of individual edges, as well as on which symptoms are most/least central). The consequence in the present study was that these popular methods tended to paint a picture of generalizability that failed to translate to the level at which networks are interpreted.

Limitations and Future Directions for Methodological Development

In interpreting these results, we should keep the limitations of the present study in mind. First, the results found here do not speak to the performance of network methods (e.g., PMRFs) beyond their application in psychopathology symptom data. For example, the Ising model was derived as a mathematical model of ferromagnetism and can be used to accurately model the behavior of systems in which individual elements (e.g., atoms) modify their behaviour to conform to other elements in their vicinity (e.g., Cipra, 1987). More broadly, PMRFs are more likely to be reliable and valid when analyzing variables that are not strongly related to one another and instead show varying relations across constructs. The intercorrelated nature of psychopathology data together with the limited reliability of single self-report items used to assess psychopathology symptoms means that PMRFs are inherently limited in their ability to model the structure of such data. Research aiming to model the dynamic causal symptom-level structure of psychopathology might better be conducted based on intensive longitudinal assessment methods of fewer symptoms that are not drawn from a single inventory designed to measure a single construct, ideally in an experimental framework, using reliable measurement (e.g., deriving latent variables of the reliable variance shared by multiple items or methods used to assess each symptom).

Second, while the analyses in the present study included a variety of sample sizes, clinical and community samples, and different mental disorder constructs, these findings may or may not generalize to other types of network analysis, disorder constructs, or other individual differences data. Future research should examine this possibility by testing the performance of a wider range of network analysis methods, types of psychopathology, and types of data (e.g., binary data). However, it is noteworthy that the data and methods we analyzed here are representative of those being used in the psychopathology network literature—for example, each symptom is assessed with a single item and all symptoms are moderately to strongly intercorrelated, which inherently increases the likelihood of instability in conditionally dependent relationships.

Third, it is likely that the limited reliability of edges in psychopathology symptom networks will necessitate the use of substantially larger sample sizes to achieve stability and replicability in network characteristics. The sample sizes in the present study (n = 365 to n = 965) are representative of the current psychopathology network literature (Epskamp & Fried, 2018; Epskamp et al., 2017), and similar analyses using other network analysis methods in much larger samples (n = 8841 and n = 9282) also yielded contradictory results based on comparing the existing suite of methods for maximizing and quantifying the stability and consistency of PMRF networks versus metrics for directly comparing the detailed network characteristics interpreted in the literature (Borsboom et al., 2017; Forbes et al., 2017). Regardless, similar tests in larger samples may find different results.

Finally, the direct metrics of consistency examined here are not necessarily the correct way to compare networks, but were selected for the purposes of examining the focal details of the networks. It would be valuable for future research to continue to develop methods for comparing a wider variety of the properties that characterize networks and their structural differences, which is an ongoing challenge for the quantification of differences between networks (Schieber et al., 2017). Another promising direction for comparing estimated network structures is in the emergence of methods for Bayesian hypothesis testing in GGMs (Williams & Mulder, 2019). Estimating networks in this framework would facilitate confirmatory testing of models consistent with network theory, as well as the comparison of competing theoretical models in real data, representing an important step forward for the field.

Overall, while our findings highlight limitations in the existing suite of methods that are widely implemented and interpreted in the network literature, we hope that the work towards understanding the appropriate applications of these methods continues. Such work might include adopting different approaches in simulation studies that test network analysis methods. To date, key simulation papers in the symptom network literature have often simulated data from models that bear little resemblance to models estimated on real-world psychopathology data. For example, the simulation studies examining the performance of bootnet used data-generating network structures with all edge weights set to be equal (usually with 50% negative edges) among eight or ten nodes with only eight or ten edges (22–29% density), respectively, to generate multivariate normal data (Epskamp et al., 2017a). Artificial data-generating structures were also used in simulation studies examining the performance of LASSO regularisation and NCT (e.g., all edges with equal weights, positive in sign, and/or with pronounced differences between data-generating networks on the features to be compared or detected; Epskamp et al., 2017b; van Borkulo et al., under review). The differences between these simulation networks and the network structures estimated in the present study (e.g., where there was 61–65% density and evident variability in the strength and sign of edges within and between networks) mirror the incongruity in the performance of the methods in simulations versus in the complex real-wold data examined here. For example, the NCT omnibus test was found to be sensitive enough to identify the difference of a single edge between two networks in simulations, but did not detect the large proportion (30%) of unreplicated edges in each of the depression and anxiety networks here. This incongruity suggests that a valuable avenue for future research would be to examine the performance of these methods in data simulated from real-world psychopathology network structures, mirroring the properties of observed data as closely as possible.

Conclusion

The networks estimated here have been described as “hypothesis-generating structures, indicative of potential causal effects” (Epskamp & Fried, in press, p. 4). Unfortunately, the relevant hypotheses for the network theory of mental disorders are based on the presence, absence, sign, and weight of individual edges, as well as on which symptoms are most/least central. These characteristics of networks were observed to vary substantially between networks in the present study—often at a level that current popular methods failed to capture—and consequently would be expected to have poor generalizability. These findings underpin our concern surrounding the increasing popularity of psychopathology network methods, given they are not well-suited to the intercorrelated nature of psychopathology symptom data, and generalizable conclusions are fundamental to the utility of their results. It is essential to not only develop sensitive and accurate methods for quantifying network reliability and replication, but also to develop a more methodologically rigorous basis for network theory. The utility of current psychopathology network methods remains severely impaired by their mismatch with network theory; ultimately, highly-partialled conditionally dependent relationships estimated in cross-sectional data no longer represent associations among the real-world symptoms of interest, and certainly do not represent the dynamic causal relationships among them.