Chemotaxis as a navigation strategy to boost range expansion

Abstract

Bacterial chemotaxis, the directed movement of cells along “chemoattractant” gradients, is among the best-characterized subjects of molecular biology^1–10. Much less is known about its physiological roles¹¹. Commonly, it is seen as starvation response when nutrients run out, or as escape response from harmful situations^12–16 . Here, we establish an alternative role of chemotaxis by systematically examining the spatiotemporal dynamics of Escherichia coli in soft agar^12,17,18: Chemotaxis in nutrient-replete conditions promotes the expansion of bacterial populations into unoccupied territories well before nutrients run out in the current environment. We show how low levels of chemoattractants act as aroma-like cues in this process, establishing the direction and enhancing the speed of population movement along the self-generated attractant gradients. This navigated range expansion process spreads faster and yields larger population gains than unguided expansion following the canonical Fisher-Kolmogorov dynamics^19,20 and is therefore a general strategy to promote population growth in spatially extended, nutrient-replete environments.

Decades of quantitative studies have elucidated how molecular signaling modulates the random run-tumble motion of individual bacterial cells, and moves them up chemoattractant gradients^1–7. In contrast, the physiological role of chemotaxis remains much more unexplored¹¹. Notably, many of the chemicals sensed by bacteria are also consumed by them^17,21. Hence, cells do not only follow the chemoattractants set by their environment, but also shape the spatial profile of attractant abundance and adjust their movement accordingly. In particular, a small group of cells can already form strong attractant gradients that drive cell movement^9,10,22–24. Here we perform a quantitative, physiological study of bacterial chemotaxis by taking into account not only chemotaxis itself, but also cell growth and metabolic reactions that lead to the self-generated attractant gradients. We use a motile strain of E. coli K-12 whose growth physiology has been extensively characterized²⁵. As with other motile E. coli strains studied, motility in our strain is enabled by an insertion element that activates the expression of the motility machinery (Supplementary Text 1.1). When inoculated at the center of a soft-agar plate, these cells swim and readily expand outwards via chemotaxis; migrating cells form a visible ring that propagates with a well-defined speed (Figure 1ab), in line with classical observations^12,17.

Figure 1. Growth dependence of expansion and swimming characteristics.

(a) Population of E. coli K-12 HE206 cells (WT, see Supplementary Text 1.1 for strain details) expanding in 0.25% soft agar with 40mM glycerol and 100μM aspartate. Photographs show population density at different times after inoculating exponentially growing cells at the center of the agar plate at initial time. Rings indicate dense bacteria at the population front. Images are representative of experiments repeated independently three times. (b) Tracking ring position over time allows precise quantification of expansion speed (slope). (c) Expansion speed is observed to increase with the growth rate. Expansion speeds are shown for HE206 cells (WT) in media with different primary carbon sources and for glycerol and glucose uptake mutants (HE433, HE443, HE268, HE269) that grow at different rates on glycerol or glucose (as controlled by varying indicuder levels, see Supplementary Text 1.2), in combination with different attractants (100μM asp, 100μM ser, 0.05% CAA), as indicated in the legend table. CAA concentration was chosen to have the same aspartate and serine content as the medium with only asp or ser. Growth rates were measured in batch culture in the presence of attractant; see Supplementary Text 1.4.2 and Supplementary Table 2. Notably, these expansion speeds are much larger than those of the Fisher-Kolmogorov dynamics (no more than a few mm/hr) as will be described shortly below. Number of biological replicates (n_{growth rate}, n_{expansion speed}) for growth and expansion speed measurements indicated in legend. Means and s.d. (for n ≥ 3) are shown.

Bacterial expansion dynamics

To characterize this expansion process quantitatively, we first investigated the dependence of this expansion speed on the state of cell growth. We used medium containing saturating amounts of a primary carbon source supplemented by small amounts of aspartate or serine as the chemo-attractant (see Supplementary Table 1 and Supplementary Text 1 for strains and growth conditions). Growth rate was determined largely by the primary carbon source, with little contribution from the aspartate and serine supplement (Supplementary Table 2). Expansion speed was clearly affected by the carbon sources used (Extended Data Figure 1a, Supplementary Table 3). This was not due to the chemotactic effect of these carbon sources, as different expansion speeds were obtained for cells growing in the same medium (glycerol + aspartate, Extended Data Figure 1b), with different steady-state growth rates attained by titrating the uptake of glycerol²⁶, which is not an attractant²¹ (Supplementary Table 2). The measured expansion speeds follow a common increasing trend with the batch culture growth rate in the respective medium, with either aspartate or serine as the attractant (red and blue symbols, Figure 1c). The very same relation was also obtained for two other widely studied motile E. coli strains (Extended Data Figure 1c), both harboring insertion elements that activate the expression of the motility machinery²⁷ (Supplementary Text 1.1). More complex medium based on Casamino acids commonly used in chemotaxis studies supports even faster growth and may be seen as extension along the same general trend (orange symbols, Figure 1c). In contrast, the expansion became much slower in the absence of a supplemented attractant, even if the primary carbon source was an attractant itself (e.g., with glucose or aspartate only), and for a Δtar mutant incapable of sensing the attractant aspartate; see Extended Data Figure 1d.

The positive growth-expansion relation is surprising in light of a widely held view, supported by gene expression data^14,25,28,29, that bacterial chemotaxis is specifically triggered by nutrient shortage to find better environments^14,21,30. To probe the origin of this positive relation, we thus first characterized the swimming speed for individual cells in different media by recording cell trajectories in well-mixed liquid culture devoid of chemotactic gradients (see Supplementary Text 1.3 for method description). Consistent with previous reports^14,15, swimming speeds were found to vary strongly in different growth phases (Extended Data Figure 2ab). However, such variations resulted from long adaptation periods during outgrowth from starvation, not due to transition out of exponential growth as commonly thought: For all the E.coli strains we probed, the swimming speed actually remained high throughout steady exponential growth, but declined rapidly upon entering starvation in both minimal and rich media (Extended Data Figure 2cd). Such behaviors, consistent with early communication by Adler³¹, suggest that motility is instead favored by E. coli during exponential growth. We next quantified the swimming characteristics during exponential growth for different growth conditions, and found that neither swimming speed nor run duration showed substantial variation at different growth rates (Extended Data Figure 2ef). It follows that cellular “diffusion” due to the random movement by run and tumbling dynamics changed little over the broad range of growth rates examined (Extended Data Figure 2g). Thus, the striking relation between expansion speed and growth rate in Figure 1c is likely a property of the collective dynamics of the propagating population rather than direct consequence of single cell characteristics.

To understand the collective expansion dynamics and its dependence on cell growth, we next observed the spatiotemporal dynamics of fluorescently labeled cells using confocal microscopy at both the population and single-cell levels (Figure 2a). At the single-cell level, we characterized the random motion of cells in agar by tracking their trajectories over time (Extended Data Figure 3ab). The results, quantified by the effective cellular diffusion coefficients across different growth conditions examined, recapitulate the finding from liquid culture that the swimming characteristics is nearly growth-rate independent over the range examined (Extended Data Figure 3c orange symbols). At the population level, we quantified bacterial growth and density profiles over long distance across the entire agar plate. We first established that the growth of bacteria in agar is indistinguishable from that in batch culture (Extended Data Figure 4a–c). Next, we analyzed the time-lapsed radial density profiles of the expanding population in minimal medium, with glycerol as the primary carbon source and a low amount of aspartate as the attractant (Figure 2b and Supplementary Video 1). The chemotactic ring is seen as a bulge in the density profile following the steep (exponential) increase at the front (Extended Data Figure 4d). Strikingly, the advance of the front bulge (~3.2 mm/h) is steadily followed by a trailing region with a broad, exponentially increasing density profile, suggesting that the outward migration of the ring is tightly coupled to the growth of bacteria behind the ring. This important feature is also observed for a population in glycerol supplemented by serine, by aspartate and serine, and in complex media (Figure 2c, Extended Data Figure 4e–h, and Supplementary Videos 2–4), suggesting that the underlying dynamical phenomenon is independent of the nature of the attractant. In contrast, for WT cells grown in glycerol alone and for Δtar cells grown in glycerol and aspartate, the much reduced expansion speeds (Extended Data Figure S1d) are accompanied by very different (flat) density profiles trailing the steep exponential rise, without recognizable density bulges; see top 2 panels of Figure 2d, with full dynamics in Supplementary Video 1 (gray line). As these populations do not chemotax, their expansion result from a combination of growth rate and random (diffusive) cell movement that may be modeled by the Fisher-Kolmogorov (FK) equation^32,33. Detailed quantitative analysis established that bacterial dynamics in these cases are indeed described by the FK solution without adjustable parameters; see Extended Data Figure 5.

Figure 2. Density profiles of expanding bacterial population.

(a)Spatiotemporal evolution of the population in agar was obtained by quantifying the local fluorescence intensity of fluorescently labeled cells throughout the agar using confocal microscopy. Tracking of single cells enabled quantitative characterization of swimming behavior at various positions and times in agar; see Extended Data Figure 3. (b) Density profiles for fluorescent strain HE274 (WT) in reference condition (40 mM glycerol + 100μM asparate) at different times, showing an advancing front marked by a density bulge and an exponential trailing region. See Extended Data Figure 4d for the appearance of the same profiles on a linear density scale. (c) Single-time density profiles for HE274 in other media with attractant(s), showing the same bulge(s) and trailing exponential region. Time-lapsed density profiles are shown in Extended Data Figure 4e–h. (d) No front bulge nor trailing exponential region were seen for WT cells in 40 mM glycerol alone or Δtar cells (HE505) in reference condition. A bulge without exponential trailing region was seen in 20 mM glucose alone, but front bulge and trailing exponential region appear for WT cells in 20 mM glucose + 100μM asparate. (e) Trajectory of front position vs time for WT cells in 40 mM glycerol or 20 mM glucose, with or without 100μM asparate. Front positions are defined by thresholds in density (OD₆₀₀ > 0.002) from confocal scans. (f) Illustration of our model of a complex medium: most nutrients are lumped together and treated as a ‘primary nutrient’ fueling cell growth, with low amounts of major chemotactic components (here aspartate and serine). In panels b-e, experiments were conducted twice with similar observations for the reference condtion (glycerol + aspartate) and once for other conditions.

Interestingly, even though glucose is an attractant^18,21, cells grown in a glucose plate exhibited a flat density profile following a bulge at the front (Figure 2d 3^rd panel, Supplementary Video S5), and the population expanded not much faster than that in plates with glycerol alone (Figure 2e black symbols). Conversely, the combination of glucose and low amounts of aspartate exhibited again the distinct density profile with a broad exponential region trailing the front bulge (Figure 2d bottom panel and Extended Data Figure 4i), along with a much faster expansion dynamics (Figure 2e red squares). Thus, it appears that the combination of an abundant primary carbon source – regardless of whether it is itself an attractant – supplemented by low amounts of attractant, is the minimal nutrient requirement needed to generate the type of behaviors generically encountered in rich media (Figure 2f). Consequently, we will adopt the simple medium used in Figure 2b, glycerol + aspartate, as our model medium (or “reference condition”) in the ensuing quantitative study.

The Growth-Expansion model

To describe the fast expansion dynamics in media with nutrient and attractant, we developed a mathematical model by extending the classical model of a propagating chemotactic ring by Keller and Segel^34,35. The original Keller–Segel front was unstable given a realistic limit of chemotactic sensitivity³⁶. Ingenious models proposed to remedy the problem^37–39 appear too restrictive to capture the simplicity and ubiquity of the observed ring propagation. We focus instead on the crucial role of bacterial growth driving population expansion. Although the inclusion of growth in chemotactic models also dates back a long time^40,41, a satisfactory understanding under general conditions is still lacking^30,42; see Extended Data Figure 6 for a review. Guided by our experiments, which established the distinct effects of a primary nutrient and a low amount of attractant on expansion (Figures 1 and 2), we explicitly modeled these two ingredients as separate dynamical variables driving bacterial growth and motility; see Figure 3a for a summary of this Growth-Expansion (GE) model and Supplementary Text 2 for details.

Figure 3. The Growth-Expansion model and its predictions.

(a) The coupled dynamics of growth and migration of the bacterial density, ρ(r, t) is modeled by treating the concentrations of the major nutrient source and the attractant as two distinct variables, n(r, t) and a(r, t), with r being the radial distance from center. Dynamics of these variables are given by Eqs. (1)-(3). The rate of cell growth λ(n, a) and attractant uptake μ(λ, a) are fixed by our measurements as discussed in Supplementary Text 2.1. Nutrients and attractants diffuse with diffusion coefficients D_n, D_a, respectively.Y denotes growth yield of the nutrient. Following the Keller-Segel model³⁴ and the coarse-grained description of chemotaxis⁴⁹, undirected swimming is described by a cell diffusion term, characterized by D. Directed movement is described by an advection term $\overrightarrow{v}$ that depends on local attractant gradients (Eq. 4), with the chemotactic coefficient χ₀ as the proportionality factor. Other details of the model are described in Supplementary Text 2.1. (b) The lone unknown parameter of the model, χ₀, is fixed by adjusting the ratio χ₀/D such that the expansion speed of the model (black line, inset) matches the experimental observation (horizontal grey line, inset). The corresponding value of χ₀/D (red dashed line, inset) is used for other simulations. Prediction of the GE model on front position at various times is shown as the solid red line; it captures well the observed dynamics of front propagation of WT cells in reference condition (red circles), including the crossover from FK dynamics (black circle and line, from Extended Data Figure 5). Solid green and brown lines show model predictions if χ₀/D used was 30% larger or smaller. (c,d) Observed and simulated density profiles at different times. The observed density bulges are less sharp due in part to limited spatial resolution of the data points (black dots). See Extended Data Figure 3e for a finer view. Black solid line indicates predicted slope of trailing region (Extended Data Figure 9a); dashed line shows slope of FK dynamics for comparison (Extended Data Figure 5). Fluorescent strain HE274 was used as the wildtype in panels (b,c), experiments were conducted twice with similar observations. (e) Predicted and observed changes in expansion speeds when varying the growth rate with different glycerol uptake rate, using HE274, HE484 and HE486 (square symbols). For HE486, three different inducer 3MBA concentration were used. Data for HE274 (n=2) represents a mean of two replicates, while expansion speeds for HE484 and HE486 are shown as mean ± s.d (n=3 biological replicates) and growth rates from single experiments. As comparison, data from Figure 1c (glycerol as carbon source) are shown as red circles. Dashed line shows prediction by scaling theory (Extended Data Figure 9) when changing only the growth rate. Solid green line shows prediction of the full GE model, including the observed dependence of model parameters, e.g. diffusion constant and uptake rate, on growth-rate.

To test predictions of the GE model, we determined most model parameters directly by independent experiments in the reference condition, including growth rates in agar (Extended Data Figure 4c), diffusion coefficients in agar (Extended Data Figure 3c), and uptake rates of aspartate (Extended Data Figure 7a–c); Supplementary Table 4 shows the full parameter list. With the molecular parameters available from the literature (Supplementary Text 2.4), only one parameter remained unknown, the chemotactic coefficient χ₀ (Figure 3a). Fixing this lone parameter by matching the asymptotic expansion speed of the model with the observed value under reference condition (Figure 3b inset), the GE model quantitatively captured main features of the population dynamics in reference condition: The dynamics of the front position (Figure 3B, red line) captures the data (red circles), including the overlap with FK dynamics (grey circles and line) at early times. The gross shape of the steady-state density profiles matches well with the experimental profile (compare Figures 3cd); in particular, the slope of the exponential trailing region (Figure 3c solid black line) is much flatter than what FK dynamics predicts (Figure 3c dashed black line). A zoomed-in analysis of the front region by using single-cell tracking allowed for additional comparisons regarding the details of the front region (Extended Data Figure 3d–h). The model also adequately accounted for the dependence of the expansion speed on the attractant concentration, long known to peak at a moderate level⁴³, for both glycerol and glucose as the primary carbon source (Extended Data Figure 7d–f). Further, the same model can quantitatively capture the slow expansion dynamics for the case where the attractant is the sole nutrient (e.g., glucose only); see Extended Data Figure 8.

We next applied the GE model to investigate the origin of the positive growth-expansion relation (Figure 1c). Since the cell diffusion coefficient depends weakly on the growth rate (Extended Data Figure 3c) while the attractant uptake rate yields a strong dependence (Extended Data Figure 7c), the latter provides a possible rationalization of the positive growth-expansion relation. Indeed, faster depletion of attractant could naively be thought to allow the front to advance faster. However, this turns out not to be case, as changing the uptake rate hardly affected the expansion dynamics, in agreement with model prediction (Extended Data Figure 7g–i and Supplementary Text 2.2). The observed growth-expansion relation (Figure 1c) can in fact be approximately accounted for within the GE model by just changing the growth rate while keeping all other parameters fixed (Figure 3e, dashed grey line). Qualitatively, the faster expansion in richer medium results from higher cell density at the front bulge, leading to faster depletion of the attractant (Extended Data Figure 7jk). More quantitatively, a simple scaling analysis captures the square-root form of the growth-rate dependence (Extended Data Figure 9a–c), and a linear dependence on the chemotactic coefficient χ₀ (Extended Data Figure 9d, which stands in contrast to the square-root dependence on χ₀ when the attractant is the sole nutrient, Extended Data Figure 8k). The full model, including the observed growth-rate dependencies of the macroscopic parameters (Extended Data Figures 3c, 7c) and assuming the independence of the molecular parameters (Supplementary Text 2.1.3), describes the observed data very well (Figure 3e, green line), without any adjustable parameters. Less is known quantitatively about how serine alone or in combination with aspartate affect the chemotactic parameters. However, the existing data appear to be captured well by the square-root form when analyzed separately for each attractant (lines of different colors in Extended Data Figure 1g), suggesting that different attractants and their combinations affect the magnitude but not the functional dependence of population expansion.

Further analysis of the GE model yields insight on how population growth and expansion are generated in a coordinated way. As indicated by the solution of the GE model (Figure 4a) and confirmed by experimental observation (Extended Data Figure 3g), cells in the front bulge region have positive drift velocities and move forward on average; they are the ‘pioneers’ of the population. Conversely, cells behind the bulge experience little chemotactic drift and can only grow locally; they are the ‘settlers’. As the pioneers advance with the front and grow in number, some pioneers would remain behind due to randomness in cellular motion (described by diffusion of cell density), effectively seeding the void region left behind by the propagating front (black arrow, Figure 4b) for colonization in the future. This coupled expansion-colonization process is illustrated explicitly in Extended Data Figure 9e by using a discrete agent-based simulation including stochastic cell movement and division (see SI Text 3). Cell-to-cell variations in swimming characteristics^24,44, which has not been included in this calculation for simplicity, is expected to further enhance the transitions between the pioneers and the settlers.

Figure 4. The expansion-colonization process.

(a) Spatial profiles of the density (ρ, green), attractant (a, mauve) and drift ($\left|\overrightarrow{v}\right|$, purple) during steady migration in co-moving frame; dashed vertical line indicates the position of maximum drift. Highlighted area (cyan) indicates the region where the attractant concentration is in the range between a₋ and a₊ (gray lines) where the chemotactic response is maximum. Full spatiotemporal dynamics of the GE model is shown in Supplementary Video S6 for both the laboratory and co-moving frame. (b) Illustration of the coupling between the front and trailing regions. Density profiles spaced by one doubling-time are shown. Orange line illustrates the density profile in a hypothetical case where the effect of diffusion is ‘turned off’ during this time. The difference, indicated by the black arrow, represents the effect of cells’ transfers from the front to the gap right behind the front, which is mediated by diffusion. (c) Size increase of populations expanding in glycerol or glucose, quantified by confocal microscopy (Supplementary Text 1.4). Populations of WT cells (colored symbols, strain HE274) increase faster with than without 100μM aspartate as attractant. Slower increase is also observed for a Δtar mutant not capable of sensing aspartate (gray triangles, strain HE505) even if aspartate was present. Differences between the size increases become noticeable at ~6 hours, corresponding to the crossover from diffusive FK dynamics to navigated range expansion (Fig. 3b). Experiments for WT cell in glycerol + asp were conducted twice with similar results, others once; see also Supplementary Table 2–3. (d) Expansion speed changing with attractant concentration. WT cells (HE206) expanding in glycerol or glucose with varied aspartate concentration (Supplementary Table 9). Expansion speeds without additional attractant are shown as dashed lines. These results confirm observation by Wolfe and Berg⁴³ and can be quantitatively accounted for by the GE model (Extended Data Figure 7ef). Points represent means of n ≥ 2 biological replicates, error bars (s.d.) shown when sample size n ≥ 3, see also Supplementary Tables S9–10. (e) Illustration comparing the navigated mode of range-expansion that involves chemotaxis (upper panel) with the unguided expansion (Fisher-Kolmogorv dynamics, bottom panel). Navigation along self-generated gradients of attractants (upper panel) allows faster expansion of the population. Remaining nutrients allow for population growth behind the front. Right panels show the corresponding density and nutrient/attractant profiles at the migrating front.

Navigated range expansion

At the population level, the expansion-colonization process sustained by a primary nutrient source and low amounts of attractant provides an effective dispersal mechanism and a clear fitness advantage. This is illustrated by the observed gain in the total population size on plates (‘population fitness’) during the expansion process (Figure 4c). In glycerol medium supplemented with aspartate, the faster propagation of the population front (Extended Data Figure 1e) accompanies the more rapid increase of the total population size compared to a population seeded in the same medium without aspartate (filled and open red circles, respectively, in Figure 4c top panel). This fitness advantage for the population is not due to the addition of aspartate as a nutrient supplement, since a Δtar mutant not able to respond to asparate chemotactically (Figure 2d) does not gain any fitness advantage with aspartate supplement (gray triangles). Further, the aspartate supplement significantly increases the population fitness even if the primary nutrient is itself an attractant, e.g., glucose (purple squares, Figure 4c bottom panel). Thus, the fitness gain specifically requires an environment with an attractant supplementing an abundant primary nutrient source regardless of whether it is an attractant itself, reflecting the requirement for attaining a boost in expansion speed as established earlier (Extended Data Figure 1e). This advantage of chemotaxis further relies on sufficiently low concentrations of the supplemented attractant (Figure 4d). Notably, this requirement is at odds with the notion of cells seeking the attractant as a source of nutrient for growth and suggests instead the role of the supplemented attractant as a signaling cue to navigate and accelerate population expansion. Indeed, by separating the roles of nutrients and navigation cues, E. coli is able to use metabolites such as aspartate and serine that are rapidly taken up^45,46 as strong attractants without concerns for their poor ability to support growth (Supplementary Table 2), while maintaining fast growth on better nutrient sources such as glucose and glycerol.

In summary, chemotaxis along self-generated gradients of low-dose attractant supplements provides a local “guide” for populations to expand rapidly into unoccupied territories, thereby giving them strong fitness advantages to grow in nutrient-replete environments. This “navigated” mode of range-expansion (upper panel, Figure 4e) is to be contrasted with the canonical, “unguided” mode of range expansion (i.e., Fisher-Kolmogorov dynamics^19,20,47 as characterized in Extended Data Figure 5), in which the population advances through the growth and random motion of cells at the front, leaving no nutrients behind the front (lower panel, Figure 4e). Notably for the navigated expansion, the guide is provided well before the population experiences any starvation. It thus manifests a built-in diversification strategy for a population with the ‘foresight’ to conquer new territories well before nutrients are depleted in the current environment. This foresight is important as turning on cell motility upon experiencing starvation will likely be too late to facilitate effective population expansion; see Extended Data Figure 10c–g.

The strategy of navigated range-expansion in nutrient-replete conditions, analyzed here for E. coli K-12 strains, is one of a number of ways chemotaxis can contribute to bacterial fitness. In other conditions, chemotaxis can be used to respond to starvation or escape from harsh enviornments such as non-optimal temperatures/pH ranges^14,15,21,30. On the other hand, navigated range expansion, involving a diversified population of pioneers and settlers to enable rapid occupation of open habitats for future colonization, may well be employed in range expansion beyond bacteria. To efficiently guide the movement of the population along the desired direction for expansion, all that is needed is a component of the unoccupied environment that can be easily sensed and modified (e.g., degraded but not consumed⁴⁸{Seymour:2010hp}), tasks that are actually much easier for higher organisms to accomplish. Thus, navigated range expansion may be readily adoptable also by higher organisms to rapidly colonize spatially extended habitats.

Methods

Strains used in this study

The reference strain for this study is HE206, a motile variant of E.coli K-12 strain NCM3722 whose physiology has been well-characterized^{25,26,50–53}. Similar to other motile E.coli strains previously studied^27,54, the strain carries an insertion element upstream of the flhDC operon to enable motility. See Supplementary Text 1.1. for the strain context. Details on all used strains (deletion mutants, titratable carbon uptake strains and fluorescently-labeled strains) and their construction are provided. As indicated in the text, comparisons are made with MG1655 and RP437, other commonly used motile E.coli strains. All strains used in this study are listed in Supplementary Table 1.

Growth medium

All growth media used in this study were based on a modified MOPS-buffered minimal medium used by Cayley et al⁵⁵. Trace micronutrients were not added into the MOPs medium, since the metal components were reported to inhibit motility of E. coli⁵⁶. To change growth conditions, different carbon sources were supplemented in the medium. When indicated, Casamino acids (CAA) and TB were used. Minimal medium for the growth of RP437, involves 4 additional amino acids. For the strains with titratable carbon uptake (glycerol or glucose), 3-methylbenzyl alcohol (3-MBA) was additionally provided as the inducer. Full details on media composition and concentrations are provided in Supplementary Text 1.2.

Strain culturing and growth rate measurement

Growth measurements were performed in a 37°C water bath shaker operating at 250 rpm. The culture volume was no more than 4.5 ml in 18 mm × 150 mm test tubes (Fisher Scientific) to limit the depth of the culture in the tube for aeration purpose. Each growth experiment was carried out in three steps: “seed culture” in LB broth, “pre-culture” and “experimental culture” in identical minimal medium. For the seed culture, one colony from fresh LB agar plate was inoculated into liquid LB and cultured at 37°C with shaking. After 4–5 hrs, cells were centrifuged and washed once with desired minimal medium. Cells were then diluted into the minimal medium and cultured in a 37°C water bath shaker overnight (pre-culture). The starting OD₆₀₀ in pre-culture was adjusted so that exponential cell growth was maintained overnight, preventing cells from reaching saturation. Cells from the overnight pre-culture were then diluted to OD₆₀₀ = 0.005–0.02 in identical pre-warmed minimal medium, and cultured in a 37°C water bath shaker (experimental culture). After cells were grown at least for three generations, OD₆₀₀ was measured around every half doubling of cell growth. At each time point, OD₆₀₀ was measured by collecting 200 μl cell culture in a cuvette (Starna Cells, Atascadero, CA) and using a spectrophotometer (Thermo Scientific). About 4–6 OD₆₀₀ data points within the range 0.04 to 0.3 were used for calculating growth rate. All the growth rates measured in this study are summarized in Supplementary Table 2.

Measurement of expansion speeds

Expansion speeds were measured using soft-agar plates containing 0.25% agar and growth media resembled to the liquid culture conditions introduced above. Attractants were additionally provided and a detailed preparation protocol is provided in Supplementary Text 1.4. Expansion speeds were either measured by the manual tracking of expanding ring positions over time (manual observation, ring position is clearly visible by eye) or by using confocal microscopy. For the manual observation, 15 ml of freshly prepared and still warm soft-agar medium was transferred into a Petri dish with 10 cm diameter, resulting a 2mm thick soft-agar layer. Agar was left to solidify for a minimum of 10 minutes at room temperature. For the confocal experiments, GFP expressing plasmids were used as fluorescent markers, strains as indicated in the legends. 8μg/ml chloramphenicol was additionally supplied into the soft-agar medium to maintain the plasmid. To prepare the soft-agar plates, 2.7 ml of the medium was transferred into a glass bottom Petri dish (Ted Pella Inc). The final thickness of the agar was approximately 1.2 mm. All the plates were freshly prepared before the assay. To start the soft-agar assay (manual observation), 2μl of cell culture from the (exponentially growing) experimental culture was transferred onto a pre-warmed soft-agar plate. The primary carbon source of the liquid culture was chosen such that it matched the growth conditions provided in the soft-agar plate. The plates were incubated at 37°C. After the population covered a circular area of at least 2 cm in radius, the radius of the population (front with chemotactic ring is clearly visible) was measured every 1–2 hours for 4–6 different time points. Expansion speeds were obtained as linear fits of the observed radii vs observation times (Fig. 1B). For convenience, the initial inoculation OD₆₀₀ used for the manual assay was varied depending on culture conditions such that ring movements could be captured during the day. The expansion speeds examined in this study are listed in Supplementary Tables 3, 9, 10. For expansion observation and density scans using microscopy, cells were always inoculated at OD₆₀₀ = 0.2 and observation was started immediately after the 2 μl cell culture was added to the agar. Expansion dynamics was analyzed by looking at the emerging spatial intensity profiles. Details of confocal imaging, intensity analysis and calibration, and the determination of growth rates within soft-agar by confocal microscopy are provided in Supplementary Text 1.4.2 – 1.4.5. Custom-made code used is available via GitHub at https://github.com/jonascremer/chemotaxis_imageanalysisexpansiondynamics.

Measurements of swimming characteristics

To quantify swimming behavior of cells in liquid culture (no gradients), we grew cells similarly as introduced before but used higher attractant concentrations to avoid the formation of temporal gradients, see Supplementary Text 1.3.1. Polyvinylpyrrolidone was added into the medium to prevent cells from binding to surfaces and to protect flagella⁵⁷. Sample volumes of about 200μl were taken at different timepoints over the course of cell growth to quantify swimming behavior, see Supplementary Text 1.3.1 for details on timing. Immediately after collection, samples were diluted to a lower OD₆₀₀ ≈ 0.005 using filtered medium. The diluted sample was then used to load a rectangular capillary and cells within the capillary were observed by acquiring videos for one minute, using a phase contrast microscope. Using a custom-made Python script, cells were detected and cell trajectories were derived. Subsequently, cell trajectories were analyzed to derive the swimming characteristics as previously reported⁵⁸. Full details on data acquisition and analysis are provided in Supplementary Text 1.3. Used custom made code is available via GitHub at https://github.com/jonascremer/chemotaxis_swimming.

Cell trajectory analysis in soft agar

To quantify diffusion behavior (undirected run and tumbling) and drift (directed run and tumbling) of swimming cells within the agar, we used time-lapse confocal microscopy allowing for the detection and tracking of individual fluorescently labeled cells (see Extended Data Figure 3 for a shorter method introduction; axes orientation and sample images shown in panels A and B). The measurement allows for the spatiotemporal resolution of swimming behavior within an expanding population. To optimize the tracking of single cells, the number of fluorescent detecetable cells was adjusted by mixing fluorescent cells with non-flucorescent cells (carrying a non-fluorescence protein⁵⁹ to minimize physiological differences of strains). Detailed methods on image acquisition, cell tracking and the statistical analysis to derive diffusion coefficients and drift are given in Supplementary Text 1.5.

Measurements of aspartate uptake

To quantify aspartate uptake, cells were grown in minimal medium supplemented with different carbon sources and 800 μM aspartate. Samples were collected at different OD during steady state growth and aspartate concentration was determined using calorimetric aspartate kit (ab102512 Abcam). Additional details are provided in Supplementary Text 1.2.2. The aspartate consumption rates measured in this study are summarized in Supplementary Table 7. For each growth condition, measurements were repeated twice.

The Growth-Expansion Model

Full details of the Growth-Expansion Model introduced in Figure 3 are provided in Supplementary Text 2. This includes the specific biological motivations for different terms used in the equations, including the terms describing attractant consumption and the nutrient dependent local growth rate (Monod type dependence^60–62. The drift term describing the directed movement along sensed gradients features Weber’s law^7,63 and response rescaling^64–66 and parameters were taken from published receptor characterications^23,67–69. Reflecting boundary conditions and initial conditions matching the experimental conditions were used, see Supplementary Text 2 for details and equations. Numerical solution of the partial differential equations was done employing an implicit scheme using Python and the module FiPy⁷⁰. Integration over time was performed with time steps dt = 0.25s, and a grid resolution with spacing dx = 10μm. Simulations were performed using a custom-made Python code which is available via GitHub at https://github.com/jonascremer/chemotaxis_simulation. Parameter used are provided in Supplementary File simulationparameters.txt; see also Supplementary Text 2.5 for additional information.

Data availability statement

Major experimental data supporting this study are provided in this manuscript or available via figshare repositories: doi.org/10.6084/m9.figshare.9639209 (confocal expansion data) and doi.org/ 10.6084/m9.figshare.9643001 (data swimming observation). Simulation data can be generated with the provided simulation code and parameter sets.

Code availability statement

Custom-made code is available via GitHub as indicated in Methods for the analysis of swimming characteristics, the analysis of expanding populations using confocal microscopy, and the numerical simulations of the Growth-Expansion Model.

Extended Data

Extendend Data Figure 1. Expansion speed measurements.

(a) Temporal evolution of front position for a population of E. coli HE206 cells (wild type) grown on soft agar plate with saturating amounts of different carbon sources (as indicated by the legend) and 100μM aspartate as attractant. Lines show linear fits. Experiments were repeated at least twice with similar results. (b) Temporal evolution of front position for HE443 cells grown on 40mM glycerol and 100μM aspartate, with different amounts of the inducer 3MBA (as indicated by legend) that titrate glycerol uptake²⁶, resulting in different growth rates (Supplementary Table 2). The experiments were repeated at least twice with similar results. (c) Expansion speed and its dependence on growth rate for the commonly used E.coli K12 strain MG1655B (red symbols) sequenced by Blattner et al and the K12 variant RP437 (blue symbols) frequently used in motility studies, see Supplementary Text 1.1. Growth conditions were changed by varying carbon source (from lower to higher growth rates: acetate, mannose, glycerol, glucose); see legend table. 100μM aspartate was added as the attractant. For the experiments with RP437, four amino acids (methionine, leucine, threonine, histidine) were provided at 1mM each into medium to sustain cell growth. Data in Figure 1C are shown in grey for comparison. Data points represent the mean of two biological replicates, except for growth rates in acetate and mannose that were from a single experiment. (d) Expansion speeds plotted against the batch culture growth rate for population grown in glycerol, glucose or aspartate as the only carbon source, without supplement of additional attractant (purple symbols). [Growth on serine is very slow (< 0.1/h) and not shown on the plot.] Expansion speeds were much slower in these media without the supplement of chemoattractant, even though glucose and aspartate are both attractants themselves^46,68. The same was observed for a Δtar knockout strain when both glycerol and aspartate were present (open triangle). See Supplementary Tables S2 and S3 for data values and sample sizes. Data of Figure 1c are shown in grey for comparison. (e, f) The difference between migration with and without additional attractant is further illustrated for growth on glycerol when growth rates are titrated (e), and for expansion when other carbon sources are provided (f). Hashed bars highlight additional increase of expansion speed (red) and growth rate (blue) when attractant is provided. In each case, supplementing low amounts of attractant(s) is seen to increase expansion speed a lot without affecting growth rate much. The graphs were created based on mean values listed in Supplementary Table S2–3. (g) Expansion speed and its dependence on growth rate when two attractants are present (20mM glycerol + 100μM asp + 100μM ser, green symbols) or for complex media (CAA + carbon source, orange symbols). Data for one attractant (taken from Figure 1C) are shown for comparison (20mM glycerol + 100μM aspartate, red symbols; 20mM glycerol + 100μM serine, blue symbols). Lines indicate fits to square-root dependencies as anticipated from a simple scaling analysis (Extended Data Figure 9d). Data points in asp + ser (green points) represent means of two biological replicates (n=2), except growth rates of HE433 and HE443 that were from a single experiment (n=1).

Extended Data Figure 2. Swimming characteristics in liquid media (well-mixed conditions, no gradients).

(a-d) Average swimming speed (purple circles) and the fraction of motile cells (gray squares) were characterized for cells taken from batch cultures along a growth curve at different optical densities (OD₆₀₀) as indicated by the green triangles. For each condition, data points are collected from a single experiment. (a) Culture was grown in LB, starting with an overnight LB culture which was sitting in saturation for 18 hours before dilution into fresh LB media at time zero. This experiment was essentially a repeat of what was done in Refs.^14,15; similar results were obtained, with motility increasing as growth progressed. Our data in the following panels suggest most of the increase in swimming speed resulted from the increased fraction of motile cells in the first two hours. (b) Culture was grown in minimal medium with 10mM glycerol and 1.7mM aspartate, starting with an overnight pre-culture (same medium) that was in saturation for about 18 hours before inoculation into fresh medium (time zero). Like what was observed for LB (panel A), it took several hours for both the motile fraction and swimming speed to recover. (c) Culture was grown in LB continuously for 10 generations, with bacterial density always kept below OD₆₀₀=0.5 before dilution to fresh LB at time zero. Both the motile fraction and the swimming speeds are high in the exponential growth phase (0–2 h) except for a dip at OD₆₀₀ ≈ 0.5. Swimming speed and motile fraction decline after the stationary phase was reached. (d) Culture was grown in the same minimal medium (glycerol + aspartate) for ~20 generations, with bacterial density maintained below OD₆₀₀ = 0.6 before measurement. As with LB (c), swimming speed and motile fraction remained high in the exponential growth phase (0–4 hr), before sharply declining after entering the stationary phase. The strong variation of the fraction of motile cells observed here is in line with previous observation on the cell-to-cell variation of swimming behavior^71,72 and can strongly affect the dynamics of migrating populations as has been investigated recently^24,73. (e-f) Swimming behavior observed in steady state growth (as for example observed in panel d for the first ~3 hours) for different (relatively fast) growth conditions and different E.coli strains (Supplementary Table 5). Swimming speeds (v) and durations between tumbling events (τ) obtained from trajectory analysis are shown in (e) and (f) respectively. Black symbols show results for the NCM3722B derived strains (HE206, HE433, HE443; growth at 37C) mainly used in this study. A similar weak dependence of quantities on growth was observed for MG1655B (red symbols, growth at 37C) and RP437 (blue symbols, growth at 30C). (g) Estimated effective diffusion coefficient, D = ν²τ, for the different growth conditions in NCM3722B derived strains. In panels (e-g), data points show the means of two biological replicates for strains HE433 and HE443 and the results of single experiments for strains HE206, MG1655B and RP437. See Supplementary Text 1.2–1.3 for methods and Supplementary Table S5 for data values and conditions. Strain details are discussed in Supplementary Text 1.1.

Extended Data Figure 3. Single-cell motility analysis in agar by confocal microscopy.

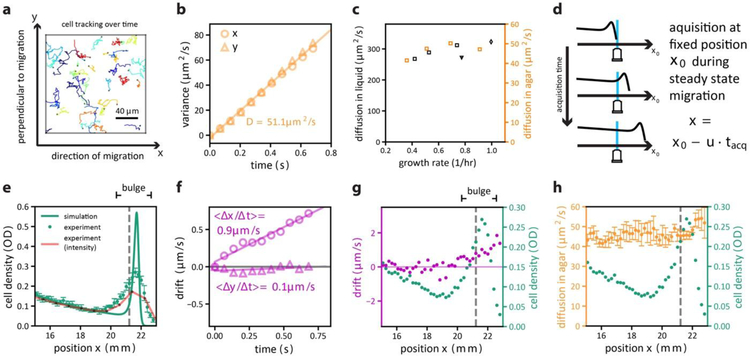
30 second videos allowing to track the movement of single cells were acquired, see Supplementary Video S7 for an example. (a) Example of trajectories derived from cell tracking analysis. Each color indicates the trajectory of one cell over a span of on average 75 frames (5.1 s). (b) Diffusive behavior was obtained by a linear fit of displacement variance over time [var(Δx) = 2DΔt]. This analysis was performed for strain HE274 (WT) growing in 40mM glycerol and 100μM aspartate (reference condition); see Supplementary Text 1.5 for a detailed method description. Data shown here are for measurements in front of the expanding population, i.e., ahead of the density peak (however diffusion coefficient obtained at different locations does not exhibit much positional dependences: see below). Repeat of experiment showed similar results. (c) Similar effective diffusion coefficients for swimming in soft-agar were obtained for other growth conditions (orange symbols, Supplementary Table 6) following the same trend as predicted from liquid culture measurements (black symbols, same as those shown in Extended Data Figure 2g). The diffusion measurements in soft-agar were repeated twice yielding similar results. The data points represent means of two biological replicates. Supplementary Table S6 for data values and conditions. (d) To resolve cellular swimming behavior of the expanding population at different spatial positions in the agar plate, videos allowing to track single cells were acquired sequentially at a fixed position (of the agar plate) over time, for different acquisition times t_acq over which videos were taken (up to several hours for each). Image direction x was aligned with direction of migration. In this setup, the migrating population (with speed u) passes the point of acquisition at a determined time, allowing us to determine the local drift speeds and diffusion coefficients relative to the front position: x = x₀ – u t_acq; see Supplementary Text 1.5 for experimental details. (e) Density obtained in this way (by cell-counting, green line) is compared to population density obtained using the approach of Extended Datat Figure 4 (fluorescence scans, red line). Spatial resolution of the latter is much coarser, each measurement point being a black dot on the red line. For comparison, the simulation result (GM model, Fig. 3) is shown in green and moderately deviates from the measured profile. (f) Analysis of average displacement along x (direction of migration) and along y (direction perpendicular to migration) over time for an acquisition time t_acq corresponding to a position at the front bulge (x = 21.3 cm, indicated by the dashed lines in panels e, g, and h). The average displacement (purple symbols) increased linearly in time along the direction of migration but was negligible perpendicular to the direction of migration (fitted purple lines show drift speed in each direction, 〈Δx/Δt〉 and 〈Δy/Δt〉). (g) Position-dependence of the drift (in the direction of expansion) was determined at different t_acq, corresponding to different positions of the expanding population. For the ease of reference, cellular densities (the data in panel e) are shown again as green symbols. Up to the resolution of the data, the drift velocity vanished to the left of the density trough (x < 19mm). (h) Position-dependence of the diffusion coefficient. Using the approach of panel b to determine the diffusion coefficient at different t_acq, we obtain the results shown as orange symbols. A moderate (~20%) increase in D is observed at the very front of the population. This spatial dependence may be due to the accumulation of faster swimming cells at the front⁹. All data in panels (e-h) were from one single expansion experiment done in reference condition (40mM glycerol+100μM aspartate; 2:1 mixture of fluorescent variant HE274 and non-fluorescent variant HE339), Similar results were obtained for one biological replicate. Error bars in panels (e,h) denote s.d. and were calculated from repeated observations at three different times during the same expansion process.

Extended Data Figure 4. Population-level observation of growth and expansion by confocal microscopy.

Densities of bacteria growing in the soft-agar were determined at various times using confocal microscopy and fluorescently labeled cells; see Supplementary Text 1.4. (a) Calibration of fluorescence intensity. Known amounts of cells were transferred from a batch culture to a fresh but cold soft agar plate. After agar solidification (< 10 min) intensity was measured. Fitted line gave relation between observed intensity (fluorescence integrated along the agar thickness) and cell density measured in batch culture (optical density OD₆₀₀). (b) Example of experiment to obtain growth rates in agar. Data is for strain HE274 (WT) grown in 40mM glycerol and 200μM aspartate. A low amount of cells were mixed uniformly into fresh soft agar plates. After agar solidification (< 10 min), fluorescence intensity was observed over time. (c) Derived growth curves in soft-agar based on experiments like the example shown in panel b. Typically, there is a fast growth regime followed by a slower regime related to oxygen consumption and limitation for OD > 0.1: with oxygen running out, cells accumulate towards the agar surface and growth becomes slower. In this work, the population was always kept in the first aerobic regime. Growth rates in the first regime (shown as colored lines and listed in Supplementary Table S2) are obtained by an exponential fit of the data and comparable to those obtained in batch culture (bar graph inset panel c). In panels (b,c) the experiment was conducted once. (d) Photo and spatiotemporal density profiles (linear intensity scale) for population expansion in reference condition (glycerol+100μM aspartate; same data as in Fig. 1A and 2B). Scale bar in photo denotes 2 cm. The confocal observations in reference conditions were repeated twice showing similar results. (e-i) Spatiotemporal density profiles (logarithmic density scale) for population expansion in different conditions, similar to those observed for the reference condition (glycerol+100μM aspartate) shown in (d). Conditions are glycerol + 100μM serine (e), glycerol + 100μM aspartate + 100μM serine (f), glycerol + 0.05% CAA (g), 1% tryptone broth (h), and glucose + 100μM apartate (i), all with strain HE274 (WT). Same color code was used to indicate time for all different runs; see the color bar scale on the right. In panels (e-i), the experiments were conducted once; expansion speeds were highly comparable to the ones measured manually.

Extended Data Figure 5. Population expansion without attractant is quantitatively captured by the Fisher-Kolmogorov dynamics.

The Fisher-Kolmogorov (FK) dynamics is a canonical model to describe the dynamics of expanding populations^19,20. For example, it has been successfully applied to investigate the expansion and evolution of non-moving bacteria at the front of dense bacterial colonies^47,74–77. Here, we probe the FK dynamics and its validity to describe swimming bacteria. The FK dynamics is driven by population growth and undirected random motion (diffusion)^32,33. To compare the predictions of FK dynamics to the expansion of bacterial population in the absence of a chemoattractant, we thus independently quantified growth rates as well as cellular diffusion for cells homogeneously distributed in soft-agar (upper two panels). We then compared observed migration speed and the density profile of the migrating population (for growth on glycerol as the sole carbon source, same as in Fig. 2d top panel) with the FK predictions (lower two panels). (a) Quantification of growth by measuring the temporal density increase of a homogeneously distributed population in agar (see Extended Data Figure 4a–c and Supplementary Text 1.4 for method details). Spatially averaged density increased exponentially with growth rate λ = 0.59/h for densities < 0.1 OD₆₀₀. For higher densities, the growth rate decreased but this regime is not important for the propagation of the front where density is low. (b) Diffusion and drift of cells homogeneously distributed in soft-agar. Analysis of recorded cell movement confirms the variance of position displacement to increase linearly in time (orange symbols) with diffusion constant D = 41.5μm²/s (linear fit of var(x) = 2 DΔt). In comparison, the average displacement of cells (purple symbols) and the calculated drift (〈ΔX/Δt〉, purple line) are small, indicating the absence of directed chemotactic movement. Data shows average over 3 independent repeats; see Extended Data Figure 3 and Supplementary Text 1.5 for method description. (c,d) Front and spatiotemporal dynamics of an expanding population. (c) Comparison of predicted expansion speed with the observed propagation of the population front. Position of the front R(t) was determined from the observed cellular densities (threshold OD₆₀₀ > 0.005); it increased linearly in time, i.e., R(t) = u_obs · t with a speed u_obs = 0.62mm/h. Dashed line denotes predicted expansion speed calculated as $u_{FK}=2\sqrt{\lambda \cdot D}=0.59 mm/h$. (d) Density profile of the population front. Observed density profile can be fitted to an exponential dependence $\rho \left(r,t\right)~e^{-k_{obs}\left(r-R\left(t\right)\right)}$ with k_obs ≈ 1.2/mm. Dashed line indicates the slope of the exponential density profile predicted by the FK equation: $k_{FK}=\sqrt{\lambda /D}=1.99/mm$. [The discrepancy likely resulted from the low spatial resolution of the very sharp density drop – the exponential dependence of the experimental profile is defined by just 3 points.] All experiments were conducted once with strain HE274 (WT), using glycerol as the carbon source (no additional attractant, glycerol cannot be sensed). Growth and cell-tracking experiments were performed with uniform cell mixture in saturating glycerol conditions (40mM). Expansion experiments were performed with 1mM glycerol.

Extended Data Figure 6. Different models of chemotaxis-driven migration.

To illustrate the difference among various models of chemotactic expansion, we show here simulation results of four different models. (a) The classical model proposed by Keller and Segel³⁴ creates a self-generated attractant gradient due to attractant consumption by the migrating population. It neglects cell growth (i.e., λ = 0 in Eq. (3) shown in Figure 3a), resulting in the conservation of the total number of bacteria. It also assumes that the attractant gradient could be detected with infinite precision, such that log-sensing (Weber’s law⁷⁸) can be implemented by cells down to arbitrary low attractant concentrations, (i.e., Eq. (4) with a₋ = 0). The latter biologically unrealistic assumption introduces a singularity that pushes all bacteria forward at a steady migration speed, which is determined by the number of cells in the population, the conserved quantity. (b) The model introduced by Novick-Cohen and Segel³⁶ fixed the singularity in the Keller-Segel model by imposing a minimal concentration for the sensing of attractant gradient (i.e., Eq. (4) with a₋ > 0). Due to the lack of cell growth, the total number of bacteria is still conserved. In this model, the density of the front bulge decays over time because once bacteria diffuse out of the front, they lose the chemotactic gradient and cannot catch up with the front anymore. The reduction in front density reduces the migration speed, which decays steadily towards zero. (c) Model including cell growth that depends on attractant concentration (nutrient=attractant). Due to growth, population size increased over time. However, since the attractant (nutrient) is mostly consumed at the front, there is not much growth behind the front and the trailing region behind the front is mostly flat. This scenario was realized and analyzed experimentally in Ref.¹⁸; see Extended Data Figure 5 for model details and discussion. (d) The Growth-Expansion model (GE) formulated in this study (Fig. 3a), including the chemotactic effect of an attractant, together with cell growth supplied by a major nutrient source. Front propagation of cells by chemotaxis is coupled to steady growth in the trailing region as described, see main text and Extended Data Figure 9. Parameter values for all models provided in Supplementary Table 8. For simplicity, simulations shown here were solved in 1d (non-radial). Green lines denote bacteria density, blue lines denote attractant (or sole nutrient) concentration, brown lines denote concentration of nutrients (in addition to the attractant). Purple lines show local drift (Eq. (4)).

Extended Data Figure 7. Aspartate uptake and further analysis of expansion dynamics.

(a-c) Characterization of aspartate uptake for different growth conditions and strains. (a) Aspartate uptake was determined using a colorimetric method to quantify remaining aspartate concentrations during growth. Full method details are provided in Supplementary Text 1.2.3. In brief, change of aspartate concentration in the media was measured during exponential growth at different cell densities (OD). Shown data are for growth with glycerol as the major carbon source (40mM) and 0.8mM initial aspartate concentration). Measurements for native aspartate uptake (WT) and for different aspartate-uptake mutants (mutants ΔgltJ and ΔgltP as well as the double mutant ΔgltJ ΔgltP). Lines show linear fit. Uptake rate was determined by multiplying obtained slope with growth rate. (b) The strains shown in (a) with different Asp uptake rates exhibit similar growth rates. For each strain, the data points were collected from a single experiment. (c) Dependence of aspartate uptake on growth rate for strains harboring native aspartate uptake. Growth is varied using WT cells (HE206, circles) grown in different sugar sources (acetate, mannose, glycerol, or glucose), or by using the glpK* mutant (HE433, triangle) or the glycerol titration mutant (HE443, squares), in glycerol with different levels of the inducer 3MBA (25, 50, or 800 μM). 0.8mM of aspartate was provided in each case for the measurement of aspartate uptake (see panel a). Line shows linear fit with parameters specified in Supplementary Text 1.2.3. Data shown in (a) and (b) were obtained for strains carrying fluorescence plasmids. Data shown in (c) were obtained for non-fluorescent strains (two biological replicates, means shown). Data, as well as strain information and media conditions including concentrations of carbon sources are provided in Supplementary Table S7. (d) Expansion dynamics with glucose as the primary carbon source. The dynamics of the front, shown to be described well by the GE model in Fig. 3b in glycerol with aspartate, is examined with the primary carbon source being glucose (20 mM). In the presence of 100μM aspartate, the observed front propagration dynamics (purple squares) is correctly captured by the GE model again (purple line), by merely replacing the growth rate by that in glucose (λ = 1.0 h⁻¹) and no additional adjustment of the chemotactic coefficient χ₀. For reference, expansion is also shown where no additional chemoattractant was provided (i.e. 0μM aspartate, open green squares), and the corresponding data where glycerol was the primary carbon source (open black circles and corresponding lines taken from Fig. 3b). (e,f) Dependence of expansion speed on attractant concentration with glycerol or glucose being the major nutrient.The observed increase of expansion speed at low attractant concentrations followed by decrease at higher concentrations – as previously observed by Wolfe and Berg⁴³- is qualitatively captured by the GE model (dashed grey lines) in both cases. A better quantitative agreement between model and data is obtained when the linear growth term in the GE model (Eq. (1) of Fig. 3a) is changed to the logistic form, i.e., λρ (1 – ρ/ρ_c). Here ρ_c is the carrying capacity, introduced to capture saturation of cell density in the front bulge; see Supplementary Text 2.3 for details. Predictions by the model are shown for different carrying capacities as colored lines in panels (e) and (f). In line with the strict requirement for oxygen when growing on glycerol and the observation that cells at high density accumulate at the agar surface when expanding with glycerol as major nutrient source (data not shown), the carrying capacity needed to resemble the observations is much lower for glycerol (e) than for glucose (f). Shown data points represent means of biological replicates (n=2 or larger), with error bars (s.d.) shown for n>=3; see Supplementary Table S9 for data values and sample sizes. (g-i) Effect of varying aspartate uptake rate on expansion speed. The GE model predicts the expansion speed to be completely independent of the attractant uptake rate if all other parameters are kept fixed (panel g, dashed black line; Supplementary Text 2.2), with differences in attractant uptake compensated by changes in bacterial densities at the front (panel h), such that the total rate of attractant depletion remains constant. This prediction is tested by characterizing the expansion dynamics of the aspartate-uptake mutants (strains HE506,HE552, HE555; see Supplementary Text 1.1, Supplementary Table 3 and 7), which exhibited up to 3-fold difference in aspartate uptake (panel a), but only ~20% change in expansion speed (panel g). The small changes are readily accounted for by incorporating the small growth rate differences between these strains (panel b) in the GE model while keeping all other parameters fixed (panel g, green crosses). Additionally, the aspartate-uptake mutants exhibited increasing peak densities at the front as predicted by compensation for reduced uptake (compare i, h). (j-k) Predicted and observed changes in density profiles when varying the growth rate by titrating glycerol uptake in strain HE486 using 25uM, 50uM and 800uM of the inducer 3MBA. For panels (g, i, k), data were obtained from a single experiment for each strain and condition.

Extended Data Figure 8. Expansion dynamics with the attractant being the sole nutrient source.

This is one of the scenarios of chemotaxis investigated previously by Koster et al¹⁸ and others⁷⁹. Here, for comparison with the dynamics presented in the main text, we show the expansion dynamics of populations grown with glucose (a chemoattractant²¹) being the sole carbon source. (a) For WT cells (HE206) spotted on 0.25% agar plate with glucose as the sole carbon source, photographs show the existence of an outer ring at the front of the expanding population for a range of glucose concentrations. Scale bar indicates 2 cm. The experiments were repeated once with similar results. (b) Dependence of expansion speed on glucose concentration. Intuitively, one may expect reducing the glucose concentration would increase the expansion speed, as it would take shorter time for the population to consume the attractant. However, the data (circles) shows that reducing the glucose concentration actually reduced population expansion speed. Data points show means of two biological replicates. (c) Direct comparison of concentration dependence of expansion speeds in glucose only (open green squares), in glycerol only (open black circles), in glycerol or in glucose with aspartate supplement varied (red circles, purple squares); data for latter condition same as those shown in Fig. 4d and Extended Figure 7ef. Expansion speed in glucose (~ 1–2 mm/h) is faster than those obtained for growth in glycerol (not an attractant) but well below the cases for which (low) amounts of attractants are supplemented. Shown data points represent means of biological replicates (n=2 or larger), with error bars (s.d.) shown for n>=3; see Supplementary Tables S9 and S10 for data values and sample sizes.To understand the expansion behavior, we first used confocal scans (d,e) to obtain the density profiles: The ring observed in the photograph is seen as a subtle density bulge at the front bounding a flat-density interior. Note the lack of an exponential trailing region, as observed when an attractant supplement is present (Fig. 2b, Extended Data Figure 4i, photographs in Fig. 1a). The observed density profiles are comparable with reports by Koster et al¹⁸, who studied expansion with galactose as the attractant and the major nutrient source. Experiments here were done with WT (HE206) in (a-c) and fluorescence cells (HE274) in (d,e). The confocal experiments were conducted once (expansion speeds are highly comparable to those measured manually). (f) To capture the observed behaviors, we modified the growth expansion model (Fig. 3a) using only one variable a to describe the attractant/nutrient. Consumption of the growth-enabling attractant is directly coupled to the increase in density via the yield Y. Fixing model parameters using available data for growth and chemotaxis on glucose (see Supplementary Text 2.4 and 2.6 with parameters used listed in Supplementary Table 4), the model generated expansion speeds (green line in panel b) and density profiles (g,h) which capture the experimental observations well; for comparison a coarse-grained spatial resolution similar to the experiments was used to display the profiles obtained by the simulations. (i) The model output can further be understood by a scaling analysis (SI Text 2.6), resulting in the simple relation u² ∝ χ₀ λ (Eq. E8.e). This relation is of the same form as the result of the Fisher-Kolmogorov dynamics, $u_{FK}=2\sqrt{D\lambda }$ (see Extended Data Figure 5), but with the chemotactic coefficient χ₀ replacing the diffusion coefficient D. (j,k) The predicted dependence of u on λ and χ₀ (black lines) are validated by numerical simulations of the model (blue circles). Importantly, the square-root dependence of the expansion speed on the chemotactic coefficient χ₀ stands in contrast to the linear dependence on χ₀ when an attractant supplement is provided (Extended Data Figure 9d) and shows that the expansion dynamics with/without the attractant supplement are two distinct classes of mathematical problems. Note that the quantitative gain in expansion speed for the case with a supplemented attrractant comes not only from the change of the dependence on the chemotactic coefficient from $\sqrt{{\chi }_0}$ to χ₀, but also from the freedom to use attractants that have large χ₀ but small λ, that can be compensated by nutrients that give larger λ. Both aspartate and serine are strong attractants but poor nutrients, and are thus most potent when used in combination with a good nutrient source. Thus, separating the role of sbustances as nutrients and as cues not only relaxes the underlying mathematical constraint but also relaxes the biological constraint so that good attractants need not be good nutrients. These results provide an important support for the central thesis of this work, that chemotactic cells gain fitness by expanding in nutrient-replete conditions as a ‘foresighted’ navigation strategy (see final discussion in the main text).

Extended Data Figure 9. Scaling analysis of expansion dynamics and illustration of the stochastic migration process.

(A) The exponential trailing region of the density profile: It is fixed by the cell growth rate λ and expansion speed u of the front: Because cells in the trailing region do not experience drift (Extended Data Figure 3g), the apparent ‘movement’ of the trailing region at the same speed as the front bulge is only possible if it has an exponential profile, i.e., ρ(r, t) ~ e^k(r−ut), with k = λ/u; see the illustration. (b) Scaling of the expansion speed with model parameters. According to the GM model (Fig. 3a), the density peak at the propagating front is determined by a balance between cell growth and back diffusion as depicted in Fig. 4b. Using a crude scaling analysis to capture this balance, we can obtain (approximately) the quantitative determinants of the propagating speed. For this, consider a sharply peaked density bulge at the front, with peak density ρ_peak and width w. The number of cells contained in the peak region, N_peak, is given by the relation (E9.a). Cell birth rate, λ · N_peak, is balanced by the back-diffusion flux, which is approximated as Dρ_peak/w, leading to the relation (E9.b). To relate to the migration speed u, we note that around the density peak the drift speed v is nearly maximal (Fig. 4A, purple line), and Eq. (4) becomes $v_{\text{max}}\approx {\chi }_0\cdot \frac{d}{dx}\text{ln}\left(a\right)$. In the scaling approach, we take u ~ v_max and with the approximation $\frac{d}{dx}\text{ln}\left(a\right)~1/w$, leading to the relation (E9.c). Combining Eq. (E9.a) - (E9.c), we obtain Eq. (E9.d) with the expansion speed increasing with the square-root of the growth rate λ. Note the χ₀/D factor appearing as prefactor in the expression for u, which is responsible for the increase in the expansion speed in the presence of chemotaxis with respect to the Fisher-Kolmogorov dynamics (Extended Data Figure 5) and to the dynamics with the attractant being the sole nutrient (Extended Data Figure 8). (c,d) Scaling results are confirmed by simulations of the GE model when varying growth rate λ (c), and chemotactic coefficient χ₀ (d). (e) To further illustrated the intricate dynamics at the front of the expanding population, we performed stochastic agent-based simulations looking at the trajectory of single cells. Shown here are cell trajectories for a few selected ones located within the population front (‘pioneers’) at time t = 6.5h. Lower panel shows 38 trajectories with color indicating the time the trajectory escaped from the front and cells switched from being pioneers to being settlers, which grow and colonize localities behind the front. Red circles indicate cell division events. Highlighted area (cyan) denotes front region with aspartate concentration in the range a₋ < a < a₊. Upper panel shows position distribution of all simulated trajectories (1000) at time t = 8 h. See Supplementary Text 3 for details.

Extended Data Figure 10. Modeled scenario of chemotaxis as a strict starvation response.

To examine the expansion characteristics of the population under the hypothetical scenario were chemotaxis is a strict starvation response, we modified the GE model (Fig. 3a) to investigate the cases when chemotaxis is either active only in slow growth conditions (a,b) or within intermediate density ranges (c-e). (a) To model chemotaxis being activated at slow growth, we introduced a strong dependence of chemotaxis on the local growth rate (orange line). In contrast to the original GE model (dashed red line) we used a chemotactic coefficient depending on growth conditions, χ₀ = χ₀(λ(n)) (orange line). Black dashed line shows the growth rate in the presence of saturating glycerol. (b) This dependence of chemotaxis on growth conditions leads to a dramatic decrease in the speed of expansion (compare orange and red dashed line). In fact, the expansion dynamics of this model resembles the case of the Fisher-Kolmogorov dynamics (gray dashed line), suggesting that chemotaxis does not boost population-level expansion when it is activated only at slow growth conditions. (c-e) We further studied the case of swimming being a density-dependent response, active only at intermediate bacterial densities as it has been observed previously in batch culture measurements¹⁵ (see data shown in panel c). Taking such a dependence of the swimming speed (v) on the local cell density (ρ) and assuming χ₀ ~ v²(ρ), we looked at the expansion dynamics for several different maximum values of the chemotactic coefficient (d,e). For all the forms of χ₀(ρ) shown in panel (d), we observed that population expansion is slowed down substantially as compared to the reference case where chemotaxis is also active at low densities (red dashed lines). Slow expansion dynamics is again similar to the Fisher-Kolmogorov dynamics, illustrating that the boost of expansion speed and population size by chemotaxis relies on chemotaxis being active at low densities. Note that in both cases analyzed, we have not included the dependence of the diffusion constant on growth rate or local densities but assumed a constant value as in the original GE model. Introducing such dependences would further reduce the speed of expansion, below even that of Fisher-Kolmogorov. The origin of the slow expansion dynamics in these models is very simple: a population cannot expand faster than its front, and the front is at low density and experiences the fastest growth rate.