Fast fit-free analysis of fluorescence lifetime imaging via deep learning

Significance

Fluorescence lifetime imaging (FLI), although capable of providing powerful biomedical insight, necessitates computationally expensive inverse solvers to obtain parameters of interest, which has limited its broad dissemination, especially in clinical settings. Hence, a real-time, user-friendly approach has the potential to transform this field. Herein, a deep neural network (DNN) architecture named fluorescence lifetime imaging network (FLI-Net) was designed to form spatially resolved quantitative images of complex fluorescence lifetimes without any user-defined parameter input during processing. Thus, FLI-Net is poised to facilitate current lifetime imaging applications, expand its dissemination, and lead to new applications, especially in preclinical and clinical settings.

Abstract

Fluorescence lifetime imaging (FLI) provides unique quantitative information in biomedical and molecular biology studies but relies on complex data-fitting techniques to derive the quantities of interest. Herein, we propose a fit-free approach in FLI image formation that is based on deep learning (DL) to quantify fluorescence decays simultaneously over a whole image and at fast speeds. We report on a deep neural network (DNN) architecture, named fluorescence lifetime imaging network (FLI-Net) that is designed and trained for different classes of experiments, including visible FLI and near-infrared (NIR) FLI microscopy (FLIM) and NIR gated macroscopy FLI (MFLI). FLI-Net outputs quantitatively the spatially resolved lifetime-based parameters that are typically employed in the field. We validate the utility of the FLI-Net framework by performing quantitative microscopic and preclinical lifetime-based studies across the visible and NIR spectra, as well as across the 2 main data acquisition technologies. These results demonstrate that FLI-Net is well suited to accurately quantify complex fluorescence lifetimes in cells and, in real time, in intact animals without any parameter settings. Hence, FLI-Net paves the way to reproducible and quantitative lifetime studies at unprecedented speeds, for improved dissemination and impact of FLI in many important biomedical applications ranging from fundamental discoveries in molecular and cellular biology to clinical translation.

Molecular imaging has become an indispensable tool in biomedical studies with great impact on numerous fields from fundamental biological investigations to transforming clinical practice. Among all molecular imaging modalities, fluorescence optical imaging is a central technique due to its high sensitivity; the numerous molecular probes available, either endogenous or exogenous; and its ability to simultaneously image multiple biomarkers or biological processes at diverse spatiotemporal scales (1, 2). Especially, fluorescence lifetime imaging (FLI) has become an increasingly popular method as it provides unique insights into the cellular microenvironment via analysis of various intracellular parameters (3), such as metabolic state (4), reactive oxygen species (5), and intracellular pH (6). Moreover, FLI’s exploitation of native fluorescent signatures has been extensively investigated for enhanced diagnostics of frequent pathologies (7–10). Additionally, FLI is one of the most accurate approaches to quantify Förster resonance energy transfer (FRET), an invaluable technique to perform nanoscale proximity assays in many biosensing and bioanalysis applications (11). FLI FRET is a powerful technique for studying molecular interactions inside living samples, including applications such as quantifying protein–protein interactions, monitoring biosensor activity (12), and ligand–receptor engagement in vivo (13). However, despite its popularity and profound impact, FLI is not a direct imaging modality and datasets need to be postprocessed to quantify fluorescence lifetime or lifetime-based parameters. Such postprocessing typically involves a model-based process in which iterative optimization methods are employed to estimate the different parameters of interest (lifetime, FRET efficiency [E%], or population fractions). Mono- or biexponential models, depending on the application at hand, are the most widely employed to analyze FLI datasets. Yet, it is notorious that the accuracy of these methods is often associated with guess parameter settings employed to constrain the inverse problem. These methods are also relatively slow and/or computationally expensive (14). This complexity together with a lack of standardized methodologies has limited the widespread use and impact of FLI, especially clinically. Recently, a fit-free lifetime quantification methodology has been proposed, the phasor approach (15). The phasor method is a graphical representation of excited-state fluorescence lifetimes. Adoption of the phasor technique has been increasing due to its simplicity that allows nonimaging experts to perform simple and fit-free analyses of the information contained in the many thousands of pixels constituting an image (16). Furthermore, the phasor formulation is independent of the sample and hence allows for the identification of fluorescent species that may not have been accounted for in a particular study’s imaging protocol. However, although the phasor method provides a graphical interface that simplifies FLI data interpretation, the mathematics underlying its computation can be challenging, its user-friendly interface requires some level of proficiency for accurate quantification (17), the approach may need to be modified for techniques such as time-gated fluorescence (18), and it requires calibration samples with known lifetime value to be quantitative (19).

In parallel, interests in data-driven and model-free processing of imaging methodologies have boomed over the last decade. Of particular note, machine-learning (ML) and deep-learning (DL) methods have recently profoundly impacted the image-processing field. For example, deep neural networks (DNNs) are currently providing high-level, robust performances in numerous biomedical applications—such as in pathology through multiple-imaging modalities (20–22), natural language processing (23), image reconstruction via direct mapping from the sensor-image domain (24), and reinforcement learning applied to drug discovery (25). DL methods are increasingly employed in molecular optical imaging applications from resolution enhancement in histopathology (26), superresolution microscopy (27), fluorescence signal prediction from label-free images (28), single-molecule localization (29), fluorescence microscopy image restoration (30), and hyperspectral single-pixel lifetime imaging (31). However, the typical application of DL methods to image processing is data driven and hence requires large training datasets that are difficult to acquire and/or not readily available.

Herein, we present a 3D convolutional neural network (CNN) architecture named fluorescence lifetime imaging network (FLI-Net) that is designed to process the typical datasets acquired by current fluorescence imaging systems. FLI-Net provides, at fast speeds, lifetime maps as well as associated quantities (i.e., lifetime species, E%, or fractional amplitude of lifetime components, such as FRET donor fraction [FD%]). To date, this 3D CNN methodology is trained to reconstruct mono- and biexponential FLI for each typical class of experiments encountered in the field, including in vitro FLI microscopy (FLIM) in cultured cells in the near-infrared (NIR) and visible range as well as in vivo NIR macroscopic FLI (MFLI) in live intact mice. For each of these cases, the data used in the training datasets were simulated over wide lifetime bounds encompassing those present in the application of interest. Furthermore, the 3D CNN is trained efficiently using a synthetic data generator to achieve state-of-the-art FLI reconstruction with experimental datasets not used during training—avoiding the need to acquire massive training datasets experimentally. Of importance, FLI-Net does not require the selection of any direct guess or user-defined parameters posttraining. FLI-Net is accurate over a large range of lifetimes (including those close to the instrument response) and has the potential to provide superior performances in photon-starved conditions. In addition, this 3D CNN is capable of processing experimental fluorescent decays acquired by either time-correlated single-photon counting (TCSCP)-based (FLIM datasets) or gated intensity charged-coupled device (ICCD)-based (MFLI datasets) instruments, which are 2 of the main FLI-based technologies employed in the field. Herein, the potential of FLI-Net is demonstrated by performing visible FLIM to quantify the metabolic status of live cells as well as reporting FRET to measure levels of receptor engagement across the visible and NIR spectra using FLIM and MFLI—covering the full range of lifetimes encountered in most current applications. In all cases, the 3D CNN performances are benchmarked against the widely used FLIM processing software SPCImage (32). Finally, we demonstrate the potential of the 3D CNN to quantify whole-body dynamic lifetime-based FRET occurrence in a live intact animal at unprecedented frame rates (≅80 ms per full whole-body image). Overall, these results demonstrate that DL methodologies, beyond classical image-processing tasks, are well suited for image formation paradigms that to date were based on inverse problem solvers. FLI-Net provides a versatile tool for fit-free analysis of complex mono- and biexponential FLI imaging processes. Due to its ease of use and fast employability, this 3D CNN should further stimulate the widespread use of FLI techniques, provide standardized quantification capabilities (as no parameter settings are required posttraining), and enable applications such as high-throughput FRET-based biosensor studies as well as real-time wide-field FLI in preclinical and clinical settings for drug screening and optical guided surgery, respectively.

FLI-Net Architecture, Training, and Validation

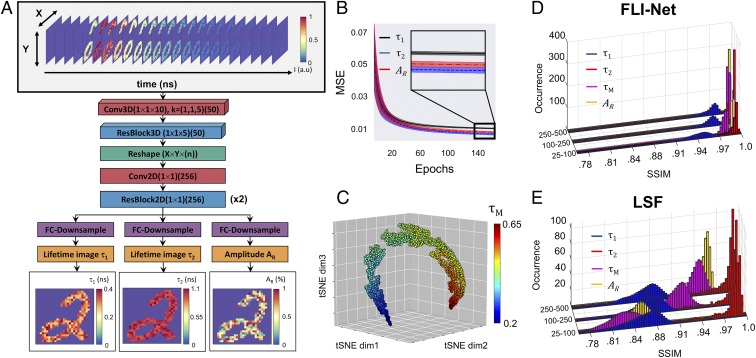
The 3D CNN FLI-Net is designed to mimic a curve-fitting approach using layers of convolutional operations and nonlinear activation functions. FLI-Net is devised such that time-resolved and spatially resolved fluorescence decays are input as a 3D data cube (x, y, t) and biexponential parameters (2 lifetimes, τ₁ and τ₂, and 1 fractional amplitude, A_R) are independently estimated at each pixel to be provided in output images of the same dimension as the input (x, y). A rendering of the architecture of FLI-Net is provided in Fig. 1A. The network architecture consists of 2 main parts: 1) a shared branch for temporal feature extraction and 2) a subsequent 3-junction split into separate branches for simultaneous reconstruction of short lifetime (${\mathit{\tau }}_1$), long lifetime (${\mathit{\tau }}_2$), and fractional amplitude of the short lifetime ($A_R$). Several design choices are critical to the performance of FLI-Net, providing the basis for a high level of sensitivity, stability, speed, and reconstruction accuracy. First, it is crucial to introduce 3D convolutions (Conv3D) along the temporal dimension at each spatially located pixel at the first layer to maximize spatially independent feature extraction along each temporal point spread function (TPSF). The use of a Conv3D layer with kernel size of (1 $\times$ 1 $\times$ 10) mitigates the potential introduction of unwanted artifacts dependent on neighboring pixel information in the spatial dimensions (x and y) during training and inference. After this step, a residual block (ResBlock) of reduced kernel length is employed. This second step enables further extraction of temporal information while reaping the benefits obtained through residual learning (elimination of vanishing gradients, no overall increase in computational complexity or parameter count, etc.) (33). The beneficial implementation of residual learning has been thoroughly documented in image classification and segmentation (34) as well as in areas of speech recognition (35). Fully convolutional networks (36), or networks designed such that input of any spatial dimensionality can be analyzed with no loss in performance, offer enormous benefit to problems where 1) prior knowledge of input size is inherently variable and 2) the experimental data of interest are memory exhaustive. After performing the common features of the whole input, the network splits into 3 dedicated fully convolutional branches to estimate the individual lifetime-based parameters of interest, i.e., short lifetime (${\mathit{\tau }}_1$), long lifetime (${\mathit{\tau }}_2$), and fractional amplitude of the short lifetime ($A_R$). In each of these branches, a sequence of convolutions is employed for down-sampling to the intended 2D image. A more detailed description of the network architecture (SI Appendix, Fig. S1) is provided in Materials and Methods and SI Appendix, SI Text.

Fig. 1.

Illustration of the 3D-CNN FLI-Net structure and corresponding metrics. During the training phase, the input to the DNN (A) was a set of simulated data voxels containing a TPSF at every nonzero value of a randomly chosen MNIST image. After a series of spatially independent 3D convolutions, the voxel underwent a reshape (from 4D to 3D) and is subsequently branched into 3 separate series of fully convolutional down-sampling for simultaneous spatially resolved quantification of 3 parameters, including short lifetime (${\mathit{\tau }}_1$), long lifetime (${\mathit{\tau }}_2$), and fractional amplitude of the short lifetime ($A_R$). (B) The 30-MSE validation curve average with corresponding SD (shaded) for each parameter. (C) t-SNE visualization obtained via the last activation map before the trijunction reconstruction, where each point represents a TPSF voxel assigned a randomized trio of lifetime and amplitude ratio values. (D and E) FLI-Net performance (D) versus LSF (E) upon evaluation of simulated TPSF voxels over 3 ranges of maximum photon count (25 to 100, 100 to 250, and 250 to 500 p.c.). Parameters of interest include ${\mathit{\tau }}_1,$ ${\mathit{\tau }}_2,$ $A_R,$ and mean lifetime (${\tau }_M,$ Eq. 2).

To obtain large datasets to train FLI-Net and ensure its architecture robustness and feature extraction efficiency as well as establish its quantitative accuracy, 10,000 TPSF voxels were generated. Each voxel was simulated using the modified National Institute of Standards and Technology (MNIST) database to obtain spatial maps of 28 $\times$ 28 pixels and subsequently generate fluorescence decays (notated $\mathrm{\Gamma }\left(\mathit{t}\right)$) at each nonzero pixel location using a biexponential model convolved with an experimental instrument response function (IRF) illustrated in Eq. 1:

$$\mathrm{\Gamma }\left(t\right)=\mathrm{I}\mathrm{R}\mathrm{F}\left(t\right)\ast \left[A_R{e}^{-t/{\text{τ}}_1}+\left(1–A_R\right)e^{-t/{\text{τ}}_2}\right].$$ [1]

Hence, the data inputs were of dimension 28 $\times$ 28 $\times$ t (SI Appendix, Fig. S2). Data were generated per class of experiments investigated herein: visible FLIM, NIR FLIM, NIR MFLI, and NIR MFLI FRET. To do so, the parameters of the biexponential model were varied over the lifetime range typically encountered in the field, including our specific experiments (visible (${\tau }_1,{\tau }_2$) ∈ [0.2 to 3] ns; NIR (${\tau }_1,{\tau }_2$) ∈ [0.2 to 1.1] ns), and the fractional amplitude A_R varied from 0 to 100% (A_R = 0 or 100% corresponds to monoexponential decays whereas every value between these extremes corresponds to biexponential decays). SI Appendix, Table S1 provides a full summary of the parameters used for training. The IRF was either generated using SPCImage in the case of FLIM data or experimentally acquired in the case of MFLI data. Finally, the photon counts (p.c.) of the maximum of the TPSF were set between either 250 or 500 (for FLIM or MFLI, respectively (SI Appendix, Table S1), and 2,000 counts followed by the addition of Poisson noise. Examples of TPSFs for FLIM or MFLI are provided in SI Appendix, Fig. S3. The training dataset was split into training (8,000) and validation (2,000) datasets. Additional information on the generation of these data is provided in Materials and Methods and SI Appendix.

To demonstrate the robustness of FLI-Net, training and validation were performed over 30 times with randomly initialized training/validation partitions in the case of a NIR-trained network as this is the most challenging case in quantitative lifetime studies due to the short lifetimes of NIR fluorophores. The plotted average of 30 validation mean-squared error (MSE) curves trained over 150 epochs with corresponding SD bounds for all 3 output branches is provided in Fig. 1B and illustrates the DNN’s excellent convergence stability. To evaluate whether the feature extraction of the shared branch was robust and effective, the output of the shared branch’s final activation layer was registered during the feedthrough of 5,000 newly simulated TPSF data voxels (not used in training or validation). These high-dimension features were flattened and projected to a 3D feature space via t-distributed stochastic neighbor embedding (t-SNE) (37). Their display as a scatter plot is provided in Fig. 1C, with each assigned color corresponding to the ground-truth (GT) value of mean lifetime (${\tau }_M,$ calculated via Eq. 2):

$${\tau }_M=A_R{\tau }_1+\left(1-A_R\right){\tau }_2.$$ [2]

The continuous gradient observed in the 3D plot of the t-SNE values versus the simulated mean lifetimes (${\tau }_m\in \left[0.2,0.65\right]$ ns) indicates an efficient and sensitive feature extraction for lifetime-based parameter estimation. Beyond feature extraction, we provide also the summary of the quantitative accuracy of the network in estimating the 3 abovementioned lifetime-based parameters (${\tau }_1,{\tau }_2,A_R$). The accuracy of these results was evaluated via the structural similarity index (SSIM) between the simulated and estimated values (SSIM = 1 indicating perfect one-to-one concordance). The SSIMs are also reported for 3 ranges of maximum photon counts (i.e., p.c._good ∈ [250 to 500]; p.c._challenging ∈ [100 to 250]; p.c._low ∈ [25,100]) as FLI imaging in biomedical applications is notoriously a photon-starved application. In all 3 cases, FLI-Net (Fig. 1D) significantly outperforms the classical least-squares fitting (LSF) (Fig. 1E) method, which as expected demonstrates worsening performances at very low photon counts ($\overline{\mathrm{S}\mathrm{S}\mathrm{I}\mathrm{M}}=0.82$). Note that although the network was trained using only TPSF data possessing intensity values greater than 500, it performs well for low photon-count levels as well (even in the 25 to 100 range with a $\overline{\mathrm{S}\mathrm{S}\mathrm{I}\mathrm{M}}=0.95$ for the worse case). To further highlight the accuracy and robustness of the network, we provide in SI Appendix, Fig. S4 examples of spatially resolved images of lifetime as estimated via FLI-Net and LSF for different p.c. along with the GT. We limit ourselves to ${\tau }_M$ and $A_R$ for simplicity. In all cases, FLI-Net predicted the absolute ${\tau }_M$ with high accuracy (mean absolute error maximum of ${\overline{\epsilon }}_{{\mathbf{\tau }}_{\mathbf{M}}}=83\pm 62$ ps in the case of low p.c.; SI Appendix, Fig. S4O) whereas LSF predictions deviated significantly at low p.c. Further, the $A_R$ quantification via FLI-Net is in much higher concordance with GT across all p.c. bounds in large contrast with LSF (SI Appendix, Fig. S4).

Overall, these training and validating results establish that FLI-Net can be efficiently and robustly trained via synthetic data representing both mono- and biexponential decays (we provide in SI Appendix, Fig. S5 an example of an alternative 2D-CNN network). Moreover, as only in such synthetic datasets the lifetime parameters absolute ground truth are known, this is the only available methodology to establish in an absolute fashion the accuracy of FLI-Net prediction. In summary, FLI-Net outperforms the classical LSF approach in estimating the 3 lifetime-based parameters that are commonly employed in FLI biomedical imaging. To further establish the usefulness and unique potential of FLI-Net, its performance was evaluated using experimental datasets after training with simulation data generated through the workflow previously described.

FLIM.

FLIM is the most widely used FLI application in biomedical imaging. For this study, we selected metabolic and FRET imaging as they are some of the most challenging, yet sought after, FLIM applications. First, the performance of FLI-Net was evaluated by quantifying the metabolic status of live cells as reported by NADH endogenous imaging. Second, FLI-Net’s capacity to quantify ligand–receptor engagement via FLIM FRET in the visible and NIR range was determined. Note that all studies hereafter are conducted using experimental datasets that have never been used in the training and validation of FLI-Net. Additionally, even if in these applications complex fluorescence decays that may reflect 3- or 4-exponential behavior can be encountered, still, it is customary in the field to use a biexponential model to process them due to relatively low photon counts.

Metabolic imaging.

Quantification of the fractional concentration between free and protein-bound NADH provides important information regarding cellular metabolic state (38). Free and protein-bound NADH possess different, yet overlapping, absorption and emission profiles (39). Since they differ significantly in fluorescence lifetime, FLIM has been used extensively for free vs. bound NADH quantification in vitro (38, 40, 41). The short-lifetime component has been indicated to reflect free NADH, while the long lifetime corresponds to bound NADH. Biexponential lifetime imaging allows for the calculation of the weighted average of NADH short- and long-lifetime components, i.e., mean fluorescence lifetime (${\tau }_M$), which has been shown to monitor metabolic response in breast cancer cells (38, 41). First, confocal FLIM data were collected from 4 human cell lines (MCF10A as a noncancerous mammary epithelial cell line and the remaining being cancer cell lines representing different types of breast cancer) using a Zeiss LSM 880 Airyscan NLO multiphoton confocal microscope equipped with an HPM-100-40 high-speed hybrid FLIM detector (GaAs 300 to 730 nm; Becker & Hickl) and a Titanium:Sapphire laser (Ti:Sa) (excitation set at 730 nm; Chameleon Ultra II, Coherent, Inc., 680 to 1,040 nm). These different cell lines, MCF10A, AU565 (HER2 positive breast cancer), T47D (estrogen receptor positive breast cancer), and MDA-MB-231 (triple-negative breast cancer), have been shown to exhibit markedly different metabolic states, as reported by NADH ${\tau }_M$ (41). Additionally, the cells were exposed to 2.5 mM of Na cyanide (NaCN), which is a well-known inhibitor of many metabolic processes leading to reduced NADH ${\tau }_M$ (41). FLIM acquisition was performed prior to exposure and after 30-min incubation of live cells with NaCN. The FLIM NADH ${\tau }_M$ images for each case are provided in Fig. 2, both for FLI-Net and for SPCImage. A visual inspection of these images shows that FLI-Net and SPCImage provide strikingly similar results. The descriptive statistics of NADH ${\tau }_M$ of SPCImage versus FLI-Net for each case are summarized in Fig. 2 I–L. The excellent concordance between the 2 analytic frameworks is highlighted in Fig. 2K by very high coefficients of determination (R² ∈ [0.985]) and a low P value (P < 1e-5). Additionally, we provide the SSIM between FLI-Net and SPCImage in Fig. 2L and SI Appendix, Fig. S6. The SSIM values indicate an excellent spatial congruence between FLI-Net and SPCImage in all cases, with the lowest measured value obtained for MDA-MB-231 cells treated with NaCN ($\overline{SSIM}=0.87$).

Fig. 2.

Visible FLIM microscopy of NADH. (A–H) Representative maps of NADH ${\tau }_M$ obtained with the commercial software SPCImage (A–D) and FLI-Net (E–H). (I and J) Averaged NADH ${\tau }_M$ values obtained across all FLIM data using both techniques. Error bars are SD, n = 3. (K) Linear regression with corresponding 95% confidence band (gray shading) of averaged NADH ${\tau }_M$ values from all cell lines pre- and postexposure to NaCN obtained via SPCImage and our DNN (slope = 1.01 (SE = 0.05); P < 1e-5; intercept = −6.9e-3 (SE = 4.2e-2); R² = 0.985); n = 3. (L) SSIM measurements for all NADH ${\tau }_M$ images. NaCN-treated cells are notated with an asterisk. Error bars are SD with n = 3. Further metrics of note (MSE; comparisons are different spatial binning, etc.) are included in SI Appendix, SI Text.

Ligand–receptor engagement.

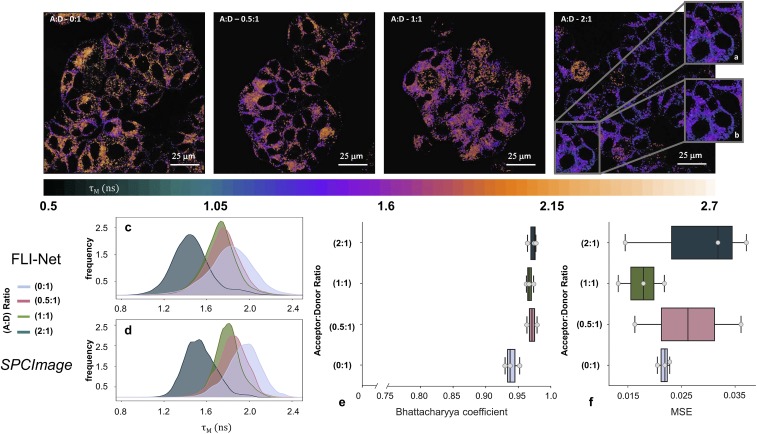
FRET is widely used in fluorescence microscopy to assay the proximity between fluorophore-labeled proteins at the nanometer range (2 to 10 nm) (42–44). FLI quantifies FRET occurrence by estimating the reduction of the fluorescence lifetime of the donor fluorophore when in close proximity to the acceptor fluorophores. When applied to receptor–ligand systems, FRET occurs when donor-labeled and acceptor-labeled ligands/antibodies bind to dimerized or cross-linked receptors (42, 45, 46) Hence, FLI FRET acts as a direct reporter of receptor engagement and internalization via the measurement of the fraction of labeled-donor entity undergoing binding to its respective receptor and subsequent endocytic internalization (13, 19, 47). Here, FLIM-FRET is performed by quantifying the reduction in the donor ${\tau }_M$ associated with FRET quenching (13, 47–49). Visible FLI FRET microscopy data were collected using a Zeiss LSM 510 equipped with an HPM-100-40 high-speed hybrid FLIM detector (GaAS 300 to 730 nm; Becker & Hickl) and a Ti:Sa laser (Chameleon) [apparatus, fluorescence labeling, and data acquisition details are described elsewhere (50)]. T47D human breast cancer cells were incubated with Tf-Alexa Fluor 488 (Tf-AF488) and Tf-AF555 visible FRET pair with a range of acceptor:donor (A:D) ratios from 0:1 to 2:1. As the A:D ratio increases, it is expected that FRET occurrence increases with the donor ${\tau }_M$ decreasing accordingly. The ${\tau }_M\text{s}$ for each condition as estimated via FLI-Net are provided in Fig. 3, Upper. In all cases, the ${\tau }_M\text{s}$ follow the decreasing trend expected as the A:D ratio increases as seen in SI Appendix, Fig. S7. Both FLI-Net and SPCImage analysis confirm this mechanistic behavior (further metrics and illustration provided in SI Appendix, Figs. S7–S9). However, in such experimental settings, it is not possible to know exactly what should be the true value of the ${\tau }_M$ parameter. Importantly, during SPCImage processing flow, a few parameters need to be user selected for optimal performances. Such user-dependent parameters can lead to relatively different ${\tau }_M$ estimations (see SI Appendix, Figs. S10 and S11 for examples). Hence, in such conditions we are limited to assess only whether FLI-Net provides similar results to SPCImage. In this regard, Fig. 3 C and D reports the respective distribution of estimated ${\tau }_M\text{s}.$ For the 4 A:D ratios tested, the mean-lifetime distributions are in reasonably high agreement between FLI-Net and SPCImage—with probability distribution maximum values shifted by less than 150 ps downward compared to SPCImage in the most different distributions. Furthermore, the Bhattacharyya coefficient (BC) was computed to measure the similarity of each paired probability distribution. As displayed in Fig. 3E (further discussed in Materials and Methods), the BCs are all very close to ≅1, indicating that FLI-Net and SPCImage provide similar ${\tau }_M$ distributions for all cases. Additionally, we computed the MSE to assess spatial congruency between the 2 postprocessing methods. As reported in Fig. 3F, the MSE values are low, indicating a good pixel–pixel correspondence. Overall, these results demonstrate that FLI-Net provides similar results to SPCImage although without the potential bias induced by user-defined parameters as in SPCImage.

Fig. 3.

Visible FLIM microscopy data. (Top) T47D human breast cancer cells were incubated with different A:D ratios of Tf-AF488 (donor, D) and Tf-AF555 (acceptor, A) for 1 h. FLI signal is reduced due to the occurrence of FRET when Tf-AF488 and Tf-AF555 bind to their respective receptor at the plasma membrane as well as during subsequent internalization of the receptor–ligand complexes. Shown are representative ${\tau }_M$ maps obtained via FLI-Net using T47D cells containing Tf-AF488 (A:D = 0:1; negative control) or different donor:acceptor ratios of Tf-AF488 and Tf-AF555 (0.5:1, 1:1, and 2:1). (A and B) Representative ROI comparison between FLI-Net (A) and SPCImage (B). (Bottom) (C and D) Distribution histograms of ${\tau }_M$ obtained via FLI-Net compared to SPCImage. (E and F) Bhattacharyya coefficient and MSE were calculated for whole images at each A:D ratio. Error bars are SD with n = 3. Further metrics of note are included in SI Appendix, SI Text (SI Appendix, Figs. S7–S9).

Beyond the quantitative and spatial accuracy of FLI-Net as demonstrated by its benchmarking against SPCImage, we compared its computational speed versus SPCImage on the same computational platform. The time required for analysis of each TCSPC voxel, which possessed 256 time points (visible FLIM) with a pixel resolution of 512 $\times$ 512, was just 2.5 s on average using our 3D CNN compared to ≅45 s with SPCImage. It is important to note that one input parameter of importance to SPCImage is the photon-count restrictions that lead to fitting only a small subset of the pixels in the input voxel, whereas FLI-Net processes the voxel’s entirety. Taking into account this embedded constraint under SPCImage, FLI-Net is ≅30 times faster than SPCImage per pixel processed (FLI-Net = 9.5e-3 ms per pixel; SPCImage = 0.28 ms per pixel). Note also that we have not focused herein on optimizing the computational efficiency of FLI-Net, and we expect even further gains in future iterations.

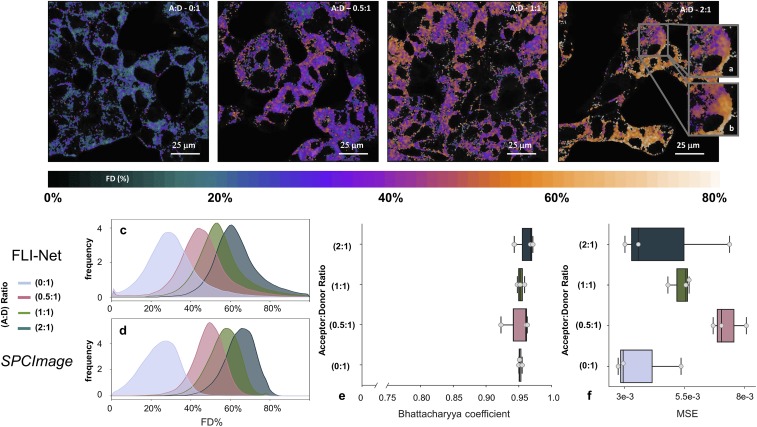
Visible FLIM takes advantage of the relatively large lifetimes of donor fluorophores in the visible range compared to the IRF temporal spread. This facilitates fitting methodologies as the IRF has minimal impact on the quantification accuracy. However, with the impetus of translating optical molecular imaging to deep tissue imaging, great efforts have been deployed over the last 2 decades to develop NIR dyes. Yet, NIR dyes are typically characterized by shorter lifetimes that can be of the order of the IRF full width at half-maximum (FWHM), rendering FLI quantification far more challenging; for example, whereas Tf-AF488 conjugates have a lifetime ≅2.5 ns, Tf-AF700 shows a donor lifetime of 1 ns, which reduces to <300 ps when undergoing FRET events in the presence of acceptor Tf-AF750. NIR microscopy data collected using a Zeiss LSM 880 confocal microscope equipped with a NIR FLIM detector (apparatus, fluorescence labeling, and data acquisition details described here) (51) were used to further test FLI-Net’s robustness during in vitro NIR FLIM FRET analysis. T47D cells were incubated with Tf-AF700 and Tf-AF750 NIR FRET pairs with a range of A:D ratios from 0:1 to 2:1. For the NIR FRET analysis and especially its in vivo applications, the parameter of interest is the fractional amplitude A_R that reports on the fraction of donor undergoing FRET (FD% or $A_R$) (42). In Fig. 4, Upper, the estimated FD% was determined using FLI-Net (the corresponding SPCImage images are shown in SI Appendix, Fig. S12, along with additional SSIM image-to-image quantification in SI Appendix, Fig. S13). As expected, as the A:D ratios increase, the FD% increases as well, as described previously (SI Appendix, Fig. S14) (19, 47). Moreover, FLI-Net results, as in the previous FLIM examples, are in good agreement both spatially and quantitatively with SPCImage results as evidenced with BCs close to ≅1 and very low MSE for all A:D ratios (Fig. 4 C and D). Finally, FLI-Net is ≅30 times faster than SPCImage per pixel processed (FLI-Net = 6.8e-3 ms per pixel; SPCImage = 0.21 ms per pixel). Even in the challenging case of NIR dyes with short lifetimes, FLI-Net shows remarkable speed and good precision in measuring FRET signal indicative of receptor engagement in cancer cells.

Fig. 4.

NIR TCSPC FLIM microscopy data. (Top) Representative FRET FD% maps obtained via FLI-Net using T47D cells containing Tf-AF700 (A:D = 0:1) or A:D ratios of Tf-AF700 and Tf-AF750 (0.5:1, 1:1, and 2:1). Cells were treated similarly to those in Fig. 3 using differently labeled Tf molecules. (A and B) Example ROI comparison between FLI-Net (A) and SPCImage (B). (Bottom) (C and D) FD% distribution overlays for both techniques. (E and F) Bhattacharyya coefficient and MSE were calculated for whole images at each A:D ratio. Error bars are SD with n = 3. Further metrics of note are included in SI Appendix, SI Text (SI Appendix, Figs. S12–S14).

MFLI

Another important application of FLI is to the imaging of tissues at the macroscopic scale (MFLI). The applications hence range from high-throughput in vitro imaging (52) to ex vivo (53) or in vivo tissue imaging (54) for diagnostics, within the framework of optical guided surgery (55), and preclinical studies (43). Particularly, there is great interest in employing NIR MFLI as in this spectral window the background fluorescence is reduced, and deep tissue imaging can be performed with high sensitivity. The technology of choice to perform MFLI is gated ICCD as it provides fast acquisition speeds over a large field of view. As a tradeoff, MFLI does not provide the efficiency of TCSPC collection and is characterized by IRF of the size of the gate employed (typically 300 ps or above). Hence, quantification of lifetime-based quantities can be very challenging. To demonstrate the potential of FLI-Net for MFLI based on gated ICCD (and hence its potential for wide-field FLI applications), its performance was evaluated in 2 settings: multiwell plate imaging with concentration-controlled mixtures of 2 NIR dye mixtures and dynamic NIR-FRET in vivo imaging in live intact, small animals.

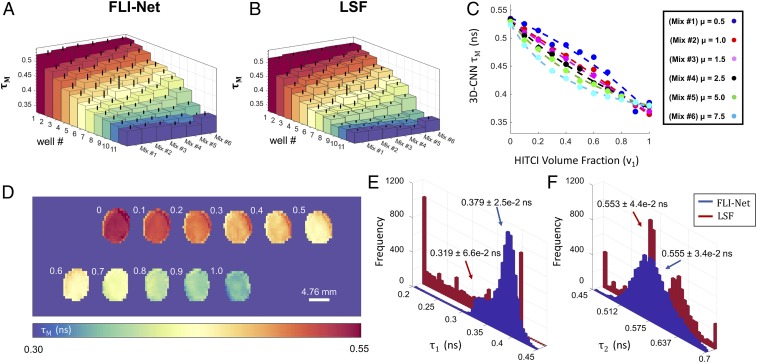
A series of MFLI data acquired from multiwell plates, each containing a volumetric fraction of 2 fluorescent dyes prepared as further described in Materials and Methods and SI Appendix, Tables S2 and S3 and in ref. 19, were used as a highly sensitive test of FLI-Net’s capability to quantitatively retrieve accurate lifetimes and fractional amplitudes in controlled settings (ranging from mono- to biexponential). Each TPSF was captured with a time-gated, wide-field MFLI apparatus described in detail elsewhere (50). Fig. 5 illustrates a sensitive comparison of FLI-Net with an LSF approach implemented in MATLAB (further described in Materials and Methods). For a one-to-one comparison, the range of ${\tau }_1$ and ${\tau }_2$ values used for TPSF generation to train the network was set to the bounds chosen for the LSF fitting. The summary of the quantification of the 2 dye lifetimes (${\tau }_1,{\tau }_2$), as well as the ${\tau }_M$ associated with the different dye ratios, for both FLI-Net and LSF is provided in Fig. 5 A and B for FLI-Net and Fig. 5 E and F for LSF. As reported, the mean ${\tau }_M$ values are in excellent agreement between LSF and FLI-Net. Similarly, the trends exhibited for ${\tau }_M$ not only follow the expected trendline but also are in agreement between the 2 estimation techniques. Note that in all cases, FLI-Net provides lifetime distributions that are centered around a single value with a relative narrow spread conversely to LSF (Fig. 5 E and F). To further highlight the mechanistic trend in ${\tau }_M$ as associated with the series of mixtures of ATTO 740 and 1,1′,3,3,3′,3′-hexamethylindotricarbocyanine iodide (HITCI), we report in Fig. 5C the FLI-Net predicted ${\tau }_M$ versus the variable volume fraction ν₁ of HITCI, ν₁ = 0, 0.1, …, 0.9, 1 and an initial concentration ratio μ = [HITCI]₀/[A740]₀ given in the key. Based on this approach, as described in Materials and Methods and SI Appendix, SI Text, it is possible to recover a value corresponding to a ratio of parameters inherent to the fluorescent species of both dyes used for the mixture based on ${\tau }_M$ as described by the linear dependence reported in SI Appendix, Figs. S15 and S16 (see ref. 19 for more details). Additionally, we provide in SI Appendix, Fig. S17 the results of ${\tau }_M$ estimation for AF700 in a different buffer mixture of PBS and ethanol (SI Appendix, Table S4 and in agreement with results in ref. 19). Such experiments demonstrate the stability of FLI-Net predictions over numerous consecutive measurements but also its ability to monitor dynamical MFLI events with accuracy even in the case of expected monolifetimes (SI Appendix, Tables S5 and S6 and Fig. S18).

Fig. 5.

Comparison of FLI-Net with LSF using MFLI of NIR dyes possessing a subnanosecond lifetime. (A and B) Mean-lifetime values obtained through MFLI of 6 dye mixtures (D) containing various volumetric fractions of 2 NIR dyes: HITCI and ATTO 740 in PBS buffer—both of which are excited at 740 nm and emit around 770 nm (further details given in SI Appendix) (19). Each of the 6 mixtures given corresponds to a differing initial volumetric fraction of the 2 fluorescent species used (µ = HITCI₀/ATTO₀) and thus a differing mechanistic trend. The values obtained from the DNN (A and C) illustrate a similar ${\tau }_M$ trend to that of the least-squares fit (B) but possess a histogram distribution that is significantly more centralized for both ${\mathit{\tau }}_1$ (E) and ${\mathit{\tau }}_2$ (F). Concentrations and ratios as well as fluorescent dye volumes used for preparation of each well-plate dataset are described in SI Appendix, Tables S2 and S3.

In Vivo Dynamical Lifetime-Based Imaging.

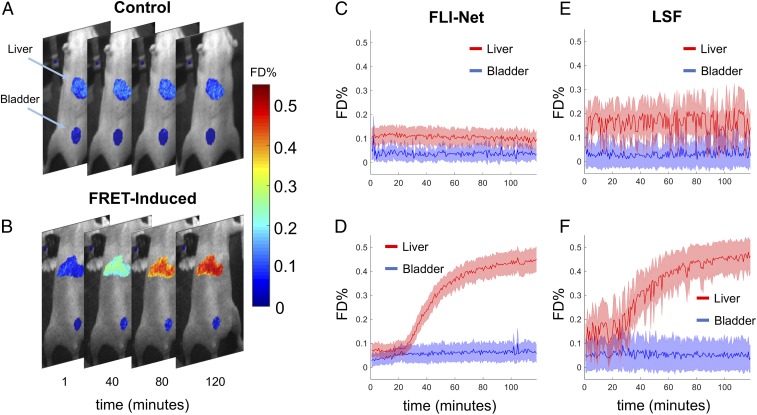
To demonstrate the applicability of FLI-Net in a dynamic setting, we performed in vivo NIR FRET imaging in live and intact small animals. As demonstrated in previous studies (47), the occurrence of FRET reports on the binding of receptor–ligand complexes (target engagement) noninvasively using the Tf-Tf receptor (TfR) system. The NIR-Tf probes label the liver, as a major site of iron homeostasis regulation displaying higher levels of TfR expression. In contrast, the urinary bladder is labeled via its role as an excretion organ due to the accumulation of free dye or small labeled peptides as degradation products (13). A total of 170 MFLI data were acquired over a 2-h time span. Each frame consisted of 256-pixel $\times$ 320-pixel $\times$ 160 time gates. An experiment with a delayed injection of the acceptor compared to the donor at A:D ratio of 2:1 was performed (donor, Tf-AF700; and acceptor, Tf-AF750) as well as a FRET negative control in which only donor was injected (A:D = 0:1; SI Appendix, Fig. S19 provided for further clarity). Fig. 6 A and B reports on the spatially resolved FRET donor fraction (FD% or $A_R$) as estimated via FLI-Net for a few frames and for the abovementioned 2 conditions. In all cases, the 2 main organs of interest, the liver and the bladder, are well resolved. Additionally, we provide the time trace of FD% over the whole 170 frames as computed for the liver and bladder regions of interest (ROIs), both for FLI-Net and for LSF, in Fig. 6 C–F. As expected, the FD% is reduced throughout the imaging period in the bladder as no TfR-Tf binding occurs, while the FD% increases sharply in the liver at A:D ratio of 2:1 due to abundant TfR expression and therefore increased NIR-labeled Tf binding and internalization in this organ. Such results are in accordance with our previous studies using the same biological system (47). Of importance, FLI-Net provided a smoother mean FD% estimate over the organs with lower average SD $\left(\mathrm{\sigma }=\left({\mathrm{\sigma }}_{\mathrm{liver}},{\mathrm{\sigma }}_{\mathrm{bladder}}\right)\right)$ across all frames $\left(\mathrm{LSF}:\left[{\mathrm{\sigma }}_{\mathrm{FRET}}=\left(0.066,0.082\right),{\mathrm{\sigma }}_{\mathrm{control}}=\left(0.058,0.085\right)\right]\right)$ (FLI-Net: $\left[{\mathrm{\sigma }}_{\mathrm{FRET}}=\left(0.037,0.041\right),{\mathrm{\sigma }}_{\mathrm{control}}=\left(0.032,0.036\right)\right])$. Additionally, at the onset of the experiments, at which time point only the donor has been injected in the animal and hence no FRET can occur, the baselines of FD% in the liver and bladder are similar (as expected) as estimated using FLI-Net conversely to the LSF estimates. Finally, FLI-Net demonstrated these remarkable performances at speeds readily employable for real-time use, ≅80 ms per voxel versus ≅7.5 $\times$ 10⁶ ms per voxel with assistance of a binary mask for the LSF.

Fig. 6.

Dynamical MFLI FRET performed over a 2-h time span in live intact mice. (A and B) Four equally spaced (in-time) MFLI-FRET image overlays obtained from 2 mice: tail-vein injected Tf-AF700 (donor-only control), control (A); and tail-vain injected Tf-AF700 (donor) followed 20 min later by injection of Tf-AF750 (acceptor), FRET induced (B). Imaging was performed over a time span of ∼2 h after Tf-AF700 injection (further detailed in SI Appendix, SI Text and Fig. S19. (C–F) comparison of LSF versus FLI-Net results for FD% (∝ Tf-TfR engagement). The shaded region associated with each curve corresponds to the SD of all values obtained for both the liver and urinary bladder at each time point. The computation time required for the LSF was >2 h using only the masked regions (liver and urinary bladder), whereas FLI-Net produced all ∼170 parameter maps, using the entire 256- $\times$ 320-pixel acquisition, in <14 s (∼80 ms per voxel).

Discussion

FLI imaging is a popular technique that enables accurate probe quantification in biological tissues, revealing unique information of great value for the biomedical community. To derive the lifetime-based quantities, model-based methodologies or graphical approaches have been proposed but they rely on relatively complex inverse formulation, may necessitate calibration samples, and/or may need to be adapted to the application investigated and instrumentation employed. In contrast, DL methodologies can deliver fast and parameter-free processing performances. Our proposed 3D CNN architecture, as well as training methodology, offers the potential of a generalized tool for fast, parameter/fit- free, quantitative FLI imaging for a wide range of applications and technologies. Especially, our methodology is centered on model-based learning that is efficient, robust, and accurate. As the training set corresponds to spatially resolved and time-resolved synthetic data, one can generate datasets over large lifetime ranges, such as in visible FLIM microscopy, and replicate typical signal-to-noise ratios encountered in biological application by controlling the photon-count levels. Such an approach avoids the need to acquire massive training datasets experimentally and can encompass numerous applications and/or technologies.

In this work, this model-based approach was leveraged to train FLI-Net based on typical experiments encountered in the field, including FLIM in the NIR and visible spectra and NIR MFLI wide-field in vivo imaging. For each case, the network was trained over a large range of potential parameters that were beyond the one expected in the designed experiments. Based on the in silico study, in which ground-truth parameters can be ascertained, we can establish that FLI-Net was accurate and robust in estimating lifetime-based parameters in the cases of both mono- and biexponential decays without setting any parameters. For instance, in the case of extreme fractional amplitudes (A_R ∈ [0 to 0.05] or A_R∈ [0.95 to 1]), FLI-Net exhibited small absolute errors in lifetime estimation conversely to LSF (SI Appendix, Fig. S18). However, as no ground truth can be obtained in such experimental settings, when benchmarking it against commonly employed fitting software, e.g., SPCImage, we could report and comment only on expected values and mechanistic trends. In all experiments, FLI-Net provided quantities that were in agreement with the expected biological outcomes. For instance, FLI-Net was able to clearly discriminate between noncancerous and cancerous cells, as well as between different types of cancer cells (AU565 and T47D vs. MDA-MB-231). In contrast to SPCImage, FLI-Net reported on a significant difference between the ${\tau }_M$ of untreated and Na cyanide-treated cells across all cell types (Fig. 2I). In the case of the cell line AU565, SPCImage quantified an increase in metabolic status after Na cyanide exposure conversely to FLI-Net and the expected effect of this metabolic inhibitor. Such results can further highlight the benefit of methodologies that do not require intrinsic calibration or user-defined parameter settings. To further emphasize this point, we provide an illustration of how a slight variation in the chosen tau initialization (SI Appendix, Fig. S10) or the choice of pixel used in the lifetime calibration routine (SI Appendix, Fig. S11) will alter the resulting distributions via SPCImage analysis. Therefore, since FLI-Net considers all pixels in the image without a priori assumptions, the wider ranges for FD% determined for both visible and NIR FLIM FRET when using FLI-Net may indicate cell environment effects on FLI measurements, which may be overlooked when using user-biased approaches that include ROI or pixel selections.

Such findings in the microscopic settings are also confirmed in the preclinical studies in which the FRET FD% prior to the delayed injection of the acceptor was in accordance with expectation for FLI-Net but overestimated when using LSF in the case of the liver. Moreover, it is important to note that FLI methodologies are well known to perform poorly in the cases of low p.c. This was also a fundamental limitation in a previous study proposing to use a basic artificial neural network (ANN), ANN-FLIM (44) that was not able to retrieve the lifetime-based parameters in all cases, especially with low p.c. Conversely, FLI-Net produced a robust estimate in such conditions as reported in the in silico study (Fig. 1D and SI Appendix, Fig. S4) and in an experimental study in which various concentrations and laser illumination powers were employed (SI Appendix, Fig. S20 with in silico equivalent in SI Appendix, Fig. S21). Such low p.c. (p.c._low ∈ [25,100]) are far below the ones typically reported for the reliable analysis of multiexponential decays (56–59) but not uncommon in biological applications. In such cases, it is customary to employ relatively large spatial binning to enable robust lifetime imaging at the cost of a decrease in spatial resolution. Indeed, herein, to obtain robust quantification via SPCImage, relatively large binning (SI Appendix, Fig. S22) was required whereas FLI-Net performs well at low levels of spatial binning (SI Appendix, Fig. S23).

Beyond enabling quantitative FLI imaging requiring user parameter input, a distinct advantage of FLI-Net, similar to the phasor approach (19), is its ability to estimate the lifetime-based parameters for a whole image at once. This is a step toward enabling the application of FLI to monitor a dynamical process and/or for clinical applications. Monitoring such a dynamical process with accuracy was demonstrated both in vitro and in vivo. Indeed, FLI-Net can process live animal MFLI quantification at speeds necessary for real-time application (≅80 ms per voxel). Hence, DL-based approaches such as the 3D-CNN presented are well positioned to profoundly impact clinical applications such as fluorescence-guided surgery or preclinical high-throughput drug screening experiments. In this context, FLI is expected to play a major role either by providing unique contrast mechanisms such as in pH-transistor-like probes (55) or by improving sensitivity for current clinically approved dyes (43). However, to date, wide-field FLI imaging formation has not been attainable at a speed relevant to current clinical practice, but perhaps FLI-Net can greatly assist in overcoming this important barrier for clinical translation.

Still, our current implementation and methodology suffer from a few shortcomings. First, as for any DL approach, the computational time to create the model-based synthetic datasets and to train the network does not allow us to produce a newly trained network on the fly. Herein, the time required to generate 10,000 TPSF voxels and subsequently train the CNN for 500 epochs was on average, 4.5 h (1 h and 3.5 h, respectively). Hence, if some experimental parameters are outside the range of the training set, a few hours can be necessary to obtain an appropriate trained network. Although, as demonstrated herein, FLI-Net can be trained over a wide parameter space such that experiments with different fluorophores and settings, i.e., in the metabolic and visible FRET imaging, can still be processed using the same trained network. Hence, we envision that a few single-trained networks, let us say for visible FLIM (Figs. 2 and 3) or NIR MFLI (Fig. 6 and SI Appendix, Figs. S17, S20, S24, and S25B), could be made available for the user to select the proper one. Additionally, the user could still have access to current tools including fitting or phasor approach for validation. Note also that the computational times reported herein are for the generation and training ab initio. Transfer learning of one trained network to another should reduce significantly the required training time. However, it is still possible that experimental data could contain values outside the range of the training set. We provide in SI Appendix, Fig. S25 such a case in which a MFLI-FRET well-plate sample was processed using FLI-Net trained with data possessing lifetime bounds largely outside of the known values. In such a case, FLI-Net reported biased quantification of lifetime but still provided the expected trend in concordance with LSF in which the parameter space was bounded to the same values used during training.

Beyond the topical application of fit-free FLI, the overall architecture of FLI-Net and the associated training methodology have potential for application across a myriad of biomedical imaging techniques that currently utilize a least-squares model-based fit for parameter extraction. It is common for many of these techniques to cite speed as a main hurdle they have yet to overcome for successful adoption into the clinical or commercial realm. We believe that this work provides ample supporting information and a robust proof of concept for similar adaptation and implementation in projects regarding analytic optimization across the field.

Materials and Methods

FLI-Net Architecture and Training Methodology.

The FLI-Net architecture consists of 2 main parts: 1) a shared branch focused on spatially independent temporal feature extraction and 2) a subsequent 3-junction split for independent reconstruction of ${\tau }_1,$ ${\tau }_2,$ and $A_R$ images simultaneously. Within the shared branch, spatially independent convolutions along time (illustrated in SI Appendix, Fig. S1 as the blue rectangular prism with kernel size of (1 $\times$ 1$\times$ 10)) were set as the network’s first layer to maximize TPSF feature extraction. A corresponding stride of k = (1,1,5), used initially to reduce parameter count and increase computational speed, resulted in no observable decrease in performance. A residual block, possessing a kernel size of (1 $\times$ 1 $\times$ 5), followed immediately afterward to further extract time-domain information.

To ultimately obtain image reconstruction of size (x $\times$ y) via a sequence of down-sampling, a transformation from 4D to 3D was required. Thus, after the 3D-residual block (output of x $\times$ y $\times$ n $\times$50) the tensor was reshaped to dimension (x $\times$ y $\times$ (n $\times$ 50)), where n corresponds to a scalar value dependent on the number of TPSF time points as well as the chosen network hyperparameters. This value can be determined via the expressions

$$P=\frac{F_{L0}}{2}\left(n_{TP}\%S\right)$$ [3]

$$n=\left(\left(n_{TP}-F_{L0}+P\right)/S+1\right),$$ [4]

where $n_{TP},$ P, $F_{L0},$ and S denote the number of time points, padding (obtained through Eq. 3), filter length along the temporal direction of the first 3D-convolutional layer (length of 10 in this study), and the corresponding stride value used in the first convolutional layer (value of 5 in this study), respectively. After this transformation, a convolutional layer of size (1 $\times$ 1) possessing 256 filters along with a subsequent residual block couplet possessing size (1 $\times$ 1) was employed before the trireconstruction junction. The (1 $\times$ 1) size of these 2D convolutional filters proved crucial in maintaining spatially independent feature extraction.

FLI-Net was written and trained using the machine-learning library Keras (60) with Tensorflow (61) backend in python. A total of 10,000 TPSFS voxels were used during training (8,000) and validation (2,000), along with a batch size dependent on the target input length along time (32 for NIR, 20 for visible). MSE was set as the loss function for each branch. The RMSprop (62) optimizer was used with an initial learning rate set to 1e-6. The network was normally trained for 250 epochs using a NVIDIA TITAN Xp GPU. This training time varied slightly depending on TPSF length, ranging between 50 s and 80 s per epoch (for voxels possessing 160 and 256 time points, respectively).

Generation of the Simulation Data.

For every training sample, an MNIST (63) binary image was chosen at random and every nonzero pixel was assigned a value of intensity (I), short lifetime (${\tau }_1$), long lifetime (${\tau }_2$), and fractional amplitude ($A_R$) (SI Appendix, Fig. S2A). These values at each pixel, along with a randomly selected IRF (an example of which is given in SI Appendix, Fig. S2B as the pink dashed line), were subsequently used in the generation of each TPSF $\left(\mathrm{\Gamma }\left(t\right)\right)$ via Eq. 1 discussed previously (FLI-Net Architecture, Training, and Validation). Further information can be found in SI Appendix and example MATLAB script in the GitHub repository (64).

Each TPSF was normalized to a maximum intensity value of one in the last step.

Preprocessing of Gated-ICCD Data.

It is common for raw fluorescence time decay data to be represented initially at each time point using a separate TIFF image. Concatenation of these along the temporal axis along with a subsequent removal of pixels possessing maximum photon counts of less than 250 was performed before the use of a Savitzky–Golay filter (65) (length 5, third order) The effect of dark noise was removed via subtraction with the mean value of time points 1 to 10 (before the IRF begins ascent). Afterward, each value was normalized to one by division with its maximum value.

Use of the Savitzky–Golay filter or a filter that preserves the slope of the TPSF’s ascent while also having no broadening effect on the curve (as is the case with Gaussian or moving average filters) was essential for analysis of the mouse data given FLI-Net sensitivity along time. SI Appendix, Fig. S5 further illustrates this reasoning.

Preprocessing of TCSPC Microscopy Data.

Given that the TCSPC microscopy data possessed significantly lower photon counts spatially relative to MFLI, local neighborhood binning was employed. The SPCImage software’s preprocessing technique involves performing this binning, along with discounting any pixels possessing a maximum photon count below a specific threshold, at every pixel before fitting (32). This processing sequence was replicated for FLI-Net datasets. A maximum photon count threshold was placed initially (normally at 3 or 4), directly followed by a local neighborhood binning (7 × 7 kernel). Unlike with the processing of the gated-ICCD data, a Savitzky–Golay filter was not employed prior to FLIM analysis.

NADH FLIM In Vitro.

All cell lines were obtained from ATCC and cultured in respective media at 37 °C and 5% CO₂. T47D and MDA-MB231 cells were grown in DMEM (Life Technologies) supplemented with 10% FBS (ATCC), 4 mM  l-glutamine (Life Technologies), and 10 mM Hepes (Sigma). AU565 cells were cultured in RPMI medium (Life Technologies) supplemented with 10% FBS and 10 mM Hepes. MCF10A cells were cultured in DMEM/F12 medium (Life Technologies) supplemented with 5% horse serum (Life Technologies), 20 ng/mL EGF (Peprotech), 0.5 mg/mL hydrocortisone (Sigma), 10 μg/mL bovine insulin (Sigma), 100 ng/mL cholera toxin (Sigma), and 50 units/mL penicillin per 50 μg/mL streptomycin (Life Technologies). For the imaging experiment, the cells were plated on MatTec 35-mm glass bottom plates at 400,000 cells per plate, cultured overnight in corresponding phenol red-free complete medium, and imaged in the same medium. In parallel, cells were incubated for 30 min with 2.5 mM NaCN in complete medium for metabolic inhibition. The FLIM imaging of NADH autofluorescence emission was performed using the Becker & Hickl HPM-100-40 detector which was attached to the NDD port on the LSM 880 using a Zeiss T-adapter that contained a 680-nm SP blocking filter (Semrock FF01-680-/SP-25 blocking edge multiphoton short-pass filter) followed by a 440/40 BP (Semrock FF01-440/40-25 single-band pass filter) at a spectral range of 420 to 460 nm. Excitation was 730 nm. The pixel dwell time was 2.58 μs and the voxel size was 512 × 512 pixels. The emission was collected for 60 s.

Visible FLIM-FRET In Vitro.

T47D cells were plated on MatTec 35-mm glass bottom plates as described above and cultured overnight. After that cells were washed with HBSS buffer and incubated for 30 min in DHB imaging medium (phenol red-free DMEM, 5 mg/mL BSA [Sigma], 4 mM l-glutamine, 20 mM Hepes [Sigma], pH 7.4) to deplete native transferrin followed by 1-h uptake of holo (iron-loaded) Tf-AF488 and Tf-AF555 (Life Technologies) with various acceptor:donor ratios in DHB solution, keeping the Tf-AF488 concentration of 20 μg/mL constant. The uptake was terminated by washing with phosphate-buffered saline and fixing in 4% paraformaldehyde. The images were acquired on a Zeiss LSM 510 equipped with a FLIM detector as described previously (66).

NIR FLIM-FRET In Vitro.

Human holo Tf (Sigma) was conjugated to Alexa Fluor 700 or Alexa Fluor 750 (Life Technologies) through monoreactive N-hydroxysuccinimide ester to lysine residues in the presence of 100 mM Na bicarbonate, pH 8.3, according to manufacturer’s instructions. T47D cells were processed for Tf uptake in the same manner as described above. NIR FLIM FRET was performed on a Zeiss LSM 880 Airyscan NLO multiphoton confocal microscope using an HPM-100-40 high-speed hybrid FLIM detector (GaAs 300 to 730 nm; Becker & Hickl) and a Ti:Sa laser (680 to 1,040 nm with excitation set at 730 nm; Chameleon Ultra II, Coherent, Inc.). The Ti:Sa laser was used in conventional one-photon excitation mode. A Semrock FF01-716/40 bandpass filter and a FF01-715/LP blocking edge short-pass filter were inserted in the beamsplitter assembly to detect the emission from Alexa 700 and to block scattered light, respectively. The 80/20 beamsplitter in the internal beamsplitter wheel in the LSM 880 was used to direct the 690-nm excitation light to the sample and to pass the emission fluorescence to the FLIM detector.

NIR MFLI Well-Plate Series.

To test the sensitivity of FLI-Net for extracting biexponential parameters, we mixed 2 NIR dyes, ATTO740 (A740, 91394-1MG-F; Sigma-Aldrich) and HITCI (252034-100MG; Sigma-Aldrich) initially prepared in PBS at various initial concentrations (SI Appendix, Table S2). For each concentration pair, different volumes of both dyes were mixed to obtain a total volume of 300 μL with volume fractions ranging from 0 to 100% (10% steps; SI Appendix, Table S3).

Dynamic NIR MFLI-FRET In Vivo.

In these experiments, the dynamics of FRET were observed by injecting Tf probes labeled with donor and acceptor at different time points. For all experiments, athymic nude female mice (Charles River) were first anesthetized with isoflurane (EZ-SA800 System; E-Z Anesthesia), placed on the imaging stage, and fixed to the stage with surgical tape (3 M Micropore) to prevent motion. A warm air blower (Bair Hugger 50500; 3 M Corporation) was applied to maintain body temperature. The animals were monitored for respiratory rate, pain reflex, and discomfort. The mice were imaged with the time-gated imaging system in the reflectance geometry, with adaptive grayscale illumination to ensure the appropriate dynamic range between the regions of interest. In particular, excitation intensity had to be reduced in the urinary bladder due to accumulation of NIR-labeled Tf over time. Two hours after tail injection of 20 μg of Tf-AF700, the FRET-induced mouse was imaged for ∼15 min before retro-orbital injection with 40 μg of Tf-AF750 (A:D ratio 2:1). Imaging was continued for another 105 min. For the negative control mouse (0:1), no further probe was injected throughout the imaging session. SI Appendix, Fig. S19 is provided for further clarity. The time-resolved MFLI-FRET imaging system used in this study is described in detail elsewhere (50).

LSF Analysis.

The LSF implementation chosen for use was based around MATLAB’s function fmincon(). The lower and upper bounds of both lifetime values were for all cases chosen to match the bounds used in generation of the TPSF data voxels used in training our model (SI Appendix, Table S1). The exceptions to this include the use of monoexponential fitting during analysis of one NIR MFLI experiment illustrated below (SI Appendix, Fig. S17).

Bhattacharyya Coefficient.

Given that every in vitro dataset possessed a distribution of values postanalysis, the addition of a metric for comparison of these probability distributions between FLI-Net output and SPCImage’s was included. To measure the degree of overlap between distributions obtained through both techniques, the Bhattacharyya coefficient was employed. Given 2 continuous probability distributions M(x) and N(x), the Bhattacharyya coefficient is calculated as

$$BC\left(M,N\right)={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\sqrt{M\left(x\right)}\sqrt{N\left(x\right)}dx},$$ [5]

where, when M(x) = N(x), or the probability distributions overlap perfectly, the Bhattacharyya coefficient is equal to 1. The metric is explained in further depth elsewhere (67).

Data Availability.

All data discussed in this paper are available to readers. We have provided a public GitHub repository (64) for dissemination of relevant data and MATLAB/python script.