Adding tests to risk based guidelines: evaluating improvements in prediction for an intermediate risk group

Abstract

Using an additional test in patients who are not at high enough risk of developing disease to confidently treat, or low enough risk to confidently not treat would seem to be a straightforward way to resolve the clinical equipoise and is recommended by many guidelines. However, clear methods for evaluating the population utility of additional tests in this group have not been established. This paper includes worked examples and simulation data to show that focus on the intermediate risk group alone can be misleading and that population utility is best evaluated across the full range of risk.

Summary points

• Measures of prediction improvement in the intermediate risk group can be biased (non-zero) when there is no true relation between the new test and the outcome

• The impact of a new test on the intermediate risk group is best assessed in the context of the full population. This includes:

  • Estimation of the model in which the new test is evaluated in the full population rather than the intermediate risk group alone

  • Use of the full population to estimate the expected prediction improvement under the null

  • Presentation of both the observed and the expected prediction improvement, or a bias correction in the case of the net reclassification improvement, in the interpretation of the overall impact

• Consider a sample of the full population if a smaller study is necessary

Decisions about treatment attempt to best balance risks and benefits, with estimation of the risk of disease prior to treatment playing a critical role in that process at both the individual and the population level. Though there is rarely a perfect threshold of risk for action, guidelines in multiple settings have arrived at useful risk cut points to inform treatment decisions. These cut points often result in three implicit or explicit strata: risk high enough to confidently treat, risk low enough to confidently not treat, and those in between, or the “intermediate risk” group. Though at the individual level, this clinical equipoise may be resolved with a discussion between doctor and patient, from a guideline perspective, the recommendation might include subsequent testing that can appropriately reclassify people into a low risk or high risk stratum and improve prediction at a population level. However, in contrast with evaluating a new marker for inclusion in the overall risk model, the process for evaluating prediction improvement in the intermediate risk group is not well developed.

Case study: cardiovascular disease risk

Risk prediction is a widely discussed tool in the prevention of cardiovascular disease and treatment of related risk factors, such as cholesterol. Current guidelines estimate risk of future cardiovascular disease events, using a risk score such as QRISK2¹ or the pooled cohort equations,² to guide treatment decisions. The joint American College of Cardiology and American Heart Association guidelines on the treatment of cholesterol,³ use a threshold of 7.5% 10 year cardiovascular disease risk to identify a subset of high risk people who might benefit from statin treatment. They also implicitly create an intermediate risk stratum of people from 5% up to 7.5% 10 year risk for potential treatment and suggest that additional factors or tests, such as family history, C reactive protein level, or coronary artery calcium score might be considered as part of individual clinician-patient discussions and decision making. Similarly, the UK National Institute for Health and Care Excellence guidelines⁴ use a threshold of 10% 10 year risk to identify high risk people for treatment and direct clinicians to take additional factors or tests into account in treatment decisions when risk is near the threshold. The Joint British Societies’ consensus recommendations⁵ call for additional research specifically directed at how new markers perform in the intermediate risk group.

Consequently, studies of new markers and tests have focused on improving prediction in the intermediate risk population. Some have measured the new marker in the entire population and calculated a measure of improvement for the intermediate risk group alone (eg,⁶). Others have measured the new marker only in the intermediate risk group and based all analyses on that group alone (eg,⁷). There have also been trials randomizing people at intermediate risk to receive additional information, such as a genetic risk score.⁸

We propose a strategy for research and evaluation of new markers for the intermediate risk group (see box 1). These are illustrated using results of a simulation study based on cardiovascular disease risk, as well as an example using real data, to highlight the consequences of different analytic choices. Our results are based on the assumption that the association between the outcome and the new test is no different in the intermediate risk group from that in the full population.

Box 1: Proposed process

• Estimate new risk model including both new marker and traditional factors in full population and evaluate the coefficient for the new marker

• If significant, proceed to other measures of evaluation, including performance in intermediate risk group

• Present any evaluation of performance in intermediate risk group along with the expected value if there were no association to provide context

• Adjust for the expected value if conducting a test or estimating a net reclassification improvement

Example with a true association

Our first example, shown in table 1, uses a model without high density lipoprotein cholesterol as the existing score and evaluates high density lipoprotein cholesterol as a new marker in the Women’s Health Study (see box 2 for additional details). As outlined in our proposed method, the first step is to estimate a risk model that includes both the new marker and the components of the established score in the full population. In such nested models, the most efficient and reliable test of independent improvement in prediction is the coefficient for the new marker.⁹ We evaluate the coefficient for the natural log of high density lipoprotein cholesterol from the model, which is statistically significant (P<0.001) when calculated in the full data. If, instead, we had used only those participants in the intermediate risk group from the established model to estimate our model, the coefficient for high density lipoprotein cholesterol would not be significant (P=0.13), likely due to a smaller sample size as well as a more limited range for the predictor variables.

Table 1.

Prediction measures examining the effect of adding high density lipoprotein (HDL) cholesterol to cardiovascular disease risk models in the Women’s Health Study

Prediction measure	Models derived using full population		Models derived using intermediate risk group
Ln HDL coefficient (SE), P value	−1.0 (0.14), <0.001		−0.52 (0.34), 0.13
Measures for changes in prediction for intermediate risk group comparing model adding HDL to model without HDL
	Original	Expected under the null
Probability of a case moving up (95% CI)*	0.27 (0.18 to 0.37)	0.22	0.45 (0.35 to 0.56)
Probability of a non-case moving up (95% CI)*	0.20 (0.18 to 0.22)	0.17	0.28 (0.27 to 0.31)
Probability of a case moving down (95% CI)*	0.14 (0.09 to 0.23)	0.19	0.16 (0.10 to 0.26)
Probability of a non-case moving down (95% CI)*	0.27 (0.25 to 0.29)	0.29	0.25 (0.23 to 0.27)
Intermediate NRI (95% CI)†	0.20 (0.05 to 0.33)	0.15	0.25 (0.10 to 0.41)
Bias corrected	0.05 (−0.10 to 0.18)		NA
Reclassification calibration for model without HDL (P value)	6.7 (0.04)		6.8 (0.03)
Reclassification calibration for model with HDL (P value)	1.6 (0.5)		0.7 (0.7)

NA=not applicable; NRI=net reclassification improvement.

*Confidence intervals calculated using Agresti-Coull method.

†Confidence intervals calculated using bootstrap.

Box 2: Women’s Health Study example

• The Women’s Health Study is a longitudinal cohort of initially healthy women followed for incident cardiovascular disease.¹⁴ Participants provided informed consent and the study was approved by the institutional review board of Brigham and Women’s Hospital. The following risk factors for cardiovascular disease have been shown to be predictive in this population: age, blood pressure, total and high density lipoprotein cholesterol, hemoglobin A_1c if diabetic at baseline, smoking, C reactive protein, and family history of premature myocardial infarction¹⁵

• We used the 24 558 women (560 events) with complete data on risk factors and known cardiovascular disease status at eight years for two scenarios:

  • We compared a model with all risk factors except high density lipoprotein cholesterol (a known strong risk factor) with a complete model including high density lipoprotein cholesterol

  • We compared the model with all the risk factors including high density lipoprotein with one adding homocysteine (a historical candidate risk factor) using a similar framework

• The reclassification used the eight year equivalents (<4%, 4% to <6%, and ≥6%) of the joint American College of Cardiology and American Heart Association 10 year risk strata (<5%, 5% to <7.5%, ≥7.5%). Models were run using the entire dataset and then rerun only in the participants with predicted intermediate risk values using the initial model (without the new marker)

Given a significant coefficient, the next step is to examine additional measures of clinical utility. In light of our setting of established risk strata, with new tests being considered only for those at intermediate risk, we focus primarily on measures that incorporate these risk strata. For simplicity we also focus on binary events, where the outcome is known at a specific time point—for example, at 10 years—though many of the methods discussed have been extended to the setting of survival models.

One simple metric of change in prediction for the intermediate risk group is the probability of cases and non-cases being reassigned to the high risk or low risk groups, similar to the sensitivity and specificity of the new marker. In our example, adding high density lipoprotein to the model calculated using all the data, reclassified 27% of the initially intermediate risk cases over the threshold into high risk. However, it also reclassified 20% of the non-cases into the high risk group.

However, some movement would be expected even with a marker not associated with cardiovascular disease. Since the full range of data are available, a table of the expected changes in predicted risk if there were no association can be calculated and used to generate an estimate of the expected value for each of the prediction measures.¹⁰ We outline this method in figure 1. Now each measure can be compared with its expected value to obtain a clearer picture of the actual improvement, as shown in table 1. For the reclassification of cases to high risk, this comparison suggests that adding high density lipoprotein cholesterol to the model does reclassify more cases to the high risk stratum than expected, though the effect above chance is small (5%). Also, fewer cases than expected are reclassified to the low risk stratum. The observed movement is larger when the model is derived only in the intermediate risk group, and the expected movement then cannot be calculated.

Fig 1.

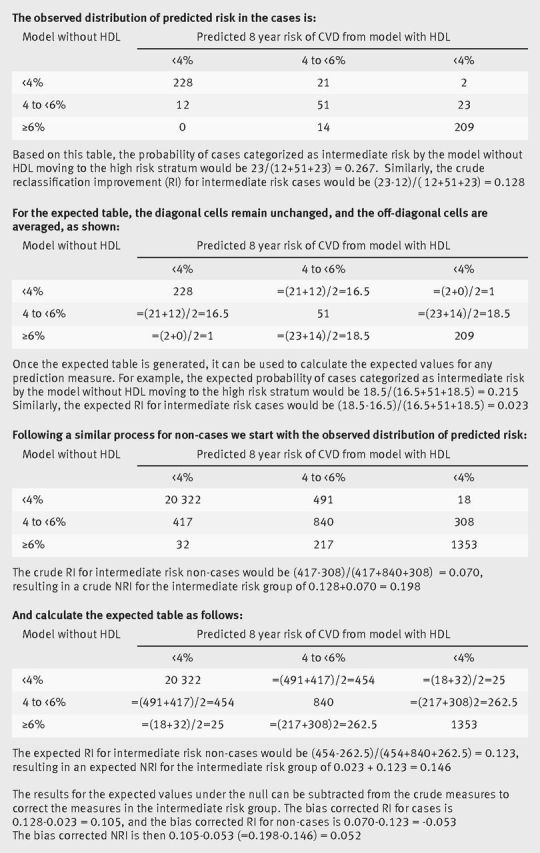
 Calculation of the expected table of predicted risk under the null for bias correction. The expected table is based on a symmetry assumption using the whole dataset and is constructed separately for the cases and controls. We use the high density lipoprotein cholesterol example in the Women’s Health Study to work through the process. HDL=high density lipoprotein; CVD=cardiovascular disease; NRI=net reclassification improvement; RI=reclassification improvement

The net reclassification improvement¹¹ summarizes whether cases have a higher probability of moving to a higher risk stratum than to a lower risk stratum and non-cases have a higher probability of moving to a lower risk stratum than to a higher risk stratum. The same strategy can be used among those who start at intermediate risk. While the expected value for the net reclassification improvement overall is 0 if there is no association we have previously shown that substantial bias may occur if the net reclassification improvement is calculated only for the intermediate group and not corrected using the method from figure 1.¹⁰ In the full data for high density lipoprotein cholesterol, the net reclassification improvement for the intermediate risk group alone has a 95% bootstrap confidence interval (0.05 to 0.33) that does not include 0, suggesting improvement in prediction. However, the 95% confidence interval for the bias corrected net reclassification improvement (observed minus expected) of (−0.10 to −0.18) does include 0, and the estimated effect is lower.

To compare the observed risk in each stratum to the average predicted risk, a reclassification calibration test can also be performed, with a significant P value suggesting a lack of fit.¹² Like the net reclassification improvement, it is usually performed on the whole table, but it can be computed in the intermediate risk subset. The regression calibration measures are also consistent with better fit in the model that includes high density lipoprotein cholesterol.

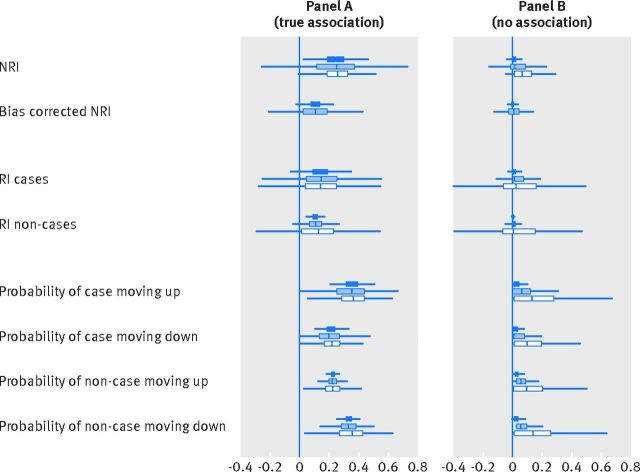
The corresponding simulation results are presented in figure 2, panel A, for a hypothetical new marker with an odds ratio of 2 for a 2 standard deviation difference. The supplemental appendix provides additional details about the simulations. The dark blue bars represent the distribution of the measures obtained if the risk model is estimated in the full population, while the white bars correspond to using only the intermediate risk group of the established score to estimate the risk model. To address the question of whether any difference is entirely due to sample size, as the intermediate risk group is inherently smaller than the full population from which it is derived, the light blue bar represents a random sample of the full population equivalent in size to the intermediate risk group, termed the scaled population. In general, the observed values are larger when the model is derived only in the intermediate risk group, where the expected values cannot be calculated.

Fig 2.

 Distribution of measures using cardiovascular disease cut points in a group at intermediate risk when the new marker has a true association (odds ratio of 2 for a 2 standard deviation difference) with the outcome (panel A) and no association (panel B). The boxes show the results when different populations are used to calculate the risk model with the new marker: dark blue boxes use the full population, light blue boxes use the scaled population (a random sample of the full population with the same number of participants as the intermediate risk population), and white boxes use the intermediate risk population as determined by the original model only. NRI=net reclassification improvement; RI=reclassification improvement

Example with no association

Our second example, shown in table 2, uses a model without homocysteine as the existing score and evaluates homocysteine as a new marker. In this example, the coefficient for homocysteine was not significant when the full population was used for model estimation or when only the group identified as intermediate risk by the established model was used. Though this confirms the importance of using the coefficient as the initial test of association, we present all the results for discussion. For all of the measures, estimates obtained from the models in the full population are consistent with the non-significant coefficient. However, the results are noticeably different when using the participants at intermediate risk for model development. In this situation, the probabilities of moving and the net reclassification improvement would suggest a large improvement, and expected values under the null cannot be calculated. Supplemental table 1 presents the full reclassification table for this example.

Table 2.

Prediction measures examining the effect of adding homocysteine to cardiovascular disease risk models in Women’s Health Study

Prediction measure	Models derived using full population		Models derived using intermediate risk group
Ln homocysteine coefficient (SE), P value	0.18 (0.11), 0.10		0.44 (0.28), 0.12
Measures for changes in prediction for the intermediate risk group comparing model adding homocysteine to model without homocysteine
	Original	Expected under the null
Probability of a case moving up (95% CI)*	0.03 (0.01 to 0.10)	0.05	0.36 (0.27 to 0.47)
Probability of a non-case moving up (95% CI)*	0.04 (0.03 to 0.05)	0.04	0.27 (0.25 to 0.30)
Probability of a case moving down (95% CI)*	0.06 (0.02 to 0.13)	0.05	0.08 (0.04 to 0.16)
Probability of a non-case moving down (95% CI)*	0.06 (0.05 to 0.07)	0.29	0.25 (0.23 to 0.27)
Intermediate NRI (95% CI)†	−0.01 (0.0 to 0.33)	0.06	0.20 (0.07 to 0.33)
Bias corrected	0.02 (−0.10 to 0.18)		NA
Reclassification calibration for model without homocysteine (P value)	1.2 (0.6)		7.5 (0.02)
Reclassification calibration for model with homocysteine (P value)	1.5 (0.5)		2.0 (0.4)

NA=not applicable; NRI=net reclassification improvement.

*Confidence intervals calculated using Agresti-Coull method.

†Confidence intervals calculated using bootstrap.

The corresponding simulation results are presented in figure 2, panel B, for a hypothetical new marker with an odds ratio of 1. Supplemental table 2 shows that the corresponding type 1 error rates are above 25% for the net reclassification improvement if the intermediate risk group is used for the model estimation, but that they are lower if the full population is used.

When symmetric cut points of half and twice the average risk in the population were used, all measures were less variable but the type 1 error rates were as high or higher, whereas correlations between the established factors and the new marker did not affect the results. Supplemental table 3 and the supplemental figures show these additional results.

Many other excellent measures of prediction exist, including the difference in the C statistic, the integrated discrimination improvement, and continuous net reclassification improvement, among others. These measures are an important part of the overall presentation and should be incorporated when evaluating the risk prediction performance of a new marker. In supplemental table 4 we have included our simulation results for the rate of type 1 errors for these measures when estimating the model with the new marker and the established risk factors in the intermediate risk group alone instead of the full population. Though the effect sizes are small, the rate of type 1 errors does increase if only the intermediate risk group is used for the integrated discrimination improvement and continuous net reclassification improvement, showing the same pattern as the categorical markers. The difference in the C statistic, on the other hand, is overly conservative in the intermediate group, as has been observed in other settings.¹³

Conclusions

Measures of model improvement may be biased when based just on the intermediate risk group. Recommendations for additional testing, even when the intermediate risk group is of primary interest, should be based on research conducted across the full spectrum of risk. This efficient design provides a more stable measure of improvement in the intermediate risk group when there is clinical justification for using the new test in the intermediate risk group only and the independent effect of the marker has been demonstrated. It also allows for reanalysis in response to changes in cut points as well as the possibility of exploring improvements in prediction in other groups. Additionally, the effect size of all prediction measures in the intermediate risk group should be presented in the context of the expected value under the null or bias corrected to avoid over-optimism.