Best Practices for Foundations in Molecular Simulations [Article v1.0]

Abstract

This document provides a starting point for approaching molecular simulations, guiding beginning practitioners to what issues they need to know about before and while starting their first simulations, and why those issues are so critical. This document makes no claims to provide an adequate introduction to the subject on its own. Instead, our goal is to help people know what issues are critical before beginning, and to provide references to good resources on those topics. We also provide a checklist of key issues to consider before and while setting up molecular simulations which may serve as a foundation for other best practices documents.

1. Introduction

Molecular simulation techniques play an important role in our quest to understand and predict the properties, structure, and function of molecular systems, and are a key tool as we seek to enable predictive molecular design. Simulation methods are useful for studying the structure and dynamics of complex systems that are too complicated for pen and paper theory, helping interpret experimental data in terms of molecular motions. Additionally, they are increasingly used for quantitative prediction of properties of use in molecular design and other applications [1–5].

The basic idea of any molecular simulation method is straightforward; a particle-based description of the system under investigation is constructed and then the system is propagated by either deterministic or probabilistic rules to generate a trajectory describing its evolution over the course of the simulation [6, 7]. Relevant properties can be calculated for each “snapshot” (a stored configuration of the system, also called a “frame”) and averaged over the entire trajectory to compute estimates of desired properties.

Depending on how the system is propagated, molecular simulation methods can be divided into two main categories: Molecular Dynamics (MD) and Monte Carlo (MC). With MD methods, the equations of motion are numerically integrated to generate a dynamical trajectory of the system. MD simulations can be used for investigating structural, dynamic, and thermodynamic properties of the system. With MC methods, probabilistic rules are used to generate a new configuration from the present configuration and this process is repeated to generate a sequence of states that can be used to calculate structural and thermodynamic properties but not dynamical properties; indeed, MC simulations lack any concept of time. Thus, the “dynamics” produced by an MC method are not the temporal dynamics of the system, but the ensemble of configurations that reflect those that could be dynamically sampled. This foundational document will focus on the concepts needed to carry out correct MD simulations that utilize good practices. Many, but not all, of the concepts here are also useful for MC simulations and apply there as well. However, there are a number of key differences, which are outside the scope of this current document.

Either method can be carried out with different underlying physical theories to describe the particle-based model of the system under investigation. If a quantum mechanics (QM) description of matter is used, electrons are explicitly represented in the model and interaction energy is calculated by solving the electronic structure of the molecules in the system with no (or few) empirical parameters, but with various approximations to the physics for tractability. In a molecular mechanics (MM) description, molecules are represented by particles representing atoms or groups of atoms. Each atom may be assigned an electric charge and a potential energy function with a large number of empirical parameters (fitted to experiment, QM, or other data) used to calculate non-bonded and bonded interactions. Unless otherwise specified, MD simulations employ MM force fields, which calculate the forces that determine the system dynamics. MM simulations are much faster than quantum simulations, making them the methods of choice for vast majority of molecular simulation studies on biomolecular systems in the condensed phase. However, typically, they are of lower accuracy than QM simulations and cannot simulate bond rearrangements. QM simulations may be too computationally expensive to allow simulations of the time and length scales required to describe the system of interest [5]. The size of the system amenable for to QM simulation also depends on what method is chosen, from high-level ab initio methods to semi-empirical methods; discussion of these methods are outside the scope of this article, and useful references are separately available [8]. Computational resources available are also an important consideration in deciding whether QM simulations are tractable. Roughly, QM simulations might be tractable with hundreds of atoms or fewer, while MD simulations routinely have tens or hundreds of thousands of atoms in the system. Much above that level, coarse-graining methods are used. They reduce resolution and computational cost. Although many of the approaches for atomistic simulations discussed here can apply to coarse-grained simulations, such simulations are not the focus of this paper and we will not discuss how coarse-grained simulations are initially built.

Speed is a particular concern when describing condensed phase systems, as we are often interested in the properties of molecules (even biomacromolecules) in solution, meaning that systems will consist of thousands to hundreds of thousands or millions of atoms. While system size alone does not dictate a classical description, if we are interested in calculations of free energies or transport properties at finite (often laboratory) temperatures, these include entropic contributions (as further discussed below) meaning that fluctuations and correlations of motions within the system affect computed properties, meaning that simulations must not only sample single optimal states but instead must sample the correct distribution of states – requiring simulations of some length. Furthermore, many systems of interest, such as polymers (biological and otherwise) have slow motions that must be captured for accurate calculation of properties. For example, for proteins, relevant timescales span from nanoseconds to seconds or more, and even rearrangements of buried amino acid sidechains can in some cases take microseconds or more, with larger conformational changes and protein folding taking even longer [9, 10]. Recent hardware innovations have made microsecond-length simulations for biological systems of 50–100,000 atoms relatively routine, and herculean efforts have pushed the longest simulations out past the millisecond range. However, the field would like to reach even longer timescales, meaning that switching to a more detailed energy model is only done with some trepidation because slower energy evaluations mean less time available for sampling. Thus the need for speed limits the use of quantum mechanical descriptions.

Thus, for the rest of this document we will restrict ourselves to classical MD.

One other important note is that, within classical molecular simulations, bond breaking and forming is generally not allowed (with notable exceptions such as reactive force fields), meaning that the topology or chemistry of a system will remain constant as a function of time. That is, the particles comprising the system move around, but the chemical identity of each molecule in the system remains a constant over the course of the simulation (with only partial exceptions, such as the case of constant pH simulations [11]). This also means that the notion of pH in molecular simulations primarily refers to the selection of fixed protonation states for the components of the system.

Here, we first discuss the scope of this document, then go over some of the fundamental concepts or science topics which provide the underpinnings of molecular simulations, giving references for further reading. Then, we introduce a variety of basic simulation concepts and terminology, with links to further reading. Our goal is not to cover all topics, but to provide some guidance for the critical issues which must be considered. We also provide a checklist to assist with preparing for and beginning a modeling project, highlighting some key considerations addressed in this work.

2. Scope of this document

There are several excellent textbooks on classical simulation methods; some we have found particularly helpful are Allen and Tildesley’s “Computer Simulations of Liquids” [12], Leach’s “Molecular Modelling” [7], and Frenkel and Smit’s “Understanding Molecular Simulations” [6], though there are many other sources. Tuckerman’s “Statistical Mechanics: Theory and Molecular Simulation” [13] may be helpful to a more advanced audience.

In principle, anyone with adequate prior knowledge (namely, undergraduate level calculus and physics) should be able to pick up one of these books and learn the required skills to perform molecular simulations, perhaps with help from a good statistical mechanics and thermodynamics book or two. In practice, due to the interdisciplinary and somewhat technical nature of this field, many newcomers may find it difficult and time consuming to understand all the methodological issues involved in a simulation study. The goal of this document is to introduce a new practitioner to some key basic concepts and bare minimum scientific knowledge required for correct execution of these methods. We also provide a basic set of “best practices” that can be used to avoid common errors, missteps and confusion in elementary molecular simulations work. This document is not meant as a full introduction to the area; rather, it is intended to help guide further study, and to provide a foundation for other more specialized best-practices documents focusing on particular simulation areas.

Modern implementations of classical simulations also rely on a large body of knowledge from the fields of computer science, programming, and numerical methods, which will not be covered in detail here.

3. Science topics

A new practitioner does not have to be an expert in all of the fields that provide the foundation for our simulation methods and analysis of the data produced by these methods. However, grasping some key concepts from each of these disciplines, described below, is essential. This section serves as a preface for Section 4 and suggestions for further reading on these subjects are provided throughout the document. In each subsection, we begin by highlighting some of the critical topics from the corresponding area, then describe what these are and why they are important to molecular simulations.

3.1. Classical mechanics

3.1.1. Key concepts

Critical concepts from classical mechanics include:

• Newton’s equations of motion

• Hamilton’s equations

• Point particles and rigid bodies

• Holonomic constraints

Molecular simulation methods work on many-particle systems following the rules of classical mechanics. Basic knowledge of key concepts of classical mechanics is important for understanding simulation methods. Here, we will assume you are already familiar with Newtonian mechanics.

Classical molecular models typically consist of point particles carrying mass and electric charge with bonded interactions (describing bond lengths, angles, and torsions) and non-bonded interactions (describing electrostatic and van der Waals forces). Sometimes it is much more efficient to freeze the internal degrees of freedom and treat the molecule as a rigid body where the particles do not change their relative orientation as the whole body moves; this is commonly done, for example, for rigid models of the water molecule. The timestep for simulation is determined by the fastest frequency motion. Due to the high frequency of the O-H vibrations, accurately treating water classically would require solving the equations of motion with a small timestep (commonly 1 fs). Thus, for computational efficiency water is often instead treated as a rigid body to allow a larger timestep (often double the length). Keeping specified objects rigid in a simulation involves applying holonomic constraints, where the rigidity is defined by imposing a minimal set of fixed bond lengths and angles through iterative procedures during the numerical integration of the equation of motion (see Section 4.6 for more on constraints and integrators).

Classical mechanics has several mathematical formulations, namely the Newtonian, Hamiltonian and Lagrangian formulations. These formulations are physically equivalent, but for certain applications one formulation can be more appropriate than the other. Many simulation methods use the Hamiltonian formulation and therefore basic knowledge of Hamiltonian mechanics is particularly important.

Classical mechanics has several conserved quantities and simulators should be familiar with these, for example, the total energy of a system is a constant of motion. These concepts play an important role in development and proper implementation of simulation methods. For example, a particularly straightforward check of the correctness of an MD code is to test whether energy is conserved.

Most books on molecular simulations have a short discussion or appendices on classical mechanics that can serve the purpose of quick introductions to the basic concepts; Shell’s book also has a chapter on simulation methods which covers some of these details [14]. A variety of good books on classical mechanics are also available and give further details on these concepts.

3.2. Thermodynamics

3.2.1. Key concepts

A variety of thermodynamic concepts are important for molecular simulations:

• Temperature and pressure

• Internal energy and enthalpy

• Gibbs and Helmholtz free energy

• Entropy

One of the main objectives of molecular simulations is to estimate/predict thermodynamic behavior of real systems as observed in the laboratory. Typically this means we are interested in macroscopic systems, consisting of 10²³ particles or more (i.e. at least a mole of particles). But properties of interest include not only macroscopic, bulk thermodynamic properties, such as density or heat capacity, but also microscopic properties like specific free energy differences associated with, say, changes in the conformation of a molecule. For this reason, it is important to understand key concepts in thermodynamics, such as temperature, pressure, entropy, internal energy, various forms of free energy, and the relationships between them. Paramount, however, is an understanding of the connection between thermodynamics and statistical mechanics, which allows us to relate macroscopic, experimental measurements to the behavior of the much smaller system that is simulated. This topic involves a variety of subtleties and thus can be a confusing and difficult, so we refer the reader to a more extensive discussion in one of several books [14, 15].

As an example, consider temperature. In a macroscopic sense, we understand this quantity intuitively as how hot or cold something is. The laws of thermodynamics provide us with a further abstraction, telling us that this is in fact the derivative of the internal energy with respect to the entropy. This mathematical definition itself is not particularly helpful, but provides a starting point for other derivations. If we want to understand temperature from the point of view of understanding molecular behavior, we finally must turn to statistical mechanics. Since molecular dynamics is mostly used to simulate behavior at the molecular or atomistic level, it is necessary to utilize statistical-mechanical expressions in computing what would be observed as the macroscopic, thermodynamic temperature.

This discussion should not provide the impression that statistical mechanics is more important than thermodynamics. The two are intimately connected and we must rely on both to successfully conduct and obtain information from MD simulations. In particular, thermodynamics provides rigid rules that must be satisfied if we are to faithfully reproduce reality. For instance, if energy is not conserved, the first law is not satisfied and we are for sure simulating a system out of equilibrium (i.e. we are somehow adding or removing energy). In this sense, the laws of thermodynamics provide us rigorous sanity checks in addition to many useful mathematical relations for computing properties. Basic thermodynamic principles thus also dictate proper simulation protocols and associated best practices.

The concept of the thermodynamic limit is important here. Specifically, as the size of a finite system is increased, keeping the particle number density roughly constant, at some point it is said to reach the thermodynamic limit where its behavior is bulk-like and no longer depends on the extent of the system. Thus, small systems will exhibit unique behaviors that reflect their microscopic size, but sufficiently large systems are said to have reached the thermodynamic limit and macroscopic thermodynamics applied. This is due to the fact that the effect of interfaces or boundaries have largely been removed, and, more importantly, that averages of system properties are now over a sufficiently large number of molecules that any instantaneous snapshot of the system roughly corresponds to average behavior (i.e. fluctuations in properties become negligible with increasing system size).

Although we usually think of thermodynamics applying macroscopically and statistical mechanics applying on the microsopic level, it is important to remember that the laws of thermodynamics still hold on average regardless of the length scale. That is, a molecule in contact with a thermal bath will exchange energy with the bath, but its average energy is a well-defined constant. This allows us to define thermodynamic quantities associated with microscopic events, such as the binding of a ligand to a protein. This is useful because it allows us to assign molecular meaning to well-defined thermodynamic processes that can only be indirectly probed by experiment. Importantly, as long as we have carefully defined our ensemble and thermodynamic path, we can apply the powerful relationships of thermodynamics to more easily calculate many properties of interest. For instance, one may use molecular dynamics to efficiently numerically integrate the Clapeyron equation and construct equations of state along phase coexistence curves [16, 17].

3.2.2. Books

Equilibrium thermodynamics is taught in most undergraduate programs in physics, chemistry, biochemistry and various engineering disciplines. Depending on the background, the practitioner can choose one or more of the following books to either learn or refresh their basic knowledge of thermodynamics. Here are some works we find particularly helpful:

• Atkins and De Paula’s “Physical Chemistry” [18], chapters 1 to 4.

• McQuarrie and Simon’s extensive work, “Physical Chemistry: A Molecular Approach” [19]

• Dill’s “Molecular Driving Forces” [15]

• Kittel and Kroemer’s “Thermal Physics” [20]

• Shell [14]: Chapters 1–15.

3.3. Classical statistical mechanics

3.3.1. Key concepts

Key concepts from statistical mechanics are particularly important and prevalent in molecular simulations:

• Fluctuations

• Definitions of various ensembles

• Time averages and ensemble averages

• Equilibrium versus non-equilibrium

Traditional discussions of classical statistical mechanics, especially concise ones, tend to focus first or primarily on macroscopic thermodynamics and microscopic equilibrium behavior based on the Boltzmann factor, which tells us that configurations r^N occur with (relative) probability exp[−U(r^N)/(k_BT)], based on potential energy function U and temperature T in absolute units. Dynamical phenomena and their connection to equilibrium tend to be treated later in discussion, if at all. However, as the laws of statistical mechanics arise naturally from dynamical equations, we will discuss dynamics first.

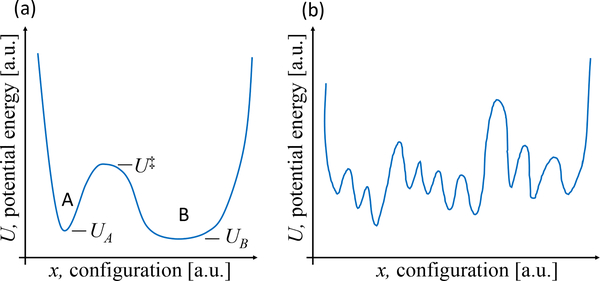
The key dynamical concept to understand is embodied in the twin characteristics of timescales and rates. The two are literally reciprocals of one another. In Fig. 1(a), assume you have started an MD simulation in basin A. The trajectory is likely to remain in that basin for a period of time – the “dwell” timescale – which increases exponentially with the barrier height, (U^‡ – U_A). Barriers many times the thermal energy k_BT imply long dwell timescales, approximated as the reciprocal of exp[(U^‡ – U_A)/(k_BT)]. The rate coefficient k_AB relates to the transition probability per unit time per amount of reactant(s). All transitions occur in a random, stochastic fashion and are predictable only in terms of average behavior. More detailed discussions of rates and rate coefficients can be found in numerous textbooks (e.g., [15, 21]).

Figure 1.

Energy landscapes. (a) A highly simplified landscape used to illustrate rate concepts and (b) a schematic of a more complex landscape with numerous minima and ambiguous state boundaries.

Once you have understood that MD behavior reflects system timescales, you must set this behavior in the context of an extremely complex energy landscape consisting of almost innumerable minima and barriers, as schematized in Fig. 1b). Each small basin represents something like a different rotameric state of a protein side chain or perhaps a tiny part of the Ramachandran spaces (backbone phi-psi angles) for one or a few residues. Observing the large-scale motion of a protein then would require an MD simulation longer than the sum of all the timescales for the necessary hops, bearing in mind that numerous stochastic reversals are likely during the simulation. Because functional biomolecular timescales tend to be on μs - ms scales and beyond, it is challenging if not impossible to observe them in traditional MD simulations. There are numerous enhanced sampling approaches [22, 23] but these are beyond the scope of this discussion and they have their own challenges which often are much harder to diagnose (see [24] and https://github.com/dmzuckerman/Sampling-Uncertainty).

What is the connection between MD simulation and equilibrium? The most precise statement we can make is that an MD trajectory is a single sample of a process that is relaxing to equilibrium from the starting configuration [21, 25]. If the trajectory is long enough, it should sample the equilibrium distribution - where each configuration occurs with frequency proportional to its Boltzmann factor. In such a long trajectory (only), a time average thus will give the same result as a Boltzmann-factor-weighted, or ensemble, average. We refer to such a system, where the time and ensemble averages are equivialent, as “ergodic.” Note that the Boltzmann-factor distribution implies that every configuration has some probability, and so it is unlikely that a single conformation or even a single basin dominates an ensemble. Beware that in a typical MD trajectory it is likely that only a small subset of basins will be sampled well - those most quickly accessible to the initial configuration. It is sometimes suggested that multiple MD trajectories starting structures can aid sampling, but unless the equilibrium distribution is known in advance, the bias from the set of starting structures is simply unknown and harder to diagnose.

A fundamental equilibrium concept that can only be sketched here is the representation of systems of enormous complexity (many thousands, even millions of atoms) in terms of just a small number of coordinates or states. The conformational free energy of a state, e.g., F_A or F_B is a way of expressing the average or summed behavior of all the Boltzmann factors contained in a state: the definition requires that the probability (or population) p^eq of a state in equilibrium be proportional to the Boltzmann factor of its conformational free energy: $p_A^{\text{eq}}~\exp \left(-F_A/k_{B}T\right)$. Because equilibrium behavior is caused by dynamics, there is a fundamental connection between rates and equilibrium, namely that $p_A^{\text{eq}}{k}_{AB}=p_B^{\text{eq}}{k}_{BA}$, which is a consequence of “detailed balance”. There is a closely related connection for on- and off-rates with the binding equilibrium constant. For a continuous coordinate (e.g., the distance between two residues in a protein), the probability-determining free energy is called the “potential of mean force” (PMF); the Boltzmann factor of a PMF gives the relative probability of a given coordinate. Any kind of free energy implicitly includes entropic effects; in terms of an energy landscape (Fig. 1), the entropy describes the width of a basin or the number of arrangements a system can have within a particular state. One way to think of this it is that entropy of a state relates to the volume of 6N-dimensional phase space that the state occupies, which in the one-dimensional case is just the width. These points are discussed in textbooks, as are the differences between free energies for different thermodynamic ensembles - e.g., A, the Helmholtz free energy, when T is constant, and G, the Gibbs free energy, when both T and pressure are constant - which are not essential to our introduction [15, 21].¹

A final essential topic is the difference between equilibrium and non-equilibrium systems. We noted above that an MD trajectory is not likely to represent the equilibrium ensemble because the trajectory is probably too short. However, in a living cell where there is no shortage of time, biomolecules may exhibit non-equilibrium behavior for a quite different reason - because they are driven by the continual addition and removal of (possibly energy-carrying) substrate and product molecules. In this type of non-equilibrium situation, the distribution of configurations will not follow a Boltzmann distribution. Specialized simulation approaches are available to study such systems [23, 26] but they are not beginner-friendly. Non-equilibrium molecular concepts pertinent to cell biology have been discussed at an introductory level (e.g. http://www.physicallensonthecell.org/). Notably, many experiments are conducted at non-equilibrium conditions; for example, membrane diffusion coefficients are commonly measured by setting up a concentration gradient across the membrane and measuring the flux. It can be tempting to the beginner to setup an MD simulation in the same manner as such an experiment. However, maintaining non-equilibrium conditions is typically more complicated in an MD simulation than in an experiment as large reservoirs are commonly required. Frequently, equilibrium methods can provide the same or similar information as a non-equilibrium experiment; users should seek to obtain familiarity with such methods before choosing to conduct a non-equilibrium MD simulation.

3.3.2. Books

Books which we recommend as particularly helpful in this area include:

• Reif’s “Fundamentals of Statistical and Thermal Physics” [27]

• McQuarrie’s “Statistical Mechanics” [28]

• Dill and Bromberg’s “Molecular Driving Forces” [15]

• Hill’s “Statistical Mechanics: Principles and Selected Applications” [29]

• Shell’s “Thermodynamics and Statistical Mechanics” [14]

• Zuckerman’s “Statistical Physics of Biomolecules” [21]

• Chandler’s “Introduction to Modern Statistical Mechanics” [30]

3.3.3. Online resources

Several online resources have been particularly helpful to people learning this area, including:

• David Kofke’s notes: http://www.eng.buffalo.edu/~kofke/ce530/Lectures/lectures.html

• Scott Shell’s notes: https://engineering.ucsb.edu/~shell/Che210d/assignments.html

3.4. Classical electrostatics

3.4.1. Key concepts

Key concepts from classical electrostatics include

• The Coulomb interaction and its long-range nature

• Polarizability, dielectric constants, and electrostatic screening

• When and why we need lattice-sum electrostatics and similar approaches

Electrostatic interactions are both some of the longestrange interactions in molecular systems and the strongest, with the interaction (often called “Coulombic” after Coulomb’s law) between charged particles falling off as 1/r where r is the distance separating the particles. Atom-atom interactions are thus necessarily long range compared to other interactions in these systems (which fall off as 1/r³ or faster). This means atoms or molecules separated by considerable distances can still have quite strong electrostatic interactions, though this also depends on the degree of shielding of the intervening medium (or its relative permittivity or dielectric constant).

The static dielectric constant of a medium, or relative permittivity ε_r (relative to that of vacuum), affects the prefactor for the decay of these long range interactions, with interactions reduced by $\frac{1}{{ϵ}_r}$. Water has a high relative permittivity or dielectric constant close to 80, whereas non-polar compounds such as n-hexane may have relative permittivities near 2 or even lower. This means that interactions in non-polar media such as non-polar solvents, or potentially even within the relatively non-polar core of a larger molecule such as a protein, are effectively much longer-range even than those in water. The dielectric constant of a medium also relates to the degree of its electrostatic response to the presence of a charge; larger dielectric constants correspond to larger responses to the presence of a nearby charge.

It turns out that atoms and molecules also have their own levels of electrostatic response; particularly, their electron distributions polarize in response to their environment, effectively giving them an internal dielectric constant. This polarization can be modeled in a variety of ways, such as (in fixed charge force fields) building in a fixed amount of polarization which is thought to be appropriate for simulations in a generic “condensed phase” or by explicitly including polarizability via QM or by building it into a simpler, classical model which includes polarizability such as via explicit atomic polarizabilities [31, 32] or via Drude oscillator-type approaches [33], where inclusion of extra particles attached to atoms allows for a type of effective polarization.

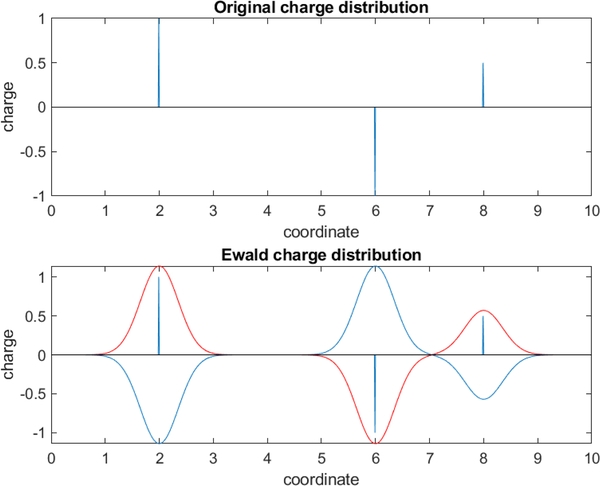
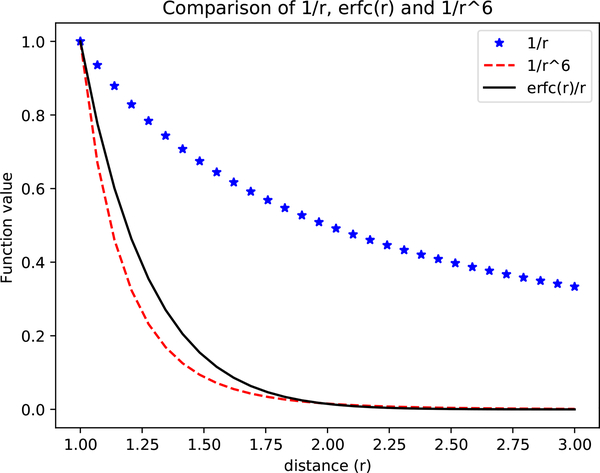
Because so many interactions in physical systems involve polarity, and thus significant long-range interactions that decay only slowly with distance, it is important to regard electrostatic interactions as fundamentally long-range interactions. Indeed, contributions to the total energy of a system from distant objects may be even more important in some cases than those from nearby objects. Specifically, since interactions between charges fall off as 1/r, but the volume of space at a given separation distance increases as r³, distant interactions can contribute a great deal to the energies and forces in molecular systems. In practice, this means that severe errors often result from neglecting electrostatic interactions beyond some cutoff distance [7, 34–37]. Thus, we prefer to include all electrostatic interactions, even out to very long ranges. Once this is decided, it leaves simulators with two main options, only one of which is really viable. First, we can simulate the actual finite (but large) system which is being studied in the lab, including its boundaries. But this is impractical, since macroscopic systems usually include far too many atoms (on the order of at least a mole or more). The remaining option, then, is to apply periodic boundary conditions (see Section 4.2) to tile all of space with repeating copies of the system. Once periodic boundary conditions are set up, defining a periodic lattice, it becomes possible to include all long-range electrostatic interactions via a variety of different types of sums which can be described as “lattice sum electrostatics” or Ewald-type electrostatics [37, 38] where the periodicity is used to make possible an evaluation of all long range electrostatic interactions, including those of particles with their own periodic images.

In practice, lattice sum electrostatics introduce far fewer and less severe artifacts than do cutoff schemes, so these are used for most classical all-atom simulation algorithms at present. A variety of different efficient lattice-sum schemes are available [38]. In general these should be used whenever long range electrostatic interactions are expected to be significant; they may not be necessary in especially nonpolar systems and/or with extremely high dielectric constant solvents where electrostatic interactions are exclusively short range, but in general they should be regarded as standard (see also Section 4.7, below).

3.4.2. Books

On classical electrostatics, we have found the undergraduate- level work by David J. Griffiths, “Introduction to Electrodynamics” [39], to be quite helpful. The graduate-level work of Jackson, “Classical Electrodynamics” [40], is also considered a classic/standard work, but may prove challenging for those without a background relatively heavy in mathematics.

3.5. Molecular interactions

3.5.1. Key concepts

Molecular simulations are, to a large extent, about molecular interactions, so these are particularly key, including:

• Bonded and nonbonded interactions

• The different types of nonbonded interactions and why they are separated in classical descriptions

• The dividing line between bonded and nonbonded interactions

Key interactions between atoms and within or between molecules are typically thought of as consisting of two main types - bonded and non-bonded interactions. While these arise from similar or related physical effects (ultimately all tracing back to QM and the basic laws of physics) they are typically treated in rather distinct manners in molecular simulations so it is important to consider the two categories separately.

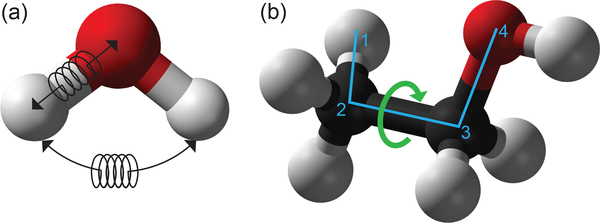
Bonded interactions are those between atoms which are connected, or nearly so, and relating to the bonds connecting these atoms. In typical molecular simulations these consist of bond stretching terms, angle bending terms, and terms describing the rotation of torsional angles, as shown in Figure 2. Torsions typically involve four atoms and are often of two types - “proper” torsions, around bonds connecting groups of atoms, and “improper” torsions which involve neighbors of a central atom; these are often used to ensure the appropriate degree of planarity or non-planarity around a particular group (such as planarity of an aromatic ring). It is important to note that the presence of bonded interactions between atoms does not preclude their also having non-bonded interactions with one another (see discussion of exclusions and 1–4 interactions, below).

Figure 2.

Standard MM force fields include terms that represent (a) bond and angle stretching around equilibrium values, using harmonic potentials with spring constants fit to the molecules and atoms to which they are applied; and (b) rotation around dihedral angles (green arrow) defined using four atoms, typically using a cosine expansion.

Nonbonded interactions between atoms are all interactions which are included in the potential energy of the system aside from bonded interactions. Commonly these include at least point-charge Coulomb electrostatic interactions and “non-polar” interactions modeled by the Lennard-Jones potential or another similar potential which describes short range repulsion and weak long-range interaction even between nonpolar atoms. Additional terms may also be included, such as interactions between fixed multipoles, interactions between polarizable sites, or occasionally explicit potentials for hydrogen bonding or other specialized terms. These are particularly common in polarizable force fields such as the AMOEBA model.

Often, the energy functions used by molecular simulations explicitly neglect nonbonded interactions between atoms which are immediately bonded to one another, and atoms which are separated by only one intervening atom, partly to make it easier to ensure that these atoms have preferred geometries dictated by their defined equilibrium lengths/angles regardless of the nonbonded interactions which would otherwise be present. This neglect of especially short range nonbonded interactions between near neighbors is called “exclusion”, and energy functions typically specify which interactions are excluded.

The transition to torsions, especially proper torsions, is where exclusions typically end. However, many all-atom energy functions commonly used in biomolecular simulations retain only partial nonbonded interactions between terminal atoms involved in a torsion. The atoms involved in a torsion, if numbered beginning with 1, would be 1, 2, 3, and 4, so the terminal atoms could be called atoms 1 and 4, and nonbonded interactions between such atoms are called “1–4 interactions”. These interactions are often present but reduced, though the exact amount of reduction differs by the energy function or force field family. For example, the AMBER family force fields usually reduce 1–4 electrostatics to $\frac{1}{1.2}$ of their original value, and 1–4 Lennard-Jones interactions to $\frac{1}{2}$ of their original value. 1–4 interactions are essentially considered the borderline between the bonded and non-bonded regions. These short-range interactions can be quite strong and there is potentially a risk of them overwhelming longer-range interactions, hence their typical reduction.

3.5.2. Books

For a discussion of molecular interactions, we recommend “Intermolecular and surface forces” by Jacob N. Israelachvili. A variety of other books discuss these from a simulation perspective, e.g. Leach [7] and Allen and Tildesley [12].

4. Basic simulation concepts and terminology

Above, we covered a variety of fundamental concepts needed for understanding molecular simulations and the types of interactions and forces we seek to model; here, we shift our attention to understanding basics of how molecular simulations actually work.

4.1. Force fields

The term “force field” simply refers to the included terms, particular form, and specific implementation details, including parameter values, of the chosen potential energy function.²

Most of the terms included in potential energy functions have already been detailed in Section 3.5, with the most common being Coulombic, Lennard-Jones, bond, angle, and torsional (dihedral) terms (Figure 2). Here, we very briefly describe the mathematical forms used to represent such interactions.

Non-bonded interactions of the Lennard-Jones form are well-described throughout the literature (for instance see Ch. 4 of Leach [7]); these model a short-range repulsion that scales as 1/r¹² and a long-range attraction that scales as 1/r⁶. Coulombic interactions, including both short and long-range components, are described in detail elsewhere in this document. To represent bonded interactions, harmonic potentials are often employed. The same is true for angles between three bonded atoms, but the harmonic potential is applied with respect to the angle formed and not the distance between atoms. Torsional terms are also commonly employed, usually consisting as sums of cosines, i.e. a cosine expansion.

While the above are perhaps the most common potentials used, there are a variety of common variations as well. More exotic potentials based on three-body intermolecular orientations, or terms directly coupling bond lengths and bending angles are also possible. Some historic force fields also added an explicit (non-Coulombic) hydrogen bonding term, though these are less frequently used in many cases today. Additionally, other choices of potential function are of course acceptable, including Buckingham or Morse potentials, or the use of “improper” dihedral terms to enforce planarity of cyclic portions of molecules. This may even include empirical corrections based on discrete binning along a particular set of degrees of freedom [43, 44], as well as applied external fields (i.e. electric fields) and force field terms describing the effect of degrees of freedom, such as solvent, that have been removed from the system via “coarse-graining.” [45] For a more in-depth discussion of common (as well as less common) force field terms, see Ch. 4 of Leach [7], or for an in-depth review of those specific to simulating biomolecules, see Ponder and Case [31].

Functional forms used to describe specific terms in a potential energy function may be vastly different in mathematical character even though they seek to describe the same physics. For instance, the Lennard-Jones potential implements an r⁻¹² term to represent repulsions, while an exponential form is used in the Buckingham potential. This results in very different mathematical behavior at very short distances and as a result differences in numerical implementation as well as evaluation efficiencies via a computer. For this reason, one functional form may be preferred above another due to enhanced numerical stability or simplicity of implementation, even though it is not as faithful to the underlying physics. In this regard, force field selection is a form of selecting a model - one should carefully weigh the virtues of accuracy and convenience or speed, and be ever-conscious of the limitations introduced by this decision (for instance, see Becker et al. [46]). It is also important to know that most MD simulation engines only support a subset of functional forms. For those forms that are supported, the user manuals of these software packages are often excellent resources for learning more about the rationale and limitations of different potential energy functions and terms (e.g. see Part II of Amber reference manuals[47] and Ch. 4 of the reference manual for GROMACS [48]).

For practical purposes, most beginning users will not be fitting a force field or choosing a functional form, but will instead be using an existing force field that already relies on a particular functional form and is available in their simulation package of choice, so for such users it is more important to know how the functional form represents the different interactions involved than to necessarily be able to justify why that particular functional form was chosen.

Many examples of force fields abound in the literature — in fact, too many to provide even a representative sample or list of citations, as most force fields are specifically developed for particular systems or categories of systems under study. However, reviews are available describing and comparing force fields for biomolecular simulations [31, 49], solid, covalently-bonded materials [50], polarizable potentials [51], and models of water [52, 53], to name just a few. Many force fields are open-source and parameter file libraries may be found through the citations in the resources above or are often distributed with molecular simulation packages. Limited databases of force fields also exist, most notably for simulations of solid materials where interatomic potentials display a much wider array of mathematical forms [54, 55].

Specification of a force field involves not just a choice of functional form, but the details of the specific parameters for all of the interacting particles which will be considered — that is, the specific parameters governing the interactions as specified by the functional form. Parameters are usually specific to certain types of atoms, bonds, molecules, etc., and include point charges on atoms if electrostatic terms are in use.

Some choices which are often considered auxiliary actually comprise part of the choice of the force field or interaction model. Specifically, settings such as the use of constraints, the treatment of cut-offs and other simulation settings affect the final energies and forces which are applied to the system. Thus, to replicate a particular force field as described previously, such settings should be matched to prior work such as the work which parameterized the force field. The choice of how to apply a cutoff, such as through direct truncation, shifting of the potential energy function, or through the use of switching functions, should be maintained if identical matches to prior work computing the properties of interest are desired. This is especially important for the purposes of free energy calculations, where the potential energy itself is recorded. However, force fields are in some cases slow to adapt to changes in protocol, so current best practices seem to suggest that lattice-sum electrostatics should be used for Coulomb electrostatics in condensed phase systems, even if the chosen force field was fitted with cutoff electrostatics, and in many cases long-range dispersion corrections should be applied to the energy and pressure to account for truncated Lennard-Jones interactions [56, 57].

For almost all force fields, many versions, variants, and modifications exist, so if you are using a literature force field or one distributed with your simulation package of choice, it is important to pay particular attention (and make note of) exactly what version you are using and how you obtained it so you will be able to accurately detail this in any subsequent publications.

As clearly described in Becker et al. [46], it is of paramount importance to understand the capabilities and limitations of various force field models that may seem appropriate for one’s work. Depending on the physics being simulated and the computational resources at hand, no force field In the literature may provide results that accurately reproduce experiment. But with so many force fields to pick from, how Is this possible? The Issue lies In what Is termed “transferability.” Simply put, a classical description of dynamics, as Implemented In MD, cannot universally describe all of chemistry and physics. At some level of finer detail, all of the potential functions described above are simply approximations. Due to this, force field developers must often make the difficult decision of sacrificing accuracy or generality. For instance, a force field may have been developed to very accurately describe a single state point, in which case It Is obvious that extensive testing should be performed to ensure that it is also applicable at other conditions. Even with force fields developed to be general and transferable, it is essential to ensure that the desired level of realism is achieved, especially if applying such a model to a new system (even more caution is advised when mixing force fields!). Either way, it is always a good idea to check results against previous literature when possible. This helps ensure that the force field is being implemented properly and, though it may seem laborious on a short-time horizon, can pay substantial dividends in the long-run.

Because this balance of accuracy versus generality and transferability can be challenging, some efforts eschew transferability entirely and instead build “bespoke” force fields, where each molecule is considered as a unique entity and assigned parameters independently of any other molecule or representation of chemical space (e.g. [58]). Such approaches offer the opportunity to assign all molecules with parameters assigned in a consistent way; however, they are unsuitable for applications where speed needs to exceed that of the parameter assignment process - so, for example, for docking of a large library of potential ligands to a target receptor, if compounds must be screened at seconds or less per molecule, such approaches may not be suitable.

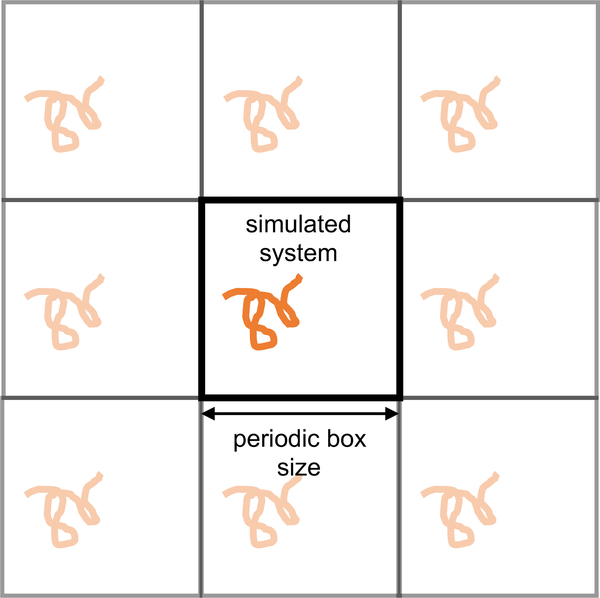
4.2. Periodic boundary conditions

Periodic boundary conditions allow more accurate estimation of bulk properties from simulations of finite, essentially nanoscale systems. More precisely, simulations of comparatively small systems with periodic boundary conditions can be a good approximation to the behavior of a small subsystem in a larger bulk phase (or at least are a much better approximation than simply simulating a nanodroplet or a finite system surrounded by vacuum). Periodic boundary conditions can alleviate many of the issues with finite size effects because each particle Interacts with periodic Images of particles In the same system. Clearly, though. It Is undesirable for a single particle to Interact with the same particle multiple times. To prevent this, a cut-off of many non-bonded interactions should be chosen that is less than half the length of the simulation box in any dimension. (However, as noted in Section 3.4 these cut-offs are not normally applied to electrostatic interactions because truncating these Interactions induces worse artifacts than does including interactions with multiple copies of the same particle. instead, what are often termed “cutoffs” that are applied to electrostatics are instead a shift from short-range to long-range treatments.) Such cut-offs Impose a natural lower limit to the size of a periodic simulation box, as the box must be large enough to capture all of the most significant non-bonded interactions. Further Information on periodic boundary conditions and discussion of appropriate cut-offs may be found in Leach [7], sections 6.5 and 6.7 and Shell [59]’s lecture on Simulations of Bulk Phases.

It Is very Important to note that periodic boundary conditions are simply an approximation to bulk behavior. They DO NOT effectively simulate an infinitely sized simulation box, though they do reduce many otherwise egregious finite-size effects. This Is most easily seen by Imagining the placement of a solute in a periodic simulation box. The solute will be replicated in all of the surrounding periodic images. The concentration of solute is thus exactly one per the volume of the box. Although proper selection of non-bonded cutoffs will guarantee that these solutes do not directly interact (hence the common claim that such systems are at infinite dilution), they may indirectly interact through their perturbation of nearby solvent. If the solvent does not reach a bulk-like state between solutes, the simulation will still suffer from obvious finite-size effects.

Macroscopic, lab-scale systems, or bulk systems, typically consist of multiple moles of atoms/molecules and thus from a simulation perspective are effectively infinite systems. We attempt to simulate these by simulating finite and fairly small systems, and, in a sense, the very idea that the simulation cell is not infinite, but simply periodic, immediately gives rise to finite-size effects. Thus, our typical goal is not to remove these completely but to reduce these to levels that do not adversely impact the results of our simulations. Finite-size effects are particularly apparent in the electrostatic components of simulations, as these forces are inherently longer ranged than dispersion forces, as discussed in Section 3.4. One should always check that unexpected long-range correlations (i.e. on the length-scale of the simulation box) do not exist in molecular structure, spatial position, or orientation. It should also be recognized that periodic boundary conditions innately change the definition of the system and the properties calculated from it. Many derivations, especially those involving transport properties, such as diffusivity [60], assume infinite and not periodic boundary conditions. The resulting differences in seemingly well-known expressions for computing properties of interest are often subtle, yet may have a large impact on results. Such considerations should be kept in mind when comparing results between simulations and with experiment.

4.3. Main steps of a molecular dynamics simulation

While every system studied will present unique challenges and considerations, the process of performing a molecular dynamics simulation generally follows these steps:

1. System preparation

2. Minimization/Relaxation

3. Equilibration

4. Production

Additional explanations of these steps along with procedural details specific to a given simulation package and application may be found in a variety of tutorials [61, 62]. It should be noted that these steps may be difficult to unambiguously differentiate and define in some cases. Additionally, it is assumed that prior to performing any of these steps, an appropriate amount of deliberation has been devoted to clearly defining the system and determining the appropriate simulation techniques.

4.3.1. System preparation

System preparation focuses on preparing the starting state of the desired system for input to an appropriate simulation package, including building a starting structure, solvating (if necessary), applying a force field, etc. Because this step differs so much depending on the composition of the system and what information is available about the starting structure, it is a step which varies a great deal depending on the nature of the system at hand and as a result may require unique tools.

Given the variable nature of system preparation, it is highly recommended that best practices documents specific to this issue and to the type of system of interest be consulted. If such documents do not exist, considerable care should be exercised to determine best practices from the literature.

Loosely speaking, system preparation can be thought of as consisting of two logical components which are not necessarily consecutive or separate. One comprises building the configuration of the system in the desired chemical state and the other applying force field parameters.

For building systems, freely available tools for constructing systems are available and can be a reasonable option (though their mention here should not be taken as an endorsement that they necessarily encapsulate best practices). Examples include tools for constructing specific crystal structures, proteins, and lipid membranes, such as Moltemplate [63], Packmol [64], and Atomsk [65].

A key consideration when building a system is that the starting structure ideally ought to resemble the equilibrium structure of the system at the thermodynamic state point of interest. For instance, highly energetically unfavorable configurations of the system, such as blatant atomic overlaps, should be avoided. In some sense, having a good starting structure is only a convenience to reduce equilibration times (if the force field is adequate); however, for some systems, equilibration times might otherwise be prohibitively long.

System preparation is arguably the most critical stage of a simulation and in many cases receives the least attention; if your system preparation is flawed, such flaws may prove fatal. Potentially the worst possible outcome is if the prepared system is not what you intended (e.g. it contains incorrect molecules or protonation states) but is chemically valid and well described by your force field and thus proceeds without error through the remaining steps — and in fact this is a frequent outcome of problems in system preparation. It should not be assumed that a system has been prepared correctly if it is well-behaved in subsequent equilibration steps; considerable care should be taken here.

Assignment or development of force field parameters is also critical, but is outside the scope of this work. For our purposes, we will assume you have already obtained or developed force field parameters suitable for your system of interest.

4.3.2. Minimization

The purpose of minimization, or relaxation, is to find a local energy minimum of the starting structure so that the molecular dynamics simulation does not immediately “blow up” (i.e. the forces on any one atom are not so large that the atoms move an unreasonable distance in a single timestep). This involves standard minimization algorithms such as steepest descent. For a more involved discussion of minimization algorithms utilized in molecular simulation, see Leach [7], sections 5.1–5.7.

4.3.3. Assignment of velocities

Minimization ideally takes us to a state from which we can begin numerical integration of the equations of motion without overly large displacements (see Leach [7], section 7.3.4); however, to begin a simulation, we need not just positions but also velocities. Minimization, however, provides only a final set of positions. Thus, starting velocities must be assigned; usually this is done by assigning random initial velocities to atoms in a way such that the correct Maxwell-Boltzmann distribution at the desired temperature is achieved as a starting point. The actual assignment process is typically unimportant, as the Maxwell-Boltzmann distribution will quickly arise naturally from the equations of motion. Since the momentum of the center-of-mass of the simulation box is conserved by Newtonian dynamics, this quantity is typically set to zero by removing the center-of-mass velocity from all particles after random assignment, preventing the simulation box from drifting.

In some cases, we seek to obtain multiple separate and independent simulations of different instances or realizations of a particular system to assess error, collect better statistics, or help gauge dependence of results on the starting structure. It is worth noting that even very small differences in initial configuration, such as small changes in the coordinates of a single atom, lead to exponential divergence of the time evolution of the system [12], meaning that simply running different simulations starting with different initial velocities will lead to dramatically different time evolution over long enough times. An even better way to generate independent realizations is to begin with different starting configurations, such as different conformations of the molecule(s) being simulated, as this leads to behavior which is immediately different. When rigid molecules are present, care must be taken to prevent components of velocities assigned along constraints from being forced to zero [66]. With a thermostat present, this only delays system equilibration, but for NVE simulations, such as might be used in hybrid MC/MD simulations, it can result in violations of equipartition and large subsequent errors [67].

4.3.4. Equilibration

Ultimately, we usually seek to run a simulation in a particular thermodynamic ensemble (e.g. the NVE or NVT ensemble) at a particular state point (e.g. target energy, temperature, and pressure) and collect data for analysis which is appropriate for those conditions and not biased depending on our starting conditions/configuration. This means that usually we need to invest simulation time in bringing the system to the appropriate state point as well as relaxing away from any artificially induced metastable starting states. In other words, we are usually interested in sampling the most relevant (or most probable) configurations in the equilibrium ensemble of interest. However, if we start in a less-stable configuration a large part of our equilibration may be the relaxation time (this may be very long for biomolecules or systems at phase equilibrium) necessary to reach the more relevant configuration space.

The most straightforward portion of equilibrium is bringing the system to the target state point. Usually, even though velocities are assigned according to the correct distribution, a thermostat will still need to add or remove heat from the system as it approaches the correct partitioning of kinetic and potential energies. For this reason, it is advised that a thermostatted simulation is performed prior to a desired production simulation, even if the production simulation will ultimately be done in the NVE ensemble. This phase of equilibration can be monitored by assessing the temperature and pressure of the system, as well as the kinetic and potential energy, to ensure these reach a steady state on average. For example, an NPT simulation is said to have equilibrated to a specific volume when the dimensions of the simulation box fluctuate around constant values with minimal drift. This definition, though not perfectly rigorous, is usually suitable for assessing the equilibration of energies, temperature, pressure, and box dimensions during equilibration simulations.

A more difficult portion of equilibration is to ensure that other properties of the system which are likely to be important are also no longer changing systematically with simulation time. At equilibrium, a system may still undergo slow fluctuations with time, especially if it has slow internal degrees of freedom - but key properties should no longer show systematic trends away from their starting structure. Thus, for example, for biomolecular simulations it is common to examine the root mean squared deviation (RMSD) of the molecules involved as a function of time, and potentially other properties like the number of hydrogen bonds between the biomolecules present and water, as these may be slower to equilibrate than system-wide properties like the temperature and pressure.

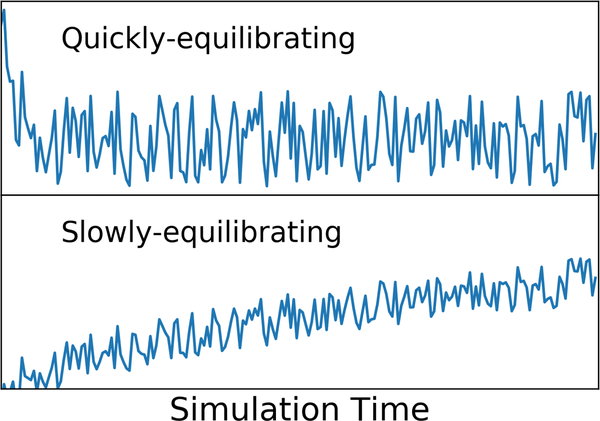
Once the kinetic and potential energies fluctuate around constant values and other key properties are no longer changing with time, the equilibration period has reached its end. In general, if any observed properties still exhibit a systematic trend with respect to simulation time (e.g. Figure 4) this should be taken as a sign that equilibration is not yet complete.

Figure 4.

Shown are graphs of a hypothetical computed property (vertical axis) versus simulation time (horizontal axis). For some system properties, equilibration may be relatively rapid (top panel), while for others it may be much slower (bottom panel). If it there is ambiguity as to whether or not a key property is still systematically changing, as in the bottom panel, equilibration should be extended.

Depending on the target ensemble for production, the procedure for the end of equilibration is somewhat different. If an NVE simulation is desired, the thermostat may be removed and a snapshot selected that is simultaneously as close to the average kinetic and potential energies as possible. This snapshot, containing both positions and velocities may be used to then start an NVE simulation that will correspond to a temperature close to that which is desired. This is necessary due to the fact that only the average temperature is obtained through coupling to a thermostat (see Section 4.4), and the temperature fluctuates with the kinetic energy at each timestep.

If the target is a simulation in the NVT ensemble at a particular density, equilibration should be done in the NPT ensemble. In this case, the system may be scaled to the desired average volume before starting a production simulation (and if rescaling is done, additional equilibration might be needed).

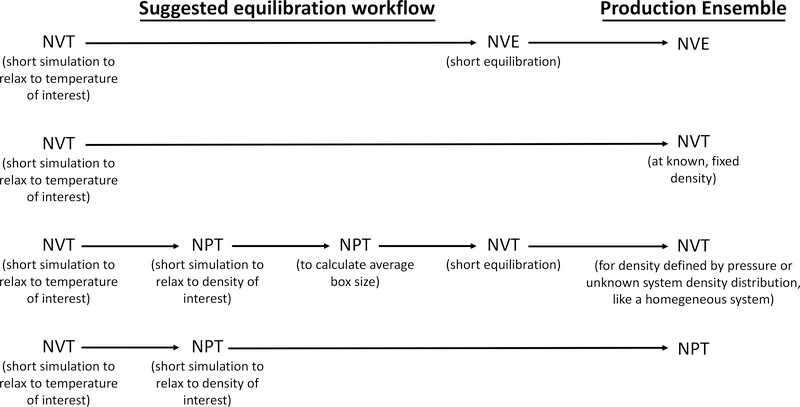
The schematic below (Figure 5) demonstrates what is generally an appropriate equilibration work-flow for common production ensembles. Clearly, this schematic cannot cover every case of interest, but should provide some idea of the general approach. For more information on equilibration procedures, see Leach [7], section 7.4 and Shell [59], lectures on Molecular dynamics and Computing properties.

Figure 5.

Common equilibration work-flows are shown; these vary depending on the target ensemble for production simulations (right). Typically, an Initial phase of equilibration at constant volume and temperature Is needed to bring the system to the desired target temperature or energy. For stability reasons, this initial phase is usually needed even if the goal is to also bring the system to a target pressure. If the production ensemble Is an NVE ensemble, an Initial NVT simulation Is usually followed by a short additional NVE equilibration before collection of production data. If the production ensemble is NVT, protocols may differ depending on whether it is necessary to allow the system to equilibrate to a particular denslty/volume or whether the volume Is selected a priori (second and third rows). And If production Is to be NPT, It Is usually equilibrated first at NVT before equilibrating to the target pressure (final row).

4.3.5. Production

Once equilibration is complete, we may begin collecting data for analysis. Typically this phase is called “production”. The main difference between equilibration and production is simply that in the production simulation, we plan to retain and analyze the collected data. Production must always be preceded by equilibration appropriate for the target production ensemble, and production data should never be collected immediately after a change in conditions (such as rescaling a box size, energy minimizing, or suddenly changing the temperature or pressure) except in very specific applications where this is the goal.

For bookkeeping purposes, sometimes practitioners choose to discard some initial production data as additional equilibration;usually this is simply to allow additional equilibration time after a change in protocol (such as a switch from NPT to NVT), and the usual considerations for equilibration apply in such cases (see Shell [59], lecture on Computing Properties).

Analysis of production is largely outside the scope of this work, but requires considerable care in computing observables and assessing the uncertainty in any computed properties. Usually, analysis involves computing expectation values of particular observables, and a key consideration is to obtain converged estimates of these properties — that is, estimates that are based on adequate simulation data so that they no longer depend substantially on the length of the simulation which was run or on its initial conditions. This is closely related to the above discussion of equilibration. Depending on the relaxation timescales involved, one may realize only after analysis of a “production” trajectory that the system was still equilibrating in some sense.

A separate Best Practices document addresses the critical issues of convergence and error analysis; we refer the reader there for more details [68] (https://github.com/dmzuckerman/Sampling-Uncertainty). For more specif c details on procedures and parameters used in production simulations, see the appropriate best practices document for the system of interest.

One other key consideration in production is what data to store, and how often. Storing data especially frequently can be tempting, but utilizes a great deal of storage space and does not actually provide significant value in most situations. Particularly, observations made in MD simulations are correlated in time (e.g. see https://github.com/dmzuckerman/Sampling-Uncertainty [68]) so storing data more frequently than the autocorrelation time results in storage of essentially redundant data. Thus, storing data more frequently than intervals of the autocorrelation time is generally unnecessary. Of course, the autocorrelation time is not known a priori which can make it necessary to store some redundant data. Disk space may also be a limiting factor that dictates the frequency of storing data, and should at least be considered. Trajectory snapshots can be particularly large. However, if there are no disk space limitations it may be best to avoid discarding uncorrelated data so sampling at intervals of the autocorrelation time may be appropriate.

If disk space proves limiting, various strategies can be used to reduce storage use, such as storing full-precision trajectory snapshots only less frequently and storing reduced-precision ones, or snapshots for only a portion of the system, more often. However, these choices will depend on the desired analysis.

For many applications, it will likely be desirable to store energies and trajectory snapshots at the same time points in case structural analysis is needed along with analysis of energies. Since energies typically use far less space, however, these can be stored more often if desired.

4.4. Thermostats

Here, we discuss why thermostats, which seek to control the temperature of a simulation, are (often) needed for molecular simulations. We review background information about thermostats and how they work, introduce some popular thermostats, and highlight common issues to understand and avoid when using thermostats in MD simulations.

4.4.1. Thermostats seek to maintain a target temperature

As mentioned above, molecular dynamics simulations are used to observe and glean properties of interest from some system of study. In many cases, to emulate experiments done in laboratory conditions (exposed to the surroundings), sampling from the canonical (constant temperature) ensemble is desired [69]. Generally, if the temperature of the system must be maintained during the simulation, some thermostat algorithm will be employed.

4.4.2. Background and How They Work

The temperature of a molecular dynamics simulation is typically measured using kinetic energies as defined using the equipartition theorem: $\frac{3}{2}N{k}_{\text{B}}T=\langle {\sum }_{i=1}^N\frac{1}{2}{m}_i{v}_i^2\rangle$. The angled brackets indicate that the temperature is defined as a time-averaged quantity. If we use the equipartition theorem to calculate the temperature for a single snapshot in time of a molecular dynamics simulation [7, 21] instead of time-averaging, this quantity is referred to as the instantaneous temperature. The instantaneous temperature will not always be equal to the target temperature; in fact, in the canonical ensemble, the instantaneous temperature should undergo fluctuations around the target temperature.

Thermostat algorithms work by altering the Newtonian equations of motion that are inherently microcanonical (constant energy). Thus, it is preferable that a thermostat not be used if it is desired to calculate dynamical properties such as diffusion coefficients; instead, the thermostat should be turned off after equilibrating the system to the desired temperature. However, while all thermostats give non-physical dynamics, some have been found to have little effect on the calculation of particular dynamical properties, and they are commonly used during the production simulation as well [70].

There are several ways to categorize the many thermostatting algorithms that have been developed. For example, thermostats can be either deterministic or stochastic depending on whether they use random numbers to guide the dynamics, and they can be either global or local depending on whether they are coupled to the dynamics of the full system or of a small subset. Many of the global thermostats can be made into local “massive” variants by coupling separate thermostats to each particle in the system rather than having a single thermostat for the whole system. There are also several methods employed by thermostat algorithms to control the temperature. Some thermostats operate by rescaling velocities outside of the molecular dynamics’ equations of motion, e.g., velocity rescaling is conducted after particles’ positions and momenta have been updated by the integrator. Others include stochastic collisions between the system and an implicit bath of particles, or they explicitly include additional degrees of freedom in the equations of motion that have the effect of an external heat bath.

4.4.3. Popular Thermostats

Within this section, various thermostats will be briefly explored, with a small description of their uses and possible issues that are associated with each. This is not an exhaustive study of available thermostats, but is instead a survey of just some of the more popular and historic thermostats used in MD.

1. Gaussian

The goal of the Gaussian thermostat is to ensure that the instantaneous temperature is exactly equal to the target temperature. This is accomplished by modifying the force calculation with the form F = F_interaction + F_constraint, where F_interaction is the standard interactions calculated during the simulation and F_constraint is a Lagrange multiplier that keeps the kinetic energy constant. The reasoning for the naming of this thermostat is due to its use of the Gaussian principle of least constraint to determine the smallest perturbative forces needed to maintain the instantaneous temperature [69]. Clearly, this thermostat does not sample the canonical distribution; it instead samples the isokinetic (constant kinetic energy) ensemble. However, the isokinetic ensemble samples the same configurational phase space as the canonical ensemble, so position-dependent (structural) equilibrium properties can be obtained equivalently with either ensemble [71]. However, velocity-dependent (dynamical) properties will not be equivalent between the ensembles. This thermostat is used only in certain advanced applications [71].

2. Simple Velocity Rescaling

The simple velocity rescaling thermostat is one of the easiest thermostats to implement; however, this thermostat is also one of the most non-physical thermostats. This thermostat relies on rescaling the momenta of the particles such that the simulation’s instantaneous temperature exactly matches the target temperature [69]. Similarly to the Gaussian thermosat, simple velocity rescaling aims to sample the isokinetic ensemble rather than the canonical ensemble. However, it has been shown that the simple velocity rescaling fails to properly sample the isokinetic ensemble except in the limit of extremely small timesteps [72]. Its usage can lead to simulation artifacts, so it is not recommended [72, 73].

3. Berendsen

The Berendsen [74] thermostat (also known as the weak coupling thermostat) is similar to the simple velocity rescaling thermostat, but instead of rescaling velocities completely and abruptly to the target kinetic energy, it includes a relaxation term to allow the system to more slowly approach the target. Although the Berendsen thermostat allows for temperature fluctuations, it samples neither the canonical distribution nor the isokinetic distribution. Its usage can lead to simulation artifacts, so it is not recommended [72, 73].

4. Bussi-Donadio-Parrinello (Canonical Sampling through Velocity Rescaling)

The Bussi [75] thermostat is similar to the simple velocity rescaling and Berendsen thermostats, but instead of rescaling to a single kinetic energy that corresponds to the target temperature, the rescaling is done to a kinetic energy that is stochastically chosen from the kinetic energy distribution dictated by the canonical ensemble. Thus, this thermostat properly samples the canonical ensemble. Similarly to the Berendsen thermostat, a user-specified time coupling parameter can be chosen to vary how abruptly the velocity rescaling takes place The choice of time coupling constant does not affect structural properties, and most dynamical properties are fairly independent of the coupling constant within a broad range [75].

5. Andersen

The Andersen [76] thermostat works by selecting particles at random and having them “collide” with a heat bath by giving the particle a new velocity sampled from the Maxwell-Boltzmann distribution. The number of particles affected, the time between “collisions”, and how often it is applied to the system are possible variations of this thermostat. The Andersen thermostat does reproduce the canonical ensemble. However, it should only be used to sample structural properties, as dynamical properties can be greatly affected by the abrupt collisions.

6. Langevin

The Langevin [77] thermostat supplements the microcanonical equations of motion with Brownian dynamics, thus including the viscosity and random collision effects of an implicit solvent. It uses a general equation of the form F = F_interaction + F_friction + F_random, where F_interaction is the standard interactions calculated during the simulation, F_friction is the damping used to tune the “viscosity” of the implicit bath, and F_random effectively gives random collisions with solvent molecules. The frictional and random forces are coupled through a user-specified friction damping parameter. Careful consideration must be taken when choosing this parameter; in the limit of a zero damping parameter, both frictional and random forces go to zero and the dynamics become microcanonical, and in the limit of an infinite damping parameter, the dynamics are purely Brownian.

7. Nosé-Hoover

The Nosé-Hoover thermostat [69] abstracts away the thermal bath from the previous thermostats and condenses it into a single additional degree of freedom. This fictitious degree of freedom has a “mass” that can be changed to interact with the particles in the system in a predictable and reproducible way while maintaining the canonical ensemble. The choice of “mass” of the fictitious particle (which in many simulation packages is instead expressed as a time damping parameter) can be important as it affects the fluctuations that will be observed. For many reasonable choices of the mass, dynamics are well-preserved [70]. This is one of the most widely implemented and used thermostats. However, it should be noted that with small systems, ergodicity can be an issue [69, 78]. This can become important even in systems with larger numbers of particles if a portion of the system does not interact strongly with the remainder of the system, such as in alchemical free energy calculations when a solute or ligand is non-interacting. Martyna et al. [78] discovered that by chaining thermostats, ergodicity can be enhanced, and most implementations of this thermostat use Nosé-Hoover chains.

4.4.4. Summary

Table 1 serves as a general summary and guide for exploring the usage of various thermostats. Knowing the system you are simulating and the benefits and weaknesses to each thermostat is crucial to successfully and efficiently collect meaningful, physical data. If you are only interested in sampling structural properties such as radial distribution functions, many of the given thermostats can be used, including the Gaussian, Bussi, Andersen, Langevin, and Nosé-Hoover thermostats. If dynamical properties will be sampled, it is preferable to turn off the thermostat before beginning production cycles, but the Bussi and Nosé-Hoover thermostats (and in cases with implicit solvent, the Langevin thermostat), can often be used without overly affecting the calculation of dynamical properties. Since dynamical properties are unimportant during equilibration, faster algorithms like the Andersen or Bussi thermostats can be used, with a switch to the Nosé-Hoover thermostat for production. Overall, the Bussi thermostat has been shown to work well for most purposes, and its use is recommended as a general-purpose thermostat.

Table 1.

Basic summary of popular thermostats. ✗ indicates that the thermostat does not fulfill the statement, ✓ indicates that the thermostat does fulfill the statement, and (✓) indicates that the thermostat fulfills the statement under certain circumstances.

Thermostat	Ensemble	Deterministic/ Stochastic	Global/ Local	Physical?	Correct Structural Properties?	Correct Dynamical Properties?
None	Microcanonical	Deterministic		✓	✓	✓
Gaussian	Isokinetic	Deterministic	Global	✗	✓	✗
Simple Velocity Rescaling	Undefined	Deterministic	Global	✗	✗	✗
Berendsen	Undefined	Deterministic	Global	✗	✗	✗
Bussi	Canonical	Stochastic	Global	✗	✓	(✓)
Andersen	Canonical	Stochastic	Local	✗	✓	✗
Langevin	Canonical	Stochastic	Local	✗	✓	✗
Nosé-Hoover	Canonical	Deterministic	Global	✗	✓	(✓)

4.5. Barostats

Here, we discuss why barostats are used, give their background, discuss roughly how they work, describe some popular options, and summarize with some recommendations.

4.5.1. Motivation

Typically, thermodynamic properties of interest are measured under open-air conditions in a laboratory, which (for short timescales) means at they are measured at essentially constant temperature and pressure. To obtain a non-atmospheric pressure, some device, like a piston, inert gas, etc., would be needed to control the pressure and volume of the system [59, 79]. Such conditions correspond to what is called the isothermal-isobaric ensemble, probably one of the most popular ensembles for MD simulations. As is the case with thermostats, if the pressure must be maintained in a simulation, a barostat algorithm will be needed to sample this ensemble.

4.5.2. Background and How They Work

Barostat algorithms control pressure alone, not temperature, so if the target ensemble is isothermal-isobaric, they must be applied with a thermostat. If a barostat is applied without a thermostat, only the number of particles (N), the pressure (P), and the enthalpy (H) of the system are held constant. This is known as the isoenthalpic-isobaric ensemble (NPH). To sample from the isothermal-isobaric ensemble (NPT), a thermostating algorithm like the ones discussed earlier must also be applied.

Much of the background information on barostats is analogous to thermostats. The pressure of a molecular dynamics simulation is commonly measured using the virial theorem (an expectation value relating to positions and forces) [7, 59]. When pairwise interactions and periodic boundary conditions are considered, different approaches are often utilized [12, 59, 79]. Regardless, these formulas give pressure as a time-averaged quantity, similar to the temperature. If we use these formulas to calculate the pressure for a single snapshot, this quantity is referred to as the instantaneous pressure. The instantaneous pressure will not always be equal to the target pressure; in fact, in the NPH and NPT ensembles, the instantaneous pressure should undergo fluctuations around the target pressure.

For the purpose of molecular modeling, consider a hypothetical system that is being compressed and/or expanded by a fictitious piston that has some mass which acts in all directions uniformly. Since the piston is acting on the system from all directions, it can be considered as applying a uniform compression or expansion. The mass of the piston can be tuned to change the compression of the system, which will change how often the particles in the system will interact with the system enclosure. These impacts from the particles on the “enclosure” will impart a stress on the system box from the surroundings and serve as a type of barostat.

The next section will describe the main differences between the many barostats that are available, and give some recommendations for proper use. Some barostats work based on scaling or rescaling the coordinates in the system (the volume and the center-of-mass coordinates of the molecules involved), whereas others work by modifying the equations of motion to ensure constant pressure.

4.5.3. Popular Barostats

Here, we introduce a few notable barostats and give a high-level summary of each, noting some key issues. This is not an exhaustive list of barostats and barostat algorithms, just a sampling of popular and historic ones used in MD.

1. Simple volume rescaling

Every time this barostat is executed, the volume of the system is modified such that the instantaneous pressure is exactly equal to the target pressure. This does not sample the proper ensemble and thus cannot be used for production sampling [59]. This also does not smoothly approach the target pressure either, which might cause very unphysical issues with the system during integration.

2. Berendsen

The Berendesen [74] weak coupling barostat is very similar to the Berendsen thermostat discussed earlier. It seeks to improve upon the simple volume rescaling method mentioned above. This is achieved by coupling the system to a weakly interacting pressure bath [74]. This bath scales the volume periodically by a scaling factor, which produces more realisitc fluctuations in the pressure as it slowly approaches the target pressure. In contrast to volume rescaling, Berendsen will approach the target pressure more realistically, but the ensemble it is sampling from is not well defined and cannot be guaranteed to be NPT or NPH. Berendsen can be useful for the beginning stages of equilibration, but should not be used for production sampling.

3. Andersen

First described by Andersen [76] in 1980, the system is coupled to a fictitious pressure bath, by adding an additional degree of freedom to the equations of motion. This behaves as if the system is being acted upon by an isotropic piston. This is similar to the Nosé-Hoover thermostat, which is also an extended system algorithm. This barostat does sample the correct ensemble. However, it is isotropic in nature and applying anisotropic pressures to parts of the system is not possible.

4. Parrinello-Rahman

The Parrinello-Rahman [80] barostat is an extension to the Andersen barostat. Unlike the Andersen barostat, Parrinello-Rahman supports the anisotropic scaling of the size and shape of the simulation box [80]. This can be quite useful in solid simulations, where phase changes can be shape changes in a crystal lattice, compared to a liquid or gas, which has no well defined shape. This barostat has essentially the same properties as the Andersen one, with the additional support anisotropy.

5. Martyna-Tuckerman-Tobias-Klein (MTTK)

The MTTK barostat has substantial similarity to the Parrinello-Rahman and Andersen barostats. When Parr- inello-Rahman’s equations of motion were discovered to hold true only in the limit of large systems, the MTTK barostat introduced alternate equations of motion to correctly sample the ensemble for smaller systems as well [81, 82]. Thus, MTTK [81, 82] is usually seen as an improvement over Parrinello-Rahman [80] for such systems.

6. Monte Carlo

Constant pressure may also be achieved by periodically performing Monte Carlo moves that adjust the system volume. For an explanation of how such moves are accepted or rejected, see “Monte Carlo simulations in other ensembles” in Shell [59]. These MC barostats are computationally advantageous in that the virial need not be computed, and they may be easily extended to accommodate anisotropic systems. They rigorously explore the correct distribution of volumes in the NPT ensemble. However, they do not preserve dynamic fluctuations. Unlike for extended system barostats, there is no sense of relaxation time over which the volume of the system responds. Instead, the rate at which the volume may respond is limited by the frequency with which MC moves are performed and the maximum allowed change in volume. Thus, long-time dynamics are not accurately reproduced in any sense for MC barostats.

4.5.4. Summary

The simple volume rescaling and Berendsen barostats are not recommended for collection of production data, as they do not sample from any correct ensemble, nor do they utilize any “realistic” approach to achieve the target pressure. They can, however, be used for approaching the target pressure. The Berendsen barostat acts in a more realistic fashion in this regard compared to the volume rescaling barostat, which itself is primarily useful only as a very stable thermostat for very early simulation stages if other algorithms have trouble beginning from particularly strained starting structures. (Alternatively, such issues can be avoided by running NVT equilibration before using a barostat, Figure 5.) Extended ensemble barostats are suitable for the production runs of most systems. It is usually not recommended to use these for the equilibration process, as these barostats do not behave as well when not near the target pressure. These can be affected by the starting configuration and pressure values much more than the Berendsen or simple volume rescaling barostats. MTTK and Parinello-Rahman allow for more flexibility in terms of the shape modulation of the simulation box. However, not all extended-ensemble barostats have been implemented all simulation engines, limiting user choice. It is recommended to begin with the Berendsen barostat to quickly bring the system to the target pressure, and then switch to an extended ensemble barostat for final equilibration and production.

4.6. Integrators

For systems consisting of more than three interacting bodies with no constrained degrees of freedom, there is no analytical solution to the equations of motion. Instead, we must approximate the dynamics in a discrete manner. This is usually termed numerical integration of the equations of motion. Algorithms to perform this integration take many forms and are usually called integrators. Here, we explain the need for integrators, discuss key criteria like energy conservation, and highlight a number of commonly used integrators.

4.6.1. Desirable integrator properties

So-called “good” integrators contain certain features that are appealing for molecular simulations. We start with the most obvious feature, which is that the integrator induces little error in the dynamics. Since integration is fundamentally about taking discrete steps to approximate continuous dynamics, this discretization process introduces errors (as can be observed by comparison to analytically soluble problems, like the harmonic oscillator). These errors are termed discretization errors, whereas additional errors called truncation errors are also accumulated through loss of precision during computer calculations. As will be discussed shortly, there are many strategies for avoiding discretization errors. For truncation errors, the only solution is to utilize a higher precision data type during calculations (i.e. use doubles instead of floats).

Integrators that minimize discretization error should preserve phase-space volume and conserve energy. If phase space volume is not preserved, then the sampled ensemble at a later timestep will not be the same as that in which the system was initialized. This means that the collected data will not in fact reflect the ensemble of interest. Luckily, this issue may be avoided simply by guaranteeing that the integrator is reversible [6]. More details may be found in Tuckerman et al. [83], but basically if the mathematical operator representing the integrator preserves phase space volume, it also satisfies the definition of reversibility: if the operator is applied to propagate forward by Δt, the starting condition may be recovered by in turn applying the operator to the result using –Δt as the timestep.

Energy conservation is also a desirable integrator property and is imperative in simulating the microcanonical (NVE) ensemble. This is a much trickier property to examine, and varies with different integrators. For instance, some classes of integrators better-preserve energy over short times, while others better-preserve energy at long times. The latter is generally preferred, though it may necessitate other sacrifices such as greater energy fluctuations away from the desired, exact system energy. When the energy does change over the course of a simulation, it is said to “drift.” The most common reason for energy drift is due to a timestep that is overly long. If the timestep is much too long, the system can become unstable and blow up (energies become very large) due to overlap of atoms. Even when the timestep is long enough that the system is still stable over long times, it may be too long for the chosen integrator to conserve energy. Other simulation parameters may also impact energy drift, such as the method of truncating forces and energies, as well as the choice of numerical precision. The latter effect, due to truncation errors, will become obvious if two simulations with different timesteps are compared. Shorter timesteps, and hence more steps to achieve a simulation of the same length, will result in more drift, since errors get larger with the number of calculations performed by the computer. This is exactly opposite to the behavior that is expected for poor energy conservation associated with discretization error, where a shorter timestep will reduce energy drift.

Overall, then, integrators do exhibit energy fluctuations that are timestep-dependent. All Verlet-equivalent integrators exhibit energy fluctuations which decrease with the square of the timestep [12], which is often an important check when assessing the correctness of an implementation. Thus, both energy drift and energy fluctuations are important criteria to understand when assessing integrators, and can be useful measures of simulation quality in the NVE ensemble.

Additionally, it is also desirable that an integrator be computationally efficient. Integrator cost mostly appears in the length of the timestep that may be taken while still avoiding discretization error. As discussed further below, the timestep must be at least an order of magnitude less than the smallest timescale of motion present in the system. However, depending on the accuracy of the integrator with respect to reproducing the true dynamics, a smaller timestep might be necessary. If the integrator requires a very small timestep to avoid discretization error, then the computational cost greatly increases. Hence, a truly “good” integrator allows for long timesteps while still achieving low discretization error. This has the added benefit of also reducing truncation error, which is proportional to the number of timesteps taken. It is worth noting that the issue of integrator choice versus timestep is not always simple; in some cases, a “better” integrator might allow longer timesteps but also carry an additional computational cost that outweighs the benefits of an increased timestep.

4.6.2. Deterministic integrators

The most commonly used integrators are variants of the Ver- let algorithm (e.g. Velocity Verlet or Leapfrog). Such integrators include terms for updating particle positions up to the order of the square of the timestep (i.e. they include forces). Inclusion of higher-order terms is favored in other families of algorithms, but generally leads to greater complexity and reduced computational efficiency at only marginal improvement in accuracy. Detailed discussion and derivation of many common integrators may be found in section 7.3 of Leach [7] and 4.3 of Frenkel and Smit [6]. Such integrators are not applicable, however, for simulations involving stochastic dynamics, as discussed below.

4.6.3. Stochastic integrators

Stochastic dynamics simulations include application of a random force to each particle, and represent discretizations of either Langevin or Brownian dynamics. A detailed description of such stochastic dynamics may be found in McQuarrie [28], Chapter 20. As detailed in Section 4.4, it is common to apply temperature control through the use of Langevin dynamics. As a brief aside, this highlights the fact that the choice of integrator is often tightly coupled to the choice of thermostat and/or barostat. Different combinations may demonstrate better performance and for expanded ensemble methods it is necessary to utilize an integrator specific to the selected temperature- or pressure-control algorithm.

With Langevin or other stochastic dynamics, the random forces usually prevent the integrator from preserving phase-space volume, which ends up dictating the choice of timestep. Specifically, despite issues with phase-space volume, some stochastic integration schemes achieve preservation of part of the full phase-space (i.e. configurations or velocities are preserved) [84] via cancellation of error. In practice these issues are easily remedied through an appropriate choice of timestep depending on the integration scheme.

Stochastic dynamics necessarily perturbs dynamics. Specifically, with Langevin or Brownian dynamics, calculations of any dynamic properties with longer timescales than the application of the random forces will be very different than those from deterministic trajectories. If one is interested in only configurational or thermodynamic properties of the system, this is of no consequence. If dynamics are of interest, the dependence of these properties on the integrator parameters (e.g. friction factor) should be assessed [70].

4.6.4. Choosing an appropriate timestep

The maximum timestep for a molecular dynamics simulation is dependent on the choice of integrator and the assumptions used in the integrator’s derivation. For the commonly used second order integrators, such as the Verlet and Leapfrog algorithms, the velocities and accelerations should be approximately constant over the timestep. Thus, the timestep is limited by the highest frequency motion present in the system, which for all-atom simulations is usually bond vibrations. It is commonly found that using a timestep that is one tenth of this vibration’s characteristic period is sufficient to conserve energy in the microcanonical ensemble. For example, if hydrogen molecules are present in the simulation box and the H-H bond vibration is the highest-frequency motion in the system with its force field harmonic force constant set to 500 N/m, the oscillation period can be calculated using the equation for simple harmonic motion ($T=2\pi \sqrt{\frac{\mu }{k}}$, where μ is the reduced mass and k is the force constant) to be 8 fs; thus, a 0.5 fs timestep can be used. As another example, if an ab initio MD simulation is being conducted in which C-H bond vibrations are known to be the highest-frequency motion, infrared spectra can be consulted to find that this bond vibration frequency will be approximately 3000 cm⁻¹, which is 11 fs; thus, either a 0.5 or 1.0 fs timestep would be recommended. For all-atom simulations with constraints on the high-frequency bonds, timesteps can be commonly increased to 2 fs; coarse-grained simulations with particles of higher mass and smaller force constants can have much larger timesteps. After choosing a timestep, a test simulation should be run in the microcanonical ensemble to ensure that the choice of timestep yields dynamics that conserve energy. The timestep should also be short enough that properties calculated from the simulation, regardless of ensemble, are independent of the chosen timestep. This is because an inappropriately large timetep can lead to subtle changes to the ensemble being simulated [7,12] and alter computed thermodynamic and transport properties, especially in stochastic simulations or those coupled to thermostats or barostats [84]. Methods also exist to increase the timestep beyond the limit imposed by the system’s highest-frequency motion. Some examples of these enhanced timestepping algorithms include multiple-timestep methods which separately integrate high-frequency motion from low-frequency motion and schemes which repartition atomic masses to decrease the highest- frequency motion seen in the system[85, 86].

4.7. Long range electrostatics

In view of the long-range nature of Coulombic interactions (Section 3.4), handling of electrostatics is particularly important in many systems. Here we describe the motivation for the different treatments of these terms, and give an overview of the core idea of the basic algorithms typically employed.

4.7.1. Motivation

The calculation of non-bonded interactions is generally the most time-consuming step of classical energy calculation. While the number of type of bonded interactions remain unchanged during an MD simulation, the strength and importance of non-bonded interactions varies substantially as a simulation proceeds.

Additionally, Coulombic interactions fall off only very slowly with distance, as r⁻¹, further complicating handling of non-bonded interactions in two different ways. First, calculating all Coulomb interactions over a periodic system results in needing to compute a sum which is conditionally convergent — that is, the value of the sum depends on the order in which it is evaluated [7], meaning we must exercise extreme care or the result will be ambiguous. Second, long-range interactions may be relevant, but determining pairwise distances is an expensive computation that grows with the square of the number of atoms involved.

As discussed in Section 4.2, simulations designed to represent bulk systems are generally performed under periodic boundary conditions, so that the electrostatic potential at any point is due to all the other charges in the system including all of their periodic copies. Given that this is the goal, a set of different methods have been developed to efficiently compute the electrostatic potential due to this infinite, periodic system.

In the early days of simulations, electrostatic interactions were often simply truncated at a particular cutoff radius (r_c). This, however, creates artificial boundary effects and other problems [12], as well as neglecting important long-range interactions.

4.7.2. Ewald Summation

The Ewald summation technique [87] provides one way to efficiently handle long-range electrostatics in periodic systems. To understand this technique, consider the relationship between the charge distribution and the Coulombic potential written in the differential form (the Poisson equation):

$${\nabla }^2\varphi (\mathit{x})=-\frac{1}{ϵ}\rho (\mathit{x})$$

where ϕ(x) is the potential at point x, ρ(x) is the charge density at point x and ε is the permittivity of the medium. The standard way to determine the potential from this equation is to first discretize the equation and then solve, but this requires the functions ρ and ϕ to be smooth. However, here, because we use point charge electrostatics, ρ is a set of delta functions.

The Ewald method is based on (temporarily) replacing the point charge distributions by smooth charge distributions in order to apply existing numerical techniques to solve this partial differential equation (PDE). The most common smooth function used in the Ewald method is the Gaussian distribution, although other distributions have been used as well. Thus the overall charge distribution is divided into a short-range or “direct space” component (ρ^sr) involving the original point charges screened by the Gaussian-distributed charge of the same magnitude (Figure 6) but opposite sign, and a long- range component involving Gaussian-distributed charges of the original sign (ρ^lr). The screening distribution is of opposite sign to allow the screened interactions to fall off rapidly with distance, as we will see below. The sum of the short-range ρ^sr and the long-range ρ^lr charge distributions is still the same as the original charge distribution.

Figure 6.

Screening charge distribution. (Top) The original charge distribution. (Bottom) Point charges can be split into Direct space (blue) and Reciprocal space charges (red). The direct space charge consists of the original charges and Gaussian-distributed screening charges of opposite sign. The reciprocal space charge is only the Gaussian-distributed charge of the original sign. Together these sum to the original charge distribution, but computation of the electrostatic potential due to each component becomes much easier.

Unlike the original, full potential, the direct space screened interaction (Figure 6, top) decays rapidly. In fact, it decays even faster than Van der Waals interactions (1/r⁶) and hence relative short cutoffs, comparable to those used for Van der Waals interactions, can be used for handling direct-space Coulomb interactions (Figure 7).

Figure 7.

Comparison of decay of the original r⁻¹ term for Coulomb interactions (blue,*), the resulting direct-space term after Gaussian screening (black,-) and the r⁻⁶ in van der Waals term (red, −.). Note: The value on the vertical axis has been scaled to allow easy visualization of the relative decay of each term.

The potential due to long-range charge interactions does not decay rapidly, and thus requires consideration of all periodic copies. This would pose severe problems if calculated via direct summation, but the smoothness of the charge p^lr (and hence potential (ϕ^lr) allows the use of fast PDE solvers. Specifically, while the sum is long-ranged in real space, taking the Fourier transform converts it into a sum in reciprocal space which is short-ranged in reciprocal space, damped by a factor exp (–k²σ²/2) where k is the reciprocal space vector and σ is the width of the Gaussian.

The final term in Ewald summation is a so-called self term which gets subtracted out of the overall sum; it is calculated only once at the beginning of the simulation as it depends only on the charge magnitudes and not their positions. It also does not contribute to the force.

4.7.3. Grid based Ewald summation

Ewald summation as described in the previous section takes O(n^3/2) time, where n is the number of charge sites. Switching to a discrete Fourier transform can reduce the cost to to O(nlog(n)). Discretization involves spreading the charge over a grid. Several common grid-based implementations are available which tackle this problem, including Particle-Particle Particle Mesh (P3M), Particle Mesh Ewald (PME) and Smooth Particle Mesh Ewald (SPME). Specifics are chosen in each case to combine accuracy, speed and ease of implementation. In this subsection, we give an overview of the grid-based approach.

Grid-based Ewald summation approaches involve five general steps:

1. Charge assignment: In this step, charges are interpolated onto the grid. While the original PME method uses Lagrangian interpolation for charge assignment, the SPME method uses the smoother cardinal B-splines (hence the name Smooth-PME) to distribute charge onto the grid.

2. Transformation of the grid to reciprocal space: A Fast Fourier Transform (FFT) is used to convert the charges on the grid to their equivalent Fourier space structure factors.

3. Energy calculation: The reciprocal space potential is calculated by solving the Poisson equation in Fourier space, and the reciprocal space potential is then stored on the grid.

4. 4. Transformation of the grid back to real space: An Inverse FFT is used to convert the reciprocal space potential back to the real space.

5. Force calculation: The force is given by the gradient of the potential. PME [35], SPME [88] and P3M [89] use different methods for calculating the force given the resulting potential.

Optimizing the performance of grid based methods can be somewhat challenging; many key choices are made in method implementation and only relative few settings are exposed to the user. Some typical options include:

• Grid dimensions or spacing: A fine grid would be slower, requiring interpolation and calculations for more grid points, but in principle accuracy should be higher.

• Screening function: The width of the Gaussian screening function can often be tuned, but the ideal width is coupled with the direct space cutoff giving limited room for tuning. In some cases alternate, non-Gaussian screening functions are available.

• Direct-space cutoff: This is typically kept at or near the value used for the van der Waals cutoff. Decreasing the cutoff improves the direct space performance but increases the complexity of the reciprocal space calculations.

In principle, it is possible to optimize settings for handling of long-range electrostatics in order to achieve considerable efficiency gains while maintaining accuracy, though this can involve considerable care [90]. For novice users, we suggest typically using well-validated or default settings for the particular method employed, and only deviating from these with careful consideration and testing.

5. Should you run MD?

A critical question before preparing an MD simulation of your system is whether you even should use MD for your system in view of the resources you have and what information you hope to obtain. MD is a tool, but it may not be the right tool for your problem. Before beginning any study, it is critical to sort out what questions you want to answer, what resources (computational and otherwise) you have at your disposal, and whether you have any information about your system(s) of interest that indicate you can realistically expect to answer those questions given a set of MD simulations. Try to understand basic concepts of statistical uncertainty ([24] and https://github.com/dmzuckerman/Sampling-Uncertainty [68]) and use these to make an educated guess regarding your chances of extracting pertinent and reliable information from your simulation.

As noted above, the frequency of the fastest vibrational motions in a system of interest sets a fundamental limit on the timestep which, given fixed computational resources, sets a limit on how much simulation time can be covered with any reasonable amount of computer time. Thus, as noted in Section 1, the longest all-atom MD simulations are on the microsecond to millisecond timescale. This means that if your system is complex and answering your questions will require sampling critical events that have a timescale of seconds or longer, MD will not be the right tool for the job. You could invest a huge amount of effort running MD simulations and find that they did not address your questions.

Ideally, you should have some information before beginning that the relevant timescales for your system might be accessible given the amount of MD you can afford to run, or you could plan a set of exploratory MD simulations to assess feasibility. But do not simply plunge in and attempt to run simulations until you find the answers to your questions, as the required timescales could end up being orders of magnitude longer than what you can afford to spend. Time is only one consideration out of many; disk storage and computer time availability can also prove limiting factors, and opportunity cost, as well, is not to be overlooked.

Ultimately, we ought to be assessing whether MD is the best tool for the job. For our problem of interest, will it really be faster to answer your questions using an MD simulation, or are there experiments which could be done which would answer the question more quickly? Maslow famously wrote, “I suppose it is tempting, if the only tool you have is a hammer, to treat everything as if it were a nail.” We do not want to end up in a position where we are running MD simulations not because they are the best tool for the job, but because they are the only tool available to us. If an experiment could answer our key questions with far less cost and time, and the questions are indeed compelling, perhaps our time might be better spent finding a suitable experimental collaborator rather than running a set of simulations. To give a concrete example, one could imagine using molecular dynamics simulations to screen a library of commercially available compounds for binding to a potential protein target, but if the compounds are commercially available at an inexpensive rate and a suitable assay is available, it might be far faster and cheaper to simply screen the compounds.

So, count the cost of your potential simulations, assess whether they realistically have a chance of answering the questions you seek to answer, and then carefully decide whether the likelihood of success is worth the cost. If not, don’t tackle that problem with MD.

6. Use your MD simulations and interpret the results with care and caution

Analysis of molecular simulations is largely outside the scope of this work; however, some words of caution are worthwhile. It is tempting, especially for those new to or outside of the area, to view simulations as providing “the answer”, giving full mechanistic insight in atomistic detail into what happens in a particular situation and why it happens. Instead, MD results are better thought of as the results of a computational experiment that results from a particular model (including force field), system composition, and protocol. The resulting simulation(s) might or might not be statistically meaningful, relevant to experiment, or useful, but results will be obtained regardless.

This, then, leads us to one of the real dangers of molecular simulations: A simulation produces results, which tempt users to interpret or overinterpret them, whether the results are meaningful or not. For example, even a very short, unequilibrated MD simulation can produce movies which appear interesting and, by virtue of the fact that they result from MD, reveal the positions of all the atoms in a system as a function of time. It’s easy to run several short MD simulations where (for example) the composition of the system is varied, and conclude that any observed differences are a result of variations in composition. But as noted in Section 4.3.3, even simulations started from the same structure but slightly different initial positions or velocities will diverge over time yielding different results, so perhaps any differences are simply a result of this divergence rather than due to the change in conditions. Thus, analysis will require great care and caution to avoid overinterpreting data, and error analysis becomes particularly critical (as discussed in https://github.com/dmzuckerman/Sampling-Uncertainty [68]).

In summary, then, do not use MD simulations simply to make movies and inspect these. Considerable care must be exercised to avoid overinterpeting the full atomistic detail they provide. While movies in some cases can be useful, proper error analysis is always essential.

7. Conclusions

Molecular simulations are particularly exciting, because they provide a detailed view into the structure and function of systems at a molecular or atomistic level. Additionally, they allow us to precisely compute thermodynamic and statistical properties and connect these to underlying motions, structure, and function. Thus MD has played a significant role in our field in suggesting new experiments, generating ideas, and helping to provide mechanistic understanding. Advances in hardware, software, methods and force fields also make MD-based calculations particularly appealing for predictive molecular design, where simulations could be used to help guide experiments to develop materials or molecules with desired properties.

Still, MD simulations require considerable care, as conducting them requires choosing a variety of settings, and the optimal choice of settings typically depends on the problem being considered. Thus, it is our hope that this document provides a helpful overview of some of the fundamental considerations for preparing and conducting MD simulations and paves the way for more specialized documents which will focus on calculations of specific properties or for specific classes of systems, since the approach employed will often need to vary depending on such choices.

This document also provides a checklist covering some of the key points raised in this work and highlighting particularly common sources of failure; we encourage readers to follow this when considering a simulation study.

Our focus here has been on the basics — focusing on things you need to understand before beginning to prepare simulations for yourself. Additionally, we have primarily focused on issues relating to how simulations are conducted, and leave data analysis for a separate treatment. As a starting point relating to data analysis, readers should probably review the Best Practices document on sampling and uncertainty estimation (https://github.com/dmzuckerman/Sampling-Uncertainty [68]).

Please remember that this is an updatable work, so we welcome contributions and suggestions via our GitHub issue tracker at https://github.com/MobleyLab/basic_simulation_training.

Figure 3.

Periodic boundary conditions are shown for a simple 2D system. Note that the simulated system is a sub-ensemble within an infinite system of identical, small ensembles.

TAKE STOCK OF YOUR PLANS.

• Count the cost: Think about what you know about the timescales of what you want to observe and determine whether it is tractable to simulate this given the size of your system, your computational resources, and the expense of the simulation. Would the questions you want to answer be better addressed a different way?

• Pick the desired ensemble (NVT, NPT, NVE, μVT)^a

• Determine reference states that you are trying to emulate/discover.

• What temperature, pressure, etc. are you interested in?

• What force field properly describes your system?

• What is already known in the literature and what data do you wish to compare to?

^aFor mixtures, the semi-grand ensemble (or osmotic ensemble) may be of interest, where the number of particles is fixed but their identities can change [12] allowing, e.g., a constant chemical potential for salt ions to be maintained [91]

PREPARE TO IMPLEMENT YOUR PLANS AND MAKE CRITICAL DECISIONS ABOUT THE SYSTEM.

• Choose a simulation package suitable for simulating that ensemble with your target force field

• Determine whether you are simulating a bulk (typically periodic) or finite system and choose the appropriate cutoff types and periodicity (full periodicity for bulk systems, partial periodicity for interfaces, etc.) as discussed in Section 4.2

• Prepare your system, paying particular attention to ensuring it contains the chemical components you want with the structures you want, and that force field parameters are assigned as intended (it is good practice to ensure that you properly implemented the force field by replicating energies, forces, or other observables from prior publications)

DETERMINE HANDLING OF CUTOFFS.

• As a general rule, electrostatics are long-range enough that either the cutoff needs to be larger than the system size (for finite systems) or periodicity is needed along with full treatment of long-range electrostatics (Section 3.4)

• Nonpolar interactions can often be safely treated with cutoffs of 1–1.5 nm as long as the system size is at least twice that, but long-range dispersion corrections may be needed (Section 4.1)

CHOOSE APPROPRIATE SETTINGS FOR THE DESIRED ENSEMBLE.

• Pick a thermostat that gives the correct distribution of temperatures, not just the correct average temperature; if you have a small system or a system with weakly interacting component choose one which works well even in the small-system limit.

• Pick a barostat that gives the correct distribution of pressures

• Consider the known shortcomings and limitations of certain integrators and thermostats/barostats and whether your choices will impact the properties you are calculating

CHOOSE AN APPROPRIATE TIMESTEP FOR STABILITY AND AVOIDING ENERGY DRIFT.

• Determine the highest-frequency motion in the system (typically bond vibrations unless bond lengths are constrained)

• As a first guess, set the timestep to approximately one tenth of the highest-frequency motion’s characteristic period

• Test this choice by running a simulation in the microcanonical ensemble, and ensure that energy is conserved

DETERMINE YOUR RUN PROTOCOL.

• Plan how you will minimize and equilibrate your system and test that your equilibration protocol actually allows you to reach equilibrium in the target ensemble (Section 4.3)

• Determine production settings, how many steps to run, and how often to store data/what data to store

• Ensure you have sufficient storage, memory, and computer time to complete the planned calculations