Abstract
The twenty-four hour sleep-wake pattern known as the rest-activity rhythm (RAR) is associated with many aspects of health and well-being. Researchers have utilized a number of interpretable, person-specific RAR measures that can be estimated from actigraphy. Actigraphs are wearable devices that dynamically record acceleration and provide indirect measures of physical activity over time. One class of useful RAR measures are those that quantify variability around a mean circadian pattern. However, current parametric and nonparametric RAR measures used by applied researchers can only quantify variability from a limited or undefined number of rhythmic sources. The primary goal of this article is to consider a new measure of RAR variability: the log-power spectrum of stochastic error around a circadian mean. This functional measure quantifies the relative contributions of variability about a circadian mean from all possibly frequencies, including weekly, daily, and high-frequency sources of variation. It can be estimated through a two-stage procedure that smooths the log-periodogram of residuals after estimating a circadian mean. The development of this measure was motivated by a study of depression in older adults and revealed that slow, rhythmic variations in activity from a circadian pattern are correlated with depression symptoms.
Keywords: Actigraphy, Depression, Rest-Activity Rhythm, Spectral, Analysis, Time Series, Wearable Technology
1. Introduction
Modern wearable technology provides a practical, noninvasive means of gathering dynamic information within a natural environment. One such type of technology is actigraphy. Actigraphs are compact, lightweight, computerized accelerometer-based devices used to monitor physical activity. Actigraphy has been used to quantify both measures of sleep [1] and measures of daytime activity [25]. As actigraphs can be worn nearly continuously over extended periods of time, such as days or weeks, actigraphy also allows researchers and clinicians to evaluate an individual’s 24-hour, or circadian, pattern of rest and activity. This pattern is commonly referred to as the rest-activity rhythm (RAR). RAR has been shown to be associated with many aspects of health. In particular, RAR provides an objective, indirect assessment of depression’s behavioral manifestations and risks [23]. Through this capacity, RAR measures have the potential to aid clinicians in monitoring risk and tailoring treatment for depression.
Applied researchers traditionally quantify RARs through two classes of subject-specific measures: parametric and nonparametric. Parametric measures are derived from the parameters of nonlinear regression models for the circadian mean function. The accompanying pseudo-F statistic of the fitted regression model is also considered as a measure of the fit of a mean circadian pattern relative to variation around this mean. Early approaches assumed a 24-hour cosinor model, while more recent approaches utilized a 5-parameter extended cosine model [15]. Nonparametric approaches assume no parametric model for the mean and are derived directly through quadratic and linear functions of the time series. These include the quadratic functions known as interdaily stability (IS), which measures the relative strength of the circadian rhythm, and intradaily variability (IV), which quantifies the amount of fragmentation of this rhythm. It should be noted that, in addition to these two classes of measures that are derived individually for actigraphy time series, there has been recent research into the use of functional regression for analyzing population parameters of actigraphy ([7], [16], [27], [31]). The focus of this article is on methods that provide interpretable subject-specific measures, which are widely used by researchers and are of interest to clinicians when treating individual patients.
The primary goals of this article are three-fold. First, we aim to summarize and provide new insights into some of the popular subject-specific parametric and nonparametric RAR measures used by applied researchers. The second goal of this article is to introduce a flexible measure of RAR variability to enhance the information currently available through existing measures. The parametric pseudo-F statistic and the nonparametric IS and IV measures all provide measures of variability. However, each of these summary measures provides information about specific, and not often well defined, sources of harmonic variability. We introduce a functional measure, which we refer to as the residual circadian spectrum (RCS), that can capture full information about harmonic variability. This measure is defined as the log-spectrum of the stochastic variability when log-activity is modeled through a parametric circadian mean plus stationary stochastic variability. The RCS curve, which quantifies the amount of variation about the circadian mean from different frequencies, can be considered a semiparametric measure in that, although a parametric form is assumed for the mean, no parametric form is assumed for the spectrum. In addition to the information provided by individual RCS curves, frequency band-collapsed summary measures can be formulated to provide low-dimensional representations that best preserve information across RCS from different subjects within a population. These frequency band measures can then be used in further analyses to elucidate biobehavioral correlates of clinical outcomes. The final goal of this paper is to investigate the relationship between RAR and depression symptoms in a study of depression in adults. In this study, it is found that RCS is associated with depression symptoms and provides additional information beyond that provided by existing parametric and nonparametric RAR measures.
The rest of this article is as follows. The motivating study of depression in adults is discussed in Section 2. Popular existing parametric and nonparametric RAR measures are discussed in Section 3. The proposed RCS measure is developed in Section 4. A discussion pertaining to summarizing RCS information from a population within frequency band-collapsed measures is given in Section 5. The data from the motivating study are analyzed in Section 6. The article concludes with a discussion in Section 7.
2. Motivating Study
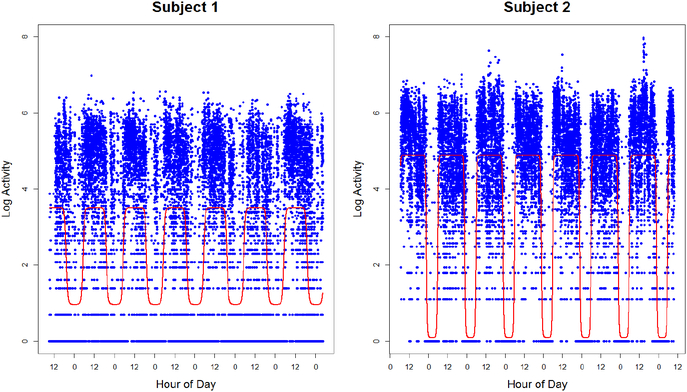
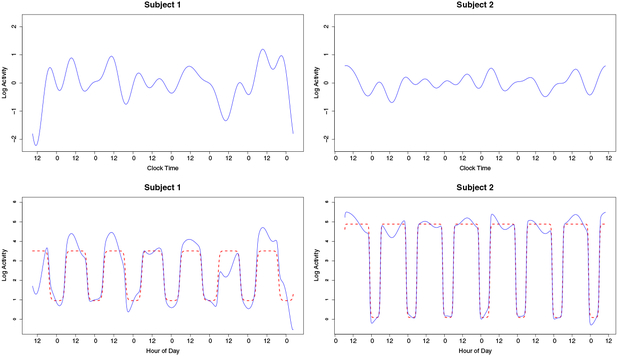
An estimated 300 million people globally suffer from depression [30], making it the leading cause of disability worldwide. Evidence suggests that RARs not only serve as a biobehavioral marker for depression, but more importantly, they represent a risk factor and a potential target for prevention [23]. We consider a study conducted at the University of Pittsburgh to better understand depression symptoms in adults. Study participants wore an Actiwatch 2 on the non-dominant wrist for approximately one week. The device included an accelerometer with a sampling rate of 32 Hz, whose data were processed to produce activity counts in 30 second epochs. Actigraphy profiles for 145 men and women aged 38–82 years, who may or may not have had a history of depression, but who had no history of other psychiatric disorders or substance abuse, were obtained. We illustrate activity counts on the logarithmic scale and display data for two subjects in Figure 1.
Fig. 1.
Log-activity counts and fitted mean circadian rhythms for two subjects in the depression study. Subject 1 (left) had a HAMD score of 52 and Subject 2 (right) had a HAMD score of 0.
Study participants underwent a clinical examination prior to being fitted with the actigraph. During this examination, the 17-item Hamilton Depression Rating Scale was administered [10]. The Hamilton Depression Rating Scale is a clinical tool for measuring depressive symptoms in which patients are rated on 17 domains by a clinician on a 3- or 5-point Likert scale, depending on the question. These scores are then totaled to compute a Hamilton Depression Score (HAMD). Larger values indicate more sever depression symptoms, with scores of 0–7 being indicative of no depression, 8–16 of mild depression, 17–23 of moderate depression, and greater than 24 of severe depression [32]. HAMD among study participants ranged from 0 to 52, with a mean of 21.15 and a standard deviation of 17.72.
3. Popular RAR Measures
There exist two popular classes of RAR measures: parametric and nonparametric. The two classes of measures are complimentary, each with its own strengths and weaknesses. The class of parametric measures, which are reviewed by Marler et al. (2006) [15], are derived from the parameters of a deterministic model for a circadian rhythm. Parametric measures have a strength in that the parameters provide interpretable measures about the shape, size and timing of the RAR. They have a weakness in that, although popular parametric models are flexible and can capture a variety of shapes, the measures are still dependent on the validity of a parametric model. Nonparametric measures, which are described by van Someren et al. (1996) [24], are defined directly by quadratic and linear statistics of the time series. They have the strength in that they do not depend on the validity of some model, but have the weakness of only quantifying a limited number of specific characteristics whose interpretations are not always direct.
3.1. Parametric Measures
Consider the time series of log-activity counts, xt, t = 1, …, T. A one is added to each count before taking the logarithm to avoid zero counts. We assume that the series represents counts within regular intervals, with there being r intervals per hour. Equivalently, we assume activity is summed within adjacent, non-overlapping epochs of length 1/r hours. In our motivating example, activity is computed within 30 second epochs where r = 120, but 1 minute (r = 60) and 1 hour (r = 1) epochs are also common. The parametric approach assumes that
| (1) |
where h is a deterministic circadian function of time (i.e. a function with a 24-hour period), is a collection of p parameters indexing the circadian function, and ϵt is a mean-zero second order stationary stochastic process. Early approaches used a cosinor model where h is a linear combination of sine and cosine functions with 24-hour periods. Although this provides a very simple model, RARs typically do not follow a pure sinusoidal pattern with a 24-hours period. Multiparameter extended cosine models take a nonlinear transformation of the 24-hour cosine function and provide flexible models of RAR with interpretable parameters. A review of a class extended cosine models is given by Marler et al. (2006) [15]. Here, we consider one specific and widely used model, which is referred to as the anti-logistic or expit model. In this model, h is parameterized by p = 5 parameters θ = (m, a, α, β, ϕ)’ such that
where expit(x) = ex/ (1 + ex) is the expit, or anti-logistic, function. For identifiability, we assume that m > 0 a > 0 α ∈ (−1,1), β > 0 and ϕ ∈ [0, 24]. The maximum value of h occurs when t = ϕ. We refer to ϕ as the acrophase, which represents the time of the day when peak activity occurs. The parameters α and β are shape parameters. The parameter α controls the amount of time spent at rest relative to active time, with more negative values indicating less resting time. The parameter β is proportional to the rate of change when transitioning from rest to activity, with larger values indicating a quicker transition between rest and peak activity.
The parameters m and a control the extremes of h. By noting that expit(x) has asymptotes at 0 and 1 for , m is commonly interpreted as the minimum and a as the amplitude (i.e. the difference between the maximum and the minimum) [15]. However, it should be noted that, given a set of shape parameters α and β, expit (β [cos {(t/r − ϕ) 2π/24} − α]) can be bounded rather far from 0 and 1. Consequently, we consider the minimum and amplitude defined as the smallest value of h(t; θ) and the difference between the largest and smallest values of h(t; θ) given the parameters θ, which can be computed as
The parameter θ is estimated though nonlinear least squares
which can be computed using Gauss-Newton [2]. Estimated circadian functions are displayed in Figure 1 for two participants in the motivating study.
In addition to the estimated parameters in θ, the psuedo-F statistic of the nonlinear regression model
where , is also reported. The psuedo-F statistic is interpreted as a measure of how well observed activity are fit by a circadian rhythm relative to variability around the circadian mean.
3.2. Nonparametric Measures
Researchers also consider a set of nonparametric measures. The nonparametric measures do not assume an underlying model for the time series of activity counts, only that they come from a second-order stationary process. Traditionally, these measures are computed using hourly activity (r = 1), but minute activity (r = 60) has also been recently considered [8]. In this article, we consider hourly epochs. There are two primary nonparametric measures of variability: interdaily stability (IS) and intradaily variability (IV).
IS is a measure of the strength of a circadian pattern. It is a signal-to-noise ratio defined as the ratio of the average square-error of hourly means from the grand mean divided by the sample variance. Formally,
where is the mean of the activity score at hour s = 1, …, 24 over multiple days of observation.
IV measures fragmentation of the circadian rhythm and is defined as
When there is high variation in hour-to-hour activity, the numerator is large. Consequently, IV is a ratio of hour-to-hour variation relative to total variability. By noting that the first differencing operator is a high-pass filter [22], one could also interpret the numerator as a measure of variability at high frequencies. Consequently, IV can also be interpreted as the percent of total variability that is accounted for by high-frequency variation.
It should also be noted that, in addition to IV and IS, nonparametric measures of minimum and maximum activity can also be considered. The nighttime activity level (L5) is the mean of the 5-hour period with lowest activity, and the daytime activity level (M10) is the mean of the 10-hour period of maximum activity. However, the focus of this article is on measures of variability, so we will not consider L5 and M10.
4. Residual Circadian Spectrum (RCS)
4.1. Definition
Thus far we have discussed three popular measures related to RAR variability: the parametric pseudo-F and the nonparametric measures IS and IV. However, these three measures offer only limited or partial information abut which rhythmic activity patterns significantly influence RAR variability. First, the pseudo-F statistic only provides a very gross measure of variation about the circadian mean with no insight into exactly how a person’s activity varies. For instance, a small pseudo-F statistic could be a result of an individual going to bed later every Friday and Saturday compared to other days, or it could be a result of an individual waking up regularly and often every night, or it could be the result of an individual alternating between hourly periods of high and low activity during the day. The measure IS provides a measure of the strength of a circadian signal relative to variance, but can also not distinguish between low-frequency variability between days and high-frequency variability within-days. The measure IV provides an understanding of the presence of high-frequency variation, but cannot speak about low-frequency variations. Our goal is to introduce a functional measure that can summarize variation from all possible rhythmic sources and pinpoint frequencies of importance.
We will assume the parametric model (1). Here, the stochastic term ϵt contains information with regards to variability about the deterministic circadian rhythm h. We will assume that ϵt has mean zero and is second-order stationary, from which we can define the autocovariance function
When γ(s) decays fast enough so that it is absolutely summable, we can define the power spectrum
The function f is periodic, such that f (ω) = f (ω + 1), and is an even function, where f (ω) = f (−ω). Due to the periodic and even nature of power spectra, we display f over frequencies between [0,1/2]. In addition, power spectra are non-negative, and we assume that f is positive, or f (ω) > 0 for ω. To aid visualization and avoid the need for constrained estimation, we consider the spectrum on the log-scale, and define
We refer to g as the residual circadian spectrum (RCS).
There is a one-to-one transformation between the autocovariance and the power spectrum, where the inverse relationship is
Substituting s = 0, it can be seen that
Consequently, the power spectrum can be thought of as a type of ANOVA decomposition, where f (ω)dω represents the amount of the total variance that is attributable to periodic variations at frequencies within some small radius dω of ω. In our motivating study, data are summarized in 30 second epochs, so that ω is in units of cycles per 30 seconds. For example, the amount of variability attributed to 12-hour variation, or one cycle per 12 hours, is given by f evaluated at ω = 1/1440 cycles per 30-second. However, for ease of interpretation, we change units to cycles per hour when reporting results.
It should be noted that, under the nonparametric model where it is only assumed that yt is second-order stationary, one could conduct a spectral analysis directly on yt rather than on the residuals from a parametric model. However, this would address the question of how much variance in activity is attributable to variability at given frequencies. We are concerned with the slightly different question that is addressed by the RCS: how much of the variance not accounted for by a mean circadian rhythm is attributable to variability at different frequencies.
4.2. Estimation
Estimation of a power spectrum traditionally begins by considering the periodogram, or the square modulus of the discrete Fourier transform. Since the variables ϵt are not observed, we take a two-step estimation procedure. In the first step, the nonlinear regression model is fit and the residuals
are computed. Then, the periodogram of the residuals are computed
for k = 1, …, K, where K = ⌊(T − 1)/2⌋, ⌊x⌋ represents the largest integer less than x, and ωk = k/T are the Fourier frequencies.
When T is sufficiently large, zk are approximately independent and distributed as . This implies that zk is an approximately unbiased but inconsistent estimator of f (ωk). A consistent estimator can be obtained by smoothing the periodogram across frequency. Many approaches are available for smoothing the periodogram, including local averaging [22], smoothing splines [26], and wavelets [17]. Here, we adopt a smoothing spline approach that minimizes a penalized Whittle likelihood. Smoothing spline estimators are obtained by minimizing penalized functions comprised of two parts: a measure of the lack of fit of an estimator to observed data and a penalty regularizing the smoothness of the estimator. The large sample distribution of the periodogram leads to the so-called Whittle likelihood [28]. The negative log-Whittle likelihood can be used as the measure of lack of fit to obtain efficient estimators ([19], [20]). We will regularize the roughness of the estimate by penalizing the integrated square second derivative of the log-spectrum. Formally, given a smoothing parameter λ > 0, we estimate the RCS as the unique periodic, even function with a finite square-integrable second derivative that minimizes
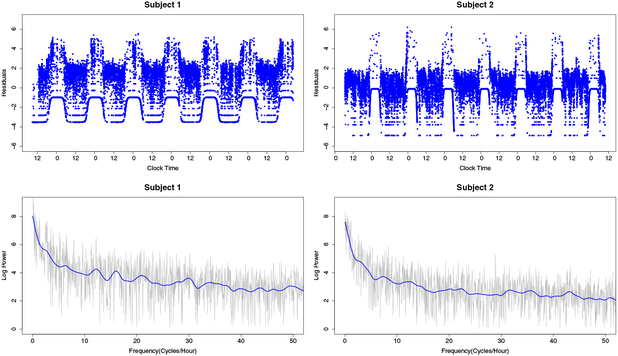
The smoothing parameter balances the smoothness of the estimated spectrum with its fit to the data. As λ → ∞, the estimated spectrum approaches a constant function of frequency and, as λ → 0, the estimated spectrum interpolates the periodogram. Estimated residuals , estimated RCS , and bias-adjusted log-periodograms, log(zk) + τ, where τ ≈ 0.577 is the Euler-Mascheroni constant, are displayed in Figure 2 for the two subjects whose activity data are displayed in Figure 1.
Fig. 2.
Residuals, bias-adjusted log-periodograms and estimated RCS for the two subjects whose activity count data are displayed in Figure 1.
The minimizer of the penalized negative log-Whittle likelihood has the form
where and the coefficients ck, k = 0, …, K, can be computed via Newton-Raphson or Fisher Scoring [9]. It should be noted this penalized Whittle likelihood estimator uses a different kernel Q than the smoothing spline estimators considered by others ([9], [19], [20]). These other approaches model the log-spectrum as smooth and periodic, but do not account for its even structure. As discussed by Krafty & Collinge (2013) [12], accounting for the even nature of the log-spectrum aides estimation, especially at the boundary near ω = 0 and ω = 1/2.
5. Frequency Band-Collapsed Summary Measures
5.1. Low Dimensional Measures
The RCS from an individual subject provides information about variability in activity from all rhythmic sources around their circadian mean. In practice, researchers and clinicians are also interested in understanding RCS within a population of subjects and in how RCS is associated with clinical and biological variables.
The infinite dimensional nature of a power spectrum as continuous function of frequency poses challenges in conducting such analyses. Although RCSs from multiple subjects could be treated as a functional variable whose association with clinical and biological variables could be assessed via functional regression models, such an approach could fail to provide interpretable, lowdimensional measures that can be used by clinicians and researchers. Utilizing the continuous nature of spectra from biological and behavioral time series, where power at neighboring frequencies can contain indistinguishable information, but where power from distant frequencies are approximately uncorre lated, researchers typically summarize spectral information within frequency bands. A frequency band is an interval of frequencies and a frequency band-collapsed measure is derived by taking a linear combination of power within the band. Popular examples include EEG, where power is commonly collapsed within the delta band of frequencies less than 4 Hz, the theta band between 4–8 Hz, the alpha between 8–15 Hz, the beta band between 16–31 Hz, and the gamma band of frequencies greater than 32 Hz, and heart rate variability, where power is collapsed into low frequencies between 0.05–0.15 Hz and high frequencies between 0.15–0.40 Hz [4].
Formally, a set of L frequency bands is defined by a partition of the frequency space into non-overlapping sets Wℓ ⊂ [0, 1/2], Wℓ ∩ Wm = 0, ℓ, m = 1, …, L, ℓ ≠ m, and associated weight functions γℓ. The weight function for the ℓth band has rapport within Wℓ such that γℓ(ω) = 0 for all ω ∉ Wℓ,. The spectral power is then summarized through the L measures defined as linear combinations of the log-spectra with weight functions γℓ. The value of the ℓth frequency band-collapsed measure for the jth subject, j = 1, …, N, is
The subject-specific scores yjℓ can then be used in analyzes of association with other variables, such as HAMD in our motivating study.
5.2. Functional Principal Component Analysis (FPCA)
Consider a collection of RCS, gj, j = 1, …, N, that can be modeled as independent realizations of a stochastic process with covariance function
An intuitive approach for optimally defining frequency bands to preserve variability among subjects is through functional principal component analysis (FPCA). The first principle component is defined as the linear combination of RCS that preserves the most variability, or maximizes
such that . Higher order components are successively defined as maximizers orthogonal to lower-order components. Formally, given weight functions for the first L − 1 components, γ1, …, γL-1, the Lth component maximizes such that and for .
The principal components can be computed through the eigenfunctions of Γ. When Γ is square-integrable, it possess the eigendecomposition
for orthonormal eigenfunctions γℓ and non-negative, non-increasing, summable eigenvalues τℓ. The eigenfunction γℓ is a weight function for the ℓth principle component and var(yjℓ) = τℓ. The eigenvalues τℓ can be used to determine the number of components for analysis by choosing L such that the fraction of variance explained (FVE) by the first L components, , relative to the total variance, is above some threshold.
5.3. Localized Functional Principal Component Analysis (LFPCA)
FPCA has been an essential tool for the analysis of functional data since the 1980’s [3]. Early methods focused on utilizing the functional or smooth nature of functional data. For example, Rice & Silverman (1991) [21] consider estimating the first FPCA at discretized values from the observed data gj = [gj(ω1), …, gj(ωK)]′, j = 1, …, N, by maximizing trace [(S – ρ0D) (γγ′)] such that γ′γ = 1, where S is the K × K sample covariance matrix, D = Δ′Δ is a K × K roughening matrix with Δ being the (K − 2) × K matrix where Δij = 1 when j ∈ {i, i + 2} Δij = −2 when j = i +1, and is zero otherwise. The parameter ρ0 controls the smoothness of the estimated component, and can be selected either subjectively or through cross-validation.
Although this approach can provide consistent estimators, the estimated eigenfunction will have non-zero support across the entire range of frequencies, even if the true component is band limited and has support only within a subinterval of frequencies. This issue, which creates complications for interpretation, is especially troublesome in our setting, were we desire low-dimensional measures that are band-limited and interpreted as power within a range of frequencies. A naive approach would be to directly add an penalty to impose localization. However, such an approach presents a non-convex and computationally intractable problem. Chen & Lei (2015) [5] proposed a solution byembedding the problem within the Fantope, or the convex hull of rank-one projection matrices, , where implies that B − A is nonnegative definite. Formally, the first estimated weight function is defined as the first eigenvector of the matrix H that maximizes
such that and ||H||1 is the matrix norm that is the sum of the absolute value of all elements of H. The tuning parameter ρ1 controls the amount of localization. This convex optimization problem can be efficiently solved through an alternating direction method of multipliers algorithm. Higher-order components can be computed similarly, but optimizing over a deflated Fantope that is orthogonal to previously estimated lower-order components.
6. Data Analysis
6.1. Estimated RCS
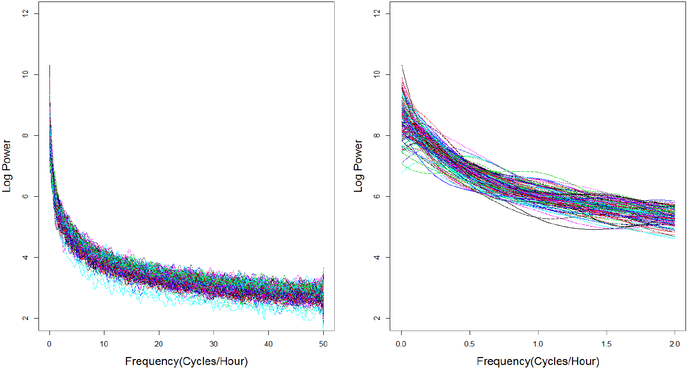
We applied the proposed procedure to the data from the study of depression in adults described in Section 2. The RCS was estimated for each subject using the smoothing spline described in Section 4.2, with smoothing parameters selected through generalized maximum likelihood [29]. Figure 3 displays the estimated RCS from all 145 subjects, both for the full range of frequencies and, to aid visualization, also restricted to the range of low frequencies up to 2 cycles per hour.
Fig. 3.
Estimated RCS curves for the entire range of frequencies (left) and restricted to low frequencies less than 2 cycles per hour (right).
6.2. Frequency Bands
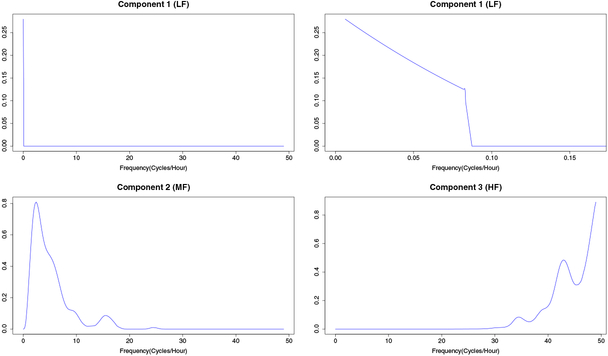
A LFPCA was conducted on the estimated RCS curves, using leave-out-one cross-validation to select the smoothing parameter ρ0, and selecting the localization parameter ρ1 and number of components L to maintain 90% of the FVE. Figure 4 displays the first 3 estimated eigenfunctions, which account 76.8%, 9.3% and 5.6% of total variability, respectively. The first component is a function of frequencies less than or equal to 2/24 cycles per hour, or two cycles per day. The second component is a function of frequencies between 2/24 cycles per hour and approximately 25 cycles per hour, while the third component is a function of frequencies greater than approximately 25 cycles per hour. We refer to these three band-collapsed measures as low-frequency (LF), middle-frequency (MF) and high-frequency (HF) power, respectively.
Fig. 4.
First L = 3 estimated LFPCA weight functions, which account for 76.8%, 9.3% and 5.6% of total variability, respectively. The first component is plotted as a function across all frequencies (top left) and within frequencies less than 4/24 cycles per hour (top right) to aid visualization.
The first component, or the LF component, accounts for the majority of variability. To examine this measure, Figure 5 graphically displays LF variation in the two subjects whose data were considered in Figures 1 and 2. A low-pass filter was applied to the residuals from the estimated deterministic circadian rhythm to maintain only variation at frequencies less than or equal to 2/24 cycles per hour. The LF score for a subject is approximately proportional to the sample variance of the low-pass filtered residual series. In Figure 5, it can be seen that Subject 1 has a higher LF score than Subject 2. The LF band is comprised of frequencies less than 2 cycles per day. This includes variation at frequencies of 1 cycle per day and slower, which account for variation in activity between days. For instance, Subject 1 experienced higher than average levels of activity during days 5 and 7, and less than average activity on days 1 and 6. The upper bound of the LF band of 2 cycles per day reflects differences in variation from the circadian mean in the morning and in the afternoon/evening on the same day. For example, during the second day, Subject l’s activity was above the circadian mean before 1pm, but below the circadian mean after 1pm. Consequently, LF can be viewed as a measure of deviation from the circadian mean due to variability in activity between days as well as due to variability between mornings and afternoon/evenings within days.
Fig. 5.
LF variation (top row), estimated deterministic circadian mean (bottom row, red dotted line) and estimated deterministic circadian mean plus LF variation (bottom row, solid blue line) for the two subjects whose data were considered in Figures 1 and 2.
6.3. Associations with Other Variables
To conduct an exploratory analysis of associations between the RCS band-collapsed measures and other variables, Table 1 displays estimated pair-wise Pearson correlation between the clinical outcome HAMD, the three RCS band-collapsed measures (LF, MF, HF), the two nonparametric measures (IS, IV), and the six traditional parametric measures (F, α, β min, amp, ϕ). The three RCS band-collapsed measures are negatively correlated with F. This is anticipated, as F is a measure of the goodness-of-fìt of the parametric circadian mean and the RCS quantifies variability of the residuals from this model. All three RCS band-collapsed measures are also negatively associated with IS; LF has the strongest association, with an estimated correlation of −60%. This is also anticipated, as IS is a measures of the strength of a daily signal and LF is comprised, in part, of daily variation. The three RCS band-collapsed measures are positively correlated with IV; MF and HF has the strongest associations, with estimated correlations of 53% and 47%, respectively. IV is a measure of the fragmentation of the circadian rhythm, which as previously discussed, is equivalent to relative variability after applying a first-difference high-pass filter to highlight hourly variation and faster, which is contained in MF and HF.
Table 1.
Estimated correlation between HAMD, the three RCS frequency-band collapsed measures (LF, MF, HF), the two nonparametric measures (IS, IV) and the six parametric measures (F, a, β, min, amp, ϕ).
| HAMD | LF | MF | HF | IS | IV | |
|---|---|---|---|---|---|---|
| HAMD | 1.00 | 0.31 | 0.20 | 0.20 | −0.23 | 0.18 |
| LF | 0.31 | 1.00 | 0.03 | 0.02 | −0.60 | 0.13 |
| MF | 0.20 | 0.03 | 1.00 | 0.08 | −0.29 | 0.53 |
| HF | 0.20 | 0.02 | 0.08 | 1.00 | −0.23 | 0.47 |
| IS | −0.23 | −0.60 | −0.29 | −0.23 | 1.00 | −0.51 |
| IV | 0.18 | 0.13 | 0.53 | 0.47 | −0.51 | 1.00 |
| F | −0.23 | −0.48 | −0.52 | −0.45 | 0.51 | −0.38 |
| α | 0.25 | 0.16 | 0.05 | 0.01 | −0.26 | 0.01 |
| β | −0.01 | −0.34 | 0.03 | 0.02 | 0.14 | 0.29 |
| min | 0.25 | 0.10 | 0.23 | 0.23 | −0.31 | 0.38 |
| amp | −0.12 | 0.06 | −0.52 | −0.54 | 0.27 | −0.59 |
| ϕ | 0.24 | 0.34 | 0.03 | 0.08 | −0.41 | 0.21 |
| F | α | β | min | amp | ϕ | |
| HAMD | −0.23 | 0.25 | −0.01 | 0.25 | −0.12 | 0.24 |
| LF | −0.48 | 0.16 | −0.34 | 0.10 | 0.06 | 0.34 |
| MF | −0.52 | 0.05 | 0.03 | 0.23 | −0.52 | 0.03 |
| HF | −0.45 | 0.01 | 0.02 | 0.23 | −0.54 | 0.08 |
| IS | 0.51 | −0.26 | 0.14 | −0.31 | 0.27 | −0.41 |
| IV | −0.38 | 0.01 | 0.29 | 0.38 | −0.59 | 0.21 |
| F | 1.00 | −0.37 | 0.25 | −0.11 | 0.24 | −0.34 |
| α | −0.37 | 1.00 | −0.21 | 0.46 | 0.04 | 0.28 |
| β | 0.25 | −0.21 | 1.00 | 0.27 | −0.27 | −0.05 |
| min | −0.11 | 0.46 | 0.27 | 1.00 | −0.43 | 0.08 |
| amp | 0.24 | 0.04 | −0.27 | −0.43 | 1.00 | −0.07 |
| ϕ | −0.34 | 0.28 | −0.05 | 0.08 | −0.07 | 1.00 |
HAMD is positively correlated with all three RCS band-collapsed measures, negatively correlated with F and IS, and positively correlated with IV. These are all consistent with previous findings, where increased variability from a stable circadian mean have been found to be associated with increased depression [23]. It is interesting to note that, out of the large number of RAR parameters investigated, LF had the highest estimated correlation with HAMD at 31%. This is exemplified by the two subjects considered in Figures 1, 2 and 5. Subject 1 had a higher LF (2074 vs. 1731) and a higher HAMD (52 vs. 0) compared to Subject 2. This result could be suggestive that both daily variation from a circadian mean and variation between morning and afternoon/evening could provide biobehavioral information that is associated with depression. To closer investigate the possible additional information provided by LF in predieting HAMD beyond that contained in existing measures, Table 2 displays the results of 4 linear regression models: HAMD regressed only on LF, HAMD regressed on LF and the two nonparametric measures, HAMD regressed on LF and F, and HAMD regressed on LF and the 5 parametric shape and location parameters. We see that LF is positively and significantly associated with HAMD, not only marginally, but also when controlling for other variables.
Table 2.
Results of 4 fitted linear regression models regression HAMD on LF, LF and F, LF and the nonparametric measures IS and IV, and LF and the five parametric shape and location parameters a, β, min, amp and ϕ.
| Estimate | Std. Error | t-Statistic | P-value | |
|---|---|---|---|---|
| Intercept | −67.3960 | 24.0749 | −2.80 | 0.0059 |
| LF | 0.0423 | 0.0115 | 3.68 | 0.0003 |
| Intercept | −49.7148 | 28.2993 | −1.76 | 0.0813 |
| LF | 0.0349 | 0.0130 | 2.68 | 0.0084 |
| F | −0.0018 | 0.0015 | −1.18 | 0.2386 |
| Intercept | −82.3788 | 40.4900 | −2.03 | 0.0439 |
| LF | 0.0430 | 0.0148 | 2.90 | 0.0044 |
| IS | 4.9836 | 14.2304 | 0.35 | 0.7268 |
| IV | 21.0823 | 12.6452 | 1.67 | 0.0979 |
| Intercept | −60.0925 | 31.9261 | −1.88 | 0.0621 |
| LF | 0.0357 | 0.0129 | 2.76 | 0.0067 |
| α | 14.8166 | 9.7457 | 1.52 | 0.1309 |
| β | 0.1182 | 0.1798 | 0.66 | 0.5119 |
| min | 3.6367 | 6.3257 | 0.57 | 0.5664 |
| amp | −2.4669 | 2.5817 | −0.96 | 0.3411 |
| ϕ | 1.3232 | 1.3014 | 1.02 | 0.3112 |
7. Discussion
Patterns of rest and activity are associated with many aspects of health and functioning. In this article, we considered their connection to depression, but they have been shown to associated with many facets of well-being. The relative inexpensiveness and accessibility of actigraphy gives researchers the ability to measure such data in a high-resolution manner, over long periods of time, in one’s natural environment. Ideally, this information can be used to inform interventions and treatments. Researchers use several subject-specific measures to quantify the RAR, but measures of variability about a mean circadian rhythm have been limited. This article introduces a new measure, RCS, which accounts for and quantifies variability of activity about a circadian mean from all rhythmic sources.
It should be noted that the procedure considered for estimating the RCS is based on the periodogram, which is defined assuming that there are no missing data. However, technical issues and, more importantly, non-wear, could lead to missing values in the activity count time series. When there is little missing data or data are missing in a periodic fashion, such as an individual removing the device at approximately the same time each day, the periodogram can be adjusted by replacing the missing values with the sample mean of the observed values and adjusting the sample size to reflect the number of observed data points [18]. If data are missing in a more complicated manner, the Lomb periodogram [14] could be used in lieu of the considered Fourier periodogram. In the case of more complicated patterns of missing data, alternative, non-periodogram based approaches for spectral estimation could be used to estimate the RCS, including maximum likelihood estimation under parametric models [22] and nonparametric time-domain approaches [13].
There remain several open problems that need to be addressed before the RCS can have applied impact. First, the RCS is computed off-line using data from a fixed time frame. A real time measure would be more practical for monitoring an individual’s risk. Second, the reliability of the RCS, and in particular of LF measures, is dependent on the number of days of activity under observation. Although anecdotal suggestions for a minimum of a week’s worth of data to allow one to capture weekly variation can be stated, the number of days required to obtain stable estimates of not only the RCS, but also other RAR parameters, is unknown. The establishment of guidelines for then number of required days to obtain stable RAR estimates, similar to guidelines established for sleep variables [11], will be a focus of future research. Third, the proposed procedure assumes that residuals are second-order stationary. If they are not, the RCS would measure some sort of average phenomenon, but its interpretation is not clear. It should be noted that similar issues arise for other RAR measures of variability as well. The extension of the proposed RCS within a locally stationary time series setting [6] to obtain time-varying spectral measures could provide useful information when residuals are not stationary. Lastly, one would ideally want to leverage other available information. This can include demographics and other information that can be collected by the wearable device, such as heart rate and light exposure. The development of a predictive measure that can fuse RAR information with other sources of data will be essential in developing tools to monitor and tailor treatments.
Acknowledgments
This work was funded by National Institutes of Health through grants R01GM113243, R01HL1104607 and K01MH112683.
References
- 1.Ancoli-Israel S, Cole R, Alessi C, Chambers M, Moorcroft W, Poliak CP: The role of actigraphy in the study of sleep and circadian rhythms. Sleep 26(3), 342–392 (2003) [DOI] [PubMed] [Google Scholar]
- 2.Bates DM, Watts DG: Nonlinear Regression Analysis and Its Applications, 2nd edn. Wiley, New York: (2007) [Google Scholar]
- 3.Besse P, Ramsay JO: Principal components analysis of sampled functions. Psychometrika 51, 285–311 (1986) [Google Scholar]
- 4.Cacioppo JT, Tassinary LG, Bernston G: Handbook of Psycholphysiology, 3 edn. Cambridge University Press, Cambridge: (2007) [Google Scholar]
- 5.Chen K, Lei J: Localized functional principal components analysis. Journal of the American Statistical Association 110, 1266–1275 (2015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Dahlhaus R: Locally stationary processes. Handbook of Statistics 30, 351–413 (2012) [Google Scholar]
- 7.Goldsmith J, Zipunnikov V, Schrack J: Generalized multilevel function-on-scalar regression and principal component analysis. Biometrics 71(2), 344–353 (2015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Gonçalves BSB, Cavalcanti PRA, Tavares GR, Campos TF, Araujo JF: Non-parametric methods in actigraphy: An update. Sleep Science 7(3), 158–164 (2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Gu C: Smoothing Spline ANOVA Models, 2nd edn. Springer-Verlag, New York; (2013) [Google Scholar]
- 10.Hamilton M: A rating scale for depression. Journal of Neurology Neurosurgury and Psychiatry 23(1), 56–62 (1960) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Israel B, Buysse DJ, Krafty RT, Begley A, Miewald M, Hall MH: Short-term stability of sleep and heart rate variability in good sleepers and patients with insomnia: For some measures, one night is enough. Sleep 35(9), 1285–1291 (2012) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Krafty RT, Collinge WO: Penalized multivariate Whittle likelihood for power spectrum estimation. Biometrika 100(2), 447–458 (2013) [Google Scholar]
- 13.Krafty RT, Zhao M, Buysse DJ, Thayer JF, Hall MH: Nonparametric spectral analysis of heart rate variability through penalized sum of squares. Statistics in Medicine 33(8), 1383–1394 (2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lomb NR: Least-squares frequency analysis of unequally spaced data. Astrophysics and Space Science 39, 447–462 (1976) [Google Scholar]
- 15.Marler MR, Gehrman P, Martin JL, Ancoli-Israel S: The sigmoidally transformed cosine curve: a mathematical model for circadian rhythms with symmetric non-sinusoidal shapes. Statistics in Medicine 25(22), 3893–3904 (2006) [DOI] [PubMed] [Google Scholar]
- 16.Morris JS, Arroyo C, Coull BA, Ryan LM, Herrick R, Gortmaker SL: Using wavelet-based functional mixed models to characterize population heterogeneity in accelerometer profiles: A case study. Journal of the American Statistical Association 101(476), 1352–1364 (2006) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Moulin P: Wavelet thresholding techniques for power spectrum estimation. IEEE Transactions on Signal Processing 42(11), 3126–3136 (1994) [Google Scholar]
- 18.Parzen E: Spectral analysis of asymptotically stationary time series. Bulletin de International de Statistique 33 (1962) [Google Scholar]
- 19.Pawitan Y, O’Sullivan F: Nonparametric spectral density estimation using penalized Whittle likelihood. Journal of the American Statistical Association 89, 600–610 (1994) [Google Scholar]
- 20.Qin L, Wang Y: Nonparametric spectral analysis with applications to seizure characterization using EEG time series. Annals of Applied Statistics 2, 1432–1451 (2008) [Google Scholar]
- 21.Rice JA, Silverman BW: Estimating the mean and covariance structure nonparametrically when the data are curves. Journal of the Royal Statistical Society, Series B 53, 233–243 (1991) [Google Scholar]
- 22.Shumway R, Stoffer D: Time series analysis and its applications. Springer: New York: (2011) [Google Scholar]
- 23.Smagula SF: Opportunities for clinical applications of rest-activity rhythms in detecting and preventing mood disorders. Current Opinions in Psychiatry 29(6) (2016) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.van Someren EJW, Hagebeuk EEO, Lijzenga C, Scheltens P, de Rooij SEJA, Jonker C, Pot AM, Mirmiran M, Swaab DF: Circadian rest-activity rhythm disturbances in Alheimer’s disease. Biological Psychiatry 40(4), 259–270 (1996) [DOI] [PubMed] [Google Scholar]
- 25.Troiano RP, Berrigan D, Dodd KW, Masse LC, Tilert T, McDowell M: Physical activity in the United States measured by accelerometer. Medicine & Science in Sports & Exercise 40(1), 181–188 (2008) [DOI] [PubMed] [Google Scholar]
- 26.Wahba G: Automatic smoothing of the log-periodogram. Journal of the American Statistical Association 75(369), 122–132 (1980) [Google Scholar]
- 27.Wang J, Xian H, Licis A, Deych E, Ding J, McLeland J, Toedebusch C, Li T, Duntley S, Shannon W: Measuring the impact of apnea and obesity on circadian activity patterns using functional linear modeling of actigraphy data. Journal of Circadian Rhythms 9(11) (2011) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Whittle P: Estimation and information in stationary time series. Arkiv fñr Matematik 2(23), 423–434 (1953) [Google Scholar]
- 29.Wood SN: Fast stable restricted maximum likelihood and marginal likelihood estimation of semiparametric generalized linear models. Journal of the Royal Statistical Society, B 73(1), 3–36 (2011) [Google Scholar]
- 30.World Health Organization: Depression Fact Sheet (2017). URL http://www.who.int/mediacentre/factsheets/fs369/en/
- 31.Xiao L, Huang L, Schrack JA, Ferrucci L, Zipunnikov V, Crainiceanu CM: Quantifying the lifetime circadian rhythm of physical activity: a covariate-dependent functional approach. Biostatistics 16(2), 352–367 (2015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Zimmerman M, Martinez JH, Young D, Chelminski I, Dalrymple K: Severity classification on the Hamilton depression rating scale. Journal of Affect Disorders 150, 384–388 (2013) [DOI] [PubMed] [Google Scholar]