Abstract
The emerging diversity of single cell RNAseq datasets allows for the full transcriptional characterization of cell types across a wide variety of biological and clinical conditions. However, it is challenging to analyze them together, particularly when datasets are assayed with different technologies. Here, real biological differences are interspersed with technical differences. We present Harmony, an algorithm that projects cells into a shared embedding in which cells group by cell type rather than dataset-specific conditions. Harmony simultaneously accounts for multiple experimental and biological factors. In six analyses, we demonstrate the superior performance of Harmony to previously published algorithms. We show that Harmony requires dramatically fewer computational resources. It is the only currently available algorithm that makes the integration of ~106 cells feasible on a personal computer. We apply Harmony to PBMCs from datasets with large experimental differences, 5 studies of pancreatic islet cells, mouse embryogenesis datasets, and cross-modality spatial integration.
Recent technological advances1 enable unbiased single cell transcriptional profiling of thousands of cells in one experiment. Projects such as Human Cell Atlas2 (HCA) and Accelerating Medicines Partnership3-5 exemplify the growing body of reference datasets of primary human tissues. While individual experiments incrementally expand our understanding of cell types, a comprehensive catalogue of healthy and diseased cells will require the ability to integrate multiple datasets across donors, studies, and technological platforms. Moreover, in translational research, joint analyses across tissues and clinical conditions will be essential to identify disease-expanded populations. Since meaningful biological variation in single cell RNA-seq datasets from different studies is often hopelessly confounded by data source6, investigators have developed unsupervised multi-dataset integration algorithms7-10. These methods embed cells from diverse experimental conditions and biological contexts into a common reduced dimensional embedding to enable shared cell type identification across datasets.
Here we introduce Harmony, an algorithm for robust, scalable, and flexible multi-dataset integration to meet four key challenges of unsupervised scRNAseq joint embedding: scaling to large datasets, identification of both broad populations and fine-grained subpopulations, flexibility to accommodate complex experimental design, and the power to integrate across modalities. We apply Harmony to a diverse range of examples, including cell lines, PBMCs assayed with different technologies, a meta-analysis of pancreatic islet cells from multiple donors and studies, longitudinal samples from mouse embryogenesis, and cross modality integration of dissociated with spatially resolved expression datasets. Harmony is available as an R package on github (https://github.com/immunogenomics/harmony), with functions for standalone and Seurat7 pipeline analyses.
Results
Harmony Iteratively Learns a Cell-Specific Linear Correction Function
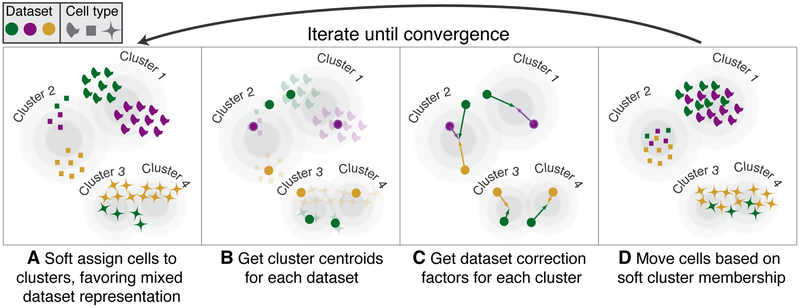
Harmony, described in detail in Supplementary Note 1, begins with a low dimensional embedding of cells, such as Principal Components Analysis (PCA), that meets 3 key criteria (online methods). Using this embedding, Harmony first groups cells into multi-dataset clusters (Figure 1A). We use soft clustering to assign cells to potentially multiple clusters, to account for smooth transitions between cell states. These clusters serve as surrogate variables, rather than actual discrete cell-types. We developed a novel soft k-means clustering algorithm that favors clusters with cells from multiple datasets (online methods). Clusters disproportionately containing cells from a small subset of datasets are penalized by an information theoretic metric. Harmony allows for multiple different penalties to accommodate multiple technical or biological factors, such as different batches and different technology platforms. Soft clustering preserves discrete and continuous topologies while avoiding local minima that might result from too quickly maximizing representation across multiple datasets. After clustering, each dataset has a cluster-specific centroid (Figure 1B) that is used to compute cluster-specific linear correction factors (Figure 1C). Since clusters correspond to cell types and states, cluster-specific correction factors correspond to individual cell-type and cell-state specific correction factors. In this way, Harmony learns a simple linear adjustment function that is sensitive to intrinsic cellular phenotypes. Finally, each cell is assigned a cluster-weighted average of these terms and corrected by its cell-specific linear factor (Figure 1D). Since each cell may be in multiple clusters, each cell has a potentially unique correction factor. Harmony iterates these four steps until convergence, until cell cluster assignments are stable.
Figure 1.
Overview of Harmony algorithm. We represent datasets with colors, and different cell types with shapes. Before we apply Harmony, principal components analysis embeds cells into a space with reduced dimensionality. Harmony accepts the cell coordinates in this reduced space and runs an iterative algorithm to adjust for data set specific effects. (A) Harmony uses fuzzy clustering to assign each cell to multiple clusters, while a penalty term ensures that the diversity of datasets within each cluster is maximized. (B) Harmony calculates a global centroid for each cluster, as well as dataset-specific centroids for each cluster. (C) Within each cluster, Harmony calculates a correction factor for each dataset based on the centroids. (D) Finally, Harmony corrects each cell with a cell-specific factor: a linear combination of dataset correction factors weighted by its soft cluster assignments made in step A. Harmony repeats steps A through D until convergence. The dependence between cluster assignment and dataset diminishes with each round.
Quantifying Performance in Cell Line Data
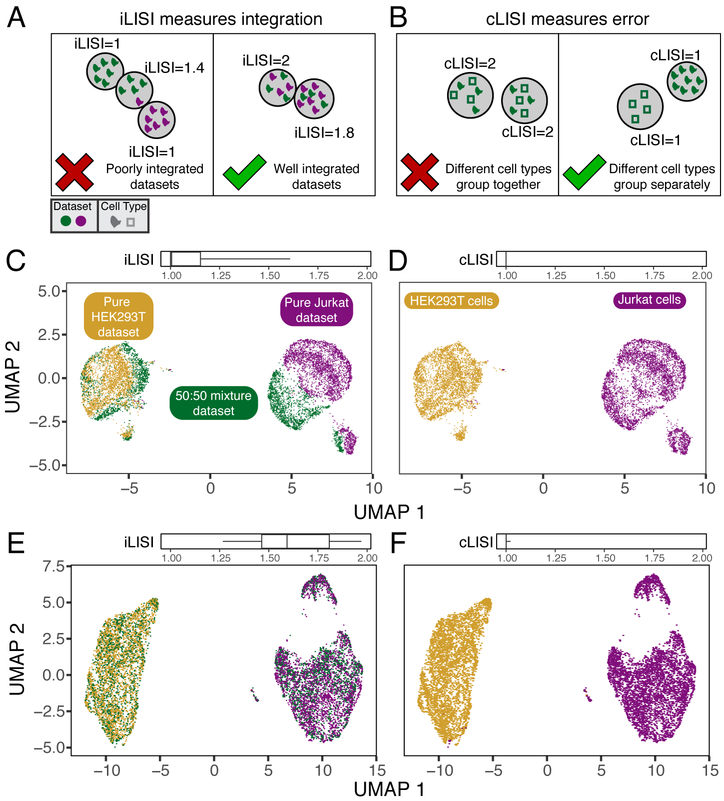
We first assessed Harmony using three carefully controlled datasets, in order to evaluate performance on both integration (mixing of datasets) and accuracy (no mixing of cell types). Perfect integration can be achieved by mixing all cells, regardless of cellular identity. Similarly, high accuracy can be achieved by partitioning cells into broad clusters without mixing datasets in small neighborhoods. In this situation, broad cellular states are defined, but fine-grained cellular substates and subtypes are confounded by the originating dataset. In order to quantify integration and accuracy of this embedding we defined an objective metric: the Local Inverse Simpson's Index (LISI, online methods) in the local neighborhood of each cell. To assess integration, we employ “integration LISI” (iLISI, Figure 2A), which defines the effective number of datasets in a neighborhood. Neighborhoods represented by only a single dataset get an iLISI of 1, while neighborhoods with an equal number of cells from 2 datasets get an iLISI of 2. Note that even under ideal mixing, if the datasets have different numbers of cells, iLISI would be less than 2. To assess accuracy, we use “cell-type LISI” (cLISI, Figure 2B), the same mathematical measure, but applied to cell-type instead of dataset labels. Accurate integration should maintain a cLISI of 1, reflecting a separation of unique cell types throughout the embedding. An erroneous embedding would include neighborhoods with a cLISI of 2, indicating that neighbors have 2 different types of cells.
Figure 2.
Quantitative assessment of dataset mixing and cell-type accuracy with cell line datasets. (A) iLISI measures the degree of mixing among datasets in an embedding, ranging from 1 in an unmixed space to B in a well mixed space. B is the number of datasets in the analysis. (B) cLISI measures integration accuracy using the same formulation but computed on cell-type labels instead. An accurate embedding has a cLISI close to 1 for every neighborhood, reflecting separation of different cell types. Jurkat and HEK293T cells from pure (purple and yellow) and mixed (green) cell-line datasets were analyzed together. Before Harmony integration, cells grouped by dataset (C) and known cell-type (D). (C) iLISI and (D) cLISI were computed for every cell's neighborhood and summarized with quantiles (5, 25, 50, 75, 95). After Harmony integration, cells from the mixture dataset are mixed into the other datasets (E), achieved by mixing Jurkat with Jurkat cells and HEK293T with HEK293T cells (F). (E) iLISI and (F) cLISI were re-computed in the Harmony embedding.
We begin with three datasets from two cells lines: (1) pure Jurkat, (2) pure 293T and (3) a 50:50 mix11. These datasets are ideal for illustration and for assessment, as each cell can be unambiguously labeled Jurkat or 293T (Supplementary Fig. 1A). A thorough integration would mix the 1799 Jurkat cells from the mixture dataset with 3255 cells from the pure Jurkat dataset and the 1565 293T cells from the mixture dataset with the 2859 from the pure 293T dataset. Thus, we expect the average iLISI to range from 1, reflecting no integration, to 1.8(=1/[(1799/(1799+2859))2+(3255/(1799+3255))2]) for Jurkat cells and 1.5(=1/[(1565/(1565+2859))2+(2859/(1565+2859))2]) for 293T cells, reflecting maximal accurate integration. Application of a standard PCA pipeline followed by UMAP embedding demonstrates that the cells group broadly by dataset and cell type. This is both visually apparent and quantified (Figure 2C,D) with high accuracy reflected by a low cLISI (median iLISI 1.00, 95% [1.00, 1.00]). However the iLISI (median iLISI 1.01, 95% [1.00, 1.61]) is also low, reflecting imperfect integration, and ample structure within each cell-type reflecting the data set of origin. After Harmony, cells from the 50:50 dataset are appropriately mixed into the pure datasets (Figure 2E). The increased iLISI (median iLISI 1.59, 95% [1.27, 1.97]) reflects the mixing of datasets, while the low cLISI (Figure 2F, median iLISI 1.00, 95% [1.00, 1.02]) reflects the accurate separation of Jurkat from 293T cells. iLISI and cLISI provide a quantitative way to compare the integration and accuracy of multiple algorithms. We repeated the integration and LISI analyses with MNN Correct, BBKNN, MultiCCA, and Scanorama and showed that they produced embeddings with statistically inferior integration (Supplementary Results, Fig. 1B, Table 1).
This benchmark demonstrates the two key metrics for assessing mixing and accuracy and shows that Harmony performs well on both metrics in a well-controlled analysis of cell-line datasets. A potential pitfall of LISI is that it is sensitive to datasets of vastly different sizes. In such a situation, most neighborhoods can be dominated by a single dataset and LISI values become difficult to interpret (Supplementary Note 2).
Harmony Scales to Large Data
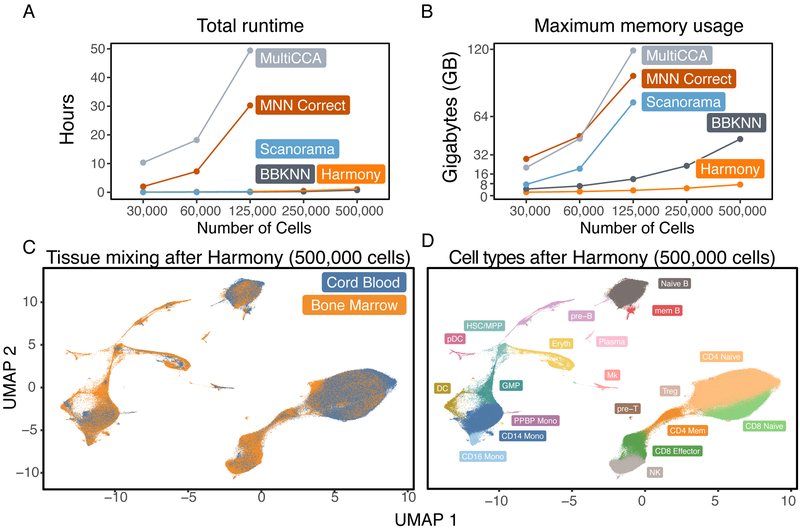
We evaluated Harmony’s computational performance, measuring both total runtime and maximum memory usage. To demonstrate Harmony’s scalability versus other methods, we downsampled HCA data12 (528,688 cells from 16 donors and 2 tissues) to create 5 benchmark datasets with 500,000, 250,000, 125,000, 60,000, and 30,000 cells. We reported the runtime and memory (Supplementary Tables 2,3) for all benchmarks. Harmony runtime scaled well for all datasets (Figure 3A), ranging from 4 minutes on 30,000 cells to 68 minutes on 500,000 cells, 30 to 200 times faster than MultiCCA and MNN Correct. The runtimes for Harmony, BBKNN, and Scanorama were comparable for datasets with up to 125,000 cells. Harmony required dramatically less memory (Figure 3B) compared to other algorithms, only 0.9GB on 30,000 cells and 7.2GB on 500,000 cells. At 125,000 cells, Harmony required 30 to 50 times less memory than Scanorama, MNN Correct and Seurat MultiCCA; these other methods could not scale beyond 125,000 cells. Importantly, Harmony returned substantially more integrated embeddings (Figure 3C) than did other competing algorithms (Supplementary Results), allowing for the identification of shared cell types (Figure 3D) across tissues and donors. These results demonstrate that Harmony is computationally efficient and capable of analyzing even large datasets (105-106 cells) on personal computers.
Figure 3.
Computational efficiency benchmarks. We ran Harmony, BBKNN, Scanorama, MNN Correct, and MultiCCA on 5 downsampled HCA datasets of increasing sizes, from 25,000 to 500,000 cells. We recorded the (A) total runtime and (B) maximum memory required to analyze each dataset. Scanorama, MultiCCA, and MNN Correct were terminated for excessive memory requests on the 250,000 and 500,000 cell datasets. The mixing between tissues in the Harmony embedding is visualized in (C). In the Harmony embedding, (D) we clustered cells and labeled populations by canonical markers: pre-T cells, CD4 Naive T cells, CD4 Memory T cells, T-regs, CD8 Naive T cells, CD8 Effector T cells, natural killer cells (NK), pre-B cells, Naive B cells, Memory B cells, plasma cells, plasmacytoid dendritic cells (pDC), conventional dendritic cells (DC), granulocyte macrophage progenitor (GMP), CD16− monocytes (CD14 Mono), CD16+ monocytes (CD16 Mono), a population of monocytes also positive for Megakaryocyte markers (PPBP Mono), Megakaryocytes (Mk), Erythroid progenitors (Eryth), and a cluster of hematopoietic stem cells and multipotent progenitor cells (HSC/MPP).
Identification of Broad and Fine-Grained PBMCs Subpopulations
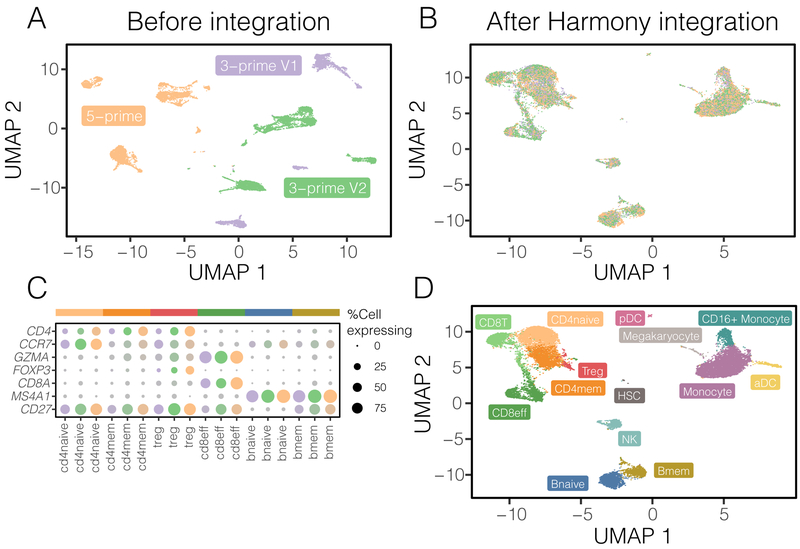
To assess how Harmony might perform under more challenging scenarios, we gathered three datasets of human PBMCs, each assayed on the Chromium 10X platform but prepared with different protocols: 3-prime end v1 (3pV1), 3-prime end v2 (3pV2), and 5-prime (5p) end chemistries. After pooling all the cells together, we performed a joint analysis. Before integration, cells group primarily by dataset (Figure 4A, median iLISI 1.00, 95% [1.00, 1.00]).
Figure 4.
Fine-grained subpopulation identification in PBMCs across technologies. Three PBMC datasets were assayed with 10X, using different library construction protocols: 5-prime (orange), 3-prime V1 (purple), and 3-prime V2 (green). Before integration (A), cells group by dataset. After Harmony integration (B), datasets are mixed together. (C) Harmony achieves the most thorough integration among datasets, while preserving (D) cell type differences. Using canonical markers (E), we identified (F) 5 shared subtypes of T cells and 2 shared subtypes of B cells. (G) Other integration algorithms fail to group these cells by subtype.
Harmony clustered the cells into biologically coherent groups (Supplementary Fig. 6A) and removed dataset-specific variation within each cluster. In the final integrated space, the datasets are well mixed (Figure 4B, median iLISI 1.96, 95% [1.36, 2.56]), more so than with other methods (Figure 4C). We confirmed that >83% of cells had a significantly (FDR<5%) higher iLISI value in Harmony than with any other algorithm (Supplementary Fig. 6B,C). To assess accuracy, within each dataset, we separately annotated (online methods) broad cell clusters with canonical markers of major expected populations (Supplementary Fig. 6D): monocytes (CD14+ or CD16+), dendritic cells (FCER1A+), B cells (CD20+), T cells (CD3+), Megakaryocytes (PPBP+), and NK cells (CD3−/GNLY+) before clustering. We observed that Harmony retained differences among cell types (Figure 4D median cLISI 1.00, 95% [1.00, 1.02]). The greater dataset integration, compared to other algorithms, affords a unique opportunity to identify fine-grained cell subtypes (Supplementary Fig. 6E). Using canonical markers (Figure 4E), we identified shared subpopulations of cells (Figure 4F) including naive CD4 T (CD4+/CCR7+), effector memory CD4 T (CD4+/CCR7−), Treg (CD4+/FOXP3+), memory CD8 (CD8+/GZMK−), effector CD8 T (CD8+/GZMK+), naive B (CD20+/CD27−), and memory B cells (CD20+/CD27+). In the embeddings produced by other algorithms, the median iLISI failed to exceed 1.1 (Supplementary Table 5). Accordingly, the subtypes identified above reside in dataset-specific, rather than dataset-mixed clusters (Supplementary Fig. 7). Importantly, we were able to maintain high quality results even as we downsampled whole populations of cells to create imbalanced datasets with non-overlapping cell types (Supplementary Results, Figs. 8-10). In both the full and downsampled PBMC datasets, Harmony was robust to the choice of parameters, particularly the diversity penalty (Supplementary Results, Fig. 11). These results show that Harmony successfully accounts for technical variation among different protocols and integrates many different cell types while preserving large-scale and fine-grained structures in the data, even with non-overlapping populations among datasets.
Simultaneous Integration Across Donors and Technologies Identifies Rare Pancreas Islet Subtypes
We considered a more complex experimental design, in which integration must be performed simultaneously over more than one source of variation. We gathered human pancreatic islet cells from five independent studies13-17, each generated with a different technological platform. Integration across these platforms is particularly challenging because of the large spread in number of cells per dataset and number of unique genes measured in each cell (Supplementary Fig. 12). Moreover, within two of the datasets13-14, the authors noted significant donor-specific effects. A successful integration of these studies must account for the effects of both different technologies and the 36 donors used in these studies. These effects may impact cell types in different ways. Harmony is the only currently available integration algorithm specifically designed for single cell data that is able to explicitly integrate over more than one variable.
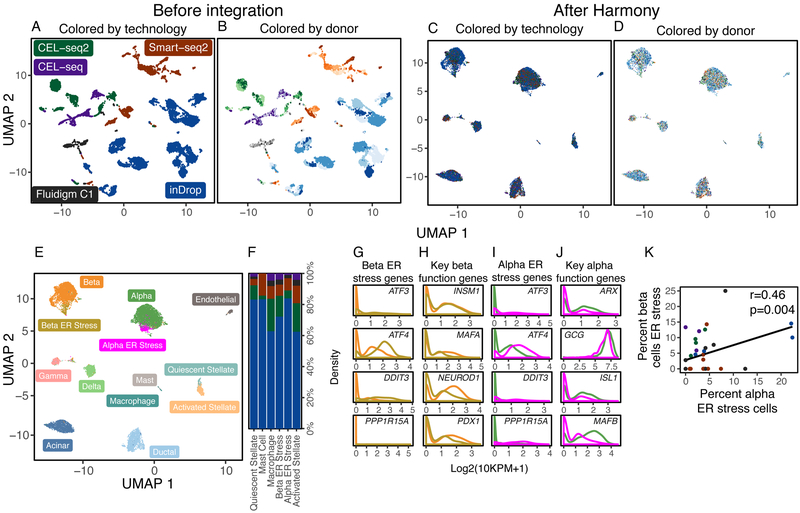
As before, we assess cell type accuracy cLISI with canonical cell types identified independently within each dataset (Supplementary Fig. 13A): alpha (GCG+), beta (MAFA+), gamma (PPY+), delta (SST+), acinar (PRSS1+), ductal (KRT19+), endothelial (CDH5+), stellate (COL1A2+), and immune (PTPRC+). Since there are two integration variables, we asses both donor iLISI and technology iLISI. Prior to integration, PCA separates cells by technology (Figure 5A, median iLISI 1.00 95% [1.00, 1.06]), donor (Figure 5B, median iLISI 1.42 95% [1.00, 5.50]), and cell type (median cLISI 1.00 95% [1.00, 1.48]). The wide range of donor-iLISI reflects that in the CEL-seq, CEL-seq2, and Fluidigm C1 datasets, many donors were well mixed prior to integration. Harmony integrates cells (Supplementary Figure 13B) by both technology (Figure 5C, median iLISI 2.17 95% [1.02, 3.91]) and donor (Figure 5D, median iLISI 5.05 95% [1.24, 10.05]), while merging cells correctly according to previously defined types (accuracy>98%, Supplementary Fig. 13C). We also benchmarked these data with BBKNN, Scanorama, MNN and MultiCCA, as well with limma18, which can correct over multiple levels. Only Harmony was able to mix both the donors and technologies substantially (Supplementary Results, Fig. 14).
Figure 5.
Integration of pancreatic islet cells by both donor and technology. Human pancreatic islet cells from 36 donors were assayed on 5 different technologies. Cells initially group by (A) technology, denoted by different colors, and (B) donor, denoted by shades of colors. Harmony integrates cells simultaneously across (C) technology and (D) donor. (E) Clustering in the Harmony embedding identified common and rare cell types, including a previously identified beta population under ER stress. Except for activated stellate cells, all rare cell types were found across the 5 technology datasets (F). The ER stress beta population was enriched for ER stress genes (G) and had decreased expression of key genes necessary for endocrine function (H). We also identified a previously undescribed population of alpha cell, also enriched for ER stress genes (I) with decreased expression of key endocrine genes (J). The abundances of the two ER stress populations were correlated across donors (K).
Harmony was able to discern rare (<2%) cell subtypes (Figure 5E) across the 5 datasets (Figure 5F). We labeled previously described subtypes using canonical markers: activated stellate cells (PDGFRA+), quiescent stellate cells (RGS5+), mast cells (BTK+), macrophages (C1QC+), and beta cells under endoplasmic reticulum (ER) stress (Figure 5G). Beta ER stress cells may represent a dysfunctional population. This cluster has significantly lower expression of genes key to beta cell identity19 and function:20 PDX1, MAFA, INSM1, NEUROD1 (Figure 5H). Further, Sachdeva et al21 suggest that PDX1 deficiency makes beta cells less functional and exposes them to ER stress induced apoptosis.
Intriguingly, we also observed an alpha cell subset that to our knowledge, has not been previously described. This cluster was also enriched with genes involved in ER stress (Figure 5I, DDIT3, ATF3, ATF4, and HSPA5). Similar to the beta ER stress population, these alpha cells also expressed significantly lower levels of genes necessary for proper function:22,23 GCG, ISL1, ARX, and MAFB (Figure 5J). A recent study24 reported ER stress in alpha cells in mice and linked the stress to dysfunctional glucagon secretion. Moreover, we found that the proportions of alpha and beta ER stress cells are significantly correlated (spearman r=0.46, p=0.004, Figure 5K) across donors in all datasets. These results suggest alpha cell injury might parallel beta cell dysfunction in humans during diabetes.25 Importantly, this rare population was nearly impossible to identify in the original studies, because they were either too rare or obscured by donor-specific variation (Supplementary Fig. 15).
Harmony Integrates Time Course Developmental Trajectories
We next evaluated Harmony’s ability to integrate datasets with smooth trajectories, rather than discrete cell types. We analyzed 15,875 cells from 8 time points of mouse haematopoiesis,26 from E6.75 to E8.5, and mixed gastrulation. This dataset presents a new challenge to Harmony: each sample was taken at a different developmental time point. Thus, no sample has all cell types represented (Supplementary Fig. 16A). Unsurprisingly, cells initially grouped by sample ID rather than by cell type (Supplementary Fig. 16B). After Harmony integration, samples are well mixed and group largely by previously defined cell type (Supplementary Fig. 16C). Encouragingly, Harmony preserved the continuous structure of the developmental cells rather than erroneously clustering cells into discrete groups. Harmony's soft clustering was critical to preserve the smoothness: it assigned cells from transitional populations to more clusters and cells in more terminal populations to fewer clusters (Supplementary Fig. 16D). With corrected Harmony embeddings, we performed trajectory analysis with DDRTree (Supplementary Fig. 16E). We recovered a branching trajectory structure that correctly captures the progression from common mesoderm and haematoendothelial progenitor populations to differentiated endothelial and erythroid populations. Interestingly, Harmony preserved the separation between the two blood progenitor populations but not in the three erythroid populations (Supplementary Fig. 16E). This suggests that these distinct erythroid populations may be an artifact of batch rather than biology. Benchmarking this analysis, (Supplementary Results), we found that except for MNN Correct, other algorithms failed to maintain smoothness or incorrectly mixed distinct progenitor populations (Supplementary Fig. 17).
Harmony Integrates Dissociated scRNAseq with Spatially Resolved Datasets
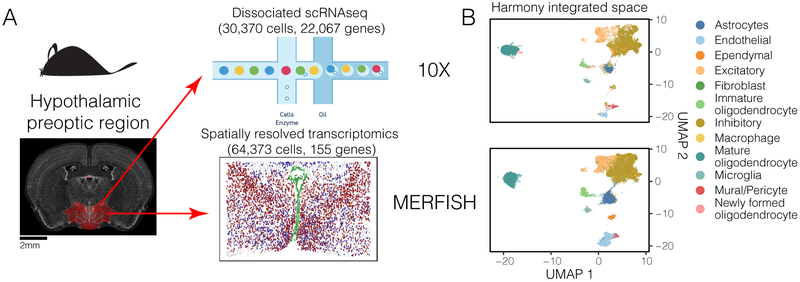
Now we consider the integration of cells measured with different modalities, measuring different aspects of a cell's biology. This type of integration is especially powerful, in that it allows inference of features measured in one modality but not the other. Harmony integrates a spatially resolved fluorescence in situ hybridization (FISH) dataset with a dissociated scRNAseq dataset from the mouse hypothalamic preoptic region (Bregma +0.5 to −0.6mm), using 154 shared genes (Figure 6A). From the embedding, we infer the spatial localization of unmeasured genes to identify previously unreported spatial patterns in neuronal transcription factors. We downloaded two datasets published by Moffit et al:27,28 30,370 cells from 6 mice measured with dissociated scRNAseq (10X) and 64,373 cells from one mouse measured with multiplexed error robust FISH (MERFISH). The spatially resolved dataset is a combination of 135 genes assayed with MERFISH and 20 assayed with two-color single molecule (smFISH). The dissociated 10X data gives information about the full transcriptome (22,067 genes post QC) but without any spatial information. In contrast, MERFISH was applied in this dataset to only a targeted number of genes. The primary challenge in this analysis is the limited number of overlapping features. Successful integration will merge similar cell types and allow inference of spatial patterns of the remaining 21,913 genes.
Figure 6.
Harmony integrates spatially resolved transcriptomic with dissociated scRNAseq datasets. (A) Cells from the hypothalamic preoptic region of mouse brain were assayed in parallel with two technologies. The full transcriptome of dissociated cells was profiled with 10X. 155 genes were profiled in-situ on intact tissue with MERFISH. (B) Harmony integrated cells from the two modalities into a shared embedding, correctly merging the 12 previously identified cell types. (C) Satb1 expression (blue), unmeasured in the MERFISH dataset, was inferred and predicted to be spatially autocorrelated in inhibitory neurons. Satb1 expression was highest in anterior slices and diminished in slices that contained ventricle-lining Ependymal cells (green). (D) Matched images from an independent in-situ hybridization experiment measuring Satb1 expression from the Allen Brain Atlas. Satb1 expression (blue) is co-localized in similar regions of the slices and diminishes with the appearance of ventricle structures (green).
Before Harmony, cells group primarily by modality (median iLISI 1.00, 95% CI [1.00, 1.04], Supplementary Fig. 18A). Harmony mixes the two modalities, 10X and MERFISH (median iLISI 1.15, 95% CI [1.00, 1.99], Figure 6B, Supplementary Fig. 18B) and merges cells based on their previous cell type labels covering 12 major neuronal and glial populations (93.7% prediction accuracy after integration vs 94% before integration, Supplementary Fig. 18C). As an independent validation, we show that the Harmony embedding agrees with the fine-grained cluster analysis in the original manuscript (Supplementary Results, Figs. 18D,E).
We next used kernel kNN regression to predict gene expression in MERFISH dataset cells, based on their nearest 10X dataset neighbors (online methods). We used five-fold cross validation to evaluate performance and found that we predicted 150 of 154 genes accurately, performing consistently better on highly expressed genes (Supplementary Results, Fig. 18F). The original manuscript identified key transcription factors that distinguished spatially distributed neuronal subtypes. After applying Harmony, we can easily identify spatially autocorrelated transcription factors. We measured the spatial autocorrelation (Moran's I) of all known vertebrate transcription factors documented in JASPAR29 (Supplementary Tables 6,7). As expected, all factors associated with a neuronal subtype were significantly (FDR<5%) spatially autocorrelated. In addition, we found 50 transcription factors significantly (FDR<5%, Moran's I > 0.1) autocorrelated in excitatory neurons and 37 in inhibitory neurons. We confirmed that these new factors were positive markers for at least one neuronal subtype. In fact, spatial correlation was significantly correlated (spearman r=0.71, p=2.6×10−62) with the AUC of that gene's best subtype (Supplementary Fig. 18G).
We next followed up on Satb1, a chromatin organizer linked with survival of mouse cortical interneurons,30 as it was strongly auto-correlated in inhibitory neurons (Moran's I=0.44). The predicted Satb1 expression was localized to anterior slices (Figure 6C). To validate this localization, we compared predicted expression to matched images of Satb1 expression from the Allen Brain Atlas.31 These images were chosen for similar anterior-posterior position (between Bregma +0.8 to −0.2mm) and ventricular morphology (in green). The measured Satb1 expression follows qualitatively similar patterns of predicted expression (Figure 6D).
These 154 genes were carefully selected by the authors to be biologically relevant to cell types in the hypothalamic preoptic region. Using correlation informed downsampling, we were able to achieve similar results with only 60 representative anchor genes (Supplementary Results, Figs. 18H,I).
Discussion:
Integration across multiple data sets is an essential component to conduct large scale inference with single cell data sets. We showed that Harmony addresses the four key challenges we laid out for single cell integration analyses: scaling to large datasets, identification of both broad populations and fine-grained subpopulations, flexibility to accommodate complex experimental design, and the power to integrate across modalities. In addition, Harmony is efficient, requiring only 7.2GB to integrate 500,000 cells; it is currently the only algorithm that enables integration of large datasets on personal computers. It can also be effective in identifying rare populations. In our meta-analysis of pancreatic islet cells, we identified a previously undescribed rare subpopulation of alpha ER stress cells. Experimental follow up on this alpha subtype and its relation to beta ER stress cells may yield insight into diabetes.
Harmony accepts a matrix of cells and covariate labels for each cell as input. Its output is a matrix of adjusted coordinates with the same dimensions as the input matrix. Hence, Harmony should be applied first before a full analysis pipeline is employed. Downstream analyses, such as clustering, trajectory analysis, and visualization, can then use integrated Harmony adjusted. Harmony does not alter the expression values of individual genes to account for dataset-specific differences. We recommend using a batch-aware approach, such as a mixed effects linear models, for differential expression analysis.
Harmony uses clusters to partition the large non-linear embeddings in which cells sit into smaller linear regions. With discrete clustering, it is possible to over-discretize the space and lose smooth transitions between populations (for examples see Supplementary Note 3). Harmony avoids over-discretization by using soft clustering. With this strategy, in the mouse embryogenesis dataset, Harmony effectively modeled both terminal populations and transition states, retaining smooth transitions and bifurcation events from a common progenitor into endothelial and hematopoietic lineages.
With the advent of high throughput single cell technologies, it is now possible to assay different interacting facets of a cells' biology. Effective synthesis of datasets across multiple modalities may help reveal such interactions. Harmony embedded spatially resolved MERFISH cells with dissociated 10X cells, despite limited overlap of genes and dramatically different capture efficiencies between these technologies. Consequently, we were able to analyze spatial patterns of gene expression on genes that were never measured with MERFISH. The ability of Harmony to integrate 10X and MERFISH and impute unmeasured gene expression relies on the quality of the overlapping set of anchor genes. Selecting the optimal anchor genes is an important open question. From our cross validation and minimal geneset analyses, we found two trends that may help guide spatial probeset design. First, we can remove correlated genes from the anchors with minimal loss in integration quality. Second, less abundant genes are more difficult to predict. Thus, a spatial probeset containing genes with lower abundance that are also maximally non-redundant should enable imputation of a large number of genes through Harmony with an appropriate scRNAseq dataset.
It is common practice to apply batch-sensitive gene preprocessing steps before application of single-cell integration algorithms. In particular, some investigators scale gene expression values within datasets separately, before pooling cells into a single matrix. While this strategy may make it easier to integrate certain datasets (Supplementary Results, Figs. 19A,B) in which all cell populations are present across all datasets, it may increase error when datasets consist of overlapping but not identical populations (Supplementary Fig. 19C). Hence, we do not use this scaling strategy in this manuscript. In our analysis pipelines, we avoid all batch-sensitive preprocessing steps. We simply concatenate the data and perform PCA on the combined data set.
Harmony models and removes the effects of known sources of variation. However, unwanted variation may also arise from unknown sources. Methods such as SVA32 and PEER33 infer and remove latent sources of variation with linear models in bulk transcriptomics. In future work, we plan to extend Harmony to identify and remove unwanted latent effects.
With the rise of automated classification algorithms, it is feasible that a user may be able to assign information about cell types prior to integration. For example, in the past, our group has used a classifier to define soft or hard identities to assign probabilistic classifications to single cells with linear discriminant analysis.3,34 Harmony has an advanced option to initialize soft cluster assignments using such probabilistic cell type assignments (See ?HarmonyMatrix). If the prior assignments are helpful, Harmony will converge to an accurate solution faster. If the prior assignments are inaccurate, Harmony can reassign cells appropriately during the clustering steps.
The Harmony framework lays the groundwork for several exciting future application. First, it can be extended to accurately model gene counts. This will allow users to apply Harmony preprocessing for methods which require full gene expression profiles, rather than low dimensional cell embeddings, such as RNA velocity35. Next, we envision specializing Harmony to quickly map cells to a multi-billion cell reference that covers a comprehensive set of tissues, organisms, and clinical conditions. This application will enable rapid comparison of cells from a single experiment against a larger reference, and in the process annotate known and novel cell types and states in seconds.
Online Methods
1. Harmony
1.1. Overview
The Harmony algorithm inputs a PCA embedding (Z) of cells, along with their batch assignments (ϕ), and returns a batch corrected embedding (). This algorithm, summarized as Algorithm 1 below, iterates between two complementary stages: maximum diversity clustering (Algorithm 2) and a mixture model based linear batch correction (Algorithm 3). The clustering step uses the batch corrected embedding to compute a soft assignment of cells to clusters, encoded in the matrix R. The correction step uses these soft clusters to compute a new corrected embedding from the original one. Efficient implementations of Harmony, including the clustering and correction subroutines, are available as part of an R package at https://github.com/immunogenomics/harmony.
Note that the correction procedure uses Z, not to regress out confounder effects. In this way, we restrict correction to a linear model of the original embedding. An alternative approach would use the output of the last iteration as input to the correction procedure. Thus, the final would be the result of a series of linear corrections of the original embedding. While this allows for more expressive transformations, we found that in practice, this can over correct the data. Our choice to limit the transformation reflects the notion in the introduction. Namely, if we had perfect knowledge of the cell types before correction, we would linearly regress out batch within each cell type.
1.2. Algorithm
| Algorithm 1 Harmony | |
|---|---|
|
|
1.3. Glossary
For reference, we define all data structures used in all Harmony functions. For each one, we define its dimensions and possible values, as well as an intuitive description of what it means in context. The dimensions are stated in terms of d: the dimensionality of the embedding (e.g. number of PCs), B: the number of batcsssshes, N: the number of samples, Nb: the number of samples in batch b, and K: the number of clusters.
The input embedding, to be corrected in Harmony. This is often PCA embeddings of cells.
The integrated embedding, output by Harmony.
R ∈ [0,1]KxN The soft cluster assignment matrix of cells (columns) to clusters (rows). Each column is a probability distribution and thus sums to 1.
ϕ ∈ {0,1}BxN One-hot assignment matrix of cells (columns) to batches (rows).
Prb ∈ [0,1]B Frequency of batches.
O ∈ [0,1]KxB The observed co-occurence matrix of cells in clusters (rows) and batches (columns).
E ∈ [0,1]KxN The expected co-occurence matrix of cells in clusters and batches, under the assumption of independence between cluster and batch assignment.
Y ∈ [0,1]dxK Cluster centroid locations in the kmeans clustering algorithm.
1.4. Assumptions about input data
In this manuscript, we always use Harmony on a low dimensional embedding of the cells. To be clear about the properties of this low dimensional space, we explicitly state three assumptions:
Cells are embedded into a low dimensional space as the result of PCA. The PCA embedding captures the variation of gene expression in a compact orthonormal space. For this reason, the default input to Harmony is now a matrix of gene expression data, normalized for library size. We then perform PCA on this high-dimensional matrix and use the eigenvalue-scaled eigenvectors as the low dimensional embedding input to Harmony.
Gene expression has been normalized for library size. In RNAseq, each cell will be sequenced to a different depth, which results in different library sizes for each cell. It is best practice to account for this source of technical variation before performing PCA. In this manuscript, we use the standard transformation akin to log CPM, described in the online methods. As a result of this depth transformation, expression values are turned into relative frequencies inside each cell. Thus, it is impossible for every gene to be upregulated in one group of cells.
The low dimensional nearest neighbor structure induced by Euclidean distance should be preserved with common similarity metrics such as cosine similarity and correlation. This can be easily checked by computing sparse nearest neighbor graphs and comparing the adjacency matrices. Cells with less than 20% overlapping neighbors can be removed as outliers. A common way to violate this assumption is to simulate cells around the origin (i.e. all embeddings equal 0). We do not find this to be the case in real scRNAseq data. This assumption is common to integration methods that use cosine distance to compare cells, such as MNN Correct and Scanorama.
2. Maximum Diversity Clustering
We developed a clustering algorithm to maximize the diversity among batches within clusters. We present this method as follows. First, we review a previously published objective function for soft k-means clustering. We then add a diversity maximizing regularization term to this objective function, and derive this regularization term as the penalty on statistical dependence between two random variables: batch membership and cluster assignment. We then derive and present pseudocode for an algorithm to optimize the objective function. Finally, we explain key details of the implementation.
2.1. Background: Entropy regularization for Soft K-means
The basic objective function for classical K means clustering, in which each cell belongs to exactly one cluster, is defined by the distance from cells to their assigned centroids.
| (1) |
Above, Z is some feature space of the data, shared by centroids Y. Rk,i can takes values 0 or 1, denoting membership of cell i in cluster k. In order to transform this into a soft clustering objective, we follow the direction of36 and add an entropy regularization term over R, weighted by a hyperparameter σ. Now, Rki can take values between 0 and 1, so long as for a given cell i, the sum over cluster memberships Σk Rki equals 1. That is, Ri. must be a proper probability distribution with support [1,K].
| (2) |
As σ approaches 0, this penalty approaches hard clustering. As σ approaches infinity, the entropy of R outweighs the data-centroid distances. In this case, each data point is assigned equally to all clusters.
2.2. Objective Function for Maximum Diversity Clustering
The full objective function for Harmony's clustering builds on the previous section. In addition to soft assignment regularization, the function below penalizes clusters with low batch-diversity, for all defined batch variables. This penalty, derived in the following section, depends on the cluster and batch identities Ω(R, ϕi) = Σi,k Rki log(Oki/Eki)ϕi.
| (3) |
For each batch variable, we add a new parameter θ. θ decides the degree of penalty for dependence between batch membership and cluster assignment. When ∀fθ=0, the problem reverts back to (2), with no penalty on dependence. As θ increases, the objective function favors more independence between batch f and cluster assignment. As θ approaches infinity, it will yield a degenerate solution. In this case, each cluster has an equivalent distribution across batch f. However, the distances between cells and centroids may be large. Finally, σ is added to this term for notational convenience in the gradient calculations.
We found that this clustering works best when we compute the cosine, rather than Euclidean distance, between Z and Y. Haghverdi et al8 showed that the squared Euclidean distance is equivalent to cosine distance when the vectors are L2 normalized. Therefore, assuming that all Zi and Yk have a unity L2 norm, the squared Euclidean distance above can be re-written as a dot product.
| (4) |
2.3. Cluster Diversity Score
Here, we discuss and derive the diversity penalty term Ω(.), defined in the previous section. For simplicity, we discuss diversity with respect to a single batch variable, as the multiple batch penalty terms are additive in the objective function. The goal of Ω(.) is to penalize statistical dependence between batch identity and cluster assignment. In statistics, dependence between two discrete random variables is typically measured with the χ2 statistic. This test considers the frequencies with which different values of the two random variables are observed together. The observed co-occurrence counts (O) are compared to the counts expected under independence (E). For practical reasons, we do not use the χ2 statistic directly. Instead, we use the Kullback Leibler Divergence (DKL), an information theoretic distance between two distributions. In this section, we define the O and E distributions, as well the DKL penalty, in the context of the probabilistic cluster assignment matrix R.
| (5) |
| (6) |
Next, we define the KL divergence in terms of R. Note that both O and E depend on R. However, in the derivation below, we expand one of the O terms. This serves a functional purpose in the optimization procedure, described later. Intuitively, in the update step of R for a single cell, we compute O and E on all the other cells. In this way, we decide how to assign the single cell to clusters given the current distribution of batches amongst clusters.
| (7) |
2.4. Optimization
Optimization of (4) admits an Expectation-Maximization framework, iterating between cluster assignment (R) and centroid (Y) estimation.
2.4.1. Cluster assignment R
Using the same strategy as36, we solve for the optimal assignment Ri for each cell i. First we set up the Lagrangian with dual parameter λ and solve for the partial derivative wrt each cluster k.
Next, we use the probability constraint to solve for .
Finally, we substitute to remove the dependency of Rki on the dual parameter λ.
| (8) |
The denominator term above makes sure that Ri sums to one. In practice (alg 2), we compute the numerator and divide by the sum.
2.4.2. Centroid Estimation Y
Our clustering algorithm uses cosine distance instead of Euclidean distance. In the context of kmeans clustering, this approach was pioneered by Dhillon et al37. We adopt their centroid estimation procedure for our algorithm. Instead of just computing the mean position of all cells that belong in cluster k, this approach then L2 normalizes each centroid vector to make it unit length. Note that normalizing the sum over cells is equivalent to normalizing the mean of the cells. In the soft clustering case, this summation is an expected value of the cell positions, under the distribution defined by R. That is, re-normalizing R.k for cluster k gives the probability of each cell belonging to cluster k. Again, this re-normalization is a scalar factor that is irrelevant once we L2 normalize the centroids. Thus, the unnormalized expectation of centroid position for cluster k would be . In vector form, for all centroids, this is Y=ZRT. The final position of the cluster centroids is given by this summation followed by L2 normalization of each centroid. This procedure is implemented in algorithm 2 in the section {Compute Cluster Centroids}.
2.5. Algorithm
| Algorithm 2 Maximum Diversity Clustering | |
|---|---|
|
|
2.6. Implementation Details
The update steps of R and Y derived above form the core of Maximum Diversity Clustering, outlined as algorithm 2. This section explains the other implementation details of this pseudocode. Again, for simplicity, we discuss details related to diversity penalty terms θ, ϕ, O, and E for each single batch variable independently.
2.6.1. Block Updates of R
Unlike in regular kmeans, the optimization procedure above for R cannot be faithfully parallelized, as the values of O and E change with R. The exact solution therefore depends an online procedure. For speed, we can coarse grain this procedure and update R in small blocks (e.g. 5% of the data). Meanwhile, O and E are computed on the held out data. In practice, this approach succeeds in minimizing the objective for sufficiently small block size. In the algorithm, these blocks are included as the Update Blocks in the for loop.
2.6.2. Centroid Initialization
We initialize cluster centroids using regular kmeans clustering, implemented in the base R kmeans function. We use 10 random restarts and keep the best one. We then L2 normalize the centroids to prepare them for spherical kmeans clustering in Algorithm 2, Maximum Diversity Clustering.
2.6.3. Regularization for Smoother Penalty
The diversity penalty term (Ebk/Obk)θ can tend towards infinity if there are no cells from batch b assigned to cluster k. This extreme penalty can erroneously force cells into an inappropriate cluster. To protect against this, we add 1 to O and E to ensure that the fraction is stable:
2.6.4. θ Discounting
The diversity penalty, weighted by θ enforces an even mixing of cells from a batch among all clusters. This assumption is more likely to break for a batch with few cells. The smaller the batch, the more likely it is, through a sampling argument, that some cell types are not represented in the batch. Spreading such a batch across all clusters would result in erroneous clustering. To prevent such a situation, we allot each batch its own θb term, scaled to the number of cells in the batch.
Above, θmax is the non-discounted θ value, for a large enough batch. The multiplicative factor ranges from 0 to 1. This factor scales exponentially for small values of batch size Nb and plateaus for sufficiently large Nb. The hyperparameter τ can be interpreted as the minimum number of cells that should be assigned to each cluster from a single batch. By default, we use values between τ=5 and τ=20.
2.6.5. K, the number of clusters
The number of clusters K used in Harmony soft clustering should be set to a value that reflects the size and complexity of the dataset. Too few clusters will not capture the number of biologically distinct cell types and states. Too many clusters will give too much weight to batch-specific outliers and prevent effective integration. As a heuristic, we assume that the datasets have at most 100 distinct cell types and that each cluster should have at least 30 cells. We set the default number of clusters, K, to lie between these two extremes, for N cells.
3. Linear Mixture Model Correction
In this section, we refer to all effects to be integrated out of the original embedding as batch effects. This does not imply that these effects are purely technical. This terminology is only meant for convenience.
3.1. Mixture of Experts model
Once we define batch-diverse clusters, we would like to remove batch-specific variation from each cluster. We achieve this with a variation on the original Mixture of Experts (MoE) model from Jordan and Jacobs38. In the context of Harmony, each cell is probabilistically assigned to a small set of experts. This assignment was computed previously in the clustering step. Conditioned on a cluster/expert, MoE assumes a linear relationship between the response and independent variables. Thus, we condition on cluster/expert k and define a Gaussian probability distribution for the response variables.
| (9) |
Here, the mean is a function of the independent variables (μk=WkT ϕ*i), while the covariance is not (σk2I). Note that the design matrix above (ϕ*) is not the same as the one used in the clustering step (ϕ). We augment the original design matrix ϕ to include an intercept term: ϕ* = 1 ∥ ϕ. These intercept terms capture batch-independent (i.e. cell type) variation in each cluster/expert. We can also achieve more complex behavior, like reference mapping (section 3.3) by modifying ϕ*.
With this generative formulation, we can solve for the parameters (Wk) of the linear model for each cluster/expert independently.
| (10) |
Above, diag(Rk) is the diagonal matrix of cluster membership terms for cluster k. Z is the matrix of original PCA embeddings
Each column in Wk corresponds to a PC dimension, from PC1 to PCd. The first row of Wk corresponds to batch-independent intercept terms. The subsequent rows (1 through B) correspond to one-hot encoded batch assignments from the original design matrix ϕ.
To get the cell specific correction values, we take the expectation of Wk wrt the cluster assignment probability distribution R. In particular, each cell is modeled by a batch independent intercept, represented in the first row of Wk (Wk[0,.]), and its batch dependent terms represented by the remaining rows: Wk[1:B,.].
| (11) |
We split Wk into two parts because we want to retain the intercept terms and remove the batch-dependent terms. To get the corrected embeddings (), we subtract the batch specific term (Σk WTk[1:B,.]ϕi) from the original embedding (Zi).
| (12) |
What remains is the cell type specific intercept Wk[0,.] and the cell specific residual ϵi.
| (13) |
Unfortunately, for the design matrix ϕ*, the formulation in equation 13 does not have a solution. This is because ϕ* is not full rank and thus ϕ* diag(Rk) ϕ*T is not invertible. This singularity arises from the fact that the sum of a one hot encoded categorical variable is equal to the intercept. To address this colinearity, we penalize non-intercept terms in Wk with an L2 norm, akin to ridge regression. This shrinks the Wk terms to 0. Just like in ridge regression, instead of inverting ϕ* diag(Rk) ϕ*T, we invert ϕ* diag(Rk) ϕ*T+λI, which is not singular. The solution for Wk now becomes:
| (14) |
λ is the ridge penalty hyperparameter. Larger values of λ will shrink Wk more towards 0. We adopt the strategy to set λ0=0, thus not penalizing the batch-independent intercept, and ∀b∈[1:B]λb to be small enough to make the solution tractable. In practice, we set ∀b∈[1:B]λb. These correction steps are summarized in algorithm 3.
3.2. Algorithm
| Algorithm 3 Mixture of Experts Correct | |
|---|---|
|
|
3.3. Reference mapping
In Supplementary Figure 13, we used Harmony to map 2 query datasets onto a reference dataset. We achieved this by modifying ϕ* so that batch terms for reference cells does not get modeled or corrected. For every cell i in a reference dataset, set ϕi*=[1, 0, … 0]. This makes Harmony explain cell i in terms of an intercept and nothing else. Since intercept terms don't get removed, cell i never changes its embedding (i.e. ).
3.4. Caveat
This section assumes the modeled data are orthogonal and each normally distributed. This is not true for the L2 normalized data used in spherical clustering. Regression in this space requires the estimation and interpolation of rotation matrices, a difficult problem. We instead perform batch correction in the unnormalized space. The corrected data are then L2-normalized for the next iteration of clustering.
4. Performance and Benchmarking
4.1. LISI Metric
Assessing the degree of mixing during batch correction and dataset integration is an open problem. Several groups have proposed methods to quantify the diversity of batches within local neighborhoods, defined by k nearest neighbor (KNN) graphs, of the embedded space. Buttner et al39 provide a statistical test to evaluate the degree of mixing, while Azizi et al40 report the entropy of these distributions. Our metric for local diversity is related to these approaches, in that we start with a KNN graph. However, our approach considers two problems that these do not.
First, the metric should be more sensitive to local distances. For example, a neighborhood of 100 cells can be equally mixed among 4 batches. However, within the neighborhood, the cells may be clustered by batch. The second problem is one of interpretation. kBET provides a statistical test to assess the significance of mixing, but it is not clear whether all neighborhoods should be significantly mixed when the datasets have vastly different cell type proportions. Azizi et al40 et al use entropy as a measure of diversity, but it is not clear how to interpret the number of bits required to encode a neighborhood distribution.
Our diversity score, the Local Inverse Simpson's Index (LISI) addresses both points. To be sensitive to local diversity, we build Gaussian kernel based distributions of neighborhoods. This gives distance-based weights to cells in the neighborhood. The current implementation computes these local distributions using a fixed perplexity (default 30), which has been shown to be a smoother function than fixing the number of neighbors. We address the second issue of interpretation using the Inverse Simpson's Index (1/Σb=1Bp(b)). The probabilities here refer to the batch probabilities in the local neighborhood distributions described above. This index is the expected number of cells needed to be sampled before two are drawn from the same batch. If the neighborhood consists of only one batch, then only one draw is needed. If it is an equal mix of two batches, two draws are required on average. Thus, this index reports the effective number of batches in a local neighborhood. Our diversity score, LISI, combines these two features: perplexity based neighborhood construction and the Inverse Simpson's Index. LISI assigns a diversity score to each cell. This score is the effective number of batches in that cell's neighborhood. Code to compute LISI is available as at https://github.com/immunogenomics/LISI. The major shortcoming of LISI is in situations with datasets with vastly different sizes. We demonstrate what happens in this situation in Supplementary Note 2.
4.1.1. Significance between embeddings
In benchmarking against other algorithms, we compared the LISI scores of Harmony to LISI scores of embeddings from other algorithms. We did this with a standard bootstrap estimation framework: first, build an empirical distribution of Harmony LISI values for each cell; then count the frequency with which the observed benchmark LISI is more extreme than bootstrapped LISI values. During the resampling phase, we reran PCA, Harmony, and LISI for every bootstrap sample. For the p-value computation, we used a 2-tailed empirical approach, adding 1 to the observed counts to avoid p=0. This calculation is described in the equation below. Let be the observed LISI value for cell i for a benchmarking algorithm. Let LISIib to be LISI value for the bth bootstrap value for cell i. We compute p as:
4.2. Time and Memory
We performed execution time and maximum memory usage benchmarks on all analyses. All jobs were run on Linux servers and allotted 6 cores and 120GB of memory. The machines were equipped with Intel Xeon E5-2690 v3 processors. To evaluate execution time and maximal memory usage, we used the Linux time utility (/usr/bin/time on our systems) with the -v flag to record memory usage. Execution time was recorded from the{Elapsed time} field. Maximum memory usage was recorded from the {Maximum resident set size} field.
4.3. Cell type prediction accuracy
In addition to cLISI, we measured the accuracy of an embedding with cell type prediction. Briefly, we predict each cell's type based on its neighboring cells and compute accuracy as the frequency of correct predictions. In detail, we compute the 30 nearest neighbors of a cell, based on cosine distance. We then weigh them with an RBF kernel with σ=0.1 width. Finally, we take the weighted sum over the neighbor's cell types and return the most likely cell type. Formally, for cell i, its 30 nearest cells NN(i), an embedding matrix Z, and cell type labels vector T, compute the most probable cell type label t:
| (15) |
4.4. Gene expression prediction
We predicted gene expression in the 10X+MERFISH analysis using a similar approach to cell type prediction above. Instead of predicting cell type labels T, we predicted gene expression yg. We predict the expression ygi take a weighted average of the observed normalized gene expression values of cell i's nearest neighbors.
| (16) |
4.5. Five fold cross validation
In the 10X+MERFISH analysis, we predicted gene expression of the 154 intersecting measured genes with a five fold cross validation framework. In this analysis, we removed a randomly sampled one fifth of the genes from both datasets before normalization. We then performed normalization, scaling, PCA, and Harmony integration from the remaining four fifths of the genes and predicted the expression of the original removed genes. We repeat this procedure for each of the 5 holdout genesets. We then repeat the entire procedure 10 times, selecting a new random partition in each iterations. We consider the mean of these 10 iterations as the predicted value of the gene. We calculated the pearson correlation between the predicted and measured expression of each gene.
4.6. Neuronal subtype correlation
To calculate the correlations between the 10X predicted clusters and the MERFISH clusters, we first subsetted the predicted gene expression matrix to the 154 intersecting 10X/MERFISH genes; we then concatenated the predicted 10X neuronal subtypes to the predicted gene expression matrix and the known neuronal subtypes to the MERFISH dataset. In both the predicted gene expression matrix and the MERFISH dataset, we calculated the average expression of the predicted 10X neuronal subtypes and known neuronal subtypes respectively. Finally, we calculated the spearman correlation between the average expression of each predicted 10X inhibitory/excitatory subtype and known MERFISH inhibitory/excitatory subtypes.
5. Analysis Details
5.1. Preprocessing scRNAseq data.
We downloaded raw read or UMI matrices for all datasets, from their respective sources. The one exception was the 3pV1 dataset from the PBMC analysis. These data were originally quantified with the hg19 reference, while the other two PBMC datasets were quantified with GRCh38. Thus, we downloaded the fastq files from the 10X website (Supplementary Table 8). We quantified gene expression counts using Cell Ranger11,41 v2.1.0 with GRCh38. From the raw count matrices, we used a standard data normalization procedure, laid out below, for all analyses, unless otherwise specified. Except for the L2 normalization and within-batch variable gene detection, this procedure follows the standard guidelines of the Seurat single cell analysis platform.
We filtered cells with fewer than 500 genes or more than 20% mitochondrial reads. In the pancreas datasets, we filtered cells with the same thresholds used in Butler et al7: 1750 genes for CelSeq, 2500 genes for CelSeq2, no filter for Fluidigm C1, 2500 genes for SmartSeq2, and 500 genes for inDrop. We then library normalized each cell to 10,000 reads, by multiplicative scaling, then log scaled the normalized data. We then identified the top 1000 variable genes, ranked by coefficient of variation, within in each dataset. We pooled these genes to form the variable gene set of the analysis. Using only the variable genes, we mean centered and variance 1 scaled the genes across the cells. Note that this was done in the aggregate matrix, with all cells, rather than within each dataset separately. With these values, we performed truncated SVD keeping the top 30 eigenvectors. Finally, we multiplied the cell embeddings by the eigenvalues to avoid giving eigenvectors equal variance.
5.1.1. Spatial analysis
The raw count 10X and MERFISH datasets were downloaded from their GEO and Dryad repositories respectively. MERFISH metadata was downloaded as a supplementary table from the Moffitt et al. publication27. Figures were generated using the 6 mice from the 10X dataset and the first naive female mouse in the MERFISH dataset. For purposes of prediction all cells labeled as 'Ambiguous' or 'Unstable' were removed from both datasets, as these represent cells with a low number of unique genes expressed, a low library size, or a non-deterministic clustering. All genes in the 10X dataset that were not expressed in any cells were removed. In the MERFISH dataset, the gene blanks were removed for integration and the Fos gene was removed (no numerical values).
In the 10X dataset, we normalized the counts by dividing the raw counts within each cell by the total number of transcripts within that cell, scaling these counts by 10,000, offsetting the counts by 1, and log transforming the counts. As the MERFISH dataset counts were already normalized by volume we only performed log transformation on the counts with an offset of 1. We then combined the two datasets by subsetting the 10X dataset to the 154 intersecting genes, concatenating the normalized count matrices, and scaling each gene through z-score transformation.
5.2. Visualization
We used the UMAP algorithm42,43 to visualize cells in a two dimensional space. For all analyses, UMAP was run with the following parameters: k=30 nearest neighbors, correlation based distance, and min_dist=0.1.
5.3. Comparison to other algorithms
We used the provided packages or source code provided by the four comparison algorithm publications.
5.3.1. MNN Correct
We used the mnn correct function, with default parameters, in the scran R package44, version 1.9.4. As input, we provided a matrix of PCA embeddings.
5.3.2. Seurat MultiCCA
We followed the suggested integration pipeline in the Seurat R package7, version 2.3.4. This included the RunMultiCCA, MetageneBicorPlot, CalcVarExpRatio, SubsetData (subset.name = "var.ratio.pca", accept.low = 0.5), and AlignSubspace functions. Unless specified, we used all default parameters for these functions. We used the same number of canonical components as the number of PCs used as input to Harmony, MNN Correct, and Scanorama. Unlike the integration examples, we did not scale data within datasets separately, unless otherwise specified. We scaled data on the pooled count matrix instead.
5.3.3. Scanorama
We used the assemble function, with precomputed PCs, from the primary github repository (brianhie/scanorama). We set knn=30 and sigma=1, to match the default comparable MNN Correct parameters. All other parameters were kept at default values. We did not use the correct function, as this included both pre-processing and integration of the data. For more equitable comparisons, we tried to use the same pre-processing pipelines for all methods and only compare only the integration steps.
5.3.4. BBKNN
We downloaded the BBKNN software from the primary github repository (Teichlab/bbknn) and followed the suggested integration pipelines, using the bbknn and scanpy umap functions. For the bbknn function, we used k=5 and trim=20 for all analyses except for the HCA datasets, in which we used k=10 and trim=30, to accommodate the larger number of cells. All other parameters were kept at default values. Because BBKNN by design constructs a batch-balanced neighborhood graph, LISI should be biased towards these neighbors. On the other hand, BBKNN does not learn a low dimensional embedding aside from UMAP. Therefore, we were forced to use the potentially biased neighborhood graph provided by the method. We felt that this was appropriate because one step of BBKNN is to prune this graph before the UMAP step. Thus, we used the pruned BBKNN graph to compute LISI.
5.4. Harmony Parameters
By default, we set the following parameters for Harmony: θ=2, K=100, τ=0, σ=0.1, block_size=0.05, ϵcluster=10−5, ϵharmony=10−4, max_itercluster=200, max_iterHarmony=10, λ=1. For the pancreas analysis, we set τ=5. We set donors to be the primary covariate (θ=2) and technology secondary (θ=4). In the spatial analysis, we used θ=3 and λ=0.05.
5.5. Identification of alpha and beta ER stress subpopulations
We identified the alpha and beta ER stress clusters in Figure 5 by performing downstream analysis, specified in this section, on the integrated joint embedding produced by Harmony. After Harmony integration, we performed clustering analysis to find novel subtypes. Clustering was done on the trimmed shared nearest neighbor graph with the Louvain algorithm45, as implemented in the Seurat package BuildSNN and RunModularityClustering functions. We used parameters resolution=0.8, k=30, and nn.eps=0. We identified several clusters within the alpha, beta, and ductal cell populations. For each cluster, we performed differential expression analysis within the defined cell type. That is, we compared alpha clusters to all other alpha cells. For differential expression, we used the R Limma package18 on the normalized data. We included technology and library complexity (log number of unique genes) as covariates in the linear models. We used the top 100 over-expressed genes for each cluster, weighted by the t-statistic, to perform pathway enrichment with the enrichR46,47 R package, using the three Gene Ontology genesets48,49. The ductal subpopulation was enriched for ribosomal genes; we did not follow up on this cluster.
5.6. Labeling cells with canonical markers
In the cell-line, PBMC, and Pancreas analyses, we labeled cells within individual datasets using canonical markers. We did this by using the standard pre-processing pipeline for each dataset, clustering (Louvain, as above), and identifying clusters specific for the canonical markers for that analysis. We used a similar strategy to identify fine-grained subpopulations of PBMCs and in the HCA 500,000 cell dataset. In these case, we clustered in the joint embedding produced by Harmony, then looked for clusters that specifically expressed expected canonical markers.
5.7. Identification of spatially autocorrelated transcription factors
To identify which of our predicted genes were transcription factors, we downloaded all known vertebrate transcription factors from JASPAR in MEME format29. We used this list of transcription factors as a reference for our predicted genes list. We assessed the degree of spatial localization of each transcription factor using Moran's I statistic. Due to the large number of cells, we found the calculation of a dense weights matrix of all pairwise distances between cells to be untenable. Therefore, after taking each slice and centering their respective cell's X and Y centroids around 0, we calculated a sparse weights matrix by finding each MERFISH cell's 30 nearest MERFISH neighbors (using centered X-centroids, centered Y-centroids, and slice Z-position as locations for each cell) excluding itself and applying an RBF kernel on the distances of each MERFISH cell's nearest neighbors with bandwidth σ=60. For each set of nearest neighbors, we divided each distance by the sum of the distances to obtain probabilities to use as weights, and input these weights into a sparse matrix. Calculations then proceeded as normal from the equation, using the sparse distance matrix as the weights matrix. Genes with significant spatial autocorrelation were evaluated at FDR 0.05. Formally, for gene g, a nearest neighbor map NN, and a 3D spatial embedding matrix X, the nearest-neighbor formulation of Moran's I is:
| (17) |
| (18) |
5.8. ISH Allen Brain Atlas access
To look at the coarse ISH data from Allen Brain Atlas, we utilized the ISH data portal31. We searched for our gene of interest (Satb1) and selected experiment number 79488931, with coronal slices. To estimate the anterior-posterior position of each slice, we used the online tool to map each slice to an Atlas reference slice. Each reference slice has a position from the Bregma, searchable in their online Allen Mouse Brain volumetric atlas 2012: https://scalablebrainatlas.incf.org/mouse/ABA12. The representative image in Figure 6A is slice 62 (282) in the volumetric atlas. We also used the Atlas annotations online to estimate the location of anatomical structures (i.e. hypothalamus and ventricles) in each slice. We downloaded 13 to 16 from experiment 79488931 and focused on a 2×2cm region around the hypothalamus.
5.9. Statistics
Statistical analysis of LISI score comparisons is described in section 4.1.1. Differential expression tests in the pancreatic islet cell analysis were performed with 2-tailed moderated t-tests, implemented in the LIMMA R package. Correlation analyses in the pancreatic islet cell and MERFISH analyses were performed using Spearman correlation.
6. Reporting Summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Data Availability
All data analyzed in this manuscript are publicly available through online sources. We included links to all data sources in Supplementary Table 8.
Code Availability
Harmony and LISI are available as R packages on https://github.com/immunogenomics/harmony and https://github.com/immunogenomics/lisi. Scripts to reproduce results of the primary analyses will be made available on https://github.com/immunogenomics/harmony2019. Additionally, vignettes are included as supplementary notes. Supplementary note 1 provides a detailed walkthrough of Harmony, connecting theoretical algorithm components to their code implementations. Supplementary note 2 demonstrates the LISI metric and how to evaluate its statistical significance. Supplementary note 1 uses Harmony with simulated datasets.
Supplementary Material
Acknowledgements
This work was supported in part by funding from the National Institutes of Health (UH2AR067677, U19AI111224, and 1R01AR063759 (to SR)) and T32 AR007530-31 (to IK). We thank members of the Raychaudhuri and Brenner labs for comments and discussion. IK and KW were funded as part of a collaborative research agreement with F. Hoffmann-La Roche Ltd (Basel, Switzerland), to SR and MBB.
Footnotes
Competing Interests Statement
IK does paid bioinformatics consulting through Brilyant LLC.
References
- 1.Svensson V, Vento-Tormo R & Teichmann SA Exponential scaling of single-cell RNA-seq in the past decade. Nature Protocols 13, 599–604 (2018). [DOI] [PubMed] [Google Scholar]
- 2.Regev A et al. The human cell atlas. Elife 6 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Zhang F et al. Defining inflammatory cell states in rheumatoid arthritis joint synovial tissues by integrating single-cell transcriptomics and mass cytometry. Nature immunology 1 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Arazi A et al. The immune cell landscape in kidneys of lupus nephritis patients. Nature Immunology 20, 902–914 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Der E et al. Tubular cell and keratinocyte single-cell transcriptomics applied to lupus nephritis reveal type I IFN and fibrosis relevant pathways. Nature Immunolology 20, 915–927 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hicks SC, Townes FW, Teng M & Irizarry RA Missing data and technical variability in single-cell RNA-sequencing experiments. Biostatistics 19, 562–578 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Butler A, Hoffman P, Smibert P, Papalexi E & Satija R Integrating single-cell transcriptomic data across different conditions, technologies, and species. Nature. Biotechnology. 36, 411–420 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Haghverdi L, Lun ATL, Morgan MD & Marioni JC Batch effects in single-cell RNA-sequencing data are corrected by matching mutual nearest neighbors. Nature Biotechnology. 36, 421–427 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hie BL, Bryson B & Berger B Efficient integration of heterogeneous single-cell transcriptomes using Scanorama. Nature Biotechnology 37, 685–691 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Polanski K, Park JE, Young MD, Miao Z, Meyer KB & Teichmann SA BBKNN: Fast Batch Alignment of Single Cell Transcriptomes. Bioinformatics btz625 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Zheng GXY et al. Massively parallel digital transcriptional profiling of single cells. Nature Communications. 8, 14049 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Li B et al. HCA data portal - census of immune cells.
- 13.Segerstolpe A et al. Single-Cell transcriptome profiling of human pancreatic islets in health and type 2 diabetes. Cell Metab. 24, 593–607 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Baron M et al. A Single-Cell transcriptomic map of the human and mouse pancreas reveals inter- and intra-cell population structure. Cell Systems 3, 346–360.e4 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lawlor N et al. Single-cell transcriptomes identify human islet cell signatures and reveal cell-type-specific expression changes in type 2 diabetes. Genome Research. 27, 208–222 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Grun D et al. De novo prediction of stem cell identity using Single-Cell transcriptome data. Cell Stem Cell 19, 266–277 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Muraro MJ et al. A Single-Cell transcriptome atlas of the human pancreas. Cell Systems 3, 385–394.e3 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ritchie ME et al. limma powers differential expression analyses for RNA-sequencing and microarray studies. Nucleic Acids Research 43, e47 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gao T et al. Pdx1 maintains β cell identity and function by repressing an α cell program. Cell Metabolism 19, 259–271 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Jia S et al. Insm1 cooperates with neurod1 and foxa2 to maintain mature pancreatic β-cell function. EMBO J. 34, 1417–1433 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Sachdeva MM et al. Pdx1 (MODY4) regulates pancreatic beta cell susceptibility to ER stress. Proc. Natl. Acad. Sci. U.S.A. 106, 19090–19095 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Katoh MC et al. MafB is critical for glucagon production and secretion in mouse pancreatic α cells in vivo. Mol. Cell. Biol. 38 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Liu J et al. Islet-1 regulates arx transcription during pancreatic islet α-Cell development. J. Biol. Chem. 286, 15352–15360 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Akiyama M et al. X-box binding protein 1 is essential for insulin regulation of pancreatic α-cell function. Diabetes 62, 2439–2449 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Burcelin R, Knauf C & Cani PD Pancreatic alpha-cell dysfunction in diabetes. Diabetes Metab. 34 Suppl 2, S49–55 (2008). [DOI] [PubMed] [Google Scholar]
- 26.Pijuan-Sala B et al. A single-cell molecular map of mouse gastrulation and early organogenesis. Nature 566, 490–495 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Moffitt JR et al. Molecular, spatial, and functional single-cell profiling of the hypothalamic preoptic region. Science 362 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Moffitt J et al. Data from: Molecular, spatial and functional single-cell profiling of the hypothalamic preoptic region (2018). URL 10.5061/dryad.8t8s248. [DOI] [PMC free article] [PubMed]
- 29.Khan A et al. JASPAR 2018: update of the open-access database of transcription factor binding profiles and its web framework. Nucleic Acids Res. 46, D260–D266 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Close J et al. Satb1 is an activity-modulated transcription factor required for the terminal differentiation and connectivity of medial ganglionic eminence-derived cortical interneurons. J. Neurosci. 32, 17690–17705 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Lein ES et al. Genome-wide atlas of gene expression in the adult mouse brain. Nature 445, 168–176 (2007). [DOI] [PubMed] [Google Scholar]
- 32.Leek JT & Storey JD Capturing Heterogeneity in Gene Expression Studies by Surrogate Variable Analysis. PloS Genet 3(9): e161 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Stegle O, Parts L, Piipari M, Winn J, Durbin R Using probabilistic estimation of expression residuals (PEER) to obtain increased power and interpretability of gene expression analyses. Nature Protocols 7, 500–507 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Mizoguchi F et al. Functionally distinct disease-associated fibroblast subsets in rheumatoid arthritis. Nature communications 9, 789 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Manno GL et al. RNA velocity of single cells. Nature 560, 494–498 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
Methods-only References
- 36.Mao Q, Wang L, Goodison S & Sun Y Dimensionality reduction via graph structure learning. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ‘15, 765–774 (ACM, New York, NY, USA, 2015). [Google Scholar]
- 37.Dhillon IS & Modha DS Concept decompositions for large sparse text data using clustering. Mach. Learn. 42,143–175 (2001). [Google Scholar]
- 38.Jordan MI & Jacobs RA Hierarchical mixtures of experts and the EM algorithm. Neural Comput. 6, 181–214 (1994). [Google Scholar]
- 39.Buttner M, Miao Z, Wolf FA, Teichmann SA & Theis FJ A test metric for assessing single-cell RNA-seq batch correction. Nature Methods 16, 43–49 (2019). [DOI] [PubMed] [Google Scholar]
- 40.Azizi E et al. Single-Cell map of diverse immune phenotypes in the breast tumor microenvironment. Cell 174, 1293–1308.e36 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Dobin A et al. STAR: ultrafast universal RNA-seq aligner. Bioinformatics 29, 15–21 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.McInnes L & Healy J UMAP: Uniform manifold approximation and projection for dimension reduction. arXiv (2018). 1802.03426. [Google Scholar]
- 43.Becht E et al. Dimensionality reduction for visualizing single-cell data using UMAP. Nature Biotechnology 37, 38–44 (2019). [DOI] [PubMed] [Google Scholar]
- 44.Lun ATL, McCarthy DJ & Marioni JC A step-by-step workflow for low-level analysis of single-cell rna-seq data with bioconductor. F1000Res. 5, 2122 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Blondel VD, Guillaume J-L, Lambiotte R & Lefebvre E Fast unfolding of communities in large networks. J. Stat. Mech: Theory Exp. 2008 (2008). [Google Scholar]
- 46.Chen EY et al. Enrichr: interactive and collaborative HTML5 gene list enrichment analysis tool. BMC Bioinformatics 14, 128 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Kuleshov MV et al. Enrichr: a comprehensive gene set enrichment analysis web server 2016 update. Nucleic Acids Res. 44, W90–7 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.The Gene Ontology Consortium. Expansion of the gene ontology knowledgebase and resources. Nucleic Acids Res. 45, D331–D338 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Ashburner M et al. Gene ontology: tool for the unification of biology. the gene ontology consortium. Nature Genetics 25, 25–29 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data analyzed in this manuscript are publicly available through online sources. We included links to all data sources in Supplementary Table 8.