Abstract
Impaired sarcoplasmic reticulum (SR) calcium transport ATPase (SERCA) gives rise to Ca2+ alternans and changes of the Ca2+release amount. These changes in Ca2+ release amount can reveal the mechanism underlying how the interaction between Ca2+ release and Ca2+ uptake induces Ca2+ alternans. This study of alternans by calculating the values of Ca2+ release properties with impaired SERCA has not been explored before. Here, we induced Ca2+ alternans by using an impaired SERCA pump under ischemic conditions. The results showed that the recruitment and refractoriness of the Ca2+ release increased as Ca2+ alternans occurred. This indicates triggering Ca waves. As the propagation of Ca waves is linked to the occurrence of Ca2+ alternans, the “threshold” for Ca waves reflects the key factor in Ca2+ alternans development, and it is still controversial nowadays. We proposed the ratio between the diastolic network SR (NSR) Ca content (Cansr) and the cytoplasmic Ca content (Cai) (Cansr/Cai) as the “threshold” of Ca waves and Ca2+ alternans. Diastolic Cansr, Cai, and their ratio were recorded at the onset of Ca2+ alternans. Compared with certain Cansr and Cai, the “threshold” of the ratio can better explain the comprehensive effects of the Ca2+ release and the Ca2+ uptake on Ca2+ alternans onset. In addition, these ratios are related with the function of SERCA pumps, which vary with different ischemic conditions. Thus, values of these ratios could be used to differentiate Ca2+ alternans from different ischemic cases. This agrees with some experimental results. Therefore, the certain value of diastolic Cansr/Cai can be the better “threshold” for Ca waves and Ca2+ alternans.
1. Introduction
Cardiac arrhythmia has long been associated with abnormal intracellular Ca2+ handling dynamics [1–4]. One useful diagnostic marker of arrhythmias is electrical alternans [5–8], which is expressed as alternated action potential durations (APDs) at the cellular level [9] and T waves on the electrocardiogram (ECG) [5], where the T wave stands for the repolarization of the ventricles and T wave alternans (TWA) indicates that the amplitude or the morphology of the T wave alternates beat-to-beat. The link between ischemia and alternans has been extensively explored [10]. Our previous simulations identified that hyperkalaemia, one component of ischemia, results in depolarization alternans [11]. Other two ischemic components, hypoxia and acidosis, lead to repolarization alternans by causing instabilities in calcium cycling [4, 11, 12]. Ca2+ alternans in ischemia can be taken as the arrhythmic triggers leading to afterdepolarization and also as the substrate facilitating reentry by inducing electrical alternans [4].
Alternans depends on instabilities of membrane voltage (Vm) [13] or/and intracellular Ca2+ handling [1, 7, 9, 14–20], due to their bidirectional couplings [3, 9, 21]. For the latter, it is known that the Ca2+ handling includes Ca2+ influx and efflux [16], and its abnormality can arise from the dysfunction of sarcoplasmic reticulum (SR) calcium transport ATPase (SERCA) [11, 13, 14], ryanodine receptor (RyR2) [1, 4, 7, 14, 16], and Ca2+ leak [13]. Under ischemic conditions, both the Ca2+ release current (Irel) [4] and the Ca2+ uptake current (Iup) decrease [4, 22] to facilitate the formation of Ca2+ alternans in an interactive manner. In this work, we will focus on Ca2+ alternans caused by an impaired SERCA pump in ischemia.
The sarcoplasmic reticulum (SR) Ca2+ release curve describes the nonlinear relationship between SR Ca2+ release content and diastolic SR Ca2+ content (Casr). The steep slope of this curve indicates that more Ca2+ is released at high diastolic SR Ca2+ content. In heart failure (HF), we have identified the primary role of the steep SR Ca2+ release curve in the genesis of alternans through simulation study [23]. Furthermore, the steep slope of the curve is also able to explain the impaired SERCA pump-caused Ca2+ alternans [19]. The onset of Ca2+ alternans in HF and in this study can be described as follows [9, 16]: when the slope of the curve is steep at certain Casr, a small increment of diastolic Casr will result in a larger Ca2+ release, where released Ca2+ cannot be completely refilled back to the SR by impaired SERCA pumps. In the following heartbeat, the decreased Casr gives rise to a smaller subsequent Ca2+ release. According to the above description, the steep slope of SR Ca2+ release curve provides the substrate for alternans onset and impaired SERCA pump enhances the susceptibility. Previous studies attribute the steep slope to Ca wave propagation [23–25] or the saturation of buffered Casr [26]. In fact, the steep slope of the curve is directly linked to the change of Irel. Then, what are the detailed changes of Irel to increase slopes? What is the factor that brings change to the Irel? To investigate these questions, we took use of “3R theory” [27] to find the answers. The “3R theory” defines three critical properties (α for “randomness”, β for “refractoriness,” and γ for “recruitment”) of a Ca spark, and we use the properties to analyze Ca2+ alternans. These properties are further introduced in the Materials and Methods section.
The propagation of Ca waves is linked to the onset of Ca2+ alternans [25, 27]. Although experimental and theoretical studies have investigated the development of Ca waves, there is a dispute regarding the definition of the “threshold” for Ca waves. Some experimental studies indicated Casr as the “threshold” [24, 28, 29], while others highlighted the role of intracellular Ca2+ concentration (Cai) [30–32]. We propose the ratio of diastolic network SR (NSR) Ca2+ content (Cansr) to diastolic Cai (Cansr/Cai) as the “threshold” for Ca waves and Ca2+ alternans, which highlights both of their roles, and finally verify it by simulations. The “threshold” of diastolic Cansr/Cai is determined by thermodynamic constraints, which provides the theoretical basis for our new “threshold.” Moreover, this new “threshold” theory may help us better understand alternans and potentially provide a novel therapeutic strategy for alternans.
2. Materials and Methods
A thermodynamic model of SR Ca pump (SERCA pump model) [22] was integrated into the human epicardial (epi) ventricular cell model (O'Hara-Rudy dynamic (ORd) model) to simulate Ca2+ alternans [33]. The ORd model can reproduce the rate dependence of Ca2+ in experiments. The SERCA pump model is built based on experimental data of the rabbit and other animals. We used it to obtain the Ca2+ uptake rate per pump and multiplied a scale factor to calculate Iup. The appropriate coefficient was determined by comparing the Iup amplitude produced by the original ORd epi cell model and the Ca2+ uptake rate per pump at steady state under normal conditions (this method was described in detail in our previous study [11]). The SERCA pump model incorporates the regulation effect of phospholamban (PLB) on Ca2+ uptake. Similar with the effect of increased pH (Figure 4 in [22]), PLB phosphorylation decreases the half-maximum Ca2+ uptake rate K0.5 [34] and increases SR Ca2+ uptake rate. During early phase of ischemia, the increased PLB phosphorylation helps to maintain the function of the SERCA pump [4]. After 20–30 minutes of ischemia, PLB dephosphorylation reduces SR Ca2+ uptake rate [4, 35]. In this work, we simulated the membrane voltage and ion concentrations after 10–20 minutes of ischemia, where phosphorylation level of PLB was kept the same as in control and the SERCA pump was impaired by ischemic components.
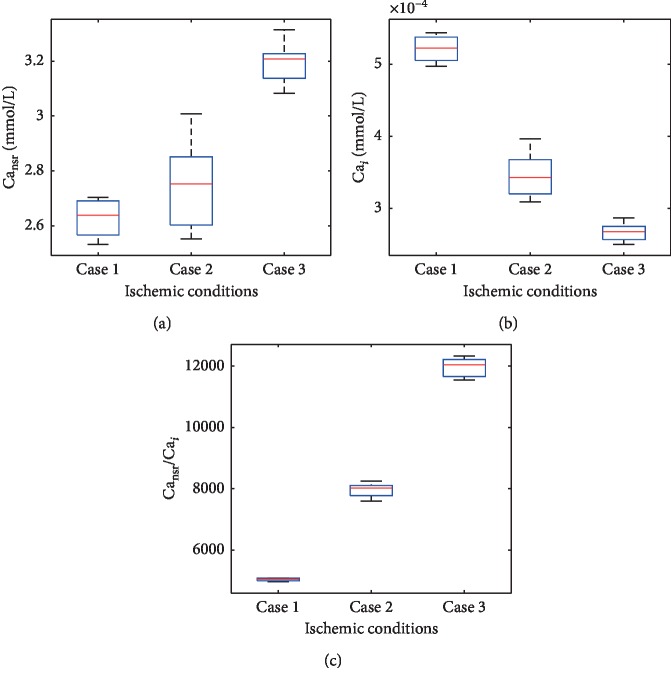
Figure 4.
Diastolic Cansr, Cai, and Cansr/Cai at the onset of Ca2+ alternans. Ca2+ alternans arises at different ranges of CLs in three ischemic cases. The ranges of CLs in ischemic cases 1, 2, and 3 are from 250 ms to 280 ms, from 250 ms to 380 ms, and from 250 ms to 300 ms.
As shown below, two Ca2+ are translated from the cytoplasm to the SR during Ca2+ uptake [22]:
| (1) |
To investigate the effect of the ischemia-impaired SERCA pump on Irel at stable state, we first compared calcium transients between control and ischemia and then applied the “3R theory” to analyze the changes of Irel achieved by decreased Iup. This investigation explained how Iup cooperated with Irel to cause Ca2+ alternans.
2.1. Conditions Setting in the Simulations
Ischemic conditions contribute to compromised metabolism and thus lead to decreased function of SERCA pumps. Specifically, hypoxia decreases intracellular ATP concentration ([ATP]i) and increases intracellular ADP concentration ([ADP]i) [36]. Meanwhile, inorganic phosphate (Pi) in the cytoplasm increases [37] and pH is decreased by acidosis [12]. According to these experimental data, we simulated three cases of ischemia (Table 1) with the cycle length (CL) of 250 ms and 350 ms, respectively to obtain Ca2+ alternans. After 1000 beats, action potentials (APs) and Ca transients were taken to be stable. Then, we analyzed them in the subsequent 1000 beats.
Table 1.
Parameters setting under different conditions.
| Conditions | [ATP]i (mmol/L) | pH |
|---|---|---|
| Ischemic case 1 | 3 | 6.5 |
| Ischemic case 2 | 3.5 | 6.6 |
| Ischemic case 3 | 4 | 6.7 |
| Control condition | 9.8 | 7 |
The CL also affects whether Ca2+ alternans can occur or not in different ischemic conditions. We attempted to find the ranges of CL in which Ca2+ alternans could arise in these three cases. In our simulations, the starting CL is 250 ms and the increasing step is 10 ms. Finally, we determined the ranges of CL in ischemic cases 1, 2, and 3, which are from 250 ms to 280 ms, from 250 ms to 380 ms, and from 250 ms to 300 ms, respectively.
2.2. The SR Ca2+ Release Curve
In our simulations, the total amount of diastolic SR Ca2+ (Casr_total (mmol)) comprised the amount of diastolic NSR Ca2+ and the junctional SR (JSR) Ca2+. The amount of Ca2+ release (Carelease(k) (mmol)) was expressed as the integral of the Ca2+ release flux (Jrel(k) (mmol/L/ms)) on the kth beat (equation (4)). Then, we used the ratio of Carelease(k) to Casr_total(k−1) to represent the fraction of SR Ca2+ release:
| (2) |
| (3) |
| (4) |
where JSR Ca2+ included free and buffered Ca2+ (Cajsr_free (mmol/L) and Cajsr_buff (mmol/L)); vnsr and vjsr represented the volume of NSR and JSR; and Casr(k) (mmol/L) and Cansr(k) (mmol/L), respectively, referred to the diastolic SR and NSR Ca2+ content on the kth beat.
2.3. Calculating Values of α, β, and γ according to “3R” Theory
In the spatially distributed calcium cycling model developed by Rovetti et al. [27], SR Ca2+ is released through CRUs. One CRU is set to have six neighbors in the 3D-distribution cell simulation [27]. As shown in equations (5) and (6), N0 represents the total number of CRUs and NK is the number of that activated on the kth beat [27], where α represents the probability of a Ca spark being activated spontaneously or by the L-type Ca2+ current (ICaL); β is the probability of a Ca spark triggered on the kth beat being unavailable during the (k + 1)th beat; γ indicates the probability of a Ca spark recruiting one of its neighboring; and f represents the percentage of secondary Ca sparks in the remaining available CRUs [27]. The number of CRUs activated on the (k + 1)th beat is given as follows [27]:
| (5) |
| (6) |
| (7) |
where <ΔCa> is the average SR Ca2+ depletion of each CRU and Casr is the average Ca2+ content of each CRU before release [27]. <Cab> refers to the average Ca2+ content of these Nk CRUs after they sparked [27]. We put Carelease(k) and Casr_total to replace <ΔCa> and CaSR to obtain equation (8). The left-hand side is SR Ca2+ concentration depletion. Thus, Carelease(k) and Casr_total(k−1), calculated from our simulations (equations (2) and (4)), were linked with NK and N0.
| (8) |
N K and N0 in equation (8) were replaced by Carelease(k), Casr_total(k−1), and <Cab>. Thus, the relationship between properties of RyRs and our simulation results was built.
| (9) |
where α, β, γ, and <Cab> are unknown parameters and others could be obtained from our simulation results. To obtain these unknown parameters, we solved equation (9) by using the MATLAB built-in lsqcurvefit function. First, the inputs of Carelease(k) and Casr_total(k−1) were calculated from simulations. Meanwhile, initial α, β, and γ were set as random values from zero to one and the initial <Cab>/(vnsr + vjsr) was from zero to the maximum Casr_total/(vnsr + vjsr). Then, these values were input to solve equation (9). Specifically, when we calculated these parameters during the short period of alternans formation, the groups of inputs were too few to obtain accurate values of these unknown parameters. We solved <Cab> in equation (9) before and after alternans onset in advance and take the value of it as a constant to input equation (9). Thus, the number of unknowns is decreased, and the remaining three unknowns are able to be obtained during the short period of alternans formation.
2.4. Definition of the Occurrence of Ca2+ Alternans
Ca2+ alternans was supposed to occur when the following criteria were met:
| (10) |
where Caamplitude(k) is defined as the amplitude of Ca2+ transient on the kth beat.
3. Results
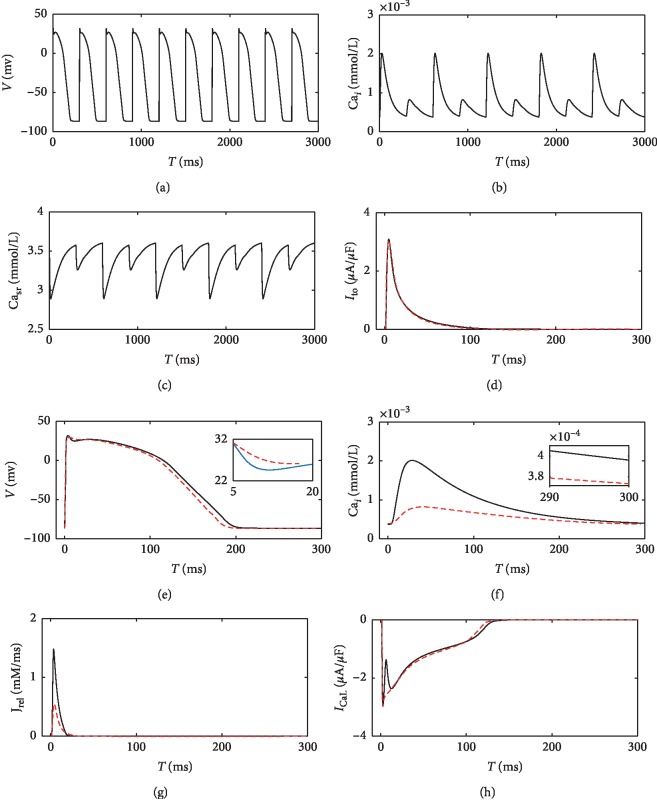
According to equation (1), increased [ADP]i, [Pi]i, and [H+]i and decreased [ATP]i result in less Ca2+ transported from the cytoplasm to the SR. The function of the SERCA pump is impaired by ischemia. As shown in Figure 1, the amplitudes of Cai and Casr alternate obviously. In contrast, diastolic Cai alternates slightly (inset of Figure 1(e)). APs also show slight alternans (Figure 1(d)), due to the Ca2+ alternans-caused fluctuation of ICaL. A larger Ca2+ release decreases ICaL, makes the transient outward current (Ito) more prominent, and leads to a slightly deeper notch of the AP. Subsequently, the voltage-dependent repolarization currents cause different repolarization phases.
Figure 1.
Alternans of APs and Ca transients and the relevant currents in ischemic case 2. Alternated APs, Cai, and Casr are shown in (a)–(c), respectively. Aligned Ito, APs, Cai, Jrel, and ICaL between two continuous APs are compared in (d)–(h), respectively, where the solid black lines stand for ischemic conditions and the dashed red lines stand for control condition. CL is 300 ms.
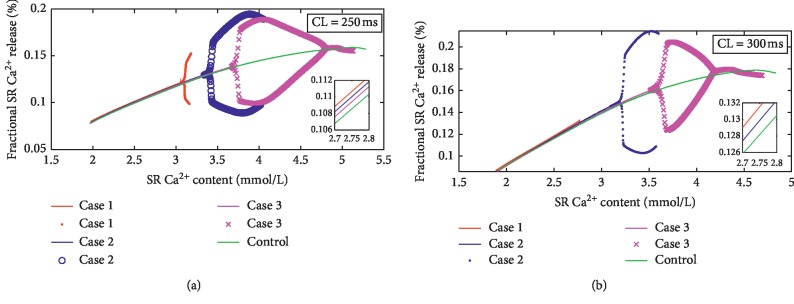
As shown in Figure 2, Ca2+ alternans can be observed in all three ischemic cases when CL = 250 ms. However, when the CL increases to 300 ms, it can only be observed in cases 2 and 3. In case 1, the maximum Casr with CL of 300 ms does not reach the value of Casr at which bifurcations occur with CL of 250 ms. In addition, the slopes of curves change slightly before alternans onset (inset of Figure 2), but the values of Casr change obviously when bifurcations occur. The values of Casr at which bifurcations occur decrease with the ischemic degree at the same CLs.
Figure 2.
SR Ca2+ release curves under control and ischemic conditions (cases 1, 2, and 3). (a) CL = 250 ms. (b) CL = 300 ms.
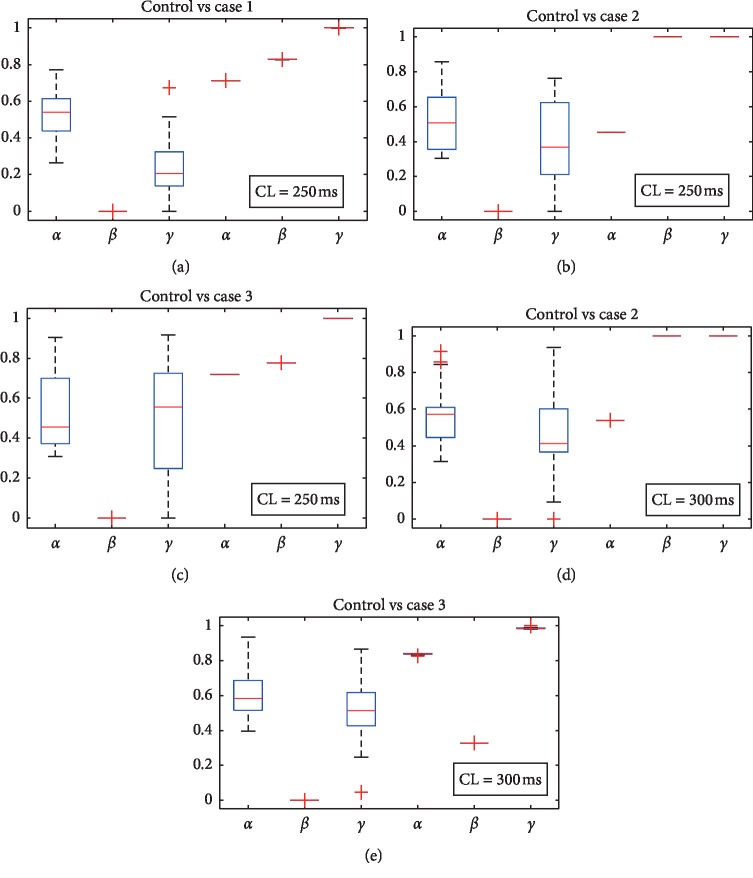
In Figure 3, α, β, and γ were obtained during the formation of Ca2+ alternans under different ischemic conditions. Compared with the control group, β and γ increase obviously in all ischemic conditions. In control condition, average β and γ are 0 and 0.42, respectively. They both increase to 1 in ischemic case 2 with CL of 300 ms. Nonetheless, α does not vary a lot.
Figure 3.
Values of α, β, and γ during the formation of Ca2+ alternans in control and ischemic cases. Twenty groups of parameter values are included in each box plot. In each panel, the left three box plots are in control conditions and the right three are under ischemia. The ranges of Casr are the same in every two contrasting groups. (a) Casr ranges from 3 to 3.7 mmol/L with the CL of 300 ms. (b) Casr ranges from 3.2 to 3.9 mmol/L with the CL of 300 ms. (c) Casr ranges from 2.8 to 3.15 mmol/L and the CL is 250 ms. (d) Casr ranges from 3 to 4 mmol/L and the CL is 250 ms. (e) Casr ranges from 3.5 to 4.4 mmol/L and the CL is 250 ms.
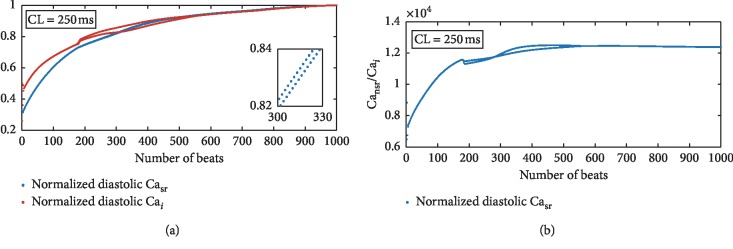
The values of diastolic Cansr, Cai, and Cansr/Cai in Figure 4 were recorded once Ca2+ alternans occurred in ischemia. On the one hand, Ca2+ alternans in case 1 or case 2 cannot be distinguished by the recorded values of Cansr (Figure 4(a)). On the other hand, there is a small difference between the values of the recorded Cai in case 2 and those in case 3 (Figure 4(b)). In contrast, the ratios vary obviously with ischemic cases. Compared with the effect of CLs, the degree of ischemia (values of [ADP]i, [Pi]i, [H+]i, and [ATP]i) affects the ratios more effectively. Furthermore, how diastolic Casr, Cai, and their ratio change with sequent heartbeats is analyzed under transient Ca2+ alternans (Figure 5). Ca2+ alternans lasts for some beats and gradually disappears in ischemic case 3 when CL = 250 ms. In the whole process of Ca2+ alternans development, diastolic Cansr, Cai, and their ratio fluctuate and increase (Figure 5). After Ca2+ alternans disappears, the ratio remains a constant value (Figure 5(b)) while the other two continue to increase (Figure 5(a)), where Casr and Cai are divided by their maximum values, respectively, to get normalized values, which are no bigger than one. This will facilitate the comparison in Figure 5(a).
Figure 5.
Normalized diastolic Cai (dashed red line in (a)), Casr (dashed blue line in (a)), and diastolic Cansr/Cai (b) under transient Ca2+ alternans. These values are recorded under ischemic case 3 during the 1000 consecutive beats.
4. Discussion
Consistent with previous study [25], fluctuations of Casr are observed during the impaired SERCA pump-caused Ca2+ alternans (Figures 1(c) and 5(a)). However, the slight fluctuations of Casr alone are insufficient to maintain Ca2+ alternans without the steep slope of Ca2+ release curve. The large fraction of Ca2+ release is demonstrated to generate Ca2+ alternans [16, 23, 25, 39]. Figure 2 shows that the curve slopes change slightly before the onset of alternans in different ischemic conditions. Subsequently, the obvious bifurcations occur in the curve. These obvious changes are the dominant factors to cause alternans. To elucidate how these bifurcations happen, we analyze how Irel is affected by impaired SERCA pump in the period of bifurcations occurrence.
I rel can be regarded as a collective effect of Ca sparks. During the formation of alternans, changes in properties of Ca sparks reflect how Irel is affected by the impaired SERCA pump. The values of β and γ increase obviously in ischemic groups compared to control without Ca2+ alternans (Figure 3). Rovetti et al. [27] concluded that large β and γ together with properly chosen α promote alternans. Our results confirmed their prediction (Figure 3).
Large β indicates long refractory period of RyRs when the CL is unchanged [27], implying a long time required for complete recovery of RyRs. Our results show that large β can be induced by the impaired SERCA pump. This can be easily understood through introducing a Ca2+ cycling hypothesis [16]: cytosolic Ca2+, taken up by the SERCA pump in the NSR, is released by the RyRs channels in the JSR. Thus, the process of transporting Ca2+ from the NSR to the JSR results in a delayed Ca2+ release after the uptake. The impaired SERCA pump slows the Ca2+ recycling process and increases RyRs refractory period. During the slow Ca2+ recycling process, the amount of Ca2+ reaching the release sites fluctuates, leading to alternated large and small Ca2+ releases. This hypothesis presents a possible mechanism underlying how SERCA pump modulates the refractoriness of the RyRs.
According to “3R theory,” large γ indicates frequent spark-induced sparks, which probably produce Ca waves. The propagation of Ca waves requires Ca diffusion to take effect. Ca diffusion is also shown to influence another behavior of synchronizing local Ca2+ release [40]. The degree of synchronization increases obviously when the “threshold” CL for alternans is approaching [40]. Because of the different dependence of pacing, Ca waves differ with the synchronization. However, when the synchronization occurs, Ca diffusion is also more likely to propagate Ca waves. The occurrence of Ca2+ alternans also promotes Ca2+ wave to propagate. On the other hand, the prolonged refractory period can produce alternated Ca waves by regulating the numbers of available CRUs. In all, large γ can either directly result from Ca2+ alternans or be induced by the prolonged refractory period.
Although we have investigated how Irel changes during the formation of Ca2+ alternans, the timing for these changes taking place is still unknown. Large γ is associated with the propagation of Ca waves. Ca waves are also linked to the onset of Ca2+ alternans. Figure 2 shows that Ca2+ alternans begin at some value of Casr. That is, that value of Casr is able to be regarded as the “threshold” for Ca waves [24, 28, 29]. This idea is also supported by the fact that increased Casr increases α and initiates Ca waves [24, 28]. However, if Casr is believed to be the “threshold” for Ca waves and Ca2+ alternans, then Ca2+ alternans should not disappear as Casr keeps rising (Figure 5(a)). In fact, whether the “threshold” of Casr determines Ca waves onset or not is also debated in other studies that tried to link Cai to the occurrence of Ca waves [30–32]. Moreover, although previous experimental study [28] supports the idea that the “threshold” of Casr determines Ca waves onset, diastolic Cai has also been associated with the frequency of release (Figures 2(a) and 2(b) of [28]). Undoubtedly, diastolic Cai also exerts influence in producing Ca waves and Ca2+ alternans. Therefore, we propose diastolic Cansr/Cai as the “threshold” of Ca waves and Ca2+ alternans, which reflects the roles of both Casr and Cai in the formation of Ca waves and Ca2+ alternans.
SERCA pumps contribute to maintain the Ca2+ concentration gradient between the SR and the cytoplasm. Since the Ca2+ uptake sites are in the NSR, diastolic Cansr/Cai is related to the Ca2+ uptake. According to equation (1), the maximum uptake rate is modulated by ischemic conditions ([ADP]i, [ATP]i, [Pi]i, and [H+]i). This means the maximum diastolic Cansr/Cai can be affected by ischemic cases. In addition, the onset of alternans is induced by ischemia, and thus its “threshold” is taken to be different with ischemic degrees. In Figure 4, the “threshold” of diastolic Cansr/Cai differs with ischemic conditions. As a contrast, neither Cai nor Cansr is able to distinguish different ischemic cases. In Figure 5, before the onset of Ca2+ alternans, Casr and Cai increase. Correspondingly, Iup goes on retaking the increasing released Ca2+ and diastolic Cansr/Cai keeps rising. However, to what extent Iup and diastolic Cansr/Cai can increase is limited by the thermodynamic constrains. Ca2+ alternans and Ca waves form when the unbalance between the Ca2+ uptake and Ca2+ release occurs. Subsequently, as diastolic Cai and Cansr keep on increasing, the Ca2+ uptake rate increases enough to uptake all released Ca2+ and Ca2+ alternans disappears. This final constant value of diastolic Cansr/Cai indicates the new balance between the Ca2+ release and Ca2+ uptake. On the other hand, if diastolic Cai or Cansr is the “threshold” for Ca waves and Ca2+ alternans, these two increasing values will initiate larger Ca waves and Ca2+ alternans will not disappear.
Xie et al. [15] demonstrated the SR Ca2+ efflux cooperates with the influx to affect the “threshold” for alternans. An intermediate SR Ca2+ uptake rate and a larger SR Ca2+ release work synergistically to produce alternans at longer CLs [16]. According to our new “threshold” theory, the limited increase of Iup contributes to unbalanced Iup and Irel and promotes abnormal intracellular Ca2+ handling. In addition, other studies demonstrated that the properties of RyRs affect the “threshold” of Casr for alternans [24, 41, 42]. When the open probability of RyRs channels increases at the same Casr [41], the Ca2+ uptake rate becomes larger accordingly. As the physiological conditions ([ADP]i, [ATP]i, [Pi]i, and [H+]i) are identical, the maximum Ca2+ uptake rate is kept the same. Thus, maximum Iup occurs at a lower Casr, resulting in a reduced “threshold” of Casr for alternans (Figure 3 of [24] and Figure 4 of [41]).
This “threshold” theory provides a new idea for changes of Irel during the formation of Ca2+ alternans. Our new “theory” shows that the unbalance between Iup and Irel begins at the “threshold” of diastolic Cansr/Cai. These two currents interact with each other and result in Ca2+ alternans. We should also note that Ca2+ alternans of case 3 is transient (Figure 5), which suggests that when Iup and Irel get balanced, Ca2+ alternans is suppressed. Therefore, this “threshold” theory may disclose a novel therapeutic strategy for Ca2+ alternans. In theory, keeping the ratio below the “threshold” stops Ca2+ alternans occurrence. In clinical, the treatment aiming at the interaction between these two currents may have a promising effect. Although direct therapeutic tools modulating the SR release channels have not been fully developed [2], the new proposed “threshold” theory can be regarded as a strong guideline for searching for new therapeutic targets.
5. Conclusion
The integrated cell model can be used to simulate the SERCA pump function in specific ischemic conditions, whereas the original ORd model cannot be used. The simulated results indicate that Ca waves can be induced by impaired SERCA pump and thus give rise to Ca2+ alternans. That is, these components of Ca cycling interact with each other to affect Ca2+ alternans development. In addition, compared with isolated changes of diastolic Casr and Cai, the value of diastolic Cansr/Cai is more appropriate to function as the “threshold” for alternans. By defining this new “threshold,” we can better explain how the interplay between the Iup and Irel causes alternans. Furthermore, this proposed “threshold” theory may help find therapeutic targets for suppressing Ca2+ alternans.
6. Limitations
This model is just used to simulate the impaired SERCA pump function during ischemia, whereas L-type calcium and other currents are also affected under ischemia, and these changes are not included in our model. We need to further improve this integrated model to simulate more accurate ischemic conditions. It is noted that the values of the three properties can be different by using different groups of inputs. The range of Cai chosen in our simulation can also determine the results by influencing the inputs. We also need to take use of other cell models to calculate values of these properties during Ca2+ alternans occurrence and identify our “threshold” theory. In addition, although we conclude that Iup and Irel interact to produce Ca2+ alternans, we just identify how the Ca release is affected by impaired SERCA pump, and the effect of Irel on Iup should also be identified in detail in the future.
Acknowledgments
This study was supported by the National R&D Program for Major Research Instruments (grant no. 61527811), the National Natural Science Foundation of China (grant no. 61701435), the Major Scientific Project of Zhejiang Lab (no. 2018DG0ZX01), the Zhejiang Provincial Natural Science Foundation of China (LY17H180003), and the Science Technology Department Program of Zhejiang Province (LGG18H180001).
Contributor Information
Yinglan Gong, Email: yinglangong@zju.edu.cn.
Ling Xia, Email: xialing@zju.edu.cn.
Data Availability
The data used to build graphs in this study are available from the corresponding author upon request.
Disclosure
Jiaqi Liu and Xiaoye Zhao are the co-first authors.
Conflicts of Interest
The authors declare that there are no conflicts of interest.
Supplementary Materials
Our supplementary files include the modified human ventricular cell model, codes, and data for plotting figures in our papers.
References
- 1.Lugo C. A., Cantalapiedra I. R., Peñaranda A., Hove-Madsen L., Echebarria B. Are SR Ca content fluctuations or SR refractoriness the key to atrial cardiac alternans?: insights from a human atrial model. American Journal of Physiology-Heart and Circulatory Physiology. 2014;306(11):H1540–H1552. doi: 10.1152/ajpheart.00515.2013. [DOI] [PubMed] [Google Scholar]
- 2.Zaza A., Rocchetti M. Calcium store stability as an antiarrhythmic endpoint. Current Pharmaceutical Design. 2015;21(8):1053–1061. doi: 10.2174/1381612820666141029100650. [DOI] [PubMed] [Google Scholar]
- 3.Landstrom A. P., Dobrev D., Wehrens X. H. T. Calcium signaling and cardiac arrhythmias. Circulation Research. 2017;120(12):1969–1993. doi: 10.1161/circresaha.117.310083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Baumeister P., Quinn T. A. Altered calcium handling and ventricular arrhythmias in acute ischemia. Clinical Medicine Insights: Cardiology. 2016;10(s1):61–69. doi: 10.4137/cmc.s39706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Verrier R. L., Klingenheben T., Malik M., et al. Microvolt T-wave alternans physiological basis, methods of measurement, and clinical utility—consensus guideline by International Society for Holter and Noninvasive Electrocardiology. Journal of the American College of Cardiology. 2011;58(13):1309–1324. doi: 10.1016/j.jacc.2011.06.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bers D. M. Calcium cycling and signaling in cardiac myocytes. Annual Review of Physiology. 2008;70(1):23–49. doi: 10.1146/annurev.physiol.70.113006.100455. [DOI] [PubMed] [Google Scholar]
- 7.Picht E., Desantiago J., Blatter L. A., Bers D. M. Cardiac alternans do not rely on diastolic sarcoplasmic reticulum calcium content fluctuations. Circulation Research. 2006;99(7):740–748. doi: 10.1161/01.res.0000244002.88813.91. [DOI] [PubMed] [Google Scholar]
- 8.Zang Y.-L., Xia L. Cellular mechanism of cardiac alternans: an unresolved chicken or egg problem. Journal of Zhejiang University Science B. 2014;15(3):201–211. doi: 10.1631/jzus.b1300177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Edwards J. N., Blatter L. A. Cardiac alternans and intracellular calcium cycling. Clinical and Experimental Pharmacology and Physiology. 2014;41(7):524–532. doi: 10.1111/1440-1681.12231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Carson D. L., Cardinal R., Savard P., Vermeulen M. Characterisation of unipolar waveform alternation in acutely ischaemic porcine myocardium. Cardiovascular Research. 1986;20(7):521–527. doi: 10.1093/cvr/20.7.521. [DOI] [PubMed] [Google Scholar]
- 11.Liu Z., Li G., Xia L., et al. In silico investigation into cellular mechanisms of cardiac alternans in myocardial ischemia. Computational and Mathematical Methods in Medicine. 2016;2016:9. doi: 10.1155/2016/4310634.4310634 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kapur S., Wasserstrom J. A., Kelly J. E., Kadish A. H., Aistrup G. L. Acidosis and ischemia increase cellular Ca2+ transient alternans and repolarization alternans susceptibility in the intact rat heart. American Journal of Physiology-Heart and Circulatory Physiology. 2009;296(5):H1491–H1512. doi: 10.1152/ajpheart.00539.2008. [DOI] [PubMed] [Google Scholar]
- 13.Nolasco J. B., Dahlen R. W. A graphic method for the study of alternation in cardiac action potentials. Journal of Applied Physiology. 1968;25(2):191–196. doi: 10.1152/jappl.1968.25.2.191. [DOI] [PubMed] [Google Scholar]
- 14.Stary V., Puppala D., Scherrer-Crosbie M., Dillmann W. H., Armoundas A. A. SERCA2a upregulation ameliorates cellular alternans induced by metabolic inhibition. Journal of Applied Physiology. 2016;120(8):865–875. doi: 10.1152/japplphysiol.00588.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Xie L.-H., Sato D., Garfinkel A., Qu Z., Weiss J. N. Intracellular Ca alternans: coordinated regulation by sarcoplasmic reticulum release, uptake, and leak. Biophysical Journal. 2008;95(6):3100–3110. doi: 10.1529/biophysj.108.130955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Weinberg S. H. Impaired sarcoplasmic reticulum calcium uptake and release promote electromechanically and spatially discordant alternans: a computational study. Clinical Medicine Insights: Cardiology. 2016;10(s1):1–15. doi: 10.4137/cmc.s39709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zhong X., Sun B., Vallmitjana A., et al. Suppression of ryanodine receptor function prolongs Ca2+ release refractoriness and promotes cardiac alternans in intact hearts. Biophysical Journal. 2016;473(21):3951–3964. doi: 10.1042/bcj20160606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kameyama M., Hirayama Y., Saitoh H., Maruyama M., Atarashi H., Takano T. Possible contribution of the sarcoplasmic reticulum Ca2+ pump function to electrical and mechanical alternans. Journal of Electrocardiology. 2003;36(2):125–135. doi: 10.1054/jelc.2003.50021. [DOI] [PubMed] [Google Scholar]
- 19.Qu Z., Liu M. B., Nivala M. A unified theory of calcium alternans in ventricular myocytes. Science Reports. 2016;6(1):p. 35625. doi: 10.1038/srep35625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Omichi C., Lamp S. T., Lin S.-F., et al. Intracellular Ca dynamics in ventricular fibrillation. American Journal of Physiology-Heart and Circulatory Physiology. 2004;286(5):H1836–H1844. doi: 10.1152/ajpheart.00123.2003. [DOI] [PubMed] [Google Scholar]
- 21.Tse G., Wong S. T., Tse V., Lee Y. T., Lin H. Y., Yeo J. M. Cardiac dynamics: alternans and arrhythmogenesis. Journal of Arrhythmia. 2016;32(5):411–417. doi: 10.1016/j.joa.2016.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Tran K., Smith N. P., Loiselle D. S., Crampin E. J. A thermodynamic model of the cardiac sarcoplasmic/endoplasmic Ca2+ (SERCA) pump. Biophysical Journal. 2009;96(5):2029–2042. doi: 10.1016/j.bpj.2008.11.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zang Y., Dai L., Zhan H., Dou J., Xia L., Zhang H. Theoretical investigation of the mechanism of heart failure using a canine ventricular cell model: especially the role of up-regulated CaMKII and SR Ca2+ leak. Journal of Molecular and Cellular Cardiology. 2013;56:34–43. doi: 10.1016/j.yjmcc.2012.11.020. [DOI] [PubMed] [Google Scholar]
- 24.Venetucci L. A., Trafford A. W., O’Neill S. C., et al. The sarcoplasmic reticulum and arrhythmogenic calcium release. Cardiovascular Research. 2008;77(2):285–292. doi: 10.1093/cvr/cvm009. [DOI] [PubMed] [Google Scholar]
- 25.Diaz M. E., O’Neill S. C., Eisner D. A. Sarcoplasmic reticulum calcium content fluctuation is the key to cardiac alternans. Circulation Research. 2004;94(5):650–656. doi: 10.1161/01.res.0000119923.64774.72. [DOI] [PubMed] [Google Scholar]
- 26.Bassani J. W., Yuan W., Bers D. M. Fractional SR Ca release is regulated by trigger Ca and SR Ca content in cardiac myocytes. American Journal of Physiology. 1995;268(5):1313–1319. doi: 10.1152/ajpcell.1995.268.5.c1313. [DOI] [PubMed] [Google Scholar]
- 27.Rovetti R., Cui X., Garfinkel A., Weiss J. N., Qu Z. Spark-induced sparks as a mechanism of intracellular calcium alternans in cardiac myocytes. Circulation Research. 2010;106(10):1582–1591. doi: 10.1161/circresaha.109.213975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Díaz M. E., Trafford A. W., O’Neill S. C., Eisner D. A. Measurement of sarcoplasmic reticulum Ca2+content and sarcolemmal Ca2+ fluxes in isolated rat ventricular myocytes during spontaneous Ca2+ release. The Journal of Physiology. 1997;501(1):3–16. doi: 10.1111/j.1469-7793.1997.003bo.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Eisner D. A., Diaz M. E., Li Y., O’Neill S. C., Trafford A. W. Stability and instability of regulation of intracellular calcium. Experimental Physiology. 2005;90(1):3–12. doi: 10.1113/expphysiol.2004.029231. [DOI] [PubMed] [Google Scholar]
- 30.Takamatsu T., Wier W. G. Calcium waves in mammalian heart: quantification of origin, magnitude, waveform, and velocity. FASEB Journal Official Publication of the Federation of American Societies for Experimental Biology. 1990;4(5):1519–1525. doi: 10.1096/fasebj.4.5.2307330. [DOI] [PubMed] [Google Scholar]
- 31.Egdell R., De Souza A. I., Macleod K. T. Relative importance of SR load and cytoplasmic calcium concentration in the genesis of aftercontractions in cardiac myocytes. Cardiovascular Research. 2000;47(4):769–777. doi: 10.1016/s0008-6363(00)00147-4. [DOI] [PubMed] [Google Scholar]
- 32.Katra R. P., Laurita K. R. Cellular mechanism of calcium-mediated triggered activity in the heart. Circulation Research. 2005;96(5):535–542. doi: 10.1161/01.res.0000159387.00749.3c. [DOI] [PubMed] [Google Scholar]
- 33.O’Hara T., Virág L., Varró A., et al. Simulation of the undiseased human cardiac ventricular action potential: model formulation and experimental validation. PLoS Computational Biology. 2011;7(5) doi: 10.1371/journal.pcbi.1002061.e1002061 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hund T. J., Rudy Y. Rate dependence and regulation of action potential and calcium transient in a canine cardiac ventricular cell model. Circulation. 2004;110(20):3168–3174. doi: 10.1161/01.cir.0000147231.69595.d3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Shintani-Ishida K., Yoshida K.-I. Ischemia induces phospholamban dephosphorylation via activation of calcineurin, PKC-α, and protein phosphatase 1, thereby inducing calcium overload in reperfusion. Biochimica et Biophysica Acta (BBA)—Molecular Basis of Disease. 2011;1812(7):743–751. doi: 10.1016/j.bbadis.2011.03.014. [DOI] [PubMed] [Google Scholar]
- 36.Ferrero J. M., Trénor B., Rodríguez B., Sáiz J. Electrical activity and reentry during acute regional myocardial ischemia: insights from simulations. Proceedings of the International Conference of the IEEE Engineering in Medicine & Biology Society; September 2003; Cancun, Mexico. pp. 3703–3715. [Google Scholar]
- 37.Ebus J., Papp Z., Zaremba R., Stienen G. Effects of MgATP on ATP utilization and force under normal and simulated ischaemic conditions in rat cardiac trabeculae. Pflügers Archiv—European Journal of Physiology. 2001;443(1):102–111. doi: 10.1007/s004240100667. [DOI] [PubMed] [Google Scholar]
- 38.Jennings R. B., Hawkins H. K., Lowe J. E., et al. Relation between high energy phosphate and lethal injury in myocardial ischemia in the dog. American Journal of Pathology. 1978;92(1):187–214. [PMC free article] [PubMed] [Google Scholar]
- 39.Weiss J. N., Karma A., Shiferaw Y., Chen P.-S., Garfinkel A., Qu Z. From pulsus topulseless: the saga of cardiac alternans. Circulation Research. 2006;98(10):1244–1253. doi: 10.1161/01.res.0000224540.97431.f0. [DOI] [PubMed] [Google Scholar]
- 40.Alvarezlacalle E., Echebarria B., Spalding J., et al. Calcium alternans is due to an order-disorder phase transition in cardiac cells. Physical Review Letters. 2015;114(10):p. 108101. doi: 10.1103/physrevlett.114.108101. [DOI] [PubMed] [Google Scholar]
- 41.Venetucci L. A., Trafford A. W., Eisner D. A. Increasing ryanodine receptor open probability alone does not produce arrhythmogenic calcium waves: threshold sarcoplasmic reticulum calcium content is required. Circulation Research. 2007;100(1):105–111. doi: 10.1161/01.res.0000252828.17939.00. [DOI] [PubMed] [Google Scholar]
- 42.Overend C. L., O’Neill S. C., Eisner D. A. The effect of tetracaine on stimulated contractions, sarcoplasmic reticulum Ca2+ content and membrane current in isolated rat ventricular myocytes. Journal of Physiology. 2010;507(3):759–769. doi: 10.1111/j.1469-7793.1998.759bs.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Our supplementary files include the modified human ventricular cell model, codes, and data for plotting figures in our papers.
Data Availability Statement
The data used to build graphs in this study are available from the corresponding author upon request.