Effect of Intravoxel Incoherent Motion on Diffusion Parameters in Normal Brain

Abstract

At very low diffusion weighting the diffusion MRI signal is affected by intravoxel incoherent motion (IVIM) caused by dephasing of magnetization due to incoherent blood flow in capillaries or other sources of microcirculation. While IVIM measurements at low diffusion weightings have been frequently used to investigate perfusion in the body as well as in malignant tissue, the effect and origin of IVIM in normal brain tissue is not completely established. We investigated the IVIM effect on the brain diffusion MRI signal in a cohort of 137 radiologically-normal patients (62 male; mean age = 50.2 ± 17.8, range = 18 to 94). We compared the diffusion tensor parameters estimated from a mono-exponential fit at b = 0 and 1000 s/mm² versus at b = 250 and 1000 s/mm². The asymptotic fitting method allowed for quantitative assessment of the IVIM signal fraction f* in specific brain tissue and regions. Our results show a mean (median) percent difference in the mean diffusivity of about 4.5 (4.9)% in white matter (WM), about 7.8 (8.7)% in cortical gray matter (GM), and 4.3 (4.2)% in thalamus. Corresponding perfusion fraction f* was estimated to be 0.033 (0.032) in WM, 0.066 (0.065) in cortical GM, and 0.033 (0.030) in the thalamus. The effect of f* with respect to age was found to be significant in cortical GM (Pearson correlation ρ = 0.35, p = 3*10⁻⁵) and the thalamus (Pearson correlation ρ = 0.20, p = 0.022) with an average increase in f* of 5.17*10⁻⁴/year and 3.61*10⁻⁴/year, respectively. Significant correlations between f* and age were not observed for WM, and corollary analysis revealed no effect of gender on f*. Possible origins of the IVIM effect in normal brain tissue are discussed.

Introduction

Diffusion MRI (dMRI) is currently being used as an important diagnostic tool, as well as a method of investigation which provides microstructural insight in neurological MRI imaging. In brain, dMRI has increasing utility for characterizing tissue composition in pathologic states (Horsfield and Jones, 2002), as well as for probing tissue microstructure (Alexander et al., 2017; Beaulieu, 2002; Jelescu and Budde, 2017; Novikov et al., 2018).

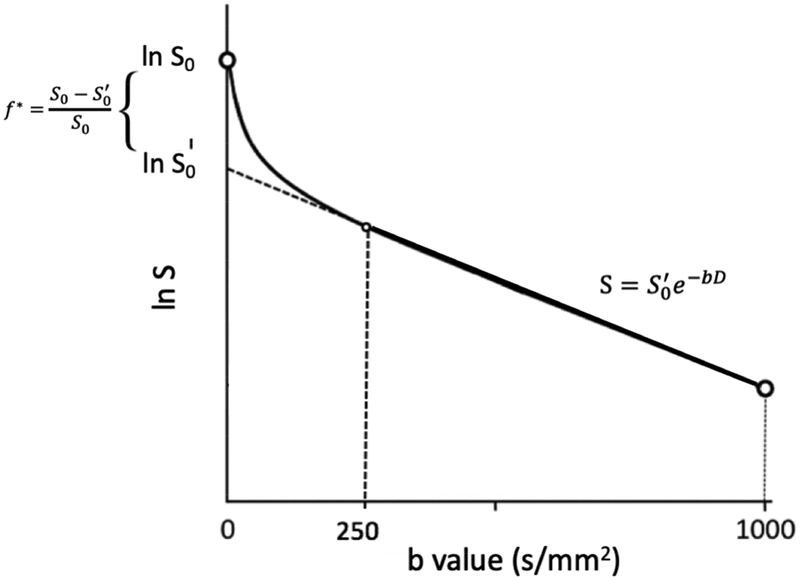
It is well-established that diffusion in biological tissue is not free (i.e., non-Gaussian), and therefore the measured dMRI signal as a function of the diffusion weighting factor, b, cannot be described by a monoexponential relationship S = S₀ ⋅ e^−bD. For moderate diffusion weightings (b ≥ 1000 s/mm²), the dMRI signal deviates from the mono-exponential functional form due to the genuine non-Gaussian diffusion characteristics of the parenchyma (Assaf and Cohen, 1998; Jensen et al., 2005; Le Bihan and Turner, 1992; Niendorf et al., 1996), including restricted and hindered diffusion due to cell membranes and organelles. Here, we focus on the dMRI signal at sufficiently low diffusion weighting, e.g. b < 250 s/mm², where it is affected by the intravoxel incoherent motion (IVIM) effect, as initially proposed by Le Bihan et al. (1988, 1986) to explain dephasing of the blood magnetization due to incoherent blood flow in capillaries.

The simplest IVIM model S(b) = S₀[f*e^−b⋅D* + (1−f*)e^−bD] seeks to capture the deviation from the monoexponential signal form at sufficiently low b-values (e.g. < 250 s/mm²) as outlined in Figure 1, with the perfusion fraction f* describing the contribution of the incoherent signal from the IVIM compartment, and the pseudodiffusion coefficient D* related to the velocity of the incoherent flow component (see below in Discussion: Causes for IVIM in normal brain). The IVIM effect is typically explained by capillary perfusion (Le Bihan et al., 1986), though other tissue compartments in the brain with specific incoherent flow patterns such as the recently proposed glymphatic system (Tarasoff-Conway et al., 2015) may also potentially contribute.

Figure 1:

Schematic representation of the measured signal in dMRI and its deviation from a monoexponential form at low b values due to the IVIM effect.

While the principles of IVIM, which separately estimates tissue diffusivity and tissue microcapillary perfusion at low b values, were initially introduced for neurological disorders (Le Bihan et al., 1986), the IVIM effect is now being more thoroughly investigated in abdominal malignancy (Kuru et al., 2014; Lemke et al., 2009; Padhani et al., 2009; Pieper et al., 2016), breast cancer (Sigmund et al., 2011), as well as hepatic and gastrointestinal disease states (Freiman et al., 2012; Guiu et al., 2012; Koh et al., 2011), which all have higher incoherent flow rates. For abdominal imaging in particular, the perfusion fraction is useful in measuring hepatic lesions (Yamada et al., 1999), as well as in diagnosing and monitoring neoplasm. Furthermore, studies have explored the perfusion fraction to identify and characterize pancreatic cancer (Kuru et al., 2014; Lemke et al., 2011), breast cancer response to therapy (Pieper et al., 2016), as well as for use as a noninvasive tool in clinical trials and drug development (Padhani et al., 2009).

In neurological tissue, IVIM modeling has been found to be useful in assessing patients with ischemic stroke (Wirestam et al., 1997), various brain pathologies, such as gliomas (Federau et al., 2014), as well as different physiological states in healthy controls (Federau et al., 2013, 2012). In addition to its use in different pathologies, it is also of interest to evaluate IVIM in normal tissue. Quantifying the impact of IVIM on the measured apparent diffusion coefficient (ADC) could be used to separate the incoherent flow effect from the overall diffusion signal, which allows for a more accurate quantification of tissue microstructure in the bulk of the tissue as opposed to the IVIM compartment, e.g. microvasculature (Henkelman et al., 1994).

Table 1 lists an overview of studies that looked at IVIM in normal brain. So far, those pilot studies included relatively small numbers of subjects, and have shown a relatively large variation in estimated IVIM signal fractions, depending on the b-range and estimation method. We report here our findings on the effect of IVIM on the dMRI signal in a retrospective whole-brain study in various brain tissue types in a cohort of 137 radiologically normal patients. Specifically, we quantify the IVIM effect at low b-values (b = 250 and 1000 s/mm²) on common dMRI whole-brain measurements using standard two-point or asymptotic fitting methods (Pekar et al., 1992; Wirestam et al., 2001), investigate its effect on age and gender, and interpret it in terms of the underlying biophysical mechanisms.

Table 1:

Selected IVIM studies of normal brain and their respective reported IVIM parameters.

Study	Brain Region	Number of Subject	b factor	Age Range	Sex	Voxel Size	D*/D	D*(*10–3 μm2/ms)	f
Faderau et. al. 2012	Full Brain	7	16 b value: 0 to 900 s/mm2	mean: 27	5 males; 2 females	1.16 × 1.16 × 4.0 mm3	7.93	7.14	0.061
Faderau et. al. 2013	Full Brain excluding CSF
	Systole	20	16 b value: 0 to 900 s/mm2	mean: 24	10 males; 10 females	1.0 × 1.4 × 5.0 mm3	14.74	11.5	0.073
	Diastole						11.8	9.2	0.07
Finkenstaedt et. al. 2017	Grey Matter	9	37 different b value: 0 to 1300 s/mm2	mean: 34; range: 22–64	6 males; 3 females	2 × 2 × 2 mm3	6.84	6.22	0.1
Here et. Al. 2017	Grey Matter	10	16 b value: 0 to 900 s/mm2			3.4 × 3.4 × 6 mm3	12.93	11.77	0.11
Meeus et. al. 2018	Grey Matter	16	3 b value: 0, 300,1000 s/mm2	mean: 26; range: 25–30		2.5 × 2.5 × 3.5 mm3			0.104
			3 b value: 0, 500,1000 s/mm2						0.141
Reischauer & Gutzeit 2017	Grey Matter	1	12 b value: 0 to 1000 s/mm2			1.57 × 1.57 × 5.0 mm3	10.13	7.7	0.11
	White Matter						10	7.2	0.07
Rydhög et. al. 2017	Comprehensive WM Protocol + JHU DTI-based atlas ROIs	1	44 b value: 0 to 800 s/mm2	30	male	1.3 × 1.3 × 4.0 mm3			0.024
		1		33	male				0.049
			5 b value: 0 to 1400 s/mm2
	Clinical WM Protocol + JHU DT1-based atlas ROIs
						2.5 × 2.5 × 2.5 mm3
Spinner et. al. 2018	Full Brain excluding CSF	11	16 b value: 0 to 900 s/mm2	mean: 27	3 males; 8 females	1.2 × 1.2 × 5 mm3	8.73	6.9	0.0846
Wirestam et. al. 2001	Thalamus	56	36 different b value: 0 to 1200 s/mm2	mean: 68.5; range: 45–83	17 males; 11 females	1.95 × 1.25 × 10 mm3		14	0.11
	Frontal WM	54						21	0.076
	All ROIs:	110						17	0.093
Wirestam et. al. 1997	Healthy Control WM	5	37 different b value: 0 to 1200 s/mm2	range: 25–32		1.95 × 1.25 × 8 mm3			0.045

Methods

Theory

In this work, we consider the IVIM+DTI signal functional form for the dMRI measured in unit direction $\widehat{g}$ with diffusion weighting b,

$$S(b,\widehat{g})=S_0\left[f^{*}{e}^{-b{D}^{*}}+\left(1-f^{*}\right)e^{-b\widehat{g}\cdot D\widehat{g}}\right],$$ (1)

where the first (IVIM) term is assumed to be isotropic, whereas the second (tissue) term is represented by the diffusion tensor D = {D_ij} (DTI approximation). We neglect the higher-order diffusion cumulants for the tissue contribution, since we limit ourselves to relatively low diffusion weighting, b ≤ 1000 s/mm².

To determine all IVIM+DTI parameters from a multi-directional measurement in the low-b case, one must have at least 4 unique b-values (shells), much like the isotropic (or a one-dimensional) analog of Eq (1) requires at least 4 independent measurements to determine its 4 parameters. Since our protocol only had 3 unique b-values: 0, 250 and 1000 s/mm², we could not directly fit Eq. (1) to the data, and used the asymptotic fitting method as originally proposed in (Pekar et al., 1992; Wirestam et al., 2001), thereby reverting to the following key assumption (Figure 1): At b ≥ 250 s/mm², the IVIM term can be fully neglected due to its sufficiently fast diffusivity D*. From the literature (Table 1), D*~7–21 mm²/s, hence e^−bD* ~ 0.17–0.005 already for b = 250 s/mm², which, after multiplying by f* (~ 0.02–0.1) makes neglecting the first term in Eq.(1) at this b-value a reasonable assumption, and leads to three practically important corollaries:

1. The DTI-estimated diffusion tensor between b = 250 and 1000 s/mm² shells corresponds to the intrinsic tissue diffusion tensor D from the second term in Eq.(1).

2. The signal taken between b = 250 and 1000 s/mm² looks as if it had no IVIM term, with a corresponding smaller amplitude S₀′ = (1 − f*)S₀, cf. Fig. 1 and Eq. (1). This prompts determining

   $$f^{*}=\frac{S_0-S_0^{\prime }}{S_0}$$ (2)

   from the two DTI fits, performed for the shells b = 0 and 1000 s/mm² yielding S₀, and for the shells b = 250 and 1000 s/mm² yielding S₀′. It should be noted that the estimate for f* here may be a lower bound for the actual IVIM signal fraction in case D* is sufficiently low such that some IVIM contribution is still present at b = 250 s/mm².
3. The apparent diffusion tensor D_app defined via representing Eq. (1) by a simple exponential, $S=S_0{e}^{-b\widehat{g}\prime D_{app}\widehat{g}}$, between b = 0 and any finite b ≥ 250 s/mm², is related to the intrinsic tissue diffusion tensor D via

   $$b{D}_{\mathit{\text{app}}}\simeq bD-\mathit{\text{ln}}\left(1-f^{*}\right)\approx bD+f^{*}.$$ (3)

   This relation follows from taking the logarithm of Eq. (1) and neglecting the first (IVIM) term; the last approximate equality is justified by taking the lowest order in expanding ln’(1 − f*) ≈ −f* at small f*. In our case, the relevant b = 1000 s/mm² in Eq. (3), from which follows Eq. (4) below.

MRI

A retrospective, HIPAA compliant study, approved by the institutional Internal Review Board (IRB), included a cohort of 137 subjects (mean age = 50.2 ± 17.8, range = 18 to 94; 62 male: mean age = 50.6 ± 17.8, range = 21 to 94; 75 female: mean age = 49.9 ± 18.0, range = 18 to 87), selected out of a total dataset of 1816 subjects who presented for clinical MRI. Only subjects who were found to have no brain abnormality on conventional MRI sequences including (T1 weighted, T2 weighted, T2 FLAIR, conventional DWI, susceptibility weighted) as determined by a board-certified neuroradiologist were included. In addition, patients were excluded with CNS disease (including migraine) based on extensive chart review by a board-certified neurologist. Patients underwent MRI on a Magnetom Prisma 3T MRI system (N=57) (Siemens AG, Erlangen, Germany) or a Skyra 3T MRI system (N=71) (Siemens AG, Erlangen, Germany). The MRI protocol included 28 diffusion-weighted images, acquired using a monopolar diffusion-weighted EPI sequence as follows: 4b = 0 images, b = 250 s/mm² along 4 directions and b = 1000 s/mm² along 20 directions (listed as Supplementary table), with the following imaging parameters: a volume of 50 slices, 130 × 130 matrix, with voxel size = 1.7 mm × 1.7 mm × 3 mm, TE = 70 ms on Prisma or TE = 95 ms on Skyra, TR = 70/3500 ms, GRAPPA with acceleration 2, and multiband 2. To correct for EPI distortions related to magnetic field inhomogeneity, one additional b = 0 image was acquired with the same parameters, except for reversed phase-encode direction (posterior-to-anterior instead of anterior-to-posterior).

Image processing

dMRI images preprocessing was performed using the DESIGNER pipeline (Ades-Aron et al., 2018), which included MP-PCA denoising using Mrtrix (Veraart et al., 2016b), correction for the rician noise floor (Koay et al. 2009), Gibbs removal using Matlab (Kellner et al., 2016), as well as EPI distortion (Andersson et al., 2003), eddy current (Jezzard et al., 1998), and motion correction (Andersson and Sotiropoulos, 2016) using the FMRIB Software Library (Smith et al., 2004).

The DTI parameters for any pair of b-shells were estimated using the weighted linear least squares method (Veraart et al., 2016a). Maps of the mean diffusivity $\text{MD}=\frac{1}{3}\text{tr}D$ calculated from the corresponding tissue diffusion tensors D_app for b = 0 and b = 1000 s/mm², and D for b = 250 and b = 1000 s/mm², as well as maps of f* according to Eq. (2), were derived for each subject, and mean values were extracted over several regions of interest (ROIs).

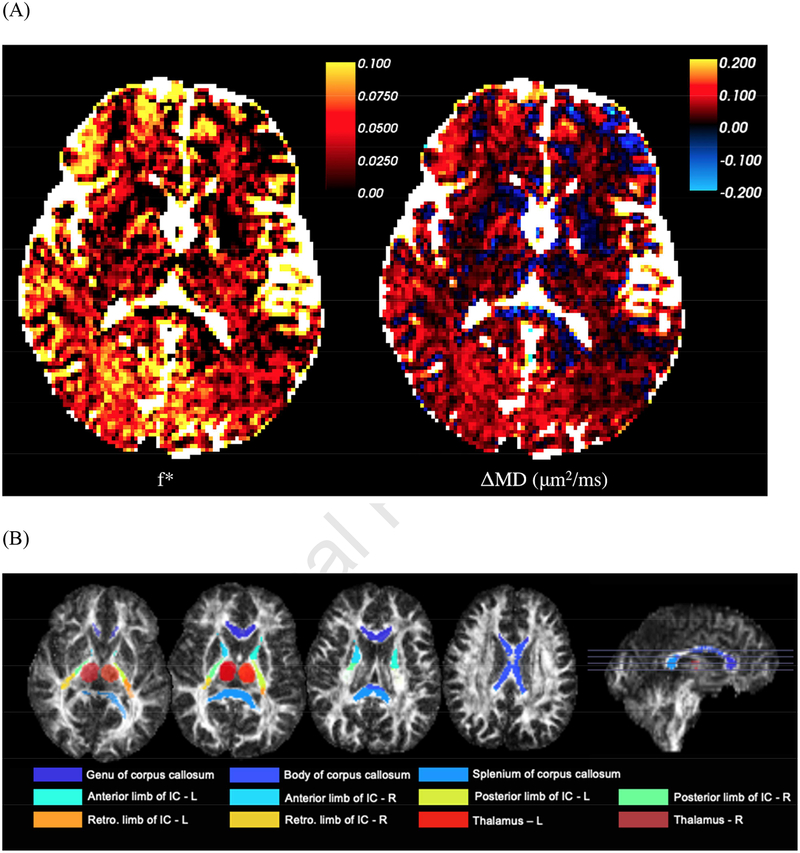
FSL FAST (Zhang et al., 2001) of the b = 0-image was used to segment ROIs for CSF and cortical GM (carefully reducing CSF and white matter partial voluming). In addition, deep gray matter was studied by manually outlining thalamus ROIs (left/right) on the b = 0-image by a resident radiologist (P.R.) for each subject (illustrated in Figure 2B). To identify white matter (WM) regions, fractional anisotropy (FA) maps were co-registered to the JHU FA atlas using FNIRT (Woolrich et al., 2009). The following WM ROIs (illustrated in Figure 2B) were chosen for follow up in this study: Genu, Body, and Splenium of the corpus callosum, anterior limb of the internal capsule (left and right), posterior limb of internal capsule (left and right), and retrolenticular limb of the internal capsule (left and right). A total WM ROI was also created by combining major WM tracts and excluding those ROIs from the JHU atlas that are a mixture of gray and white matter, and/or very small and contaminated by partial volume effects.

Figure 2:

A representative subjects’ (55 year old female) brain parametric maps. (A) Panel 1: The map of IVIM fraction f*. Panel 2: The difference ΔMD = MD_app − MD. CSF has been colored white. This difference is mostly positive — and given by f*, cf. Eq. (4), exemplifying the degree of overestimation of the tissue diffusivity due to IVIM based on estimating it from b = 0. (B) Axial and sagittal slices of the regions of interests used in this study overlaid on the FA image.

Statistics

The difference between regional MD-values based on fitting the diffusion tensor to b = 0 and b = 1000 s/mm² vs b = 250 and b = 1000 s/mm² was computed using a one-tailed student’s t-test. Next, Pearson correlation coefficients were calculated to assess the effect of age on f* values in cortical gray matter, white matter, and the thalamus, and analysis of covariance (ANCOVA) with age (if significant) as covariates was performed to evaluate the effect of gender.

Results

A representative subject’s (55 year old female) map of f*, Eq. (2), is shown in Figure 2A panel 1. The difference between this subject’s apparent mean diffusivity MD_app calculated from the apparent diffusion tensor D_app estimated between b = 0 and b = 1000 s/mm², and MD calculated from the intrinsic tissue diffusion tensor D estimated between b = 250 and b = 1000 s/mm², is shown in Figure 2A panel 2. The thalamus and WM ROIs used in the subsequent analysis are shown for this representative subject in Figure 2B.

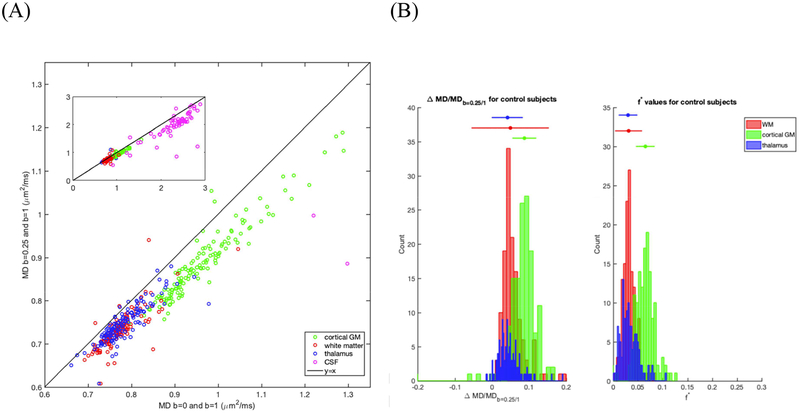
The observed scatter plot between the calculated median MD extracted for all subjects over the regions of interest — WM, cortical GM, thalamus and CSF — from b = 0 and b = 1000 s/mm², and b = 250 and b = 1000 s/mm², is shown in Figure 3A. We observe that most of the subjects’ values fall below the unit-slope line, exemplifying the overestimation of MD when calculated between b = 0 and b = 1000 s/mm², cf. also Fig 2B. The mean (median) MD difference from the MD calculated using b = 250 and b = 1000 s/mm² for WM was calculated to be 0.044 (0.036) μm²/ms (p < 0.01), 0.077 (0.078) μm²/ms in cortical GM (p < 0.01), 0.032 (0.035) μm²/ms in the thalamus (p < 0.01), and 0.31 (0.29) μm²/ms in CSF (p < 0.01). A one-tailed test is used here, as we hypothesized that the diffusion coefficients estimated when choosing b-values closer to 0 s/mm² will systematically overestimate the actual diffusion coefficient. Note that both the one tailed t-test as well as two-tailed t-test were statistically significant, as all p-values < 0.01.

Figure 3:

Differences in MD and in f* calculated from using b = 0–1000 s/mm² and b = 250–1000 s/mm² in CSF (magenta), Thalamus (blue), WM (red), and cortical GM (green) across 137 healthy subjects. (A) Scatter plot of the calculated difference in mean MDs over cortical GM, WM, and CSF of each ROI. Reference line of y=x is shown in black in both panels. (B) Histograms of the percent change in MD with respect to MD from b = 250–1000 s/mm² (panel 1) and histograms of f* (panel 2). 4 subjects not shown in WM and 1 subject not shown in cortical GM for ease of visualization.

Figure 3A shows both cortical and thalamus GM, WM and CSF, where we note that representing the CSF compartment with Eq (1) leads to large “perfusion fractions” in the IVIM model, potentially due to partial voluming or turbulent flow in the CSF. Because the CSF compartment is wholly fluid, going forward, we will focus on brain parenchyma (cortical GM, thalamus and WM), where the strong correlation between MD_b=0/1000 and MD_b=250/1000 observed is a consequence of Eq. (3) for the corresponding diffusion tensors, taken at b = 1000 s/mm²:

$${\text{MD}}_{\text{app}}\approx \text{MD}+f^{*}/b$$ (4)

Figure 3B shows histograms of the mean values over all subjects for ΔMD with respect to MD calculated using b = 250 and b = 1000 s/mm² (panel 1) and f* (panel 2). The mean (median) value of the distribution of the percent difference of ΔMD with respect to MD calculated using b = 250 and b = 1000 s/mm² for WM is 4.5 (4.9)%, for cortical GM is 7.8 (8.7)%, and for thalamus is 4.3 (4.2)% (1 erroneous value excluded from WM calculation).

Similarly, for f*, the mean (median) value is 0.033 (0.032) in WM, 0.066 (0.065) in cortical GM, and 0.033 (0.030) in the thalamus. To extract the mean values and assess the effect of age and gender (described next), few erroneous values (i.e. 4 patients for cortical GM, 2 patients for WM) were filtered out with a cutoff of 0 < f*< 0.3 limit suggested in the literature (Federau, 2017). Values of f* and MD in specific WM region of interests (ROI) are listed in Table 2. WM ROIs had f* of 0.032 (0.029) ± 0.007 (0.007) compared to 0.033 (0.032) in the total WM ROI.

Table 2:

Mean (median) values of the patient cohort for the calculated mean MD value and the mean f*in different brain regions at both b value pairs, as well as calculated mean and standard deviations for f* and ΔMD for several white matter regions.

ROI	ΔMD/MD (median) ± std	f* ± std
Cortical GM	0.078 (0.087) ± 0.010	0.066 (0.065) ± 0.018
Thalamus R	0.043 (0.040) ± 0.043	0.033 (0.030) ± 0.019
Thalamus L	0.043 (0.042) ± 0.041	0.033 (0.030) ± 0.019
White Matter	0.045 (0.049) ± 0.117	0.033 (0.032) ± 0.014
Genu	0.051 (0.048) ± 0.047	0.037 (0.034) ± 0.023
Body	0.050 (0.047) ± 0.044	0.039 (0.036) ± 0.024
Splenium	0.015 (0.013) ± 0.040	0.022 (0.018) ± 0.019
anterior limb of internal capsule R	0.058 (0.057) ± 0.048	0.039 (0.038) ± 0.022
anterior limb of internal capsule L	0.062 (0.050) ± 0.126	0.036 (0.033) ± 0.023
posterior limb of internal capsule R	0.036 (0.038) ± 0.040	0.028 (0.027) ± 0.016
posterior limb of internal capsule L	0.047 (0.048) ± 0.040	0.033 (0.032) ± 0.018
retrolenticular limb of internal capsule L	0.024 (0.026) ± 0.035	0.024 (0.022) ± 0.015
retrolenticular limb of internal capsule R	0.034 (0.033) ± 0.034	0.027 (0.025) ± 0.016

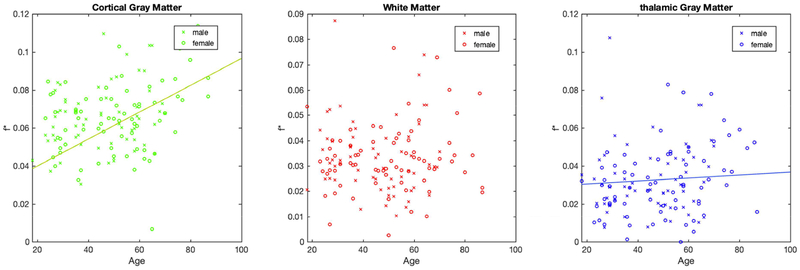
Figure 4 shows scatter plots of f* with respect to subjects’ age at the time of scanning. Significant increases of f* with age were found in the cortical GM (Pearson correlation ρ = 0.35, p = 3*10⁻⁵) and the thalamus (Pearson correlation ρ = 0.20, p = 0.022), with an on average positive increase in f* of 5.17*10⁻⁴/year and 3.61*10⁻⁴/year respectively, but not in the white matter (ρ = 0.15, p = 0.07). Figure 4 also shows the gender of all subjects. Using ANCOVA, no effect of gender on f* was found.

Figure 4:

Scatter plots of f* as a function of patient age at time of scan, showing significant increases with age in cortical GM (green) and thalamus (blue) (shown by regression lines), while not in WM (red). For all regions, no differences were found between females (circles) and males (crosses).

Discussion

The purpose of this study is to evaluate the contribution of IVIM to DTI parameters as assessed by performing DTI fits for diffusion data for b = 0–1000 s/mm² and b = 250–1000 s/mm², respectively. While similar two-point methods (also known as asymptotic fitting) have been previously applied to study the effect of IVIM in brain tumors (Cohen et al., 2013), to study optimal b value ranges for perfusion insensitive ADC measurements (Freiman et al., 2012), and to optimize b values when measuring ADC (Xing et al., 1997), the effect of IVIM in normal appearing brain parenchyma using this approach has not been reported so far. Using a large cohort of radiologically normal subjects, we observed a slight deviation from the mono-exponential model in WM, and a larger deviation in thalamus GM, cortical GM, and CSF (Figure 3A). In what follows, we will discuss the effect of IVIM’s characteristics in different brain regions, potential effects of age and sex, as well as elaborate on the possible origins of IVIM in normal brain, along with limitations and potential outlook.

IVIM-values in normal brain

We observed that the estimated f* of 0.066 for cortical GM is about twice as large as f* of 0.033 in the WM, which is qualitatively in agreement with the literature values reported for different brain regions (Table 1). The reported range for f* is 0.02–0.08 for white matter and 0.10–0.14 for gray matter or 0.05–0.08 for brain parenchyma. GM f*, typically estimated on the order of 0.1, is slightly higher than our reported value of f* = 0.066. Potential differences may be due to partial volume from white matter (lowering the overall f*), as well as the use of the two-point method where the minimum b-value of 250 mm²/ms could potentially still have a significant IVIM component (Meeus et al. 2018). Our values for f* in the thalamus ROIs were ≈ 0.03, which were closer to the values observed for WM than cortical GM, and can be understood as these ROIs are a mixture of gray and white matter.

In our WM ROI analysis, we observe overall a relatively small variation in f* among the individual ROIs that agrees with the mean value over the overall WM ROI. While we control for SNR bias - diffusion images are processed using our in-house developed DESIGNER pipeline (Ades-Aron et al., 2018) which does map the noise floor accurately (Veraart et al., 2016b) and subsequently corrects for rician bias (Koay et al., 2009) - we recognize that our segmentation may suffer to some extent from partial voluming, in particular in those ROIs adjacent to CSF (e.g. body corpus callosum) and/or gray matter, which may have resulted in slightly increased f* in those regions. Similarly, partial voluming may also been seen in the CSF where the MD values calculated for the CSF, which were on the order ≈2.1 to 2.3 μm²/ms, in contrast to the more commonly observed values of ≈3.0 μm²/ms. In Figure 3A, while most of the data is clustered in ≈2.5 to 3.2 μm²/ms which is in agreement with reported CSF MD values, about 15–20% are outside the range (greater than 3.2 μm²/ms or less than 2.5 μm²/ms). The deviations for these samples may be indicating turbulent flow in the CSF, or may indicate partial voluming in our segmentation. Further studies with more b values and higher resolution to reduce partial volume effects are imperative to increase the confidence of these measurements.

Effect of age and gender on IVIM f* fraction

Our results showed an increase for cortical GM and the thalamus in f* versus subject age, but no significant change for WM. Assuming that IVIM is due to brain vasculature, the observed increase of f* with age in GM could potentially be explained in terms of faster atrophy in GM cellular than vascular tissue. While atrophy has been reported for cellular (Giorgio et al., 2010) and vascular tissue (Leenders et al., 1990), a direct comparison of the two still needs to be performed. Establishing the effect of age may also be confounded by inherent partial volume effects and related CSF contamination, set to increase with age due to atrophy, and thereby yielding consistently larger f* values with age. In addition, our results showed no effect of sex on f* (Figure 4), neither with respect to age nor at baseline, and hence do not indicate that normal brain IVIM is different between sexes.

Causes for IVIM in normal brain

The IVIM effect in the brain is conventionally explained in terms of the vascular brain network (Le Bihan, 1990; Le Bihan and Turner, 1992). In the physical picture to explain this, two distinct flow regimes can be distinguished. The short-time regime is when the flow along each capillary segment can be viewed as locally straight, i.e. the distance vt. traveled over the diffusion time. ≃ 50ms is shorter than the capillary gyration radius lc ≈ 100μm (correlation length of the capillary network (Pawlik et al., 1981)), i.e.,v ≪v_c = l_c/t ≈ 2 μm/ms = 2 mm/s for our experiment. In this case, angular averaging over isotropically distributed straight capillary segments yields the sinc-model for the signal (Le Bihan, 1990), S = sinc(qvt) ≃ 1 – bD*, where b = q²t^:. and the pseudo-diffusion coefficient $D^{*}(v,t)\simeq v^{2}t/6\equiv D_c^{*}(t)\cdot {\left(v/v_c\right)}^2,v\ll v_c$, where we introduced the characteristic pseudo-diffusion coefficient scale $D_c^{*}(t)=v_c^{2}t/6=l_c^2/6t\approx 33$ μm²/ms for our diffusion time. In this random-flow picture, the IVIM D*(t) actually grows linearly with diffusion time in this slow-flow regime. In the opposite, long-time or fast-flow regime v ≫v_c, the flow randomizes and the molecular displacements along each tortuous capillary begin to resemble a Brownian path, such that their displacements become incoherent (giving the name to the IVIM phenomenon), and the pseudo-diffusion coefficient approaches a time-independent value $D^{*}(v)\simeq v{l}_c/6\equiv D_c^{*}\cdot v/v_c,v\gg v_c$. Here we again wrote the result in terms of the characteristic value $D_c^{*}(t)$estimated above, but its time-dependence cancels out due to the v/v_c factor. To summarize, for a fixed diffusion time, D*(v)grows quadratically for small velocities and then linearly for large velocities.

Experimentally, we can be in short- or long-time (slow- or fast-flow) regimes or intermediate regimes in between them. While the velocity of blood through arteries is on the order of ≈ 40 cm/s to ≈100 cm/s (Kellner et al., 2016), corresponding to the fast-flow regime, in brain capillaries it is on the order of ≈ 1mm/s measured through capillaroscopy in rats and doppler ultrasound in humans (Mathura et al., 2001). Similar studies show that in humans the mean red blood cell velocity is 2.43 ± 0.08 mm/s in arterioles and precapillaries < 5pm (Ivanov et al., 1981), 0.79 ± 0.03 mm/s in cerebral capillaries, and 0.47 ± 0.37 mm/s in human skin capillaries (Stücker et al., 1996). As the vessel generation number increases and vessel radius decreases, blood velocity substantially decreases. This phenomenon is mathematically described by Murray’s law, which describes the branching of the arterial system and that blood flow in a vessel is proportional to the cube of its radius (Murray, 1926). As blood slows in the capillaries, the IVIM regime switches from the long-time or fast-velocity regime of incoherent flow, to the short-time or slow-velocity regime of the coherent flow. From the above references, for the typical capillary, v = 1mm/s, and we can estimate $D^{*}\approx D_c^{*}/4\approx 8$ μm²/ms, with lower velocities potentially bringing it even closer to the genuine water diffusivity value. Furthermore, the gyration radius of the capillaries should also vary depending on position and their diameter, which potentially brings the IVIM regime closer to the short-time of coherent flow. For most velocities, the above estimates are in line with the values D*~5–21 μm²/ms (Table 1) which practically justify neglecting the IVIM effect for our non-zero b-shells. We also note that consideration of diffusion time can be useful not only for these extremal regime estimates but also for contrast variation and more detailed modeling of IVIM effects (Kennan et al., 1994). In vivo preclinical brain studies (Fournet et al., 2017) and clinical liver studies (Wetscherek et al., 2015) have begun to demonstrate these approaches. Flow-compensated diffusion gradients (Ahlgren et al., 2016) provide another means to probe time-dependent IVIM.

If vascular, the IVIM effect will also depend on the composition of each brain region, GM, WM. Indeed, primarily only large blood vessels continue to the WM towards the ventricular angle (Nonaka et al., 2003), resulting in a less tortuous network of vessels with fewer contradictory flow vectors and smaller blood volume (He and Yablonskiy, 2007) leading to a smaller IVIM effect in WM. In line with this, we observed that the estimated f* for cortical GM is nearly twice as large as f* in WM, which is also likely influenced by well-known blood volume fractions in these tissues (Kuppusamy et al., 1996; Leenders et al., 1990). This qualitative agreement suggests that the IVIM effect is caused by the brain vasculature and predominantly present in GM, and is further evidenced by correlations between healthy brain IVIM metrics with other measures of blood perfusion (Federau, 2017) as well as with the cardiac cycle (Federau et al., 2013).

In addition to the well-documented incoherent blood flow effect, one could speculate that non-blood flow may contribute to the IVIM parameter f*. In particular, recent work (Iliff et al., 2012; Kress et al., 2014; Louveau et al., 2015; Tarasoff-Conway et al., 2015) has suggested the importance of interstitial bulk flow (ISF) in protein clearance in the brain through CSF. ISF, which is largely facilitated by the astroglial aquaporin-4 channels and now known as the glymphatics system, has been speculated to contribute to brain CSF clearance, which also includes CSF movement to the ventricles and subarachnoid space, as well as perivascular drainage from the periarterial space to the lymphatics (Tarasoff-Conway et al., 2015). However, the presence of ISF through brain extracellular space has been subsequently disputed using diffusion-advection modeling (Jin et al., 2016), which suggested that diffusion alone (without convection) was enough to account for experimental transport studies in brain parenchyma.

Overall, the extent of ISF and whether it can be measured through IVIM remains controversial and needs to be better understood. Recent work from (Hare et al., 2017) showed that with CSF nulled, D* values notably decreased and a monoexponential model adequately described the diffusion signal in brain, thereby suggesting IVIM being sensitive to the CSF rather than brain microvasculature. Conversely, Rydhog et.al. (2017) found both free water and vascular fractions to be measurable in brain tissue. Blood-nulled DWI studies of the liver (Lemke et al., 2010) have also demonstrated a dramatic reduction of the IVIM signature, so it also seems prudent to monitor the accuracy of any tissue nulling strategy.

Another analysis that could help further elucidate the origin of IVIM in normal brain would be to vary the echo time and evaluate its effect on IVIM parameters, particularly f*, as the difference in T2-relaxation between CSF and brain tissue is substantially larger as compared to blood and brain tissue. Along these lines, variable echo time IVIM studies in the liver (Lemke et al., 2010) have illustrated this modulation of IVIM signal weights and provided opportunity for correcting the measured vascular fraction for relaxation weighting.

Limitations

This retrospective study has some limitations that may be addressed in future research. First, only two nonzero b-values were employed, only allowing to study the IVIM signal fraction f*. It would be useful to find the optimal balance of b-values and SNR, as done in Lemke et al.’s work (2011) which studied the optimal distribution of b values using Monte Carlo simulations for different IVIM regimes and applied it to the abdomen. Similarly, Meeus et al. recently quantified the reproducibility of f and D in various SNR models at low, medium, and high perfusion fractions (Meeus et al., 2018), and proposed optimal b value distributions of b = 500 and 1000 s/mm² for low perfusion models (as observed in brain), though the exact deviations depended upon the image acquisition protocol and inputted IVIM parameters. In future work, it would be of interest to explore more specifically the inflection point of the signal curve described in Figure 1, and have additional b-values around b = 100 s/mm², with enough directions (>6) to estimate IVIM anisotropy.

Next, our voxel sizes limited the regional analysis of IVIM, and made our results prone to partial volume effects, in particular for the cortical GM, and to a much lesser extent to the WM, which was studied in more regional detail. In addition, we did not have high resolution T1 or T2 data available to perform segmentation of GM ROIs. We recommend future work to expand upon this analysis with T1 and T2 data to allow for segmentation of GM ROIs and following up with analysis analogous to our WM ROI calculations to see if this can unveil any further insight.

Third and last, although we label our patient population as “controls,” these patients were recruited from a clinical population, which may not represent true normal controls. While it may be of interest to repeat this in healthy volunteers, studying the current population is also of interest as they represent those that need to be clinically distinguished from pathological states.

Outlook

The changes in MD due to IVIM reported here suggest this effect is overall small in normal brain, implying that dMRI data over an extensive range is needed in normal brain tissue when performing bi-exponential fitting to avoid error-prone values. While the focus of this work was to quantify IVIM in a radiologic healthy cohort of patients, we recommend exploring the effect of IVIM in disease states in order to develop a deeper understanding of tissue microstructure in different pathologies. Baseline DWI volumes have been found to be useful in assessing clinical stroke (Suo et al., 2016), and IVIM has been suggested as a key diagnostic tool for stroke within the first 12 hours of onset (Schellinger et al., 2010), where the perfusion fraction values have been reported to considerably decrease in the infarcted brain region (Wirestam et al., 1997). Furthermore, the observed dependency of increasing IVIM in brain with age prompts for further exploration, particularly because elderly patients are more prone to developing cerebrovascular accidents which are associated with white matter lesions (Kobayashi et al., 1997; Steingart et al., 1987), lower cerebral blood flow (Tzourio et al., 2001), cognitive decline, dementia, white matter lesions (Cees De Groot et al., 2000; Longstreth et al., 1996), and depression (Hickie et al., 1997).

It would also be of interest to examine IVIM in neurodegenerative disease, such as Alzheimer’s, to better understand the origin of IVIM in brain. Insight could be gained by comparing against the known sequential changes of amyloid and tau deposition in GM (Braak and Braak, 1991; Guo et al., 2010), given the recent research interest in the glymphatic system in AD (Tarasoff-Conway et al., 2015). If IVIM is correlated to the glymphatic system, measuring changes in the observed IVIM effect over time in pathologic states could provide further insight into the progression of disease. However, efforts remain warranted to isolate the effect of the glymphatic system from other mechanisms contributing to IVIM.

Conclusion

In summary, we evaluated the effect of IVIM in the brain of 137 subjects by performing DTI on diffusion data with either b = 0 or b = 250, and b = 1000 s/mm². Derived MD-values including the b = 0 signal are consistently larger compared to when one excludes the b = 0 signal, suggesting contribution from IVIM to the dMRI signal decay. IVIM fraction calculated from our experiments was calculated to be on the order of ≈7% in cortical GM, ≈3% in WM, and ≈3% in the thalamus, suggesting that IVIM is predominantly present in cortical GM and caused by brain microvasculature. The effect of f* with respect to age was found to be significant in cortical GM (p = 3*10⁻⁵) and the thalamus (p = 0.022) with an average increase in f* of 5.17*10⁻⁴/year and 3.61*10⁻⁴/year, respectively, while significant correlations between f* and age were not observed for WM. Corollary analysis revealed no effect of gender on f*, and potential causes discussed in detail.

Highlights.

• Study of the effect of IVIM on the diffusion brain signal in 137 radiologically normal subjects

• Comparison of DTI parameters derived from b = 0 and 1000 s/mm² versus from b = 250 and 1000 s/mm²

• MD changes, with corresponding IVIM signal fractions, are ≈4% in white matter and ≈8% in cortical gray matter

• IVIM signal fraction increases with age in cortical gray matter and thalamus

• Possible origins of the IVIM effect in normal brain are discussed

Abbreviations:

IVIM

Intravoxel incoherent motion

dMRI

diffusion MRI

b

diffusion weighting factor

ADC

apparent diffusion coefficient

f*

perfusion fraction

D*

pseudodiffusion coefficent

MD

mean diffusivity

FA

fractional anisotropy

WM

white matter

GM

gray matter

CSF

cerebrospinal fluid

ISF

interstitial bulk flow