Learning Similar Actions by Reinforcement or Sensory-Prediction Errors Rely on Distinct Physiological Mechanisms

Abstract

Humans can acquire knowledge of new motor behavior via different forms of learning. The two forms most commonly studied have been the development of internal models based on sensory-prediction errors (error-based learning) and success-based feedback (reinforcement learning). Human behavioral studies suggest these are distinct learning processes, though the neurophysiological mechanisms that are involved have not been characterized. Here, we evaluated physiological markers from the cerebellum and the primary motor cortex (M1) using noninvasive brain stimulations while healthy participants trained finger-reaching tasks. We manipulated the extent to which subjects rely on error-based or reinforcement by providing either vector or binary feedback about task performance. Our results demonstrated a double dissociation where learning the task mainly via error-based mechanisms leads to cerebellar plasticity modifications but not long-term potentiation (LTP)-like plasticity changes in M1; while learning a similar action via reinforcement mechanisms elicited M1 LTP-like plasticity but not cerebellar plasticity changes. Our findings indicate that learning complex motor behavior is mediated by the interplay of different forms of learning, weighing distinct neural mechanisms in M1 and the cerebellum. Our study provides insights for designing effective interventions to enhance human motor learning.

Introduction

The ability to learn new motor behaviors is a fundamental feature of the animal kingdom. Humans constantly carry out motor behaviors that are essential and define our way of living from brushing teeth and getting dressed to play sophisticated sports or musical instruments. The complexity of learning and performing these ubiquitous behaviors becomes evident following an illness or injury that results in motor deficits. Recent research focused on understanding how humans acquire knowledge of new motor tasks indicated that multiple forms of learning are in play (Haith and Krakauer 2013; Taylor and Ivry 2014), including cognitive strategies (Taylor et al. 2014), developing internal models of movement dynamics (Shadmehr et al. 2010), use-dependent (Diedrichsen et al. 2010; Verstynen and Sabes 2011; Mawase et al. 2017) and reinforcement mechanisms (Huang et al. 2011; Izawa and Shadmehr 2011). Indeed, motor tasks developed in the laboratory have manipulated the weight each of these forms of learning have when acquiring new motor behaviors (Criscimagna-Hemminger et al. 2010; Izawa and Shadmehr 2011; Shmuelof et al. 2012; Therrien et al. 2016). Importantly, it has been argued that these forms of learning depend on different neuronal mechanisms. For instance, research on patients with cerebellar damage has shown that developing internal models to reduce sensory-prediction errors (i.e., error-based or adaptation learning) (Wolpert et al. 1995) heavily depends on the cerebellum (Tseng et al. 2007; Synofzik et al. 2008); while brain stimulation studies indicated that this type of learning leads to changes in cerebellar excitability (Jayaram et al. 2011; Schlerf et al. 2012). Yet, little is known about the potential physiological markers underlying reinforcement forms of learning in humans.

In the motor domain, reinforcement forms of learning have been referred as a success (reward)-based process in which actions leading to successful outcome are reinforced, whereas those leading to unsuccessful outcome are avoided (Sutton and Barto 1998). This form of learning is traditionally thought to engage basal ganglia and primary motor cortex (M1) loops (Doya 2000), relying on dopamine as a main neurotransmitter (Wickens et al. 2003; Wise 2004). Interestingly, human (Ueki et al. 2006; Kishore et al. 2012) and animal studies (Molina-Luna et al. 2009; Guo et al. 2015) indicate that dopaminergic projections to M1 help drive neurophysiological plasticity in M1 such as long-term potentiation (LTP)-like plasticity. M1 LTP-like plasticity has also been described as a neurophysiological phenomenon associated with motor learning and retention of learned motor memories (Rioult-Pedotti et al. 1998, 2000; Rosenkranz et al. 2007; Cantarero et al. 2013a, 2013b), although these studies used motor tasks that cannot disentangle the exact form of learning. Considering that the same motor behavior can be acquired using different forms of learning (Huang et al. 2011), here we tested two distinct neurophysiological mechanisms when people learn similar actions by relying on different forms of learning. We hypothesized that learning heavily via reinforcement will result in LTP-like plasticity changes in M1, but not cerebellar excitability modifications, while learning mainly via sensory-prediction errors will result in cerebellar modifications but not LTP-like plasticity changes in M1.

We first investigated the presence of neurophysiological changes when subjects trained in a visuomotor adaptation task (experiments 1 and 2). This task introduces a sudden perturbation to the sensorimotor system, requiring subjects to adapt motor commands in order to minimize prediction errors via vector feedback (Wolpert et al. 1995). Recent behavioral studies have suggested that learning this task mainly, but not exclusively, relies on cerebellar-dependent error-based forms of learning especially early on in the training; while other forms of learning, such as reinforcement, become relevant later on in the training when performance becomes asymptotic and successful movements are repeated (Huang et al. 2011; Shmuelof et al. 2012). Therefore, we predicted that learning this task would be associated with the presence of M1 LTP-like plasticity changes late but not early on during training, whereas the cerebellum would show excitability changes only early on, as previously described by measuring cerebellar-M1 connectivity (Schlerf et al. 2012). To further discern the relationship between reinforcement and error-based forms of learning, we assessed the same two neurophysiological markers when subjects learned a similar motor action via training on a task relying on reinforcement mechanisms (Therrien et al. 2016). Here, subjects only received success-based binary feedback (“success” or “failure”) instead of vector error feedback (experiment 3).

Materials and Methods

Participants

The study was approved by the Johns Hopkins University School of Medicine Institutional Review Board and was in accordance with the Declaration of Helsinki. A total of 59 healthy subjects (24.2 ± 5.1 years, including 32 females, mean ± standard of deviation (SD)) were recruited for the study. All individuals were right handed and were naïve to the purpose of the study. They provided written informed consent before participating in the study. None of the subjects had a history of neurological disease and/or psychological disorders and were taking medications.

Neurophysiological Assessments

We used a previously described protocol that combines transcranial magnetic stimulation (TMS) and transcranial direct current stimulation (tDCS) to assess the presence of learning-related LTP-like plasticity changes in M1 (Cantarero et al. 2013a, 2013b). Briefly, the protocol consists of determining whether the facilitatory anodal tDCS (AtDCS) effects, thought to be mediated through mechanisms akin to LTP plasticity due to the dependency on NMDA and TrK B receptors activation via BDNF (Nitsche and Paulus 2000; Liebetanz et al. 2002; Nitsche et al. 2003; Fritsch et al. 2010), are saturated after learning motor tasks relative to AtDCS effects in the absence of any motor training. As previously shown, if motor learning is associated with LTP formation in M1 then the AtDCS effects to M1 should be occluded after training (Rioult-Pedotti et al. 1998, 2000; Rosenkranz et al. 2007; Cantarero et al. 2013a, 2013b; Spampinato and Celnik 2017).

To determine cerebellar excitability changes, we used a paired-pulse TMS technique that probes the strength of the cerebellar inhibition (CBI) exerted over the contralateral M1. A number of studies demonstrated that TMS to the cerebellum results in subsequent inhibition of the contralateral M1 (Ugawa et al. 1995; Pinto and Chen 2001; Daskalakis et al. 2004; Galea et al. 2009). This has been interpreted as modulation of the inhibitory output from the cerebellar cortex to dentate nucleus, which in turn has excitatory connections with M1 via the thalamus (Celnik 2015; Grimaldi et al. 2016). Importantly, previous studies have shown that the magnitude of CBI is modulated by noninvasive brain stimulation protocols to the cerebellum (Galea et al. 2009; Popa et al. 2010), and when learning adaptive motor tasks (Jayaram et al. 2011; Schlerf et al. 2012). These effects were found in the absence of M1 excitability changes, indicating that the CBI modulation is predominantly mediated by cerebellar excitability changes.

MEP Measures

We stimulated the left M1 using a 70-mm-diameter figure-of-eight coil connected to TMS (Bistim² stimulator; Magstim) to elicit motor-evoked potential (MEP) of the first dorsal interosseous (FDI) muscle of the right hand. We used a neuro-navigation system (BrainSight; Rogue Research) to ensure consistency of stimulation location throughout assessments. We first coregistered the subjects’ heads to a standard magnetic resonance image in the system. Then, we identified the “hotspot” as the optimal area for eliciting MEPs in the resting FDI. The coil was placed tangentially to the scalp with the handle pointed backward at a 45° angle with respect to the anteroposterior axis. MEPs were recorded with electromyography (EMG) using disposable surface electrodes placed over the FDI. EMG signals were sampled at 5 kHz with a band-pass filter of 10–1000 Hz, visually displayed online, and analyzed off-line using MATLAB (R2015b; MathWorks). We defined peak-to-peak MEP amplitude as the index of corticospinal (M1) excitability.

Potentiation Effects of AtDCS on M1 Excitability

We first determined the stimulus intensity needed to evoke an MEP with peak-to-peak amplitude of around 1 mV (Stimulus intensity 1 mV, S1mV), and recorded 10 MEPs (preAtDCS MEP) using this intensity with a randomized interstimulus interval of 4–6 s. Then, we delivered tDCS through two 25 cm² sponge electrodes soaked in a saline solution using portable direct current stimulator (Chattanooga Ionto; Chattanooga group), with the anodal electrode centered over the left motor “hotspot” of FDI, the cathodal electrode positioned over the right supra-orbital area. In this manner, we applied direct current for 7 min at intensity of 1 mA. Immediately after the cessation of tDCS, we recorded 10 MEPs using predetermined stimulator intensity of S1mV and repeated the same assessment every 5 min for 15 min (postAtDCS MEP: P0–P15) to account for possible temporal variation in the AtDCS response across participants. To assess the potentiation effects of AtDCS we normalized the average of 10 MEP amplitudes for each time point to the average of 10 MEP amplitudes of preAtDCS MEP. In other words, changes in MEP amplitudes were expressed as a ratio relative to the preAtDCS MEP amplitude. We have previously shown that this tDCS protocol resulted in increased excitability after effects (Cantarero et al. 2013a, 2013b).

Assessment of Learning-Related M1 LTP-like Plasticity Changes

In a “baseline” session, we first evaluated the potentiation effects of AtDCS on M1 excitability when subjects were at rest in the absence of any motor training. As an indication of global potentiation effects of AtDCS, we calculated the grand average of normalized postAtDCS (P0, P5, P10, and P15) MEP amplitudes. In a different day, we performed identical measurements after subjects trained the motor tasks, and compared the potentiation effects with those of the baseline session. We determined the presence of learning-related LTP-like plasticity changes in M1 when we observed less increase in postAtDCS MEP amplitudes (i.e., less potentiation effects) after motor training compared to the baseline session (Cantarero et al. 2013a, 2013b). This implies that the resources needed to increase MEP amplitudes by AtDCS were used during motor learning.

CBI Measures

As an index of cerebellar excitability, we assessed the magnitude of CBI to the contralateral M1 using a paired-pulse TMS technique. This was done by delivering a TMS conditioning stimulus (CS) over the right cerebellar cortex 5 ms before a test stimulus (TS) over the left M1 (Ugawa et al. 1995; Pinto and Chen 2001; Daskalakis et al. 2004; Galea et al. 2009; Schlerf et al. 2012). To avoid potential artifacts caused by antidromic stimulation of the pyramidal tract itself with the cerebellar CS (Fisher et al. 2009), the intensity of cerebellar CS was set at less than the brainstem active motor threshold. The brainstem threshold for pyramidal tract activation was tested with a 110-mm-diameter double-cone coil centered over the inion with the stimulator current directed downward (Ugawa et al. 1995). The threshold was defined as the nearest 5% stimulator output that elicited an MEP of 50 μV in the pre-activated FDI muscle in five of 10 pulses. Then, the intensity of cerebellar CS was set at 5% less than the brainstem threshold, or 70% of maximum stimulator output (MSO) was used if the threshold was not observed at 80% of MSO. The TS over the left M1 was delivered using a 70-mm-diameter figure-of-eight coil. Note that the stimulator intensity was adjusted to S1mV at each time point (see “Experimental protocols” section). In a set of 20 TS over the left M1, 10 TS (selected at random) occurred 5 ms after a cerebellar CS delivered with the double-cone coil centered over the right cerebellar cortex 3 cm lateral to the inion (conditioned TS), whereas the remaining 10 TS were collected without a CS (unconditioned TS). An interstimulus interval across TS was randomized between 4 and 6 s. The magnitude of CBI was computed as the ratio of the conditioned/unconditioned TS MEPs.

To prove that changes in CBI were not accompanied with excitability changes in M1, we also assessed M1 excitability separately but at similar time points to those for CBI measures. For this, we applied single-pulse TMS to the left M1 with a randomized interstimulus interval of 4–6 s. We recorded 10 MEPs at a predetermined stimulator intensity of S1mV. Note that the same stimulator intensity was consistently used for all time points (see “Experimental protocols” section). We evaluated the level of M1 excitability by calculating the average of 10 MEP amplitudes.

Motor Tasks

Reaching with Vector Feedback (Experiments 1 and 2)

Subjects performed a center-out reaching task, moving a visually displayed cursor from a central starting location through one of eight radial targets in a slicing movement (Fig. 1a,b). Subjects were seated approximately 45 cm in front of a vertical computer monitor (1280 × 1024-pixel resolution). They were instructed to move a digitizing stylus attached to their right index finger over a horizontal digitizing tablet (48.8 × 30.5 cm active area, Intuos4 XL; Wacom) located on a table. Subjects put their forearm on an arm support with approximately 45° horizontal adduction and 90° flexion in the shoulder, and 45° flexion in the elbow. The tablet and subjects’ forearm were covered by a box to prevent subjects from directly looking at their hand while moving. The position of the stylus, sampled at 60 Hz through a custom Matlab program, corresponded to the position of a yellow 1.5-mm-diameter cursor displayed on a black screen such that moving the stylus forward moved the cursor upward. The mapping between the stylus and the displayed cursor displacement was set as 1:2.

Figure 1.

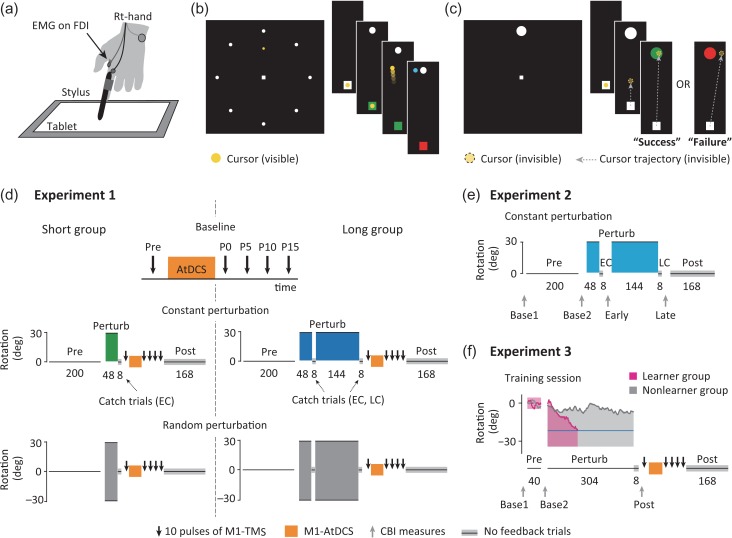
Experimental protocols. (a) Experimental setups. (b) Motor task for experiments 1 and 2. Subjects performed a center-out reaching controlling a yellow cursor from a central starting position to one of eight white targets while receiving online and endpoint cursor feedback (blue dot). Right panels show enlarged monitor for display purpose. (c) Motor task for experiment 3. Subjects performed a reaching from a central starting position to one target. Binary feedback (target color) about task performance was presented instead of vector cursor feedback. (d) Schematic representation of experiment 1. In a first-day “baseline” session, the AtDCS effects on M1 excitability were evaluated in the absence of motor training. Then in different days subjects participated in two counter-balanced crossover design sessions. Briefly, they trained the task in three blocks; preperturbation (Pre), perturbation (Perturb), and postperturbation blocks (Post). During the Perturb block, either a 30° (“constant perturbation” session) or trial-by-trial pseudo-randomized rotations (“random perturbation” session) were applied to cursor movement. The AtDCS effects were evaluated after the Perturb block. The numbers under each block represent the amount of trials. Note that the main difference between short and long groups was that the long group performed one additional Perturb block. (e) Schematic representation of experiment 2. Subjects participated in two-day counter-balanced crossover design sessions where training the same task as the long group in experiment 1 (the random perturbation session is not shown). CBI was obtained before (Base1) and after (Base2) the Pre block, and after the first (Early) and the second Perturb blocks (Late). (f) Schematic representation of experiment 3. After a baseline session where the AtDCS effects were evaluated (not shown in the panel), subjects trained the task through three blocks in a second-day “training” session. During the Perturb block, a range for task success (shaded area in magenta and gray) was shifted from the original range used in the pre block toward clockwise direction according to a moving average of the previous 10 reach angles (examples are shown in magenta and gray lines). The Perturb block terminated when the moving average reached a predetermined certain degree (blue horizontal line), otherwise it terminated when the number of trials reached 304. The AtDCS effects were evaluated after the Perturb block, and CBI measures were performed before (Base1) and after the Pre block (Base2), and after the Perturb block (Post).

Subjects performed rapid “shooting” movements to white 2-mm-diameter targets displayed in one of eight positions arrayed radially at 10 cm from a central starting position (0, 45, 90, 135, 180, −135, −90, and −45°). In this manner, subjects attempted to move the cursor from a white 3-mm-square centered in the middle of the screen (starting position) through the visible target in a straight line with no corrections. Subjects were instructed not to stop at the target but to strike through it as accurately as possible. In addition, they were instructed to use finger movements as much as possible to control the cursor displacement instead of using wrist movements.

Each trial started with moving the finger such that the cursor was positioned within the starting position. After maintaining this position for 500 ms, one of the targets was presented and the central starting position turned green. Upon presentation of the target, subjects started to move their finger so that the cursor crossed through the target. When the cursor passed through the invisible boundary circle centered around the starting position with a 10-cm radius, online feedback of the cursor location was hidden but the boundary point (endpoint) was marked with a blue 1.5-mm-diameter circle. Also, the central starting position turned red. When needed a high- or low-pitched auditory tone informed subjects that the movement (time from the starting position to endpoint) was either too fast (<87.5 ms) or too slow (>137.5 ms), respectively. In other words, the task was designed so that the movements were not ballistic, but constrained to be executed within a predefined time period. This time window was selected based on prior studies from our group (Galea et al. 2011; Schlerf et al. 2012; Spampinato and Celnik 2017) and based on our past experience showing that participants performing reaching movements within this time window are able to execute the task with no clear indication of online corrections (i.e., sub-movements, changes on movement speed). Subjects were reminded to try to hit the target and, as a secondary goal, try to complete the movement in the time allowed (Table 1). After each trial, subjects moved back to the starting position during which a yellow ring indicating a distance from current cursor position to the starting position was provided. By moving toward the starting position, a yellow ring became progressively smaller. This ring was used to guide subjects to the starting position without additional adaptation occurring between trials. When the cursor was within 1.25 cm from the central starting position, the ring was transformed into the cursor, allowing subjects to precisely position the cursor within the central square. The eight different targets were presented pseudorandomly so that every set of eight consecutive trials (=epoch) included one of each of the target positions.

Table 1.

Movement time (ms)

	Constant	Random
Experiment 1
Short group	132 ± 14	127 ± 11
Long group	135 ± 15	141 ± 12
Experiment 2	126 ± 13	134 ± 17

	Training
Experiment 3
Learner group	251 ± 35
Nonlearner group	273 ± 27

Values indicate the average (±SD) movement time (ms) across participants in each session in each experiment.

Reaching with Binary Feedback (Experiment 3)

Subjects performed a reaching task involving a rapid finger movement in the same setup used in the former two experiments (Fig. 1a). The critical difference in this motor task was that subjects only received binary feedback (“success” or “failure”) at the end of each trial instead of vector cursor feedback (Therrien et al. 2016). The cursor on the monitor was invisible when moving toward the target; while the target’s color turned green if the invisible cursor passed through a “success range” (e.g., between the target’s bounds) or red if it missed a range (Fig. 1c). We adopted this motor task so that subjects acquired a new reaching that leads to a similar kinematic solution (i.e., similar amount of angular deviation in reaching from the original movement direction) with heavily relying on reinforcement mechanisms.

In the task, subjects attempted to move a yellow 1.5-mm-diameter cursor from a white 3-mm-square starting position centered in the middle of the screen toward a white 16-mm-diameter target in a straight line with no corrections. The visible target was always displayed at 90°, 10 cm superior to the starting position (Fig. 1c). A trial begins with a period when subjects moved their finger such that the cursor was positioned inside the central starting position. Once the cursor was held in the starting position for 500 ms, the target appeared on the screen. Upon presentation of the target, subjects started to move their finger so that the cursor crossed through the target. However, the cursor disappeared immediately after it moved out (>0.3 mm) of the starting position, and therefore, subjects did not receive online and endpoint cursor feedback. Instead, reinforcing binary color feedback (green: success, red: failure) was presented to subjects at the moment when the invisible cursor passed through the invisible 10-cm radius boundary circle centered around the starting position. When needed a high- or low-pitched auditory tone informed subjects that their movements were either too fast (<175 ms) or too slow (>375 ms). Again, this time window was selected based on our prior studies (see above) to diminish the opportunity for online corrections. We verbally instructed subjects to obtain as many green targets as possible and, as a secondary goal, to complete the movement in the time window allowed (Table 1). After each trial, subjects moved back to the starting position guided by a yellow ring that indicates the distance of the current cursor position from the central starting position. When the invisible cursor was within 1.25 cm from the central starting position, the ring was transformed into the visible cursor.

Experimental Protocols

Experiment 1

We sought to investigate the presence of learning-related LTP-like plasticity changes in M1 early and later on during training the visuomotor adaptation task (Fig. 1b). We recruited 28 participants (23.7 ± 5.2 years, including 15 females, mean ± SD) for three-day experimental sessions (Fig. 1d). In a first-day baseline session, we evaluated the AtDCS potentiation effects on M1 excitability when subjects were at rest in the absence of any motor training. Importantly, recent studies indicated that the AtDCS effects show between-individual variability, namely a number of subjects do not show clear potentiation (“non-responder”) even after the application of AtDCS (Lopez-Alonso et al. 2014, 2015; Wiethoff et al. 2014). Therefore, we screened out those subjects based on the results in the baseline session. We defined subjects as non-responders when we found (1) grand average of normalized MEP amplitude across postAtDCS time points (P0, P5, P10, and P15) did not exceed 1.0 (i.e., smaller than preAtDCS MEP) or (2) normalized MEP amplitude exceeded 1.0 in less than half (i.e., only once) of the four postAtDCS time assessments. A total of 8 subjects met this exclusion criteria and were not invited to the subsequent experimental sessions. The other 20 subjects were randomly assigned into one of two groups: short (n = 10, 25.2 ± 6.3 years, including 5 females) or long (n = 10, 23.4 ± 4.8 years, including 7 females) groups. Both groups participated in two randomly assigned, counter-balanced crossover design sessions separated by at least 24 h (Fig. 1d). In a “constant perturbation” session, the subjects trained in the center-out reaching task with a constant 30° counter-clockwise visuomotor transformation (perturbation) in the relationship between the movement of the finger and a screen cursor, leading to trial-to-trial adjustments in the finger reaching direction to achieve the goal of the task (i.e., visuomotor adaptation). In a “random perturbation” session, the subjects trained in the same task under the condition that seven different pseudo-randomized transformations (−30, −20, −10, 0, 10, 20, and 30°) were applied in each trial. The random perturbation session was set as a control condition, in which the subjects experienced movement execution and errors without learning a new visuomotor mapping.

In each session, both groups first performed a preperturbation block (200 trials = 25 epochs) without any visuomotor perturbation to familiarize themselves with the task and movement demands. After this, they performed a perturbation block (48 trials = six epochs) in which either constant or randomized perturbations were applied to the cursor movements. Only the long group continued with an additional perturbation block (144 trials = 18 epochs). Our previous work demonstrated that the process of adaptation to the constant visuomotor perturbation was still not completed during the first perturbation block but reached asymptote during the second block (Schlerf et al. 2012). We inserted catch trials consisting of eight, no visual feedback trials at the end of the first (early catch: EC) and the second (late catch: LC) perturbation block. In the catch trials, the cursor disappeared once it moved out (>0.3 mm) of the central starting position so that subjects did not receive online and endpoint cursor feedback. We adopted these trials to evaluate the magnitude of corrected reach angle (i.e., the amount of learning) that subjects acquired through the perturbation blocks. Note that we did not provide any explicit cue to make subjects aware of the coming of catch trials. After completion of the perturbation blocks, the AtDCS potentiation effects on M1 excitability were evaluated as done in the baseline session. During the evaluation, we placed a pillow under the subject’s right hand and instructed them to relax the entire upper limb without changing their arm position. By observing the potentiation effects in the short and long groups, we assessed the presence of learning-related M1 LTP-like plasticity changes early and late during the training, respectively. After this, both groups of subjects completed a postperturbation block consisting of no visual feedback trials (168 trials = 21 epochs). We adopted this block to evaluate the robustness of retention of learned movements.

Experiment 2

We evaluated changes in cerebellar excitability early and late during the training in the same reaching task as in experiment 1 (Fig. 1b). A new group of 8 subjects (24.0 ± 6.0 years, including 4 females, mean ± SD) participated in two randomly assigned, counter-balanced sessions in which they performed the reaching task with either constant or randomized visuomotor perturbations (Fig. 1e). Each session was separated by at least 24 h. The subjects completed the training of the task in the same manner as in the long group of experiment 1: a 200 trial preperturbation block, a 48 trial first perturbation block, a 144 trial second perturbation block, and a 168 trial postperturbation block. Eight catch trials were inserted at the end of each perturbation block (EC, LC). To evaluate the changes in cerebellar excitability, we assessed the magnitude of CBI before (Base1) and after the preperturbation block (Base2) as baseline measurements, and immediately after the first (Early) and second perturbation blocks (Late). We also evaluated M1 excitability at the same time breaks used for the CBI measures, by recording MEP amplitudes from M1 TMS only.

Experiment 3

We recruited a new group of subjects for two-day experimental sessions (Fig. 1f). A total of 23 subjects (24.9 ± 4.7 years, including 13 females, mean ± SD) participated in a first-day baseline session where we evaluated the AtDCS effects on M1 excitability when the subjects were at rest in the absence of any motor training (Fig. 1d). We screened out 3 subjects as non-responders as defined in experiment 1. The remaining 20 subjects (24.9 ± 4.9 years, including 11 females) proceeded on to a second-day “training” session at least 24 h later where they trained in the reaching task with success-based binary feedback through three experimental blocks (Fig. 1f). The subjects first performed a preperturbation block (40 trials = five epochs) in which the success range was kept constant between the target’s bounds (90° ± 4.5° on the screen), followed by a perturbation block in which the success range changed from the original one. Here, the right bound of the range shifted −30° (i.e., clockwise direction), which remained the same throughout the block. In contrast, the left bound shifted trial-by-trial according to a moving average of an individual subject’s reach angle in previous 10 trials (Fig. 1f). Reach angle was defined as the angle between the line connecting the starting position to the center of the visible target and the line connecting the starting position to the endpoint in reaching. This manipulation has been shown to reinforce subjects’ reaching toward a clockwise direction in a gradual manner (Therrien et al. 2016). Importantly, the perturbation block ended when the mean of the previous 10 reach angles approached a certain prespecified degree, so that the total magnitude of reaching corrections made was comparable to that of the short group from experiment 1. We adopted this protocol to make a clear contrast that compared two subject groups that learned similar actions; one group learned heavily relying on error-based mechanisms (the short group in experiment 1), while the other group learned via reinforcement mechanisms. To establish the termination criterion, we computed the mean reach angle of the last eight trials (one epoch) during the perturbation block for each individual in the short group (−21.4 ± 1.4° ranging from −14.6 to −29.9, mean ± SEM), and randomly assigned these angles to each subject’s criterion angle to end the block. In cases where subjects did not approach their predetermined angle, we terminated the perturbation block when the number of attempts reached 304 trials. After the perturbation block, subjects performed eight catch trials (one epoch) consisting of no-feedback trials in which the target always turned black irrespective of reaching performance. Finally, the subjects performed a postperturbation block (168 trials = 21 epochs) comprising the same setting as the catch trials. For neurophysiological assessments, we evaluated the magnitude of CBI before (Base1) and after the preperturbation block (Base2) as baseline measurements, and immediately after the perturbation block (Post). We also evaluated changes in M1 excitability at the same time breaks used for the CBI measures. The AtDCS effects on M1 excitability were assessed in the period between the perturbation and the postperturbation blocks.

Importantly, some subjects could successfully reach the criterion angle during the perturbation block (total number of trials in the block: 107.9 ± 18.3 trials, mean ± SEM), while others could not reach it even after 304 attempts. In other words, they could not learn to correct the reaching via success-based binary feedback. Therefore, we classified the former subject group as “leaner” (n = 12, 25.1 ± 4.7 years, including 7 females, mean ± SD) and the latter as “nonlearner” (n = 8, 24.6 ± 5.4 years, including 4 females), and analyzed them separately. The nonlearner group constituted the ideal control group that helped dissociate physiological changes related to true learning rather than simple movement execution.

Data Analysis

Behavioral Analysis

Task performance was quantified in each trial using reach angle, the angle between the line connecting the starting position to the center of the target and the line connecting the starting position to the endpoint in reaching. Trials in which subjects failed to move the cursor far enough to pass through the target on the first reaching attempt and then made a second corrective reaching were excluded from analysis. In addition, we excluded trials in which reaching angle exceeded 60° or movement time exceeded 600 ms. Excluded trials accounted for less than 5% of all trials on average (1.6 ± 0.3%, 2.8 ± 0.9%, and 4.3 ± 0.7% for experiments 1, 2, and 3 respectively, mean ± SEM). To analyze changes in reach angle during task training, we computed the average reach angle across eight consecutive trials (reaching toward eight different targets = one epoch) for experiments 1 and 2. In a similar vein, to analyze the data of experiment 3 matching the first two experiments we defined the average of eight trials as one epoch, even though there was only one target in the task. However, since participants performed different number of trials during the perturbation block in experiment 3 (recall that the cutoff threshold here was based on the amount of learning but not on the trial number), to be able to compare the effects across groups we defined one epoch as the average across 10% of the total number of trials. For example, when the total number of trials was 90 in a participant we used nine trials (10% of 90 trials) as an epoch for this participant. In case 10% of trials were not a round number, we rounded up to the nearest integer. For example, if the total number of trials was 73 (10% of trials was 7.3), the trial numbers (trial_n) included in each epoch were trial₁ to trial₇, trial₈ to trial₁₅, and trial₁₆ to trial₂₂, etc.

Using mean reach angle in the catch trials as the outcome measure, we compared the amount of learning across groups. For experiment 1, we applied an unpaired t-test (two-tailed) between the last catch trials of the short (i.e., EC) and the long groups (i.e., LC). For experiment 2, we applied a mixed-effect, repetitive measure, analyses of variance (ANOVA_RM), to confirm that the amount of learning was comparable between the subject group from experiment 2 and the long group from experiment 1, with between-subject factor for group and within-subject factor for time (EC, LC). For experiment 3, we applied an unpaired t-test (two-tailed) between the catch trials of the learner group and the short group from experiment 1 to check if the amount of learning was well-controlled. Using mean reach angle at the first and the last epochs during the postperturbation block, we also compared the robustness of retention of learned movements (i.e., resistance to forgetting) between the groups by applying a mixed-effect ANOVA_RM with between-subject factor for group and within-subject factor for time (first, last).

Neurophysiological Analysis

In the process of MEP analysis, MEPs were discarded from the analysis when there was pre-EMG activation or when amplitudes were greater than two standard deviations from the mean amplitudes for the given measurement. On average, we discarded 0.1 ± 0.2 (0.7 ± 0.9%, mean ± SD) and 0.1 ± 0.1 (1.3 ± 1.8%) pulses for the short and the long groups, respectively, in experiment 1; 0.3 ± 0.2 (3.3 ± 2.4%) in experiment 2; and 0.2 ± 0.2 (1.6 ± 1.6%) and 0.1 ± 0.1 (1.0 ± 0.9%) pulses for the learner and the nonlearner group respectively in experiment 3.

To assess the presence of learning-related LTP-like plasticity changes in M1, we first evaluated the magnitude of the AtDCS potentiation effects for each experimental session by computing the grand average of normalized MEP amplitude across postAtDCS time points (P0, P5, P10, and P15). Then, for experiment 1, we compared these values among the groups and sessions by applying a mixed-effect ANOVA_RM with between-subject factor for group (short, long) and within-subject factor for session (baseline, constant, random). We additionally performed Bonferroni’s multiple comparison test as post hoc analysis to evaluate the difference between the baseline session and the other sessions for each group. For experiment 3, we applied a mixed-effect ANOVA_RM with between-subject factor for group (learner, nonlearner) and within-subject factor for session (baseline, training). For post hoc analysis, we further applied a paired t-test (two-tailed) to evaluate the difference between the two sessions for each group.

To assess the difference in the magnitude of CBI between sessions in experiment 2, we applied ANOVA_RM with within-subject factors for session (constant, random) and time (Base1, Base2, Early, Late). For post hoc analysis, we used paired t-tests (two-tailed) for each time point to compare the difference between the sessions. For experiment 3, we applied a mixed-effect ANOVA_RM with between-subject factor for group (learner, nonlearner) and within-subject factor for time (Base1, Base2, Post). We also used the same statistical analysis to compare MEP amplitudes acquired by single-pulse TMS.

All statistical analyses were performed using SPSS (version 20; IBM, Armonk). Effects were considered significant if P ≤ 0.05. Effect sizes were reported in Cohen’s d value (d) for t-test, and partial eta squared value (η_p²) for ANOVA, respectively.

Results

M1 LTP-like Plasticity Develops Late, but not Early When Learning via Vector Feedback

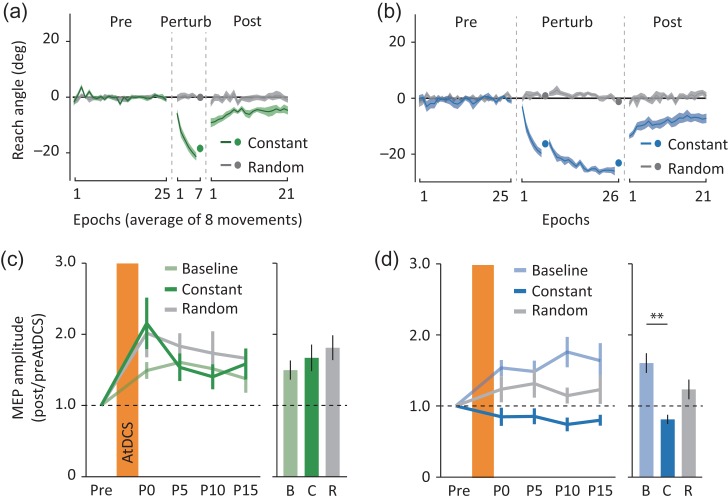
We found in experiment 1 that both, the short and the long groups gradually shifted the reaching direction only when exposed to the constant perturbation, but not when exposed to the random perturbation (Fig. 2a,b). This indicates that both groups accumulated significant amounts of information only when exposed to constantly transformed visuomotor mapping. However, when we compared the total amount of learning between the two groups, we found that the short group adapted less, whereas the long group seemed to compensate more for the perturbation. This difference resulted in significantly greater angular deviation in the catch trials at the end of the perturbation block for the long group (−23.17 ± 0.82°, mean ± SEM) relative to the short group (−18.44 ± 1.36°: t₁₈ = 3.0, P = 0.008, d = 1.40, see Supplementary Fig. S1a). This group difference persisted in the subsequent postperturbation block (mixed-effect ANOVA_RM, main effect of group: F_1,18 = 5.7, P = 0.03, η_p² = 0.24, see Supplementary Fig. S1b), resulting in comparable amounts of gradual shift toward baseline reaching directions from the first (−9.21 ± 1.65° and −13.68 ± 0.85° for the short and the long group) to the last epoch (−4.81 ± 1.45° and −7.19 ± 1.65°; main effect of time: F_1,18 = 14.4, P = 0.001; group × time interaction: F_1,18 = 0.5, P = 0.48, η_p² = 0.03). In contrast, neither group could systematically accumulate trial-to-trial learning in the random perturbation session (Fig. 2a,b). This is depicted by both groups showing little and comparable changes in angular deviation in the catch trials at the end of the perturbation block (−0.06 ± 0.57° and −1.18 ± 1.00° for the short and the long group: t₁₈ = 1.0, P = 0.34, d = 0.46).

Figure 2.

Results for experiment 1. (a, b) Reach angle for the short (a) and the long groups (b). Positive values indicate counter-clockwise deviation. Solid lines and shaded areas show the mean and standard errors of the mean (SEM) for each eight trial epoch for the constant perturbation (green for the short and blue for the long groups) and the random perturbation sessions (gray). Colored dots show the mean reach angles in the catch trials. Dashed vertical lines indicate short breaks between the blocks. (c, d) The AtDCS effects on M1 excitability for the short (c) and the long groups (d). MEP amplitudes normalized to that of preAtDCS are presented for each time point (Pre, P0…P15). Solid lines and vertical error bars show the mean and SEM of normalized MEP for the baseline (light green and light blue), the constant perturbation (green and blue), and the random perturbation sessions (gray). Bar graphs and vertical error bars depict the mean and SEM of grand average of postAtDCS MEPs (P0–P15) for each session. Dashed horizontal lines represent the normalized MEP amplitude of preAtDCS (i.e., 1.0). **P < 0.01 (with Bonferroni’s multiple comparison).

When we evaluated the effects of AtDCS on M1 excitability, we found clear difference across sessions and groups (mixed-effect ANOVA_RM, group × session interaction: F_2,36 = 7.3, P = 0.002, η_p² = 0.29, Fig. 2c,d). This distinction was not explained by the difference in the baseline (preAtDCS) MEP amplitude (see Supplementary Table S1). The short group revealed comparable magnitude of potentiation effects both after training in the random (1.81 ± 0.18, mean ± SEM: Bonferroni correction, P = 0.58) and the constant perturbation sessions (1.67 ± 0.19: P = 1.00) relative to the baseline session (1.50 ± 0.13, Fig. 2c). On the contrary, the long group showed clear occlusion of the potentiation effects after training in the constant perturbation (0.81 ± 0.07: P > 0.001) compared to the one in the baseline session (1.60 ± 0.14), an effect that was not present after training in the random perturbation (1.23 ± 0.14: P = 0.11, Fig. 2d). These findings indicate that M1 develops LTP-like plastic changes late, but not early, when adapting to a visuomotor perturbation. This is because later in the practice more repetitions result in successful movements (asymptotic phase) weighting more reinforcement contributions. Importantly, we did not find signs of occlusion after training in the random perturbation (see Supplementary Fig. S2 for individual data). This indicates that M1 LTP-like plastic changes are specifically associated to learning, rather than the simple execution of movements.

Cerebellar Excitability Changes Early When Learning via Vector Feedback

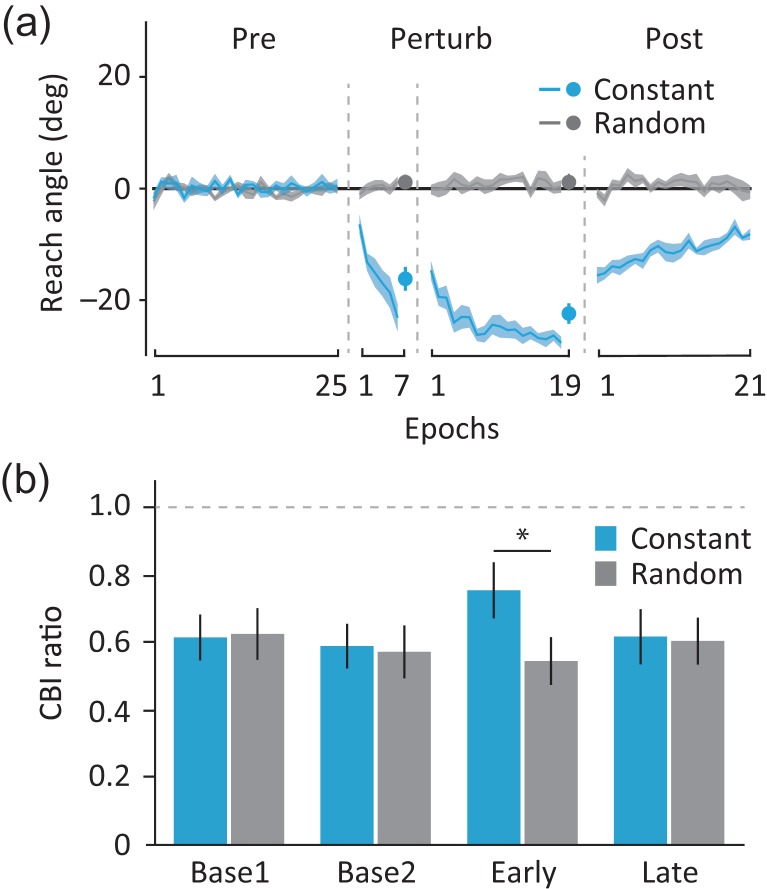
In experiment 2, similar to experiment 1, we found gradual accumulation of trial-to-trial learning only when the subjects dealt with constant perturbation but not in the randomized situation (Fig. 3a). Importantly, the magnitude of angular deviation in the catch trials at the end of the first (−16.19 ± 2.12°) and the second perturbation blocks (−22.43 ± 1.84°) were comparable to that observed in the long group from experiment 1 (mixed-effect ANOVA_RM, group × time interaction: F_1,16 = 0.18, P = 0.68, η_p² = 0.01, see Supplementary Fig. S1c). Similarly, both groups showed comparable magnitude of angular deviation and a return to baseline levels of performance from the first (−15.57 ± 1.50°) to the last epoch (−8.20 ± 0.99°) during the postperturbation block (mixed-effect ANOVA_RM, main effect of time: F_1,16 = 28.0, P < 0.001, η_p² = 0.64; main effect of group: F_1,16 = 1.2, P = 0.29, η_p² = 0.07; group × time interaction: F_1,16 = 0.1, P = 0.74, η_p² = 0.01, see Supplementary Fig. S1d).

Figure 3.

Results for experiment 2. (a) Reach angle. Solid lines and shaded areas show the mean and SEM of eight trial epochs for the constant (light blue) and random perturbation sessions (dark gray). (b) CBI Results. Bar graphs and vertical error bars indicate the mean and SEM of CBI ratio (the ratio of the conditioned/unconditioned TS MEP amplitude) for the constant (light blue) and the random sessions (dark gray) at each time point (Base1, Base2, Early, Late). Dashed horizontal line indicates the normalized unconditioned TS MEP amplitude (i.e., 1.0). *P < 0.05 (two-tailed paired t-test).

When we assessed CBI, we found a selective reduction only early during training with the constant perturbation (ANOVA_RM, session × time interaction: F_3,21 = 3.6, P = 0.03, η_p² = 0.34, Fig. 3b). Importantly, we confirmed that there was no systematic difference in the amplitude of unconditioned TS MEPs across sessions and time points (see Supplementary Table S2). While there was no significant difference in CBI between the sessions (constant and random) at baseline assessments (Base1, 0.61 ± 0.07 and 0.62 ± 0.08: t₇ = 0.2, P = 0.85; Base2, 0.59 ± 0.07 and 0.57 ± 0.08: t₇ = 0.3, p = 0.80), the magnitude of CBI decreased early on during learning the constant perturbation (Early, 0.75 ± 0.08 and 0.54 ± 0.07: t₇ = 2.5, P = 0.04). The reduction of CBI returned to baseline levels later on in the training, reaching comparable levels between the sessions (Late, 0.62 ± 0.08 and 0.60 ± 0.07: t₇ = 0.3, P = 0.81, see Supplementary Fig. S3 for individual data). Importantly, the modulation of CBI was observed in the absence of M1 excitability changes (ANOVA_RM, main effect of time: F_3,21 = 0.2, P = 0.86, η_p² = 0.03; main effect of session: F_1,7 = 0.9, P = 0.38, η_p² = 0.11; time × session interaction: F_3,21 = 1.0, P = 0.41, η_p² = 0.13, see Supplementary Table S3). These findings are consistent with a prior study showing changes in the magnitude of CBI early on during adaptation to a constant visuomotor perturbation (Schlerf et al. 2012), when error-based forms of learning would be critically engaged in developing an internal model of the new environment.

Learning via Binary Feedback Elicits M1 LTP-like Plasticity, but not Cerebellar Excitability Changes

Results in experiments 1 and 2 showed that the cerebellum exhibited excitability changes early on during adapting to a constant visuomotor perturbation, whereas M1 exhibited LTP-like plasticity changes late but not early on during the adaptation. However, it could be argued that the lack of M1 LTP-like plasticity changes early on during adaptation is due to less amount of learning (i.e., smaller correction in the reaching direction), independently of weighted learning mechanisms engaging at each phase. To exclude this assertion and further discern the relationship between reinforcement and error-based forms of learning, we assessed the same neurophysiological markers when subjects learned a similar amount of angular deviation in reaching via training on a task that heavily relies on reinforcement mechanisms. We predicted that learning the same magnitude of angular deviations only via success-based binary feedback (reinforcement signals) would lead to M1 LTP-like plasticity, but no cerebellar excitability changes. In other words, the opposite neurophysiological pattern to that observed when learning the same angular deviations through error-based mechanisms.

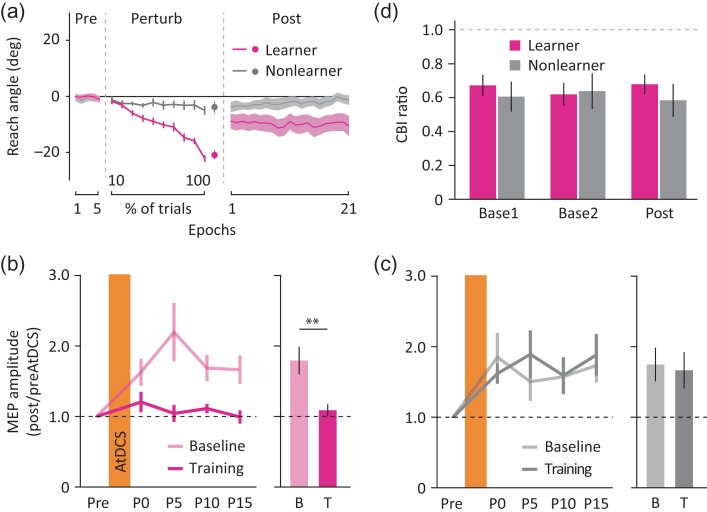
The subjects in experiment 3 were divided into the learner and the nonlearner groups based on task performance during the perturbation block (Fig. 4a). While the percentage of task success during the preperturbation block was comparable between the learner (71.0 ± 5.4%, mean ± SEM) and the nonlearner groups (68.8 ± 2.7%, two-tailed unpaired t-test, t₁₈ = 0.4, P = 0.71, d = 0.15), the leaner group showed greater percentage of success (63.7 ± 1.9%) than the nonlearner group (52.1 ± 0.9%, two-tailed unpaired t-test, t₁₈ = 6.6, P < 0.001, d = 2.21) during the perturbation block. Importantly, we confirmed that the magnitude of angular deviation in the catch trials in the learner group (−20.77 ± 1.62°, mean ± SEM) was comparable to that in the short group from experiment 1 (two-tailed unpaired t-test, t₂₀ = 1.1, P = 0.28, d = 0.48, see Supplementary Fig. S1e). However, during the postperturbation block, the learner group showed a trend toward better retention of the learned reaching angle; in other words, less gradual shift from the first (−8.80 ± 2.73°) to the last epoch (−10.58 ± 3.61) when compared to the short group (mixed-effect ANOVA_RM, group × time interaction: F_1,20 = 3.8, P = 0.07, η_p² = 0.16, see Supplementary Fig. S1f).

Figure 4.

Results for experiment 3. (a) Reach angle. Solid lines and shaded areas indicate the mean and SEM of each eight trial epoch for the learner (magenta) and the nonlearner groups (dark gray). Only for the Perturb block, the mean of every 10%-trial bin instead of eight trial epochs was calculated. (b, c) The AtDCS effects on M1 excitability for the learner (b) and the nonlearner groups (c). Solid lines and vertical error bars indicate the mean and SEM of normalized MEP amplitudes for the baseline (light magenta and light gray) and for the training sessions (magenta and dark gray) at each time point. Bar graphs and vertical error bars depict the mean and SEM of grand average of postAtDCS MEPs. (d) CBI results. Bar graphs and vertical error bars indicate the mean and SEM of CBI ratio for the learner (magenta) and the nonlearner groups (dark gray) at each time point (Base1, Base2, Post). P < 0.01 (two-tailed paired t-test).

When applying AtDCS after the perturbation block, we found significant differences in the potentiation effects between the learner and the nonlearner groups (mixed-effect ANOVA_RM, group × session interaction: F_1,18 = 8.6, P = 0.009, η_p² = 0.32, Fig. 4b,c). Note that there was no meaningful difference in the amplitude of preAtDCS MEP across groups and sessions since it was controlled to some extent to meet the amplitude around 1 mV (see Supplementary Table S1). The learner group showed significantly less AtDCS-induced potentiation after the training (1.09 ± 0.09, mean ± SEM) relative to the baseline session (1.79 ± 0.20: two-tailed paired t-test, t₁₁ = 4.6, P = 0.001, Fig. 4b). In contrast, this effect was not present in the nonlearner group (baseline, 1.75 ± 0.24; training, 1.67 ± 0.26: t₇ = 0.7, P = 0.53, Fig. 4c). As predicted, we found no systematic difference in the magnitude of CBI throughout the experiment regardless of whether the subjects successfully learned (Base1, 0.67 ± 0.06; Base2, 0.62 ± 0.07; Post, 0.68 ± 0.06) or not the task (Base1, 0.61 ± 0.09; Base2, 0.64 ± 0.10; Post, 0.58 ± 0.10, Fig. 4d). This was supported by a mixed-effect ANOVA_RM that revealed no statistical significance across groups and time (main effect of group: F_1,18 = 0.2, P = 0.65, η_p² = 0.01; main effect of time: F_2,36 = 0.1, P = 0.96, η_p² = 0.003; group × time interaction: F_2,36 = 1.4, P = 0.25, η_p² = 0.07, see Supplementary Fig. S4 for individual data). Importantly, we confirmed that the amplitude of unconditioned TS MEPs was comparable and approximately 1 mV across groups and time points (see Supplementary Table S2). Similar to the result of CBI, we found no systematic changes in M1 excitability throughout the experiment (mixed-effect ANOVA_RM, main effect of group: F_1,18 = 1.6, P = 0.22, η_p² = 0.08; main effect of time: F_2,36 = 1.0, P = 0.38, η_p² = 0.05; group × time interaction: F_2,36 = 2.65, P = 0.08, η_p² = 0.13, Supplementary Table S3). These neurophysiological findings further support our claim that learning motor behavior via reinforcement mechanisms is exclusively linked to the development of M1 LTP-like plasticity changes but not cerebellar plasticity modifications.

In summary, the learner group of experiment 3 arrived to a comparable amount of angular deviation in reaching as the short group from experiment 1. While the former learned the task via binary feedback, the latter learned via online and endpoint vector feedback, weighting differently reinforcement and error-based learning mechanisms respectively. The learner group heavily relying on reinforcement showed M1 LTP-like plasticity changes, but no cerebellar excitability changes; whereas the short group mainly relying on error-based mechanisms expressed cerebellar excitability but no M1 LTP-like plasticity changes. This double dissociation clearly points to learning-related LTP-like plasticity changes in M1 as a marker of engaging reinforcement processes, whereas cerebellar excitability changes as a marker of error-based forms of learning.

Discussion

Learning complex motor skills, like hitting a baseball, involves multiple processes such as reinforcement and sensory-prediction error-based forms of learning. Here, we added to the evidence that these different processes can be used to learn similar motor actions (Huang et al. 2011; Therrien et al. 2016). Importantly, our study shows in healthy young individuals that these two forms of learning rely on different neural substrates, each engaging distinct neurophysiological mechanisms, one involving the motor cortex and the other one the cerebellum. These findings suggest that manipulating one form of learning could be used to compensate another mechanism that has been damaged due to neurological diseases. For instance, in patients with cerebellar lesions who experience abnormalities in error-based learning, Therrien et. al were able to train them to learn a motor task via reinforcement feedback (Therrien et al. 2016). However, this concept warrants further testing in older adults and patient populations.

Reinforcement learning has been defined as one form of learning that relies on scalar measures of outcome such as success or failure, where behavior leading to a successful outcome is reinforced while another leading to a failure is avoided (Sutton and Barto 1998). This form of learning is driven by “reward prediction errors”, consisting of differences between actual and predicted rewards. Specifically, if the reward is better than predicted (positive prediction error) the behavior leading to the reward will be repeated. In contrast, if the reward is worse than predicted (negative prediction error) the behavior will be avoided the next time around (Schultz 2016). This form of learning is implemented by dopaminergic neurons in the midbrain that change their level of activity when reward itself or reward prediction errors are encountered (Schultz 1986; Schultz et al. 1997; Pan et al. 2005; Pessiglione et al. 2006). It is likely that a similar dopamine-dependent physiological process drove the learning of the motor task in our experiment 3. Here, successful or unsuccessful outcome would result in positive or negative reward prediction errors prompting subjects to explore and learn the correct reaching movements. The contribution of dopaminergic activity to this form of learning is supported by behavioral studies in Parkinson’s disease patients who experience reduced variation of movements as a function of unsuccessful outcome (Pekny et al. 2015).

If reinforcement forms of learning rely on dopaminergic activity in the midbrain, why did we observe the expression of M1 LTP-like plasticity changes in association with greater engagement of this learning? Previous animal research has shown that dopamine affects neuronal excitability in M1 via direct dopaminergic projections from the ventral tegmental area (Molina-Luna et al. 2009; Hosp et al. 2011). For instance, eliminating dopaminergic terminals in M1 or dopaminergic cells in the ventral tegmental area impairs the expression of LTP in M1 and interferes with learning of new motor skills (Molina-Luna et al. 2009; Hosp et al. 2011). Specifically, dopamine-dependent D1 receptors within M1 have been implicated to be critical for structural dendritic spine plasticity and LTP synaptic plasticity (Guo et al. 2015). Dopamine is also likely to influence synaptic efficacy in M1 via basal ganglia-M1 loops receiving inputs from the substantia nigra (Gaspar et al. 1992; Williams and Goldman-Rakic 1998; Hosp et al. 2011). Indeed, the capacity of M1 to undergo plastic changes in response to excitability-modulating noninvasive brain stimulation protocols is impaired in Parkinson’s disease patients in the absence of dopamine agonist medications (Morgante et al. 2006; Ueki et al. 2006; Suppa et al. 2011; Kishore et al. 2012). Therefore, it is conceivable to reason that engaging dopamine-dependent reinforcement forms of learning can lead to the expression of learning-related LTP-like plasticity changes in M1.

The present study indeed revealed that learning motor tasks that heavily rely on reinforcement mechanisms is associated with the expression of learning-related LTP-like plasticity changes in M1. To learn the motor task in experiment 3, subjects relied on binary feedback and thus reinforcement processes. As argued by others (Huang et al. 2011), we also predicted that to learn the adaptation task of experiments 1 and 2 reinforcement forms of learning would also be engaged in the later stages of the training. Although subjects learn to make the cursor reach the target via vector feedback, a process generally thought to be mediated by formation of internal models (i.e., error-based learning) (Shadmehr et al. 2010; Krakauer and Mazzoni 2011), at later stages of the training when the errors are greatly decreased, the subjects in the long group experienced significant number of successful movements leading to “reward” and increase propensity to repeat the same movements (Huang et al. 2011). Thus, we think the reliance on reinforcement mechanisms is what drove the formation of LTP-like plasticity in M1 when learning via binary feedback, as well as later on during learning via vector feedback as in the long group of experiment 1.

Here, we assessed the expression of LTP-like plasticity by determining the presence of occlusion of AtDCS effects on M1 excitability. Electrophysiological studies demonstrated that the application of AtDCS over M1 elicits long-lasting increases in M1 excitability through processes that resemble LTP plasticity changes due to the involvement of NMDA receptor activity (Nitsche and Paulus 2000; Liebetanz et al. 2002; Nitsche et al. 2003; Fritsch et al. 2010). However, the exact cellular mechanisms and the specific brain regions modulated by AtDCS remain incompletely understood. Previously we have shown that AtDCS effects on M1 excitability are occluded when the stimulation is applied immediately after learning a skill motor task (Cantarero et al. 2013a, 2013b; Spampinato and Celnik 2017). This phenomenon, well characterized in animal models (Rioult-Pedotti et al. 1998, 2000, 2007), can be interpreted by the learning using up LTP resources resulting in a lack of potentiation when AtDCS is applied after the training.

We found that some subjects in experiment 3 did not successfully correct their reaching toward the desired direction (i.e., nonlearner group) resulting in no M1 LTP-like plasticity changes. This was despite the fact that the nonlearner group performed greater number of trials than the learner group (number of trials was 304 in the nonlearner group vs. 107 in the learner group on average). This provided the ideal control to differentiate learning versus execution effects on plasticity changes. In other words, mere movement repetition without learning a new motor pattern was not sufficient to drive LTP-like M1 plasticity changes. If M1 LTP-like plasticity results from simple movement execution then the nonlearner group should have experienced larger plasticity changes. A similar situation was also present in experiment 1 where training with random perturbations, resulting in no learning, did not induce cerebellar or M1 plasticity changes.

Unlike experiment 3, we did not find any nonlearner in experiments 1 and 2; (see Supplementary Figs S2 and S3). This is because the reinforcement-based task is more difficult. Here, participants were required to find the correct movements based on binary feedback signaling only “success” or “failure” in the absence of any vector error feedback. In other words, in experiment 3, unlike the other two experiments, subjects have no cursor to track and thus no information of the magnitude and direction of errors. Importantly, the fact that the invisible success range, but not the visible target, gradually shifted across trials was not intuitive for naïve participants. Nonetheless, it remains unclear why some subjects in experiment 3 could not learn the task using the binary feedback. A recent study suggested that a balance of two sources of movement variability, exploration variability and motor noise, are keys to optimize reinforcement forms of learning (Therrien et al. 2016). In particular, exploration variability, defined as the one subjects have full awareness, is thought to help update estimates of correct movements as a function of binary feedback of performance outcome. Motor noise, on the other hand, is defined as variability of which subjects are unaware. Based on this model, we could speculate that the subjects in the nonlearner group might have less exploratory variability, which was suboptimal to learn the reinforcement-based task in the course of predetermined number of trials. Other possibilities remain such as subjects not paying attention or not really caring to learn the task. Future studies will need to address why some people are not able to learn a motor task.

In contrast to the link between reinforcement forms of learning and M1 plasticity, we found cerebellar excitability changes (i.e., reduction of CBI) early on during visuomotor adaptation when error-based forms of learning are greatly engaged. This is consistent with our previous finding in visuomotor and locomotor adaptation paradigms (Jayaram et al. 2011; Schlerf et al. 2012). We interpret this reduction of CBI to be indicative of reduced Purkinje cell activity as described in nonhuman primate investigations (Medina and Lisberger 2008). This research has shown that cerebellar-dependent motor learning is linked to a depression of parallel fiber/Purkinje cell synaptic activity (Ito 2002), triggered by climbing fiber inputs signaled when movements are inaccurate or erroneous (Simpson et al. 1996; De Zeeuw et al. 1998; Kitazawa et al. 1998). Thus, if Purkinje cell activity is reduced due to the learning, then a conditioning TMS pulse over the cerebellum of the same intensity as baseline will engage only partially the cerebello-dentato-thalamo-cortical pathway releasing inhibition of M1 activity triggered by a subsequent test pulse (Celnik 2015).

Interestingly, although the short group and the subjects that learned in experiment 3 acquired a similar amount of angular deviation in reaching, we found less forgetting (i.e., greater memory retention) in the learner group of experiment 3. Note that this group learned the new reaching patterns mainly via reinforcement. This result is consistent with previous behavioral findings which showed that training motor skills or adaptive motor tasks under explicit positive reinforcement feedback (i.e., rewarding) impact the strength of the memory trace and facilitate retention of learned movements (Abe et al. 2011; Shmuelof et al. 2012; Galea et al. 2015; Therrien et al. 2016). Our finding also implies that motor memories acquired through different amount of contributions between reinforcement and error-based mechanisms would be represented by differently weighed neuronal networks (Debas et al. 2010). Nevertheless, when comparing retention across these experiments it is important to consider that the nature of the tasks is different across experiments 1–2 and 3. For example, given that the number of targets and trials are different across the experimental tasks, subjects had to deal with different challenges to arrive to similar motor commands. In other words, although the ultimate kinematics executed were comparable across experiments, it is possible that participants learned slightly different challenges such as to counteract potential interference across target directions, reduce motor noise related to multiple targets, different number of trials leading to different fatigue states, etc. These distinguishing features across tasks might engage slightly different neuronal substrates and might also affect the magnitude of memory retention across experiments.

Although our findings indicate a relationship between each form of learning and a specific neural substrate, it is likely that other brain regions not tested here are also involved in these forms of learning. For instance, human imaging studies have shown that both learning via reinforcement as well as via error-based mechanisms are associated with functional connectivity changes between sensorimotor regions in cerebral cortex and subcortical structures including the cerebellum and the basal ganglia (Vahdat et al. 2011; Sidarta et al. 2016). Thus, our results demonstrate clear dissociable plasticity changes in a subset of the neural substrates likely relevant to the two different forms of learning. In addition, it should be noted that our findings do not exclude that other forms of learning (c.f., cognitive strategy and use-dependent mechanism), not tested in the present study, are involved when learning our motor tasks.

The purpose of this study was to understand whether learning results in LTP-like plasticity changes as probed by occlusion of anodal tDCS effects. To this end, we screened out non-responders to AtDCS effects at baseline, prior to training. Therefore, we could not verify whether participants not responding to AtDCS show a reduced or abnormal capacity to learn motor tasks that rely on reinforcement mechanisms. This provocative concept that stems out from our current results could be investigated in future studies.

In conclusion, our study shows a double dissociation where learning actions via reinforcement processes leads to LTP-like plasticity changes in M1 but not cerebellar excitability changes; while learning a similar kinematic direction via error-based mechanisms results in cerebellar excitability changes but not M1 LTP-like plasticity. This indicates that learning complex motor behavior appears to rely on the interplay of different forms of learning, weighting distinct neural mechanisms in M1 and the cerebellum. The results provide insights for designing effective interventions using noninvasive brain stimulations to enhance human motor function in healthy people and patients with neurological diseases.

Authors' Contribution

S.U., F.M., and P.C. designed research; S.U. performed research; S.U. and F.M. analyzed data; S.U., F.M., and P.C. wrote the paper.

Funding

National Institute of Health (Grant RO1 HD073147), JSPS KAKENHI (Grant-in-Aid for JSPS fellows, 25–4917) and JSPS Overseas Research Fellowships to S.U. and the Rothschild Fellowship of Yad Hanadiv Foundation to F.M.