Abstract
Spatial attention is thought to be the “glue” that binds features together (e.g., Treisman & Gelade, 1980)—but attention is dynamic, constantly moving across multiple goals and locations. For example, when a person moves their eyes, visual inputs that are coded relative to the eyes (retinotopic) must be rapidly updated to maintain stable world-centered (spatiotopic) representations. Here we examined how dynamic updating of spatial attention after a saccadic eye movement impacts object-feature binding. Immediately after a saccade, participants were simultaneously presented with four colored and oriented bars—one at a precued spatiotopic target location—and instructed to reproduce both the color and orientation of the target item. Object-feature binding was assessed by applying probabilistic mixture models to the joint distribution of feature errors: feature reports for the target item could be correlated (and thus bound together) or independent. We found that compared to holding attention without an eye movement, attentional updating after an eye movement produced more independent errors, including illusory conjunctions—in which one feature of the item at the spatiotopic target location was mis-bound with the other feature of the item at the initial retinotopic location. These findings suggest that even when only one spatiotopic location is task-relevant, spatial attention—and thus object-feature binding—is malleable across and after eye movements, heightening the challenge that eye movements pose for the binding problem and for visual stability.
“Where’s my coffee mug? Did I grab the right set of keys? One, two, three kids, all here!” Object recognition is a crucial part of everyday life, yet visual objects are each composed of multiple visual features (e.g., color, shape, texture) that must be processed and integrated together into a cohesive object-level representation (i.e., “the binding problem”; Treisman, 1996). The crux of Anne Treisman’s Feature Integration Theory (Treisman & Gelade, 1980) is that spatial attention serves as the “glue” that binds features together. The idea is that features falling within the same spatial window of attention are grouped together into an integrated object (e.g., Duncan, 1984; O’Craven, Downing & Kanwisher, 1999; Schoenfeld et al., 2003). Consequently, conditions of limited attention can lead to failures of object-feature binding (i.e., binding between multiple feature dimensions), as evidenced by “illusory conjunctions”, such as viewing a green square and a red circle, but reporting a green circle (Treisman & Schmidt, 1982; see also Wolfe & Cave, 1999). The strong consensus is that the ability to maintain a precise spatial focus of attention is critical for preserving object integrity (Nissen, 1985; Reynolds & Desimone, 1999; Pertzov & Husain, 2013; Schneegans & Bays, 2017; Treisman & Gelade, 1980).
Visual attention, however, is rarely singular or static. In the real world, multiple objects with multiple features are simultaneously present in the environment, and attention is constantly moving across multiple goals and locations. Previous work has demonstrated striking errors of binding under dynamic conditions of spatial attention (Dowd & Golomb, 2019; Golomb, L’Heureux, & Kanwisher, 2014; Golomb, 2015). In one set of studies (Golomb et al., 2014), participants were presented with an array of simple, single-feature objects (i.e., colored squares) and were asked to reproduce the color of a target item (i.e., continuous-report paradigm; Wilken & Ma, 2004). Covert spatial attention was cued to shift from one location to another, to split across two locations simultaneously, or to hold stable across an eye movement. Probabilistic mixture modeling (e.g., Bays, Catalao, & Husain, 2009; Zhang & Luck, 2008) found that shifting attention produced more “swap errors” (i.e., misreporting a non-target color; see Bays, 2016), while splitting attention resulted in a blending between the two attended colors. Intriguingly, holding covert attention across an eye movement produced both types of errors, discussed below. More recently, we extended this paradigm to probe multi-feature objects, using a joint continuous-report (i.e., reproduce both the color and orientation of a target) and joint probabilistic modeling to fit responses from multiple feature dimensions simultaneously (Dowd & Golomb, 2019; see also Bays, Wu, & Husain, 2011). We found that splitting attention across multiple locations degraded object integrity (e.g., reporting the color of the target but an incorrect orientation), while rapid shifts of spatial attention maintained bound objects, even when reporting the wrong object altogether (e.g., reporting both the color and the orientation of the swapped object).
In the current study, we focus on a special case of dynamic attention: saccadic eye movements. Eye movements pose a unique challenge to visual stability because visual inputs are coded relative to the eyes, in “retinotopic” coordinates, which are constantly moving—yet we perceive and act upon stable world-centered “spatiotopic” representations. Thus, retinotopic information must be rapidly updated with each eye movement. It has been suggested that neurons may “remap” their receptive fields in anticipation of a saccade (Duhamel, Colby, & Goldberg, 1992), and spatial attention can also shift predictively to a remapped location (Rolfs, Jonikaitis, Deubel, & Cavanagh, 2011). However, remapping of spatial attention may not be as rapid or efficient as it seems. In addition to “turning on” the new location, there seems to be a second stage of “turning off” the previous location: For a brief window of time after each eye movement, spatial attention temporarily lingers at the previous retinotopic location (the “retinotopic attentional trace”; Golomb, Nguyen-Phuc, Mazer, McCarthy, & Chun, 2010; Talsma, White, Mathôt, Munoz, & Theeuwes, 2013) before updating to the correct spatiotopic location (e.g., Golomb, Chun, & Mazer, 2008; Mathôt & Theeuwes, 2010; see also Jonikaitis, Szinte, Rolfs, & Cavanagh, 2013). The idea is that attention can be allocated to a new retinotopic location before it disengages from the previous retinotopic location, resulting in a transient period in which both locations are simultaneously attended (Golomb, Marino, Chun, & Mazer, 2011; see also Khayat, Spekreijse, & Roelfsema, 2006).
Like dynamic shifts and splits of covert spatial attention, dynamic remapping of spatial attention across saccades also induces errors of feature perception: Golomb and colleagues (2014) included a condition where participants were instructed to reproduce the color of an item appearing at a spatiotopic target location at different delays after a saccade; the target location was cued before the saccade, so that the retinotopic coordinates needed to be remapped with the saccade. Critically, a different non-target color was simultaneously presented at the retinotopic trace location. When the color array was presented at a short delay following the saccade (50 ms), there were two distinct types of errors: On some trials, participants made swap errors and misreported the color of the retinotopic distractor instead of the target—as if spatial attention was stuck at the pre-saccadic retinotopic location instead of updating to the spatiotopic location. More intriguingly, on other trials, color reports were systematically shifted toward the color of the retinotopic distractor (similar to the blending seen in the Split Attention condition of the same study), consistent with the premise that spatial attention was temporarily split between the two locations during remapping. Importantly, at longer post-saccadic delays (500 ms), subjects accurately reported the spatiotopic color. Together, these results suggest that that even incidental and residual spatial attention after an eye movement (i.e., the retinotopic trace) is sufficient to distort feature representations. How then does dynamic remapping of spatial attention impact visual object integrity?
Here, we examine object-feature binding during the crucial post-saccadic period of dynamic attentional remapping. As in Dowd and Golomb (2019), we asked participants to reproduce multiple features at a target location, allowing us to assess object-feature binding by modeling responses from multiple feature dimensions simultaneously (see also Bays et al., 2011). However, while our previous paper manipulated dynamic spatial attention by cueing different spatial locations while the eyes remained fixated, the current study examines dynamic remapping of attention induced by a saccadic eye movement—comparing performance at different delays after a saccade to performance with no saccade at all. In other words, we combined the saccadic remapping manipulation of Golomb and colleagues (2014) with the multi-feature design of Dowd & Golomb (2019). We predicted that if attentional remapping results in a transient splitting of spatial attention across the spatiotopic target location and the retinotopic trace location, object integrity should degrade during this period. However, when spatial attention does not need to remap (i.e., no saccade) or has completely updated after a saccade, object integrity should be maintained. Evidence for transient “un-binding” of visual objects would imply that spatial attention—and thus object-feature binding—is malleable across and after eye movements, heightening the challenge of visual stability.
Method
Our participant recruitment techniques, target sample size, exclusion rules, stimuli, task design and procedure, and statistical models and analyses were pre-registered on the Open Science Framework (http://osf.io/y495a) prior to data collection.
Participants
Data from 25 participants (ages 18 to 34; 17 female) from The Ohio State University were included in the final analyses, according to our pre-registered power analyses. Pre-registered exclusion criteria required that each participant complete at least 10 blocks (320 trials) across two 1-hour experimental sessions. Pre-registered exclusion criteria also required that each participant’s pTCTO parameter estimate (as explained below) be greater than 0.5, as an indication that they were performing the task correctly, but no subject’s data were excluded for this reason. However, there was one more volunteer whose data resulted in pTCTO > 0.5, but their associated estimates of feature precision (σ) were > 2.5 standard deviations from all other participants—indicating poor performance and making it difficult to interpret the other model parameters for this subject. (In the current model, pTCTO is directly impacted by precision, such that an extremely large σ parameter may inflate estimates of pTCTO.) Thus, we also excluded the data from this volunteer; this exclusion criterion was not pre-registered. All participants reported normal or corrected-to-normal visual acuity and color vision, received course credit or $10/hour, and provided informed consent in accordance with The Ohio State University institutional review board.
Stimuli & Procedure
Stimuli were presented on a 21-inch flatscreen ViewSonic Graphic Series G225f CRT monitor with a refresh rate of 85 Hz and screen resolution of 1280 × 1024 pixels, using Matlab and the Psychophysics Toolbox extensions (Kleiner, Brainard, & Pelli, 2007). Subjects were positioned with a chinrest approximately 60 cm from the monitor in a dimly lit room. Eye position was monitored with a desktop-mounted EyeLink 1000 eye-tracking system and the Eyelink Toolbox (Cornelissen, Peters, & Palmer, 2002), which were calibrated using a nine-point grid procedure and sampled observers’ left eyes at 500 Hz. No drift corrections were utilized, but participants were recalibrated between blocks as needed. The monitor was color-calibrated with a Minolta CS-100 colorimeter.
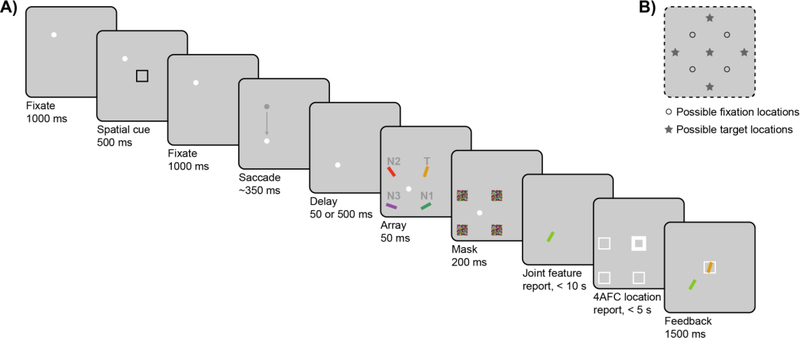
Figure 1A illustrates an example trial sequence. Each trial began with the presentation of a white fixation dot (diameter of 0.6°) presented at one of four locations on the screen (the corners of an imaginary 10.5° × 10.5° square, Figure 1B). Once participants had accurately fixated for 1,000 ms, as determined by real-time eye-tracking, the trial continued as follows:
Figure 1.
(A) Example trial sequence for a Saccade trial. Participants were cued to covertly attend to a spatial pre-cue and reproduce both the color and orientation (i.e., joint continuous-report) of whichever stimulus subsequently appeared at that cued (spatiotopic) location. On No-Saccade trials, participants maintained fixation at a single location across the trial. On Saccade trials, the fixation dot moved to a new location prior to stimulus presentation, and participants had to accurately make a saccade to the new fixation location. The array appeared at either 50 ms or 500 ms after completion of the saccade, followed by a mask array. For the joint-feature report, participants adjusted a probe bar presented at fixation to match the color and orientation of the target item. After the joint-feature report, participants additionally reported the location of the target item. In this example, the target item is the upper-right yellow bar, marked “T”, and the critical N1 non-target is the lower-right green bar, marked “N1”. On Saccade trials, the critical N1 non-target appears at the same retinotopic location as the initial spatial cue, i.e., relative to fixation. Gray labels shown in the example are illustrative only and were not displayed during the actual task. (B) In this task, there were four possible fixation locations (open circles) and five possible target locations (gray stars).
A single spatial black cue (black 4° × 4° square outline, stroke width = 0.1°) was presented (7.4° eccentricity from fixation) for 500 ms. Participants were instructed to covertly attend to the cued location. After another 1,000-ms fixation period, on half of the trials, the fixation dot jumped to a horizontally or vertical adjacent position. On these Saccade trials, subjects had to immediately move their eyes to the new location. On the other half of trials (No-Saccade trials), the fixation dot remained at the original location, and subjects held fixation for a similar amount of time based on average saccadic latency from a previous experiment (350 ms, Golomb et al., 2014; see also Supplement S3). Both the location of the cue (five possible locations on the screen, Figure 1B) and the presence and direction of the saccade were randomized.
After a delay of either 50 ms or 500 ms1 from the time of successful saccade completion (as determined by real-time eye-tracking), an array of four colored and oriented bars (0.75° × 4°) appeared at equidistant locations around fixation (7.4° eccentricity) for 50 ms. One of these stimuli appeared at the same spatiotopic (absolute) location of the cue—this was the “target” (T) that subjects were supposed to report. On Saccade trials, another stimulus occupied the same retinotopic location (relative to the eyes) as the cue—this was the critical non-target (N1). The other adjacent non-target (N2) and the diagonal non-target (N3) were considered control items. In No-Saccade trials, the cued location was both spatiotopic and retinotopic, so “N1” and “N2” were arbitrarily assigned to the stimuli adjacent to the target.
The color of the target item was chosen randomly on each trial from 180 possible colors, which were evenly distributed along a 360° circle in CIE L*a*b* coordinates with constant luminance (L* = 70, center at a* = 20, b* = 38, and radius 60; Zhang & Luck, 2008). The colors of the remaining stimuli were chosen so that the adjacent items (N1 and N2) were equidistant in opposite directions (90° clockwise or counterclockwise deviation along the color wheel, with direction randomly varying from trial to trial), and the item at the diagonal location (N3) was set 180° away in color space. The orientation of the target item was also chosen randomly on each trial from a range of angles 0°–180°, and N1 and N2 were likewise equidistant in opposite directions (45° clockwise or counterclockwise deviation), with N3 set 90° away. Feature values for color and orientation were set independently, as was the direction of deviation for each feature. The stimulus array was followed by 200 ms of masks (squares colored with a random color value at each pixel location, covering each of the four stimulus locations).
Participants then made a joint continuous-report response, reporting the color and orientation of the target item. A single probe bar with random initial values for color and orientation was presented at fixation (i.e., the second fixation location in Saccade trials). Participants were instructed to adjust the color and orientation of the probe item to match the features of the target. The probe’s features were adjusted using two sets of adjacent keys on either side of same keyboard: [z] and [x] (left-color) and [,<] and [.>] (right-orientation). Pressing down on one set of keys caused the probe to rotate through the 180° range of possible orientations (steps of 1°; [.>] clockwise, [,<] counterclockwise); pressing down on the other set of keys caused the probe’s color to cycle through the 360° space of possible colors (steps of 2°; [x] clockwise, [z] counterclockwise). Participants could adjust the two features in any order. To input their response, participants pressed the space bar. Accuracy was stressed, and there was a time limit of 10 s.
Then participants also made a 4-alternative-forced-choice location response: Four location placeholders (white 4° × 4° square outlines, stroke width = 0.1°) were displayed at the four stimulus locations around fixation. Pressing the right-hand set of keys rotated through each location and bolded the placeholder (stroke width = 0.3°). Participants were instructed to select the cued (spatiotopic) location and input their response by pressing the space bar, with a time limit of 5 s.
At the end of the trial, participants were shown feedback for 1,500 ms: The reported color-orientation response was shown at fixation, and the actual target item was displayed in its original location. The reported location was displayed as a white outline on the same screen.
At any point in the trial, if the subject’s eye position deviated more than 2° from the correct fixation location, or if saccadic latency was greater than 600 ms, the trial was immediately aborted and repeated later in the block. All participants completed 10–16 blocks (as time permitted) of 32 intermixed 2 × 2 (Saccade vs. No-Saccade, Early vs. Later) trials, resulting in 80–128 trials of each saccade-delay condition, across two separate experimental sessions. Only the first session began with fixation training and practice trials (6 No-Saccade, 12 Saccade). Trials were discarded if subjects made no color and no orientation adjustments before inputting their response (< 0.1%). For No-Saccade trials, the delay manipulation should have, in practice, made no difference; with no saccade being triggered, the array simply appeared 1,400 ms or 1,850 ms after the offset of the spatial cue. Indeed, there was no statistically significant difference in pTCTO (as explained below) when No-Saccade-Early and No-Saccade-Later trials were analyzed separately. Thus, No-Saccade trials were collapsed across Early and Later delays and analyzed as a single condition for all subsequent analyses.
Joint-Feature Analyses
On each trial, response error was calculated as the angular deviation between the continuous probe report and the cued target item, for each feature separately (θC = color error, range −180° to 180°; θO = orientation error, range −90° to 90°). For Saccade trials, although the direction of N1 varied randomly in relation to T (clockwise or counterclockwise in terms of color or orientation space), we aligned the responses on each trial so that errors toward the N1 feature were always coded as positive deviations (+90° or +45°), and errors toward N2 as negative deviations (–90° or −45°).
To quantify the amount of object-feature binding, we adopted the same mixture modeling approach as in Dowd and Golomb (2019; as based on Bays et al., 2009; Bays et al., 2011; Golomb et al., 2014; Zhang & Luck, 2008). Within each single feature dimension, responses could be attributed to either reporting the target (T, a von Mises distribution centered on the target feature value), misreporting the critical retinotopic non-target (N1, a von Mises distribution centered on the N1 feature value), or random guessing (U, a uniform distribution across all feature values). Our focus here was on dynamic remapping of spatial attention from the retinotopic N1 location to the spatiotopic T location; thus, because responses to N2 and N3 were theoretically less relevant, our model of interest does not specify separate distributions centered on those items. In this model, what few responses do occur to N2 and N3 would be absorbed by U (see Supplement S1 for additional information and an alternative model incorporating all of these parameters).
Critically, we modeled color and orientation as joint probability distributions, fitting responses from both feature dimensions simultaneously (Bays et al., 2011; Dowd & Golomb, 2019). In the Simple Joint Model, we modeled the three types of feature reports described above (T, N1, and U) for each dimension, resulting in 9 response combinations of color (3) and orientation (3), plus 4 parameters for the concentrations κC and κO () and means μC and μO of the target. The joint distribution of responses was thus modeled as:
where θC and θO are the reported feature errors, and m is the number of joint color-orientation response combinations, with mSimple = 1:9. αm is the probability of each response combination, and pm represents the joint probability density distribution for that combination. Table 1 lists each of the nine combinations and associated probability density functions. For example, the joint probability distribution of reporting the target color and the N1 non-target orientation would be pTCN1O = .
Table 1.
Simple Joint Model response distributions combined across both non-spatial feature dimensions
| Response type | mSimple | Response combination | Joint probability density | |
|---|---|---|---|---|
| Correlated | Correlated target | 1 | TCTO | |
| Correlated swap | 2 | N1CN1O | ||
| Independent | Illusory conjunction | 3 | TCN1O | |
| 4 | N1CTO | |||
| Unbound target | 5 | TCUO | ||
| Unbound nontarget | 6 | UCTO | ||
| 7 | N1CUO | |||
| 8 | UCN1O | |||
| Random guessing | 9 | UCUO | γCγO | |
Note. For the current experiment, the Simple Model was restricted to the spatiotopic T and critical retinotopic N1 items, given our theoretical focus on remapping spatial attention.
Joint-feature response distributions were fit using Markov chain Monte Carlo (MCMC), as implemented through custom Matlab scripts (available on Open Science Framework) using the MemToolbox (Suchow, Brady, Fougnie, & Alvarez, 2013) on the Ohio Supercomputer Center (Ohio Supercomputer Center, 1987). The MCMC procedure sampled three parallel chains across as many iterations as necessary to achieve convergence, according to the method of Gelman and Rubin (1992). We collected 15,000 post-convergence samples and used the posterior distributions to compute the maximum-likelihood estimates of each parameter, as well as its 95% highest posterior density interval (HDI). For our primary analyses using the Simple Model, we adopted a standard within-subject analytical approach: Parameter estimates were obtained separately for each individual subject and each trial type, then evaluated with frequentist significance testing. Post-hoc tests were evaluated with the appropriate Bonferroni-correction for multiple comparisons. As a supplementary analysis, we also fit the data using a Full Joint Model, which includes mixtures of T, N1, N2, N3, and U; more details can be found in the Supplement.
Results
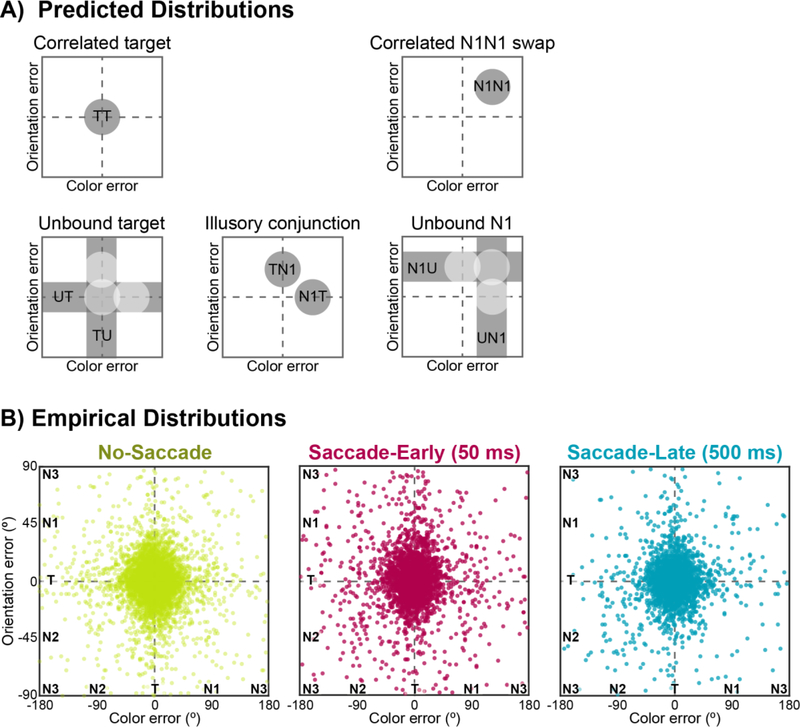
By probing both color and orientation on each trial, we examined whether errors in recalling multiple features of the same object were correlated (and thus bound together) or independent (and unbound) immediately after an eye movement. Figure 2 visualizes the joint distribution of responses by plotting individual trials in joint-feature space, where the vertical and horizontal axes correspond to the color and orientation errors, respectively.
Figure 2.
Visualizations of color-orientation reports in joint-feature space, plotted as error relative to actual target feature values: color responses are shown along the x-axis, and orientation responses are shown along the y-axis. For visualization purposes, we have flattened joint-feature space; both feature dimensions are in fact circular, such that +180° is identical to – 180° in color space. The schematics in (A) show predicted distributions for possible response types, with correlated responses on the top row and independent responses on the bottom row. The scatterplots in (B) plot trial-by-trial empirical error distributions separately for No-Saccade, Saccade-Early, and Saccade-Late trials. Each dot represents the corresponding color and orientation response for a single trial, aggregating across subjects.
“Object integrity” was inferred from contrasting correlated responses (i.e., reporting both the color and orientation of the same item) with independent responses (i.e., reporting only one feature of an item) (see Table 1 and Figure 2A for predicted distributions). Correlated target responses thus refer to reporting both features of the correct target item (TCTO), which would be represented as a two-dimensional Gaussian density centered on the origin (0° error). Correlated N1CN1O “swap” errors refer to misreporting both features of the retinotopic N1 distractor, which would be represented as a two-dimensional Gaussian density on the positive-slope diagonal of joint-feature space. Failures in object-feature binding, on the other hand, would result in independent responses, such as reporting the color of an item without also reporting the orientation of the same item. Independent errors could be due to reporting only one feature of the target and guessing the other (unbound target; e.g., TCUO); reporting only one feature of the N1 non-target and guessing the other (unbound N1; e.g., N1CUO); or mis-binding the features of the target and the N1 non-target (illusory conjunction; e.g., TCN1O). For instance, in joint-feature space, independent target errors are represented as a distribution of responses along the horizontal or vertical axes of joint-feature space (i.e., centered on zero error in one dimension but not the other; Figure 2A).
Figure 2B presents scatterplots of the empirical data, collapsed across all participants, for No-Saccade, Saccade-Early, and Saccade-Later trials. We quantified the different response types with joint-feature probabilistic models, and the corresponding parameter estimates from the Simple Model are summarized in Table 2 and Figure 3.
Table 2.
Simple Joint Model Parameter Estimates (N = 25)
| No Saccade | Saccade - 50 ms Delay | Saccade - 500 ms Delay | |
|---|---|---|---|
| pTCTO | .864 (.131) | .802 (.164) | .864 (.117) |
| pN1CN1O | .005 (.007) | .005 (.006) | .006 (.008) |
| pTCN1O | .013 (.018) | .017 (.018) | .013 (.017) |
| pN1CTO | .013 (.012) | .014 (.012) | .007 (.007) |
| pTCUO | .020 (.024) | .027 (.041) | .019 (.025) |
| pUCTO | .022 (.036) | .030 (.052) | .025 (.025) |
| pN1CUO | .005 (.008) | .010 (.013) | .008 (.013) |
| pUCN1O | .005 (.008) | .012 (.020) | .004 (.004) |
| pUCUO | .053 (.063) | .082 (.107) | .053 (.071) |
| μC | 1.00 (5.55) | 0.16 (6.23) | 1.20 (6.75) |
| μO | 0.17 (2.05) | −0.01 (3.04) | 0.34 (3.15) |
| σC | 21.90 (6.37) | 24.35 (11.55) | 21.20 (7.20) |
| σO | 13.03 (2.78) | 14.84 (4.79) | 13.11 (4.82) |
Group means, with standard deviations presented in parentheses. μC and σC range from −180° to +180°, while μO and σO range from −90° to +90° ()
Figure 3.
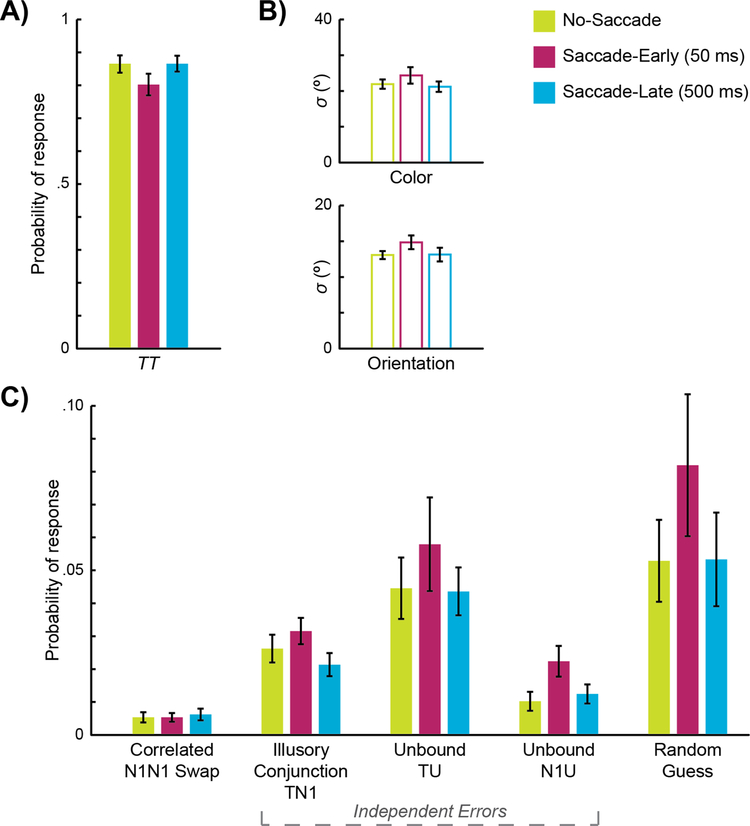
Simple Joint Model maximum-likelihood parameter estimates. The graphs in (A) present group means of best-fit estimates for the probability of correlated target responses (TCTO) and in (B) the standard deviations of the TCTO distribution for color (σC) and orientation (σO) for each condition. The graphs in (C) present the proportion of erroneous responses (i.e., non-TCTO) that can be attributed to correlated N1CN1O swaps; different types of independent errors: illusory conjunctions (e.g., TCN1O), unbound targets (e.g., TCUO), and unbound non-targets (e.g., N1CUO); and random guesses. Error bars represent standard errors.
Joint-Modeling Results
Across all conditions, the vast majority of responses were attributed to reporting both features of the correct target item (correlated target responses), as reflected in the scatterplots as a central density of responses at the origin (Figure 2B) and the overall high proportion of TCTO responses in Figure 3A. Critically, as predicted, the saccade manipulation degraded performance. Presenting the array 50 ms after a saccade resulted in greater feature errors, with a significantly lower probability of correlated target responses (TCTO) in Saccade-Early trials compared to No-Saccade trials, t(24) = 3.48, p = .002, d = 0.70. However, when the array was presented 500 ms after a saccade, performance rebounded, with significantly greater correlated target responses in Saccade-Late trials compared to Saccade-Early trials, t(24) = 3.60, p = .001, d = 0.72, and no difference between Saccade-Late and No-Saccade trials, t(24) = 0.02, p = .987, d < 0.01 (Figure 3A). The standard deviations of both color (σC) and orientation (σO) responses were also greater for Saccade-Early trials than the other conditions (Figure 3B; see Table 3 for all comparisons), indicating less precise feature reports when spatial attention was still updating immediately after a saccade. The performance drop for Saccade-Early trials was not simply because the task was too hard; random guessing (i.e., UCUO) was only marginally significantly different across conditions, F(2, 48) = 2.79, p = .071, n2 = .03. While there are a number of factors that could contribute to an increase in random guessing or a decrease in precision immediately after a saccade, including increased task difficulty, noisy encoding, and/or attentional resources at the saccade landing point (e.g., Schneider, 2013), a benefit of our joint-feature model is that we can explore specific types of feature-binding errors on top of these more general performance indicators.
Table 3.
Summary of Comparisons for Simple Model Response Types and Parameters
| Test Statistic | Significance | Effect size | ||
|---|---|---|---|---|
| TT | ANOVA: Condition Post-hoc t-tests | F(2, 48) = 10.3 | p < .001* | η2= .301 |
| NoSacc vs. Sacc50 | t(24) = 3.48 | p =.002** | d = 0.70 | |
| NoSacc vs. Sacc500 | t(24) = 0.02 | p = .987 | d < 0.01 | |
| Sacc50 vs. Sacc500 | t(24) = 3.60 | p = .001** | d = 0.72 | |
| All Non-TT Errors | 3×2 ANOVA Condition | F(2, 48) = 5.55 | p = .007* | η2= .018 |
| Error (Correlated vs. Independent) |
F(1, 24) = 40.5 | p < .001* | η2= .508 | |
| Interaction | F(2, 48) = 5.69 | p =.014* | η22 = .018 | |
| Correlated N1N1 | ANOVA: Condition | F(2, 48) = 0.08 | p = .925 | η22 = .003 |
| Independent Errors | ANOVA: Condition Post-hoc t-tests | F(2, 48) = 5.78 | p = .006* | η22 = .194 |
| NoSacc vs. Sacc50 | t(24) = 2.77 | p = .011** | d = 0.55 | |
| NoSacc vs. Sacc500 | t(24) = 0.22 | p = .831 | d = .04 | |
| Sacc50 vs. Sacc500 | t(24) = 2.46 | p = .021* | d = 0.49 | |
| Independent Errors | 3×2 ANOVA Condition | F(2, 48) = 5.78 | p = .006* | η22 = .031 |
| Error (f, Unbound T, Unbound N1) | F(2, 48) = 12.6 | p < .001* | η22 = .215 | |
| Interaction | F(4, 96) = 0.48 | p = .754 | η22 = .004 | |
| Illusory TN1 | ANOVA: Condition | F(2, 48) = 2.54 | p = .090 | η22 = .096 |
| Unbound T | ANOVA: Condition | F(2, 48) = 2.06 | p = .139 | η22 = .079 |
| Unbound N1 | ANOVA: Condition Post-hoc t-tests | F(2, 48) = 4.23 | p = .020* | η22 = .150 |
| NoSacc vs. Sacc50 | t(24) = 2.30 | p = .031* | d = 0.46 | |
| NoSacc vs. Sacc500 | t(24) = 0.72 | p = .478 | d = .14 | |
| Sacc50 vs. Sacc500 | t(24) = 2.17 | p = .040* | d = 0.44 | |
| UU | ANOVA: Condition | F(2, 48) = 2.79 | p = .071 | η22 = .104 |
| σC | ANOVA: Condition Post-hoc t-tests | F(2, 48) = 5.06 | p =.010* | η22 = .174 |
| NoSacc vs. Sacc50 | t(24) = 2.04 | p = .052 | d = 0.41 | |
| NoSacc vs. Sacc500 | t(24) = 1.13 | p = .268 | d = 0.23 | |
| Sacc50 vs. Sacc500 | t(24) = 2.64 | p =.014** | d = 0.53 | |
| σO | ANOVA: Condition Post-hoc t-tests | F(2, 48) = 3.38 | p = .042* | η22 = .124 |
| NoSacc vs. Sacc50 | t(24) = 2.58 | p = .017** | d = 0.52 | |
| NoSacc vs. Sacc500 | t(24) = 0.09 | p = .931 | d = 0.02 | |
| Sacc50 vs. Sacc500 | t(24) = 2.38 | p = .026* | d = 0.48 | |
| μC | ANOVA: Condition One-sample t-tests | F(2, 48) = 0.99 | p = .381 | η22 = .039 |
| NoSacc vs. 0 | t(24) = 0.90 | p = .378 | d = 0.18 | |
| Sacc50 vs. 0 | t(24) = 0.12 | p = .902 | d = 0.02 | |
| Sacc500 vs. 0 | t(24) = 0.89 | p = .384 | d = 0.18 | |
| μO | ANOVA: Condition One-sample t-tests | F(2, 48) = 0.30 | p = .746 | η2= .012 |
| NoSacc vs. 0 | t(24) = 0.41 | p = .686 | d = 0.08 | |
| Sacc50 vs. 0 | t(24) = 0.02 | p = .982 | d < 0.01 | |
| Sacc500 vs. 0 | t(24) = 0.55 | p = .587 | d = 0.11 |
denotes statistical significance at p < .05
denotes statistical significance at p < .017 (Bonferroni-corrected for multiple post-hoc comparisons) Post-hoc t-tests reported only for significant main effects.
Our critical question was, what types of binding errors occur when spatial attention is dynamically updating immediately after a saccade? One hypothesis is that remapping is simply a single-stage process of shifting attention that occurs with variable latency (such that on some trials, attention has already updated to the spatiotopic (T) location, and on others, it is still stuck at the initial retinotopic (N1) location)—which should primarily produce greater correlated N1CN1O swap errors in Saccade-Early trials, similar to the Shift condition of Dowd and Golomb (2019). However, we hypothesize that remapping instead occurs in two temporally-overlapping stages (see Golomb et al., 2014), such that spatial attention is transiently split across the spatiotopic target (T) location and the retinotopic trace (N1) location immediately after the saccade— which should produce greater independent errors in Saccade-Early trials, similar to the Split condition of Dowd and Golomb (2019).
We first analyzed Simple Model parameter estimates with a broad repeated-measures ANOVA across error type (correlated N1CN1O swaps vs. all independent responses; see Table 1) and condition (No-Saccade, Saccade-Early, Saccade-Late), revealing a significant interaction effect, F(2, 48) = 5.69, p = .006, n2 = .01. Thus, we followed up with two separate repeated-measures ANOVAs across condition, first for correlated N1CN1O swaps, F(2, 48) = 0.08, p = .925, n2 < .01, and then for all independent responses, F(2, 48) = 5.78, p = .006, n2 = .04. As illustrated in Figure 3C, correlated N1CN1O swap errors were overall rare and not significantly different across conditions. However, independent errors were significantly more frequent in Saccade-Early compared to No-Saccade trials, t(24) = 2.77, p = .011, d = 0.55, and marginally more frequent in Saccade-Early compared to Saccade-Late trials, t(24) = 2.46, p = .021, d = 0.49 (compared to Bonferroni-corrected thresholds of p = .017).
To deconstruct further, we then examined whether the Saccade-Early increase in independent errors was attributable to increased illusory conjunctions (e.g., TCN1O), unbound targets (e.g., UCTO), and/or unbound non-targets (e.g., N1CUO). Previous single-feature studies demonstrated that in the critical period immediately after a saccade, participants produced more “mixing” errors, or a blending between the spatiotopic target and retinotopic distractor colors (Golomb et al., 2014). Although we found no evidence of mixing within feature-dimensions here (means μC and μO of the target were not different from zero nor different across conditions, ps> .38; see Table 3), illusory conjunctions could potentially be thought of as participants producing mixing across feature-dimensions—such that they “mis-bind” one feature of the target with one feature of the retinotopic distractor (i.e., an illusory conjunction between T and N1). The other types of independent errors can be thought of as “un-binding” (i.e., reporting only one feature of one item). A repeated-measures ANOVA across condition and independent error type (illusory conjunction, unbound target, unbound non-target) revealed a significant main effect of condition, F(2, 48) = 5.78, p = .006, n2 = .02 (identical to the one-way ANOVA from before), and a significant effect of error type, F(2, 48) = 12.6, p < .001, n2 = .14, revealing that across all conditions, unbound targets occurred more often than illusory conjunctions or unbound non-targets. However, there was not a significant interaction effect, F(4, 96) = 0.48, p = .754, n2< .01 (Figure 3C). The lack of an interaction suggests that the increase in independent errors for Saccade-Early trials was not driven more by one sub-type of independent error than the others. Thus, while the pattern of results supports an increase in illusory conjunctions (i.e., mixing across feature-dimensions), increased independent errors immediately after a saccade are not driven by illusory conjunctions alone; instead, the results suggest that dynamic spatial remapping after a saccade leads to a breakdown of object-feature binding more generally.
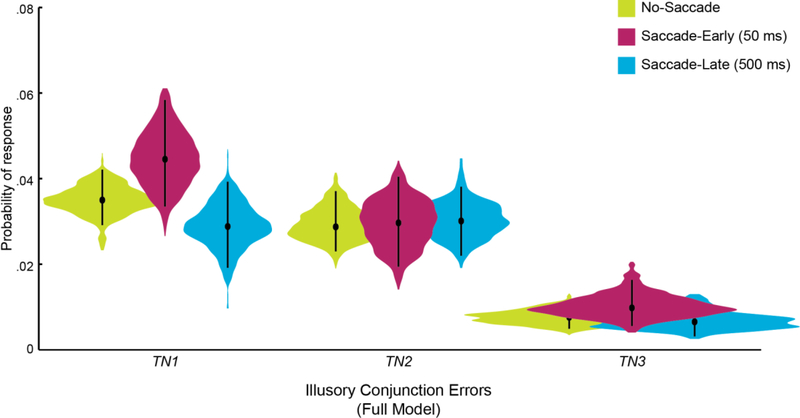
The Simple Model used to generate the results above assumes that independent errors stem from reporting a single feature from the target or the retinotopic N1 non-target. Given our theoretical focus on remapping spatial attention across these two critical locations, illusory conjunctions were defined in the Simple Model as binding between spatiotopic T and retinotopic N1 items specifically (e.g., TCN1O). But were illusory conjunctions between T and the retinotopic N1 distractor actually more likely than between T and the control N2 distractor? To confirm that the retinotopic N1 location was indeed the critical non-target that triggered illusory conjunctions, we used the supplemental Full Model parameter fits to compare across combinations of T with all of the non-target items (e.g., TCN1O, TCN2O, TCN3O). For Saccade-Early trials, participants were numerically more likely to report illusory conjunctions between T and N1 items (pTCN1O + pN1CTO = .042, 95% HDI [.031 .056]) than illusory conjunctions between T and N2 items (pTCN2O + pN2CTO = .028 [.017 .038]), with only a slight overlap between their 95% HDIs (Full Model parameter estimates were considered significantly different if their 95% HDIs did not overlaps; Kruschke, 2011). In contrast, in No-Saccade and Saccade-Late trials, the TN1 and TN2 probabilities were nearly equal (Figure 4; HDIs overlap almost entirely).
Figure 4.
Full Joint Model maximum a posteriori estimates for independent target errors suggest that the retinotopic N1 distractor specifically interfered with performance. For each response type (i.e., combinations of T with each non-target, and a uniform distribution), a violin plot illustrates the posterior distribution of each parameter over 15,000 post-convergence samples. The black dots mark each parameter’s best-fit estimate, and the whiskers represent the 95% highest density interval. The Full Model was fit for each condition (upper right legend) separately, collapsed across all subjects. See Supplement S1 for more information.
Discussion
Our perception of visual stability is facilitated by the dynamic remapping of visual information across eye movements (e.g., Duhamel et al., 1992), but this process is not as rapid or efficient as previously thought (e.g., Golomb et al., 2008; 2010; Mathôt & Theeuwes, 2010). Here, we examined how the remapping of spatial attention across saccades impacts visual object integrity.
We tested the hypothesis that for a brief period of time after each eye movement, spatial attention lingers at the previous retinotopic location (e.g., Golomb et al., 2008; 2010), such that attention is transiently split across the correct spatiotopic location and the retinotopic trace location. Previous work has demonstrated that in the absence of eye movements, splitting covert spatial attention across multiple locations degrades object integrity, whereas rapid shifts of spatial attention maintain bound objects (Dowd & Golomb, 2019). In the current pre-registered study, participants were not explicitly attending to two different locations, but rather were told to maintain attention at a single spatiotopic location across a saccade. Nevertheless, we found that immediately after a saccadic eye movement, participants made more erroneous feature reports. It was not simply that participants randomly guessed more (marginal increase in UCUO responses immediately after a saccade), but specifically, participants reported more independent feature errors (i.e., illusory conjunctions, unbound target, and unbound non-target responses)—as if spatial attention were indeed briefly split across multiple locations on some trials.
These failures of object-feature binding after a saccade were both temporally and spatially specific. The increase in independent errors was present only when objects were presented a short interval (50 ms) after each eye movement; performance rebounded when the objects were presented after a longer post-saccadic delay (500 ms), consistent with a short-lived “retinotopic attentional trace” that decays after ~150 ms (Golomb et al., 2008). The errors themselves also seemed to reflect interference from residual attention at another (i.e., the retinotopic trace) location: The increase in independent errors included both un-binding (i.e., reporting only one feature of either the spatiotopic T or retinotopic N1 item; unbound errors) and mis-binding (i.e., associating one feature of the spatiotopic T item with the other feature of the retinotopic N1 item; illusory conjunctions) of features. In the supplementary Full Model analyses, illusory conjunctions were also numerically more likely for the spatiotopic T and retinotopic N1 items than for the spatiotopic T and equidistant control N2 items, supporting the idea of spatial interference by residual retinotopic attention.
One initial hypothesis was that residual retinotopic attention during dynamic remapping would result in an increase in illusory conjunctions between spatiotopic T and retinotopic N1 items. However, we found that that the increase in independent errors immediately after a saccade was not driven by these illusory conjunctions alone. Instead, increased independent errors may have been more reflective of general un-binding, which mimics the pattern found when participants intentionally and covertly split attention between two cued spatial locations (Split vs. Hold conditions of Dowd & Golomb, 2019)—in that study, splitting attention across two locations also resulted in greater independent errors compared to maintaining attention at one location, and this increase was significantly driven by unbound targets rather than illusory conjunctions or unbound non-targets. Taken together, these results suggest that dynamic spatial remapping after a saccade is akin to splitting covert attention in that it leads to a general breakdown of object-feature binding.
These results demonstrate perceptual consequences consistent with a two-stage, or dual-spotlight, model of remapping, in which “turning on” of the new retinotopic location is distinct from “turning off” the previous retinotopic location, allowing for a brief window of time during which both locations are simultaneously attended (e.g., Golomb et al., 2011). Previous studies have demonstrated systematic distortions within a single feature dimension immediately after an eye movement (e.g., reporting the blending of colors at spatiotopic T and retinotopic N1 locations; Golomb et al., 2014). By highlighting the integration of multiple features into objects, the current results provide yet more support that remapping of attention across eye movements results in a temporary splitting of attention across both locations. An alternative single-stage process of remapping would predict that a single focus of spatial attention shifts from one location to another, such that at a given moment, attention is either at the updated (spatiotopic) location or stuck at the initial (retinotopic trace) location. If this were the case, we would expect remapping to involve primarily a shift of attention, which should preserve object integrity in this multi-feature paradigm (as in the exogenously-induced Shift condition of Dowd & Golomb, 2019). In other words, a simple shift of attention would result in a mixture of some trials in which attention had successfully remapped (resulting in correlated target TCTO responses) and some trials in which attention was still at the previous retinotopic location (resulting in correlated N1CN1O swap errors). However, in the current study, there was no increase in correlated N1CN1O swap errors immediately after a saccade. Moreover, if the speed of such a hypothetical remapping-shift was faster than an exogenously-induced shift (i.e., Dowd & Golomb, 2019), then attention should have already finished remapping to the new retinotopic location by the time the array was presented, such that there would be similar rates of correlated TCTO responses immediately and later after a saccade—which was not the case. Another alternative single spotlight (i.e., serial) model might posit that attention shifts rapidly back and forth between the previous retinotopic and new retinotopic locations, with limited attention at either location (cf. Jans, Peters, & De Weerd, 2010), resulting in an increase in independent errors. However, it is unclear how this back-and-forth account would apply to dynamic remapping after a saccade, where there are clear priorities in retinotopic space (i.e., from trace to new). Instead, the increase in independent errors suggests that spatial attention was transiently split across multiple locations, within a single trial, similar to the covert attention Split condition of Dowd & Golomb (2019).
It should be noted that the present study examines “feature integration” in the sense of Treisman’s Feature Integration Theory (Treisman & Gelade, 1980)—the idea that spatial attention serves as the “glue” that binds different features of an object together, when multiple objects are simultaneously present in the visual field. Thus, the goal was to test how dynamic spatial attention induced by a saccade influences object-feature binding, for multi-feature stimuli presented immediately after an eye movement. This is not to be mistaken with transsaccadic feature integration (integrating features presented at different points in time before, during, and after an eye movement; e.g., blending of pre-saccadic and post-saccadic orientation or color; Melcher, 2005; Oostwoud Wijdenes, Marshall, & Bays, 2015). Our question here is not how features are perceptually integrated over time across an eye movement, nor whether an object presented prior to an eye movement preserves its integrity across the saccade (e.g., Hollingworth, Richard, & Luck, 2008; Shafer-Skelton, Kupitz & Golomb, 2017), but rather how the process of attentional remapping across a saccade impacts object-feature binding. Nevertheless, it is interesting to note that previous studies have induced the mis-binding or un-binding of features by breaking transaccadic object correspondence, such that attention might be split between separate pre-saccadic and post-saccadic object representations (Poth, Herwig, & Schneider, 2015). Compare that to the current study, in which mis-binding and un-binding of features arise for objects presented immediately after a saccade, such that attention might be split between separate spatial locations. Here, the process of dynamically remapping attention presents yet another instance of the binding problem (Treisman, 1996; Wolfe & Cave, 1999).
Treisman’s initial concept of linking multiple feature dimensions via spatial attention (Treisman & Gelade, 1980) has been extended into a multitude of studies that argue that spatial location serves as the anchor for object-feature binding (e.g., Nissen, 1985; Pertzov & Husain, 2013; Reynolds & Desimone, 1999; Schneegans & Bays, 2017; Vul & Rich, 2010; see also Schneegans & Bays, 2018). But such space-binding models do not necessarily account for changing spatial reference frames (i.e., retinotopic versus spatiotopic) across eye movements (e.g., Schneegans & Bays, 2017; see also Cavanagh, Hunt, Afraz, & Rolfs, 2010). The current findings demonstrate that even when only one spatiotopic location is task-relevant, dynamic remapping across eye movements can produce, even transiently, multiple foci of attention, and this can result in a breakdown of object integrity. We speculate that this breakdown is a bug rather than a feature of the visual system; i.e., that when our attention is overly taxed, there may be suboptimal consequences for visual perception. The disruption of object-feature binding when attention is remapped and when spatial reference frames are updated thus poses a unique challenge for models of object-feature integration. Nevertheless, the current results also more broadly emphasize the importance of a single locus of spatial attention for intact object integrity (see also Dowd & Golomb, 2019). Overall, these failures of object integrity after eye movements not only underline the importance of spatial attention, but also suggest how vulnerable object perception may be in the real world, when our eyes are constantly moving across multiple objects with multiple features in the environment.
Supplementary Material
Significance.
Visual object perception requires integration of multiple features, and according to Treisman’s Feature Integration Theory, spatial attention is critical for object-feature binding. But attention is dynamic, especially when our eyes are moving. Here, we examined how the updating of spatial attention across saccadic eye movements—and its consequences for how attention is deployed—impacts visual object integrity. Probabilistic mixture modeling revealed more independent errors, including illusory conjunctions, immediately after a saccade. This work has important implications for our understanding of how spatial attention is remapped across eye movements, as well as the broader challenge of object integrity and visual stability.
Open Practices Statement.
The participant recruitment techniques, target sample size, exclusion rules, stimuli, task design and procedure, and statistical models and analyses were pre-registered on the Open Science Framework (http://osf.io/y495a) prior to data collection. Materials are available on OSF at https://osf.io/btsyz/.
Acknowledgements
We thank Alexandra Haeflein, Chris Jones, Robert Murcko, and Samoni Nag for assistance with data collection.
Funding
This study was funded by grants from the National Institutes of Health (R01-EY025648 to J. D. Golomb, F32–028011 to E. W. Dowd) and the Alfred P. Sloan Foundation (to J. D. Golomb).
Footnotes
Publisher's Disclaimer: This Author Accepted Manuscript is a PDF file of a an unedited peer-reviewed manuscript that has been accepted for publication but has not been copyedited or corrected. The official version of record that is published in the journal is kept up to date and so may therefore differ from this version.
Because of the screen refresh rate (85 Hz), actual presentation durations were a few ms shorter. For instance, a 50-ms duration was actually 47 ms, and a 500-ms duration was actually 496 ms. Simulus presentation durations have been rounded up for consistency with previously published experiments (e.g., Golomb et al., 2014; Golomb, 2015; Dowd & Golomb, 2019).
References
- Bays PM (2016). Evaluating and excluding swap errors in analogue tests of working memory Nature Publishing Group, 1–14. 10.1038/srep19203 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bays PM, Catalao RFG, & Husain M (2009). The precision of visual working memory is set by allocation of a shared resource. Journal of Vision, 9(10), 7–7. 10.1167/9.10.7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bays PM, Wu EY, & Husain M (2011). Storage and binding of object features in visual working memory. Neuropsychologia, 49(6), 1622–1631. 10.1016/j.neuropsychologia.2010.12.023 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cavanagh P, Hunt AR, Afraz A, & Rolfs M (2010). Visual stability based on remapping of attention pointers. Trends in Cognitive Sciences, 14(4), 147–153. 10.1016/j.tics.2010.01.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cornelissen FW, Peters EM, & Palmer J (2002). The Eyelink Toolbox: Eye tracking with MATLAB and the Psychophysics Toolbox. Behavior Research Methods, Instruments, & Computers, 34, 613–617. [DOI] [PubMed] [Google Scholar]
- Dowd EW, & Golomb JD (2019). Object-feature binding survives dynamic shifts of spatial attention. Psychological Science. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duhamel JR, Colby CL, & Goldberg ME (1992). The updating of the representation of visual space in parietal cortex by intended eye movements. Science, 255(5040), 90–92. 10.1126/science.1553535 [DOI] [PubMed] [Google Scholar]
- Duncan J (1984). Selective attention and the organization of visual information. Journal of Experimental Psychology: General, 113(4), 501–517. 10.1037/0096-3445.113.4.501 [DOI] [PubMed] [Google Scholar]
- Gelman A, & Rubin DB (1992). Inference from Iterative Simulation Using Multiple Sequences. Statistical Science, 7(4), 457–472. 10.1214/ss/1177011136 [DOI] [Google Scholar]
- Golomb JD (2015). Divided spatial attention and feature-mixing errors. Attention, Perception, & Psychophysics, 77(8), 2562–2569. 10.3758/s13414-015-0951-0 [DOI] [PubMed] [Google Scholar]
- Golomb JD, Chun MM, & Mazer JA (2008). The Native Coordinate System of Spatial Attention Is Retinotopic. Journal of Neuroscience, 28(42), 10654–10662. 10.1523/JNEUROSCI.2525-08.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golomb JD, L’Heureux ZE, & Kanwisher N (2014). Feature-Binding Errors After Eye Movements and Shifts of Attention. Psychological Science, 25(5), 1067–1078. 10.1177/0956797614522068 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golomb JD, Marino AC, Chun MM, & Mazer JA (2011). Attention doesn’t slide: spatiotopic updating after eye movements instantiates a new, discrete attentional locus. Attention, Perception, & Psychophysics, 73(1), 7–14. 10.3758/s13414-010-0016-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golomb JD, Nguyen-Phuc AY, Mazer JA, McCarthy G, & Chun MM (2010). Attentional Facilitation throughout Human Visual Cortex Lingers in Retinotopic Coordinates after Eye Movements. Journal of Neuroscience, 30(31), 10493–10506. 10.1523/JNEUROSCI.1546-10.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hollingworth A, Richard AM, & Luck SJ (2008). Understanding the function of visual short-term memory: Transsaccadic memory, object correspondence, and gaze correction. Journal of Experimental Psychology: General, 137(1), 163–181. 10.1037/0096-3445.137.1.163 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jans B, Peters JC, & De Weerd P (2010). Visual spatial attention to multiple locations at once: The jury is still out. Psychological Review, 117, 637–682. 10.1037/a0019082 [DOI] [PubMed] [Google Scholar]
- Jonikaitis D, Szinte M, Rolfs M, & Cavanagh P (2013). Allocation of attention across saccades. Journal of Neurophysiology, 109(5), 1425–1434. 10.1152/jn.00656.2012 [DOI] [PubMed] [Google Scholar]
- Khayat PS, Spekreijse H, & Roelfsema PR (2006). Attention Lights Up New Object Representations before the Old Ones Fade Away. Journal of Neuroscience, 26(1), 138–142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kleiner M, Brainard D, & Pelli D (2007). What’s new in Psychtoolbox-3? Perception, 36, ECVP Abstract Supplement. [Google Scholar]
- Kruschke JK (2011). Bayesian Assessment of Null Values Via Parameter Estimation and Model Comparison. Perspectives on Psychological Science, 6(3), 299–312. 10.1177/1745691611406925 [DOI] [PubMed] [Google Scholar]
- Mathôt S, & Theeuwes J (2010). Gradual Remapping Results in Early Retinotopic and Late Spatiotopic Inhibition of Return. Psychological Science, 21(12), 1793–1798. 10.1177/0956797610388813 [DOI] [PubMed] [Google Scholar]
- Melcher D (2005). Spatiotopic Transfer of Visual-Form Adaptation across Saccadic Eye Movements. Current Biology, 15(19), 1745–1748. [DOI] [PubMed] [Google Scholar]
- Nissen MJ (1985). Accessing features and objects: Is location special? In Posner MI & Marin OS (Eds.), Attention and Performance XI (pp. 205–219). [Google Scholar]
- O’Craven KM, Downing PE, & Kanwisher N (1999). fMRI evidence for objects as the units of attentional selection. Nature. [DOI] [PubMed] [Google Scholar]
- Oostwoud Wijdenes L, Marshall L, & Bays PM (2015). Evidence for optimal integration of visual feature representations across saccades. Journal of Neuroscience, 35(28), 10146–10153. 10.1523/jneurosci.1040-15.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pertzov Y, & Husain M (2013). The privileged role of location in visual working memory. Attention, Perception, & Psychophysics, 76(7), 1914–1924. 10.3758/s13414-013-0541-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poth CH, Herwig A, & Schneider WX (2015). Breaking object correspondence across saccadic eye movements deteriorates object recognition. Frontiers in System Neurosciences, 9, 176 10.3389/fnsys.2015.00176 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reynolds JH, & Desimone R (1999). The role of neural mechanisms of attention in solving the binding problem. Neuron, 24(1), 19–29. 10.1016/s0896-6273(00)80819-3 [DOI] [PubMed] [Google Scholar]
- Rolfs M, Jonikaitis D, Deubel H, & Cavanagh P (2011). Predictive remapping of attention across eye movements. Nature Neuroscience, 14(2), 252–256. 10.1038/nn.2711 [DOI] [PubMed] [Google Scholar]
- Schneegans S, & Bays PM (2017). Neural architecture for feature binding in visual working memory. Journal of Neuroscience, 37(14), 3913–3925. 10.1523/JNEUROSCI.3493-16.2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneegans S, & Bays PM (2018). New perspectives on binding in visual working memory British Journal of Psychology. Advance online publication. 10.1111/bjop.12345 [DOI] [PubMed] [Google Scholar]
- Schneider WX (2013). Selective visual processing across competition episodes: A theory of task-driven visual attention and working memory. Philosophical Transactions of the Royal Society B: Biological Sciences, 368(1628), 20130060 10.1098/rstb.2013.0060 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schoenfeld MA, & Tempelmann C (2003). Dynamics of feature binding during object-selective attention. Proceedings of the National Academy of Sciences, 100(20), 11806–11811. 10.1073/pnas.1932820100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shafer-Skelton A, Kupitz CN, & Golomb JD (2017). Object-location binding across a saccade: A retinotopic spatial congruency bias. Attention, Perception, & Psychophysics, 79(3), 765–781. 10.3758/s13414-016-1263-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suchow JW, Brady TF, Fougnie D, & Alvarez GA (2013). Modeling visual working memory with the MemToolbox. Journal of Vision, 13(10), 9–9. 10.1167/13.10.9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Talsma D, White BJ, Mathôt S, Munoz DP, & Theeuwes J (2013). A retinotopic attentional trace after saccadic eye movements: Evidence from event-related potentials. Journal of Cognitive Neuroscience, 25(9), 1563–1577. 10.1162/jocn_a_00390 [DOI] [PubMed] [Google Scholar]
- Treisman AM, & Gelade G (1980). A feature-integration theory of attention. Cognitive Psychology, 12(1), 97–136. [DOI] [PubMed] [Google Scholar]
- Treisman A, & Schmidt H (1982). Illusory Conjunctions in the Perception of Objects. Cognitive Psychology, 14, 107–141. 10.1093/acprof:osobl/9780199734337.003.0019 [DOI] [PubMed] [Google Scholar]
- Treisman A (1996). The binding problem. Current Opinion in Neurobiology, 6(2), 171–178. 10.1016/S0959-4388(96)80070-5 [DOI] [PubMed] [Google Scholar]
- Vul E, & Rich AN (2010). Independent Sampling of Features Enables Conscious Perception of Bound Objects. Psychological Science, 21(8), 1168–1175. 10.1177/0956797610377341 [DOI] [PubMed] [Google Scholar]
- Wilken P, & Ma WJ (2004). A detection theory account of change detection. Journal of Vision, 4(12), 1120–1135. 10.1167/4.12.11 [DOI] [PubMed] [Google Scholar]
- Wolfe JM, & Cave KR (1999). The psychophysical evidence for a binding problem in human vision. Neuron, 24(1), 11–17. 10.1016/s0896-6273(00)80818-1 [DOI] [PubMed] [Google Scholar]
- Zhang W, & Luck SJ (2008). Discrete fixed-resolution representations in visual working memory. Nature, 453(7192), 233–235. 10.1038/nature06860 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.