Development of algorithmic dementia ascertainment for racial/ethnic disparities research in the U.S. Health and Retirement Study

Abstract

Background:

Disparities research in dementia is limited by lack of large, diverse, and representative samples with systematic dementia ascertainment. Algorithmic diagnosis of dementia offers a cost-effective alternate approach. Prior work in the nationally-representative Health and Retirement Study (HRS) has demonstrated that existing algorithms are ill-suited for racial/ethnic disparities work given differences in sensitivity and specificity by race/ethnicity.

Methods:

We implemented traditional and machine learning methods to identify an improved algorithm that (a) had ≤5 percentage point difference in sensitivity and specificity across racial/ethnic groups, (b) achieved ≥80% overall accuracy across racial/ethnic groups, and (c) achieved ≥75% sensitivity and ≥90% specificity overall. Final recommendations were based on robustness, accuracy of estimated race/ethnicity-specific prevalence and prevalence ratios compared to those using in-person diagnoses, and ease of use.

Results:

We identified six algorithms that met our pre-specified criteria. Our three recommended algorithms achieved ≤3 percentage point difference in sensitivity and ≤5 percentage point difference in specificity across racial/ethnic groups, as well as 77%−83% sensitivity, 92–94% specificity, and 90–92% accuracy overall in analyses designed to emulate out-of-sample performance. Pairwise prevalence ratios between non-Hispanic whites, non-Hispanic blacks, and Hispanics estimated by application of these algorithms are within 1% to 10% of prevalence ratios estimated based on in-person diagnoses.

Conclusions:

We believe these algorithms will be of immense value to dementia researchers interested in racial/ethnic disparities. Our process can be replicated to allow minimally biasing algorithmic classification of dementia for other purposes.

INTRODUCTION

As the global population ages, the burden of dementia is expected to grow to epidemic proportions.¹ Unfortunately, the time and cost associated with formal dementia ascertainment has limited research in crucial areas, particularly that related to racial/ethnic disparities in dementia. Classifying dementia algorithmically in existing, representative samples offers a cost-effective alternate approach allowing an expanded the scope of research.

Algorithms developed previously for classifying dementia status in the nationally representative Health and Retirement Study (HRS) all used data collected in the HRS to predict dementia status formally ascertained through in-person assessment in participants of an HRS sub-study, the Aging Demographics and Memory Study (ADAMS).^2–6 In previous work,⁷ we evaluated the predictive performance of these algorithms, which we will refer to as the Herzog-Wallace², Langa-Kabeto-Weir^3,5, Wu⁴, Crimmins⁵, and Hurd⁶ algorithms. This work⁷ demonstrated that naïve application of these algorithms using a single threshold to classify dementia status resulted in substantially different performance across demographic subgroups. Notably, across racial/ethnic groups, sensitivity is typically higher, but specificity is typically lower among non-Hispanic blacks and Hispanics compared to non-Hispanic whites. Therefore, naïve application of these algorithms to the HRS or other similar studies for dementia racial/ethnic disparities research will lead to substantial bias and misleading conclusions due to differential misclassification.

Given the limitations of existing algorithms, and in response to the national priority to address racial/ethnic disparities in dementia as codified in the 2011 US National Alzheimer’s Project Act (NAPA), our goal was to develop and distribute an algorithm that performs comparably across racial/ethnic groups for use in dementia racial/ethnic disparities research leveraging the HRS.

METHODS

Overview

We defined three racial/ethnic groups of interest based on self-reported race and ethnicity: non-Hispanic white, non-Hispanic black, Hispanic. Considering performance metrics achieved by existing algorithms,⁷ our goal was to identify an algorithm that met the following criteria:

• ahad comparable sensitivity and specificity across racial/ethnic groups, defined as differences of ≤5 percentage points across pairwise comparisons
• bachieved ≥80% accuracy in all racial/ethnic groups
• cachieved ≥75% sensitivity and ≥90% specificity overall

In the event that multiple algorithms met these criteria, we applied two additional criteria:

• dwhich algorithm best reproduced estimates quantifying the disparities in dementia across race/ethnicity groups found in the ADAMS data
• ewhich algorithm was easiest to implement

To accomplish this, we re-evaluated the performance of existing algorithms using alternate classification cut-offs, developed a new logistic algorithm incorporating additional predictors, and developed new algorithms using machine learning approaches. Unfortunately, we were unable to account for potential differences in predictors across groups by training a separate algorithm for each race/ethnicity group due to the small number of minority participants in ADAMS. We instead relied on two alternate approaches: we included interaction terms between race/ethnicity and various predictors in the new logistic and machine learning models, and we evaluated the performance of both existing and new algorithms using race/ethnicity-specific classification cut-offs. Here, we provide details of this process and present all resulting algorithms that meet criteria (a) through (c). Ultimately, we recommend and distribute algorithms chosen based on criteria (d) and (e) for dementia disparities research using the HRS.

Data Sources

The HRS is a nationally representative, longitudinal study of adults aged ≥50.⁸ Enrollment began in 1992, and additional waves have been enrolled to maintain a steady-state sample of approximately 19,000 persons at any given wave. Interviews have been conducted biennially since 1998, with use of proxy respondents when participants are not willing or able to complete an interview. HRS interviews include questions on sociodemographic and socioeconomic characteristics, health behaviors and social engagement, medical history, health and cognitive status, as well as cognitive testing.

ADAMS selected a subsample of HRS participants aged ≥70 at the time of completing the 2000 or 2002 HRS interview using a stratified random sampling approach. 856 participants completed systematic dementia ascertainment for prevalent dementia in 2001–2003 (Wave A), and those without dementia at baseline were re-assessed for incident dementia at up to three additional time points through 2009 (Waves B, C, and D). Details of the dementia ascertainment approach are described elsewhere.^9–11

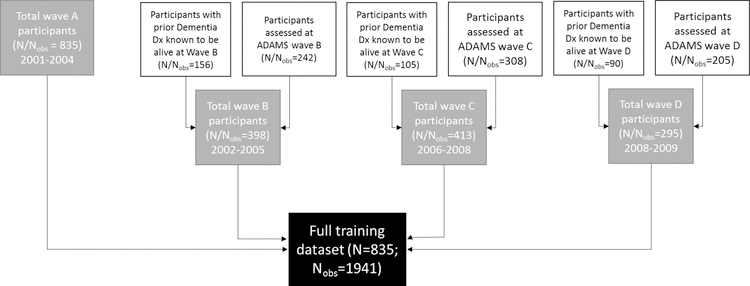
We used repeated data from all ADAMS participants at all time points where we could accurately assign dementia status to maximize information available. We linked data from each ADAMS participant at each ADAMS assessment wave to HRS data from the nearest prior HRS interview wave. For participants who were not re-examined at Waves B, C, or D due to a prior dementia diagnosis but who were known to be alive at the median ADAMS assessment date for each wave, we assigned a diagnosis of dementia and linked this to data from the closest HRS interview wave prior to the median ADAMS assessment date (Figure). We excluded participants who did not identify as non-Hispanic white, non-Hispanic black, or Hispanic given the small number of participants who met these criteria. Unless otherwise specified, we weighted all analyses (i.e. development of all new algorithms and evaluation of all algorithms) to recover performance in a representative sample of U.S. adults over age 70. We describe our process for computing weights in eAppendix 1. HRS and ADAMS participants provided informed consent at data collection. The George Washington University Institutional Review Board approved this research.

FIGURE.

Derivation of training dataset from ADAMS data

Predictors

We considered all predictors used in existing algorithms (i.e., the Herzog-Wallace², Langa-Kabeto-Weir^3,5, Wu⁴, Crimmins⁵, and Hurd⁶ algorithms), as well as additional factors that were (a) hypothesized to be associated with cognitive decline or dementia onset¹² and (b) consistently available in the HRS with minimal missingness (<5%). Additionally, given that change in cognition or function is an integral part of the diagnostic criteria for dementia,¹³ we considered variables quantifying changes in cognition, physical functioning, and social engagement. Finally, we considered interactions that we believed to be meaningful, including interactions between cognitive predictors and both race/ethnicity and respondent status (self-respondent vs. proxy-respondent). eTable 1 lists the predictor set. We used HRS data pre-processed by the RAND corporation (Longitudinal File 2014 (V2))¹⁴ for relevant data when available, and the core HRS files for data not included in the RAND dataset, as in our prior work.⁷

Statistical Analyses

Evaluation of existing algorithms using alternate global and race/ethnicity-specific cut-offs

To begin, we considered the two existing summary score cutoff-based algorithms (Herzog-Wallace², Langa-Kabeto-Weir^3,5, details are provided in eAppendix 2). We computed these algorithm scores and classified dementia status using every possible score threshold for each observation. Next, we compared algorithmic dementia classifications resulting from application of each global threshold and each race/ethnicity-specific threshold combination to the ADAMS diagnoses to compute overall and race/ethnicity-specific sensitivities and specificities for comparison against our criteria.

We similarly evaluated whether use of alternate global or race/ethnicity-specific predicted probability thresholds would result in classifications that met our requirements for the three existing regression-based algorithms (Crimmins⁵, Hurd⁶, and Wu⁴). We estimated predicted probabilities of dementia in our new dataset using the coefficients from the Wu and Crimmins algorithms as published,^4,5 and from the Hurd algorithm as re-estimated in our previous work (coefficients provided in eTable 2).⁷ We assigned dementia status using probability thresholds ranging from 0.01 to 0.99 in increments of 0.01 and compared algorithmic classifications to the ADAMS diagnoses to compute race/ethnicity-specific sensitivities, specificities, and accuracies, and evaluated whether any global or race/ethnicity-specific combinations of thresholds resulted in classifications that met our pre-specified criteria.

Development of a new algorithm using a traditional approach

Next, we developed a new logistic algorithm (Expert Model, eTable 1), with covariates chosen based on the subject matter expertise of one author, (MCP), an epidemiologist with over a decade’s experience studying risk factors for ADRD and related outcomes, with reference to current epidemiologic evidence¹² and with the aim of improving predictive ability in minority groups. We followed the Wu model and used the missing-indicator method to fit a single logistic regression to predict dementia status for both self- and proxy-respondents in our new dataset.⁴ Because no comparable external validation dataset was available, we estimated expected out-of-sample performance (i.e., sensitivity, specificity, and accuracy) across a range of probability thresholds (0.01 to 0.99 in increments of 0.01) applied to predictions obtained using 10-fold cross-validation. We evaluated these to determine whether we could achieve our pre-specified criteria through application of any global or race/ethnicity-specific thresholds to the Expert Model.

Development of new algorithms using machine learning

Finally, we derived multiple new algorithms using a variety (library) of common machine learning models (Table 1). We implemented the Super Learner two-stage ensemble algorithm using the full set of predictors in eTable 1, including hard-coded interactions. Briefly, in the first stage, Super Learner employs K-fold cross validation to determine the risk associated with each constituent algorithm (i.e., divides the data into K randomly selected and non-overlapping equally-sized sets, fits each constituent algorithm to all combinations of K – 1 of the sets and computes the corresponding prediction error in the held-out set). Super Learner then averages the cross-validated risk for each constituent function across all folds to identify the function that achieved highest predictive accuracy. In the second stage, Super Learner applies the Broyden-Fletcher-Goldfarb-Shanno (BFGS) quasi-Newton algorithm attributing weights to the constituent functions that maximize non-negative binomial likelihood when combined in the Super Learner ensemble. ^15–17 We first fit Super Learner with 10-fold cross-validation including only constituent prediction functions of the same classifier family to identify the function from each family with the lowest average cross-validated risk and/or that achieved highest accuracy most frequently across the ten folds (Table 1). We then fit Super Learner using the identified constituent prediction functions from different families and calculated out-of-sample performance metrics for each constituent function and the ensemble predictor across a range of predicted probability thresholds, similar to the approach used when evaluating the Expert Model. We then compared the resulting performance metrics against our criteria to determine whether we could achieve our pre-specified criteria through application of any global or race/ethnicity-specific thresholds to the machine learning models.

TABLE 1.

Constituent learner functions considered and selected for use in the final Super Learner ensemble

Family	Available functions	Description	Functions selected for further consideration and inclusion in final SuperLearner ensemble
Boosting	gbm	Gradient boosting model	gbm
LASSO	biglasso	LASSO	biglasso
Elastic net	glmnet at alpha levels 0.1 – 0.9 (in 0.1 increments)	Elastic net regularized logistic regression model with varying levels of the mixing parameters between LASSO (alpha = 1) and ridge (alpha = 0)	glmnet, alpha = 0.5 glmnet, alpha = 0.8 glmnet, alpha = 0.9
K-nearest neighbor	knn	K-nearest neighbors	knn
	kernelKnn	Kernel-based K-nearest neighbors
Decision trees / regression trees	cforest	Conditional random forests	Cforest randomForest
	dbarts	Discrete Bayesian additive regression trees samples
	extraTrees	Extremely randomized trees
	ipredbagg	Bagging for classification, regression and survival trees
	randomForest	Random forest
	ranger	Fast implementation of random Forests / recursive partitioning
	rpart	Recursive partitioning and regression trees
	rpartPrune	Recursive partitioning and regression trees with pruning
Support vector machine	svm	Support vector machines	ksvm
	ksvm	Kernel-based support vector machines

Identification and comparison of algorithms that met our criteria

Both existing and new algorithms were trained and initially evaluated on slightly different versions of the data. The existing regression-based algorithms were all originally trained on unique subsets of linked HRS-ADAMS data.^4,5,7 We trained our new algorithms on maximum-information samples, containing the subset of the HRS-ADAMS observations with non-missing data for all potential predictors for the machine learning algorithms (N_obs=1688, N=777), and non-missing data for chosen predictors for the Expert Model (N_obs=1917, N=834). Thus, to ensure fairness in our evaluation process, we not only evaluated model performance in the maximum information samples for each of the existing regression-based algorithms (range N_obs=1809 to N_obs=1939, N=818 to N=835) and new algorithms, but we also (a) evaluated the performance of the Expert Model out-of-sample predictions in the smaller sample used for training the machine learning algorithm, and (b) conducted complete case, head-to-head comparison of all existing and new regression-based algorithms in a sub-sample of observations with complete data for every predictor used in every model (N_obs=1571, N=756). Only model/threshold combinations that met our pre-specified criteria regardless of sample (i.e. maximum information samples and complete case sample) were eligible to be recommended, which has the added benefit of eliminating overfit models that are unduly sensitive to small changes in the data.

For a subset of the algorithms, we identified multiple threshold combinations that met our criteria and were robust to variations in sample. Thus, for a given model, we selected a single threshold combination that produced estimates of race/ethnicity-specific dementia prevalence and prevalence ratios across racial/ethnic groups that were closest to those observed in ADAMS diagnoses.

We then applied criteria (d) and (e) to select algorithms for recommendation and distribution. When applying criteria (d), we considered performance not only in our primary weighted samples, but also in the full unweighted samples, as well weighted and unweighted subsets of the data, to consider the robustness of our conclusions. Specifically, we evaluated the models separately in observations from waves A and B (i.e. representative of the age >70 population in 2002), and in observations from waves C and D (i.e. representative of the age >70 population in 2006) using our newly derived weights, as well as in observations from wave A only using wave A cross-sectional sampling weights provided by ADAMS.¹⁸

Finally, we used the bootstrap percentile method to obtain 95% confidence intervals for the performance metrics of our recommended algorithms to provide an illustration of our uncertainty and to allow full comparison to our prior work. As we were concerned about the potential for overfitting in the newly developed recommended models, we compared their cross-validated performance metrics to their apparent performance metrics evaluated based on in-sample predictions, as large differences across cross-validated and apparent performance metrics would indicate overfitting. 95% confidence intervals around apparent performance were estimated using the bootstrap percentile method. Due to our weighting procedure (eAppendix 1), we selected, with replacement, on unique individuals in waves A and B, and on unique individuals in waves C and D, to draw 10,000 bootstrap samples.

All analyses were completed using SAS version 9.4 or R version 3.4.4. Code for assigning dementia classifications using our recommended algorithms and derived classifications for all HRS participants ages 65 and older at HRS waves between 2000 and 2014 are available on our GitHub page (https://github.com/powerepilab/AD_Algorithm_Development).

RESULTS

Selected characteristics of the HRS/ADAMS samples used for training our Expert Model (N_obs=1917, N=834) and machine learning algorithms (N_obs=1688, N=777), as well as the sub-sample of observations with complete data on predictors for all models (Expert Model, machine-learning models, Wu, Hurd, and Crimmins models, N_obs=1571, N=756) are provided in eTable 3. There are no notable differences in the distribution of dementia or characteristics across samples before or after application of weights.

No set of global or race/ethnicity-specific cut-offs for either the Herzog-Wallace or Langa-Kabeto-Weir summary score-based algorithms led to results that met our pre-specified criteria. For the Wu, Crimmins, and Hurd algorithms, several combinations of race/ethnicity-specific probability thresholds resulted in dementia classifications that met our pre-specified criteria when evaluated in the full samples for each algorithm. However, only the Hurd model findings were robust when applied to the sample of observations with complete data for all algorithms. Race/ethnicity-specific performance metrics of the Hurd algorithm using the chosen threshold combination are provided in Table 2.

TABLE 2.

Weighted out-of-sample predictive performance of Hurd mode, Expert Model, and machine-learning models at chosen race/ethnicity-specific probability thresholds ^a

	Score cutoff	Sensitivity	Specificity	Overall Accuracy
(1) Hurd model b
Non-Hispanic white	0.19	79%	95%	92%
Non-Hispanic black	0.25	78%	90%	87%
Hispanic	0.27	81%	91%	89%
Overall	-	79%	94%	92%
(2) Expert Model c
Non-Hispanic white	0.27	77%	93%	91%
Non-Hispanic black	0.32	78%	89%	86%
Hispanic	0.46	75%	91%	87%
Overall	-	77%	93%	90%
(3) Gradient boosting model d
Non-Hispanic white	0.20	81%	93%	91%
Non-Hispanic black	0.28	80%	88%	87%
Hispanic	0.48	77%	90%	88%
Overall	-	81%	93%	91%
(4) Conditional random forests model d
Non-Hispanic white	0.27	81%	94%	92%
Non-Hispanic black	0.35	80%	89%	87%
Hispanic	0.45	79%	90%	88%
Overall	-	81%	93%	92%
(5) LASSO model d
Non-Hispanic white	0.25	83%	93%	91%
Non-Hispanic black	0.19	85%	89%	88%
Hispanic	0.34	82%	90%	88%
Overall	-	83%	92%	91%
(6) Super Learner ensemble d
Non-Hispanic white	0.24	83%	93%	92%
Non-Hispanic black	0.27	81%	89%	87%
Hispanic	0.36	80%	89%	87%
Overall	-	83%	93%	91%

^aCutoffs chosen to recover, as close to possible, true dementia prevalence ratios across race/ethnicity groups in the weighted ADAMS sample

^bPerformance metrics achieved in full sample of observations with non-missing Hurd predictors (N=1855)

^cPerformance metrics achieved in full sample of observations with non-missing expert logit model predictors (N=1917)

^dPerformance metrics achieved in full sample of observations with non-missing predictors used for training machine learning models (N=1688)

Regression coefficients of the Expert Model are shown in eTable 4. Several combinations of race/ethnicity-specific thresholds resulted in dementia classifications that met our three pre-specified criteria and were robust to variation in sample when applied to the out-of-sample predicted probabilities. We show the race/ethnicity-specific performance metrics using the chosen threshold Table 2, which best recovered prevalence ratios across race/ethnicity groups in the ADAMS data.

Finally, among machine-learning functions, the gradient boosting, conditional random forests, and LASSO models, as well as the Super Learner ensemble produced out-of-sample estimates that resulted in performance metrics which met the three pre-specified criteria and that were robust to variation in sample. Chosen race/ethnicity-specific thresholds and associated performance metrics for each model are shown in Table 2. Coefficients for the LASSO-reduced logistic model are in eTable 5.

Areas under the curve (AUCs) were high across all algorithms that met criteria (a)–(c), overall (range: 0.948 to 0.959) and by racial/ethnic group (non-Hispanic whites range: 0.953 to 0.963, non-Hispanic blacks range: 0.910 to 0.944, Hispanics range: 0.926 to 0.944, eFigure 1). Comparing receiver–operator characteristic (ROC) curves across algorithms, predictive performance is consistently better among non-Hispanic whites, and most models performed least well for Hispanics.

Comparison of dementia prevalence and prevalence ratio estimates based on ADAMS diagnoses versus those based on algorithmic classifications in the full weighted data are provided in Table 3. All algorithms over-estimated dementia rates despite high specificities due to the high proportion of non-dementia cases. All models performed similarly in estimating prevalence ratios between non-Hispanic blacks and whites (2%−6% lower than prevalence ratios based on ADAMS diagnoses), but the Expert Model performed best in estimating prevalence ratios between non-Hispanics and Hispanics (0%−4% lower than prevalence ratios based on ADAMS diagnoses).

TABLE 3.

Comparison of race/ethnicity-specific dementia prevalences, and prevalence ratios between race/ethnicity groups based on ADAMS gold-standard diagnoses vs. algorithmic diagnoses in the full training sample, weighted to represent the US age >70 population

	ADAMS (true) diagnoses	Algorithmic diagnoses Estimated prevalence (difference between estimated and true prevalences) Estimated prevalence ratio (ratio of estimated to true prevalence ratios)
		Hurd probit model	Expert Model	Gradient boosting model	Conditional random forests	LASSO	Super Learner
True and estimated dementia prevalence
Non-Hispanic white	15.6%	17.0% (1.4%)	17.8% (2.2%)	18.5% (2.9%)	17.6% (2.0%)	18.8% (3.2%)	18.6% (3.0%)
Non-Hispanic black	25.9%	27.6% (1.7%)	28.4% (2.5%)	29.3% (3.4%)	28.5% (2.6%)	30.4% (4.5%)	29.2% (3.3%)
Hispanic	20.0%	23.6% (3.6%)	22.5% (2.5%)	23.5% (3.6%)	24.2% (4.3%)	24.6% (4.7%)	25% (5.1%)
True and estimated prevalence ratios
Non-Hispanic black vs. white	1.66	1.62 (0.98)	1.60 (0.96)	1.59 (0.96)	1.62 (0.97)	1.61 (0.97)	1.57 (0.94)
Hispanic vs. Non-Hispanic white	1.28	1.39 (1.08)	1.26 (0.99)	1.27 (1.00)	1.37 (1.07)	1.31 (1.03)	1.34 (1.05)
Non-Hispanic black vs. Hispanic	1.30	1.17 (0.90)	1.26 (0.97)	1.25 (0.96)	1.18 (0.91)	1.23 (0.95)	1.17 (0.90)

Similar trends are observed in weighted analyses of data from waves A and B (eTable 6), and data from waves C and D (eTable 7). In weighted analyses of only wave A observations (Table 4) the new algorithms uniformly performed poorly in estimating prevalence ratios comparing Hispanics to non-Hispanic whites and blacks due to substantial over-estimation of Hispanic dementia prevalence. Prevalence across all racial/ethnic groups were over-estimated to a greater degree by algorithms in unweighted analyses across sub-sets of the data (eTable 6, eTable 7, and eTable 8). However, while model-based estimates of prevalence ratios comparing non-Hispanic blacks and whites in unweighted analyses reasonably recovered prevalence ratios based on ADAMS diagnoses, estimates comparing Hispanics to non-Hispanic whites and blacks were more variable.

TABLE 4.

Comparison of race/ethnicity-specific dementia prevalences, and prevalence ratios between race/ethnicity groups based on ADAMS gold-standard diagnoses vs. algorithmic diagnoses in wave A, weighted to represent US age >70 population in 2002

		Algorithmic diagnoses Estimated prevalence (difference between estimated and true prevalences) Estimated prevalence ratio (ratio of estimated to true prevalence ratios)
	ADAMS (true) diagnoses	Hurd probit model	Expert Model	Gradient boosting model	Conditional random forests	LASSO	Super Learner
True and estimated dementia prevalence
Non-Hispanic white	12.4%	14.9% (2.5%)	17.2% (4.9%)	17.8% (5.4%)	17.8% (5.4%)	18.7% (6.4%)	19.0% (6.6%)
Non-Hispanic black	22.2%	28.0% (5.8%)	27.4% (5.2%)	30.0% (7.8%)	26.3% (4.2%)	32.0% (9.8%)	30.8% (8.6%)
Hispanic	10.8%	16.7% (5.9%)	23.1% (12.3%)	25.8% (14.9%)	27.2% (16.4%)	32.8% (22%)	32.6% (21.8%)
True and estimated prevalence ratios
Non-Hispanic black vs. white	1.79	1.88 (1.05)	1.59 (0.89)	1.69 (0.94)	1.48 (0.83)	1.71 (0.95)	1.62 (0.90)
Hispanic vs. Non-Hispanic white	0.87	1.12 (1.28)	1.34 (1.54)	1.45 (1.65)	1.53 (1.75)	1.75 (2.01)	1.72 (1.97)
Non-Hispanic black vs. Hispanic	2.05	1.68 (0.82)	1.18 (0.58)	1.17 (0.57)	0.97 (0.47)	0.97 (0.47)	0.94 (0.46)

Based on our analyses, there is no single “best” algorithm that performs consistently well in recovering prevalence ratios between race/ethnicity groups across the full training sample and its subsamples. When considering only comparisons between non-Hispanic whites and blacks, the Hurd and LASSO models perform consistently well relative to other algorithms. However, when considering all three pairwise comparisons, the Expert Model performs better. With regard to ease of use, traditional regression models (Expert Model, Hurd, LASSO) can be reproduced with knowledge of the final coefficients, while application of the other machine learning models is more complex. Compared to the Expert Model, all other models are complicated by inclusion of change and lag variables requiring at least two waves of data, increasing the likelihood of data missingness and limiting their use in potential new settings. Given model performance and these considerations, we recommend the Expert, LASSO, and Hurd models, recognizing that one may be better than another depending on the goal, as discussed below.

For purposes of comparability with results comparing performance of existing algorithms,⁷ 95% confidence intervals for performance metrics of the three recommended algorithms are provided in eTable 9. While performance metrics in the overall sample and among non-Hispanic whites are very precise, confidence intervals for performance metrics among non-Hispanic blacks and Hispanics (particularly for sensitivity) are wide due to small sample sizes. Finally, to address the concern that the algorithms may be overfit, we compared performance metrics evaluated on in-sample predictions to those evaluated on out-of-sample predictions. We confirm that the neither the Expert or LASSO models are severely overfit, given that in-sample predictions were 0–1 percentage points higher in the LASSO model (developed using machine learning) and 1–4 percentage points higher in the Expert Model (eTable 10). Considering the differences between model-estimated prevalence ratios and ADAMS diagnoses-estimated prevalence ratios (Table 3), and the magnitude of confidence intervals around estimated performance metrics (eTable 9), application of these models for examining disparities will be most reliable in contexts where disparities are relatively large.

DISCUSSION

Given the lack of large, nationally representative samples with formal dementia ascertainment, development of a dementia prediction algorithm that minimizes difference in predictive performance across race/ethnicity groups is crucial for advancing disparities research. We identified three such algorithms that can be used in HRS: the Hurd model, our Expert Model, and our LASSO model. These algorithms achieved ≤3 percentage point difference in sensitivity and ≤5 percentage point difference in specificity across racial/ethnic groups, as well as 77%−83% sensitivity, 92–94% specificity, and 90–92% accuracy overall. In terms of ease of use, the Expert model requires the fewest variables and does not include variables quantifying change from the prior wave. The Expert model also produces the best overall performance when considering all three racial/ethnic groups. Nonetheless, we also recommend use of our re-estimated Hurd model (with newly identified race/ethnicity-specific cutoffs) or LASSO model when only comparing non-Hispanic whites and blacks. However, both of these models require availability of additional variables, including change from prior status, which precludes use prior to the second HRS interview. Thus, even when contrasts of non-Hispanic whites and non-Hispanic blacks are of primary interest, it may be preferable to implement the Expert model, which still performs well but only requires predictors from a single time point.

Our goal was to minimize cross-group differences in sensitivity and specificity (i.e., characteristics of the test). While this goal is related to the idea of fairness, as popularized by the machine learning community, we note that it is not synonymous with several common notions of fairness, e.g. statistical parity and calibration.¹⁹ Future efforts may focus on applying novel methods recently introduced in the classification fairness literature.^20–26 However, we anticipate that they are unlikely to reliably improve on our efforts here given the relatively small sample and number of predictors available. This work demonstrates that popular machine-learning models are not superior to traditional regression-based models when the sample size and predictor set is relatively small.

To our knowledge, our work is the first to identify an algorithm for classifying dementia in HRS with the explicit goal of achieving equal sensitivity and specificity across race/ethnicity groups. We have conducted several sensitivity analyses to ensure that our results are robust to variations in the data. Notably, the race/ethnicity-specific cut-offs identified for each recommended algorithm result in classifications that meet our pre-specified criteria in both the sample with maximum available observations specific to each algorithm, and in the common sample with complete cases across all existing and new algorithms. This ensured that our evaluation and comparison of algorithms was fair, which protected against recommendation of overfit models. We have also posted our code on GitHub to reproduce our algorithmic diagnoses to increase reproducibility and use of these algorithms.

However, our work has limitations. Notably, we cannot recommend application of the algorithms to data beyond the HRS without first validating their performance, given that model predictors and performance may be sensitive to cohort and study procedural differences (especially in machine learning algorithms), as well as cross-cultural differences. Unfortunately, we were unable to identify an external validation sample with both sufficient coverage of predictors and systematic dementia ascertainment. We hope to have the opportunity to evaluate these algorithms against such a sample in the future, and the Health Cognitive Aging Project (HCAP) may provide such an opportunity. However, given that investigators will continue to use the HRS to conduct research related to dementia disparities in the meantime, we believe that our work remains important and timely by providing tools to make those studies more sound. Furthermore, we believe that our approach can be applied to other data to train study- or country-specific algorithms if the performance of our recommended algorithms prove to differ substantially in future validation studies.

We also caution that, while we advocate for their use, the recommended algorithms have limitations. First, comparisons including Hispanics must be made with caution. Because of the small number of Hispanic participants in ADAMS, we have less confidence in the models’ ability to adequately ascertain dementia status in Hispanics. Furthermore, the ADAMS sample does not include Hispanics with more than a high school degree; considering that education level may impact cognitive test scores, the algorithms’ performance metrics presented here may not reflect their performance in a truly nationally representative sample for Hispanics. Second, the algorithms assume a time-invariant relationship between predictors and dementia status, which may limit their application to data collected at times far outside the ADAMS observations period (2000–2009). Additionally, we do not recommend use of these algorithms to HRS waves before 2000 or to participants aged <70: proxy respondents in 1998 (outside of our training sample) appear to be substantially different (better cognition, fewer ADLs/IADLs) from proxy respondents from 2000 and later, and ADAMS only considered those aged ≥70,. Finally, our goal was to predict prevalent dementia at a given time point. Our past work indicates that algorithmic diagnoses are better at identifying prevalent rather than incident dementia, because they are better at identifying moderate to severe dementia than mild dementia. This makes sense, given that cognitive decline leading to dementia is typically gradual, but limits use of algorithmic diagnoses for some applications.

In conclusion, we recommend and have distributed code to reproduce three algorithms that we deem appropriate for use in racial/ethnic dementia disparities research in the nationally-representative HRS. We believe the availability of these algorithms will facilitate efforts in dementia racial/ethnic disparities research. Our process can be replicated to allow minimally biasing algorithmic classification of dementia for other similar purposes.