Patient Specific Characterization of Artery and Plaque Material Properties in Peripheral Artery Disease

Abstract

Patient-specific finite element (FE) modeling of atherosclerotic plaque is challenging, as there is limited information available clinically to characterize plaque components. This study proposes that for the limited data available in vivo, material properties of plaque and artery can be identified using inverse FE analysis and either a simple neo-Hookean constitutive model or assuming linear elasticity provides sufficient accuracy to capture the changes in vessel deformation, which is the available clinical metric. To test this, 10 human cadaveric femoral arteries were each pressurized ex vivo at 6 pressure levels, while intravascular ultrasound (IVUS) and virtual histology (VH) imaging were performed during controlled pull-back to determine vessel geometry and plaque structure. The VH images were then utilized to construct FE models with heterogeneous material properties corresponding to the vessel plaque components. The constitutive models were then fit to each plaque component by minimizing the difference between the experimental and the simulated geometry using the inverse FE method. Additionally, we further simplified the analysis by assuming the vessel wall had a homogeneous structure, i.e. lumping artery and plaque as one tissue. We found that for the heterogeneous wall structure, the simulated and experimental vessel geometries compared well when the fitted neo-Hookean parameters or elastic modulus, in the case of linear elasticity, were utilized. Furthermore, taking the median of these fitted parameters then inputting these as plaque component mechanical properties in the finite element simulation yielded differences between simulated and experimental geometries that were on average around 2% greater (1.30–5.55% error range to 2.33–11.71% error range). For the homogeneous wall structure the simulated and experimental wall geometries had an average difference of around 4% although when the difference was calculated using the median fitted value this difference was larger than for the heterogeneous fits. Finally, comparison to uniaxial tension data and to literature constitutive models also gave confidence to the suitability of this simplified approach for patient-specific arterial simulation based on data that may be acquired in the clinic.

1. Introduction

In the United States, approximately 8.4 million people over the age of 40 have peripheral arterial disease (PAD) [1]. Left untreated, PAD can cause severe tissue ischemia, ulcerations, and gangrene, which may eventually lead to limb amputation. Approximately 25% of patients with PAD have worsening limb symptoms over 5 years, with 7% requiring revascularization and 4% requiring amputation [2]. Revascularization is commonly approached via endovascular therapies, mainly stenting. However, the failure rate of endovascular therapies is high, with restenosis occurring in 27% of patients and occlusions in 19% within three years of the intervention [3]. Stent fracture is a common cause of such events, with similarly high incidence rates [4,5]. The high prevalence is thought to result from the strenuous mechanical environment in the arteries. The bending and flexion of limbs during locomotion leads to significant forces being exerted on both the arterial wall and the stent which, over thousands of cycles, leads to fatigue failure in the stent struts [6]. In addition, plaque and wall composition greatly affect the locations and magnitudes of stress concentrations on the stent struts. For example, calcifications lead to stiffer regions on the arterial wall that can impede strut motion, leading to higher stress magnitudes.

Intravascular ultrasound (IVUS) allows vessel geometry and morphology to be measured in vivo, with virtual histology (VH) providing a means for identifying different plaque components that are present [7]. From the 2D IVUS-VH images, a 3D finite element (FE) model can be constructed with patient specific geometry, including heterogeneous material properties representative of the artery wall as well as the various plaque components [8]. By deploying a stent into the vessel in silico, such FE models can be then utilized to assess the viability of stents and the risk of fracture by applying displacements and loading similar to those experienced during locomotion. The performance of differing stent designs can then be compared via simulation, in order to select the optimum stent for the patient that minimizes the risk of stent fracture and restenosis. In order to obtain accurate results from FE models, however, accurate material properties must be utilized in the simulations. Unfortunately, the reported literature values for constitutive response of the individual plaque components and the atherosclerotic wall vary greatly (Table 1). In addition, many plaque components for which mechanical response have been identified do not have the same description as those identified by VH. Finally, the degree of patient specificity of each plaque component and the arterial wall is not clear. This introduces significant uncertainty in computational modeling of the artery.

Table 1.

A comparison of different strain energy functions and coefficients used to describe atherosclerotic artery wall and plaque components.

Bennetts et al. 2013 [27]
$W=C_{10}\left(I_1-3\right)+C_{01}\left(I_2-3\right)+C_{20}{\left(I_1-3\right)}^2+C_{11}\left(I_1-3\right)\left(I_2-3\right)+C_{30}{\left(I_1-3\right)}^3$
	C10 (kPa)	C01 (kPa)	C20 (kPa)	C11 (kPa)	C30 (kPa)
Artery	18.90	2.75	590.4	857.0	0
Fibrous plaque	1.4	0	7.3	0	5.8
Fatty plaque	1.6	0	9.3	0	11
Necrotic core	0.7	0	22.0	0	−0.45
Calcified Plaque	2.5	0	16.4	0	7
Bukala et al. 2014 [43]
$W=C_{10}\left(I_1-3\right)+C_{01}\left(I_2-3\right)+C_{20}{\left(I_1-3\right)}^2+C_{11}\left(I_1-3\right)\left(I_2-3\right)+C_{02}{\left(I_2-3\right)}^2$
	C10 (kPa)	C01 (kPa)	C20 (kPa)	C11 (kPa)	C02 (kPa)
Coronary Artery	18.90	2.75	590.4	857.0	0
Cellular Plaque	−88.31	106.2	113.7	893.8	−966.7
Calcified Plaque	−3025	3107	107390	−234700	137220
Yang et al. 2009 [55]
$W=c_1\left(I_1-3\right)+D_1\left[\text{exp}\left(D_2\left(I_1-3\right)\right)-1\right]+\frac{K_1}{2K_2}[\mathrm{e}\mathrm{x}\mathrm{p}[K_2{\left(I_4-1\right)}^2-1]$
	c1 (kPa)	D1 (kPa)	D2	K1 (kPa)	K2
Artery (Circ.)	28.14	1.31	11.5
Artery (Axial.)	14.07	0.655	9.2
Artery (Anisotropic)	8.29	0.907	3.1	8.82	3.7
Lipid core	0.5	0.5	0.5
Calcified	281.4	13.1	11.5

Huang et al. 2001 [56]
$W=D_1\left[\text{exp}\left(D_2\left(I_1-3\right)\right)-1\right]$
	D1 (kPa)	D2
Artery	2.645	8.365
Fibrous plaque	5.105	20
Lipid pool	0.05	13
Calcified	18.80	0.5

Morlacchi et al. 2014 [44]
$W=C_{10}\left({\overline{I}}_1-3\right)+C_{20}{\left({\overline{I}}_1-3\right)}^2+C_{30}{\left({\overline{I}}_1-3\right)}^3+C_{40}{\left({\overline{I}}_1-3\right)}^4+C_{50}{\left({\overline{I}}_1-3\right)}^5+C_{60}{\left({\overline{I}}_1-3\right)}^6$
	C10 (kPa)	C20 (kPa)	C30 (kPa)	C40 (kPa)	C50 (kPa)	C60 (kPa)
Artery	268.9	625.7	−2091.3	21953	−66842.5	74924.3
Cellular plaque	2.38	1.89	−388.0	3730	−2540	573.0

In addition to the parameters in Table 1 other studies have attempted to characterize the mechanical behavior of atherosclerotic plaques and the individual components. Uniaxial tensile and shear testing has been used extensively to characterize plaques from various arteries including aorta, carotid, and iliac arteries, although, most assume plaque homogeny or test specific components such as the fibrous cap due to the difficulty in testing individual components and thus are somewhat limited in their application to FE modeling [9–15]. However, in some cases plaques were imaged prior to testing to identify the predominant plaque type and this was used to distinguish the mechanical properties of the different samples. Furthermore, in some cases individual components were identified and tested with Teng et al. performing uniaxial testing of fibrous caps, lipid pools and intraplaque hemorrhages for carotid arteries and Holzapfel et al. performing mechanical testing on fibrous caps, fibrotic plaque and calcification on iliac arteries [14,16]. Uniaxial tension testing has also been utilized to fit constitutive model parameters for studies in Table 1 and for further studies including those which have utilized FE modeling and have evaluated stent performance [17–20]. In particular, Teng et al. investigated several commonly used constitutive models fitting to uniaxial tension test data and then further evaluated them through FE simulations of an idealized plaque [21]. Plaque components have also been evaluated using indentation test with Ebenstein et al. performing nanoindentation of plaque components and Chai et al. have utilized microindentation and inverse FE analysis to probe the mechanical properties of specific plaque components in vitro and fit them to a common constitutive model [22–24]. Inverse FE analysis has also been utilized by Akyildiz et al. for characterization of local plaque material properties with ultrasound displacement imaging utilizing a neo-hookean constitutive model to characterize the plaque mechanical response [25]. Finally, inverse FE analysis has been used with MRI to characterize plaque mechanical behavior again using a neo-hookean constitutive model [25,26]. However, the latter two studies did not identify plaque structure with the same spatial resolution as can be acquired by IVUS-VH. Therefore, in contrast to previous inverse FE studies to identify plaque mechanical properties, the present work can be applied to investigate the individual plaque component mechanical properties non-destructively with a higher degree of spatial resolution and using techniques that are applied routinely when evaluating patient plaque morphology.

The goal of this study was to find a means of determining material properties of diseased peripheral arteries using IVUS-VH imaging and FE modeling. To do this, we used a previously implemented work flow to convert IVUS-VH images to ABAQUS input files for FE simulations [8,27]. Then, utilizing inverse FE analysis, we determined material parameters of each component. A simple neo-Hookean model was utilized to describe the arterial wall components and to further reduce model complexity and provide a clinically applicable approach a linear elastic material was also considered. As this requires no ex vivo data this method can be easily extended to in vivo and provide patient specific simulation of PAD to inform clinical decision making.

Methods

2.1. Pressure Inflation Testing

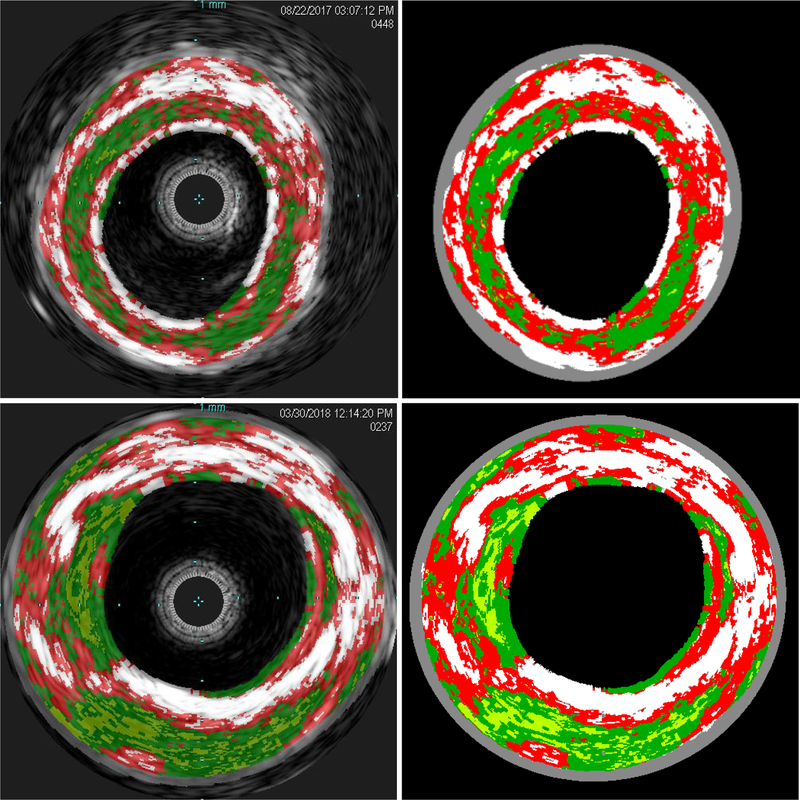
After receiving Mayo Clinic Institutional Review Board approval (IRB 14–009261), ten human cadaveric peripheral arteries were collected and stored at −70°C until testing. Before testing the samples, they were defrosted in a refrigerator at 4 °C overnight. Excess fatty tissue was carefully removed using surgical scissors. Any bifurcations were sealed with suture to prevent leakage while minimizing the effect on the recorded IVUS-VH. The tissue was then mounted onto custom fixtures that were attached at the top and bottom of the in vitro chamber to enable vessel pressurization, and the fixtures were connected to the plastic tubing using clamps. The samples were mounted such that the artery was held straight with the minimum axial tension applied. We noted in trial experiments that no buckling was observed at high pressure with this minimal tension and this was also observed in the samples tested for this manuscript. The IVUS catheter was inserted into the vessel through a side port that minimized fluid outflow, and then the chamber was sealed and filled with body temperature saline. The full configuration can be seen in Figure 1. Pressure measurement was performed using pressure transducers (PendoTECH, Princeton, NJ) and the pressure was recorded and controlled by specialized software (Harvard Apparatus, Holliston, MA) [28]. IVUS images were captured with an eagle eye platinum catheter (Philips N.V., Amsterdam, Netherlands) and acquisition performed on a Volcano IVUS machine (Philips N.V., Amsterdam, Netherlands). Automatic pullback was performed at 0.5 mm/s at a baseline pressure (10 mmHg) to obtain images of the baseline geometry and to ensure artery perfusion with saline, and then pressures of 60, 80, 120, 160 and 200 mmHg were sequentially applied. VH images were acquired at approximately 0.2 frames/mm using an ECG simulator (he Instruments, Lake Worth, FL, USA) to replicate patient cardiac electrical activity, due to VH being ECG gated. VH was collected for the initial 10 mmHg pressure only due to difficulties in accurately acquiring images at higher pressures. VH results identified arterial wall (grey) and four different plaque components; calcification (white), fibrous plaque (dark green), fatty plaque (light green), and necrotic core (red) (Figure 2).

Figure 1.

Images detailing the experimental assembly. Plastic tubing is inserted into each end of the vessel and held with cable ties (a). This tubing in turn is inserted into the fixtures by clamps (b) that are attached into the bioreactor (c), which is then filled with body temperature saline. The image (d) shows the full assembly with IVUS machine (1), catheter pullback device (2), and bioreactor (3) identified.

Figure 2.

Representative IVUS-VH images extracted from the machine (left) and the segmented images for input into the finite element input file synthesis python scripts (right) for a 63 year old female patient (top, case 3) and a 87 year old male (bottom, case 8). Grey is arterial wall, light green is fatty plaque, dark green is fibrous plaque, red is necrotic core, and white is calcification.

2.2. Finite Element Model Creation

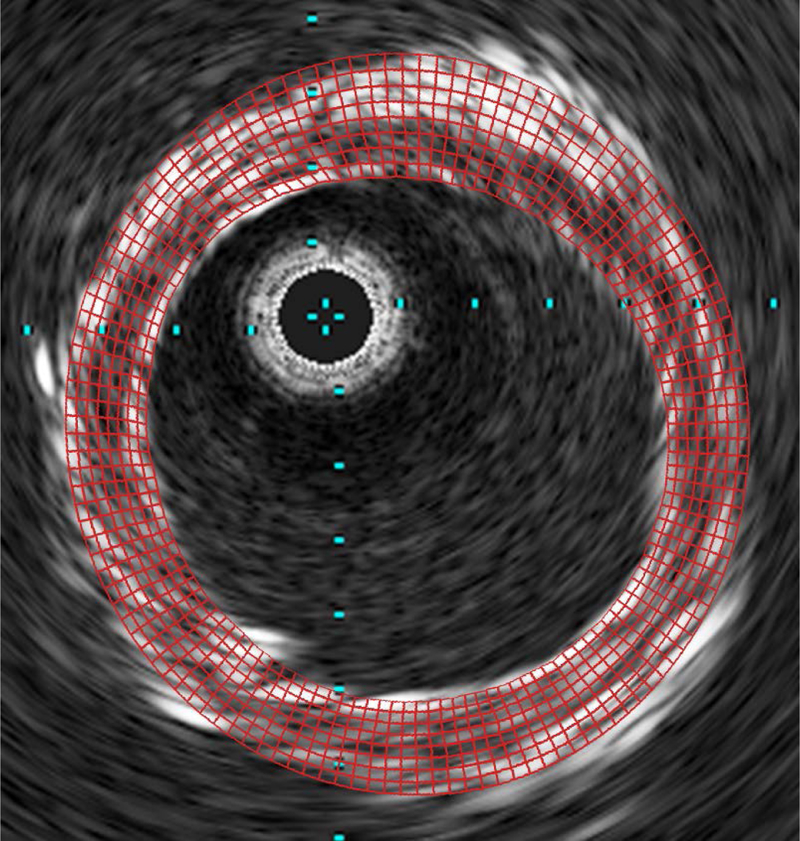
Due to the inhomogeneity of the vessel wall, an analytical approach to fit material properties is not suitable and thus an inverse FE approach was employed. Inner and outer boundaries of the IVUS-VH images were extracted, and these boundaries were used to convert the stack of images into a cylindrical hex mesh with 128 (circumferential) X 8 (radial) 8-node brick elements (C3D8H) in the plane of the IVUS-VH images, and 1 element covering five images out-of-plane (along the vessel axial direction). Element-specific material properties were determined by first identifying the pixels from the IVUS-VH images that lie in each element of the mesh. Then, the element-specific material properties were determined by calculating the weighted average, based on the number of pixels of each material type in each element, of the corresponding SEF polynomial coefficients [8]. Averaging across five images out-of-plane along the axial direction was performed as initial studies showed this reduced simulation time by nearly fivefold while causing an insignificant increase in model error. As there are on average 280 slices per artery this is a substantial reduction in simulation time for optimization. Once the element-specific material properties were determined, the mesh was filtered in order to smooth spatial discontinuities between images. The final finite element model is shown for two artery segments in Figure 3. The mean number of pixels per element across all cases was 555 ± 128 and the average element dimensions were 0.164 mm by 0.208 mm with 1 mm element length in the z axis as it is composed of an average of 5 VH slices that are 0.2 mm apart.

Figure 3.

Finite element model generated by python scripts for case 3 in the unloaded and loaded configuration (a and b) and case 8 in the loaded and unloaded configuration (c and d). Von Mises stress is shown to highlight the effects of heterogeneous mechanical properties on stress distribution.

Simulations were performed using Abaqus (version 6.14–2, standard) (Simulia, Providence, RI, USA). Pressures were applied to the inner wall to mimic experimental loading; and nodes on the axial end faces of the model were fixed in the axial direction and free to expand in the radial direction. These constraints were chosen to replicate the in vitro constraints. By selecting VH images 1 mm away from the clamped ends of the vessel this ensured that the effect of the clamping on vessel expansion was negligible.

2.3. Segmentation and Registration

Semi-automatic segmentation of the artery lumen was performed using 3D Slicer (http://www.slicer.org [29]). Prior to segmentation, the IVUS DICOM images were processed using a custom Python script (Python Software Foundation, https://www.python.org/), implementing SimpleITK functions [30,31]: (1) a vector image was converted to a scalar image using the first image index, (2) the image was resampled to every 5^th slice, and finally (3) a 5 × 5 × 5 pixel median filter was applied. Virtual histology images were registered to the 10 mmHg IVUS images by specifying the IVUS location of the first and last VH image. The remaining VH images were assumed to be equally spaced between the first and last IVUS longitudinal coordinates. The end point of the IVUS data collection (first sign of narrowing at the clamp site) was used to register IVUS images of the remaining pressure levels to the 10 mmHg IVUS coordinates.

2.4. Hyperelastic Nonlinear Fitting

Hyperelastic arterial wall material properties were defined with a Neo-Hookean SEF:

$$W_{NH}=\mathrm{ }{C}_{10}\mathrm{ }(I_1-3)$$ (1)

where I₁ is the first invariant of strain such that I₁ tr(C) where C is the right Cauchy-Green deformation tensor and C₁₀ is the mechanical constant. The arterial wall and all plaque constituents were assumed incompressible. This constitutive model was chosen to reduce computational complexity, requiring optimization of only one coefficient per material.

This model was chosen to simplify the fitting procedure as more complex strain energy functions have additional terms that will increase the number of parameters to be sought by five for each term added which with the clinically available data will reduce the fidelity of the optimization. Additionally, choices of constitutive model are limited to those which the constants are linear (i.e. polynomial strain energy functions) such that material averaging is representative. Finally, anisotropic models such as the Holzapfel-Gasser-Odgen model would require local characterization of plaque fiber orientations which is highly taxing in vitro for the element sizes in this model and in vivo is limited to specialized techniques which are beyond the scope of this study [32,33].

Two models were considered for this optimization: a heterogeneous model distinguishing between the plaque components and the arterial wall, and a homogeneous model where the same Neo-Hookean SEF was used to describe the entire vessel. For the heterogeneous model, the coefficient for fatty plaque was not optimized to reduce the computational complexity because it constituted a negligible overall proportion of the plaque composition (mean proportion <1%). Therefore, coefficients for necrotic core (red), calcification (white) and fibrous plaque (green), along with the arterial wall (grey) were optimized and fatty plaque (light green) was assigned literature values (Table 1, Bennetts et al. 2013) [27]. The homogeneous model was considered to further simplify the optimization, as only one C₁₀ value was required rather than four in the heterogeneous model.

Material properties were found via an inverse FE method, where a vector of model parameters is optimized to minimize the error between computationally predicted and experimentally measured vessel diameters. The difference between the maximum and minimum vessel diameters, assuming an elliptical cross-section, for each VH slice was calculated for each pressure level and the resulting cost function vector minimized. This is represented numerically as

$$\begin{gathered} x*=\underset{x}{\text{argmin}}{\left|\left[{|d_{max}^{comp}-d_{max}^{exp}|}_{60},{|d_{min}^{comp}-d_{min}^{exp}|}_{60}, \\ {|d_{max}^{comp}-d_{max}^{exp}|}_{80},{|d_{min}^{comp}-d_{min}^{exp}|}_{80}, \\ {|d_{max}^{comp}-d_{max}^{exp}|}_{120},{|d_{min}^{comp}-d_{min}^{exp}|}_{120}, \\ {|d_{max}^{comp}-d_{max}^{exp}|}_{160},{|d_{min}^{comp}-d_{min}^{exp}|}_{160}, \\ {|d_{max}^{comp}-d_{max}^{exp}|}_{200},{|d_{min}^{comp}-d_{min}^{exp}|}_{200}\right]\right|}^2. \end{gathered}$$ (2)

Here, ${\mathit{d}}_{max}^{comp}$ and ${\mathit{d}}_{min}^{comp}$ are vectors of the computed maximum and minimum lumen diameters, respectively, calculated by assuming each image slice of the vessel has an elliptical shape and finding the minimum and maximum internal diameter from nodal coordinates. Next, ${\mathit{d}}_{max}^{exp}$ and ${\mathit{d}}_{min}^{exp}$ are vectors of the maximum and minimum experimental lumen diameter calculated by finding the maximum and minimum diameters of DICOM frames registered to the VH slices during in vitro pressurization. There was an average of 55 entries for all vectors.

The optimization was performed with a trust-region-reflective algorithm using the lsqnonlin function within MATLAB 2016b (The MathWorks Inc., Natick, MA, USA). For the homogeneous fitting, initial studies found that only one starting point was required to find the optimum parameter. The optimization was bounded with a lower bound of 1 kPa and an upper bound of 1000 kPa. The heterogeneous fitting was performed over multiple, randomly assigned, initial start-points, and the best fit was selected. This increased the likelihood that the estimated parameter values represented a globally optimal set [34]. The optimization was bounded to ensure physically plausible values (Table 2) with the fittings from the homogeneous case used to inform the selection of these bounds. To assist in finding representative coefficients, all 20 initial starting points were generated such that $C_{10}^{calc}>C_{10}^{nec}+C_{10}^{fib}+C_{10}^{artery}$, where $C_{10}^{calc}$, $C_{10}^{nec}$, $C_{10}^{fib}$ and $C_{10}^{artery}$ were randomly assigned starting points for the Neo-Hookean parameters for calcified plaque, necrotic core, fibrous plaque and artery, respectively.

Table 2.

Upper and lower bounds for the optimization procedure for both Neo-Hookean coefficient and elastic modulus.

	${\mathit{C}}_{10}^{\mathit{a}\mathit{r}\mathit{t}\mathit{e}\mathit{r}\mathit{y}}$ (kPa)	${\mathit{C}}_{10}^{\mathit{n}\mathit{e}\mathit{c}}$ (kPa)	${\mathit{C}}_{10}^{\mathit{f}\mathit{i}\mathit{b}}$ (kPa)	${\mathit{C}}_{10}^{\mathit{c}\mathit{a}\mathit{l}\mathit{c}}$ (kPa)
Upper Bound	150	150	150	310
Lower Bound	1	1	1	3
	Eartery (kPa)	Enec (kPa)	Efib (kPa)	Ecalc (kPa)
Upper Bound	1000	1000	1000	3000
Lower Bound	1	1	1	3

2.4.1. Validation, Sensitivity Analysis, and Literature Comparison

While the goodness-of-fit from the inverse FEA establishes the first level of confidence, validation and comparison to existing constitutive models allows for further assurance to the reliability of the fitted parameters. For experimental material property validation, uniaxial tensile tests were performed on three segments cut from the arteries used for cases 2, 3, 4, 8, and 9. Arteries were cut open axially and flattened into a rectangular sheet. Next, a dog-bone-shaped punch (gage region width 3 mm) was used to cut samples in the circumferential direction. The test was performed at a quasi-static testing rate of 0.1 mm/s in open air at room temperature, and no samples underwent preconditioning to correspond to the inflation testing. The median data sets were fit to the neo-Hookean constitutive model (with the first principal first Piola Kirchhoff stress, P₁, and the stretch along the axis of extension, λ, related by P₁ = 2C₁₀(λ − λ⁻²)) shown previously using a standard curve fitting procedure. Additionally, a sensitivity study was performed where simulations were performed with the homogeneous fitted C₁₀ doubled and halved and the percentage difference between simulated and experimental vessel diameters calculated. Finally, for additional comparison, the FE models of each artery were run with constitutive models from three previous publications [18,27,35]. These works all utilized a polynomial constitutive model of the form

$$W=C_{10}\left(I_1-3\right)+C_{01}\left(I_2-3\right)+C_{20}{\left(I_1-3\right)}^2+C_{11}\left(I_1-3\right)\left(I_2-3\right)+C_{30}{\left(I_1-3\right)}^3.$$ (3)

Barring Lally et al. the studies chosen all define the five plaque components in similar terms to this study. Lally et al. defines the plaque as a homogeneous entity and, thus, was treated similarly to homogeneous plaque in this study. The polynomial strain energy function chosen for these studies has all its constants defined linearly and so the meaning of the averaged constants for different plaque components, for constructing the finite element models, is relatively clear unlike for strain energy functions with exponential terms where the meaning of the averaged parameters becomes less obvious. Finally, there is little information on the mechanics of peripheral artery plaque mechanics and, thus, data were chosen where available for polynomial strain energy functions. The resulting error values for each strain energy function and the error values from the heterogeneous and homogeneous fits and the median fitted values for each artery were compared using a Kruskal-Wallis test followed by a multi-comparison test. This test was chosen due to the observed positive skew of the data. The statistical analysis was performed in MATLAB 2016b (The MathWorks Inc., Natick, MA, USA) where the multi-comparison test adjusts the significance level accordingly.

Further (in silico) validation was performed by assigning known material parameters (the mean of the heterogeneous parameters given in Table 2) to a FE model generated from IVUS-VH imaging of a new artery at the baseline pressure. This FE model was then given the same boundary conditions as for the neo-Hookean FE models used for the fittings and the resulting nodal displacements recorded and used to calculate the deformed geometry. A fitting procedure was then performed to the in silico deformed geometry and the acquired neo-Hookean parameters compared to the parameters assigned to the initial FE model. If the fitting procedure is representative and repeatable then the parameters will be the same. In addition, to further test the robustness of the fitting procedure to noise, noise was added to the deformed geometry and the fitting procedure again performed. This noise was pseudorandom values drawn from the standard normal distribution scaled by the mean range of the data multiplied by five. This on visual observation gave a sufficiently noisy signal without losing the overall data pattern (Supplementary Figure 1).

2.5. Linear Fitting

As the zero stress state cannot be found directly in vivo the hyperelastic material has limited application clinically without further, computationally expensive, processing. However, if linear elasticity is assumed then the zero stress state is not required and the systolic vessel geometry can be simulated using the diastolic pressure geometry and the pressure difference. Such linear conditions can be reasonably assumed, as deformation between diastole and systole in femoral arteries is often less than 10% [36,37]. Furthermore, inverse FE for nonlinear analyses is relatively slow and requires multiple data points recorded at different pressures to fit hyperelastic materials accurately, further increasing optimization time. Such long optimization times are impractical for patient-specific modeling of arterial walls for clinical applications. Linear FE analyses are computationally less expensive than their nonlinear counterparts, and in the present analysis required fewer data points (clinically two data points, 80 and 120 mmHg, would be required). By taking IVUS-VH images at measured maximum and minimum pressures in vitro and utilizing the work flow that will be described in Section 3, the mechanical response may be determined and subsequent computational analysis of possible treatment methods evaluated in situ. To test this, fitting to a linear elastic material model was performed again by inverse FE according to

$$x*=\underset{x}{\text{argmin}}{\left|\left[{|d_{max}^{comp}-d_{max}^{exp}|}_{80},{|d_{min}^{comp}-d_{min}^{exp}|}_{80},{|d_{max}^{comp}-d_{max}^{exp}|}_{120},{|d_{min}^{comp}-d_{min}^{exp}|}_{120}\right]\right|}^2$$ (4)

where the terms of Eq. (4) are defined in the previous section. Differing from the hyperelastic optimization, fitting pressures for linear elastic optimization were only applied at 80 and 120 mmHg, to replicate the diastolic and systolic in vivo pressures. Like before the optimization was bounded to ensure physically plausible values, however, initial studies found that multiple starting points were not required as the lowest error was found regardless of the starting point. Thus, only one set of initial parameters was generated that satisfied the following inequality, E^calc > E^nec + E^fib + E^artery, where E^calc, E^nec, E^fib and E^artery are the randomly assigned starting points of the elastic moduli for calcified plaque, necrotic core, fibrous plaque and artery, respectively. As stated in Section 2.4, both heterogeneous and homogeneous models were considered with homogeneous fitted parameters the basis for the bounds of the heterogeneous fits.

The linear fittings would better emulate clinical conditions if the VH images were recorded at 80 mmHg in the experimental procedure, and were then subsequently loaded by 40 mmHg in silico to replicate the in vivo systolic pressure. However, difficulties in acquiring VH images at pressures higher than 10 mmHg (due to the limited diameter range of the field-of-view) rendered this option impossible for most of the vessels. Nevertheless, as this was a linear analysis it was assumed that the vessel stiffness between 0 and 120 mmHg was equivalent to the vessel stiffness between 80 and 120 mmHg. To test this assumption, IVUS-VH images were captured at 80 mmHg for the only artery where this was possible (case 6, which had a small enough outer diameter to fit in the field-of-view at higher pressures) and converted into a finite element mesh in the same manner as for the baseline VH images. The finite element model was then assigned the heterogeneous and homogeneous fitted linear elastic material properties found by the methods in the previous paragraph and pressurized by 40 mmHg to replicate at total representative systolic pressure of 120 mmHg. If the linear material assumption holds, then the mean wall diameter should be similar to the value when the baseline finite element model was pressurized by 120 mmHg.

As in Section 2.4 in silico validation was performed by assigning known material parameters (the mean of the heterogeneous parameters given in Table 5) to a FE model generated from IVUS-VH imaging of a new artery at the baseline pressure. This FE model was run with the same boundary conditions as for the linear elastic FE models used for the fittings and the deformed geometry calculated. The fitting procedure was then performed using the in silico deformed geometry and the acquired elastic moduli compared to those assigned to the initial FE model. Additionally, as in Section 2.4 noise was added to the deformed geometry and the fitting procedure again performed.

Table 5.

Parameters obtained by fitting a neo-Hookean constitutive model to the uniaxial tension data in Figure 7.

Case	2	3	4	8	9
C10 (kPa)	172.9	67.33	179.7	188.8	74.0

Finally like for the neo-Hookean material, a sensitivity study was performed where simulations were performed with the fitted elastic modulus doubled and halved and the percentage difference between the simulated and experiment vessel diameters calculated.

3. Results

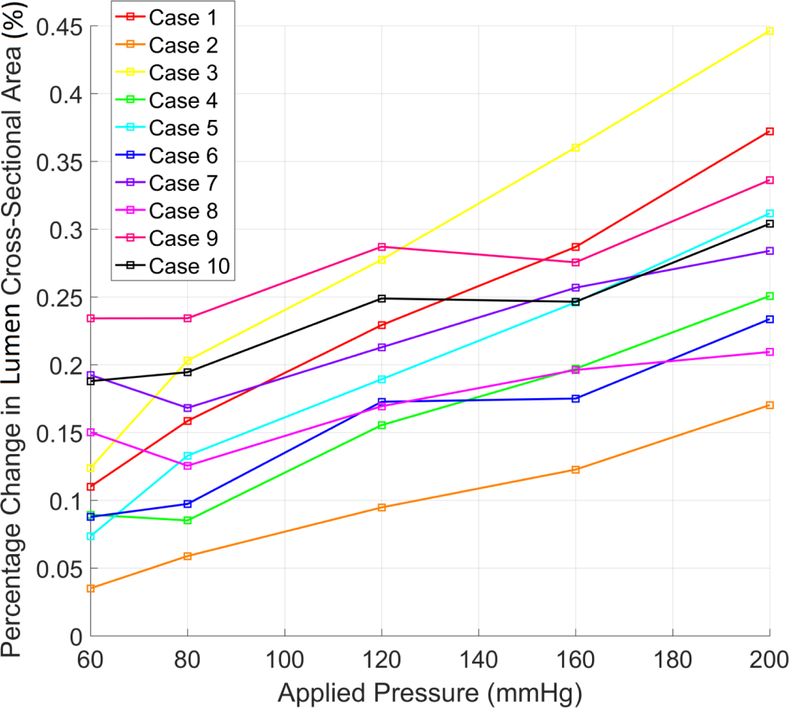
Pressure-inflation testing results can be seen in Figure 4 for vessel cross-sectional area. Overall, there is an increase of vessel area with pressure with case 3 showing the largest increase and overall gradient and case 2 the lowest. However, the cross-sectional area plateaus and slightly decreases for many cases at different pressures.

Figure 4.

Percentage change in lumen cross-sectional area compared to baseline measurement versus applied interior pressure for each case.

3.1. Hyperelastic Nonlinear Fitting

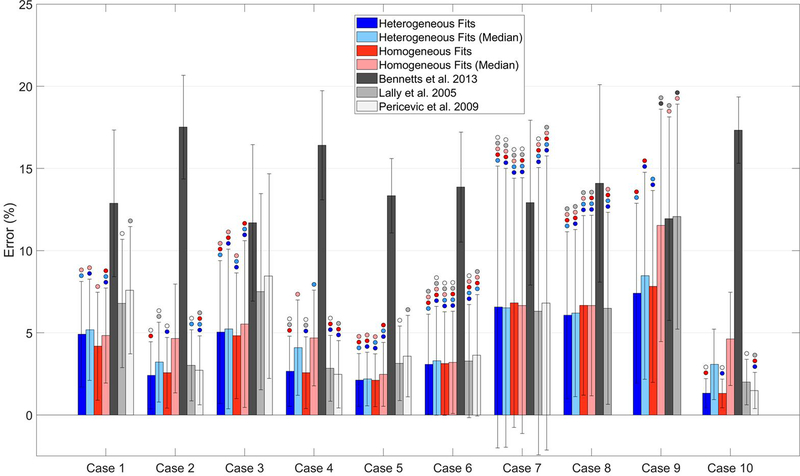
An overlay of the finite element mesh for the fitted parameters for case 4 and the IVUS DICOM at the same axial position for a representative slice at 200 mmHg is shown in Figure 5. There can be seen a good association between the simulated and experimental geometries. For the optimization, all starting points yielded the different parameters sets at the end of the procedure. The best fit parameters, from the multiple starting points selected, for the homogenous wall are given in Table 3, where it can be seen that all fitted C₁₀ values are relatively closely grouped (median and interquartile range are 79.60 and 65.99 kPa respectively). The lowest value was 40 for case 9 and the highest 143 kPa for case 10. The percentage error, also shown in Figure 6, (found by normalizing the difference between the experimental and simulated vessel diameters at each pressure) is above 5% for cases 7, 8, and 9. For the heterogeneous plaques again the starting points yielded different parameters at the end of the optimization procedure. Compared to homogeneous fittings there is greater variability between the samples with the median of artery, fibrous plaque, necrotic core and calcification at 69.41 (85.88), 26.20 (46.20), 12.20 (27.60), and 149.3 (17.90) kPa (interquartile range shown in parentheses) respectively. Comparing the error for the fitted parameters of each artery to the error for the median fitted parameters, it can be seen that the error is larger for both homogeneous and heterogeneous models, as would be expected (Figure 6). However, the difference is less than 1% for most cases in the heterogeneous models, and no more than 2%. Additionally, for the homogeneous models the difference between the errors is larger but still below 3% for all cases bar case 9 and 10. Comparing these errors to the errors resulting from using material models from the literature (Figure 6), it can be seen that only the models of Lally et al. and Pericevic et al. [18,35] have comparable error values for some cases. In contrast, the model from Bennetts et al. showed significantly higher (p< 0.05) error for all cases. Comparing the errors for Lally et al. to those calculated from the median fitted values, it can be seen that the results of this study show statistically significant lower errors (p<0.05) for less than half of the cases (cases 1, 3, 5 and 9 for heterogeneous fits and cases 1, 3 and 5 for homogeneous fits). Comparing the errors from the model proposed by Pericevic et al. to that from the median fitted values, it can again be seen that the results of this study show significantly lower errors (p<0.05) for only 3 cases for both heterogeneous and homogeneous fits (cases 1, 3 and 5). However, the model proposed by Pericevic failed to converge for two cases limiting its application.

Figure 5.

A representative overlay of the finite element mesh from Case 1 on the corresponding IVUS DICOM slice at 200 MPa.

Table 3.

Hyperelastic fitted arterial wall and plaque SEF coefficients for heterogeneous and homogeneous wall structure. Also shown are the mean percentage difference between experimental and computational vessel minimum and maximum diameters calculated at each image slice (Geometry Difference (%)) and the standard deviations of the error values calculated at each slice (% Diff StDev). Additionally the percentage difference between experimental and computational vessel minimum and maximum diameters at each slice for the median fitted parameters is also given (Geometry Difference (median fit, %)) and the standard deviation of the error values at each slice for the median fitted parameters (Geometry Difference StDev (median fit, %) ).

Homogeneous C10 (kPa)
Case	1	2	3	4	5	6	7	8	9	10	Median
Whole model	69.31	139.0	58.34	135.3	92.09	82.82	73.95	76.38	40.87	143.8	79.60
Geometry Difference (%)	4.16	2.57	4.82	5.60	2.11	3.13	6.84	6.67	7.82	1.31
Geometry Difference (%) StDev	3.31	2.15	3.82	3.66	1.60	3.16	7.56	5.46	5.85	0.87	-
Geometry Difference (median fit, %)	4.83	4.66	5.53	4.86	2.48	3.20	6.87	6.69	11.53	4.63	-
Geometry Difference StDev (median fit, %)	2.89	3.31	5.08	2.91	1.94	3.11	7.79	5.50	7.07	2.84	-
Heterogeneous C10 (kPa)
Artery	15.82	119.7	14.20	113.8	37.31	11.01	101.7	101.5	25.40	101.7	69.41
Fibrous Plaque	38.47	58.36	13.93	117.2	46.37	12.13	13.78	11.45	12.16	108.6	26.20
Necrotic core	12.41	10.02	11.99	106.4	38.42	10.82	11.28	10.02	18.05	114.4	12.20
Calcification	149.0	209.2	149.4	149.1	149.2	149.2	167.4	167.0	105.8	167.1	149.3
Geometry Difference (%)	4.92	2.41	5.04	2.66	2.12	3.07	6.56	6.07	7.41	1.33	-
Geometry Difference (%) StDev	3.21	2.04	4.34	2.14	1.61	3.03	8.57	5.08	5.47	0.89	-
Geometry Difference (median fit, %)	5.18	3.22	5.23	4.09	2.19	3.29	6.59	6.20	8.47	3.08	-
Geometry Difference StDev (meidan fit, %)	3.08	2.43	4.86	2.90	1.63	3.31	8.48	5.08	6.30	2.14	-

Figure 6.

A comparison of the mean error (± standard deviation) for each case for the fitted parameters in this study (Table 2) and for constitutive models from three previous studies. Bars marked with a circle are not significant with respect to the bar of the same color as the circle.

A sensitivity study for the homogeneous fits was performed to better understand the nature of the fittings. The fitted C₁₀ values were increased and decreased by a factor of 2, and the resulting error values plus/minus the standard deviations are given in Table 4. For double C₁₀, the error values tend to be around 50–80% greater than in Table 3, with no mean values (bar case 9) exceeding 10%. For half C₁₀, the error values were larger for every case, except case 3, compared to the doubled C₁₀ values, with most mean errors more than twice those in Table. Additionally, for halved C₁₀, some cases did not converge for all pressures; in particular, case 2 only converged for 60 and 80 mmHg. Overall, the vessel is less sensitive to large increases in stiffness compared to large decreases in stiffness, although the errors were relatively small in both cases when considering the large changes in vessel stiffness.

Table 4.

Sensitivity study results in homogeneous wall material parameters. Fitted parameters were increased or decreased by a factor of two for both Neo-Hookean and linear elastic material models and the resulting mean errors and standard deviations (StDev) are shown. Superscripted numbers indicates that the following pressures were eliminated from mean due to model convergence issues.

Double Fitted C10
Case	1	2	3	4	5	6	7	8	9	10
Geometry Difference (%)	7.81	3.99	7.88	3.75	4.94	5.23	7.67	8.12	11.57	2.90
Geometry Difference (%) StDev	3.62	3.05	5.95	2.94	2.76	4.09	9.20	6.51	7.07	1.76
Half Fitted C10
Case	1200	2120, 160, 200	3	4	5	6	7160,200	8200	9200	10
Geometry Difference (%)	10.52	5.60	5.71	5.57	10.43	9.73	8.47	9.46	14.36	5.85
Geometry Difference (%) StDev	8.12	3.84	4.29	3.47	7.38	7.22	7.02	7.44	11.59	3.43
Double Fitted Elastic Modulus
Case	1	2	3	4	5	6	7	8	9	10
Geometry Difference (%)	6.90	3.11	5.43	3.03	4.36	3.91	6.29	6.78	9.25	2.34
Geometry Difference (%) StDev	3.11	2.64	4.94	3.07	2.40	3.99	8.06	5.75	6.18	1.49
Half Fitted Elastic Modulus
Case	1	2	3	4	5	6	7	8	9	10
Geometry Difference (%)	8.32	3.89	14.98	4.85	5.33	8.83	10.71	9.57	13.30	3.57
Geometry Difference (%) StDev	5.33	2.72	6.50	2.37	2.58	4.39	6.33	6.25	7.31	1.81

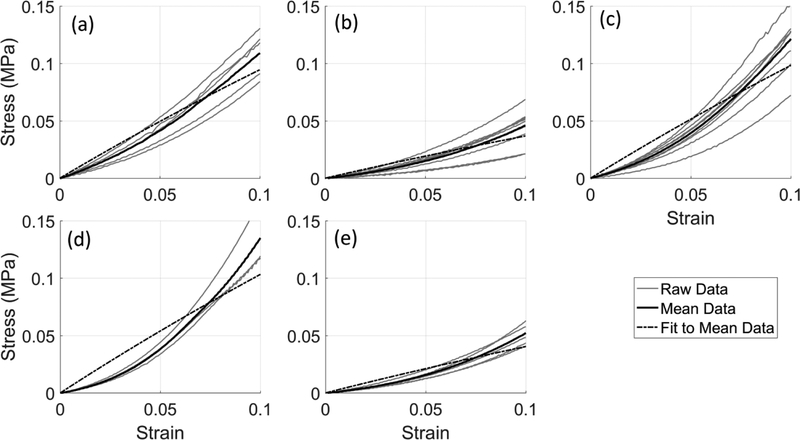
3.1.1. Validation

Validation was performed by fitting neo-Hookean coefficients to uniaxial tension data of five arteries previously evaluated in this study (Cases 2, 3, 4, 8, and 9). The uniaxial tension curves and the mean curve for each artery are shown in Figure 7. Overall, the fit to the tensile behavior was good, but did not effectively capture the strain stiffening behavior. However, the magnitudes of the C₁₀ coefficients fitted to this uniaxial data for each artery (Table 5) are relatively similar to all cases for the homogeneous fits in Table 3 except case 8.

Figure 7.

Circumferential tensile stress versus strain response for case 2 (a), case 3 (b), case 4 (c), case 8 (d), and case 9 (e). Mean and subsequent curve fit to the mean are also given.

The results of the in silico validation can be seen in Table 6. The fitted parameters are near identical to the assigned parameters with only a small difference for the artery wall. In addition, the parameters acquired from fitting to the noisy data are also in good association.

Table 6.

Parameters assigned to the FE models to acquire the in silico deformed geometry utilized for the corresponding validation and the resulting fitted parameters for both neo-Hookean and linear elastic materials. Fitted parameters to the noisy deformed geometry are also given.

	Neo-Hookean Parameters (kPa)			Elastic Moduli (kPa)
	Assigned	Fitted	Fitted (noisy)	Assigned	Fitted	Fitted (noisy)
Artery	64.21	62.94	21.62	313.5	314.4	454.7
Fibrous Plaque	43.25	43.00	37.69	57.96	56.41	108.2
Necrotic Core	34.38	34.26	63.07	109.6	110.3	49.01
Calcification	156.24	156.00	145.83	737.9	738.4	738.4

3.2. Linear Fitting

The fitted parameters for the homogenous wall are given in Table 7. Here, it can be seen that the fitted values for elastic modulus are not as closely grouped as they are for C₁₀ (Table 3) the homogeneous elastic modulus median was 292.2 (411) kPa, compared to 79.60 (65.99) kPa (interquartile range shown in parentheses) for C₁₀. The lowest value was 111.0 kPa for case 9 and the highest 844.7 kPa for case 2. For the heterogeneous model coefficients, there is also greater variability between the samples, with the median coefficients of artery, fibrous plaque, necrotic core and calcification at 133.94 (475.99), 36.44 (81.31), 54.76 (168.54) and 538.35 (638.7) kPa (interquartile range shown in parentheses), respectively. The errors for the median fitted parameters are, expectably, higher than the errors for the fitted parameter to each artery. However, as with the hyperelastic fits, the difference between the errors is small (although the linear elastic fits only fit to two pressures rather than five for the hyperelastic fits and so the error would be expected to be lower). The homogeneous models showed differences less than 4% for all cases bar case 9 and 10, and the heterogeneous models showed differences less than 3% for all cases bar case 10.

Table 7.

Linear elastic fitted arterial wall and plaque SEF coefficients for heterogeneous and homogeneous wall structure. Also shown are the mean percentage difference between experimental and computational vessel minimum and maximum diameters calculated at each image slice (Geometry Difference (%)) and the standard deviations of the error values calculated at each slice (% Diff StDev). Additionally the percentage difference between experimental and computational vessel minimum and maximum diameters at each slice for the median fitted parameters is also given (Geometry Difference (median fit, %)) and the standard deviation of the error values at each slice for the median fitted parameters (Geometry Difference StDev (median fit, %) ).

Homogeneous Elastic Modulus (kPa)
Case	1	2	3	4	5	6	7	8	9	10	Median
Whole model	279.2	844.7	158.5	678.5	422.3	279.2	278.6	267.5	111.0	792.4	279.2
Geometry Difference (%)	3.79	2.59	4.84	2.98	2.00	3.15	6.15	5.62	5.61	1.39	-
Geometry Difference (%) StDev	2.88	2.26	4.06	2.43	1.59	2.93	6.45	4.74	3.91	0.97	-
Geometry Difference (median fit, %)	3.81	6.01	5.03	5.99	3.18	3.15	6.17	5.59	10.89	6.30	-
Geometry Difference StDev (median fit, %)	2.86	3.65	4.48	2.82	2.06	2.93	6.45	4.79	6.62	2.50	-
Heterogeneous Elastic Modulus (kPa)
Artery	11.41	989.1	10.04	11.22	11.41	357.8	197.1	487.4	70.78	989.1	133.9
Fibrous Plaque	10.23	15.92	64.87	11.79	17.92	13.89	181.8	103.0	54.95	95.20	36.44
Necrotic core	179.1	11.36	10.02	10.56	477.6	36.85	181.8	10.04	72.67	105.5	54.76
Calcification	481.3	1255	560.5	1549	511.7	460.1	516.2	604.9	320.3	1120	538.4
Geometry Difference (%)	3.52	2.37	3.83	2.71	1.96	2.83	5.55	4.86	5.08	1.30	-
Geometry Difference (%) StDev	2.70	2.07	3.60	2.44	1.56	2.40	6.99	3.88	3.69	0.92	-
Geometry Difference (median fit, %)	3.67	5.53	4.46	5.94	3.17	2.89	5.91	6.65	5.74	5.31	-
Geometry Difference StDev (median fit, %)	2.73	3.55	3.88	3.03	2.06	2.68	7.62	4.63	3.99	2.43	-

Similar to the hyperelastic material model, a sensitivity study for the homogeneous fits was performed to better under the nature of the low error values (Table 4). Doubling the elastic modulus led to varied increases in mean error with more than double for case 5 and a marginal increase of case 4. When the elastic modulus is halved the error is higher for all cases compared to doubling the elastic modulus. Case 3 in particular has a mean error three times greater than for the fitted elastic modulus. Like for the hyperelastic sensitivity study this indicates that the vessel deformation is not strongly sensitive to large changes in vessel stiffness. Doubling vessel stiffness has a relatively small effect on vessel deformation and while reducing vessel stiffness had a larger effect this was still relatively small considering the large changes to the vessel stiffness.

Finally, it was assumed that that the vessel stiffness between 0 and 120 mmHg was equivalent to the vessel stiffness between 80 and 120 mmHg such that the fitted parameters are applicable to a clinical scenario. This assumption was tested by obtaining VH images at 80 mmHg for case 6 then pressurizing an FE model generated from these images by 40 mmHg and comparing the vessel deformation to an additional simulation where an FE model generated from VH images at 10 mmHg was pressurized by 120 mmHg. It was found that the mean percentage difference between the experimental and computational mean vessel diameter for the heterogeneous plaque was 4.24 ± 2.82% and for homogeneous plaque was 3.62 ± 2.71%. This indicates that the assumption was acceptable and the fitted parameters may be considered applicable to the clinical loading scenario.

3.2.1. Validation

The results of the in silico validation can be seen in Table 6. The fitted parameters are the sufficiently similar to the assigned parameters to have confidence in the procedure. In addition, the parameters acquired from fitting to the noisy data are in the same magnitude with calcification in particular showing near identical magnitude.

3.3. Simulation and Optimization Time

Simulation time was reduced, on average, from approximately 10 minutes for the neo-Hookean material to 5 minutes for the linear elastic materials. The total optimization time was reduced from, on average, over two weeks to around 24 hours, mostly as a result of the simplified optimization procedure. However, for heterogeneous models an additional time consideration was the model generation, including the material averaging, which regardless of material type took approximately 5 minutes. Consequently, with this in addition to the simpler optimization problem the homogeneous material optimization took considerably less time, reducing neo-Hookean material optimization to less than one week and linear elastic material optimization to around 8 hours.

4. Discussion

While significant work has been performed in categorizing the mechanical properties of atherosclerotic plaques, the most common methods for determining the fitted constitutive model parameters is ex vivo testing of explanted samples. This is disadvantageous for use clinically as, for obvious reason, this cannot be applied to patient arteries and ex vivo samples show large variation in mechanical response (Table 1). Thus, it is currently unclear how applicable any given constitutive model or its parameters are to an individual patient. With these points in mind, we utilized the data available clinically (i.e., the vessel geometry and plaque composition identified by IVUS-VH, and the internal pressure in the vessel) to fit a simple Neo-Hookean constitutive model and a linear elastic material. Then, the error for each fit was calculated and analyzed.

The low errors seen for both homogeneous and heterogeneous fittings in Table 3 demonstrate the capability of a simple strain energy function to describe the loading behavior of the arterial wall for the data available clinically. This may be partially explained by the relatively low sensitivity of the FE vessel diameter to doubling or halving C₁₀ i.e. the mean vessel diameter will be somewhat unchanged providing the material stiffness is with an acceptable tolerance. However, the low variability in the homogeneous fitted parameters is at odds to the pressure-inflation data (Figure 4), where there is much greater variability. Nevertheless, this is encouraging as it demonstrates that high variability in vessel distortion is not necessarily reflected in the fitted values. Considering this finding in conjunction with the finding of low sensitivity to material parameters, it is possible that a general lumped parameter may be able to describe the displacement behavior of all arteries undergoing such loading conditions with an acceptable tolerance.

For validation, the relative similarity between the C₁₀ values from the uniaxial tensile tests (Table 5) is a promising indication of the accuracy of the lumped values to describe the circumferential arterial behavior. However, case 8 showed a large dissimilarity between the fitted C₁₀ values, which may be because the tested samples had stiffer plaque components than the majority of the remaining vessel wall. Regardless, the value is still within an acceptable tolerance given the differences between uniaxial and pressure-inflation testing procedures.

As an additional means of assessing the quality of the parameters obtained from the material curve fitting a comparison was performed using three sets of literature values. The error values were calculated for each artery for each parameter set and compared. For all arteries the errors calculated using the model proposed in Bennetts et al. were significantly higher than the fitted parameters. The models proposed by Lally et al. and Pericevic et al. produced lower errors that were comparable for some cases to those from the fitted values in this study. However, the constitutive model utilized by Lally et al. has two components, artery wall and stenotic plaque. Thus, the plaque is assumed homogeneous. Homogeneous plaque distribution has limited application compared to the heterogeneous plaque as the stress distributions will differ greatly. Furthermore, for more advanced modeling applications such as in silico stent deployment heterogeneous plaque models will have likely more accurate stent stress distribution than homogeneous plaques. Additionally, the model by Lally et al. shows good association to these ten arteries but it cannot be assumed this extends to all PAD arteries. However, the homogenous fitting procedure can be applied to new arteries and determine specific material properties that are likely to be more accurate than those of Lally et al. In addition, while the parameters from Pericevic et al. are plaque component specific two models failed to converge when utilizing them. This highlights the need for a fitting procedure as the model convergence is sensitive to the material parameters.

As shown in Table 1, it is more common to use more complex strain energy functions with greater strain stiffening, as reported in many other studies [38–41]. One such study by Vychytil et al. fitted the Neo-Hookean model and Fung hyperelastic anisotropic constitutive models to experimental data from a pressure inflation test [42]. They found that the Fung model gave a superior fit to the Neo-Hookean model, showing strain-softening. Such behavior was not seen in our pressure inflation or tensile tests. However, we assume isotropy of the artery in the present study, due to the difficulty in acquiring axial deformation information required to fit an anisotropic model (a problem also present in vivo), and to reduce modeling complexity to allow for faster material fitting. To this end, we assumed the circumferential direction is the predominant loading direction during physiological pressures, and more so during treatment processes such as balloon angioplasty [18,43,44]. Furthermore, due to the relatively low percentage change in vessel diameter, such that the infinitesimal strain theory could be assumed, we also evaluated a simple linear elastic FE model to improve optimization time. Similar to the hyperelastic model, the errors from the linear model, for both heterogeneous and homogeneous fits, were low, although errors from the linear approach were evaluated at only two pressures, 80 mmHg and 120 mmHg, representative of diastolic and systolic pressures, respectively. However, unlike the hyperelastic fits, the sensitivity of the elastic fitted parameters is far higher for some cases therefore it is unlikely a general parameter set can be applied for the homogeneous model when using an even simpler constitutive model. When comparing the C₁₀ parameter to the elastic modulus for the homogeneous fits it can be seen that generally the magnitude of the respective parameters coincides for each case with the highest and lowest values of the respective mechanical properties occurring for the same cases. While this is expected as the increase in vessel diameter when pressurized will be directly dependent on the vessel stiffness it still indicates consistency in the fitting procedure. This, however, is less apparent for the heterogeneous fits, where unlike for the homogeneous fits the elastic moduli of plaque components for some cases are less than the corresponding C₁₀ value. This is likely due to the additional complexity in the fitting procedure, such that many combinations of plaque component elastic modulus give an equally low error. Comparing the fitted elastic modulus for the plaque components to values calculated by Lee et al. from dynamic compression testing, the non-calcified plaque components are less stiff in this work and the calcification is also approximately an order of magnitude less stiff [45]. By contrast, in Tracqui et al. they found, using atomic force microscopy, a mean necrotic core elastic modulus that was considerably less stiff than in our study and fibrous plaque had similar stiffness [46]. In the work by Baldewsing et al. they used ultrasound imaging and FE modeling to determine plaque component elastic modulus and found necrotic core mechanical properties comparable to this study for in vitro plaque but calcification far stiffer in their work [47]. However, for in vivo plaque the calcification had comparable values to this work but necrotic core was considerably less stiff in their study. These differences in elastic modulus may be a result of the different loading behavior with compression likely yielding a different response to pressure-inflation, and the patient specificity of the plaque properties. Finally, as mentioned previously, due to difficulties in the experimental arrangement of VH, we could only capture pressures above baseline for case 6. Therefore this was utilized as a means for validating the linear elastic assumption. The low errors demonstrate that the linear elastic assumption holds, although further samples would provide more assertion to this claim. However, when comparing these errors to the sensitivity data, the low sensitivity of the former may indicate that the error would be low for a wide range of material parameters.

An alternative approach for determining arterial wall mechanical response in vivo is elastography. Mascarenhasa and colleagues used ultrasound elastography to determine aortic wall mechanical properties under physiological loading conditions [48]. As in the present study, the wall was inflated to beyond physiological pressures and modelled as a neo-Hookean material. They found the average shear modulus to be 92 kPa, which is similar to our values for homogeneous arterial wall (G = 2C₁₀, with G the shear modulus), although our vessels were likely stiffened by disease and calcification, thus increasing the shear modulus. However, no additional testing was performed on the arteries in Mascarenhasa et al. to validate their material parameters, although they compared well with previous validated studies. Yet another approach is shear wave imaging, which was utilized in vivo in Couade et al. to measure human carotid artery shear modulus [49]. Again, they found shear moduli similar to our homogeneous values (mean was 130 KPa at systole and 80 KPa at diastole), although as in [31], this was performed on healthy tissue and no comparison with mechanically tested arterial tissue from the same artery was performed for validation. The last widely investigated approach for minimally invasive in vivo imaging is acoustic radiation force impulse imaging. One such study by Dhal and coworkers investigated carotid artery atherosclerotic plaque mechanical properties [50]. Tests were performed in vivo on volunteers with high or low cardiovascular disease risk. They found the stiffness of homogeneous plaques was no different to vascular tissue, while heterogeneous plaque had distinguishable hard and soft regions with a stiff cap covering the soft region. However, as this was a feasibility study, they did not acquire mechanical properties which would allow comparison with this study.

4.1. Limitations

The linear fittings would better emulate clinical conditions if the VH images were recorded at 80 mmHg in the experimental procedure and then subsequently loaded by 40 mmHg in silico to replicate the in vivo systolic pressure. However, VH limitations prevented us from acquiring images at pressures higher than 10 mmHg for cases other than case 6. Nevertheless, we assumed that since this was a linear analysis, the change in vessel diameter between 80 and 120 mmHg would be the same regardless. This assumption was partially verified by our investigation with case 6; however, further investigation would be required to analyze whether the low errors obtained in this study are indeed reflected when fully replicating in vivo loading.

During artery preparation suture was utilized to seal the vessel branches and efforts were made to utilize as little suture as possible so that it did not influence the VH images while still ensuring a good seal. In post processing the effect of the suture on the resulting VH images was minimized, and branching occurred in only a small proportion of the vessel wall, so it is unlikely that this had a significant effect on the results obtained. However, this resulted in the vessel having high leakage at high pressures such that the loading/unloading of the vessel was erratic and could not be reasonably controlled to conduct a preconditioning protocol. This difference in mechanical response compare to a preconditioned artery will be reflected in the fitted mechanical parameters and thus this must be considered when interpreting these values.

For the neo-Hookean fittings necrotic core showed similar mechanical properties to fibrotic plaque and arterial wall. As necrotic core is formed of a lipid pool it should show weaker mechanical response than the other components. One reason for this disparity may be that necrotic core is often found around calcification in the VH images and thus it may be that this influenced the fitted necrotic core and resulted in it being artificially stiffer. Alternatively, the artifacts in IVUS image may have resulted in incorrectly identified necrotic core when it was a different component which in turn would have led to an artificially stiffer value from the optimization procedure. For the linear elastic tissue this may have been exacerbated by the reduced data available. An initial requirement was that calcification had to be stiffer than the sum of the other components for all starting points. Further restrictions were not applied so that the problem wasn’t over constrained and artificially guided to an optimum solution. However, in future further constraints on the mechanical response to of necrotic core may be required to further ensure physical plausibility.

Residual stresses were not included in the finite element models. It has been shown in previous studies that residual stress can greatly affect stress magnitude and location of stress concentrations in models of both healthy and diseased arterial walls [51–53]. However, there is currently no means of determining residual stresses in vivo. Also, it is likely that each plaque type will have differing residual stresses (or no residual stress), and that the residual stress will vary for the same plaque type based on the position axially, radially and circumferentially [54]. Therefore, because of the likely inaccuracies and to simplify the simulation, we opted to neglect residual stresses as part of the simulation. Consequently, care must be taken when interpreting the fitted constitutive model parameters as they incorporate the influence of the residual stresses and the actual material property.

Finally, our tests were conducted with arteries held in body temperature saline, while in vivo the artery is surrounded by adjacent tissues. This is unlikely to affect the IVUS signal, but the tissue will deform differently in our in vitro tests, as there is no surrounding tissue to push back on the expanding arterial wall. Thus, caution must be taken when using the fitted parameters elsewhere as this effect is likely incorporate into the parameters such that the actual material parameters may differ. Therefore, further testing would be required to evaluate whether this fitting procedure would still be applicable when including surrounding tissues.

5. Conclusions

In this study, we utilized IVUS-VH imaging to obtain geometric information from atherosclerotic and heavily diseased human cadaveric femoral arteries during in vitro pressure inflation testing. Due to a lack of reliable constituent material information in the literature and the difficulty in individually characterizing the material response of plaque components, we employed an inverse FE procedure to determine material behavior. The inverse FE procedure was performed assuming the artery was heterogeneous and assuming the entire geometry was homogeneous. In addition, in an attempt to decrease computational time to increase the applicability of this method in a clinical setting, we repeated this inverse FE procedure assuming linear elastic material properties (again considering both a heterogeneous and a homogeneous case), and compared these results to the hyperelastic material results. Overall, it was found that the fitted parameters for both heterogeneous and homogeneous walls had low errors and that when the means of the fitted parameters were placed in FE simulations the difference between simulated and experimental results were also low. Furthermore, when the homogeneous fitted parameters were doubled and halved the errors showed a relatively small increase indicating a relatively low sensitivity to large changes in the wall stiffness. Finally, compared to literature values, the median fitted homogeneous and heterogeneous parameters showed superior or better correspondence to the experimental data. Therefore, for clinically available data i.e. vessel morphology and vascular pressure, a simple constitutive model can sufficiently describe the vessel even beyond physiological pressure. Additionally, if wall heterogeneity is not required a homogeneous wall structure can accurately recreate vessel deformation.