Correcting Undersampled Cardiac Sources in Equivalent Double Layer Forward Simulations

Abstract

Electrocardiographic Imaging (ECGI) requires robust ECG forward simulations to accurately calculate cardiac activity. However, many questions remain regarding ECG forward simulations, for instance: there are not common guidelines for the required cardiac source sampling. In this study we test equivalent double layer (EDL) forward simulations with differing cardiac source resolutions and different spatial interpolation techniques. The goal is to reduce error caused by undersampling of cardiac sources and provide guidelines to reduce said source undersampling in ECG forward simulations. Using a simulated dataset sampled at 5 spatial resolutions, we computed body surface potentials using an EDL forward simulation pipeline. We tested two spatial interpolation methods to reduce error due to undersampling triangle weighting and triangle splitting. This forward modeling pipeline showed high frequency artifacts in the predicted ECG time signals when the cardiac source resolution was too low. These low resolutions could also cause shifts in extrema location on the body surface maps. However, these errors in predicted potentials can be mitigated by using a spatial interpolation method. Using spatial interpolation can reduce the number of nodes required for accurate body surface potentials from 9,218 to 2,306. Spatial interpolation in this forward model could also help improve accuracy and reduce computational cost in subsequent ECGI applications.

1. Introduction

Electrocardiographic Imaging (ECGI) non-invasively describes the electrical activity on the surface of the heart and is increasingly being used to diagnosis and treatment of cardiac arrhythmias. ECGI relies heavily on ECG forward models, yet recent research has shown these models to produce more error than commonly thought [1] and that properly sampled cardiac sources can play a role in reducing error [7]. Despite the risk of increased error, ECG forward models are often subsampled to reduce computational cost. Guidelines for cardiac source resolution and interpolation tools are needed to improve the accuracy of ECG forward and subsequent ECGI calculations.

Mitigating error due to insufficient cardiac source resolution can be dependent on the type ECG forward model being used. The challenge originates from the nature of the cardiac activation wave because it is characterized by high gradients of transmembrane and extracellular potentials in a small region of space. Undersampling the activation wavefront can produce temporal noise from large regions of the tissue becoming active simultaneously. A previous study was able to reduce error due to spatial undersampling of the transmembrane currents in a finite element (FEM) model by spatially averaging the values [5]. For other types of source models, such as using activation times with the equivalent double layer (EDL) [3], spatial averaging may not be effective in reducing error due to spatial resolution. However, using EDL with a boundary element method (BEM) formulation provides an other methods to spatially interpolate cardiac surface data from undersampled sources for use in the ECG forward simulation.

In this paper, we propose new spatial interpolation schemes for use in an EDL forward simulation and tested them with varying source resolution. The goal of the study was to use these interpolation schemes to reduce or eliminate errors due to undersampling the cardiac sources, including temporal irregularities. We also sought to provide some guidelines for appropriate sampling resolutions for the cardiac surface in order to effectively use the EDL simulation with different spatial interpolations. Our results show that these techniques can be an effective solution to reducing error due to cardiac sampling.

2. Methods

We analyzed the effect of different cardiac source resolutions and different spatial interpolation methods on body surface potentials generated with the ECG forward simulation. We used five mesh resolutions and computed the EDL model with two spatial interpolation methods, triangle weighting and triangle splitting, in addition to testing without added interpolation. We evaluated computed body surface potentials against a set of ground truth potentials generated using a BEM transmembrane potential forward model.

2.1. ECG Forward Simulation

The ECG forward simulation used in this study is the EDL forward model [3]. EDL transmembrane potential (TMP) sources are parameterized to allow reformulation of the forward simulation in term of the local activation times of the cardiac tissue. For this study, the other phases of the action potential were ignored. Therefore, only the ventricular activation was simulated on the body surface.

Spatial Interpolation

In addition to the constant and linear interpolation of the TMP over each facet of the cardiac surface, we tested two methods for performing spatial interpolation of the activation times to reduce error due to low spatial resolution: triangle weighting and triangle splitting.

Triangle Weighting incorporates the activation times for the three vertices for each triangular face then scales that face’s contribution to the source geometry based on how much of it is activated. This implementation requires solving the EDL for the triangular faces, instead of the vertices, yet activation times for each vertex.

Triangle Splitting is effectively adaptively refining the cardiac mesh along the activation wave front. For each time step, partially activated faces are subdivided into activated and inactivated regions. Using this adapted ventricular tessellation at each sample moment, the transfer function from ventricular surface to body surface is computed anew to find the ECGs at that moment.

2.2. Comparison Studies

The ground truth dataset used in this study consisted of simulated TMPs forward computed to the torso. The TMP were calculated at the maximum cardiac mesh resolution (147,458 nodes, mean edge length of 0.78 mm) using a bidomain simulation with a Ten Tusscher ionic model, with rule-based tissue anisotropy and conduction velocity of 1 m/s. The body surface potentials were then computed from the TMP using BEM. The torso mesh used contained 1520 nodes and had a mean edge length of 23 mm. The torso was modeled as homogeneous with a conductivity of 1 S/m.

To test various cardiac sampling resolutions, the cardiac mesh and TMPs were subsampled at 4 resolutions with edge lengths of 12.4 mm (578 nodes, resolution 0), 6.21mm (2,306 nodes, resolution 1), 3.1 mm (9,218, resolution 2), and 1.6 mm (36,866 nodes, resolution 3). These subsampled cardiac sources combined with the full resolution mesh (resolution 4) comprised the 5 source resolutions tested in this study. For each resolution, we computed body surface potentials using the EDL model without spatial interpolation, with triangle weighting, and with triangle splitting. Simulated body surface potentials were compared to the ground truth using root mean squared voltage (Ē), relative root mean square error (rRMSE), and correlation (ρ), as defined as follows:

$$\overline{E}=\frac{\Vert {\Phi }_{\left\{gt,s\right\}}\Vert }{\sqrt{n}}$$ (1)

$$rRMSE=\frac{\Vert {\Phi }_{gt}-{\Phi }_s\Vert }{\Vert {\Phi }_{gt}\Vert }$$ (2)

$$\rho =\frac{{\Phi }_{gt}^{{\rm T}}{\Phi }_s}{\Vert {\Phi }_{gt}\Vert \Vert {\Phi }_s\Vert }$$ (3)

where Φ_{gt,s} is a vector of either ground truth or simulated body surface potentials, n is the number of body surface electrodes,Φ_gt is a vector of the ground truth body surface potentials, and Φ_s is a vector of the associated simulated body surface potentials.

3. Results

Using different cardiac source sampling altered the computed body surface potentials in that the error in computed body surface potentials was reduced as the spatial resolution increased. Using spatial interpolation techniques also affected body surface potentials, yet the results were less dependent on the technique.

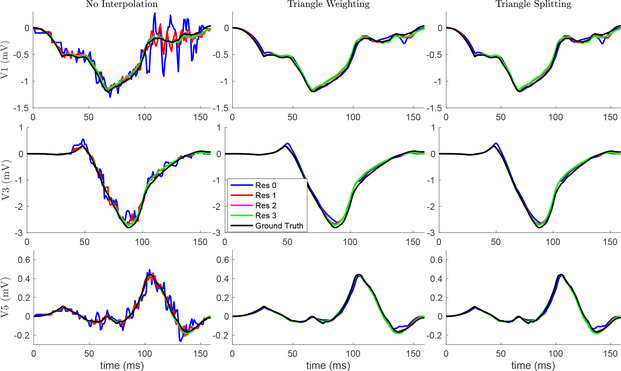
The resolution of the cardiac sources and spatial interpolation affected the ECG signals computed with the forward simulation (Figure 1). When the lowest resolution cardiac surface was used, the ECG signals contained high frequency artifacts that are reduced in amplitude as resolution increases, and are missing altogether from the highest resolution and the ground truth. These artifacts are greatly reduced or eliminated using either of the spatial interpolation methods. There is no observable difference between the two methods’ effects on the ECG signals.

Fig. 1.

Effect of spatial resolution and interpolation on ECG recordings. Ground truth and three cardiac surface resolutions are shown in each plot. The three rows represent precordial leads (v1, v3, and v5). Columns represent interpolation method. The ECGs simulated with Res 4 were nearly indistinguishable from those of Res 3.

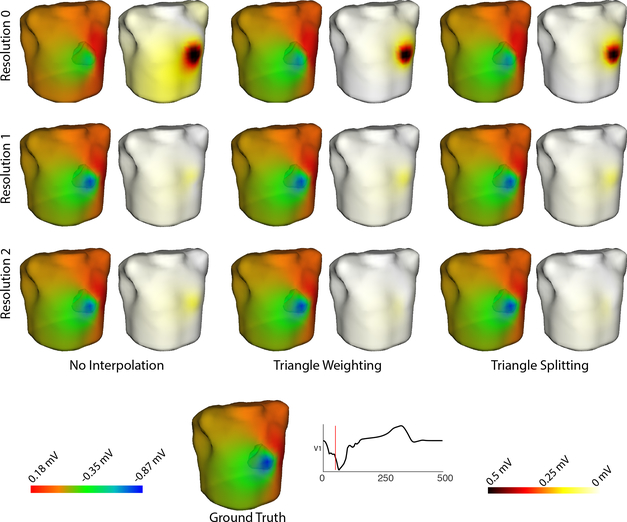
The predicted body surface potential maps were also affected by cardiac mesh resolution and interpolation method (Figure 2). Although the predicted potential maps are overall qualitatively similar to the ground truth, the greatest difference occurs near the extrema. As the resolution increases, the potential maps more closely align with those of the ground truth. Using either spatial method also reduces the difference between the predicted potential map and the ground truth.

Fig. 2.

Effect of spatial resolution and interpolation on body surface potential maps. Ground truth and three cardiac surface resolutions are shown. Difference maps are also included. The three rows represent cardiac surface resolution. Columns represent interpolation method. There were minimal qualitative differences between potential maps generated with Res 2 and those generated with higher source sampling (Res 3 & 4) maps generating higher

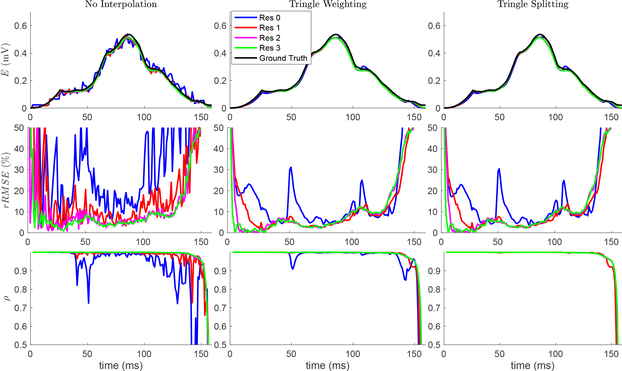
Figure 3 illustrates the Ē, rRMSE, and the ρ for the predicted body surface potentials over the ventricle activation. Similar to the ECG signal tracings, there is high frequency oscillations in the metrics over time using the low resolution cardiac surfaces (resolution 0 and 1) in the ECG forward simulation. These oscillations are reduced with mesh resolutions 2 and higher for the Ē and ρ, yet rRMSE still shows oscillations with resolution 2. These oscillations are reduce or eliminated with when spatial interpolation methods are used, even with the lowest cardiac source resolution. The two methods produced similar levels of improvement, with the exception of two remaining transient reductions in correlation with resolution 0 and triangle weighting, which are not present with triangle splitting. Interestingly, the rRMSE error remains high at the beginning and end of ventricular activation, regardless of resolution or spatial interpolation. Likewise, the ρ is very low at the end of ventricular activation for all resolutions and spatial interpolation methods.

Fig. 3.

Effect of spatial resolution and interpolation on all body surface potentials. Three cardiac surface resolutions are shown in each plot, and the ground truth is shown in the Ē plots. The three rows represent a metric (Ē, rRMSE and ρ). Columns represent interpolation method. The plot of the temporal metrics of Res 4 were nearly indistiguishable from Res 3.

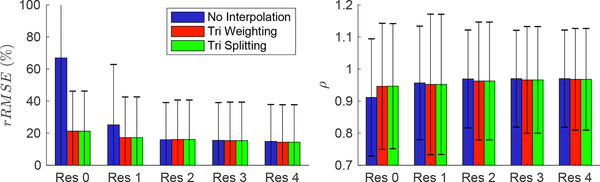
Figure 4 illustrates the mean rRMSE and ρ in simulated body surface potentials for all cardiac surface resolutions and spatial interpolation methods. Similar to the trend seen in Figure 3, the rRMSE is highest and the ρ the lowest with resolution 0 and no spatial interpolation. The rRMSE reduces and ρ increases when mesh resolution increases or spatial interpolation is used. There was no observable difference between spatial interpolation methods based on the mean error metrics of the predicted body surface potentials. The rRMSE remained somewhat high despite the increased resolution and interpolation (minimum rRMSE of 14.4 %). When we excluded the last 10 ms of the body surface potentials from the metric calculation, the rRMSE reduced by ~ 5 % for all cases except with resolution 0 and no interpolation.

Fig. 4.

Mean effect of spatial resolution and interpolation on all body surface potentials. The mean metric value over ventricular activation is shown, with the error bars representing standard deviation.

4. Discussion

The results presented in this study demonstrate that the sampling resolution of the cardiac sources can effect the ventricular activation body surface potentials computed with an EDL forward model. Additionally, the results show that spatial interpolation methods can mitigate or eliminate errors due to sampling resolution. The presented data also provide some insight into the resolution needed for EDL simulations.

The high frequency oscillation observed when predicting ECG signals with lower resolution cardiac sources (Figure 1) are expected when using EDL and BEM theory. The relatively low resolution of the source mesh increases the relative contribution of each source point or face within the simulation and the time difference between neighboring regions becoming activated. Each of these effect contribute to increased discontinuity in the electric field that is manifest as high frequency oscillations. These effects can be smoothed through the forward calculation, yet with lower resolutions, this smoothing does not adequately eliminate the high frequency artifacts. The error in the forward simulation was also manifested through changes in extrema location in the body surface potential maps (Figure 2). Similar behavior was demonstrated in previous studies analyzing the effect of source sampling error on forward simulations [5,7]. Interestingly, the error generated from reduced cardiac sampling is easier to observe by analyzing temporal signals than body surface potential maps, despite the error originating from spatial processes. While this discrepancy could be attributed to the complex nature of visualizing multidimensional data, it highlights the need for careful analysis of the sampling requirements for ECG forward simulations.

The spatial interpolation methods, triangle weighting and triangle splitting, both improved the accuracy of the predicted body surface potentials (Figure 1, 2, 3, & 4) to a similar level. Either method improved simulation accuracy from a low resolution (resolution 0) cardiac source to match or exceed the accuracy of a simulation from a higher resolution (resolution 1, Figure 4). Furthermore, using spatial interpolation, ECG signals calculated from the coarsest cardiac sources could be smoother and more closely match the ground truth than those generated with 20 times the number of nodes (resolution 2, Figure 1). Both interpolation methods performed comparably, despite triangle splitting requiring more computational resources to compute.

The results from this dataset also indicate some possible guidelines for the spatial resolution cardiac source data for EDL simulations. Without spatial interpolation, the forward simulation required at least 9,218 nodes (resolution 2) to generate ECG signals with minimal artifact and reduced noise. However, with spatial interpolation, similar smoothness in ECG signals can be achieved with as few 578 nodes (resolution 0) and a similar level of error can be achieved with 2,306 nodes (resolution 1).

The guidelines and the interpolation tools presented have only been tested on a limited dataset. To expand the scope of these guidelines and tools, more geometries and activation profiles need to be tested. However, we anticipate a similar outcome based on previous published [5,7] and results, as well as observations obtained from other, unpublished, simulations. This study also only evaluated the effect of cardiac sampling on body surface potentials during ventricular activation, excluding the plateau and repolarization stages of cardiac activity. It is possible to apply the interpolation methods to the plateau and repolarization phases, yet we expect the effect to be negligible because the spatial gradients of the cardiac sources is much lower than during activation. However, the ground truth dataset did include these stages, which provides an explain for the large error near the end of ventricular activation (Figure 3). Excluding this time points reduced the overall error (Figure 4, Section 3), suggesting that overall accuracy metrics could be improved by including the plateau phase and non-zero ST potentials to better represent late ventricular activation.

Although this study focused on the effect of cardiac source sampling on the ECG forward simulation, the result also have implications for ECGI applications. First, accurate forward simulations are needed for ECGI because many studies use simulated data to test new techniques [4,9]. Second, the errors associated with cardiac source sampling highlight a growing need to provide quantified uncertainty to both ECG forward models and ECGI [8,6,2], especially those designed for clinical use. Finally, similar strategies of generating accurate results with lower mesh resolution can improve ECGI by making complex solutions less computationally expensive, e.g., when using non-linear optimization with forward computed solutions to guess the next iterations [3].

We conclude that cardiac source resolution is an important consideration in EDL forward simulations. This study also suggested a possible minimum resolution for EDL and we introduced some spatial interpolation tools that may help mitigate errors from reduced cardiac sampling. These results will help improve ECG forward models which will lead to more accurate and new ECGI techniques to diagnose and treat cardiac arrhythmias.