Anodic stimulation misunderstood: preferential activation of fiber orientations with anodic waveforms in deep brain stimulation

Abstract

Objective.

During deep brain stimulation (DBS), it is well understood that extracellular cathodic stimulation can cause activation of passing axons. Activation can be predicted from the second derivative of the electric potential along an axon, which depends on axonal orientation with respect to the stimulation source. We hypothesize that fiber orientation influences activation thresholds and that fiber orientations can be selectively targeted with DBS waveforms.

Approach.

We used bioelectric field and multicompartment NEURON models to explore preferential activation based on fiber orientation during monopolar or bipolar stimulation. Preferential fiber orientation was extracted from the principal eigenvectors and eigenvalues of the Hessian matrix of the electric potential. We tested cathodic, anodic, and charge-balanced pulses to target neurons based on fiber orientation in general and clinical scenarios.

Main results.

Axons passing the DBS lead have positive second derivatives around a cathode, whereas orthogonal axons have positive second derivatives around an anode, as indicated by the Hessian. Multicompartment NEURON models confirm that passing fibers are activated by cathodic stimulation, and orthogonal fibers are activated by anodic stimulation. Additionally, orthogonal axons have lower thresholds compared to passing axons. In a clinical scenario, fiber pathways associated with therapeutic benefit can be targeted with anodic stimulation at 50% lower stimulation amplitudes.

Significance.

Fiber orientations can be selectively targeted with simple changes to the stimulus waveform. Anodic stimulation preferentially activates orthogonal fibers, approaching or leaving the electrode, at lower thresholds for similar therapeutic benefit in DBS with decreased power consumption.

1. Introduction

Nearly two decades after initial approval of deep brain stimulation (DBS), it has grown into an established surgical intervention for movement disorders such as essential tremor, Parkinson’s disease, and dystonia (Pizzolato and Mandat 2012, Wichmann and DeLong 2006) as well as a potential treatment option for a number of intractable psychiatric disorders. Effectiveness of DBS varies across patients. Its success depends on appropriate surgical target and stimulation parameter selection. Although target selection can be challenging, computational modeling has been used to help visualize stimulation spread to neural targets like nuclei or fiber tracts to improve our understanding of target activation (Butson et al 2007, Butson et al 2013, Noecker et al 2018). The volume of tissue activated (VTA) was developed to approximate activation around a lead through the use of multicompartment NEURON models arranged tangentially around the electrode (Butson and McIntyre 2005, Butson et al 2007). In an effort to save computational time by avoiding NEURON simulations, a number of methods approximate activation with ellipsoidal fits of the VTA (Mädler and Coenen 2012, Chaturvedi et al 2013), voltage isosurfaces (Martens et al 2011), electric field isolevels (Åström et al 2012), and second difference thresholds (Anderson et al 2018). The spread of activation can help determine which regions might correspond to clinical benefits or side effects. However, a key feature ignored in the majority of analyses is the influence of fiber orientation on activation trends. In this paper, we expand upon prior work in Anderson et al (2018) by using the Hessian of the electric potential to explore the role of orientation in axon activation.

Cathodic stimulation is used in nearly all clinical DBS applications (Volkmann et al 2006). Generally, cathodic and anodic stimuli result in different sites of action potential initiation (API). In straight axons perpendicular to a stimulating electrode, cathodic activation occurs at the node(s) nearest the electrode and anodic activation occurs at nodes farther away (McIntyre and Grill 1999, Basser and Roth 2000). Sites of API for cathodic and anodic stimulation are noted by arrows in figure 1(A). Axons are understood to be more excitable during cathodic stimulation, and many studies report larger anodic thresholds compared to cathodic thresholds (Ranck 1975, Basser and Roth 2000, Zhang and Grill 2010). In some cases, however, the presence of a local cell body enables lower anodic thresholds than cathodic thresholds (McIntyre and Grill 1999, 2000, 2002). Nonetheless, modern DBS stimulators programmed in a monopolar configuration are capable of only cathodic settings, potentially arising from a previously incomplete understanding of extracellular stimulation or a vestige of the first DBS technology.

Figure 1.

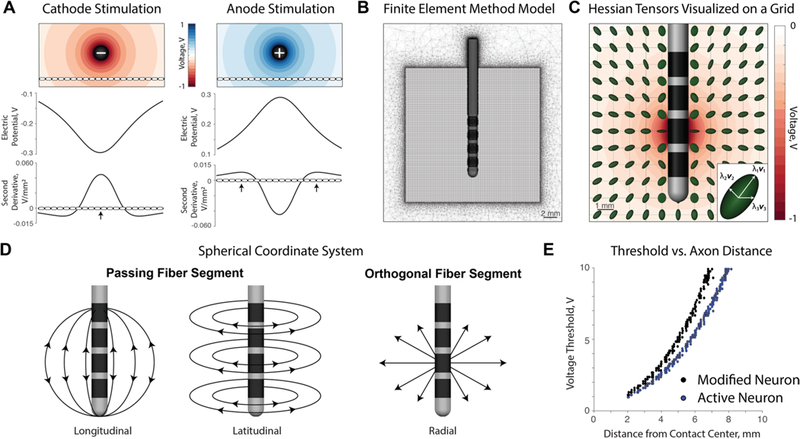
(A) The electric potential and second derivative plotted along an axon passing tangentially to the electrode. Action potentials initiate at points of sufficiently positive second derivatives: the center node closest to the electrode for cathodic stimulation and the distal nodes away from the electrode for anodic stimulation. (B) The finite element method (FEM) model consists of a tetrahedral mesh around a Medtronic 3389 lead. The Hessian was calculated on a 20 × 20 × 20mm grid with a resolution of 0.1 mm around the lead. (C) Normalized Hessian matrices visualized as 3D tensors on a subgrid given contact 1 as a cathode. Each tensor is composed of eigenvalues and eigenvectors, which represent second derivatives along principal neuron orientations. (D) A spherical coordinate system is used to describe fiber orientations throughout the paper. Orientations can be categorized into longitudinal, latitudinal, and orthogonal directions with respect to the electrode. (E) A modified neuron model was used in this paper in order to isolate firing at the location of the Hessian tensor. The active neuron is an MRG axon, and the modified neuron is an MRG axon with all compartments being passive except the center compartment.

If a monopolar configuration cannot generate a sufficiently large therapeutic window (i.e. the difference in thresholds between adequate symptom alleviation and side effects), the programmer may investigate bipolar configurations with one contact as an anode. In clinical practice, these bipolar configurations have been used to avoid side effects (Volkmann et al 2006, Deli et al 2010). The literature supports this approach with the claim that bipolar stimulation activates axons projecting through a more localized tissue volume (Ranck 1975, Basser and Roth 2000, McIntyre et al 2004, Zhang et al 2009). Given that axons with local cell bodies can be activated with anodic stimulation at lower voltages, it is possible that bipolar stimulation activates a different set of axons within that volume.

In this study, we demonstrate that cathodic stimulation preferentially activates axon segments passing adjacent to the electrode, whereas anodic stimulation preferentially activates axon segments approaching or leaving the electrode.

2. Materials and methods

2.1. Finite element model

For this work, we reference methods similar to those of Anderson et al (2018) regarding the finite element method (FEM) and the use of the Hessian matrix in approximating neural activation. We solved the bioelectric field problem in SCIRun 4.7 (Scientific Computing and Imaging (SCI) Institute, University of Utah, Salt Lake City, UT) using a FEM model. A tetrahedral mesh was generated over a volume of 100 mm × 100 mm × 100 mm with the Medtronic 3389 lead positioned in the center of the volume. Centered within the large volume, a smaller cube sized 20 mm × 20 mm × 20 mm with 0.1 mm grid spacing was solved at a higher mesh resolution on which the Hessian matrix could be calculated to avoid interpolation errors (figure 1(B)). The tetrahedral mesh as a whole consisted of ~9 million nodes, and the Poisson equation was solved with a linear solver to find the electric potential at each node.

The Medtronic 3389 electrode was chosen as the lead model for this study because it is a commonly used clinical electrode. The Medtronic 3389 lead consists of four cylindrical contacts, each 1.5 mm in height, with conductivity σ = 1 × 10⁶ S m⁻¹, and separated by a 0.5 mm cylindrical insulator with conductivity σ = 1 × 10⁻¹⁰ S m⁻¹ (Wei and Grill 2005, Miocinovic et al 2006). For this study, we used a simplified isotropic conductivity volume with the tissue medium represented by 0.1 S m⁻¹ isotropic conductivity tensors in order to achieve an electrode impedance of approximately 1000 Ω (Butson et al 2006, Satzer et al 2014).

We solved for the monopolar electric potential with a Dirichlet node at −1 V at the center of the active contact and Dirichlet boundary conditions (0 V) to represent a distant return anode on the outer bounding box of the computational model. We solved for bipolar contact configurations using two point sources of opposite signs, each positioned in the center of their respective contacts. For this study, cathodic monopolar stimulation was done with contact 1 set to −1 V, and bipolar stimulation was done where contact 1 was set to −0.5 V and contact 2 was +0.5 V so that the difference between the voltages was one volt for comparison between the monopolar and bipolar configurations.

2.2. Hessian matrix

In order to determine preferential fiber orientation patterns, we calculated the Hessian matrix of the second spatial partial derivatives of electric potential at each node of the 20 mm × 20 mm × 20 mm grid. The Hessian matrix at each node can be visualized as an anisotropic 3D tensor (figure 1(C)). Each eigenvalue of the Hessian matrix represents the second derivative of the electric potential along the respective eigenvector. The second spatial derivative across nodes of Ranvier, known as the activating function, can be used to approximate activation from an extracellular source (Rattay 1986, 1999): a larger second derivative corresponds to a higher likelihood of axon firing at that node point (figure 1(A)).

Preferential fiber orientation patterns can be represented through the eigenvalues and eigenvectors of the Hessian. The Hessian tensor has three eigenvalues, which represent the second derivatives in the directions governed by the eigenvectors. The primary eigenvalue represents the largest second derivative, and thereby the primary eigenvector is the preferred activation orientation of a neuron for cathodic activation. In contrast, the tertiary eigenvalue represents the lowest second derivative—which must be a negative value since the Hessian trace is required to be zero according to the Poisson equation—and corresponds to a theoretical inhibition of the axon along the direction of the tertiary eigenvector. We classify fiber orientations into three categories of direction as defined by a spherical coordinate system: (1) longitudinal, (2) latitudinal, and (3) radial/orthogonal relative to the source (figure 1(D)). For simplicity, longitudinal and latitudinal segments are referred to as passing axon segments, whereas orthogonal segments are axons segments approaching or leaving the electrode. In this study, we characterized the preferential orientation of activation around cathode, anode, and bipolar configurations.

2.3. NEURON model

In order to verify the activation trends predicted by the Hessian, we used NEURON 7.4 to run multicompartment neuron models for neurons in the orientations of the eigenvectors. The neurons are modeled as 5.7 μm myelinated axons with defined compartments representing the nodes of Ranvier, paranodal, and internodal sections according to the MRG NEURON model (McIntyre et al 2002, Butson et al 2007). Electric potentials are mapped through linear interpolation onto each neural segment based on the position of the modeled neuron in space to determine whether extracellular stimulation causes neuron firing.

The Hessian matrix can be used to inform upon whether a neuron segment will fire an action potential at any given fiber orientation. To test the ability of the Hessian to predict neuron firing thresholds, we restricted the site of API to be at the node where the Hessian was calculated. To do this, the center node of Ranvier of each neuron was placed at a grid point on a down-sampled 26 × 51 grid where the Hessian was calculated. All NEURON compartments except the center node are made passive so that the center node is the only site of API. Despite the modified neurons having only one active compartment, the remaining compartments still experience electric potential influence and enable axial current contribution, a key feature to firing in the cable equation (McNeal 1976). The modified neurons have higher threshold amplitudes compared to the classic MRG neurons, likely due to the reduced transmembrane currents across passive nodes (figure 1(E)).

2.4. Threshold for a variety of conditions

We varied the stimulus waveform applied to the neurons to determine how changes in the stimulus waveform might alter the preferential activation of neurons based on axon orientation. At each grid node, the modified 81-compartment neurons were extended in the directions of the primary, secondary, and tertiary eigenvectors. Firing thresholds were calculated using a binary search algorithm on a down-sampled 26 × 51 grid for faster computational time. Activation thresholds were determined for neurons stimulated by unbalanced cathodic and anodic waveforms, as well as stimulus regimes where the charge-balancing phase was 100%, 50%, 25%, 10%, 5%, and 2.5% of the leading phase amplitude, as shown in figure 4(A). The area under the charge-balancing phase was maintained, so that given a larger amplitude, a shorter width was used. An interphase interval of 100 μs was used to separate the leading phase from the charge-balancing phase. The extracellular influence of each phase of the waveform was calculated using linear interpolation of the FEM electric potential solution onto multicompartment cable models centered at each point on the 26 × 51 downsampled grid. The simulations were run over 250ms at 130 Hz, and a neuron was considered to be active if each waveform period resulted in an action potential. Exponential fits were used to characterize the relationship between threshold of firing and distance to the center of the active contact.

Figure 4.

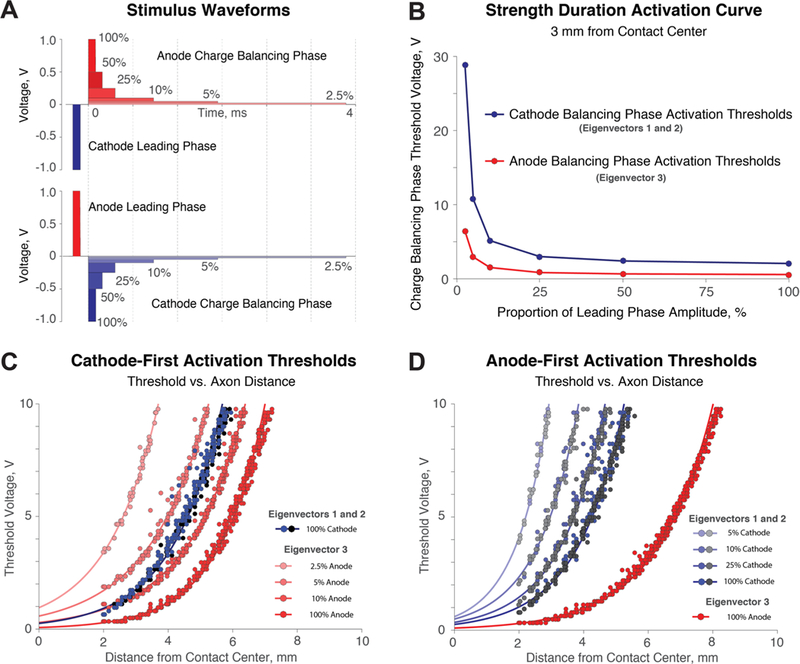
(A) Cathode- and anode- first stimulus regimes with varying charge-balancing phases of 100%, 50%, 25%, 10%, 5%, and 2.5% of the leading phase amplitude. (B) Strength duration curve for the charge-balancing phase for passing fibers (blue) or orthogonal fibers (red) for neurons 3 mm away from the contact center. (C) Cathode-first stimulation with varying amplitudes of the anodic charge balancing phase. Changes to the balancing either select against or in favor of orthogonally oriented fibers (third eigenvector). (D) Anode-first stimulation with varying amplitudes of the charge-balancing phase. Orthogonal fibers are highly excitable in all anode-first waveform scenarios.

2.5. Patient-specific model

In order to demonstrate clinical application of this study, we explored preferential activation of fiber orientations in a Parkinson’s disease patient with DBS for the subthalamic nucleus (STN). For the patient, we acquired preoperative T1-, T2-, multishell diffusion-weighted (DW) magnetic resonance images (MRIs), and postoperative computed tomography (CT). We corrected the DW-MRI acquisitions for distortions using HySCO (Ruthotto et al 2012, 2013) and registered all imaging modalities to the T1-MRI using ANTS (Avants et al 2009). We registered the PD25-atlas (Xiao et al 2015) to the patient imaging to obtain segmentations of deep brain structures. To obtain a representation of the internal capsule (IC), we processed the DW-MRI data with DSIStudio (http://dsi-studio.labsolver.org) using the restricted diffusion imaging (RDI) algorithm (Yeh et al 2017) for multishell DW data. Based on the fractional anisotropy (FA) visualization, we manually segmented the anterior part of the IC and implemented the segmented volume as a region of interest (ROI). To obtain tractography of the hyperdirect pathway, we used the segmentation of the anterior limb of the IC as a ROI and a segmentation of the STN from the PD25 atlas as the seed region. We computed 417 tracts for both the IC and the hyper-direct pathway.

The Medtronic 3389 lead was positioned according to the post-operative CT imaging for the DBS patient; however, the lead was shifted 1.0 mm in the anterior direction to avoid overlap of the lead with the hyperdirect pathway we defined using tractography. We wanted to demonstrate a clinically relevant example with a lead location that might represent a typical lead location; it is typical to see a 2 mm deviation in lead placement (Patel et al 2002, Burchiel et al 2013). The influence of DBS stimulation was tested on the tractography that we generated using NEURON simulations. With NEURON modeling, we aimed to explore the differences between activation patterns of anodic stimulation and cathodic stimulation on fiber pathways associated with therapeutic benefits and side effects.

3. Results

3.1. Preferential fiber orientation

We found that cathodic stimulation and anodic stimulation each activate certain fiber orientations selectively as indicated by the primary, secondary, and tertiary eigenvector directions. The second derivatives along the principal eigenvector directions are shown in figure 2 for monopolar and bipolar cases. At a given location, the primary eigenvector represents the orientation of fibers most likely to fire an action potential, and the tertiary eigenvector represents the orientation of fibers in which API will be most suppressed. The likelihood that a particular fiber orientation will induce firing depends on the sign and the magnitude of the respective eigenvalue. Around a cathodic source, the positive primary and secondary eigenvalues indicate that the preferential directions of activation are in the longitudinal and latitudinal directions around the electrode. During monopolar stimulation, the primary and secondary eigenvalues have similar median amplitudes, implying that neurons in the primary and secondary eigenvector directions are activated at similar thresholds. In contrast, orthogonal neurons are inhibited because the tertiary eigenvalues are negative. Additionally, the eigenvalue magnitudes associated with the orthogonal direction are approximately twice as large as with the primary and secondary directions. The Hessian indicates that monopolar cathodic stimulation promotes activation of axon segments passing adjacent to the electrode and selects against orthogonal axon segments, leaving or approaching the electrode.

Figure 2.

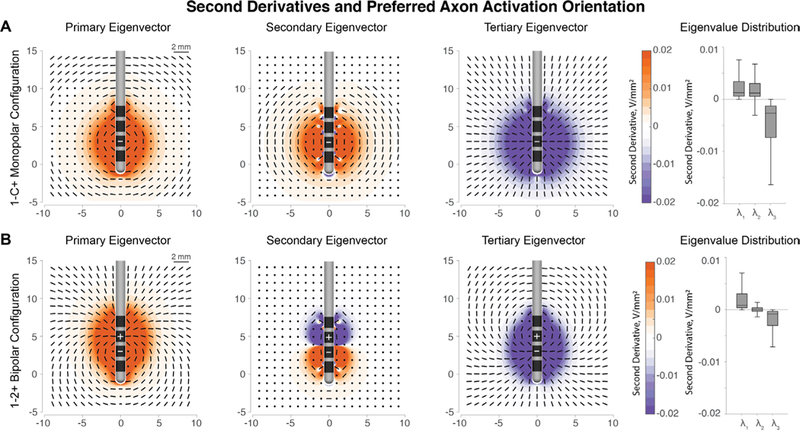
(A) Primary, secondary, and tertiary eigenvector orientations for cathodic stimulation at contact 1 of the Medtronic 3389 lead. Longitudinal and latitudinal fibers (passing fibers) have positive second derivatives, which correspond to an increased likelihood of firing. The orthogonal direction defined by the tertiary eigenvector has negative second derivatives. The median amplitude of the tertiary eigenvalues is twice that of the primary and secondary eigenvalues, implying large inhibition of orthogonal fibers. (B) Eigenvector directions remain the same around the cathode, but the activation patterns are reversed around the anode. Note: box-whisker plots are plotted without outliers for clarity.

During bipolar stimulation, the same orientation patterns of activation hold true around the cathode electrode, with passing fibers being preferred over orthogonal fibers. However, the recruitment order of neuron orientation reverses around the anode. Orthogonal neurons are preferentially activated around the anode, whereas the longitudinal and latitudinal neurons are inhibited due to the negative second derivatives.

3.2. Recruitment order based on fiber orientation

The Hessian predicts that cathodic stimulation activates passing axons and anodic stimulation activates axons leaving or approaching the electrode (orthogonal). To explore the validity of fiber orientation activation trends informed by the Hessian, we used NEURON models to verify the preferential activation order. For an unbalanced cathodic waveform, as predicted, neurons in the primary and secondary eigenvector directions fire action potentials, whereas neurons in the tertiary eigenvector directions (orthogonal) do not (figure 3(A)). Firing behavior matches the predictions made by the Hessian matrix and verifies that the activating function can serve as a predictor of neuron activation. Activation thresholds for neurons in any direction are predicted by the respective eigenvalue, with lower firing thresholds appearing when the second derivative values are higher.

Figure 3.

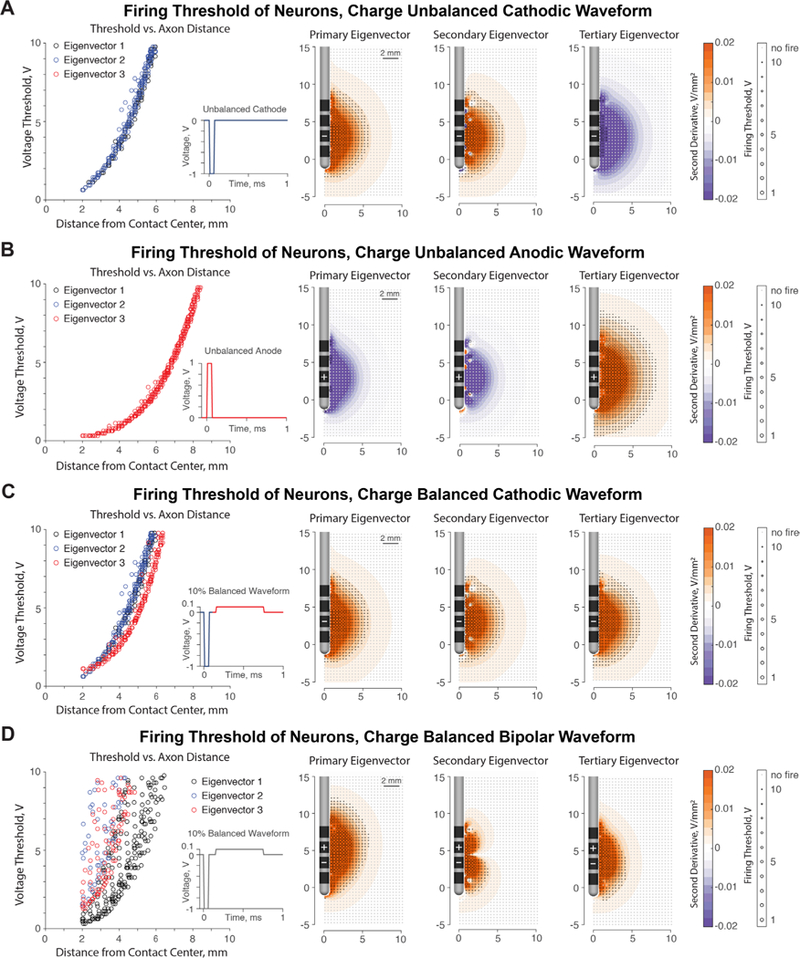
(A) An unbalanced cathodic pulse causes firing of neurons oriented in the primary and secondary eigenvector directions, which represent passing axons (positive second differences, in orange). Neurons in the tertiary eigenvector orientation do not fire, as predicted by the eigenvalues (negative second differences, in purple). (B) An unbalanced anodic pulse reverses the fiber orientation recruitment from the cathodic pulse. Orthogonal neurons (tertiary eigenvector from the cathodic pulse) fire exclusively, whereas adjacent passing axons do not fire. (C) In a 10% charge balancing cathode-first stimulus regime, neurons at all orientations are approximately equally likely to fire due to the cathodic and the anodic component of the pulse. (D) Firing thresholds for the bipolar stimulation case, 1–2+ configuration. There is a larger range of activation thresholds for neurons along the principal eigenvectors due to the combination of passing and orthogonal fiber segments within the primary and tertiary eigenvectors (as shown in, figure 2(B)). The differing firing thresholds on the secondary eigenvector is due to the differing influence of the cathodic phase and the anodic phase on latitudinal fibers. Ultimately, the second derivatives calculated from the Hessian predict firing for the respective fiber orientation. Note: Distance to contact center is measured from nearest active contact.

We applied an unbalanced anodic waveform to the primary, secondary, and tertiary eigenvectors calculated from the FEM solution (figure 3(B)). The orthogonal neurons associate with positive eigenvalues due to the flipped waveform and generate action potentials in response to an anodic stimulus. The longitudinal and latitudinal neurons, which fired with a cathodic pulse, do not fire with anodic stimulation. During anodic stimulation, orthogonal neurons fire at lower thresholds than the passing fibers did under cathodic stimulation. Lower firing thresholds for orthogonal neurons are due to the fact that tertiary eigenvalue amplitudes are twice as large as the primary and secondary eigenvalue amplitudes.

In response to a biphasic waveform that contains a cathodic phase followed by an interphase delay and a charge-balancing anodic phase at 10% of the amplitude but 10 times the duration, neurons in all fiber orientations can fire (figure 3(C)). The longitudinal and latitudinal orientations fire due to the cathodic phase, and the orthogonal directions fire during the anodic phase. A cathode-first waveform with a 10% balancing anodic phase does not have a preference of which fiber orientations are activated; the orthogonal orientations fire at approximately the same thresholds as the longitudinal and latitudinal directions according to the threshold versus axon distance plot.

The activation of fiber orientations is more complicated for the bipolar stimulation configuration (figure 3(D)); there is a greater range in activation thresholds for each eigenvector. The primary and tertiary eigenvectors contain a combination of highly excitable orthogonal fibers around the anode and moderately excitable longitudinal fibers around the cathode, as shown in figure 2(B). The secondary eigenvector consists entirely of latitudinal, passing fibers, which exhibit different excitability from the cathodic and anodic components of the waveform. Ultimately, the second derivatives predict activation of the neurons along the respective eigenvector orientations.

3.3. Selective activation of neuron populations based on changes in waveform

Modifying the cathodic and anodic portions of the DBS wave-form can selectively target fiber orientations (figure 4). We learn from figure 3 that, in general, cathodic stimulation activates adjacent passing fibers, whereas anodic stimulation activates fibers leaving or approaching the electrode. However, for safe and effective stimulation, stimulus waveforms must be charge balanced (Merrill et al 2005). By varying the cathodic and anodic components of a waveform, we can selectively activate passing neurons or orthogonal neurons. We tested the ability to selectively activate fiber orientations by varying the amplitude and duration of the charge balancing in cathode- and anode-first waveforms. Strength-duration curves of charge-balancing pulse ratios 3 mm away from the active contact center (figure 4(B)) highlight that axon segments approaching or leaving the electrode are highly excitable with anodic stimulation. For cathode-first stimulation (figure 4(C)), we found that using a charge-balancing amplitude of 2.5% and 5% will prioritize firing of longitudinal and latitudinal axons, a 10% balancing pulse amplitude will activate all fiber orientations similarly, and a 100% balancing pulse amplitude will preferentially activate orthogonal fibers. For anode-first stimulation (figure 4(D)) the orthogonal neurons will be preferentially activated regardless of the balancing pulse amplitude. The equation and coefficients used for the exponential fits in figures 4(C) and (D) can be seen in the Appendix.

For an STN DBS patient, we virtually isolated the IC and the hyperdirect pathway (HD) from coregistered T1- and diffusion- weighted MRI data. Activation of the IC is associated with side effects while stimulation of the STN and the afferent HD pathway is associated with possible therapeutic benefit (Tamma et al 2002, Gradinaru et al 2009, Henderson 2012). Near the STN, the fiber orientations of the IC and HD tracts are different: the IC passes the lead vertically and the HD approaches the lead orthogonally.

We demonstrated through a theoretical example that anodic stimulation could be used for clinical benefit as well. From figure 3, we saw that orthogonal fibers are preferentially activated by anodic stimulation, so we tested to see whether the HD pathway can be preferentially activated with anodic stimulation. We found that the activation threshold of the HD pathway was reduced by approximately half in the monopolar and bipolar stimulation regimes with anodic stimulation (figure 5(B)). The IC also exhibited a decrease in the firing threshold for monopolar anodic stimulation, likely attributable to orthogonal components in the vertically oriented IC. However, using a bipolar configuration greatly reduced the activation of the IC, for both anode- and cathode- first stimulation. We also included IC and HD threshold analysis for a symmetrically balanced waveform condition (figure 5(C)); the activation thresholds of cathode- and anode- first stimulation were nearly identical. The thresholds for activation of the HD pathway was reduced to nearly half of the cathode-first 10% balanced regime.

Figure 5.

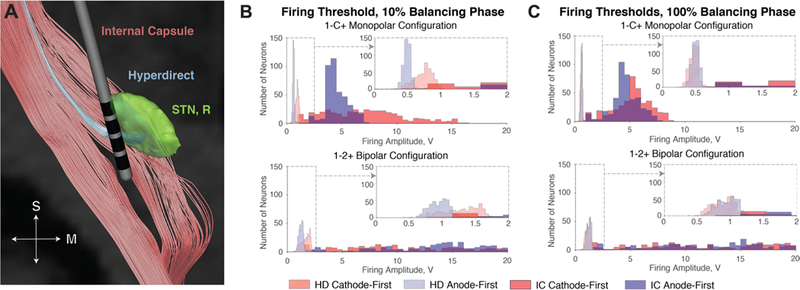
(A) Visualization of HD and IC tracts with respect to the STN (right) and lead. (B) Firing threshold histograms for HD and IC tracts given cathodic and anodic stimulation for 10% balancing. Anodic stimulation reduces threshold voltage of orthogonally oriented fibers. As a result, the HD is activated by a smaller voltage with anodic stimulation rather than cathodic stimulation. The orthogonal components of the IC are activated at lower thresholds as well, but bipolar stimulation reduces the spread of activation in the IC. (C) Firing histograms using symmetrically balanced pulses exhibit lower firing thresholds for both the HD and IC, but bipolar stimulation avoids the IC.

4. Discussion

The primary outcome of this simulation study is to demonstrate the selective activation of passing fibers with cathodic stimulation versus selective activation of orthogonal fibers with anodic stimulation. The Hessian matrix, a mathematical representation of activation, was able to inform us of a previously unknown biophysical relationship between fiber orientation and axon activation. We verified the activation patterns predicted by the Hessian matrix through NEURON models. An advantage of the Hessian is that it can efficiently estimate neuron activation in any direction, potentially allowing it to serve as a more comprehensive activation volume predictor than models using a single fiber orientation.

A secondary outcome of this experiment is that orthogonal fibers are activated by anodic stimulation at lower thresholds than passing fibers given the same amplitude of cathodic stimulation. It might be possible to take advantage of the highly excitable nature of the orthogonal neurons in clinical application in terms of power consumption. Since every neuron around a lead must have segments that approach or leave the lead (orthogonal), anodic stimulation could activate nearby axons at lower thresholds than cathodic stimulation.

This study offers a mechanistic explanation for the results in a number of previous studies in which anodic stimulation was investigated. A recent study explored anodic versus cathodic stimulation in a clinical setting in 10 Parkinson’s disease patients implanted with DBS in the STN (Kirsch et al 2018). The study used a conventional stimulus waveform using a 10% charge-balancing regime for both cathode-first and anode-first stimulation. Kirsch et al (2018), found that anodic stimulation significantly decreases MDS-UPDRS III motor scores when compared to both off stimulation and cathodic stimulation in the suprathreshold stimulation case. It was found that anodic therapeutic and side effect thresholds were greater than the cathodic case, but the therapeutic window was wider for the anodic case. Additionally, bradykinesia metrics were significantly improved by anodic stimulation versus cathodic stimulation (58.6% versus 39.8%). The authors postulate that improvements in clinical response in the anodic case may be due to the differential activation of beneficial fibers based on fiber orientation by anodic stimulation. Our findings support the possible explanation made in Kirsch et al (2018) on the differing clinical effects of anodic stimulation.

Another recent study by De Jesus et al (2018) found improved tremor outcomes in DBS in the ventralis intermedius nucleus of the thalamus (VIM) for essential tremor by using a larger anodic component in the DBS waveform. The study compared the use of a square biphasic pulse, with an anodic charge-balancing phase magnitude equal to the cathodic leading phase magnitude, to the conventional 10% charge-balancing regime. The square biphasic pulse is identical to the symmetrically balanced pulse we ran in figure 4(F) and demonstrated reduced firing threshold of fiber tracts associated with clinical benefit. We believe that De Jesus et al (2018) found improved tremor response with a square biphasic pulse because of the increased activation contribution of the anodic phase of the waveform. The anodic phase of the waveform would activate the orthogonal population of axons near the VIM, which might be a part of the fiber pathways associated with clinical benefit.

Our results indicate that anodic stimulation has lower firing thresholds in the orthogonal fiber orientations. These results could explain lower anodic thresholds in applications of cortical stimulation where fibers are largely orthogonal to the surface of the brain (Cornelia et al 1998). In the same study, brain stem simulation saw lower thresholds with cathodic stimulation than with anodic stimulation. The different activation thresholds reported in this study may be explained by the different orientations of the fibers being targeted. Cortical fibers are orthogonal to the electrode source while brainstem fibers traveling from the cortex to the spine pass adjacent to the electrode source.

A number of computational studies also demonstrate that fibers with cell bodies in proximity to the active electrode can be activated with lower thresholds using anodic stimulation (McIntyre and Grill 1999, 2000, 2002). Such a finding supports the results in our study since a cell body essentially serves as a current sink.

For bipolar configurations, around the anode contact, orthogonal neurons will be activated first at lower voltages. In contrast, the longitudinal and latitudinal neurons do not experience firing around the anode. In the future, it might be possible to intelligently use complex bipolar configurations, especially coupled with novel directional leads, to activate neurons within a target and avoid side effect inducing regions given knowledge of fiber orientations from diffusion tensor imaging. The different activation patterns based on fiber orientation are relevant to approaches estimating the VTA. In a monopolar stimulation case, for the conventional 10% balancing regime for cathode-first stimulation, all fiber orientations fire at approximately the same thresholds (figure 3(C)). Standard methods of monopolar VTA estimation for a cathode-first, 10% balancing regime likely estimate the VTA reasonably well since there is no preferential fiber orientation selectivity in that case. However, based on this study, standard VTA methods are unlikely to hold up in cases with different stimulus waveforms or anodic contacts, such as in bipolar stimulation, where there exists differential fiber selectivity.

This study might also explain the existence of virtual cathodes in tangential fibers, which are present during anodic stimulation at more distal nodes (figure 1(A)). In tangential fibers, the nodes where API and the virtual cathode appear are partially orthogonal to the lead. This study implies that activation is not due to a ‘virtual’ cathode, but rather due to outright activation of orthogonal segments by the anode. Largely, we believe that the excitatory nature of anodic stimulation has been misunderstood for decades. In fact, anodic stimulation does not counteract a desired stimulation effect (Hofmann et al 2011), but, rather, it preferentially activates neurons approaching or leaving the electrode.

4.1. Limitations

The MRG neurons that we used in this study have been modified to limit API to nodes where the Hessian was calculated to verify the predictive power of the Hessian. Since it would be an incorrect assumption to map distal API back to a center node, we modified the neuron dynamics so that only the center node could initiate an action potential. Additionally, in the NEURON modeling, we assumed linear fiber orientations along each eigenvector, but fiber orientation can vary along a neuron. Firing behavior might change based on different axial current influence from neighboring nodes, but it is not possible to take into account all possible neuron pathways in our simulations. Given these modifications to the neurons, we saw higher firing thresholds than the classic MRG neuron.

Additionally, the Hessian is limited in its approximation because it defines the response of a neuron in a time-independent scenario. The activating function can be used to predict neural activation, but only through activating function versus threshold relationships tested at varying pulse widths. We tested the 5.7 μm myelinated fiber model, and while the activating function relationships will vary for other axon diameters, the overall patterns of cathodic and anodic stimulation will hold for all fiber types that follow the cable equation. The Hessian is limited to activation approximation according to neuronal cable theory, which refers to infinitely long fibers. Therefore, the presence of a soma or other morphological variations could change the threshold curves. The limitations listed above mainly affect the observed voltage thresholds, and further characterization of activating function threshold values is necessary. However, these limitations do not undermine the observed relationship between fiber orientation and activation that the Hessian has revealed. In fact, we plan to further explore the prediction of the Hessian not only on activation of axons but also on the inhibition of axons through network models. Since the primary eigenvalue indicates the first instance of neuron activation in the eigenvector orientation, with full characterization of function and firing thresholds, the Hessian could be used as a novel volume of activation that considers activation in all fiber orientations.

5. Conclusions

From the study, we have determined that cathodic and anodic stimulation exclusively activate passing fibers and orthogonal fibers, respectively. This study reveals that anodic stimulation directly activates orthogonal axons at lower thresholds than the thresholds of passing fibers due to cathodic stimulation. Targeting fiber orientations is possible with simple modifications to the anodic and cathodic components of the DBS waveform. Fiber orientation selectivity may be useful in targeting stimulation to therapeutic fibers and avoiding side effect-inducing fiber tracts. There may be clinical applications of anodic stimulation for therapeutic benefit or widening the therapeutic window.

Appendix.

The exponential fits in figures 4(C) and (D) were made following the form shown in equation (A.1), where x is distance from the active contact center in mm and V_th is the firing threshold in Volts.

$$V_{th}=A{e}^{kx}.$$ (A.1)

The curves for cathode-first 25% and 50% and anode-first 2.5% and 50% were calculated as listed in table A1, but visualizations of the fits were not shown in figure 4 for clarity.

Table A1.

Exponential Fit Coefficients for equation (A.1) representing firing threshold versus distance relationships plotted in figures 4(C) and (D).

	Exponential fit coefficients
	Cathode-first		Anode-first
Leading phase	A	k	A	k
	0.252	0.648	0.093	0.585
Balancing pulse, %	A	k	A	k
2.5	0.950	0.637	0.947	1.138
5	0.577	0.543	0.597	0.963
10	0.290	0.554	0.491	0.784
25	0.135	0.612	0.343	0.723
50	0.089	0.668	0.289	0.706
100	0.068	0.713	0.253	0.700