ADMMBO: Bayesian Optimization with Unknown Constraints using ADMM

Abstract

There exist many problems in science and engineering that involve optimization of an unknown or partially unknown objective function. Recently, Bayesian Optimization (BO) has emerged as a powerful tool for solving optimization problems whose objective functions are only available as a black box and are expensive to evaluate. Many practical problems, however, involve optimization of an unknown objective function subject to unknown constraints. This is an important yet challenging problem for which, unlike optimizing an unknown function, existing methods face several limitations. In this paper, we present a novel constrained Bayesian optimization framework to optimize an unknown objective function subject to unknown constraints. We introduce an equivalent optimization by augmenting the objective function with constraints, introducing auxiliary variables for each constraint, and forcing the new variables to be equal to the main variable. Building on the Alternating Direction Method of Multipliers (ADMM) algorithm, we propose ADMM-Bayesian Optimization (ADMMBO) to solve the problem in an iterative fashion. Our framework leads to multiple unconstrained subproblems with unknown objective functions, which we then solve via BO. Our method resolves several challenges of state-of-the-art techniques: it can start from infeasible points, is insensitive to initialization, can efficiently handle ‘decoupled problems’ and has a concrete stopping criterion. Extensive experiments on a number of challenging BO benchmark problems show that our proposed approach outperforms the state-of-the-art methods in terms of the speed of obtaining a feasible solution and convergence to the global optimum as well as minimizing the number of total evaluations of unknown objective and constraints functions.

1. Introduction

Bayesian optimization (BO) has been shown to be a powerful tool for solving optimization problems whose objective functions are unknown and expensive to evaluate (Brochu et al., 2010a; Martinez-Cantin et al., 2007; Hutter et al., 2011; Torn and Zilinskas, 1989). For example, in drug design (Azimi et al., 2012; Scott, 2010; Brochu et al., 2010b), where the goal is to maximize the efficacy of a drug, the evaluation of the objective function, i.e., drug efficacy, across multiple drug formulations requires producing and testing new drugs, which would be subject to resource and cost limitations. As another example, minimizing the validation error of a machine learning model, such as hyperparameter tuning of a deep neural network (LeCun et al., 2015), involves many evaluations of the objective function,i.e., the validation error, where each evaluation requires training and evaluating a new model (Bergstra et al., 2011; Hoffman et al., 2014; Snoek et al., 2012; Swersky et al., 2013).

In many real-world problems, the desired solution, in addition to optimizing the objective function, must satisfy constraints that are also unknown and expensive to evaluate (Shahriari et al., 2016). For example, in the drug design problem, the goal is often to maximize the drug efficacy while limiting its side effects. In the hyperparameter tuning problem in machine learning, the optimal hyperparameters not only must minimize the validation error, but also must ensure that the prediction time of the learned model is sufficiently short. The majority of existing work on BO has focused on the unknown-objective problem (Jones et al., 1998; Kushner, 1964; Lizotte, 2008; Jones, 2001; Hernández-Lobato et al., 2014; Cox and John, 1992; Wu et al., 2017), while only a few recent reports have addressed the problem in the unknown-objective unknown-constraint setting (Snoek, 2013; Gelbart et al., 2014; Gardner et al., 2014; Bernardo et al., 2011; Hernández-Lobato et al., 2015; Picheny et al., 2016; Gramacy et al., 2016; Picheny, 2014), (see Section 4 for a review).

1.1. Existing Challenges & Paper Contributions

In this subsection, we describe some of the limitations of the state-of-the-art constrained Bayesian optimization methods. First, several of these methods, including Expected Improvement with Constraints (EIC) (Schonlau et al., 1998; Snoek, 2013; Gelbart et al., 2014), Integrated Conditional Expected Improvement (IECI) (Bernardo et al., 2011) and Expected Volume Reduction (EVR) (Picheny, 2014), require a feasible initial point. However, in practice, a feasible point is often not available; hence, these algorithms require finding a feasible point first, which consumes part of the computational budget. Second, most existing constrained BO methods, including EIC, IECI, EVR, Augmented Lagrangian for Bayesian Optimization (ALBO) (Gramacy et al., 2016) and Slacked-augmented Lagrangian for Bayesian Optimization (Slack-AL) (Picheny et al., 2016), require joint evaluation of the objective function and all constraints at a candidate point in each step, in order to quantify its utility for finding a global optimum. However, for a large class of problems, labeled as “decoupled”, the objective function and the constraints can each be evaluated independently. This can be especially advantageous in settings where some functions might be significantly more expensive to evaluate than the others (Gelbart, 2015). For example, in the hyperparameter tuning problem, evaluating the prediction time may not require training the model and is often much cheaper than evaluating the validation error. Thus, methods that require joint evaluation of all unknown functions, including EIC, IECI, EVR, ALBO, and Slack-AL could increase the overall cost of solving decoupled problems more than might be necessary. Third, the majority of existing methods, including IECI, EVR, ALBO and Predictive Entropy Search with Constraints (PESC) (Hernández-Lobato et al., 2015), do not have closed form expressions for the so-called ‘acquisition function’, which is a key step in the BO algorithm. Thus, these methods need to approximate the acquisition function, typically via algorithms such as Expectation Propagation (Minka, 2001) or Monte-Carlo Sampling (Picheny et al., 2013), which often suffer from implementation difficulty and slow execution time, or may cause instabilities (Picheny et al., 2016; Gelbart, 2015). Finally, most of the BO methods fix a computational budget in terms of either wall-clock time or the number of function evaluations, and stop when the budget is exhausted. However, this budget is an additional parameter which must be hand tuned, and the performance of the BO method typically is highly dependent on it. A value that is too small may result in missing easy improvement while one that is too large might incur additional cost for an insignificant gain. Thus, having an automatic stopping criterion is highly desirable while many BO methods, including EIC, IECI, EVR and PESC, lack such a criterion.

In this paper, we propose a novel constrained BO framework for optimizing an unknown objective function subject to unknown constraints that resolves all the aforementioned challenges. First, we reformulate the problem into an equivalent unconstrained optimization. Since the joint (Bayesian) optimization of the unconstrained problem over the unknown objective function and unknown augmented constraints is challenging, we introduce auxiliary variables, one per constraint, and then force these variables to be equal to the the original variable, resulting in an equivalent constrained formulation, where the constraints are now known. The new formulation allows to perform the (Bayesian) optimization over each term independently, decoupling the objective function optimization from constraint satisfaction. To efficiently solve our proposed optimization, we adopt the Alternating Direction Method of Multipliers (ADMM) framework (Boyd et al., 2011; Hong and Luo, 2017; Parikh et al., 2014), which leads to solving an ‘optimality subproblem’, and a ‘feasibility subproblem’ for each constraint, at each iteration. The optimality subproblem minimizes the objective function close to current solutions of the feasibility subproblems, while each feasibility sub-problem searches for a feasible solution of its constraint close to the current solution of the optimality subproblem. Our framework, which we call Alternating Direction Method of Multipliers for Bayesian Optimization (ADMMBO), provides the following advantages compared to the state-of-the-art methods (see Table 1 for a summary).

Table 1:

Advantages of ADMMBO with respect to the state-of-the-art methods.

Advantages	Infeasible initialization	Decoupled problems	Closed-form acquisition func.	Stopping criterion
EIC	–	–	✓	–
IECI	–	–	–	–
PESC	✓	✓	–	–
EVR	–	–	–	–
ALBO	✓	–	–	✓
Slack-AL	✓	–	✓	✓
ADMMBO	✓	✓	✓	✓

– Unlike many existing methods, ADMMBO can start from an infeasible initial point and gradually move towards a feasible point via solving the feasibility subproblems.

– Due to its separation of the optimizations over each expensive to evaluate function, i.e., objective function and each constraint, ADMMBO can handle decoupled problems efficiently, without requiring joint evaluation of all such functions at each candidate point.

– Because it decomposes the overall problem into separate subproblems, each involving only one expensive to evaluate function, resulting in simpler BO steps, ADMMBO may be able to facilitate derivation of closed-form acquisition functions.

– ADMMBO offers a well-defined stopping criterion, inherited from ADMM, which in practice avoids unnecessary function evaluations. The stopping criterion is satisfied when the solutions of the optimality and feasibility subproblems converge to each other.

– Our experiments empirically show that ADMMBO achieves good solutions significantly faster than the state-of-the-art methods, is relatively insensitive to initialization, and requires fewer function evaluations to find desirable solutions. Moreover, our results suggest that ADMMBO’s performance does not depend on whether the optimal solution lies on the boundary of or inside the feasible region, and is also insensitive to the relative volume of the feasibility region.

1.2. Paper Organization

In Section 2, we review both BO and the ADMM algorithm that we build upon. We motivate and introduce our proposed reformulation of the constrained problem and present our ADMMBO algorithm to solve this reformulated optimization in Section 3. In Section 4, we discuss existing related work on constrained BO that handles unknown-objective unknown-constraint optimization problems. We present experimental results on synthetic and real data in Section 5. Finally, in Section 6, we discuss our results and open avenues for future research and conclude the paper.

2. Background

In this section, we review the underlying components of our proposed method: Bayesian Optimization in its standard settings, with a focus on EI as the acquisition function, and the ADMM algorithm.

2.1. Bayesian Optimization

Bayesian optimization (Shahriari et al., 2016; Brochu et al., 2010b) addresses the problem of finding a global minimum (or maximum), x*, of an objective function f (x) over a bounded box $\mathcal{B}\in {ℝ}^d$, where f is unknown but available to evaluate pointwise via computationally costly queries. Thus, the goal is to find x* with as few evaluations of f (x) as possible. Given a collection of initial points in $\mathcal{B}$ and their observed objective values, denoted by $\mathcal{F}={\left\{\left(x_l,f\left(x_l\right)\right)\right\}}_{l=1}^n$, BO methods iteratively suggest the next best candidate x_l+1, and evaluate the corresponding objective value at iteration l + 1. More specifically, to find x_l+1, BO first assumes a prior probability model for the unknown function f, denoted by p[f (x)], and then uses the observed data, $\mathcal{F}$, to update the posterior probability $p[f(x)|\mathcal{F}]$. This posterior is then used to build an acquisition function, denoted by α(x), which provides an estimate of the optimization usefulness of any candidate point $x\in \mathcal{B}$ if it is chosen as x_l+1 for the next function evaluation. In contrast to f (x), the acquisition function α(x) has a known form and can be maximized over $x\in \mathcal{B}$, using analytical or numerical optimization techniques. The optimum of the acquisition function provides a recommendation for x_l+1 that is used to evaluate f (x_l+1) and then to update the data $\mathcal{F}$ accordingly. BO iteratively repeats this process, guiding the search towards sampling a global minimizer of f.

Many BO methods assume that the unknown function f (x) is a Lipschitz continuous bounded function over $\mathcal{B}$, and then model p[f (x)] as a Gaussian Process (GP) (Močkus, 1975; Jones et al., 1998; Hernández-Lobato et al., 2014; Kushner, 1964; Cox and John, 1992). GPs are non-parametric Bayesian models which are widely used in the Bayesian optimization literature since they provide a flexible fit for modeling unknown functions. Moreover given GP models, some acquisition functions give closed-form expressions, which can be efficiently optimized with numerical optimization techniques (Rasmussen and Williams, 2006; Houlsby et al., 2012). As an example, which we will then employ in the exposition of our method below, we describe a popular acquisition function called Expected Improvement (Jones et al., 1998; Brochu et al., 2010b). Given data $\mathcal{F}$, let f ⁺ denote the best objective value achieved by the points in $\mathcal{F}$. Then the improvement of any given point x, denoted by I(x), corresponds to the improvement of f (x) relative to f ⁺, i.e., $I(x)\triangleq \max \left(0,f^{+}-f(x)\right)$. An efficient strategy in BO would be to choose the next candidate for function evaluation by finding a point x which offers the largest improvement (Jones et al., 1998). However, since f (x) is unknown and expensive to evaluate pointwise, it is difficult to calculate improvement I(x). Alternatively, Expected Improvement of x, denoted by EI(x), is an acquisition function which computes the expectation of I(x) with respect to $p[f(x)|\mathcal{F}]$. Močkus (1975); Jones et al. (1998); Brochu et al. (2010b) has shown that assuming a GP model for p[f (x)], the Expected Improvement can be computed using the closed-form expression

$$EI(x)=E_{f|\mathcal{F}}[I(x)]={\sigma }_f(x)\left[\frac{m_f(x)-f^{+}}{{\sigma }_f(x)}\mathrm{\Phi }\left(\frac{m_f(x)-f^{+}}{{\sigma }_f(x)}\right)+\varphi \left(\frac{m_f(x)-f^{+}}{{\sigma }_f(x)}\right)\right],$$ (1)

where the expectation is computed with respect to the posterior probability $p[f(x)|\mathcal{F}]$. Here, Φ(•) denotes the normal cumulative distribution function, $\varphi (\cdot )$ is the standard normal probability density function, and m_f(x) and σ_f(x) are the posterior mean and standard deviation of p[f(x)|F], respectively. All four of these components can be cheaply and easily evaluated for any given x. Thus, one advantage of EI(x) over I(x) is that EI(x) can be cheaply evaluated pointwise without requiring evaluation of f(x). Moreover, according to (1), EI(x) can be efficiently maximized using numerical optimization techniques to suggest the most promising point (from the perspective of EI) for function evaluation.

2.2. Alternating Direction Method of Multipliers (ADMM) Optimization

Our reformulation of the optimization of an unknown-objective unknown-constraint problem allows us to build a framework based on a popular numerical optimization technique, ADMM (Boyd et al., 2011; Hong and Luo, 2017; Parikh et al., 2014), which we briefly review here. Consider the problem of minimizing f (x) + g(x) with respect to x, where $x\in {ℝ}^d\text{and}f,g:{ℝ}^d\to ℝ$. Specifically, consider the case where separately minimizing f (x) and g(x) is relatively easy, while optimizing their sum is challenging. For example in the Least Absolute Shrinkage and Selection Operator (LASSO) problem (Tibshirani, 1996; Mota et al., 2013), we are interested in minimizing $\Vert Ax-b{\Vert }_2^2+\lambda \Vert x{\Vert }_1$with respect to x, with an overdetermined dictionary, A. While each term can be easily minimized, it is much harder to minimize the sum of the two terms. ADMM is a powerful numerical optimization method which handles such cases (Boyd et al., 2011; Hong and Luo, 2017).

In order to minimize f (x) + g(x), ADMM first defines an auxiliary variable $z\in {ℝ}^d$ for the function g, and considers the following optimization, which is equivalent to the original minimization problem,

$$\underset{x,z}{\min }f(x)+g(z)\text{s.t}.x=z.$$ (2)

To solve (2), ADMM first builds the augmented Lagrangian function (ALF) for (2), where the ALF provides an unconstrained surrogate function for the constrained problem. Specifically, ALF augments the objective function of a constrained problem with terms penalizing the infeasibility of the constraints. These penalty terms include the product of the feasibility gap with a dual variable vector, also called a Lagrange multiplier vector, and the squared Euclidean norm of the feasibility gap. More specifically, ALF for (2) is given by

$$L_{\rho }(x,z,y)\triangleq f(x)+g(z)+y^T(x-z)+\frac{\rho }{2}\Vert x-z{\Vert }_2^2,$$ (3)

where $y\in {ℝ}^d$ denotes the Lagrange multiplier vector corresponding to the constraint, x – z is the feasibility gap, and ρ is a positive penalty parameter.

Starting from an initial value for y, z, ADMM iteratively updates the values of variables x, y, z by minimizing the ALF, until convergence. Let x^k, z^k, y^k denote the values of variables at iteration k. At iteration k + 1, ADMM solves two optimization problems, one over x while fixing z = z^k and y = y^k and one over z while fixing x and y, and updates the Lagrange multiplier vector afterwards. More specifically, at iteration k + 1, ADMM solves

$$\begin{array}{l}{x}^{k+1}=\underset{x}{\text{argmin}}{L}_{\rho }\left(x,z^k,y^k\right)=\underset{x}{\text{argmin}}f(x)+{\left(y^k\right)}^T\left(x-z^k\right)+\frac{\rho }{2}{\Vert x-z^k\Vert }_2^2,\\ z^{k+1}=\underset{z}{\text{argmin}}{L}_{\rho }\left(x^{k+1},z,y^k\right)=\underset{z}{\text{argmin}}g(z)+{\left(y^k\right)}^T\left(x^{k+1}-z\right)+\frac{\rho }{2}{\Vert x^{k+1}-z\Vert }_2^2,\\ y^{k+1}=y^k+\rho \left(x^{k+1}-z^{k+1}\right).\end{array}$$ (4)

The primal residual is defined as $r^{k+1}\triangleq x^{k+1}-z^{k+1}$, i.e., the gap between the main variable x and the auxiliary variable z, and the dual residual can be shown to be $s^{k+1}\triangleq -\rho \left(z^{k+1}-z^k\right)$ (Boyd et al., 2011; Hong and Luo, 2017). Assuming f and g are closed, proper and convex, and also that the unaugmented Lagrangian $L_{\rho }(x,z,y)-\frac{\rho }{2}\Vert x-z{\Vert }_2^2$has a saddle point, Boyd et al. (2011) proves that as $k\to \infty ,r^k\to 0,f\left(x^k\right)+g\left(z^k\right)\to p^{*}$, and $y^k\to y^{*}$ where p* is the optimal objective value of primal problem (2) and y* is the dual optimal point. The necessary and sufficient optimality conditions for the ADMM problem are primal feasibility and dual feasibility, and they are effecively met in practice when the ${\mathcal{l}}_2$-norm of both the primal and dual residuals of (2) fall below an appropriately small tolerance. Boyd et al. (2011) shows that ADMM can be extended to problems optimizing sum of more than two functions. In this situation, ADMM defines a distinct auxiliary variable z_i for each additional function g_i, i = 1,…, N, and enforces each such variable to be equal to the main variable x. The rest of the algorithm naturally follows. See (Boyd et al., 2011), chapter 7 for a detailed discussion.

3. Constrained Bayesian Optimization via ADMMBO

In this section, we describe our proposed framework, which we refer to as ADMMBO, for solving the Bayesian optimization problem under unknown constraints. More specifically, we consider the constrained optimization problem of

$$\begin{array}{l}\underset{x\in \mathcal{B}}{\min }f(x)\\ \text{s.t}.c_i(x)\le 0,i=1,\dots ,N,\end{array}$$ (5)

where, $\mathcal{B}\subset {ℝ}^d$ is a bounded domain and $f,c_i:{ℝ}^d\to ℝ$ are unknown functions which can be evaluated pointwise. However, such evaluations are expensive. Our goal is to determine a sampling procedure for x that sequentially approaches a global optimum, x*, with as few function queries from f and all c_i’s as possible.

To tackle the problem, we first reformulate (5) into the unconstrained optimization

$$\underset{x\in \mathcal{B}}{\min }f(x)+{\displaystyle \sum _{i=1}^{N}M}1\left(c_i(x)>0\right),$$ (6)

where 1(•) is an indicator function, which is one when its argument is true and is zero otherwise, and M is a positive constant. For a sufficiently large M, the constrained problem in (5) will be equivalent to the unconstrained one in (6).

Proposition 1.

Given Lipschitz continuity of f and compactness of $\mathcal{B}$, f is bounded for every x in $\mathcal{B}$. Let ${\eta }_{\mathcal{l}}$ and ${\eta }_u$ denote, respectively, the lower and upper bound of f, i.e., ${\eta }_{\mathcal{l}}\le f(x)\le {\eta }_u,\forall x\in \mathcal{B}$. Assume the feasible region of (5) is non-empty. For $M>{\eta }_u-{\eta }_{\mathcal{l}}$, the unconstrained optimization in (6) will be equivalent to (5).

Proof.

Let J(x) denote the value of the objective function of (6). For any infeasible point of (5) $x_i\in \mathcal{B}$, we have $J\left(x_i\right)\ge {\eta }_{\mathcal{l}}+M,$ since the minimum value that f can attain is ${\eta }_{\mathcal{l}}$ and the second term in (6) will be at least M, as x_i is infeasible for at least one constraint. On the other hand, for any feasible point $x_f\in \mathcal{B}$ of (5), we have $J\left(x_f\right)\le {\eta }_u.$ Since $M>{\eta }_u-{\eta }_{\mathcal{l}},$ we always have J(x_f) < J(x_i), hence (6) always finds a feasible solution, which makes the second term of the objective function vanish. As a result, the minimization in (6), obtains the minimizer of f, which satisfies all the constraints, hence being equivalent to (5).

A key observation in our proposed framework is that while jointly minimizing the objective function in (6) is difficult, individually minimizing each term of the objective function using Bayesian optimization allows independent function evaluations for f and each c_i. More specifically, we can minimize f (x) with respect to x by assuming a GP model for p[f (x)] and using BO afterwards. Similarly, we can minimize 1(c_i(x) > 0) with respect to x by assuming a GP model for p [c_i(x) and using it to build a Bernoulli random variable with parameter ${\theta }_i\triangleq p\left[c_i(x)>0\right]$ to represent 1(c_i(x) > 0), and then applying BO. In contrast, optimizing the entire objective function in (6) is difficult and also may require joint function evaluations for f and every c_i. To take advantage of the simplicity of individually optimizing each term in the objective function of (6), we introduce N auxiliary variables, one per constraint function, and consider the following optimization problem

$$\begin{gathered} \underset{x,z_1,\dots ,z_N\in \mathcal{B}}{\min }f(x)+{\displaystyle \sum _{i=1}^{N}M}1\left(c_i\left(z_i\right)>0\right) \\ \text{s.t}.x=z_i,i=1,\dots ,N. \end{gathered}$$ (7)

which clearly is equivalent to (6). Notice that in contrast to the unknown-objective unknown-constraint problem in (5), in (7) the equality constraints are known (deterministic) and only the objective function is unknown. Moreover, each of the unknown terms in the objective function of (7) is defined over a different variable, leading to a variable separation property which we will take advantage of. Next, we describe how ADMMBO combines Bayesian optimization with an ADMM-inspired framework to solve (7) efficiently.

3.1. ADMMBO Formulation

In this section, we describe our approach to combine the ADMM algorithm with BO steps to solve the proposed equivalent reformulation in (7). We first need to build the ALF for the optimization in (7), which is given by

$$L_{\rho }\left(x,z_i,y_i\right)=f(x)+{\displaystyle \sum _{i=1}^N\left[M1\left(c_i\left(z_i\right)>0\right)+y_i^T\left(x-z_i\right)+\frac{\rho }{2}{\Vert x-z_i\Vert }_2^2\right]}=f(x)+{\displaystyle \sum _{i=1}^N\left[M1\left(c_i\left(z_i\right)>0\right)+\frac{\rho }{2}{\Vert x-z_i+\frac{y_i}{\rho }\Vert }_2^2-\frac{\rho }{2}{\Vert y_i\Vert }_2^2\right]},$$ (8)

where $y_i\in {ℝ}^d$ is a Lagrange multiplier vector, and ρ is a positive penalty parameter. Note that the second line in (8) follows from the first line by completing the square and reordering terms. Having formed the ALF, to apply the ADMM algorithm, as discussed in Section 2.2, we initialize the unknown variables and the Lagrange multiplier vectors and at ADMM iteration k, we solve for each variable in turn, using BO, having fixed the rest. More specifically, for (8), the k^th ADMM iteration will become

$$\begin{array}{l}{x}^{k+1}=\underset{x\in \mathcal{B}}{\text{argmin}}f(x)+{\displaystyle \sum _{i=1}^N\frac{\rho }{2}}{\Vert x-z_i^k+\frac{y_i^k}{\rho }\Vert }_2^2,\\ z_i^{k+1}=\underset{z_i\in \mathcal{B}}{\text{argmin}}M1\left(c_i\left(z_i\right)>0\right)+\frac{\rho }{2}{\Vert x^{k+1}-z_i+\frac{y_i^k}{\rho }\Vert }_2^2,\forall i=1,\dots ,N\\ y_i^{k+1}=y_i^k+\rho \left(x^{k+1}-z_i^{k+1}\right),\forall i=1,\dots ,N.\end{array}$$ (9)

The x update, which we refer to as the optimality subproblem, minimizes the unconstrained objective function of the original problem in (5), f, plus a sum of quadratic terms that force the solution to be close to the feasible region. On the other hand, each z_i update, which we refer to as feasibility subproblems, looks for a feasible point of the constraint c_i that is also close to the unconstrained optimum found in the optimality subproblem.

Since both the optimality and feasibility subproblems involve unknown objectives, we solve each of them using Bayesian optimization with unconstrained acquisition functions. Thus, in ADMMBO there are two levels of iteration: ADMM iterations (from now on referred to as main loop iterations), and BO iterations, which are performed to solve each subproblem during each main loop iteration. ADMMBO’s general framework allows it to incorporate any unconstrained acquisition function, including EI, Predictive Entropy Search (PES)(Hernández-Lobato et al., 2014), and Knowledge Gradient (KG)(Wu et al., 2017), as best fits a given problem. For example, while PES is reported to outperform EI by Hernández-Lobato et al. (2014),but has also been reported to be relatively slow due to its need to sample x* and compute expectation propagation approximations (Hernández-Lobato et al., 2016). EI has a closed-form solution which, in practice, may make it faster than PES (Jones et al., 1998). The choice of acquisition function for each subproblem in any main loop iteration of ADMMBO is a matter of user preference and does not change ADMMBO’s structure. In this paper we chose to use EI to solve both the optimality and feasibility subproblems because of its wide popularity and because its structure more easily leads to closed form solutions. In addition, while we could have modeled the objective function of each subproblem with a single GP, this would have ignored available partial knowledge about the structure of these objectives. Instead, we designed a specific Bayesian model for each subproblem objective that takes advantage of this knowledge to better guide the optimization. We show that EI still maintains a closed-form solution given these new Bayesian models.

3.1.1. Expected Improvement for the Optimality Subproblem

For the k^th main loop iteration, the optimality subproblem associated with (9) requires optimizing the sum of the unknown objective function, f, and a known function, i.e.,

$$\underset{{}_{x\in B}}{\min }{u}^k(x),\text{where}{u}^k(x)\triangleq f(x)+{\displaystyle \sum _{i=1}^N\frac{\rho }{2}}{\Vert x-z_i^k+\frac{y_i^k}{\rho }\Vert }_2^2.$$ (10)

As f (x) is an unknown function, we solve (10) via BO by assuming that f follows a GP prior. Since $z_i^k\text{and}{y}_i^k$ are given and fixed, the second term in the definition of u^k(x) is constant for any given x. Thus, we can still model p [u^k(x)] as a GP. Given observed data $\mathcal{F}={\left\{\left(x_l,f\left(x_l\right)\right)\right\}}_{l=1}^n,x_l\in \mathcal{B},$ we compute ${\mathcal{U}}^k={\left\{\left(x_l,u^k\left(x_l\right)\right)\right\}}_{l=1}^n$ and denote the best objective value of (10) so far by u^k+. Then, similar to the standard EI, we compute the Expected Improvement for the optimality subproblem, which will be

$$\begin{gathered} EI(x)=E_{u^k|\mathcal{u}k}\left[\max \left(0,u^{k+}-u^k(x)\right)\right] \\ ={\sigma }_{u^k}(x)\left[\frac{m_{u^k}(x)-u^{k+}}{{\sigma }_{u^k}(x)}\mathrm{\Phi }\left(\frac{m_{u^k}(x)-u^{k+}}{{\sigma }_{u^k}(x)}\right)+\varphi \left(\frac{m_{u^k}(x)-u^{k+}}{{\sigma }_{u^k}(x)}\right)\right], \end{gathered}$$ (11)

where m_u^k(x), σ_u^k(x) are, respectively, the mean and standard deviation of the posterior distribution p[u^k(x)|$\mathcal{u}$^k]. Thus, for any given x, we can calculate its EI via (11).

3.1.2. Expected Improvement for the Feasibility Subproblem

For k^th main loop iteration, the i^th feasibility subproblem associated with (9) requires optimizing the sum of an unknown function and a known function, i.e,

$$\underset{z_i\in \mathcal{B}}{\min }{h}_i^k\left(z_i\right),\text{where}{h}_i^k\left(z_i\right)\triangleq 1\left(c_i\left(z_i\right)>0\right)+\frac{\rho }{2M}{\Vert x^{k+1}-z_i+\frac{y_i^k}{\rho }\Vert }_2^2.$$ (12)

Let us call $q_i^k\left(z_i\right)=\frac{\rho }{2M}{\Vert x^{k+1}-z_i+\frac{y_i^k}{\rho }\Vert }_2^2.$ Since c_i(z_i) is unknown, we solve (12) via BO by assuming that c_i follows a GP prior. Then, we model 1(c_i(z_i) > 0) as a Bernoulli random variable with the parameter ${\theta }_i\triangleq p\left[c_i\left(z_i\right)>0\right].$ Since $x_i^{k+1}\text{and}{y}_i^k$ are given and fixed, $q_i^k\left(z_i\right)$ will be constant for any given z_i. Thus, we model $h_i^k\left(z_i\right)$ as a shifted Bernoulli random variable, again with the parameter θ_i, which is equal to $q_i^k\left(z_i\right)+1$ with probability θ_i, and equal to $q_i^k\left(z_i\right)$ with probability 1 – θ_i. Note that 1 – θ_i for any z_i is a Gaussian Cumulative Distribution Function (CDF) based on the marginal Gaussianity of GPs (Houlsby et al., 2012; Gardner et al., 2014; Rasmussen and Williams, 2006). Given ${\mathcal{C}}_i={\left\{\left(z_{l,i},c_i\left(z_{l,i}\right)\right)\right\}}_{l=1}^{m_i},z_{l,i}\in \mathcal{B},$ we generate ${\mathcal{H}}_i^k={\left\{\left(z_{l,i},h_i^k\left(z_{l,i}\right)\right)\right\}}_{l=1}^{m_i}$ using C_i, and denote the best objective value of (12) by $h_i^{k+}.$ We then compute the Expected Improvement for the i^th feasibility subproblem, which is given by

$$EI\left(z_i\right)=E_{h_i^k|{\mathcal{H}}_i^k}\left[\max \left(0,h_i^{k+}-h_i^k\left(z_i\right)\right)\right]=\max \left(0,h_i^{k+}-q_i^k\left(z_i\right)-1\right){\theta }_i+\max \left(0,h_i^{k+}-q_i^k\left(z_i\right)\right)\left(1-{\theta }_i\right),$$ (13)

Given any $z_i,\text{if}{h}_i^{k+}-q_i^k\left(z_i\right))$ is non-positive, then EI(z_i) is zero. If $h_i^{k+}-q_i^k\left(z_i\right)$ lies between zero and one, the first term in (13) is zero while the second term has a positive value. When $h_i^{k+}-q_i^k\left(z_i\right)$ is larger than one, both terms are positive. Thus, we can simplify (13) to

$$EI\left(z_i\right)=\{\begin{array}{ll}0,\hfill & \text{if}{h}_i^{k+}-q_i^k\left(z_i\right)\le 0\hfill \\ \max \left(0,h_i^{k+}-q_i^k\left(z_i\right)\right)\left(1-{\theta }_i\right),\hfill & \text{if}0<h_i^{k+}-q_i^k\left(z_i\right)\le 1\hfill \\ \max \left(0,h_i^{k+}-q_i^k\left(z_i\right)\right)\left(1-{\theta }_i\right)+\max \left(0,h_i^{k+}-q_i^k\left(z_i\right)-1\right){\theta }_i,\hfill & \text{else}.\hfill \end{array}$$ (14)

Notice that according to the closed-form expressions in (11) and (14), Els can be cheaply evaluated pointwise at any given point. As a result, these acquisition functions can be maximized with standard numerical optimization methods such as DIRECT or stochastic gradient descent (Finkel, 2003; Bottou, 2010)

3.2. ADMMBO Algorithm

Algorithm 3.1 summarizes the steps of ADMMBO. The parameters to the algorithm are the search space $\beta .$ the coefficient M, the number of initial function evaluations for the objective function n, number of initial function evaluations for each constraint m_i for i = 1,…, N, the maximum number of ADMM iterations K, the ADMM’s penalty parameter ρ, and the total BO iteration budget, the maximum number of function evaluations throughout the algorithm. We distribute this budget among main loop where at iteration k, α^k denotes the BO budget for the optimality subproblem and ${\beta }_i^k$ is the BO budget for i^th feasibility subproblem, the tolerances for the stopping criterion ϵ, and a confidence parameter δ to determine the final solution returned in the case that the budget is exhausted before convergence.

Algorithm 3.1.

ADMMBO

1:	Input: $\mathcal{B},n,m_i,\delta ,K,{\alpha }^k,{\beta }_i^k,\rho ,ϵ,M;\forall i=1,\dots ,N,\forall k=1,\dots ,K$
2:	Randomly generate ${\left\{x_l\in \mathcal{B}\right\}}_{l=1}^n\text{and}{\left\{z_{l,i}\in \mathcal{B}\right\}}_{l=1}^{m_i},\forall i=1,\dots ,N$
3:	Initialize: $k=1,{\mathcal{F}}^1={\left\{\left(x_l,f\left(x_l\right)\right)\right\}}_{l=1}^n,{\text{C}}_i^1={\left\{\left(z_{l,i},c_i\left(z_{l,i}\right)\right)\right\}}_{l=1}^{m_i},y_i^1=0,z_i^1=0,$ S = False;
4:	while (k ≤ K) and (S == False) do
5:	$\left[x^{k+1},{\mathcal{F}}^{k+1}\right]\leftarrow \text{OPT}\left({\mathcal{F}}^k,\mathcal{B},{\alpha }^k,z_i^k,y_i^k\right)$ (See Algorithm 3.2)
6:	for i = 1,…, N do
7:	$\left[z_i^{k+1},{\mathcal{C}}_i^{k+1}\right]\leftarrow \text{FEAS}\left({\mathcal{C}}_i^k,\mathcal{B},{\beta }_i^k,x^{k+1},y_i^k\right)$ (See Algorithm 3.3)
8:	$y_i^{k+1}=y_i^k+\rho \left(x^{k+1}-z_i^{k+1}\right)$
9:	$r^{k+1}[i]=x^{k+1}-z_i^{k+1}$
10:	$s^{k+1}[i]=-\rho \left(z_i^{k+1}-z_i^k\right)$
11:	end for
12:	if $\left({\Vert r^{k+1}\Vert }_2\le ϵ\right)\text{and}\left({\Vert s^{k+1}\Vert }_2\le ϵ\right)$ then S = True
13:	end if
14:	k ← k + 1
15:	end while
16:	if S==True then   Output: xk+1
17:	else
	Output: argmin $\underset{x\in {\mathcal{F}}^K\cup {\mathcal{C}}_1^K\cup \dots \cup C_N^K}{\text{argmin}}{E}_{f|\mathcal{F}K}[f(x)]\text{s.t}.p\left[c_i(x)\le 0\right]\ge 1-\delta$
18:	end if

Algorithm 3.1 works as follows: first in order to build the initial datasets $\mathcal{F}\text{and}{\mathcal{C}}_i,$ the algorithm randomly generate n and m_i samples in the search space $\mathcal{B},$ and then evaluate f and c_i at the corresponding points (lines 2 – 3). After initializing the parameters (line 3), ADMMBO iterates through its main loop until it reaches the total BO iteration budget or the stopping criterion is satisfied (line 4). At the k^th iteration of the main loop, ADMMBO solves the optimality subproblem with BO given budget α^k. Specifically, this step is done by calling the Algorithm 3.2, denoted OPT, which outputs a desirable solution of the optimality subproblem and the updated dataset $\mathcal{F}$ (line 5). Then, for each constraint i, ADMMBO performs the following steps: first it solves the corresponding feasibility subproblem with BO given budget ${\alpha }_i^k,$ by calling the algorithm 3.3, denoted FEAS, which outputs a good solution of the i^th feasibility subproblem and the updated dataset C_i (line 7). Then, ADMMBO updates the corresponding Lagrange multipliers and components of the primal and dual residuals (lines 8 – 10). Afterwards, at the end of each main loop iteration, it checks the stopping criterion, i.e. whether the ${\mathcal{l}}_2\text{-norms}$ of the primal and dual residuals are smaller than or equal to a chosen tolerance (line 12). If the stopping criterion is satisfied, the algorithm stops and reports the most recent x as the desirable solution for the unknown-objective unknown-constraint problem (5) (line 17). Otherwise, it keeps iterating. After reaching the maximum number of total iterations without meeting stopping criterion, ADMMBO reports a final recommendation for the desirable solution of (5). This recommendation is the point belonging to the merged data $\mathcal{F}\cup {\mathcal{C}}_1\cup \dots \cup {\mathcal{C}}_N$ which has the lowest expected objective value subject to the posterior probability of satisfying the constraints being at least 1 – δ, where δ is a parameter representing the maximum acceptance probability that a final solution is infeasible.

Algorithm 3.2.

OPT

1:	Input: $\mathcal{F}={\left\{\left(x_l,f\left(x_l\right)\right)\right\}}_{l=1}^n,\mathcal{B},\alpha ,z_i,y_i;i=1,\dots ,N$
2:	Initialize: ${\mathcal{F}}^1=\mathcal{F}$
3:	for t = 1,…, α do
4:	Given ${\mathcal{F}}^t,\text{compute}{\mathcal{U}}^t=\{{(x_l,f\left(x_l\right)+{\displaystyle {\displaystyle \sum _{i=1}^N}\frac{\rho }{2}}{\Vert x_l-z_i+\frac{y_i}{\rho }\Vert }_2^2\}}_{l=1}^n$
5:	Update the GP posterior $p\left[u(x)|{\mathcal{U}}^t\right]$
6:	$x^t\leftarrow \arg {\max }_{x\in \mathcal{B}}EI(x)$ (use expression (11) for EI(x))
7:	${\mathcal{F}}^{t+1}={\mathcal{F}}^t\cup \left\{\left(x^t,f\left(x^t\right)\right)\right\}$
8:	n ← n + 1
9:	end for
10:	xmin = argmin $f(x)+{\displaystyle {\displaystyle \sum _{i=1}^N}\frac{\rho }{2}}{\Vert x-z_i+\frac{y_i}{\rho }\Vert }_2^2$
11:	Output: [xmin, Fα]

Algorithm 3.3.

FEAS

1:	Input: ${\mathcal{C}}_i={\left\{\left(z_{l,i},c_i\left(z_{l,i}\right)\right)\right\}}_{l=1}^{m_i},\mathcal{B},{\beta }_i,x,y_i$
2:	Initialize: $C_i^1=C_i$
3:	for t = 1,…,βi do
4:	Given ${\mathcal{C}}_i^t,\text{compute}{\mathcal{H}}_i^t={\left\{\left(z_{l,i},1\left(c_i\left(z_{l,i}\right)>0\right)+\frac{\rho }{2M}{\Vert x-z_{l,i}+\frac{y_i}{\rho }\Vert }_2^2\right)\right\}}_{l=1}^{m_i}$
5:	Update the GP posterior $p\left[c_i\left(z_i\right)|{\mathcal{C}}_i^t\right]$
6:	$z_i^t\leftarrow \arg {\max }_{z_i\in \mathcal{B}}EI\left(z_i\right)$ (use expression (13) for EI(zi))
7:	${\mathcal{C}}_i^{t+1}={\mathcal{C}}_i^t\cup \left\{\left(z_i^t,c_i\left(z_i^t\right)\right)\right\}$
8:	mi ← mi + 1
9:	end for
10:	$z_{\min }=\underset{z_i\in {\mathcal{C}}_i^{{\beta }_i}}{\text{argmin}}1\left(c_i\left(z_i\right)>0\right)+\frac{\rho }{2M}{\Vert x-z_i+\frac{y_i}{\rho }\Vert }_2^2$
11:	Output: $\left[z_{\min },{\mathcal{C}}_i^{{\beta }_i}\right]$

Algorithm 3.2, denoted by OPT, solves the optimality subproblem with BO under a budget α. For α iterations, OPT repeats the following steps: Given y_i z_i, and dataset $\mathcal{F}$, it computes $\mathcal{U}$ and updates the GP posterior $p[u(x)|\mathcal{U}].$ Then, OPT uses this posterior to compute EI(x) using equation (11) and maximizes it over $x\in \mathcal{B}.$ It evaluates the objective function f at the global optimum of EI(x), and updates data $\mathcal{F}$ accordingly. After a iterations, OPT gives a final recommendation for the solution of the optimality subproblem, and outputs the most updated data $\mathcal{F}$.

Algorithm 3.3, denoted by FEAS, solves each feasibility subproblem with BO under a budget β_i. For β_i iterations, FEAS repeats the following steps: Given x, y_i, and data ${\mathcal{C}}_i,$ it computes ${\mathcal{H}}_i.$ Then, FEAS updates the GP posterior $p\left[c_i\left(z_i\right)|{\mathcal{C}}_i\right]$ and use this posterior and ${\mathcal{H}}_i$ to compute EI(z_i) using equation (13). Next, it maximizes EI(z_i) over $z_i\in \mathcal{B},$ evaluate the constraint C_i at the optimum of the EI(z_i) and updates C_i accordingly. After β_i iterations, the algorithm gives a final recommendation of the solution for the feasibility subproblem, and outputs the most updated data C_i.

ADMMBO has the potential to be parallelized at two different levels: first, the feasibility subproblems are independent and can be solved independently, in parallel (lines 6 – 11 in Algorithm 3.1). Second, BO iterations at OPT and FEAS (lines 3 – 9 in Algorithm 3.2 and 3.3) can be parallelized according to a scheme suggested by Snoek et al. (2012) where a new candidate location is selected according to not only the observed data, but also the locations of pending function evaluations. Both parallelization will lead to speed up of ADMMBO.

3.2.1. Hyperparameter Tuning for ADMMBO

ADMMBO has two sets of parameters: BO-dependent parameters, which are commonly used by other constrained BO methods, and ADMM-dependent parameters, which lend themselves to the ADMM framework of ADMMBO. BO-dependent parameters are B, a box defining the search space, n and m_i, the number of initial random samples at which to evaluate f and each c_i, respectively, δ, the parameter used if ADMMBO does not converge, and a total BO iteration budget.

ADMM-dependent parameters are K, the maximum number of iterations in the main loop, along with ${\alpha }^k\text{and}{\beta }_i^k,$ the BO iteration budgets for the optimality and i^th feasibility subproblems during the k^th main loop iteration. These three hyperparameters should be jointly set in a way that ${\displaystyle {\sum }_{k=1}^K\left({\alpha }^k+{\displaystyle {\sum }_{i=1}^N{\beta }_i^k}\right)}$ equals to the total BO iteration budget. ρ is the ADMM penalty parameter, and ϵ is a small tolerance which controls the stopping rule for the algorithm. We provide guidance on how to set these hyperparameters in practice in section 5.1. Finally, M controls the penalization of infeasibility. In Proposition 1, we suggest to set the value of M based on the range of f over $\mathcal{B}.$ The unconstrained range of f is known for many user-defined objectives. For example, if we define f as the validation error of a machine learning model, this range equals, the maximum possible error, 1, minus the minimum possible error 0, 1 – 0 = 1. Since the unconstrained range of f is an upper bound for the range of f over $\mathcal{B}$, we can use it to set M. However, this range might be unknown in practice. In such cases, we recommend setting the value of M equal to a large number with respect to any likely value of f, which can be chosen based on the application domain. As long as M is reasonably large, its precise value does not affect the performance of ADMMBO in practice. In section 5.7, we illustrate that ADMMBO’s performance is not sensitive to the choice of M over a very wide range of values.

3.2.2. Convergence in Practice

Convergence guarantees for ADMM only hold for convex problems (Boyd et al., 2011). However, here only limited information is available about the objective function and the feasible set and thus often the convexity of the problem is unknown. If f is a convex function and the feasible set is a convex set, ADMM has convergence guarantees given each subproblem is solved exactly. In ADMMBO,however, the subproblems have unknown objectives which the algorithm solves using BO methods. These methods offer exact solutions only given an unlimited budget, which is not realistic in practice. For a limited budget, BO methods find approximate solutions for the subproblems, and thus similar to the rest of the BO state-of-the-art, ADMMBO cannot offer convergence guarantees.

However, in fact, we have chosen ADMM precisely to build upon the many studies that have found that ADMM exhibits a good empirical performance even if the convergence conditions are not satisfied (Xu et al., 2016; Wang et al., 2015; Hong et al., 2016). We report in section 5 that ADMMBO converged for the non-convex problems we tested.

4. Related Work

Two general strategies have been introduced to extend Bayesian optimization to constrained Bayesian optimization with unknown constraints. One strategy is to modify the acquisition function within the Bayesian optimization framework, that the acquisition function simultaneously takes into account the feasibility of a candidate point along with its objective value. Most previous work falls into this category, including EIC, IECI, EVR, and PESC (Schonlau et al., 1998; Snoek, 2013; Gelbart et al., 2014; Gardner et al., 2014; Bernardo et al., 2011; Picheny, 2014; Hernández-Lobato et al., 2015). The second strategy merges Bayesian optimization with numerical optimization techniques which are designed to deal with constrained optimization problems. To the best of our knowledge, to date there is only one such approach in this category for BO, ALBO, along with its Slack-AL variant, (Gramacy et al., 2016; Picheny et al., 2016). We describe some existing methods in both categories next.

4.1. Constrained BO using Modified Acquisition Functions

Several proposed acquisition functions for BO problems with unknown constraints are extensions of EI (Jones et al., 1998). One such extension, Expected Improvement with Constraints is reported by Schonlau et al. (1998); Snoek (2013); Gelbart et al. (2014), and Gardner et al. (2014). Given a point x, EIC calculates the expectation of the improvement of the objective value of x over the best observed objective value evaluated at a feasible point so far, and then weight it by the probability of feasibility of x. Assuming independent Gaussian process models for the objective function and constraints, EIC yields closed-form solutions based on the standard normal CDF and PDF. Bernardo et al. (2011) proposed another variation of EI, Integrated Expected Conditional Improvement, based on a one-step look-ahead strategy. Given a candidate point x, IECI measures how much reduction in the improvement of the objective value of a typical point x’ is expected, if we have previously evaluated the objective value of x and augmented our data with it. IECI does not have a closed-form solution, and thus its integral is computed numerically over a grid of x’. This limits the application of IECI to small dimensional problems (Hernández-Lobato et al., 2015; Shahriari et al., 2016).

In addition to EI-based methods, there is a class of information-based acquisition functions designed to reduce a chosen measure of uncertainty about the location of the global optimum. Thus, for a candidate point, such methods evaluate the reduction in their uncertainty measure which will be obtained by evaluating its objective value. Expected Volume Reduction proposed by Picheny (2014) uses the expected volume of the feasible region as its measure of uncertainty. For a point x, EVR first computes the probability that, for any given point x’ f (x’) is less than the minimum of the best observed f so far corresponds to a feasible point and f (x). It then integrates that probability against the probability of feasibility of x’ over all x’. Another information-based acquisition function, Predictive Entropy Search with Constraints (PESC) uses entropy as its uncertainty measure. Specifically, PESC first calculates the differential entropy of the posterior of the global optimum and then for a point x, measures how much reduction is expected in this entropy if we evaluate the objective function and constraints at point x (Hernández-Lobato et al., 2015).

4.2. Constrained BO using Numerical Optimization

In addition to the approaches based on BO with a modified acquisition function, there is a second category that solves the unknown constraint problem using ideas from the field of numerical optimization. Many numerical optimization algorithms tackle a constrained problem by reformulating it into two or more coupled unconstrained problems, which are generally easier to handle, and then solving them via alternating iterations (Nocedal and Wright, 2006). Here, where the constrained problem involves unknown functions, the idea is to define unconstrained surrogate problems using numerical optimization techniques, and then solve these problems, which still involve unknown functions, with BO. The first, and to-date only, methods in this category are based on the augmented Lagrangian method.

Gramacy et al. (2016) proposed the Augmented Lagrangian for BO, ALBO, which uses the Augmented Lagrangian Function (ALF) to formulate unconstrained surrogate problems, and then solves them using EI as acquisition function. The challenge in the proposed approach is that ALF of the original problem involves a complicated mixture of unknown functions. Thus, the previous calculations for the EI, which assumed a single GP model, do not hold any more. Building a probabilistic model for this mixture objective and recalculating EI based on it is a challenging task. As a result, EI calculations in ALBO do not result in closed form solutions, and so this method relies on Monte-Carlo approximation. To address this issue, Picheny et al. (2016) introduced Slack-AL by modifying the original problem to include a slack variable and then applying the augmented Lagrangian method on the modified problem. The authors optimized the modified ALF with EI iterations. It turns out that the modified ALF in Slack-AL is easier to solve than the ALF in ALBO. As a result, the Expected Improvement in Slack-AL, in contrast to ALBO, has a closed-form expression, and may be evaluated with library routines.

5. Experiments

In this section, we evaluate the performance of ADMMBO on several synthetic problems, studied in the constrained Bayesian optimization literature (Gardner et al., 2014; Gramacy et al., 2016; Picheny et al., 2016), as well as on the problem of hyperparameter tuning for a fast neural network on the MNIST digit recognition dataset (LeCun, 1998; Hernández-Lobato et al., 2015). We compare ADMMBO with four state-of-the-art constrained Bayesian optimization methods¹: EIC (Gelbart et al., 2014; Gardner et al., 2014), ALBO (Gramacy et al., 2016), Slack-AL (Picheny et al., 2016) and PESC (Hernández-Lobato et al., 2015).

5.1. Implementation Details

In all the synthetic problems, discussed below, similar to (Hernández-Lobato et al., 2015; Picheny et al., 2016; Gramacy et al., 2016), we assume that f and c_i follow independent GP priors with zero mean and squared exponential kernels. For the problem of hyperparameter tuning in Neural Networks on the MNIST dataset, we assume that f and c_i, follow independent GP priors with zero mean and with Matérn 5/2 kernels (Hernández-Lobato et al., 2015). For ADMMBO, in all the experiments we set M = 50, ρ = 0.1, ϵ = 0.01, δ = 0.05 and initialize $y_i^1$ with a zero vector and and $z_i^1\text{with}\min (\mathcal{B}).$ Further, in all the experiments, we set the total BO iteration budget to 100(N +1), where N is the number of constraints of the optimization. We empirically observed that ADMMBO performed best when we assign a higher BO budget for the first iteration of the algorithm. Thus, we set ${\alpha }^1={\beta }_i^1=20$ for the first iteration and ${\alpha }^k={\beta }_i^k=2,2\le K$ for the rest. Considering total BO budget and the budgets for the optimality and feasibility subproblems, we set K = 40. We initialize datasets $\mathcal{F}\text{and}{\mathcal{C}}_i\text{with}n=m_i=2$ points. Notice that initial points are randomly generated and will not necessarily be feasible.

The convergence speed of ADMM in practice depends on the value of the penalty parameter ρ (Boyd et al., 2011). Specifically, a large value of ρ imposes a large penalty on violating the primal feasibility and thus encourages small primal residuals. On the other hand, a small value of ρ increases the penalty on the dual residual, encouraging it to be small, but at the same time also reduces the penalty on primal feasibility, resulting in a larger primal residual. To improve the convergence speed of ADMMBO in practice and to make the performance less sensitive to the choice of the penalty parameter ρ, following (Boyd et al., 2011), we use the penalty ρ^k at iteration k, where

$${\rho }^{k+1}=\{\begin{array}{ll}{\tau }^{incr}{\rho }^k\hfill & \text{if}{\Vert r^k\Vert }_2>\mu {\Vert s^k\Vert }_2\hfill \\ {\rho }^k/{\tau }^{decr}\hfill & \text{if}{\Vert s^k\Vert }_2>\mu {\Vert r^k\Vert }_2\hfill \\ {\rho }^k\hfill & \text{otherwise}.\hfill \end{array}$$ (15)

We set $\mu =10\text{and}{\tau }^{incr}={\tau }^{decr}=2$ similar to (Boyd et al., 2011; Hong and Luo, 2017).

5.2. Performance Metrics

To test the sensitivity of different algorithms to the initialization of $\left\{\mathcal{F},{\mathcal{C}}_1,\dots ,{\mathcal{C}}_N\right\},$ we run each algorithm for each synthetic problem with 100 random initializations and for the hyperparameter tuning problem for 5 random initializations. For each method after each additional function evaluation, we report the median of the best observed objective value at a feasible point, over all random initializations. This median is shown by a solid curve in our figures (Figures 1 to 6). For each method, we start to report results (show the median curve) once all 100 runs have found a feasible point. The budget at which each method attains such a point over 100 runs is denoted by a dashed vertical line in our figures. Moreover, the variability of the performance is illustrated after different number of function evaluations by reporting the 25/75 percentiles of the best feasible objective value over the 100 runs. Moreover, in Figures 1 to 4, we depict the feasible region of our 2-dimensional problems, their global and local optima, as well as the final recommendation provided by each method given a specific budget, among 100 runs.

Figure 1:

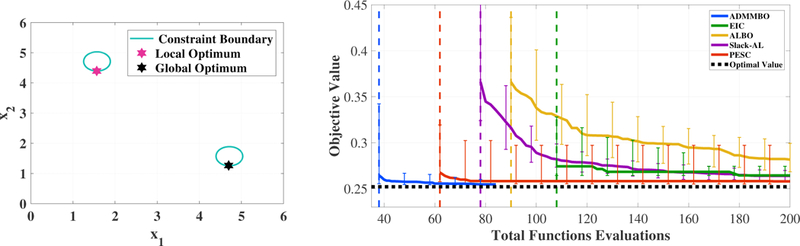
Left: feasible region of (16) consists of two oval regions. The pink and black stars show,respectively, the local and global optimizer. Right: the curve of the median and 25/75 percentiles of the best objective value found by each method, among 100 runs that obtain a feasible solution, as a function of the total budget for function evaluation. We report the results of each method for a budget once all of its 100 runs obtain a feasible solution.

Figure 6:

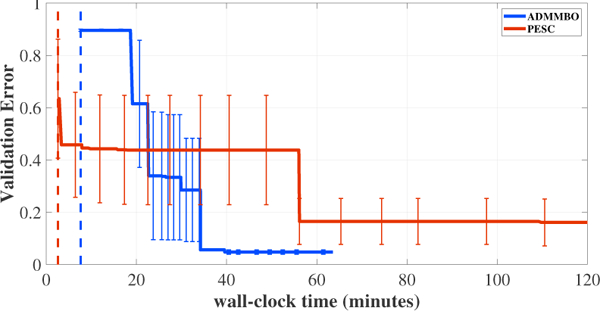
Comparison between ADMM and PESC for hyperparameter tuning for a neural network with short prediction time.

Figure 4:

The feasible region of (17) and the best solutions obtained by ADMMBO (left), EIC (middle) and PESC (right) after 50 function evaluations, over 100 runs. For each method, each point represents the final solution of that method over one run, after 50 total function evaluations.

5.3. Test Problem with a Small Feasible Region

Consider the following optimization problem, studied also in (Gardner et al., 2014),

$$\begin{array}{cc}\stackrel{\min }{{}_{x\in \mathcal{B}}}& \sin \left(x_1\right)+x_2\\ \text{s.t}.& \sin \left(x_1\right)\sin \left(x_2\right)+0.95\le 0,\end{array}$$ (16)

where $\mathcal{B}={[0,6]}^2.$ This is a challenging problem since both the objective function and the constraint are highly non-linear. Moreover, the feasible region with respect to the bounded parameter space $\mathcal{B}$ is small, hence, finding a feasible point is difficult.

The left plot in Figure 1 shows the feasible region of (16) and its global and local optima, while the right figure shows the median of the objective value of the best feasible point, obtained by each method, among 100 runs as a function of total number of function evaluations. As the results demonstrate, ADMMBO outperforms EIC, ALBO, Slack-AL and PESC in terms of finding the global optimum at a lower budget. Moreover, ADMMBO is the first method to find a feasible point in all 100 runs, followed by PESC second and then the others. Only ADMMBO, ALBO, and Slack-AL have defined stopping criteria, and of those three only ADMBBO reaches its criterion and stops before the pre-set budget is exhausted. Figure 2 shows the best points obtained by ADMMBO, ALBO, and Slack-AL after 100 function evaluations, over 100 runs. Over all runs, ADMMBO has consistently found a feasible solution very close to the global optimum (black star in the left figure in Figure 1). However, the best points obtained by ALBO and Slack-AL are scattered throughout the entire feasible region and not necessarily close to the global optimum. Note that in a few runs, the best solutions found by these two methods are outside the feasible region, and thus are infeasible. We observe that ALBO and Slack-AL require a higher budget in order to converge to the global optimum of (16).

Figure 2:

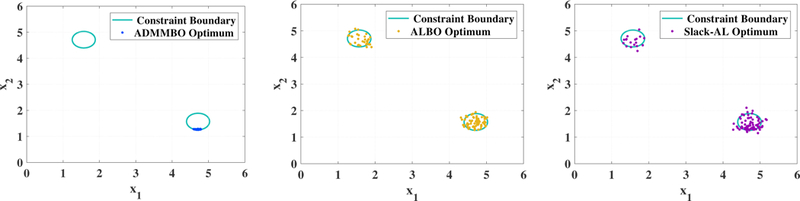
Feasible region of (16) and the best solutions obtained by ADMMBO (left), ALBO (middle) and Slack-AL (right) after 100 function evaluations, over 100 runs. For each method, each point represents the final solution of that method over one run, after 100 total function evaluations.

5.4. Test Problem with Multiple Constraints

Our second benchmark problem is a toy two dimensional problem introduced first in (Gramacy et al., 2016), and used later in (Picheny et al., 2016; Hernández-Lobato et al., 2015). We have chosen this problem specifically to test our ADMMBO on a problem with multiple constraints. More specifically, for $\mathcal{B}={[0,1]}^2,$ we consider the optimization problem

$$\begin{gathered} \underset{x\in \mathcal{B}}{\min }{x}_1+x_2 \\ \mathrm{s}.\mathrm{t}.0.5\sin \left(2\pi \left(x_1^2-2x_2\right)\right)+x_1+2x_2+1.5\le 0,-x_1^2-x_2^2+1.5\le 0. \end{gathered}$$ (17)

The left plot in Figure 3 shows the feasible region of (17) and its global and local optimizers, and the right plot shows the performance of different methods as a function of the number of function evaluation budget. The layout is the same as for the previous figure. Again, ADMMBO achieves the best performance in terms of converging to the global optimum at a lower budget, followed by PESC. We believe this is due to the fact that both ADMMBO and PESC can handle decoupled problems, including this example, via single function evaluations, while EIC, ALBO and Slack-AL enforce joint function evaluations at each step. Moreover, as the plot demonstrates, ADMMBO and ALBO are the first methods that arrive at a feasible point over 100 runs at a lower number of function evaluations.

Figure 3:

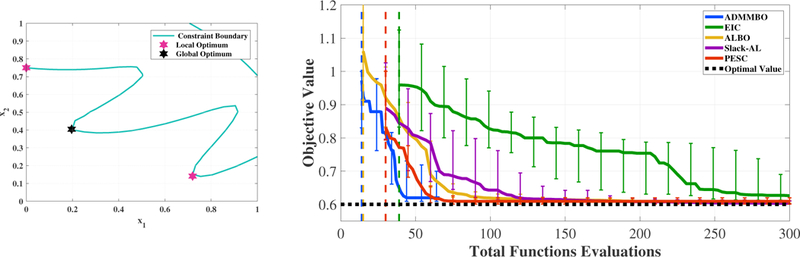
Left: feasible region of the optimization problem (17). Right: performance of different methods as a function of the total budget for function evaluation.

Figure 4 shows the best points obtained by ADMMBO, EIC, and PESC after 50 function evaluations, over 100 runs. Over all runs, ADMMBO and PESC have found solutions very close to the global or local optima (black and pink stars in the left figure in Figure 3). However, EIC was unable to narrow down its search toward such an optimum, and thus its proposed solutions are scattered throughout the entire feasible region. According to the Figure 3, all methods, including EIC, ultimately converge to the global optimum. However, ADMMBO and PESC achieve this sooner and at a lower budget.

5.5. Test Problem in Higher Dimensions

We chose the first two problems, defined over a two-dimensional space, in order to be able to visualize the feasible regions, global and local optima, as well as the final solution of different algorithms. Here, we evaluate the performance of ADMMBO on a test problem which is defined over a higher dimensional space. This is a modification of the example in (Picheny et al., 2016), where the constraint is the Hartman 4-dimensional function. This function was used as an equality constraint in (Picheny et al., 2016), however, we modified it as an inequality constraint to follow the format of (5). More specifically, for $\mathcal{B}={[0,1]}^4,$ we consider the optimization problem

$$\begin{array}{ll}\stackrel{\min }{{}_{x\in \mathcal{B}}}\hfill & {\displaystyle \sum _{i=1}^4{x}_i}\hfill \\ \text{s.t}.\hfill & 1.1923\left[{\displaystyle \sum _{i=1}^4{E}_i}\exp \left(-{\displaystyle \sum _{j=1}^4{A}_{ji}}{\left(x_j-P_{ji}\right)}^2\right)-1.1\le 0\right],\hfill \end{array}$$ (18)

where A_ji, E_i and P_ji denote, respectively, the entries of

$$A=\left[\begin{array}{cccc}10.00& 0.05& 3.00& 17.00\\ 3.00& 10.00& 3.50& 8.00\\ 17.00& 17.00& 1.70& 0.05\\ 3.50& 0.10& 10.00& 10.00\end{array}\right],E=\left[\begin{array}{l}1.0\hfill \\ 1.2\hfill \\ 3.0\hfill \\ 3.2\hfill \end{array}\right],P=\left[\begin{array}{cccc}0.131& 0.232& 0.234& 0.404\\ 0.169& 0.413& 0.145& 0.882\\ 0.556& 0.830& 0.352& 0.873\\ 0.012& 0.373& 0.288& 0.574\end{array}\right].$$

As Figure 5 shows, ADMMBO and PESC compared to EIC, ALBO, and Slack-AL achieve lower value of the objective function after a smaller number of function evaluation. However, similar to other examples, ADMMBO arrives at a feasible point after fewer number of functions evaluations compared to PESC. As an interesting observation, in the budget range of [5,25], ADMMBO shows a flat curve, which we speculate is due to being at a local minima, however, finally ADMMBO escapes this local minimizer. Again, as this figure shows, an advantage of ADMMBO compared to existing work is its efficient stopping criterion that allows our algorithm to terminate before consuming the total budget, hence, avoiding unnecessary function evaluations.

Figure 5:

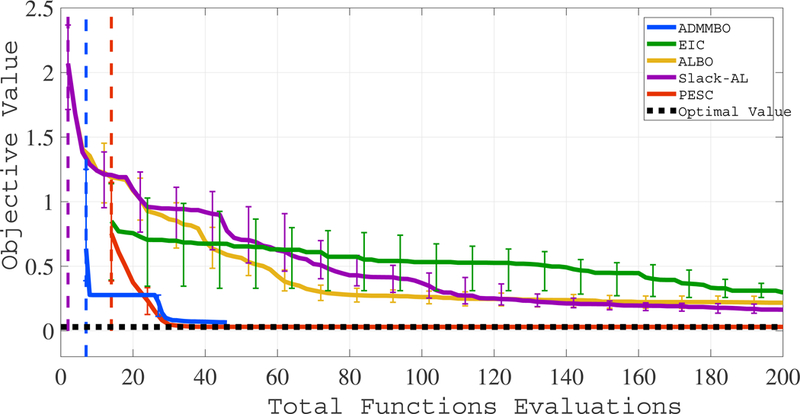
Performance of different algorithms solving (18) as a function of the total budget for function evaluation.

5.6. Tuning a Fast Neural Network

In our last experiment, we tune the hyperparameters of a a three-hidden-layers fully connected neural network for a multiclass classification task using MNIST dataset (LeCun, 1998; LeCun et al., 2015). A version of this experiment was previously reported in (Hernández-Lobato et al., 2015). We train the network using stochastic gradient descent with momentum. We consider the optimization problem of finding a set of hyperparameters that minimize the validation error subject to the prediction time being smaller than or equal to 0.045 second on NVIDIA Tesla K80 GPU. ² Here, we focus on eleven hyperparameters: learning rate, decay rate, momentum parameter, two drop out probabilities for the input layer and the hidden layers as well as two regularization parameters for the weight decay, the weight maximum value, the number of hidden units in each of the 3 hidden layers, and the choice of activation function (RELU or sigmoid). We define B = [0 1; 0 1; 0 1; –4 1; 0 100; –4 0; –3 0; 50 500; 50 500; 50 500; 0 1]. We build our network using Keras with TensorFlow backends (Chollet et al., 2015; Abadi et al., 2016). We compute the prediction time as the average time of 1000 predictions, over a batch size of 128 (Hernández-Lobato et al., 2015).

We compare ADMMBO only with PESC, since as previously reported (Hernández-Lobato et al., 2015, 2016) (and also consistent with our results on the synthetic experiments), PESC typically outperforms EIC and ALBO. Moreover, among state-of-the-art methods, ADMMBO and PESC are the only ones capable of handling decoupled problems, and thus are a good fit for this experiment. Note that since the computational cost of evaluating the validation error and the prediction time are significantly different, we show the results in terms of total wall-clock time rather than the total number of function evaluations.

As the results in Figure 6 show, PESC performed better at first. PESC found the first feasible set of hyperparameters slightly faster than ADMMBO, and also was able to find hyperparameters with lower validation error compared to the hyperparameters suggested by ADMMBO. However, around 18 minutes after initializing the algorithms, ADMMBO’s performance started to improve and outperformed PESC from minute 22 on. For example, at minute 40, ADMMBO found a desirable set of hyperparameters resulting in 0.05 validation error and less than 0.045 seconds prediction time. After the same time, PESC’s suggested hyperparameter result in a shorter prediction time less than 0.045 seconds, but their validation error was around 0.45. One interesting observation is that ADMMBO terminated after around one hour, satisfying its stopping criterion, avoiding extra expensive evaluations.

5.7. Sensitivity Analysis on M and ρ

In this section, we report on an evaluation of the sensitivity of ADMMBO to the hyperparameters M and ρ. In the first set of experiments, we set the value of M to 20 and ran ADMMBO for fifteen uniformly distributed initial values of ρ ∈ [0.0001, 2], while keeping the rest of the hyperparameters as in 5.1. In Figure 7 we report on some selected cases, to avoid cluttering the figure. The figure illustrates that ADMMBO’s performance was not very sensitive to the initial value of ρ. In particular, for initial ρ = 2, ADMMBO attained a feasible point over all 100 runs after no more than 27 function evaluations, while for other values of ρ, the same was achieved after roughly 15 evaluations. Even with ρ = 2, at budget 15, 91 out of 100 runs had already found a feasible solution. The vertical dashed line in Figure 7 shows the budget at which the last run found a feasible solution.

Figure 7:

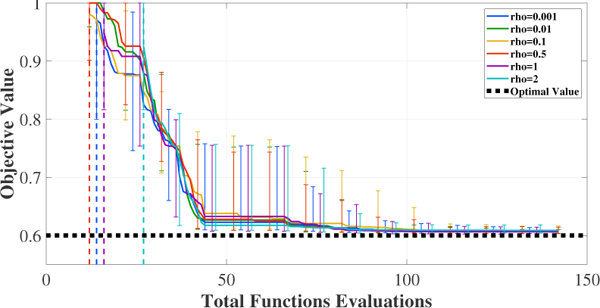
Performance of ADMMBO solving (17) given M = 20 and different values of ρ.

In the second set of experiments, we set the value of ρ to 0.1 and ran ADMMBO for ten uniformly distributed values of M ∈ [0.001,2] as well as M = 100,1000. As Figure 8 shows,again reporting on a subset of the values tested for clarity, the performance of ADMMBO did not depend strongly on the precise value of M as long as it was large enough. Note that in problem (17), the range of f over $\mathcal{B}$ was 2. Even for M < 2, ADMMBO found good solutions, failing only when M was 4 order of magnitude smaller than the bound. Also, ADMMBO with different values of M found a feasible point over 100 runs at the same budget. Finally, given all different combinations of M and ρ, ADMMBO always converged before spending the total iteration budget of 300.

Figure 8:

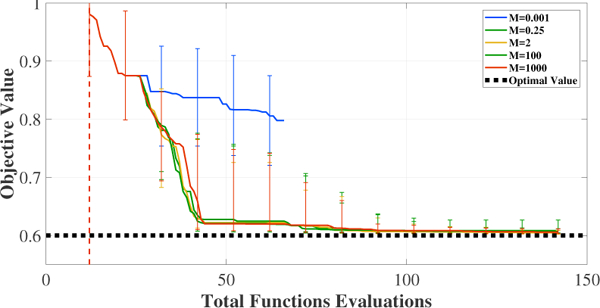
Performance of ADMMBO solving (17) given M = 0.1 and different values of M.

6. DISCUSSION

In this paper, we address the problem of solving an optimization whose objective function and constraints are unknown and available to evaluate pointwise, but at high computational cost. We proposed a novel constrained Bayesian optimization algorithm, called ADMMBO, which merges ADMM, a powerful tool from numerical optimization, with Bayesian optimization techniques. ADMMBO defines a set of unconstrained subproblems, over the modified objective function and over modified constraints, and iteratively solves them using Bayesian optimization on each subproblem. Some key advantages of ADDMBO are its ability to start from an infeasible point, its ability to effectively handle decoupled problems, the ability to find closed-form acquisition functions, and its stopping criterion. We showed the effectiveness of ADMMBO through experiments on benchmark problems and the problem of hyperparameter tuning for a fast neural network for digit recognition. ADMMBO consistently outperformed existing methods and obtained the feasible optimum with the fewest number of black-box evaluations. We speculate that the reason behind this rapid convergence is that ADMMBO typically first finds the unconstrained optimum of the problem, and then finds for the closest point to that optimum which belongs to the feasible set, which turns out to be an effective search strategy.

There are several ways in which we believe ADMMBO could be extended or improved. One would be to enable ADMMBO to handle problems with unknown equality constraints. A straightforward approach would be to rewrite an equality constraint as a pair of inequality constraints and employ our current algorithm. Since ADMMBO is highly parallelizable (lines 6 – 11 in Algorithm 3.1 can be implemented in parallel), increasing the number of constraints may not be a significant computational barrier. However, investigating more principled ways of handling equality constraints is a topic for future investigation. Another extension of clear interest is to speed up ADMMBO through augmenting the problem with environmental variables which directly affect the duration of function evaluations (Klein et al., 2016). For example, in tuning the hyperparameters of a neural network, the size of the training set or the number of epochs can be regarded as such variable. Then, similar to Snoek et al. (2012), one can penalize ADMMBO’s acquisition functions with the inverse duration of function evaluations. We speculate that this may lead to finding a good solution for the unknown optimization problem as quickly as possible. A further extension concerns developing a comprehensive budget management strategy. This will be useful specifically in cases where we have partial knowledge about the unknown functions, in particular an estimate of the relative computational complexity of the objective and constraint functions. In this setting, we may be able to leverage such estimates to more efficiently distribute the budget. Another direction worth exploring is the flexibility within the ADMMBO framework to adopt different random process models (beyond independent GPs) and different acquisition functions (beyond EI). In particular using Predictive Entropy as acquisition function with approximations potentially similar to PESC-F would seem to be a promising approach to explore, given both the results in the literature and the relative success of PESC in our experiments. With any new acquisition function we would face the challenge of efficiently optimizing it. Acquisition functions are often multi-modal and complex, and it is an open question how best to carry out this particular optimization step.

Finally, we mention one current limitation of ADMMBO, which is the number of hyperparameters. Good values will clearly speed up the optimization time of ADMMBO. In our experiments here, we followed the default initialization suggested in (Boyd et al., 2011; Hong and Luo, 2017) for the ADMM-related parameters and were able to obtain favorable results. However, for more complex problems, an adaptive initialization policy, potentially similar to ρ’s adaption rule based on primal and dual residuals suggested by Boyd et al. (2011), might make the algorithm less sensitive to the possibility of a poor parameter setting.