Covariate-Adjusted Region-Referenced Generalized Functional Linear Model for EEG Data

Summary

Electroencephalography (EEG) studies produce region-referenced functional data in the form of EEG signals recorded across electrodes on the scalp. It is of clinical interest to relate the highly structured EEG data to scalar outcomes such as diagnostic status. In our motivating study, resting state EEG is collected on both typically developing (TD) children and children with Autism Spectrum Disorder (ASD) aged two to twelve years old. The peak alpha frequency (PAF), defined as the location of a prominent peak in the alpha frequency band of the spectral density, is an important biomarker linked to neurodevelopment and is known to shift from lower to higher frequencies as children age. To retain the most amount of information from the data, we consider the oscillations in the spectral density within the alpha band, rather than just the peak location, as a functional predictor of diagnostic status (TD vs. ASD), adjusted for chronological age. A covariate-adjusted region-referenced generalized functional linear model (CARR-GFLM) is proposed for modeling scalar outcomes from region-referenced functional predictors, which utilizes a tensor basis formed from one-dimensional discrete and continuous bases to estimate functional effects across a discrete regional domain while simultaneously adjusting for additional non-functional covariates, such as age. The proposed methodology provides novel insights into differences in neural development of TD and ASD children. The efficacy of the proposed methodology is investigated through extensive simulation studies.

1 |. INTRODUCTION

Children with Autism Spectrum Disorder (ASD) display a wide range of cognitive ability compared to their typically developing (TD) peers, yet the neural processes underlying this variability are not well understood.¹ In our motivating study, resting-state electroencephalograms (EEG) were recorded on both ASD and TD children aged two to twelve years old, allowing researchers to compare and contrast neural processes between the two diagnostic groups over a wide developmental range. Of particular interest was the location of a single prominent peak in the spectral density located within the alpha frequency band (6–14 Hz) called the peak alpha frequency (PAF). PAF has been shown to index neural development in TD children, where it shifts from lower to higher frequencies as children grow older.^2,3 Recent research suggests that this chronological shift (from lower to higher frequencies) in PAF is delayed or possibly absent in children with ASD.^1,4 This phenomena can be seen in our motivating data where slices of the group-specific bivariate mean surface of the spectral density (across age and frequency) at ages 30, 60, 90 and 120 months from the T8 electrode are plotted in Figure 1(a). The PAF, resembled by the location of the ‘humps’ in the spectral density, is more pronounced and displays a greater shift with age in the TD children compared to their peers diagnosed with ASD.

FIGURE 1.

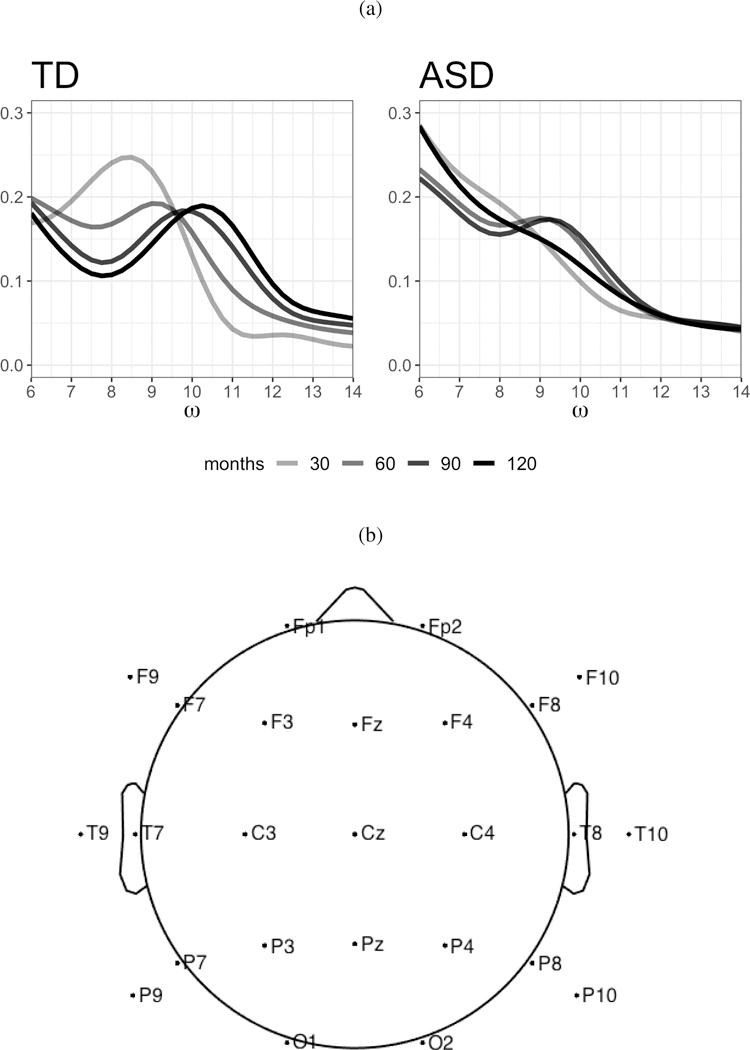
(a) Slices of the group-specific bivariate mean alpha band spectral density (across age and frequency (6–14 Hz)) at ages 30, 60, 90 and 120 months from the T8 electrode. Darker lines correspond to older children. (b) A schematic diagram of the 10–20 system 25 electrode montage.

While the PAF location is well defined in sample averages, estimating a subject-electrode specific PAF presents many challenges, including the variability in estimation of the spectral densities and the potential for multiple local maxima.⁵ In addition, identifying a single PAF inherently collapses information in the data across the alpha frequency band into a single number. To retain the most information from the data, we consider the spectral density across the alpha band as a functional observation and model associations between alpha band spectral dynamics and diagnostic status. In our motivating study, EEG signals are observed uninterrupted for several minutes across a high density electrode array and the continuous signal is divided into two-second segments before Fast Fourier Transform (FFT) to guarantee stationarity. The spectral density is then averaged across segments to increase the signal-to-noise ratio. The resulting spectral densities obtained across electrodes form the region- referenced functional data, with the spectral densities and the electrodes referred to as the functional and regional dimensions of the data. In order to model the association between diagnostic status and the high-dimensional EEG data, two methodological obstacles must be addressed. First, EEG signals recorded at each electrode result in a region-referenced functional predictor for which an appropriate functional regression model does not exist. Second, the relationship between the alpha band spectral dynamics and diagnostic status is expected to change with age and thus the potential regression model must allow for covariate- adjustments when estimating functional effects. To address both issues, we propose the covariate-adjusted region-referenced generalized functional linear model (CARR-GFLM) that jointly estimates covariate-adjusted functional effects at each region by first projecting the regression function onto a tensor basis and then performing dimension reduction to produce a well-posed problem.

Since the introduction of the functional linear model (FLM) by Ramsay and Dalzell⁶, functional regression methods have been formalized into three categories based on the role of the functional data object: (1) scalar-on-function, (2) function-on- scalar, and (3) function-on-function regression models.^7,8 Given that our goal is to relate a region-referenced functional predictor (region-referenced EEG spectral densities) to a scalar response (ASD diagnostic status), we restrict our discussion to relevant scalar-on-function regression methods (SoFR) particularly with respect to multivariate (i.e. multiple functional signals defined on possibly different domains) and multi-dimensional (i.e. two- or higher-dimensional functional signals defined continuously on a single domain) functional predictors. Hastie and Mallows⁹ were the first to formally define a FLM for a Gaussian response and Marx and Eilers¹⁰ broadened this foundational model to include exponential family responses by proposing a generalized FLM (GFLM). Both models have been extended to accommodate multilevel functional predictors and adapted to non-parametric and non-linear frameworks.¹¹ Considerable methodological development has focused on appropriate regularization strategies for settings in which multivariate or multi-dimensional functional predictors are observed, where estimation is often performed via projection of the corresponding regression function(s) onto smooth basis functions with regularization imposed via the basis coefficients. While regularization for multivariate functional predictors is enforced within each distinct functional domain (Zhu et al¹²; Gerthreiss et al¹³; Lian¹⁴), regularization for multi-dimensional functional predictors is enforced by assuming continuity across the functional domain (Marx and Eilers¹⁵; Reiss and Ogden¹⁶; Goldsmith et al¹⁷). Specific to EEG and local field potentials, recent works by Gao et al^18,19 develop methods for vector-valued electrical potentials recorded from multiple electrodes but these models focus on capturing longitudinal dynamics and cluster structures over the course of a recording session, respectively, rather than modeling associations with a scalar response.

Our proposed CARR-GFLM makes two important contributions to the existing literature. First, to our knowledge no SoFR method accommodates region-referenced functional predictors, i.e. correlated functional data observed over a non-smooth regional domain. To address this challenge, we consider a tensor basis that is a mixture of discrete and continuous basis functions. A corresponding penalty structure is developed to ensure smoothness of the regression function within each region along the functional dimension, with joint penalization across the regional domain. Second, we allow for the region-referenced regression function to vary across a continuous covariate, in our application, age. In the setting of a one-dimensional functional predictor, Wu et al²⁰ proposed a varying-regression functional linear regression model where regression effects not only vary across functional time but also across a scalar covariate. Authors estimate regression effects by targeting the functional covariance processes conditional on specific values of the scalar covariate via kernel smoothing methods. This estimation approach does not scale up well for higher dimensional functional data (e.g. region-referenced EEG spectral densities) given the reliance on computationally intensive kernel methods. Different from the approach in Wu et al²⁰, we add age as an argument to the tensor basis considered in estimation. The tensor basis is formed as a kronecker product of a marginal bases in the functional, regional and covariate domains leading to greater computational efficiency. The resulting number of tensor basis functions may exceed the number of subjects in some applications; hence we further consider the singular value decomposition (SVD) of the design matrix as in Reiss and Ogden^16,21 to ensure the problem is well-posed.

Note that existing SoFR methods do not provide an adequate covariate-adjusted modeling framework for region-referenced functional predictors. Given that region-referenced functional predictors are observed over a discrete regional domain, methods for multi-dimensional functional predictors which assume continuity of the regression function across each dimension cannot be used in the analysis of region-referenced functional predictors. Considering the functional signal from each region as multivariate functional data and applying existing multivariate GFLM (m-GFLM) techniques would require either a global regularization parameter across all dimensions or a separate regularization parameter for each region, both of which are undesirable due to the possibility of under fitting or over fitting the data, respectively. In addition to less than desirable regularization, existing multivariate methods do not allow for covariate adjustments when modeling the regression effects, as these adjustments have only been proposed in the literature for a single functional predictor by Wu et al²⁰. We show the favorable predictive performance of the proposed CARR-GFLM in comparison to the existing simpler approaches of m-GFLM, ignoring covariate effects, and a multivariate GFLM with a linear interaction term between the covariate and the functional predictor (m-GFLMi) in simulation studies and data applications.

The paper is organized as follows. Section 2 introduces the proposed model and develops estimation and inferential procedures. Section 3 discusses application of the proposed method to resting state EEG data from our motivating study, focusing on inference and interpretation of the estimated regression coefficients. Section 4 assesses performance of the proposed methodology via a simulation study. We conclude with a brief discussion in Section 5.

2 |. THE PROPOSED COVARIATE-ADJUSTED REGION-REFERENCED GFLM

2.1 |. Statistical framework and modeling

Suppose for i = 1,... n subjects, we observe the data {y_i,X_i(a_i,r,ω),a_i}, where y_i is a scalar response, X_i(a_i,r,ω) is a region-referenced functional predictor observed at region r, r = 1,…,R, frequency ω, ω ∈ Ω and non-functional scalar covariate a_i ∈ A ⊂ ℝ. While Ω and A are both continuous domains, they represent a functional and a non-functional covariate domain, respectively. The predictor X_i(a_i, r, ω) is assumed square-integrable and smooth over the functional domain Ω. Given our motivating data, we assume a_i is a scalar covariate though it could constitute a real valued vector of continuous covariates. For notational convenience, a regular grid for observations is assumed in the regional and functional dimensions, however, note that for sparse data applications in either the regional or functional dimension or both, the hybrid principal components analysis (HPCA) of Scheffler et al²² can be used to reconstruct the full functional predictor. Throughout the remainder of the paper, scalars will be represented by lower case letters (b), vectors by lower case bold letters (b), and matrices by upper case bold letters (B).

First consider the region-referenced GFLM allowing for a region-referenced functional predictor,

$$\begin{gathered} y_i~\mathcal{F}\left({\mu }_i,\vartheta \right) \\ g\left({\mu }_i\right)=\sum _{r=1}^R\int \left\{X_i(r,\omega )-\eta (r,\omega )\right\}\beta (r,\omega )d\omega =\sum _{r=1}^R\int X_i^c(r,\omega )\beta (r,\omega )d\omega \end{gathered}$$ (1)

where ℱ is an exponential family distribution with conditional expectation ${\mu }_i=E\left\{y_i|X_i(r,\omega ),\vartheta \right\},\vartheta$ denoting the vector of nuisance parameters and g(·) denoting an invertible link function. The region-referenced mean curve for all subjects is denoted by η(r, ω) = E{X_i(r, ω)} and the mean centered subject-specific functional predictor which captures subject-level deviations from the region-referenced mean curve is denoted by $X_i^c(r,\omega )=X_i(r,\omega )-\eta (r,\omega )$ . The region-referenced regression function β(r, ω) models the linear association between g(μ_i) and $X_i^c(r,\omega )$, where β(r, ω) is not assumed to be smooth across the R regions. Note that the region-referenced GFLM in (1) is different from a multivariate GFLM with R separate functional predictors (possibly evaluated over different functional domains) in that the R functional predictors considered for (1) all represent spectral densities evaluated over the same domain, hence modeled in the next section with a single tensor basis and a combined smoothing parameter. Fixing R =1 yields a standard GFLM for a functional predictor and scalar response as described in Marx and Eilers¹⁰.

Next, consider the proposed CARR-GFLM where the regression relationship changes as a function of a non-functional covariate. In our motivating data for example, the association between a subject’s diagnostic status and alpha band spectral dynamics depends on chronological age. Thus, the proposed model for region-referenced functional predictors is given by

$$g\left({\mu }_i\right)=\sum _{r=1}^R\int \left\{X_i\left(a_i,r,\omega \right)-\eta \left(a_i,r,\omega \right)\right\}\beta \left(a_i,r,\omega \right)d\omega =\sum _{r=1}^R\int X_i^c\left(a_i,r,\omega \right)\beta \left(a_i,r,\omega \right)d\omega$$ (2)

where ${\mu }_i=E\left\{y_i|X_i\left(a_i,r,\omega \right),a_i,\vartheta \right\}$,$\eta (a,r,\omega )=E\left\{X_i\left(a_i,r,\omega \right)|a_i\right\}$,$X_i^c\left(a_i,r,\omega \right)$ and β(a_i,r,ω) denote the conditional expectation, the region-referenced mean surface, the mean-centered subject-specific functional predictor and the regression function that now all depend on the covariate a, respectively. The regression function β(a_i,r,ω) in a specific region r is assumed to be smooth in both the functional domain Ω and the covariate domain A, allowing borrowing of information across the range of the covariate values observed in the sample in estimation. For a fixed a, the regression function β(a_i,r,ω) captures the different weights placed on the functional predictor across the frequency domain and how these relations change over the R regions. Changes over a add to this interpretation by depicting how this regression relation can vary over the different values of the covariate a. The proposed model reduces to the varying-coefficient functional linear model of Wu et al²⁰ for R =1.

The regression function β(a_i,r,ω) is approximated by a linear combination of basis functions that are formed as a tensor product of discrete and continuous marginal basis functions in a, r, and ω,

$$\beta (a,r,\omega )\approx \sum _{k_a=1}^{K_a}\sum _{k_r=1}^{K_r}\sum _{k_{\omega }=1}^{K_{\omega }}{\varphi }_{k_a}(a){\varphi }_{k_r}(r){\varphi }_{k_{\omega }}(\omega ){\theta }_{k_a,k_r,k_{\omega }}$$

where the basis functions in a and m, denoted by ${\varphi }_{k_a}(a)$ and ${\varphi }_{k_{\omega }}(\omega )$, respectively, can be chosen to be any set of continuous basis functions appropriately combined with a quadratic penalty, such as functional principal components or B-splines. The basis functions in r, denoted by ${\varphi }_{k_r}(r)$ , is a set of discrete basis functions such that span $\left[{\left\{{\varphi }_{k_r}(r)\right\}}_{k_r=1}^{K_r}\right]\subseteq {ℝ}^R$(e.g. columns of an identity matrix). The unknown coefficients of the projection, denoted by ${\theta }_{k_a,k_r,k_{\omega }}$ are collected into the vector θ and are estimated. Note that the total number (K_a, K_r and K_ω) of basis functions considered in each dimension, is chosen to be sufficiently large to capture the regression function behavior before penalization. The shape of the resulting regression function can be controlled by both the choice of the marginal basis functions and the quadratic penalization of θ. We follow Wood²³ to construct a general penalty structure which is formed by a kronecker sum of marginal penalties along each dimension a, r and ω,

$$\mathrm{pen}(\theta |\lambda )={\theta }^{\text{T}}P(\lambda )\theta ,$$

$$P(\lambda )={\lambda }_a\left(P_a\otimes I_{K_r}\otimes I_{K_{\omega }}\right)+{\lambda }_r\left(I_{K_a}\otimes P_r\otimes I_{K_{\omega }}\right)+{\lambda }_{\omega }\left(I_{K_a}\otimes I_{K_r}\otimes P_{\omega }\right),$$

where λ = (λ_a, λ_r, λ_ω) denotes a vector of positive penalty parameters and P_a, P_r, and P_ω denote the positive semi-definite penalty matrices, that control the degree of smoothness or shrinkage along each marginal dimension. For the dimensions along which the regression function is expected to be smooth (i.e. the functional and covariate dimensions), a differencing penalty can be used for a B-spline basis to penalize rapid change in the coefficients. In case of the regional dimension, the regression function is not assumed to be smooth and the choice of penalty structure requires more deliberation. In situations where there is no a priori knowledge of the dependency of the functional effects among regions, a ridge penalty would promote smaller coefficients without imposing a prior dependency structure. If prior knowledge is available, one way to induce dependency across regions would be through a Gaussian Markov Random Field prior which have been applied in spatial analysis and generalized additive models.^24,25 The choice of the penalty structure plays an important role in inference through the posterior distribution of the coefficient vector θ and should be considered carefully.

To our knowledge, this is the first application of a tensor basis formed from a mixture of discrete and continuous basis functions for estimating functional regression effects. Note that the proposed penalty structure with one penalty parameter for each marginal dimension, strikes a balance between under smoothing and increased computational burden with a larger number of penalty parameters and over smoothing with a smaller number of penalty parameters. For example, penalizing the regression function in each region separately would lead to R separate pairs of penalty parameters (λ_ra, λ_rm), r = 1,… ,R, increasing the number of penalty parameters and hence the computational burden significantly. Alternatively, λ_r, can be set to zero, effectively controlling smoothness across Ω. and A at each region with just two parameters, possibly leading to over smoothing.

2.2. ǀ Estimation and inference

The proposed CARR-GFLM model is fit using the general additive model (GAM) framework of Wood²⁵ for which there exists both stable optimization routines and theory for inference via confidence intervals. The region-referenced mean surface η(a, r, ω) is estimated prior to model fitting separately for each region based on pooled data across all subjects via smoothing achieved by projection onto a tensor basis of penalized marginal B-splines in a and ω. Estimation and smoothing parameter selection are carried out by restricted maximum likelihood (REML) methods. Let (ω₁,…, ω_H) denote the regular functional grid where the region-referenced functional predictor is observed. The proposed CARR-GFLM in (2) can be written in matrix notation as,

$$\begin{gathered} \sum _{r=1}^R\int X_i^c\left(a_i,r,\omega \right)\beta \left(a_i,r,\omega \right)d\omega \approx \sum _{r=1}^R\int X_i^c\left(a_i,r,\omega \right)\sum _{k_a=1}^{K_a}\sum _{k_r=1}^{K_r}\sum _{k_{\omega }=1}^{K_w}{\varphi }_{k_a}\left(a_i\right){\varphi }_{k_r}(r){\varphi }_{k_{\omega }}(\omega ){\theta }_{k_a,k_r,k_w}d\omega \\ \approx \sum _{r=1}^R\sum _{h=1}^H\sum _{k_a=1}^{K_a}\sum _{k_r=1}^{K_r}\sum _{k_{\omega }=1}^{K_{\omega }}{w}_h{X}_i^c\left(a_i,r,{\omega }_h\right){\varphi }_{k_a}\left(a_i\right){\varphi }_{k_r}(r){\varphi }_{k_{\omega }}\left({\omega }_h\right){\theta }_{k_a,k_r,k_{\omega }} \\ =\left[{\mathbf{\Phi }}_a{\otimes }_r\left\{XW\left({\mathbf{\Phi }}_r\otimes {\mathbf{\Phi }}_{\omega }\right)\right\}\right]\theta \end{gathered}$$ (3)

where ⊗ and ⊗_r denote the standard and the row kronecker products, respectively. For two matrices with the same number of rows, the row kronecker product ⊗_r forms a new matrix by taking the kronecker product of the rows of each matrix. In (3), ${\mathbf{\Phi }}_a=\left\{{\varphi }_{k_a}{\left(a_i\right)}_{k_a=1,\dots ,K_a}^{i=1,\dots ,n}\right\}$denotes an n × K_a matrix with ith row containing evaluations of the marginal basis functions at a_i; and ${\mathbf{\Phi }}_r=\left\{{\varphi }_{k_r}{(r)}_{k_r=1,\dots ,K_r}^{r=1,\dots ,R}\right\}$and ${\mathbf{\Phi }}_{\omega }=\left\{{\varphi }_{k_{\omega }}{\left({\omega }_h\right)}_{k_{\omega }=1,\dots ,K_{\omega }}^{h=1,\dots ,H}\right\}$denote R × K_r and H × K_ω matrices, respectively, whose columns contain evaluations of the marginal basis functions in r and m. The predictor matrix X is a n × RH matrix containing the vectorized subject-specific functional predictor $X_i^c\left(a_i,r,\omega \right)$ in its ith row. Finally, $W=\mathrm{diag}\left\{{\left(w_{rh}\right)}_{r=1,\dots ,R}^{h=1,\dots ,H}\right\}$ denotes the RH × RH diagonal matrix of weights that correspondingly sum across the R regions and is used to approximate the integral in m. More information on defining appropriate marginal basis function can be found in Wood²⁵.

The coefficient vector θ is estimated by penalized least squares, with the penalized log-likelihood given by

$${\mathcal{l}}_p(\theta ,\lambda ,\vartheta |y)=\mathcal{l}(u,\vartheta |y)-\frac{1}{2}\mathrm{pen}(\theta |\lambda )$$

where $\mathit{u}=g^{-1}\left(\left[{\mathbf{\Phi }}_a{\otimes }_r\left\{XW\left({\mathbf{\Phi }}_r\otimes {\mathbf{\Phi }}_{\omega }\right)\right\}\right]\theta \right)$ and $\mathcal{l}(u,\vartheta |y)={\sum }_{i=1}^n\mathcal{l}\left({\mu }_i,\vartheta |y_i\right)$denotes the log-likelihood function for the response distribution $\mathcal{F}\left({\mu }_i,\vartheta \right)$. The penalized log-likelihood is maximized using REML rather than generalized cross-validation (GCV) due to the superior performance of REML reported in numerical studies.²⁶ The penalized likelihood can be maximized in a number of different ways. One popular approach is to treat λ as a precision parameter in a generalized linear mixed model.^23,27 However, this often produces covariance structures that are difficult to implement in standard software; a challenge that can be circumvented by suitable transformations of the marginal basis functions that divide the coefficient vector into sets of fixed effects and independent and identically distributed Gaussian random effects. This solution may still not be desirable since it introduces additional penalty parameters that may be hard to interpret.²⁸ We opt to maximize the penalized likelihood with the gam () function in the R package mgcv which finds an approximate REML criterion via Laplace approximation and optimizes the approximated likelihood using Newton-Raphson updates. The procedure iterates between estimating the λ and θ using standard penalized regression methods.^25,29

By projecting the regression function β(a, r, ω) onto a tensor basis, we perform an initial dimension reduction step. However, for SoF regression with multi-dimensional predictors, the number of basis functions may still greatly exceed the number of subjects, suggesting that the dimension of the basis is too large to be estimated well and further dimension reduction may be needed. Rather than restricting the number of basis functions in the tensor product, we perform a second dimension reduction step by only retaining the leading right singular vectors of the design matrix $\mathit{D}={\mathbf{\Phi }}_a{\otimes }_r\left\{XW\left({\mathbf{\Phi }}_r\otimes {\mathbf{\Phi }}_{\omega }\right)\right\}$ as in Reiss and Ogden^16,21. Therefore, we minimize the penalized log-likelihood based on the response mean function,

$$u=g^{-1}\left(D{V}_q\tilde{\theta }\right),$$ (4)

where V_q denotes the matrix containing the q leading columns from the singular value decomposition UEV^T of the design matrix D and $\tilde{\theta }$ denotes the coefficient vector for the reduced dimensional design matrix DV_q. In applications, we retain the minimum number of components q that explain 95% of the total variation in the design matrix D, i.e. q is the minimum number of components that satisfy $\sum _{s=1}^q{\kappa }_s^2/{\sum }_{s=1}^{K_a{K}_r{K}_{\omega }}{\kappa }_s^2>.95$ , where k_s are the ordered singular values from the SVD of D. The penalty structure can easily be updated to accommodate the SVD of the design matrix,$\mathrm{pen}(\tilde{\theta }|\lambda )={\tilde{\theta }}^{\text{T}}{V}_q^{\text{T}}P(\lambda )V_q\tilde{\theta }$ . This dimension reduction serves two purposes, (1) it ensures that there is a unique solution that maximizes the penalized log-likelihood and (2) it allows for the use of the inferential machinery of mgcv which requires that the number of coefficients is less than or equal to the number of subjects. As emphasized earlier, this is a common issue with multi-dimensional predictors in SoF regression where the dimension of the scalar response may be much lower than the dimension of the functional predictors.

Due to the quadratic penalty, estimates of the coefficient vector $\tilde{\mathit{\theta }}$ (associated with the the reduced dimensional design matrix DV_q) are biased and thus naive point-wise confidence intervals calculated based on the covariance matrix of the estimated coefficient vector can produce poor coverage. Therefore, we adopt the Bayesian point-wise confidence intervals described in Wood³⁰ which are based on the large sample limit of the posterior distribution $\tilde{\mathit{\theta }}|\mathit{y}$, which can be obtained by a default option in gam(). More specifically,

$$\tilde{\mathit{\theta }}|\mathit{y}~\mathcal{N}\left[\mathit{\gamma },{\left\{{\mathit{V}}_q^{\text{T}}{\mathit{D}}^{\text{T}}\mathit{Z}\mathit{D}{\mathit{V}}_q+{\mathit{V}}_q^{\text{T}}\mathit{P}(\mathit{\lambda }){\mathit{V}}_q\right\}}^{-1}\right]$$

where γ denotes the estimate of $\tilde{\theta }$ , Z denotes an n × n matrix containing entries $Z_{ii}={\left\{g^{\prime }{\left({\mu }_i\right)}^{2}V\left({\mu }_i\right)\right\}}^{-1}$with μ_i equal to the ith entry of u in (4), V denotes the variance function such that V(μ_i)σ² is equal to the variance of y_i and σ² is a scale parameter defined by ℱ. The covariance of $\tilde{\theta }|y$ can be adjusted by V_q in order to recover the posterior distribution of θ|y. The Bayesian point-wise confidence intervals have been reported to lead to better coverage than those based on the covariance of the parameter estimates. We study the finite sample properties of the proposed methodology including coverage of the proposed Bayesian point-wise confidence intervals in the simulations of Section 4.

3 |. DATA ANALYSIS

3.1 |. Data structure and methods

In our motivating study, EEG data was sampled at 500 Hz for two minutes using a 128-channel HydroCel Geodesic Sensor Net on 58 ASD and 39 TD children 25 to 144 months old (groups were age matched). EEG recordings were made under an ‘eyes-open’ paradigm in which bubbles were presented on a screen in a sound-attenuated room.¹ Four electrodes near the eyes were removed prior to recording, in order to improve the comfort of the subjects. To facilitate independent component analysis for identification of artifacts, the data was interpolated to the international 10–20 system 25 electrode montage (R = 25) by spherical interpolation as described in Perrin et al³¹ and implemented in the function eeg_interp from EEGLAB³² (Figure 1(b)). Following interpolation and ICA, the signal was reconstructed without components attributed to non-neural sources of signal, such as electromyogram (EMG) or non-stereotyped artifacts, and re-referenced to the average of all electrodes. For spectral analysis, the first 38 seconds of artifact free EEG data was used for each subject, where 38 seconds was the minimum amount of artifact free data available on all the subjects. Spectral density estimates were obtained by Welch’s method. ³³ The 38 second EEG signal was divided into two second Hanning windows with 50% overlap and transformed into the frequency domain via FFT. For each electrode, the spectral densities at each overlapping segment were averaged, resulting in electrode-specific estimates of the spectral density.

Since the interest is on the location of the dominant alpha peak and the general shape of the alpha band spectral dynamics more than alpha band power, the alpha (Ω = (6 Hz, 14 Hz)) spectral density normalized to a unit area (through division by its integral) is considered as the region-referenced functional predictor to facilitate comparisons across electrodes and subjects. As a result of the sampling scheme, the grid along the functional domain has a frequency resolution of .25 Hz and thus includes H = 33 points. Smooths of the region-referenced mean surface η(a, r, ω) are obtained as described in Section 2.2 using a tensor basis of penalized cubic B-splines (with 15 and 4 degrees of freedom in the frequency and age domains, respectively) and second degree difference penalties along each dimension. In order to avoid bias in estimation of the region-referenced mean surfaces due to the observed imbalance in sample size between diagnostic groups, we re-weight the data such that the two diagnostic groups contribute equally to the region-referenced mean surface smoothing. The mean centered subject-specific functional predictors,$X_i^c\left(a_i,r,\omega \right)=X_i\left(a_i,r,\omega \right)-\eta \left(a_i,r,\omega \right)$, are obtained by subtracting age conditional slices of η(a, m,ω) from the observed subject-specific alpha spectral densities.

The regression function β(a, r, ω) is estimated by projection onto a tensor basis formed as the product of basis functions along the age, region/electrode and frequency dimensions. The marginal basis matrices Φ_a and Φ_ω are formed as evaluations of cubic B-splines with K_a = 5 and K_ω = 10 degrees of freedom, respectively. The regional basis matrix is equal to Φ_r = [1_R, I_R] with K_r = 26, where 1_R is an R × 1 vector of 1’s. Second order marginal difference penalties are utilized for both P_a and P_ω to ensure smoothness over the functional and age domains. Given that we do not have any prior knowledge regarding the dependency of alpha spectral effects across electrodes, we employ a ridge style penalty across the regional dimension, P_r = [0_R, I_R], where 0_R is an R × 1 vector of 0’s. The zero entry along the diagonal of P_r corresponds to the basis vector 1_R which is left unpenalized to absorb the common effect across all electrodes. The remaining regional basis vectors are penalized and loadings on them represent the electrode-specific deviations from the overall effect across the scalp. The number of columns in the resulting design matrix D is K_aK_rK_ω = 1300.

We carry out comparisons between the proposed CARR-GFLM and the existing approaches of m-GFLM and m-GFLMi. For the m-GFLM, the region-referenced alpha spectral densities are treated as multivariate functional data where the functional effect at each region is estimated by projection onto a basis of cubic B-splines with ten degrees of freedom. The m-GFLMi includes a main effect of age as well as a linear interaction term between age and the region-referenced alpha spectral densities for which an additional set of functional effects are estimated. For each functional effect, regularization is enforced using a separate smoothing parameter with a second degree difference penalty. Similar to CARR-GFLM, the number of basis functions for m-GFLM and m-GFLMi is too large to be estimated well and the portion of the design matrix encoding functional effects is reduced by SVD with appropriate adjustments made to the penalty structure. The number of columns (i.e. rank) of the SVD reduced design matrices for the CARR-GFLM, m-GFLM, and m-GFLMi models is 66, 57, and 50, respectively, accounting for approximately 99% of the total variation. The threshold for the proportion of variation explained is slightly higher in the data analysis than suggested in Section 2.2 in order to ensure model convergence. Models are fit using the gam() function from mgcv (version 1.8–24) on a 2.4 GHz 6-Core Intel Xeon processor operating R (version 3.5.1) with a mean computation time of 26.6 seconds based on ten runs. Penalty parameters are selected via REML and estimated to be λ_a = 0.0063, λ_r = 0.0042, and λ_ω = 0.0078.

3.2 |. Data analysis results

Slices of the region-referenced mean surface η(a, r, ω) representing the electrode-specific mean alpha spectral density at ages 30, 60, 90, and 120 months for the T8 and T10 electrodes (right temporal) are given in Figure 2 . Across subjects and electrodes, the PAF increases with increasing chronological age. Since functional predictors are supposed to retain group differences to predict diagnostic status, region-referenced mean surfaces are estimated across subjects (rather than within diagnostic groups) and subtracted from the observed alpha spectral densities to obtain the mean-centered functional predictors $X_i^c\left(a_i,r,\omega \right)$ used in modeling. It is expected that, on average, subjects within each diagnostic group will deviate from the region-referenced mean surfaces in a distinct manner, allowing for characterization of patterns in the alpha spectral density that are predictive of ASD diagnosis.

FIGURE 2.

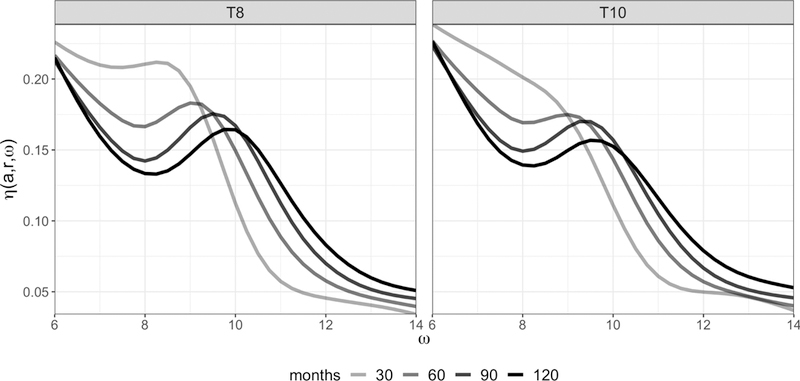
Slices of the region-referenced mean surface η(a, r, ω) representing the electrode-specific mean alpha spectral density at ages 30, 60, 90, and 120 months for the T8 and T10 electrodes. Darker lines correspond to older children.

The results from fitting the CARR-GFLM model to our motivating data for the T8 electrode are shown in Figure 3 and are representative in shape and sign of other electrodes across the scalp. In order to visualize information across chronological age, results are shown as cross sections at 30, 60, 90, and 120 months. The T8 electrode is highlighted because among all electrodes it produces the highest average contribution to the log-odds of ASD diagnosis,$1/n{\sum }_{i=1}^n{\int }_{\Omega }\left|X_i^c\left(a_i,r,\omega \right)\widehat{\beta }\left(a_i,r,\omega \right)\right|d\omega$ , which can be interpreted as a measure of the absolute effect of a given electrode across all subjects. Referring to Figure 1(b), the three electrodes with the highest average contribution to the log-odds of ASD diagnosis, the T8, T10, and F8 electrodes, are located in the right temporal and frontal region of the scalp, suggesting differences in these brain regions have the strongest effect on whether a subject is predicted to have an ASD diagnosis. The average mean-centered functional predictors for the TD and ASD children displayed in in Figure 3 (top row) provide insights into group differences. On average at 30 months old, TD children display higher alpha power between 8 to 10 Hz. This changes over the course of development and by 120 months ASD children display higher alpha power between 6 to 10 Hz and TD children show higher power between 10 to 12 Hz.

FIGURE 3.

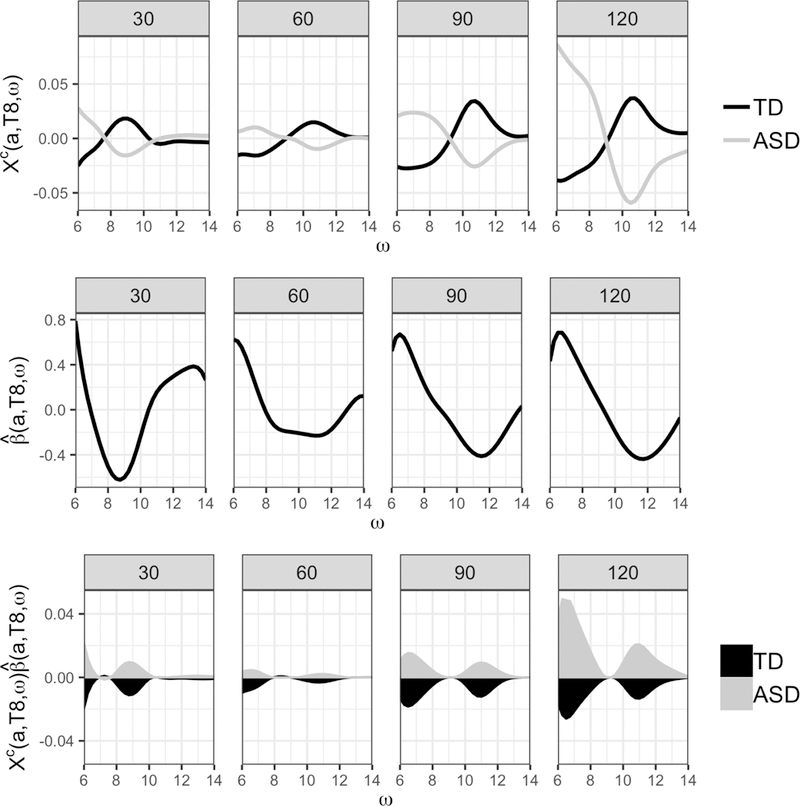
The results from fitting the CARR-GFLM model to the resting state EEG data for the T8 electrode. Results are presented with increasing age from 30 to 120 months organized by column. (top row) The average mean-centered functional predictor for (black) TD children and (grey) ASD children. (middle row) Cross sections of the estimated regression function. (bottom row) The point-wise product of the top two rows where the shading represents the average area under the curve for the (black) TD children and (grey) ASD children.

The slices of the estimated regression function $\widehat{\beta }(a,r,\omega )$ for the T8 electrode are plotted in Figure 3 (middle row). The estimated regression function puts mostly negative weight on the spectral density for frequencies between 8 to 10 Hz and positive weight for frequencies between 10 to 14 Hz for subjects aged 30 to 60 months. After 60 months the shape of the regression function begins to flip, with positive weight on frequencies between 6 and 10 Hz and negative weight for those between 10 and 14 Hz. The Bayesian point-wise confidence intervals are wide including zero, due to the small sample size within diagnostic groups; however they exclude zero at 11.25 Hz for children between 124 to 134 months (not shown). The point-wise product of the average mean-centered functional predictors for each group and the regression function are displayed in Figure 3 (bottom row) where the shading represents the area under the curve for each group which ultimately encapsulates the linear effect on the log odds of ASD diagnosis. Before 60 months, the average TD child has a PAF between 8 to 10 Hz and hence due to the negative weighting by the regression coefficient, this results in a predicted probability of ASD diagnosis that is less than .5. Similarly, since the average TD child of age older than 60 months have PAF between 10 to 14 Hz, a negative weight in that domain results in a predicted probability of ASD diagnosis that is again less than .5. Similar descriptions can be formed for the ASD group and on average the areas under the curve produced by the point-wise products formed in Figure 3 (bottom row) are in accordance with the true diagnostic status.

To get a better sense of the predictive performance of the CARR-GFLM in our data across electrodes stratified by developmental age, we look at the predicted probabilities of ASD diagnosis and their associated 95% confidence intervals for the study subjects in Figure 4 (top row). The 95% confidence intervals are calculated on the logit scale based on the posterior distribution of $D{V}_q\tilde{\theta }|y$ (see Section 2.2) and then transformed onto the probability scale. If subjects are classified based on a threshold of .5, then at younger and older ages CARR-GFLM discriminates between the two groups well. However, between 50 and 75 months the model has some trouble distinguishing the two diagnostic groups. This is likely because the differences in the alpha spectrum between the two groups are minimal at the median study age, suggesting the greatest group differences in alpha spectral dynamics occur at younger and older ages. In order to contrast the predictive performance of the CARR-GFLM with the existing models of m-GFLM and m-GFLMi, we compare performance measures including sensitivity (sens = $P\{\widehat{ASD}|ASD\}$), specificity (spec = $P\{\widehat{TD}|TD\}$ ), and the area under the receiver operating characteristic curve (AUC). Predicted probabilities are estimated using leave-one-out cross validation (LOOCV) in which each subject is iteratively withheld from the model data, models are fit, and then probabilities are predicted for the withheld subject. The CARR-GFLM (sens = .602; spec = .663; AUC = .635) outperforms both m-GFLM (sens = .527; spec = .588; AUC = .553) and m-GFLMi (sens = .822; spec = .363; AUC = .593) in terms of both balance between sensitivity and specificity and AUC.

FIGURE 4.

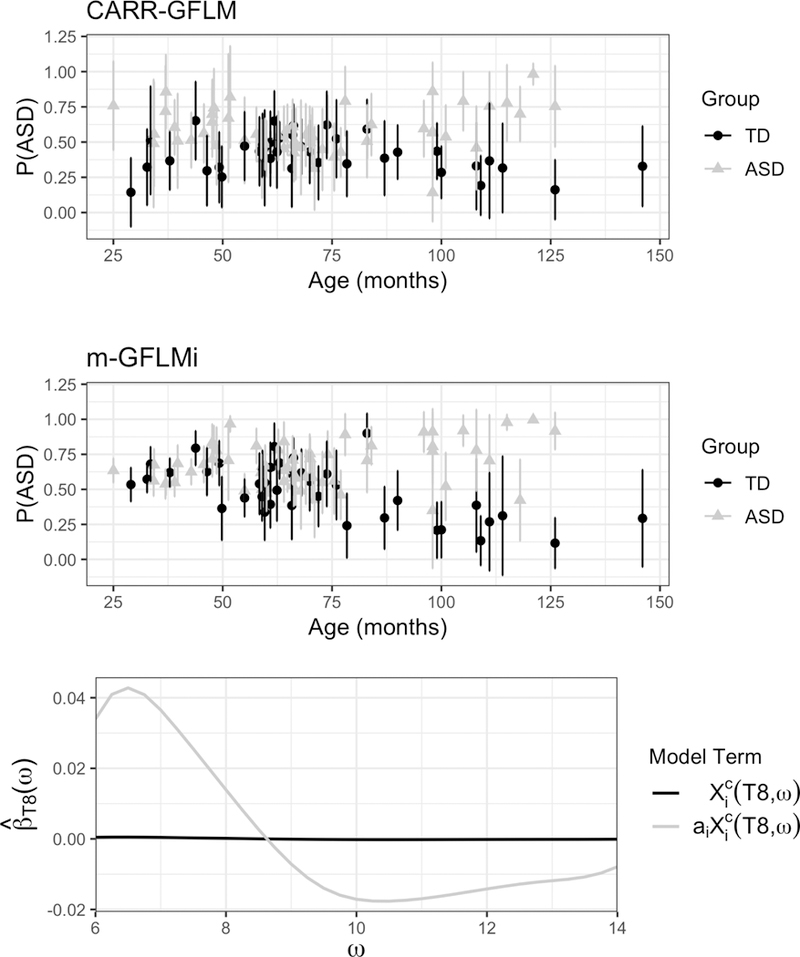
(top and middle row) The predicted probabilities of ASD diagnosis and their associated 95% confidence intervals for the study subjects, with true group membership denoted by black for TD and grey for ASD for the CARR-GFLM (top) and m-GFLMi (middle) models. (bottom row) The estimated regression functions for the main effects and interaction term from the T8 electrode for the m-GFLMi model.

It is clear from the superior performance of the CARR-GFLM and m-GFLMi models compared to m-GFLM that including age improves prediction of ASD diagnosis. To determine why CARR-GFLM outperforms m-GFLMi despite the fact that both models account for age, we consider the estimated regression functions from the T8 electrode for both models. For m-GFLMi (Figure 4 (bottom row)), the association between the alpha spectral densities and ASD diagnosis is modeled as a function of two terms, the main effect, $X_i^c(T8,\omega )$ , and the interaction term, $a_i{X}_i^c(T8,\omega )$. The estimated regression function for the main effect is flat compared to the estimated regression function of the interaction term which assumes a relatively linear decreasing trend with a positive weight on the alpha spectral density between 6 to 9 Hz and a negative weight between 9 to 14 Hz. These effects get stronger as children age. On the other hand, CARR-GFLM (Figure 3 (middle row)), allows the regression function to vary in a non-linear manner across age, with the sign and shape of the regression function shifting across development. The benefit of the greater flexibility of CARR-GFLM over m-GFLMi is visible in the predicted probabilities for each model. While both models struggle to differentiate between the two groups between 50 and 75 months, CARR-GFLM (Figure 4 (top row)) is able to discriminate between the two diagnostic groups at younger ages between 25 and 50 months while m-GFLMi (Figure 4 (middle row)) shows a clear bias towards a diagnosis of ASD, likely induced by the more rigid linear modeling structure.

4 |. SIMULATION

We assess the finite sample performance of the proposed methodology across a range of simulation settings. The data generating process for the simulation is described in Section 4.1 and simulation results are deferred to Section 4.2.

4.1 |. Data generation

Binary scalar outcomes are simulated from y_i ~ Bernoulli(μ_i), i = 1,… ,n, where the subject-specific probabilities are formed on the log odds scale through the linear model $\mathrm{logit}\left({\mu }_i\right)=\sum _{r=1}^R\int X_i^c\left(a_i,r,\omega \right)\beta \left(a_i,r,\omega \right)d\omega$ . The functional and covariate grids are chosen as 50 and 30 equidistant points in [0,1], respectively, with data generated for a total of R = 15 regions. For each subject, the observed covariate values are simulated from a discrete uniform distribution defined on the covariate grid in [0,1]. The regression function β(a, r, ω) is constructed to vary both across regions and along the functional and covariate domains,

$$\beta (a,r,\omega )=\{\begin{array}{ll}{(-1)}^{r}2\cos (\omega r\pi /6+\pi a),\hfill & r=1,\dots ,8\hfill \\ {(-1)}^{r}2\sin \{\omega (r-8)\pi /6+\pi a\},\hfill & r=9,\dots ,15.\hfill \end{array}$$

The subject-specific functional predictors are formed by $X_i\left(a_i,r,\omega \right)=\sum _{k=1}^5{\xi }_{ikr}{\psi }_k(\omega )$ , with a common set of basis functions ψ_k(ω), k = 1,…, 5, across the 15 regions, where ψ_k(ω) are cubic B-splines and the vector of subject-specific scores is generated from ${\xi }_{ik}={\left({\xi }_{ik1},\dots ,{\xi }_{ikR}\right)}^{\text{T}}~\mathcal{M}\mathcal{V}\mathcal{N}\left(\mathbf{0},{\mathrm{\Sigma }}_k\right)$ . The r × r covariance matrix Σ_k controls the regional dependency of the functional predictors by inducing correlations between a subject’s scores for the kth spline basis across the R regions. The covariance matrix Σ_k is chosen to have a compound symmetric structure with diagonal entries equal to one and off diagonal entries equal to ρ, a tuning parameter for the level of dependency across regions. For simplicity, we set η(a_i, r, ω) to zero.

We perform 500 Monte Carlo runs across nine simulation settings: three sample sizes (n = 200,500,1000) and three levels of regional dependency (ρ = 0.0,0.1,0.3). We use the relative squared error $\mathrm{RSE}(a,r,\omega )=\Vert \widehat{f}(a,r,\omega )-f(a,r,\omega )2\Vert /{\Vert f(a,r,\omega )\Vert }^2$ to assess the regression function estimates, where $\Vert f(a,r,\omega ){\Vert }^2=\sum _{r=1}^R\iint f^2(a,r,\omega )dad\omega$ . The coverage probability of the Bayesian point-wise confidence intervals as a function of a, r and ω, is assessed by recording the proportion of times the regression function estimates lie within the confidence interval over the 500 Monte Carlo runs. For each Monte Carlo run at a fixed sample size n, we generate n + 200 samples, where first n is used for estimation and the additional 200 samples are reserved as a validation set for assessing prediction accuracy. Prediction accuracy is assessed by the AUC in the validation sets. The use of validation sets with a common number of observations (200 samples) allows for comparisons of the AUC from different simulation settings.

The region-referenced mean curves are estimated by pooling data across subjects and performing bivariate penalized smoothing over the functional and covariate domains with a tensor basis of penalized cubic B-splines (with 10 and 5 degrees of freedom in the functional and covariate domain, respectively). In addition, second order difference penalties are used along the functional and the covariate dimension, similar to the data analysis. The marginal basis matrices Φ_a and Φ_ω are formed as evaluations of the cubic B-splines with K_a = 5 and K_ω = 5 degrees of freedom, respectively, and the regional basis matrix is equal to Φ_r= [1₁₅, I₁₅] with K_r = 16. First order marginal difference penalties are utilized for both P_a and P_ω to ensure smoothness over the functional, and the covariate domains. For the regional domain, a ridge style penalty P_r = [015, I15] is employed as in the data analysis. The model for all simulation settings has K_a × K_r × K_Ω = 400 coefficients and for each Monte Carlo run SVD is used to reduce the dimension of the design matrix such that the resulting columns account for at least 95% of the total variation. Across simulation settings, the rank of the SVD reduced design matrix increases with sample size and decreases as a function of ρ, with the median rank at ρ = 0.0 equal to 93, 128, 145, for n = 200,500, and 1000, respectively. Moving from ρ = 0.0 to ρ = 0.3, the median rank decreases by approximately 20 at each sample size. The median penalty parameters across 500 Monte Carlo runs for n = 500; ρ = 0.0 are λ_a = .0033, λ_r = .0036, and λ_ω = .0043, with penalty parameters displaying no median trend across sample size or dependency structure but slightly more variation among Monte Carlo runs at n = 200 compared to larger sample sizes. The average computation times based on ten iterations for Monte Carlo runs at n = 200,500,1000 are 7.6, 15.4, and 29.1 seconds, respectively. Predictive performance of CARR-GFLM is compared to the existing methods of m-GFLM and m-GFLMi with functional effects estimated by projection onto a basis of cubic B-splines with five degrees of freedom and second degree differencing penalties.

4.2 |. Results

Figure 5 displays the results from 500 Monte Carlo runs under each simulation setting, with RSE values for the regression function β(a, r, ω) (top row) and coverage probabilities for the Bayesian point-wise confidence intervals (bottom row). As expected, RSE values decrease as sample size increases with the median RSE reduced by approximately a factor of 3 moving from n = 200 to n = 1000 at each level of regional dependency. For a fixed sample size, an increase in regional dependency produces a modest but consistent increase in median RSE (RSE is increased by 7.2% with ρ changing from 0.0 to 0.3 at n = 200). With increasing ρ, functional predictors at each region share more information and the estimated regression function may lose precision much akin to when a multivariate regression experiences multicollinearity. The true and estimated regression function β(a, r, ω) at three regions from the Monte Carlo run with the median RSE (0.327) for n = 500 and ρ = 0.1 is shown in Figure 6 . Despite the non-negligible RSE, the shape, periodicity, and magnitude of the regression function is well preserved, suggesting that the accumulation of estimation error is evenly distributed across the regression functions from each region rather than being concentrated within a few regions. Note that n = 200 is a small sample size for functional regression settings, especially for binary functional regression. This explains the relatively high median RSE values observed for n = 200 (ranging between 0.57 and 0.65 for varying values of ρ). The coverage probabilities for each simulation setting approaches the nominal level of 95% as sample size increases. For sample sizes n = 500 and 1000, the median coverage observed is consistently larger than .83. Since the confidence intervals considered are point-wise, they are not expected to hit the nominal level uniformly over all a, r and ω. However for n = 200, coverage decreases significantly with increasing ρ. This may be due to the fact that the rank of the resulting design matrix after SVD is the smallest at n = 200 and ρ = .3, leading to narrower confidence intervals. Note that because coverage probabilities are calculated at each (a, r, ω), the number of points considered 15 * 30 * 50 = 22,500 is large and thus outliers have been jittered horizontally to improve presentation.

FIGURE 5.

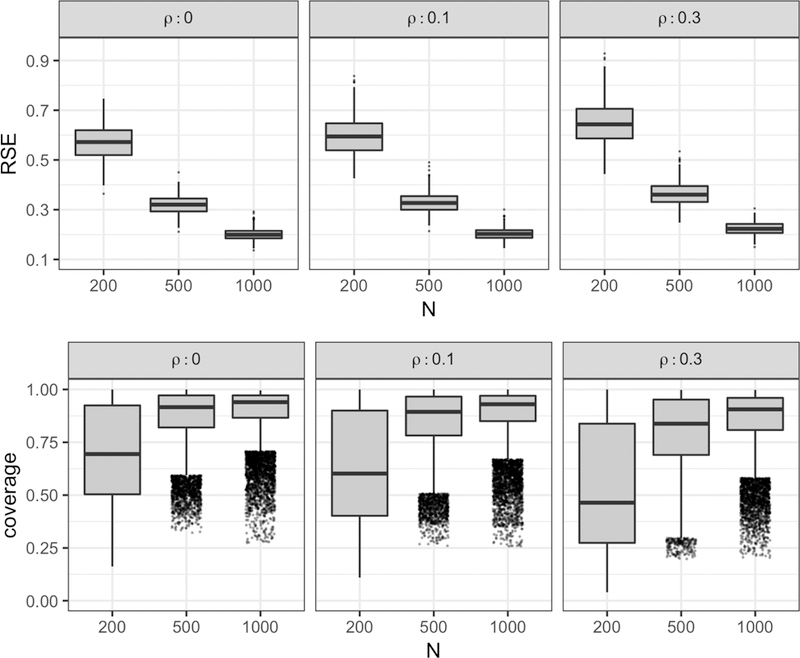
The simulation results from 500 Monte Carlo runs under each simulation setting (ρ = 0,0.1,0.3 in columns and n = 200,500,1000 in columns within panels). RSE values for the regression function β (a, r, ω) (top row) and the coverage probability for the Bayesian point-wise confidence intervals for a nominal level of 95% ((bottom row) are provided. Outliers are jittered horizontally to improve presentation.

FIGURE 6.

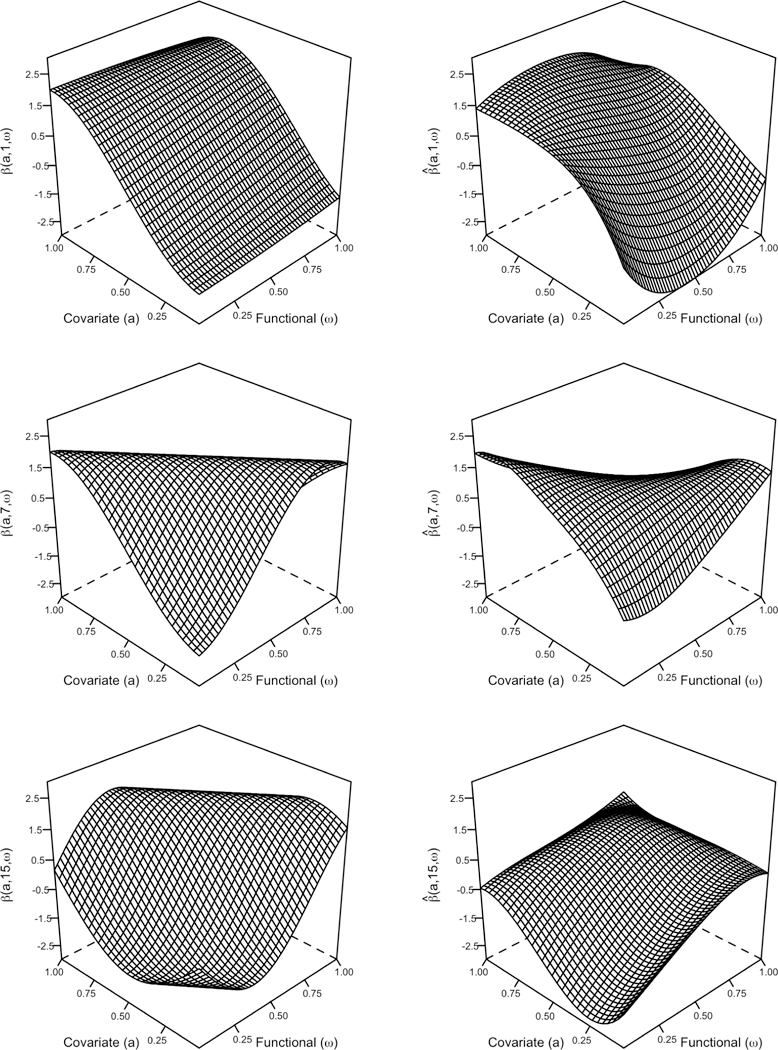
The true (left column) and estimated (right column) regression function β (r,a,ω) for regions r = 1,7,15 (descending rows) from the Monte Carlo run with the median RSE (0.327) under the simulation design, n = 500; ρ = 0.1.

Figure 7 compares the AUC from CARR-GFLM (top row) with m-GFLM (middle row) and m-GFLMi (bottom row) over 500 Monte Carlo runs under each simulation setting. For all models, the median AUC for the validation sets improves with increasing sample size and decreases with increasing regional dependency, though the differences observed for regional dependency are small. At each simulation setting, a descending trend is observed for median AUCs as one moves from CARR-GFLM to m- GFLMi to m-GFLM. While the median AUC for CARR-GFLM is greater than .80 for sample sizes greater than n = 200, m-GFLM and m-GFLMi fail to exceed a median AUC of .75 for any simulation setting, suggesting that incorporating flexible covariate-adjustments is essential for predictive performance even at large sample sizes. The overall good AUC for CARR- GFLM suggests that despite the high model complexity, the regularization induced by the quadratic penalty and SVD avoids overfitting and allows for generalization of the fitted model to newly observed data.

FIGURE 7.

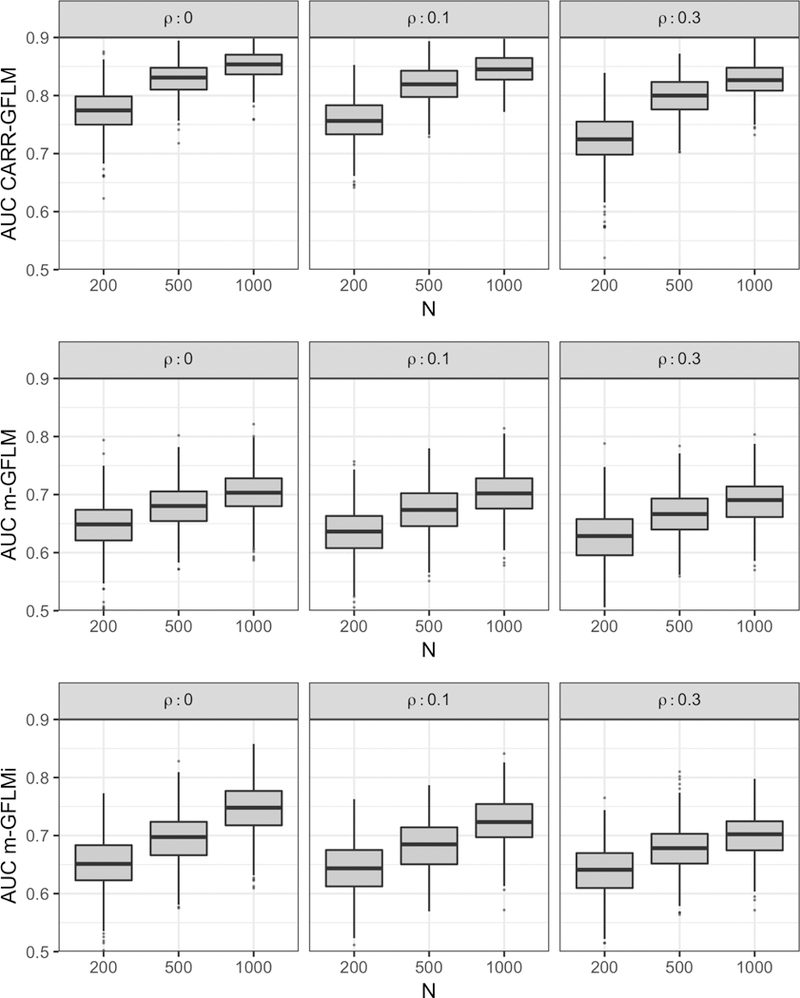
The AUC for the validation data sets from 500 Monte Carlo runs under each simulation setting (ρ = 0,0.1,0.3 in columns and n = 200,500,1000 in columns within panels) for the CARR-GFLM (top row), mGFLM (middle row), and m-GFLMi (bottom row).

5 |. DISCUSSION

We propose a covariate-adjusted region-referenced generalized functional linear model (CARR-GFLM) that estimates functional effects across a non-smooth regional domain while simultaneously adjusting for observed covariates. The proposed estimation procedure projects the regression function onto a tensor basis formed from a kronecker product of one-dimensional discrete and continuous basis functions. The tensor structure allows for construction of a flexible penalty structure that induces regularization along each dimension while at the same time controlling the number of shrinkage parameters. Even for a three-dimensional regression function, the number of elements in the tensor basis will often greatly exceed the number of observed subjects and thus SVD is utilized to reduce the dimension of the design matrix allowing the proposed model to be fit in standard software. The model can be generalized to accommodate a vector of covariates by introduction of additional marginal bases in the kronecker product.

The proposed method is used to model associations between diagnostic status and alpha band spectral dynamics in ASD and TD children across a broad developmental range. The challenge in estimating a single PAF at each electrode is a voided by considering the full alpha spectral density, where the information on the developmental stage of the child is integrated into the model by adjusting for chronological age. Thus, based on EEG data alone, we find that differences across the scalp in alpha band spectral dynamics between ASD and TD children at similar ages can predict diagnostic status reasonably well. This finding suggests that developmental differences in the alpha band spectral density may provide a promising point of further investigation into the underlying neural differences between ASD and TD children. Performance of the CARR-GFLM model is compared to existing methods in both the data analysis and the simulation study and is found to provide superior prediction and inference. While the proposed model is motivated by a developmental EEG study, the methodology can be considered in applications involving other brain imaging modalities with a regionally-referenced functional predictor and an additional set of covariates.

Abbreviations:

PAF

peak alpha frequency

FFT

Fast Fourier Transform