Artefact detection and quality assessment of ambulatory ECG signals

Highlights

• •A novel way for ECG quality assessment is proposed, based on the posterior probability of an artefact detection classifier.
• •A good performance was obtained when testing the classifier on two independent (re)labelled datasets, thereby showing its robustness. The performance was better, compared to a heuristic method and comparable to another machine learning algorithm.
• •A significant correlation was observed between the proposed quality assessment and the annotators level of agreement.
• •Significant decreases in quality level were observed for different noise levels.

Abstract

Background and Objectives

The presence of noise sources could reduce the diagnostic capability of the ECG signal and result in inappropriate treatment decisions. To mitigate this problem, automated algorithms to detect artefacts and quantify the quality of the recorded signal are needed. In this study we present an automated method for the detection of artefacts and quantification of the signal quality. The suggested methodology extracts descriptive features from the autocorrelation function and feeds these to a RUSBoost classifier. The posterior probability of the clean class is used to create a continuous signal quality assessment index. Firstly, the robustness of the proposed algorithm is investigated and secondly, the novel signal quality assessment index is evaluated.

Methods

Data were used from three different studies: a Sleep study, the PhysioNet 2017 Challenge and a Stress study. Binary labels, clean or contaminated, were available from different annotators with experience in ECG analysis. Two types of realistic ECG noise from the MIT-BIH Noise Stress Test Database (NSTDB) were added to the Sleep study to test the quality index. Firstly, the model was trained on the Sleep dataset and subsequently tested on a subset of the other two datasets. Secondly, all recording conditions were taken into account by training the model on a subset derived from the three datasets. Lastly, the posterior probabilities of the model for the different levels of agreement between the annotators were compared.

Results

AUC values between 0.988 and 1.000 were obtained when training the model on the Sleep dataset. These results were further improved when training on the three datasets and thus taking all recording conditions into account. A Pearson correlation coefficient of 0.8131 was observed between the score of the clean class and the level of agreement. Additionally, significant quality decreases per noise level for both types of added noise were observed.

Conclusions

The main novelty of this study is the new approach to ECG signal quality assessment based on the posterior clean class probability of the classifier.

1. Introduction

Electrocardiogram (ECG) is one of the primary screening tools of the cardiologist. It measures the electrical activity of the heart during a short period of time to obtain a better understanding of its functioning. During this screening, the subject is requested to lay still in a supine position to avoid possible signal distortions.

Despite high detection rates, some problems might remain unnoticed due to the limited intermittent sampling and lack of cardiac stress during the measurement. Therefore, the patient is often equipped with an ambulatory monitoring device [1].

Ambulatory devices allow patients to be monitored during daily life, instead of in a protected hospital environment. This results in a drastic increase of the detection window and, thereby, the likelihood of identifying dysfunctions. However, taking the recording procedure out of the hospital increases the exposure to noise.

Noise can originate from a variety of sources, such as the power line, muscle activity or electrode movement. All of these sources affect the recording in a different way. For instance, muscle activity and power line interference respectively cause abrupt and continuous alterations of the signal. All these alterations can be categorized as artefacts. Since artefacts could profoundly reduce the diagnostic quality of the recording, it is important to deal with them accordingly. Two distinct approaches can be used to handle artefacts: ECG denoising and assessment of the acceptability of the recorded ECG [2]. This study will focus on the latter approach.

Silva et al. stated that: ”Rigorous quality control is essential for accurate diagnosis, since alterations during the actual recording might result in inappropriate treatment decisions” [3]. To mitigate this problem, automated algorithms are needed to detect artefacts and to quantify the quality of the recorded signal [4]. Two closely related approaches can be distinguished to assess the acceptability of the recorded ECG: detection and quantification. The first approach consists of a simple binary, clean or contaminated, classification. One example of where this might be used is at the front end of the acquisition process. The user could be provided with rapid, binary feedback and, if required, make adjustments in the recording set-up or, worst case scenario, re-start the recording.

A variety of signal quality indices and algorithms were proposed in line with this approach as a result of the Physionet/Computing in Cardiology (CinC) challenge of 2011 [5], [6], [7], [8]. The challenge aimed at encouraging the development of software for mobile phones by recording an ECG and providing useful feedback about its quality [3]. The best performing algorithm was developed by Xia et al. [5]. In line with other proposed methods, their algorithm consists of multiple stages, namely: flat line detection, missing channel identification and auto- and cross-correlation thresholding. Amplitude features such as, minimum and maximum amplitude or range and differences with previous samples were also frequently used. However, due to different saturation levels between recording devices, these features restrict the usability of the algorithms.

The rationale for the second approach, quality quantification, is that different study objectives require different quality levels. For instance, heart rate variability (HRV) studies do not require the same, high, quality level as T-wave alternans or beat classification studies. This prompted a number of authors to propose a multi-level quantification of the signal quality [9], [10], [11]. For example, Li et al. proposed a five level signal quality classification algorithm which divided the signals in five bins: clean, minor noise, moderate noise, severe noise and extreme noise [11].

In this study, we propose a novel method for the detection of artefacts and quantification of the signal quality. The autocorrelation function (ACF) is used to characterize the ECG signal, since it facilitates the separation of clean and contaminated segments [12]. From the ACF, descriptive features are extracted and fed to a RUSBoost classifier. We propose to use the posterior probability of the clean class as an indication of the quality of the signal.

The first objective of this study is to evaluate the robustness of the proposed artefact detection method by training it on one dataset and testing it on two independent datasets. The second objective is to evaluate the novel signal quality index by comparing it to the agreement of the annotators and the level of noise.

2. Methods

2.1. Data

ECG recordings were used from three different studies: (1) a sleep study conducted by the University hospitals Leuven (UZ Leuven), Belgium, (2) the PhysioNet/Computing in Cardiology (CinC) Challenge of 2017 and (3) a stress study conducted by imec.

2.1.1. Sleep dataset

This dataset was intended for sleep apnea classification, but it has been previously used for artefact detection in [12]. All signals were reviewed for artefacts and annotated by a medical doctor with experience in interpreting polysomnographic signals, including ECG.

The dataset was recorded in the sleep laboratory of the UZ Leuven and consists of 16 single-lead (lead II) ECG recordings, originating from 16 different patients. A total of 152 hours and 12 minutes of signal was acquired with a sampling frequency of 200 Hz.

In sleep apnea research, it is common practice to first divide the recordings in one minute segments and subsequently analyse each recording on a minute-by-minute basis [12]. Implementation of this procedure resulted in a total of 9132 one-minute segments, which included 295, or 3.2%, contaminated segments.

2.1.2. CinC dataset

The PhysioNet/Computing in Cardiology Challenge of 2017 was intended for the differentiation of atrial fibrillation (AF) from noise, normal and other rhythms in short term ECG recordings. All recordings, lasting from 9 to 60 seconds, were sampled at 300 Hz and stored as 16-bit files with a bandwidth of 0.5–40 Hz.

In total, the dataset consists of 12,186 ECG recordings, of which 8528 recordings were provided for training. Only the normal rythm and noisy class were selected for this paper. They accounted for a total of 5334 recordings. A more detailed description of the dataset can be found in [13].

2.1.3. Stress dataset

This dataset was recorded to detect and quantify stress in daily life using different physiological metrics, including ECG. The single-lead (lead II) ECG signals were recorded with the Health Patch (imec, Leuven, Belgium), which has a sampling frequency of 256 Hz. The device was previously used in another stress study to measure ECG and acceleration [14].

The subjects were instructed to wear this patch for five consecutive days and to remove it only while working out. They were also provided with a waterproof cover to protect the patch while showering. One day of one subject was selected to test the proposed algorithm.

This ECG signal was divided in segments of 30 seconds, resulting in a total of 2879 segments.

2.2. (Re)labelling of the data

During the CinC challenge, participants noted that some recordings of the non-noisy classes were actually very noisy [13]. Therefore, the organizers decided to re-check all recordings and provide new labels if necessary. However, despite these adjustments, the organizers of the CinC challenge stated that: ”The kappa value, κ, between many data remained low even after relabelling, indicating that the training data could be improved.” [13]. Additionally, no labelling of the Stress dataset was present prior to this study. Therefore, it was opted to have our own (re)labelling procedure for the CinC and Stress datasets.

Each segment was (re)labelled by four independent annotators according to the following rule:

”If the annotator is able to confidently distinguish all R-peaks in the segment, then the segment is labelled as clean. Otherwise, it is labelled as contaminated.”

All annotators are engineers working in the signal processing domain with varying experience in ECG analysis. The most experienced annotator has seven years of experience and the least experienced has about one year. The annotators had no knowledge of the original labels.

2.3. Pre-processing

Each ECG segment was filtered by means of zero phase, 2^nd order high- and 4^th order low-pass Butterworth filters with cut-off frequencies at 1 Hz and 40 Hz, respectively. These filters ensure the removal of baseline wander and high frequency noise, without altering the information contained in the characteristic waves of the ECG.

2.4. Feature extraction

First, we segmented the filtered ECG segments into epochs of five seconds, with 80% overlap. This window width was selected, since in [12], it provided the best results.

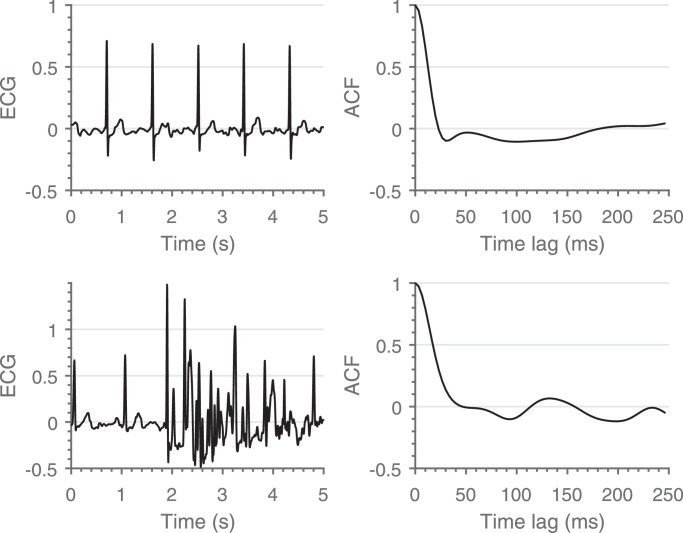
Then, each five seconds epoch is characterized by its ACF. An example of the difference between the ACF’s of a clean and a contaminated segment is shown in Fig. 1. The maximum time lag was restricted to 250 ms to ensure inclusion of the different waveforms, without including consecutive heartbeats.

Fig. 1.

Comparison between a clean (top) and a contaminated (bottom) segment. A clear difference between the shape of both ACF’s can be observed.

Based on previous work, we selected three features from the ACF’s to characterize the ECG segments [15]:

2.4.1. First (local) minimum

We assume that the shape of the ACF during the first time lags is primarily defined by the shift of the R-peak towards the S-wave. Following this assumption, the first (local) minimum of the ACF should coincide with the shift of the R-peak towards the deepest point of the S-wave.

As a first step, the first (local) minimum was selected in every ACF derived from the five seconds epochs. Afterwards the overall minimum of the whole segment was computed, which results in a single value per segment.

Extensive lengthening of this interval could be an indication of a flat line, while extensive shortening could relate to high-frequency artefacts.

2.4.2. Maximum amplitude at 35 ms

The second feature is highly related to the first feature, since it is a measure of the amplitude of an estimation of the first (local) minimum in an average clean segment.

To derive one value for the whole segment, a similar approach as the first feature was applied. First, the amplitude at 35 ms was selected in every ACF derived from the five seconds epochs. Afterwards, the overall maximum of these amplitudes was computed, which results in one value per segment.

High values of this feature could indicate a flat line or a technical artefact with a high amplitude and large width.

2.4.3. Similarity

The third feature, was selected based on the assumption that ECG signals do not have abrupt alterations between consecutive small windows. To detect these alterations, we crafted a feature that represents the similarity between the different five seconds epochs.

It is defined by computing the maximum euclidean distance between all ACF’s, computed from the five seconds epochs, in a time lag interval between 30 ms and 115 ms. These values were empirically determined.

The steepness of the first downward slope is an indication for erroneous segments. However, it is already taken into account in the first two features. Hence we did not include the first 30 ms for this feature. 115 ms was selected as an end point for the similarity feature since we observed no added value for an extended window length.

The larger the distance, the less similar the ACF’s in that interval and the more likely that the segment contains abrupt alterations.

2.5. Classification

Instead of randomly selecting the training set, we used the fixed-size algorithm [16]. This algorithm maximizes the Renyi entropy of the training set, such that the underlying distribution of the entire dataset is approximated. As a result, the main characteristics of the whole dataset are represented in the training set, which consists of 70% of the whole dataset. This algorithm is applied on the three datasets separately to derive three training and test sets.

The first objective of this study is to test the robustness of the proposed algorithm. Hence, one dataset was used to train the classifier and the other two were used for independent testing. The Sleep dataset was used for the initial classifier training, since a gold standard was provided by a medical doctor.

The percentage of contaminated segments of the Sleep dataset is substantially lower compared to the clean percentage, 3.2% vs. 96.8%. This class imbalance challenges traditional classification algorithms, since the majority class might be favoured [17]. In this study, we used the classification algorithm proposed by Seiffert et al., which combines random under sampling (RUS) and boosting into a hybrid, ensemble classification algorithm named RUSBoost [18]. Previous research has shown great reference results in case of class imbalance [17].

Decision trees were selected as weak learners, since they are well-suited for ensemble classifiers, such as the one we use [19]. Each decision tree was trained with the CART algorithm and deep trees were used with a minimal leaf size of five. The learning rate of the ensemble was set at 0.1, which requires more learning iterations, but often achieves better accuracy.

In addition to the selection of the right weak learner, one of the most important hyper-parameters is the number of weak learners of the ensemble. We used a standard 10-fold cross-validation approach to select the number of weak learners. The maximum number of weak learners was fixed at 500 and the mean squared classification error of the folds was used as decisive metric.

To evaluate the robustness of the proposed approach, we compared the classification performance of two models. The first model is trained on the Sleep dataset and the second model is trained on the entire dataset. Additionally, to illustrate the effectiveness of the proposed algorithm, the performance of two other algorithms, a heuristic [20] and a machine learning algorithm [21], were also evaluated and compared with the results obtained with our models.

2.6. Quality indicator

RUSBoost is a probabilistic classifier, which means that it does not only output the most probable class, but also the probability for each class. Hence, besides providing a clean or contaminated label, also the probability of each class is provided based on the relative weight across the set of decision trees.

For each sample, each class and each decision tree, this relative weight is obtained by dividing the number of training samples of each class by the total number of training samples in the selected leaf. These weights are averaged over all decision trees in the ensemble to obtain the overall class weight. When we normalize these weights, we obtain a probability for each class ranging between 0 and 1.

Mounce et al. used the class probabilities to produce a more fine grained and focussed assessment of the risk of iron failure in drinking water [17]. In this study we propose a similar approach, but applied to the level of quality of ECG signals. The probability of the clean class was transformed to a quality score ranging from 0% to 100%, or in other words, from too contaminated to process to perfectly clean.

The obtained score is taken as the quality level of the signal. Since this score reflects the certainty of the algorithm, it is expected that it closely relates to the certainty/agreement of the annotators.

To evaluate the proposed algorithm, we created a dataset with known SNR levels. We corrupted the clean signals of the Sleep dataset with recorded artefacts from the PhysioNet noise stress test database (NSTDB) [22]. This database contains samples of three types of noise: electrode motion (EM), baseline wander (BW) and muscle artefact (MA). Only EM and MA were considered, since baseline wander is usually not a cause for erroneous R-peak detection. Contaminated signals were generated at five contamination levels, according to [11].

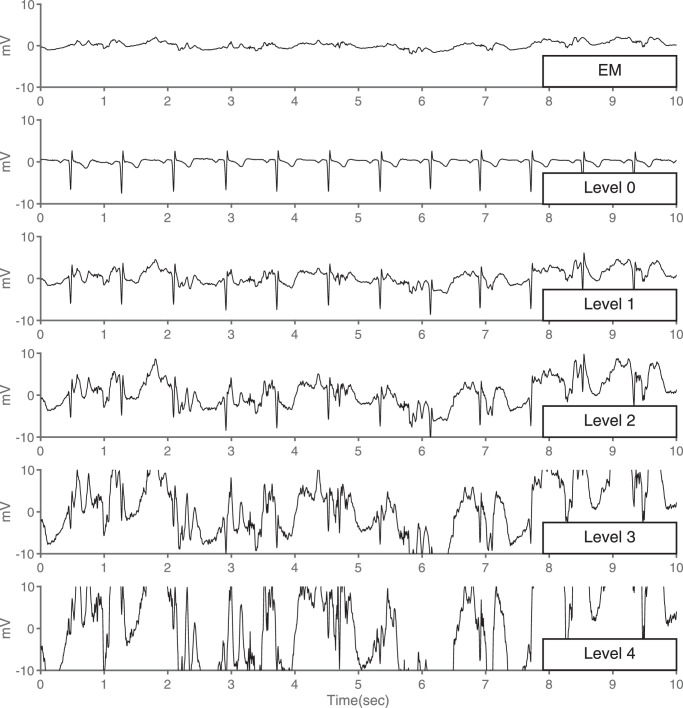
To enlarge the amount of segments, we divided the clean signals and artefact samples in 10 seconds. For each clean ECG segment, an artefact segment was randomly selected and a calibrated amount was added to the clean one. The SNR of the resulting signals was defined as described in [21]. An example of the resulting signals is shown in Fig. 2. The obtained results were compared with the modulation spectrum-based ECG quality index (MS-QI), described in [23].

Fig. 2.

Impact of Electrode Motion on ECG signal quality. EM: Electrode Motion noise, Level 0: Clean ECG signal, Level 1: Minor contamination, Level 2: Moderate contamination, Level 3: Severe contamination, Level 4: Extreme contamination. The quality of the ECG signal decreases with the increase of electrode motion (EM) noise increases.

2.7. Performance metrics

To quantify the agreement between the different annotators, we computed two different metrics: (1) the percentage of agreement and (2) the Fleiss’ kappa.

2.7.1. Percentage of agreement

All segments were classified into three classes: ‘Perfect agreement’, when all four annotators agreed, ‘Moderate agreement’, when three annotators agreed, or ‘Disagreement’, when no majority voting was possible.

2.7.2. Fleiss’ kappa

One of the drawbacks of the percentage of agreement is the lack of correction due to chance. The Fleiss’ kappa is a relatively simple, yet powerful, metric that considers the possibility that the agreement has occurred by chance [24]. Kappa values can vary between -1 and 1, but are between 0 and 1 if the observed agreement is due to more than chance alone. The closer to 1, the stronger the agreement [25].

To evaluate the classification model on the two independent datasets, we computed four different performance metrics: sensitivity (Se), which is the proportion of clean signals that have been correctly classified; specificity, wich is the proportion of contaminated signals that have been correctly classified; negative predictive value (NPV), which is the proportion of correctly classified contaminated signals over all signals labeled as contaminated; and the area under the ROC curve (AUC). The latter is more suitable than the overall accuracy, since it is not sensitive to the class imbalance [18].

The aforementioned metrics are applicable when the ground truth is clearly predefined or when all annotators agree. However, for the labelling of artefacts, it might be possible that different annotators have different opinions, and subsquently assign different labels for the same segment. Therefore, we assessed the performance by the weighted sensitivity (wSe), weighted specificity (wSp), and accordingly, the weighted AUC (wAUC), as proposed by Ansari et al. [26]. In contrast to majority voting, these metrics take all raters’ opinions into account. Thus, also the minority votes, which would be ignored when using majority voting, are used to quantify the overall satisfaction of the raters. Note that when there is 100% agreement, the weighted and classical metrics are equal.

To evaluate the effectiveness of the proposed quality index, we ranked the quality score against the agreement of the annotators on the clean class. The Pearson correlation coefficient was computed to quantify the correlation. Additionally, the quality scores for the different noise types and contamination levels were compared using a Kruskal-Wallis test.

All analysis were performed using MatlabR2017a^TM (The Mathworks, Natick, MA, USA).

3. Results

3.1. Inter-rater agreement

Despite the great difference in experience, the annotators were in agreement on 72.3% of the CinC and 91.9% of the Stress dataset. Additionally, the kappa values ranged from substantial ( > 0.61) for the CinC dataset, to almost perfect ( > 0.81) for the Stress dataset (Table A.1). This indicates that the high level of agreement was not due to chance.

3.2. Model performance

To evaluate the robustness of the proposed approach, we compared the classification performance of two models. The first model is trained on the Sleep dataset and the second model is trained on a combined subset of the three datasets. For the Stress and CinC datasets, only the segments in the âPerfect agreementâ subset were considered.

The model that was trained on the Sleep dataset achieved a mean squared classification error of under 2% when 40 or more weak learners were used. Additionally, the classification error stagnated at 140 weak learners. Therefore, we retained 140 weak learners and removed the excessive weak learners. This is likely to have minimal effect on the predictive performance of the model, since the selected weak learners give near-optimal accuracy.

We used the same methodology for the second model, which resulted in a model consisting of 90 weak learners, corresponding to an average classification error of 4.3%.

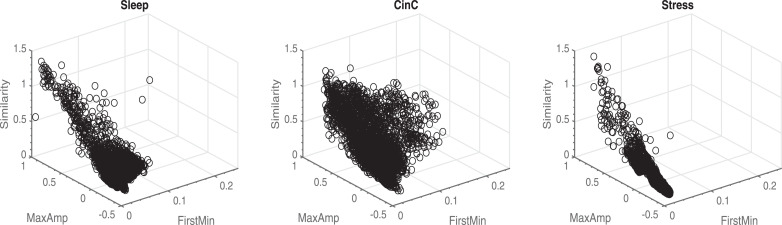
From Table 1 we can observe that similar performances were obtained with the first model compared to the second one. All performance metrics were above 0.89. Regarding NPV, better results were obtained for the CinC and Stress sets for the second model. This might be due to a different spread of the features in the three datasets. In Fig. 3, we can observed that the features of the CinC dataset have a larger spread, compared to the other two datasets. Overall, both models outperformed the method of [20], which had a particularly low NPV on the Sleep dataset, and achieved similar performance scores compared to the method of [21].

Table 1.

Classification performance on independent test sets. Model 1: Trained on the Sleep dataset, Model 2: Trained on the three datasets, Orphanidou et al. [20], Clifford et al. [21].

	Test Sleep				Test CinC				Test Stress
	Model 1	Model 2	Orphanidou et al.	Clifford et al.	Model 1	Model 2	Orphanidou et al.	Clifford et al.	Model 1	Model 2	Orphanidou et al.	Clifford et al.
Se	1.000	1.000	0.892	0.999	0.932	0.977	0.945	0.981	0.993	1.000	0.987	0.993
Sp	0.966	0.910	0.876	0.828	0.966	0.947	0.88	0.892	1.000	0.996	1.000	0.996
NPV	1.000	1.000	0.211	0.965	0.896	0.960	0.906	0.998	0.984	1.000	0.972	0.997
AUC	0.999	1.000	/	0.992	0.988	0.993	/	0.982	1.000	1.000	/	1.000

Fig. 3.

Feature space of the three training datasets. A larger spread can be observed in the CinC dataset compared to the other datasets.

3.3. Quality assessment index

Since the performance of the second model was slightly better, compared to the first one, we used that model for the evaluation of the quality assessment index.

In the previous section, only the segments with ‘Perfect agreement’ were used for testing. Hence the weighted and non-weighted performance metrics are the same. When adding the ‘Moderate agreement’ subsets, we used the weighted performance metrics to take also the minority votes into account.

We observed a decrease in the weighted performance metrics with wSe = 0.794, wSp = 0.787 and wAUC = 0.928 for the CinC dataset and wSe = 0.966, wSp = 0.848 and wAUC = 0.970 for the Stress dataset.

These results indicate that the segments in the ‘Moderate agreement’ subset are more difficult to classify. We hypothesized that this difficulty is not only reflected in the performance of the classifier, but also in the probability of the predicted class.

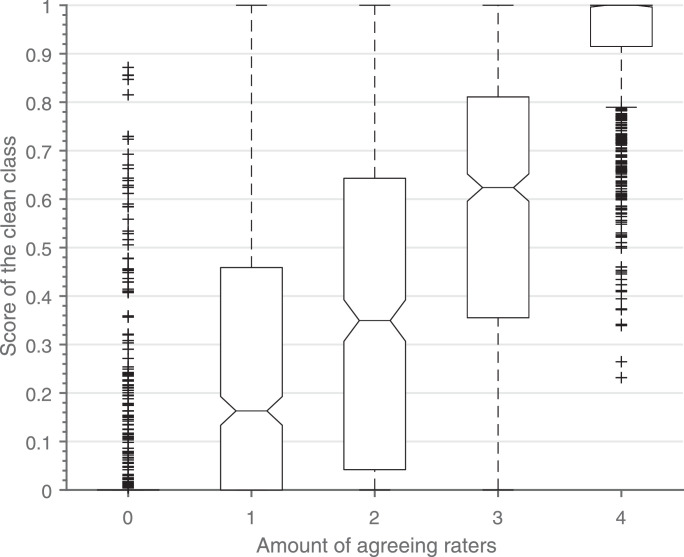
The boxplots in Fig. 4 show an increase of the score of the clean class with respect to the amount of annotators that agree on the clean class. A Pearson correlation coefficient of 0.8131 was obtained. This confirms the assumption that the score of the clean class is closely related to the certainty/agreement of the annotators.

Fig. 4.

Boxplot of the score of the clean class vs. the amount of annotators agreeing on the clean class. Outliers are shown as plus signs. The different categories consist of respectively 685, 589, 485, 636 and 1268 segments.

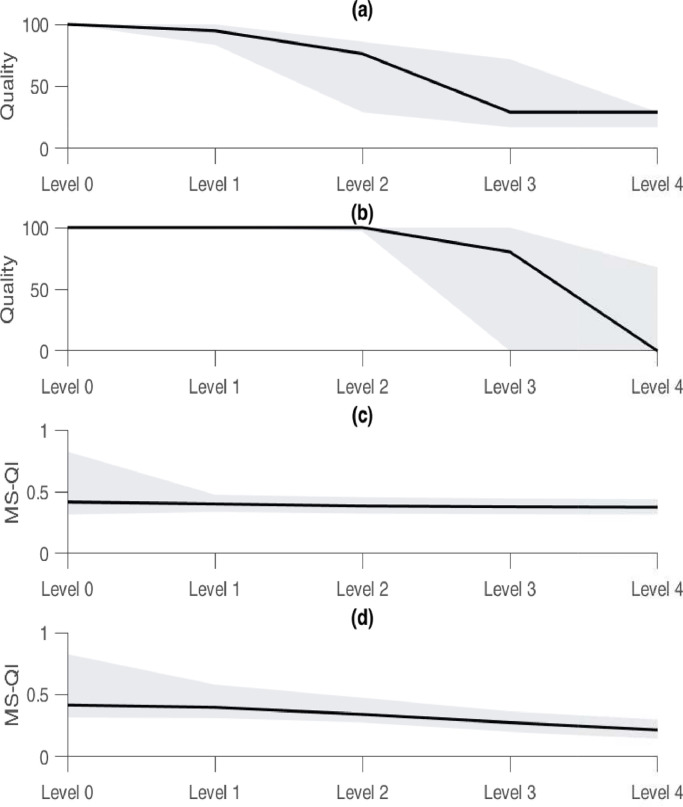
The last experiment consisted of testing the proposed quality indication on a dataset with known SNR levels and comparing the results with the MS-QI. Two types of realistic ECG noise, EM and MA, at different SNR levels from the NSTDB were added to create a simulated dataset. Significant positive correlations (0.65 and 0.65) were observed for both types of noise (p < 0.01) and the quality values of the EM and MA noise significantly decreased with the increasing noise levels (Fig. 5). However, the inter-noise quality values also differed significantly (p < 0.01).

Fig. 5.

Comparison between the proposed quality index and the modulation spectrum-based quality index (MS-QI). The quality of the EM (a) and MA (b) noise both significantly decrease, to a different extent, with the increasing noise level. The same can be observed for the MS-QI. The boundaries of the gray area indicate the 25th and 75th percentiles, and the solid line the median.

In the case of the MS-QI, also significant correlations were observed for both types of noise (p < 0.01). However, the correlation coefficients were substantially lower (0.15 and 0.41). Additionally, similar significant decreases per noise level could be observed for the MS-QI (p < 0.01). Besides these observed differences, the main difference between both algorithms is the computation time. Averaged for 1000 segments, it takes 0.215 ± 0.016 seconds to compute the MS-QI for a segment of 10 seconds, while the proposed metric takes only 0.046 ± 0.005 seconds.

4. Discussion

In this study we presented an automated method for artefact detection and continuous signal quality assessment, based on the ACF and a RUSBoost classifier. The main novelty is the new approach to signal quality assessment, using the posterior probability of the clean class of the RUSBoost classifier as an estimation of the quality of the ECG segments.

The first objective of this study was to evaluate the robustness of the proposed algorithm by training it on one dataset and testing it on two independent datasets. Due to the low level of agreement between the annotators of the CinC dataset and the lack of labelling in the Stress dataset we performed our own (re)labelling procedure. Relabelling (parts) of a freely available dataset was already done by other authors [21], [27], [28].

The newly labelled datasets were used to test the robustness of the proposed model. Firstly, the model was trained on the Sleep dataset and subsequently tested on the ‘Perfect agreement’ subset of the other two datasets. Very high performance metrics on the test sets were obtained, indicating that the model can be applied on data obtained in different recording conditions without substantial performance loss. Furthermore, this highlights the robustness of the model, since the data was recorded with different sampling frequencies, acquired with different systems and segmented with different segment lengths.

Secondly, the model was trained on a training set derived from all datasets and tested on a test subset of the ‘Perfect agreement’ subset. In this set-up all recording conditions were taken into account when training the model. Although only slightly, the overall performance of the model increased. This is particularly observable for the NPV in the CinC dataset. This might be due to a different spread of the feature space of the three datasets, as shown in Fig. 3.

The difference between the datasets could be explained by a couple of factors:

4.1. Amount of subjects

The CinC dataset consists of ECG signals of many different subjects, while the Sleep and Stress dataset consist of 16 and 1 subject respectively.

4.2. Clean vs. Contaminated

The CinC dataset contains more contaminated segments, compared to the other two datasets, as shown in Table A.1. This might be due to the way of recording. The CinC dataset recordings were made by a hand held device, while the other two were made with electrodes attached to the body.

The performance of the proposed model was compared with a heuristic [20] and a machine learning algorithm [21]. We have shown that the proposed model outperforms [20]. This algorithm is intrinsically linked to the performance of a peak detector, which could hinder the performance of the method. Since our method is solely based on features derived from the ACF of small ECG segments, it is not subjected to this type of problems.

A similar performance is obtained compared to the machine learning algorithm of [21]. This method also uses peak detection, but, instead of using the obtained RR-intervals, it compares the output of two peak detection algorithms. This is a more robust methodology, compared to [20].

The advantage of the method proposed in this paper is that only 3 features are needed to obtain an accurate performance. However, a drawback of this study is that the model was trained and tested on a dataset which mostly consisted of normal sinus rhythm. Previous studies have shown that signal quality classification algorithms experience a reduction in performance on an arrhythmia database when it was not explicitly retrained using signals containing arrhythmia episodes [11]. We expect the model to be only marginally influenced by abnormal rhythms, but more affected by abnormalities which change the shape of the heartbeat significantly, e.g. pre-mature ventricular contractions. This hypothesis will be further investigated in the future.

The obtained Pearson correlation coefficient of 0.8131 confirms the hypothesis that the certainty of the algorithm, quantified by the score of the clean class, is closely related to the certainty/agreement of the annotators. This motivated the proposal to use the score of the clean class as a new quality assessment index. One of the big advantages of this method is that no additional parameters have to be tuned, after the model is compacted. This is in contrast with [29], where an extra coefficient needs to be chosen when spectral or statistical noise is present.

As a last experiment, we tested the proposed quality indication on a dataset with known SNR levels and compared the results with the MS-QI [23]. Firstly, we observed an overall quality level of 100% (25th percentile=100% and 75th percentile=100%) for the clean segments, according to the proposed algorithm. This indicates that, at least for the clean signals, there is a correct estimation of the quality. However, the MS-QI’s of the clean segments were substanually lower, compared to the values in the original paper. This might be explained by the way that the clean segments were generated/selected. In [23], clean signals were generated using ecgsyn, a Matlab function which is available in Physionet. While in this paper, from the clean segments of the Sleep datset, the segments with the highest quality were selected by an in-house quality estimation algorithm [12]. In this algorithm, the segments are pre-processed by means of a band pass Butterworth filter with cutoff frequencies of 1 Hz and 40 Hz. Hence, since the MS-QI does not contain any filtering operation, it might be that it underestimates the quality of the clean segments.

Secondly, we observed significant quality decreases per noise level for both types of added noise for the proposed metric. However, in contrast to what was expected, the quality of the segments that are contaminated with EM noise do not decrease to 0%. This might be due to the similar morphology and frequency content of the EM noise and the QRS complex. A comparable issue was reported by Li et al. when testing their signal quality indices [29].

Despite these promising findings, we also found significant inter-noise differences, both for the proposed index and the MS-QI. This might indicate that the algorithm reacts differently to different types of noise. An explanation might be that, although the SNR values are chosen according to clinical usage, the shape of the different noise types remains different. This has limited influence on more elaborate algorithms, where more features are used, such as the one of [11], but in the proposed method, only three features derived from the ACF are used. All three features are (QRS-) shape dependent and are thus heavily influenced by the shape of the noise. Therefore, the selected features might not be optimal. On the contrary, it is very probable that the quality assessment can be improved by including statistical, frequency or other features. This will be investigated in future work.

One of the limitations of this study is that the window size for the initial feature extraction was not tuned to produce optimal results. Additional investigation into the optimal window size might result in better performance of the model. Since it is desired to remove as few data points as possible, the model would benefit from a smaller window size.

5. Conclusions

We have developed an automated, accurate and robust artefact detection algorithm, based on the ACF and the RUSBoost algorithm. We have shown that, when training the classification model on one specific dataset, it is robust enough to accurately predict the labels in other datasets. Although, as expected, the prediction is more accurate when we model the other conditions as well.

The main novelty of this study is the new approach to ECG signal quality assessment. We suggest to exploit the posterior class probability of the RUSBoost classifier and to use the probability for the clean class as a novel quality assessment index. This allows users to identify periods of data with a pre-defined level of quality, depending on the task at hand.

Declaration of Competing Interest

The authors do not have financial and personal relationships with other people or organisations that could inappropriately influence (bias) their work.

Appendix A

Table A.1.

Table A.1.

Overview of the CinC and Stress dataset (re)labelling.

	CinC			Stress
	Clean	Cont.	All	Clean	Cont.	All
Perfect	2404	1453	3857 (72%)	1817	829	2646 (92%)
Moderate	518	523	1041 (20%)	118	66	184 (6%)
Disagree			436 (8%)			49 (2%)
Fleiss’ kappa			0.686			0.901