Economic Modelling of Chronic Kidney Disease: A Systematic Literature Review to Inform Conceptual Model Design

Abstract

Background

Chronic kidney disease (CKD) is a progressive condition that leads to irreversible damage to the kidneys and is associated with an increased incidence of cardiovascular events and mortality. As novel interventions become available, estimates of economic and clinical outcomes are needed to guide payer reimbursement decisions.

Objective

The aim of the present study was to systematically review published economic models that simulated long-term outcomes of kidney disease to inform cost-effectiveness evaluations of CKD treatments.

Methods

The review was conducted across four databases (MEDLINE, Embase, the Cochrane library and EconLit) and health technology assessment agency websites. Relevant information on each model was extracted. Transition and mortality rates were also extracted to assess the choice of model parameterisation on disease progression by simulating patient’s time with end-stage renal disease (ESRD) and time to ESRD/death. The incorporation of cardiovascular disease in a population with CKD was qualitatively assessed across identified models.

Results

The search identified 101 models that met the criteria for inclusion. Models were classified into CKD models (n = 13), diabetes models with nephropathy (n = 48), ESRD-only models (n = 33) and cardiovascular models with CKD components (n = 7). Typically, published models utilised frameworks based on either (estimated or measured) glomerular filtration rate (GFR) or albuminuria, in line with clinical guideline recommendations for the diagnosis and monitoring of CKD. Generally, two core structures were identified, either a microsimulation model involving albuminuria or a Markov model utilising CKD stages and a linear GFR decline (although further variations on these model structures were also identified). Analysis of parameter variability in CKD disease progression suggested that mean time to ESRD/death was relatively consistent across model types (CKD models 28.2 years; diabetes models with nephropathy 24.6 years). When evaluating time with ESRD, CKD models predicted extended ESRD survival over diabetes models with nephropathy (mean time with ESRD 8.0 vs. 3.8 years).

Discussion

This review provides an overview of how CKD is typically modelled. While common frameworks were identified, model structure varied, and no single model type was used for the modelling of patients with CKD. In addition, many of the current methods did not explicitly consider patient heterogeneity or underlying disease aetiology, except for diabetes. However, the variability of individual patients’ GFR and albuminuria trajectories perhaps provides rationale for a model structure designed around the prediction of individual patients’ GFR trajectories. Frameworks of future CKD models should be informed and justified based on clinical rationale and availability of data to ensure validity of model results. In addition, further clinical and observational research is warranted to provide a better understanding of prognostic factors and data sources to improve economic modelling accuracy in CKD.

Electronic supplementary material

The online version of this article (10.1007/s40273-019-00835-z) contains supplementary material, which is available to authorized users.

Key Points for Decision Makers

This review provides an overview of how chronic kidney disease (CKD) is typically modelled, with glomerular filtration rate (GFR) and albuminuria, respectively, typically utilised as the key prognostic factor within CKD and diabetes model frameworks.

Most of the models identified were Markov models and/or utilised input data at cohort mean levels, and many of the current methods did not explicitly consider patient heterogeneity or underlying disease aetiology, except for diabetes, providing limited clinical rationale for the choice of model design.

Given the heterogenous nature of individual CKD patients’ characteristics and clinical prognoses, a model structure designed around the prediction of individual patients’ GFR trajectories may be preferred over cohort-based modelling frameworks when simulating patients with CKD. However, model choice should be informed and justified based on clinical rationale and availability of data to ensure validity of model results.

Introduction

Chronic kidney disease (CKD) is a progressive condition with heterogenous aetiology that leads to irreversible damage to the kidneys and is associated with an increased incidence of cardiovascular events and mortality [1–6]. The age-standardised global prevalence of CKD stages 1–5 among adults aged ≥ 20 years in 2010 was approximately 10.4% in men and 11.8% in women and continues to rise, fuelled by ageing populations and the increasing incidence of diabetes and hypertension [7, 8]. Currently, more than two million patients with CKD worldwide have been estimated to require renal replacement therapy (RRT) through dialysis or kidney transplantation [9]. In addition, the humanistic and economic burdens of CKD increase significantly as renal function declines, and patients at CKD stage 3 or above are at 1–14 times higher risk for cardiovascular and overall mortality compared with the general population [4]. Moreover, patients with CKD often experience health-related quality of life (HRQoL) impairments and increased healthcare costs [4, 10]. Because of the need for intensive treatment, the largest costs and impacts on HRQoL are incurred when patients reach CKD stage 5 (glomerular filtration rate [GFR] < 15 mL/min/1.73 m²) or end-stage renal disease (ESRD), which is irreversible and where patients often require RRT [11, 12].

Cardiovascular disease (CVD) and CKD are closely interrelated, and the reduction of systolic blood pressure, blood glucose and other cardiovascular risk factors via drug treatment and/or lifestyle modifications are key components of CKD management. Renin–angiotensin–aldosterone system inhibitors, which confer both cardio- and reno-protective benefits through their anti-hypertensive effect, have been the cornerstone of CKD treatment for many years [13, 14] and are often prescribed in addition to statins and anti-platelet therapy [15–19]. While the risk of developing CKD of certain aetiologies can be reduced through medical and/or lifestyle interventions, others cannot, and the main goals of CKD management are to delay the rate of progression to ESRD to limit cardiovascular risk, preserve HRQoL and restrain healthcare costs. However, the underlying aetiology is often predictive of both the likely treatment strategy and the clinical prognosis.

As novel treatments for CKD become available and require evaluation for inclusion into drug formularies, estimates of economic (optimisation of budget usage) and clinical (maximisation of population benefits) outcomes are needed to guide payer reimbursement decisions. Given the significant costs associated with ESRD management, the rate of progression to ESRD is a significant determinant of cost effectiveness. However, the long-term outcomes of CKD, such as ESRD incidence, are not always sufficiently captured over the duration of clinical studies, and time to ESRD often varies widely between patients [20], making extrapolation necessary yet challenging. The choice of model structure may also play a key role in the validity of these extrapolations, underlining the importance of understanding the implications of selecting a particular conceptual modelling approach. With these challenges in mind, the aim of the present review was to systematically review published economic models that simulated long-term outcomes of kidney disease to qualitatively describe the chosen model designs, rates of CKD progression and the incorporation of CVD in a population with CKD.

Methods

Literature Search and Data Extraction

This review was conducted according to the PRISMA-P (Preferred Reporting Items for Systematic reviews and Meta-Analyses Protocols) guidelines [21]. A search strategy was devised using a specified set of search terms for each database (Tables 1–6 in Resource 1 of the Electronic Supplementary Material [ESM]). In brief, the search was designed to identify economic modelling publications that included adult patients with/without CKD in whom CKD progression was evaluated.

Searches were conducted in MEDLINE, Embase, the Cochrane Library and EconLit on 10 November 2017. To identify additional publications that may have modelled progression of kidney disease as part of another disease model, we conducted a supplementary search in MEDLINE to identify systematic literature reviews detailing economic models for diabetes or hypertension. We also searched the websites of the following health technology assessment agencies: UK National Institute for Health and Care Excellence, Canadian Agency for Drugs and Technologies in Health and the Australian Pharmaceutical Benefits Advisory Committee. Bibliographies of eligible articles were also searched for potential publications of interest to the review.

Titles and abstracts of the identified citations were screened by a single reviewer following specific PICOS (population, interventions, comparators, outcomes and study design) eligibility criteria (Table 7 in Resource 1 of the ESM). In brief, studies were included if they described an economic model of adult patients with/without CKD in whom CKD progression was evaluated. The model structure must have included the progression of kidney disease and any health economic outcome, including (but not restricted to) quality-adjusted life-years, incremental cost-effectiveness ratios, life-years gained or costs. Studies were limited to English language only. Abstracts/titles that did not meet the eligibility criteria were excluded; full-text publications were obtained for the remaining citations. The screening process was repeated using the PICOS criteria for full-text articles to obtain a final set of included publications that described economic models characterising CKD progression, regardless of the intervention or comparator being assessed.

Information on model characteristics (including structure, perspective, health states and disease setting), disease progression, event utility, costs, sensitivity analyses, drivers of cost effectiveness, validation procedures and model limitations were extracted from all included publications.

Analysis of Time to End-Stage Renal Disease (ESRD) or Death

Where reported, transition and mortality rates were extracted from publications to qualitatively describe the choice of model parameterisation on disease progression, such as time to and time with ESRD. To facilitate comparison of rates of CKD disease progression, transition rates from each eligible published model were used to estimate time to ESRD or death (ESRD/death) and time with ESRD within a simple Markov model framework. Such analyses were undertaken individually for each model and limited to decision trees and Markov models that reported sufficient data to allow such analyses. Published models were excluded from these analyses if transition rate data were not reported in sufficient detail or if regression-based simulation approaches were modelled because of their complexity. Models were also excluded if they were designed to model a horizon of < 10 years.

Health states were defined based on those reported in each individual model publication (Fig. 1 in Resource 2 of the ESM). Where possible, analyses were initiated with a standard patient profile, defined as patients aged 50 and from CKD stage 1, normo-albuminuria or earliest disease stage modelled, to provide a consistent reference point. The cycle length reported in each publication was utilised and the time to ESRD/death and time with ESRD subsequently calculated by estimating the time spent in each of the modelled health states. A maximum horizon of 50 years (up to the age of 100) was modelled across all analyses to limit the uncertainty between modelled outcomes.

Results

Summary of Included Models

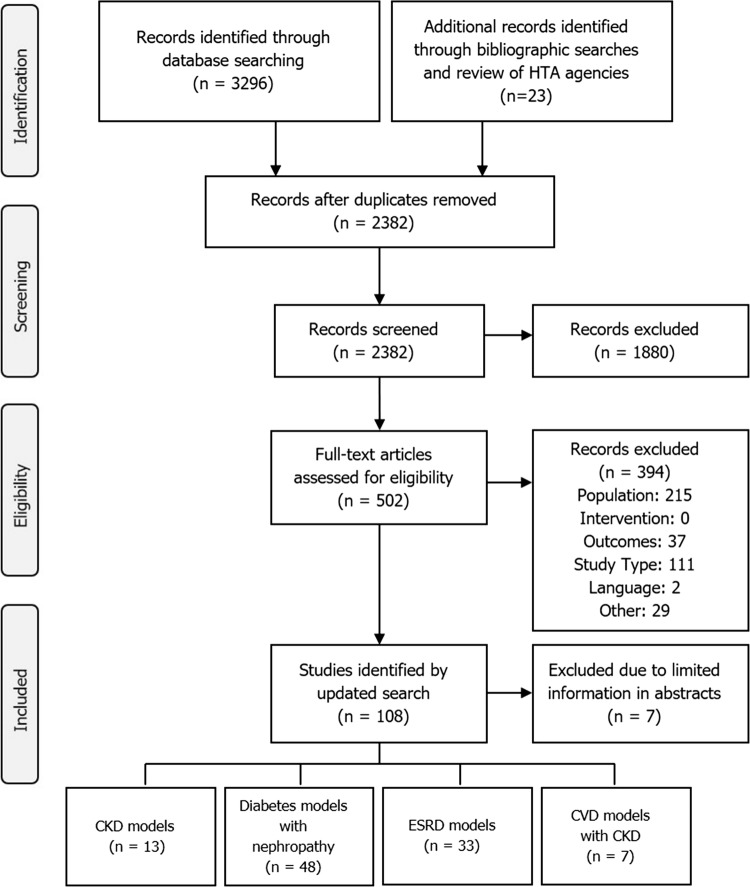
The search identified 2382 citations, excluding any duplicate publications (Fig. 1). During the screening of titles and abstracts, a further 1880 citations were excluded. Upon full-text assessment of the remaining 502 articles, 101 models met criteria for inclusion, which were classified into CKD models (n = 13), diabetes models with nephropathy (n = 48), ESRD-only models (n = 33) and cardiovascular disease (CVD) models with CKD components (n = 7).

Fig. 1.

PRISMA (Preferred Reporting Items for Systematic Reviews and Meta-Analyses) diagram showing the model-selection process. CKD chronic kidney disease, CVD cardiovascular disease, ESRD end-stage renal disease, HTA health technology appraisal

Models were assessed using the Consolidated Health Economic Evaluation Reporting Standards (CHEERS) checklist for economic evaluation of health interventions, which assesses whether all key elements of model structure, parameterisation and approach have been clearly reported [22]. In 15 (15%) models, all elements of the CHEERS checklist were included, with 79 (78%) models including ≥ 80% of applicable elements (Resource 3 of the ESM). Often there was no single table of modelling assumptions; instead, structural or other assumptions underpinning the models were reported in relevant sections of the publication. The most infrequently reported elements were conflicts of interest (47%), measurement and valuation of preference-based outcomes (34%) and sources of funding (30%).

Chronic Kidney Disease (CKD) Models

Framework and Disease Pathway

In 13 publications that described unique CKD models, a Markov model was most commonly used (ten publications [77%]) [23–32], including two models that were developed to inform clinical and policy decisions in improving CKD care: the Chronic Kidney Disease Model [31] and the SHARP CKD-CVD model [32] (Table 1). A further model, the CKD Health Policy Model, was also developed to inform policy-making decisions and used a microsimulation approach [33]. Across models, CKD was generally described and modelled as a single disease. Other aetiologies included CKD and hypertension [26] and CKD and hepatitis C virus genotype [25], but a general population of individuals was more common [23, 24, 27, 33]. Where reported, the underlying disease aetiologies are described in Supplementary Table 8 (Resource 4 of the ESM). Also, an overview of the model settings, health states related to kidney disease, approach to model CKD progression, approach to modelling cardiovascular events, discounting, sensitivity analyses, drivers of cost effectiveness and approach to model validation is available in Supplementary Tables 8–10 (Resource 4 of the ESM).

Table 1.

Summary of model structural framework and the method of disease progression across identified chronic kidney disease and diabetes models

N	Model structure	Model structure sub-category	CKD progression (as described by model publication)	References
CKD models (N = 13)
9	Markov model	Multistate Markov model	Transition probabilities	[23]
		Markov model	GFR decline	[24]
		Semi-Markov model	Transition probabilities	[25]
		Markov model	Estimated GFR decline, transition probabilities	[26]
		Markov model	Transition probabilities	[27]
		Markov model	Estimated GFR decline, transition probabilities	[28]
		Markov model	Transition probabilities	[30]
		Markov model	Transition probabilities	[29]
		Markov model	Risk equations	[32]
1	Simulation model	Microsimulation model	Estimated GFR decline	[163]
3	Combination	Markov model and Monte Carlo simulation	Relative risk of progression	[36]
		Decision tree and Markov model	Transition probabilities	[35]
		Markov model and Monte Carlo simulation	GFR decline	[31]
Diabetes models (N = 48)
25	Markov model	Markov model	Transition probabilities	[115]
		Markov model	Transition probabilities	[118]
		Markov model	Transition probabilities	[90]
		Markov model	Transition probabilities	[79]
		Markov model	Transition probabilities	[98]
		Markov model	Transition probabilities	[116]
		Markov model	Transition probabilities	[53]
		Markov model	Creatinine clearance decline	[124]
		Markov model	Transition probabilities	[92]
		Markov model	Transition probabilities	[100]
		Markov model	Transition probabilities	[89]
		Markov model	Transition probabilities	[164]
		Markov model	Transition probabilities	[85]
		Markov model	Transition probabilities	[120]
		Markov model	Transition probabilities	105
		Markov model	Transition probabilities	[88]
		Markov model	Transition probabilities	[110]
		Markov model	HbA1c levels	[86]
		Markov model	Transition probabilities	[102]
		Markov model	Transition probabilities	[103]
		Markov model	Risk equations	[104]
		Markov model	Transition probabilities	[113]
		Markov model	Transition probabilities	[74]
		Semi-Markov model	Transition probabilities	[117]
		Semi-Markov model	Transition probabilities	[107]
13	Simulation model	Discrete-event simulation model	Transition probabilities	[121]
		Microsimulation model	Risk equations	[109]
		Microsimulation model	Incidence rates	[91]
		Discrete-event simulation model	Risk equations	[95]
		Microsimulation model	Risk equations	[93]
		Microsimulation model	Transition probabilities	[83]
		Object-oriented simulation model	Risk equations	[112]
		Microsimulation model	Risk equations	[99]
		Discrete-event simulation model	Transition probabilities	[101]
		Microsimulation model	Transition probabilities	[96]
		Discrete-event simulation model	Transition probabilities	[84]
		Monte Carlo simulation model	Transition probabilities	[87]
		Microsimulation model	Not reported	[106]
2	Decision tree	Decision tree	Creatinine clearance decline	[96]
		Decision tree	Probabilities	[82]
8	Combination	Markov model and Monte Carlo simulation	Transition probabilities	[94]
		Markov model and Monte Carlo simulation	Transition probabilities	[119]
		Markov model and microsimulation	Transition probabilities	[122]
		Semi-Markov model and Monte Carlo simulation	Transition probabilities	[81]
		Markov model and Monte Carlo simulation	Hazard rate (per year)	[97]
		Markov model and Monte Carlo simulation	Risk equations	[114]
		Markov model and Monte Carlo simulation	Transition probabilities	[80]
		Decision tree and Markov model	Transition probabilities	[111]

Decision tree: Defined as a cohort-level model that uses a tree-like model of decisions and their possible consequences, where transitions are limited to those specified by the particular nodes included in the decision tree. Markov model: A more fluid extension of the decision tree principle, defined as a type of cohort-based mathematical model containing a finite number of mutually exclusive health states, with time periods of uniform length, in which the probability of movement from one state to another depends on the current state. Semi-Markov model: As a Markov model but incorporating a time-dependency factor whereby transition rates are dependent on the time spent in a health state and are, thus, not constant. Multi-state Markov model: As a Markov model but has explicitly described the calculation of transition rates as accounting for dependencies between events. Simulation model: Defined as a patient-level model in which patient disease progression is simulated individually and where health states are not modelled as mutually exclusive. Microsimulation model: As a simulation model but providing more granularity/detail (e.g. where a simulation model may model ESRD as a single state, a microsimulation model may model health states within the ESRD state such as dialysis or transplant). Object-oriented simulation model: Defined as a person-by-person, object-by-object simulation, spanning from biological details to the care processes, logistics, resources and costs of healthcare systems. Monte-Carlo simulation model: Defined as a form of modelling where model inputs are drawn from distributions and are not treated as fixed values, with the model run multiple times to provide a probabilistic distribution of results. Discrete-event simulation: Discrete-event simulation is a computer-modelling technique used in economic evaluation of health interventions in which individual patient experience is simulated over time, and events occurring to the patient and the consequences of such events are tracked and summarised. Unlike other models, in discrete-event simulation, movements between patients’ health states are usually driven by events that may occur at varying times (rather than during cycles of fixed length), and time-to-event distributions are required for each event. Event likelihoods are driven by individual patient characteristics, which are recorded at baseline and may be updated as the patient experience (events, new health states) accumulates

CKD chronic kidney disease, ESRD end-stage renal disease, GFR glomerular filtration rate, HbA_1c glycated haemoglobin

In general, models were based on a core structure defined by health states for CKD according to (estimated or measured) GFR, in line with stratifications in the National Kidney Foundation Kidney Disease Outcomes Quality Initiative (NKF KDOQI) guidelines [34] (Fig. 2). However, four models did not apply this structure [23, 27, 35, 36]. Boersma et al. [23] modelled CKD according to the presence of albuminuria (normoalbuminuria, microalbuminuria and macroalbuminuria). Ferguson et al. [27] divided model states into normal kidney function; low, intermediate and high risk of progression to kidney failure; being on dialysis; and surviving with a kidney transplant. Howard et al. [36] simulated the annual progression of patients from the development of risk factors (specifically hypertension, proteinuria and diabetes [with no albuminuria, microalbuminuria or macroalbuminuria]) through CKD stage 1–4 to ESRD and RRT. In most studies, patients initiated RRT with dialysis and had the option to receive a transplant. However, a number of studies did not differentiate between type of RRT, instead defining RRT as dialysis or transplant. For hypertension and proteinuria states, patients in this modelling study had an annual probability of progressing to ESRD requiring RRT, where CKD progression was not explicitly modelled. Finally, Okubo et al. [35] formulated a Markov model using separate sub-models for patients with CKD with and without diabetes. In both, kidney disease was modelled as the probability of ESRD. All models included transition to death.

Fig. 2.

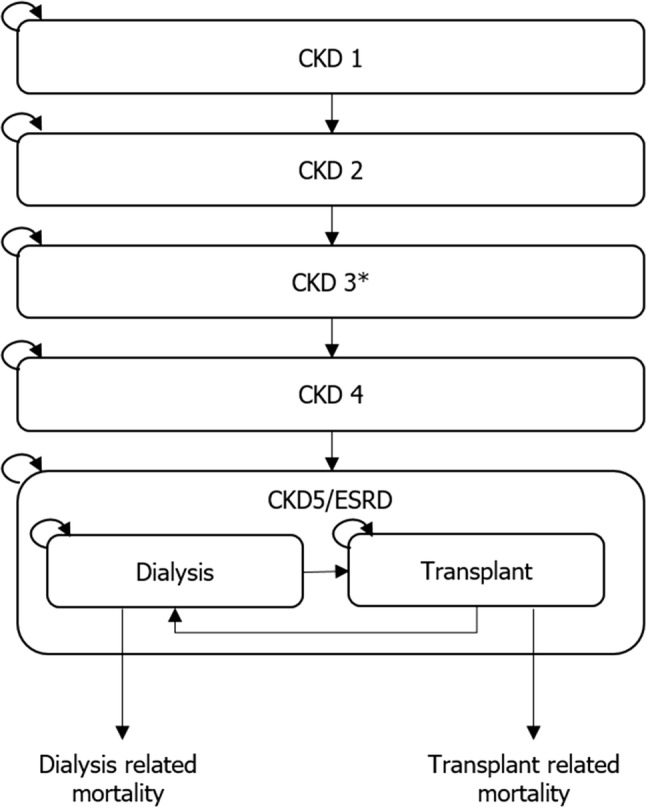
Example of the core model structure of chronic kidney disease models. CKD chronic kidney disease, ESRD end-stage renal disease. *CKD stage 3 may be further stratified into CKD stage 3a and CKD stage 3b. Note: Patients could progress to death from any health state

There were four common variations to the core structure of reported models (Fig. 2): (1) modelling CKD stage 3 as a single health state or stratified into CKD stage 3a and 3b; (2) the initial CKD stage (i.e. whether patients began in early or advanced CKD stages); (3) presenting CKD stage 5 as a single state (ESRD) or stratified into non-dialysis ESRD, dialysis or kidney transplant; and (4) using separate sub-models for diabetes and CKD that informed the overall model. Where reported, ESRD models defined ESRD as (measured or estimated) GFR < 15 mL/min/m²; the initiation rules for RRT were less consistent. Four models assumed initiation of RRT (dialysis or transplant) immediately after the incidence of ESRD [29, 30, 32, 36], whereas four models assumed a delay in the initiation of RRT; one model assumed RRT was initiated 1 year after ESRD incidence [33], two models initiated RRT at a GFR < 10 mL/min/m² [28, 31] and one assumed a static transition probability to RRT [25].

Characterisation of CKD Progression

In summary, five models (38%) predicted CKD outcomes based on rates of annual GFR decline, four models (31%) used GFR transition probabilities and two models (15%) used albuminuria transition probabilities.

Models based on GFR health states predicted CKD outcomes based on rates of GFR decline or transition probabilities. Erickson et al. [26] used published observations from large observational cohorts of comparable patient populations to estimate the mean annual rate of estimated GFR decline. This annual rate was applied to all CKD stages (progression from stage 3a to stage 5 CKD). Boulware et al. [24] and the CKD Health Policy Model [33] modelled progression through CKD stages based on GFR decline and albuminuria status. In the CKD Health Policy Model, a person would be assigned an initial estimated GFR and subsequently experience annual decreases in estimated GFR based on rates derived from a clinical trial by Boulware et al. [24] that varied according to CKD stage, presence of albuminuria and diabetes, and hypertension status. The model by Levy et al. [28] modelled the functioning kidney as a single health state; estimated GFR was assumed to decline linearly from estimated GFR 3a until ESRD. The Chronic Kidney Disease model [31] utilised GFR changes based upon a distribution derived from an analysis of a primary dataset of patients with CKD followed for 5 years [37] that was adjusted for age, race, current CKD stage, hypertension, diabetes, proteinuria, and CVD.

Four models [25, 27, 29, 30] utilised transition probabilities between CKD stages to model (estimated or measured) GFR decline. Elbasha et al. [25] derived probabilities from a targeted review of the published literature, Ferguson et al. [27] calculated probabilities based on estimated GFR values and adapted longitudinal data on CKD progression and regression rates from the indigenous cohort within the Alberta Kidney Disease Network [38], and Nuijten et al. [29, 30] used a published study by Keith et al. [39] to derive transition probabilities.

In the two models [23, 36] that used albuminuria states to model CKD progression, annual transition probability and mortality rates differed by proteinuria stage and were based on data from the PREVEND (Prevention of Renal and Vascular End Stage Disease) study [40].

Within the SHARP CKD-CVD policy model, the CKD sub-model utilised participant data from the SHARP (Study of Heart and Renal Protection) trial—a randomised trial assessing the effects of lowering low-density lipoprotein cholesterol in patients with CKD—to inform disease progression [32, 41]. For each year of follow-up, data collected during that year were used to categorise participants into respective health states (one of five CKD states, on maintenance dialysis, or having undergone a kidney transplant). Participants not receiving RRT could progress to (or remain in) any CKD category, with transition probabilities estimated using multivariate multinomial logistic regression.

Two models predicted improvement in health over time (e.g. CKD stage 2 to stage 1): Boersma et al. [23] and Ferguson et al. [27] allowed patients to transition to improved states of health during the model horizon, the former through transitions between macro-, micro- and normo-albuminuria, and the latter between CKD stages 1–4.

Four models [25–28] adapted mortality rates from baseline populations using age- and sex-specific life tables from the country of study and modified them using relative risks or hazard ratios to derive CKD stage-specific all-cause mortality. Another approach was to derive mortality rates from large cohort studies [23, 29, 30]. Where modelled, mortality rates for those surviving with a transplant or those on dialysis, as well as the chance of graft failure, were taken from national registries.

ESRD-Only Models

Rather than modelling disease progression through its full spectrum (CKD stage 1–5), 33 models described an ESRD population (e.g. CKD stage 5 or a dialysis population). Across ESRD-only models, the costs and benefits of different dialysis modalities was the primary outcome assessed [42–51]. In addition, the cost effectiveness of treating hyperphosphatemia or anaemia, secondary conditions associated with CKD progression, were commonly modelled (e.g. use of sevelamer with calcium carbonate for patients receiving dialysis with hyperphosphatemia [52]).

Of these models, 19 (58%) modelled patients from the explicit state of dialysis or transplant, and the remaining 14 (42%) initiated patients from a pre-dialysis health state with or without ESRD, including health states describing pre-dialysis CKD stage 5 and other broader CKD health state definitions. Most models focusing on ESRD only used Markov modelling techniques (28 publications [42–45, 47, 48, 50–71]); among the remaining models, one [49] used a decision tree and another a microsimulation approach [46], and two further models used a Markov model with a decision tree component [58, 72]. An overview of the models is provided in Supplementary Tables 11–13 (Resource 5 of the ESM).

In general, models employed a core structure based on four health states: pre-dialysis, dialysis, transplantation and death. The majority of models assumed the initiation of dialysis or transplantation at model initiation, with only two notable exceptions, the models by Shechter et al. [73] and Lee et al. [46], where dialysis was not initiated until GFR thresholds of < 10 and < 9 mL/min/m², respectively. Within the dialysis state, patients could switch between haemodialysis and peritoneal dialysis modalities. Patients could progress from the pre-dialysis state to dialysis or directly to kidney transplant; they could also reach the transplant state through progression from the dialysis state. Upon transplant, patients could remain in continued graft function or experience graft failure, whereby they returned to the dialysis state.

There were two common variations to this structure: first, models differed in the approach to modelling dialysis and, second, they differed on how kidney function was modelled post-transplant. Dialysis was modelled as a single health state [44, 51, 52, 55, 66, 68, 71, 74], as two separate health states for haemodialysis and peritoneal dialysis [45, 48–50, 56, 58, 62, 63, 67], as three separate health states [47, 65], or as four separate health states [43, 70] that included home haemodialysis, satellite haemodialysis, hospital haemodialysis and continuous ambulatory peritoneal dialysis [43]. Two models reported the use of five different dialysis modalities [42, 57]. Regarding graft function post-transplant, the majority of models included a rate of graft failure, upon which patients would return to the dialysis health state. Four models included a post-transplant health state [44, 46, 60, 65].

In general, ESRD-only models used various forms of transition rates to model the proportion of pre-dialysis patients progressing to dialysis or transplant, as described briefly in Supplementary Tables 10–19 (Resources 5–7 of the ESM) [42–45, 47–52, 54, 56, 57, 60, 62–67, 70, 75]. These were usually derived using data obtained from national renal registries relevant to the country perspective of the model, such as the Norwegian Renal Registry [76], the UK Renal Registry [75] or the Dutch Renal Replacement Registry [77].

Diabetes Models with Nephropathy

Framework and Disease Pathway

Diabetic nephropathy is a microvascular complication of diabetes and a leading cause of ESRD [78]. In total, 48 unique diabetes models were identified that modelled nephropathy using two different approaches. The first approach modelled diabetes through estimated glycated haemoglobin (HbA_1c) change with time. The models included a sub-model of nephropathy as a long-term complication of diabetes; other complications included retinopathy and neuropathy. The second approach exclusively modelled the progression of nephropathy in diabetic patients through albuminuria health states, without modelling diabetes progression or HbA_1c. Twelve (25%) were models of type 1 diabetes mellitus (T1DM) [74, 79–89], 22 (46%) were models of type 2 diabetes mellitus (T2DM) [90–111] and seven (16%) were models of both T1DM and T2DM [112–117]. The remaining models evaluated either diabetes with hypertension [118–120], pre-diabetes [121, 122], or diabetes with more advanced kidney disease [123, 124]. The majority of models were Markov (n = 25 [52%]) or microsimulation (n = 7 [15%]) models (Table 1). An overview of the models is provided in Supplementary Tables 14–16 (Resource 6 of the ESM).

Irrespective of the type of diabetes, most models applied a core sub-model structure of diabetic nephropathy based on a disease pathway of five health states: no nephropathy (or normoalbuminuria), microalbuminuria, macroalbuminuria (or gross proteinuria), ESRD (comprising dialysis or transplant as absorbing states) and death (Fig. 3). Some models also included a health state of macroalbuminuria with impaired (estimated or measured) GFR.

Fig. 3.

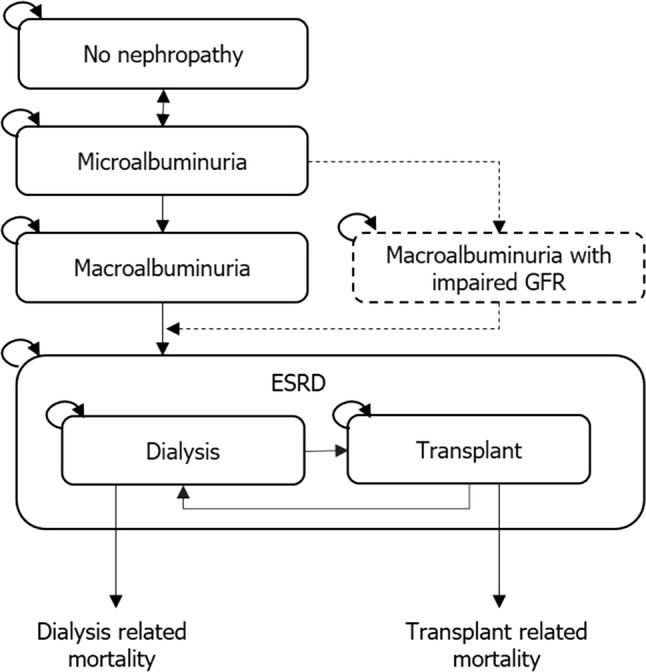
Example of the core model structure of the nephropathy component of diabetes models with nephropathy. CKD chronic kidney disease, ESRD end-stage renal disease, GFR glomerular filtration rate. Note: Patients could progress to death from any health state

Generally, in models focusing on diabetic nephropathy, patients could progress from no nephropathy to microalbuminuria, from which they could either return to no nephropathy or progress to macroalbuminuria with or without impaired GFR. Once in a state of macroalbuminuria, with or without impaired GFR, patients could progress to ESRD. Across all diabetic nephropathy models, RRT (dialysis or transplant) was not explicitly defined in 15 models and not modelled entirely in nine models. When RRT was included in a model, it was typically initiated upon the incidence of ESRD (22 models) or after the first year of ESRD (one model). Patients with ESRD could usually progress from dialysis to transplant and, following graft failure, from transplant to dialysis; both the dialysis and the transplant health states were associated with an increased risk of mortality.

Characterisation of CKD Progression

Generally, in T1DM models, transition rates or transition probabilities informed nephropathy progression, with the source of disease progression commonly derived from the DCCT (Diabetes Control and Complications Trial), a major clinical trial conducted from 1983 to 1993 [125] or the randomised clinical trial of captopril for the inhibition of diabetic nephropathy [126]. Similarly, T2DM models tended to use transition rates or transition probabilities to model the progression of diabetic nephropathy. Two studies, the USRDS (United States Renal Data System) national database and the UKPDS (UK Prospective Diabetes Study), were used to inform transition rates or probabilities across many of the models. The JADE model [95], UKPDS OM1 model [96], UKPDS OM2 model [99] and the IHE cohort model [104] developed risk equations using data mainly derived from the UKPDS, among other sources.

Models including both T1DM and T2DM disease states also applied transition rates or transition probabilities to predict diabetic nephropathy progression. Information was generally sourced from different studies to inform separate rates/probabilities for T1DM and T2DM. The EAGLE [114] and CORE [115] diabetes models with CKD components used separate sources for ESRD only (T1DM [127], T2DM [128]), with the latter model employing three additional studies [126, 129, 130] to inform T2DM transition probabilities. Furthermore, in the CORE diabetes model, patients were screened for the presence of micro- or macroalbuminuria; once either was detected, they could be treated with angiotensin-converting enzyme inhibitors. Patients in receipt of angiotensin-converting enzyme inhibitors progressed at a different rate from those not receiving these medications.

In all models, patients in the ESRD health state received dialysis or renal transplant. The decision to transition to dialysis was typically based on a weighted average of dialysis modalities (haemodialysis and peritoneal dialysis) that either reflected country-specific treatment patterns or were derived from contemporary studies. The rate at which patients progressed from dialysis to transplant or from transplant to dialysis, and the mortality risk multiplier attributable ESRD, were typically informed by country-specific registry data.

Cardiovascular Morbidity and Mortality

Given the interrelationship between CKD and CVD, the incorporation of cardiovascular morbidity and mortality was assessed across identified models. In CKD models, the most commonly reported cardiovascular events were myocardial infarction (five models [23, 25, 26, 31, 33]) and stroke (four models [25, 26, 31, 33]). In two models, the Framingham risk equations were used to estimate baseline cardiovascular event hazards that were subsequently multiplied by CKD-specific hazard ratios reflecting the increased risk of cardiovascular events independently associated with CKD stage [26, 33]. In one of these models [26], a relative risk reduction for myocardial infarction and stroke was applied to the baseline risk based on statin use. The relative risk reductions for CKD stage 3 (3a and 3b) and stage 4 were obtained from a published meta-analysis [131] and the SHARP trial [41], respectively. The authors assumed that statins did not reduce cardiovascular risks for patients with CKD stage 5. The second publication, describing an adapted version of the SHARP CKD-CVD policy model [33], included CVD as a separate sub-model, with health states including non-vascular death, vascular death, non-fatal major atherosclerotic event and non-fatal haemorrhagic stroke. Elbasha et al. [25] also used CKD stage-specific hazard rates for myocardial infarction and stroke, although they were applied to baseline probabilities reported in the underlying Framingham risk equation publications. Boersma et al. [23] used transition probabilities for cardiovascular event incidence that were estimated based on the PREVEND study [40]. In Howard et al. [36], patients had an annual probability of experiencing a fatal or non-fatal cardiovascular event based on clinical history (diabetes, hypertension, proteinuria) obtained from the general literature. Models of ESRD did not include CVD components.

In models focusing on patients with diabetic nephropathy, CVD was most commonly incorporated using risk equations or transition probabilities. Equations from the Framingham Heart Study [132, 133] or UKPDS [96, 134] were most commonly used to model cardiovascular events, including myocardial infarction and stroke. Transition probabilities were estimated based on data derived from various sources, including DCCT [125], MARVAL [135] and UKPDS [96, 134].

In addition to the models described, a further seven models of CVD were identified that included a CKD component [136–142]. An overview of the models is provided in Supplementary Tables 17–19 (Resource 7 of the ESM). In six of these models, CKD was incorporated through a single ESRD health state, and one model [141] included a sub-model for the progression of nephropathy. The main approach to modelling cardiovascular events by these models was to use transition probabilities. Probabilities were typically age and sex specific and derived from the Framingham risk equation or Framingham data/studies. Two models adjusted the risk of cardiovascular events for hypertension treatment but assumed such treatment had no comparable impact on the risk of CKD progression [138, 141].

Time to and Time with ESRD

Transition rates consistent with the core model structures presented in Figs. 2 and 3 were extracted from eligible studies and are summarised in Table 2. Overall, there was greater availability of transition rate data for model structures based on albuminuria than for CKD stage-based models defined by GFR, which would be expected given the greater number of diabetes models with CKD components identified. Significant variability was observed across several reported transition rates. Most notably, the annual transitions from CKD stage 3 to CKD stage 4 and the transitions from ESRD/dialysis to death ranged from 0.008 to 0.405 and 0.008 to 0.626, respectively. All extracted transition rates are summarised in Resource 8 in the ESM.

Table 2.

Summary of annual transition rates reported in identified studies

Transition	Mean	Median	Minimum	Maximum	No. of observations	References
CKD transitions
CKD 1 to CKD 2	0.053	0.053	0.022	0.083	2	[25, 30]
CKD 1 to death	0.040	0.040	0.040	0.040	1	[30]
CKD 2 to CKD 3	0.071	0.054	0.002	0.175	4	[25, 27, 30]
CKD 2 to death	0.027	0.027	0.003	0.051	2	[27, 30]
CKD 3 to CKD 4	0.182	0.151	0.008	0.405	6	[25, 27, 29, 30]
CKD 3 to death	0.041	0.063	0.005	0.063	5	[27, 29, 30]
CKD 4 to CKD 5/ESRD	0.067	0.059	0.010	0.148	12	[25, 27, 29, 30, 53, 54, 58, 61]
CKD 4 to death	0.080	0.062	0.008	0.177	10	[27, 29, 30] [58, 61, 66]
Nephropathy-related transitions
No nephropathy to microalbuminuria	0.028	0.027	0.003	0.060	24	[23, 74, 79, 88, 92, 98, 103, 111, 117, 141]
No nephropathy to death	0.026	0.006	0.000	0.194	16	[23, 74, 79, 80, 88, 92, 113, 117]
Microalbuminuria to macroalbuminuria	0.044	0.030	0.001	0.157	18	[23, 74, 79, 88, 92, 103, 110, 111, 117]
Microalbuminuria to death	0.038	0.014	0.000	0.119	17	[23, 74, 79, 88, 92, 102, 110, 117]
Macroalbuminuria to ESRD	0.040	0.012	0.001	0.158	17	[23, 74, 79, 88, 92, 110, 111, 117]
Macroalbuminuria to death	0.101	0.086	0.007	0.289	15	[23, 74, 79, 88, 92, 110, 117]
ESRD transitions
ESRD/dialysis to transplant	0.055	0.040	0.005	0.150	14	[27, 30, 43, 44, 48, 51, 107, 118, 120]
ESRD/dialysis to death	0.177	0.146	0.008	0.626	56	[27, 30, 35, 43–45, 48, 51, 53, 58, 59, 61, 63, 66, 74, 79, 88, 92, 94, 98, 107, 110, 111, 117, 118, 120, 121, 136, 138, 141]
Transplant to dialysis	0.082	0.084	0.040	0.118	4	[27, 30, 118]
Transplant to death	0.053	0.050	0.012	0.093	12	[27, 30, 51, 61, 107, 118, 120]

Assumptions: Where relevant, transitions were matched to a baseline patient age of 50 years. Where ranges were reported, the midpoint of the range was extracted. Where male and female rates were reported, the average of the two was extracted. Duration of diabetes was assumed to be 10 years if not reported and required to calculate transition rates. All transitions are presented as annual probabilities. Depending on the model, ESRD includes non-dialysis ESRD and dialysis

CKD chronic kidney disease, ESRD end-stage renal disease

The mean rate of progression from CKD stage 4 to ESRD was greater than that from macroalbuminuria (0.067 vs. 0.043, respectively); conversely, the mean rate of progression from CKD stage 4 to death was lower than that from macroalbuminuria (0.080 vs. 0.101, respectively). As anticipated, across transition rates relating to model structures based on albuminuria, the rate of progression to death increased as disease severity increased, with a less clear pattern observed among transitions relating to a CKD stage-based model structure defined by GFR. Patients with ESRD/dialysis were at the greatest risk of mortality (mean rate 0.177); following transplant, the rate of transition to death was comparable to that in earlier disease stages (mean rate 0.053).

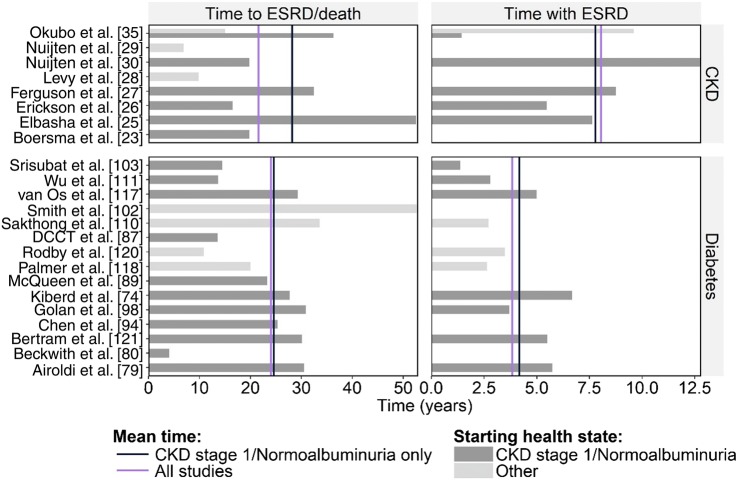
In total, eight CKD models and 15 diabetes models with CKD components reported enough information to evaluate expected time to ESRD/death and/or time with ESRD. Significant parameter variability existed between models in both time to ESRD/death and time with ESRD, with only small improvements in consistency observed when considering just those models where starting health states were aligned (i.e. all patients initiated at CKD stage 1 or normoalbuminuria) (Fig. 4).

Fig. 4.

Predicted time to end-stage renal disease (ESRD) or death and with ESRD. CKD chronic kidney disease

Such parameter variability was likely due to the heterogeneity in patient characteristics and disease severity across studies. The reported age of patients varied from 13 to 75 years, with most models evaluating a cohort aged between 30 and 50 years. The majority of CKD models initiated patients at CKD stage 1, with only two exceptions: Levy et al. [28] (CKD stage 3b/4) and Erickson et al. [26] (CKD stage 2). However, significant heterogeneity existed with respect to patients’ disease background, the most notable of which were the models by Elbasha et al. [25] and Erickson et al. [26], which modelled cohorts with hepatitis C and early autosomal dominant polycystic kidney disease, respectively. Among diabetes models with nephropathy, there was reasonable consistency with respect to starting health state, with only four of the 15 models not initiating patients in the state of normoalbuminuria. The most notable differences in disease background were the modelling of T1DM or T2DM, and within those settings, the choice of diabetes treatment.

Further, published models eligible for this analysis typically followed the core model structure identified earlier in this review, based on either CKD stage or albuminuria. Some variability existed with respect to explicitly incorporated health states outside of these core structures, where the number of health state transitions varied from two in the simplest model to 26 in the most complex. Such differences in health state definition likely influenced differences in progression estimates.

Mean time to ESRD/death was relatively consistent across CKD models and diabetes models with nephropathy. In CKD models, mean time to ESRD/death was 28.2 years when patients were initiated from the earliest CKD stage (21.6 years when initiating patients in the starting health state defined in the model publication) and 24.6 years in diabetes models with CKD components (24.0 years when initiating patients in the starting health state defined in the model publication). When evaluating time with ESRD, CKD models predicted extended ESRD survival over diabetes models with nephropathy (mean time with ESRD: 8.0 vs. 3.8 years).

Discussion

This review qualitatively describes how the progression of kidney disease was incorporated in economic models. Models focusing purely on CKD are typically based on (estimated or measured GFR) decline, with GFR progression predominantly based on a linear rate of decline, which could be adjusted for age, race, CKD stage, prevalence of proteinuria and clinical history (hypertension or diabetes). In comparison, diabetes models with nephropathy, where most of the economic models included nephropathy as a separate microvascular sub-model within the overall model, were most frequently based on the presence of albuminuria, where CKD progression was most commonly modelled with the use of transition probabilities calculated for progression between albuminuria health states. There were exceptions to these general rules, and the choice of modelling framework was likely driven by numerous factors, such as perspective, intervention, indication and underlying data sources used to inform disease progression, among other considerations.

The preference to model GFR over albuminuria (or vice versa) was not immediately clear and not typically justified in modelling publications; however, it may relate to the focus and structure of models in the two disease areas. For example, models focusing on CKD typically predicted health state occupancy in line with CKD stages in patients with established CKD, for which GFR provides an explicit delineator. In contrast, diabetes models with nephropathy typically aimed to predict the presence of ESRD based on a reported baseline prevalence of albuminuria, an established predictor of ESRD in patients with diabetes, often in patients with no history of CKD [143, 144]. However, while the choice of prognostic factor may be relatively straight forward within the context of specific modelling frameworks informed by the availability of data, the clinical rationale for any preference is much less well-defined [145]. Consensus does exist among the published literature with respect to the natural trajectory of albuminuria and GFR, with changes in albuminuria considered variable, with both negative and positive changes often observed in short timeframes, and changes in GFR usually considered to be progressive (i.e. monotonically decreasing). However, two studies predicted improvement in GFR and albuminuria health states [23, 27], in line with the literature suggesting that renal function can improve in a subset of patients [146–148]. Nevertheless, it has been suggested that the two variables be used in conjunction to predict the progression of CKD [145, 149].

There were some limitations to our review. First, only English articles were included in the search. However, this included the vast majority of the articles published, and research suggests that exclusion of non-English articles is unlikely to result in bias [150]. Second, only primary publications of models were included as they were deemed to contain the most relevant information regarding the model. Third, the review was limited to the information available in the study publication. Fourth, titles and abstracts of the identified citations were screened by a single reviewer. For uncertainties surrounding the relevance of a study, the corresponding full text was obtained, so a decision was made based on a thorough assessment of the study.

Across all models, a common author-identified limitation was the quality and quantity of the data sources that were used to inform the model, such as using data from clinical trials with a short duration, despite a longer follow-up study being more appropriate to model disease progression. For models of CKD without diabetes, limitations surrounded the modelling of CKD progression, including the lack of data for estimating the rate of decline in kidney function for people with neither diabetes nor hypertension [24], lack of stratification of CKD states according to albuminuria [25], and the assumption that GFR declines linearly [28]. In models of CKD with diabetes, a number of authors cited the use of risk equations derived from the Framingham Heart Study as a limitation to predicting cardiovascular events in those with CKD.

Interestingly, most models that captured the risk of CVD predicted an increase in cardiovascular risk as CKD progressed; conversely, only two models predicted an increased risk of CKD progression as a function of CVD incidence [23, 92]. However, it should be noted that the modelling of these components was often relatively simplistic and failed to provide clinical justification or rationale for the choice of modelled relationship. Across all models, cardiovascular-related risk was most frequently derived from the Framingham Heart Study, with estimates modified to reflect differences in specific geographical populations or patient characteristics. The Framingham risk equations are an extremely well-validated set of equations derived from a large cohort of patients (over multiple generations) followed-up over several decades and have helped identify major cardiovascular risk factors and their impact on the evolving risk of CVD [151–156]. However, the generalisability of the Framingham equations to a CKD population is uncertain, given the equations were derived using data from a population-based cohort with a low prevalence of CKD [157]. Various studies have demonstrated that patients with CKD have a higher prevalence of CVD than can reasonably be explained based on traditional cardiovascular risk factors, suggesting that CKD itself, or other unknown factors, are additionally impacting on patients’ cardiovascular risk [3, 158, 159]. As a result, the Framingham risk equations demonstrate poor overall accuracy in predicting cardiovascular events in individuals with CKD, emphasising the need for the development of cardiovascular risk equations in patients with CKD specifically to support future cost-effectiveness studies [156].

Across models, CKD was generally described and modelled as a single disease, thus ignoring (perhaps relevant) differences in aetiologies. However, the interventions under evaluation were typically indicated across all CKD aetiologies and targeted to other diseases rather than to CKD itself, with decision makers most interested in an evaluation of cost effectiveness across the entire CKD population (cohort level as opposed to individual patient level). Further, while specific CKD aetiologies were not often defined or cited, modelled populations were usually defined based on an underlying clinical trial design, which typically limited patient heterogeneity through specific inclusion/exclusion criteria. Therefore, within this context, a simplification or generalisation of CKD aetiologies may be considered appropriate.

The clinical course of CKD progression (CKD stage 1–4) to ESRD is known to vary substantially across patients and may be influenced by various risk factors, including CKD aetiology, sex, presence of comorbidities (e.g. diabetes and CVD), anaemia, hypertension and proteinuria [160, 161]. Such heterogeneity in underlying disease poses challenges in the accurate modelling of CKD progression, and the models identified often did not consider these factors. Overall, the body of evidence on prognostic factors related to disease outcomes is relatively large in the field of diabetes, with a greater volume of prospective studies from which disease progression estimates can be derived or multivariable risk equations utilised. However, the tendency across all identified models was to capture input data at the mean rather than the observed patient-level variation, which often precluded the ability to capture true patient heterogeneity. More commonplace was the independent sampling of input data, through probabilistic sensitivity analysis to approximate heterogeneity, although this approach is associated with inherent limitations and does not actually capture how relevant differences in patients’ clinical profiles affect cost-effectiveness outcomes.

The time it takes a patient to reach ESRD/death, and the time for which a patient resides in the ESRD state, is of significance, particularly from the health economics perspective, since ESRD is associated with a significant resource burden and, consequently, may influence cost-effectiveness decisions. While there was general agreement amongst model type with respect to mean time to ESRD/death, mean time with ESRD was typically shorter among CKD models than among diabetes models with nephropathy. Such a difference may possibly be attributed to the excess morbidity and mortality associated with diabetes. In addition, a difference in the age distribution of patients may be a contributing factor. Overall, given the relatively large variations in time to and time with ESRD and their potential influence on health economics studies, we suggest that further research may be undertaken to fully quantify the differences across models’ structures and better understand the heterogeneity between modelled populations and model designs, and the likely causes of such differences.

The heterogeneity with respect to both patient characteristics and disease outcome prediction, combined with a reasonable body of evidence, does seem to contribute to a wide use of microsimulation models (compared with Markov-based cohort models) in the field of diabetes. However, the rationale for model selection was often not cited in the various model publications identified in this review, and estimates of CKD progression in diabetes models with CKD components still rely heavily on a limited number of older datasets that may not fully capture contemporary patient care. Even though (at least) a similar level of patient and disease heterogeneity exists in the field of CKD, a Markov design was relatively common for simulating CKD progression. This may be driven by the limited data available to characterise the true variation in CKD progression patterns, although several risk equations are currently available [162]. It could be hypothesised that the economic modelling of CKD is less well-researched than that of diabetes because of the significant advancements in the treatment of diabetes over recent years and paralleled advancements in modelling methodologies. With the expected development of new CKD treatment options, we anticipate that our understanding of the most appropriate modelling methods for CKD will improve, with this review providing a basis from which further discussion may be considered.

Conclusion

Typically, GFR is used within CKD model frameworks and albuminuria in diabetes model frameworks. The prognostic ability of GFR to predict CKD progression is well-established in patients with CKD (both with and without diabetes). This, combined with the heterogenous nature of individual patients’ GFR and albuminuria trajectories, provides rationale for a model structure designed around the prediction of individual patients’ GFR trajectories. However, most models identified by this review were cohort based and/or utilised input data at cohort mean levels, limiting the consideration of clinically relevant differences between patients’ course of disease. Frameworks of future CKD models should be informed and justified based on clinical rationale and data availability to ensure validity of model results. In addition, further clinical and observational research is warranted to provide a better understanding of prognostic factors and data sources to improve economic modelling accuracy in CKD.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Author Contributions

DS led the design and implementation of the research and the writing of the manuscript and undertook the systematic literature review. TW contributed to the design and implementation of the research, the analysis of the data and the writing of the manuscript. SR led and undertook the systematic literature review and contributed to the writing of the manuscript. PM provided senior review and technical expertise and contributed to the design of the research. HVH provided senior review, contributed to the design and implementation of the research and supported manuscript development. All named authors meet the International Committee of Medical Journal Editors (ICMJE) criteria for authorship for this manuscript, take responsibility for the integrity of the work as a whole, and have given final approval to the version to be published. As guarantor and corresponding author, DS takes full responsibility for the work as a whole and the decision to submit and publish the manuscript.

Data Availability

All data generated or analysed during this study are included in this published article and the Supplementary Material.

Compliance with Ethical Standards

Funding

Sponsorship for this work and article processing charges were funded by AstraZeneca.

Conflict of interest

DS, TW, SR and PM are employees of Health Economics and Outcomes Research Ltd. and received funding from AstraZeneca to undertake the research outlined in this study. HVH is an employee of AstraZeneca.