Finding the sweet spot: What levels of larval mortality lead to compensation or overcompensation in adult production?

Abstract

Extrinsic mortality impinging on negatively density-dependent populations can result in no change in the number of survivors (compensation) or an increase (overcompensation) by releasing the population from density-dependent effects on survivorship. The relationship between the level of extrinsic mortality (i.e., percentage of mortality) and the level and likelihood of overcompensation is theoretically important, but rarely investigated. We tested the hypothesis that overcompensation occurs below a threshold value of extrinsic mortality that is related to density-dependent mortality rate, and that additive extrinsic mortality occurs above this threshold. This hypothesis predicts that survivorship vs. extrinsic mortality will: 1) be best described by a two-segmented model with a threshold; 2) have a slope >0 below the threshold; and 3) have a slope=−1 above the threshold. We also tested whether mortality imposed by real predators and random harvest have equivalent effects on adult production, and whether magnitude of overcompensation is related to species sensitivity to density-dependence. These hypotheses were tested in the container mosquitoes Aedes aegypti, A. albopictus, A. triseriatus, and Culex pipiens (Diptera: Culicidae). Cohorts of 150 larvae were exposed to random harvest of 0–70% two days after hatch or to predation by 1–3 Mesocyclops longisetus (Crustacea: Copepoda). Overcompensation occurred in A. aegypti in a pattern consistent with predictions. Aedes triseriatus showed strong overcompensation but no evidence of a threshold, whereas A. albopictus and C. pipiens had survival consistent with compensatory mortality but no evidence of a threshold. Compared to random harvest, mortality from predation yielded greater adult production in A. aegypti and A. albopictus, lesser adult production in C. pipiens, and no difference in adult production in A. triseriatus. Our results are largely consistent with our hypothesis about overcompensation, with the caveat that thresholds for additive mortality appear to occur at very high levels of extrinsic mortality. Magnitudes of overcompensation for the three Aedes were inversely related to survival in the 0% mortality treatment, consistent with our hypothesis that overcompensation is related to sensitivity to density-dependence. A broad range of extrinsic mortality levels can yield overcompensation, which may have practical implications for attempts to control pest populations.

Introduction

Population responses to extrinsic sources of mortality, such as harvesting and predation, have traditionally been assumed to result in a net reduction in population size. Extrinsic mortality, it would be reasoned, interacts additively with intrinsic mortality sources such as intraspecific resource competition. Under certain circumstances, however, extrinsic mortality may produce less intuitive results. Populations regulated by negative density-dependent effects are constrained by intrinsic mortality or reductions in reproduction rates as population sizes approach and exceed the carrying capacity of their habitats (Sibly et al. 2005). Extrinsic mortality affecting such populations can result in the production of the same (compensation; Fig. 1B), or a greater (overcompensation; Fig. 1A, D), number of surviving individuals in subsequent life-stages as would occur without the extrinsic mortality (De Roos et al. 2007, Zipkin et al. 2008, Sandercock et al. 2011). Compensation / overcompensation may occur when extrinsic mortality kills individuals that would have otherwise died of intrinsic mortality sources. If removal of these individuals leads to greater per capita resource levels for the surviving population, overcompensation may occur. Under some circumstances, overcompensation can result in the “Hydra effect” (Abrams and Matsuda 2005, Abrams 2009), wherein extrinsic mortality results in an increase in a population’s equilibrium size.

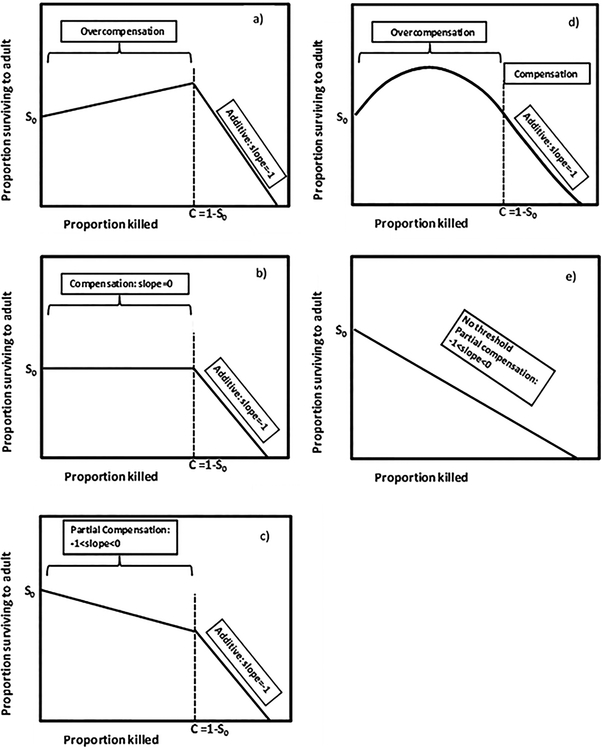
Figure 1.

Postulated relationships of proportion surviving to adulthood vs. proportion killed by extrinsic mortality as described by Sandercock et al. (2011). Panels A, B, C illustrate two-segmented models with linear change in proportion surviving below the threshold mortality C at which mortality becomes additive. In Sandercock et al.’s (2011) formulation, and in panels A, B, and C, the value of C = 1-S₀, where S₀= proportion surviving when extrinsic mortality = 0. Panel D illustrates a two-segmented model with a quadratic relationship of proportion surviving vs. proportion killed, with C = 1-S₀. Panel E illustrates an unsegmented model with no threshold C.

Overcompensation leading to the hydra effect was first postulated in Ricker (1954), whose fishery-based models yielded population density increases in response to extrinsic mortality of immatures. These related phenomena have been the subject of multiple theoretical studies to determine the conditions under which the may occur (reviewed by Abrams 2009 and Schröder et al. 2014). The timing of extrinsic mortality relative to density-dependent mortality is predicted to be a key factor in determining whether overcompensation and increases in population density will occur (Jonzen and Lundberg 1999, Ratikainen et al. 2008, Abrams 2009, Zipkin et al. 2009, Hilker and Liz 2013, McIntire and Juliano 2018). Mortality occurring before the onset of density-dependence is predicted to lead to overcompensation (Jonzen and Lundberg 1999, Abrams 2009), and this prediction has been supported in controlled laboratory experiments (McIntire and Juliano 2018). Life history traits can further influence the occurrence of overcompensation (De Roos et al. 2007, Zipkin et al. 2009, Karatayev and Kraft 2015). Population regulation by maturation versus reproduction determines whether overcompensation can occur in the juvenile and adult stage (De Roos et al. 2007), and high reproduction rates and static maturation rates are postulated to increase the chances of overcompensation in adults (Zipkin et al. 2009, Karatayev and Kraft 2015).

Overcompensatory mortality and the hydra effect are predicted for many food web structures (Cortez and Abrams 2016). Despite multiple theoretical studies of overcompensation and the hydra effect, there are relatively few empirical examples in natural or laboratory populations. Compensatory mortality has been demonstrated in response to predation (Nannini and Juliano 1998), harvest (Weber et al. 2016), and parasitism (Washburn et al. 1991). Overcompensation has been demonstrated in response to harvest (Nicholson 1954, Cameron and Benton 2004, Zipkin et al. 2008, McIntire and Juliano 2018), parasitism (Washburn et al. 1991), and real or simulated toxin exposure (Agudelo-Silva and Spielman 1984, Moe et al. 2002). Previous studies have investigated the effects of extent of extrinsic mortality on population sizes (Slobodkin and Richman 1956, Fryxell et al. 2005), but we have found no empirical studies testing the quantitative predictions of how extent of extrinsic mortality in one life stage affects overcompensation in the production of the next stage.

The extent of extrinsic mortality impinging on a population (i.e., the percentage of the population killed), as opposed to timing of mortality, is expected to affect strongly whether compensation or overcompensation occurs (Boyce et al. 1999, Ratikainen et al. 2008, Abrams 2009, Zipkin et al. 2009). There should be a threshold above which extrinsic mortality is additive to intrinsic mortality sources (Boyce et al. 1999, Ratikainen et al. 2008, Abrams 2009) (Fig. 1). This additive response is predicted to occur when extrinsic mortality exceeds the level of density-dependent mortality (Sandercock et al. 2011). Above this threshold, extrinsic mortality removes a portion of the population that exceeds the portion that would have died due to density-dependent effects, thus lowering survivorship and potentially affecting density. Understanding the relationship between level of mortality and overcompensation is important theoretically, but also practically, for making decisions about managed populations. However, only one empirical study examines this relationship (Sandercock et al. 2011) and showed partially compensatory response to harvest, which reduced population size but at a lower magnitude than the amount harvested. While this demonstrated neither perfect compensation nor overcompensation, it demonstrates a strong relationship between level of mortality and compensation, as predicted by theory (Boyce et al. 1999, Ratikainen et al. 2008, Abrams 2009, Zipkin et al. 2009).

The strength of density-dependent effects regulating a population should affect the magnitude of increase in survivorship induced by extrinsic mortality. Stronger density-dependent effects result in greater reduction in survivorship at high densities than do weak density-dependent effects. This greater reduction yields the potential for a greater effect of the release from density dependence when extrinsic mortality occurs. By this logic, populations facing stronger density-dependence are predicted to have greater magnitude of overcompensation than similar populations facing weaker density-dependence. This predicted relationship between the strength of density-dependent effects and overcompensation is untested. Sandercock et al. (2011) presented models postulating a relationship between survivorship due solely to density-dependent effects, with no extrinsic mortality (S₀), and a threshold for extrinsic mortality (C=1-S₀), above which extrinsic mortality becomes additive (Fig. 1). The value of S₀ provides a measure of the strength of density dependent effects on survival (lower S₀ implies greater density-dependent death). The model postulates that with extrinsic mortality below the threshold, overcompensation (Fig. 1a), compensation (Fig. 1b), or partial compensation (Fig. 1c) may occur, or survivorship may have a nonlinear, concave downward relationship to proportion killed by extrinsic mortality (Fig. 1d). The threshold may also be absent (Fig. 1e). This flexible model can be tested by fitting a segmented regression model (Motulsky and Arthur 2004) to data on survivorship vs. proportion extrinsic mortality, and testing whether a threshold (C) exists, whether the threshold C=1-S₀, whether the slope is greater than 0 (overcompensation), not different from 0 (compensation), between 0 and −1 (partial compensation), or not different from −1 (additivity). A quadratic, rather than a linear, model provides a simple test for the nonlinearity (Fig. 1d).

The purpose of this study is to test the effects of multiple levels of extrinsic mortality of larvae on overcompensation of adult production. We tested this in four container mosquitoes (Diptera: Culicidae): Aedes aegypti, A. albopictus, A. triseriatus, and Culex pipiens. These species are suited for studies of overcompensation because they experience strong negative-density dependence in their aquatic larval stages (Dye 1984, Léonard and Juliano 1995, Lord 1998, Alto et al. 2012). There is evidence for (Maciá and Bradshaw 2000, McIntire and Juliano 2018) and against (Ower and Juliano 2019) overcompensation in container mosquitoes. None of the cited studies have tested the model of Sandercock et al. (2011) by testing for the predicted relationships between extrinsic mortality level and adult production embodied in Fig. 1.

To compare responses to controlled random removal and natural mortality sources, we included in our experiment random harvest of larvae and predation on larvae by Mesocyclops longisetus (Crustacea: Copepoda) as sources of extrinsic mortality. Mesocyclops longisetus occurs from South America to the southern United States (Gutiérrez-Aguirre and Suárez-Morales 2001). Their range partially overlaps the ranges of each of the four mosquito species tested here, and M. longisetus are commonly found in the water-filled containers with larval mosquitoes (Gutiérrez-Aguirre and Suárez-Morales 2001, Marten and Reid 2007). They are voracious, size-selective predators of early instar mosquito larvae (Soumare et al. 2004), and individuals can kill up to 38 larvae per day (Marten et al. 1994). Mesocyclops species prey preferentially on Aedes over Culex larvae (Marten et al. 1994, Soumare et al. 2004), but feeding preferences for the three Aedes species are unknown. Past empirical studies on overcompensation in mosquitoes have used random harvesting (McIntire and Juliano 2018) or predation (Nannini and Juliano 1998) as sources of mortality, but none have compared the two. Differences in the effects of the two mortality sources (e.g., selectivity of mortality by predators, biomass remaining as partially consumed victims, or anti-predator behavior modifications in prey) may result in differences among these species in likelihoods or levels of overcompensation.

Based on past theoretical predictions (Boyce et al. 1999, Ratikainen et al. 2008, Abrams 2009, Zipkin et al. 2009) and the work of Sandercock et al. (2011), we hypothesize that: overcompensation occurs below a threshold value C of extrinsic mortality; the threshold C=1-S₀; and additive mortality occurs above this threshold. If this hypothesis is correct, we predict that data on survivorship vs. extrinsic mortality level will: 1) be better described by a two-segmented model with threshold C=1-S₀ (Fig. 1a–d), rather than an unsegmented model lacking a threshold (Fig. 1e); 2) have a slope significantly >0 for at least part of the range of extrinsic mortality (Fig. 1a, d); 3) have a slope for extrinsic mortality above the threshold C that is not significantly different from −1 (Fig. 1a–d). We further postulate that if mortality imposed by real predators and random harvest are equally unselective with respect to prey traits, they will yield similar levels of overcompensation in adult production for similar levels of mortality; alternatively, if real predators selectively remove individuals with a greater or lesser chance of dying due to density-dependent intrinsic mortality, or if real predators have non-consumptive effects, such as inducing reduced foraging (Abrams 2009, McIntire and Juliano 2018), then we expect the two mortality sources to yield different levels of overcompensation.

In comparing the species, we postulate that differential competitive abilities and responses to larval density will be associated with likelihood and levels of overcompensatory mortality in response to the same level of extrinsic mortality. Overcompensation requires the release of a population from density-dependent effects, so that populations under stronger density-dependent regulation should exhibit greater levels of overcompensation. Resource competition appears to be strong in larvae of container mosquitoes (reviewed by Juliano 2009, 2010), and general theory (Chase and Leibold 2003) and experiments with these mosquitoes (Murrell and Juliano 2012) indicate that ability to maintain survival and population growth at low per capita resource levels is the main determinant of competitive ability. Based on the competitive abilities of the four species in this experiment (reviewed by Juliano 2009, 2010; Reiskind and Lounibos 2009, Murrell and Juliano 2012, O’Neal and Juliano 2013), we predict levels of overcompensation in the four species will be, from greatest to least, C. pipiens, A. triseriatus, A. aegypti, and A. albopictus, as this series coincides with their increasing competitive abilities.

Methods

Mosquitoes and M. longisetus used in this study were from laboratory colonies at Illinois State University, Normal, IL (See Appendix Methods for colony origins and rearing protocols). Four days prior to the beginning of the experiment, 500 ml plastic containers were filled with 400 ml ultrapure water, 1g dried live oak leaves (Quercus viriginiana) collected from Vero Beach, FL, 0.05 g dried decorated crickets (Gryllodes sigillatus), and 100 μl microbial inoculum collected from a rain-filled bucket in Merwin Nature Preserve, Lexington, IL. Lids were placed on the containers with holes for ventilation. Containers were housed in an environmental chamber at 25°C until the beginning of the experiment to allow the establishment of a microbial community to serve as food resources for mosquito larvae.

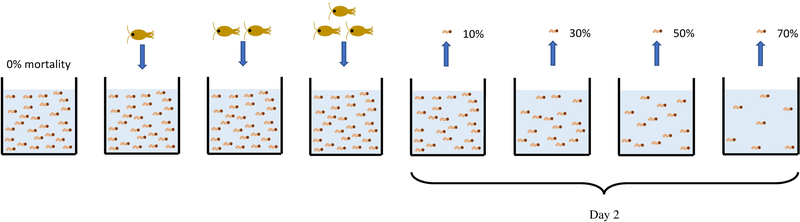
Containers (n=201) were randomly assigned a species and mortality treatment. Mortality treatments consisted of either a percentage of the cohort (0, 10, 30, 50, or 70%) to be removed at random on day 2, or the addition of 1, 2, or 3 female M. longisetus (Appendix S1 Fig. S1). On day 0 of the experiment, 150 mosquito hatchlings (Appendix Methods for hatching procedures) of one species were added to appropriate containers, and M. longisetus were added to predator treatment containers. This initial density of mosquito larvae was chosen based on preliminary trials testing different resource amounts and densities and is consistent with high field densities reported for our study species (e.g., Juliano et al. 2004, Johnson and Sukhdeo 2013, Camara et al. 2016). Containers were returned to the environmental chamber, which maintained a 14:10 light:dark photoperiod. Random mortality treatments were applied on day 2, which is the time most likely to induce overcompensation in experimental populations of container mosquitoes (McIntire and Juliano 2018).

On days 16 and 30, 0.5g dried live oak leaves and 0.025g dried decorated crickets were added to each Aedes container, and on days 9, 16, 23, and 30, the same amounts were added to the C. pipiens containers. More frequent resource additions were used for C. pipiens because initial trials using the same feeding schedule as the Aedes containers failed to produce adults in all C. pipiens treatments. Containers were checked daily for pupae, which were removed and placed in 0.92 ml vials with cotton stoppers. Pupae were stored in the environmental chamber and checked daily for emergence, and the date of emergence for each individual was recorded. All individuals reaching adulthood were counted as survivors. Temporal blocks ended when no larvae remained, with a maximum duration of 84 days.

Statistical analyses

This experiment was conducted in incomplete temporal blocks (n=8) over a period of 9 months. Blocks were incomplete due to egg availability. A single quantitative mortality variable (hereafter “mortality”) was created to enable comparison of random extrinsic mortality and predator-induced extrinsic mortality. This mortality variable was the percent of individuals removed on day 2 for random mortality treatments and the percent mortality by predation through day 2 for predator treatments. Because Aedes and Culex species were given different food treatments, they were analyzed separately.

We analyzed these data in two ways. First, number of survivors per container was analyzed using a generalized linear mixed model (PROC GLIMMIX, SAS 9.4) to fit a descriptive polynomial to the data, and to test for differences due to predator treatment and mosquito species. Models including predator presence/absence, species (Aedes analysis only), mortality, mortality², mortality³, and all two-way interactions as fixed effects, and block included as a random effect, were evaluated. Higher-order polynomial terms were not tested in models without lower-order terms. To account for over-dispersion, a negative binomial error distribution was used. Because the species*mortality interaction was significant in the Aedes analysis (see Results), separate regressions were run to determine the best model for each species. Corrected Akaike’s information criteria (AICc; Sugiura 1978) were compared to determine the best model, and the model with the lowest evidence ratio was used to generate predictions in the case of A. aegypti, A. triseriatus, and C. pipiens. The two best A. albopictus models had similar AICcs (Appendix S1: Table S1), so excluding the second-best model would discard valuable information. The best model contained the predator effect alone, whereas the second-best model contained predator and a cubic relationship to mortality. Since the third and fourth best models contained the linear and quadratic relationships to mortality, respectively, and the evidence ratio for the fourth model was relatively low (E=2.044), these four models were averaged (Anderson 2008) to predict numbers of survivors and standard errors, which were weighted by their respective model weights (w_i) when all unselected models were excluded (Appendix Table S2). These four models had a combined weight of w_i=0.7037 relative to all possible models (Appendix SI Table S1, sum of w_i from top 4 models).

A second analysis was designed to test for overcompensation, compensation, or additivity by testing hypotheses about the slopes of the relationship, to test for the presence of the threshold C, and whether C=1-S₀, where S₀ is the intercept on the vertical axis (Fig. 1). For this purpose, we modeled the relationship of proportion surviving to adulthood vs. proportion morality on day 2 using PROC NLMIXED in SAS 9.4 and compared five different models for each species: two-segmented models with linear relationships above and below the threshold (Fig. 1a–c); two-segmented models with a quadratic relationship below, and a linear relationship above the threshold (Fig. 1d); and one-segmented linear relationships (i.e., no threshold; Fig. 1e). For two-segmented models with a threshold, we tested models with the threshold constrained to be C=1-S₀, and models where the threshold was unconstrained and estimated as a parameter of the regression model. All models included the effect of predator presence/absence and the random block effect. We also tested segmented threshold models postulating negative binomial, log normal, and Poisson error, and in all cases, they were poorer descriptions of the data than models postulating normally distributed error, which are the models we report. We used AICc to determine which model best described the data, and hypothesis tests on parameters to test for overcompensation (slope>0) and partial compensation (0>slope>−1). Slopes not significantly different from 0, or not significantly different from −1, were interpreted as being consistent with compensation or additivity, respectively. For unconstrained models, we tested whether C differed significantly from 1-S₀.

We analyzed post-treatment intrinsic mortality for each species using generalized linear mixed models in the events/trials mode with a binomial distribution of error and a logit link function (PROC GLIMMIX, SAS 9.4). Treatment was a fixed effect and block a random effect. For each replicate, trials were the number of larvae on day 2 after extrinsic mortality treatments, and events were the number dying after day 2 (=larvae on day 2 – adults produced). Least squares means were compared using Tukey’s method.

Results

Polynomial models

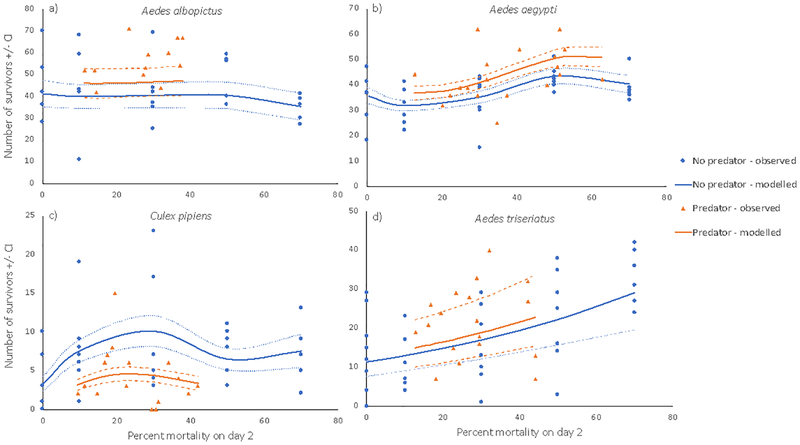
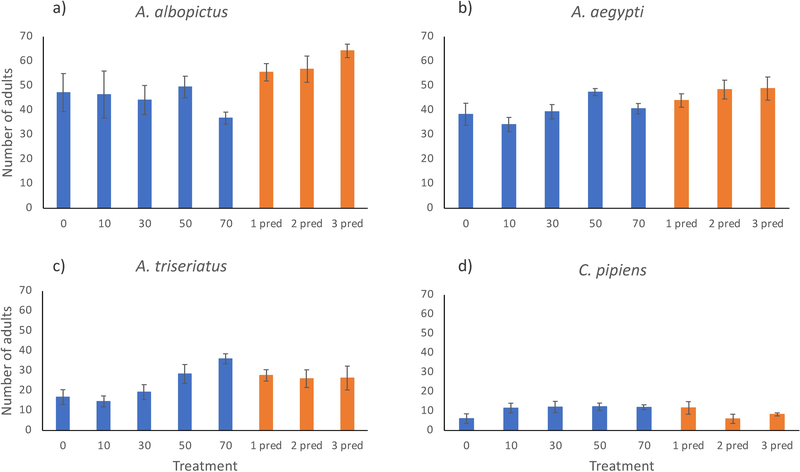
The mean number of adults produced with no extrinsic mortality for C. pipiens, A. triseriatus, A. aegypti, and A. albopictus were 6, 17, 38, and 47, respectively (Appendix S1 Fig. S2). The mortality*species interaction was significant in the analysis of the three Aedes species (F_2,132 = 15.55, p<0.0001). Therefore, we report here the results from the single-species analyses. The model average prediction for A. albopictus incorporated predictions from the predator-only (w_i=0.3376), predator + a cubic relationship to mortality (w_i=0.3054), predator + linear effect of mortality (w_i=0.1919), and predator + a quadratic relationship to mortality (w_i=0.1651) models (Appendix S1 Table S1). This model-averaged prediction showed no change in number surviving to adulthood with added mortality (compensation) over the range of 0 to 50% mortality, and an apparent decrease in survival to adulthood at 70% mortality (Appendix S1 Table S1, Fig. 2a). Mortality by predation resulted in significantly more surviving adults compared to that for a similar level of random mortality, with predator treatments yielding 3.74–7.19 more survivors depending on the model (Appendix S1 Table S2).

Figure 2.

Observed and predicted numbers of surviving Aedes albopictus (a), A. aegypti (b), Culex pipiens (c), and A. triseriatus (d) reaching adulthood after exposure to a range of mortality treatments on or by day 2, based on polynomial regressions. Random mortality was applied to no-predator treatments (circles) by randomly removing 0, 10, 30, 50, or 70% of the initial cohort size (150) on day 2. Predator treatments (triangles) received 1, 2, or 3 female M. longisetus at the start of the experiment, and the percent mortality by day 2 was determined by counting the number of surviving mosquito larvae. Predicted curves for the no-predator (blue) and predator (orange) treatments plot the polynomial function produced by generalized linear mixed models. Dashed lines show 95% confidence intervals. Predicted values were calculated using the models with the lowest AICc’s for A. aegypti, A. triseriatus, and C. pipiens and using model weights to average the four models with the lowest AICc’s for A. albopictus. The effect of predator was significant for all species except A. triseriatus.

The A. aegypti and C. pipiens data were each best described by the models containing predator and a cubic relationship to mortality (Appendix S1 Tables S3 and S4), whereas the A. triseriatus data were best described by a model containing only the linear effect of mortality (Appendix S1 Table S5). The effect of predator was significantly positive for A. aegypti with an estimate of 5.80 more adults produced in predator treatments, and negative for C. pipiens with an estimate of 1.88 fewer adults produced in predator treatments, compared in both cases to adult production with a similar level of random mortality (Appendix S1 Table S6, Fig. 2b, c). The polynomial for Aedes aegypti indicates overcompensation at 50% mortality compared to 0% mortality (Fig. 2b). Aedes triseriatus clearly showed overcompensation across all mortality levels, with a linear increase in survivors with greater random or predator-induced mortality (Appendix S1 Table S6, Fig. 2d). The polynomial for Culex pipiens showed an apparent overcompensatory response at all levels of random mortality, with the greatest number of survivors produced in the 30% mortality level (Appendix S1 Table S6, Fig. 2c). Predator-induced mortality did not suggest overcompensation (Fig. 2c).

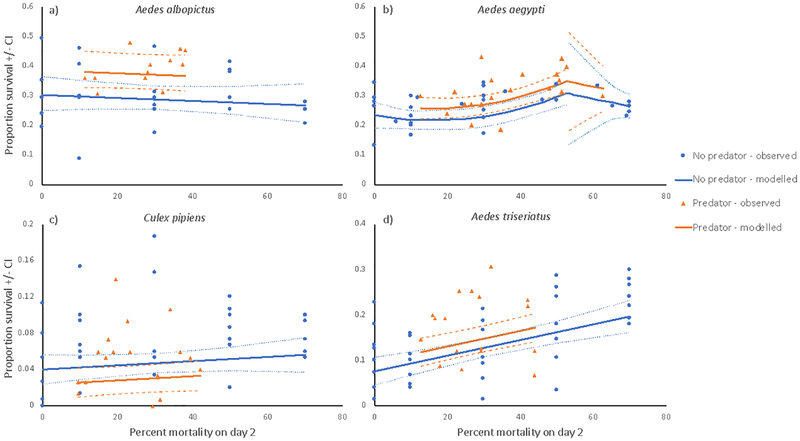
Segmented models

One-segmented linear models without the threshold were the best models for A. albopictus, A. triseriatus, and C. pipiens (Table 1, Fig. 3, Appendix S1 Table S7). The quadratic two-segmented threshold model with C estimated from the data was best for A. aegypti (Appendix S1 Table S7), and C was significantly different from the predicted 1-S₀ (Table 1; t=2.05, df=48, P=0.0475). The curvilinear trend for A. aegypti below the threshold was clearly positive (Fig. 3) and dominated by a significant positive quadratic term (b_3, Table 1), indicating significant overcompensation. In all three species where the one-segmented model was best, the second-best model was the linear two-segmented model with the threshold C constrained to C=1-S₀ (Appendix S1 Table S7). Slopes of the regression (b₁) were positive for A. triseriatus and C. pipiens, and significantly greater than 0 for A. triseriatus (Table 1, Fig. 3), indicating significant overcompensation. The slopes for A. albopictus and C. pipiens were not significantly different from 0, and thus consistent with compensation (Table 1, Fig. 3). For A. albopictus, A. triseriatus, and C. pipiens the one-segmented model slopes were always significantly greater than −1 (Table 1), so mortality was never additive. For A. aegypti the slope above the estimated threshold C (b₂) was negative and not significantly different from −1 (Table 1), and thus consistent with additive mortality above the threshold C. Predator effects were positive and significant (A. albopictus and A. aegypti, Table 1) or not significant (A. triseriatus, P=0.2530) for all Aedes and negative and nearly significant (P=0.0775) for C. pipiens (Table 1).

Table 1.

Parameter estimates for the segmented generalized linear mixed models

Species	Best model	S0 (SE)	b1 (SE)	b2 (SE)	b3 (SE)	C (SE)	Predator effect (SE)	H0: b1 or b2 = −1
Aeg	2 segments, quadratic; C is free;	0.2349 (0.0219) ***	−0.9451 (0.6413)	−0.5742 (0.7153)	2.9577 (1.0662) **	0.5267 (0.1146) ***	0.0406 (0.0154) *	b2 NS
Albo	1 segment	0.3030 (0.0216) ***	−0.1657 (0.1966)				0.0834 (0.0292) **	b1 ***
Tris	1 segment	0.0761 (0.0155) ***	2.2680 (0.9013) *				0.0202 (0.0175)	b1 ***
Culex	1 segment	0.0401 (0.0081) ***	0.5758 (0.5961)				−0.0166 (0.0092)	b1 *

Note: Best models based on AICc (Table S7) for proportion surviving (S_A) vs. proportion killed by day 2 (K), with parameter estimates. S₀=proportion surviving with K=0; C=threshold where slope changes for segmented models with C is estimated from the data or C=1-S₀ in constrained models; b₁=linear effect below the threshold C; b₂=linear effect above the threshold C (absent in unsegmented models); b₃=quadratic effect below the threshold C; Predator effect = Additive effect of real predation vs. random removals, modeled as independent of values of K (i.e., no predator*K interaction). All models include an additive random effect of experimental block. The last column tests the null hypothesis of additive mortality (Slope=−1) for either b₁ or b₂.

^*P<0.05,

^**P<0.01,

^***P<0.001

^†Aedes aegypti;

^‡Aedes albopictus;

^§Aedes triseriatus;

^¶Culex pipiens

Figure 3.

Observed and predicted proportion surviving to adulthood for Aedes albopictus (a), A. aegypti (b), Culex pipiens (c), and A. triseriatus (d) after exposure to a range of mortality treatments on or by day 2, based on segmented nonlinear regressions to test the threshold model (Sandercock et al. 2011). Treatments described in Fig. 2. Predicted curves for the no-predator (blue) and predator (orange) treatments plot the best segmented model based on nonlinear regression. Dashed lines show 95% confidence intervals. Predicted values were calculated using the models with the lowest AICc’s for each species.

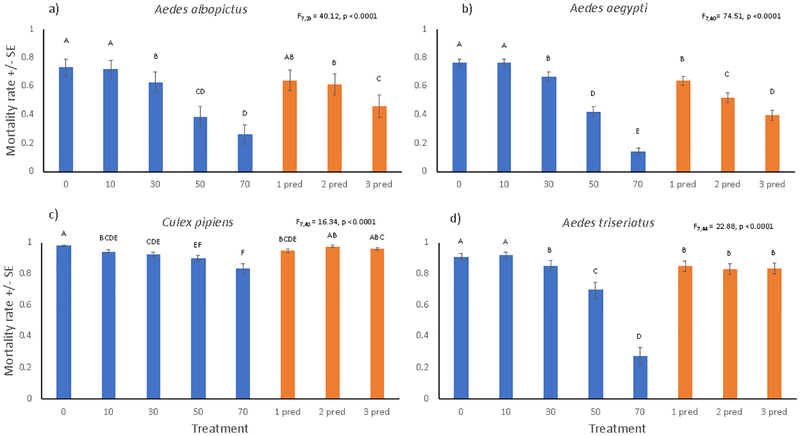
Post-treatment intrinsic mortality decreased significantly with increasing extrinsic mortality for all species (Fig. 4). Thus, survivors of extrinsic mortality gained a significant survival benefit via release from density-dependent mortality, particularly with greater extrinsic mortality. Post-day-2 mortality yielded detectable pairwise differences among predator treatments only for A. albopictus and A. aegypti (Fig. 4).

Figure 4.

Least squares mean (±SE) cumulative post-treatment mortality rates from day 2 until the last larva pupated or died (1- [number of adults produced/ number of larvae on day 2]). Within each panel, the F statistic tests the null hypothesis of no treatment effect, and least squares means associated with the same letter are not significantly different based on Tukey’s test.

Discussion

Our polynomial vs. segmented analyses served different purposes. The segmented models are ideally suited for testing for overcompensation, compensation, or additivity in a clear and objective way, and for determining if the threshold for additive mortality exists. The continuous curves produced by polynomials cannot provide clear answers to these questions. In contrast the polynomials provide the best test for differences among Aedes species in the relationships of survivors to extrinsic mortality (via the test for interactions of mortality with species) and provide the most powerful tests for effects of random vs. predator-induced mortality on survivorship. We will discuss the implications of each of these analyses.

Overcompensation, compensation, additivity, and thresholds

The low numbers of adults produced in the 0% mortality treatments demonstrate that the densities and resource levels used in this experiment were sufficient to induce strong negative-density dependence. Statistically significant overcompensation of adult production was present in A. aegypti (up to 50% mortality) and A. triseriatus (up to 70% mortality). Production of adults by A. albopictus and C. pipiens was consistent with compensatory mortality, though caution is needed in this interpretation because it is based on the regression slopes being not significantly different from 0. It remains striking that for these two species, killing as many as 70% of the larvae on day 2 yields no detectable reduction in adult production. Our three predictions based on Sandercock et al. (2011) were clearly supported strongly for A. aegypti with a significant positive slope, and a slope beyond the threshold not different from −1, indicating additive mortality. The threshold at which the slope changes was, however, significantly different from the predicted 1-S₀. Results for A. triseriatus are also consistent with this model, because of the significantly positive slope and the threshold of 1-S₀ predicted to occur at an extrinsic mortality rate greater than any we used (1-S₀ is estimated to be 1−0.094=0.906; see Table 1). For C. pipiens, the predictions are not supported, but neither can they be refuted as the slope is positive, but not significant (Table 1), and the predicted mortality threshold of 1-S₀ would again fall at a value greater than any we implemented (1-S₀=0.940). For A. albopictus we found no evidence of overcompensation, and our hypothesis is not supported, because we failed to find any evidence of a threshold. The most striking finding about A. albopictus is the consistency of numbers of adults produced across a wide range of extrinsic mortality rates. All these Aedes show considerable plasticity of adult size in response to differences in per capita food (e.g., Wormington and Juliano 2014), and that plasticity may contribute to the stability of adult production despite major changes in density. This raises an interesting question for future research: Does that plasticity of adult size contribute to biomass overcompensation in response to extrinsic mortality (De Roos et al. 2007)?

Mortality by predation versus random harvest

Based on the polynomial models it is clear that these Aedes differed in their responses to extrinsic mortality. Further, mortality by predation led to significantly greater adult production than did random mortality in A. aegypti and A. albopictus. Random mortality in this experiment was imposed by randomly removing individuals from the containers, resulting in the complete loss of biomass represented by the harvested individuals. In contrast, predation by M. longisetus releases feces and unconsumed body parts to the system, potentially enhancing resources for the microorganisms on which surviving mosquitoes feed, which may contribute to the greater numbers of adults produced in predator treatments. Furthermore, the selectivity of the random and predator-induced mortalities likely influenced the difference in adult production. Individuals were selected at random for removal in harvest treatments, whereas predators are likely selective for prey traits. We expect M. longisetus would preferentially kill smaller, slowly-developing individuals, or any individuals debilitated by crowding. If this selective removal of less robust larvae occurred with real predation, it may have resulted in higher-quality survivors than did our random removal treatments, with correspondingly greater likelihood of survival to adulthood. For A. triseriatus, predator present/absent had no significant effect, though the trend was for greater adult survivorship with predators vs. random mortality (Fig. 2, 3).

In contrast to A. aegypti and A. albopictus, fewer C. pipiens adults were produced when exposed to predation than to random mortality. Culex are thought to be less vulnerable than Aedes to predation by copepods (Marten and Reid 2007), and if copepod predation in this experiment was less for C. pipiens than for the Aedes, the result may be a lesser overcompensatory effect on survivorship of C. pipiens to adulthood (Abrams 2009, McIntire and Juliano 2018). We analyzed day 2 survivorship for the predator treatments and the no-predator replicates (prior to manipulation) and found a significant interaction of species and predator number, but the important difference was that A. aegypti was significantly more vulnerable to predation by 3 copepods than all other species (data not shown). Thus, we find no evidence that C. pipiens is less vulnerable to copepod predation than Aedes in general. The reason for the opposite responses to predation vs. random removals among these genera remain unexplained.

Our analyses of post-treatment mortality rates (Fig. 4) show the benefits of extrinsic mortality that accrue to the survivors. A wide range of intensities of extrinsic mortality (30–70%) result in detectable decreases in post-treatment mortality of survivors for all three of the Aedes.

Competitive ability and overcompensation

We also predicted that competitive ability of these species would be related to both the level of overcompensation and survival in the absence of extrinsic morality (S₀). In natural settings and in laboratory microcosms, A. albopictus is the best competitor, followed by A. aegypti, A. triseriatus, and C. pipiens (reveiwed by Juliano 2009, 2010; Reiskind and Lounibos 2009, Murrell and Juliano 2012, O’Neal and Juliano 2013), and competitive abilities are often determined by a species’ ability to persist at low per capita resource levels (Chase and Leibold 2003, Murrell and Juliano 2012). In our experiment, per capita resource availability was lowest with 0% mortality, so that S₀ provides a measure of ability to compete for resources. Estimated S₀ for the four species were in the order we predicted: C. pipiens<A. triseriatus<A. aegypti<A. albopictus (Table 1), which suggests that density dependent effects are greatest for C. pipiens and least for A. albopictus. We thus predicted overcompensatory responses to be greatest for C. pipiens, followed by A. triseriatus, then A. aegypti, and least for A. albopictus. One way to quantify the magnitude of the overcompensatory response is by the slopes of the segmented linear regressions below the threshold (i.e., b₁ in Table 1). Larger positive slopes indicate greater overcompensation, whereas slopes<0 indicate partial to no overcompensation. This comparison is complicated by the nonlinearity found in the best model for A. aegypti (Table 1) so that the slope is not constant. The results in Table 1 are partly consistent with this prediction, with the notable exception of C. pipiens. The steepest slope is for A. triseriatus and is significantly greater than 0 (Table 1). For A. aegypti, we will use for comparison the linear slope from the second-best model, which is 0.4974±0.1910 (Slope±SE) and also significantly greater than 0 (P=0.0122; Appendix S1 Table S7). The slope for A. albopictus is slightly negative but not significantly different from 0 (Table 1). Thus, the three Aedes species fall in the order predicted by competitive ability and S_0. Slope for C. pipiens is positive and somewhat greater than that for A. aegypti. However, it is not significantly different from 0 (Table 1), so it clearly does not fit our prediction. Lack of overcompensation in Culex is consistent with a field study of its congener, C. restuans (Ower and Juliano 2019). Because resource availability was greater for C. pipiens than for the Aedes, its response may not be comparable to those of the Aedes. Culex pipiens did not survive well under any of our experimental conditions, perhaps because this species is adapted to water with very high nutrient levels. Thus, our prediction about competitive ability and overcompensation is supported only for the three Aedes in the experiment.

Lack of overcompensation by A. albopictus is somewhat surprising, as an experiment on effects of mortality timing on overcompensation with A. albopictus (McIntire and Juliano 2018) with the same resource levels, but initial cohorts of 250 larvae exposed to 48% random mortality at day 2 yielded a strong overcompensation response. The greater cohort size with the same initial quantity of resources that we used with smaller cohorts in the present study indicates greater density-dependent effects in early in their experiment, which would be expected to yield greater overcompensation with similar mortality. A second experiment by McIntire and Juliano (2018) found compensation in A. triseriatus in response to extrinsic mortality, which contrasts with the overcompensation observed for A. triseriatus in the present study. These two experiments on A. triseriatus used similar initial per capita amounts of detritus, so that further experiments are needed to understand why overcompensation responses vary within a species.

The shift to additive mortality above the threshold in A. aegypti is consistent with predictions of theory (Boyce et al. 1999, Ratikainen et al. 2008, Abrams 2009, Zipkin et al. 2009, Sandercock et al. 2011). The absence of this result in our A. triseriatus and C. pipiens suggests that extrinsic mortality levels in this study were not sufficiently high to exceed the threshold to induce additive mortality. For A. albopictus, our results are inconsistent with predictions, as our best model did not include a threshold (Appendix S1 Table S7). However, the second-best model for A. albopictus had an Akaike weight only slightly worst than the best model (Table S7), and it included a threshold constrained to be equal to 1-S₀ (Table S7). For all three of the species for which the one-segment model with no threshold was best, the second-best model was the two-segment model with C=1-S₀ (Table S7). Thus, our results may well be consistent with the predictions from Sandercock et al. (2011). The high level of density-dependent mortality observed in mosquitoes in the absence of extrinsic mortality suggests that further experiments need to use experimental levels of extrinsic mortality that are very high (e.g., 90%).

Practical implications

Quantitative relationships of overcompensation to extrinsic mortality are critical for effectively managing pest populations (Zipkin et al. 2009). Interventions aimed at control of density-dependent populations can lead to counter-productive results (Agudelo-Silva and Spielman 1984, Buckley et al. 2001, Pardini et al. 2009). The four mosquito species used in this study are targets of control efforts because of their importance as vectors of viruses (Eldridge et al. 2000). Our results demonstrate the potential importance of control strategies that minimize the risk of imposing mortality levels that are offset by a release from density-dependence. To avoid inducing overcompensation, control strategies must result in sufficiently high levels of mortality to surpass the threshold for additive mortality demonstrated by the target population. We believe that species- and site-specific field studies are needed to determine what this threshold is for natural populations.

Mesocyclops longisetus has been successfully used as a biocontrol agent of several mosquito species, including the three Aedes species tested in this study (Marten et al. 1994, Soumare and Cilek 2011). Our results suggest the success of M. longisetus at reducing mosquito populations is not only dependent on predation rate of individuals, but also on copepod numerical response, which was necessarily absent in our short-term experiment. Introductions of M. longisetus for mosquito control must use large numbers of copepods and growth of a large copepod population is needed to avoid overcompensation in mosquito adult production (Soumare and Cilek 2011).

For mosquitoes that are vectors, the interaction of density dependence and extrinsic mortality may affect mosquito population vectorial capacity in ways that go beyond changing number of adults (Bara et al. 2015). Larval density reduction can increase adult size and longevity, which increases vectorial capacity (Reiskind and Lounibos 2009), and decrease vector competence, which decreases vectorial capacity (Alto et al. 2008). Thus, density reductions of larvae via extrinsic mortality may thus have complex and potentially counterproductive effects on vector borne disease.

First Appendix

Methods

Laboratory Colony Rearing

The Culicidae used in this study were from laboratory colonies at Illinois State University, Normal, IL, that were initiated with field-collected larvae and pupae from: New Orleans, LA (A. aegypti); Tyson Research Center in Eureka, MO (A. triseriatus); Harrisburg, PA (A. albopictus); and Normal, IL (C. pipiens). The colonies had been maintained in the lab for approximately 3 years (A. aegypti), 2.5 years (A. albopictus), and 1 year (A. triseriatus and C. pipiens). Adults were provided blood meals from anesthetized guinea pigs (Cavia porcellus) and mice (Mus musculus; Illinois State University IACUC# 842043). Eggs from the three Aedes species were deposited on seed germination paper and allowed to embryonate for at least two weeks. Culex pipiens eggs were deposited in a timothy hay (Phleum pratenase)/oak leaf (Quercus virginiana) infusion.

Mesocyclops longisetus used in this study were taken from a laboratory colony maintained at Illinois State University in Normal, IL, which originated from a colony maintained at the Florida Medical Entomology Laboratory (FMEL) in Vero Beach, FL. The colony was housed at room temperature in 2-quart plastic storage containers and provided Paramecium caudatum approximately bi-monthly as food resources.

Experimental Setup

Eggs from the three Aedes species were hatched by placing strips of egg papers in vials containing 0.4 g/l Difco™ nutrient broth (Becton, Dickinson and Company, Sparks, MD) mixed with ultrapure water and stored for 24 hours at 25°C. Culex pipiens eggs were collected on the day as oviposition and stored in ultrapure water at 25°C for 24 hours. At the start of the experiment, hatchling larvae of all species were rinsed in ultrapure water prior to counting.

For random mortality treatments, each container was emptied into an enamel pan and leaves were removed and set aside. Surviving larvae in predator containers were counted and returned to the containers with the leaves, and the percent mortality by day 2 due to predation was determined as the proportion of the initial 150 larvae that were missing or dead. Predators were difficult to detect with certainty in these containers, so they were not removed. Random mortality treatments were applied by randomly removing surviving larvae until the number of remaining individuals equaled the appropriate percentage of the original cohort size (150). After stirring the water with larvae in the pan, an array of 6 PVC pipes 4 cm long and 2.5 cm in diameter were placed in the water, trapping larvae within the pipes. A random number generator was used to select one of the numbered pipes, and larvae were removed from that section. This was repeated three times before removing the pipes, stirring the contents, and replacing the pipes. This process was repeated until the desired number of survivors remained in each container. Larvae removed were set aside for each species and added, as needed, to any random mortality container with fewer survivors than needed for its assigned mortality treatment. The average number of survivors by day 2 in random mortality treatments was 138, and all 0% mortality containers required an addition of mosquitoes to reach 150. Thus, at 2 days, we precisely controlled the numbers of larvae surviving in random mortality containers.

Figure S1.

Experimental design. Single-species cohorts of 150 hatchlings were exposed to predation or artificial mortality. For predator treatments, 1–3 M. longisetus were added to containers at the beginning of the experiment. For random mortality treatments, 10, 30, 50, 70% of the initial 150 individuals were randomly removed on day 2.

Figure S2.

Mean (±SE) number of adults produced for each mortality treatment applied to cohorts of A. aegypti (a), A. albopictus (b), A. triseriatus, (c), and C. pipiens (d). Mortality treatments consisted of either random harvest of 10, 30, 50, or 70% of the initial 150 individuals on day 2 (blue columns) or predation from 1, 2, or 3 M. longisetus (orange columns).

Table S1.

Generalized linear mixed models testing the effects of predator (pred) and polynomial effects of mortality up to the cubic term on survivorship in A. albopictus

Model Effects	AICc	ΔAICc	exp(−.5*ΔAICc)	wia	Ea	wib	Eb
Pred	308.91	0.00	1.00	0.24	1.00	0.34	1.00
Pred mortality mortality2 mortality3	309.11	0.20	0.90	0.21	1.11	0.31	1.11
Pred mortality	310.04	1.13	0.57	0.14	1.76	0.19	1.76
Pred mortality mortality2	310.34	1.43	0.49	0.12	2.04	0.17	2.04
None	310.69	1.78	0.41	0.10	2.44
Mortality	311.33	2.42	0.30	0.07	3.35
Pred mortality mortality2 mortality3 mortality*pred	312.17	3.26	0.20	0.05	5.10
Pred mortality mortality*pred	312.41	3.50	0.17	0.04	5.75
Pred mortality mortality2 pred*mortality	313.23	4.32	0.12	0.03	8.67
Pred mortality mortality2 mortality3 mortality*pred mortality2*pred	315.53	6.62	0.04	0.01	27.39
Pred mortality mortality2 mortality3 mortality*pred mortality2*pred mortality3*pred	317.10	8.19	0.02	0.00	60.04
Sum	-	-	4.21	-	-

Note: Weight of evidence (w_i) is calculated as exp(−0.5*AICc)/∑exp(−0.5*ΔAICc) and estimates the probability the model is correct. The evidence ratio (E) is calculated as w_(max)/w_i and expresses how much more likely the best model is than the given one. Higher values indicate a less likely model.

^aindicates w_i and E values when all models are included in calculations.

^bindicates w_i and E values when only the 4 models incorporated in the model average prediction are included in calculations.

Table S2.

Parameter estimates for the four models used to calculate model-averaged prediction values for A. albopictus

Model Effects	Intercept	p>0	Pred	p>0	Mortality	p>0	Mortality2	p>0	Mortality3	p>0
Pred	39.53	0.0013	7.19	0.04	-	-	-	-	-	-
Pred mort	42.19	0.0014	7.14	0.05	0.0021	0.22	-	-	-	-
Pred mort mort2	39.50	0.0019	3.74	0.29	0.0065	0.25	0.0001	0.12	-	-
Pred mort mort2 mort3	43.34	0.0021	6.26	0.11	−0.0188	0.16	0.0008	0.08	0.0000	0.04

Note: Values were produced in a generalized linear mixed model testing the effects of predator (pred) and mortality up to the cubic term on survivorship.

Table S3.

Generalized linear mixed models testing the effects of predator (pred) and mortality up to the cubic term on survivorship in A. aegypti

Model Effects	AICc	ΔAICc	exp(−.5*ΔAICc)	wi	E
Pred mortality mortality2 mortality3	377.39	0.00	1.00	0.42	1.00
Pred mortality	378.90	1.51	0.47	0.20	2.13
Pred mortality mortality*pred	379.98	2.59	0.27	0.12	3.65
Pred mortality mortality2 mortality3 mortality*pred	380.07	2.68	0.26	0.11	3.82
Pred mortality mortality2	381.46	4.07	0.13	0.05	7.65
Pred mortality mortality2 mortality3 mortality*pred mortality2*pred	382.51	5.12	0.08	0.03	12.94
Pred mortality mortality2 pred*mortality	382.65	5.26	0.07	0.03	13.87
Mortality	382.81	5.42	0.07	0.03	15.03
Pred mortality mortality2 mortality3 mortality*pred mortality2*pred mortality3*pred	384.59	7.20	0.03	0.01	36.60
Pred	391.89	14.50	0.00	0.00	1408.10
None	395.62	18.23	0.00	0.00	9090.63
Sum	-	-	2.38	-	-

Note: Weight of evidence (w_i) is calculated as exp(−0.5*AICc)/∑exp(−0.5*ΔAICc) and estimates the probability the model is correct. The evidence ratio (E) is calculated as w_(max)/w_i and expresses how much more likely the best model is than the given one. Higher values indicate a less likely model.

Table S4.

Generalized linear mixed models testing the effects of species, predator (pred), and mortality on survivorship in Culex pipiens

Model Effects	AICc	ΔAICc	exp(−.5*ΔAICc)	wi	E
Pred mortality mortality2 mortality3	294.08	0.00	1.00	0.30	1.00
Pred mortality mortality*pred mortality2 mortality3	295.68	1.60	0.45	0.13	2.23
pred mortality mortality*pred mortality2	295.85	1.77	0.41	0.12	2.42
Pred mortality mortality*pred mortality2 mortality2*pred mortality3 mortality3*pred	296.18	2.10	0.35	0.10	2.86
pred mortality	296.25	2.17	0.34	0.10	2.96
pred mortality mortality*pred mortality2 mortality2*pred	297.23	3.15	0.21	0.06	4.83
pred mortality mortality*pred mortality2 mortality2*pred mortality3	297.33	3.25	0.20	0.06	5.08
mortality	297.76	3.68	0.16	0.05	6.30
pred mortality mortality*pred mortality2 mortality2*pred mortality3	297.78	3.70	0.16	0.05	6.36
mortality mortality2 mortality3	300.83	6.75	0.03	0.01	29.22
Pred	301.64	7.56	0.02	0.01	43.82
None	303.32	9.24	0.01	0.00	101.49
Sum	-	-	3.34	-	-

Note: Weight of evidence (w_i) is calculated as exp(−0.5*AICc)/∑exp(−0.5*ΔAICc) and estimates the probability the model is correct. The evidence ratio (E) is calculated as w_(max)/w_i and expresses how much more likely the best model is than the given one. Higher values indicate a less likely model.

Table S5.

Generalized linear mixed models testing the effects of predator (pred) and mortality up to the cubic term on survivorship in A. triseriatus

Model Effects	AICc	ΔAICc	exp(−.5*ΔAICc)	wi	E
Mortality	420.61	0.00	1.00	0.54	1.00
Pred mortality	422.48	1.87	0.39	0.21	2.55
Pred mortality mortality2	424.23	3.62	0.16	0.09	6.11
Pred mortality mortality*pred	424.48	3.87	0.14	0.08	6.92
Pred mortality mortality2 pred*mortality	426.48	5.87	0.05	0.03	18.82
Pred mortality mortality2 mortality3	426.62	6.01	0.05	0.03	20.19
Pred mortality mortality2 mortality3 mortality*pred	428.43	7.82	0.02	0.01	49.90
Pred mortality mortality2 mortality3 mortality*pred mortality2*pred	429.34	8.73	0.01	0.01	78.65
Pred mortality mortality2 mortality3 mortality*pred mortality2*pred mortality3*pred	429.97	9.36	0.01	0.01	107.77
None	434.93	14.32	0.00	0.00	1286.91
Pred	437.22	16.61	0.00	0.00	4044.04
Sum	-	-	1.85	-	-

Note: Weight of evidence (w_i) is calculated as exp(−0.5*AICc)/∑exp(−0.5*ΔAICc) and estimates the probability the model is correct. The evidence ratio (E) is calculated as w_(max)/w_i and expresses how much more likely the best model is than the given one. Higher values indicate a less likely model.

Table S6.

Parameter estimates from the best polynomial models for A. aegypti, A. triseriatus, and C. pipiens.

A. aegypti
Effect	Estimate	Std Er	DF	t Value	Pr > |t|
Intercept	3.7286	0.1168	4	31.93	<.0001
Predator −	−0.1502	0.06018	43	−2.5	0.0165
Predator +	0	.	.	.	.
Mortality	−0.01939	0.01198	43	−1.62	0.1128
Mortality2	0.000873	0.000376	43	2.32	0.0249
Mortality3	−8.16E-06	0	43	−2.7	0.0099
A. triseriatus
Intercept	2.4634	0.1948	4	12.65	0.0002
Mortality	0.01327	0.002984	50	4.45	<.0001
C. pipiens
Intercept	0.3699	0.313	4	1.18	0.3027
Predator −	0.8311	0.2416	43	3.44	0.0013
Predator +	0	.	.	.	.
Mortality	0.114	0.01701	43	6.7	<.0001
Mortality2	−0.00339	0.000239	43	−14.14	<.0001
Mortality3	0.000027	0	43	2.15	0.0374

Table S7.

Segmented models fit using PROC NLMIXED, (SAS 9.4) with block effect omitted, and a normal distribution of error

Model description	AICc	ΔAICc	exp(−0.5*ΔAICc)	Model weight (wi)	Evidence ratio (E)
Models for Aedes albopictus
1 segment	−71	0	1	0.636	1
2 segments, linear below C, C=1-S0	−68.2	2.8	0.247	0.157	4.055
2 segments, linear below C, C unconstrained	−67.6	3.4	0.183	0.116	5.474
2 segments, quadratic below C, C=1-S0	−66.3	4.7	0.095	0.067	10.486
2 segments, quadratic below C, C unconstrained	−64.9	6.1	0.047	0.030	21.115
			1.572
Models for Aedes aegypti
2 segments, quadratic below C, C unconstrained	−146.5	0	1	0.508	1
1 segment	−145.3	1.2	0.549	0.279	1.822
2 segments, linear below C, C unconstrained	−143.5	3.0	0.223	0.113	4.482
2 segments, linear below C, C=1-S0	−142.8	3.7	0.157	0.080	6.360
2 segments, quadratic below C, C=1-S0	−140.1	6.4	0.041	0.021	24.533
			1.970
Models for Culex pipiens
1 segment, linear	−203.0	0	1	0.594	1
2 segments, linear below C, C=1-S0	−200.5	2.5	0.287	0.170	3.490
2 segments, quadratic below C, C=1-S0	−200.3	2.7	0.259	0.154	3.857
2 segments, linear below C, C unconstrained	−197.8	5.2	0.074	0.044	13.464
2 segments, quadratic below C, C unconstrained	−197.5	5.5	0.064	0.038	15.643
			1.684
Models for Aedes triseriatus
1 segment, linear	−143.5	0	1	0.581	1
2 segments, linear below C, C=1-S0	−141.0	2.5	0.287	0.166	3.490
2 segments, quadratic below C, C=1-S0	−141.0	2.5	0.287	0.166	3.490
2 segments, linear below C, C unconstrained	−138.3	5.2	0.074	0.043	13.464
2 segments, quadratic below C, C unconstrained	−138.3	5.2	0.074	0.043	13.464
			1.722

Note: Weight of evidence (w_i) is calculated as exp(−0.5*AICc)/∑exp(−0.5*ΔAICc) and estimates the probability the model is correct. The evidence ratio (E) is calculated as w_(max)/w_i and expresses how much more likely the best model is than the given one. Higher values indicate a less likely model.