EMG-informed musculoskeletal modeling to estimate realistic knee anterior shear force during drop vertical jump in female athletes

Abstract

Background:

The anterior cruciate ligament is the primary structural restraint to tibial anterior shear force. The anterior force occurring at the knee during landing contributes to anterior cruciate ligament injury risk, but it cannot be directly measured experimentally.

Purpose:

The objective of this study was to develop electromyography-informed musculoskeletal simulations of the drop vertical jump motor task and assess the contribution of knee muscle forces to tibial anterior shear force.

Study Design:

cross-sectional study.

Methods:

Musculoskeletal simulations were used to estimate the muscle forces of thirteen female athletes performing a drop vertical jump using an electromyography-informed method. Muscle activation and knee loads that resulted from these simulations were compared to the results obtained with the more common approach of minimization of muscle effort (optimization-based method). Quadriceps-hamstrings and quadriceps-gastrocnemius co-contractions were progressively increased and their contribution to anterior shear force was quantified.

Results:

The electromyography-informed method produced co-contraction indexes more consistent with electromyography data than the optimization-based method. The muscles that presented the largest contribution to peak anterior shear force were the gastrocnemii likely from their wrapping around the posterior aspect of the tibia. The quadriceps-hamstring co-contraction provided a protective effect on the ACL and reduced peak anterior shear force by 292 N with a co-contraction index increase of 25% from baseline (31%), whereas a quadriceps-gastrocnemius co-contraction index of 61% increased peak anterior shear force by 797 N compared to baseline (42%).

Conclusion:

An increase in gastrocnemius contraction, which might be required to protect the ankle from the impact with the ground, produced a large quadriceps-gastrocnemius co-activation, increasing peak anterior shear force.

Clinical Relevance:

A better understanding of each muscle’s contribution to anterior shear force and, consequently, anterior cruciate ligament tension may inform subject-specific injury prevention programs and rehabilitation protocols.

1. INTRODUCTION

Anterior cruciate ligament (ACL) rupture is a common and devastating injury in adolescent and young athletes, and its short- and long-term consequences can be highly detrimental over the life of an individual ³. Non-contact ACL tears are associated with highly dynamic motor tasks, such as landing from a jump and pivoting while running ^{9, 29}. The drop vertical jump (DVJ) task has been used to identify ACL injury risk factors ^{32-34, 36}. The DVJ is a simple motor task that mimics landing and jumping movements performed often by athletes of several sport disciplines. This task concurrently accomplishes multiple neuromotor objectives: it decelerates the body center of mass and prepares the body for the subsequent jump, while protecting distal joints (ankle and knee) that could be affected by the impact with the ground (as demonstrated by the natural tendency to decelerate smoothly), as well as using muscles efficiently. The quick transition from braking to propulsion requires all the muscles spanning the knee to exert large forces in a limited time window. Specifically, the quadriceps, hamstrings and gastrocnemius activate to generate knee extension, hip extension, and ankle plantarflexion torques, respectively.

The role of several lower limb muscles with respect to ACL function was previously investigated in cadaveric studies. Although there is no unanimous consensus ^{5, 57}, the quadriceps and the gastrocnemius are considered antagonists of the ACL at low knee flexion angles (0-50°), as they produce tibial anterior shear force (ASF) ^{21, 41, 44, 61}. On the contrary, the hamstrings generate a posterior tibial force and have consistently been reported to decrease ACL strain ^{41, 54}. Although a few attempts to replicate in vitro the dynamic conditions of a landing activity have been made ^{7, 30, 61}, the combination of the complex neuromuscular coordination, large joint angular velocities, and impact loads that occur in vivo cannot be replicated on a cadaveric specimen.

ACL strain in response to muscle activation has been measured in vivo by inducement of muscle contraction with transcutaneous electrical muscle stimulation, which confirmed that the gastrocnemius is an antagonist of the ligament ²⁴. However, these muscle contractions were not representative of the highly dynamic loading conditions associated with ACL injuries. Electromyography (EMG) signals are commonly used to measure muscle activity in vivo during dynamic activities. For example, co-activation of rectus femoris (ACL antagonist) and biceps femoris (ACL agonist) was examined by calculating the co-contraction index (CI) from EMG data collected on male subjects during DVJ from different heights ³⁷. However, co-activation of the quadriceps and gastrocnemius has never been investigated during landing. In addition, studies that solely focus on EMG data are limited by the fact that a direct translation of an EMG signal to muscle force and its mechanical impact on ACL strain is not possible.

Musculoskeletal simulations have also been employed to analyze the biomechanics of single- or double-leg landing ^{40, 48, 51, 59}. The main advantage of computational modeling is that internal variables not accessible in vivo, such as muscle forces, can be estimated. The solution of the muscle redundancy problem represents a challenge when estimating muscle forces from kinematic and kinetic data collected in vivo ²². The majority of the studies that simulated landing bypassed this problem using optimal criteria, such as the minimization of muscle activation, which has been shown to perform well with activities of daily living like level walking ⁴. However, this strategy cannot predict the muscle co-contraction evident in the EMG patterns collected during DVJ, in which the neuromuscular system simultaneously accomplishes different and partially conflicting objectives. Alternative strategies that use experimentally measured EMG signals as inputs to the muscle force prediction algorithm have been used to simulate multiple motor tasks, but not dynamic activities associated with non-contact ACL injury risk, such as DVJ ^{2, 42, 52, 56}. Therefore, there is a need to quantify realistic muscle forces during dynamic tasks, consistent with muscle activity collected in vivo, and assess their contribution to ASF, which is primarily resisted by the ACL.

The primary goals of this study were (a) to estimate muscle forces during DVJ for a number of athletes accounting for the subject-specific muscle activity measured with surface EMG (EMG-informed method); and (b) compare the resulting muscle activations to the predictions obtained with an optimal recruitment strategy that minimizes muscle activity (optimization-based method). The musculoskeletal simulation strategy was then used to pursue three corollary objectives: (i) identify the contribution of each knee muscle to ASF peak; (ii) explain the ACL antagonist role of the gastrocnemius by its geometric features; and (iii) quantitatively evaluate the effect of quadriceps-hamstrings (Q-H) and quadriceps-gastrocnemius (Q-G) co-contraction on knee ASF.

2. METHODS

2.1. Experimental set up

Experimental data from thirteen female high school volleyball players were used for this study (height 169 ± 6 cm, mass 62 ± 5 kg) ²⁸. Informed written consent, approved by the Cincinnati Children’s Hospital institutional review board, was obtained (approval number: 15-009007).

A 10-camera motion analysis system (Eagle cameras, Motion Analysis Corporation, Santa Rosa, CA) was used to capture three-dimensional marker trajectories. Thirty-seven reflective markers were placed on the subject, as previously described ²⁷. Ground reaction force was captured with two force platforms (AMTI, Watertown, MA) embedded in the floor. The trials were collected in EVaRT (Version 5, Motion Analysis Corporation, Santa Rosa, CA) with synchronized video (240 Hz) and analog data (force and EMG; 1200 Hz). A telemetry surface electromyography system (TeleMyo 2400, Noraxon) was used to record muscle activity on the right lower extremity. The unit specifications included an amplifier gain of 2000, hardware bandpass filter of 10–500 Hz, an input impedance of >1MΩ and a common-mode rejection ratio of >100 dB. Disposable, self-adhesive Ag/AgCl dual electrodes with sensor diameter of 1 cm and interelectrode distance of 2 cm (Noraxon #272, Scottsdale, AZ) were applied to 8 muscles on the right lower limb: biceps femoris, semitendinosus, rectus femoris, vastus lateralis, vastus medialis, gastrocnemius medialis, hip adductors, and gluteus medius. Electrode placement was determined using protocols described previously in the literature ^{10, 15}.

EMG signals were first processed with a 10–400 Hz bandpass eighth order Butterworth filter, then rectified and filtered with a 6 Hz low-pass second order Butterworth filter, and finally, normalized to the peak processed EMG value measured for the subject across all the motor activities performed during data collection, which included maximum voluntary contractions and DVJ from different drop heights (15, 30 and 45 cm) ⁴⁶. To collect maximum voluntary contractions, the subjects were seated on a dynamometer (Biodex Medical Systems, Shirley, NY) with the trunk perpendicular to floor, the hip flexed to 90°, and the knee flexed to 60° ¹¹. Each subject performed three maximum effort isometric contractions of the quadriceps and hamstrings muscle groups. Each isometric contraction lasted 5 s with a 30-s rest between each trial.

The three DVJ trials from a 30-cm drop height were used for the musculoskeletal simulations described hereafter.

2.2. Musculoskeletal simulations

A generic musculoskeletal model ⁵³ was scaled in OpenSim ¹⁹ to match the size and body proportions of each subject based on marker data collected during a static trial. The generic model was modified to include tibiofemoral abduction/adduction and internal/external rotation as independent degrees of freedom (not constrained to flexion angle), since female athletes exhibit large knee rotations in the frontal and transverse planes during DVJ ^{26, 34}, not consistent with the passive knee kinematics originally implemented in the model ⁶⁰. In addition, the maximum isometric force of each muscle was increased by 50% to enable the muscles to generate the required joint torques during landing, as previously done in other studies ^{40, 48}.

A summary of the musculoskeletal simulation pipeline is shown in Fig. 1a. Inverse kinematics and inverse dynamics were performed in OpenSim for the three DVJ trials collected for each subject to derive joint angles and net torques. A previously presented method based on direct collocation was used to solve the muscle redundancy problem and estimate muscle activations consistent with the experimental net torques, muscle moment arms and musculotendon lengths ¹⁶. Muscle forces were estimated only for the subject’s right leg. For each degree of freedom, an ideal actuator that can produce torque instantaneously was added to the model to guarantee problem feasibility in the presence of modeling and measurement errors. The optimization-based method (not including EMG data as input) minimized the following objective function:

$$J={\int }_{t_0}^{t_f}\left(\sum _{i=1}^m{a}_i^2+w_1\sum _{k=1}^K{a}_{\mathit{Tk}}^2\right)\mathit{dt}$$

where the integral time window (t₀, t_f) goes from 150 ms before impact with the ground (IC – 150) to 300 ms after impact (IC + 300), m is the number of muscles in the model, a_i is the activation of muscle i (0 ≤ a_i ≤ 1), K is the number of degrees of freedom, a_Tk is the activation level of the ideal actuator k (−1 ≤ a_Tk ≤ 1), and w₁ is the weight penalizing the use of the ideal actuators. Initial contact with the ground (IC) was defined as the time frame at which a ground force larger than 10 N was recorded. A weight w₁ = 1 was used. The ideal actuator k could generate a torque

$$T_k=a_{\mathit{Tk}}{T}_K^{\mathit{max}}$$

where $T_K^{\mathit{max}}$ is its maximum torque. Larger maximum torques (10,000 Nm rather than 10 Nm) were chosen for the two secondary rotations of the knee (ab/adduction and internal/external) because their net joint torque is mostly explained by the contribution of unmodeled components, such as tibiofemoral contact and ligaments.

Fig. 1:

Workflow of the study. (a) Pipeline developed to estimate muscle forces for the three DVJ trials performed by the thirteen subjects analyzed in this study. Motion capture data and ground forces were used to calculate joint angles and joint net torques in OpenSim (inverse kinematics and dynamics, respectively). The time window analyzed in this study is depicted in the bottom left corner of (a). Specifically, the landing phase was divided into three regions: before contact (BC = IC-150 ms to IC), after contact 1 (AC1 = IC to IC+100 ms), and after contact 2 (AC2 = IC+100 to IC+300 ms). Muscle moment arms and musculotendon lengths for each trial were calculated through the Muscle analysis tool in OpenSim, and, together with the joint torques from inverse dynamics, were input to the two methods used to estimate muscle forces: the optimization-based method, in which only muscle activity squared was minimized, and the EMG-informed method in which an additional term constraining muscle activations to track the shape of EMG measures delayed by 40 ms to account for the electromechanical delay (see the Methods section for a more complete version of the objective functions, including also the ideal actuators). The muscle forces estimated with the two methods were used to perform a joint reaction analysis in OpenSim and calculate the anterior shear force produced on the tibia by the combined effect of muscle and ground forces. The DVJ trial that best approximated the average ASF obtained with the EMG-informed method was selected to assess the sensitivity of peak ASF predictions to a number of model parameters. (b) Three sensitivity analyses were performed: sensitivity to muscle forces, to the anterior/posterior location of the gastrocnemius wrapping object on the tibia, and to quadriceps-hamstrings and quadriceps-gastrocnemius co-contraction.

The objective function of the direct collocation method was modified as follows to track subject-specific experimentally measured EMG signals in the EMG-informed method, to Afschrift et al. ²:

$$J={\int }_{t_0}^{t_f}\left(\sum _{i=1}^m{a}_i^2+w_1\sum _{k=1}^K{a}_{Tk}^2+\sum _{j=1}^{m_{EMG}}{w}_2(s_j{\widehat{a}}_j-a_j{)}^2\right)\mathit{dt}$$

where m_EMG = 14 is the number of muscles tracking EMG data, ${\widehat{a}}_j$ is the normalized EMG profile to be tracked by muscle j delayed by 40 ms to represent the electromechanical delay between muscle excitation and activation ^{14, 62}, w₂ = 1,000 is a weighting factor, and s_j is a scaling factor and an optimization variable used to impose similarity only in shape (not in magnitude) between the normalized-delayed EMG profiles and predicted muscle activations ², since errors in EMG measurement and normalization may limit the reliability of the profile magnitude ^{17, 56}. Since the first term of the objective function aims to minimize muscle activation, lower bounds were imposed to the scaling factors s_j to avoid a null activation of ‘co-contracting’ muscles such as the hamstrings. Specifically, a lower bound of 0.8 was used for the hamstrings, and 0.5 was used for every other muscle tracking EMG data. An upper bound of 1.5 was used for every muscle, even though the upper bound a_i ≤ 1 on predicted activations was still enforced. Some muscles on which EMG was not collected tracked the signal from muscles belonging to the same group (Tab. 1). Specifically, the semimembranosus tracked the signal from the semitendinosus and the gastrocnemius lateralis tracked the signal from the gastrocnemius medialis. In addition, the gluteus medius was modeled with three separate musculotendon units (gluteus medius 1, 2, 3) and all of them tracked the same EMG signal.

Tab. 1:

Assignment of EMG data to model muscles for the EMG-informed method.

EMG Profile	Muscle model
Biceps femoris	Biceps femoris long and short head
Semitendinosus	Semitendinosus, semimembranosus
Rectus femoris	Rectus femoris
Vastus lateralis	Vastus lateralis
Vastus medialis	Vastus medialis
Gastrocnemius medialis	Gastrocnemius medialis and lateralis
Hip adductors	Adductor brevis and longus
Gluteus medius	Gluteus medius 1,2,3

Method 4 presented in Kellis et al. (2003) ³⁷ was used to calculate the Q-H and Q-G CIs both with the experimental EMG data and the activation results from the optimization-based and EMG-informed methods:

$${\mathrm{CI}}_{EMG}=\frac{{\int }_{t_{\mathit{start}}}^{t_{\mathit{end}}}{\mathrm{EMG}}_{ant}\mathit{dt}}{{\int }_{t_{\mathit{start}}}^{t_{\mathit{end}}}({\mathrm{EMG}}_{ago}+{\mathrm{EMG}}_{ant})\mathit{dt}}$$

$${\mathrm{CI}}_{model}=\frac{{\int }_{t_{\mathit{start}}}^{t_{\mathit{end}}}{a}_{\mathit{ant}}\mathit{dt}}{{\int }_{t_{\mathit{start}}}^{t_{\mathit{end}}}(a_{\mathit{ago}}+a_{\mathit{ant}})\mathit{dt}}$$

where the subscripts ago and ant indicate ‘agonist’ and ‘antagonist’ muscles, according to the following definition, which will be used hereafter: the hamstrings and gastrocnemius were considered ‘antagonist’ because they generate a knee flexion torque during DVJ, whereas the net torque needed throughout the activity according to inverse dynamics is an extension torque. Conversely, the quadriceps are defined as ‘agonist’ because they produce an extension torque. When multiple EMG signals were available for a muscle group, they were averaged (e.g. EMG from the semitendinosus and biceps femoris were averaged to calculate the EMG_ant profile for the Q-H CI). Three landing phases were used for the calculation of the CI:

• before contact (BC) = (t_start = IC – 150 ms,t_end = IC

• after contact 1 (AC1) = (t_start = IC,t_end = IC + 100 ms)

• after contact 2 (AC2) = (t_start = IC + 100 ms,t_end = IC + 300 ms).

Joint reactions (including ASF and knee compressive force) resulting from muscle forces, ground reaction forces, and inertial forces were calculated with OpenSim using the muscle forces and ideal torques estimated with the two methods (Fig. 1a).

2.3. Model evaluation

Three sensitivity analyses were performed to assess the role of knee muscles with respect to knee loads. The three analyses were performed on the trial that presented the ASF predicted profile most similar to the average profile.

2.3.1. Contribution of muscle forces to knee loads

The force in each muscle i was in turn increased by 10 N (ΔF_i) and the effect of this change on peak ASF and compressive load was evaluated (Fig. 1b, left). The contribution of each muscle to peak ASF was calculated as

$$F_{i2\mathit{ASF}}=\frac{\Delta {\mathrm{ASF}}_{peak}}{\Delta F_i}\times 100$$

where F_i2ASF is the increase/decrease of peak ASF due to the change in F_i, described as a % of ΔF_i. F_i2ASF represents the portion of the force exerted by muscle i translating into ASF when the model is in the pose corresponding to the time frame at which peak ASF occurs.

2.3.2. Contribution of the gastrocnemius wrapping geometry to knee loads

The gastrocnemius was previously reported to be an ACL antagonist because of its wrapping around the posterior aspect of the tibia and other posterior muscles, such as the soleus ^{21, 24}. The musculoskeletal model used in this study represents this geometrical property of the muscle with a cylindrical wrapping surface on the back of the tibia (Fig. 1b, middle). To assess the sensitivity of predicted ASF to this geometrical feature, three modified versions of the musculoskeletal model were created by anterior translation of the wrapping surface by 10, 20, 30 mm. The EMG-informed method and the joint reaction analysis were repeated with the modified models to assess the subsequent changes in peak ASF (Fig. 1b, middle).

2.3.3. Contribution of muscle co-contraction to knee loads

Q-H and Q-G co-contractions were simulated by increasing the predicted activation profiles of the hamstrings and gastrocnemius (antagonist muscles) by 0.1, 0.2, and 0.3 (Fig. 1b, right). The activations of the quadriceps (agonist muscles) were also modified to compensate for the extra flexion torque generated by the antagonists. First, the change in flexion torque was calculated:

$$F_i^{\mathit{new}}=f\left(a_i^{\mathit{new}},l_i^{\mathit{MT}}\right)$$

$$\Delta {\tau }_{\mathit{knee}}={\mathrm{MA}}_i^{knee}(F_i^{\mathit{new}}-F_i^{\mathit{bl}})$$

where f(∙) represents the Hill-type model equations, $a_i^{\mathit{new}}$ is the modified activation of muscle i, $l_i^{\mathit{MT}}$ is the musculotendon length of muscle i, $F_i^{\mathit{new}}$ and $F_i^{\mathit{bl}}$ are the new and baseline muscle forces, and ${\mathrm{MA}}_i^{knee}$ is the moment arm of muscle i with respect to the knee flexion degree of freedom. This extra torque (Δτ_knee) was then split equally into three and the activations needed by the vastus lateralis, vastus medialis and rectus femoris to compensate with three corresponding extension torques were back-calculated:

$$F_i^{\mathit{new}}=\frac{\Delta {\tau }_{knee}}{{\mathrm{MA}}_i^{knee}}-F_i^{\mathit{bl}}$$

$$a_i^{\mathit{new}}=f^{-1}(F_i^{new},l_i^{MT})$$

The new sets of muscle forces for the six co-contraction cases (Q-H with hamstrings activations +0.1, +0.2, +0.3; Q-G with gastrocnemius activations +0.1, +0.2, +0.3) were used to calculate new joint reactions. In addition, the new CIs were calculated and related to changes in ASF.

2.4. Statistical analyses

The Pearson-product correlation coefficients and RMSD between model-predicted muscle activations and experimental EMG data were calculated and used to statistically compare the estimated activations from the optimization-based and EMG-informed methods with a paired t-test. Q-H and Q-G CIs were compared between EMG, optimization-based, EMG-informed methods with a repeated-measures ANOVA and a Bonferroni correction for multiple comparisons. Statistical differences between ASF and compressive force predicted with the two methods were calculated with paired t-tests. Statistical significance was set at p < 0.05. The percent increases or decreases in peak ASF due to artificially increasing Q-H and Q-G CIs were calculated to assess the impact of muscle co-contraction on anterior loading. Post hoc power and effect size analyses were performed with G*Power 3 ²³ for all statistical tests.

3. RESULTS

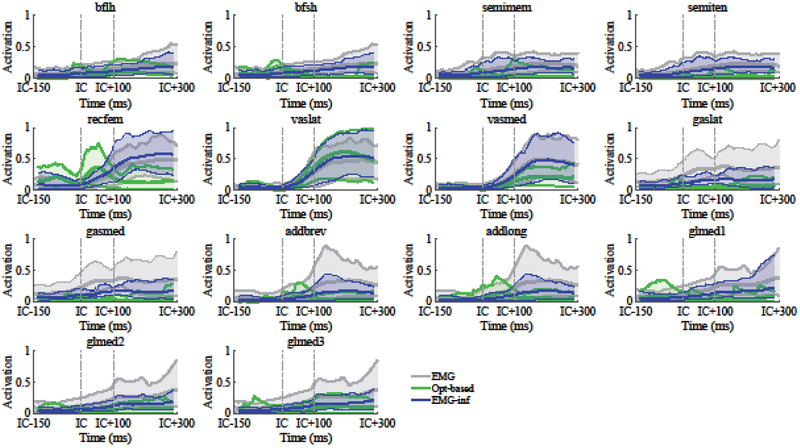
Statistical power > 0.8 and effect size > 0.5 were obtained for all the statistical comparisons performed in this study, except for the repeated-measures ANOVA that compared Q-G CIs during the BC landing phase that presented an effect size of 0.3. Normalized EMG data presented significantly larger correlation coefficients with the muscle activations estimated with the EMG-informed method than with the optimization-based method (p < 0.001, r_emg-inf = 0.78 ± 0.25 vs. r_opt-based = 0.22 ± 0.56; Fig. 2). The muscle that presented the lowest average correlations between EMG and optimization-based predictions was the biceps femoris short head (r = −0.56). Significantly lower RMSD between activation predictions and normalized EMG were also observed with the EMG-informed method (p < 0.001, RMSD_emg-inf = 0.11 ± 0.05 vs. RMSD_opt-based = 0.18 ± 0.05).

Fig. 2:

Muscle activations estimated with the optimization-based method (green) and EMG-informed method (blue), compared to normalized and delayed (40 ms) EMG measurements (see Tab. 1 for the pairing between model muscles and EMG data). Solid lines represent the data averaged across all the DVJ trials (3 trials for 13 subjects), whereas shaded regions represent the corresponding 5-95% confidence bounds. The data from the different trials were synchronized based on the initial contact (IC) time. A time window starting from 150 ms before IC and ending 300 ms after IC was selected. Vertical dashed lines in correspondence of IC and IC+100 ms are shown. See the text and Fig. 1a for a description of the three landing phases.

Optimization-based Q-H and Q-G CIs were significantly smaller than both EMG-informed and experimental CIs in all of the analyzed landing phases (p < 0.001; BC = before contact, AC1 = after contact 1, AC2 = after contact 2; Fig. 3a and 3b; see Fig. 1 for a visual description of the three phases). EMG-informed CIs were smaller than experimental CIs only during AC2 for the Q-H co-contraction (p < 0.001; Fig. 3b), and during every landing phase for the Q-G co-contraction (BC: p < 0.01; AC1 and AC2: p < 0.001; Fig. 3b).

Fig. 3:

(a) Average agonist (solid lines) and antagonist (dashed lines) activations, and sum between the two (dotted lines), for both the quadriceps-hamstrings (Q-H, top-left) and quadriceps-gastrocnemius (Q-G, top-right) co-contractions, calculated using EMG data (gray), EMG-informed results (blue), and optimization-based results (green). (b) Co-contraction indexes calculated according to method 4 described in Kellis et al. (2003) (CI = antagonist/(agonist+ antagonist)) and compared between EMG and simulation predictions during the three landing phases (see the text and Fig. 1a for a description of the three landing phases). The black dots represent the actual numbers for all the trials, whereas the colored bars represent the average across trials. Significant differences between each case were evaluated with repeated-measures ANOVAs and Bonferroni corrections for multiple comparisons (*** = p < 0.001; ** = p < 0.01; * = p < 0.05; no star= p > 0.05).

ASF and compressive forces predicted for the two methods were different mostly after IC (Fig. 4a). EMG-informed peak ASF occurred during AC1 and was larger than the corresponding optimization-based ASF at the same time frame (p < 0.001), and a larger posterior tibial shear force was predicted with the EMG-informed method during AC2 (p < 0.001). The average peak ASF for the EMG-informed method was 245 N and occurred 30 ms after IC. Compressive force at peak ASF was significantly larger when using the EMG-informed method compared to the optimization based-method (on average 4047 N vs. 2266 N, respectively; p < 0.001; Fig. 4a).

Fig. 4:

(a) Anterior shear forces (ASF, top-left) and compressive forces (bottom-left) estimated with the joint reaction analysis for the optimization-based (green) and EMG-informed (blue) methods. Solid lines represent the data averaged across all the DVJ trials (3 trials for 13 subjects), whereas shaded regions represent the corresponding 5-95% confidence bounds. A positive force corresponds to an anterior force on the tibia by the combination of muscle, ground, and inertial forces, resisted by the unmodeled joint components (the primary restrain to the tibia in the anterior direction is provided by the ACL). The black solid line represents the joint reactions estimated for trial 3 of subject 11, which was the trial presented the EMG-informed ASF prediction closest to the average prediction (solid blue line). Vertical dashed lines in correspondence of IC and IC+100 ms are shown. The dashed red line represents the time of average ASF peak. Both peak ASF and compressive force at peak ASF were significantly different between the two methods (p < 0.001). (b) Sensitivity to muscle force increase/decrease. % portion of the muscle force change (±10 N) translating into tibial ASF (top-right) and compressive force (bottom-right). A positive/negative number indicates that the corresponding change in muscle force generated an increase/decrease in tibial ASF.

The trial selected for the sensitivity analyses was trial 3 from subject 11, as it presented the ASF profile most similar to the average ASF (Fig. 4a, black line). When each muscle force was in turn increased by 10 N, the quadriceps, gastrocnemius, and tensor fasciae latae increased the ASF at its peak, whereas the hamstrings, sartorius and gracilis decreased it (Fig. 4b). An average of 45% of the force in the gastrocnemius muscles translated into ASF, whereas 15% of the quadriceps force turned into ASF. The hamstrings produced an opposite effect, with an average of 55% of their force translating into posterior shear force. An increase in the force exerted by each muscle spanning the knee produced a corresponding increase in compressive force, and the % force translating into compressive force ranged from 78% (semitendinosus) to 99% (tensor fasciae latae) (Fig. 4b).

Since the gastrocnemius was the muscle with the highest % force transferred to ASF at ASF peak, the contribution of its wrapping surface on the posterior aspect of the tibia was analyzed (Fig 5a and 5b). An anterior translation of the wrapping object of 10 and 20 mm reduced the ASF peak by 94 and 187 N, respectively, whereas a translation of 30 mm produced a negative anterior/posterior reaction force (corresponding to a posterior shear force) (Fig. 5c). Consistently, the % force translated from the gastrocnemius to the ASF decreased on average by 22% for every 10 mm displacement of the wrapping surface (Fig. 5d). However, the moment arms of the gastrocnemius muscles with respect to knee flexion were also affected by the change in geometry. Specifically, the RMSD and the correlation coefficient between the model-estimated gastrocnemius medialis moment arm and the average in vitro measurement from Buford et al. (1997) progressively increased (RMSD = 2.9 to 7.0 mm) and decreased (r = 0.87 to 0.39), respectively, with anterior translation of the wrapping object (Fig. 5e). Similar changes were not observed for the moment arm profile of the gastrocnemius lateralis throughout the flexion range (0-120°), even though a visible increase of the RMSD at flexion angles < 70° was observed (4.3 to 8.0 mm; Fig. 5e).

Fig. 5:

(a) representation of the anterior push of the gastrocnemius onto the posterior aspect of the proximal tibia, modeled as a cylindrical wrapping surface. The gastrocnemius pushes the tibia anteriorly with a force equal to the vector sum (gray arrow) of two vectors directed as the proximal and distal parts of the muscle (middle red arrows), acting where each portion of the muscle starts wrapping onto the cylinder. (b) Baseline location of the wrapping surface (opaque) compared to the location of the object after an anterior translation of 30 mm (solid). (c) Changes in ASF produced by the anterior translation of the wrapping object (baseline = black; 10 mm = blue, 20 mm = red; 30 mm = yellow). (d) % portion of the force change in the gastrocnemius medialis and lateralis translating into ASF compared between the four models (baseline and with translated object) when 10 N were added (+ sign) or subtracted (−sign). A positive/negative number indicates that the corresponding change in muscle force generated an increase/decrease in tibial ASF. (e) Gastrocnemius medialis (top-right) and lateralis (bottom-right) moment arms estimated with the four models (baseline and with translated object) and compared to gold-standard in vitro measures from Buford et al. (1997) (mean = black thin line, one standard deviation = gray region).

An increase in Q-H co-contraction during DVJ produced a decrease in ASF and an increase in compressive force (Fig. 6). Specifically, when the hamstrings activation was increased by 0.1, 0.2, and 0.3, the CI increased by 17%, 23%, and 25% during AC1, and by 8%, 12%, and 14% during AC2 (Fig. 6a and 6b). Correspondingly, the ASF peak (which occurred during AC1) decreased by 68, 176, and 292 N (becoming a posterior shear force with a CI of 56%, which occurred when the hamstrings activation was increased by 0.3), whereas the compressive force at the time of ASF peak increased by 660, 1158, and 1693 N (Fig. 6c).

Fig. 6:

(a) Hamstrings activation increased by 0.1, 0.2, and 0.3 (top-left) and corresponding quadriceps activation adjustment to compensate for the extra flexion torque generated by the hamstrings. Only the activation changes for the biceps femoris short head (bfsh), semimembranosus (semimem), vasuts lateralis (vaslat) and vastus medialis (vasmed) are shown for brevity, even though the activations of the biceps femoris long head, semitendinosus, and rectus femoris were also changed. (b) Quadriceps-hamstrings (Q-H) co-contraction indexes (CI) recalculated after the increase in activation, compared to baseline CIs. (c) Changes in ASF and compressive force due to the changes Q-H muscle activations.

An increase in gastrocnemius activation by 0.1, 0.2, and 0.3 produced a Q-G CI increase of 11%, 16%, and 19% during AC1, and of 11%, 17%, and 21% during AC2 (Fig. 7a and 7b). The larger Q-G co-contraction increased both ASF peak and compressive force. ASF peak with highest CI reached a peak of 1001 N, whereas compressive force at ASF peak increased up to 6385 N (Fig. 7c). Therefore, changes in Q-H and Q-G co-activations produced opposite trends on peak ASF (Fig. 8).

Fig. 7:

(a) Gastrocnemius activations increased by 0.1, 0.2, and 0.3 (top-left) and corresponding quadriceps activation adjustment to compensate for the extra flexion torque generated by the gastrocnemius. Only the activation changes for the vasuts lateralis (vaslat] and vastus medialis (vasmed) are shown for brevity, even though the activation of the rectus femoris was also changed. (b) Quadriceps-gastrocnemius (Q-G) co-contraction indexes (CI) recalculated after the increase in activation, compared to baseline CIs. (c) Changes in ASF and compressive force due to the changes Q-G muscle activations.

Fig. 8:

Peak ASF as a function of Q-H (light gray) and Q-G (dark gray] co-contraction indexes (CI) obtained by artificially increasing the activations of the antagonist muscles (see text and Figs. 6 and 7 for more details). An increase in Q-H CI produced a decrease in peak ASF due to the line of action of the hamstrings, which is directed posteriorly, whereas an increase in Q-G CI produced a substantial increase in peak ASF, since the quadriceps and gastrocnemius pull and push the tibia anteriorly, respectively. This data can be interpreted as a lower bound in ACL force during landing, as the ACL is the primary restrain for the anterior translation of the tibia, and the ligament also restrains secondary knee rotations as abduction and internal rotation.

3. DISCUSSION

A musculoskeletal modeling approach was used to estimate muscle forces and tibial ASF for thirteen female athletes performing a DVJ. The contribution of each muscle and agonist-antagonist co-activations to peak ASF was quantified. Q-G co-contraction was identified as a potential cause for increase in peak ASF.

Since the ACL is the primary structural restraint to anterior tibial translation, an ASF applied to the tibia will be primarily resisted by the ligament ^{13, 55}. However, ACL strain has also been shown to increase when knee abduction and internal rotation torques are combined with ASF ^{38, 45}. In this study, the effect of multiplanar knee loads on ACL strain could not be assessed because the knee representation in the musculoskeletal model lacks the level of detail needed to quantify ligament strain (ligaments, contact geometries, and menisci were not included). However, since abduction and internal rotation moments occur at the knee during DVJ ³⁴, the ASF estimates presented in this study can be interpreted as a lower bound of the actual force resisted by the ACL during landing.

Pflum et al. (2004) performed a more comprehensive multi-scale simulation of drop landing, which included a knee model with 12 degrees of freedom and average tibiofemoral and patellofemoral contact geometries. However, only one landing simulation from a single subject was performed, and the sensitivity of ACL force to model parameters and muscle co-contraction was not assessed. The results presented in Pflum et al. (2004) are consistent with the current study, which indicate that the total shear force was directed anteriorly in the first 70 ms of the landing phase (61 ms on average in our study), with a peak ACL force of 253 N at 40 ms, and then switched to a posterior force. The peak ASF predicted in the current study with the EMG-informed method was 245 ± 207 N and occurred at 30 ms after IC. In Pflum et al. (2004), the quadriceps and hamstrings generated anterior and posterior shear forces, respectively, consistent with the sensitivity analysis performed in this study.

Optimization-based hamstrings and gastrocnemius activations were smaller in comparison to predictions obtained with the EMG-informed method, which indicated that an optimal criterion such as the minimization of muscle effort does not correctly capture the neuromuscular strategies employed during a complex activity such as DVJ. The EMG-informed CIs were also more consistent with experimental data (Fig. 3a and 3b), which demonstrated that ‘sub-optimal’ Q-G and Q-H co-activations occur at the knee during landing. Neuromuscular recruitment does not optimally calculate muscle activations using an internal dynamic representation of the body, but aims to achieve competing goals with habitual ‘sub-optimal’ strategies ^{18, 43}. An additional agonist-antagonist co-contraction that was not analyzed in this study is the one between ankle plantarflexors (gastrocnemius and soleus) and dorsiflexors (tibialis anterior). Since the ground reaction forces occurring after IC generate a dorsiflexion torque throughout the whole landing phase, a tibialis anterior activation is not required according to a neuromuscular strategy that aims to minimize muscle effort, as demonstrated by an average activation of 0.07 predicted with the optimization-based method. Conversely, the EMG-informed method induced the gastrocnemius, together with the soleus, to generate a plantarflexion torque larger than the dorsiflexion torque from ground forces, which triggered the activation of the tibialis anterior to balance for it. Even though tibialis anterior EMG was not collected in this study, the timing of its activation predicted with the EMG-informed method was consistent with previously reported EMG collected during a side cutting task ³⁹, which is an activity associated to ACL injury and presents impact forces similar to DVJ ⁴⁷. The co-contraction of ankle muscles at impact with the ground might be motivated by a neuromuscular strategy adopted to protect the ankle and might be the cause of the ‘sub-optimal’ contraction of the gastrocnemius (and, consequently, of the Q-G co-activation). Ankle sprains are the most common acute musculoskeletal injuries occurring during sports ²⁵, they are often caused by impacts on uneven or unexpected terrain ⁶, and injury risk can be reduced by active co-contraction of the muscles spanning the joint²⁰.

The two agonist-antagonist co-contractions at the knee analyzed in this study produced opposite effects on ASF Larger Q-H co-contraction simulated by artificially increasing the hamstrings activation reduced peak ASF even though the compensatory contraction of the quadriceps had the opposite effect. This is motivated by the line of action of the hamstrings at the time of peak ASF, which is better aligned to the anterior/posterior axis of the tibia than the patellar tendon, which increases the ratio of hamstrings force that translates into posterior shear force in comparison to the quadriceps. When the gastrocnemius activation was increased by 0.1, 0.2, and 0.3, and the quadriceps activation was also increased to generate a knee extension torque equivalent to the extra flexion torque (producing Q-G CIs of 54%, 58%, and 61% during AC1), the ASF peaked at 576, 817, and 1001 N, respectively. Although the quadriceps and gastrocnemius have opposite roles in the flexion/extension degree of freedom of the knee, both muscle groups act as ACL antagonists during landing. Fleming et al. (2001) demonstrated in vivo that ACL strain increased when the quadriceps and the gastrocnemius generated force singularly and at the same time. The current study investigated the mechanism by which the gastrocnemius generates an ASF by changing the anterior/posterior location of its wrapping surface at the tibia. When the wrapping object was moved anteriorly by 10, 20, and 30 mm, the % force in the gastrocnemius that translated into ASF was decreased from 34% to 24%, 12%, and 0%, respectively, which demonstrated that the wrapping of the muscle around the posterior aspect of the tibia is the primary responsible for this mechanism (Fig. 5). The change in the muscle moment arm due to the wrapping surface displacement demonstrated the anatomical validity of the original position of the surface in the model developed by Rajagopal et al. (2016), since it correctly replicated gold-standard in vitro measurements ¹².

A secondary effect of larger knee muscle co-contraction is the increase in compressive force. A previous in vitro study showed that compressive force produced an anterior shift of the neutral position of the knee, which was greatest at 30° of tibiofemoral flexion (5.2 mm when a compressive load of 444 N was applied) and increased by three times when the ACL was sectioned, which indicated that compressive force loads the ACL ⁵⁸. This can be explained by the shape of the lateral tibial plateau, which presents a posterior slope that pushes anteriorly the tibia when compressive force is applied through the femur. The posterior tibial slope has been previously reported to be an anatomical factor associated to ACL injury risk ^{8, 31}. A recent computational study confirmed that impulsive compressive force and knee abduction torque increase ASF and ACL force during landing ⁴⁹. In the current study, a simulated increase in Q-H CI of 17%, 23%, and 25% during AC1, caused the compressive force to increase by 21%, 37%, and 54%, respectively. An increase in compressive force after IC may produce an additional ASF by means of the posterior tibial slope, which potentially reduces the protective role of a contraction of the hamstrings.

A number of limitations were present in this study. First, the inherent limitations of surface EMG, such as the variability due to electrode placement, skin impedance, crosstalk between muscles, and normalization, may have affected our results ¹⁷. In particular, the subject-specific normalization to the maximum processed EMG value might result in the overestimation of activity magnitude, if the muscle did not fully activate throughout the data collection. To address this limitation, additional design variables were added to the EMG-informed muscle optimization to scale the normalized EMG data and provide flexibility in terms of activation magnitude. A 0.5 lower bound was used for the gastrocnemius scaling factor because using 0.8, as for the hamstrings, resulted in the saturation of the tibialis anterior activation and in no activation of the soleus, which was not a realistic scenario. An additional limiting factor was that EMG data for the tibialis anterior muscle was not collected in this study and the EMG-informed method could not include a constraint for this muscle. Finally, the conclusions of this investigation cannot be generalized to males, as only female athletes were examined, and sex differences in co-contraction levels and ASF could not be quantified.

In conclusion, a muscle force prediction strategy based on subject-specific muscle activity was developed in this study to estimate the contribution of each muscle spanning the knee to ASF during DVJ, which is associated with increased ACL injury risk. Co-contraction of knee extensors and flexors was simulated and the changes in ASF during the first 100 ms after IC were quantified. The ‘sub-optimal’ activation measured for the gastrocnemius might be motivated by the need to stabilize and protect the ankle during impact with the ground and cause an increase in ASF.