Abstract
Objective:
Develop a web-based calculator that predicts the likelihood of experiencing multiple, competing outcomes prospectively over five, ten, and 15 years.
Methods:
Baseline demographic and medical data from a healthy and racially and ethnically diverse cohort of 161,808 postmenopausal women, aged 50–79 at study baseline, who participated in the Women’s Health Initiative (WHI) was used to develop and evaluate a risk-prediction calculator designed to predict individual risk for morbidity and mortality outcomes. Women were enrolled from 40 sites arranged in four regions of the U.S. The calculator predicts all-cause mortality, adjudicated outcomes of health events (i.e. myocardial infarction [MI], stroke, and hip fracture), and disease (lung, breast, and colorectal cancer). A proportional sub-distribution hazards regression model was used to develop the calculator in a training dataset using data from three regions. The calculator was evaluated using the C-statistic in a test dataset with data from the fourth region.
Results:
The predictive validity of our calculator measured by the C-statistic in the test dataset for a first event at five and 15 years, was as follows: MI 0.77, 0.61, stroke 0.77, 0.72, lung cancer 0.82, 0.79, breast cancer 0.60, 0.59, colorectal cancer 0.67, 0.60, hip fracture 0.79, 0.76, death 0.74, 0.72.
Conclusion:
This study represents the first large scale study to develop a risk prediction calculator that yields health risk prediction for several outcomes simultaneously. Development of this tool is a first step towards enabling women to prioritize interventions which may decrease these risks.
Keywords: Risk prediction, Post-menopausal women, Women’s Health Initiative, Comorbidity
INTRODUCTION
Health care providers and patients share a common interest in the accurate prediction of risk for both morbidity (i.e., various disease outcomes) and mortality based on the individual patient’s lifestyle, family history and other risk factors. Because some risk factors, e.g. smoking, may increase the impact of several diseases (e.g. cardiovascular disease, cancer), accurate prediction of a specific disease outcome (i.e., cardiovascular disease or cancer) is a complicated endeavor. Many clinically available risk prediction algorithms do not account for competing risks. Competing risks are events that preclude, or reduce the importance, for an individual, of the outcome of interest. The development and evaluation of a tool that could accurately incorporate competing outcomes into the risk prediction of a specific diseases (i.e., a calculator that accounts for risk of cancer-related morbidity and mortality whilst predicting risk for cardiovascular disease) would represent a significant clinical advancement.
There are several widely available risk algorithms for predicting morbidity among older adults, including women. These include, i.e. the ACC/AHA Pooled Cohort Equations (http://tools.acc.org/ascvd-risk-estimator-plus) 1, the Framingham heart disease risk score (https://www.framinghamheartstudy.org/risk-functions/)2, the Gail risk score for breast cancer risk (http://www.cancer.gov/bcrisktool/)3, the Reynolds risk calculator for cardiovascular disease (www.reynoldsriskscore.org/)4, and the Fracture Risk assessment Tool (FRAX) (https://www.shef.ac.uk/FRAX/tool.jsp)5 tool for evaluating fracture risk. While some incorporate competing risks, others do not.
None of these tools predict the risk of multiple disease outcomes simultaneously. This limits their clinical utility, particularly with respect to post-menopausal women, as the likelihood of multiple, competing morbidities increases with age. For example, women at high risk of having a myocardial infarction (MI) have a shorter average life-span, lowering their likelihood of developing breast cancer or experiencing hip fracture relative to women at low risk of MI. Failure to incorporate the competing cardiovascular risk into a risk prediction algorithm for breast cancer or hip fracture would be expected to yield results that are limited in value to patient and provider. Further, these prevention efforts might receive less attention because of focus on less lethal conditions and the opportunity for clear guidance to engage the patient with meaningful primary and secondary prevention efforts may be lost.
Another example of this is observed in the widely used FRAX algorithm for predicting hip fracture risk. Paradoxically, when using FRAX to assess older women the fracture risk decreases with age (see Leslie et al.6). This misleading “decrease” in fracture risk is a manifestation of this algorithm’s lack of individualization of risk of death, instead using the average risk of death for a woman the same age. In contrast, appropriate risk prediction that accounts for competing health risks will show that for a woman with a long-life expectancy, fracture risk increases with age. Ideally, one should be able to predict the risk of specific outcomes, such as fracture, while accounting for the risk of other outcomes. Specifically, calculators designed to provide women, and their providers, with information about the probabilities of a particular outcome occurring first, are warranted. Nevertheless, to our knowledge, no published health risk calculators yet accomplish this.
In the present work, we aim to address this literature gap by developing and evaluating a risk calculator that addresses multiple, competing morbidity (myocardial infarction, MI, stroke, lung, breast and colorectal cancer, hip fracture) and mortality (all causes of death) risks simultaneously. The calculator will account for competing risks and yield estimates of the probability of each outcome occurring first, offering at least a preliminary mechanism for prioritizing health prevention and maintenance efforts based upon women’s most immediate risks. We will accomplish this using data collected from the large, diverse cohort of postmenopausal women who participated in the Women’s Health Initiative (WHI) and examine the veracity of our risk prediction tool for five-, ten-, and 15-year risk of outcomes.
METHODS
Study population
The WHI recruited a diverse cohort of 161,808 healthy, postmenopausal women aged 50–79 years at baseline from four geographical regions throughout the U.S.7 Recruitment efforts (baseline) occurred between 1993–1998. The WHI consisted of an observational study (OS) cohort and four clinical trial (CT) cohorts (a low-fat diet intervention, two trials of menopausal hormone and an overlapping trial of supplemental calcium and vitamin D). All women in the OS and CT cohorts are used in the current analysis to develop the risk prediction models. The scientific rationale, study design, eligibility criteria, and baseline characteristics of these studies have been previously reported.7
In this study we use outcomes reported, confirmed by record, and adjudicated by independent panels of study physicians using standardized protocols during the main WHI study (1993–2005) and the first extension study (2005–2010). 115,400 women (86% of survivors) enrolled in the extension study and no new participants were added. Mortality data are available for all participants. Institutional review boards at participating institutions approved procedures and protocols. All participants provided written informed consent.
Primary outcomes
The primary outcomes for this analysis were chosen based on their clinical relevance and frequency in the study population (incidence of ~2% or greater at 15 years). Predictive models were built for: 1) MI, 2) stroke, 3) lung cancer, 4) breast cancer, 5) colorectal cancer, 6) hip fracture, and 7) death from any cause, as defined by WHI.8 We considered outcomes occurring within five, ten and 15 years of baseline. The supplement contains additional details on the outcome definitions and adjudication.
Risk predictor definitions
During the baseline clinic visit, each study participant completed self-administered questionnaires on demographics, medical history, medications, smoking, diet, physical activity and other lifestyle-related factors, and had blood pressure, weight, and height measured (https://www.whi.org/researchers/studydoc/SitePages/Home.aspx). Waist circumference was measured to nearest 0.5 cm at the narrowest part of the torso at the end of a normal expiration. Risk predictors selections were made a priori and were guided by previously identified risk factors and calibrated using existing (i.e., published) risk algorithms. See the supplement for additional details on the risk predictors.
Statistical methods
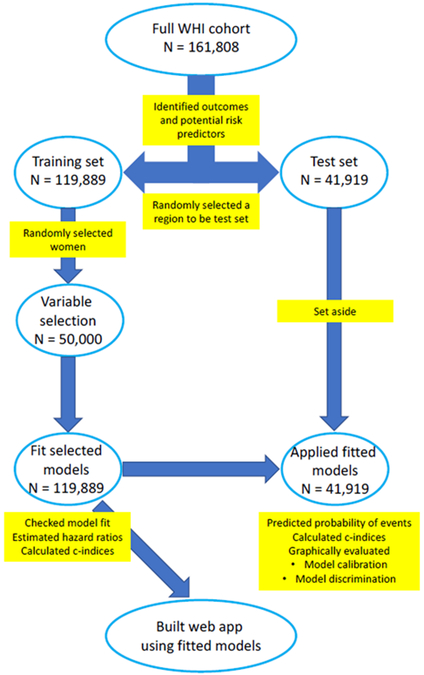
A diagram to summarize the steps to build and fit the models is displayed in Figure 1. We began by splitting the data into a training and a test dataset by randomly selecting one of the four similarly sized WHI geographic regions to be the test dataset. This approach exploits regional differences, allowing us to evaluate model performance in a geographically distinct cohort in the absence of an external validation. The southern WHI region was used as the test dataset and women from the other three WHI regions (Northeast, Midwest, and West) comprised the training dataset. All model building and model checking was performed on the training dataset. The test dataset was used to evaluate the prediction model’s performance. We compared the distribution of risk predictors in the test and training set using standardized difference, a measure of the difference in means between two groups expressed in units of standard deviations.9
Figure 1: Summary of steps to build and fit models using Women’s Health Initiative (WHI) data.
As the goal was to create a calculator to predict the probability of a woman having one specific outcome (e.g., cardiovascular event) before another outcome (e.g., cancer diagnosis), we used a competing risk framework to build the prediction model. Competing risk algorithms model the time until an event occurs in a period when more than one event type is possible. A separate model was fit for each outcome and time point to obtain a predicted probability for each event type at five, ten, or 15 years. The models use data from baseline to predict the probability of the event. We fit the proportional sub-distribution hazards regression model described in Fine and Gray10. The proportional hazards assumption was evaluated by visually examining Schoenfeld residuals and no apparent violations were identified.
Our primary approach treats any event besides the primary outcome of interest as a competing event, which differs from the classical definition of a competing event as one that precludes the event of interest from occurring. This “event first” approach should facilitate risk prediction that provides an individual with information about her probability of experiencing one health event relative to another. In other words, it should predict an individual patient’s likelihood of MI, relative to the likelihood of stroke, hip fracture, breast, lung, or colorectal cancer diagnoses, or death from any cause. In the decision-making process, we believe a woman would benefit by understanding the probability of ever experiencing the event of interest (MI in the example above) the context other health events. To address this concern, we additionally fit models for each event type where the only competing risk is death and additionally present these predicted probabilities (“event ever”). The participants were followed until the first occurrence of any outcome in the “event first” approach and until the outcome of interest or death in the “event ever” approach; loss to follow-up (last visit through September 30, 2010 used as last date of follow-up); or completion of 15 years of follow-up, whichever came first. Additional details about the modeling approaches are contained in the supplement.
Variables included in the main effects analyses were chosen a priori for inclusion in the predictive models. We also used variable selection to select two-way interactions from a pre-specified list for inclusion in the models.11,12 Additional details on the variable selection methods are provided in the supplement. The models were fit to the full training data set to estimate coefficients to be used in obtaining predictions.
Missing data were imputed using the methods described in the supplement.13,14 Missing values were minimal; imputation was needed for only 1% of the nearly 14.5 million data points. However, despite the small overall proportion of observations missing, the 1% of missing data points were distributed evenly across the women and imputation was used because 44% of women were missing data on one or more risk predictor (Appendix Figure 1).
To evaluate the model calibration, we plotted predicted risk vs. the observed event rate. In a well-calibrated model, the predicted risk will approximate observed risk. We calculated the concordance statistic (C-statistic) to assess model discrimination15. Model discrimination is also graphically displayed in Kaplan-Meier plots stratified by predicted risk quintile. In models with good discrimination, the women in each predicted risk quintile will have differing survival curves, indicated by distinct and correctly ordered survival curves in the stratified Kaplan-Meier plot.
All statistical analyses were performed in R version 3.2.316. The ‘mice’ R package was used to multiply impute the data, the ‘cmprsk’17 package was used to fit the competing risk models, and the ‘crrstep’18 was used in the variable selection. The risk prediction model is implemented in an interactive, web-based application (app) that was created using Shiny.
RESULTS
We included 161,808 women in our study (119,889 in the training set, 41,919 in the test set) and had complete follow-up for 98% of women at five years, 78% at ten years, 45% at 14 years, and 27% at 15 years. Baseline data for women in the training set, comprised of 3 regions, and the test set, the WHI south region, are shown in Table 1. The training set is 85% non-Hispanic white, 6% non-Hispanic black, and 9% reporting other race/ethnicities. The test set is 75% non-Hispanic white, 17% non-Hispanic black, 7% Hispanic, and 2% reporting other race/ethnicities. The mean age is 63.5 years in the training set and 62.4 years in the test set (See Table 1). Race/ethnicity, age, age at first birth, and number of pregnancies differ between the training and test regions.
Table 1. Baseline demographic, medical, and lifestyle characteristics of the Women’s Health Initiative (WHI) cohort.
The table contains the N (%) in each cell unless otherwise noted.
| Variables | Training Set (Northeast, Midwest, West Regions) (N = 119,889) |
Test Set (South Region) (N = 41,919) |
Standardized Difference |
|---|---|---|---|
| Age, mean (SD) | 63.54 (7.21) | 62.37 (7.25) | 0.163 |
| Race/Ethnicity | 0.414 | ||
| American Indian or Alaska Native | 543 (0.5) | 170 (0.4) | |
| Asian or Pacific Islander | 3,933 (3.3) | 257 (0.6) | |
| Non-Hispanic Black | 7,696 (6.4) | 6,922 (16.6) | |
| Hispanic | 3,755 (3.1) | 2,729 (6.5) | |
| Non-Hispanic White | 10,2142 (85.4) | 31,399 (75.1) | |
| Other | 1,507 (1.3) | 342 (0.8) | |
| Incomea | 0.103 | ||
| < $10,000 | 4,572 (4.0) | 2,365 (5.9) | |
| $10-20K | 13,524 (11.7) | 4,975 (12.4) | |
| $20-35K | 27,706 (24.0) | 8,959 (22.4) | |
| $35-50K | 23,157 (20.1) | 7,755 (19.4) | |
| $50-75K | 22,479 (19.5) | 7,469 (18.7) | |
| $75-100K | 10,126 (8.8) | 3,487 (8.7) | |
| $100-150K | 6,935 (6.0) | 2,502 (6.3) | |
| > $150,000 | 3,666 (3.2) | 1,257 (3.1) | |
| Don't know | 3,135 (2.7) | 1,249 (3.1) | |
| Occupationa | 0.070 | ||
| Managerial/professional | 46,499 (42.0) | 16,005 (42.1) | |
| Technical/sales/admin | 33,365 (30.1) | 10,758 (28.3) | |
| Service/labor | 19,832 (17.9) | 6,716 (17.7) | |
| Homemaker only | 10,993 (9.9) | 4,544 (12.0) | |
| Diabetes | 6,824 (5.7) | 2,794 (6.7) | 0.041 |
| Medical history | |||
| High cholesterol | 15,716 (13.9) | 5,819 (14.8) | 0.026 |
| Migraine | 12,642 (11.2) | 4,452 (11.3) | 0.005 |
| Atrial fibrillation | 5,171 (4.4) | 1,899 (4.6) | 0.012 |
| Stroke | 1,558 (1.3) | 607 (1.4) | 0.013 |
| Myocardial infarction | 2,747 (2.3) | 957 (2.3) | <0.001 |
| Gallbladder disease or gallstones | 19,560 (16.4) | 6,627 (16.0) | 0.012 |
| Underactive thyroid | 17,602 (15.6) | 5,479 (14.1) | 0.043 |
| Overactive thyroid | 3,215 (2.9) | 1,040 (2.8) | 0.009 |
| Hypertension | 39,918 (33.5) | 14,353 (34.6) | 0.023 |
| Broke bone | 44,622 (39.2) | 14,682 (36.9) | 0.047 |
| Hip fracture at age 55+ | 619 (0.7) | 215 (0.7) | 0.005 |
| Treated hypertension | 0.029 | ||
| Never hypertensive | 75,241 (66.3) | 25,833 (65.3) | |
| Untreated hypertension | 9,288 (8.2) | 3123 (7.9) | |
| Treated hypertension | 29,041 (25.6) | 10,611 (26.8) | |
| Age at menarche | 0.044 | ||
| < 9 | 1,598 (1.3) | 607 (1.5) | |
| 10 | 6,349 (5.3) | 2,021 (4.8) | |
| 11 | 18,322 (15.3) | 6,467 (15.5) | |
| 12 | 31,052 (26.0) | 10,961 (26.3) | |
| 13 | 34,762 (29.1) | 11,833 (28.4) | |
| 14 | 15,925 (13.3) | 5,527 (13.3) | |
| 15 | 6,564 (5.5) | 2,510 (6.0) | |
| 16 | 3,633 (3.0) | 1,416 (3.4) | |
| > 17 | 1,246 (1.0) | 368 (0.9) | |
| Ever breastfeed | 61,152 (51.5) | 21,053 (51.0) | 0.01 |
| Ovaries removed | 0.082 | ||
| None | 85,234 (72.0) | 28,108 (68.4) | |
| One | 8,257 (7.0) | 3,309 (8.1) | |
| Both | 22,730 (19.2) | 8,825 (21.5) | |
| Unknown number removed | 983 (0.8) | 451 (1.1) | |
| Part of an ovary removed | 1,173 (1.0) | 386 (0.9) | |
| Breast biopsy (yes/no) | 26,579 (23.3) | 10,151 (25.6) | 0.053 |
| Number of pregnancies | 0.108 | ||
| Never pregnant | 11,172 (9.4) | 3,718 (8.9) | |
| 1 | 7,863 (6.6) | 3,439 (8.3) | |
| 2-4 | 69,593 (58.3) | 25,379 (61.0) | |
| 5+ | 30,775 (25.8) | 9,092 (21.8) | |
| Number of term pregnancies | 0.150 | ||
| Never pregnant | 11,172 (9.4) | 3,718 (8.9) | |
| Never had term pregnancy | 2,923 (2.5) | 1,318 (3.2) | |
| 1 | 9,859 (8.3) | 4,346 (10.5) | |
| 2 | 28,883 (24.2) | 11,388 (27.4) | |
| 3 | 28,943 (24.3) | 9,896 (23.8) | |
| 4 | 18,696 (15.7) | 5,861 (14.1) | |
| 5+ | 18,742 (15.7) | 5,017 (12.1) | |
| Age at first birth | 0.168 | ||
| Never pregnant | 11,172 (10.3) | 3,718 (10.0) | |
| Never had term pregnancy | 2,923 (2.7) | 1,318 (3.5) | |
| < 20 | 13,764 (12.7) | 6,789 (18.3) | |
| 20-29 | 71,666 (66.0) | 22,561 (60.7) | |
| 30+ | 9,128 (8.4) | 2,787 (7.5) | |
| Mom alive | 29,324 (24.8) | 11,734 (28.5) | 0.084 |
| Dad alive | 10,193 (8.7) | 4,097 (10.1) | 0.047 |
| Relatives’ medical history | |||
| Myocardial infarction | 59,568 (52.4) | 20,605 (52.4) | <0.001 |
| Broke bone | 44,287 (40.0) | 14,828 (38.6) | 0.029 |
| Number of family members with diabetes | 0.092 | ||
| None | 76,175 (67.1) | 25,145 (64.2) | |
| 1 | 25,987 (22.9) | 9,118 (23.3) | |
| 2 | 7,353 (6.5) | 2,951 (7.5) | |
| 3 | 2,318 (2.0) | 1,134 (2.9) | |
| 4+ | 1,652 (1.5) | 836 (2.1) | |
| Breast cancer (Female) | 21,365 (18.8) | 7,045 (17.9) | 0.023 |
| Colorectal cancer (Female) | 9,584 (8.4) | 3,152 (8.0) | 0.015 |
| Colorectal cancer (Male) | 10,252 (9.1) | 3,149 (8.1) | 0.036 |
| Age mother had myocardial infarction | 0.037 | ||
| No MI | 73,873 (77.4) | 23,717 (75.9) | |
| < 55 | 2,694 (2.8) | 920 (2.9) | |
| 55-64 | 4,491 (4.7) | 1,569 (5.0) | |
| > 65 | 13,591 (14.2) | 4,788 (15.3) | |
| Yes, don't know age | 779 (0.8) | 259 (0.8) | |
| Age father had myocardial infarction | 0.023 | ||
| No myocardial infarction | 64,925 (65.3) | 21,495 (64.4) | |
| < 55 | 7,118 (7.2) | 2,405 (7.2) | |
| 55-64 | 9,779 (9.8) | 3,396 (10.2) | |
| > 65 | 16,558 (16.7) | 5,713 (17.1) | |
| Yes, don't know age | 975 (1.0) | 372 (1.1) | |
| Lactose-free diet | 5,878 (5.0) | 1,955 (4.9) | 0.008 |
| Moderate exercise b | 0.064 | ||
| None | 60,078 (52.9) | 21,970 (55.8) | |
| 1 day/week | 13,079 (11.5) | 4,309 (10.9) | |
| 2 days/week | 13,038 (11.5) | 4,256 (10.8) | |
| 3 days/week | 14,436 (12.7) | 4,885 (12.4) | |
| 4 days/week | 5,091 (4.5) | 1,654 (4.2) | |
| >4 days/week | 7,860 (6.9) | 2,326 (5.9) | |
| MET-hours per week from walking (mean, SD) b | 4.80 (6.07) | 4.34 (5.80) | 0.076 |
| Alcohol intake | 0.305 | ||
| Non-drinker | 10,311 (8.7) | 7,341 (17.7) | |
| Past drinker | 21,391 (18.0) | 8,757 (21.1) | |
| < 1 drink/month | 15,201 (12.8) | 4,725 (11.4) | |
| < 1 drink/week | 25,351 (21.3) | 7,586 (18.3) | |
| 1-6 drinks/week | 32,254 (27.1) | 8,919 (21.5) | |
| 7+ drinks/week | 14,624 (12.3) | 4,124 (9.9) | |
| Years smoking, mean (SD) | 3.68 (1.62) | 3.58 (1.62) | 0.062 |
| Resting pulse, mean (SD), beats per 30s | 34.74 (5.85) | 34.91 (6.59) | 0.027 |
| Height, mean (SD), cm | 161.65 (6.63) | 162.06 (6.73) | 0.060 |
| Weight, mean (SD), kg | 73.34 (16.75) | 74.10 (17.35) | 0.045 |
| BMI, mean (SD), kg/m2 | 27.95 (5.89) | 28.05 (6.08) | 0.018 |
| Waist, mean (SD), cm | 86.59 (13.82) | 86.19 (13.89) | 0.029 |
| Hip, mean (SD), cm | 106.30 (12.22) | 106.78 (12.37) | 0.039 |
| Systolic blood pressure, mean (SD), mmHg | 127.30 (17.57) | 127.62 (18.24) | 0.018 |
| Taking aspirin | 26,466 (22.1) | 8,376 (20.0) | 0.051 |
| Taking statins | 9,007 (7.5) | 3,236 (7.7) | 0.008 |
| General health | 0.117 | ||
| Excellent | 20,617 (17.3) | 6,771 (16.3) | |
| Very good | 49,955 (41.9) | 15,681 (37.8) | |
| Good | 38,635 (32.4) | 14,407 (34.7) | |
| Fair | 9240 (7.7) | 4222 (10.2) | |
| Poor | 840 (0.7) | 392 (0.9) | |
SD = standard deviation, MET = metabolic equivalent of task, BMI = body mass index
The socioeconomic variables income and education are provided to compare the women who are in the test and training set. They were not included in the risk prediction models.
The physical activity variables included in the risk prediction model were calculated from these variables and other physical activity variables.
Regarding morbidity and mortality data, the observed 15-year cumulative frequencies of the outcomes were MI 4%, stroke 4%, lung cancer 2%, breast cancer 7%, colorectal cancer 2%, hip fracture 2%, and death 13% (Table 2). Appendix Table 1 shows the C-statistics for the training sets and test sets at five, ten, and 15 years in the event-first models. The C-statistics for training and test samples at fifteen years for the event-first models are as follow: MI 0.71, 0.61, stroke 0.70, 0.72, lung cancer 0.77, 0.79, breast cancer 0.59, 0.59, colorectal cancer 0.61, 0.60, hip fracture 0.76, 0.76, death 0.71, 0.72. The estimated hazard ratios for each prediction variable are displayed for all models (Appendix Table 1).
Table 2. Prevalence of outcomes within five, ten, and 15 years of baseline in all Women’s Health Initiative (WHI) women.
| 5 years | 10 years | 15 years | |
|---|---|---|---|
| Myocardial infarction | 2063 (1.27%) | 4,324 (2.67%) | 5,836 (3.61%) |
| Stroke | 1,938 (1.20%) | 4,253 (2.63%) | 6,151 (3.80%) |
| Lung cancer | 905 (0.56%) | 1,989 (1.23%) | 2,933 (1.81%) |
| Breast cancer | 4,321 (2.67%) | 8,007 (4.95%) | 10,745 (6.64%) |
| Colorectal cancer | 1,011 (0.62%) | 1,923 (1.19%) | 2,610 (1.61%) |
| Hip fracture | 904 (0.56%) | 2,458 (1.52%) | 3,895 (2.41%) |
| Death | 4,341 (2.68%) | 11,850 (7.32%) | 20,408 (12.61%) |
The distribution of predicted risk for selected outcomes at 15 years is displayed in Appendix Figure 2. Model calibration for the event-first models is displayed in Appendix Figure 3. Overall, the models were well-calibrated as demonstrated by predicted rates consistent with observed rates. The breast and colorectal cancer predictions yielded slightly higher risk than rates actually observed in the data. The stroke predictions yielded slight underestimations of risk, relative to observed rates, among women in the highest risk deciles. Death was modestly, but consistently, over-predicted in the test set, particularly for women in the higher risk deciles.
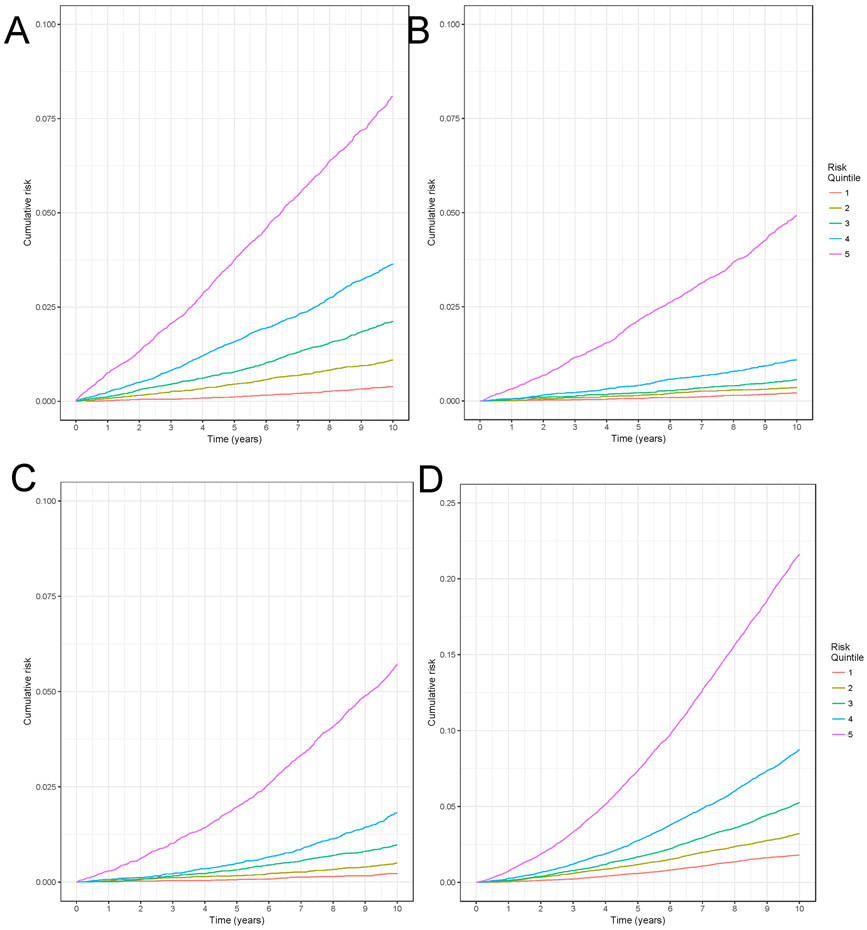
Model discrimination is graphically demonstrated by the differences in cumulative risk by quintile of predicted risk in Figure 2. As can be seen, the cumulative risk curves diverge over time indicating the model discriminates risk well.
Figure 2: Stratified Kaplan-Meier plot to evaluate model discrimination for A) myocardial infarction, B) lung cancer, C) hip fracture, D) death.
Note that the vertical axis is truncated to 0.1 in panels A, B, and C and to 0.25 in panel D. They do not extend to 1 due to the rarity of the events. Each line represents the lowest to highest risk quintile, according to a woman’s risk as predicted by the 10-year model for myocardial infarction, lung cancer, hip fracture, and death in the test set. In a model that discriminates well, we would expect that the highest risk quintile would have the highest cumulative risk and the lowest risk quintile would have the lowest observed cumulative risk
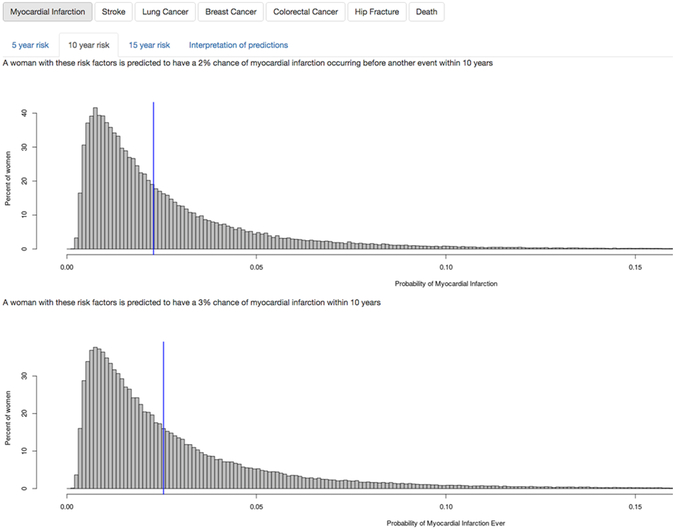
From the models that were developed, an interactive, web-based application (i.e., app) was produced. An image of the output produced by the app appears in Figure 3. The app can be accessed at https://hedlin.shinyapps.io/shiny/. The graphs at the bottom of the app show the woman’s risk compared to age- and ethnicity-matched women. The first graph shows a woman’s probability of having the event of interest prior to any other event in the next five, ten, or 15 years (based on the event-first models). The second graph shows a woman’s probability of having the event of interest ever within five, ten, or 15 years (based on the event-ever models).
Figure 3: Screenshot of web-based app.
DISCUSSION
We used the rich data resources of the WHI to develop and evaluate a calculator to predict the five, ten, and 15-year risk of multiple disease and mortality outcomes in a diverse cohort of postmenopausal women aged 50–79 years. Discrimination was excellent for MI, stroke, lung cancer, hip fracture, and death through 10 years (C-statistics 0.73–0.89 in training and test sets), and remains very good for stroke, lung cancer, hip fracture, and death through 15 years (C-statistics 0.70–0.79). Discrimination was more modest for breast and colorectal cancer at each time point (C-statistics 0.59–0.66 in training and test sets), however, and results suggested that the calculator over-predicted all-cause mortality in the test cohort.
Taken together, these findings offer an optimistic picture for the value and utility of the risk prediction tool in healthy post-menopausal women. Further research, particularly efforts to externally validate this tool with additional data sets will bolster our understanding of the tool’s generalizability and offer evidence-based guidance for the refinement of its predictive models. This study represents the first large scale study to develop a risk prediction calculator that yields health risk prediction for several outcomes simultaneously, and thus offers a novel contribution to the literature.
Despite its novelty, our study findings are consistent with prior literature in several important ways. First, this risk calculator produces C-statistics similar to published C-statistics from existing risk estimators for most outcomes, although some outcomes (breast cancer, for example) have slightly lower C-statistics for reasons we note below. 1, 19, 20, 21, 22, 23, 24, 25 Unlike its predecessors, risk information is entered once and risk predictions for seven common health outcomes (i.e. MI, stroke, lung cancer, breast cancer, colorectal cancer, hip fracture, and death) are yielded simultaneously.
Our study has several methodological limitations that warrant discussion. First, our risk calculator was developed on women, aged 50–79 (baseline) who participated in WHI. As such, generalizability may be limited, and this work may be particularly relevant to U.S. based postmenopausal women whose health profile is similar to those recruited into WHI. Further, WHI represents a cohort of women from an earlier era in women’s health. As such several unique health era factors, e.g. the state of premenopausal women’s health care, availability and dosing of hormone-based therapies, and general state of the knowledge about women’s postmenopausal risk for cancer and cardiovascular disease for WHI women, particularly the oldest group, i.e., those aged 70 and older at baseline, warrant consideration as they too could influence the generalizability of our findings.
Second, while we internally validated the calculator by splitting the WHI data into training and test datasets that leveraged the considerable variability by region (particularly with respect to race/ethnicity), external validation efforts, i.e., using another dataset entirely, are needed and would help to refine and ready the calculator for dissemination and use. However, external validation efforts are beyond the scope of the current paper. The code used to build our models is available to other researchers who would like to externally validate or create a risk calculator for men or populations with other racial/ethnic compositions, for example. We underscore the importance of external validation and fully acknowledge the inherent challenge here as identifying a data set that is matched to WHI in terms of size and comprehensive health scope may prove difficult.
Third, the calculator’s predictions for breast cancer are not as robust as other published risk calculators because we were unable to include outcome-specific predictors such as BRCA1 or BRCA2 mutations, or the number of breast biopsies for breast cancer. Our aim was to develop a tool for women who are not known to be at high risk of a condition to weigh the risks of various events. If she or her physician know she is at high risk of an event, for example knowing she has a BRCA mutation, this tool will not improve the ability to predict that event.
It is possible the models could be improved by introducing variables, such as lipids, bone mineral density, or genetic mutations, which were not available in the entire Women’s Health Initiative cohort. At the same time, because we are making predictions for a range of outcomes, the amount of data needed to make the predictions is large and these additional variables may not be generally available to women. Entering many variables into the risk calculator is time consuming but only needs to be done once for multiple outcomes.
Strengths of the present study include the fact that we developed and evaluated this tool on a very large and diverse cohort of postmenopausal women, in a high quality (WHI) dataset with a myriad of health and health risk variables and adjudicated morbidity and mortality outcomes. The risk-prediction model underlying the calculator has been internally validated by splitting the cohort into different regions of the country with different characteristics. Further, the WHI dataset afforded us the opportunity for long-term follow-up, up to 15 years, with relatively complete ascertainment of events--a rare strength afforded by few available datasets.
Conclusions
The present work presents the development and internal validation of an easy-to-use calculator that can yield meaningful and accurate short, medium and long-term risk predictions for multiple competing outcomes simultaneously. This represents a significant advance in the available treatment planning, health prevention and health maintenance “tools” for postmenopausal women, and the health care providers who care for them. Implications for women’s health policy and practice might relate to the need to educate providers about use of comprehensive health risk prediction tools, including responsible use of these calculators, and cautious interpretation of findings, particularly when salient disease predictors (i.e., bone mineral density, or genetic mutations) are absent from the algorithm. Guidance regarding best practices for interpreting findings that contrast with their clinical judgment and discussion of delicate matters of health priorities and intervention strategies with patients whose personal priorities and values may conflict with health prevention and intervention strategies (i.e., smoking cessation to reduce MI risk) are also warranted.
Designed for use in postmenopausal women, this risk prediction algorithm was developed and validated on a select group of women and results may therefore not be fully generalizable to other population. Nevertheless, this work offers a highly valuable empiric foundation for calculators of this sort, and it is our hope that this work will encourage further research efforts that will increase our understanding of meaningful strategies for morbidity and mortality risk prediction in this population.
Supplementary Material
Appendix Figure 1. Heatmap visualization of missing baseline data. Each row corresponds to a single woman and the columns correspond to risk predictors included in our model. The small red areas indicate missing data and blue represents available data.
Appendix Figure 2. Histograms of predicted risk for A) MI, B) lung cancer, C) hip fracture, D) death at ten years. The horizontal axis shows a woman’s predicted risk and the vertical axis shows the number of women to display the distribution of predicted risk for all outcomes in the test set.
Appendix Figure 3. Graphical display of model calibration for A) MI, B) lung cancer, C) hip fracture, D) death. The black curve displays the predicted risk (vertical axis) over 10 years according to the model by a woman’s risk percentile (horizontal axis) for myocardial infarction, lung cancer, hip fracture, and death in the test set. The blue dots represent the observed event rate for women in each decile of predicted risk to graphically display how well the predictions from our model agree with the observed data. In well-calibrated models, the blue dots representing the observed data will follow the line representing the model prediction.
Appendix Table 1: C-statistics from event-first models fit to the training and test data
Appendix Table 2a: Hazard ratios (95% confidence intervals) estimated from the 5-year event first models in training set.
Appendix Table 2b: Hazard ratios (95% confidence intervals) estimated from the 10-year event first models in training set.
Appendix Table 2c: Hazard ratios (95% confidence intervals) estimated from the 15-year event first models in training set.
Acknowledgments
The views expressed in this manuscript are those of the authors and do not necessarily represent the views of Stanford School of Medicine, the University of California, Davis, School of Medicine, the Department of Veterans Affairs, or any other institution associated with the authors on this manuscript. Drs. Haley Hedlin and Marcia Stefanick had full access to all of the data in the study. As such, they assume full responsibility for the data integrity as well as the accuracy of analyses.
The WHI is funded by the National Heart, Lung, and Blood Institute; National Institutes of Health (NIH), US Department of Health and Human Services. The NIH had no role in the study design; the data collection, analysis, or interpretation of data; in the writing of the report; or in the decision to submit the paper for publication.
The Women’s Health Initiative programs is funded by the National Heart, Lung, and Blood Institute, NIH, US Department of Health and Human Services through contracts, HHSN268201100046C, HHSN268201100001C, HHSN268201100002C, HHSN268201100003C, HHSN268201100004C.
Sources of funding: NIH
Footnotes
Conflicts of interest/financial disclosures: Jennifer G Robinson: Research grants to Institution: Acasti, Amarin, Amgen, Astra-Zeneca, Esai, Esperion, Merck, Pfizer, Regeneron, Sanofi, Takeda. Consultant: Amgen, Merck, Novo-Nordisk, Pfizer, Regeneron, Sanofi
References
- 1.Goff DC Jr, Lloyd-Jones DM, Bennett G, et al. 2013 ACC/AHA guideline on the assessment of cardiovascular risk: a report of the American College of Cardiology/American Heart Association Task Force on Practice Guidelines. Circulation. 2014; 129(25 Suppl 2): S49–S73. [DOI] [PubMed] [Google Scholar]
- 2.Wilson PW, D’Agostino RB, Levy D, Belanger AM, Silbershatz H, Kannel WB. Prediction of coronary heart disease using risk factor categories. Circulation. 1998; 97(18): 1837–47. [DOI] [PubMed] [Google Scholar]
- 3.Gail MH, Brinton LA, Byar DP, et al. Projecting individualized probabilities of developing breast cancer for white females who are being examined annually. J Natl Cancer Inst. 1989; 81(24): 1879–86. [DOI] [PubMed] [Google Scholar]
- 4.Ridker PM, Buring JE, Rifai N, Cook NR. Development and validation of improved algorithms for the assessment of global cardiovascular risk in women: the Reynolds Risk Score. JAMA. 2007; 297(6): 611–9. [DOI] [PubMed] [Google Scholar]
- 5.Kanis JA, Oden A, Johnell O, et al. The use of clinical risk factors enhances the performance of BMD in the prediction of hip and osteoporotic fractures in men and women. Osteoporosis International. 2007; 18(8): 1033–46 [DOI] [PubMed] [Google Scholar]
- 6.Leslie WD, Lix LM, Wu X, Manitoba Bone Density Program. Competing mortality and fracture risk assessment. Osteoporosis International. 2013; 24(2): 681–8. [DOI] [PubMed] [Google Scholar]
- 7.The Women’s Health Initiative Study Group. Design of the Women’s Health Initiative clinical trial and observational study. Controlled Clinical Trials. 1998; 19(1): 61–109 [DOI] [PubMed] [Google Scholar]
- 8.Curb JD, McTiernan A, Heckbert SR, et al. Outcomes ascertainment and adjudication methods in the Women’s Health Initiative. Annals of Epidemiology. 2003; 13(9 Suppl): S122–8 [DOI] [PubMed] [Google Scholar]
- 9.Austin PC. Using the standardized difference to compare the prevalence of a binary variable between two groups in observational research. Communications in Statistics - Simulation and Computation. 2009; 38(6): 1228–34. [Google Scholar]
- 10.Fine JP and Gray RJ. A proportional hazards model for the subdistribution of a competing risk. JASA 1999; 94:496–509. [Google Scholar]
- 11.Kuk D and Varadhan R. Model selection in competing risks regression. Statistics in Medicine. 2013; 32(18): 3077–88. [DOI] [PubMed] [Google Scholar]
- 12.Volinsky CT and Raftery AE. Bayesian information criterion for censored survival models. Biometrics 2000; 56(1): 256–262. [DOI] [PubMed] [Google Scholar]
- 13.van Buuren S Flexible Imputation of Missing Data. 2nd ed. New York: Chapman & Hall/CRC Press; 2018. [Google Scholar]
- 14.White IR and Royston P. Imputing missing covariate values for the Cox model. Statistics in Medicine. 2009; 28(15): 1982–98 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Harrell FE Jr., Califf RM, Pryor DB, Lee KL, Rosati RA. Evaluating the yield of medical tests. JAMA. 1982; 247: 2543–2546 [PubMed] [Google Scholar]
- 16.R Core Team. R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria: URL https://www.R-project.org/, 2015. [Google Scholar]
- 17.Gray B cmprsk: Subdistribution Analysis of Competing Risks. R package version 2.2–7. https://CRAN.R-project.org/package=cmprsk, 2014. [Google Scholar]
- 18.Varadhan R and Kuk D. crrstep: Stepwise covariate selection for the Fine & Gray competing risks regression model. R package version 2015–2.1. https://CRAN.R-project.org/package=crrstep, 2015. [Google Scholar]
- 19.van Kempen BJ, Ferket BS, Kavousi M, et al. Performance of Framingham cardiovascular disease (CVD) predictions in the Rotterdam Study taking into account competing risks and disentangling CVD into coronary heart disease (CHD) and stroke. Int J Cardiol. 2014; 171(3): 413–8. [DOI] [PubMed] [Google Scholar]
- 20.Pencina MJ, D’Agostino RB Sr, Larson MG, Massaro JM, Vasan RS. Predicting the thirty-year risk of cardiovascular disease: the Framingham Heart Study. Circulation. 2009; 119(24), 3078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Anothaisintawee T, Teerawattananon Y, Wiratkapun C, Kasamesup V, Thakkinstian A. Risk prediction models of breast cancer: a systematic review of model performances. Breast Cancer Research and Treatment. 2012; 133(1), 1–10. [DOI] [PubMed] [Google Scholar]
- 22.Crandall CJ, Larson JC, Watts NB et al. Comparison of fracture risk prediction by the US Preventive Services Task Force strategy and two alternative strategies in women 50–64 years old in the Women’s Health Initiative. The Journal of Clinical Endocrinology & Metabolism. 2014; 99(12): 4514–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.D’Amelio AM Jr, Cassidy A, Asomaning K, et al. Comparison of discriminatory power and accuracy of three lung cancer risk models. British Journal of Cancer. 2010; 103(3): 423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Tammemagi CM, Pinsky PF, Caporaso NE, et al. Lung cancer risk prediction: prostate, lung, colorectal and ovarian cancer screening trial models and validation. Journal of the National Cancer Institute. 2011; 103(13): 1058–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Park Y, Freedman AN, Gail MH. Validation of a colorectal cancer risk prediction model among white patients age 50 years and older. Journal of Clinical Oncology. 2009; 27(5): 694. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix Figure 1. Heatmap visualization of missing baseline data. Each row corresponds to a single woman and the columns correspond to risk predictors included in our model. The small red areas indicate missing data and blue represents available data.
Appendix Figure 2. Histograms of predicted risk for A) MI, B) lung cancer, C) hip fracture, D) death at ten years. The horizontal axis shows a woman’s predicted risk and the vertical axis shows the number of women to display the distribution of predicted risk for all outcomes in the test set.
Appendix Figure 3. Graphical display of model calibration for A) MI, B) lung cancer, C) hip fracture, D) death. The black curve displays the predicted risk (vertical axis) over 10 years according to the model by a woman’s risk percentile (horizontal axis) for myocardial infarction, lung cancer, hip fracture, and death in the test set. The blue dots represent the observed event rate for women in each decile of predicted risk to graphically display how well the predictions from our model agree with the observed data. In well-calibrated models, the blue dots representing the observed data will follow the line representing the model prediction.
Appendix Table 1: C-statistics from event-first models fit to the training and test data
Appendix Table 2a: Hazard ratios (95% confidence intervals) estimated from the 5-year event first models in training set.
Appendix Table 2b: Hazard ratios (95% confidence intervals) estimated from the 10-year event first models in training set.
Appendix Table 2c: Hazard ratios (95% confidence intervals) estimated from the 15-year event first models in training set.