Helical fibrillar microstructure of tendon using serial block-face scanning electron microscopy and a mechanical model for interfibrillar load transfer

Abstract

Tendon's hierarchical structure allows for load transfer between its fibrillar elements at multiple length scales. Tendon microstructure is particularly important, because it includes the cells and their surrounding collagen fibrils, where mechanical interactions can have potentially important physiological and pathological contributions. However, the three-dimensional (3D) microstructure and the mechanisms of load transfer in that length scale are not known. It has been postulated that interfibrillar matrix shear or direct load transfer via the fusion/branching of small fibrils are responsible for load transfer, but the significance of these mechanisms is still unclear. Alternatively, the helical fibrils that occur at the microstructural scale in tendon may also mediate load transfer; however, these structures are not well studied due to the lack of a three-dimensional visualization of tendon microstructure. In this study, we used serial block-face scanning electron microscopy to investigate the 3D microstructure of fibrils in rat tail tendon. We found that tendon fibrils have a complex architecture with many helically wrapped fibrils. We studied the mechanical implications of these helical structures using finite-element modelling and found that frictional contact between helical fibrils can induce load transfer even in the absence of matrix bonding or fibril fusion/branching. This study is significant in that it provides a three-dimensional view of the tendon microstructure and suggests friction between helically wrapped fibrils as a mechanism for load transfer, which is an important aspect of tendon biomechanics.

1. Introduction

Tendon's hierarchical structure allows for load transfer between its fibrillar elements across multiple length scales [1–3], which results in remarkable capabilities to withstand stress and endure repetitive loading [4]. The microscale structure and function are particularly important, because this is the scale where the cells and their surrounding collagen fibrils interface, and these mechanical interactions can have important physiological and pathological contributions. In particular, there is evidence of microscale sliding and shear load transfer that is highly likely to represent sliding between fibrils at small strains (less than 2%); and at larger strains this microscale sliding is non-recoverable, indicating tissue damage [5–7]. However, the underlying mechanisms of load transfer between tendon fibrils are still unknown. Tendon fibrils are collagenous structures (diameter ∼100 nm) that are the building blocks of tendon microstructure [8]. The fibrils are responsible for supporting external mechanical loading. Interfibrillar matrix molecules such as glycosaminoglycan chains (GAG) have been postulated to be responsible for load transfer between fibrils [9,10]; however, removal of a wide range of interfibrillar matrix components, including GAG, does not affect the mechanical response [11], or has minimal consequences [12]. It is not likely that the load transfer in tendon is solely, or majorly, mediated via the interfibrillar matrix. Thus, the microscale architecture of the collagen fibrous network itself is likely to have a role in mediating load transfer.

Serial block-face scanning electron microscopy (SBF-SEM) makes it possible to visualize the three-dimensional (3D) microscale architecture of tissue in great detail, and to reveal the fibrillar architecture with several mechanical implications [13,14]. SBF-SEM is an advanced electron microscopy technique that takes sequential SEM images of the cross-section of tissue; these images combine to provide a 3D view of the microstructure [14,15]. Using SBF-SEM with a short scan depth (8.7 µm), our group showed that there is a small fibril angular dispersion and that the fusion/branching of small fibrils might be responsible for interfibrillar load transfer [11]. Longer scan depths (approx. 100 µm) showed that fibril fusion/branching and fibril ends also exist in tendons [16], and that helical fibril patterns form in microscale during tendon development in juvenile tail tendons [17,18]. The existence of helical fibrils in collagen microscale and nanoscale was shown using 2D light, atomic force, electron and X-ray scattering microscopy in tendons and other collagenous tissues [19–26]; however, these visualizations do not provide the details of the 3D fibrillar structures.

Experimental observations and finite-element (FE) modelling suggest that helical structures in tendon may have significant mechanical effects. The rotation and high Poisson's ratio observed during tendon's axial loading have been attributed to such structures [27–29]. Furthermore, some FE models have studied the groups of helical fibrils by combining the fibrils with interfibrillar matrix in a mesh to produce the nonlinear stress response of fascicles [28,30]. Despite the potential of helical fibril organization to affect tendon's microscale mechanics, little is known about individual groups of helically wrapped fibrils and their mechanical implications. We hypothesized that helical wrapping can induce frictional load transfer between fibrils, allowing for mechanical interfibrillar load transfer without an intermediate matrix. This would imply that friction between helically wrapped fibrils can contribute to load transfer, in addition to interfibrillar matrix shear and fibril fusion/branching.

The scope of this contribution was to visualize the 3D fibril organization of rat tail tendon and to study the potential of interfibrillar friction within helically wrapped groups of fibrils to serve as a mechanism for load transfer. First, we visualized the microstructure of tendon in three dimensions using SBF-SEM. We found a complex network, with many helically wrapped fibrils. These observations informed the second part of this study, in which we used FE analysis to test the hypothesis that frictional contact between helically wrapped fibrils can transfer stress (load) between fibrils without a need for a mediating matrix. This study elucidates new aspects of tendon microstructure, providing a detailed image of fibril tortuosity, fusion/branching and organization into helical groups. Importantly, our results establish interfibrillar friction as a new mechanism for interfibrillar load transfer, among the several proposed mechanisms, advancing our knowledge about microscale structure–mechanics relationships.

2. Methods

2.1. Serial block-face scanning electron microscopy imaging

A tail tendon fascicle from a three-month-old male Sprague–Dawley rat was dissected as previously described [31], and used for SBF-SEM imaging. To prepare for imaging, the fascicle was equilibrated in PBS for 8 h, consistent with other studies [31,32], which may have increased interfibrillar spacing and fibril diameter [33], but likely did not alter overall structure such as tortuosity, and then soaked overnight at 4°C in a solution of 2% glutaraldehyde and 2% paraformaldehyde in 0.1 M sodium cacodylate buffer. The sample was subsequently stained and resin-embedded, according to established techniques [14].

The transverse cross-section was scanned in series under 1.78 kV in low-vacuum pressure with 3 µs dwelling time using an Apreo VolumeScope (Thermo Fisher Scientific, Waltham, MA, USA). After the end of the scanning of each section, a 200 nm layer of the block's face was removed by means of a mechanical slicer and the scanning was repeated. Alignment was maintained by keeping the block fixed in place throughout the imaging process. The in-plane resolution of the scans was 10 nm pixel⁻¹ with 432 slices that covers a total volume of (20.27 µm × 16.74 µm × 86.20 µm), where the third dimension is measured along the fascicle's axial direction.

2.2. Segmentation and data analysis

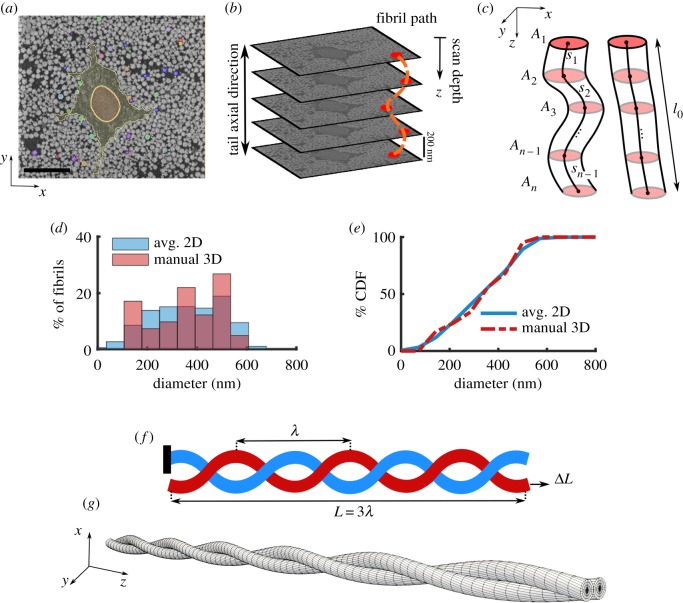
The SEM images were smoothed using a Gaussian blur filter and a representative subset of fibrils were manually segmented through the entire 3D image stack (figure 1a). Only fibrils that spanned the entire image stack, as many fibrils did not entirely fit in the scanned volume or some fibrils were otherwise discontinuous, were used for analysis (n = 42 fibrils). The segmentation was done using Seg3D (seg3d.org). Since the axial distance between subsequent images was small (200 nm), the fibrils appear as approximately circular spots that move in-plane allowing for the fibrils to be inspected and tracked through the image stack (figure 1a–c).

Figure 1.

(a) Representative SEM image and in-plane segmentation (scale bar, 5 µm), (b) SBF-SEM imaging process showing sequential stacks of images and a schematic fibril label (dotted orange line) along the tendon length, (c) schematics of fibrils with large (left) and low (right) tortuosity that shows the cross-sectional area (A_i) of fibrils throughout the scan depth and the incremental distance (s_i) between the centre of the fibrils. By comparing the (d) distribution and (e) cumulative distribution function (CDF) of the diameter using the averaged 2D automatic segmentation of all fibrils (blue) and the 3D manual segmentation of a subset of 42 fibrils (red), it is evident that the manually segmented fibrils are a representative of the full fibril population. (f) For the FE analysis, a model with three full turns is used (L = 3λ). The boundary condition is that one fibril (blue) is anchored (left), while the other fibril (red) is pulled in the axial direction (arrow, right) to a deformation of ΔL = Lε. (g) The mesh used for the FE simulations shows that the fibrils were initially in contact throughout the length. (Online version in colour.)

To confirm that the manually segmented fibrils were a representative selection of all the fibrils, we segmented all fibrils in each of 10 equally spaced 2D sections by thresholding (ImageJ, imagej.nih.gov). The distribution of fibril diameter was calculated and compared to that of the manual 3D fibril segmentations by using the Wilcoxon rank-sum test (figure 1d,e). The distributions were similar, and the median of the fibrils were not different (p = 0.927), confirming that the manually segmented fibrils were a representative sample. The manual 3D fibril segmentations were used for all subsequent analysis.

To determine the variation in fibril diameter along the length, we calculated the normalized diameter of each fibril in each section in the image stack. The normalized diameter for a fibril at section i is defined as

$$\overline{d\hspace{0.17em}}(z_i)=\frac{d(z_i)}{\tilde{d}},$$ 2.1

where z_i is the scan depth, $d(z_i)=\sqrt{4A_i/\pi }$ is the diameter of the fibril, A_i is the cross-sectional area of the fibril and $\tilde{d}$ is the median of d(z_i) across all sections (figure 1c). To quantify the complexity of the fibrillar network, we calculated the per cent tortuosity for each fibril as

$$\tau =\left(\frac{{\sum }_{i=1}^{N-1}{s}_i}{l_0}-1\right)\times 100.$$ 2.2

Here, l₀ is the end-to-end distance of the fibrils, and s_i is the magnitude of the 3D vector between adjacent fibril slice centroids and N is the number of sections (figure 1c). Half of the segmented fibrils (n = 21) were in helical groups; for these groups, we calculated the pitch (λ) by diving the total scan depth (86.20 µm) by the average number of turns. Note that tortuosity is a combination of tortuosity along the helical axis and of the helical turns themselves. For a high aspect ratio helix, as in this study, the contribution from the helical turns is small.

2.3. Statistics

The variation in diameter of fibrils along the length was tested by calculating, for each section, the 95% confidence interval of normalized diameter (equation (2.1)). To test the correlation between fibril diameter and tortuosity, we conducted a linear regression analysis between $\tilde{d}$ and τ for the fibrils in the helical groups and others, separately, using Pearson's correlation method. Statistical significance was defined as p < 0.05.

2.4. Finite-element analysis of helical fibril structures

Helical wrapping of fibrils around each other was a commonly observed feature, and we hypothesized that this helical wrapping may provide interfibrillar load transfer. To study this, we developed a 3D FE model of a pair of helical fibrils in contact (figure 1f,g) using FEBio software (FEBio2.8 febio.org) [34]. Based on the SBF-SEM microstructural analysis, the fibril diameter was taken to be 200 nm (within the range, median [min, max], of segmented fibril diameters 378 [128, 565] nm, see Results), and consistent with previous values for fibril diameter using TEM measurements of the median diameter of 144 nm for non-incubated and 161 nm for PBS-incubated samples [32]. Additionally, the helix pitch was set at 40 µm (within the range of measured pitch 38 [20, 86] µm, see Results). The entire model included three full fibril revolutions (i.e. L = 3λ, where L is the total length). The boundary condition was set as that each fibril had one free end. In one fibril, the opposite end was anchored; in the other fibril, it was set to move to create 8% axial strain (figure 1f). The value of 8% was selected from experimental data as the maximum tissue strain that fibrils may experience prior to tissue failure [5].

We used an isotropic compressible neo-Hookean constitutive relation for the fibrils [35,36]

$$\mathit{\Psi }(I_1,\hspace{0.17em}J)=\frac{E}{4(1+\nu )}(I_1-3)-\frac{E}{2(1+\nu )}\ln J+\frac{E\nu }{2(1+\nu )(1-2\nu )}{(\ln J)}^2.$$ 2.3

Where Ψ is the strain energy, I₁ is the first invariant of the right Cauchy–Green strain tensor, J is the Jacobian of deformation, E is Young's modulus, and ν is Poisson's ratio.

To solve the frictional contact problem between the fibrils, we employed the penalty method regularized with an augmented Lagrangian scheme that has been implemented in FEBio [37]. This is a surface-to-surface method, which is a robust algorithm to solve frictional contact problems that would require specialized smoothing, or higher order shape function by using a node-to-surface method [37]. In the initial configuration, the fibrils were in contact along the entire length. We used a mesh consisting of 20 160 elements (hexahedral trilinear and linear pentahedral wedge) elements and 23 478 nodes based on a mesh sensitivity analysis (figure 1g). To improve the stability of the contact algorithm, we used an auxiliary frictionless external cylindrical sheath with a weak modulus (10% of fibril modulus) to prevent separation in the intermediate steps of the iterative FE solver (see electronic supplementary material, figure S1). The auxiliary sheath was effective in increasing the stability of the model, and did not alter the final solutions. This was confirmed by using different moduli for the sheath between 0.1% and 1000% of the fibril modulus; the same mechanical response was produced in each case.

The reaction force at the anchored end of the fixed fibril was divided by the cross-sectional area and used as the measure for load transfer. To assess the sensitivity of the load transfer, we performed a one-at-a-time parametric sensitivity analysis by varying the model parameters in a range according to the reported values in the literature for fibril properties and measured range in this study, as summarized in table 1 [6,38–40,42–45]. According to the summary of literature parameter, the initial values for model parameter sensitivity analysis for solid material were set as E = 1 GPa, ν = 0.2. The friction parameter between fibrils was set as μ = 0.5, and the helix pitch was set as λ = 40 µm. Since the experimental data for the frictional coefficient of fibril-on-fibril are not available, we used an estimated range (0 < μ < 2) based on AFM indentation tests [45]. We studied the following cases by changing one parameter at a time: E = 0.1–10 GPa, ν = 0–0.4, μ = 0–2, λ = 20–80 µm. The maximum value of Poisson's ratio was set to 0.4, which was a practical decision to avoid computational singularity due to the isotropic material incompressibility limit of ν = 0.5.

Table 1.

Collagen fibril's mechanical properties for the FE analysis: Young's modulus (E), Poisson's ratio (ν), frictional coefficient (μ) in tendon unless otherwise noted.

E (GPa)	ν	µ	method	tissue	ref.
0.1–10	0–0.4	0–2	—	rat tail	current study's range for modelling
0.326 ± 0.112	—	—	tensile test MEMS	rat patellar	[38]
0.6 ± 0.2	—	—	tensile test AFM	bovine achilles	[39]
0.3–1.2	—	—	atomistic modelling	—	[40]
1.6 ± 0.4	—	—	shear-lag curve fitting	rat tail	[6,41]
1.2–2.2	—	—	indentation AFM	bovine achilles	[42]
3.75–11.5	0–0.5	—	indentation AFM	rat tail	[43]
—	2.1 ± 0.7	—	X-ray diffraction	bovine pericardium	[44]
—	—	∼0.4	indentation AFM	collagen film	[45]

To evaluate the spatial distribution of the induced stress and deformation in the fibrils, we plotted axial stress and we also plotted the normalized displacement ($\overline{u}$) relative to the mid-section of each fibril along the axial direction. We defined normalized displacement as

$$\overline{u}(z)=\frac{1}{\lambda }\left(u(z)-u\left(\frac{L}{2}\right)\right).$$ 2.4

Here, u(z) is the axial displacement at position z along the fibril length.

3. Results

3.1. Microstructure of fibrils and serial block-face scanning electron microscopy

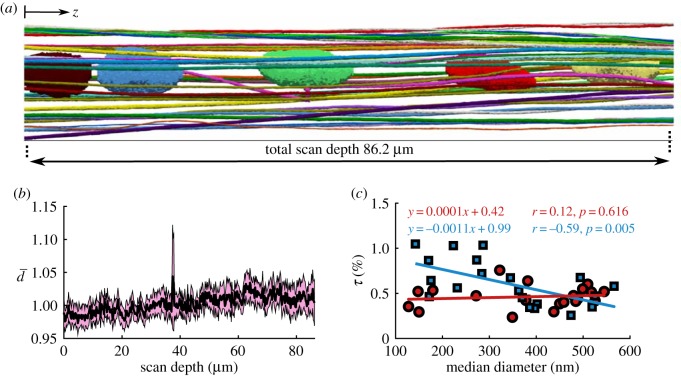
To describe the microstructure of tendon, we segmented fibrils from the SBF-SEM images in 3D. The segmentation indicated that although the fibrils are mostly axially aligned, they create a complex network around the cells (figure 2a). From the manually segmented fibrils, we quantified the fibril diameter throughout the scan depth (equation (2.1)) and the per cent tortuosity (equation (2.2)). As expected, the fibrils' diameter did not vary along the scanned fibril length of 86.20 µm (figure 2b), which is consistent with previous findings [16]. Note that the normalized fibril diameter (equation (2.1)) was not significantly different from one across the scan depth (figure 2b). This observation supports the use of a single median diameter value assigned to each fibril for correlation with the tortuosity. We quantified the per cent tortuosity (τ) of each segmented fibril (equation (2.2)), and calculated its correlation with the median diameter of the fibrils. This showed that for all of the fibrils, τ was small (less than 1%) and for the fibrils in helical groups, tortuosity was correlated with diameter (r = −0.59, p < 0.05), where for the other fibrils, it was the same across the diameter sizes (r = 0.12, p = 0.616) (figure 2c). As a result, the smaller fibrils in helical groups are more likely to have higher tortuosity, and thus have a more complex structure. For the tortuosity analysis, one fibril that made a right-angle turn and passed through the cell membrane (figure 3c, discussed below) was not included in the correlation.

Figure 2.

(a) Lateral view of the 3D segmentation along the scan length with cell nuclei. Although the fibrils are primarily axially oriented, they have a complex 3D network. (b) The 95% confidence interval (highlighted in pink) of the normalized diameter ($\overline{d}$, equation (2.1)) contains the unity value throughout the scan depth with less than 5% variation, which indicates that the diameter of the fibrils does not change along the scan depth. (c) Per cent tortuosity (τ, equation (2.2)) was calculated as a measure of the complexity of the fibrillar structure for the fibrils in helical groups (marked with blue squares) and the other fibrils (marked with red circles) separately. The helical fibril tortuosity was correlated with the diameter, with the small diameter fibrils being more tortuous; however, tortuosity was uniform for the other fibrils. (Online version in colour.)

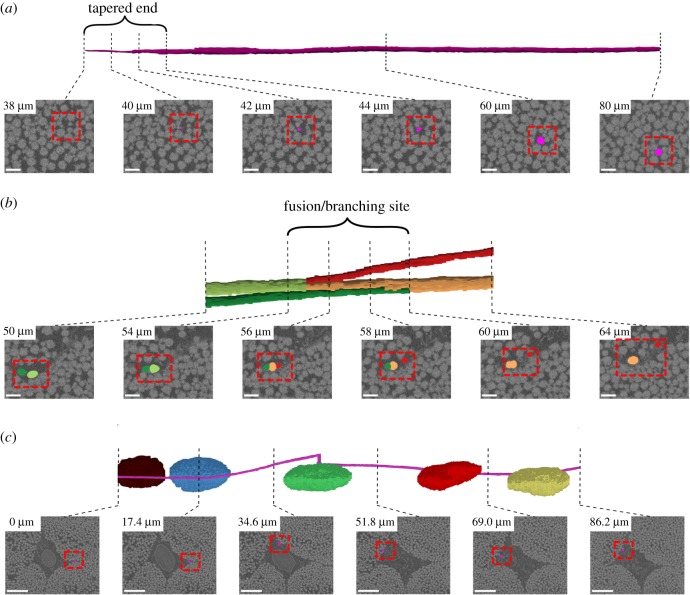
Figure 3.

Three interesting but isolated structural features were observed: (a) tapered fibril end, (b) fibril fusion/branching and (c) a helical fibril that wrapped around cells (only the nuclei are shown). For each feature, the first row includes the 3D segmentation, and the second row shows the segmentation mask overlaid on the SEM section image (dashed red box). In (a,b), scale bar, 1 µm, for (c), scale bar, 5 µm. (Online version in colour.)

We made several isolated structural observations that have potential mechanical implications: tapered fibril end (figure 3a; electronic supplementary material, video SV1), fibril fusion/branching (figure 3b; electronic supplementary material, video SV2), and one fibril that wrapped around the cells (figure 3c; electronic supplementary material, video SV3). For the tapered fibril end, in the last approximately 4 µm of the fibril length (scan depth of 38–42 µm), a reduction in fibril diameter was evident, where the fibril gradually fades away in the image sequence when approaching from the deeper scanned layers (figure 3a). At the fusion/branching site, a small fibril merges with a larger one, and in the subsequent scanned images, the larger resulting fibril branches into two distinct ones. The fusion/branching site approximately spanned 6 µm, where at least two fibrils were not distinguishable (figure 3b). Another interesting feature was one fibril that made almost a full turn around the cells (figure 3c). These features were interesting but were isolated observations in the dataset.

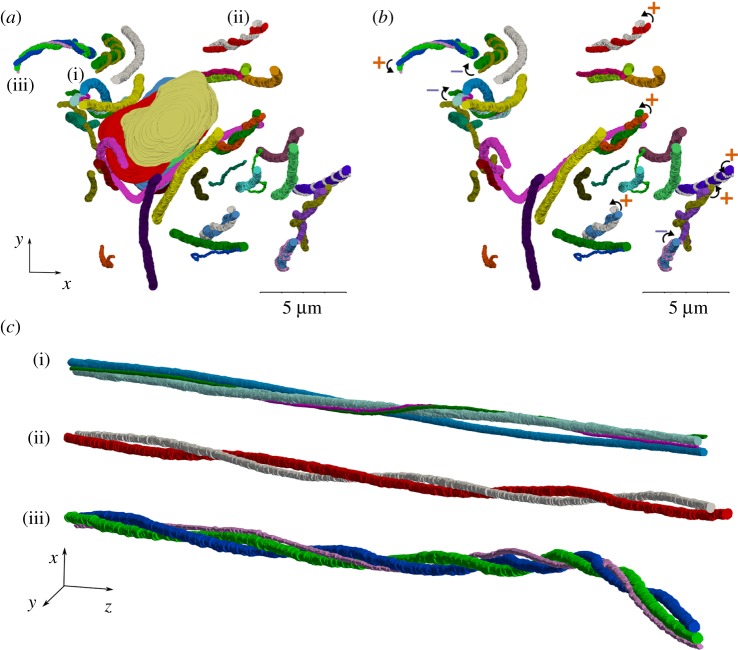
When looking at the axial view of the fibrils, we observed several helical structures (figure 4; electronic supplementary material, video SV4). In particular, many fibrils locally wrapped around each other, which contained two, three or more fibrils with both left- and right-handed helical configuration (figure 4; electronic supplementary material, video SV5). Half (21 out of 42 fibril) of the fibrils that we segmented were in helical groups, although the sampling was not purely random. Of these helical fibrils, 13 fibrils had a right-handed twist and eight were left-handed (figure 4b). These fibrils made an average of 2.2 ± 0.7 turns around each other along the scan length (figure 4c), that also corresponds to an average 45 ± 18 µm helical pitch (λ, the axial length of one full turn as described in figure 1f).

Figure 4.

Many helical structures were observed in the axial view of the fibrils that are evident in the figures (a) with and (b) without the cell nuclei. The helical fibril groups have both right (marked with +ccw curve) and left-handed (marked with – cw curve) twist. (c) Three examples of the groups of twisting fibrils with pitch ranging from 22 to 86 µm. (Online version in colour.)

3.2. Finite-element simulations of the helical fibrils

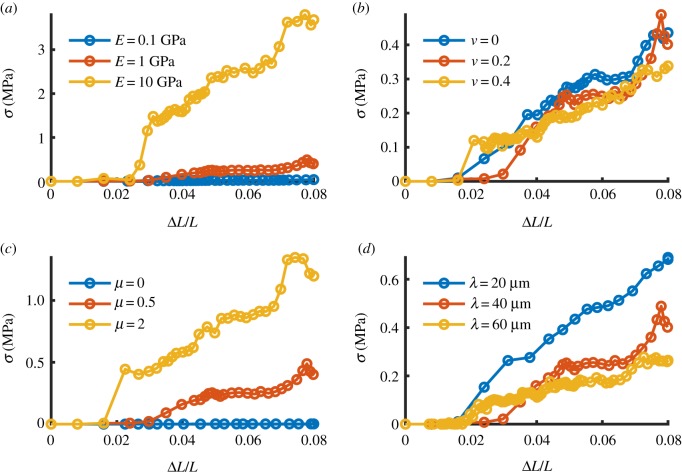
We used an FE model to test our hypothesis that frictional contact between helically wrapped fibrils can transfer stress (load) between fibrils without a need for a mediating matrix. The stress transfer was proportional to the fibril's tensile modulus (figure 5a). Further parametric studies indicated that there is no change to the transferred stress with a change in Poisson's ratio (ν) (figure 5b). As expected, the transferred load increased with an increase in frictional coefficient (μ) (figure 5c). Our results show that the load transfer decreased with an increase in pitch (λ) (figure 5d).

Figure 5.

FE analysis of stress transfer due to friction between helically grouped fibrils. Base material properties E = 1 GPa, ν = 0.2, μ = 0.5, λ = 40 µm. The transferred stress (a) increases with fibril modulus E, and (b) is insensitive to Poisson's ratio ν, (c) increases with frictional coefficient µ and (d) decreases with increasing helix pitch λ. (Online version in colour.)

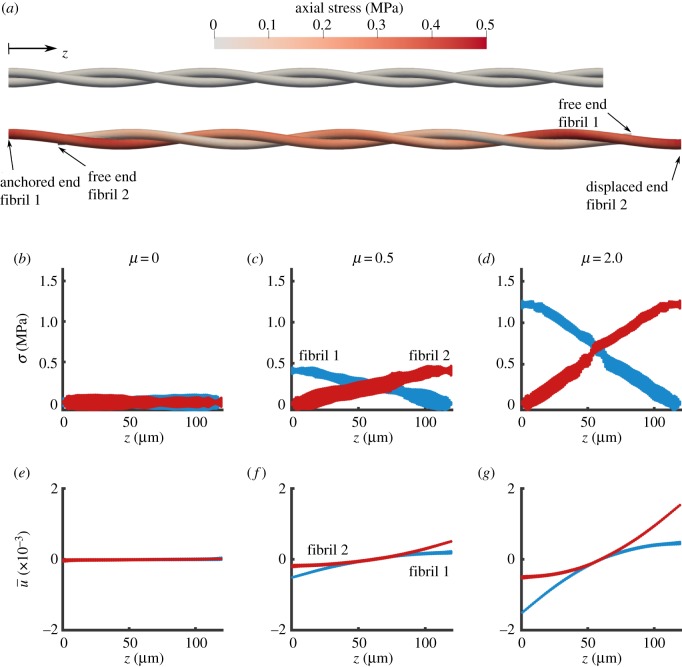
To evaluate the spatial distribution of stress and deformation along the length of each fibril and its dependence on the friction coefficient, we plotted the axial stress and axial displacement ($\overline{u}$, equation (2.4)) at maximum displacement of the pulled fibril (figure 6). The fibril stress was zero with no friction (μ = 0, figure 6b) and it increased with higher friction coefficient (figure 6c,d). The axial stress varied linearly along the length of the fibril, increasing with distance from the free boundary and the stress in each fibril was the mirror image of the stress in the other one (figure 6a–d), which is in accordance with the static equilibrium condition. Similarly, for the fibril deformation, in the zero friction case, there was no axial deformation, hence the fibrils slid freely (figure 6e). When friction was increased, the induced deformation also increased, showing a plateau at the free ends indicating no strain, which confirms the stress-free boundary condition imposed on the model (figure 6f,g).

Figure 6.

FE simulation of two helically wrapped fibrils. (a) Axial stress distribution in the fibrils for the undeformed (top) and deformed (bottom) states for µ = 0.5. The geometrical scale is compacted 10 times in the axial direction for clarity. (b–d) Stress along the length of the fibrils, and (e–g) normalized displacement ($\overline{u}$, equation (2.4)) along the length of the fibrils for various choices of friction coefficient µ. With no friction (µ = 0), there was no σ or $\overline{u}$ (b,e). As the frictional coefficient increases, the stress and the deformation increases for µ = 0.5 (c,f) and for µ = 2 (d,g). The model parameters are E = 1 GPa, ν = 0.2, λ = 40 µm. (Online version in colour.)

4. Discussion

In this study, we visualized the microscale structure of tendon fibrils in 3D using SBF-SEM and studied the mechanical implications of helical fibrils as a mechanism for interfibrillar load transfer using FE analysis. We found that tendon fibrils are not purely parallel structures and there are many helical fibrils that wrap around each other and in groups. Our FE analysis indicated that in addition to other potential mechanisms of load transfer (interfibrillar matrix and fusion/branching of smaller fibrils), the helical fibrils can also mediate load transfer through frictional mechanical contact.

4.1. Microstructure of fibrils and serial block-face scanning electron microscopy

We observed helical structures that twisted around each other (figure 4). The existence of helical fibrils was previously reported [19,25], and were suggested to be left-handed [22]; however, our findings showed a similar number of the left-handed and right-handed helical fibrils (figure 4b). The formation of the helical structure has been explained based on a fibripositor model of fibril assembly [17,46] and the helicity of subfibrillar structures [19]. The helical fibril structures explain the rotation of tendon in tension [27]. Additionally, they have been used as an explanation for the macro-scale mechanical behaviour of tendon, in particular for the low stiffness at small deformations and the large tensile Poisson's ratio [28,29]. The grouping of fibrils into helices can mediate load transfer by inducing frictional contact between fibrils during axial loading.

We observed some interesting but isolated features that can have implications for load transfer and loading on cells. For load transfer, we observed a tapered fibril end and fusion/branching, which agree with previous findings [16], with the difference that the tapered end in this study was observed in a ‘straight’ fibril in contrast with the hairpin shape in the previous study. As previously suggested by Szczesny et al. [11], an instance of fusion/branching, such as the one described above, could mediate load transfer between fibrils via direct physical connection. A free fibril end like the tapered end can also mediate load transfer by allowing microscale sliding and shear stress, which is a well-documented phenomenon in experimental studies [5,6,29]. Additionally, we observed a fibril that wrapped around the cells, which indicates that during axial loading, lateral compression can be exerted on the cells affecting tendon mechanotransduction [47]. Our fibril diameters and distribution of diameters (figure 1d,e) were larger than the juvenile tail tendon fibrils [17], and it was consistent with the other tendon studies in mature rat tail tendon [48]; however, the incubation in PBS, although facilitating the preparation of the sample for fixation and staining by increasing interfibrillar spacing, could have increased the fibril diameter [32,33]. Another potential source of error for fibril diameter would be calculation of diameter based on the assumption of circular area used in this study. Due to the small dispersion angles of the fibrils, this effect should be minimal, however, for future analysis, especially when tortuosity is high, methods such as elliptical fitting could provide a more accurate measurement of fibril diameter [14]. Fibril distribution has recently been related to circadian control [49]; however, our study did not control time of day or address this potential mechanism.

The fibril structure assessment was subject to some limitations. The SBF-SEM technique generates large 3D datasets and segmentation is consequently difficult compared to 2D SEM, creating practical limitations in data collection and analysis [16]. Although we consequently chose to do in-depth manual segmentation for only one sample, we performed several scans of additional fascicles and these scans showed similar structural features. Additionally, although the helical fibrils were easily observed and represented approximately half of the segmented fibrils, based on the current analysis, we may not conclude that in general half of the fibrils in tendon are in helical groups; related to this, it is possible that scans that cover larger axial lengths of fibrils would reveal helices with larger pitch length.

Future work using 3D automated segmentation will be needed to establish the frequency of helical fibrils and quantify helical pitch across a population. Such automatic segmentation methods could then be implemented in studies involving multiple animals at various ages, disease states, or in transgenic mouse models. Such applications would be highly instrumental in determining mechanisms of tendon development and disease, and in developing and testing tendon therapies. A separate limitation of the microstructural analysis is that our observations only included a region near the tenocytes, and other regions further away from the cells might have a different structure. Furthermore, we only scanned the tail tendon, which is a low-stress tendon; further investigation is needed to confirm the existence of helical fibril groups in other tendons.

4.2. Finite-element simulations of the helical fibrils

Interfibrillar load transfer by friction in a helical contact does not require interfibrillar matrix bonding, but the sum of its contribution over many fibrils and its relative magnitude in comparison to other load transfer mechanisms, such as chemical bonding, remains unknown. Here, the estimated magnitude of the transferred fibril stress (approx. 0.2–4 MPa) was low compared to the ultimate stress of the fibrils—typically in the range of 90 MPa [38] which matches the stress of a single fibril's tensile response based on our model parameters (see electronic supplementary material, figure S2). The large variation in mechanical parameters of fibrils (table 1) and the unknown accumulation among hundreds of fibrils hinders accurate calculation of the total load transferred in situ by the interfibrillar friction mechanism. Of particular importance, the fibril-on-fibril friction coefficient is unavailable. Thus, more experimental measurements of single fibrils and groups of fibrils are needed for more accurate estimations.

The variations in fibril stress transfer and displacement observed in the parametric FE sensitivity analysis make physical sense (figure 6). In particular, the dependence of transferred stress with modulus and frictional coefficient are expected based on Hooke's law and Coulomb's friction law, respectively, and they were shown using our FE model (figure 5a,c). Note, however, that while this study used the relatively simplified model of friction contact, additional mechanisms, such as hydrodynamic friction, molecular asperity and nonlinear dependence of friction coefficient to normal traction and other nano- and microscale tribological effects may be at play to induce load transfer between and within fibrils in the physiological system [50–53]. The decrease in reaction force by increasing the pitch of the helix, which is shown in figure 5d, can be explained by a reduction in lateral compression (normal force) on the fibrils as the pitch angle decreases and the fibrils become more parallel. The lack of dependence on Poisson's ratio was an unexpected observation that might be due to the high aspect ratio of the fibril's geometry or due to the isotropy of the constitutive relation (figure 5b). Large Poisson's ratio in tension ($\nu \sim 2$) have been reported for individual fibrils [44], which is greater than the isotropic limit of ν = 0.5. To include the effect of the Poisson ratio on the interfibrillar load transfer, anisotropy of the isolated fibril material may need to be incorporated. The curves in figure 5 were not smooth, which is potentially related to the nature of frictional contact that can switch between slip and stick conditions and cause jitter (imagine moving heavy house furniture on ceramic); however, the trends are clear, and this does not affect the outcome of the sensitivity analysis.

Interfibrillar friction causes a gradient of axial stress in the fibril. In the simulated cases (figure 6), the spatial distribution of stress variation and deformation match the distributions of stress and deformation based on established shear lag theories as applied to tendon fibrils [41]. By using frictional contact, we were able to replicate the linear response in shear lag [41], but did not reach a constant stress plateau, predicted by the shear lag model with an intermediating matrix material. Although a region of constant stress is likely to appear with a larger number of helical turns in the model, it would be extremely difficult to achieve convergence in our FEM contact model with a longer length. Moreover, our actual scan length was only 86.20 µm and our current FEM is already extrapolated to a maximum length of 180 µm. Thus, if we were to model an even longer length, we would have to extrapolate even further, which we do not think is appropriate. To further put this study in the context of prior research on theory of wire ropes, it should be mentioned that, unlike helical ropes such as elevator and bridge cables, which are continuous strands with only a small and local effect of friction [54,55]; in tissue, experimental observations demonstrate significant non-symmetrical microscale sliding that mediates load transfer. The interfibrillar sliding requires implementation of friction and contact; hence, we used the FE method for this problem over the classical wire rope theory [54].

There remains open questions regarding the physical existence and frequency of free fibril ends in mature tendon [16,56] and our single sample only demonstrated one free end; however, it is important to note that experimental tensile data suggest there are ‘effective’ free fibril ends that allow microscale sliding [57]. It is possible that fibril ends may exist in the form of tapered ends (such as figure 3a) or as physically weak links along the fibril length that can act as an ‘effective end’ due to its high compliance [58]. Further investigations are required to explore these microstructures and their contribution to interfibrillar sliding and shear load transfer. Regardless of how the effective fibril ends occur, the experimental evidence of microscale sliding and shear load transfer supports our FE model based on friction and its inherent boundary condition assumption for free fibril ends.

In conclusion, we used SBF-SEM to visualize the 3D microscale tendon structure of the fibrillar network, and used FE analysis to demonstrate that helically arranged fibrils can have the mechanical function of frictional interfibrillar load transfer. Our results showed novel microstructural configurations of collagen fibrils and cells in tendon and we showed that interfibrillar friction should be considered as another potential mechanism for interfibrillar load transfer, in addition to the previously postulated mechanisms of interfibrillar matrix shear and direct load transfer through fibril junctions. This study shows that a combined approach of SBF-SEM imaging and FE modelling is a powerful tool to study structure–mechanics relationships in tendon microstructure.

Data accessibility

The raw SBF-SEM images are available at https://zenodo.org/record/2560801. FEBio open-source code is publicly available at https://febio.org. All of the material supporting the findings of this study are available from the authors.

Authors' contributions

B.N.S. contributed to all aspects of this study; D.M.E. and J.L.C. contributed to study design and analysis. B.N.S. and J.R.N. contributed to SBF-SEM data analysis; B.N.S. and J.L.C. contributed to SBF-SEM data acquisition; B.N.S. and J.M.P. contributed to finite-element analysis. All of the authors contributed to the writing and preparation of the manuscript.

Competing interests

The authors do not have any conflict of interests to disclose.

Funding

The funding for this study was made available from NIH-NIBIB (grant no. R01-EB002425). Microscopy access was supported by grants from the NIH-NIGMS (P20 GM103446), the NSF (IIA-1301765) and the State of Delaware.

Disclaimer

The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH.