Abstract
Respiratory syncytial virus (RSV) is a common virus that can have varying effects ranging from mild cold-like symptoms to mortality depending on the age and immune status of the individual. We combined mathematical modelling using ordinary differential equations (ODEs) with measurement of RSV infection kinetics in primary well-differentiated human bronchial epithelial cultures in vitro and in immunocompetent and immunosuppressed cotton rats to glean mechanistic details that underlie RSV infection kinetics in the lung. Quantitative analysis of viral titre kinetics in our mathematical model showed that the elimination of infected cells by the adaptive immune response generates unique RSV titre kinetic features including a faster timescale of viral titre clearance than viral production, and a monotonic decrease in the peak RSV titre with decreasing inoculum dose. Parameter estimation in the ODE model using a nonlinear mixed effects approach revealed a very low rate (average single-cell lifetime > 10 days) of cell lysis by RSV before the adaptive immune response is initiated. Our model predicted negligible changes in the RSV titre kinetics at early times post-infection (less than 5 dpi) but a slower decay in RSV titre in immunosuppressed cotton rats compared to that in non-suppressed cotton rats at later times (greater than 5 dpi) in silico. These predictions were in excellent agreement with the experimental results. Our combined approach quantified the importance of the adaptive immune response in suppressing RSV infection in cotton rats, which could be useful in testing RSV vaccine candidates.
Keywords: respiratory syncytial virus, ordinary differential equations, viral kinetics, adaptive immunity, cotton rats, nonlinear mixed effects modelling
1. Introduction
Almost every individual is infected with respiratory syncytial virus (RSV) by age 2 years [1]. Although RSV infection usually does not cause any concern in healthy adults, it can cause serious morbidity and even death in children [1], immune-compromised individuals [2] and the elderly [2]. RSV infection is a major cause of hospital admissions and death worldwide in children under 5 years of age [3]. Despite the public health relevance of RSV infection there is no vaccine or antiviral therapy available and treatment is merely supportive [4].
RSV is a negative strand RNA enveloped virus with three surface glycoproteins: the (G) glycoprotein, the fusion (F) glycoprotein and the small hydrophobic protein. The virus infects the ciliated epithelial cells lining the airways of the respiratory tract by first attaching to the host cell plasma membrane via the G protein and then fusing its membrane with the membrane of the cell, a process mediated by the F protein [5,6]. Once the RSV nucleocapsid enters the cytoplasm, its polymerase produces mRNA and replicates its genome, using the host cell machinery to produce proteins and to assemble virions that are released into the local environment [5].
RSV owes its middle name to its F protein that also causes infected cells to fuse with neighbouring cells, resulting in giant cells (syncytia) containing multiple nuclei. Syncytia are more common in RSV-infected immortalized cells in tissue culture [7] than in vivo [8]. Both the innate and adaptive immune responses of the host limit RSV infection but the effectiveness of the adaptive response depends on the age of the individual [9]. The innate response is mediated by cytokines (e.g. interferons (IFNs), interleukins and growth factors) generated by the epithelial cells, macrophages, neutrophils and natural killer (NK) cells [9]. Pre-existing, maternal antibodies in neonates also play an important inhibitory role in infection initiation [10]. It takes several days (greater than or equal to 4 days) for the adaptive immune response of cytolytic CD8+ T cells, helper CD4+ T cells and antibody-producing B cells to begin to affect the infection [9].
The relative roles of the components of the innate and adaptive immune response in controlling RSV infection are not well understood. Challenges of investigating these aspects in the high-risk group, namely neonates, immune-compromised adults and the elderly contribute to this problem. This presents a major roadblock in developing vaccines and antiviral therapies.
Animal models such as cotton rats infected with laboratory strains of RSV have been successfully employed to analyse the role of the immune response in regulating RSV infection [11,12]. To this end, we combined mathematical models [13–17], based on population dynamics of viruses and the host immune response, with published [12,18] and new viral titre measurements in cotton rats to determine the roles of the adaptive and innate immune responses in controlling the viral infection. Population dynamic models have been successfully employed for describing kinetics of human immunodeficiency virus (HIV) [13,19,20], hepatitis C virus (HCV) [21] and influenza A virus (IAV) [14,15,22,23] infections within the host and some of these models have been used to develop vaccination strategies against these infections. Several population dynamic models have been developed to describe RSV infection kinetics in vitro [24–26] and in vivo [27,28]. These studies [24,27] generalize viral kinetic models developed for IAV infection for describing RSV kinetics. However, RSV and IAV infection within the host differ in several key aspects, such as IAV infection may be more self-limiting due to rapid death of target cells [8,14], whereas RSV induces few obvious cytopathic effects in vivo [8,29]. In addition, the adaptive immune response, an important regulator of RSV infection, is not considered in the above computational models describing RSV infection. The model developed here shows the importance of the adaptive immune response in generating key features of RSV infection in cotton rats which cannot be captured by simple extensions of IAV models or by the suppression of RSV replication by the innate response (e.g. type I IFN) alone. We performed detailed parameter estimation by applying a nonlinear mixed effects modelling approach [16,30] to RSV titre measurements in cotton rats of ages ranging from 3 days to 11 months. In addition, model parameters in the absence of the adaptive immune response were estimated using measurement of RSV titre and infected cells in primary well-differentiated human bronchial epithelial (HBE) cell cultures. Finally, we tested model predictions affirmatively with experiments carried out in CD8+ T-cell depleted and cyclophosphamide-treated cotton rats. Our results demonstrate the role of the adaptive immune response; in particular, the lysis of the RSV-infected epithelial cells by CD8+ T cells.
2. Results
The following four key steps were carried out to evaluate the role of the adaptive immune response in particular the CD8+ T-cell response in regulating the RSV titre kinetics in the lungs of cotton rats.
2.1. Development of a simple population dynamic model for RSV titre infection in cotton rats
2.1.1. Evaluation of distinct features of RSV kinetics
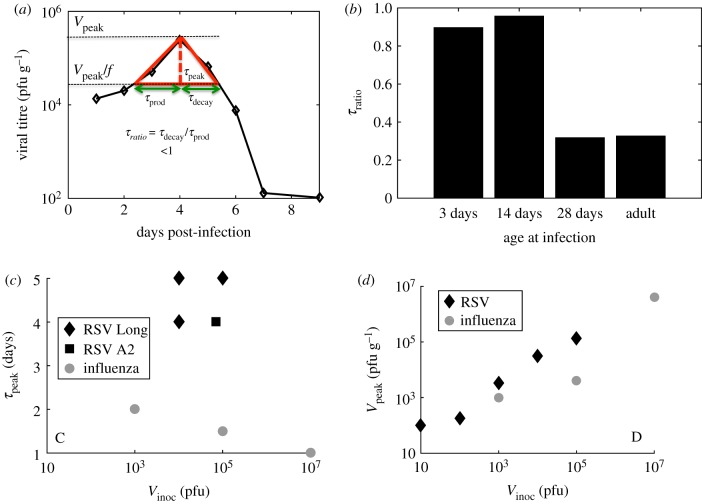
We used viral titre measurements in cotton rats inoculated with RSV reported by Prince et al. [12] to evaluate relevant timescales and to characterize the shape of the viral titre kinetic curve. We analysed the kinetic trajectories followed by the geometric means of the RSV titres measured in three animals [12]. The following timescales were calculated (figure 1a): (1) peak time (τpeak) or the time when the viral titre reached its maximum (or peak) value (Vpeak) post-infection, (2) production time (τprod) or the time duration over which the viral titre increased f-fold to reach its peak value, (3) decay time (τdecay) or the time duration where the viral titre decreased f-fold from its peak value. We used f-values of 10, 5 or 2 in our calculations. A dimensionless variable τratio = τdecay/τprod characterizes the shape of the RSV viral titre kinetic curve, i.e. τratio < 1 (or τratio > 1) indicates a slower (or faster) timescale for the production of RSV in the early stages (t ≤ τpeak) of the infection compared to the timescale for the reduction of the viral load after the peak titre is reached. We found that the RSV titres measured in the lungs of cotton rats at different ages (3 days (neonate), 14 days, 28 days or six to eight weeks (adult)) produced τratio ≤ 1 (feature#1) (figure 1b). This behaviour appears to distinguish RSV from influenza A virus (IAV) kinetics [31] in the lung of cotton rats and the IAV titre obtained from the nasal wash of human volunteers [14] which has τratio > 1. We analysed uncertainties in τratio estimation for the RSV titre data [12] in the lungs of cotton rats and for the IAV titre data [14] measured in the nasal wash of human subjects in electronic supplementary material, figure S1. The IAV titre in the lungs of the cotton rats, unlike inbred laboratory mice and humans, becomes undetectable in approximately 1–3 days due to the presence of the antiviral Mx protein [33] in the cytoplasm of infected cells in cotton rats. This specific feature (i.e. τratio < 1) of RSV titre kinetics appears to be organ dependent as the RSV titre kinetics in the nose of the same cohort of cotton rats displayed a τratio ≥ 1 at several ages of the animal cohorts.
Figure 1.
Shape features of RSV titre kinetics. (a) Schematic diagram defining τprod, τdecay, τpeak and τratio. The diamond symbols show the geometric averages of RSV titres measured in the lungs of cotton rats at age 3 days as reported in Prince et al. [12]. (b) Shows values of τratio calculated for f = 10 for the RSV titre kinetics in the lung of cotton rats of different ages (3 days to adults) as reported in Prince et al. [12]. We performed a linear interpolation to evaluate τprod and τdecay. The errors in the calculation of τratio are discussed in electronic supplementary material, figure S1. (c) Variation of τpeak with V0 for RSV (black diamonds and squares) and influenza A infection (grey circles) in cotton rats [31]. The diamonds and squares show the data obtained for infections by Long strain RSV (data for V0 = 104 pfu reported in ref. [12] and for V0 = 105 pfu in [32]) and RSV-A2 (also from the data in our experiments shown in electronic supplementary material, figure S8), respectively. (d) Variation of Vpeak with V0 for RSV [18] (black diamonds) and influenza A infection (grey circles) in cotton rats [31]. The data for influenza A infection in (c) and (d) are obtained from Ottolini et al. [31]. (Online version in colour.)
Next, we analysed the variation of τpeak and Vpeak with increasing inoculation dose (Vinocul) in cotton rats. Several experiments show τpeak for RSV infection occurs at roughly 4–5 days post-infection (dpi) irrespective of the Vinocul over a 10- to 100-fold range [12,32,34–36] (feature #2) (figure 1c). Additionally, experiments by Prince et al. [18] suggested the viral titre at 4 dpi, which we assumed to be equal or close to Vpeak, increased monotonically with increasing Vinocul (feature #3) (figure 1d). For influenza A infection in cotton rats, τpeak decreased but Vpeak increased with increasing Vinocul for the viral loads measured in the lungs (figure 1c,d) [31]. Thus, some of the above features (feature #1 and feature #2) appear to be specific to RSV infection in the lungs of cotton rats. Previous studies have used similar variables such as τpeak, duration of infection (∼τprod + τdecay) and Vpeak to characterize viral titre kinetics in adenovirus [37] and influenza A [22,38] infections, however, these studies did not investigate the variations of these variables, in particular τratio, with model parameters as we discuss later in the text.
We set out to develop a minimal model that is able to capture the above features of RSV kinetics. As a caveat, we note there are several features of the RSV titre kinetics we do not attempt to model here, e.g. the RSV titre in the lung of the cotton rats show the presence of plateaus or multiple peaks in 28-day-old or adult cotton rats [12]. The presence of these characteristics is more common in the RSV kinetics measured in the trachea (see fig. 2 in [12]) and in the nose (fig. 3 in [12]). These features could arise due to the interplay between RSV and type I IFNs that inhibit RSV replication (see Discussion). IFNs are induced within hours of RSV infection as a component of host innate immunity [9,39]. Therefore, capturing these features in a mathematical model will require a more complicated model with many unknown parameters. Since measurements of viral titres at only a few time points are available, it is likely that multiple complex models with parameters lying in wide ranges of possible values may be able to explain the data. This will make drawing mechanistic conclusions from the analysis difficult. Thus, here we pursue modelling a few broad features of the RSV titre kinetics as described above with a minimal model.
2.1.2. Description of RSV titre kinetics using ODEs
We developed a minimal model (figure 2) to describe the RSV titre kinetics in cotton rats in terms of the number of ciliated target cells (T), RSV-infected cells (I), and free virus (V). In the model, ciliated target cells become infected by RSV [8,40] and produce infected cells at rate βTV. The infected cells then produce and release virus particles, virions, at rate pI into the local environment. The infected cells are destroyed by RSV at rate δI and virions are cleared at rate cV from the local environment (figure 2). The adaptive immune response (e.g. CD8+ T-cell response), A, is modelled as a binary variable which changes from zero to unity at t = tA. The adaptive immune response eliminates the infected cells with rate δAI A. These processes are described by the following set of coupled ordinary differential equations (ODEs).
| 2.1 |
| 2.2 |
| 2.3 |
where H(x) denotes the Heaviside step function, where H(x) = 0 for x < 0 and H(x) = 1 for x ≥ 1.
Figure 2.
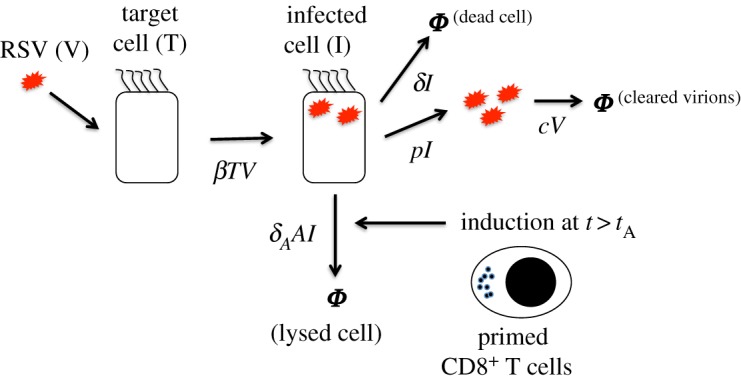
Schematic diagram for the processes described in the RSV model. Ciliated target cells (T) are infected by RSV virions (V) by a rate (βTV) producing infected cells (I). The variables (e.g. T, I, V) describing the biological entities are denoted in regular fonts and their abundances in the ODEs are indicated in italics (e.g. T, I, V). The infected cells produce new RSV virions at a rate (pI), and undergo apoptosis at a rate δI due to RSV infection. Free virions are cleared at a rate cV from the local environment due to mucociliary activity or lose infection capability. After a time lag tA post-infection, primed CD8+ T cells lyse RSV-infected cells with a rate δAIA. The CD8+ T-cell response (A) is modelled by a step function which changes from 0 to 1 at t = tA. (Online version in colour.)
The above ODEs minimally describe attachment and entry of RSV into the ciliated target cells followed by production and release of virions by the infected cells. Experiments using infection of human epithelial cells in tissue culture suggest RSV to be only mildly cytopathic [8]. We also note that the same ODEs in equations (2.1)–(2.3) with δA = 0 have been used by Baccam et al. [14] to model influenza A kinetics in humans. Pawelek et al. [23] considered a similar increase in the rate of lysis of infected cells, induced by a delayed adaptive response, in a model describing equine influenza A infection in horses. The model developed by Pawelek et al. [23] is more detailed than that in equations (2.1)–(2.3), and is composed of target cells, infected cells, host cells refractory to viral infection, free virus and IFNs. The term describing the adaptive immune response ( = δAIA) plays a key role in capturing the specific features of RSV titre kinetics (see the next section for details). Below we provide justifications regarding the processes considered in our model.
The adaptive immunity against RSV infection is complex and is mediated by T-cell and B-cell responses activated by RSV antigens processed and presented by antigen presenting cells. Activated CD8+ T cells clear the infection by directly eliminating infected epithelial cells. In addition, CD4+ T cells and regulatory T cells participate in limiting the infection by influencing B cell responses and controlling the cytokine milieu [9]. In cotton rats, CD8+ and CD4+ T-cell responses are initiated around 4 dpi. In mice, CD8+ T cells start expanding around 4 dpi and peaks between 8 and 10 days following RSV infection [41]. The description of the CD8+ T-cell response in the model ignores such gradual increases. Activated B cells secrete antibodies to neutralize the virus, however, these neutralizing antibodies arise in cotton rats at later times (greater than or equal to 6 dpi in experiments by Prince et al. [12]) when the RSV titres are already receding. In our experiments, neutralizing antibodies were detected around day 12 when the RSV titres reached very low or undetectable values. Therefore, we did not account for neutralizing antibodies in our model.
We found that depletion of CD4+ T cells in our experiments does not change viral clearance indicating that during the acute phase the CD4+ T-cell response does not play a substantial role in clearance (electronic supplementary material, table S1). Therefore, we assumed only the CD8+ T-cell response in the minimal model. The nature of the CD8+ T-cell response can be complex [9], however, we modelled the response minimally by a binary variable A that is turned on at a time tA post-infection. This is done in the spirit of finding the simplest model that can be used to describe the viral titre kinetics by approximating the kinetics of many other parts of the immune and host-response associated with the infection. We compared the above model with a model where kinetics of the CD8+ T-cell response increases continuously during the infection and is explicitly described [15] (electronic supplementary material, text S1, table S2 and figure S2). In this model, activated CD8+ T cells undergo clonal expansion and lyse infected cells (I), and the activation of the CD8+ T cells is induced by the infected cells. The model with a continuously increasing CD8+ T-cell response does not generate a better fit to the data from Prince et al. [12] and shows a continuous decrease in the peak time τpeak as the inoculation dose is increased (electronic supplementary material, text S1, table S2 and figure S3). The comparison of the fits across the models were performed using the Akaike information criterion (AIC) [42].
We investigated whether innate immune responses mediated by IFNs (type I IFN such as IFNα and IFNβ) alone were able to describe the RSV titre kinetics measured by Prince et al. [12] and others [12,18,32,34–36]. Blanco et al. [39] showed that IFNα mRNA peaks at 1 dpi, and mRNA expression for IFNγ, which is secreted by cytotoxic T cells and NK cells, is induced at 1 dpi and peaks at 4 dpi in the lungs of RSV-infected cotton rats. There is a time delay of few hours (e.g. approx. 7 h for an immune response protein Trfd1 in dendritic cells [43]) between the changes in mRNA expression and the changes in protein levels [43]. We applied a model developed by Baccam et al. [14] that included an IFNα response to describe the above data. In this model, IFNα is induced by IAV infected cells after a time delay (τ) and suppresses viral replication. Our calculations showed that for values of τ ≤ 1 dpi, the above model was not able to describe all three features of RSV titre kinetics as discussed in the previous section (electronic supplementary material, table S2 and figures S2 and S3). However, for a larger value (approx. 4.5 dpi) of the delay τ, which is much longer than the delay in IFNα response observed by Blanco et al. [39], the above model captures the three main features of the RSV titre kinetics (electronic supplementary material, text S1, table S2 and figures S2 and S3). For the large value of τ, the above model becomes mechanistically similar to our model where a large and sudden decrease in viral replication is introduced after t > 4 dpi. Therefore, though the model with τ ≈ 4.5 dpi was able to describe the RSV titre kinetics, the IFNα response in the model was inconsistent with the experimental observations. We also investigated if the innate immune response alone in an IAV infection model proposed by Handel et al. [15] is able to describe the RSV infection kinetics in the lungs of cotton rats. The model developed by Handel et al. [15] included a generic innate immune response that suppressed viral replication and can potentially describe IFN responses. We found that the above model without any adaptive immunity described the RSV titre kinetics well; however, the variation of the peak RSV titre Vpeak and the peak time τpeak with increasing inoculation dose (Vinocul) did not reproduce the trends measured by Sami et al. [18] (figure 1) (electronic supplementary material, text S1, table S2 and figures S2 and S3). Thus, the IFN response alone, with experimentally observed timescales, in two different models that contained the basic processes of RSV kinetics was not able to describe all the features of the RSV kinetics. Since our model with a CD8+ T-cell response alone was able to capture the main features of the RSV titre kinetics we chose not to account for any IFN response in our model in order to keep the number of parameters at minimum. In addition, maternal antibodies [9] were not detected in the cotton rats in our experiments and thus we did not include their effect in our model.
Recent work [25] showed that the loss of infectivity of RSV A Long strain is better described by a non-exponential decay (e.g. Weibull decay ∝ exp(−(ct)k) where k < 1). The modification of the rate (∼[k(ct)k−1]cV) of viral clearance that produced a Weibull distributed non-exponential clearance of RSV in our model did not produce a better fit to the available RSV titre kinetics data in the lungs of cotton rats compared to the linear rate of viral clearance in equation (2.3) (electronic supplementary material, text S1, table S2 and figure S2). Next, we investigated if the simple model in Baccam et al. [14] with a Weibull decay in viral clearance is able to described the RSV titre kinetics. We found that if the parameter k in the above model is increased to large values (k ≈ 16.5), it is able to capture the three main features of the RSV titre kinetics (electronic supplementary material, text S1, table S2 and figures S2 and S3). However, Beauchemin et al. [25] estimated k to be around 0.3 in their in vitro experiments. The simple model in Baccam et al. [14] with a large k value in the Weibull decay generates a large increase in viral clearance after t > 4 dpi and produces a similar effect as the CD8+ T cells response in our model. Since the relation between the CD8+ T-cell response and parameters in the above modification of the Baccam et al. [14] model becomes tenuous and it is difficult to biologically justify parameter values (e.g. k) in this model we did not pursue developing our models along this direction any further.
2.1.3. Elimination of the infected cells by the CD8+ T-cell response in the ODE model is necessary for generating key features of RSV infection kinetics
An important difference between our minimal model (equations (2.1)–(2.3)) and that in Baccam et al. [14] is the inclusion of the CD8+ T-cell response via the –δAIA term in equation (2.3). Here, we analyse the key role played by this term in generating the three basic features of the RSV titre kinetics. The detailed parameter estimation for our model is described in the next two sections. We found that the presence of the CD8+ T-cell-induced elimination of the infected cells is important for generating these features. In the absence of this response (or δA = 0), the RSV titre kinetics were limited to the region τratio ≥ 1(figure 3a). Note, when δA = 0, the resulting ODE model is the same as that used by Baccam et al. [14] to describe influenza A infection in humans. By contrast, for δA ≠ 0, τratio spanned a wider region (0 < τratio ≤ 1 and τratio > 1) which included the measured values of τratio and the peak time for the RSV titre kinetics in cotton rats (figure 3a). Furthermore, the increase of the peak RSV titre Vpeak and the weak dependency of the peak time τpeak with increasing inoculum dose (V0) was captured by our model only for δA ≠ 0 (figure 3b,c). Note that the comparison in figure 3b shows a smaller value of Vpeak at the lowest inoculation dose (10 plaque-forming units (pfu)) than that predicted in the model; such slower increases of Vpeak with increasing V0 at low V0 values could arise in the model due to specific forms (e.g. Michaelis–Menten) of dependence of the CD8+ T-cell expansion on viral titres [37] which are not considered in our model.
Figure 3.
The adaptive immune response (δA ≠ 0) in the minimal model is essential for generating the unique features of RSV titre kinetics. (a) Values of τratio and τpeak obtained for the viral titre kinetics in the ODE model with (δA ≠ 0; RSV model) and without (δA = 0; IAV model) the adaptive immune response. 458285 number of cases for the RSV model and 460492 number of cases for the IAV model are shown. The above data were generated by varying parameters (β, δ, δA, tA, p, c and V0) in the ODE model (equations (2.1)–(2.3)) 10 000-fold across base values (electronic supplementary material, table S3). The τratio in the above cases were evaluated at f = 10, f = 5 or f = 2. The qualitative features for the data do not depend on the specific value of f. See main text and figure 1a for the definition of f. (b) The filled diamonds show the data obtained from Sami et al. [18]. Variation of Vpeak with Vinoc in the ODE model with (δA ≠ 0; RSV model) and without (δA = 0; IAV model) the adaptive immune response. The ODE model was solved for a V0 = const. × Vinoc. The constant was evaluated by estimating V0 (table 3) by fitting the ODE model to the RSV titre kinetics at a Vinoc = 104pfu for adult cotton rats measured by Prince et al. [12], i.e. const = 104 pfu/(2.4 × 103 pfu). Vpeak for other Vinoc values were calculated by evaluating V0 using V0 = const. × Vinoc and then solving the ODEs by setting the rest of the parameters to the values estimated for adult cotton rats (tables 2 and 3). (c) Variation of τpeak with V0 in the ODE model with (δA ≠ 0; RSV model with parameters for adult cotton rats as shown in tables 2 and 3) and without (δA = 0; IAV model) the adaptive immune response. The measured data (filled diamonds and squares) for RSV shown in figure 1c are provided here as reference. (Online version in colour.)
2.2. Modelling kinetics of RSV infection of human bronchial epithelial cultures grown in vitro
We modelled RSV infection kinetics in HBE cultures in vitro with three main goals: (1) evaluate how well the ODE model without an adaptive immune response (δA = 0) is able to capture the in vitro kinetics. (2) Estimate parameters in the model. Since in the in vitro experiments performed here we measured the kinetics of both the number of infected cells (I) and the RSV titre (V) at many time points and control the inoculation dose (V0) and the number of target cells (T0), these measurements provide well defined data to constrain parameter estimates in the model. (3) Use the estimated parameters as an initial guess for the model parameters for fitting the ODE model to the in vivo RSV titre measurements. The parameter estimation for the in vivo model was carried out using nonlinear mixed effects modelling [42] which involves optimization of cost functions in large dimensions. Therefore, the parameter estimates are often sensitive to the initial guesses and the allowed ranges for the parameter values [16,30]. We will assume that the common model parameters estimated in the in vitro experiments for HBE cultures provide biologically relevant values and therefore use these values as initial guesses for estimating parameters for RSV infection in the cotton rat.
The HBE cells were grown in tissue culture and were infected with a human strain of recombinant RSV expressing green fluorescent protein (rgRSV) [8]. Each tissue culture well was washed with 100 µl of medium every 24 h and the RSV titre in the 100 µl of washed medium was measured (see Material and methods for details). We set δA = 0 for the RSV infection model of in vitro infection since there is no adaptive immune response in this case. Equation (2.3) was modified to account for the periodic removal of RSV in the following manner. The RSV titre, V(t), was reduced by a fixed fraction (λ) of V(t) at the times t = tr ≡ {24 h, 48 h, 72 h, 96 h, and so on} when the culture was washed with the medium. The viral kinetics for tr + Δ ≤ t ≤ tr + 24 h (Δ → 0) was evaluated by numerically solving equations (2.1)–(2.3) with δA = 0 and initial conditions at t = tr + Δ as T(tr + Δ) = T(tr), I(tr + Δ) = I(tr), and V(tr + Δ) = V(tr) − λ V(tr). λV(tr) and I(tr) were fitted with their experimental counterparts over a span of 13 dpi (figure 4). The fits to the RSV titres and the number of infected cells averaged over two experiments are shown in figure 4. The parameters T0, p, I0, V0 and c were determined from the experiment and a simple analysis of the kinetics (see Material and methods). V0 was known from the experimental protocol. The two model parameters β and δ were estimated using nonlinear least squares where the sum of the squares of the difference between the values obtained for the model simulation and in vitro measurements corresponding to the logarithms of the viral titre and the number of infected cells was minimized for a fixed value of λ. The calculations were performed using the lsqcurvefit subroutine in MATLAB that uses the Levenberg–Marquardt algorithm [44]. The confidence intervals (CIs) were calculated using the nlparci subroutine in MATLAB that evaluates the CI using a linear approximation of the sum of the square residuals (SSR) [45] and by using the Jacobian and the SSR outputs obtained from lsqcurvefit at the estimated parameter values for the calculation. Next, we evaluated the minimum value of the cost function at different values of λ (electronic supplementary material, figure S4). The parameter values, the CIs, and the reproductive number R0 = βpT0/(cδ) are shown in table 1 for λ = 0.3, where the cost function was at the minimum for all the values of λ that were considered (electronic supplementary material, figure S4). R0 provides an estimate of the average number of new infections initiated by a single-infected cell [46]. Fit of the model in equations (2.1)–(2.3) at δA = 0 with different initial conditions or different sets of fitting parameters generated marginally better fits (electronic supplementary material, table S4C) or did not improve the fits (electronic supplementary material, table S4A).
Figure 4.
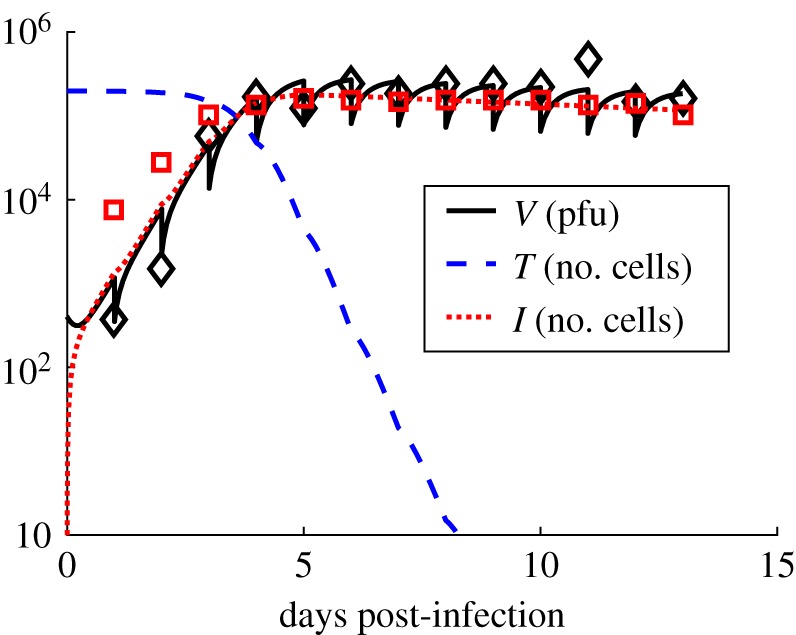
Model fits for the RSV infection in vitro. Shows the kinetics of the numbers of target cells (T) (dashed line), infected cells (I) (dotted line) and the free RSV virions (V) (solid line in black) in our ODE model describing infection of HBE cells by rgRSV in vitro where the free RSV virions were removed (or washed out) each day for measuring the viral titre. The data from the experiment for V and I are shown in open black diamond and open red square symbols, respectively. The sudden decrease at each day in the viral titre represents the removal of the medium for the measurement. We assumed that a fixed fraction λ of the V is removed during the measurement. λ is set to 0.3 for the data shown above. The other parameters are set to the values in table 1 in the main text. (Online version in colour.)
Table 1.
Estimated parameter values and confidence intervals (95% CI) for the model fits (figure 4) to the data measured in vitro experiments with HBE.
| T0 (no. cells) | V0 (no. pfu) | I0 (no. cells) | β (pfu−1 d−1) | δ (d−1) | p (pfu cell−1 d−1) | c (d−1) | R0 |
|---|---|---|---|---|---|---|---|
| 198 000 | 400a | 0a | 1.317 × 10−5 (1.106 × 10−5 − 1.567 × 10−5) | 0.0555 (0.0215 – 0.1434) | 3.83a | 2.3a | 78.24 |
aValues known from experimental protocol or calculated by analysing the measured data.
We further investigated whether including a temporal delay in infection of RSV by HBEs and the release of the virions by the infected cells lead to a better fit to the data (further details in the electronic supplementary material, text 2, table S4 and figure S5). Following the approach in Kakizoe et al. [47], we included an eclipse phase in the model, where infected HBE cells contain the viral genome and possibly viral proteins but do not produce free virus. We considered two situations where the time delay in virus production due to the presence eclipse phases is distributed exponentially or non-exponentially (Erlang distribution [47]). Comparison of the models with the eclipse phase and the model described in equations (2.1)–(2.3) for δA = 0 using AICc scores showed that if the HBE cells in the model residing in the eclipse phase are assumed to generate fluorescent proteins and hence are counted as infected cells then the models with the eclipse phase are better suited than the model without the eclipse phase to describe the RSV infection kinetics in the HBEs (electronic supplementary material, text 2, tables S4A and S4C, and figure S5). The model with the eclipse phase with an exponential or a non-exponential distribution of time delays described the data almost equally well. The above results suggest that intercellular processes related to synthesis of RSV proteins are likely to be active in the eclipse phase but there is a delay in assembly and budding of RSV. However, further investigations are required to establish this result. Therefore, for the sake of parsimony we use the simpler model in equations (2.1)–(2.3) to model the in vivo kinetics.
2.3. Estimation of model parameters for RSV kinetics in the lungs of cotton rats
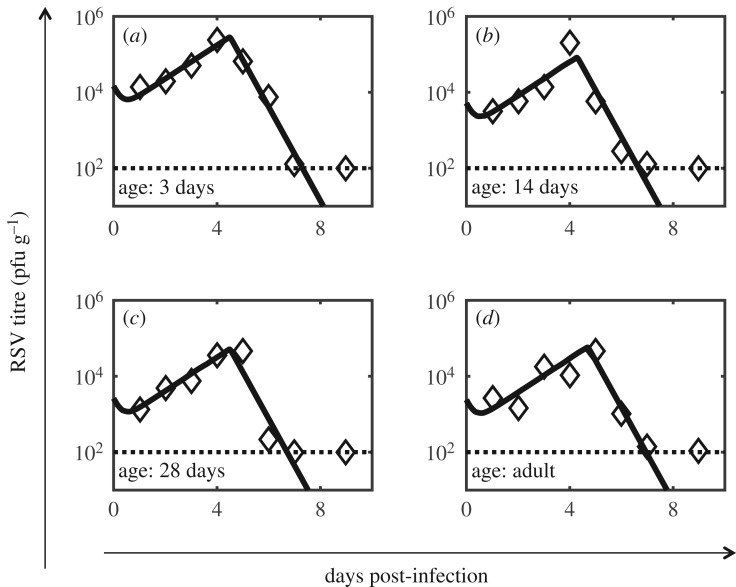
We modelled RSV infection of target epithelial cells (T0) present in a gram of lung tissue in cotton rats. We used the data published in Prince et al. [12], where cotton rats of different ages were infected with the Long strain of RSV. The parameter estimation and their dependence on the age of the cotton rat cohorts were carried out using nonlinear mixed effects modelling [16,30] (details in Material and methods section). T0 and I0 were held fixed at 1 × 107 cells and 0 for all ages. Assuming 10% of the cells in the large and small airways in the lung are ciliated epithelial cells and that there are about 108 cells in 1 g of lung tissue in cotton rats we estimated T0 ≈ 1 × 107 cells. The fraction of ciliated cells is possibly larger (approx. 30%) if only the cells in large airways are considered. When we increased T0 three times the value quoted above, the value of β decreased about threefold and the rest of the parameters remained the same. Therefore, we fixed the value of T0 to 1 × 107 cells for all the calculations here. We first considered the parameters, to be random unknown parameters that varied with age a. The logarithms of the parameters θa were assumed to vary randomly across ages with a normal distribution with mean values μ and standard deviations ω [16,42,48]. The differences between the logarithms of viral titres measured in vivo (or v(data)) and computed in the model (or v(model)) were assumed to follow a normal distribution with zero mean and a variance σ2. The likelihood function where was maximized to estimate the parameter values. The distribution for parameter p was centred around the value μp = 3.83 pfu (cell)−1 d−1 to constrain value of p to biologically reasonable values as changes in p were compensated by β due to the dependence between p and ß in the model (see electronic supplementary material, text S3 and figure S6). Additionally, δA was constrained to be less than or equal to 30 d−1 to maintain biologically reasonable values. Details of the method are described in Material and methods. The numerical calculations were performed using the software package Monolix [42]. In order to determine the variability of the maximum-likelihood estimate (MLE) of θa across ages we evaluated the standard deviations ω for the parameters (electronic supplementary material, table S5) which quantified the variations of the parameters across ages. (approx. 0.76) and (2.43 × 10−8) showed the largest and the lowest value, respectively. The standard deviations for V0 and tA were greater than 0.01 while the rest of the parameters were distributed with standard deviations less than 10−6. The low variability in parameter values of β, p and c indicated that the age-specific variations in these parameters with low standard deviations cannot be resolved well using the available viral titre data points. Therefore, we considered β and c as age independent but unknown population parameters in our next parameter estimation step (p was fixed at 3.83 pfu (cell)−1 d−1 to constrain covariations between β and p). The estimated population parameters δ and δA were associated with large values of 95% CIs (see Material and methods and electronic supplementary material, table S5 for details) providing empirical evidence for the lack of identifiability [42] of δ and δA. Therefore, in order to evaluate a reasonable range of values for δ and δA we simultaneously varied δ and δA over a biologically feasible range, and at each value of {δ, δA} we estimated the other parameters and calculated the corresponding AIC value (electronic supplementary material, figure S7). The AIC values indicated that the best fit to the data occurred in the range 0 < δ < 5 d−1 and 5 d−1 < δA < 50 d−1 (electronic supplementary material, figure S7) where the alternate models are larger than the minimum AIC model by < 2 points. If δ assumes similar values in vivo as estimated approximately 0.05 d−1 in vitro (table 1), then the cytolysis of RSV-infected cells will contribute minimally in the time duration (approx. 4–5 dpi) the viral titre reaches the peak. Therefore, we chose value δ = 0, and set δA = 30 d−1 for estimating the rest of the parameters below. The age-dependent random parameters were chosen to be and T0 and I0 were fixed to the same values as in the previous estimation. The estimated parameters and their 95% CIs are listed in tables 2 and 3. The fits to the data are shown in figure 5. Calculations of correlations between the parameters show that except β − c (Corr ∼ 0.8) and β − V0 (Corr ∼ −0.54), the other pairs are weakly (|Corr| < 0.5) correlated (electronic supplementary material, table S6B).
Table 2.
Estimated values and the 95% CIs for the age independent parameters in the in vivo model describing the RSV titre kinetics in the lungs of cotton rats measured in Prince et al. [12].
| T0 (no. cells) | I0 (no. cells) | ß (pfu−1 d−1) | δ (d−1) | p (pfu cell−1 d−1) | δA (d−1) | c (d−1) |
|---|---|---|---|---|---|---|
| 1 × 107a | 0a | 1.07 × 10−7 (8.27 ×10−8 − 1.38 × 10−7) | 0.0a | 3.83* | 30.0a | 2.99 (2.68–3.33) |
aThe parameters are not estimated by fitting.
Table 3.
Estimated age-dependent parameters V0(a) and tA(a) for the in vivo model describing the RSV titre kinetics the lungs in cotton rats measured in Prince et al. [12].
| age (a) | V0(a) (no. pfu g−1) | tA(a) (day) |
|---|---|---|
| 3 days | 1.46 × 104 | 4.47 |
| 14 days | 5.20 × 103 | 4.26 |
| 28 days | 2.62 × 103 | 4.47 |
| adult | 2.40 × 103 | 4.68 |
Figure 5.
Model fits for the RSV titre kinetics in the lungs of cotton rats. The model fits to the data obtained from Prince et al. [12] are shown for the RSV titre kinetics in the lungs of the cotton rats where the animal cohorts of age (a) 3 days, (b) 14 days, (c) 28 days and (d) six to eight weeks (adults) were infected with the Long strain of RSV. The estimated parameter values are shown in tables 2 and 3. The dashed horizontal line shows the level of detection.
The standard errors, the percentage errors, and the standard deviations (ω) for the distributions pertaining to these parameters are shown on electronic supplementary material, table S6. The estimates show that V0(a) varies substantially across the age a more than any of the other age-dependent parameters. V0(a) also shows a systematic decrease with increasing age which could be due to the increasing size of the lungs as the animal ages (see Discussion). The variation of tA(a) with the age is less than a day which is smaller than the time intervals (1 day) of the measurements. The value of c increased slightly (i.e., from 2.3 d−1 in vitro to 2.99 d−1 [2.68–3.33] in vivo) from its value estimated in vitro. This small increase could appear surprising as the virus in the lung can additionally be cleared by phagocytic cells as well as by the mucociliary escalator. However, the in vitro system (HBE cells in medium) considered here might not represent the in vivo system (cells in the microenvironment in the lungs of cotton rats) because the in vitro system is devoid of the above additional host-mediated clearance mechanisms. The decrease in the value of β for the in vivo model compared to the in vitro model is mainly due to the change in the unit from the in vitro to the in vivo estimate (electronic supplementary material, text S4), and the estimated value of δ or its value for the in vitro estimate is too small to have an appreciable effect on the RSV titre kinetics for the duration of the infection. Thus, the decay in the RSV titre kinetics in vivo appears to be mainly controlled by the introduction of the CD8+ T-cell response (non-zero δA) to the in vitro model.
2.4. Test of model predictions: CD8+ T-cell response induces faster decline in RSV kinetics
We decreased the value of δA in the best-fit model developed in the last section to predict the changes in the RSV titre kinetics when the CD8+ T-cell response is suppressed. Our model simulations showed that reducing δA resulted in slower decay of the viral titre after the titre peak (Vpeak) is reached (figures 6 and 7). However, the kinetics before attaining the peak titre remained the same (figures 6 and 7). We tested this prediction by comparing RSV titre kinetics measured in the lungs of the wild-type and the CD8+ T-cell depleted geriatric (aged over nine months; figure 6) or adult cotton rats (figure 7). We provide further details below regarding the experiments and the modelling that was performed. Cotton rats at different ages, namely, neonates, adult and geriatric (over nine months), were inoculated intranasally with 105 TCID50 of strain RSV-A2. Homogenates from the nose and lung were titrated at various days after infection. The nonlinear mixed effects model developed for estimating parameters in the previous section was applied to the lung RSV titres (electronic supplementary material, figure S8). The estimated parameters are listed in electronic supplementary material, tables S7–S9. The estimation of the parameters δ and δA encountered similar issues with identifiability as that we faced for fitting the data in Prince et al. [12]. We performed a similar analysis by varying δ and δA (electronic supplementary material, figure S7) and choose fixed values of δ and δA at δ = 0 and δA = 30 d−1. Most of the parameter values estimated were of the same order of magnitude as those estimated for the data in Prince et al. [12]. The main differences in the estimated parameters for the Prince et al. [12] data and our dataset was in V0(a) which was smaller than that estimated in the previous section. The correlations between the estimated parameters are shown in electronic supplementary material, table S8C. The values of β and c were slightly higher than their counterparts estimated in the previous section. The parameters, V0, tA and c, showed larger age-dependent variations compared to the other parameters; the values are listed in electronic supplementary material, table S8B.
Figure 6.
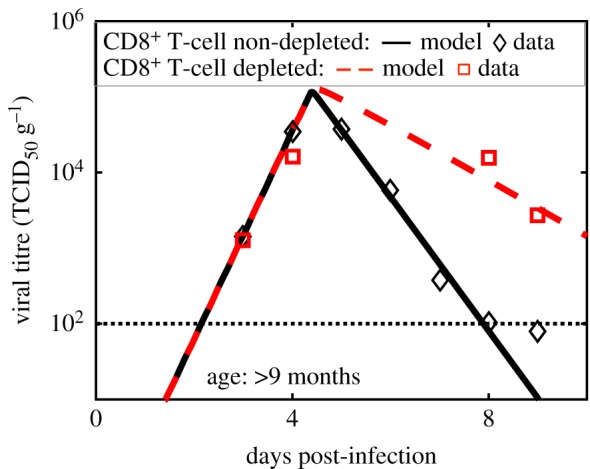
Test of model prediction for the RSV titre kinetics in the lungs of CD8+ T-cell depleted geriatric cotton rats. The model (dashed line) predicted that reduction of the strength (δA) of the CD8+ T-cell response alone by approximately threefold does not affect the RSV titre at early stages (less than 4 days) of infection, however, it increases the RSV titre at later days (greater than 4 days). This model prediction was tested by measuring RSV titre kinetics in the lungs of the CD8+ T-cell non-depleted and CD8+ T-cell depleted geriatric (age ∼ 270+ days) cotton rats. As predicted by the model, the RSV titres in the CD8+ T-cell depleted cotton rats do not change appreciably from their counterpart in the CD8+ T-cell non-depleted at 3 and 4 dpi, however, at later stages of infection (5 and 6 dpi), the RSV titres in the lungs of the immunosuppressed cotton rats are substantially larger than that in the CD8T cell non-depleted cotton rat. (Online version in colour.)
Figure 7.
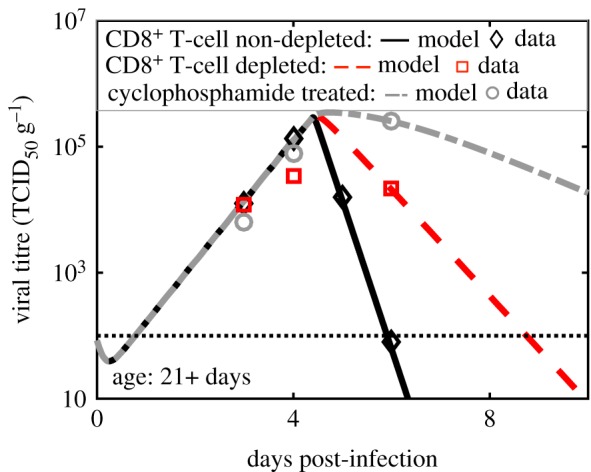
Test of model prediction for the RSV titre kinetics in the lungs of CD8+ T-cell depleted or cyclophosphamide-treated adult cotton rats. The model prediction regarding the reduction of CD8+ T-cell response was tested by measuring RSV titre kinetics in the lungs of CD8+ T-cell non-depleted, CD8+ T-cell depleted, and cyclophosphamide-treated geriatric (age ∼ 270+ days) cotton rats. In cyclophosphamide-treated cotton rats, all rapidly replicating cells are depleted thus the adaptive immune response is severely blocked in these animals. Depletion was modelled by reducing δA alone by approximately fivefold and cyclophosphamide treatment was modelled by reducing δA alone by 10-fold. The varying effects only take place approximately after 5 days. Similar to figure 7, the model prediction is in excellent agreement with the measurements. (Online version in colour.)
These predictions were compared against RSV titre kinetics measured over 9 days in lungs of CD8+ T-cell depleted geriatric (figure 6) and adult (figure 7) cotton rats (see Material and methods for details). The δA values in the best-fit models for the adult and the geriatric cotton rats were reduced about fivefold and threefold, respectively, to generate predictions for RSV titre kinetics in those animals. The model predictions were in excellent agreement with the experiments (figures 6 and 7).
The model prediction was also tested in cotton rats injected with the drug cyclophosphamide, a drug that suppresses the adaptive immune response by inhibiting cell proliferation. The effect of cyclophosphamide was modelled by decreasing δA 10-fold. The RSV titre kinetics in the lungs of cyclophosphamide injected adult cotton rats agreed well with the model prediction (figure 7), where the RSV titre kinetics in the cyclophosphamide-treated cotton rats did not change appreciably from that of the control during the early stages (less than 4 dpi) of the infection but increased substantially at later days (more than 4 dpi). The RSV titres measured in the nose of CD8+ T-cell depleted or cyclophosphamide-treated cotton rats agreed qualitatively with the model predictions as well (electronic supplementary material, figures S9 and S10).
3. Discussion
We developed a simple ODE model to describe RSV titre kinetics in the lungs of cotton rats. The model described several unique features of RSV titre kinetics, estimated key parameters pertaining to RSV infection, and demonstrated the importance of the CD8+ T-cell response in the decline of the RSV titre in the lungs of cotton rats. The ODE model generated quantitative predictions regarding the RSV titre kinetics in CD8+ T-cell depleted or immune-suppressed cotton rats that were in excellent agreement with experiments. Previous modelling efforts described RSV titre kinetics using ODEs in vitro [25,26], in ferrets [28] and in human subjects [27]. These models did not investigate the role of the adaptive immune response in regulating the RSV infection kinetics. Therefore, the minimal model developed here provides an experimentally validated simple mathematical model with predictive power for investigating RSV titre kinetics in the presence of an adaptive immune response in cotton rats.
RSV infection induces cytokine responses (e.g. type I IFN) which suppress RSV replication in cotton rats [39] as well as in humans [9]. We analysed the influence of IFNα on RSV replication by fitting several models [14,15] that were developed to describe suppression of influenza A infection by IFNα to the RSV titre kinetic data. However, comparisons of the AIC values (electronic supplementary material, table S2) and analysis of the necessary features of RSV infection (electronic supplementary material, figure S3) showed that our minimal model with the CD8+ T-cell response better described all the features of RSV titre kinetics in the lungs compared to the other models with realistic values of parameters. The above comparison and the higher RSV titres in CD8+ T-cell depleted cotton rats demonstrate that IFNα response alone is not sufficient to explain the RSV infection dynamics in the lungs of the cotton rats.
The ODE model developed for RSV titre kinetics in vivo was modified to describe RSV titre kinetics in vitro where HBE cells were infected with a human strain of recombinant RSV expressing green fluorescent protein (rgRSV). The model incorporated specific steps following the in vitro experiments where RSV virions were washed from the culture wells every 24 h and measured (details in Material and methods section). We estimated model parameters for the RSV kinetics by fitting the model with the measured values of RSV titres in the supernatant and the counts of infected cells. The estimate of the reproductive number [46] R0 in vitro is approximately 80 suggesting a high infection capability of RSV (i.e. approx. 80 new infections initiated on average by a single-infected cell during its lifetime). The estimated replication rate in vitro is high, (approx. 3 pfu per day per infected cell), and the average timescale for HBE cell death due to RSV infection is more than 10 days, which indicates that RSV infection is not readily cytopathic. The low rate of infected cell death and large RSV replication rate contributed towards the large value of R0 in vitro. The fit of the in vitro data (electronic supplementary material, figure S5) to a model with eclipse phase indicated that there could be a time delay between the infection of the host cells by RSV and the production of the free virions by infection cells, and, the intercellular processes related to synthesis of RSV proteins are likely to be active within the host cells residing in the eclipse phase. Models including the eclipse phase [26] have been used previously to describe RSV infection kinetics in vitro, however, those modelling studies did not fit the kinetics of infected cell populations as we report here.
The parameter estimates for the in vivo data were much less constrained compared to that for the in vitro data as the RSV titres alone were measured in vivo. We used nonlinear mixed effects modelling [16,30] to estimate the model parameters, as well as their dependences on the age of the RSV-infected cotton rats. The values of the parameters δ and c that generated best model fits to the RSV titre kinetics measured in Prince et al. [12] were similar to that estimated for the in vitro measurements. The value of δ, the rate of infected cell death due to RSV infection alone, were less than 0.1/day both in vitro and in vivo demonstrating that cell apoptosis by RSV infection is not a major factor in eliminating infected cells during the course (greater than 10 days) of the infection. Estimation of the parameter δA (approx. 30 d–1) showed that CD8+ T cells eliminated the infected cells at a high rate where the number of infected cells decreased by a log in 0.1 days after the CD8+ T cells was induced. Accurate estimations of δ and δA were not possible as these parameters turned out to be poorly identifiable. Measurement of the kinetics of infected cells could help to better estimate these parameters. The age dependency of the RSV titre kinetics in the lung appeared to be predominately captured by the systematic decrease of V0 with increasing age. Since the size of the lung increases as cotton rats age, the amount of inoculum initiating infection in a fixed volume of lung (or V0) decreases with increasing age. This could underlie the age-dependent behaviour of V0 we found in our parameter estimation.
The values of model parameters appeared to depend on the strain of RSV used for infecting the cotton rats. Prince et al. [12] used the Long strain of RSV, whereas our experiments used the RSV-A2 strain. Some of the estimated parameters (ß and c) for the RSV titres measured in our experiments were slightly higher compared with those estimated for the data in Prince et al. [12]. Similar values of the parameters δ and δA produced the best fits to the model in both the experiments. However, V0 shows a decrease with increasing age for the infection with the Long strain of RSV, whereas this systematic decrease is absent in the infection with the RSV-A2 strain, and the values of V0 were larger for the Long strain (electronic supplementary material, tables S7–S9). Thus, the values of some of the model parameters appear to depend on the specific strain used in infecting the cotton rats, however, the mechanisms underlying this dependence remain unclear at this point.
Several RSV titre mean trajectories in the nose and trachea of cotton rats contained more than one peak [12]. However, it is difficult to assess if the RSV titre in the same animal showed multiple peaks over time because the animals were sacrificed at each measurement. Given the small sample size of the animal cohort (three cotton rats per cohort) the presence of the multiple peaks in the geometric average of the RSV titre could be attributed to animal-to-animal variation of the RSV titre. However, if the multiple peaks in the geometric average of the RSV titre are representative of the actual RSV titre kinetics in an individual cotton rat, such behaviour can arise due to the interplay between induction of IFNs by RSV and the suppression of viral replication by the IFNs. Baccam et al. [14] showed a time delay in the induction of IFNα and the suppression of the viral replication by IFNα could produce multiple peaks in IAV titre kinetics. This is because the IFNs decrease viral load by suppressing viral replication, however, lowering the viral load also decreases the induction of IFNs thereby increasing viral replication, thus, the viral titre decreases after the first peak and then increases again to generate a second peak. Similar mechanisms can be included in the simple model to describe potential multiple peaks in the RSV titre as well.
The approach carried out here combining simple mechanistic modelling and measurements of RSV titres shows the usefulness of simple mathematical models in deciphering mechanisms that underlie RSV production kinetics in cotton rats. The RSV disease in children can be caused by the tissue damage generated by a dysregulated host immune response to the RSV infection where the severity of the disease is associated with the intensity of the pro-inflammatory response [49]. Though the virus initiates the host-response the relationship between the viral load and the dysregulated immune response is not well understood [50]. Vaccine candidates aim to deal with both the RSV viral load and the inflammatory response. Extending the simple model developed here to describe the associated inflammatory response could be an attractive future direction. Recent experiments measuring a wide variety of inflammation markers in animal models [51] and human subjects [52] could provide useful datasets for this exercise. Viral kinetic models ranging from a simple mechanistic model such as the one considered here to complex multiscale models that are extensions of these simple models have been widely successful for viral infections such as HIV, HCV and influenza in understanding basic mechanisms of viral infections as well as designing therapies pertaining to antiviral drugs and vaccine candidates [53]. A recent study [54] provides such an example where a simple RSV kinetic model was combined with pharmacokinetic and pharmacodynamics models to describe the effects of a nucleoside viral replication inhibitor drug. We hope the simple model studied here will play a similar role for RSV infection.
4. Material and methods
4.1. Experiments
4.1.1. Preparation of HBE cultures
4.1.1.1. HBE cell recovery and culture
The nasal respiratory epithelium was sampled using a cytology brush and the cells were recovered as previously reported [55]. Mucus was removed through treatment with 14.3 µM 2-mercaptoethanol and cells were cultured using the mCRC method [55]. At passage 1, all cells in the culture were basal cells. Basal cells were plated onto collagen-coated 0.33 cm2 transwell membranes at 2 × 104 cells per membrane as previously described [55]. At confluence, the medium was changed to PneumaCult-ALI Base Medium containing the 10X supplement, the 100X supplement, heparin, and hydrocortisone (Stem Cell Technologies, Vancouver, BC, Canada).
4.1.1.2. Inoculation of HBE cultures with RSV, imaging and virus yield
On differentiation day 21, HBE cultures were washed with DMEM to remove mucous and inoculated with 400 pfu of recombinant green fluorescent protein (GFP) expressing RSV strain A2 (rgRSV224) [56] in 50 µl of DMEM for 4 h at 37°C. Each day post-infection wells were imaged to quantify GFP fluorescence. Fluorescence was quantified with the MIPAR program (MIPAR Image Analysis; Worthington, OH) by multiplying the mean intensity fluorescence by the surface area fraction of fluorescence. A separate set of wells were washed with 100 µl of DMEM containing 10% FBS, and the wash was snap frozen on dry ice and stored at −80°C for later quantification. The number of infectious viruses in each wash was quantified by serial dilution titration on HEp-2 cells in 96-well plates and counting the green fluorescent foci at 24 h post-inoculation.
4.1.2. In vivo measurements
4.1.2.1. Animals
Inbred cotton rats (Sigmodon hispidus) were obtained from Envigo, Inc. (Indianapolis, IN) and housed in standard polycarbonate cages in a barrier system, or obtained from an in house breeding colony. Corncob bedding (Cincinnati Labs Supply) was used for all experimental animals. Environmental conditions were constant at 22 ± 2°C, 30–70% relative humidity, and 12 L : 12 D cycle. Cotton rats of both sexes between day 3 days and 11 months of age were used. Euthanasia was performed via CO2 inhalation. Cotton rats were purchased specific pathogen-free and maintained in colonies free of endo- and ectoparasites, mouse parvovirus 1 and 2, minute virus of mice, mouse hepatitis virus, murine norovirus, Theiler murine encephalomyelitis virus, mouse rotavirus, Sendai virus, pneumonia virus of mice, reovirus, Mycoplasma pulmonis, lymphocytic choriomenginitis virus, mouse adenovirus and ectromelia virus according to quarterly health monitoring of sentinel (CD1) mice exposed to 100% pooled dirty bedding from colony animals at each cage change.
4.1.2.2. Infection
Cotton rats were anaesthetized via isoflurane inhalation before being inoculated intranasally with virus diluted in PBS to a final inoculation volume of 100 µl (10 µl for neonates).
4.1.2.3. Virus
Stocks of RSV A/2 were grown in HEp-2 cells in MEM/2% fetal bovine serum. When infection reached a cytopathic effect of approximately 80%, cells were scraped from the flask in the growth media. The cells were briefly frozen at −80°C, thawed, and centrifuged at 3000 r.p.m. for 15 min at 4°C to remove all large cellular debris. The supernatant was collected and placed on top of 15 ml of a 35% sucrose cushion and centrifuged at 15 000 r.p.m. in a Sorval SS 34 rotor for 5 h at 4°C to pellet the virus. Virus pellets were re-suspended in MEM/10% trehalose, and TCID50 was determined by titration on Hep-2 cells [57]. Each virus stock was aliquoted and frozen in liquid nitrogen. Aliquots were thawed immediately prior to use and were only used once to prevent loss of titre due to repeated cycles of freeze–thaw.
4.1.2.4. CD8+ T-cell depletion
Cotton rats were inoculated on day −1, 1 and 3 after infection with 0.5 mg of a cotton rat CD8 alpha specific monoclonal antibody [58].
4.1.2.5. Cyclophosphamide treatment
Cotton rats were injected with 150 mg kg−1 cyclophosphamide (Sigma-Aldrich) intraperitoneally on day −4, day −2 and day 0 of infection.
4.1.2.6. Statistical analysis
Data are represented as means ± s.d. Statistical significance was determined by multiple t-tests using the Holm–Sidak method, with alpha = 0.05, and each cell type was analysed individually, without assuming a consistent s.d. Data were analysed using Prism version 7.00 for Windows (GraphPad Software, La Jolla, CA, USA).
4.2. In silico modelling
4.2.1. In vitro estimates of T0, V0, I0, p and c
T0 was by calculated by assuming that about 30% of the total number of epithelial cells in the culture is ciliated. The total number of cells in the surface of the well was estimated to be about 660 000 cells by counting the number of cells in a cross-section, then estimating the diameter of a single epithelial cell by assuming a cell to be a sphere, and finally calculating the number of cells that can be present on the surface of the culture. The number of infected cells was calculated in experiments using the proportion of the fluorescent target cells. Note the number of T0 can vary depending on the human donors and the fraction of the cililated cells in the HBEs can also vary between 30 and 80%. We carried out an alternate case of parameter estimation where we assumed 70% of the cells are ciliated (electronic supplementary material, table S4D). The parameter values in electronic supplementary material, table S4D when used as initial conditions did not change the estimations for the in vivo data. The parameter c was determined from the measurement of the decay of RSV in vitro [59]. We fitted an exponential decay (∝ exp(−ct)) to the data (fig. 3 in [59]) showing the decay of surviving fraction of Long RSV strain at between 0 and 2.0 days at 37°C in [59]. The linear fit estimated c as 2.3 d−1. We assumed this value of c to hold for the rgRSV strain in our in vitro experiments. The parameter p was determined by assuming that the viral titre and the infected cell kinetics reach the steady state beyond 8 dpi, i.e. dI/dt = dV/dt = 0. Thus, at the steady state, pISS = cVSS or p = cVSS/ISS, where, ISS and VSS are the steady values of I and V, respectively. ISS is measured in the experiments (figure 4) and VSS is related to the measured viral titre (VSS(measured)) as VSS = VSS(measured)/λ, where λV is the amount of RSV titre removed from the culture to estimate the number of RSV virions (see main text for details). We estimated p ( = cVSS(measured)/(λ ISS)) to be equal to 3.83 pfu cell−1 d−1 using λ = 0.3. V0 (=400 pfu) and I0 (=0) were known from the experimental protocol.
4.2.2. Extraction of data from published literature
We used a software tool GraphClick (http://www.arizona-software.ch/graphclick/) to extract data from Prince et al. [12] (fig. 1 and 3 in their manuscript), Sami et al. [18] (fig. 1 in their manuscript) and Ottolini et al. [31] (fig. 3 in their manuscript). The extracted data are made available to the readers in an excel file provided with the manuscript. We also used GraphClick to extract data from fig. 3 of [59].
4.2.3. Nonlinear mixed effects modelling of RSV titre kinetics in cotton rats of different ages
The temporal profiles of RSV titres measured in the lungs of the cotton rats showed differences with respect to age (figure 5). Therefore, we modelled the RSV infection kinetics in cotton rats with parameter values that depended on the age (a in {3 days, 14 days, 28 days, Adult}) of the animal. We employed a nonlinear mixed effects approach that models age-specific parameters as random effects. For each time point t in (1, 2, 3, 4, 5, 6 and 7) dpi and for each age a, we computed the logarithm of the geometric mean RSV titre (denoted log10 V(data)(t, a)) at a particular time t, where the geometric mean was taken over three cotton rats in an animal cohort of age a. The parameters of the nonlinear mixed effects model were estimated by maximum likelihood (ML), which (provided that there is a unique maximum) finds the set of parameter values that makes the RSV titre log10[V(data)(t, a)] most probable. Given the age-specific random effects parameters, and the fixed parameters (T0 and I0), V(model)(t, θa) was obtained by numerically solving the ODEs in equations (2.1)–(2.3). For brevity, we will denote log10[V(data)(t, a)] and log10[V(model)(t, θa)] as v(data)(t,a) and v(model)(t, θa), so that the nonlinear mixed effects model is more succinctly expressed by: . Here, the residual error (denoted hε) may depend on fixed parameters (or measured covariates) through the function h, whereas, ε is distributed as a normal distribution of zero mean and an unknown variance σ. We assume that ε(t) is independent of age and h = 1. We also fixed σ to the standard deviation in the dataset σ(data) = 1/(# of timepoints × # of age groups × # of animals in the animal cohort)∑{t,a,α} (v(data)(α) (t,a) − v(data) (t,a))2 ≈ 0.5, where v(data)(α) (t,a) denotes the log of the RSV titre measured at time t in a cotton rat (indexed by α) that belong in the animal cohort of age a. For our dataset for inoculation with RSV-A2 strain σ(data) = 0.244. θais given by the sum of two components: unknown but fixed (i.e. age independent) parameters μ, and random parameters ηa that depend on the age a, i.e. θa = μ + ηa. The random vector ηa is assumed to be independent and identically distributed (iid) following a specified probability distribution function (e.g. normal distribution with zero mean and an unknown variance ω). The joint probability distribution function is given by where, ρ = {σ, μ, ω}, is the likelihood function:
The likelihood function is maximized to evaluate the maximum-likelihood estimates (MLE) of the unknown fixed parameters, namely μ, and the variances of the ω of the random parameters.
The probability distribution for each age-specific parameter vector θa is estimated from the conditional probability distribution, where is the ML estimate of ρ. Computing the ML estimates of the model parameters involves optimization of high-dimensional cost functions. The landscape of the cost function for nonlinear models is typically multimodal, containing more than one local maximum. As such, parameter estimates are often dependent on the initial guesses for the parameter values, which are then used to seed the search. In order to get a sense of the range and the initial guess for the model parameters we first fitted the model for measurements in an in vitro experiment where both the RSV load and number of infected cells can be measured at many time points and the inoculation dose and the number of target cells can be clearly controlled.
The in vivo estimations were carried out using the in vitro estimates of the common parameters (table 1) as initial conditions to a simulated annealing algorithm in Monolix, with initial guesses of tA = 4.5 days and δA = 25 day−1 A−1. In order to set δA < 30 d−1 A−1, Monolix requires to estimate a value (δA)actual = 30 – (δA)estimated. The simulated annealing algorithm is designed to converge to the neighbourhood of the global maximum of the likelihood. The parameter outputs from the simulated annealing simulations were used (after 2000 exploratory steps) as initial guesses for a Nelder–Mead simplex algorithm in Monolix to converge to the local maximum from the neighbourhood provided by the simulated annealing. The unit of β was changed for the in vivo models following the formula derived in the electronic supplementary material, text S4. In the Monolix software package, we used no variability for fixed parameters, with five burn-in iterations, 2000 exploration iterations, 200 smoothing iterations (no auto-stop permitted) and the simulated annealing option defined as previously stated. The parameter values do not dependent appreciably on the specific value of the large number (greater than 2000) of iterations that was performed (electronic supplementary material, figure S11). All Monolix project files used can be found in the data available to the readers.
4.2.3.1. Calculation of the confidence intervals
For a specific population parameter θpop, the 95% CIs are given by [42]
where and s.e. ≡ standard error.
The standard errors are calculated from the inverse of the Fisher Information Matrix estimated within the software package Monolix (2018R1) [42].
Supplementary Material
Acknowledgements
Portions of this were done under the auspices of the UD Department of Energy under contract 89233218CNA000001. D.W. and J.D. acknowledge the computation support provided by the Ohio Supercomputer Center (OSC). D.W. acknowledges help from the Monolix staff with using the software.
Ethics
All animal experiments were approved by the Institutional Animal Care and Use Committee of The Ohio State University.
Data accessibility
All Monolix project files used can be found in the electronic supplementary material.
Authors' contributions
D.W., M.E.P., S.N. and J.D. planned the projects. D.W. and K.U. developed computational models and carried out simulations. D.W., W.C.L.S., A.S.P. and J.D. analysed data. M.E.P., S.D.R. and S.N. planned the experiments. O.H., P.C., T.K. carried out the experiments. All the authors contributed to the writing of the manuscript and the electronic supplementary material.
Competing interests
We declare we have no competing interests.
Funding
This work was partially supported by NIH grant nos. R01-GM103612 to J.D., P01-AI112524 to M.E.P. and S.N., and R01-AI078881 and R01-OD011095 to A.S.P., and a grant from the Cystic Fibrosis Foundation to M.E.P.
References
- 1.Smyth RL, Openshaw PJ. 2006. Bronchiolitis. Lancet 368, 312–322. ( 10.1016/S0140-6736(06)69077-6) [DOI] [PubMed] [Google Scholar]
- 2.Falsey AR, Hennessey PA, Formica MA, Cox C, Walsh EE. 2005. Respiratory syncytial virus infection in elderly and high-risk adults. New Engl. J. Med. 352, 1749–1759. ( 10.1056/NEJMoa043951) [DOI] [PubMed] [Google Scholar]
- 3.Paramore LC, Ciuryla V, Ciesla G, Liu L. 2004. Economic impact of respiratory syncytial virus-related illness in the US. Pharmacoeconomics 22, 275–284. ( 10.2165/00019053-200422050-00001) [DOI] [PubMed] [Google Scholar]
- 4.Mazur NI, et al. 2015. Lower respiratory tract infection caused by respiratory syncytial virus: current management and new therapeutics. Lancet Respir. Med. 3, 888–900. ( 10.1016/S2213-2600(15)00255-6) [DOI] [PubMed] [Google Scholar]
- 5.Hacking D, Hull J. 2002. Respiratory syncytial virus—viral biology and the host response. J. Infect. 45, 18–24. ( 10.1053/jinf.2002.1015) [DOI] [PubMed] [Google Scholar]
- 6.Hicks SN, Chaiwatpongsakorn S, Costello HM, McLellan JS, Ray W, Peeples ME. 2018. Five residues in the apical loop of the respiratory syncytial virus fusion protein F2 subunit are critical for its fusion activity. J. Virol. 92, 00621-18 ( 10.1128/JVI.00621-18) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Tristram DA, Hicks W, Hard R. 1998. Respiratory syncytial virus and human bronchial epithelium. Arch. Otolaryngol. Head Neck Surg. 124, 777–783. ( 10.1001/archotol.124.7.777) [DOI] [PubMed] [Google Scholar]
- 8.Zhang L, Peeples ME, Boucher RC, Collins PL, Pickles RJ. 2002. Respiratory syncytial virus infection of human airway epithelial cells is polarized, specific to ciliated cells, and without obvious cytopathology. J. Virol. 76, 5654–5666. ( 10.1128/JVI.76.11.5654-5666.2002) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Openshaw PJ, Chiu C, Culley FJ, Johansson C. 2017. Protective and harmful immunity to RSV infection. Annu. Rev. Immunol. 35, 501–532. ( 10.1146/annurev-immunol-051116-052206) [DOI] [PubMed] [Google Scholar]
- 10.Niewiesk S. 2014. Maternal antibodies: clinical significance, mechanism of interference with immune responses, and possible vaccination strategies. Front. Immunol. 5, 446 ( 10.3389/fimmu.2014.00446) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Niewiesk S, Prince G. 2002. Diversifying animal models: the use of hispid cotton rats (Sigmodon hispidus) in infectious diseases. Lab. Anim. 36, 357–372. ( 10.1258/002367702320389026) [DOI] [PubMed] [Google Scholar]
- 12.Prince GA, Jenson AB, Horswood RL, Camargo E, Chanock RM. 1978. The pathogenesis of respiratory syncytial virus infection in cotton rats. Am. J. Pathol. 93, 771. [PMC free article] [PubMed] [Google Scholar]
- 13.Nowak M, May RM. 2000. Virus dynamics: mathematical principles of immunology and virology. Oxford, UK: Oxford university press. [Google Scholar]
- 14.Baccam P, Beauchemin C, Macken CA, Hayden FG, Perelson AS. 2006. Kinetics of influenza A virus infection in humans. J. Virol. 80, 7590–7599. ( 10.1128/JVI.01623-05) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Handel A, Longini IM, Antia R. 2010. Towards a quantitative understanding of the within-host dynamics of influenza A infections. J. R. Soc. Interface 7, 35–47. ( 10.1098/rsif.2009.0067) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Best K, Guedj J, Madelain V, de Lamballerie X, Lim SY, Osuna CE, Whitney JB, Perelson AS. 2017. Zika plasma viral dynamics in nonhuman primates provides insights into early infection and antiviral strategies. Proc. Natl Acad. Sci. USA 114, 8847–8852. ( 10.1073/pnas.1704011114) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Smith AM, Ribeiro RM, Perelson AS. 2018. Population dynamics of host and pathogens. In Systems immunology (eds Jayaprakash Ciriyam, Das Jayajit), pp. 265–278. Boca Raton, FL: CRC Press. [Google Scholar]
- 18.Sami IR, Piazza FM, Johnson SA, Darnell ME, Ottolini MG, Hemming VG, Prince GA. 1995. Systemic immunoprophylaxis of nasal respiratory syncytial virus infection in cotton rats. J. Infect. Dis. 171, 440–443. ( 10.1093/infdis/171.2.440) [DOI] [PubMed] [Google Scholar]
- 19.Perelson AS, Neumann AU, Markowitz M, Leonard JM, Ho DD. 1996. HIV-1 dynamics in vivo: virion clearance rate, infected cell life-span, and viral generation time. Science 271, 1582–1586. ( 10.1126/science.271.5255.1582) [DOI] [PubMed] [Google Scholar]
- 20.Lu C-L, et al. 2016. Enhanced clearance of HIV-1-infected cells by broadly neutralizing antibodies against HIV-1 in vivo. Science 352, 1001–1004. ( 10.1126/science.aaf1279) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Neumann AU, Lam NP, Dahari H, Gretch DR, Wiley TE, Layden TJ, Perelson AS.. 1998. Hepatitis C viral dynamics in vivo and the antiviral efficacy of interferon-α therapy. Science 282, 103–107. ( 10.1126/science.282.5386.103) [DOI] [PubMed] [Google Scholar]
- 22.Hadjichrysanthou C, Cauët E, Lawrence E, Vegvari C, de Wolf F, Anderson RM. 2016. Understanding the within-host dynamics of influenza A virus: from theory to clinical implications. J. R. Soc. Interface 13, 20160289 ( 10.1098/rsif.2016.0289) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Pawelek KA, Huynh GT, Quinlivan M, Cullinane A, Rong L, Perelson AS. 2012. Modeling within-host dynamics of influenza virus infection including immune responses. PLoS Comput. Biol. 8, e1002588 ( 10.1371/journal.pcbi.1002588) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Gonzàlez-Parra G, De Ridder F, Huntjens D, Roymans D, Ispas G, Dobrovolny HM. 2018. A comparison of RSV and influenza in vitro kinetic parameters reveals differences in infecting time. PLoS ONE 13, e0192645 ( 10.1371/journal.pone.0192645) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Beauchemin CA, Kim Y-I, Yu Q, Ciaramella G, DeVincenzo JP. 2019. Uncovering critical properties of the human respiratory syncytial virus by combining in vitro assays and in silico analyses. PLoS ONE 14, e0214708 ( 10.1371/journal.pone.0214708) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Pinky L, Dobrovolny HM. 2016. Coinfections of the respiratory tract: viral competition for resources. PLoS ONE 11, e0155589 ( 10.1371/journal.pone.0155589) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.González-Parra G, Dobrovolny HM. 2015. Assessing uncertainty in A2 respiratory syncytial virus viral dynamics. Comput. Math. Methods Med. 2015, Article ID 567589 ( 10.1155/2015/567589) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.González-Parra G, Dobrovolny HM. 2019. The rate of viral transfer between upper and lower respiratory tracts determines RSV illness duration. J. Math. Biol. 79, 467–483. ( 10.1007/s00285-019-01364-1). [DOI] [PubMed] [Google Scholar]
- 29.Zhang L, Collins PL, Lamb RA, Pickles RJ. 2011. Comparison of differing cytopathic effects in human airway epithelium of parainfluenza virus 5 (W3A), parainfluenza virus type 3, and respiratory syncytial virus. Virology 421, 67–77. ( 10.1016/j.virol.2011.08.020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lavielle M, Mentré F. 2007. Estimation of population pharmacokinetic parameters of saquinavir in HIV patients with the MONOLIX software. J. Pharmacokinet. Pharmacodyn. 34, 229–249. ( 10.1007/s10928-006-9043-z) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Ottolini MG, Blanco JC, Eichelberger MC, Porter DD, Pletneva L, Richardson JY, Prince GA. 2005. The cotton rat provides a useful small-animal model for the study of influenza virus pathogenesis. J. Gen. Virol. 86, 2823–2830. ( 10.1099/vir.0.81145-0) [DOI] [PubMed] [Google Scholar]
- 32.Prince GA, Prieels J-P, Slaoui M, Porter DD. 1999. Pulmonary lesions in primary respiratory syncytial virus infection, reinfection, and vaccine-enhanced disease in the cotton rat (Sigmodon hispidus). Lab. Invest. 79, 1385–1392. [PubMed] [Google Scholar]
- 33.Verhelst J, Parthoens E, Schepens B, Fiers W, Saelens X. 2012. Interferon-inducible Mx1 protein inhibits influenza virus by interfering with functional viral ribonucleoprotein complex assembly. J. Virol. 86, 13 445–13 455. ( 10.1128/JVI.01682-12). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Grieves JL, Yin Z, Durbin RK, Durbin JE. 2015. Acute and chronic airway disease after human respiratory syncytial virus infection in cotton rats (Sigmodon hispidus). Comp. Med. 65, 315–326. ( 10.1016/j.compbiomed.2015.07.025) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Wyde PR, Chetty SN, Timmerman P, Gilbert BE, Andries K. 2003. Short duration aerosols of JNJ 2408068 (R170591) administered prophylactically or therapeutically protect cotton rats from experimental respiratory syncytial virus infection. Antiviral Res. 60, 221–231. ( 10.1016/j.antiviral.2003.07.002) [DOI] [PubMed] [Google Scholar]
- 36.Blanco JC, Pletneva LM, Oue RO, Patel MC, Boukhvalova MS. 2015. Maternal transfer of RSV immunity in cotton rats vaccinated during pregnancy. Vaccine 33, 5371–5379. ( 10.1016/j.vaccine.2015.08.071) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Li Y, Handel A. 2014. Modeling inoculum dose dependent patterns of acute virus infections. J. Theor. Biol. 347, 63–73. ( 10.1016/j.jtbi.2014.01.008) [DOI] [PubMed] [Google Scholar]
- 38.Vegvari C, Hadjichrysanthou C, Cauet E, Lawrence E, Cori A, de Wolf F, Anderson RM. 2016. How can viral dynamics models inform endpoint measures in clinical trials of therapies for acute viral infections? PLoS ONE 11, e0158237 ( 10.1371/journal.pone.0158237) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Blanco JC, Richardson JY, Darnell ME, Rowzee A, Pletneva L, Porter DD, Prince GA. 2002. Cytokine and chemokine gene expression after primary and secondary respiratory syncytial virus infection in cotton rats. J. Infect. Dis. 185, 1780–1785. ( 10.1086/340823) [DOI] [PubMed] [Google Scholar]
- 40.Johnson SM, McNally BA, Ioannidis I, Flano E, Teng MN, Oomens AG, Walsh EE, Peeples ME. 2015. Respiratory syncytial virus uses CX3CR1 as a receptor on primary human airway epithelial cultures. PLoS Pathog. 11, e1005318 ( 10.1371/journal.ppat.1005318) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Schmidt ME, Varga SM. 2018. Cytokines and CD8T cell immunity during respiratory syncytial virus infection. Cytokine. ( 10.1016/j.cyto.2018.07.012) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Lavielle M. 2014. Mixed effects models for the population approach: models, tasks, methods and tools London, UK: Chapman and Hall. [Google Scholar]
- 43.Liu Y, Beyer A, Aebersold R. 2016. On the dependency of cellular protein levels on mRNA abundance. Cell 165, 535–550. ( 10.1016/j.cell.2016.03.014) [DOI] [PubMed] [Google Scholar]
- 44.Press WH, Teukolsky SA, Vetterling WT, Flannery BP. 2007. Numerical recipes 3rd edition: the art of scientific computing. Cambridge, UK: Cambridge University Press. [Google Scholar]
- 45.Bates DM, Watts DG. 1988. Nonlinear regression analysis and its applications. New York, NY: Wiley. [Google Scholar]
- 46.Ribeiro RM, Qin L, Chavez LL, Li D, Self SG, Perelson AS. 2010. Estimation of the initial viral growth rate and basic reproductive number during acute HIV-1 infection. J. Virol. 84, 6096–6102. ( 10.1128/JVI.00127-10) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Kakizoe Y, Nakaoka S, Beauchemin CA, Morita S, Mori H, Igarashi T, Aihara K, Miura T, Iwamib S. 2015. A method to determine the duration of the eclipse phase for in vitro infection with a highly pathogenic SHIV strain. Sci. Rep. 5, 10371 ( 10.1038/srep10371) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Lavielle M, Ribba B. 2016. Enhanced method for diagnosing pharmacometric models: random sampling from conditional distributions. Pharm. Res. 33, 2979–2988. ( 10.1007/s11095-016-2020-3) [DOI] [PubMed] [Google Scholar]
- 49.Openshaw PJ, Chiu C. 2013. Protective and dysregulated T cell immunity in RSV infection. Curr. Opin. Virol. 3, 468–474. ( 10.1016/j.coviro.2013.05.005) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Johansson C. 2016. Respiratory syncytial virus infection: an innate perspective. F1000Research 5(F1000 Faculty Rev):2898 ( 10.12688/f1000research.9637.1) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Boukhvalova M, Yim K, Blanco J. 2018. Cotton rat model for testing vaccines and antivirals against respiratory syncytial virus. Antiviral Chem. Chemother. 26, 2040206618770518 ( 10.1177/2040206618770518) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Bohmwald K, Gálvez NM, Canedo-Marroquín G, Pizarro-Ortega MS, Andrade-Parra C, Gomez-Santander F, Kalergis AM. 2019. Contribution of cytokines to tissue damage during human respiratory syncytial virus infection. Front. Immunol. 10, 452 ( 10.3389/fimmu.2019.00452). ( 10.3389/fimmu.2019.00452) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Canini L, Perelson AS. 2014. Viral kinetic modeling: state of the art. J. Pharmacokinet. Pharmacodyn. 41, 431–443. ( 10.1007/s10928-014-9363-3) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Patel K, et al. 2018. Respiratory syncytial virus-A dynamics and the effects of lumicitabine, a nucleoside viral replication inhibitor, in experimentally infected humans. J. Antimicrob. Chemother. 74, 442–452. ( 10.1093/jac/dky415) [DOI] [PubMed] [Google Scholar]
- 55.Reynolds SD, et al. 2016. Airway progenitor clone formation is enhanced by Y-27632-dependent changes in the transcriptome. Am. J. Respir. Cell Mol. Biol. 193, A1470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Hallak LK, Spillmann D, Collins PL, Peeples ME. 2000. Glycosaminoglycan sulfation requirements for respiratory syncytial virus infection. J. Virol. 74, 10 508–10 513. ( 10.1128/JVI.74.22.10508-10513.2000) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Green MG, Petroff N, La Perle K, Niewiesk S. 2018. Characterization of cotton rat (Sigmodon hispidus) eosinophils, including their response to respiratory syncytial virus infection. Comp. Med. 68, 31–40. [PMC free article] [PubMed] [Google Scholar]
- 58.Streif S, Pueschel K, Tietz A, Blanco J, Meulen VT, Niewiesk S. 2004. Effector CD8+ T cells are suppressed by measles virus infection during delayed type hypersensitivity reaction. Viral Immunol. 17, 604–608. ( 10.1089/vim.2004.17.604) [DOI] [PubMed] [Google Scholar]
- 59.Hambling M. 1964. Survival of the respiratory syncytial virus during storage under various conditions. Br. J. Exp. Pathol. 45, 647. [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All Monolix project files used can be found in the electronic supplementary material.