Relationship between inorganic ion distribution, resting membrane potential, and the ΔG′ of ATP hydrolysis: a new paradigm

Abstract

Cell membrane potential and inorganic ion distributions are currently viewed from a kinetic electric paradigm, which ignores thermodynamics. The resting membrane potential is viewed as a diffusion potential. The 9 major inorganic ions found in blood plasma (Ca²⁺, Na⁺, Mg²⁺, K⁺, H⁺, Cl⁻, HCO₃⁻, H₂PO₄⁻, and HPO₄²⁻) are distributed unequally across the plasma membrane. This unequal distribution requires the energy of ATP hydrolysis through the action of the Na⁺-K⁺ ATPase. The cell resting membrane potential in each of 3 different tissues with widely different resting membrane potentials has been shown to be equal to the Nernst equilibrium potential of the most permeant inorganic ion. The energy of the measured distribution of the 9 major inorganic ions between extra- and intracellular phases was essentially equal to the independently measured energy of ATP hydrolysis, showing that the distribution of these 9 major ions was in near-equilibrium with the ΔG′ of ATP. Therefore, thermodynamics does appear to play an essential role in the determination of the cell resting membrane potential and the inorganic ion distribution across the plasma membrane.—Veech, R. L., King, M. T., Pawlosky, R., Bradshaw, P. C., Curtis, W. Relationship between inorganic ion distribution, resting membrane potential, and the ΔG′ of ATP hydrolysis: a new paradigm.

BACKGROUND

Recently a review article was published entitled “The enduring legacy of the ‘constant field equation’ in membrane ion transport” (1). In the article, the authors state that “Thermodynamic equations are not applicable, because ion transport in cells is out of equilibrium.” We fundamentally disagree with this statement. Over the past 35 yr, a basic understanding of thermodynamics applied to membrane ion distribution and resting membrane potential has been reported (2–5). We summarize these contributions here and address several outstanding questions in this field using the understanding gained from these findings.

THE DISTRIBUTION OF IONS RELATED TO THE ACTIVITY OF THE SODIUM-POTASSIUM ATPASE AND TO THE INDEPENDENTLY MEASURED ΔG′ OF ATP

The Na⁺-K⁺ ATPase pump creates a Gibbs-Donnan equilibrium in which Na⁺ is the external functionally impermeant cation. The charge on this external Na⁺ is opposite in sign and nearly equal in magnitude to that of the internal impermeant anionic Gibbs-Donnan polyanionic material. This Gibbs-Donnan system balances the colloid-osmotic pressure established by the presence of these intracellular macromolecules to maintain cell volume. The gradients of the other 8 major inorganic ions are linked to the sodium gradient by a series of transporters. The cytoplasmic ΔG′ of ATP can be calculated from the measurement of cellular metabolite concentrations (6). For example, substrate and product levels of the glyceralydehyde-3-phosphate dehydrogenase–3-phosphoglycerate kinase reactions can be used as previously described (6) and recently reviewed (4).

THE ENERGY OF THE ION GRADIENTS OF THE 9 MAJOR INORGANIC IONS BETWEEN THE EXTRA- AND INTRACELLULAR PHASES OF THE CELL IS EQUAL TO THE FREE ENERGY OF ATP HYDROLYSIS

Although it has been long known that the development of an extracellular Na⁺ gradient requires the energy of ATP hydrolysis (7), it took several more decades for the magnitude of the energy of ATP hydrolysis in vivo to be determined (6). The ATP couple, [ATP]/([ADP]×[P_i]), participates in hundreds of reactions, allowing the ΔG′ of ATP to control a wide range of the reactions of cellular metabolism (8).

The distribution of intra- and extracellular H₂O was estimated using the ³H₂O and ¹⁴C inulin spaces in 3 cell types with resting membrane potentials (measured by a KCl electrode) of −83 mV for heart (9), −28 mV for liver (10), and −7 mV for red blood cells. Na⁺, K⁺ Mg²⁺, and Ca²⁺ were measured by atomic absorption spectroscopy, Cl⁻ by chloridometry, and HCO₃⁻, HPO₄²⁻, and H₂PO₄⁻ were measured enzymatically. The pH was calculated from measured HCO₃⁻ and CO₂ using the Henderson-Hasselbalch equation (11). Free [Mg²⁺] was calculated from the measured citrate:isocitrate ratio (12). Three tissues that have the widest range of resting membrane potential were chosen.

E_N [ION]_O/I IS CALCULATED FROM THE MEASURED ION CONCENTRATION AND THE NERNST EQUATION. THE E_N, RESTING MEMBRANE POTENTIAL IS MEASURED BY KCL ELECTRODE

One can compare the contribution of voltage of the individual ions in the 3 tissues. This is achieved by plotting the voltages for the individual ion distributions against the resting membrane potentials. The Nernst potential, E_N, of each of the 9 major inorganic ions between extra and intracellular phases was calculated using the Nernst equation:

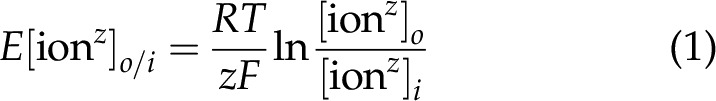where R is the gas law constant 8.3145 × 10⁻³ kJ/mole; F is the Faraday constant 96.485 kJ/V/mol, T is absolute temperature or 311.15 in degrees Kelvin, o is out, and i is in.

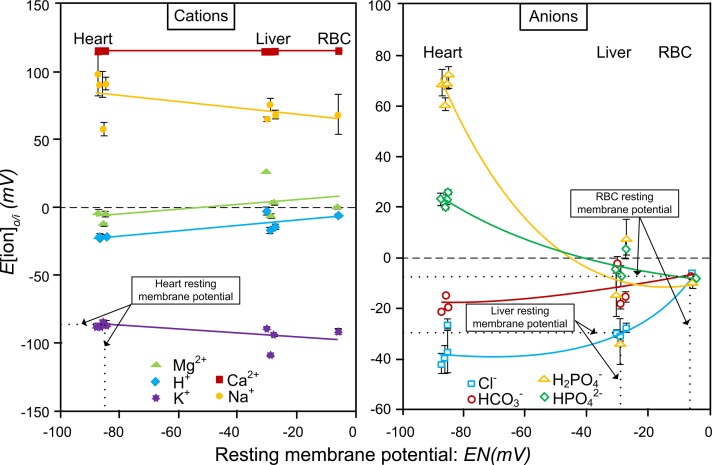
The Nernst potential for any ion in 2 phases is given in Eq. 1. The plots of voltage for each individual ion in heart, liver, and red blood cells are shown in Fig. 1. The 3 tissues are shown above their resting membrane potentials.

Figure 1.

The calculated Nernst potentials of the individual inorganic ions in tissues is plotted vs. the resting membrane potentials, E_N. The x axis is the resting membrane potential of each of the 3 tissue types. The intersection of the measured resting membrane potential on the x axis for the 3 tissues, heart, liver, and red blood cell with the resting potential calculated on the y axis is shown by dotted lines for each of the 3 tissues. This intersection identifies the ions reflecting the resting membrane potential. For the heart, K⁺ reflects the resting potential at −83 mV; for the liver, Cl⁻ reflects the resting membrane potential at −28 mV, and for the red blood cell Cl⁻ and HCO₃⁻, both reflect the resting membrane potential at −7 mV (11).

The resting membrane potential of cells from the 3 tissues was a Nernst equilibrium potential (13) of the most permeant ion (Fig. 1), which is not a diffusion potential. The most permeant ion is determined by the ion with the ΔG′[ion]_o/i that approaches zero (Eq. 2).

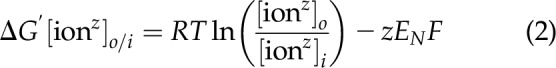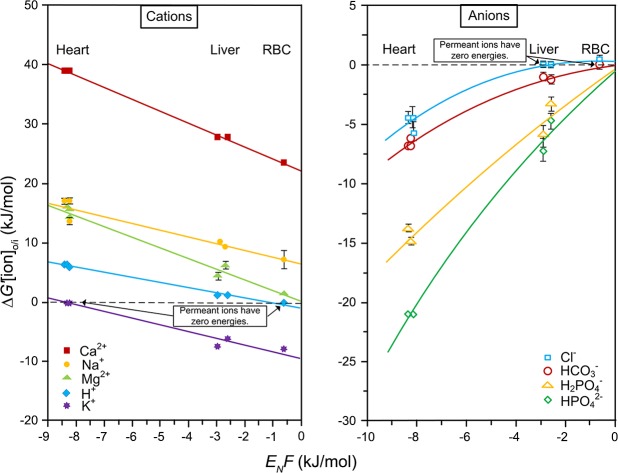
This can be seen in Fig. 2, which in the case of heart was K⁺, in liver was Cl⁻, and in the red blood cell was Cl⁻ and HCO₃⁻. The resting membrane potential is therefore not a diffusion potential as has been widely taught, demonstrating that thermodynamics do apply. The establishment and maintenance of the membrane potential and the distribution of the 9 major inorganic ions across the plasma membrane represent a Gibbs-Donnan equilibrium system that is based on thermodynamics.

Figure 2.

The energies of the 9 major inorganic ions between the intra- and extracellular phases. The ΔG′ [ion]_o/i is shown for 3 cell types with greatly different resting membrane potentials. The resting membrane potential (E_N) times the faraday constant F is plotted on the x axis. Equation 2) is plotted on the y axis. The ion that has an energy approaching zero is the most permeant ion. The resting membrane potential of the 3 tissues was a Nernst equilibrium potential (13) of the most permeant ion, which in the case of heart was K⁺, in liver was Cl⁻, and in red blood cells was Cl⁻ and HCO₃⁻.

For the energies one plots ΔG[ion]_o/i against the resting membrane potential times the Faraday constant.

It was further shown that that ΔG′[cation]_o/i formed linear relationships with the energy of the resting membrane potentials, E_N × F, for the 3 cell types tested. In contrast, the energy of the anions (ΔG′[anion]_o/i) formed curvilinear relationships with the resting membrane potential, reflecting the differing amounts of impermeant intracellular Donnan-active anionic macromolecules that are balanced by impermeant extracellular Na⁺ ions created by the Na⁺-K⁺ ATPase. The gradients of the other major inorganic ions were related to the gradient of the Na⁺ ion and linked to one another by ion transporters in the electroneutral and osmoneutral system. The 3 cell types tested each formed a Gibbs-Donnan near-equilibrium system wherein the resting membrane potential was equivalent to the Nernst equilibrium potential of the most permeant ion (Table 1).

TABLE 1.

Concentrations of EC and IC inorganic ions in heart, liver, and red blood cells

	Perfused beating heart			Liver		Red blood cell, control
Ion/location	Glucose	G + insulin	G + ketones	Control	+ Na acetate
Ca2+ EC	1.1	1.1	1.1	1.1	1.07	1.07
Ca2+ IC	0.0002	0.0002	0.0002	0.0002	0.0002	0.0002
Na+ EC	144	144	149	146 ± 1	170 ± 2	144
Na+ IC	6.5 ± 5.2	5.6 ± 1.8	5.1 ± 0.8	12.3 ± 1.2	10.7 ± 1.5	8.8 ± 6.3
Mg2+ EC	0.5	0.5	0.5	0.52 ± 0.0	0.51 ± 0.02	0.52 ± 0.02
Mg2+ IC	1.2 ± 0.03	0.72 ± 0.3	0.74 ± 0.1	0.43 ± 0.0	0.97 ± 0.01	0.5
pH external	7.42	7.39	7.4	7.37 ± 0.03	7.52 ± 0.0	7.40
pH internal	7.06 ± 0.01	7.05 ± 0.2	7.04 ± 0.03	7.12 ± 0.07	7.12 ± 0.1	7.29 ± 0.0
K+ EC	5.9	5.9	5.9	5.22 ± 0.1	3.9 ± 0.3	5.16 ± 0.3
K+ IC	142 ± 3	147 ± 5	141 ± 6	175 ± 1	229 ± 2	153 ± 5
Cl− EC	127	127	127	103 ± 1	95.4 ± 1	108 ± 1
Cl− IC	47.9 ± 3.6	29.4 ± 5.5	36.1 ± 11	36.7 ± 2.3	30.8 ± 2.2	83.4 ± 2.9
HCO3− EC	25	25	25	26.7 ± 0.5	36.5 ± 1.4	26.7 ± 0.5
HCO3− IC	14.3 ± 0.2	14.4 ± 0.5	12 ± 0.4	15.1 ± 1.1	19.0 ± 1.6	22 ± 0.7
H2PO4− EC	0.18	0.19	0.19	0.22 ± 0.01	0.11 ± 0.01	0.39 ± 0.01
H2PO4− IC	2.43 ± 0.2	1.8 ± 0.2	2.9 ± 0.2	0.356 ± 0.08	0.48 ± 0.01	0.27 ± 0.02
HPO42− EC	0.91	0.90	0.91	0.95 ± 0.03	0.67 ± 0.04	1.9 ± 0.1
HPO42− IC	5.4 ± 0.4	4.03 ± 0.3	6.26 ± 0.4	0.91 ± 0.2	1.55 ± 0.45	1.0 ± 0.1

The values are given as means ± SEM in units of micromoles per milliliter. H2O free intracellular [Ca²⁺] was assigned as 0.2 μM in all tissues (11). EC, extracellular; IC, intracellular.

IS THERE AN EQUATION THAT CAN RELATE THE GIBBS FREE ENERGY OF THE ACTIVE TRANSPORT DRIVEN BY ATP TO THE DISTRIBUTION OF ALL 9 MAJOR INORGANIC IONS IN EQUILIBRIUM?

Knowledge of the ΔG′ ATP has allowed for an estimate of the extent and direction of the gradient of Na⁺ between the extra- and intracellular phases of perfused heart, with a resting membrane potential of −83 mV that was found to be in near-equilibrium with the reaction of the Na⁺ pump in the presence of an open K⁺ channel in Eq. 3: following statement (3):

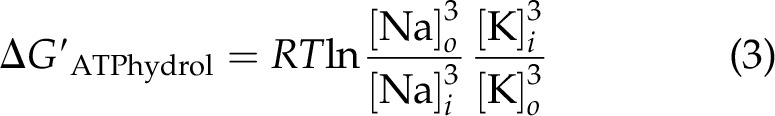However, this electroneutral osmoneutral statement cannot be written for tissues where there is no open K⁺ channel. The gradients of the 9 major inorganic ions defined in Krebs and Henseleit (14) and the initial hemodialysis fluids were therefore also examined (15). The energy of the 9 ions between intra- and extracellular phases was found to vary between 53 and 60 kJ/mol as stated in Eq. 4:

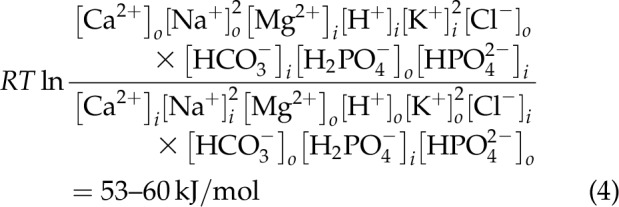The energy of the 9 ion gradients was then compared with the independently determined ΔG′ of ATP hydrolysis in the same 3 tissues. The results of the comparison are given in Table 2.

TABLE 2.

The values of ΔG′ ATP of hydrolysis measured compared with the calculated ΔG′ from the 9 ion empirical equations

ΔG′ (kJ/mol)	Perfused beating heart			Liver		Red blood cell, control
	Glucose	G + insulin	G + R-3-hydroxybutyrate	Control	+Na acetate
ATP	−54.2 ± 0.6	−58.0 ± 0.2	−57.0 ± 0.3	−56.5 ± 0.4	−56.1 ± 0.7	−57.1 ± 0.4
9 ions	53.3 ± 0.1	57.0 ± 2.5	59.0 ± 1.8	54.0 ± 0.7	60.3 ± 1.1	53.0 ± 0.6

ΔG′ of ATP and ΔG′ of 9 ions calculated using Eq. 5 in heart, liver, and red blood cells (11).

The energy of the distribution of the 9 ions between the intra- and extracellular spaces were linked to one another, to the ΔG′ of ATP, and to the resting membrane potential in an osmoneutral and electroneutral manner as shown in Eq. 5, where the energy of Na⁺ transport is linked to the transport of the other 9 ions. The driving forces are established by the excess intracellular impermeant anions that set up the Gibbs-Donnan system (16, 17).

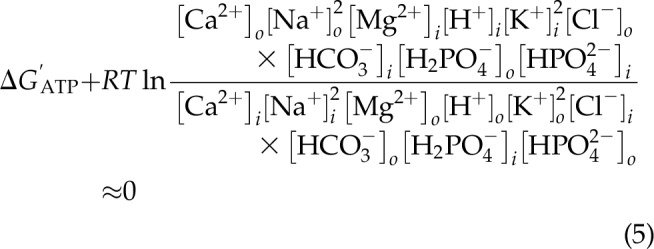The finding that the energy of the 9 major inorganic ions is essentially the same as that of the ΔG′ of ATP demonstrates that this ionic distribution is in near-equilibrium with the energy of ATP hydrolysis.

RECENT FINDINGS

The equation shown in Eq. 5 was selected by a computer search to give an electroneutral osmoneutral reaction, which was equivalent to the ΔG′ of ATP. In the time since the empirical equation was matched to the data, there has been much progress in identifying and characterizing many plasma membrane ion transporters. It is therefore of interest to determine why [Na⁺] and [K⁺] are present in the equation as second-order (squared) terms while the other 7 major ions are present as first-order terms.

The transport reaction of the 3 Na⁺-2 K⁺ ATPase is seen in Eq. 6:

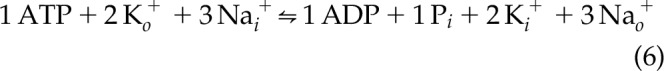The order of Na⁺ is 2 in Eq. 5, although at first glance it might be predicted to be 3. If 1 writes a mass action equation for the 3 Na⁺-2 K⁺ ATPase, the Na⁺ term would be cubed and the K⁺ term would be squared. The Na⁺ is transported from in to out, so the product 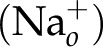appears in the numerator.

If a secondary active transporter is present, such as a Na⁺-dependent ion cotransporter, then:

In this reaction, the 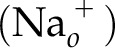is the reactant and so it is placed in the denominator. Thus, when combining Eq. 6 and Eq. 7, 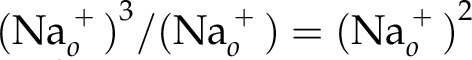. Therefore, the ability of the Na⁺ gradient to drive the transport of other ions likely leads to the factoring out of 1 order in the Na⁺ term, bringing the total order to 2.

MATTERS OF CONTROVERSY AND UNANSWERED QUESTIONS

It is widely thought that the origin of the resting negative membrane potential of nerve and muscle cells (18) resulted from the diffusion of a small fraction of the excess intracellular K⁺ ions to the extracellular phase, creating a “diffusion potential.” This concept formed a basic premise that has been taught in neuroscience classes for over 50 yr (1, 19). The action potential of the axon is thought to result from a reversal of membrane permeability in which the Na⁺ ion becomes transiently much more permeant than K⁺ (20). The Goldman–Hodgkin–Katz equation is essentially a kinetic equation based on the relative permeance of the 3 ions K⁺, Na⁺, and Cl⁻. This equation as reported in 1949 is shown in Eq. 8:

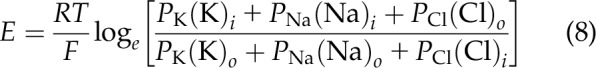where E represents the resting membrane potential of the squid axon where the relative permeability of the 3 ions considered was taken to be: P_K = 1, P_Na = 0.04, and P_Cl = 0.45 (19).

We propose that in high-voltage tissue, such as nerve and muscle, the K⁺ is the permeant ion as represented in the Goldman–Hodgkin–Katz equation. However, K⁺ is not permeant in other tissues, such as liver or red cell, so the Goldman–Hodgkin–Katz equation does not apply. Rather, the most permeant ion has a permeance of 1 and determines the measured resting membrane potential. The distribution of the 9 major inorganic ions form a Gibbs-Donnan near-equilibrium system in which the energies of the ion distribution are related to one another in near-equilibrium with the energy of ATP hydrolysis as stated in Eq. 5.

PROSPECTS AND PREDICTIONS

The finding that the gradients of the 9 major inorganic ions are dependent upon each other and to the energy of ATP hydrolysis provides new insights into the use of intravenous (IV) therapy. For example, a decrease in cellular phosphorylation potential is then expected to alter the gradients of the 9 major inorganic ions. Therefore, IV fluids that contain an energy substrate to restore the phosphorylation potential as well as a balanced ionic composition to prevent activation of the Na⁺-K⁺ ATPase will likely be of therapeutic benefit.

AUTHOR CONTRIBUTIONS

R. L. Veech wrote the first draft; M. T. King performed much of the research cited, contributed content, and validated the math and data; R. Pawlosky contributed content; P. C. Bradshaw contributed content and edited for comprehension; and W. Curtis made the graphics, initial outline, and contributed content.