Effects of marker type and filtering criteria on Q_ST-F_ST comparisons

Abstract

Comparative studies of quantitative and neutral genetic differentiation (Q_ST-F_ST tests) provide means to detect adaptive population differentiation. However, Q_ST-F_ST tests can be overly liberal if the markers used deflate F_ST below its expectation, or overly conservative if methodological biases lead to inflated F_ST estimates. We investigated how marker type and filtering criteria for marker selection influence Q_ST-F_ST comparisons through their effects on F_ST using simulations and empirical data on over 18 000 in silico genotyped microsatellites and 3.8 million single-locus polymorphism (SNP) loci from four populations of nine-spined sticklebacks (Pungitius pungitius). Empirical and simulated data revealed that F_ST decreased with increasing marker variability, and was generally higher with SNPs than with microsatellites. The estimated baseline F_ST levels were also sensitive to filtering criteria for SNPs: both minor alleles and linkage disequilibrium (LD) pruning influenced F_ST estimation, as did marker ascertainment. However, in the case of stickleback data used here where Q_ST is high, the choice of marker type, their genomic location, ascertainment and filtering made little difference to outcomes of Q_ST-F_ST tests. Nevertheless, we recommend that Q_ST-F_ST tests using microsatellites should discard the most variable loci, and those using SNPs should pay attention to marker ascertainment and properly account for LD before filtering SNPs. This may be especially important when level of quantitative trait differentiation is low and levels of neutral differentiation high.

1. Introduction

Geographical and temporal differentiation in mean values of quantitative traits are of commonplace occurrence in animal and plant populations. Before such differentiation can be ascribed to adaptation, two premises need to be fulfilled. First, the observed differentiation needs to be genetically based rather than environmentally induced. Second, the observed differentiation has to have been caused by directional natural selection instead of neutral processes, such as gene flow or genetic drift. Comparative studies of quantitative trait and molecular marker differentiation (Q_ST-F_ST tests) provide a way of identifying footprints of directional selection as a cause of population differentiation in quantitative traits (reviewed in [1–5]). The rationale behind Q_ST-F_ST comparisons is simple: the level of genetically based population differentiation in quantitative traits (i.e. Q_ST) is compared with that in neutral marker loci (i.e. F_ST). If Q_ST > F_ST, this provides evidence for adaptive population differentiation, as only directional selection is expected to elevate divergence in quantitative traits above the neutral expectation. Similarly, if Q_ST < F_ST, this would be indicative of uniform stabilizing selection that has prevented populations from diverging less than would be expected under random genetic drift alone. An outcome of Q_ST ≈ F_ST would be inconclusive: the null-hypothesis of differentiation by genetic drift could not be rejected (e.g. [1]). While the majority of studies using the Q_ST-F_ST (reviewed in [3,4,6]) or a related approach [7,8] to test for the adaptive nature of quantitative trait differentiation have found support for it, there is a concern that many of these studies might have tested Q_ST against overly liberal (i.e. too low) F_ST estimates [9,10]. This concern stems from the fact that most Q_ST-F_ST comparisons have used microsatellite markers for F_ST estimation. Since microsatellite loci are highly variable due to their high mutation rates [11,12], they may underestimate levels of neutral genetic differentiation [13–16], and hence, render Q_ST-F_ST comparisons biased towards finding evidence for adaptive differentiation [9,10]. Recent advances in sequencing technology have started to replace microsatellite markers with single-locus polymorphisms (SNPs) as the tool of the trade-in population genetic investigations of non-model organisms [17–19]. Since SNP loci are (mostly) bi-allelic and experience, on average, lower mutation rates than microsatellite loci, they might provide a way to obtain less biased estimates of neutral baseline differentiation than microsatellite loci [9,20]. However, since per nucleotide mutation rates are highly variable, and may vary depending on their genomic location [21,22], SNP loci may not automatically yield less biased neutral baseline estimates of divergence (as measured by F_ST) than microsatellites. Similarly, not all SNPs are or behave as being neutral; they may be subject to various forms of selection depending on their genomic location and/or functionality [23–25]. For instance, hitchhiking under positive and background selection can increase allele frequency shifts between populations, especially in genomic regions of low recombination [26–28]. Bias in the estimation of the neutral baseline from SNP data could also arise from analytical methods involved in marker selection and F_ST estimation [29]. Specifically, different averaging methods to estimate F_ST across loci have been shown to yield different results between studies [29], which should be particularly concerning in the context of Q_ST-F_ST comparisons. On the other hand, F_ST estimates can be affected by ascertainment bias (sensu [17]) when the selected markers are not representative of the variability observed in all sampled individuals. They can also be sensitive to how rare low-frequency alleles are collected and filtered from the data [30–33], and how each researcher decides to deal with markers that are in linkage disequilibrium (LD) with each other [34]. The latter issue may be particularly important in Q_ST-F_ST studies where divergent populations differing in their LD patterns are compared: due to methodological constraints, typically, only a small subset of SNPs can be included and failure to account for LD in marker selection for one or more populations in the data has potential to bias F_ST estimates. To the best of our knowledge, there have not been any studies of these effects of SNPs filtering in the context of Q_ST-F_ST comparisons, although the problem of defining neutral baseline differentiation level has been well recognized in related contexts (e.g. [25,35,36]).

The aim of this study was to explore how marker type and various filtering criteria could influence inferences from Q_ST-F_ST comparisons through their effect on estimates of neutral baseline differentiation. To this end, we used empirical data on quantitative trait and microsatellite differentiation among four populations of nine-spined sticklebacks (Pungitius pungitius) used in an earlier Q_ST-F_ST study [8]. These data were supplemented with information on variability in millions of SNP loci and over 18 000 in silico genotyped microsatellite loci to see how marker type and different filtering criteria influenced the neutral baseline differentiation level as reflected in F_ST. In particular, we were interested to evaluate the conjecture (cf. [10]) that Q_ST-F_ST comparisons using highly variable microsatellite markers could be biased towards finding evidence for adaptive differentiation. Because the P. pungitius study system is known for its particularly high level of quantitative trait differentiation [8,37,38], we also simulated genomic datasets under varying levels of Q_ST-F_ST divergence and evaluated the different marker types' ability to detect the signature of divergent selection under different evolutionary scenarios in this particular system.

2. Material and methods

2.1. Phenotype data

The phenotype data used here were adopted from an earlier study [8] which used a full-sib mating design comprised of 92 F₁-generation nine-spined stickleback individuals from four populations (Baltic Sea, n = 21; White Sea, n = 24, Bynastjärnen, n = 22, Pyöreälampi, n = 25) and five families per population. Five morphological traits including standard length (M1), body depth (M2), head length (M3), pelvic girdle length (M4) and caudal peduncle length (M5), as well as two behavioural traits including aggressiveness (B1) and propensity for risk-taking (B2) of all 92 individuals were quantified as described in Herczeg et al. [37,38]. The study populations are highly differentiated in most of these traits, and the available evidence suggested that this differentiation has been driven by natural selection stemming from local adaptation to pond environments (Bynastjärnen & Pyöreälampi) lacking piscine predators [8,37–39].

2.2. Genetic data

An assembled and annotated reference genome (110× coverage) for P. pungitius from a Pyöreälampi individual [40] was used for obtaining the genetic data. SNP data and in silico microsatellite data were obtained by whole genome resequencing of 10 female individuals from each of the above-mentioned four populations. The processing and analysis of these are explained in detail below. The empirical microsatellite data for 12 loci were the same as that used by Karhunen et al. [8].

2.3. Variant calling

The 40 samples for this study were processed as a part of a larger sample set (n = 140) that included populations not used in this study. For each sample, the sequence reads were mapped to the reference genome with bwa (v. 0.7.12; [41]) using default options, duplicate reads were removed with SAMtools (v. 1.3.1; [42]) and those around indels were realigned with GenomeAnalysisToolkit's IndelRealigner (GATK; v. 3.4; [43]). Each sample was then called with GATK HaplotypeCaller using mode ‘discovery’, output format ‘gvcf’, and emit and call confidence of 3 and 10, respectively. The full sample set was jointly genotyped with GATK GenotypeGVCFs. From this, the 40 samples from the four study populations were extracted and their analysis continued in isolation.

2.4. SNP filtering

The full datasets consist of 3 806 181 SNPs that are variable within the four populations and have data for at least 80% of the individuals in each population. We applied different SNP filtering criteria to obtain the following three datasets: (i) SNPs in all genomic regions (ALL), (ii) the SNPs in non-coding regions excluding exons and repeat regions and their immediate neighbourhood (50 bp of flanking sequence) (NONCOD) and (iii) the SNPs in synonymous third codon position (C3SYNO). C3SYNO includes variable third codon positions that were inferred to contain synonymous substitutions by the R package VariantAnnotation (v. 1.18.1; [44]). From these, we removed sites with missing genotype data or monomorphic among the study samples and the three final datasets consisted of 1 702 105, 1 165 221 and 41 927 SNPs, respectively. To account for the possibility of ascertainment bias [17,29], we also filtered markers based on their variability in the marine populations. This is because F_ST can be seen as either a parameter of the evolutionary process, or a statistic derived from observed samples. As such, it is used to measure correlation between randomly drawn alleles from a single population relative to either the most recent common ancestral population or the combination of the two population samples [29]. Under the former definition, the markers included in the analysis should have been variable in the ancestral population; alternatively, markers can often be ascertained by their variability in an outgroup or maximally diverged modern populations. In our case, the marine populations are representative of the ancestral genetic variation and represent the geographical extremities among the study populations. Hence, variability-based marker ascertainment was done using the two marine populations and for each category, markers invariable in either of the marine populations were excluded.

2.5. Effect of LD on F_ST

Filtering of SNP dataset based on the degree of linkage between loci is a common pruning method in population genomics studies. For Q_ST-F_ST comparison, no clear guidelines are available on whether SNPs in LD should or should not be included in the data used for F_ST estimation. A general assumption is that unlinked markers should be preferred as they provide a closer estimation of what would be expected under neutrality. For practical and computational reasons, LD pruning should at least be performed on the basis that some Q_ST-F_ST methods—particularly MCMC-based approach—cannot handle large numbers of markers. Consequently, we investigated the effect of LD pruning on the estimation of F_ST by using genome-wide sets of unlinked SNPs to estimate the mean and variance of F_ST. Two different approaches were used to extract a subset of unlinked SNPs from the full SNP datasets. First, a thinning approach was applied to select roughly 2000 SNPs located at ca 150–200 kb from each other, and the rest of the SNPs were discarded. The thinning approach was carried out with VCFtools [45]. Second, we used the more sophisticated LD pruning approach of Zheng et al. [46] implemented in the R package SNPrelate. This approach divides each chromosome first into multiple 500 kb non-overlapping sliding windows. Within each sliding window, a single SNP was firstly randomly included into the active set, and this was followed by including another SNP into the active set if its correlation (as defined by the LD composite measure; [47,48]) with the SNPs in the active set was lower than a defined threshold. This procedure was repeated for all the SNPs in the same sliding window. A sequence of LD-values ranging from 0.05 to 0.95 (the pruned data have low LD when the threshold is small) were used to evaluate how the F_ST estimates were affected by the changes of LD. To see how the thinning and sliding window approaches influenced the baseline F_ST levels as estimated from the data, we evaluated F_ST as a function of standardized (to the total number of markers in the data) marker number included into the estimation. If the pruning is effective, we would expect no relationship between F_ST and number of markers included into the estimation. However, if the pruning is ineffective and linked markers become included into the data, we expect to see that the F_ST varies as a function of number of markers included. Comparison of LD between pond and marine populations was done by calculating the mean LD (defined as squared composite measure; [47,48]) between all the SNP pairs within each non-overlapping 500 kb sliding window across the genome.

2.6. In silico microsatellite analysis

The in silico microsatellite discovery and genotyping was performed with Tandem repeats finder (TRF; v. 4.09; [49]) and RepeatSeq (v. 0.8.2; [50]), respectively. Dinucleotide repeats were identified in the P. pungitius reference genome using TRF with options ‘2 7 7 80 10 20 2 -f -d -m -h’. The parameter values are as recommended by the software developers with the exception of the last two, minimum score (20) and maximum period size (2). From the output, repeat loci were chosen with the following criteria: period and consensus pattern of 2, length of 10–20 copies, alignment score of 100 and distance of at least 500 bp to the previous locus. The selected loci were genotyped in the 40 study samples using RepeatSeq. The output was processed using bcftools [42] and custom scripts, and the resulting data analysed using the R package diveRsity (v. 1.9.89; [51]). After removing loci with more than 20% missing data in any population, the resulting dataset contained 18 824 microsatellite loci.

2.7. Estimation of local recombination rate

Since variation in recombination rate along chromosomes can influence patterns of polymorphism and hence F_ST through background and/or hitchhiking selection (e.g. [28,52]), we explored how the F_ST in our data was influenced by variation in recombination rate. To this end, the local recombination rate was estimated using a sex-averaged genetic map (an improved [40] version of that reported in [53]). First, non-monotonic regions were manually removed and outlier markers discarded by performing loess regression (α = 0.2, degree = 1), interpolating genetic distance from physical positions and removing any points that lie further than 2 cM from the line. Using the remaining regions and markers, we estimated the local recombination rate by performing loess regression on a fixed number of markers (α adjusted to include 250 markers, degree = 2) and predicting the change on genetic distance for a pair of adjacent physical positions. We could estimate the local recombination rate for 54.7% of the genome (electronic supplementary material, figure S1). Although a small fraction of the genome still got negative rate estimates, a great majority of sites had inferred recombination rates between 0 and 20 cM Mb⁻¹ (mean = 6.6). Using the inferred rate, the genome was split into two roughly equally large subsets of regions with low (1–7 cM Mb⁻¹) and high (7–15 cM Mb⁻¹) local recombination rates, discarding the loci with either no rate estimate or an estimate from the extreme ends of the rate distribution (electronic supplementary material, figure S2a). The microsatellite loci were further divided into those with few (1–4), intermediate (5–8) and many (9–21) alleles, the two extremes approximately corresponding to the first and fourth quartile of the distribution (electronic supplementary material, figure S2b). F_ST was separately estimated for the different subsets of SNP dataset NONCOD and the microsatellite data. Since the impact of background selection was expected to be weak in small pond populations subjected to strong drift, the impact of recombination rate on F_ST was assessed only in the two large marine populations (LEV & HEL).

2.8. Outlier analyses

Since loci linked to selected sites are expected to show elevated F_ST [36], we used two approaches to identify possible outliers and evaluate their impact on baseline F_ST: BayeScan [54] and OutFLANK [33]. In both methods, the outliers were detected while controlling for the false discovery rate with a liberal p = 0.1 threshold.

2.9. F_ST estimation and comparison

We investigated whether different estimation methods would yield critically different F_ST values as expected from previous studies [29]. First, we used the Weir & Cockerham [55] theta estimator of F_ST. This estimator can be efficiently obtained even from genome-wide datasets, and it was used for estimation of both single and multilocus F_ST. This estimator was used to (i) calculate the pairwise F_ST values for each individual marker and produce empirical F_ST distributions for different SNP (using VCFtools; [45]) and microsatellite datasets (R package diveRsity; [51]), and (ii) evaluate how different ways of filtering and pruning the SNP data can affect the estimation of the neutral baseline F_ST (using R package SNPrelate; [46]). We then combined the estimates across loci using either the ‘ratio of average' (ROA) or the ‘average of ratio' (AOR) [29].

2.10. Q_ST-F_ST comparisons

We used two approaches to conduct the Q_ST-F_ST comparisons: the Bayesian Driftsel [7] and the frequentist QstFstComp approach [56,57]. One advantage of the former over the latter approach is that it has been shown to be more powerful in detecting signatures of selection even when the number of populations is low (see [58] for a detailed statistical demonstration). However, since the standard Q_ST-F_ST comparisons continue to be widely used, and because they might be more intuitive in providing direct comparison of the quantities of F_ST and Q_ST, QstFstComp tests were included for comparison. Driftsel provides two test statistics, referred to as S and H statistics. S statistic accounts for patterns of relatedness among populations, as well as ancestral genetic correlations among the traits of interest [58]. S-values close to zero are indicative of stabilizing selection; those close to one indicate directional selection; and values close to 0.5 are consistent with evolution due to drift [58]. In addition to the factors accounted for with the S statistic, the H statistic allows the environment to be accounted for by including similarity in the distribution of population means and habitat parameters [8]. In other words, the H statistics allows one to test whether population means from similar habitats are more similar than expected by random genetic drift. Following the testing criteria proposed in Karhunen et al. [8], S or H > 0.95 implies that a quantitative trait has evolved under divergent selection at the 95% credibility level, whereas S or H < 0.05 would imply stabilizing selection at the same credibility level. The default non-informative priors were used in the Driftsel analyses. 15 000 Markov chain Monte Carlo (MCMC) samples of the posterior distribution were simulated, by considering the first 5000 as a burn-in, and the remaining were stored in every 10th iteration, so that eventually 1000 MCMC samples were used for calculating S and H statistics. We calculated both statistics for all datasets, using the binary habitat type (pond versus marine) as the input data for the distance matrix of the environmental covariates required by Driftsel [8]. The frequentist QstFstComp constructs a null distribution of the difference between Q_ST and F_ST using a parametric simulation approach. The sampling error of the F_ST was evaluated by random sampling (i.e. bootstrapping) of the given loci, and the expected distribution of the Q_ST under neutrality was simulated on the basis of the mean F_ST. The observed Q_ST-F_ST quantity was compared with 1000 samples simulated from the Q_ST-F_ST null distribution for a statistical test of neutrality, from where uncertainty quantities (p-values and confidence intervals) were derived. If Q_ST-F_ST quantity is positive, and p < 0.05, the quantitative trait in question is inferred to have been subject to divergent selection. The QstFstComp was not applicable to the microsatellite loci with more than 10 alleles due to software limitation. Since both methods, and in particular the MCMC-based Driftsel approach, are computationally very demanding, we restricted all the analyses to 2000 loci. For SNP analyses, SNP loci obtained with the thinning approach (see above) were derived from the ALL, NONCOD and C3SYNO datasets. Likewise, loci for in silico microsatellite analyses were obtained with the thinning approach, and the analyses were conducted separately for all loci irrespectively of their variability, only loci with a low number of alleles, and only loci with a high number of alleles. Finally, we investigated the effect of marker ascertainment (cf. SNP filtering section above and [29]) on Q_ST-F_ST comparisons. For each genomic dataset (i.e. ALL, NONCOD and C3SYNO) and each set of in silico microsatellites, we ran Driftsel using full datasets and using loci ascertained based on their variability in the marine populations. QstFstComp was also run for each genomic dataset using unascertained and ascertained SNP markers.

2.11. Simulation study

A simulation study was conducted to evaluate the ability of Driftsel and QstFstComp to detect signatures of divergent selection with different marker types and varying levels of Q_ST-F_ST divergence. Because our empirical data show a high level of quantitative trait differentiation, the rationale here was to simulate different levels of Q_ST-F_ST divergence to evaluate the effect of marker types on Q_ST-F_ST inference in a more general context. To do so, a population genomic dataset of four sub-populations corresponding to our four study populations (Helsinki [HEL], White Sea [LEV], Bynastjärnen [BYN] and Pyöreälampi [PYO]) was first simulated using the software fastsimcoal2 [59,60]. Simulations were based on the most likely demographic history of real nine-spined stickleback populations (electronic supplementary material, figure S3 and see [61–63]): first, a population split was modelled between the two marine (LEV and HEL) sub-populations from an ancestral population 5000 and 4000 generations ago, respectively. Then the pond populations (BYN and PYO, respectively) split from HEL and LEV, 600 generations before present and experienced bottleneck for 300 subsequent generations. Each population consisted of 200 individuals. Like in the real stickleback genome, we simulated 20 chromosomes (sex chromosomes were not simulated). Each chromosome contained four LD blocks: one comprising 250 SNPs, and the other three 25 microsatellites each. The recombination rate was set to be 10⁻⁵ between loci within each of the LD blocks. In the three microsatellite LD blocks, mutation rates were specified to be 5 × 10⁻⁶ (low mutation rate; Mi_l) 5 × 10⁻⁵ (medium mutation rate; Mi_m) and 5 × 10⁻⁴ (high mutation rate; Mi_h), with 10, 22 and 64 alleles, respectively. We then randomly picked 10 individuals from each of the four sub-populations, and used both SNPs and microsatellites as neutral markers to estimate F_ST. To simulate the quantitative traits, we randomly picked 20 individuals from each of the four sub-population as founders, and then used a full-sib design to simulate 10 full-sib families (five offspring per family) within each of the sub-populations which evolved through 30 generations using a simulation procedure similar to that used in Karhunen et al. [7].

This simulation scheme was used to model different divergence scenarios corresponding to varying intensity of selection. Specifically, different evolutionary forces over the 30 generations were applied as follows: in scenario (i), the populations bred completely randomly without any selection (neutral scenario; Q_ST = F_ST). In scenarios (ii) to (iv), populations were subjected to increasing levels of directional selection (Q_ST > F_ST) by multiplying the neutral pattern by a factor of 1.5, 2 or 4, respectively, thus generating weak (ii), moderate (iii) and strong selection (iv). All the genetic and environmental parameters needed in simulations were specified in the same way as in Karhunen et al. [7]. Due to the high computational cost of MCMC-based approach (approx. 24 h for each run), the whole simulation procedure was replicated 10 times, and the averaged performances of both Driftsel and QstFstComp on the replicated datasets were recorded.

3. Results

3.1. F_ST comparisons: effects of marker type, genomic location and averaging approach

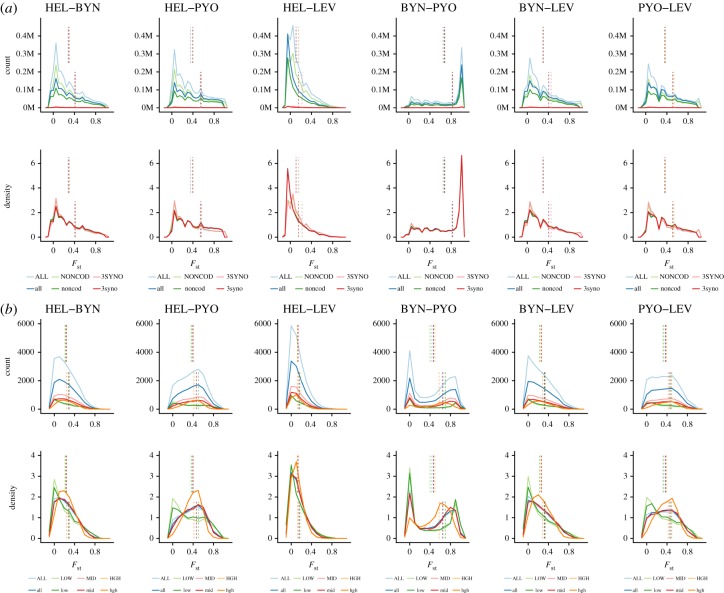
The estimated neutral baseline for the three SNP datasets based on the Weir & Cockerham [55] theta estimator of F_ST was around 0.51, with very narrow credibility intervals (electronic supplementary material, table S1). Hence, the mean and distribution of F_ST values were not significantly affected whether estimated using all, non-genic or genic loci (electronic supplementary material, table S1; figure 1). However, all of these values were significantly higher than the F_ST = 0.35 estimated from the 12 microsatellite loci used by Karhunen et al. [8]. While the F_ST = 0.37 estimated from the in silico genotyped microsatellite loci was similar to that of Karhunen et al.'s [8] estimate, comparison of estimates calculated for the different sets of microsatellites differing in their variability (see electronic supplementary material, figure S4 for details of variability in these loci) revealed that the F_ST estimates declined with increasing variability (electronic supplementary material, table S2; figure 1). The effect of marker variability on F_ST was particularly clear from the distribution of F_ST values: microsatellites with few alleles (1–4) were skewed towards extreme F_ST values and looked most similar to equivalent distributions for SNPs (figure 1); those with intermediate numbers of alleles (5–8) had the broadest distribution of F_ST and most strongly differed between the population pairs, whereas the ones with many alleles (9–21) were least diverged across the different population pairs (figure 1).

Figure 1.

Distribution of per locus pairwise F_ST. Values of per locus F_ST were estimated between all pairs of the four populations based on: (a) 3 806 181 SNP loci and (b) 18 824 microsatellite loci. Colours represent for each marker type the different datasets used to estimate F_ST estimate: in (a) all SNP loci (‘ALL' dataset; blue), non-coding/non-repeat sites (‘NONCOD' dataset; green) and codon third position synonymous changes (‘C3SYNO' dataset; red); light colours (in capitals) indicate full datasets whereas dark colours (in lowercase) show the distributions for loci ascertained by variability in marine populations. Absolute counts of sites (top) and density plots (bottom) are shown. Loci with minor allele frequency below 0.025 were discarded. In (b), F_ST for full microsatellite data (‘ALL' dataset; blue) and three subsets of data containing either low (1–4; ‘LOW'), moderate (5–8; ‘MID’) or high (9–21; ‘HIGH') number of alleles per locus. In all plots, dashed vertical lines indicate the mean value for the corresponding category: the upper and lower halves show the average of ratios and the ratio of averages, respectively.

We further compared two approaches for combining F_ST estimates across loci: average of ratios (AOR) and ratio of averages (ROA). Overall, ROA gave consistently higher estimates of F_ST than AOR (figure 1). The relative difference between the two approaches differed between comparisons and data types, but was the smallest for the two least diverged populations, FIN-HEL and RUS-LEV. While the three SNP datasets produced identical F_ST estimates under both averaging approaches, the relative order of marker categories in the microsatellites dataset changed drastically: the F_ST estimates based on highly variable microsatellites were clearly the lowest when using ROA, whereas they were one of the highest when using AOR (figure 1b).

3.2. F_ST comparisons: effects of variability-based ascertainment and minor allele filtering

We compared the F_ST estimates from the full data with those estimated from loci ascertained using the two marine populations, FIN-HEL and RUS-LEV. The effects of ascertainment differed between population comparisons, datasets and averaging approaches (figure 1). Notably, the greatest impact among SNP-based estimates was in the comparison of populations used for the ascertainment, whereas the estimates for the two pond populations—neither included in the ascertainment—were virtually unchanged (figure 1a). Among microsatellites, variability-based ascertainment only affected estimates based on the least variable category (figure 1b).

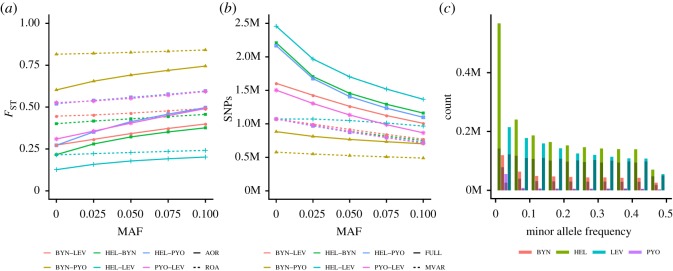
Another approach to reduce the impact of rare, novel variants is to filter the data using minor allele frequency (MAF). We tested the MAF filtering using SNP data and found that it had clear effects on F_ST estimates when using average of ratios (AOR) but only subtle effects when using ratio of averages (ROA; figure 2a). The effect on data ascertained by variability in marine populations was minimal (data not shown). This is consistent with the fact that the variability-based ascertainment itself heavily reduces the number of SNPs and the MAF filtering have only a minimal additional effect (figure 2b). Another notable effect of variability-based ascertainment was the changes in the shape of minor allele frequency: although the number of variable SNPs was reduced in all populations, the relative impact on numbers of low-frequency alleles was drastically different in the highly variable marine populations, especially on FIN-HEL, than in the small pond populations (figure 2c).

Figure 2.

Effect of minor allele frequency (MAF) cut-offs on mean F_ST estimated from the NONCOD SNP dataset. (a) Mean F_ST for different population pairs as a function of MAF, (b) number of SNPs retained, (c) site frequency spectrum for the four populations using the bin width of 0.05. In (a), solid and dashed lines indicate the two averaging approaches, average of ratios (AOR) and ratio of averages (ROA) whereas in (b) they indicate full data (FULL) and loci ascertained by variability (MVAR). In (c), dark shading shows the effect of ascertainment by variability in marine populations.

3.3. F_ST comparisons: effects of recombination rate

The effects of local recombination rate on F_ST between the two marine populations were statistically significant, but subtle. For SNPs, the average per-locus F_ST was 0.1265 and 0.1352 (t-test: p < 2.2 × 10⁻¹⁶) in regions of low and high recombination rate, respectively, while for microsatellite loci with few alleles, they were 0.1403 and 0.1540 (t-test: p < 0.05; electronic supplementary material, figure S2c). The differences were consistent but not significant for microsatellite loci with an intermediate number of alleles (mean F_ST 0.140 and 0.145, p = 0.15) while that for the most allele-rich loci were incongruent with the other categories of markers albeit not significantly so (0.1234 and 0.1186, p = 0.36; electronic supplementary material figure, S2c).

3.4. F_ST comparisons: effects of outliers

Outlier analyses did not detect any outliers either in the SNP nor microsatellite datasets, suggesting that outliers had little influence on mean F_ST estimates in our data (results not shown).

3.5. F_ST comparisons: effects of LD

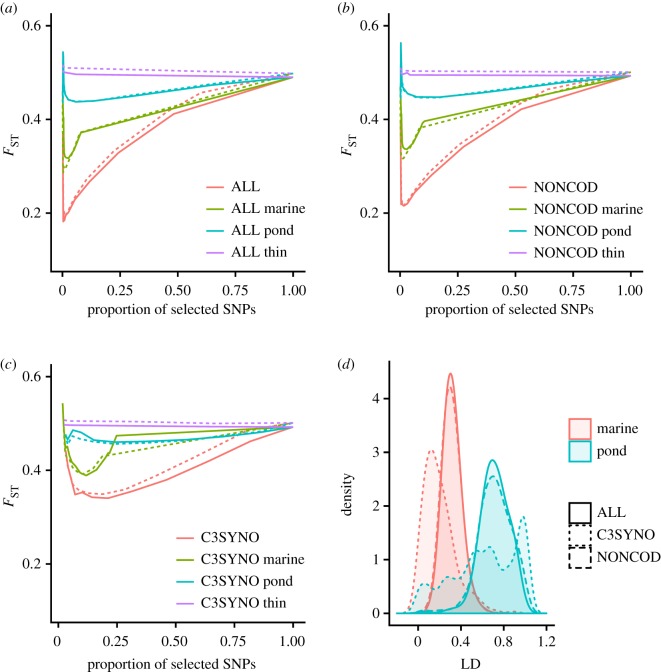
For all three SNP datasets, pruning of SNPs with the distance thinning approach had little effect on the mean F_ST: it remained constant irrespective of the number of SNPs sampled for estimation (figure 3a–c). The LD-based pruning yielded quite different results: when pooled data were used, the mean F_ST was heavily deflated for all three SNP datasets over much (0.1–0.7) of the parameter range (figure 3a–c). More specifically, this deflation was most marked at the lower end of this LD threshold range, generating a positive correlation between F_ST and the proportion of SNPs sampled (figure 3a–c). Only when the LD-threshold was set to be less than 0.1 or greater than 0.7 (corresponding to selection of less than 2000 or greater than 20 000 SNPs in C3SYNO), the sampled unlinked SNPs yielded F_STs similar to that in the full datasets (figure 3a–c). As we employed LD-based pruning separately for pond and marine populations, the F_ST values were more similar (but still somewhat deflated) to those obtained with the thinning approach (figure 3a–c). Although the extent of LD differs in different populations (figure 3d), this is unlikely to explain the F_ST deflation in the LD-based pruning.

Figure 3.

Effect of LD pruning on F_ST estimated from different datasets. Results are shown for (a) all SNPs (‘ALL' dataset), (b) non-coding/non-repeat sites (‘NONCOD' dataset) and (c) codon third position synonymous changes (‘C3SYNO' dataset). For each dataset, solid lines are colour coded to depict results obtained with the thinning approach (purple), or sliding window approach for all pooled populations (red), marine populations only (green) or pond populations only (blue). Dashed lines depict the same results after removing loci with MAF < 0.05. (d) The distribution of the average degree of linkage disequilibrium (LD) in marine and pond populations as estimated from non-overlapping 500 kb sliding windows across the genome.

3.6. Q_ST-F_ST tests: effects of marker type and filtering

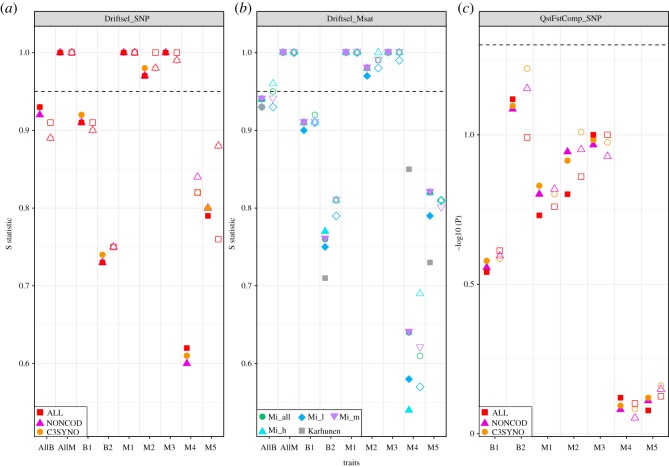
Irrespectively of the marker type or filtering criteria used, the Driftsel analyses detected significant signals of divergent natural selection for most of the traits while QstFstComp detected only very weak and non-significant signals of divergent selection (figure 4; electronic supplementary material, table S1–S7). In all analyses, Driftsel results were also fully consistent with earlier results based on 12 microsatellite loci ([8]; figure 4; electronic supplementary material, table S1, S5). Filtering of SNP data did not affect the outcomes: both Driftsel and QstFstComp yielded the same inference across datasets (i.e. ALL, NONCOD, C3SYNO; figure 4; electronic supplementary material, tables S1, S3, S5, S7). Marker type (i.e. microsatellites or SNP) did not influence the outcome of the Driftsel analyses: all traits displaying evidence for divergent natural selection with SNP markers did also with microsatellite markers (figure 4). Similarly, marker type did not influence the outcome of the QstFstComp analyses (figure 4; electronic supplementary material, table S4).

Figure 4.

Effect of marker ascertainment, marker type and filtering of SNP dataset on Q_ST-F_ST comparisons. Results of Driftsel analyses using SNP and microsatellite markers (a,b, respectively) and QstFstComp using SNP markers (b) are shown. (b) The Driftsel results with the 12 microsatellites used in [8] (Karhunen; grey squares) as well as for different sets of in silico microsatellites: all (Mi_all; green circles), ones with low number of alleles (Mi_l; blue diamonds); with intermediate number of alleles (Mi_m; purple triangles), and with high number of alleles (Mi_h; cyan triangles). (a,c) The results of Driftsel and QstFstComp, respectively, using all SNPs (‘ALL' dataset, red squares); non-coding/non-repeat sites (‘NONCOD' dataset, pink triangles) and codon 3rd position synonymous changes (‘C3SYNO’ dataset, orange circles). Values of the S statistic (Driftsel) or (−log10) p-values (QstFstComp) are reported on the y-axis and dashed lines correspond to the significance threshold for each method. For all panels, filled and open shapes correspond to whether or not the full datasets (filled) or datasets with variability-based ascertained markers (open) were used.

3.7. Q_ST-F_ST tests: effects of marker ascertainment

Marker ascertainment did not influence the outcome of the QstFstComp analyses, regardless of the type of genomic dataset used (figure 4; electronic supplementary material, tables S3, S4, S7). The ascertainment did influence the outcome of the Driftsel analyses for microsatellite markers, however (figure 4). Specifically, Driftsel detected a significant signal of divergent selection on the multivariate behaviour phenotype (‘AllB'; figure 4; electronic supplementary material, table S6) when in silico microsatellites were used. However, this effect disappeared when using only in silico microsatellites with low to mid number of alleles (figure 4; electronic supplementary material, table S6). Moreover, the effect of marker ascertainment on the outcome of Driftsel was more pronounced when the H statistic [8] was computed (electronic supplementary material, figure S5). For this test, both NONCOD and C3SYNO ascertained SNP datasets failed to detect signal of divergent selection on behavioural traits (‘AllB' and ‘B1'; electronic supplementary material, figure S5) and morphological traits (‘M2' and ‘M3'; electronic supplementary material, figure S5). Similarly, the ALL SNP and Mi_h datasets failed to detect signals of selection for the first behavioural trait (‘B1'; electronic supplementary material, figure S5) when using ascertained markers. The ALL SNP dataset also failed to detect the signal of selection for the second morphological trait (‘M2'; electronic supplementary material, figure S5) when using ascertained markers.

3.8. Simulation study

F_ST values estimated by the Driftsel method were 0.49, 0.47, 0.43 and 0.31 for the SNP, Mi_l, Mi_m and Mi_h datasets, respectively, thus approaching the F_ST estimates obtained from the real stickleback data (electronic supplementary material, table S1 and S2). Under the scenarios (i) and (ii) (i.e. Q_ST ≈ 0.45–0.68), the S statistics estimated from the Mi_h data were considerably higher than the estimates obtained with SNP or Mi_l datasets (electronic supplementary material, figure S6(a) and table S9), but in general, the averaged S statistics of all the datasets were under the significance threshold (0.95) to identify the divergent selection. In scenario (iii) (i.e. Q_ST ≈ 0.85), the S statistic of Mi_h set started to go beyond the significance threshold, and had better power to identify the signature of selection compared with other datasets. In scenario (iv) with strong signature of selection (i.e. Q_ST ≈ 0.99), the S statistic among all the datasets were consistent, and they all indicated strong selection signals (S ≈ 0.99). By contrast, the p-values of all the datasets by using the QstFstComp method did not reach the significance level even in scenario (iv) (electronic supplementary material, figure S6(b)), and the power to detect signature of selection appeared to be consistently low (electronic supplementary material, table S9).

4. Discussion

In accordance with earlier suggestions [9,10], our results indicate that microsatellite markers can indeed yield an overly liberal neutral baseline for Q_ST-F_ST tests, and this problem increases with increasing marker variability. Yet this made little difference for the outcome of the Q_ST-F_ST tests in the stickleback data: SNP and microsatellite data yielded the same evolutionary inference. Similarly, we found little evidence to suggest that the genomic location of SNP-markers would markedly influence the F_ST estimates. Filtering of the SNP data for minor alleles had some impact on the estimation of F_ST when using AOR, but the magnitude of this impact was low and varied from one population comparison to another. However, the ascertainment of the markers by variability in marine populations had a relatively large but inconsistent effect: it changed the F_ST estimates when comparing populations used in ascertainment, but had virtually no impact on the comparison of pond populations. Worryingly, the direction of change differed between comparisons from slight increase to significant decrease. If the results are generalizable to other systems involving a greater number of populations with less extreme divergences, the choice of populations used for marker ascertainment may have a relatively large impact on F_ST estimates, and thus, on the neutral baseline divergence estimation. Hence, our results highlight some challenges (and opportunities) which the earlier Q_ST-F_ST studies based on low marker numbers did not meet. In the following, we will briefly discuss the implications of these findings for comparative studies of quantitative trait and molecular marker differentiation.

We compared two approaches for combining F_ST estimates across loci: average of ratios (AOR) and ratio of averages (ROA). Although AOR has been shown to be affected by rare alleles and underestimate the F_ST [29], it often seems the most natural way to compare subsets of genomic estimates (e.g. in sliding window analyses), and is probably still widely used [29]. Our analyses confirmed that ROA gives consistently higher estimates of F_ST than AOR. The relative difference between the two approaches differed between comparisons, but, more interestingly, the relative order F_ST estimates also changed within a comparison between different sets of markers: in our analysis of microsatellite data, the F_ST estimates based on highly variable loci were clearly the lowest with ROA but among the highest with AOR. As a side note, when doing the analyses, we learned that the proper averaging approach, ROA, has been made unnecessarily difficult as many softwares only output estimates of the sitewise ratio of variances. For example, the popular software VCFtools could be easily changed to output also the numerator and denominator of the F_ST estimates, and thus, allow computing ROA for arbitrary subsets of loci.

One of the major concerns in the application of Q_ST-F_ST tests for adaptive differentiation has been the likely underestimation of neutral genetic differentiation when highly variable microsatellite markers are used [9,10]. Our results comparing F_ST values estimated using a very large number of microsatellite loci with differing levels of variability do indeed suggest, in accordance with earlier studies [13,14], that highly variable loci deflate F_ST estimates. However, to which degree this constitutes a concern for Q_ST-F_ST studies depends also on the degree of differentiation in quantitative traits. In the case of the stickleback data analysed here, this made little difference for the outcome of the Driftsel analyses: although the F_ST values were lower for microsatellite than for SNP loci, all the tests that rejected the null hypothesis of differentiation by drift with microsatellites also did so with SNPs. However, this point should be treated cautiously because of the nature of our data. Very high degree of quantitative trait differentiation among marine and freshwater nine-spined sticklebacks are well documented and have been attributed to divergent natural selection for a suite of ecologically important traits [8,37]. Such a marked differentiation is not the norm in empirical Q_ST-F_ST studies where the degree of differentiation can be more subtle (e.g. [64,65]). Hence, the observed insensitivity of the Q_ST-F_ST tests towards biases in the neutral baseline F_ST should not be considered as a general rule. However, the particular case of the sticklebacks could be viewed as an exception confirming the rule: marker type and variability have the potential to bias the neutral baseline F_ST, and although they are less likely to affect inferences involving strong quantitative trait differentiation (i.e. high Q_ST), they should be particularly acknowledged when degree of quantitative trait differentiation is at low to moderate levels. This view is reinforced by the effect of marker ascertainment on the outcome of our Q_ST-F_ST tests. Although the observed effect was trait-specific and confined to highly variable microsatellites in Driftsel analyses, we found that Q_ST-F_ST inference can be influenced by marker type and filtering criteria, even when Q_ST is high.

One critical assumption underlying Q_ST-F_ST analyses is that the markers used for estimation of F_ST are unlinked, as inclusion of tightly linked markers in F_ST estimation can lead to biases in neutral expectations. This assumption is not discussed much in the Q_ST-F_ST literature, where the major methodological concerns have instead been in the estimation of Q_ST (e.g. [66,67]), as well as in the effect of marker variability on F_ST. One reason for the lack of concern over possible effects of LD is that most Q_ST-F_ST studies have used relatively few markers, and the likelihood of sampling tightly linked loci with few markers is low. With genome-scale data, accounting for LD can become a major concern, as linked markers do not provide independent information about the evolutionary history and demography of the study populations [34,68]. Using two different approaches to account for LD, we discovered that the LD-based sliding window approach [46], which is a commonly used tool in genome-wide association and population genetic studies (e.g. [69–72]), may lead to gross underestimation of F_ST. The reason for this appeared to be the strong structure among our study populations that created an impression of LD when the data were pooled. The pond populations had low nucleotide diversity (cf. figure 2c) and many loci showing variation in the marine populations were either fixed or nearly fixed in the ponds. Such differentiated loci showed high F_ST between the populations but also appeared to be in high LD with each other and were preferentially pruned by the sliding window approach. As such, a severe downward bias in F_ST ensued. In fact, LD pruning methods developed for populations with homogeneous LD structure are known to result in misleading outcomes when applied to data from structured populations [73]. Hence, care should be taken when pruning linked markers from multiple-population data, and as demonstrated here, a simple distance thinning approach can maintain the genetic structure of the original data and avoid downward bias in F_ST which could lead to overly liberal Q_ST-F_ST tests. Moreover, our results suggest that the LD-based approach may work relatively well when the LD is estimated from one population or a set of closely related populations; in our case, thinning based on pond populations worked the best (figure 3a–c).

The question of how loci with low minor allele frequencies should be dealt with in population genomic investigations is contentious. Because such loci exhibit high sampling variance, and carry very little information about populations' demographic histories, it is commonly argued that they should be excluded from F_ST estimation (e.g. [31,33], but see [30]). We observed that F_ST was sensitive to decisions about minor allele filtering cut-off points: the higher the cut-off point, the higher the F_ST became. However, the magnitude of this effect varied from one population pair to another, apparently because of the fairly large differences in the frequency of minor alleles among populations. What may be useful to note is that the effect of minor allele filtering on F_ST may depend on how it is calculated [29]. The mean F_STs can be obtained by averaging locus-specific F_ST estimates, or by first calculating the average (within and between populations) variances of all the SNPs and then estimating the mean F_ST of those. Since the individual F_STs of the low-frequency variants are small, they weigh down the average F_ST as obtained with the first approach. However, since the low-frequency variants have very small allelic variances, their influence on the mean F_ST as estimated from the second approach (which is the one used by Driftsel and other Q_ST-F_ST comparison methods) is small. Hence, given their relatively small contribution to F_ST, and in order to err on the conservative side, we believe that it would be justified to remove low-frequency alleles (e.g. MAF < 0.025) when estimating the F_ST baseline for Q_ST-F_ST tests. Their inclusion would have only a minor impact and tend to make tests of adaptive hypotheses slightly more liberal.

We found that F_ST estimates for SNPs and less variable microsatellite loci were on average slightly, but significantly higher in regions of high than low recombination. While this effect was small, it is noteworthy since the difference was in the opposite direction than expected. Namely, background and hitchhiking selection are expected to have stronger effects on allele frequencies in areas of low than high recombination. This is because linkage between neutral and selected loci is tighter in the areas of low recombination [27,28,74]. In fact, several studies have documented negative correlations between population differentiation and recombination rate [75–82]. On the other hand, introgression between fish species was recently shown to be more common in regions of high recombination [83] and possibly the weaker linkage to negatively selected sites allow loci with smaller adaptive effects to diverge between populations. This would create correlation between genetic divergence and recombination rate, and could explain the slightly elevated F_ST values. Although the effect we observed was so subtle that it did not have practical consequences for our Q_ST-F_ST comparisons, recombination rate and degree of population differentiation are often found to go hand-in-hand. Future Q_ST-F_ST studies should thus pay particular attention to how the markers in test panels are distributed in respect to variation in recombination rate or its proxies, such as their location relative to centromeres (e.g. [82]).

Interestingly, we did not detect any outlier loci in our analyses, suggesting that their impact on baseline F_ST estimates, and hence on the outcome of our Q_ST-F_ST tests, can be assumed to be negligible. However, the fact that no outliers were detected does not mean that they did not exist in the data: given the extremely strong impact of genetic drift on the genetic constitution of the pond populations, as for instance reflected in the generally very high F_ST estimates and lack of low-frequency alternative alleles, the outlier tests were probably ill-suited for detecting footprints of selection against such a highly divergent neutral background (e.g. [36]). However, even if some outliers might have become included in the data, it is likely that their impact is small given that a few high-F_ST loci make little difference for the overall F_ST when averaged over a large number of unlinked and presumably neutral loci.

Q_ST-F_ST comparisons have a long history in evolutionary biology (reviewed in [4]), and recent years have seen several methodological refinements to the basic approach (e.g. [8,56–58,84]). Here, we employed two recently developed approaches and although our aim was not to provide formal performance comparisons between the two methods, we discovered that the Driftsel approach recovered consistently more evidence for selection in our data than the QstFstComp approach. This was expected, as the Driftsel approach has been shown to have more power to detect footprints of selection than other types of Q_ST-F_ST tests, especially when the number of populations is small and the impact of random genetic drift is strong [58]. Our simulations further confirm the validity of this inference. Under a scenario of profound quantitative trait divergence (Q_ST > F_ST), Driftsel was consistently able to detect the signal of selection, irrespective of the marker set used, whereas QstFstComp approach failed to do so. Under the scenario of intermediate differentiation, neither of the two approaches was able to pick up the signal of selection, albeit the Driftsel approach applied to highly variable markers showed tendency towards this. This observation underlines the validity of the concerns associated with the use of highly variable markers in Q_ST-F_ST comparisons [9,10]. The generally poor performance of both Driftsel and QstFstComp approaches in detecting signatures of selection in our simulated datasets can be explained by two factors. First is the high level of neutral baseline differentiation used in the simulations, and the second is the small number of populations used. As shown earlier, the performance of both approaches increases with decreasing impact of drift and increasing number of populations included into analyses [58].

Another illuminating lesson from our comparisons was that increasing the number of microsatellite loci (from 12 to 2000) used for F_ST estimation did not influence the outcome of our Q_ST-F_ST tests. However, given the many possible sources of error and bias in estimating neutral baseline differentiation, including as many judiciously filtered markers as possible, may be warranted. This also highlights the need for further developments in the current Q_ST-F_ST testing tools. Although Driftsel is in principle capable of handling infinite number of loci, the run-times for individual tests quickly become prohibitive once the number of markers starts to exceed a few thousand. A nature of the stochastic sample-based MCMC algorithm is that the larger number of SNPs included, the slower the algorithm will converge to the target posterior distribution, and more iterations will be needed. Hence, fine-tuning of the underlying algorithm to meet the demands of modern-day marker-panels is needed. For example, a deterministic variational Bayes (VB) algorithm [85,86] might provide a faster alternative to analyse large-scale SNP data with the Driftsel model.

Finally, it may be also worth stressing that Q_ST-F_ST tests are prone to biases stemming from the choice of study design used to obtain quantitative genetic parameters needed for the estimation of Q_ST. Specifically, the use of full-sib design, such as used in the present study, yields estimates of additive genetic variance potentially confounded with dominance variance [87]. However, dominance variance tends to reduce, rather than inflate Q_ST [88,89]. Thus, even if non-additive inheritance were at play in the differentiation among our stickleback populations, our results would most likely still be rather conservative in respect to the detection of signals of divergent selection.

5. Conclusion

In conclusion, our empirical investigation of genetic variation and differentiation based on large numbers of SNP and microsatellite loci shows that both under- and overestimation of the neutral baseline level of differentiation can occur depending on the filtering and ascertainment of marker data. The results highlight the fact that marker ascertainment, but sometimes also minor allele filtering, might influence the outcome of Q_ST-F_ST tests through their effects of F_ST, especially if the degree of quantitative trait divergence is low. Similarly, while pruning of tightly linked markers from the SNP panels is needed to avoid biased neutral estimates of differentiation, standard filtering methods developed for data from unstructured populations may result in serious biases if populations are strongly differentiated. However, once founded on carefully assembled SNP-panels and sound quantitative genetic data, Q_ST-F_ST comparisons continue to provide a useful framework for testing the adaptive basis of population differentiation in ecologically important quantitative traits. Our findings and considerations suggest that for Q_ST-F_ST comparisons, SNP-markers are preferable over microsatellites, and if microsatellites are to be used, loci from the lower end of the allele number distribution should be preferred over those from the higher end.

Data accessibility

R scripts for the simulation study are attached as electronic supplementary material. SNP and in silico microsatellite data are available within the Dryad Digital Repository: https://dx.doi.org/10.5061/dryad.c2fqz6140 [90].

Authors' contributions

J.M. conceived the study; A.L. and Z.L. designed the methodology; all authors contributed to collecting of the data; A.L. processed the genomic data; A.L. and Z.L. analysed the data; J.M. and A.F. led the writing of the manuscript. All authors contributed critically to the drafts and gave final approval for publication.

Competing interests

We have no competing interests.

Funding

We were supported by the Academy of Finland (grant nos 134728, 250435 and 265211 to J.M.).