Deconstructing the sources of genotype-phenotype associations in humans

Abstract

Efforts to link variation in the human genome to phenotypes have progressed at a tremendous pace over the past couple of decades, and have revealed that most human traits are affected by a large number of genetic variants across the genome. To interpret these associations, and to use them reliably, in particular for phenotypic prediction, a better understanding of the many sources of genotype-phenotype associations is necessary. We summarize the progress that has been made in this direction in humans, notably in decomposing direct and indirect genetic effects as well as population structure confounding. We discuss the natural next steps in data collection and methodology development, with a focus on what can be gained by analyzing genotype and phenotype data from close relatives.

Introduction

Not long ago, genetic analyses were performed using trait values (phenotypes) in families, without genetic data. Discovery of readily measurable genomic markers enabled the identification of disease genes by linkage analysis, without prior knowledge of the underlying mechanisms (1). This led to the identification of the gene responsible for X-linked phagocytic disorder chronic granulomatous disease in 1986, followed by other Mendelian diseases such as cystic fibrosis (2), Huntington disease (3), as well as the breast cancer genes (4, 5). This approach was also applied to study common, complex diseases, including type-2 diabetes and autism, but failed to provide replicable findings.

The second major development came with high-throughput single-nucleotide-polymorphisms (SNP) arrays, which allowed for the genotyping of hundreds of thousands of SNPs simultaneously, giving rise to the genome-wide association study (GWAS) (6). A GWAS tests each SNP for association with the phenotype, without family data. The success of GWAS started with the discovery that CFH contributes to Age-related Macular Degeneration (AMD) based on analyzing 96 cases and 50 controls (7). Subsequent increases in sample sizes, with some now over 2 million (8), have led to discovery of thousands of genetic variants affecting hundreds of human traits. Results from GWAS hold the promise of identifying novel drug targets (9, 10), among other applications.

The power of a GWAS to identify a trait-affecting SNP depends on the fraction of trait variation explained by the SNP, which increases in proportion to the square of the effect size and the heterozygosity. As heterozygosity is higher for more common variants, initial successes were mainly for susceptibility variants with a minor allele frequency above 5%. Even if a common variant is not directly analyzed, it is likely to be strongly correlated with a genotyped SNP nearby, due to the lack of ancestral recombination events between them. This correlation is “local” linkage-disequilibrium, or local LD. Non-local LD, correlations between variants that are not physically close, can result from non-random mating. Due to local LD, GWAS usually does not directly identify the specific causal variant, only localizing its approximate genomic position. Fine-scale mapping, which often requires functional analysis and experimentation, is needed to identify causal variants (11).

The majority of common variants found by GWAS to affect disease risk have low to modest effects (increasing the odds of disease by less than 1.5 fold per risk allele) (12, 13). GWAS applied to whole exome and genome sequencing, along with statistical imputation of sequence-level variants into samples genotyped by SNP-arrays, has led to discovery of some rarer variants with large effects (14). Although the trait variance explained by genome-wide significant (GWS) loci has increased, for most complex traits, the variance explained by GWS loci is only a fraction of the estimated heritability. This gap, labelled the ‘missing heritability’, is discussed further below (12, 15).

For complex traits, identifying all the causal variants and elucidating their underlying mechanisms remains a distant goal. However, GWAS data can be used for prediction from genotypes, notably with polygenic scores (PGS). PGS combine the estimated effects of multiple genetic variants to provide a predicted trait value for an individual. Many applications of PGS have been investigated, such as identification of individuals with substantially elevated genetic risk of heart disease (16). Despite the demonstrated value of PGS, questions regarding robustness and interpretation, i.e. what is driving the predictive power, have started to surface (17, 18).

In GWAS, it is widely acknowledged that associations can be biased by population stratification: primarily association between ancestry and environment effects. Methods adjusting for ancestry, together with replication (19), lend confidence that most GWS associations with common SNPs are true positives. However, this does not mean that bias is eliminated, nor the nature of genotype-phenotype associations properly characterized. We aim to lay out here the different contributions to genotype-phenotype association, the difficulties they introduce, and propose possible solutions.

Effects captured by GWAS associations

The association between a genetic variant and phenotype can be decomposed into the direct effect of the variant, the indirect genetic effect of the variant, and confounding effects (Figure 1). An example would be a variant that has a direct effect on educational attainment (EA) when inherited, and an indirect effect through parental behavior/nurture (20). The same variant could also have an indirect on health through parental nurture but little to no direct effect. Direct effects incorporate a wide range of causal pathways, some neither simple nor “direct”, e.g. variants in CHRNA5 affect lung cancer risk through their association with smoking quantity (21). Furthermore, the direct effect here can include effects of other variants in local LD. Importantly, the typical GWAS conducted without family data can only estimate the sum of the direct and indirect effects (combined effect), and not the two separately.

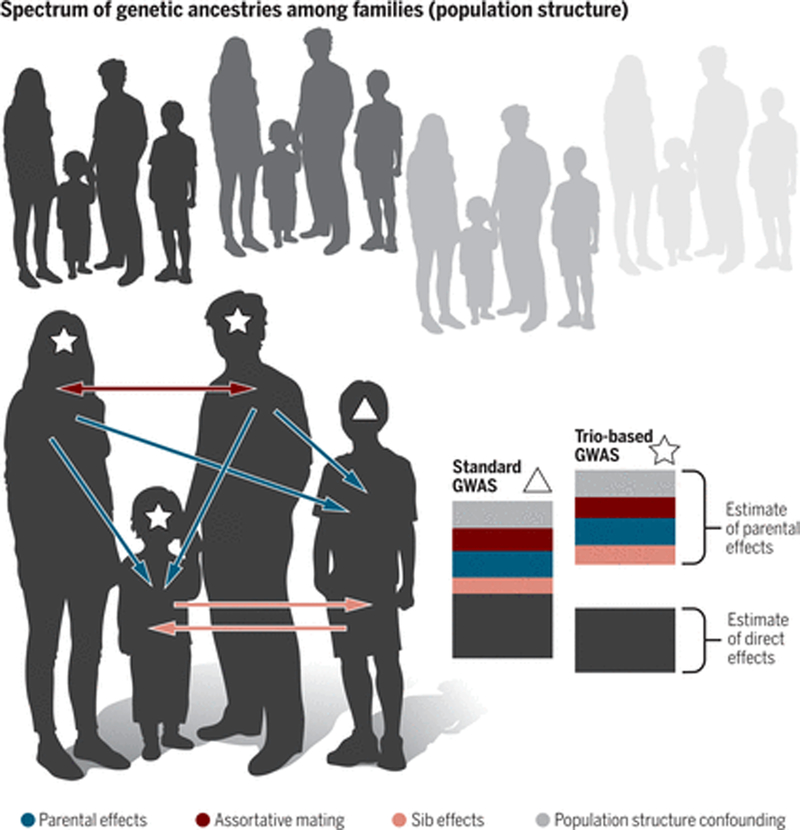
Figure 1. The signals captured by GWAS of distantly related individuals and families.

[For figure designer: Instead of the box above with population structure confounding, a ring of families, each in a slightly different shade of green, with this family as the focal one. Whatever exact color the focal family is, the black boxes to the right should be in that shade.]

When based on distantly related individuals, estimates of effect sizes of SNPs on a trait include direct genetic effects (in black) as well as a number of other effects, including confounding due to population structure (in green), assortative mating for the trait or a correlated one (in blue), indirect genetic effects from parents (in purple) and sib effects (in red). Family-based GWAS (such as the use of a trio) uses parental genotypes as controls to separate direct from indirect genetic effects and other confounding effects (20), as illustrated in the decomposition to the right. In this figure, we ignore effects of local LD.

Under an additive model for the joint effects of variants, we define a genetic component as a linear combination of the genotypes of all the causal variants with weights proportional to the true (direct, indirect, or combined) effects (Fig. 2 legend). The genetic components for direct effect and indirect effect are distinct, but can be correlated with a strength that depends on the genetic correlation between the proband phenotype of interest and the phenotypes of the relatives through which the indirect effects are mediated. As an example, this correlation is probably strong for EA and weak for body mass index (BMI) (20). The relative strengths of these two genetic components and their correlation determine the correlations with the combined effect genetic component. Importantly, because the PGS constructed from a typical GWAS uses estimates of the combined effects, its predictive power can sometimes be substantially stronger than what can be explained by the direct effects alone (20).

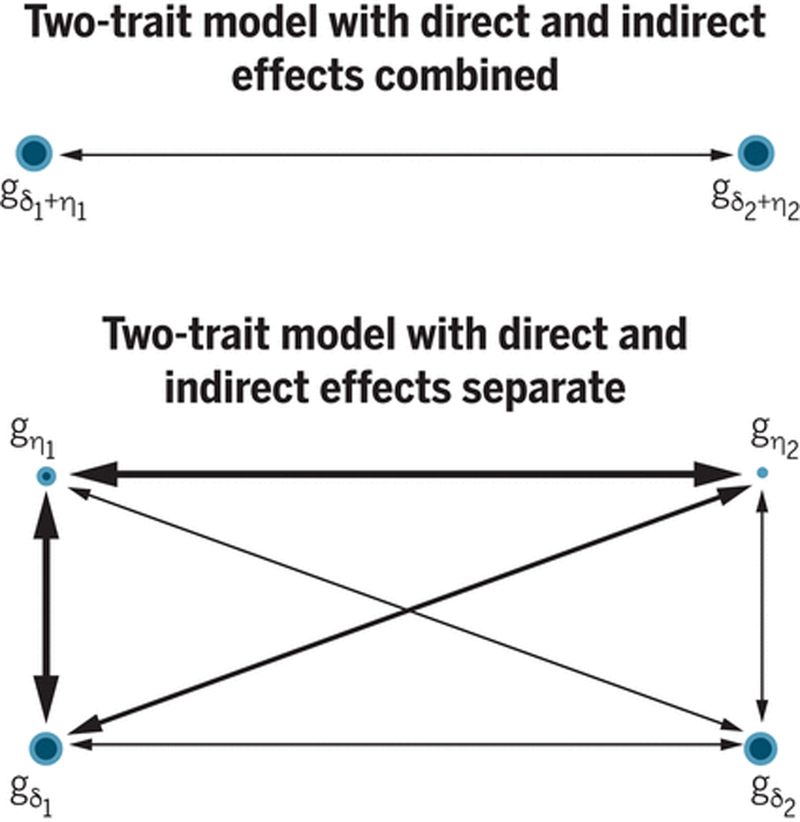
Figure 2. Two-trait genetic models with direct and indirect effects combined or separated.

For a trait, assuming an additive model, the genetic component combining direct and indirect effects is $g_{\delta +\eta }=\sum _i\left({\delta }_i+{\eta }_i\right)g_i$, where g_i, δ_i, and η_i, denote the genotype, the direct effect, and the indirect effect, of variant i respectively. With two traits (1 and 2), there are two magnitudes and one correlation (top panel). For each trait, the combined genetic component can be separated into the direct effect component, $g_{\delta }={\sum }_i{\delta }_i{g}_i$, and the indirect effect component, $g_{\eta }={\sum }_i{\eta }_i{g}_i$. The two-trait model becomes one with four genetic components and six pairwise correlations between them (bottom panel). For the canonical example illustrated here, where trait 1 could be EA and trait 2 could be BMI, the size of • indicates the magnitude of a component, and the thickness of a connecting line indicates the strength of the correlation.

Genetic effects can contribute to the associations between traits through pleiotropy. A two-trait model of pleiotropy (top panel of Fig. 2) of the combined effects has 3 parameters: the variances explained by the combined effect genetic components of the two traits, and the correlation between them. This correlation has been estimated for many pairs of traits using GWAS data (22). By separating out direct and indirect effect components, the model (bottom panel of Fig. 2) has 10 parameters, including the magnitudes of 4 direct and indirect effect genetic components, and 6 correlations. The full model cannot be estimated using standard GWAS, so we currently have little understanding of the extent to which direct and indirect genetic effects contribute differently to pleiotropy.

Confounding Effects

The association between a genetic variant and a phenotype could reflect, in part, a correlation with some other causal phenomena (environmental or genetic) rather than a true causal effect of the SNP on the phenotype. This type of confounding arises from the presence of non-random mating leading to population structure. There are at least three sources of confounding in GWAS: (i) environmental confounding: where allele frequencies and environmental effects vary in a correlated way across different geographic regions or subpopulations; (ii) genetic confounding: when allele frequency differences between subpopulations correlate with frequency differences of other alleles with causal effects; or (iii) assortative mating confounding: when there is assortative mating for the trait or a correlated trait, a variant with a causal effect on the trait becomes correlated with other variants with causal effects. Its association with the trait will then capture its own causal effect plus a fraction of that of the other variants. While the forms of confounding are conceptually different, in practice they are often intertwined.

Adjusting for confounding in GWAS

Principal component (PC) adjustment is a common technique used to remove some of the population structure related confounding effects (23). Ideally, the principal components used for adjustments are strongly correlated with the environmental confounding component and uncorrelated with the direct genetic effect component. If the direct effect component is substantially correlated with the confounding components, PC adjustment will remove some of the direct genetic effects as well as confounding effects.

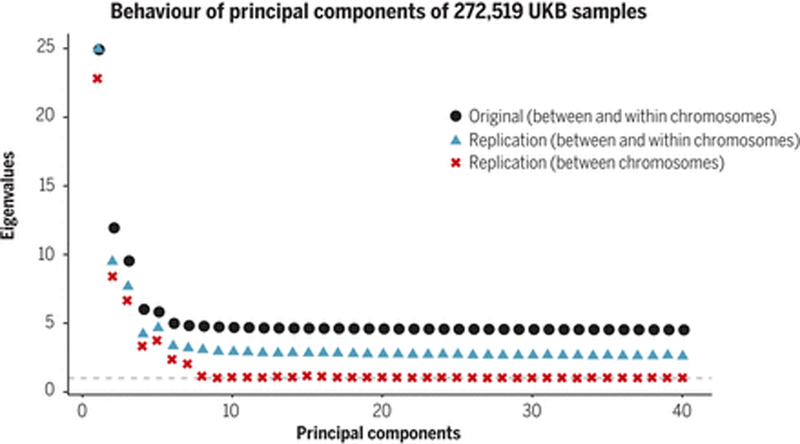
The assortative mating confounding component (iii) is, by its nature, nearly perfectly correlated with the sum of the direct and indirect components. Assortative mating for traits like height and EA (24) leads to non-local LD of variants with direct and indirect effects, which PCs capture. Thus, in theory, PC adjustment could adjust away most of the direct effect component. In practice, this does not happen. Even with a very large sample size, the inferred PCs are likely to be mostly noise beyond a few strong (often geographic) signals. Results from the UKB white British (WB) sample highlight this point (Figure 3): beyond the first 8 strongest PCs, PCs computed from a sample of 272,519 individuals (25) appear to be mainly driven by sampling noise and local LD within chromosomes. The noise can mask subtle population structure that can lead to confounding in GWAS even after PC adjustment (26).

Figure 3. Behavior of principal components of 272,519 UK Biobank samples.

We examine the degree to which principal components are capturing real population structure by examining whether the genetic variance (eigenvalues) explained by top 40 principal components inferred from 146,082 SNPs in 272,519 UK Biobank White British (WB) samples replicates in an independent sample of WB. A replication eigenvalue above 1 indicates that the inferred principal component is capturing replicable correlations between SNPs, either local-LD (within chromosome) or population structure (mostly between chromosomes). Original (black squares): eigenvalues of the principal components in the original set of 272,519 WB individuals. Replication (blue triangles): eigenvalue-equivalents, i.e. variances of the linear combinations of SNP using weights inferred from the original set and standardized genotypes in the replication set of 64,969 WB individuals. Replication (between chromosome only) (red crosses): using the same replication set, but eigenvalue-equivalents computed by ignoring the covariances of SNP-pairs within the same chromosomes, and counting only the covariances of SNP-pairs on different chromosomes, which includes 94.8% of all SNP-pairs. The average eigenvalue for the last 32 PCs decreases from 4.37 for the original set to 2.61 for the replication set and further to 1.03 for the between chromosome set, indicating those PCs are mostly capturing noise and local-LD rather than population structure.

Fitting linear mixed models (LMMs) is an alternative to PC adjustment. These methods perform a type of regression on a set of SNPs where the effect of each SNP is modelled as a ‘random effect’ drawn from a normal distribution (27). LMMs have long been used for trait prediction in animal breeding (28). In human studies, LMM association testing typically consists of estimating the effect of a focal SNP as a ‘fixed effect’, while modelling random effects for a set of other SNPs. Naive LMMs computation scales with the cube of sample size, and thus alternative computational approaches have been developed to handle large GWAS sample sets (29).

The appeal of LLMs is improved modelling of population stratification and sample relatedness (27). LMMs are often used in combination with PCA adjustment and can account for more complicated patterns of stratification by modelling the effects of (nearly) all measured SNPs, capturing both real genetic effects and stratification effects (27). Furthermore, LMM methods can lead to improved estimation of SNP effects and their sampling errors over linear regression in the presence of sample relatedness (27). LMMs can also reduce bias in SNP effect estimates due to assortative mating (30). However, current LMM GWAS methods do not remove the contribution of indirect genetic effects.

Using family genotype data

Given the parental genotypes, an offspring’s genotype is determined by random segregation of genetic material during meiosis. This random segregation is uncorrelated with indirect genetic effects from relatives and other confounding effects. Parental genotypes can thus be used as controls to obtain unbiased estimates of direct genetic effects (20, 31) (Fig. 1). Similarly, genetic differences between siblings are a result of random Mendelian segregation in the parents during meiosis. The genetic differences between siblings are therefore not confounded with indirect genetic effects from parents, population stratification, and assortative mating. However, methods using the differences in sibling genotypes estimate the direct effect minus the indirect effect from the sibling, and hence only provide unbiased direct effect estimates when the indirect genetic effect of the sibling is zero.

The study of indirect genetic effects has a long history in animal breeding (13). In humans, most studies of indirect genetic effects have used PGS derived from GWAS that do not distinguish between direct and indirect genetic effects (Figure 4) (20). However, when direct and indirect genetic effects are not perfectly correlated, that approach cannot give the full picture (32). Ideally, GWAS should be performed with parental or sibling genotypes as controls and measures of indirect genetic effects. However, the power of this approach is currently limited as large samples with genotyped siblings and/or parents are uncommon. Furthermore, as only around half of the genetic variation in a population is within-families, substantially larger samples of families are required to obtain the same study power as standard GWAS analysis. Therefore, methods combining information from standard GWAS and from analysis of families are needed.

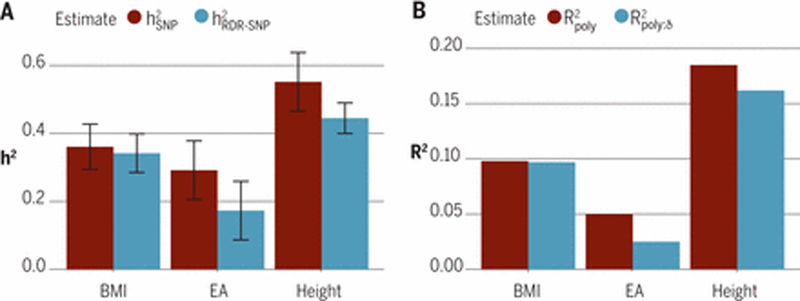
Figure 4. Shrinkage of polygenic prediction and heritability estimates using within-family designs using Icelandic data (20, 31).

A) An estimate of the SNP heritability using transmitted alleles is given by $h_{\text{SNP}}^2$; and an estimate of the SNP heritability using a within family method, relatedness disequilibrium regression (RDR), is given by $h_{\text{RDR}-\text{SNP}}^2$. Statistically significant differences (P<0.05, one-sided z-test) were observed for EA $h_{\text{SNP}}^2/h_{\text{RDR}-\text{SNP}}^2$ = 1.72 (P=7.6×10⁻³) and height $h_{\text{SNP}}^2/h_{\text{RDR}-\text{SNP}}^2$ = 1.24 (P=0.015). B) The variance explained by regression of trait onto polygenic score is given by #”_ol_y; the variance explained by a polygenic score when its effect is estimated using a within-family (trio) design is given by $R_{\text{poly}}^2\cdot \delta$. We emphasise the relative size of the estimates from within-family methods ($h_{\text{RDR}-\text{SNP}}^2$ and $R_{\text{poly}:\delta }^2$) to between-family methods ($h_{\text{SNP}}^2$ and $R_{\text{poly}}^2$). Between family methods capture indirect genetic effects from relatives and, potentially, population stratification and assortative mating in addition to the heritability captured by within-family methods. Trait abbreviations: BMI, body mass index; EA, educational attainment (years).

Heritability

Traditionally, heritability has been estimated from comparing correlations between identical and non-identical twins. In addition to identifying specific causal loci, it is possible to use GWAS data to estimate the phenotypic variation explained by the genetic variation captured by the SNPs (and variants in LD with them) on a genotyping array, called ‘SNP heritability’, $h_{\text{SNP}}^2$ (33). While estimates of $h_{\text{SNP}}^2$ imply that the common genetic variations assayed on a typical genotyping array collectively explain substantially more phenotypic variance than the GWS variants, estimates of $h_{\text{SNP}}^2$ tend to be substantially lower than estimates of heritability from twin studies (15), part of the ‘problem of missing heritability’. Some, but far from all, of this gap is explained by effects of imputed variants that are not in strong LD with markers on a typical genotyping array (13, 34). One possibility is that much of the remaining missing heritability is explained by very rare variants (35).

A widely-used method, GREML, estimates $h_{\text{SNP}}^2$ by measuring the strength of the relationship between phenotypic similarity and genome-wide genetic similarity (estimated from SNPs), which varies even for the distantly related individuals typically used in GWAS (36). This approach provides an estimate of the total variance explained by the combined direct and indirect effects of probands’ alleles (20, 31). The extent to which indirect genetic effects and population stratification have contributed to estimates of $h_{\text{SNP}}^2$ (Figure 4) is not known, nor is the bias induced by assortative mating on both within and between family estimates of heritability.

It is also important to note that the total variance explained by the combined direct and indirect effects differs from the traditionally defined heritability, which is about direct effects only. However, it is a parameter of interest, as it defines an upper bound of genetic prediction from probands’ alleles. An implication is that the upper limit of genetic prediction for a trait could often be larger than the heritability (18).

Some recent methodological developments

LD score regression

With the explosion of GWAS, approaches have been developed to better use and interpret their results. Notably, LD score regression (LDSC) was developed to distinguish the effects of confounding due to population stratification from causal genetic effects on GWAS test statistics (37). Assuming a highly polygenic architecture, the GWAS test statistic for an individual SNP is expected to increase with its LD score (a measure of the genetic variation tagged by a SNP through local LD), due to increasing correlation with causal variants. However, the average test statistic across all SNPs is raised by population stratification, due to correlation between alleles and differences in mean trait values between subpopulations (37–39). By estimating how much population stratification induced confounding inflates the average test statistic, the LDSC intercept can be used to adjust the GWAS test statistics. LDSC can also be used to estimate the correlation between SNP effects on different traits (22), to partition contributions to SNP heritability from different functional categories of variants (40), and to facilitate multi-trait meta-analysis (41).

A key assumption of LDSC is that allele frequency differences between subpopulations are independent of LD scores (37). However, a correlation between LD scores and allele frequency differences can be induced by forms of linked selection such as background selection (26). Thus, questions remain about the reliability of the LDSC measure of population stratification bias.

Mendelian Randomisation

Mendelian randomization (MR) uses genetic data to improve causal inference in epidemiology (42). If a genetic variant affects trait A, and trait A affects trait B, then variants that affect trait A are expected to affect trait B. Genetic variants that affect trait A can be used to determine if an association between trait A and trait B reflects a causal influence of trait A on trait B, given that the genetic variants affect trait B only through their effect on trait A, and that the genetic variants are not correlated with any confounding factors. MR has proven successful in refuting false causal hypotheses derived from observational data, such as the association between HDL cholesterol levels and cardiovascular disease (43) and the reduced risk of cardiovascular disease in moderate drinkers in western societies (44).

MR usually relies on SNP effect estimates from GWAS without families, which can be biased by population stratification, indirect genetic effects from relatives, and assortative mating (45). Within-family MR methods have been proposed to address these concerns, and shown that previous MR estimates of causal effects of height and BMI on EA were spurious (45).

A further challenge for MR analyses is widespread pleiotropy: if a SNP affects trait B through a trait other than trait A, then it is not a valid instrument for inference of the causal effect of trait A on trait B. While methods have been developed to address this problem, their effectiveness can depend on prior knowledge about the confounding pathway (46).

Gene-by-environment interactions

A gene-environment (GxE) interaction occurs when a genetic variant’s effect on a trait differs in different environments (47). Such GxE interactions are distinct from gene-environment correlation, which can result from, for example, indirect genetic effects from relatives. In humans, robustly replicated examples of GxE interactions are rare outside of pharmacogenomics (48, 49). One exception is an interaction between variants in the FTO locus and physical activity affecting BMI (50, 51).

Power to detect GxE interactions in GWA studies is likely to have been low due to small effect sizes and multiple-testing burden. One way to increase the power to detect GxE is to look for interactions between environmental factors and PGS (52, 53). This method is effective when genetic variants affecting a trait interact with environmental factors in similar ways, but cannot identify interactions between environmental factors and specific genetic variants. LMMs can be applied to detect a component of phenotypic variance arising from the interaction between genome-wide genetic variants and an environmental factor (54), but cannot pinpoint interactions with specific genetic variants. Genetic variants involved in GxE interactions affect the variability of a trait (55, 56), which can be exploited to reduce the search space of potential interactions by restricting to variants with evidence for an effect on phenotypic variability. However, methodological challenges remain: interaction effects and genetic effects on phenotypic variability are sensitive to the scale of measurement (56, 57), and the effects of population stratification on estimates of GxE are not well characterized. Furthermore, causality of GxE interaction effects is hard to establish, since the interaction may be with an unmeasured environmental factor that is correlated with measured environmental factor(s), and the broader socio-environmental factors that may structure the environmental exposure are often unknown.

Portability of phenotypic prediction

The accuracy of prediction based on PGS depends on the trait’s heritability and the power of the existing GWAS (notably on the sample size and genetic architecture) (28). For a handful of traits, such as height for which the current prediction accuracy is ~25% (58), existing scores are already informative in sets of individuals similar to those in which the GWAS was conducted.

Polygenic scores do not perform as well in predicting phenotypes of individuals that differ from those included in the GWAS set. Some of the reasons are understood and arise from differences in ancestry. Notably, since PGS are a weighted sum of allele counts and allele frequencies vary across the globe (due to genetic drift and natural selection), alleles that contribute to trait variation in the GWAS are less likely to be present or may even be absent in more distantly related individuals. The prediction accuracy of PGS is also expected to decrease across ancestry groups because GWAS do not identify causal sites, but sets of possible causal sites in local LD; since local LD patterns depend on population histories, the associations observed in one population will tend to capture causal SNPs less well in others. As expected, recent studies report that the incremental R² for a wide range of traits is lower in individuals whose ancestries differ from those of the GWAS set (59, 60).

In addition to allele frequency and LD differences, other factors may contribute to decreased PGS predictive ability: the extent of environmental variance may differ among groups of different ancestry or selected by different enrollment criteria (18), and phenotype measurement may differ across groups. Moreover, effect sizes of variants may differ due to gene by gene (GxG) and gene by environment (GxE) interactions. Changes in effect sizes may be particularly important for traits to which indirect effects or assortative mating make a large contribution, as such factors could be culturally and environmental contingent. Here it becomes essential to decompose the nature of the signals identified in GWAS in order to identify which components (e.g., direct vs indirect effects) provide more readily generalized predictions.

Outlook

For many complex traits, GWAS has changed the landscape of genetic investigations and our understanding of genetic architectures — from lacking a single reliably replicated association to having thousands of variants with robust associations. Notably, GWAS does not require family data, facilitating the collection of large sample sizes. Recently, however, the unique properties of family data are being brought back to the forefront. For one, some rare variants with strong effects only exist in extended families. Most importantly, for deeper and more subtle questions, family data such as parent-offspring trios and sib-pairs may be necessary to separate out direct from indirect effects and other confounding factors. Statistically, one natural extension is to extend the study unit from an individual to the nuclear family. In this regard, it is worth noting that as sample sizes increase, close relatives will inevitably be collected, due to saturation of the population.

A remaining challenge is the issue of ascertainment bias—when study samples differ systematically from the population. Most sample sets are biased towards individuals of European ancestry (60) as well as towards individuals with higher social economic status and greater health (61), along with other unknown biases. While not necessarily introducing false positives, these ascertainment biases limit the portability of GWAS findings (18, 60). Particularly salient in this regard are GxE interactions, not only over space—that is across populations at a given time—but over time, given the massive secular trends in environment that have occurred and continue to occur. This consideration applies to health traits, education-related traits, and fertility traits, which affect selection pressures. In this regard, it is important to sample not only different ancestries and current environments but, where possible, to also collect data on multiple generations.

Glossary

Assortative mating

when couples that produce offspring select one another on the basis of particular phenotypes.

Fine-scale mapping

refers to approaches that aim to identify which variant or variants are likely to be causal among the set of associated variants identified in a GWAS.

Heritability

measures the proportion of phenotypic variation explained by the direct effects of all genetic variants in a population at a given time.

Heterozygosity

the probability that two alleles at a site differ; assuming Hardy-Weinberg equilibrium and considering a bi-allelic site, this measure of genetic diversity is given by 2p(1 - p), where p is the allele frequency.

Imputation

a statistical method that infers the genotypes of individuals at variants not directly measured on a genotyping array by reference to complete genome sequence data.

Indirect genetic effect

the effect of a genetic variant in one individual on the trait of another individual through the environment

Genome-wide significant (GWS) associations

variants associated with the phenotype at a significance level chosen to overcome the multiple testing burden, usually set at p<5×10⁻⁸.

Linkage analysis

tests for co-segregation of phenotypes and genotypes within families.

Pleiotropy

the common observation that many SNPs that are associated with one trait are also associated with other traits. Related to the concept of genetic correlation.

Principal component

A principal component is an inferred axis of genetic variation in a sample. A principal component is a linear combination of genotypes of SNPs, where each SNP has a ‘loading’ giving its contribution to the principal component.

Polygenic risk scores (PGS)

weighted sum of alleles carried by an individual, where the weights are given by effect sizes estimated in GWAS.