Nanoscale Distribution of Nuclear Sites by Super-Resolved Image Cross-Correlation Spectroscopy

Abstract

Deciphering the spatiotemporal coordination between nuclear functions is important to understand its role in the maintenance of human genome. In this context, super-resolution microscopy has gained considerable interest because it can be used to probe the spatial organization of functional sites in intact single-cell nuclei in the 20–250 nm range. Among the methods that quantify colocalization from multicolor images, image cross-correlation spectroscopy (ICCS) offers several advantages, namely it does not require a presegmentation of the image into objects and can be used to detect dynamic interactions. However, the combination of ICCS with super-resolution microscopy has not been explored yet. Here, we combine dual-color stimulated emission depletion (STED) nanoscopy with ICCS (STED-ICCS) to quantify the nanoscale distribution of functional nuclear sites. We show that super-resolved ICCS provides not only a value of the colocalized fraction but also the characteristic distances associated to correlated nuclear sites. As a validation, we quantify the nanoscale spatial distribution of three different pairs of functional nuclear sites in MCF10A cells. As expected, transcription foci and a transcriptionally repressive histone marker (H3K9me3) are not correlated. Conversely, nascent DNA replication foci and the proliferating cell nuclear antigen(PCNA) protein have a high level of proximity and are correlated at a nanometer distance scale that is close to the limit of our experimental approach. Finally, transcription foci are found at a distance of 130 nm from replication foci, indicating a spatial segregation at the nanoscale. Overall, our data demonstrate that STED-ICCS can be a powerful tool for the analysis of the nanoscale distribution of functional sites in the nucleus.

Significance

Several methods are available to quantify the proximity of two labeled molecules from dual-color images. Among them, image cross-correlation spectroscopy (ICCS) is attractive because it does not require a presegmentation of the image into objects and can be used to detect dynamic interactions. Here, we combine for the first time, to our knowledge, ICCS with super-resolution stimulated emission depletion (STED) microscopy (STED-ICCS) to quantify the spatial distribution of functional sites in the nucleus at the nanoscale. Our results show that STED-ICCS, in addition to quantifying the colocalized fraction, detects characteristic nanometer distances associated to correlated nuclear sites. This work shows that STED-ICCS can be a powerful tool to quantify the nanoscale distribution of functional sites in the nucleus.

Introduction

Healthy genome regulation and maintenance rely on the proper spatiotemporal coordination between several nuclear functions. Alterations in chromatin organization are often linked to human diseases (1). Representative examples are DNA transcription and replication, two fundamental genomic processes that can potentially compete for the same DNA template. Replication and transcription both occur within the highly packed chromatin environment and must be tightly coordinated in time and space to avoid interference and generation of DNA damage (2). Alterations in the coordination of replication and transcription represent a major source of genomic instability, a hallmark of cancer (3). Therefore, deciphering the coordination between nuclear functions at a high spatial and temporal resolution is important to understanding its role in health and disease. Genome-scale sequencing methods provide high-resolution maps of spatiotemporal regulation of genomic processes (4,5). However, they do not provide any information on spatial localization and lack single-cell resolution. In this context, optical imaging methods are emerging as complementary tools to investigate genome organization and structure in intact single-cell nuclei (6).

The simplest approach to study spatial organization of two labeled molecules consists in the analysis of dual-color images for the presence of colocalized signal, i.e., signal that overlaps within the two detection channels. Colocalization is a measurement of the co-distribution of two probes at a spatial scale defined by the resolution of the optical microscope. In conventional optical microscopy, this spatial scale is limited by diffraction to ∼250 nm. For this reason, alternative strategies have been developed to investigate cellular processes at the nanoscale. For instance, a popular method to probe molecular distances in the nanometer range is Förster resonance energy transfer (FRET) (7, 8, 9), but unfortunately, FRET is not sensitive when distances are larger than ∼10 nm. Similarly, in situ proximity ligation assay (PLA) is a powerful method to visualize proximity of two labeled species, but its sensitivity does not exceed 40 nm (10,11). This scenario changed dramatically with the introduction of super-resolution microscopy (also called nanoscopy), namely the ensemble of microscopy techniques providing optical resolution below the diffraction limit (12). For instance, in single-molecule localization microscopy (SMLM), the fluorophores are sequentially switched on and off and localized with high precision on each frame, resulting in images with a resolution down to ∼20 nm (13, 14, 15). In stimulated emission depletion (STED) microscopy, the fluorophores are selectively switched off at the periphery of the diffraction-limited detection spot by a second, doughnut-shaped laser beam, producing an immediate improvement of spatial resolution down to ∼50 nm (16). Thus, super-resolution microscopy can be used to probe spatial organization in the 20–250 nm range, which corresponds to the range of higher-order organization of chromatin in the nucleus. This nanoscale spatial organization can be studied in a “static” way, from images of fixed cells, or in a “dynamic” way, from acquisition of super-resolution data in live cells.

Methods that provide a quantitative measure of colocalization from static multicolor super-resolution images can be divided into two major groups: object-based methods, which perform a segmentation of the image into objects before analyzing their relative spatial distributions, and pixel-based methods, which extract correlation coefficients from pixel intensities (17,18). In general, object-based analysis can be performed on any type of super-resolution image as long as the target objects are well-resolved and identified. In particular, object-based methods are often the methods of choice in SMLM, in which the acquired data are already segmented into a list of x, y coordinates of individual molecules (19, 20, 21, 22, 23). In principle, object-based analysis provides a full description of the spatial distribution of the two labeled species: in fact, knowledge of the object coordinates allows 1) mapping the locations of the specimen with a higher level of proximity and 2) performing a statistical analysis of the relative distance between the particles. On the other hand, a great advantage of pixel-based methods is that they do not require a presegmentation of the images into objects but rely on the calculation of coefficients from the pixel intensity values (24,25). Pixel-based methods are routinely applied to quantify spatial distributions in multicolor super-resolution images (26, 27, 28).

A method to study interactions in a “dynamic” way is fluorescence cross-correlation spectroscopy (FCCS), the dual-channel version of fluorescence correlation spectroscopy (FCS) (29). In FCCS, the fraction of interacting particles is extracted from the analysis of temporal intensity fluctuations originating from changes in fluorophore concentration within a small observation volume, typically defined by the focal spot of a confocal microscope (30,31). Both FCS and FCCS have been applied to study the mobility and interactions of molecules in the nucleus (32, 33, 34). Interestingly, the very same formalism of FCS and FCCS can be applied to the analysis of the spatial intensity fluctuations found in images. Image correlation spectroscopy and image cross-correlation spectroscopy (ICCS) are the spatial variants of FCS and FCCS, respectively (35). Notably, ICCS can be used as a pixel-based method to analyze the spatial distribution in static images as well (36). Thus, ICCS appears as an extremely versatile method that can offer several advantages compared to other analysis approaches, namely it does not require a presegmentation of the image into objects and can be used to detect dynamic interactions (37, 38, 39). Dreier et al. have previously shown that the synergic application of STED super-resolution imaging and confocal ICCS reveals the dynamics of liposomes at the human skin barrier (40). However, despite its potential, the combination of ICCS with super-resolution microscopy has not been fully explored yet.

Here, we show that the combination of dual-color STED nanoscopy with ICCS (STED-ICCS) can be used to quantify the relative nanoscale spatial distribution of distinct nuclear foci. In particular, we show that STED-ICCS can provide, to some extent, some of the attractive features of an object-based analysis but without requiring a presegmentation of the super-resolved image. In fact, we are able to 1) map the locations within nuclei with a higher level of proximity and 2) determine whether the particles are correlated at a certain nanoscale distance. First, the analysis is tested on simulated images of nuclear foci at variable densities and compared with an object-based analysis performed on the same simulated data sets. Then, the STED-ICCS analysis is tested on dual-color STED images of model samples based on DNA origami bearing green and red fluorophores located at a characteristic distance of 20 or 100 nm. These data demonstrate that STED-ICCS can provide nanoscale information on the distance between correlated particles. Finally, to validate the STED-ICCS method on a biological sample, we quantify the relative nanoscale spatial distribution of three different pairs of nuclear sites in MCF10A cells. As expected, transcription foci and a transcriptionally repressive histone marker (histone 3 lysine 9 tri-methylated (H3K9me3)) show the minimum level of colocalization and a random relative distance distribution. Conversely, nascent DNA replication foci and the proliferating cell nuclear antigen (PCNA) protein have a high level of proximity and are correlated at a nanometer distance scale that is close to the limit of our experimental approach. Notably, nascent DNA replication foci and transcription foci are found to be partially correlated but at a distance of ∼100 nm, indicating that the two functional sites are spatially segregated at the nanoscale. Overall, these data demonstrate that STED-ICCS can be a powerful tool for the analysis of relative nanoscale spatial distribution of functional sites in the nucleus.

Materials and Methods

Cell culture

Human mammary epithelial cells MCF10A were grown in Dulbecco’s modified Eagle’s medium (Merck KGaA, Darmstadt, Germany)/Ham’s F12K (Thermofisher Scientific, Waltham, MA) medium (1:1) containing 5% horse serum, 1% penicillin/streptomycin, 2 mM L-glutamine, 10 μg/mL insulin, 0.5 μg/mL hydrocortisone, 50 ng/mL cholera toxin (all from Merck KGaA), and 20 ng/mL epidermal growth factor (PeproTech, Rocky Hill, NJ), at 37°C in 5% CO₂. For fluorescence microscopy measurements, cells were seeded on glass coverslips coated with 0.5% (w/v) gelatin (Sigma-Aldrich, St. Louis, MO) and cultured for 18 h in growth medium. Cells were incubated for 20 min with the synthetic nucleotides 5-ethynyl-2′-deoxyuridine 10 μM (EdU) (Thermo Fisher Scientific, Waltham, MA) and 5-bromouridine 10 mM (BrU) (Sigma-Aldrich) to allow labeling of replication and transcription, respectively. Upon nucleotide incorporation, cells were washed with phosphate-buffered saline (PBS) and fixed with 4% paraformaldehyde (w/v) for 10 min at room temperature.

Sample preparation

For immunostaining, MCF10A cells were permeabilized with 0.1% (v/v) Triton X-100 in blocking buffer (BB), composed of 5% w/v bovine serum albumin in PBS, for 1 h at room temperature. To recognize nascent DNA (transcription) and RNA (replication) filaments, incorporated BrU and EdU were labeled, respectively. For BrU detection, cells were incubated overnight at 4°C with a primary rabbit antibody anti-BrdU (Rockland Immunochemicals, Limerick, PA) diluted at 1:1000 in BB, followed by three 15-min rinses in BB. EdU incorporation was detected using the Click-iT EdU imaging kit (Thermo Fisher Scientific) according to the manufacturer instructions but replacing the kit’s azide-Alexa488 with Azide-PEG3-biotin-conjugated (Merck) at a 1:500 dilution to allow the subsequent immunostaining. After the click reaction, cells were washed with PBS and incubated with the primary mouse antibody anti-biotin (Merck) diluted at 1:1000 in BB for 1 h at room temperature. To detect PCNA and EdU, incorporated EdU nucleotides were conjugated with biotin-azide using the Click-iT EdU imaging kit as previously described. Samples were then incubated with primary antibodies anti-biotin (1:1000 dilution in BB) and anti-PCNA in rabbit IgG (Santa Cruz Biotechnology, Dallas, TX) (1:500 dilution in BB) at the same time for 1 h at room temperature. To detect transcriptionally active and repressed chromatin, we labeled BrU and H3K9me3, respectively. The cells were simultaneously incubated with primary antibody anti-BrdU as previously described and anti-H3K9me3 in mouse IgG (Abcam, Cambridge, UK) at a 1:800 dilution overnight at 4°C in BB.

After three 15 min rinses in BB, cells were incubated with secondary antibodies (1:200 dilution) for 1 h at room temperature in BB, upon which cells were washed with BB three times for 15 min. The secondary antibodies were Atto532 and Chromeo488 conjugated with goat anti-mouse IgG (Rockland Immunochemicals) and anti-rabbit IgG (Abcam), respectively. All samples were washed with PBS and water before mounting with Mowiol (Sigma-Aldrich).

DNA origami structures containing the two fluorophores Chromeo488 and Atto532 at a well-defined distance of either d = 20 nm or d = 100 nm were purchased from GATTAquant (custom nanorulers; GATTAquant, Hiltpoltstein, Germany).

Experiments

All imaging experiments were performed on a Leica TCS SP5 gated-STED microscope, using an HCX PL APO 100×100/1.40/0.70 oil immersion objective lens (Leica Microsystems, Mannheim, Germany). Emission depletion was accomplished with a 592 nm STED laser. Excitation was provided by a white laser at the desired wavelength for each sample. For imaging of MCF10A nuclei, Chromeo488 was excited at 470 nm and its fluorescence emission detected at 480–530 nm, with 1–10 ns time gating using a hybrid detector (Leica Microsystems). Atto532 excitation was performed at 532 nm and the emission collected between 545 and 580 nm by a hybrid detector, with time gating of 2.5–6 ns. The two channels were acquired in line-sequential mode, and the excitation and depletion power were adjusted separately for each channel. 512 × 512 pixel images were acquired with a pixel size of 40 nm. Similar settings were used for imaging the 100- and 20-nm nanorulers.

Simulations

Dual-color images of nuclear foci were simulated using MATLAB (The MathWorks, Natick, MA). For each channel, the object consisted in a variable number N of point-like emitters distributed randomly inside a circular area with a diameter of 16 μm (41). The images were made by 512 × 512 pixels with a pixel size of 40 nm. The maximal total number of photons detected from a single pixel position from a single particle was set to S = 40. For each channel, the object was convolved with a Gaussian point spread function (PSF) with a full width at half-maximum (FWHM) of 120 nm, and a uniform background level B = 3 was added within the circular region. Finally, the resulting images were corrupted by Poisson noise. Poisson noise was introduced to each pixel at a level based on the pixel value using the MATLAB function “imnoise.” To simulate the uncorrelated sample, the foci were distributed randomly in both channels. To simulate a partially colocalized sample, a number N/4 of foci in the second channel was set to have the same coordinates of N/4 foci in the first channel. To simulate the sample colocalized in a zone, the colocalized foci were forced to be in a specific quarter of the circular area. The total number of foci in each channel was varied from N = 100 to N = 10,000.

The simulations reported in Figs. S1–S3 were generated by randomly distributing N = 500 particles in the green channel and then locating each of the N = 500 red particles at a given distance d and a random orientation relative to a particle in the green channel. The images were all made by 256 × 256 pixels. The signal level S, the background level B, and the width of the PSF in each channel were varied as specified in the captions. In the simulations reported in Fig. S6, the images were all made by 128 × 128 pixels, and the pixel size was set to 40 nm. The first frames were generated by randomly distributing N = 1000 green-red particles correlated at the specified distance d. To simulate movement of the particles, in each consecutive frame, the green-red particles were moved by half a pixel in random directions and their relative orientation varied by 0.1 rad. The signal level was set to S = 15, and the background level was set to B = 1.5.

ICCS and local ICCS

The ICCS analysis was performed in MATLAB (The MathWorks) using a custom code. The two-dimensional (2D) image correlation functions were calculated as

$$G_{ij}\left({\delta }_x,{\delta }_y\right)=\frac{I_i\left(x,y\right)I_j\left(x+{\delta }_x,y+{\delta }_y\right)}{I_i\left(x,y\right)I_j\left(x,y\right)}-1,$$ (1)

where I₁(x,y) and I₂(x,y) are the images in the first and the second channel, respectively, and the angle brackets indicate averaging over all the selected pixels of the image. The two autocorrelation functions were obtained by setting i = j = 1 and i = j = 2, respectively, whereas the cross-correlation function was obtained by setting i = 1 and j = 2. The numerator in Eq. 1 was calculated by a 2D fast Fourier transform algorithm. Before calculation, a region of interest (ROI) corresponding to the nucleus was defined and all the pixels outside this ROI were assigned an intensity value equal to the average value inside ROI, as reported previously (42). This step is useful to minimize the effects of nuclear borders on the correlation functions.

The 2D correlation functions were then converted into radial one-dimensional correlation functions G_ij(δ_r) by performing an angular mean, as described previously (43). The resulting radial correlation functions were then fitted to a Gaussian model

$$G_{ij}\left({\delta }_r\right)=G_{\infty }+G_{ij}\left(0\right)exp\left(-{\delta }_r^2/w_{ij}^2\right)$$ (2)

to extract the amplitude parameters G_ij(0) and the width parameters w_ij. Note that the width parameter w represents the 1/e² radius of a Gaussian function and is related to the FWHM by the relationship w = FWHM/(2ln2)^1/2.

The amplitude parameters were used to calculate the coefficients of colocalizations M₁ and M₂ (36):

$$M_1=G_{12}\left(0\right)/G_{22}\left(0\right),$$ (3)

$$M_2=G_{12}\left(0\right)/G_{11}\left(0\right).$$ (4)

The colocalized fraction f_ICCS was then calculated as the arithmetic mean of the two coefficients M₁ and M₂. The broadening of the cross-correlation function with respect to the corresponding autocorrelation function has been evaluated with the parameter Δw = w₁₂ − w_cc, where w_cc = ((w₁₁² + w₂₂²)/2)^1/2. The value of Δw was converted into a distance value d_ICCS using the empirical relationship d_ICCS = (Δw/C)^1/2, where the value of the constant C was determined from simulated data (Figs. S1 and S3).

To discard bad cross-correlation function fits, we excluded 1) fits with a χ²-value 50 times larger than the χ²-value of the autocorrelation function fit; 2) fits with a width w₁₂ too different compared to the average autocorrelation function widths (r_w < 0.5 or r_w > 2, where r_w = w₁₂/(w₁₁w₂₂)^1/2); and 3) fits with a negative offset G_∞ (G_∞ < −0.2 G₁₂(0)). In all these cases, we set f_ICCS = 0.

The local ICCS analysis consisted in performing ICCS iteratively on small, 69 × 69 pixels wide subregions of the full-size image. For each subregion, the local auto- and cross-correlation function were calculated and the parameters G_ij(0), w_ij, and f_ICCS were extracted as described for ICCS analysis. In addition to the conditions described above, we excluded local autocorrelation fits with an amplitude 10 times larger than the amplitude of the global autocorrelation function and local cross-correlation fits with an amplitude two times larger than the amplitude of the local autocorrelation function. The calculation was limited to N_samp = 100 sampling subregions centered on N_samp pixels uniformly distributed over the image. Then, the resulting values were interpolated to produce a map of the same size of the full-size image.

A user-friendly version of the MATLAB script used in this work is available at https://github.com/llanzano/ICCS.

Object-based analysis and relative distance distribution

The central coordinates of the foci in each channel were obtained using the JaCoP plugin (44) in ImageJ (45). For each channel, an intensity threshold was set manually. The minimal size of the particles was set to 2 pixels. The algorithm provided the coordinates of all the localized particles in each channel and the values of distance from each particle in the first channel from all the particles in the second channel. In the simulations, particles were considered colocalized if their distance was lower than 50 nm. In the biological samples, particles were considered colocalized if their distance was lower than 140 nm. All the values of distance were used to build the relative distance distribution (RDD) histogram. To estimate the random component in the cumulative RDD histogram, a linear fit of the data through the origin was performed in the range 250–500 nm. This linear component was then subtracted from the data to obtain an RDD without the random component.

Results

Simulations: Super-resolved ICCS is a robust method to characterize relative spatial distribution at high densities of foci

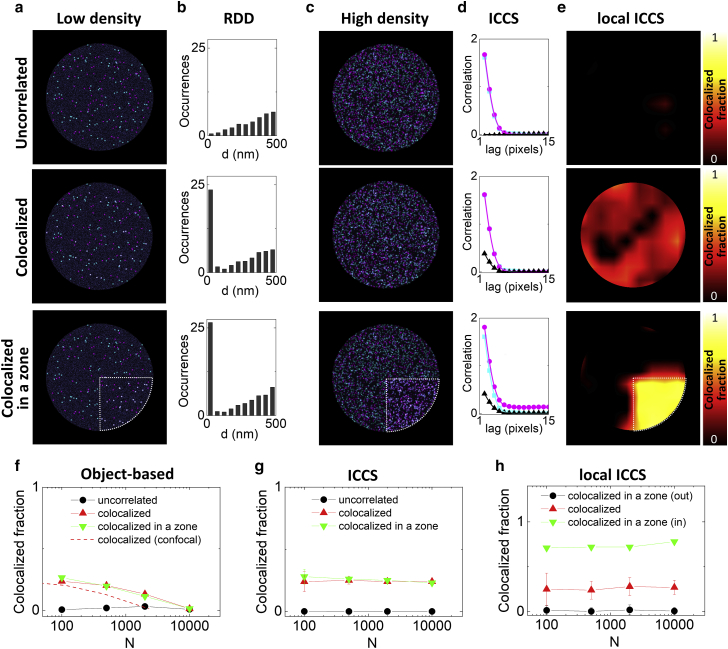
To compare super-resolved ICCS with object-based analysis, we simulated dual-color images of nuclear foci at variable densities (Fig. 1). In each channel, the nuclear foci were simulated as N point-like particles distributed in a 16-μm-wide circular region (41) and convoluted with a Gaussian PSF with an FWHM of three pixels, corresponding to 120 nm. We simulated distributions of foci randomly distributed in each channel (uncorrelated), with a fraction f_coloc = 0.25 of foci colocalizing in the two channels (colocalized) and with a fraction f_coloc = 0.25 of foci colocalizing only in a specific subportion of the image (colocalized in a zone). The total number of foci in each channel was varied from N = 100 to N = 10,000. These simulations are intended to test the analysis workflow and not as a model of the more complex distributions and patterns that can be found in real samples.

Figure 1.

Comparison between super-resolved ICCS and object-based analysis on simulated data. (a) Simulated dual-color images of nuclear foci at low density (total number of foci, N = 100), assuming a random distribution of foci in each channel (uncorrelated), a 25% of foci colocalization in the two channels (colocalized) and a 25% of foci colocalizing only in a specific subportion of the image (colocalized in a zone), indicated by the dashed contour. The data were simulated with a PSF size of FWHM = 120 nm. (b) Relative distance distributions (RDDs) obtained by object-based analysis of the simulated images. (c) Simulated dual-color images of nuclear foci at high density (total number of foci, N = 2000). (d) Spatial correlation functions of the images shown in (c). Shown are the cross-correlation function (black triangles) and the single-channel autocorrelation functions (magenta dots and cyan squares) along with the corresponding fits (solid lines). (e) Local ICCS maps of the images shown in (c). The color map represents the value of parameter f_ICCS calculated on a moving subregion of 69 × 69 pixels. (f) Colocalized fraction extracted from object-based analysis of the simulated data as a function of the number of foci N. The dashed red line shows the trend for the colocalized sample when the PSF size is FWHM = 250 nm. (g) Colocalized fraction extracted by ICCS analysis of the simulated data as a function of the number of foci. (h) The value of f_ICCS extracted from the local ICCS map inside (in) and outside (out) the colocalization zone for the “colocalized in a zone” sample is compared with the value of f_ICCS in the “colocalized” sample. To see this figure in color, go online.

At low density, the foci are easily localized in the xy plane, and the relative distance between every center in one channel and every center in the other channel can be calculated from their center positions (Fig. 1 a) according to the localization-based approach. The resulting RDD has a linearly growing trend for the uncorrelated sample, as expected from purely geometrical considerations (Fig. 1 b). For the other two samples in Fig. 1 a (colocalized and colocalized in a zone), the RDD shows an additional peak at a distance zero, corresponding to the fraction of colocalized foci, superimposed with the linear trend due to the random distribution (Fig. 1 b). At higher densities of foci (Fig. 1 c), the colocalized fraction retrieved with the object-based analysis (Fig. 1 f, triangles) deviates from the simulated value (f_coloc = 0.25). In particular, a deviation of 20% from the expected value is obtained when the number of foci is N = 500 (Fig. 1 f). For comparison, considering an FWHM value typical of diffraction-limited microscopy, FWHM_conf = 250 nm, a deviation of 20% is obtained already when the number of foci is N = 115. This is due to the lower accuracy in determining the center positions of the foci during the segmentation process.

On the other hand, ICCS is able to determine the colocalized fraction independently of the density of foci (Fig. 1 g). In ICCS, the colocalized fraction f_ICCS is extracted from the fitting of the image auto- and cross-correlation functions (42,46). The amplitude of the cross-correlation function is zero for the uncorrelated sample (Fig. 1 d, top), whereas it is positive for both colocalized samples (Fig. 1 d, mid and bottom). In the range of foci densities explored here, the value of colocalized fraction retrieved by ICCS is consistent with the simulated value (Fig. 1 g), in keeping with previous studies (36). Thus, super-resolved ICCS can be used to determine the fraction of cross-correlated particles also when the density of foci is too high for non-super-resolved methods or, equivalently, when the improvement of spatial resolution is not sufficient to resolve the foci.

An apparent disadvantage of ICCS, in comparison with object-based approaches, is that it provides only an average description of the properties of the sample in the region analyzed. In fact, the two correlated samples shown in Fig. 1 c (colocalized and colocalized in a zone) produce almost identical correlation functions (Fig. 1 d) despite a very different colocalization pattern. Thus, ICCS can be used to extract a value of the colocalized fraction at high density of foci but does not specify where the foci are colocalized. To partially overcome this limitation, we performed local ICCS analysis, i.e., ICCS performed on small subregions of the image (Fig. 1, e and h). It has been previously shown that if the spatial correlation function is calculated locally, one can get maps of physical parameters such as protein velocity (47), particle size (43), or diffusion coefficient of a probe (48,49). Local ICCS can be used to generate a map of the value of the colocalized fraction extracted by fitting the local auto- and cross-correlation functions (Fig. 1 e). The local ICCS maps show that the two correlated samples (colocalized and colocalized in a zone) have a very different pattern, despite containing the same total fraction of colocalized foci. The spatial resolution of the local ICCS map depends on the size of the subimage employed for the local analysis. For instance, in the example of Fig. 1 e, the size of the subimage was set to 69 × 69 pixels.

Measurements on model systems: STED-ICCS detects particles correlated at a distance

Another limitation of super-resolved ICCS, when compared to object-based analysis, is that it cannot be used to perform a complete statistical analysis of the relative distance between the particles. This feature of object-based analysis is particularly useful to detect characteristic nanometer distances associated with intermolecular complexes (20). Here, we aim to show that even if it is not able to provide a full statistical analysis, super-resolved ICCS can provide information on the average distance between correlated particles.

In super-resolved ICCS, the shape of the cross-correlation function is dependent upon the distance d between the two probes and the effective spatial resolution of the STED microscope in the two channels. For two single spots located at distance d along a given direction, if the single-channel 2D autocorrelation functions have width w₁₁ and w₂₂, the corresponding 2D cross-correlation function has a width equal to w_cc = ((w₁₁² + w₂₂²)/2)^1/2 and is shifted from the origin of an amount d along the same direction (50). In most real cases, however, the particles are found at all possible orientations with respect to each other. This has two effects on the cross-correlation function, namely a reduction of its amplitude and an increase of the value of its width compared to the value w_cc expected for perfectly coaligned spots. The broadening of the cross-correlation function can be evaluated as Δw = w₁₂ − w_cc. Importantly, Δw is a parameter sensitive only to the average distance between correlated particles, whereas the amplitude-related parameter f_ICCS is sensitive also to the relative number of correlated particles. Thus, the Δw can be used to estimate the distance associated to the correlated particles. To actually convert values of Δw into values of distance, we performed simulations of particles correlated at variable distances and measured the broadening of the cross-correlation function (Fig. S1). We investigated the effect of a varying level of background noise in the determination of this calibration curve (Fig. S2). We did not find a significant dependence for background levels comparable to those present in our data (Fig. S2). In contrast, we found a more critical dependence of the calibration curve from the width of the PSF in the two channels (Fig. S3).

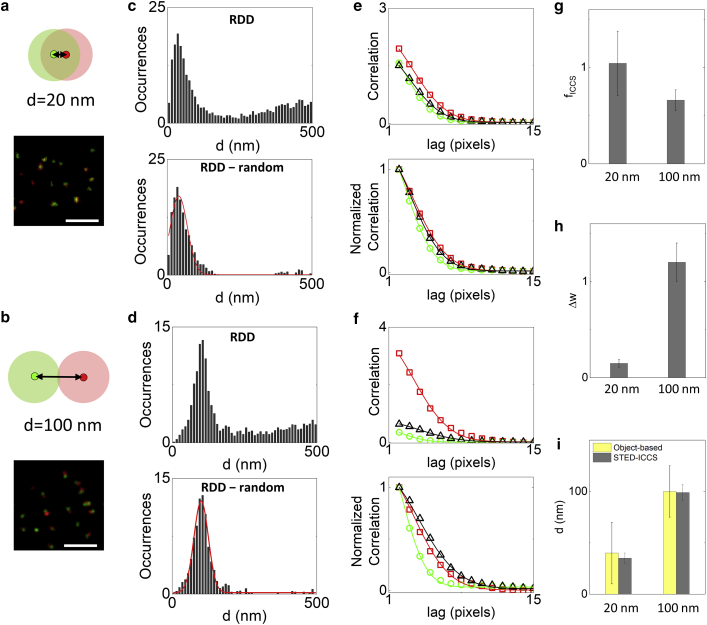
To demonstrate, experimentally, that super-resolved ICCS can extract characteristic correlation distances, we performed STED-ICCS on optical nanorulers, i.e., DNA origami structures designed to contain the same two fluorophores used in our experiments (Chromeo-488 and Atto-532) at a well-defined distance of either d = 20 nm or d = 100 nm (Fig. 2, a and b). First, we characterized the samples by object-based analysis. The spatial resolution achieved in these STED images was ∼95 nm in the green channel and ∼130 nm in the red channel, as determined from the FWHM of line profiles (Fig. S4). Considering an average number of photons detected per spot per channel N ∼ 30 and a 10% background noise level, this translates to an estimated localization precision σ_G ∼ 13 nm and σ_R ∼ 20 nm in the green and red channels, respectively (51). This propagates to an expected uncertainty (σ_G² + σ_R²)^1/2 ∼ 24 nm in the estimation of the relative distance d. The distributions of distances obtained from the object-based analysis of STED images of optical nanorulers are reported in Fig. 2, c and d. They contain a peak superimposed to a linear growing component. The distance peak value found in the RDD of the 100-nm nanorulers was d_100nm = 100 ± 25 nm (mean ± SD), in keeping with the expected value. These data indicate that at the imaging conditions of this sample, we can measure distances with a precision σ_d ∼ 25 nm. This sets a lower limit to the distances that can be detected with our experimental setup. In line with this, the distance peak value found in the RDD of the 20-nm nanorulers was d_20 nm = 40 ± 30 nm.

Figure 2.

STED-ICCS of model samples. (a and b) Schematic drawing and representative dual-color STED images of the optical nanorulers. These model systems consist of Chromeo-488 and Atto-532 fluorophores located at a fixed distance of 20 nm (a) and 100 nm (b) on engineered DNA nanorulers. The shaded circles schematically represent the PSF. Scale bars, 1 μm. (c and d) Object-based analysis for the 20-nm (c) and 100-nm (d) nanorulers. Shown are the RDD histograms before (top) and after (bottom) subtraction of the uncorrelated random component. Solid red lines are Gaussian fits of the data (d_20 nm = 40 ± 30 nm, d_100 nm = 100 ± 25 nm, mean ± SD). (e and f) Raw (top) and normalized (bottom) correlation functions of the representative images shown in (a) and (b). Shown are the cross-correlation function (black triangles) and the red (red square) and green (green circles) channel autocorrelation functions along with the corresponding fits (solid lines). (g) Colocalized fraction extracted from STED-ICCS analysis. (h) Cross-correlation function broadening obtained from STED-ICCS. (i) Values of distances determined by object-based analysis and STED-ICCS. To see this figure in color, go online.

Then, we performed STED-ICCS on the same samples. As expected, STED-ICCS detected a positive cross-correlation for both samples (Fig. 2, e and f), with the colocalized fraction being higher in the 20-nm nanorulers (f_ICCS = 1.04 ± 0.3, mean ± SD) than in the 100-nm nanorulers (f_ICCS = 0.66 ± 0.11, mean ± SD) (Fig. 2 g). More interestingly, the parameter Δw, related to the broadening of the cross-correlation function (Fig. 2 h), was higher in the 100-nm nanorulers (Δw = 1.2 ± 0.2 pixels, mean ± SD) than in the 20-nm ones (Δw = 0.15 ± 0.04 pixels, mean ± SD). According to the simulations, the measured values of Δw correspond to the distance values d_ICCS = 99 ± 8 nm for the 100-nm nanorulers and d_ICCS = 35 ± 5 nm for the 20-nm nanorulers, which are in agreement with the peak values found with object-based analysis (Fig. 2 i). Note that the smaller uncertainty in the value of d_ICCS is due to the fact that each STED-ICCS measurement is performed on an image containing several tens of nanorulers, whereas in the object-based analysis, the distance is measured on each identified pair of objects.

Thus, the relative broadening of the STED-ICCS cross-correlation function can provide nanoscale information on the distance between particles that are not distributed randomly.

Measurements in cell nuclei: STED−ICCS quantifies the relative nanoscale distribution of functional nuclear sites

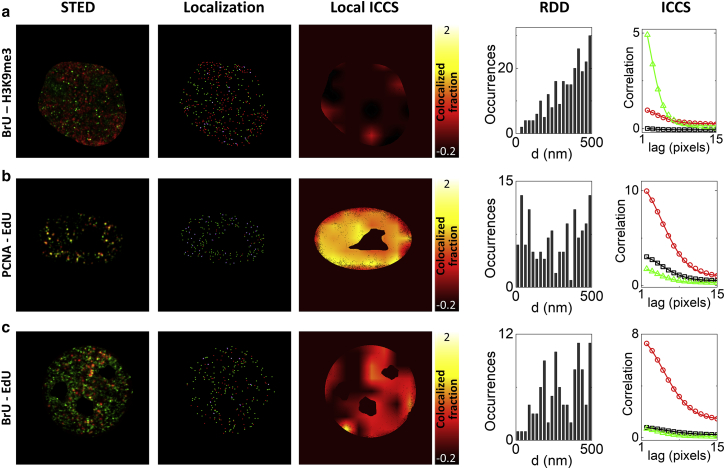
As validation of our STED-ICCS method, we characterized the nanoscale spatial distribution of three different pairs of functional nuclear sites in the diploid mammary epithelium cells MCF10A. We compared the nanoscale spatial distribution of 1) transcription foci (labeled through incorporation of the nucleotide analog BrU) versus a transcriptionally repressive histone marker (H3K9me3) (Fig. 3 a), 2) nascent DNA replication foci (labeled through incorporation of the nucleotide analog EdU) versus the replication machinery protein PCNA during the early S phase (Fig. 3 b), and 3) transcription foci (BrU) versus nascent DNA replication foci (EdU) during the early S phase (Fig. 3 c). The STED-ICCS analysis was compared with an object-based analysis performed on the same data set.

Figure 3.

Analysis of nuclear foci by STED-ICCS and object-based localization. Analysis of representative STED images of MCF10A cells acquired upon labeling of (a) BrU (green) and H3K9me3 (red), (b) PCNA (green) and EdU (red), and (c) BrU (green) and EdU (red). Shown are (from left to right) the dual-color STED image, the positions of the colocalized (cyan) and non-colocalized (red and green) foci recovered by particle localization, the map of the colocalized fraction recovered by local ICCS, the RDD histogram, and the spatial correlation functions recovered by ICCS. The ICCS plot shows the cross-correlation function (black triangles) and the red (red squares) and green (green circles) channel autocorrelation functions along with the corresponding fits (solid lines). Scale bars, 4 μm. To see this figure in color, go online.

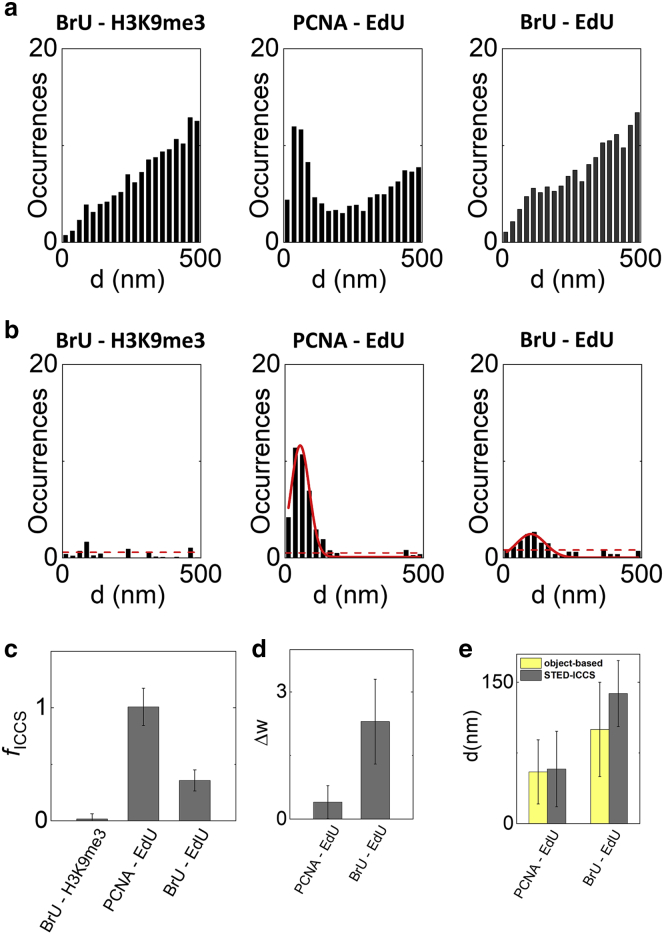
Representative dual-color STED images of the three samples are reported in Fig. 3. For each image are shown the map of localized spots along with the calculated RDD, the image auto- and cross-correlation functions, and the map of the colocalized fraction obtained by local ICCS (Fig. 3). Overall, there was an agreement between the colocalized fraction extracted by the object-based analysis, f_obj, and that extracted by STED-ICCS, f_ICCS, for the different samples (Fig. S5). Differences in the absolute values (f_ICCS was systematically higher than f_obj) are probably related to the specific settings of each analysis. For instance, in the object-based analysis, an intensity threshold value was set manually for each image, whereas in the ICCS analysis, we did not perform any background subtraction. Notably, the local ICCS maps can be used to visualize, in STED-ICCS, the regions of the nuclei with a higher level of proximity, similarly to what can be done with object-based analysis (Fig. 3). The average colocalization fractions retrieved from the STED-ICCS analysis are reported in Fig. 4 c. Transcription foci and the transcriptionally repressive histone marker H3K9me3 show the minimal level of colocalization (f_ICCS = 0.02 ± 0.05, mean ± SD, n = 17 cells), in keeping with the evidence that H3K9me3 is an epigenetic marker of repressive heterochromatin replicating during the late S phase and not associated with active transcription (52). This result is confirmed by object-based analysis, in which transcription and H3K9me3 show a random-like RDD (Fig. 4, a and b). Conversely, DNA replication foci and the PCNA protein have the maximal level of colocalization (f_ICCS = 1.01 ± 0.16, mean ± SD, n = 19 cells), in agreement with the role of the PCNA protein in orchestrating the replication process (53). Transcription foci and DNA replication foci in the early-S-phase cells exhibit an intermediate level of colocalization (f_ICCS = 0.36 ± 0.09, mean ± SD, n = 22 cells). However, this analysis does not show whether this difference in the level of colocalization is due to a different distribution at the nanoscale.

Figure 4.

Relative nanoscale spatial distribution of the investigated nuclear sites in MCF10A cells. (a and b) Cumulative results of the object-based analysis. Shown are the RDD histograms before (a) and after (b) subtraction of the uncorrelated random component. Solid red lines are Gaussian fits of the data (PCNA-EdU: d = 55 ± 34 nm, mean ± SD, n = 19 cells; BrU-EdU: d = 100 ± 50 nm, mean ± SD, n = 22 cells). The dashed red lines indicate the SD of the data in the range 250–500 nm after subtraction of a linear fit of the uncorrelated component. (c and d) Cumulative results of the STED-ICCS analysis. (c) Colocalized fraction extracted from STED-ICCS analysis. (d) Cross-correlation function broadening extracted from STED-ICCS. (e) Values of distances extracted by object-based analysis and STED-ICCS for the correlated samples. To see this figure in color, go online.

To get insight into the relative nanoscale distribution of the correlated functional sites, we analyzed the broadening of the cross-correlation function, Δw (Fig. 4 d), and compared it with the RDD derived from the object-based analysis (Fig. 4, a and b). The RDD of DNA replication foci and the PCNA protein revealed a peak distance of 55 nm (d_PCNA-EdU = 55 ± 34 nm, mean ± SD, n = 19 cells). STED-ICCS detected a broadening Δw_PCNA-EdU = 0.4 ± 0.4 pixels (mean ± SD, n = 19 cells) corresponding to a distance value of d_PCNA-EdU = 58 ± 40 nm. The values of distance detected by the two methods are very close to the limit of our experimental approach, as determined with the 20-nm optical nanorulers (d_obj = 40 nm and d_ICCS = 35 nm). A higher level of inaccuracy might also come from the use of primary and secondary antibodies. Moreover, we analyzed only single optical sections that represent only a projection of the distribution of nuclear foci in three dimensions. This could result in underestimation of the recovered distance values. Besides these technical considerations, we should also take into account that the EdU signal labels the DNA sequences that were replicating during the previous 20 min and that PCNA not only tethers polymerases to DNA during replication but also participates in nonreplicative DNA synthesis events (e.g., DNA repair) and other cell functions that extend well beyond DNA synthesis.

The RDD of transcription and DNA replication foci in early-S-phase cells exhibited a quasirandom relative distance distribution (Fig. 4 b). After subtraction of the random component, the RDD showed a small peak, indicating a positive correlation at a distance of d_BrU-EdU = 100 ± 50 nm (mean ± SD, n = 22 cells) (Fig. 4 b). Interestingly, STED-ICCS detected a broadening Δw_BrU-EdU = 2.3 ± 1.0 pixels (mean ± SD, n = 22 cells) corresponding to a distance value d_BrU-EdU = 138 ± 35 nm (Fig. 4, b, d, and e). Thus, STED-ICCS was able to reveal a correlation between these nuclear sites in the ∼100-nm range, similarly to the object-based analysis. The nonrandom distribution in the BrU-EdU sample is consistent with the cell population that was analyzed; during the early S phase, replicating DNA is mainly euchromatic and gene-rich. Most of the genes contained within these regions are generally expressed during the early S phase, and importantly, although their transcription is time-controlled to avoid transcription-replication clashes, it is still very close to ongoing replication not only in space but also in time, both before and after DNA synthesis. Thus, in the early S phase, transcription and replication operate on the same portion of the genome, thus explaining proximity of the corresponding BrU and EdU signals (54). In summary, STED-ICCS detected a small but positive correlation between replication and transcription (quantified by the parameter f_ICCS) but indicated spatial segregation at the nanoscale (quantified by the parameter d_ICCS), in keeping with a long-standing model of genome organization suggesting spatial segregation between replication and transcription (2,54).

Discussion

In this work, we have explored the use of super-resolution STED imaging combined with ICCS to investigate the relative nanoscale spatial distribution of nuclear foci. There are three main technical points that characterize super-resolved ICCS. The first important aspect is that being based on the calculation and fit of the image spatial correlation functions, super-resolved ICCS does not require a presegmentation of the images into objects. To illustrate the consequences of this point, we have performed ICCS and object-based analysis on simulated data of point-like particles at different densities and spatial resolutions. These simulations indicated that ICCS could be applied even at high densities of foci, whereas the object-based analysis was affected by a decreasing accuracy in the presegmentation process when the spatial resolution was not sufficient to resolve the foci. Another consequence of this point, which might be relevant in the context of high-throughput studies, is that the computational speed of ICCS depends on the number of pixels, but not on the number of objects in the image. A second technical aspect is that in super-resolved ICCS, the colocalized fraction is estimated from the amplitude of the image cross- and autocorrelation functions calculated over the image. Compared to object-based analysis, this calculation does not specify where the foci are colocalized. In this respect, we have shown that a local super-resolved ICCS analysis can be used to map the value of the colocalization coefficient across the sample and partially compensate for this limitation. The third important aspect is related to the detection of characteristic correlation distances. In the object-based approaches, it is possible to perform a complete statistical analysis of the relative distance between the particles and detect characteristic nanometer distances associated to intermolecular complexes (20). In this respect, we have shown that the broadening of cross-correlation function in super-resolved ICCS can also provide quantitative information on the nanoscale distance between correlated particles.

To validate our approach, we performed STED-ICCS on dual-color STED images of model and biological samples and compared the results with an object-based analysis performed on the same data sets. In particular, the object-based quantification was presented in terms of an RDD, representing the histogram the distance values between particles. However, we expect that any other type of quantitative analysis applied to the list of coordinates of the positions of the foci, such as radial distribution functions or Ripley’s functions (20,21), would give similar results. We quantified by STED-ICCS the relative nanoscale distribution of three pairs of functional nuclear sites. Notably, STED-ICCS was able to detect not only a value of colocalized fraction but also the characteristic correlation distance associated to correlated nuclear sites. In particular, PCNA was found in close association with EdU-labeled replication foci with a detected distance of ∼50 nm, very close to the experimental limit of the analysis. On the other hand, transcription foci were found at a distance of 130 nm from EdU-labeled replication foci, indicating a spatial segregation at the nanoscale despite both transcription and replication taking place on the same portion on the genome during the early S phase of the cell cycle. Overall, there was a good agreement between STED-ICCS and the object-based analysis, demonstrating that even without requiring a presegmentation, STED-ICCS can provide some of the most attractive features of an object-based analysis.

An important point to discuss is how general is the applicability of our method. We have shown experimental data obtained on model and fixed biological samples by dual-color STED imaging. In particular, in the conditions of our experiments, we achieved a lateral resolution on the order of ∼100 nm. The same type of nanoscale ICCS analysis could be applied to other types of “static” super-resolution images, including images obtained with SMLM. In the case of SMLM, a segmentation of the data is already available, making object-based colocalization analysis the method of choice. Nevertheless, we believe that the ICCS analysis could be useful as an independent cross-validation of the results obtained with object-based approaches.

Even more interesting appears to be the application of our method to the analysis of “dynamic” super-resolution images, for which an object-based analysis is less straightforward. Indeed, the super-resolved ICCS analysis can also be applied to nonstatic samples (Videos S1 and S2) to extract the colocalization fraction and/or the characteristic correlation distances (Fig. S6). In our data, a spatial resolution of the order of ∼100 nm was sufficient to characterize the relative nanoscale spatial distribution of the three pairs of functional nuclear sites investigated in our samples. The same spatial resolution could be achieved, in principle, with many live-cell super-resolution imaging approaches. For instance, structured illumination microscopy and its point-scanning equivalent image scanning microscopy are super-resolution techniques compatible with live-cell imaging, even if their resolution improvement is limited to a factor of ∼2 (12). The same STED nanoscopy includes several variants developed to reduce the STED beam intensity and its potentially photodamaging effects (41,55,56). Thus, we expect that our ICCS formalism could be applied to live-cell super-resolved images obtained, for instance, by dual-color STED- or structured-illumination-microscopy-based setups (57). As a final remark, we note that our method is based on the analysis of spatial auto- and cross-correlation functions, and, in principle, it could be adapted to other approaches based on spatial cross correlations and compatible with nanoscopy, for instance, raster ICCS or line-scanning spatial correlation spectroscopy (37,39). From this perspective, we believe that our work could be useful to establish, in the near future, a new type of dynamic analyses that cannot be obtained with other static super-resolution techniques.

Author Contributions

L.L., M.F., and A.D. designed research. M.O., M.J.S., L.F., and S.P. prepared samples. M.O., M.J.S., L.L., and P.B. performed experiments. L.L. and L.S. wrote software. L.L., L.S., M.O., and I.C. analyzed data. All authors contributed to the interpretation of the results. L.L. wrote the manuscript with input from all other authors.

Editor: Tom Misteli.