Abstract
Understanding how cell subpopulations in a tissue impact overall system function is challenging. There is extensive heterogeneity among insulin-secreting β-cells within islets of Langerhans, including their insulin secretory response and gene expression profile, and this heterogeneity can be altered in diabetes. Several studies have identified variations in nutrient sensing between β-cells, including glucokinase (GK) levels, mitochondrial function, or expression of genes important for glucose metabolism. Subpopulations of β-cells with defined electrical properties can disproportionately influence islet-wide free-calcium activity ([Ca2+]) and insulin secretion via gap-junction electrical coupling. However, it is poorly understood how subpopulations of β-cells with altered glucose metabolism may impact islet function. To address this, we utilized a multicellular computational model of the islet in which a population of cells deficient in GK activity and glucose metabolism was imposed on the islet or in which β-cells were heterogeneous in glucose metabolism and GK kinetics were altered. This included simulating GK gene (GCK) mutations that cause monogenic diabetes. We combined these approaches with experimental models in which gck was genetically deleted in a population of cells or GK was pharmacologically inhibited. In each case, we modulated gap-junction electrical coupling. Both the simulated islet and the experimental system required 30–50% of the cells to have near-normal glucose metabolism, fewer than cells with normal KATP conductance. Below this number, the islet lacked any glucose-stimulated [Ca2+] elevations. In the absence of electrical coupling, the change in [Ca2+] was more gradual. As such, electrical coupling allows a large minority of cells with normal glucose metabolism to promote glucose-stimulated [Ca2+]. If insufficient numbers of cells are present, which we predict can be caused by a subset of GCK mutations that cause monogenic diabetes, electrical coupling exacerbates [Ca2+] suppression. This demonstrates precisely how metabolically heterogeneous β-cell populations interact to impact islet function.
Significance
Biological tissues contain heterogeneous populations of cells. Insulin-secreting β-cells within the islets of Langerhans are critical for regulating blood glucose homeostasis. β-cells are heterogeneous, but it is unclear how the islet response is impacted by different cell populations and their interactions. We use a multicellular computational model and experimental systems to predict and quantify how cellular populations defined by varied glucose metabolism interact via electrical communication to impact islet function. When glucose metabolism is heterogeneous, electrical coupling is critical to promote electrical activity. However, when cells deficient in glucose metabolism are in the majority, electrical activity is completely suppressed. Thus, modulating electrical communication can promote islet electrical activity after dysfunction caused by gene mutations that impact glucose metabolism.
Introduction
Most biological tissues are multicellular systems in which a diverse range of cellular elements function collectively through dynamic interactions. Understanding the function of such a multicellular system requires understanding the characteristics of the constituent cell population and the way in which these populations interact over a defined architecture. As such, the dynamics of multicellular systems often show complex emergent behaviors (1, 2, 3, 4). Many diseases can arise from genetic variations that impact molecular and cellular function. Given the complexities of multicellular systems, effectively predicting how molecular and cellular dysfunctions lead to tissue and organ dysfunction and cause disease is challenging.
The islets of Langerhans are micro-organs located within the pancreas that are critical for regulating blood glucose homeostasis. Complex multicellular dynamics occur between insulin-secreting β-cells and other endocrine cell types that underlie regulated hormone secretion. Death or dysfunction of β-cells that results in a reduction or absence of insulin secretion is the main cause of diabetes. Glucose metabolism and cellular excitability are key features of β-cell insulin secretion. Specifically, upon elevated blood glucose, glucose is transported into the β-cell and phosphorylated by the low-affinity hexokinase, glucokinase (GK), which is the rate-limiting step in glucose metabolism (5). The increase in ATP/ADP inhibits ATP-sensitive K+ (KATP) channels, causing membrane depolarization and activation of voltage-gated calcium channels and generating bursts of action potentials. The elevated oscillations in intracellular free-calcium activity ([Ca2+]) trigger pulses of insulin granule exocytosis (6, 7, 8). In the absence of elevated ATP/ADP, KATP channels remain open, hyperpolarizing the cell, preventing voltage-gated calcium channel activation, and suppressing [Ca2+].
β-cells in the islet are electrically coupled by Connexin36 (Cx36) gap-junction channels (9, 10, 11). As a result of electrical coupling, β-cells exhibit coordinated [Ca2+] oscillations under elevated glucose and are uniformly silent under basal glucose (9,11, 12, 13, 14). β-cells are functionally heterogeneous, showing variations in electrical activity and insulin secretion (15, 16, 17, 18), as well as varying gene expression profiles (19, 20, 21). However, as a result of electrical coupling, β-cells within the islet show near-identical [Ca2+] responses and oscillatory dynamics (11). Nevertheless, the overall [Ca2+] response across the islet can be impacted by β-cell populations. In a normal islet, nearly all β-cells are capable of responding to elevated glucose. However, a small number of inexcitable cells that remain hyperpolarized at elevated glucose can reverse this response and silence the whole islet (22, 23, 24). Conversely, a small number of highly excitable cells alone may support the uniformly elevated [Ca2+] dynamics (25). Understanding how different cell populations characterized by different molecular signatures interact and affect overall islet function is lacking.
We and others have previously examined how heterogeneity in KATP channel activity and electrical coupling impact overall islet [Ca2+] (9,22,24,26). However, both single-cell-based studies and in situ analysis have demonstrated that β-cells exhibit substantial heterogeneity in glucose metabolism (27), which includes varying GK expression (21,25,28), metabolic fluxes (29, 30, 31, 32), or mitochondrial function (19,21). Although extensive heterogeneity in glucose metabolism exists within the islet, it is not clear how cell subpopulations with differing GK expression or levels of glucose metabolism influence each other via electrical coupling.
Computational models have been utilized to examine how islet function is impacted by different cellular populations. For example, the frequency of islet [Ca2+] oscillations can be predicted by the relative numbers of slow-oscillating and fast-oscillating β-cells and their electrical coupling (33,34). In the presence of a broad heterogeneous population, electrical coupling was also suggested to sharpen the islet response (34). We computationally predicted this concept, in which electrical coupling allows the islet to withstand a critical number of inexcitable cells and show near-normal glucose-stimulated [Ca2+]. Beyond this critical number, the islet sharply transitions to lack any glucose responsiveness (22,26), despite there being a population of β-cells that would otherwise be capable of responding to glucose. Computational models have also predicted that electrical coupling increases the impact of human KATP channel mutations that cause neonatal diabetes mellitus (NDM) (26). These models predicted islet dysfunction was reversible upon modulating electrical coupling for many mutations by allowing a population of β-cells to show [Ca2+] elevations. Mutations to GCK that reduce its activity can cause monogenic diabetes, either mature onset diabetes of the young (MODY) or NDM (35,36). Prior computational studies therefore suggest that electrical coupling may play an important role upon heterogeneity to GK activity, including mediating how mutations to GCK impact islet function.
In this study, we apply experimental and computational approaches to examine the role of gap-junction-mediated electrical coupling between β-cells in the presence of heterogeneity to GK activity. We examine how a defined population deficient in GK and glucose metabolism impacts islet function and how electrical coupling mediates the impact of this subpopulation. We also examine how electrical coupling between a broad heterogeneous population of cells impacts islet function and compare this with endogenous heterogeneity in the islet. Importantly, we compare how these results with heterogeneous GK activity compare to prior studies examining heterogeneity in KATP channel conductance. Finally, we predict how human GCK mutations impact islet function and the roles that heterogeneity in glucose metabolism and electrical coupling play in mediating the impact of these mutations.
Materials and Methods
Ethics statement
All experiments were performed in compliance with the relevant laws and institutional guidelines and were approved by the University of Colorado Institutional Biosafety Committee and Institutional Animal Care and Use Committee (B-95817(05)1D).
Animal care
The generation of GKlox/lox (Glucokinase with loxP sites flanking exon2), Pdx-CreER (β-cell-specific inducible Cre), and Cx36−/− (Connexin36 global knockout) mice has been described previously (37, 38, 39). Expression of variable GK deficiency was achieved by crossing GKlox/lox and Pdx-CreER mice and inducing GK deletion in 8- to 24-week-old mice by one to five daily doses of tamoxifen (50 mg/kg bodyweight or 5 mg/kg bodyweight, as indicated) administered intraperitoneally. Littermates lacking Pdx-CreER or GK loxP sites or wild-type C57BL/6 mice were used as controls. Mice were held in a temperature-controlled environment with a 12 h light/dark cycle and given food and water ad libitum.
In vivo measurements
Blood glucose was measured 3 times/wk using a glucometer (Ascensia Contour; Bayer, Basel, Switzerland) and averaged over days 10–15 post-tamoxifen induction. Plasma insulin was measured at day 15 post-tamoxifen induction from plasma extracted from blood samples centrifuged for 30 min at 3000 rpm at 4°C and assayed using mouse ultrasensitive insulin ELISA (Alpco, Salem, NH).
Islet isolation
Pancreas dissection and islet isolation were performed in mice under ketamine and xylazine anesthesia that were subsequently euthanized via exsanguination and cervical dislocation or bilateral thoracotomy. Islets were isolated by collagenase injection into the pancreas through the pancreatic duct; the pancreas was harvested and digested, and islets were handpicked (40,41). Islets were maintained in RPMI 1640 medium at 11 mM glucose (Invitrogen, Carlsbad, CA) supplemented with 10% fetal bovine serum, 100 U/mL penicillin, 100 μg/mL streptomycin, at 37°C under humidified 5% CO2 for 24–48 h before study.
Calcium imaging
Isolated islets were loaded with 4 μM Fluo-4 AM (Invitrogen) for 45 min at 37°C in imaging medium (125 mM NaCl, 5.7 mM KCl, 2.5 mM CaCl2, 1.2 mM MgCl2, 10 mM Hepes, 2 mM glucose, and 0.1% bovine serum albumin (pH 7.4)) and were imaged in 35 mm glass bottom dishes maintained at 37°C. Fluo-4 fluorescence was imaged on a confocal microscope (LSM800; Zeiss, Oberkochen, Germany) with a 40×1.2 NA water immersion objective, 488 nm diode laser for excitation, and 490–550 nm bandpass emission filter. Images were acquired at 1 frame/s for 2 min at 2 mM glucose and for 5 min at 11 mM glucose after 15 min of glucose stimulation. 20 mM KCl was then added during continuous imaging. Microscope settings (integration time, scan time, gain, laser power) were constant for all images collected within the same day. For mannoheptulose (MH) experiments, after imaging islets at 11 mM glucose, islets were imaged for 5 min after either 3, 5, or 10 mM MH was applied for 15 min at 11 mM glucose.
NAD(P)H imaging
NADH(P)H autofluorescence was imaged under two-photon excitation using a tunable mode-locked Ti:sapphire laser (Coherent Chameleon; Coherent, Santa Clara, CA) set to 710 nm for excitation. Fluorescence emission was detected at 425–475 nm using a non-descanned detector. A z-stack of six images was taken at 2 μm intervals starting 10 μm from the bottom of the islet. Images were acquired at both 2 mM and 15 min after 20 mM glucose stimulation. Microscope settings (scan time, gain, laser power) were constant for all images collected within the same day.
Image analysis
All images were analyzed using custom MATLAB (The MathWorks, Natick, MA) scripts. For calcium imaging, a 5 × 5 smoothing filter was first applied. Areas with very low to no fluorophore staining were excluded from analysis by excluding pixels at or below the average fluorescence of a manually chosen background area. Saturated areas were also removed by limiting the area to intensities below the maximum. To determine whether a cell was active, a peak detection algorithm was used to determine whether areas of the islet had peak amplitudes greater than 1.5 times the average of quiescent reference cells (32). A quiescent reference cell (or background region if no cells were quiescent) was chosen manually and showed no significant fluctuations in intensity during the entire time course. The fraction of active area was then calculated as the number of pixels detected as active relative to the total number of pixels that were not excluded as background in the defined islet. Activity maps are presented in hue saturation value (HSV) format, with the hue representing the [Ca2+] oscillation synchronization, as described previously (11). Briefly, cross-correlation coefficients (between 0 and 1) were calculated between every pixel area and a reference consisting of the average [Ca2+] fluorescence of the whole islet. This was calculated only for areas of the islet determined as active (see above). For MH treatments, [Ca2+] activity was normalized to the activity of the islet at 11 mM glucose.
NAD(P)H images were analyzed by averaging the intensity across the z-stack for the islet. For each experimental condition these intensity values were normalized to mean NAD(P)H intensity at 2 mM of islets from control mice that were acquired on the same day. The average intensity at 2 mM was subtracted from the average intensity at 20 mM to obtain the NAD(P)H response for the islet.
Coupled β-cell electrical activity model
The coupled β-cell model with and without stochastic noise was described previously (26) and adapted from the published Cha-Noma single-cell model (42,43), with modifications to the ATP dependence as previously described (44). All code was written in C++ and run on JANUS (University of Colorado, Boulder, CO) or Rosalind (University of Colorado, Denver, CO) supercomputers. Model code is included in Data S1.
The membrane potential (Vi) for each β-cell i is related to the sum of individual ion currents, as described by (42)
| (1) |
where the gap-junction-mediated current ICoup (22) is
| (2) |
NADH concentration ([Re]) was calculated by solving the following differential equation (42):
| (3) |
where Jglc is the flux of glycolysis, Jβ,ox is flux of β-oxidation, and Jop is the flux of oxidative phosphorylation and ATP production. N = 2.5 stochiometric conversion of NADH to ATP, and Rvol = 2.5, the ratio of the volume of the cytosol/the mitochondria. ATP and ADP (bound (b) and free (f)) relationships have been previously described (42):
| (4a) |
| (4b) |
The KATP channel current is (42)
| (5) |
where gK(ATP) is the open-channel conductance and × p0K(ATP) is the channel open probability.
Modeling changes in GK activity
The flux of glycolysis, which is limited by the rate of GK activity in the β-cell, is described as
| (6) |
where kglc is the maximal rate of glycolysis (equivalent to GK activity), which was simulated as a normal distribution with a mean of 0.000126 ms−1 and standard deviation (SD) of 10% of the mean. [Retot] = 10 mM, the total amount of pyrimidine nucleotides. The ATP and glucose dependence of glycolysis (GK activity) is
| (7) |
where [G] is the extracellular concentration of glucose, hgl is the Hill coefficient, KG is the half-maximal concentration of glucose, and KmATP is the half-maximal concentration of ATP.
GK deletion simulations, in which GK was deleted in a population of cells, were modeled with a rate of glycolysis kglc = 0 ms−1 in randomly distributed cells. The number of cells that received the deletion was defined as the fraction PMut multiplied by the number of cells (1000).
For GK inhibition simulations, decreases in kglc were modeled as
| (8) |
GK mutations that cause MODY2 or permanent neonatal diabetes mellitus (PNDM) were previously described in terms of their enzyme kinetics, , , and , by (36,45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58) and were first simulated as
| (9) |
To account for variability in the control wild-type GK kinetics between studies (Table S1), GK parameters , , and for each mutation were expressed relative to the wild-type GK parameter from the same study , , and . Thus,
| (10a) |
| (10b) |
| (10c) |
| (11) |
We also simulated MODY-2 mutants as a heterogeneous mutant:
| (12) |
Simulation data analysis
All simulation data analysis was performed using custom MATLAB scripts. The first 2000 time points were excluded to allow the model to reach a stable state. Cells were considered active if membrane potential Vm exceeded −45 mV. The fraction of cells that were active was determined relative to the total number of simulated cells (1000).
Duty cycle was determined as the fraction of the [Ca2+] oscillations spent above a threshold value during the time course analyzed. This threshold value was determined as 50% of the average amplitude at 11 mM glucose with no changes in rate of glycolysis. Duty cycle was reported as the average across all cells in the simulated islet.
Average parameters within a population of cells were calculated using a single simulation when the islet lacked electrical coupling (gcoup = 0 pS) and when a fraction of the cells was active. This corresponds to either PMut = 0.50 (Fig. 1) or kglc′ = (1 − 0.65) × kglc (Fig. 3). Each parameter was averaged over time when applicable and across all GK− and GK+ cells (Fig. 1) or active and nonactive cells (Fig. 3).
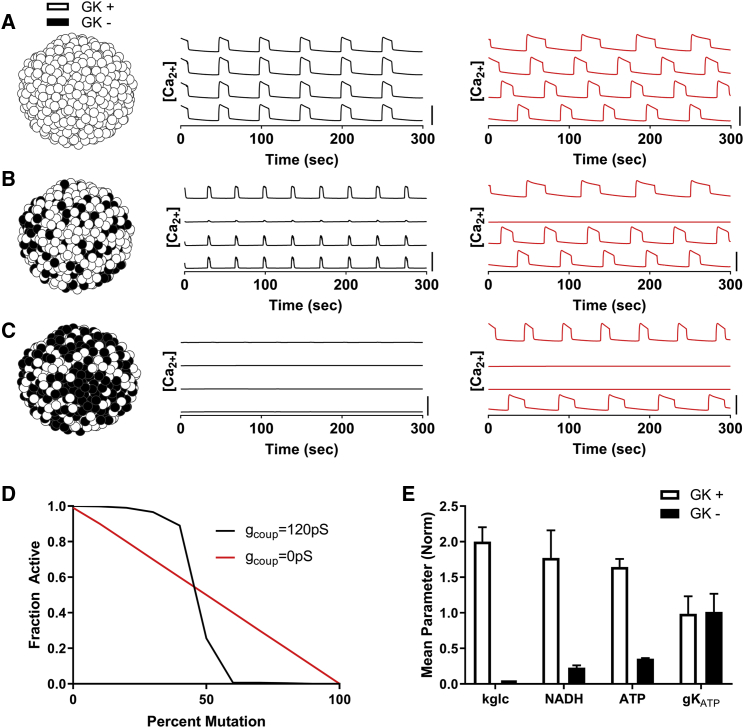
Figure 1.
Simulating how metabolically deficient cells impact islet function via electrical coupling. (A) Simulations of an islet with normal GK activity are shown. Left: schematic of GK activity across simulated islet. Middle: time courses of [Ca2+] for four individual cells within the simulated islet for gcoup = 120 pS (black line). Right: time courses of [Ca2+] for four individual cells within the simulated islet for gcoup = 0 pS (red line). (B) shows the same as in (A) but for simulations in which 40% of cells have no GK activity (GK−, black cells). (C) shows the same as in (A) but for simulations in which 60% of cells have no GK activity. (D) Fraction of cells showing depolarization and elevated [Ca2+] activity (“active cells”) in simulated islets versus the percentage of cells deficient in GK is shown for gcoup = 120 and 0 pS. (E) Average parameter values in simulation for cells with normal GK activity (GK+) compared to cells deficient in GK activity (GK−) at 50% GK− cells are shown. Error bars in (E) represent SD over 500 cells. All simulations were run at 11 mM glucose. Scale bars in (A)–(C) represent 0.5 μM. To see this figure in color, go online.
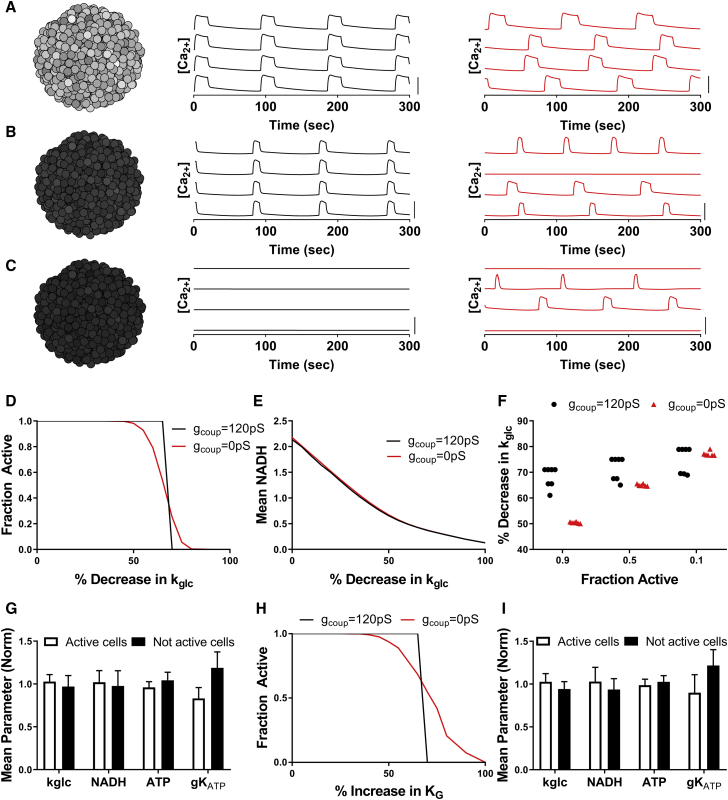
Figure 3.
Simulations predicting how heterogeneity in metabolic activity impact islet function via electrical coupling. (A) Simulation of islet with normal GK (kglc) activity is shown. Left: schematic of heterogeneous GK activity across simulated islet. Darker cells represent reduced activity. Middle: time courses of [Ca2+] for representative cells within the simulated islet with gcoup = 120 pS. Right: time courses of [Ca2+] for representative cells within the simulated islet for gcoup = 0 pS. (B) shows the same as in (A) for a simulated islet with a 60% decrease in kglc activity across the islet. (C) shows the same as in (A) for a simulated islet with a 70% decrease in kglc activity across the islet. (D) The fraction of cells showing elevated [Ca2+] (“active cells”) in a representative simulated islet versus fractional decrease in kglc (decreasing GK activity) for gcoup = 120 and 0 pS is shown. (E) Mean NADH across a representative simulated islet versus fractional decrease in kglc for gcoup = 120 and 0 pS is shown. (F) The decrease in kglc required to reduce [Ca2+] to 0.9, 0.5, or 0.1 of normal levels, with either gcoup = 120 pS or gcoup = 0 pS, is shown. Data are representative of simulations with six random number seeds (gcoup = 0 pS) and seven seeds (gcoup = 120 pS). (G) Average parameter values in [Ca2+] active cells and nonactive cells within a simulated islet are given, with gcoup = 0 pS and a 65% decrease in kglc. (H) The fraction of active cells, as in (D), versus increases in the half-maximal concentration of glucose (KG) is shown, with gcoup = 120 pS (black) and gcoup = 0 pS (red). (I) Average parameter values, as in (G), are shown, with gcoup = 0 pS and a 70% increase in KG. Data in (G) and (I) represent mean ± SD. Scale bars in (A)–(C) represent 0.5 μM. To see this figure in color, go online.
When simulation results were binned according to oral glucose tolerance test (OGTT) values, “mild” mutations had a 2 h OGTT result of <145 mg/dL, “moderate” mutations had an OGTT result of 145–175 mg/dL, and “severe” mutations had an OGTT value of >175 mg/dL. Simulation results were also binned according to HbA1c and were characterized as mild if HbA1c < 6.5%, moderate if HbA1c was 6.5–7.0%, and severe if HbA1c > 7.0%.
Statistical analysis
All statistical analysis was performed in Prism (GraphPad, San Diego, CA). Either a Student’s t-test or a one-way ANOVA with Dunnett post hoc analysis was utilized to test for significant differences between [Ca2+] activity, ΔNAD(P)H, plasma insulin, blood glucose, and simulation results. Matched pairs of Cx36+/+ and Cx36−/− islets were chosen as islets imaged on the same day, and a paired t-test was used to determine significance. If uneven numbers of islets with the same genotype were imaged on the same day, their results were averaged before the paired t-test was performed. Linear regression was used to evaluate the correlation between [Ca2+] activity, plasma insulin, or blood glucose versus ΔNAD(P)H. Outliers were removed from experimental data sets based on the interquartile range (IQR). Data were first grouped by genotype, then outliers identified as any data point outside of [Q1 − 1.5 × IQR, Q3 + 1.5 × IQR] where Q1 and Q3 are the first and third quartiles, respectively. Data are reported as mean ± standard error (SE) or mean ± SD when indicated. For data in Figs. 5 e and S6, some groups failed normality by an Anderson-Darling normality test (MATLAB), and therefore a nonparametric ANOVA (Kruskal-Wallis) and Dunn’s post hoc analysis was used. Data are reported as mean ± SE unless otherwise indicated.
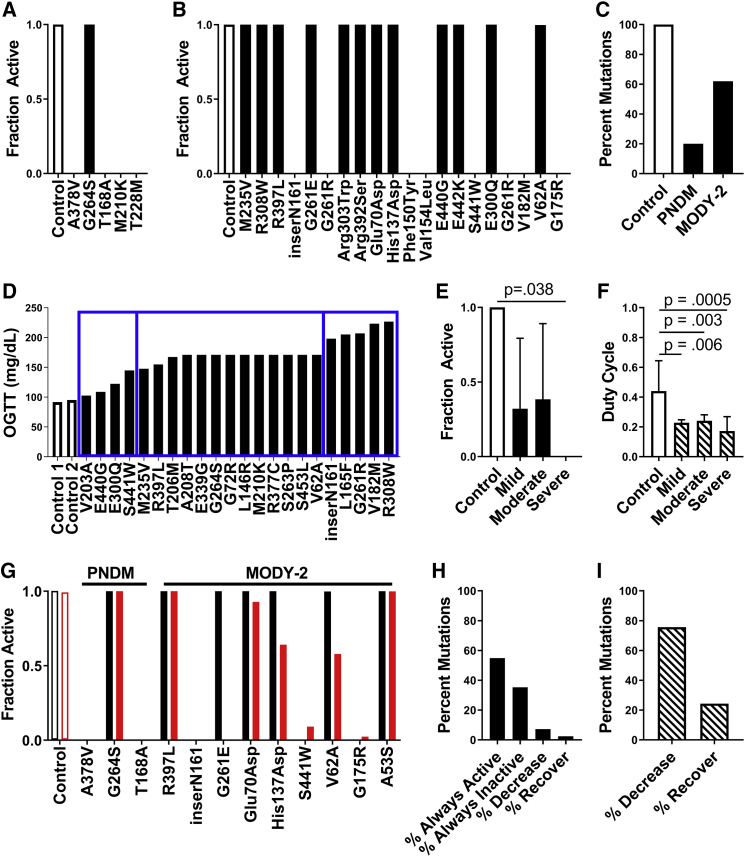
Figure 5.
Simulations predicting how GCK mutations underlying monogenic diabetes impact islet function via electrical coupling. (A) The fraction of cells showing elevated [Ca2+] activity (“active cells”) in simulated islets from all PNDM mutations at 20 mM glucose is shown. (B) The fraction of active cells in simulated islets for a representative subset of MODY2 mutations at 20 mM glucose is shown. For all mutations, see Fig. S2. (C) Percentage of all mutations tested that had high islet [Ca2+] activity (>90% active cells) for control (n = 1), PNDM (n = 5), and MODY2 (n = 82) at 20 mM glucose is shown. (D) OGTT results for a set of individuals with MODY2 mutations are shown, with bins indicating the severity of dysglycemia for mild, moderate, and severe mutations (left to right, blue rectangles). (E) The mean fraction of active cells from simulations of mutations in (D) at 11 mM glucose is shown, averaging over the disease severity and considering homozygous mutations. (F) Average duty cycle for mutations in (D) at 11 mM glucose is shown, averaging over the disease severity and considering heterozygous mutations. All simulations in (A)–(F) were run with gcoup = 120 pS. Data in (E and F) represent mean ± SD. (G) The fraction of active cells in simulated islets for a representative subset of PNDM and MODY2 mutations with gcoup = 120 pS (black) and gcoup = 0 pS (red) at 20 mM glucose is shown. (H) Percent of all MODY2 mutations that maintain the same activity (always active, always inactive), decrease, or increase (recover) [Ca2+] activity when gcoup is reduced from 120 to 0 pS is shown, considering homozygous mutations at 20 mM glucose. (I) Percent of all MODY2 mutations in which the duty cycle decreases or increases (recovers) when gcoup is reduced from 120 to 0 pS is shown, considering heterozygous mutations at 11 mM glucose. To see this figure in color, go online.
Results
Computational model predicts how discrete populations of metabolically deficient cells impact islet function
Previous studies have demonstrated how excitable and inexcitable cells (defined by KATP channel activity) interact within the islet via electrical coupling. Given that glucose metabolism varies extensively between previously identified β-cell subpopulations, we first set out to examine how cells with high and low levels of glucose metabolism interact. We simulated islets at elevated glucose with varying numbers of cells lacking GK activity. Simulated islets with normal electrical coupling and normal GK activity showed elevated [Ca2+] with coordinated oscillatory dynamics closely matching previously published models (Fig. 1 a; (11,22,42,59)). As the number of cells lacking GK activity (GK−) increased in number up to ∼40% of GK− cells, the simulated islet retained normal coordinated [Ca2+] elevations, albeit with a reduced plateau fraction (Fig. 1 b). However, above ∼50% GK− cells, the simulated islet lacked elevation in [Ca2+] (Fig. 1 c), with all remaining GK+ cells remaining silent. In the absence of electrical coupling, as the number of GK− cells was increased, the disruption to [Ca2+] was more gradual (Fig. 1, a–c), with all remaining GK+ cells responding. Thus, with fewer than ∼40% GK− cells, the absence of electrical coupling diminished [Ca2+] compared to in the presence of coupling (Fig. 1 d). However, with greater than 50% GK− cells, the absence of electrical coupling increased [Ca2+]. Simulated GK− cells showed reduced ATP and NADH levels but normal KATP open-channel conductance (Fig. 1 e), as expected.
Thus, simulations predict the islet requires ∼50% of the cells to have near-normal glucose metabolism to show glucose-stimulated [Ca2+]. Below this number, the islet will sharply transition to lack any glucose-stimulated [Ca2+]. However, in the absence of electrical coupling, the change in [Ca2+] is gradual, and only cells with near-normal glucose metabolism will show glucose-stimulated [Ca2+].
Experimentally testing how discrete populations of metabolically deficient cells impact islet function
To experimentally test these computational model predictions, we used a mouse model in which GK deficiency is induced in a population of β-cells. We focused on testing 1) that the threshold number of GK-deficient cells required to sharply suppress islet [Ca2+] is ∼50% and 2) that above this threshold number of GK-deficient cells, a loss of gap-junction electrical coupling elevates [Ca2+].
GKlox/lox;Pdx-CreER mice received doses of tamoxifen totaling between 10 mg/kg body weight (bw) and 250 mg/kg bw. For mice receiving tamoxifen doses of 50–250 mg/kg bw, blood glucose levels were elevated significantly compared to control mice (see Materials and Methods), with no significant difference in blood glucose between groups within this range (Fig. S1). Below this dosage (10–25 mg/kg bw), mice remained euglycemic, similar to control mice. Plasma insulin levels were significantly lower than control mice for tamoxifen doses 50–250 mg/kg bw (Fig. S1).
We isolated islets from these GKlox/lox;Pdx-CreER mice and control mice that received varying tamoxifen dosages. We performed two-photon imaging of NAD(P)H to assess changes in the islet metabolic response (Fig. 2 a). The NAD(P)H response decreased with increasing tamoxifen dosage (Fig. 2 a), with mice receiving doses of 50–250 mg/kg bw having significantly lower responses than in controls (Fig. 2 b). This showed good correlation with blood glucose and plasma insulin (Fig. S1). We also performed [Ca2+] imaging to assess changes in the islet electrical response (Fig. 2 c). Doses of 10–25 mg/kg bw did not significantly impact [Ca2+], with coordinated [Ca2+] oscillations remaining, showing varying patterns of slow or fast oscillations. In contrast, doses of 50–250 mg/kg bw led to significantly lower [Ca2+] than in controls (Fig. 2, d and e). However, the remaining [Ca2+] elevations were coordinated, indicating electrical coupling was not substantially diminished (Fig. 2 e). For mice receiving doses of 50–250 mg/kg bw, KCl treatment elevated [Ca2+] across the majority of the islet, equivalent to in control islets (Fig. 2 f), indicating that the disruption to [Ca2+] is not due to cell death or de-differentiation but rather an absence of metabolic regulation of electrical activity and [Ca2+].
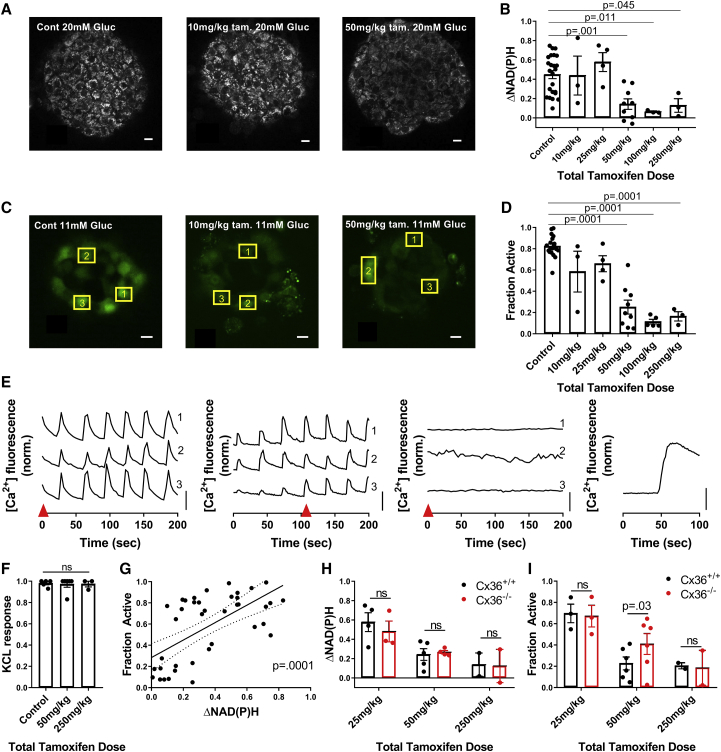
Figure 2.
Experimentally demonstrating how metabolically deficient cells impact islet function via gap-junction coupling. (A) Representative images of NAD(P)H at 20 mM glucose in islets from GKlox/lox;Pdx-CreER mice injected with differing levels of tamoxifen, as indicated, are shown. (B) Change in NAD(P)H from 2 to 20 mM (ΔNAD(P)H) compared to total tamoxifen dose is shown. For control, n = 24 mice; for 10 mg/kg, n = 3; for 25 mg/kg, n = 4; for 50 mg/kg, n = 9; for 100 mg/kg, n = 3; and for 250 mg/kg, n = 3 (two to seven islets per mouse). (C) Representative images of fluorescence from the [Ca2+]-sensitive dye Fluo-4 at 11 mM glucose when injected with varying amounts of tamoxifen are shown. (D) The fraction of cells showing elevated [Ca2+] activity (“active cells”) at 11 mM glucose compared to total tamoxifen dose is shown. For control, n = 19 mice; for 10 mg/kg, n = 3; for 25 mg/kg, n = 4; for 50 mg/kg, n = 9; for 100 mg/kg, n = 5; and for 250 mg/kg, n = 3 (two to seven islets per mouse). (E) Representative time courses of individual cells, shown by yellow boxes in (C), at 11 mM glucose within islets from mice treated with varying amounts of tamoxifen are given (from left to right: control, 10, 50, 250 mg/kg with KCl). Red arrow in (E) indicates time point at which images in (C) are displayed. (F) The fraction of cells showing elevated [Ca2+] after KCl compared to total tamoxifen dose is shown. For control, n = 5 mice; for 50 mg/kg, n = 6; and for 250 mg/kg, n = 3 (two to four islets per mouse). (G) Scatter plot (dots) plus linear regression ±95% confidence interval (solid and dashed lines) of mean active cells for islets from GKlox/lox;Pdx-CreER mice versus mean ΔNAD(P)H for islets from the same mice (n = 41 mice) are given. p represents significance of linear trend slope. (H) A comparison of ΔNAD(P)H for islets from GKlox/lox;Pdx-CreER;Cx36+/+ and GKlox/lox;Pdx-CreER;Cx36−/− mice for the tamoxifen doses indicated is shown. For 25 mg/kg, n = 4; for 50 mg/kg, n = 5; and for 250 mg/kg, n = 2 (two to seven islets per mouse). (I) A comparison of fraction of active cells at 11 mM glucose for islets from GKlox/lox;Pdx-CreER;Cx36+/+ and GKlox/lox;Pdx-CreER;Cx36−/− mice is shown for the tamoxifen doses indicated. For 25 mg/kg, n = 3; for 50 mg/kg, n = 6; and for 250 mg/kg, n = 2 (two to seven islets per mouse). Scale bars in (A) and (C) represent 10 μm; scale bars in (E) represent dF/F of 50%. Error bars in (B), (D), (F), (H), (I) represent SEM. To see this figure in color, go online.
The greatest decline in glucose-stimulated [Ca2+], from ∼70 to ∼20% of the islet showing elevated [Ca2+], occurred between 25 and 50 mg/kg bw tamoxifen dosage. Given the lack of an associated fluorescent reporter, we were unable to directly quantify the percentage of cells showing GK deletion. To account for the spread in NAD(P)H response at each tamoxifen dosage, for each animal, we compared the decline in [Ca2+] with the corresponding NAD(P)H response (Fig. 2 f). The sharp decline in [Ca2+] occurred around an NAD(P)H response of ∼0.15–0.2 (Fig. 2 f), which is ∼30–50% of the mean NAD(P)H response in control islets (Fig. 2 b). This suggests that a sudden decline in [Ca2+] occurs upon a 50–70% loss in metabolic activity, which is equivalent to a complete loss of metabolic activity in 50–70% of cells, assuming mosaic activation of Pdx-CreER and GK deletion. This is consistent with the simulated islet results (Fig. 1), in which greater than 50% GK− metabolically deficient cells leads to a dramatic decrease in [Ca2+].
We next tested whether a decrease in Cx36 and electrical coupling can increase [Ca2+] for levels of GK deletion above the threshold at which [Ca2+] is suppressed. We examined islets from age-matched GKlox/lox;Pdx-CreER;Cx36+/+ and GKlox/lox;Pdx-CreER;Cx36−/− mice after tamoxifen injection. 50 mg/kg bw tamoxifen is the smallest dose that led to markedly decreased [Ca2+] in the presence of Cx36 (Fig. 2 d). At this dose, similar NAD(P)H responses were observed in the presence and absence of Cx36, consistent with similar GK deletion (Fig. 2 g). Despite this, there was a significant elevation in [Ca2+] activity in islets lacking Cx36, consistent with simulation predictions (Fig. 2 h). Islets from mice treated with either lower tamoxifen doses at which islet [Ca2+] is near normal (25 mg/kg bw) or higher doses at which islet [Ca2+] is suppressed (250 mg/kg bw) showed similar [Ca2+] irrespective of Cx36. This is also consistent with model predictions.
Therefore, islets lacking GK in a subpopulation of metabolically deficient β-cells show behavior in good agreement with computational model predictions. There exists a threshold number of ∼50% β-cells at which GK deficiency causes a sharp suppression in [Ca2+], and this suppression depends on gap-junction electrical coupling.
Computational model predicts how a distribution of metabolically active or inactive populations impacts islet function
We have examined how the islet responds with two distinct cell populations with either elevated metabolic activity (normal GK) or deficient metabolic activity (deficient GK). Although some studies have suggested distinct subpopulations exist within the islet with differing metabolic activity (19,25), other studies have demonstrated that a continuous distribution of metabolic activity is present (29,31). Within a continuous distribution, a “metabolically deficient” population of cells may fall below some threshold metabolic activity required for stimulating [Ca2+]. We therefore simulated islets with a continuous distribution of GK activity between cells. With a normal distribution of GK activity, elevated [Ca2+] with coordinated oscillatory dynamics were observed in the presence of electrical coupling, but these oscillatory dynamics lacked coordination in the absence of electrical coupling (Fig. 3 a). As the mean GK activity was reduced in the presence of electrical coupling, coordinated [Ca2+] elevations were maintained until a certain decrease in GK activity, at which point there was a transition to a complete absence of [Ca2+] elevation (Fig. 3, b–d). In the absence of electrical coupling, the decline in [Ca2+] was more gradual as GK activity was reduced (Fig. 3, b–d). The change in NAD(P)H, indicating metabolic activity, was similar across the islet in the presence and absence of electrical coupling (Fig. 3 e). As such, when the decrease in GK activity was low (<70% decrease) and the islet was metabolically active, the absence of electrical coupling decreased [Ca2+] because some cells lacked elevated [Ca2+] (Fig. 3, d and f). However, with greater decreases in GK activity (>70%) such that the islet was metabolically deficient, the absence of electrical coupling increased [Ca2+] because some cells maintained elevated [Ca2+]. In the absence of electrical coupling, the population of cells in which [Ca2+] elevations remained had slightly higher metabolic activity (higher kgly, NADH levels), and lower KATP open-channel conductance (gKATP) (Fig. 3 g) and thus were more excitable. When excluding heterogeneity in gKATP, similar observations were made when GK activity was reduced (Fig. S2): the population of cells in which [Ca2+] elevations remained had higher metabolic activity (higher kgly, NADH levels). Thus, elevated metabolic activity was sufficient for the cells to be more excitable.
GK kinetics can be impacted in additional ways, such as substrate affinity (60). To understand more generally how islet function can be impacted by changes in GK activity, we simulated islets with other perturbations to GK kinetics. When the affinity for glucose is reduced (increasing KG), the islet showed uniform elevated [Ca2+] until the affinity was reduced ∼2-fold (KG increased by ∼70%), at which point [Ca2+] declined sharply (Fig. 3 h). In the absence of electrical coupling, the decline in [Ca2+] was more gradual (Fig. 3 h), whereas the population of cells in which [Ca2+] elevations remained had higher metabolic activity (higher NADH) and lower KATP open-channel conductance (gKATP) (Fig. 3 i). Reducing the affinity for ATP (by increasing KmATP) or increasing the Hill coefficient for glucose affinity had much weaker effects on islet activity (Fig. S3). Inclusion of stochastic noise under conditions of decreased GK activity also elevated [Ca2+] (Fig. S3), consistent with prior predictions (26).
Thus, upon a distribution of cellular metabolic activity, similar results were observed as with two distinct populations of cells. The islet transitions from islet-wide [Ca2+] elevations to a complete lack of [Ca2+] according to the mean GK level: a lower mean GK level results in more cells falling into being metabolically deficient. The simulations specifically predict the islet requires >30% of the cells to have near-normal glucose metabolism to show islet-wide glucose-stimulated [Ca2+]. This behavior again depends on electrical coupling, whereby in the absence of electrical coupling, the decline is gradual, and excitable cells with near-normal glucose metabolism remain active.
Experimentally testing how endogenous metabolically active or inactive populations impact islet function
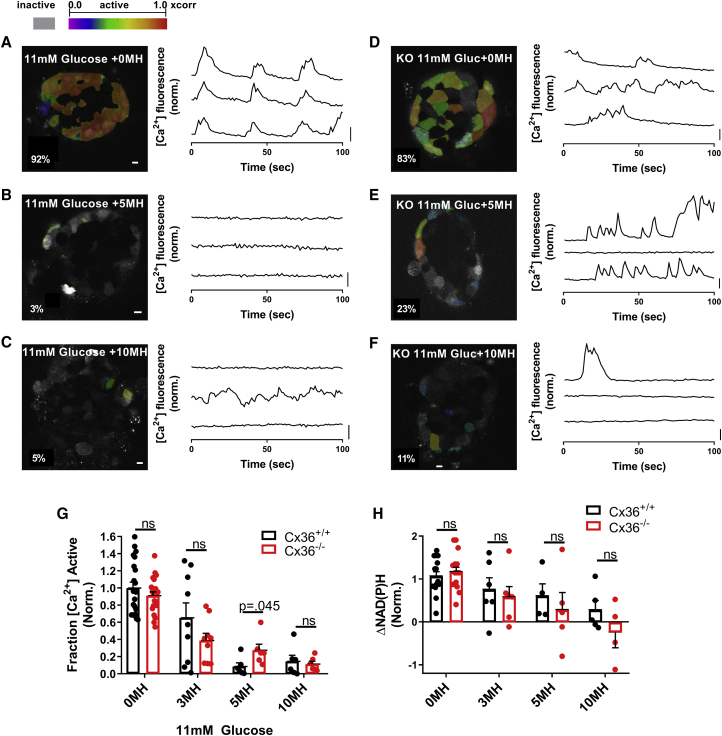
To experimentally test these model predictions, we reduced GK activity across the islet with the GK inhibitor MH in the presence (Cx36+/+) and absence (Cx36−/−) of gap-junction coupling. In both the presence and absence of gap-junction coupling, increasing concentrations of MH decreased [Ca2+] (Fig. 4, a–f). In islets from Cx36+/+ mice, the decline in [Ca2+] was modest for low MH concentrations (3 mM), but a substantial decline occurred between 3 and 5 mM MH and no further decline between 5 and 10 mM MH (Fig. 4 g). However, in islets from Cx36−/− mice, the decline in [Ca2+] was more gradual up to the maximal 10 mM MH. At 5 mM MH, at which [Ca2+] was almost completely suppressed in islets from Cx36+/+ mice, [Ca2+] was significantly higher in islets from Cx36−/− mice, in which ∼30% of cells continued to show elevated [Ca2+] (Fig. 4, e and g). For all MH treatments, the NAD(P)H response was similar between islets from Cx36+/+ mice and Cx36−/− mice (Fig. 4 h), indicating that the differences in [Ca2+] are not a result of differing metabolic activity, which is consistent with simulated data (Fig. 3 e).
Figure 4.
Experimentally demonstrating how heterogeneity in metabolic activity impacts islet function via gap-junction coupling. (A) Imaging [Ca2+] in wild-type islet at 11 mM glucose with 0 mM MH is shown. Left: false color map of regions of elevated [Ca2+] activity in a wild-type islet. Right: time courses of [Ca2+] activity in three individual cells within the islet, as measured by Fluo-4 fluorescence. (B) shows the same as in (A) but at 11 mM glucose with 5 mM MH. (C) shows the same as in (A) but at 11 mM glucose with 10 mM MH. (D) Imaging [Ca2+] in Cx36−/− islet at 11 mM glucose with 0 mM MH: time courses of [Ca2+] activity as in (A). (E) shows the same as in (D) but at 11 mM glucose with 5 mM MH. (F) shows the same as in (D) but at 11 mM glucose with 10 mM MH. (G) The fraction of islet with elevated [Ca2+] activity with increasing MH concentration for Cx36+/+ and Cx36−/− islets is shown. (H) Change in NAD(P)H from 2 to 20 mM glucose with increasing concentration of MH for Cx36+/+ and Cx36−/− islets is shown. For [Ca2+] activity experiments, n = 21 mice for 0 mM MH, n = 9 for 3 mM, n = 6 for 5 mM MH, and n = 6 for 10 mM MH (one to seven islets per mouse). For NAD(P)H experiments, n = 15 mice for 0 MH, n = 6 for 3 mM, n = 5 for 5 mM MH, and n = 5 for 10 mM MH (one to six islets per mouse). Data in (D) and (E) are normalized to the mean [Ca2+] activity for 0 mM MH. Scale bars in (A)–(F) images represent 10 μm; scale bars in (A)–(F) time courses represent dF/F of 20%. Error bars in (G) and (H) represent SEM. To see this figure in color, go online.
Thus, there is good agreement with simulations that demonstrate a sharp decrease in [Ca2+] in the presence of gap-junction electrical coupling as a result of decreased GK activity but a gradual decrease in [Ca2+] in the absence of gap-junction coupling. There is also good agreement with simulations in which 30–40% of cells maintain elevated [Ca2+] in the absence of gap-junction coupling for a level of GK activity sufficient to suppress [Ca2+] in the presence of gap-junction coupling.
Computational predictions for gap-junction coupling and GCK mutations that cause diabetes
Our results indicate that gap-junction electrical coupling substantially impacts islet function when GK activity is heterogeneous. This includes enabling a large minority of metabolically active cells to increase [Ca2+] across the islet and exacerbating the decline in [Ca2+] when a majority of cells show deficient metabolic activity. We next applied our computational model to examine the role of electrical coupling in the presence of GCK mutations that cause NDM or MODY. We simulated the islet and included altered GK kinetics based upon the biochemical characterization of GCK mutations that cause MODY or PNDM (Table S1; (36,45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58)). The majority of PNDM GCK mutations (4/5) suppressed [Ca2+] at elevated glucose (Fig. 5 a). In comparison, only a subset of MODY GCK mutations (∼35%) suppressed [Ca2+] at elevated glucose (Fig. 5 b; Fig. S4), showing more moderate impact than PNDM mutations (Fig. 5 c). MODY mutations are single-allele variants; thus, when modeling half of GK with normal kinetics, MODY GCK mutations reduced the [Ca2+] oscillation plateau fraction compared to controls (Fig. S5).
We next compared simulation predictions for the impact of GCK mutations with corresponding clinical assessments for the loss of glucose control. We specifically examined a set of mutations for which patients had received OGTTs and segmented the mutations into three classes (“mild,” “moderate,” and “severe”) according to the level of glucose intolerance (2 h blood glucose) (Fig. 5 d). ∼50% of both mild and moderate mutations suppressed [Ca2+]. However, all severe mutations suppressed [Ca2+] (Fig. 5 e). When accounting for MODY mutations being single-allele variants, the [Ca2+] oscillation plateau fraction was reduced to a greater degree by severe mutations compared to mild or moderate mutations (Fig. 5 f). Similar results in terms of suppression of [Ca2+] or impact on [Ca2+] oscillation plateau fraction were observed considering HbA1c, albeit with reduced difference between mild, moderate, and severe mutations (Fig. S6). These data show a good correlation between the clinical severity of GCK mutations and the simulated impact on [Ca2+].
With this agreement, we examined the impact of electrical coupling on [Ca2+] upon GCK mutations. We simulated all MODY and PNDM mutations in the absence of electrical coupling and compared [Ca2+] to simulations in the presence of electrical coupling (Fig. S4). No PNDM mutation showed a change in [Ca2+], but a subset of MODY mutations (∼10%) showed changes in [Ca2+] in the absence of electrical coupling (Fig. 5, g and h). This impact of removing electrical coupling included increases in [Ca2+] for a subset of mutations in which [Ca2+] was normally suppressed and a reduction in [Ca2+] for different mutations in which [Ca2+] remained active (Fig. 5, h and i). Thus, gap-junction-mediated electrical coupling plays a partial role in mediating islet dysfunction caused by GCK mutations.
Discussion
β-cells in the islet respond collectively to glucose, despite the individual β-cells themselves being highly heterogeneous. Prior studies have demonstrated that small changes in the oscillatory properties or glucose responsiveness of individual β-cells can lead to large changes in the collective behavior of the whole islet (22,25,32,33). Heterogeneity in metabolic activity between β-cells is extensive (28,29,31). In this study, we controlled the heterogeneity in GK activity between β-cells to examine how electrical coupling between metabolically heterogeneous cells impacts islet function. Using computational models and experimental systems, we discovered that small changes in the number of cells with deficient GK and glucose metabolism led to large changes in islet [Ca2+]. Electrical coupling was important, mediating either the recruitment of metabolically deficient cells to show elevated [Ca2+] or the suppression of metabolically active cells to suppress [Ca2+]. Based on these results, computational models further predicted a role for changes in electrical coupling to impact islet dysfunction in monogenic diabetes that results from mutations to GCK.
Cell heterogeneity and phase transitions within the islet network
Our previous work examined the impact of heterogeneity in KATP channel activity in the islet using computational models and experimental systems (22,61). β-cells were rendered inexcitable via expression of mutant KATP channels that do not close in response to elevated metabolism, thus hyperpolarizing the cell. As the number of these inexcitable β-cells was progressively increased, the islet initially showed near-normal responses. However, at some critical number of inexcitable cells, there was a sharp transition between islet-wide [Ca2+] elevations and complete suppression of [Ca2+]. Here, our computational and experimental results demonstrate similar findings, as predicted. As the number of metabolically deficient cells caused by reduced or absent GK activity is increased beyond a critical threshold (40–50%), there is a sharp transition between islet-wide [Ca2+] elevations and complete suppression of [Ca2+]. The remaining cells with normal GK are suppressed via electrical coupling by the metabolically deficient cells. This is supported by results in the absence of coupling in which remaining metabolically active cells show elevated [Ca2+] (Fig. 1). Our experimental results are consistent with these findings: the lowest level of GK deletion (in ∼50% of cells) sufficient to suppress islet [Ca2+] shows elevated [Ca2+] in the absence of gap-junction coupling (Fig. 2).
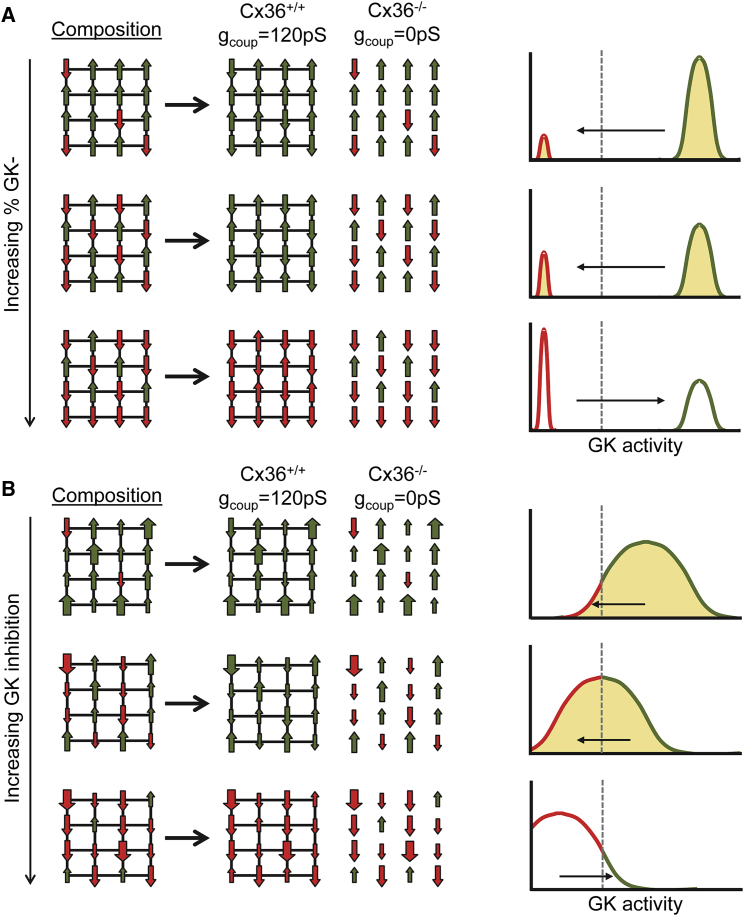
We observed similar results whether GK activity was partially reduced across all cells in the islet (Figs. 3 and 4). Computationally (Fig. 3), there was a level of GK reduction at which there existed a sharp transition between islet-wide [Ca2+] elevations and complete suppression of [Ca2+]. This transition occurred when 30–40% of cells had sufficient metabolic activity to show [Ca2+] elevations if electrically isolated. Experimentally (Fig. 4), the lowest concentration of MH that was sufficient to fully suppress islet [Ca2+] (5 mM) only suppressed [Ca2+] in a subset of cells in the absence of gap-junction coupling, leaving ∼30% of cells active. The correspondence between computational and experimental results (Fig. S7) indicates the presence of broad metabolic heterogeneity within the islet. Thus, when GK activity is partially inhibited, less metabolically active cells will have insufficient glucose metabolism to elevate [Ca2+], whereas more metabolically active cells will have sufficient glucose metabolism to elevate [Ca2+]. If there are sufficient numbers of cells capable of elevating [Ca2+] (predicted to be 30–50%; Fig. S7), they can resist being suppressed by less metabolically active cells, and the islet can elevate [Ca2+]. These findings are summarized in Fig. 6.
Figure 6.
Model summarizing how cells higher in GK and lower in GK interact within the islets via gap-junction electrical coupling. (A) A schematic illustrating how composition of the islet under a bimodal distribution (as in Figs. 1 and 2) impacts activity is given. Left: green up arrows represent metabolically normal cells that can elevate [Ca2+], red down arrows represent metabolically deficient cells that cannot elevate [Ca2+]. When deficient cells are in the majority, electrical coupling cannot mediate the recruitment of elevated [Ca2+] (green). Right: equivalent histogram illustrating the same concept in which left-pointing arrow and shading represent recruitment and right-pointing arrow and empty space represent suppression. (B) shows the same as in (A) for a continuous distribution of metabolic activity (as in Figs. 3, 4, and 5). Large green up arrows represent highly metabolically active cells, large red down arrows represent highly metabolic deficient cells. The dashed line represents threshold GK activity for [Ca2+] elevation, determining the relative number of “metabolically deficient” and “metabolically active” cells. To see this figure in color, go online.
Of note, we do observe differences in this study compared to prior studies. Previously, when examining heterogeneity in KATP channel activity, the number of inexcitable cells (cells with elevated KATP activity) required to suppress [Ca2+] across the islet was 20–40% (depending whether KATP overactivity was in a defined population of cells or broadly distributed (61)). This number is smaller than the number of metabolically deficient cells required to suppress islet-wide [Ca2+], which was 50–70%. Thus, populations of metabolically deficient cells are less effective at suppressing islet [Ca2+] than cells with elevated KATP activity. Conversely, this means smaller populations of metabolically active cells are effective at stimulating islet [Ca2+]. This has significant implications for the role of metabolic heterogeneity in islet function (see discussion below). The residual ATP levels in metabolically deficient cells will partially close KATP channels, and therefore, cells with elevated KATP activity may transmit greater hyperpolarizing current across the islet compared to metabolically deficient cells. Furthermore, in our model, elevated ATP also regulates voltage-gated calcium channel activity, thus providing additional depolarization and Ca2+ entry at elevated glucose. Thus, cells with increased GK and metabolic activity may also transmit greater depolarizing current across the islet compared to cells with lower KATP activity. We were unable to precisely measure NAD(P)H changes on a cell-by-cell basis and therefore cannot exclude the presence of metabolic coupling. Furthermore, the percentage of cells in which GK was deleted (Fig. 2) was inferred from the change in NAD(P)H activity and so may deviate slightly. However, by modeling changes only in GK and electrical coupling, our computational model results and experimental results are in close agreement for both GK deletion (Figs. 1 and 2) and GK inhibition (Figs. 3 and 4) when the percentage of cells rendered inactive is quantified.
Therefore, after changes in glucose metabolism, a certain number of β-cells will show sufficient metabolism to elevate [Ca2+]. If this is above some critical number, then the islet will elevate [Ca2+], whereas below this number, a complete loss of glucose-stimulated [Ca2+] occurs. In the absence of electrical coupling, the population of β-cells with sufficient metabolism to elevate [Ca2+] will not be suppressed. These cells have sufficient GK activity for ATP generation and KATP closure but may also have low KATP conductance or other factors that promote elevated electrical activity and insulin release.
Implications for islet physiology
It has long been known that β-cells in the islet are functionally heterogeneous (16), including heterogeneity in GK expression, glucose metabolism, and mitochondrial function (28,30,31). Recently, using transcriptome, protein labeling, surface markers, or fluorescent reporters, specific subpopulations have been defined with diminished GK expression or reduced mitochondrial function or glucose metabolism (27). Our results indicate quantitatively how changes in the proportion of these cell subpopulations with deficient GK or glucose metabolism will impact islet function. Assuming the electrical coupling remains unchanged between subpopulations, the islet will remain tolerant to cells low in glucose metabolism and recruit these deficient cells to show elevated [Ca2+]. However, when they form a substantial majority (above 50–70%), islet electrical activity will be disrupted.
That the majority of β-cells need to be deficient in glucose metabolism for islet [Ca2+] to be suppressed means that gap-junction electrical coupling generally serves to mediate the recruitment of metabolically deficient cells. Upon a minority of 30–50% of metabolically deficient β-cells, gap-junction electrical coupling mediates their activation by more metabolically active cells. Indeed, our computational and experimental results upon uniform changes in GK activity indicate that as few as ∼30% of metabolically active β-cells can recruit and elevate [Ca2+] across the islet (Figs. 3 and 4). Therefore, cells with high levels of glucose metabolism play an important role for elevating [Ca2+] across the islet via electrical coupling. This is in agreement with recent studies examining how metabolically active cells can recruit and maintain elevated [Ca2+] across the islet (25,32). As such, the preferential disruption of metabolically active cell populations under pathogenic conditions could critically impact islet function.
Despite the important role a large minority of metabolically active cells may play in elevating [Ca2+] in metabolically deficient cells, some studies have demonstrated that subpopulations low in glucose metabolism also show lower GJD2 expression (encoding Cx36) (19). As a result, with increasing numbers of cells low in glucose metabolism, the islet electrical activity may trend toward the behavior we observe in the absence of electrical coupling. Cells low in glucose metabolism may not be recruited to elevate [Ca2+], and islet [Ca2+] elevations may remain in a population of metabolically active cells even if large numbers of cells are deficient in glucose metabolism. Thus, remodeling of electrical coupling may be protective against large numbers of cells with deficient glucose metabolism.
We simulated a Gaussian distribution of glucose metabolism that agreed well with our experimental results. However, recent studies have indicated that small populations of cells, characterized by high electrical coupling and GK expression, play a substantial role in coordinating islet electrical activity (25). Other highly metabolic subpopulations may also exist. Thus, within the populations of GK+ cells able to elevate [Ca2+] across the islet, a smaller subpopulation may dominate this recruitment.
It is also important to understand other ways in which altered GK activity may impact the islet. Give the link between glucose and gap-junction coupling (62), cells with higher glucose metabolism may also show elevated gap-junction coupling, thus impacting the recruitment of [Ca2+]. Paracrine signals that rely on metabolic products such as glutamate may be disrupted by reduced GK activity and impact islet responses (63,64). Furthermore, hormone secretion from other endocrine cells, such as α-cell glucagon secretion, depends on GK activity (65). Altered glucagon secretion would impact insulin release (and [Ca2+] to a lesser extent). Furthermore, in our MH experiments (Fig. 4), GK activity is reduced in all islet cells, whereas in our GK deletion experiments (Fig. 2), only β-cell (and δ-cell) GK is deleted. The difference in paracrine signals between the two experiments could conceivably explain the different thresholds for suppression. However, in each case, model results show that loss of GK activity in β-cells and electrical coupling is sufficient to explain experimental results. Understanding the distribution of glucose metabolism, electrical coupling, and the role for other aspects of islet function will be important for future work.
Implications for monogenic diabetes
Many forms of monogenic diabetes arise from mutations to genes that encode components regulating insulin secretion (66). We previously applied computational models to demonstrate that eliminating electrical coupling could blunt the effect of many mutations to KATP channel subunits that cause NDM (26). This relies on electrical coupling mediating the hyperpolarization and suppression of [Ca2+] by more inexcitable cells expressing mutant ATP-insensitive KATP channels. Our experimental and computational results show a role for electrical coupling in mediating islet-wide suppression of [Ca2+] by inexcitable cells that show decreased GK activity. For large decreases in GK activity (e.g., upon 5 mM MH), a reduction in electrical coupling elevates [Ca2+]. Thus, we rationalized that for a subset of GCK mutations that cause diabetes, reducing electrical coupling may recover islet function.
Our computational model, which described experimental data well, also generated results that were consistent with clinical data regarding GCK mutations. Mutations that cause NDM suppressed [Ca2+] to a greater degree than mutations that cause MODY2, and those MODY2 mutations associated with poorer glucose control (OGTT or HbA1c) caused a greater reduction in [Ca2+]. Thus, we can be confident that the model can predict the effect of GCK mutations. The computational model predicts that reducing electrical coupling improves [Ca2+] elevations in a small number of mutations. This is consistent with the relatively narrow range of reduced GK or percentage of cells low in GK over which electrical coupling mediates a suppression of islet [Ca2+] (Figs. 1 and 3). The larger set of mutations in which electrical coupling promotes elevations in islet [Ca2+] is consistent with the idea that electrical coupling can mediate more metabolically active cells to elevate [Ca2+] in metabolically inactive cells (see discussion above). Thus, elevating electrical coupling may improve islet function in the face of GCK mutations, especially if electrical coupling is diminished by factors such as poor glucose control.
There are important considerations when modulating electrical coupling to promote β-cell [Ca2+] in the face of GCK mutations. Firstly, the terminal measurement we have made is glucose-regulated [Ca2+], which follows close agreement with our computational model. However, a deficiency of GK and glucose metabolism will impact the production of mitochondrial-derived amplifying factors that enhance insulin secretion (67). Paracrine signals such as glutamate (63,64), somatostatin, or glucagon may also be disrupted and impact islet responses. Therefore, although modulating gap-junction electrical coupling can improve [Ca2+] upon GK deficiency, the elevation of insulin secretion may be modest given β-cells with low glucose metabolism would show low amplification. This may be overcome by stimulating incretin pathways such as GLP1R activation that amplify insulin secretion. We also note that our model is based upon a mouse islet and has been validated by mouse model data. The cytoarchitecture and electrical regulation differ in human islets, and there may be differences in GK action and electrical coupling in regulating islet function. However, experimental data in human islets as to the role of heterogeneity and gap-junction electrical coupling are limited, and thus, our ability to accurately simulate these properties and validate their role in the human context is limited. Nevertheless, our mouse-based computational model provided good agreement with clinical data, supporting our results and conclusions. Examining the role of heterogeneity in glucose metabolism and electrical coupling in regulating human islet function is an important goal for future work.
Conclusions
The results from this study illustrate how gap-junction-mediated electrical coupling coordinate the response of metabolically heterogeneous β-cells within the islet. Using both experimental systems and computational models, we have demonstrated that gap-junction electrical coupling robustly coordinates the [Ca2+] response in the presence of high levels of metabolic heterogeneity. Electrical coupling promotes islet [Ca2+] elevations when low numbers of metabolically deficient β-cells are present but suppresses islet [Ca2+] elevations when higher numbers of metabolically deficient β-cells are present. Computational models support these findings, showing relevance to monogenic diabetes involving GCK mutations, in which modulating electrical coupling can promote islet [Ca2+] elevations for certain mutations. Therefore, we provide further understanding of how β-cell subpopulations regulate islet function via cell-cell communication.
Author Contributions
J.M.D. designed and performed research, developed analytical tools, performed analysis, and wrote the manuscript. N.W.F.L. designed and performed research, developed analytical tools, and performed analysis. R.A.P. performed research. W.E.S. performed research. O.M. performed research. M.J.W. performed research and developed analytical tools. R.K.P.B. verified results and wrote the manuscript.
Acknowledgments
The authors thank Dr. Chris Rhodes for sharing the GKlox/lox mice.
This work was supported by National Institutes of Health grants R01 DK102950 and R01 DK106412 and Juvenile Diabetes Research Foundation Grant 5-CDA-2014-198-A-N (to R.K.P.B.). Experiments were performed through the use of the University of Colorado Anschutz Medical Campus Advance Light Microscopy Core (P30 NS048154, UL1 TR001082), islet isolation was performed in the Barbara Davis Center Islet Core (P30 DK057516), and utilization of the JANUS supercomputer was supported by the National Science Foundation (CNS-08217944) and the University of Colorado.
Editor: Raimond Winslow.
Footnotes
JaeAnn M. Dwulet and Nurin W. F. Ludin contributed equally to this work.
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2019.10.037.
Supporting Material
References
- 1.Winfree A.T. Biological rhythms and the behavior of populations of coupled oscillators. J. Theor. Biol. 1967;16:15–42. doi: 10.1016/0022-5193(67)90051-3. [DOI] [PubMed] [Google Scholar]
- 2.White J.A., Chow C.C., Kopell N. Synchronization and oscillatory dynamics in heterogeneous, mutually inhibited neurons. J. Comput. Neurosci. 1998;5:5–16. doi: 10.1023/a:1008841325921. [DOI] [PubMed] [Google Scholar]
- 3.Strogatz S.H. Exploring complex networks. Nature. 2001;410:268–276. doi: 10.1038/35065725. [DOI] [PubMed] [Google Scholar]
- 4.Kepler T.B., Marder E., Abbott L.F. The effect of electrical coupling on the frequency of model neuronal oscillators. Science. 1990;248:83–85. doi: 10.1126/science.2321028. [DOI] [PubMed] [Google Scholar]
- 5.Matschinsky F.M. Glucokinase as glucose sensor and metabolic signal generator in pancreatic beta-cells and hepatocytes. Diabetes. 1990;39:647–652. doi: 10.2337/diab.39.6.647. [DOI] [PubMed] [Google Scholar]
- 6.Ashcroft F.M., Rorsman P. K(ATP) channels and islet hormone secretion: new insights and controversies. Nat. Rev. Endocrinol. 2013;9:660–669. doi: 10.1038/nrendo.2013.166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ammälä C., Eliasson L., Rorsman P. Exocytosis elicited by action potentials and voltage-clamp calcium currents in individual mouse pancreatic B-cells. J. Physiol. 1993;472:665–688. doi: 10.1113/jphysiol.1993.sp019966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Rorsman P. The pancreatic beta-cell as a fuel sensor: an electrophysiologist’s viewpoint. Diabetologia. 1997;40:487–495. doi: 10.1007/s001250050706. [DOI] [PubMed] [Google Scholar]
- 9.Speier S., Gjinovci A., Rupnik M. Cx36-mediated coupling reduces beta-cell heterogeneity, confines the stimulating glucose concentration range, and affects insulin release kinetics. Diabetes. 2007;56:1078–1086. doi: 10.2337/db06-0232. [DOI] [PubMed] [Google Scholar]
- 10.Moreno A.P., Berthoud V.M., Pérez-Armendariz E.M. Biophysical evidence that connexin-36 forms functional gap junction channels between pancreatic mouse beta-cells. Am. J. Physiol. Endocrinol. Metab. 2005;288:E948–E956. doi: 10.1152/ajpendo.00216.2004. [DOI] [PubMed] [Google Scholar]
- 11.Benninger R.K., Zhang M., Piston D.W. Gap junction coupling and calcium waves in the pancreatic islet. Biophys. J. 2008;95:5048–5061. doi: 10.1529/biophysj.108.140863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ravier M.A., Güldenagel M., Meda P. Loss of connexin36 channels alters beta-cell coupling, islet synchronization of glucose-induced Ca2+ and insulin oscillations, and basal insulin release. Diabetes. 2005;54:1798–1807. doi: 10.2337/diabetes.54.6.1798. [DOI] [PubMed] [Google Scholar]
- 13.Head W.S., Orseth M.L., Benninger R.K. Connexin-36 gap junctions regulate in vivo first- and second-phase insulin secretion dynamics and glucose tolerance in the conscious mouse. Diabetes. 2012;61:1700–1707. doi: 10.2337/db11-1312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Benninger R.K., Head W.S., Piston D.W. Gap junctions and other mechanisms of cell-cell communication regulate basal insulin secretion in the pancreatic islet. J. Physiol. 2011;589:5453–5466. doi: 10.1113/jphysiol.2011.218909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Zhang M., Goforth P., Satin L. The Ca2+ dynamics of isolated mouse beta-cells and islets: implications for mathematical models. Biophys. J. 2003;84:2852–2870. doi: 10.1016/S0006-3495(03)70014-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Pipeleers D.G. Heterogeneity in pancreatic beta-cell population. Diabetes. 1992;41:777–781. doi: 10.2337/diab.41.7.777. [DOI] [PubMed] [Google Scholar]
- 17.Salomon D., Meda P. Heterogeneity and contact-dependent regulation of hormone secretion by individual B cells. Exp. Cell Res. 1986;162:507–520. doi: 10.1016/0014-4827(86)90354-x. [DOI] [PubMed] [Google Scholar]
- 18.Van Schravendijk C.F., Kiekens R., Pipeleers D.G. Pancreatic beta cell heterogeneity in glucose-induced insulin secretion. J. Biol. Chem. 1992;267:21344–21348. [PubMed] [Google Scholar]
- 19.Bader E., Migliorini A., Lickert H. Identification of proliferative and mature β-cells in the islets of Langerhans. Nature. 2016;535:430–434. doi: 10.1038/nature18624. [DOI] [PubMed] [Google Scholar]
- 20.Dorrell C., Schug J., Grompe M. Human islets contain four distinct subtypes of β cells. Nat. Commun. 2016;7:11756. doi: 10.1038/ncomms11756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Karaca M., Castel J., Kargar C. Exploring functional beta-cell heterogeneity in vivo using PSA-NCAM as a specific marker. PLoS One. 2009;4:e5555. doi: 10.1371/journal.pone.0005555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hraha T.H., Westacott M.J., Benninger R.K. Phase transitions in the multi-cellular regulatory behavior of pancreatic islet excitability. PLoS Comput. Biol. 2014;10:e1003819. doi: 10.1371/journal.pcbi.1003819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Nittala A., Ghosh S., Wang X. Investigating the role of islet cytoarchitecture in its oscillation using a new β-cell cluster model. PLoS One. 2007;2:e983. doi: 10.1371/journal.pone.0000983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Rocheleau J.V., Remedi M.S., Piston D.W. Critical role of gap junction coupled KATP channel activity for regulated insulin secretion. PLoS Biol. 2006;4:e26. doi: 10.1371/journal.pbio.0040026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Johnston N.R., Mitchell R.K., Hodson D.J. Beta cell hubs dictate pancreatic islet responses to glucose. Cell Metab. 2016;24:389–401. doi: 10.1016/j.cmet.2016.06.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Notary A.M., Westacott M.J., Benninger R.K. Decreases in gap junction coupling recovers Ca2+ and insulin secretion in neonatal diabetes mellitus, dependent on beta cell heterogeneity and noise. PLoS Comput. Biol. 2016;12:e1005116. doi: 10.1371/journal.pcbi.1005116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Benninger R.K.P., Hodson D.J. New understanding of β-cell heterogeneity and in situ islet function. Diabetes. 2018;67:537–547. doi: 10.2337/dbi17-0040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Jetton T.L., Magnuson M.A. Heterogeneous expression of glucokinase among pancreatic beta cells. Proc. Natl. Acad. Sci. USA. 1992;89:2619–2623. doi: 10.1073/pnas.89.7.2619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Piston D.W., Knobel S.M., Magnuson M.A. Adenovirus-mediated knockout of a conditional glucokinase gene in isolated pancreatic islets reveals an essential role for proximal metabolic coupling events in glucose-stimulated insulin secretion. J. Biol. Chem. 1999;274:1000–1004. doi: 10.1074/jbc.274.2.1000. [DOI] [PubMed] [Google Scholar]
- 30.Heimberg H., De Vos A., Schuit F. Heterogeneity in glucose sensitivity among pancreatic beta-cells is correlated to differences in glucose phosphorylation rather than glucose transport. EMBO J. 1993;12:2873–2879. doi: 10.1002/j.1460-2075.1993.tb05949.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kiekens R., In ’t Veld P., Pipeleers D. Differences in glucose recognition by individual rat pancreatic B cells are associated with intercellular differences in glucose-induced biosynthetic activity. J. Clin. Invest. 1992;89:117–125. doi: 10.1172/JCI115551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Westacott M.J., Ludin N.W.F., Benninger R.K.P. Spatially organized β-cell subpopulations control electrical dynamics across islets of langerhans. Biophys. J. 2017;113:1093–1108. doi: 10.1016/j.bpj.2017.07.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Zimliki C.L., Mears D., Sherman A. Three roads to islet bursting: emergent oscillations in coupled phantom bursters. Biophys. J. 2004;87:193–206. doi: 10.1529/biophysj.103.038471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Smolen P., Rinzel J., Sherman A. Why pancreatic islets burst but single beta cells do not. The heterogeneity hypothesis. Biophys. J. 1993;64:1668–1680. doi: 10.1016/S0006-3495(93)81539-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Vionnet N., Stoffel M., Cohen D. Nonsense mutation in the glucokinase gene causes early-onset non-insulin-dependent diabetes mellitus. Nature. 1992;356:721–722. doi: 10.1038/356721a0. [DOI] [PubMed] [Google Scholar]
- 36.Njølstad P.R., Søvik O., Bell G.I. Neonatal diabetes mellitus due to complete glucokinase deficiency. N. Engl. J. Med. 2001;344:1588–1592. doi: 10.1056/NEJM200105243442104. [DOI] [PubMed] [Google Scholar]
- 37.Zhang H., Fujitani Y., Gannon M. Efficient recombination in pancreatic islets by a tamoxifen-inducible Cre-recombinase. Genesis. 2005;42:210–217. doi: 10.1002/gene.20137. [DOI] [PubMed] [Google Scholar]
- 38.Degen J., Meier C., Willecke K. Expression pattern of lacZ reporter gene representing connexin36 in transgenic mice. J. Comp. Neurol. 2004;473:511–525. doi: 10.1002/cne.20085. [DOI] [PubMed] [Google Scholar]
- 39.Postic C., Shiota M., Magnuson M.A. Dual roles for glucokinase in glucose homeostasis as determined by liver and pancreatic beta cell-specific gene knock-outs using Cre recombinase. J. Biol. Chem. 1999;274:305–315. doi: 10.1074/jbc.274.1.305. [DOI] [PubMed] [Google Scholar]
- 40.Scharp D.W., Kemp C.B., Lacy P.E. The use of ficoll in the preparation of viable islets of langerhans from the rat pancreas. Transplantation. 1973;16:686–689. doi: 10.1097/00007890-197312000-00028. [DOI] [PubMed] [Google Scholar]
- 41.Koster J.C., Remedi M.S., Nichols C.G. Hyperinsulinism induced by targeted suppression of beta cell KATP channels. Proc. Natl. Acad. Sci. USA. 2002;99:16992–16997. doi: 10.1073/pnas.012479199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Cha C.Y., Nakamura Y., Noma A. Ionic mechanisms and Ca2+ dynamics underlying the glucose response of pancreatic β cells: a simulation study. J. Gen. Physiol. 2011;138:21–37. doi: 10.1085/jgp.201110611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Cha C.Y., Santos E., Noma A. Time-dependent changes in membrane excitability during glucose-induced bursting activity in pancreatic β cells. J. Gen. Physiol. 2011;138:39–47. doi: 10.1085/jgp.201110612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Silva J.R., Cooper P., Nichols C.G. Modeling K,ATP--dependent excitability in pancreatic islets. Biophys. J. 2014;107:2016–2026. doi: 10.1016/j.bpj.2014.09.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Davis E.A., Cuesta-Muñoz A., Matschinsky F.M. Mutants of glucokinase cause hypoglycaemia- and hyperglycaemia syndromes and their analysis illuminates fundamental quantitative concepts of glucose homeostasis. Diabetologia. 1999;42:1175–1186. doi: 10.1007/s001250051289. [DOI] [PubMed] [Google Scholar]
- 46.Gloyn A.L., Odili S., Matschinsky F.M. Insights into the structure and regulation of glucokinase from a novel mutation (V62M), which causes maturity-onset diabetes of the young. J. Biol. Chem. 2005;280:14105–14113. doi: 10.1074/jbc.M413146200. [DOI] [PubMed] [Google Scholar]
- 47.Sagen J.V., Odili S., Matschinsky F.M. From clinicogenetic studies of maturity-onset diabetes of the young to unraveling complex mechanisms of glucokinase regulation. Diabetes. 2006;55:1713–1722. doi: 10.2337/db05-1513. [DOI] [PubMed] [Google Scholar]
- 48.Barbetti F., Cobo-Vuilleumier N., Cuesta-Muñoz A.L. Opposite clinical phenotypes of glucokinase disease: description of a novel activating mutation and contiguous inactivating mutations in human glucokinase (GCK) gene. Mol. Endocrinol. 2009;23:1983–1989. doi: 10.1210/me.2009-0094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Capuano M., Garcia-Herrero C.M., Sacchetti L. Glucokinase (GCK) mutations and their characterization in MODY2 children of southern Italy. PLoS One. 2012;7:e38906. doi: 10.1371/journal.pone.0038906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Cuesta-Muñoz A.L., Tuomi T., Matschinsky F.M. Clinical heterogeneity in monogenic diabetes caused by mutations in the glucokinase gene (GCK-MODY) Diabetes Care. 2010;33:290–292. doi: 10.2337/dc09-0681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.García-Herrero C.M., Galán M., Navas M.A. Functional analysis of human glucokinase gene mutations causing MODY2: exploring the regulatory mechanisms of glucokinase activity. Diabetologia. 2007;50:325–333. doi: 10.1007/s00125-006-0542-7. [DOI] [PubMed] [Google Scholar]
- 52.Turkkahraman D., Bircan I., Gloyn A.L. Permanent neonatal diabetes mellitus caused by a novel homozygous (T168A) glucokinase (GCK) mutation: initial response to oral sulphonylurea therapy. J. Pediatr. 2008;153:122–126. doi: 10.1016/j.jpeds.2007.12.037. [DOI] [PubMed] [Google Scholar]
- 53.Valentínová L., Beer N.L., Gloyn A.L. Identification and functional characterisation of novel glucokinase mutations causing maturity-onset diabetes of the young in Slovakia. PLoS One. 2012;7:e34541. doi: 10.1371/journal.pone.0034541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.García-Herrero C.M., Rubio-Cabezas O., Navas M.A. Functional characterization of MODY2 mutations highlights the importance of the fine-tuning of glucokinase and its role in glucose sensing. PLoS One. 2012;7:e30518. doi: 10.1371/journal.pone.0030518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Njølstad P.R., Sagen J.V., Matschinsky F.M. Permanent neonatal diabetes caused by glucokinase deficiency: inborn error of the glucose-insulin signaling pathway. Diabetes. 2003;52:2854–2860. doi: 10.2337/diabetes.52.11.2854. [DOI] [PubMed] [Google Scholar]
- 56.Byrne M.M., Sturis J., Bell G.I. Insulin secretory abnormalities in subjects with hyperglycemia due to glucokinase mutations. J. Clin. Invest. 1994;93:1120–1130. doi: 10.1172/JCI117064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Zelent B., Odili S., Matschinsky F.M. Mutational analysis of allosteric activation and inhibition of glucokinase. Biochem. J. 2011;440:203–215. doi: 10.1042/BJ20110440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Galán M., Vincent O., Navas M.A. Effects of novel maturity-onset diabetes of the young (MODY)-associated mutations on glucokinase activity and protein stability. Biochem. J. 2006;393:389–396. doi: 10.1042/BJ20051137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Fridlyand L.E., Ma L., Philipson L.H. Adenine nucleotide regulation in pancreatic beta-cells: modeling of ATP/ADP-Ca2+ interactions. Am. J. Physiol. Endocrinol. Metab. 2005;289:E839–E848. doi: 10.1152/ajpendo.00595.2004. [DOI] [PubMed] [Google Scholar]
- 60.Liang Y., Kesavan P., Matschinsky F.M. Variable effects of maturity-onset-diabetes-of-youth (MODY)-associated glucokinase mutations on substrate interactions and stability of the enzyme. Biochem. J. 1995;309:167–173. doi: 10.1042/bj3090167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Hraha T.H., Bernard A.B., Benninger R.K. Dimensionality and size scaling of coordinated Ca(2+) dynamics in MIN6 β-cell clusters. Biophys. J. 2014;106:299–309. doi: 10.1016/j.bpj.2013.11.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Farnsworth N.L., Hemmati A., Benninger R.K. Fluorescence recovery after photobleaching reveals regulation and distribution of connexin36 gap junction coupling within mouse islets of Langerhans. J. Physiol. 2014;592:4431–4446. doi: 10.1113/jphysiol.2014.276733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Marquard J., Otter S., Lammert E. Characterization of pancreatic NMDA receptors as possible drug targets for diabetes treatment. Nat. Med. 2015;21:363–372. doi: 10.1038/nm.3822. [DOI] [PubMed] [Google Scholar]
- 64.Satin L.S., Kinard T.A. Neurotransmitters and their receptors in the islets of Langerhans of the pancreas: what messages do acetylcholine, glutamate, and GABA transmit? Endocrine. 1998;8:213–223. doi: 10.1385/ENDO:8:3:213. [DOI] [PubMed] [Google Scholar]
- 65.Basco D., Zhang Q., Thorens B. α-cell glucokinase suppresses glucose-regulated glucagon secretion. Nat. Commun. 2018;9:546. doi: 10.1038/s41467-018-03034-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Murphy R., Ellard S., Hattersley A.T. Clinical implications of a molecular genetic classification of monogenic beta-cell diabetes. Nat. Clin. Pract. Endocrinol. Metab. 2008;4:200–213. doi: 10.1038/ncpendmet0778. [DOI] [PubMed] [Google Scholar]
- 67.Henquin J.C. Triggering and amplifying pathways of regulation of insulin secretion by glucose. Diabetes. 2000;49:1751–1760. doi: 10.2337/diabetes.49.11.1751. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.