Abstract
Steel modular building structures are being increasingly adopted for a variety of building applications since their method of construction, despite being relatively new, offers many benefits over conventional constructional methods. Even though their behaviour under gravity (dead and live) loads is generally well understood, their response to lateral dynamic loads such as seismic and wind loads, is relatively less known. Due to their unique structural detailing, their structural response and failure patterns under lateral dynamic loading can vary considerably from that exhibited by conventional structures. Limited research has shown that under lateral loadings, modular structures tend to fail at the columns which are critical members whose failure can lead to partial or total collapse of the structure. This paper aims to mitigate this by shifting the failure away from the columns to inter-modular connections which can be allowed to deform in a ductile manner. Towards this end, this paper proposes two innovative inter-modular connections and investigates their performance under monotonic and cyclic lateral loading using comprehensive validated numerical techniques. The proposed connections have an additional steel plate and resilient layers to provide increased ductility and dissipation of seismic energy with desired ductile failure mechanisms. Three-dimensional numerical models of the proposed connections are developed in ABAQUS software considering geometric and material nonlinearities, as well as contact formulations to accurately capture their response to the lateral loads and failure propagations. The numerical model is verified based on experimental results in the literature and used for extensive parametric studies. Seismic reliance of the proposed connections in terms of ductility, failure patterns, and energy absorption are compared with those of a standard inter-modular connection currently used in modular buildings. The outcome of this study demonstrates that the proposed connections have superior dynamic performances compared to the standard inter-modular connections in use today. New information generated through this study will enable to improve life safety and dynamic performance of modular building structures under typical gravity loads as well as under seismic loading.
Keywords: Civil engineering, Construction engineering, Structural analysis, Structural engineering, Structural mechanics, Failure mechanism, Innovative inter-modular connection, Lateral loading, Seismic mitigation, Steel modular structures
Civil engineering; Construction engineering; Structural analysis; Structural engineering; Structural mechanics; Failure mechanism; Innovative inter-modular connection; Lateral loading; Seismic mitigation; Steel modular structures
1. Introduction
1.1. Background
An emerging trend in the construction of medium-rise structures is modular construction or three-dimensional “pre-fabricated construction systems” [1]. It differs from conventional construction as it involves the prefabrication of individual volumetric units (modules) off-site in factory-controlled settings (off-site manufacture or OSM) which are then assembled on-site, expediting the construction process while maintaining quality and safety standards [2].
Modular buildings have a wide range of applications as both temporary (re-locatable) and permanent structures. Modules may be manufactured in standard sizes and shapes for buildings that require repetitive units or be designed to meet more innovative architectural requirements [3]. The speed and ease of construction combined with greater quality of manufacture in factory-controlled settings have made them a popular solution to increasing demands for development. Modular projects from around the world include the Little Hero apartment building in Melbourne, Australia, the Clement Canopy in Singapore, the Murray Grave project in the UK and the megaprojects at Hudson Yards in Brooklyn, New York [4, 5].
However, modular buildings are different from traditional structures “in terms of behaviour, detailing requirements and method of construction” [3]. Their design and detailing are not covered by many of the established building codes around the world and modular structures continue to be designed according to conventional theories. The study of the effect this has on their dynamic performance is still as relatively new to the research field as modular buildings are to the construction field. While most modular buildings are designed to sustain gravity loads (including self-weight of modules), their performance under dynamic loading such as wind, combined actions of wind and gravity loads, seismic loads and accidental loading cases is not generally considered. This results in designers and construction engineers being reluctant to let an assembly of modules stand alone and instead most modular structures consist of lateral load resisting systems such as in-situ reinforced concrete/monolithic steel cores, podiums and bracing systems [6, 7, 8], which prevent these buildings from being ‘purely’ modular [9].
One of the most important differences between modular and conventional structures lies in the inter-modular connections. Whereas conventional steel structures have a high degree of connectivity, modular units are generally only attached to other units at their corners and are discontinuous along the remaining portions of their structural interfaces [10, 11]. While the individual modules have greater stiffness and strength in their box-like frame, the inter-modular connections are the primary determinants of the integrity and robustness of the entire structural system [12]. Fig. 1 depicts a medium-rise steel modular structural frame and the individual box-like modules. Structural integrity needs to be ensured with robust connections between modules that help to maintain structural stability during an earthquake event that imposes large time-varying loads [13]. The connections allow the units to rotate and deform independently to each other due to the discontinuity between modules, thus imposing high stresses on vertical and horizontal connections and increasing inter-storey drifts. This is amplified during seismic events when combined with resonant effects.
Fig. 1.
(a) 3D view of medium-rise steel modular structural frame (b) Schematic diagram of typical inter-modular connections within the modular system (c) 3D view (d) front view and (e) side view of a single modular unit (frame).
In addition to this, most inter-modular connections do not contribute to the energy dissipating capacity of the structure. In current practices followed in the assembly of modular structures, the individual modules are connected together using three major types of connections: bolted, screwed and welded [12]. Their inability to deform in a ductile manner leads to unfavourable failure mechanisms which can threaten the entire structure. As concluded from the analysis of a ten-storey medium-rise steel modular building, modular structures form plastic hinges in critical column members when subjected to earthquake loads and typical inter-modular connections do not contribute to resisting lateral loads due to “over-conservative designs and lack of knowledge about their actual behaviour” [14, 15]. Current solutions for seismic mitigation in conventional structures include methods such as installation of dampers and base isolation [16, 17, 18]. The main aim of the present study however is to enable a purely, or exclusively, modular building structure without any external lateral load resisting systems. These factors warrant research into novel types of connections more suited to modular structural systems than conventional connections. The connection should contribute towards energy dissipation during seismic events and enable to shift potential failure points from critical columns to the connections which can be replaced after the seismic event.
1.2. Need and motivation for this research
Limited research on modular frames has shown that under lateral loadings, modular structures tend to fail at the columns which are critical members whose failure can lead to partial or total collapse of the structure. This paper aims to mitigate this by shifting the failure away from the columns to inter-modular connections which can be allowed to deform in a ductile manner. This will not only prevent the failure of critical members in the modular building but will also enable easier retrofitting by replacing the failed connection after the loading event. Towards this end, this paper proposes two innovative inter-modular connections and investigates their performance under monotonic and cyclic lateral loading using comprehensive validated numerical techniques. The proposed connections have an additional steel plate and resilient layers to provide increased ductility and dissipation of seismic energy with desired ductile failure mechanisms. These connections will shift the main failure locations away from critical structural members such as columns to the connection area and provide superior seismic mitigation.
The proposed novel bolted connections with energy dissipating mechanism and high ductility for steel modular structures can replace the current practice of field welding. One advantage of using bolted connections in steel modular structures is the ability to disassemble the connection and separate the modules, when necessary. This is not possible when adjacent modules are completely welded to each other which is a more permanent connection. Welding can only be done between similar materials while bolting can be done between two different materials which can be more convenient for modular structures resulting in hybrid connections such as that presented in this study. Also, when modules are stacked vertically and horizontally, it will be difficult to weld around the columns at the connection regions and to achieve necessary penetration and fusion levels for seismic performance due to difficulty in access after installation. This often leads to vulnerabilities such as incomplete penetration welds that result in weld root damage [19]. This combined with other factors such as poor workmanship at the site can lead to unsafe welds that are not up to engineering specifications. In addition, welding at the site can be costly and time-consuming [20]. Bolted connections, on the other hand, are designed under factory controlled settings and can be manufactured as a part of the modules prior to assembling, preserving quality and saving money. There have been studies on the lateral response of similar column-to-column bolted connections in seismic frames [21, 22, 23].
Bolt-and-plate connections used currently in modular constructions are unable to deform in a plastic manner to dissipate large amounts of kinetic energy from lateral dynamic loads and can fail at crucial points such as the bolts or at critical column locations. This is evidenced by the limited research available to date [15]. The proposed connections overcome these issues of bolted connections while enhancing their advantages by providing an energy dissipating mechanism in the connection that will also lessen the critical loads at vulnerable points in the structure. The above information highlight the need and motivation for this research.
2. Design
2.1. Proposed innovative bolted connection
A novel inter-modular connection is presented in this paper and two of its variations are investigated. The proposed connections (including the variants) can be used at the junction between eight (interior connection between two storeys) or four adjacent modules (exterior connection between two storeys). An interior connection is investigated in this paper and is as illustrated in Fig. 2. To simplify the numerical model, as well as to save computational effort, a symmetrical portion of this connection (consisting of four modules) will be analysed in the present study. Fig. 3 shows the schematic views of three types of inter-modular connections, C1, C2 and C3, studied in this paper (symmetrical models shown in E-W direction with respect to Fig. 3) while Fig. 4 shows the perspective views of C1 and C2 in a global modular frame. The transverse beams of the modules have been omitted for simplicity. C1 and C2 are the proposed types of connections while C3 is a general bolted connection used for comparison purposes in this study. They form a connection between adjacent modules and are capable of transferring both vertical and lateral forces to which the corner supported modules may be subjected to. However, C1 and C2 connections are able to allow modular structures to withstand greater dynamic loads with increased energy dissipation.
Fig. 2.
(a) 3D view of inter-modular connection at an interior junction of eight modules (transverse beams are omitted for clarity) (b) Plan view of the interior connection.
Fig. 3.
Schematic diagrams of the columns and inter-modular connections in: (a) C1 (b) C2 and (c) C3 (dimensions are in mm).
Fig. 4.
Perspective views of (a) C1 (b) C2 in the modular structure as interior joints (red demotes the steel connector plate and yellow denotes the resilient layers).
The Australian Standard 4100 defines a connection as a collection of structural members, “connection components” and “connectors” which transfer applied forces and provide stability to the overall structure [24]. In both variations of the connection, the primary components are the columns, column plates which are welded to the ends of the columns and M20 bolts. The columns are square hollow sections which represent the corner columns of the modules with transverse beams welded to them. The cross-section dimensions of the beams and columns are limited by factors such as the dimensions and carrying capacities of the vehicles used to transport individual modules and the conditions of the routes taken during transport. Hollow sections show superior compressive resistance under the same load conditions but contribute only a small percentage of the building mass and so reduces gravity loads. The radius of gyration of a hollow section is higher than that of the weak axis of an open section which reduces its slenderness ratio, λ and the probability of failure by buckling. The global buckling behaviour is also a function of the ratio width-to-wall thickness (d/t) of hollow sections until local buckling becomes the predominant failure mode [25, 26]. Each column is 0.5m in length in the numerical analyses and this reduces buckling effects when the connection is isolated for analyses. The standard height of the columns in modular units depend on the structural and building requirements and is typically about 3m. M20 Grade 8.8 High Strength Friction Grip bolts are used in each of the connections, C1, C2 and C3. High Strength Friction Grip Bolts (HSFG) allow connections to be extremely efficient under fluctuating loads such as those experienced under time-variant seismic loads. Two bolts per column plate are used (making a total of eight bolts in an interior connection connecting eight modules) as the required number of bolts to carry the shear and axial forces generated in the connection while also resulting in simplified construction. A different arrangement of bolts may also achieve this, however, the present configuration has been found to be suitable for this study.
Compared to conventional bolt-plate connections, the proposed connection type C1 shown in Fig. 3a contains an additional steel connector plate which forms the centre of the connection. This plate is separated from the columns above and below with the use of washers as spacers. The major path of load transfer in this connection is through bolt bearing since the column end-plates and connector plate do not come into contact to generate friction. This additional plate is expected to deform and contribute to the overall connection energy dissipation which will effectively reduce the seismic energy transferred to the modules.
In the proposed connection type C2, a resilient material, such as rubber, is interlayered between the steel column plates and steel connector plate, as shown in Fig. 3b. This connection can be classified as a friction-type connection as force transfer between the connector plate and resilient layers are induced due to resultant friction [20]. The resilient layers will provide additional damping to the system which will reduce the need for extreme connector plate deformation, further protecting all components of the modular structure. Both connections are bolt-and-plate type connections which can be manufactured in a factory along with the modules. This makes them cost-efficient in manufacture. In this study, both connection types C1 and C2 are compared against a general (traditional) bolted connection, C3, to capture the differences in performance. As shown in Fig. 3c, connection C3 consists of columns, column plates and bolts that are of these same dimensions as those of C1 and C2 and will not be varied.
3. Methodology
3.1. Finite element analysis
When numerically simulating modular structures, it is vital to model the “configuration and dynamic characteristics” of the structure as realistically as is possible given the limitations of the modelling techniques in order to capture their true behaviour [11]. Most finite element analyses simulate inter-modular connections as rigid, semi-rigid, pinned or as springs to simulate full penetrating welds, partial welds and bolt-plate connections [3, 11, 27, 28]. However, when numerically modelling these connections, it has been observed that most bolted connections behave nonlinearly and are semi-rigid due to various factors such as geometric discontinuities and stress concentrations in parts of the bolt-plate assemblies and contact-status changing the frictional slip between the bolt and clamped surfaces [29]. The extent of rigidity and associated behaviour depend on both geometric and material characteristics of the connection. Proper connection design and analysis are crucial as under-design can cause failure in the connection region while over-design can have negative economic consequences. This is especially true for modular structures where the inter-modular connections also contribute to the lateral stability of the structure during seismic events.
Therefore, it prompts the need to conduct accurate analyses of inter-modular connections with parametric studies to develop the most effective type of inter-modular connection in terms of geometry, stiffness, strength capacity, type of materials and cost. In the present study, detailed three-dimensional finite element models are analysed using ABAQUS v 16.4.2 [30] to study the proposed novel inter-modular connection and its variations to draw realistic conclusions regarding their performance and capacity under dynamic loads. The modelling techniques have been validated with existing experimental and numerical data in the literature.
3.1.1. Finite element model and parametric study
The three-dimensional finite element models developed for this study are given in Figs. 5 and 6. The model presented is a symmetrical half-model depicting eight adjacent modules connected both vertically and horizontally. C1 has a steel connector plate at mid-height while C2 consists of two additional resilient layers. C3 is a normal bolted connection expected to be used in current modular structure designs. The columns are modelled at 0.5m lengths to simplify the model and are assumed to be fully welded to the column plates at the base and that brittle failure is avoided. The weld is assumed to be a complete penetration joint as recommended by EN 1998-1, 2003 for seismic design and is modelled by merging the columns and column plates together to allow them to behave as one part [19]. The load is distributed at the column ends with the use of analytical rigid plates in ABAQUS which eliminates local damages that will cause premature failure of the connection.
Fig. 5.
3D views of the (a) unmeshed and (b) meshed 3D finite element models developed in ABAQUS.
Fig. 6.
Front views of connection types (a) C1 (b) C2 and (c) C3.
The parametric study considered both material and geometric parameters. Table 1 provides details of the models developed for connections C1 and C2 for the parametric study. The main parameters that were varied are: the connector plate thickness, the resilient layer thickness, material properties of the resilient layers, the number of interlayers, and axial compressive forces and type and magnitude of lateral loads applied on the columns. The column cross-sections, bolt sizes and column plate dimensions were kept constant as they have been designed for typical gravity loads, intra-modular robustness during transport, assembly and service life. The dimensions of the column plates used as the base of columns are 240 × 240 × 10mm, the column cross-section dimensions are 150 × 150 × 4.5mm and the diameter of the bolts are 20 mm. The bolts, designated M20 bolts, are Grade 8.8 Structural steel bolts which were found adequate to sustain typical gravity loads in steel modular frames. The positioning of the bolts within the connection system were based on the investigation of several bolt configurations and the current configuration was found to be adequate. Washers (5mm height, Grade 8.8) were used in C1 to achieve space between the different plates and was modelled with the same material properties and mesh detail as the M20 bolts. The same dimensions were also used for the columns and bolts in C3. The four column plates used for C3 include 2 plates that are 240 × 240 × 10 (in mm) and two plates that are 490 × 250 × 10mm. The shear moduli of the resilient layers were varied in the range of 0.3–2.5MPa which encompasses a wide variety of rubber-like materials.
Table 1.
Dimensions and material properties used in the model for parametric analyses.
| Connection Type | Connector Plate dimensions (mm) | Resilient Layer dimensions (mm) | Resilient Layer shear modulus (MPa) |
|---|---|---|---|
| C1 | 490 × 250 × 5 | - | - |
| 490 × 250 × 10 | - | - | |
| 490 × 250 × 20 | - | - | |
| C2 | 490 × 250 × 10 | 490 × 250 × 5 | 0.3 |
| 490 × 250 × 10 | 490 × 250 × 10 | 0.3 | |
| 490 × 250 × 10 | 490 × 250 × 20 | 0.3 | |
| 490 × 250 × 20 | 490 × 250 × 10 | 0.3 | |
| 490 × 250 × 20 | 490 × 250 × 20 | 0.3 | |
| 490 × 250 × 10 | 490 × 250 × 5 | 0.6 | |
| 490 × 250 × 10 | 490 × 250 × 5 | 1.2 | |
| 490 × 250 × 10 | 490 × 250 × 5 | 1.8 | |
| 490 × 250 × 10 | 490 × 250 × 5 | 2.5 |
3.2. Material modelling
3.2.1. Steel
A bilinear stress-strain relationship with kinematic strain hardening was used to model the non-linear material behaviour of the steel components of the connection [31]. The steel components that are common to all models, C1 – C3, are the hollow square section columns, column plates and M20 bolts. C1 and C2 have an additional steel connector plate. Since structural hollow sections are composed of the same structural steel as other structural cross-sections, they have the same mechanical properties based on the method of production: hot-rolled or cold-rolled. AS/NZS 1163 provides information on cold formed structural steel hollow sections including standard sizes, production methods, allowed connecting methods and other mechanical properties [26]. A Young's Modulus (E) of 200GPa and a Poisson's ratio of 0.3 were specified for all steel components. The yield stress for the columns, column plates and connector plate was considered to be 450MPa. The M20 bolts have a theoretical tensile yield strength of approximately 640MPa and a tensile ultimate strength of approximately 880MPa [24]. Strain hardening was assumed to be 2% of the Young's Modulus. ABAQUS defines the stress-strain curve in terms of true stress (and true strain and plastic strain values which are calculated from nominal stress and strain values as follows:
| (1) |
| (2) |
| (3) |
The kinematic hardening plasticity model considers both the Bauschinger effect and the von Mises yield criterion and is the metal plasticity model recommended by ABAQUS [30]. Geometrical nonlinearities were taken into account by activating NLGEOM in ABAQUS to include large displacement effects.
3.2.2. Resilient layer
For this study, the interlayer resilient material is initially taken to be rubber and its material properties are varied in the parametric study to reflect other possible rubber-like materials (Table 1). To capture the hyper-elastic behaviour of nearly incompressible rubber-like materials, the Neo-Hookean form of a hyper-elastic constitutive model is defined as the material model for rubber and is specified in terms of coefficients and . These coefficients form a part of the strain potential energy equation pertaining to the Neo-Hookean hyper-elasticity model as given in Eq. (4) where is the strain energy per unit volume, is the first deviatoric strain invariant and is the elastic volume ratio [30, 32, 33].
| (4) |
and are calculated from the initial shear modulus and bulk modulus respectively.
| (5) |
| (6) |
This hyper-elastic model captures the nonlinear, nearly elastic response of rubber subjected to large strains while eliminating local instabilities [34]. While material nonlinearity is considered by defining the appropriate material models, geometric nonlinearities are allowed by considering the large displacement theory during analyses.
3.3. Finite element mesh and boundary conditions
The mesh was selected to achieve optimum convergence of results while maintaining computational efficiency. According to conclusions drawn in [35], the use of solid elements, despite requiring a higher computational effort, yields the most accurate results by applying frictional contact areas and element stiffness more precisely. Therefore, C3D8R, a general purpose 8-node linear brick element with reduced integration and hourglass control is used for the finite element mesh of all the steel components [36]. The element size of the bolts were smaller than that of the other steel components to improve the accuracy of the contact formulations. The resilient layer is modelled with C3D8RH elements which have an additional hybrid formulation to account for hyper-elasticity and near-incompressibility. Hourglass modes are overcome by reducing the mesh-size as appropriate and allowing the rubber to exhibit some compressibility (D1 > 0). The model of C1 consisted of approximately 33670 elements and 53308 nodes while C2 had 58178 elements and 90644 nodes and C3 had 30860 elements and 48964 nodes. As recommended by ANSI/AISC 341-16, it is necessary to use pretension bolts in seismic force-resisting frame bolt-and-plate type connections which are subjected to highly reversible loads. This will allow the bolted-connections to be slip-critical (termed “slip-resistant” by BS EN 1993-1-8) which will prevent, even though not completely eliminate, excessive shearing deformations between connected components. The design preload required can be calculated as per Eq. (7) retrieved from BS EN 1993-1-8 Clause 3.6.1(2) where, is the ultimate bolt tensile strength, is the tensile stress area and is taken as 1.1 from Table 2.1 under Clause 2.2 of BS EN 1993-1-8:2005 [37]. Fixed constraints were imposed at the base of the connection.
| (7) |
3.4. Contact modelling
The Coulomb friction model is adapted in modelling the frictional contact between the interlayers in all connections. It can be used to approximate the amount of friction force generated between the interlayers by the normal force acting on the connection. Different friction coefficients (μ) were defined to model the contact between steel and steel and between resilient layer material and steel. This also prevents penetration between surfaces. The penalty method was utilized to solve the frictional forces since it is less computationally expensive.
3.5. Load application
3.5.1. Axial loads
An axial force equal to 10% and 20% of the design section capacity in axial compression (Ns) of the square hollow section column was applied on the column in turn and kept constant while the lateral loads (discussed in section 3.5.2) were applied. This takes into account that in a global structure, connections will be subjected to compressive axial loads, such as from gravity and would simulate the combined effects of bending moment and axial loads. Eq. (8) extracted from Australian Institute of Steel Construction for the Design of Structural Steel Hollow Section Connections was used to calculate Ns [38].
| (8) |
Where; is 0.9 (Table 3.4 of AS 4100), is the form factor (1.0 in this case), is the net area of cross-section and is the yield stress of the hollow section [38].
3.5.2. Monotonic and cyclic loads
Monotonic and cyclic analyses of the connection were performed in ABAQUS to obtain load-displacement (F-Δ) pushover and hysteresis curves. The amount of energy dissipation was also obtained from these results calculated as the area under the F-Δ hysteresis curves. A lateral force is applied at the top of the columns (as shown in Fig. 5). For the pushover curves, this lateral force was monotonically increased while for the hysteresis curve, a quasi-static cyclic loading was applied.
The loading history for the cyclic loading was adapted from the loading protocol presented by FEMA 461 as shown in Fig. 7 [39].
Fig. 7.
Loading protocol adopted for the numerical study.
3.6. Validation of the finite element model using reference test results
The modular connection models and numerical modelling techniques discussed in the previous sections are validated against experimental and numerical results from the literature [14] where a module-to-module connection was designed and tested as shown in Fig. 8. The connection forms the junction between four adjacent modular units, similar to the connection studied in this paper. This standard bolted connection type is an example of modular connections used at present in the construction industry and formed the basis for connection type C3 investigated in the parametric study of this paper. However, the standard connection lacks the additional connector plate and/or resilient layers included in the proposed innovative connections that can enhance the energy dissipation and the structural capacity of modular structures as is described in the present study.
Fig. 8.
(a) Dimensions of modular connection used for validation (b) experimental set-up in [14] (c) schematic diagram of experimental set-up in [14] (d) method of load application and bolt shear plane as shown in ANSYS [14] (e) ABAQUS model (meshed) used in present study.
A 3D model of the experimental set-up in [14] was developed using ABAQUS for validation purposes and its load-deformation capacity was compared to that obtained through experimental testing and numerical modelling. The present study modelled the connection design with a bolt diameter of 12 mm in a 14 mm round type bolt hole. The columns were allowed to move in the direction of the lateral force applied and the main region observed was the shear plane for the bolts as shown in Fig. 8d.
C3D8R solid elements were used for all components which included the columns (SHS of dimensions (150 × 150 × 9 mm), column plates and four M12 bolts. Material properties for structural steel as provided in [14] were input to the model. The same boundary conditions as the experiment are imposed on the model with the top and bottom of one column plate fixed while the other is allowed to slide. The frictional contact between the plates are defined using a penalty friction formulation where a tangential friction coefficient is specified.
A comparison of the load-displacement results from the present model illustrate that the model developed in the present study closely follows the numerical results obtained in [14] and is shown in Fig. 9. Until approximately 0.9 mm, there is a rapid deformation due to the slip of the connection whereby bolt bearing will occur. Beyond this, due to the bolt bearing, the stiffness of the connection is altered which changes the rate of deformation under applied load. After 2.1 mm, the bolts undergo shear deformations as well, which means that the overall connection stiffness is now governed by both bolt bearing and bolt shear. This validation provides confidence in using the present modelling techniques to study the effects of parameters and capture the general behaviour of inter-modular connections with material and geometric nonlinearities and subjected to lateral loads.
Fig. 9.
Comparison of the vertical deformation of the column plate under shearing loads.
4. Results and discussion
Force-controlled monotonic and cyclic load numerical analyses were conducted on the models listed in Table 1 to determine parameters such as their load capacities, energy dissipation and deformation mechanisms. Axial forces equal to 0%, 10% and 20% of the design section capacity of the column in axial compression were applied in turn and kept constant on the columns (in the vertical direction) when monotonic and quasi-static loads were applied on the column tips (in the lateral direction) until the maximum tensile stress specified in the constitutive material model is exceeded anywhere in the connection components. This would signify the ultimate capacity of the connection before failure. The deformed shapes and von Mises stress patterns observed at the early stages of monotonic loading for C1 (with a connector plate of 10 mm thickness), C2 (with a connector plate of 10 mm thickness and resilient layers of 5 mm thickness) and the normal bolted connection C3 are shown in Figs. 10, 11 and 12 respectively.
Fig. 10.
Deformed shapes of C1 (a) front view (b) 3-D view at early loading stages.
Fig. 11.
Deformed shapes of C2 (a) front view (b) 3-D view at early loading stages.
Fig. 12.
Deformed shapes of C3 (a) front view (b) 3-D view at early loading stages.
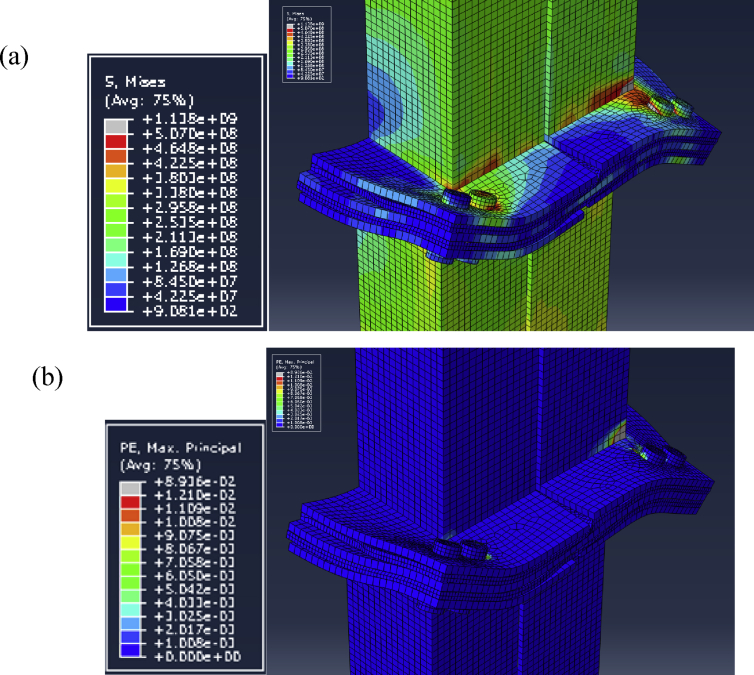
With the application of the load at the tip of the column (Fig. 5), the component layers of steel and/or rubber in C1 and C2 undergo tilting and provide additional rotational and displacement ductility to the connection. As Fig. 12 shows, C3 also undergoes tilting due to the bending moments generated at the connection due to the lateral loading. Fig. 13 illustrates the deformations that the steel connector plate in C1 in the y (vertical) direction to exemplify the rotational and tilting behaviour of the connector plate. Fig. 14 depicts the main failure region of connection C2 in terms of von Mises stress and plastic strain. This pattern and failure region is similar to that observed for C1 as well. The analysis is terminated when the maximum defined tensile strength and its corresponding plastic strain are first exceeded anywhere in the model. The maximum load corresponding to this is taken as the ultimate load sustained and is an indication of the overall deformability and load-capacity of the connection. Therefore, weld failure is the ultimate failure mode. Prior to that, most of the energy dissipation happens due to material yielding of the column plates and deformations in the connector plate. The location of this failure region shifts between the four column plates depending on the type of connection and the varying thicknesses and material properties of the steel and resilient layers. There are no plastic yielding observed anywhere in the column, other than the weld area at ultimate failure. The bolts do not show critical stresses due to their higher yield and tensile strengths. This confirms that bolt failure is unlikely in all these connection types. Additionally, deformations vary with variations in component parameters as elucidated by the parametric study.
Fig. 13.
(a) Undeformed connector plate in C1 (b) deformation of connector plate in a C1 type connection in +y (vertical) direction.
Fig. 14.
(a) von Mises stress variation (b) plastic strains at ultimate load of a C2 type connection.
4.1. Monotonic loading
Fig. 15 shows the load-displacement (F-Δ) pushover curves obtained under monotonic loading for C1 with varying connector plate thicknesses and axial compressive loads (Ns); where Δ is the lateral displacement of the upper module columns. The pushover curves show three major stages of deformation; the elastic deformation up to the critical yield point, yield development, and strain hardening and stiffness degradation until ultimate tensile failure. The connection models were subjected to 20%, 10% and 0% of the design section capacity in axial compression (Ns) and as Fig. 15 demonstrates, the higher the axial compressive force, the higher the post-yield stiffness and lower the total connection displacement. Generally, as the axial load increases, the deformation rate decreases as seen from Figs. 15 and 16, however, the later load capacity is sustained. This shows that when installed into a global modular structure, with higher realistic axial loads, the ductility of the connection can reduce due to the combined actions of axial and lateral forces. This shows that when installed into a global modular structure, with higher realistic axial loads, the lateral load capacity and ductility of the connection can reduce due to the combined actions of axial and lateral forces. All C1 connections showed a maximum load capacity in the range 250–280kN when failure occurred.
Fig. 15.
Pushover curves for C1 with connector plate of thickness (a) 5 mm (b) 10 mm (c) 20 mm (under different Ns) (d) effect of varying connector plate thickness under 20% Ns.
Fig. 16.
Pushover curves for C2 with (a) 10 mm connector plate, 5 mm rubber (b) 10 mm connector plate, 10 mm rubber (c) 10 mm connector plate, 20 mm rubber (d) 20 mm connector plate, 10 mm rubber (e) 20 mm connector plate, 20 mm rubber (under different Ns).
Results on the effects of connector plate thickness on performance of C1 connections show that connector plate thicknesses of 5 mm and 10 mm give similarly high ultimate displacements However, a 20 mm thick connector plate produces the least ultimate displacement, when all three thicknesses are compared. Therefore, a thicker column plate will be more resistant to initial deformations and so will not exhibit additional ductility and energy dissipation. In addition, the higher the magnitude of the applied axial loads on the columns, the lower the ultimate displacements and higher the required yield load.
Figs. 16 and 17 demonstrate the load-displacement (F-Δ) pushover curves obtained for C2 with varying connector plate thicknesses, resilient layer thicknesses, resilient material properties, number of total layers and axial compressive loads (Ns). These results demonstrate more pronounced effects of the chosen parameters. The resilient layer is initially assumed to be rubber with a shear modulus of 0.3 MPa and two resilient layers are provided for each connection to sandwich the steel connector plate.
Fig. 17.
Ultimate loads and displacements (under 20% Ns) with variations in (a) number of steel and rubber layers (b) shear moduli (c) connector plate and resilient layer thicknesses.
One of the main parameters investigated was the effect of connector plate and resilient layer thicknesses on connection performance. Similar to C1, this connection is also analysed under 20%, 10% and 0% of the design column axial compressive loads. As seen in Fig. 16a–c, the specimens show a pushover response similar to that observed for C1 connections but exhibit a greater ductility in most instances. When considering the effect of resilient layer thickness only, a common behaviour pattern is observable and illustrates that varying only the resilient layer thickness does have some effect on the overall connection performance. However, the highest lateral displacement of column, and therefore highest ductility and energy dissipation, is exhibited by the specimen with a 20 mm steel connector plate and two 10 mm rubber layers as shown in Fig. 16d. This is in contrast to results obtained for C1 with a 20 mm thick connector plate, but without a rubber (resilient) layer which showed considerably lower ultimate displacement (Fig. 15c). When the thickness of the connector plate is increased to match the thickness of the resilient layers, as shown in Fig. 16e, the overall connection displacement reduces. These results validate that including a resilient layer provides a higher load and displacement capacity and also demonstrate that pairing the resilient layer with a thicker connector plate can lead to increased ductility and energy dissipation.
Fig. 17 captures the effects of some of the important connection parameters. Fig. 17a shows that the connection with one steel connector plate and two resilient layers has a higher ultimate displacement and hence ductility compared to a connection with two connector plates and three resilient layers. The ultimate load is denoted as F. Therefore, increasing the number of connector plates and resilient layers does not guarantee a better performance which could be due to increased connection stiffness. In addition, the number of plates/layers that can be contained within a connection is limited by factors such as limitation in overall connection thickness, ease of assembly and overall cost. The shear modulus () of the resilient layers also has a significant effect on connection behaviour as elucidated in Fig. 17b. The results obtained are for C2 connections with one 10 mm thick steel connector plate and two 5 mm thick resilient layers but with different values. An increase in shear moduli causes an increase in ultimate displacement and load capacity of the connection until a certain threshold after which the capacity reduces drastically with increased shear moduli. This is evident from the results obtained for shear moduli values of 1.8 MPa and 2.5 MPa as shown in Fig. 17b. This could be due to increased connection stiffness with the use of stiffer resilient materials. The results in Fig. 17c show that when rubber layers are included in a connection with a thicker connector plate, it can lead to greater ductility and energy dissipation as also demonstrated by the results of connection type C2 (Fig. 16). Despite this, if the connector plate thickness is also increased (for example, to 20 mm) to match the rubber layer thickness (20 mm), the ultimate displacement and load capacity of the connection decreases again. This implies that the connection works more effectively if the steel connector plate is thicker than the resilient layers.
Fig. 18 compares the ultimate mid-plate rotation of the steel connector plate with the ultimate lateral displacement of the column for all monotonic analyses, excluding those models with a 20 mm thick connector plate since they show smaller mid-plate rotations in comparison to the other models. The rotations are calculated using the small angle approximation method. This defines the relationship between the rotation of the connector plate and the displacement capacity of the connection up to failure. The results show that for C2 connections with the resilient layers, a smaller mid-plate rotation can yield a higher ultimate connection displacement which relates to a higher amount of dissipated energy. The mid-plate rotation of C1 (square) needs to be higher to obtain the same ultimate displacements as C2 (diamond). The ultimate displacement vs rotation of the connector plate can be seen to exhibit an approximately linear behaviour as shown in Fig. 18. This behaviour is compatible with what was also observed visually in Fig. 14 where most part of the connector plate is in the non-plastic range.
Fig. 18.
Ultimate lateral displacement of columns vs mid-plate rotation of connector plate of C1 and C2 connections.
The load-displacement (F-Δ) pushover curves for the normal bolted connection (C3) under 20%, 10% and 0% axial compressive loads (Ns) are shown in Fig. 19a. It can be seen that they do not display any significant trends. They are compared with those of C1 and C2 in Fig. 19b. It is evident that the simple normal bolted connection (C3), as used in modular structures today, falls short in terms of ductility and energy dissipation when compared to the performance of C1 and C2 connections. It also requires a higher load to yield, portions of which may be transferred to the bolts and cause premature failure in them due to tension or shear failure. The superior performance of the C2 connection proposed in this study is evident as it shows a significant ductility enhancement, which protects the bolts and will result in more robust modular structures that perform better under dynamic loading through increased energy absorption.
Fig. 19.
(a) pushover curves for normal bolted connection, C3 under different Ns values (b) comparison between C1 (with 10 mm thick connector plate), C2 (with 10 mm thick connector plate and 10 mm thick resilient layers) and C3, under 20% Ns
4.1.1. Ductility ratio and initial stiffness
The ductility of each connection is deduced through the “energy balance approach” used by Mander et al. [40] and is tabulated in Table 2. It follows that the additional energy per unit volume which can be calculated from the area under the curves after the yield point corresponds to additional ductility before failure. Therefore, in this study, the ductility coefficient is defined as;
| (9) |
Table 2.
Performance indicators of the connections.
| Model | (kN.m) | (kN.m) | (kN/m) | |
|---|---|---|---|---|
| C1 – CP = 5 mm (20% Ns) | 3.3064 | 0.2819 | 11.73 | 62766.48 |
| C1 – CP = 5 mm (10% Ns) | 6.0477 | 0.3998 | 15.13 | 55007.01 |
| C1 – CP = 5 mm (0% Ns) | 16.2397 | 0.4779 | 33.98 | 49160.63 |
| C1 – CP = 10 mm (20% Ns) | 3.2723 | 0.4719 | 6.93 | 56879.17 |
| C1 – CP = 10 mm (10% Ns) | 6.1644 | 0.4342 | 14.20 | 52903.70 |
| C1 – CP = 10 mm (0% Ns) | 15.5254 | 0.5018 | 30.94 | 47990.12 |
| C1 – CP = 20 mm (20% Ns) | 2.5763 | 0.5055 | 5.10 | 47282.44 |
| C1 – CP = 20 mm (10% Ns) | 4.4800 | 0.3179 | 14.09 | 54824.79 |
| C1 – CP = 20 mm (0% Ns) | 9.7761 | 0.3319 | 29.45 | 53218.41 |
|
C3 (20% Ns) Plate thickness = 10 mm |
0.4891 | 0.2379 | 2.06 | 78505.27 |
|
C3 (10% Ns) Plate thickness = 10 mm |
0.5308 | 0.2964 | 1.79 | 73236.11 |
|
C3 (0% Ns) Plate thickness = 10 mm |
0.6712 | 0.3271 | 2.05 | 69275.95 |
|
C2 – CP = 10 mm Rubber = 5 mm (20% Ns) |
5.3745 | 0.3632 | 14.80 | 55546.35 |
|
C2 – CP = 10 mm Rubber = 5 mm (10% Ns) |
19.0375 | 0.4589 | 41.49 | 49367.09 |
|
C2 – CP = 10 mm Rubber = 5 mm (0% Ns) |
15.6519 | 0.4499 | 34.79 | 48794.25 |
|
C2 – CP = 10 mm Rubber = 10 mm (20% Ns) |
16.4552 | 0.4301 | 38.26 | 52371.28 |
|
C2 – CP = 10 mm Rubber = 10 mm (10% Ns) |
15.1486 | 0.4337 | 34.93 | 50791.64 |
|
C2 – CP = 10 mm Rubber = 10 mm (0% Ns) |
16.7343 | 0.5577 | 30.01 | 43990.80 |
|
C2 – CP = 10 mm Rubber = 20 mm (20% Ns) |
13.1383 | 0.3668 | 35.82 | 56304.98 |
|
C2 – CP = 10 mm Rubber = 20 mm (10% Ns) |
5.436 | 0.2834 | 19.18 | 61327.08 |
|
C2 – CP = 10 mm Rubber = 20 mm (0% Ns) |
14.6775 | 0.3603 | 40.74 | 54747.37 |
|
C2 – CP = 20 mm Rubber = 10 mm (20% Ns) |
21.2314 | 0.3987 | 53.25 | 43191.21 |
|
C2 – CP = 20 mm Rubber = 10 mm (10% Ns) |
24.3127 | 0.4403 | 55.22 | 39376.07 |
|
C2 – CP = 20mm Rubber = 10mm (0% Ns) |
25.7655 | 0.4575 | 56.32 | 36956.52 |
|
C2 – CP = 20 mm Rubber = 20 mm (20% Ns) |
17.5602 | 0.6372 | 27.56 | 41977.35 |
|
C2 – CP = 20 mm Rubber = 20 mm (10% Ns) |
17.1467 | 0.6236 | 27.50 | 41427.10 |
|
C2 – CP = 20 mm Rubber = 20 mm (0% Ns) |
19.2727 | 0.627 | 30.74 | 40140.29 |
|
C2 – CP = 10 mm Rubber = 5 mm (20% Ns) No. of Layers = 5 |
3.201 | 0.2016 | 15.88 | 65268.95 |
|
C2 – CP = 10 mm Rubber = 5 mm (20% Ns) Shear Modulus = 0.6 |
2.0394 | 0.3051 | 6.68 | 55644.11 |
|
C2 – CP = 10 mm Rubber = 5 mm (20% Ns) Shear Modulus = 1.2 |
2.348 | 0.369 | 6.36 | 54166.67 |
|
C2 – CP = 10 mm Rubber = 5 mm (20% Ns) Shear Modulus = 1.8 |
8.6996 | 0.4038 | 21.31 | 56470.59 |
|
C2 – CP = 10 mm Rubber = 5 mm (20% Ns) Shear Modulus = 2.5 |
7.428 | 0.3693 | 20.11 | 60000.10 |
In the above Eq. (9), is energy dissipated after the yield point, and is energy dissipated up to the yield point. As calculated in Table 2, the ductility ratio is lowest for the normal simple bolted connections and highest for the connections with the resilient layers. This gives an indication of the better performing connections and enables the selection of an optimum connection with the largest ductility capacity. According to the results, the maximum calculated ductility ratio is 56.32 for a connection with a 20 mm connector plate coupled with two resilient layers of 10 mm thickness each and a shear modulus of 0.3 MPa. However, this value was obtained when there was no axial compression forces and is a conservative value. Under 20% Ns, this same connection (C2) still exhibits a high ductility value of 53.25. The lowest ductility values are displayed by the normal connection C3 which has a ductility ratio of 2.06 under 20% Ns. This behaviour is also reflected by the initial stiffness values calculated for the connections. The initial stiffness of the connection prior to yielding is calculated from the slope of the elastic portion of the pushover curves and is denoted by Normal bolted connections (C3) are the stiffest connections with the highest initial stiffness values. This shows that steel inter-modular connections as used in construction today are stiff connections with limited dynamic performance. In contrast, the lowest initial stiffness values are shown by the C2 connection with a 20 mm connector plate and two resilient layers of 10 mm thickness each (shear modulus is 0.3 MPa) which also provided the highest ductility. The best performing connection configurations are further summarized in Table 3.
Table 3.
Performance indicators of best performing connection types.
| Model | (kN.m) | (kN.m) | (kN/m) | |
|---|---|---|---|---|
| C1 – CP = 5 mm (20% Ns) | 3.3064 | 0.2819 | 11.73 | 62766.48 |
|
C2 – CP = 20 mm Rubber = 10 mm (20% Ns) |
21.2314 | 0.3987 | 53.25 | 43191.21 |
|
C3 (20% Ns) Plate thickness = 10 mm |
0.4891 | 0.2379 | 2.06 | 78505.27 |
4.2. Cyclic loading
Fig. 20 depicts the hysteresis curves obtained for C1 with three different connector plate thicknesses under an axial compression loading of 20% of Ns. Fig. 21 shows the hysteresis curves developed for some of the C2 models with the resilient layers, also under 20% of Ns.
Fig. 20.
Hysteresis curves for C1 with connector plate thickness of (a) 5 mm (b) 10 mm and (c) 20 mm.
Fig. 21.
Hysteresis curves for C2 (a) 10 mm connector plate, 5 mm resilient layer, is 0.3 MPa (b) 10 mm connector plate and 10 mm resilient layer, is 0.3 MPa (c) 10 mm connector plate and 20 mm resilient layer, is 0.3 MPa (d) 20 mm connector plate, 10 mm resilient layer, is 0.3 MPa (e) 20 mm connector plate and 20 mm resilient layer, is 0.3 MPa (f) 10 mm connector plate, 5 mm resilient layer, is 1.2 MPa.
All the C1 and C2 models subjected to cyclic loads show wide hysteresis curves that display high ductility and energy dissipation. The hysteresis curves of C1 type connections are stable on both negative and positive sides, with reduced pinching, providing an effective energy dissipation mechanism. While the hysteresis curves obtained for C2 shows a similar pattern, they appear to be more unstable which is related to the hyper-elasticity of rubber. The load/displacement capacity shown under cyclic loads is less than that under monotonic loads and this could be explained due to fatigue and the effects of residual deformations.
The amount of energy dissipated can be quantified as the area enclosed within the hysteresis loops and is illustrated in Fig. 22. The bars correspond to Figs. 20 and 22 where the shaded bars represent C1 connections and the solid bars represent C2 connections. An axial compressive load of 20% of Ns was selected for all cyclic models to simulate the axial loads present in a global frame to prevent over-estimation of performance parameters.
Fig. 22.
Quantification of the energy dissipated under cyclic loads corresponding to Figs. 21 and 22 ( is 0.3 MPa).
Both the energy dissipation values and the hysteresis curves for C1 connections show that, when subjected to dynamic loads, a connection with a connector plate of 20 mm thickness gives the highest energy dissipation despite showing a lower ductility ratio ( = 5.10) under monotonic loads (Table 2). Despite having smaller ductility ratios than C2 type connections, C1 connections show increased energy dissipation. This is due to the repeated yielding of the steel connector plate under cyclic loading. However, when all connections are compared, the C2 type connection with thin resilient layers (10 mm) paired with a thicker steel connector plate (20 mm) showed the highest amount of energy dissipation as also predicted by the results obtained for monotonic loading which showed a very high ductility ratio of 53.25 under 20% axial load. Overall, under cyclic loads, the performance capacities of the connections parallel the results obtained for monotonic loads to some extent while some differences are also observed.
5. Conclusions
Modular building structures find increasing applications today as their construction method offers many benefits over traditional construction methods. Through their response under vertical gravity loads is reasonably well understood, their performance under lateral dynamic loads such as wind and seismic loads is relatively less known. Limited research in this area has shown that under lateral dynamic loading these modular building frames fail at columns which are critical members whose failure can lead to partial or total collapse of the structure. To mitigate this adverse behaviour, this research proposed innovative inter-modular connections that can shift the failure region away from the column to the connection which can be replaced after the dynamic event. Two variations of this novel connection are proposed for joining adjacent modules in the construction of medium-rise steel modular structures. They have a greater energy absorbing capability under seismic loads and add further value to the modular construction techniques which have the advantages of being more efficient and cost-effective.
The present study used numerical techniques calibrated with experimental data from published research to assess the performance of the connection types under monotonic and cyclic loads. The use of an extensive 3D model, though computationally expensive, yielded more accurate insight into the behaviour of the connections. The results obtained from the finite element models developed in ABAQUS v 16.4.2 demonstrate the viability of this connection to be used as an inter-modular connection. Overall, the results demonstrate that the proposed connections provide a strategy to mitigate failure in critical modular members by enabling failure points to be shifted away from the columns to the inter-modular connections. The proposed C1 and C2 connections are able to show a superior performance to the standard bolted connection C3. Design information on the proposed connections is briefly presented in the following section on the main conclusions of the present study. Modular structures may be constructed from many materials such as precast concrete and timber but this study focused on steel modular buildings which fall under permanent modular construction (PMC).
The main conclusions derived from this study include:
-
(1)
The proposed innovative connection, with its two variations C1 and C2, show greater ductility and energy dissipation capacity than the simple bolted connection used as inter-modular connections in current practice (C3) and is, therefore, a superior type of connection. This connection is applicable for use under dynamic loading conditions such as earthquake actions.
-
(2)
The ultimate failure region of the connection was the weld region between the column and column plate and the analyses were terminated when this was significant. However, prior to this, the column plates deformed and yielded. This suggests that the formation of plastic hinges is limited to the connection region and is away from critical primary structural members such as columns.
-
(3)
A range of parameters were analysed to identify the most effective arrangement of connections C1 and C2 while comparing their dynamic performance to that of a traditional bolted connection (C3) used in modular structures today. These analyses demonstrated that variations in steel connector plate thickness, resilient layer thickness, number of overlapping steel and resilient material layers and material properties of the resilient material all contribute to the connection performance.
-
(4)
The optimum connection type, from the models considered for this parametric study, is the connection with a 20 mm connector plate with two added resilient layers (10 mm thickness and a shear modulus of 0.3 MPa) which showed the highest energy dissipation and ductility ratios. The superior performance of the C2 connection proposed in this study is evident in its significant ductility enhancement. When compared to other connection models, it is evident that pairing a thicker steel connector plate and a thinner resilient layer provides an efficient inter-modular connection.
-
(5)
Increasing the number of layers of overlapping connector plates and resilient layers result in a stiffer connection with limited deformation capabilities. A higher number of plates/layers also affects the connection workability and the ease of construction.
-
(6)
The shear modulus () of the resilient layers also has a significant effect on connection behaviour. An increase in shear moduli causes an increase in ultimate displacement and load capacity of the connection until a limit is reached after which the capacity reduces with increased shear moduli.
-
(7)
Generally, the proposed connections (C1 and C2) perform better than the traditional bolted connection C3 due to additional yielding and energy dissipation from the steel connector plate (in C1 and C2) and damping from the resilient layers (C2). As C2 showed increased ductility and energy dissipation with certain variations in parameters, it can be recommended for use in steel modular structures for seismic resistance.
Declarations
Author contribution statement
Sukhi V. Sendanayake: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
David P. Thambiratnam & Nimal Perera: Conceived and designed the experiments; Wrote the paper.
Tommy Chan & Sanam Aghdamy: Contributed reagents, materials, analysis tools or data; Wrote the paper.
Funding statement
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Competing interest statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
References
- 1.Lawson R. Developments in pre-fabricated systems in light steel and modular construction. Struct. Eng. 2005;83(6):28–35. [Google Scholar]
- 2.Lawson M., Ogden R., Goodier C. CRC Press; 2014. Design in Modular Construction. [Google Scholar]
- 3.Fathieh A., Mercan O. Structures Congress 2014. ASCE; 2014. Three-dimensional, nonlinear, dynamic analysis of modular steel buildings. [Google Scholar]
- 4.Gunawardena T., Ngo Tuan, Mendis Priyan, Aye Lu, Crawford Robert, Alfano Jose. 2013. A Holistic Model for Designing and Optimising Sustainable Prefabricated Modular Buildings. [Google Scholar]
- 5.Generalova E.M., Generalov Viktor P., Kuznetsova Anna A. Modular buildings in modern construction. Procedia Eng. 2016;153:167–172. [Google Scholar]
- 6.Lawson R.M., Richards J. Modular design for high-rise buildings. Proc. Inst. Civil Eng.-Struct. Buildings. 2010;163(3):151–164. [Google Scholar]
- 7.Park H.K., Ock J.-H. Unit modular in-fill construction method for high-rise buildings. KSCE J. Civil Eng. 2015:1–10. [Google Scholar]
- 8.Ramaji I.J., Memari A.M. Proceedings of the 1st Residential Building Design and Construction Conference. 2013. Identification of structural issues in design and construction of multi-story modular buildings. [Google Scholar]
- 9.Farnsworth D. 2014. Modular Building Unit Connection System. Google Patents. [Google Scholar]
- 10.Lawson R., Ogden R. ‘Hybrid’light steel panel and modular systems. Thin-Walled Struct. 2008;46(7):720–730. [Google Scholar]
- 11.Annan C., Youssef M., El Naggar M. Seismic vulnerability assessment of modular steel buildings. J. Earthq. Eng. 2009;13(8):1065–1088. [Google Scholar]
- 12.Yu C. Vol. 65. Woodhead Publishing; 2016. (Recent Trends in Cold-Formed Steel Construction. Woodhead Publishing Series in Civil and Structural Engineering). [Google Scholar]
- 13.Johnson R.B., Mahamid M. Proc., ASCE Structures Congress. ASCE; 2010. Design of steel connections for tie forces. [Google Scholar]
- 14.Gunawardena T. 2016. Behaviour of Prefabricated Modular Buildings Subjected to Lateral Loads. [Google Scholar]
- 15.Gunawardena T., Ngo T., Mendis P. Behaviour of multi-storey prefabricated modular buildings under seismic loads. Earthquake Struct. 2016;11(No. 6) [Google Scholar]
- 16.Rahmani Samani H. The effects of dynamic loading on hysteretic behavior of frictional dampers. Shock Vib. 2014;2014 [Google Scholar]
- 17.Samani H.R., Mirtaheri M., Zandi A.P. Experimental and numerical study of a new adjustable frictional damper. J. Constr. Steel Res. 2015;112:354–362. [Google Scholar]
- 18.Jangid R., Kelly J. Base isolation for near-fault motions. Earthq. Eng. Struct. Dyn. 2001;30(5):691–707. [Google Scholar]
- 19.CEN, prEN . 2003. 1998-1-Eurocode 8: Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions and Rules for Buildings. [Google Scholar]
- 20.ISDAG . 2012. Bolted Connections - I.www.steel-insdag.org cited 2017; Available from: [Google Scholar]
- 21.Hu Y. Cyclic tests of fully prefabricated concrete-filled double-skin steel tube/moment-resisting frames with beam-only-connected steel plate shear walls. Thin-Walled Struct. 2019:106272. [Google Scholar]
- 22.Hu Y. Experimental seismic performance of CFDST-steel beam frames with different construction details. J. Constr. Steel Res. 2019;162:105736. [Google Scholar]
- 23.Hu Y. Seismic behavior of concrete-filled double-skin steel tube/moment-resisting frames with beam-only-connected precast reinforced concrete shear walls. Arch. Civil Mech. Eng. 2019;19(4):967–980. [Google Scholar]
- 24.SA A. Standards Australia; Sydney: 1998. 4100-1998 Steel Structures. [Google Scholar]
- 25.Wardenier J., Packer J.A., Zhao X.L., Van der Vegte G.J. Bouwen met Staal Rotterdam; The Netherlands: 2002. Hollow Sections in Structural Applications. [Google Scholar]
- 26.AS/NZS1163 . 2016. Cold-formed Structural Steel Hollow Sections. [Google Scholar]
- 27.Annan C., Youssef M., El Naggar M. Experimental evaluation of the seismic performance of modular steel-braced frames. Eng. Struct. 2009;31(7):1435–1446. [Google Scholar]
- 28.Annan C., Youssef M.A., El-Naggar M.H. Proceedings of the Ninth Canadian Conference on Earthquake Engineering. Canada; Ottawa, ON: 2007. Seismic performance of modular steel braced frames. [Google Scholar]
- 29.Maggi Y., Gonçalves R.M., Leon R.T., Ribeiro L.F.L. Parametric analysis of steel bolted end plate connections using finite element modeling. J. Constr. Steel Res. 2005;61(5):689–708. [Google Scholar]
- 30.Abaqus V. Dassault Systemes Simulia Corporation; 2014. 6.14 Documentation. [Google Scholar]
- 31.Chen W.-F., Han D.-J. J. Ross publishing; 2007. Plasticity for Structural Engineers. [Google Scholar]
- 32.Kim B., Lee Seong Beom, Lee Jayone, Cho Sehyun, Park Hyungmin, Yeom Sanghoon, Park Sung Han. A comparison among Neo-Hookean model, Mooney-Rivlin model, and Ogden model for chloroprene rubber. Int. J. Precis. Eng. Manuf. 2012;13(5):759–764. [Google Scholar]
- 33.Shahzad M., Kamran Ali, Siddiqui Muhammad Zeeshan, Farhan Muhammad. Mechanical characterization and FE modelling of a hyperelastic material. Mater. Res. 2015;18(5):918–924. [Google Scholar]
- 34.Bradley G., Chang P., McKenna G. Rubber modeling using uniaxial test data. J. Appl. Polym. Sci. 2001;81(4):837–848. [Google Scholar]
- 35.Kim J., Yoon J.-C., Kang B.-S. Finite element analysis and modeling of structure with bolted joints. Appl. Math. Model. 2007;31(5):895–911. [Google Scholar]
- 36.Kim T.S., Kuwamura H. Finite element modeling of bolted connections in thin-walled stainless steel plates under static shear. Thin-Walled Struct. 2007;45(4):407–421. [Google Scholar]
- 37.BS EN 1993-1-8 . 2005. Eurocode 3: Design of Steel Structures - Part 1-8: Design of Joints. Authority: The European Union Per Regulation 305/2011, Directive 98/34/EC, Directive 2004/18/EC. [Google Scholar]
- 38.Syam A., Chapman B. 1996. Design of Structural Steel Hollow Section Connections Volume 1: Design Models. [Google Scholar]
- 39.Federal Emergency Management Agency (FEMA) 461. Federal Emergency Management Agency; Washington, DC: 2007. [Google Scholar]
- 40.Mander J.B., Priestley M.J., Park R. Theoretical stress-strain model for confined concrete. J. Struct. Eng. 1988;114(8):1804–1826. [Google Scholar]