Early osteointegration evaluation of porous Ti6Al4V scaffolds designed based on triply periodic minimal surface models

Abstract

Background

The graded porous structures were designed using triply periodic minimal surfaces models to mimic the biomechanical properties of bone. The mechanical properties and bone formation ability were evaluated to explore the feasibility of the design method in bone tissue engineering.

Methods

The scaffolds were designed using a P-surface with different pore sizes. All materials were fabricated using 3D printing technology and the mechanical properties were tested by an electronic universal testing device. The biomechanical properties were then analyzed by finite element method, while the ontogenesis of the material in vivo was examined by implanting the scaffolds for five weeks in pigs.

Results

According to the obtained results, the pore size ranged between 100 μm to about 700 μm and porosity were around 49.54%. The graded porous architectures can decrease the stiffness of implants and reduce the stress shielding effect. In addition, these porous structures can stimulate bone ingrowth and achieve a stable interface between implants and surrounding bone tissues after 5 weeks' implantation. The micro-CT results also demonstrated the obviously bone formation around all the porous structures.

Conclusion

To sum up, the triply periodic minimal surfaces based graded porous structure is effective in decreasing the stress shielding effect, promoting early osteogenesis and osteointegration. This is the first research to explore the effect of this kind of porous structures on bone formation in vivo where the obtained results supported the previous theoretical research on the application potential in bone tissue engineering.

The translational potential of this article

Porous architecture designed using triply periodic minimal surface models can achieve gradually changed pore size and appropriate porosity for bone regeneration. This kind of structure can mimic the Young’s modulus of natural bone tissue, improve the stress transmission capability and dismiss the stress shielding effect. It also can stimulate the early bone integration in vivo and enhance the binding force between bone and implants, which may bring a new design method for orthopaedic implants and their surface structure.

Introduction

The bone has a prominent role in motion, support and protection of the human body. With the increased population growth and increased life expectancy, a rapid increase in musculoskeletal disorders, fractures and osteoporosis, which gives rise to bone-related medical treatment, has been observed, especially in elderly populations [1], [2] Over the past decades, a number of artificial implants have been developed, including artificial bones and joints, plates, screws and dental implants. Metallic biomaterials such as stainless steel (Young's modulus: 190 GPa), cobalt–chromium alloys (Young's modulus: 230 GPa) and tantalum (Young's modulus: 187 GPa) have been used to fabricate implant devices [3], [4]. Compared with the aforementioned metals, titanium (Young's modulus: 110 GPa) is a low modulus metal, with nonallergenic qualities and excellent biocompatibility, which has been applied in many orthopaedic and dental applications. Nevertheless, this material is elastic, has low wear resistance and is stiffer than the cortical bone (Young's modulus: 7–30 GPa) [5]. The mismatch of Young's moduli between implants and bone tissues is vital in stress shielding, a universal phenomenon after implantation, which results in the nonhomogeneous stress transfer between the implants and the surrounding bone tissue. As a result, the bone tissues can become atrophic and gradually lose the load-bearing capability, which may cause osteoporosis and fracture around the implants [6]. In addition, the bone resorption around the implants can lead to an unstable interface between bone and implants, which can be regarded as the high risk for early implantation failure [7], [8]. To address these issues and to construct a long-lasting implant, the porous design is introduced to mimic the elasticity modulus and yield the strength of the nature bone [9]. The modulus is significantly lower in the porous structure, and the stress shielding may be alleviated. The interconnected pores generally result in significant osteointegration and better fixation of implants [10], [11], [12]. Moreover, the porous structure can provide interfacial adhesion between implants and the surrounding bone, which enables an enhanced bonding and a shorter healing time. The exchange of nutrients and vascularisation are also improved with appropriate porous characteristics (pore size, pore shape and pore size distribution) [13], [14], [15]. Previous studies have shown that the titanium scaffolds with a pore size ranging from 100 to 500 μm and a porosity of approx. 50% are ideal for bone ingrowth. Although the higher porosity and pore size, such as 500–1000 μm, are favourable for bone ingrowth, the strength of the implant is constantly decreasing [12]. Therefore, designing a porous structure with adequate modulus is critical for the application of titanium alloys in bone tissue repair.

Triply periodic minimal surfaces (TPMSs), which can exhibit periodicity in three independent directions in three-dimensional (3D) space, have been regarded as an effective tool for designing scaffolds with gradual and regular porous structure [9], [16]. Because of its specific design, the porosity and the pore architecture can be generated by defining weight functions and spatially dependent porosity function [17]. The porous structure with minimal surfaces can be realised using this method. The concept of minimal surface defined in differential geometry of surfaces is the surface with a mean curvature of zero that can be indefinitely extended in three periodic directions [18]. Coincidentally, the mean curvature of trabecular bone is close to zero, which may promote the bone tissue regeneration on such surfaces [19]. Besides the comparability of curvature, TPMS-based designs have some other advantages. For example, the cell differentiation is more active because of cellular interconnectivity with the complex inner structure [20]. In addition, compared with the typical lattice network structure, the stress concentration can be decreased because of the smooth joints and the gradual porous design [17]. These special characteristics make TPMS-based designs appropriate for fabricating bone scaffolds or the surface structure of implants.

Despite the structure design, the production of scaffolds has an important aspect in fabrication process and includes accurate control of pore size, pore distribution and pore interconnectivity. Nevertheless, the fine and stable physicochemical properties make titanium alloys difficult to match with porous structures. Traditional fabrication techniques such as powder sintering, plasma spray coating, fibre bonding and phase separation allow the regulation of only few parameters, such as porosity and pore size [21]. The development of 3D printing technology has significantly improved the controllability of the network architecture. The most common 3D printing techniques used for fabrication of titanium alloys are selective laser melting (SLM), selective laser sintering, electron beam melting and laser engineered net shaping [22], [23]. Numerous studies have used SLM and electron beam melting techniques to fabricate porous titanium scaffolds with the mechanical properties of different designs, such as permeability, fatigue and moduli, that have been thoroughly explored using in vitro testing [17], [18], [24]. Nevertheless, only a few studies have explored the effect of materials on bone tissue in vivo, as well as the bone integration ability in the host.

In the present study, three kinds of scaffolds were designed using a P-surface to form different pore sizes and pore distributions to mimic the physical properties of natural bone. The stress transmission abilities were analysed by finite element (FE) simulation. SLM was used for production of porous Ti6Al4V scaffolds. The titanium powder can be completed melted under the high-power solid-state lasers and form 3D entities after cooling [25]. The internal and external shape of 3D printing products can be closer to the computer-aided design model, ensuring that the scaffold pore characteristics can meet the requirements of bone formation. Finally, an in vivo study on Bama mini pigs was conducted to evaluate the osteointegration at the early stage of bone healing process.

Materials and methods

The experiment was divided into three parts: scaffold design, FE simulation and in vivo testing. All methods in this study were carried out in accordance with relevant guidelines and regulations. All experimental protocols in this study were approved by the Ethics Committee of Drum Tower Hospital affiliated to the Medical School of Nanjing University (Nanjing, China).

Scaffold design based on the TPMS modelling method

After extracting the isosurface by the marching cube method, the corresponding stereolithography (STL) model was conveniently extracted. The typical P-, D- and G-surfaces of the TPMS are triangulated and separately visualised, as shown in Figure 1A and B. The TPMS coordinates were defined by the Weierstrass formula [26], [27], as shown in formula (1):

$$\{\begin{array}{c}x=Re\underset{\omega 0}{\overset{\omega 1}{\int }}{e}^{i\theta }\left(1-{\omega }^2\right)R\left(\omega \right)d\omega \\ y=Re\underset{\omega 0}{\overset{\omega 1}{\int }}{e}^{i\theta }\left(1+{\omega }^2\right)R\left(\omega \right)d\omega \\ z=Re\underset{\omega 0}{\overset{\omega 1}{\int }}{e}^{i\theta }\left(2\omega \right)R\left(\omega \right)d\omega \end{array}$$ (1)

where ω represents a complex variable, θ is an angle called Bonnet and $R\left(\omega \right)$ represents a function that varies with different surfaces. For P-, D- and G-surfaces of the TPMS, $R\left(\omega \right)$ can be expressed by the formula (2):

$$R\left(\omega \right)=\frac{1}{\sqrt{1-14{\omega }^4+{\omega }^8}}$$ (2)

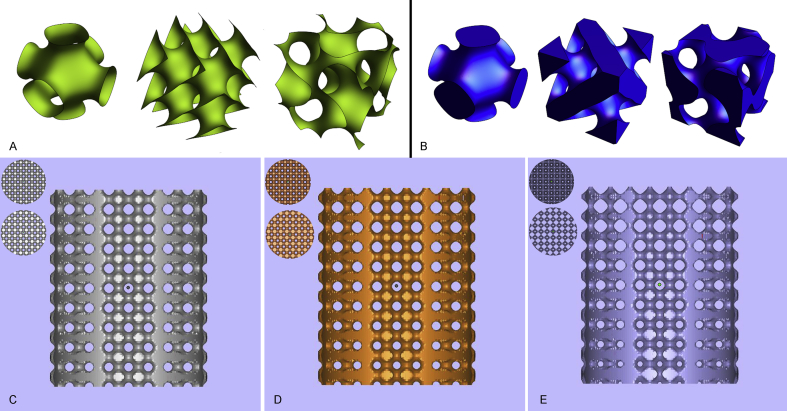
Figure 1.

General view of TPMS-based models. (A) Triangulation of a nonclosed implicit surface: P-surface, D-surface and G-surface. (B) Triangulation of typical closed implicit surface: P-surface, D-surface and G-surface. The cylindrical graded porous structure with the pore diameter distribution range from (C) 300–500 μm, (D) 200–600 μm and (E) 100–700 μm. The top and bottom view of each structure is shown in the upper left corner. TPMS = triply periodic minimal surface.

Compared with the parametric TPMS, the approximate TPMS periodic surface is generally defined and can be expressed using the formula (3):

$$\varnothing \left(r\right)=\sum _{k=1}^K{A}_{k}cos\left[\frac{2\pi \left(h_k\cdot r\right)}{{\lambda }_k}+p_k\right]=C$$ (3)

where γ represents position vectors of Euclidean space, $A_k$ represents amplitude factor, $h_k$ is the kth grid vector in the reciprocal space, ${\lambda }_k$ represents the periodic wavelength, $p_k$ represents the phase offset and C is a constant.

The control of the TPMS modelling is adjusted by the trigonometric parameters in the function. As shown in Eq. (3), the parameters involved in the surface modelling were $A_k$, $h_k$, ${\lambda }_k$, $p_k$ and the standard value $\varnothing {\left(r\right)}_0=C$. In this study, the P-surface was chosen as the porous scaffold unit to fabricate porous structures. Herein, several different porous scaffolds were obtained by different parameter values assigned by$C$, as shown in Table 1.

Table 1.

Mathematical characterisation of P-surface graded structures and their relative density.

TPMS	Periodic trigonometric function	$C$	Relative density
P	$\varnothing \left(r\right)=\cos \left(2\pi x\right)+\cos \left(2\pi y\right)+\cos \left(2\pi z\right)+C$	0.04z	Graded 45–55%
		0.08z	Graded 40–60%
		0.16z	Graded 30–70%

TPMS = triply periodic minimal surface.

Eventually, we defined multigroup porous structures (with size: Φ8 × 10 mm) by defining the scaffolds according to the constitutive equations presented in Table 1. The change rate in the size of the porous structures along the z-axis was different. The structure of the three types of porous scaffolds is shown in Figure 1C–E.

FE simulation

The load and boundary constraints

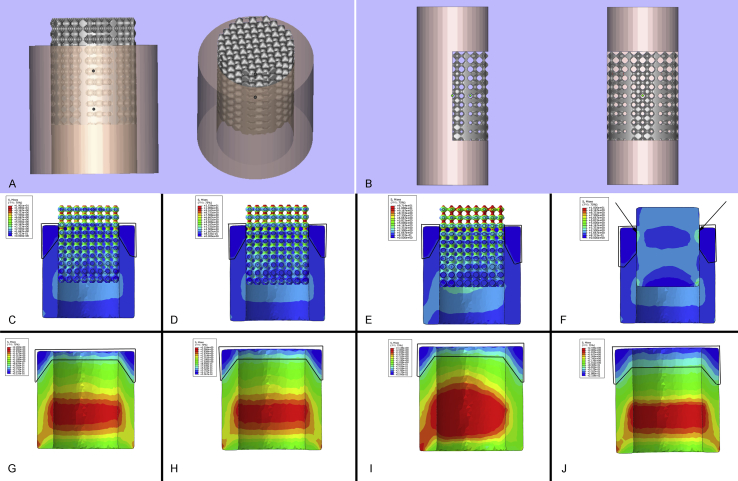
We herein designed two FE simulation tests. The first and second FE simulation tests were designed to observe the stress transmission and the stress shielding of the structures, and the assembly methods are shown in Figure 2A and B. In the first test, the porous scaffolds and the block were plugged into a hollow base, which is defined as the material properties of cortical bone. The bottom of the hollow base was immobilised, and a vertical force (100 N, a quarter of body weight of Bama mini pigs) was applied on the top of the porous scaffold and the block. The surfaces between the base and porous scaffold/block structure were defined as a kinematic constraint and allowed the plate to uniquely move in the vertical direction.

Figure 2.

The stress transmission result of FE simulation. The assembly methods of (A) the first FE simulation test and (B) the second FE simulation test. The section views of stress transmission in (C) D1, (D) D2, (E) D3 and (F) the nonporous block structure. The threshold was set to 10 MPa in the above 4 stress nephograms. The position of Region 1 is indicated by the frames, and the stress concentration is pointed out by arrows in (F). The scaffold part was removed, and the section views of the base in (G) D1, (H) D2, (I) D3 and (J) the nonporous block structure are demonstrated. The threshold was set to 2 MPa in the above 4 stress nephograms. The position of Region 2 is indicated by the frames. FE = finite element.

In the second test, all the scaffolds were divided into two halves; one of the halves was embedded into the cylinder base. The bottom of the cylinder base was immobilised, and a vertical force (100 N, a quarter of body weight of Bama mini pigs) was applied on the top of the base. The surfaces between the scaffold and base were defined as the first FE simulation test.

Furthermore, the elastic modulus of the porous structure was simulated by Abaqus/Explicit FE code (SIMULIA, Rhode Island, USA) with a compression speed of 0.5 mm/min, and the load applied on the samples was increased to 100 KN at last.

FE model operation

The geometry of porous scaffolds was constructed and then exported as an STL file using Wolfram Mathematica 11.0 software (Wolfram Research, IL, USA). The assembly units used in the two FE simulation tests were made using Materialise Magics 19.0 software (Materialise, Leuven, Belgium). All the data were exported as STL files, and the meshing was operated using Materialise 3-matic 11.0 software (Materialise, Leuven, Belgium). The finished models were imported and assembled using Abaqus 2017 (Dassault Systemes, France). The porous scaffold, the nonporous block and the bases were considered isotropic and linear elastic. The scaffold and the block were defined as Ti6Al4V alloys, and the bases were defined as bone material. The material parameters were selected from the literature, as shown in Table 2 [28], [29].

Table 2.

The properties of materials used in FE simulation.

	Density (kg/m3)	Young's modulus (GPa)	Yield strength (MPa)	Poisson's ratio
Ti6Al4V	4430	105	830	0.31
Bone	1700	7.8	85	0.3

FE = finite element.

In vivo testing

3D printing and scaffold preparation

The porous scaffolds with a diameter of 8 mm and height of 10 mm were used for in vivo testing. Those materials were fabricated using an SLM 3D printing device (EOSINT M280; EOS Ltd., Munich, Germany). The optimal parameters of SLM process used in the 3D printing are expressed in Table 3. The surface topography of the 3D printing scaffolds was observed using a scanning electron microscope (Hitachi Ltd., Tokyo, Japan). The porosity of the scaffolds was calculated by using the formula, $P=\frac{\text{V}0-\text{V}}{\text{V}0}\times 100\%$. Here, V₀ represents the apparent volume of the solid Ti6Al4V cylinder, and V represents the absolute volume of the porous scaffolds. All the numerical values of the volume were obtained using Magics 19.0 software. According to the standard (ISO 13314:2011 [30]) for compression of porous and cellular metals, the compression modulus of the scaffold was tested using an electronic universal testing device (CMT5105; MTS Systems Corp., MN, USA) equipped with a 100-kN load cell and a compression speed of 0.5 mm/min. Each kind of scaffold was tested on three samples. All the implants were ultrasonically cleaned three times using acetone, ethanol and deionised water before use.

Table 3.

The 3D printing parameters.

Laser power (W)	Scan speed (mm/s)	Hatch spacing (mm)	Layer thickness (mm)	Laser focus (mm)	Atmosphere
180	1350	0.1	0.03	0.08	Argon

3D = three-dimensional.

Experimental animals and operation procedure

A total of 8 male Bama mini pigs, weighting 25.55 ± 0.84 kg, were randomly divided into four groups (two pigs for each group). All the animals were housed in an environment with a temperature of 22 ± 1 °C, relative humidity of 50 ± 1% and light/dark cycle of 12/12 h. In addition, all animal studies (including the euthanasia procedure which was performed using lidocaine and propofol) were carried out in compliance with the regulations and guidelines of the Ethics Committee of Drum Tower Hospital affiliated to the Medical School of Nanjing University and conducted according to the Animal Research: Reporting of In Vivo Experiments (ARRIVE) and the Institutional Animal Care and Use Committee (IACUC) guidelines.

All the implants were implanted at the distal region and proximal region of the right tibia bone. Cefuroxime sodium was intramuscularly injected for 3 d after operation to avoid infection. All animals were killed at the 5th week after operation, to measure the effect of early bone integration.

Micro–computed tomography analysis

The tibia bones were harvested and scanned using a M1001 micro–computed tomography (CT) system (Hiscan Information Technology, Jiangsu, PRC) at 90 kV, 89 μA, a field of view of 63.9 mm and a nominal isotropic image voxel size of 62.4 μm. The obtained images were converted to Digital Imaging and Communications in Medicine (DICOM) files for the following analysis. The 3D reconstruction of the scaffold and newborn bone were operated using MIMICS 19.0 software (Materialise, Leuven, Belgium). To avoid the impact of metal artefact, we used high voltage and the same threshold value to segment the titanium and bone tissue.

Biomechanical testing

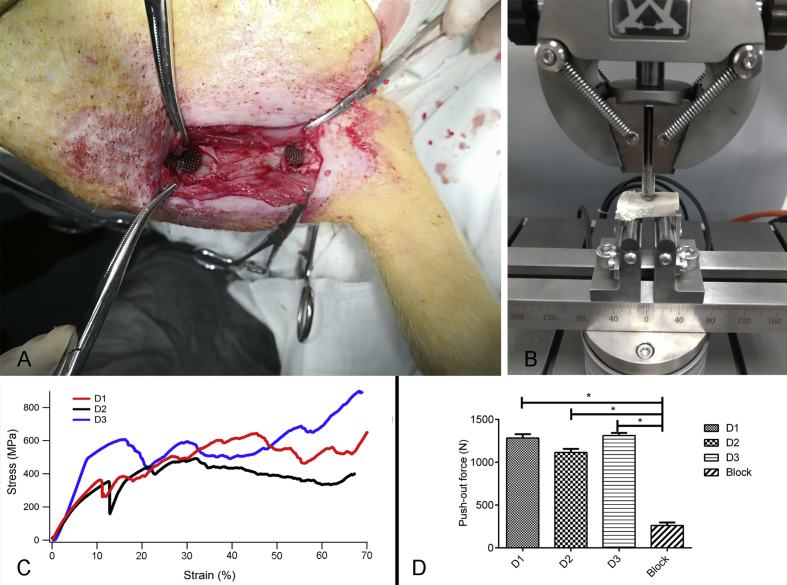
The samples used for biomechanical testing (push-out test) were cut into 30-mm lengths, and soft tissues attached to the samples were removed before testing. The push-out tests were carried out using a universal mechanical testing machine (ElectroPlus E3000; Instron, MA, USA) with a bending testing program. A loading rate of 0.1 mm/min was used to gradually separate the implant and the bone tissue, and the maximum failure load was recorded as the push-out force.

Histological analysis

After performing micro-CT analysis, the harvested femurs were fixed overnight in formalin at 4 °C. The samples were then rinsed with distilled water, dehydrated through graded alcohols and embedded in polymethyl methacrylate without decalcification. Thin sections of 30-μm thickness were cut using a diamond-coated saw (310 CP; EXAKT, Germany). The sections were stained with Goldner's trichrome and then observed using a fluorescence microscope (Olympus Corp., Tokyo, Japan).

Statistical analysis

The statistical analysis and exponential curve fitting were performed using SPSS 19.0 software (SPSS Inc., IL, USA) and IGOR Pro 6.12 software (WaveMetrics Inc., OR, USA). Data were presented as mean ± standard deviation and evaluated using an unpaired Student t-test. A p-value < 0.05 was considered statistically significant.

Results

Structure characteristics

The pore structure of three porous metal titanium parts with different pore structures was interconnected, and the diameter of the pore ranged from 100 μm to about 700 μm. The pore diameter distribution range of Model 1 was 300–500 μm (defined as D1), of Model 2 was 200–600 μm (defined as D2) and of Model 3 was 100–700 μm (defined as D3). Besides, the pore structure of D1 was relatively gentle from the upper to lower part; the pore size of D2 was gradually reduced from top to bottom, while the pore size of D3 was very obvious from the upper to lower part, and the diameter of the upper pore was the largest of all the printing parts. These structural forms corresponded exactly with the design idea of linear gradual change of the pore structure considered in the design of the model, and the porosity of D1 to D3 was 49.53%, 49.54% and 49.56%, respectively.

FE simulation test

The colour changes (from red to dark blue) represented the stress variation from large to small on the stress nephogram. Because the stress on the scaffolds was significantly higher than the base, the threshold value was adjusted after the part of the scaffold was removed. The results of Figure 2C–F demonstrated the stress transmission ability of porous and solid scaffolds. The stress gradually decreased on all the porous structures. However, the stress concentration was observed on the solid scaffold (as showed with the arrow in Figure 2F). In addition, the dark blue area around the top of the base increased (the area represented by frames in Figure 2C–F, defined as Region 1; the values are shown in Table 4), meaning that the stress applied on the base was decreased. The same results can be found in Figure 2G–J. The area range from light blue to dark blue around the top of the solid scaffold was larger than that of the three porous scaffolds (the area represented by frames in Figure 2G–J, defined as Region 2; the values are shown in Table 4).

Table 4.

The area of stress distribution.

	D1 (mm2)	D2 (mm2)	D3 (mm2)	Block (mm2)
Region 1	9.538	10.114	10.286	14.652
Region 2	22.938	25.346	26.947	47.822

The results related to the stress shielding effect of the porous structure are shown in Figure 3A–H. The colours around the implantation region were obviously different between TPMS architectures and the solid scaffold. According to the colour changes, we concluded that the stress shielding effect was notably reduced in the TPMS-based porous structures. In the D1 and D2 groups, the inner sides of the base which were directly connected with the scaffolds were light blue, and the outer sides were green, which indicated that the stress around this region ranged from 1.879 MPa to 1.169 MPa (mean values were 1.715 MPa and 1.731 MPa). In the D3 group, the correlated region was red and green, which indicated that the stress was above 1.557 MPa (mean value was 1.998 MPa). In the solid scaffold group, the region was light blue and dark blue, indicating that the stress was from 0.564 MPa to 1.704 MPa (mean value was 1.456 MPa).

Figure 3.

The stress shielding result of FE simulation. The general views of the stress shielding result in (A) D1, (B) D2, (C) D3 and (D) the nonporous block structure. The threshold was set to 3.3 MPa in the above 4 stress nephograms. The scaffold part was removed, and the views of the base in (E) D1, (F) D2, (G) D3 and (H) the nonporous block structure are demonstrated. The threshold was set to 3.3 MPa in the above 4 stress nephograms. The stress variation is indicated by arrows in (G) and (H). FE = finite element.

Porous scaffold characterisation

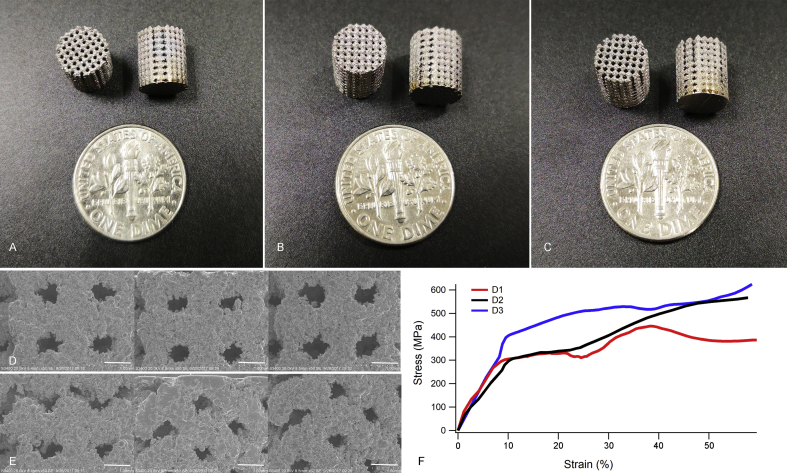
The general view of the three types of porous scaffolds is shown in Figure 4A–C. The cylinder scaffolds with a diameter of 8 mm and height of 10 mm were fabricated for the subsequent implantation experiment. The surface topography of the top side and lateral side observed by the scanning electron microscope is shown in Figure 4D and E. The pore size was similar to our previous design, and the surfaces were irregular. The compressive stress–strain curve calculated by FE simulation is shown in Figure 4F; the values of Young's modulus and yield strength are shown in Table 5.

Figure 4.

The results of 3D printing. The general views of 3D printing entities. The cylindrical scaffolds with a diameter of 8 mm and height of 10 mm were made. The pore size and the changing rate were obviously different in (A) D1, (B) D2 and (C) D3. The SEM micrographs show the surface morphology of the (D) top views and (E) the lateral views of the three groups (Scale bar: 500 μm). (F) The strain–stress curve calculated by FE simulation. 3D = three-dimensional; FE = finite element; SEM = scanning electron microscope.

Table 5.

Scaffold properties.

	D1	D2	D3	Block
Young's modulus by FE simulation (GPa)	3.45	2.59	4.064	123.86
Young's modulus by compressive testing (GPa)	3.505 ± 0.17	3.073 ± 0.33	7.326 ± 0.24	118.89 ± 5.73
Yield strength by FE simulation (MPa)	338.346	331.324	494.684	1135.59
Yield strength by compressive testing (MPa)	363.124 ± 11.29	353.359 ± 8.63	606.013 ± 17.51	1170.74 ± 22.68
Maximum failure load by compressive testing (MPa)	1282.50 ± 45.45	1114.62 ± 42.13	1312.31 ± 31.28	1358.34 ± 19.77

FE = finite element.

The implantation surgery and the biomechanical test are shown in Figure 5A and B. The compressive stress–strain curve tested using the universal mechanical testing machine is demonstrated in Figure 5C. The results of biomechanical testing are shown in Figure 5D. The maximum failure load of the porous scaffold group is significantly higher than that of the nonporous block structure; values are shown in Table 5 (P < 0.05). These results show that the strength of binding between the scaffold and the bone interface can be enhanced in all porous structures.

Figure 5.

The mechanical test and the in vivo test. (A) The implantation position on the tibial bone of the Bama mini pig. (B) The biomechanical test was carried out using a universal mechanical testing machine. (C) The strain–stress curve of the compression test using a universal mechanical testing machine. (D) The result of the biomechanical test, the maximum failure load was regarded as the push-out force, with *P < 0.05.

Early osteointegration evaluation

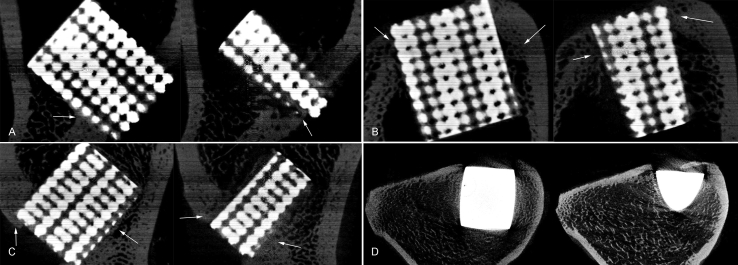
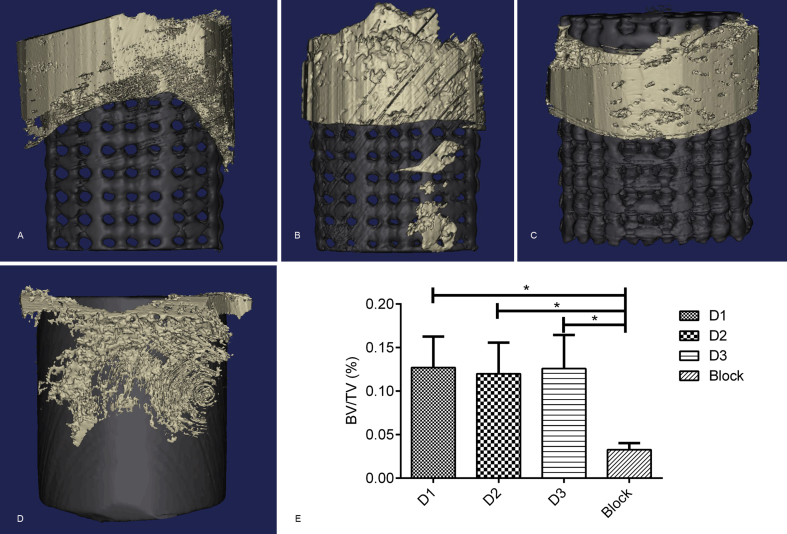
All pigs recovered well from anaesthesia and the operative procedure. No implant dislocation and incision infection occurred during the experiment. Five weeks after implantation, bone formation was observed in both groups through micro-CT; yet, significant differences were found in the bone volume between the TPMS-based graded porous structures and the nonporous block structure. Moreover, two sections of each group were selected to examine the bone integration effect of each scaffold (one section was located in the middle, and the other one was located outside). Despite the interference of metal artefacts, we found some active osteogenesis effect around all the porous structures in every section (represented by arrows in Figure 6A–C). For the nonporous block group, a significant gap between the implant and bone was observed around the scaffold (Figure 6D). The 3D reconstruction results are shown in Figure 7A–D; significant differences were found in the bone volume between TPMS-based scaffolds and the nonporous block structure. The bone volume/total volume was 12.71 ± 3.556%, 11.99 ± 3.581%, 12.84 ± 3.874% and 3.28 ± 0.752%, respectively (Figure 7E).

Figure 6.

The micro-CT results of (A) D1, (B) D2, (C) D3 and (D) the nonporous block structure. The center section and the lateral section are demonstrated, and the arrows represent the region with active osteogenesis effect. CT = computed tomography.

Figure 7.

The 3D reconstruction of (A) D1, (B) D2, (C) D3 and (D) the nonporous block structure. The black part represents the scaffold, and the silver part represents the newborn bone tissue.(E) The bone volume was notably different between TPMS-based structures and the nonporous block structure, and the BV/TV is shown. 3D = three-dimensional; BV = bone volume; TPMS = triply periodic minimal surface; TV = total volume.

The position of the stained sections is shown in Figure 8A. In Goldner's trichrome staining, the blue-green colour represents the regenerating bony tissue. The general view of each section is demonstrated on the top. Our results suggested that the interfaces between bone and implants are more stable in TPMS-based porous scaffold groups. From the magnifying view of Figure 8B, a clear gap can be seen between the bone (defined as B in the figure) and scaffold (defined as S in the figure). Nevertheless, in Figure 8C–E, it is obvious that the newborn bone tissues closely surround the scaffolds.

Figure 8.

The histological results. (A) The position of sections. The Goldner's trichrome staining of (B) D1, (C) D2, (D) D3 and (E) the nonporous block structure. Scale: 50 μm. The general view of each section is demonstrated on the top. B represents the bone tissues, and S represents the scaffold.

Discussion

In the present study, we designed three porous structures using TPMS models, and we evaluated the early osteointegration capability of these structures in vivo. Some previous studies have explored the mechanical properties, permeability and fatigue behaviour of different TPMS-based architectures and theoretically confirmed the feasibility of the application in tissue engineering [31], [32], [33], [34]. Nevertheless, only a few studies have been carried out on real animals. According to our experiments in the pig model, the bone ingrowth can be observed at the periphery of all the graded porous scaffolds few weeks after implantation. As for the solid Ti6Al4V scaffold group, although the implantation region was near the metaphysis and the surrounding was full of trabecular bone, the bone formation was still weak around the implants. The biomechanical test also supported this phenomenon; the push-out force of TPMS-based groups can reach as high as 1100 N–1300 N after only 5 weeks of implantation, that were 5-fold to 6-fold versus the nonporous block group. Compared with previous studies which examined different kinds of titanium implants (200–800 N at 8–24 weeks) [35], [36], [37], the bending force between bone and TPMS-based scaffolds in our study was much higher at the early stage of implantation. These results can be explained through the advantages of the TPMS-based porous architectures. The unique design method enables the porous scaffold to mimic the natural bone, thus improving its biomechanical and microstructure properties. The larger pore interconnections of the TPMS-based scaffolds have shown to induce faster cell proliferation by providing a sufficient supply of oxygen and nutrients for cells located in the centre of the scaffold [32]. In addition, the interaction between the porous structures and the bone material was analysed by FE simulation. The equivalent stiffness of the three structures was designed to mimic the bone tissue, led to a superior stress transmission ability and significantly decreased stress shielding effect.

The curvature of the surface on which cells reside in particular has been proved to play a fatal role in determining the tissue regeneration rate [18], [38]. Compared with convex and planar surfaces, the bone tissue is more likely to grow on the concave surface because of the existence of surface tensile stresses that may prevent tissue from going onto the convex surface [39], [40]. This means that lower curvature results in higher levels of bone tissue regeneration. Herein, the P-surface was chosen as the cell unit because of its bony structure. To enhance the interconnectivity, a nonclosed implicit architecture has replaced the typical closed implicit one. Because of the minimal curvature and the complexity of the interconnected structure, the TPMS-based porous scaffolds demonstrated the magnificent osteoconductive and osteoinductive characteristics for bone remodelling and bone ingrowth during the healing process.

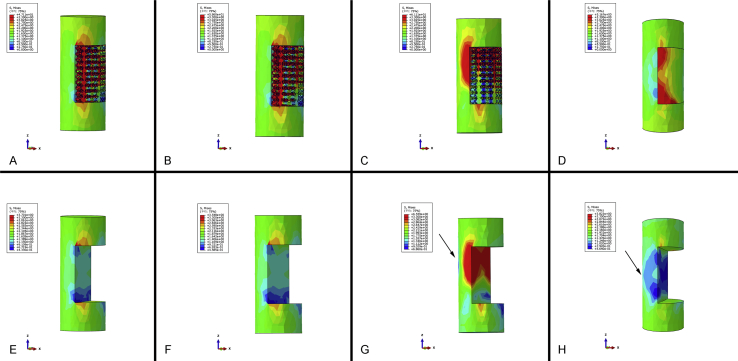
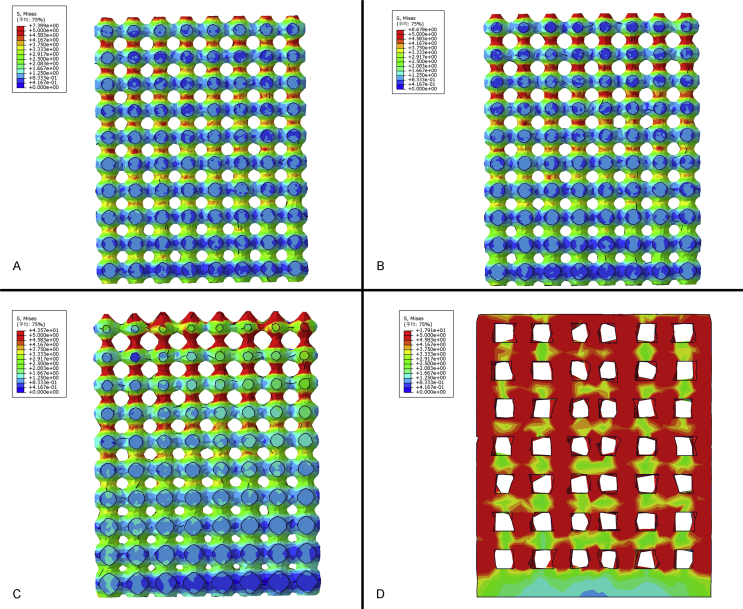
The natural bone has a graded structure, the outer cortical bone is solid and dense, and the inner cancellous bone is spongy honeycombed structure [41], [42]. There are limitations in conventional computer-aided design methods to control the spatial distributions of heterogeneous pore architectures. In TPMS-based models, we can easily achieve the gradual changing of the pore size along the z-axis by altering the constant in the function. Moreover, the continuous change of Young's modulus can be realised. Compared with the homogeneous porous structure, the biomechanical properties appear to be more suitable for implantation. As shown in Figure 9, a supplementary FE simulation about the internal stress transmission of scaffolds was processed. A vertical force of 50 N was applied on the top of each scaffold, and the results of stress distribution were significantly different between gradual and homogeneous structures with the threshold of 5 MPa. The peak value of stress in the D1 and D2 structures was 7.389 MPa and 8.678 MPa, respectively. In the D3 structure, this value peaked at 43.57 MPa. The peak value just appeared at the bottom and gradually decreased below the threshold because of the continuous curvature of their struts. But the stress was much higher on the homogeneous structure. The peak value of stress was 17.91 MPa, and the stress was still higher than the threshold even in the last porous layer close to the bottom, suggesting that the total stress on the homogeneous porous structure was much higher than the graded porous structure. This phenomenon may lead to a more stable mechanical property and a longer implantation life in graded porous implants. More importantly, the gradually changed pore size can contain the optimal size and porosity for bone ingrowth. For some early implantation failure in dental and orthopaedic applications, the implants with poor stability and lack of complete bone ingrowth are high-risk factors [7], [8]. The space in the scaffolds has a momentous role in osteogenesis and vascularisation, which can lead to biological fixation at an early stage of bone healing [43].

Figure 9.

The internal stress transmission of (A) D1, (B) D2, (C) D3 and (D) a homogeneous porous scaffold. The threshold was set to 5 MPa.

There are some limitations in the present study. Because there are only a few studies about the bone formation in vivo, to minimise the interference of different unit cell types in stimulating osteogenesis, only one of them was introduced in the design of graded porous scaffolds. To investigate the application potential in orthopaedics, architectures containing more unit cell types should be tested in the future. In addition, 4–5 weeks is enough time for observing the early bone formation in large animals. Nonetheless, the time period is still not long enough for comprehensively evaluating the osteogenesis and osteointegration capability. The animal model used in our study was an implantation model, and the interaction between the TPMS-based structures and the in vivo circumstance under load bearing also need to be explored.

Conclusion

In the present study, we designed three TPMS-based porous structures with different change rates in the size of the porous structures along the z-axis. The mechanical properties of these structures are similar to natural bone tissue. The FE simulation results indicated that the stress transmission capability of the TPMS-based architecture was better than the solid homogeneous porous structure. In addition, the in vivo experiment was introduced to evaluate the early osteointegration ability. Micro-CT and histological results proved that the graded porous structures can stimulate bone formation. This study is the first in vivo research to explore the osteointegration capability of TPMS-based models. The results of our study have corroborated the previous theoretical research about the application potential of TPMS-based models in bone tissue repair.

Conflicts of Interest

The authors have no conflicts of interest to disclose in relation to this article.