Abstract
In August 2017 the National Center for Health Statistics (NCHS), part of the U.S. Federal Statistical System, published new standards for determining the reliability of proportions estimated using their data. These standards require an individual to take the Korn-Graubard confidence interval (CI), along with CI widths, sample size, and degrees of freedom, to assess reliability of a proportion and determine if it can be presented. The assessment itself involves determining if several conditions are met. This manuscript presents kg_nchs, a postestimation command that is used following svy: proportion. It allows Stata users to (a) calculate the Korn-Graubard CI and associated statistics used in applying the NCHS presentation standards for proportions, and (b) display a series of three dichotomous flags that show if the standards are met. The empirical examples provided show how kg_nchs can be used to easily apply the standards and prevent Stata users from needing to perform manual calculations. While developed for NCHS survey data, this command can also be used with data that stems from any survey with a complex sample design.
Keywords: health survey data, complex sample design, effective sample size, Clopper-Pearson confidence interval, exact confidence interval, health care, National Ambulatory Medical Care Survey, survey design
1. Introduction
When calculating a confidence interval (CI) for proportions, the default setting in Stata is to calculate the “exact” CI, known in the broader literature as the Clopper-Pearson binomial CI (Clopper and Pearson 1934). This CI is more optimal with proportions based on a small number of events as opposed to other CIs, such as the Wald (Newcombe 1998; Dean and Pagano 2015). However, to calculate this CI for proportions estimated for survey data that use a complex, multi-stage cluster design, an adjustment specified by Korn and Graubard (1998) should be applied. This adjustment is applicable when analyzing data from many nationally-representative health surveys, which often use samples with a complex design (Korn and Graubard 1999).
The Korn-Graubard adjustment to the Clopper-Pearson CI (or more simply, the Korn-Graubard CI) is also a key component in presentation standards for proportions that are published by the National Center for Health Statistics (NCHS) (Parker et al. 2017). NCHS is part of the U.S. Federal Statistical System, and is the principal health statistics agency of the U.S. Department of Health and Human Services. The agency’s mission is to provide statistical information that will guide actions and policies to improve the health of the American people. In August 2017, NCHS began using the Korn-Graubard CI, along with information on CI width, sample size, and degrees of freedom, to assess the reliability of a proportion, and determine whether or not it can be presented as an official estimate. Researchers using NCHS survey data who wish to follow these same presentation standards must now calculate the Korn-Graubard CI, and use this CI to apply them.
In this manuscript, the postestimation command kg_nchs is presented, which serves two functions. First, it draws from the results stored by Stata’s svy: proportion command and uses them to calculate the Korn-Graubard CI for each proportion, in addition to the effective sample size and absolute and relative CI widths. Second, kg_nchs automatically reviews these results and uses them to produce a series of dichotomous flags that determine whether a proportion meets the various components of the NCHS presentation standards for proportions. While this command was developed for NCHS survey data, its utility is much broader in that it can also be used with data from any survey with a complex sample design.
2. Korn-Graubard confidence intervals
2.1. Calculation
The Korn-Graubard CI involves a modification to the binomial CI frequently used in a non-survey setting (Korn and Graubard, 1998), and was developed for use when estimating proportions using a sample with a complex design, and when the proportion and/or sample size is small (Gray et al., 2004). To calculate the Korn-Graubard CI for proportionp (Korn and Graubard, 1998) as used in the kg_nchs command, the effective sample size is needed. The effective sample size (n*) is defined as the sample size divided by the design effect (Kish, 1965). The approach used here for its calculation is
| (1) |
or the product of p and its complement (1-p) divided by variance of p. Here p is the proportion, (1-p) is the complementary proportion, and var(p) is the variance of p. Limits are set such that when p=0, then n*=n (where n is the sample size). The effective sample size is then adjusted by the degrees of freedom df, or the difference in number of primary sampling units (PSUs) and number of strata. This df-adjusted effective sample size () is defined as
| (2) |
Here, the unadjusted effective sample size n* is multiplied by the t distribution of n-1 divided by the t distribution of df, squared (note ∝ represents the significance level). Limits are also placed here such that if p=0, then .
The next series of steps in calculating a Korn-Graubard CI is to adjust the number of x positive responses for , such that
| (3) |
The number of positive responses (x) is then used to calculate v1 through v4 degrees of freedom, which are needed to calculate the F distribution, and ultimately to produce the Korn-Graubard CI:
| (4) |
| (5) |
| (6) |
| (7) |
Finally, the confidence interval (Korn and Garubard 1998) can be calculated for x number of positive responses, with the df-adjusted effective sample size of n*f, where the lower limit of the interval (pL) is
| (8) |
and the upper limit of the interval (pU) is
| (9) |
2.2. NCHS presentation standards for proportions
The NCHS Data Presentation Standards for Proportions (Parker et al. 2017) were developed to assess the reliability of a proportion, and determine whether it should be presented. It should be noted that these standards do not address issues surrounding confidentiality, which may also be separately assessed to determine if a proportion should not be presented. In addition, while these standards primarily focus on estimates calculated from survey data, they also discuss estimates resulting from population data (specifically NCHS vital statistics). However, the Korn-Graubard CI does not apply to estimates from population data, and therefore does not apply to the kg_nchs command discussed below. While the text in this section provides a brief description of the NCHS standards and how to use the Korn-Graubard CI to apply them, Stata users are encouraged to read the full report to gain a complete understanding. The report can be found at: https://www.cdc.gov/nchs/data/series/sr_02/sr02_175.pdf.
Prior to assessing the reliability of a proportion using the NCHS standards, a few final calculations are needed using the Korn-Graubard CI; specifically, the absolute and relative widths of the CI. Here the absolute width of the Korn-Graubard CI is defined by . In regards to the relative widths, these are calculated for both the proportion p and its complement (1-p). Here the relative width for p is defined as , and for 1−p as .
According to the NCHS standards (Parker et al. 2017), proportion p is considered unreliable and would not be presented if any of the following are true: (a) n<30 or n*<30, (b) the absolute width of its Korn-Graubard CI is ≥0.30, or (c) its absolute CI width is >0.05 and <0.30, and its relative CI width is >130% of the proportion. These thresholds were decided upon for the standards while keeping in mind that the Korn-Graubard CI is known to be conservative (Brown, Cai, and DasGupta, 2001; Gray et al., 2004).
If any of the aforementioned conditions are met, proportion p is suppressed. However, the NCHS standards also give attention to additional considerations. Specifically, in instances where: (a) the absolute CI width is ≤0.05 and either p=0 or 1-p=0, or where (b) the absolute CI width is ≤0.05 and df<8. In these instances, a statistical review of the estimate should be given to determine whether or not it would be able to be presented, or should be suppressed. While within NCHS this review would be performed by a clearance official, for general Stata users this review might entail a manual assessment by either the user him/herself, or a knowledgeable statistician.
The final consideration needed when applying the NCHS standards is to assess the reliability of the complement of proportion p. During instances where p is presented, its complement (1-p) should also have the NCHS standards applied to it in order to assess the complement’s reliability. If 1-p is found to be unreliable, per standards p can still be presented; however, a footnote should be added that states its complement does not meet the standards. Note that this assessment of 1-p should be given regardless as to whether 1-p is intended to be presented.
3. The kg_nchs command
3.1. Syntax
The syntax is simply
kg_nchs
As this is a postestimation command for proportions using survey data, it can only be executed immediately following a svy: proportion command. An error message will result if used following any other command, including proportion without the svy prefix.
3.2. Description
The kg_nchs postestimation command uses the output from a svy: proportion command to generate two sets of results, all contained in a single table. In the first set of results, each proportion and its standard error are used to calculate a number of statistics. These include the complementary proportion, Korn-Graubard 95% CI, effective sample size (adjusted for degrees of freedom), the absolute Korn-Graubard CI width, and the relative Korn-Graubard CI widths (multiplied by 100) for both the proportion and its complement.
The second set of results pertain directly to the NCHS standards, and for each proportion presents three separate dichotomous flags (0=no; 1=yes). The first of these flags signals if a proportion meets all presentation standards, and is considered reliable. The second flag signals if a proportion is flagged for statistical review. The third and final flag pertains to the complementary proportion. This flag signals if the complement meets all presentation standards, and is considered reliable. Used together, these flags provide Stata users with a quick method of assessing whether a proportion meets these comprehensive standards, without the need for performing manual calculations.
3.3. Understanding Degrees of Freedom and Restriction Following the over() Option
For complex sample surveys, one general rule of thumb is to calculate degrees of freedom as the number of PSUs minus the number of strata. It should be noted this is not the only way. For example, when calculating national estimates using NCHS’ National Health Interview Survey, degrees of freedom are assumed to be large enough for a normal approximation, and degrees of freedom may be calculated as n-1 (National Center for Health Statistics, 2006; Parker et al., 2017). However, number of PSUs minus the number of strata is the approach used with the majority of NCHS surveys (Parker et al., 2017) and in Stata software, and therefore this approach is used in the kg_nchs postestimation command.
As degrees of freedom play a critical role in both the adjustment of the effective sample size, and determining if a proportion should be flagged for statistical review, Stata users should have a clear understanding of how degrees of freedom are calculated for use in the kg_nchs postestimation command. The PSU and strata counts used in this calculation by Stata are for all observations included in the preceding svy: proportion command (not those associated with each specific proportion listed in Stata’s Results window). When calculating the Korn-Graubard 95% CI for a specific subgroup, it may be improper to use the counts for all observations as this could lead to inflated PSU and strata counts; especially for instances with smaller subgroups. More explicitly, this leads to a problem if kg_nchs would be used following a svy: proportion command with the over() option. In such an instance, Stata would use the PSU and strata counts for all observations, and would not capture those counts specific to each subpopulation of the variable(s) specified in the over() option.
Therefore, to prevent the incorrect PSU and strata counts from being used, the kg_nchs postestimation command is designed so it cannot be used following the svy: proportion command when it is accompanied with the over() option. If this command is given with the over() option, an error message will result. Instead, Stata users may use the subpop() option with the svy prefix. The result will be a more accurate calculation; one that is guaranteed to correctly estimate the degrees of freedom and accurately calculate the df-adjusted effective sample size.
4. Empirical examples
The proceeding examples use public-use data from the 2014 National Ambulatory Medical Care Survey (NAMCS), which consists of a total of 45,710 patient visits. NAMCS is an annual survey conducted by NCHS that is representative of ambulatory visits made to nonfederal, office-based physicians in the United States. Details on the design, methods, and content of NAMCS can be found elsewhere (National Center for Health Statistics, 2017).
The following example uses 2014 NAMCS data and the svy: proportion command to estimate the proportion of visits to office-based physicians made by patients with congestive heart failure, and the kg_nchs postestimation command to calculate the Korn-Graubard CIs and assess if the resulting proportions meet NCHS standards.

Here 1.6% of visits were made by patients with congestive heart failure, while 98.4% were made by patients without this chronic condition. The kg_nchs command shows that both of these proportions are reliable (i.e., flag A=1), as each meets the conditions for reliability detailed by the NCHS standards: n*>30, an absolute Korn-Graubard CI width <.30, and a relative CI width of ≤130%. Neither proportion requires statistical review (i.e., flag B=0), as although the absolute CI width is ≤0.05, neither proportion is equal to 0 or 1, and the df>8. In addition, for each proportion its complement is also reliable (i.e., flag C=1).
The next example again examines office-based physician visits by patients with congestive heart failure, but in this instance among the subgroup of Hispanic women aged ≥65 years. With a smaller subgroup of 440 observations, reliability issues exist.

Here approximately 3.9% of visits were by Hispanic females aged >65 years with congestive heart failure. The Stata results from the kg_nchs command show that the relative Korn-Graubard CI width is >130. Therefore, the proportion does not meet the standards, is not considered reliable, and would not be presented (i.e., flag A=0). Notice that as this proportion is considered unreliable, both flags B and C are not applicable and will display a “.” in the results table for this proportion.
For the complement, 96.1% of visits were by Hispanic females aged >65 years without congestive heart failure. This proportion meets NCHS standards (i.e., flag A=1) and does not require statistical review (i.e., flag B=0). However, its complement is considered unreliable (i.e., flag C=0), and therefore Stata users applying these standards would add a footnote stating such.
The example below examines office-based physician visits by Hispanic male patients aged 18–44 years. Among this subpopulation, not a single visit was by a patient who had congestive heart failure. Rather, 100.0% of visits by Hispanic males aged 18–44 were by persons who had never been diagnosed with congestive heart failure.

Recall the limits specified above state that when a proportion is 0, the effective sample size is set to the nominal sample size; in this instance 376. Thus, as the kg_nchs results show, according to NCHS standards both of these proportions are reliable (i.e., flag A=1). However, both of these estimates would be flagged for statistical review (i.e., flag B=1) as the absolute Korn-Graubard CI width is ≤0.05 and the proportion (or its complement) is equal to 0. In addition, for these instances kg_nchs will not show the relative CI widths in the Stata Results window.
The final example details why the kg_nchs postestimation command cannot be used following a svy: proportion command that uses the over() option. Here the proportion of office-based physician visits by non-Hispanic black patients aged 18–44 years, 45–64 years, and ≥65 years with congestive heart failure is estimated. As noted above, in such instances an error message would be generated by the postestimation command.
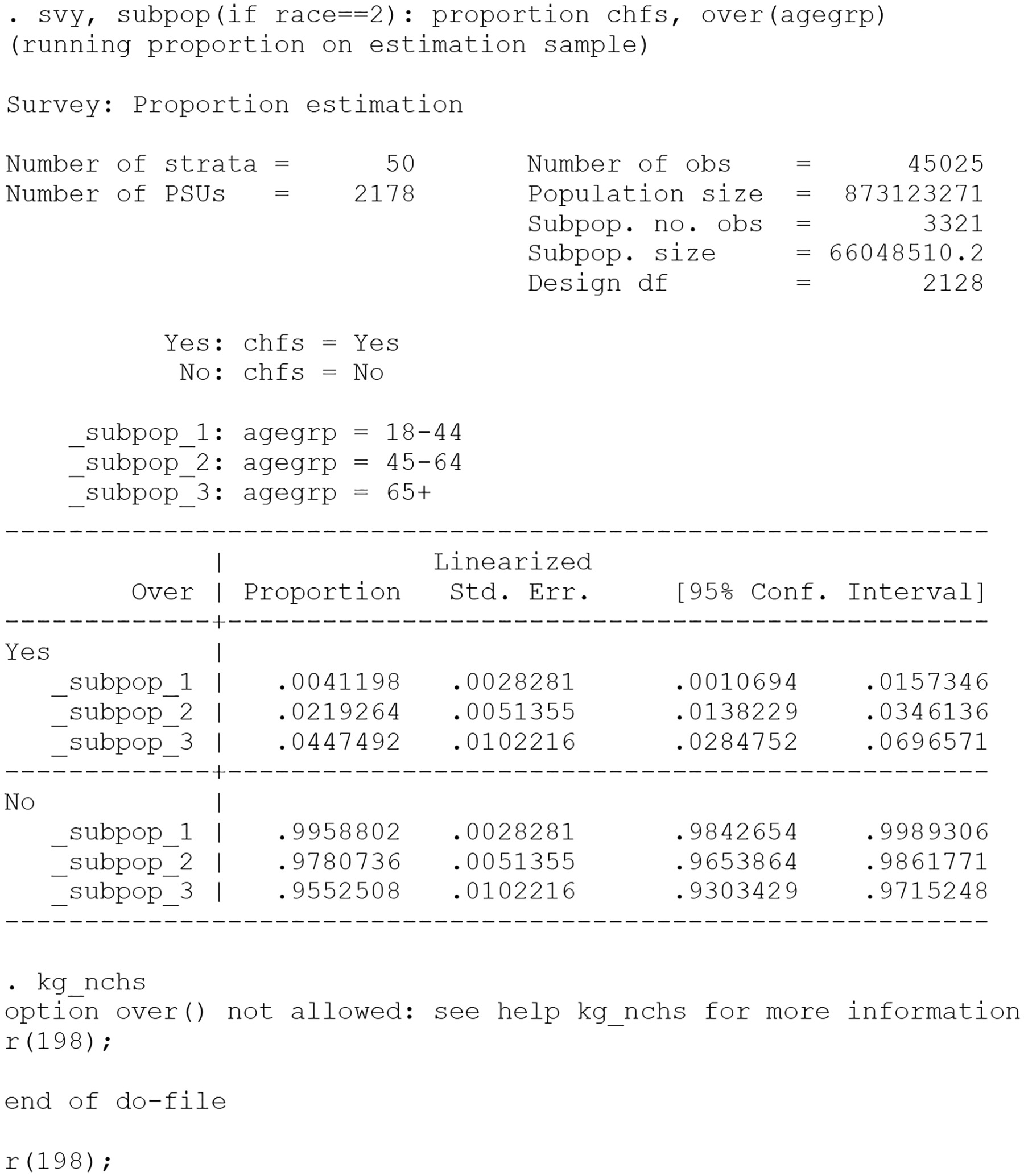
This restriction prevents the use of an inaccurate number of degrees of freedom (in the Results immediately above, 2,218) from being used when adjusting the effective sample size for each subgroup. As an alternative, Stata users would generate separate svy: proportion commands for each subgroup using the subpop() option, as shown below for the subgroup of visits by non-Hispanic black patients aged ≥65 years:

For visits by non-Hispanic black patients with congestive heart failure, the age group >65 years has a different number for degrees of freedom (i.e., 2,062) than the original example if kg_nchs was allowed to follow a svy: proportion command with an over() option (i.e., 2,128). This restriction prevents the miscalculation of the df-adjusted effective sample size, and allows for an accurate assessment of the NCHS standards.
5. Conclusion
The kg_nchs postestimation command produces the Korn-Graubard CI, and a series of related statistics that are needed to determine if a proportion is considered reliable per NCHS presentation standards (Parker et al., 2017). It also displays three dichotomous flags that prevent the need for manual comparison of these results to the conditions that comprise these standards. Thus, using kg_nchs with svy: proportion is an easy and efficient method that allows Stata users to accurately determine if a proportion meets the NCHS Data Presentation Standards for Proportions. While this command was developed for use with NCHS data, it can also be used with any dataset that stems from a survey with a complex sample design.
6. Acknowledgements
Note that all views expressed in this manuscript are those of the author, and do not necessarily reflect those of the Centers for Disease Control and Prevention or National Center for Health Statistics. I would like to thank the following individuals for “beta testing” the kg_nchs command, or helping me to verify the command’s results either manually or with SAS/SUDAAN software: Yutaka Aoki, Jessica Lendon, Frances McCarty, Lauren Rossen, Clint Thompson, and Ben Zablotsky. I would also like to thank NCHS staff who developed the Data Presentation Standards for Proportions, provided me feedback, and encouraged me to pursue the development of kg_nchs.
7 References
- Brown LD, Cai TT, and DasGupta A 2001. Interval estimation for a binomial proportion. Statistical Science 16(2): 101–133. [Google Scholar]
- Clopper CJ, and Pearson ES 1934. The use of confidence or fiducial limits illustrated in the case of the binomial. Biometrika 26(4): 404–413. [Google Scholar]
- Gray A, Haslett S, Kuzmicich G 2004. Confidence intervals for proportions estimated from complex sample designs. Journal of Official Statistics 20(4): 705–723. [Google Scholar]
- Newcombe RG 1998. Two-sided confidence intervals for the single proportion: Comparison of seven methods. Statistics in Medicine 17(8): 857–872. [DOI] [PubMed] [Google Scholar]
- Dean N, and Pagano M 2015. Evaluating confidence interval methods for binomial proportions in clustered surveys. Journal of Survey Statistics and Methodology 3(4): 484–503. [Google Scholar]
- Kish L 1965. Survey Sampling. New York, NY: John Wiley & Sons, Inc. [Google Scholar]
- Korn EL, Graubard BI 1998. Confidence intervals for proportions with small expected number of positive counts estimated from survey data. Survey Methodology 24(2): 193–201. [Google Scholar]
- Korn EL, and Graubard BI 1999. Analysis of Health Surveys. New York, NY: John Wiley & Sons, Inc. [Google Scholar]
- National Center for Health Statistics. 2006. Variance Estimation Guidance, 2006–2015 (Adapted from the 2006–2015 NHIS Survey Description Documents). Hyattsville, MD: National Center for Health Statistics. [Google Scholar]
- National Center for Health Statistics. 2017. 2014 NAMCSMicro-data File Documentation. Hyattsville, MD: National Center for Health Statistics. [Google Scholar]
- Parker JD, Talih M, Malec DJ, Beresovsky V, Carroll M, Gonzalez JF Jr., et al. 2017. National Center for Health Statistics data presentation standards for proportions. Vital and Health Statistics 2(175): 1–14. [PubMed] [Google Scholar]


