Estimating the Distribution of Random Parameters in a Diffusion Equation Forward Model for a Transdermal Alcohol Biosensor

Abstract

We estimate the distribution of random parameters in a distributed parameter model with unbounded input and output for the transdermal transport of ethanol in humans. The model takes the form of a diffusion equation with the input being the blood alcohol concentration and the output being the transdermal alcohol concentration. Our approach is based on the idea of reformulating the underlying dynamical system in such a way that the random parameters are now treated as additional space variables. When the distribution to be estimated is assumed to be defined in terms of a joint density, estimating the distribution is equivalent to estimating the diffusivity in a multi-dimensional diffusion equation and thus well-established finite dimensional approximation schemes, functional analytic based convergence arguments, optimization techniques, and computational methods may all be employed. We use our technique to estimate a bivariate normal distribution based on data for multiple drinking episodes from a single subject.

1. Introduction

Researchers and clinicians studying and treating alcohol dependence have long sought the means to continuously and quantitatively monitor blood alcohol levels in naturalistic settings. The ability to do this would be extremely valuable for advancing a wide range of alcohol research and clinical treatment domains, including how alcohol concentrations relate to drinking motives, physical responses to alcohol, behaviors, decision-making, negative consequences, and environmental situational factors over the course of a drinking episode and across drinking episodes. At present the only ways to collect alcohol consumption data in the field are the self-report diary and the breath analyzer, both of which require the active participation of the subject and generally yield inaccurate estimates of blood alcohol level when obtained during naturalistic drinking episodes.

Recently, biosensors that measure transdermal alcohol concentration (TAC), the amount of alcohol diffusing through the skin (Fig. 1.1), have been developed and used, but primarily only as abstinence monitors (for example, in court mandated monitoring of DUI offenders). Because TAC data does not consistently correlate with breath/blood alcohol concentrations (BrAC/BAC) across individuals, devices, and environmental conditions, these devices have not experienced wide-spread acceptance among the research and clinical communities. Indeed, BAC and BrAC are currently, and historically have been, the standard measures of alcohol level intoxication among alcohol researchers and clinicians and unfortunately there is currently no well-established method for producing reliable estimates of BrAC/BAC (eBrAC/eBAC) from TAC data.

Figure 1.1.

(Left Panel) The WRISTAS™ 7 transdermal alcohol biosensor, (Right Panel) The Alcohol Monitoring System (AMS) Secure Continuous Alcohol Monitoring (SCRAM) system.

The transport and filtering of alcohol by the skin is affected by a number of factors that differ across individuals (e.g., skin layer thickness, porosity, and tortuosity, etc.) and across drinking episodes within individuals (e.g., body and ambient temperature, humidity, subject activity level, skin hydration, vasodilation, etc.). The implication is that, regardless of how reliable and accurate transdermal alcohol device hardware becomes at measuring TAC, the raw TAC data will never consistently map directly onto BrAC/BAC across individuals and drinking episodes.

In our work to date on determining eBrAC/eBAC from TAC (see, for example, [5] and [16]), we have taken a strictly deterministic approach to converting TAC to either BAC or BrAC. First principles physics-based models (a one-dimensional diffusion equation with either infinite or finite speed of propagation and input and output on the boundary) were fit to individual calibration data to capture the forward process - the transport of ethanol molecules from the blood, through the skin, and its measurement by the sensor. The result is TAC expressed as a convolution of BAC or BrAC with a kernel or filter. We then deconvolve an estimate of the BAC or BrAC from the biosensor measurements of TAC.

To greatly reduce the burden on researchers/clinicians and participants/patients and thus significantly increase the feasibility of using these devices, we have been investigating ways to eliminate the need to calibrate the sensor’s data analysis system to each individual, each sensor, and across varying current environmental conditions. In particular, we have been investigating the use of our first principles physics/physiological based models to describe the dynamics common to the entire population (interpreted broadly to include all individuals, devices, and environmental conditions) and then to attribute all un-modeled sources of uncertainty (primarily due to variations in physiology, hardware, and the environment) observed in individual data to random effects. We refer to this as a population model; it takes the form of our earlier deterministic transport models, but with the parameters now being random variables whose distributions are to be estimated based on aggregate population data.

We assume an underlying mathematical framework describing the system dynamics that are common to all individuals, environmental conditions, and devices in the population (e.g., the physics-based model for the transport of ethanol from the blood, through the skin, and measurement by the sensor), but that individual members of the population exhibit variation in the parameters appearing in the model (e.g., the rate at which the alcohol is transported, evaporates, etc.). We then assume that the sensor measures the sum or mean of all of these effects. This is realized in the form of a model based on random partial differential equations and boundary conditions, and then, instead of fitting the unknown parameters in the model directly to individual data, we now estimate the distribution of the random parameters (in the form of probability measures or density functions) based on aggregate population data. In this way, the fit describes the mean behavior of the population.

We consider the (in general, infinite dimensional) discrete time initial value problem given by

$$x_{k+1}=g\left(t_k,x_k,u_k;q\right)$$ (1.1)

$$x_0\text{\hspace{0.17em}given},$$ (1.2)

and assume that it describes the dynamics of a process common to the entire population. In addition, it is assumed that we are able to observe some function of the state, or solution, of (1.1), (1.2), x(u;q) = {x_k(u,q)}, and the input, u = {u_k}, as given by the output or observation equation

$$y_k(u,q)=h\left(x_k(u,q),u_k;q\right).$$ (1.3)

In equations (1.1)–(1.3) it is assumed that the parameters q are contained in a set Q, the set of admissible parameters, and that their values are specific to a particular individual (interpreted broadly) member of the population. The objective is to estimate the parameters, q, or more precisely their distribution, based on population or aggregate data rather than data for a particular individual. We assume 𝓆 is a random vector with support set Q and that 𝓆~π(ρ), where π(ρ) is a family of distributions or push forward measures parameterized by ρ and defined on a sigma field of subsets of Q where $\rho \in \mathcal{R}$, $\mathcal{R}$ the set of feasible parameters. We will assume π(ρ) is defined in terms of a joint density function f(ρ); f(ρ) is absolutely continuous, non-negative, and

$$\pi (A;\rho )=P(𝓆,\in A)={\int }_Q{\chi }_{A}d\pi (\rho )={\int }_{A}f(q;\rho )dq,$$

for A an event, where $\rho \in \mathcal{R}$.

The statistical model for the population data upon which the estimation is to be based assumes that the observed data points can be represented by the expected value of the output of the model plus random error. We assume that we have ν subjects and μ_i noise-corrupted observations for the i^th subject. For $\rho \in \mathcal{R}$, we define

$$v_{i,j}(\rho )=E_{\pi (\rho )}\left[y_{i,j}\left({\tilde{u}}_i,𝓆\right)\right]={\int }_{Q}h\left(x_{i,j}\left({\tilde{u}}_i,q\right),{\tilde{u}}_{i,j};q\right)d\pi (\rho )={\int }_{Q}h\left(x_{i,j}\left({\tilde{u}}_i,q\right),{\tilde{u}}_{i,j};q\right)f(q;\rho )dq,$$ (1.4)

for j = 0,1, …, μ_i, i = 1, …, ν, the mean behavior of the population at time t_j given that the distribution of the parameters 𝓆 is described by the measure π(ρ). In (1.4), x_i and y_i are given by (1.1) – (1.3) with $u={\tilde{u}}_i$ and x₀ = x_i,0. As is typically the case in standard linear regression, we assume our observations are given by

$$V_{i,j}=v_{i,j}\left({\rho }_0\right)+{\epsilon }_{i,j}=E_{\pi \left({\rho }_0\right)}\left[y_{i,j}\left({\tilde{u}}_i,q\right)\right]+{\epsilon }_{i,j}={\tilde{y}}_{i,j}\left({\tilde{u}}_i,{\rho }_0\right),j=0,1,\dots ,{\mu }_i,i=1,\dots ,v,$$ (1.5)

where the ε_i,j, j = 1, …, μ_i, i = 1, …,ν, represent measurement noise which are assumed to be independent, identically-distributed random variables with mean 0 and common variance σ², and ${\rho }_0\in \mathcal{R}$ represents the true values of the parameters.

Our estimation problem minimizes prediction error based on a least squares (or MLE if ε_i,j~N(0, σ²)) approach. For V = {V_i,j}, our estimator $\widehat{\rho }$ is given by

$$\begin{gathered} V=\left\{V_{i,j}\right\},\text{ our estimator }\widehat{\rho }\text{\hspace{0.17em}is\hspace{0.17em}given\hspace{0.17em}by\hspace{0.17em}}\widehat{\rho }=arg\underset{\rho \in \mathcal{R}}{\text{min}}J\left(\rho ;V\right) \\ =arg\underset{\rho \in \mathcal{R}}{\text{min}}\left\{{\sum }_{i=1}^v{J}_{i,\mu }(\rho ;V)+\lambda (\rho )\right\} \\ =arg\underset{\rho \in \mathcal{R}}{\text{min}}\left\{{\sum }_{i=1}^v{\sum }_{j=0}^{{\mu }_i}{\alpha }_{i,j}{\left|v_{i,j}(\rho )-V_{i,j}\right|}^2+\lambda (\rho )\right\} \end{gathered}$$ (1.6)

where λ(ρ) is a regularization term, $\mu ={\left\{{\mu }_i\right\}}_{i=1}^v$, the α_i,j are positive weights, ν_i,j(ρ) is given by (1.4) and V = {V_i,j} by (1.5). In general (and in fact, in the problem of interest to us here), the fact that the dynamical system (1.1)–(1.3) may be (or is) infinite dimensional, means that the optimization problem given in (1.6) is not directly amenable to computation. Consequently, when we apply these ideas to the alcohol biosensor problem in Section 2 below, we replace the infinite dimensional state equation with a finite dimensional approximation. Relevant convergence issues which are the central focus of our research, are discussed in Section 4. We note that if one is trying to estimate the shape of f and the parameters ρ are the coefficients of basis elements with the dimension of the feasible parameter space $\mathcal{R}$ increasing in dimension in order to achieve some level of convergence, then the presence of regularization in the form of the term λ(ρ), would likely be essential. In our studies here, we are not estimating the shape of f and the dimension of $\mathcal{R}$ is fixed and relatively low (~10), and hence we found that regularization was unnecessary. Consequently we do not include λ(ρ) (i.e. we assume λ(ρ) = 0) in the remainder of our treatment below. It would not however, be difficult to include it, and we may do that in future work where the focus is either the estimation of the shape of the density or the corresponding measure, π, as in [4].

Our problem as posed is a classic mixed effects model (see, for example, [6,7], and the numerous references contained therein) featuring both inter- and intra-subject variation and uncertainty. The standard statistical model requires a function, which describes the relationship between the observations and the design variables of the form

$$y_{ij}=f\left(x_{ij},q_i\right)+{\epsilon }_{ij},i=1,\dots ,v,j=1,\dots ,{\mu }_i,$$

where y_ij is the j^th observation from the i^th individual, the $x_{ij}^{\prime }s$ are the known design or state variables, the q_i’s are the parameters specific to i^th individual, and ε_ij (typically ~N(0, σ²)) are i.i.d. with mean zero and common variance σ². Moreover, it is also assumed that q_i = h(c_i, μ, η_i) where c_i’s are the known vectors of the covariates, μ is the unknown vector of fixed effects, and the η_i are random, for example, η_i~N(0, Ω). In our case here, in this model, the parameters to be estimated are μ, σ, Ω with Ω the covariance matrix. When f and h are linear, estimation of these parameters is relatively straight forward using standard approaches. However, when f is nonlinear, or even more complex, for example, as in our case here wherein, due to the PDE-based model, a closed form finite dimensional representation is unavailable, and there is a clear lack of independence in the observations, a number of significant statistical and computational challenges result. Indeed, the state variables, x_ij, in our model are the solution of a partial differential equation and consequently the representation for the function f is in terms of a semigroup of infinite dimensional operators on a Hilbert space whose dependence on the parameters, q_i, is highly nonlinear. As a result the use of any estimation technique that relies on a likelihood (e.g. MLE, EM, Stochastic Approximation Expectation Minimization, Bayesian estimation with MCMC, etc.) can be daunting (see, for example, [10]). Indeed, such an approach would in one way or another, likely involve repeated simulation requiring repeated solution of the PDE which is something we are trying to avoid. Another method involves estimating the state from the observations, then using nonlinear regression together with the PDE to estimate the parameters. In our case we have a one dimensional measurement of an infinite dimensional state and observability could very likely be an issue. Also, if one opted to use the Kalman filter to estimate the state based on the observations, its implementation is essentially equivalent to solving the PDE and would itself require finite dimensional approximation. In general, this approach often yields inaccurate estimates.

Along with measurements across different subjects, we have longitudinal measurements for each subject, which of course one would expect to be dependent. In addition, from a pharmacokinetic (PK) standpoint, our definition of “subject” or population is somewhat non-standard in that it refers to not only individual participants and their various physiological differences, but also environmental conditions suchas temperature and humidity, etc. as well as hardware related uncertainties. Thus, in our model, the q_i’s describe unmodeled phenomena present both across different individuals and within the same individual. Indeed our working hypothesis is that each observation represents a sum or average of any number of diffusion processes all at work simultaneously. In addition, because human subjects are involved, it would be both costly and time consuming to collect simultaneous BrAC and TAC data from enough individuals wearing enough sensors and under sufficiently varied environmental conditions to estimate the distribution of the q_i’s directly. Consequently, although it can have bias problems [14], it seemed most appropriate that our estimator in (1.6) take the form of what is known in the PK literature as the naïve pooled data estimator.

Our general approach relies to some extent on two relatively recent papers: 1) Banks and Thompson’s framework for the estimation of probability measures in random abstract evolution equations and the convergence of finite dimensional approximations in the Prohorov metric [4], and 2) Gittelson, Andreev, and Schwab’s theory for random abstract parabolic partial differential equations with dynamics defined in terms of coercive sesquilinear forms [9]. The approach in [9] is novel in the way that it treats the random variable as another “space-like” independent variable in the PDE. In this way, finite dimensional approximation is handled in much the same way that it is for the standard deterministic space variables. We use the framework in [9] together with the generation and approximation results from linear semigroup theory, (i.e. the Hille-Yosida-Phillips and Trotter Kato theorems, see, for example, [3, 11, 15]) to establish that the sufficient conditions for a Banks–Thompson-like convergence result are satisfied in the case of regularly dissipative systems with random parameters whose distributions can be described by appropriately parameterized probability density functions.

For a number of reasons, the approach we take here, and in particular our population model as defined in Section 3 below, is especially well suited for our estimation problem as given in (1.6) with the underlying dynamics (1.1), (1.2) being described by a random PDE. Indeed, 1) it does not require repeated simulation, 2) it takes particular advantage of the underlying parabolic structure of the model’s state equation, 3) it lends itself extremely well to functional analytic arguments for convergence of the estimators based on finite dimensional approximation, the central focus of this study, 4) based on our working hypothesis concerning our data as stated in the previous paragraph and the statistical model given in (1.5), the output of the population model is precisely what is required to evaluate the naïve pooled data based performance index, J (ρ; V) given in (1.6), and 5) it is especially well suited for deconvolving an estimate of BrAC from TAC which is our ultimate goal [20].

In this paper, we focus solely on the application of our framework to the alcohol biosensor problem outlined above. The abstract functional analytic approximation and convergence theory on which the results presented here are based was established in [18] and [19]. In addition, in our treatment here, we are only concerned with the fitting of the random parameters in the forward model. The inverse problem involving the deconvolution of the BAC/BrAC from the TAC signal once the forward model with random elements has been fit is treated elsewhere [20].

An outline of the remainder of the paper is as follows. In Section 2 we discuss our diffusion based distributed parameter model for the transdermal transport of ethanol, its abstract formulation as an infinite dimensional dynamical system with unbounded input and output, and the corresponding discrete-time input-output system on which our general framework is based. In Section 3 we discuss the treatment of initial value problems involving regularly dissipative operators with random coefficients as in [9] and [17], and apply it to the system of interest to us here discussed in Section 2. Section 4 outlines our finite dimensional approximation and convergence results, in Section 5 we discuss a consistency result for our estimator, and in Section 6 we present and discuss our numerical results using actual experimental/clinical data for the alcohol biosensor problem. Section 7 contains a brief discussion of future research, and some concluding remarks.

We use standard notation throughout. For example, we denote the space of square Lebesgue or Bochner integrable functions defined on an interval (a, b) with range in the normed linear space X by L₂ (a, b; X), and we use C(a, b; X) when the functions are continuous. When $X=ℝ$, the range space is omitted. For normed linear spaces X and Y, $\mathcal{L}(X,Y)$ denotes the space of bounded (continuous) linear operators defined on X with range in Y. Unless explicitly stated otherwise, all Hilbert space norms are the ones induced by the standard inner product on that space. We occasionally use “dot” notation to denote weak or strong derivatives with respect to time.

2. A Distributed Parameter Model for a Transdermal Alcohol Biosensor and its Abstract Formulation

Our ethanol transport model is based on diffusion, or Fick’s law, and consequently it is described by abstract parabolic operators. When formulated abstractly in a Gelfand triple setting, these operators are examples of what are known as regularly dissipative operators and can be shown to generate analytic or holomorphic semigroups (see [11, 15, 22]).

After converting to what are essentially dimensionless quantities (see [16]), we obtain the input/output model

$$\frac{\partial \phi }{\partial t}\left(t,\eta \right)=q_1\frac{{\partial }^2\phi }{\partial {\eta }^2}(t,\eta ),0<\eta <1,t>0$$ (2.1)

$$q_1\frac{\partial \phi }{\partial \eta }\left(t,0\right)-\phi \left(t,0\right)=0,t>0,$$ (2.2)

$$q_1\frac{\partial \phi }{\partial \eta }\left(t,1\right)=q_{2}u\left(t\right),t>0$$ (2.3)

$$\phi (0,\eta )={\phi }_0,0<\eta <1$$ (2.4)

$$\text{y}(\text{t})=\text{\hspace{0.17em}φ}(\text{t},0),\text{\hspace{0.17em}t\hspace{0.17em}}>0,$$ (2.5)

in the form of an initial-boundary value problem for a one dimensional diffusion equation with input and output on the boundary and two unknown parameters, q = (q₁,q₂). In the system (2.1) – (2.5) φ(t, η) is essentially the concentration of ethanol in the interstitial fluid in the epidermal layer of the skin at depth η and time t, u is the concentration of alcohol in the blood (BAC) as measured by a breath analyzer (BrAC), and y is the (TAC). The boundary condition (2.2) models the evaporation of ethanol at the skin surface, condition (2.3) captures the exchange of ethanol molecules between the (blood fed) dermal and epidermal layers of the skin. The output equation (2.5) models the biosensor measured TAC at the skin surface. We assume that there is no alcohol in the skin initially, so in general φ₀ = 0 in (2.4).

Using the tools of functional analysis and linear semi-group theory, we reformulate (2.1) – (2.5) as a discrete-time SISO system with state space an infinite dimensional Hilbert space. In (2.1)–(2.5) the input and output are on the boundary and consequently the resulting continuous time input and output operators are unbounded with respect to the usual state space for such a system, L₂(0,1). However, in the discrete or sampled time formulation which is of primary interest to us here, they become bounded.

Let V and H be Hilbert spaces with the embeddings V ↪ H ↪ V* dense and continuous, where V* denotes the space of continuous linear functionals on V. Let 〈·,·〉 and | · | denote the H inner product and norm, respectively, and let ∥·∥, denote the norm on V. For q ∈ {Q, d_Q}, a compact metric space, let $\text{a}\left(\text{q};\cdot ,\cdot \right):\text{\hspace{0.17em}V\hspace{0.17em}}\times \text{\hspace{0.17em}V\hspace{0.17em}}\to ℝ$ be a bilinear form satisfying the following three conditions:

• i(Boundedness) |a(q; ψ_1, ψ₂) | ≤ α₀∥ψ₁∥∥ψ₂∥, ψ₁, ψ_{2 ∈ V, q ∈ Q,}
• ii(Coercivity) a(q; ψ_, ψ) + λ₀|ψ|² ≥ μ₀∥ψ∥², ψ ∈ V, q ∈ Q
• iii(Measurability) For ψ₁, ψ₂ ∈ V, the map q → a(q; ψ₁,ψ₂) is measurable with respect to all measures π(ρ), $\rho \in \mathcal{R}$.

For q ∈ {Q, d_Q} let b(q), c(q) ∈ V*, and consider an input/output system in weak form as given by

$${\langle \dot{\phi },\text{\hspace{0.17em}ψ}\rangle }_{{\text{V}}^{*},\text{V}}+\text{\hspace{0.17em}a}\left(\text{q};\text{\hspace{0.17em}φ},\text{\hspace{0.17em}ψ}\right)={\langle \text{b}\left(\text{q}\right),\text{\hspace{0.17em}ψ}\rangle }_{{\text{V}}^{*},\text{V}}\text{u},\text{y\hspace{0.17em}}={\langle \text{c}\left(\text{q}\right),\text{\hspace{0.17em}φ}\rangle }_{{\text{V}}^{*},\text{V}},\text{\hspace{0.17em}ψ},\text{\hspace{0.17em}φ\hspace{0.17em}}\in \text{\hspace{0.17em}V,}$$ (2.6)

where φ(0) = φ₀, ∈ H and 〈·,·〉_v*,v denotes the natural extension of the H inner product to the duality pairing between V and V*. If we set $\text{W}\left(0,\text{\hspace{0.17em}T}\right)=\left\{\text{ψ}:\text{\hspace{0.17em}ψ\hspace{0.17em}}\in {\text{L}}_2\left(0,\text{\hspace{0.17em}T};\text{\hspace{0.17em}V}\right),\dot{\psi }\in {\text{L}}_2\left(0,\text{\hspace{0.17em}T};{\text{V}}^{*}\right)\right\}$ and u ∈ L₂ (0, T) it can be shown (see, for example, [13]) that the system (2.6) admits a unique solution φ ∈ W(0, T) that depends continuously on u ∈ L₂(0, T). It follows that W(0, T) ⊆ C(0, T, H) and that y ∈ L₂ (0, T).

For q ∈ Q, the q-dependent bilinear form on V × V, $\text{a}\left(\text{q};\cdot ,\cdot \right):\text{V\hspace{0.17em}}\times \text{\hspace{0.17em}V\hspace{0.17em}}\to ℝ$, defines a bounded linear operator $\text{A}\left(\text{q}\right)\in \mathcal{L}\left(\text{V},{\text{V}}^{*}\right)$ by 〈A(q)ψ₁, ψ₂〉_v*,v = −a(q; ψ₁, ψ₂), for ψ₁, ψ₂ ∈ V. Then, if we let $\mathcal{H}$ denote any of the spaces V, H or V*, we can consider the linear operator A(q) to be the unbounded linear operator, $\text{A}\left(\text{q}\right)\text{:\hspace{0.17em}}{\text{D}}_{\text{q}}\subset \mathcal{H}\to \mathcal{H}$ where D_q = V in the case $\mathcal{H}={\text{V}}^{*}$, and ${\text{D}}_{\text{q}}=\left\{\text{ψ\hspace{0.17em}}\in \text{\hspace{0.17em}V:\hspace{0.17em}A}\left(\text{q}\right)\text{ψ\hspace{0.17em}}\in \mathcal{H}\right\}$ in the case $\mathcal{H}=\text{\hspace{0.17em}H}$ or $\mathcal{H}=\text{\hspace{0.17em}V}$. It can then be shown (see, for example, [2,3,22]) that A(q) is a closed, densely defined unbounded linear operator on $\mathcal{H}$ and it is the infinitesimal generator of an analytic semigroup of bounded linear operators, {e^A(q)t: t ≥ 0} on $\mathcal{H}$.

For q ∈ Q, define the bounded linear operators $\text{B}\left(\text{q}\right):ℝ\to {\text{V}}^{*}$ and $\text{C}\left(\text{q}\right):\text{\hspace{0.17em}V\hspace{0.17em}}\to ℝ$ by 〈B(q)u, ψ〉_V*,V = 〈b(q), ψ〉_V*,Vu, and C(q)ψ = 〈c(q), ψ〉_V*,V, respectively, for ψ ∈ V and $\text{u\hspace{0.17em}}\in ℝ$. The input/output system can now be written formally in the standard state space form as

$$\begin{gathered} \dot{\text{x}}\left(\text{t}\right)=\text{\hspace{0.17em}A}\left(\text{q}\right)\text{x}\left(\text{t}\right)+\text{\hspace{0.17em}B}\left(\text{q}\right)\text{u}\left(\text{t}\right), \\ \text{y}\left(\text{t}\right)=\text{\hspace{0.17em}C}\left(\text{q}\right)\text{x}\left(\text{t}\right),\text{\hspace{0.17em}t\hspace{0.17em}}>0,\text{\hspace{0.17em}x}\left(0\right)={\text{x}}_0\in H \end{gathered}$$ (2.7)

where the state x(t) = φ(t,·). Using the fact that {e^A(q)t: t ≥ 0} is an analytic semigroup on the spaces V, H and V*, it follows that a so called mild solution ([11,15]) to the state equation in (2.7) x is given by

$$x\left(t;q\right)={\text{e}}^{\text{A}\left(\text{q}\right)\text{t}}{x}_0+{\int }_0^{\text{t}}{\text{e}}^{\text{A}\left(\text{q}\right)\left(t-s\right)}\text{B}\left(\text{q}\right)\text{u}\left(\text{s}\right)ds,t\ge 0,$$ (2.8)

where x in (2.8) is in W(0, T).

Now let a sampling time τ > 0 and x₀ ∈ V be given, and consider zero order hold inputs of the form u(t) = u_i, t ∈ [iτ, (i + 1)τ), i = 0,1,2,…. Then, under the assumptions we have made here thus far (see [19]), it can be shown that using (2.8), it follows from the properties of analytic semigroups generated by regularly dissipative operators that

$$x_{i+1}=\widehat{A}\left(q\right)x_i+\widehat{B}\left(q\right)u_i,y_i=\widehat{C}\left(q\right)x_i,i=0,1,2,\dots ,$$ (2.9)

where $\widehat{\text{A}}\left(\text{q}\right)={\text{e}}^{\text{A}\left(\text{q}\right)\tau }\in \mathcal{L}(\text{V},\text{\hspace{0.17em}V})$, $\widehat{\text{B}}\left(\text{q}\right)={\int }_0^{\tau }{\text{e}}^{\text{A}\left(\text{q}\right)\text{s}}\text{B}\left(\text{q}\right)\text{ds\hspace{0.17em}}\in \mathcal{L}(ℝ,\text{\hspace{0.17em}V})$, $\widehat{C}\left(q\right)=\text{\hspace{0.17em}C}\left(\text{q}\right)=\text{\hspace{0.17em}c}\left(\text{q}\right)\in \mathcal{L}(\text{V},ℝ)={\text{V}}^{*}$, x_i = x(iτ) and y_i = y(iτ), i = 0,1,2, ….

Boundedness of the operators $\widehat{\text{A}}\left(\text{q}\right)$ and $\widehat{\text{B}}(\text{q})$ in (2.9) follows once again from the fact that {e^A(q)t: t ≥ 0} is an analytic semigroup on V, H and V* ([2,3,13,22]). Indeed, the coercivity assumption, Assumption (ii) (possibly together with a change of variables), implies that we may assume without loss of generality that the operator A(q) from either H into H or V into V*, is invertible with bounded inverse. Consequently, it follows that

$$\begin{gathered} \widehat{\text{B}}\left(\text{q}\right)={\int }_0^{\tau }{\text{e}}^{\text{A}\left(\text{q}\right)\text{s}}\text{B}\left(\text{q}\right)\text{ds}={\text{A}{\left(\text{q}\right)}^{-1}{\text{e}}^{\text{A}\left(\text{q}\right)\text{s}}\text{B}\left(\text{q}\right)|}_0^{\tau } \\ =\left(\widehat{\text{A}}\left(\text{q}\right)-\text{\hspace{0.17em}I}\right)\text{A}{\left(\text{q}\right)}^{-1}\text{B}\left(\text{q}\right) \\ =\left(\widehat{\text{A}}\left(\text{q}\right)-\text{I}\right)\text{A}{\left(\text{q}\right)}^{-1}\text{b}\left(\text{q}\right)\in \mathcal{L}(\text{V},\text{\hspace{0.17em}R}). \end{gathered}$$

Let Q be a closed and bounded subset of ${ℝ}^2$ endowed with the Euclidean metric, let H = L₂ (0,1) together with the standard inner product $\langle {\psi }_1,{\psi }_2\rangle ={\int }_0^1{\psi }_1(x){\psi }_2(x)dx$, and norm denoted by | · |, and let V be the Sobolev space V = H₁(0,1) together with its standard inner product $\langle \langle {\psi }_1,{\psi }_2\rangle \rangle ={\int }_0^1{\psi }_1(x){\psi }_2(x)dx+{\int }_0^1{\psi }_1^{\prime }(x){\psi }_2^{\prime }(x)dx$ and norm denoted by ∥·∥. Then we have the usual dense and continuous embeddings 𝑉 ↪ 𝐻 ↪ 𝑉*, where 𝑉* denotes the space of distributions dual to 𝑉. The forms and functions $a(q;\cdot ,\cdot ):V\times V\to ℝ$, $b(q;\cdot ):V\to ℝ$ and $c(\cdot ):V\to ℝ$ are given by

$$a\left(q;{\psi }_1,{\psi }_2\right)={\psi }_1\left(0\right){\psi }_2\left(0\right)+q_1{\int }_0^1{\psi }_1^{\prime }\left(x\right){\psi }_2^{\prime }\left(x\right)dx,{\psi }_1,{\psi }_2\in V$$ (2.10)

〈b(q), ψ〉_v*,v = q₂ ψ(1), and 〈c(q), ψ〉_v*,v = ψ(0), for ψ ∈ V. It follows that b(q) = q₂ δ (· − 1) ∈ V* and c(q) = δ ∈ V*, where δ denotes the Dirac delta distribution, or unit impulse at zero. It is not difficult to argue that Assumptions (i)-(iii) hold for the form a(·; ·, ·) as given in (2.10) above. See [19] for a more abstract, detailed and rigorous description of how we deal with input signals on the boundary of the domain.

3. Systems Governed by Regularly Dissipative Operators with Random Parameters

In this section, we use ideas from [9] to consider systems of the form (2.1)–(2.5) with the parameters q ∈ Q random. Let 𝓆 be a p dimensional random vector with support in ${\Pi }_{i=1}^p\left[a_i,b_i\right]$ where $-\infty <\overline{\alpha }<a_i<b_i<\overline{\beta }<\infty$. Let $\overrightarrow{a},\overrightarrow{b}\in {ℝ}^p$ be given by $\overrightarrow{a}=\left[a_i\right]$ and $\overrightarrow{b}=\left[b_i\right]$, and let Θ be a parameter set that is a compact subset of ${ℝ}^r$ for some r. We assume that 𝓆 has distribution described by the absolutely continuous cdf, $F\left(q;\overrightarrow{a},\overrightarrow{b},\theta \right)$, or equivalently by the push forward measure $\pi =\pi \left(\overrightarrow{a},\overrightarrow{b},\theta \right)$, where θ ∈ Θ.

Let a(q; ·, ·) denote a sesquilinear form on V × V satisfying the conditions (i) - (iii) given in Section 2, and in particular that the function q ↦ a(q; ν, w) is π–measurable for any ν, w ∈ V. By appropriately defining new function spaces, it is possible to embed the randomness in the sesquilinear form a(𝓆; ⋅, ⋅), or equivalently in the operator, A(𝓆), in (2.7) into these spaces. Consequently, the input output system (2.7) can be stated in a way that makes the stochasticity in the operators, the state and the output effectively invisible and thus amenable to analysis and approximation using standard (deterministic) linear semigroup theory. In effect, the random variables are treated the same way as the space variables in the underlying PDE.

Toward this end, we define $\mathcal{V}=L_{\pi }^2(Q;V)$ and $\mathcal{H}=L_{\pi }^2(Q;H)$. It then follows that $\mathcal{V}$, $\mathcal{H}$, ${\mathcal{V}}^{*}$ form a Gelfand triple of separable Hilbert spaces with $\mathcal{V}\subseteq \mathcal{H}\subseteq {\mathcal{V}}^{*}$ by identifying $\mathcal{H}$ with its dual ${\mathcal{H}}^{*}$ and identifying ${\mathcal{V}}^{*}$ with the Bochner space $L_{\pi }^2\left(Q;V^{*}\right)$. We also define the π-averaged sesquilinear form $a(\cdot ,\cdot ):\mathcal{V}\times \mathcal{V}\to ℂ$ by

$$a(v,w)={\int }_{Q}a\left(q;v\left(q\right),w\left(q\right)\right)d\pi =E_{\pi }\left[a\left(\mathcal{q};v\left(\mathcal{q}\right),w\left(\mathcal{q}\right)\right)\right]$$ (3.1)

where, υ, $w\in \mathcal{V}$. Assumptions (i) and (ii) guarantee that a(·, ·) given in (3.1) is a bounded and coercive sesqui-linear form on $\times \mathcal{V}$, and therefore that -a induces a bounded linear map $\mathcal{A}$ from $\mathcal{V}$ into ${\mathcal{V}}^{*}$. It follows (see, once again, for example, [2,3,22]) that the operator $\mathcal{A}:\text{ Dom}(\mathcal{A})\subseteq \mathcal{H}\to \mathcal{H}$ where $\text{Dom}(\mathcal{A})=\left\{v\in \mathcal{V}:\text{\hspace{0.17em}Av\hspace{0.17em}}\in \mathcal{H}\right\}$ is the infinitesimal generator of an analytic semigroup of bounded linear operators $\mathcal{T}=\left\{\mathcal{T}(t):t\ge 0\right\}$ on $\mathcal{H}$, and, moreover, that $\mathcal{T}$ can be extended to an analytic semigroup on ${\mathcal{V}}^{*}$ and restricted to an analytic semigroup on $\mathcal{V}$.

We assume that the maps q ↦ 〈b(q), ψ(q)〉_v*,v, and q ↦ 〈c(q), ψ(q)〉_v*,v are π–measurable for any $\text{ψ\hspace{0.17em}}\in \mathcal{V}$, and that ∥b (q)∥_v* and ∥c(q) ∥_v* are uniformly bounded for q ∈ Q. (Assuming that b, $c\in {\mathcal{V}}^{*}$ would be fine as well.) We then define the two bounded linear operators $\mathcal{B}:ℝ\to {\mathcal{V}}^{*}$ and $\mathcal{C}:\mathcal{V}\to ℝ$ by the expressions $\langle \mathcal{B}\text{u},v\rangle ={\int }_Q{\langle \text{b}\left(\text{q}\right),v(q)\rangle }_{{\text{V}}^{*},\text{\hspace{0.17em}V}}d\pi \left(q\right)u=E_{\pi }\left[{\langle \text{b}(\mathcal{q}),v(\mathcal{q})\rangle }_{{\text{V}}^{*},\text{V}}\right]u$ and $\mathcal{C}v={\int }_Q{\langle \text{c}(\text{q}),v(q)\rangle }_{{\text{V}}^{*},\text{V}}d\pi (q)=E_{\pi }\left[{\langle \text{c}(q),v(q)\rangle }_{{\text{V}}^{*},\text{V}}\right]$, respectively, for $v\in \mathcal{V}$ and $u\in ℝ$.

We then consider the continuous time input/output system set in the spaces $\mathcal{V}$, $\mathcal{H}$, ${\mathcal{V}}^{*}$, given by

$$\dot{x}\left(\text{t}\right)=\mathcal{A}x\left(\text{t}\right)+\mathcal{B}\text{u}\left(\text{t}\right),$$ (3.2)

$$𝓎\left(t\right)=\mathcal{C}x\left(\text{t}\right),t>0,x\left(0\right)=x_0\in \mathcal{H}.$$ (3.3)

The mild solution to the initial value problem given in (3.2), (3.3) is then given by

$$x\left(\text{t}\right)=\mathcal{T}\left(t\right)x_0+{\int }_0^t\mathcal{T}(t-s)\mathcal{B}\text{u}\left(\text{s}\right)ds,t\ge 0,$$ (3.4)

and therefore, from (3.3), for 𝑡 ≥ 0, that

$$𝓎\left(t\right)=\mathcal{C}\mathcal{T}\left(t\right)x_0+{\int }_0^t\mathcal{C}\mathcal{T}\left(t-s\right)\mathcal{B}\text{u}\left(\text{s}\right)ds,$$ (3.5)

Once again let the sampling time τ > 0 be given and consider zero order hold inputs of the form u(t) = u_i, t ∈ [iτ, (i + 1)τ), i = 0,1,2, …. Set $x_{\text{i}}=x(\text{i}\tau )$ and let $y_{\text{i}}=y(\text{i}\tau )$, i = 0,1,2, …. It then follows from the variation of parameters formula for systems governed by analytic semigroups, (3.4), and (3.5) that

$$x_{j+1}=\widehat{\mathcal{A}}{x}_j+\widehat{B}{u}_j,{𝓎}_j=\widehat{C}j,j=0,1,2,\dots$$ (3.6)

with $x_0\in \mathcal{V}$, where $\widehat{\mathcal{A}}=\mathcal{T}(\tau )\in \mathcal{L}(\mathcal{V},\mathcal{V})$, $\widehat{\mathcal{B}}={\int }_0^{\tau }\mathcal{T}(s)\mathcal{B}\text{ds\hspace{0.17em}}\in \mathcal{L}(ℝ,\mathcal{V})$, and $\widehat{C}=\mathcal{C}\in \mathcal{L}(\mathcal{V},ℝ)={\mathcal{V}}^{*}$. Boundedness of the operators $\widehat{\mathcal{A}}$ and $\widehat{\mathcal{B}}$ follows from the fact that $\left\{\mathcal{T}(t):\text{\hspace{0.17em}t\hspace{0.17em}}\ge 0\right\}$ is an analytic semigroup on $\mathcal{V}$, $\mathcal{H}$ and ${\mathcal{V}}^{*}([2,3,13,22])$. Once again, without loss of generality, we may assume that $\mathcal{A}:\text{ Dom}(\mathcal{A})\subset {\mathcal{V}}^{*}\to {\mathcal{V}}^{*}$ is invertible with bounded inverse, from which it follows that $\widehat{\mathcal{B}}={\int }_0^{\tau }\mathcal{T}(s)\mathcal{B}\text{ds\hspace{0.17em}}={\mathcal{A}}^{-1}\mathcal{T}(s){\mathcal{B}|}_0^{\tau }=(\widehat{\mathcal{A}}-\text{I}){\mathcal{A}}^{-1}\mathcal{B}\in \mathcal{L}(ℝ,\mathcal{V})={\mathcal{V}}^{*}$.

It can be shown ([9,17]) that $x\text{(}t\text{)}$ given by (3.4) agrees π-almost everywhere with x(t) given in (2.8) for all t ≥ 0, and consequently it follows that $\mathcal{y}\text{(t) = }\mathcal{C}x\text{(t) =\hspace{0.17em}}{E}_{\pi }[\text{y}(\text{t};\mathcal{q})]=E_{\pi }[\text{C}(\mathcal{q})\text{x}(\text{t};\mathcal{q})]$, for all t ≥ 0, and therefore that

$${\mathcal{y}}_i=\widehat{C}{x}_i=E_{\pi }\left[y_i(\mathcal{q})\right]=E_{\pi }\left[\widehat{C}\left(\mathcal{q}\right){\text{x}}_i\left(\mathcal{q}\right)\right].$$ (3.7)

We refer to (3.2),(3.3) or (3.6),(3.7) as our population model.

4. Finite Dimensional Approximation, Convergence and Computational Considerations

In light of the final expression in Section 3, we may formulate our estimation/optimization problem (1.6) as follows: $(\mathcal{P})$ Given v data sets $\left({\tilde{u}}_i,{\tilde{y}}_i\right)={\left({\left\{{\tilde{u}}_{i,j}\right\}}_{j=0}^{{\mu }_i-1},{\left\{{\tilde{y}}_{i,j}\right\}}_{j=0}^{{\mu }_i}\right)}_{i=1}^v$, determine ${\overrightarrow{a}}^{*}=\left[a_i^{*}\right]$, ${\overrightarrow{b}}^{*}=\left[b_i^{*}\right]$ and θ* ∈ Θ, feasible, which minimize

$$J\left(\overrightarrow{a},\overrightarrow{b},\theta \right)={\sum }_{i=1}^v{{\sum }_{j=0}^{{\mu }_i}\left|{\mathcal{y}}_j\left({\tilde{u}}_i,\overrightarrow{a},\overrightarrow{b},\theta \right)-{\tilde{y}}_{i,j}\right|}^2,$$

where ${\left\{{\mathcal{y}}_j\left({\tilde{u}}_i,\overrightarrow{a},\overrightarrow{b},\theta \right)\right\}}_{j=0}^{{\mu }_i}$ is given as in (3.6) with $u_j={\tilde{u}}_{i,j},j=0,1,2,\dots ,{\mu }_i-1,\text{ and }i=1,2,\dots ,v$. ∎

Henceforth we assume that the measures $\pi =\pi (\overrightarrow{a},\overrightarrow{b},\theta )$ are described by a family of joint density functions $f=f(\overrightarrow{a},\overrightarrow{b},\theta )$, and let $\overline{Q}={\Pi }_{i=1}^p[\overline{\alpha },\overline{\beta }]$. We will require the following assumptions on the family of densities $f(\overrightarrow{a},\overrightarrow{b},\theta )$:

• ivThe maps $(\overrightarrow{a},\overrightarrow{b},\theta )\mapsto f(q;\overrightarrow{a},\overrightarrow{b},\theta )$ are continuous on ${ℝ}^p\times {ℝ}^p\times \text{\hspace{0.17em}Θ}$ for π-almost every $q\in \overline{Q}={\prod }_{i=1}^p\left[\overline{\alpha },\overline{\beta }\right]$.
• v
  There exist positive constants γ, δ such that

  $$0<\gamma \le f(q;\overrightarrow{a},\overrightarrow{b},\theta )\le \delta <\infty ,$$

  for π-almost every $q\in \overline{Q}={\prod }_{i=1}^p\left(\overline{\alpha },\overline{\beta }\right)$.

Assumptions (i)-(v) are sufficient to establish that the maps $(\overrightarrow{a},\overrightarrow{b},\theta )\mapsto {\mathcal{y}}_k\left({\tilde{u}}_i,\overrightarrow{a},\overrightarrow{b},\theta \right)$ are continuous for k = 0,1,2, …,μ_i − 1, and i = 1,2, …,ν, and therefore that the map $(\overrightarrow{a},\overrightarrow{b},\theta )\mapsto J(\overrightarrow{a},\overrightarrow{b},\theta )$ is continuous. Consequently it follows from compactness that problem $(\mathcal{P})$ has a solution.

Solving problem $(\mathcal{P})$ requires finite dimensional approximation. For each N = 1,2, …., let $\overline{\mathcal{H}}=L_{\pi }^2(\overline{Q};H)$, and $\overline{\mathcal{V}}=L_{\pi }^2(\overline{Q};V)$. Let ${\overrightarrow{a}}^{\text{N}}=\left[a_i^N\right]$ and ${\overrightarrow{b}}^{\text{N}}=\left[b_i^N\right]$ be vectors in ${ℝ}^p$ with $-\infty <\overline{\alpha }<a_i^N<b_i^N<\overline{\beta }<\infty$, and let θ^N ∈ Θ, and set $Q^N={\prod }_{i=1}^p\left[a_i^N,b_i^N\right]$, ${\mathcal{H}}^N=L_{\pi }^2\left(Q^N;H\right)$, and ${\mathcal{V}}^N=L_{\pi }^2\left(Q^N;V\right)$. Let ${\mathcal{U}}^N$ be a finite dimensional subspace of ${\mathcal{V}}^N$. Let ${\mathcal{J}}^{\text{N}}:\overline{\mathcal{H}}\to {\mathcal{H}}^N$ be such that $\text{Im}\left({\mathcal{J}}^{\text{N}}\right)={\mathcal{H}}^N$ and ${\left|{\mathcal{J}}^{\text{N}}\text{x}\right|}_{{\mathcal{H}}^N}\le {\left[\text{x}\right]}_{\overline{\mathcal{H}}}$. Let ${\mathcal{P}}^{\text{N}}:{\mathcal{H}}^N\to {\mathcal{U}}^N$ be the orthogonal projection of ${\mathcal{H}}^N$ onto ${\mathcal{U}}^N$ and define ${\mathcal{J}}^{\text{N}}≔{\mathcal{P}}^{\text{N}}\circ {\mathcal{J}}^{\text{N}}$. Define ${\mathcal{A}}^{\text{N}}:{\mathcal{U}}^N\to {\mathcal{U}}^N$ by

$$\begin{gathered} \langle {\mathcal{A}}^{\text{N}}{\text{v}}^{\text{N}},{\text{w}}^{\text{N}}\rangle =-a\left({\text{v}}^{\text{N}},{\text{w}}^{\text{N}}\right) \\ =-{\int }_{Q^N}a\left(q;{\text{v}}^{\text{N}}\left(q\right),{\text{w}}^{\text{N}}\left(q\right)\right)d{\pi }^N\left(q\right) \\ =-{\int }_{Q^N}a\left(q;{\text{v}}^{\text{N}}\left(q\right)\text{,\hspace{0.17em}}{\text{w}}^{\text{N}}(q)\right)f\left(q;{\overrightarrow{a}}^{\text{N}},{\overrightarrow{b}}^{\text{N}},{\theta }^N\right)dq, \end{gathered}$$

where, v^N, ${\text{w}}^{\text{N}}\in {\mathcal{U}}^N$.

Using assumptions (i)-(v), it can then be shown (see Sirlanci et. al. [18,19]) that ${\mathcal{A}}^{\text{N}}\in \text{\hspace{0.17em}G}\left(\text{M},{\text{λ}}_0\right)$ on ${\mathcal{U}}^N$ (i.e. that ${\left|e^{{\mathcal{A}}^{\text{N}}t}\right|}_{{\mathcal{H}}^N}\le M{e}^{{\text{λ}}_{\text{o}}t}$, t ≥ 0), where the constants M and λ₀ are independent of N. Suppose further that for some λ ≥ λ₀, ${\left|{\mathcal{J}}^{\text{N}}{\text{R}}_{\text{λ}}(\mathcal{A})\text{x\hspace{0.17em}}-{\text{R}}_{\text{λ}}\left({\mathcal{A}}^{\text{N}}\right){\mathcal{J}}^{\text{N}}\text{x}\right|}_{{\mathcal{H}}^N}\to 0$ as N → ∞, for every $\text{x\hspace{0.17em}}\in \overline{\mathcal{H}}$, where ${\text{R}}_{\lambda }(\mathcal{A})$ and ${\text{R}}_{\text{λ}}\left({\mathcal{A}}^{\text{N}}\right)$ denote respectively the resolvent operators $\mathcal{A}$ and ${\mathcal{A}}^{\text{N}}$ at λ. It then follows, from a version ([1,18,19]) of the Trotter Kato theorem (see, for example, [11,15]) that allows for the state spaces to depend on the parameters, $\left({\overrightarrow{a}}^{\text{N}},{\overrightarrow{b}}^{\text{N}},{\theta }^N\right)$, that

$${\left|{\mathcal{J}}^{\text{N}}\mathcal{T}\left(t\right)\text{x\hspace{0.17em}}-e^{{\mathcal{A}}^{\text{N}}t}{\mathcal{J}}^{\text{N}}\text{x}\right|}_{{\mathcal{H}}^N}\to 0\text{\hspace{0.17em}as\hspace{0.17em}N\hspace{0.17em}}\to \infty$$

for $\text{x\hspace{0.17em}}\in \overline{\mathcal{H}}$, uniformly in t in compact intervals of [0, ∞).

Define the operators ${\mathcal{B}}^{\text{N}}:ℝ\to {\mathcal{U}}^N$ and ${\mathcal{C}}^{\text{N}}:{\mathcal{U}}^N\to ℝ$ by

$$\langle {\mathcal{B}}^{\text{N}}u,{\text{v}}^{\text{N}}\rangle =\underset{Q^N}{\int }{\langle \text{b}\left(\text{q}\right),{\text{v}}^{\text{N}}\left(q\right)\rangle }_{{\text{V}}^{*},\text{V}}f\left(q;{\overrightarrow{a}}^{\text{N}},{\overrightarrow{b}}^{\text{N}},{\theta }^N\right)dqu,$$

and

$${\mathcal{C}}^{\text{N}}{\text{v}}^{\text{N}}={\int }_{Q^N}{\langle \text{c}\left(\text{q}\right),{\text{v}}^{\text{N}}\left(q\right)\rangle }_{{\text{V}}^{*},\text{V}}f\left(q;{\overrightarrow{a}}^{\text{N}},{\overrightarrow{b}}^{\text{N}},{\theta }^N\right)dq,$$

where ${\text{v}}^{\text{N}}\in {\mathcal{U}}^N$, and $u\in ℝ$ and consider the sequence of finite dimensional optimization problems given by

$\left({\mathcal{P}}_{\mathit{N}}\right)$ Given ν data sets ${\left\{\left({\tilde{u}}_i,{\tilde{y}}_i\right)\right\}}_{i=1}^v$, determine ${\overrightarrow{a}}^{\text{N}*}=\left[a_i^{N*}\right]$, ${\overrightarrow{b}}^{\text{N}*}=\left[b_i^{N*}\right]$ and θ^N* ∈ Θ, feasible, which minimize

$$J^N\left(\overrightarrow{a},\overrightarrow{b},\theta \right)={\sum }_{i=1}^v{\sum }_{j=0}^{{\mu }_i}{\left|{\mathcal{y}}_j^N\left({\tilde{u}}_i,\overrightarrow{a},\overrightarrow{b},\theta \right)-{\tilde{y}}_{i,j}\right|}^2,$$

where ${\left\{{\mathcal{y}}_j^N\left({\tilde{u}}_i,\overrightarrow{a},\overrightarrow{b},\theta \right)\right\}}_{j=0}^{{\mu }_i}$ is given by

$$x_{i,j+1}^N={\widehat{\mathcal{A}}}^N{x}_{i,j}^N+{\widehat{\mathcal{B}}}^N{\tilde{u}}_{i,j},{𝓎}_{i,j}^N={\mathcal{C}}^N{x}_{i,j}^N,j=0,1,2,\dots {\mu }_i,$$ (4.1)

with $x_{i,0}^N=0\in {\mathcal{U}}^N$, where ${\widehat{\mathcal{A}}}^N=e^{{\mathcal{A}}^{\text{N}}\tau }\in \mathcal{L}\left({\mathcal{U}}^N,{\mathcal{U}}^N\right)$, ${\widehat{\mathcal{B}}}^N={\int }_0^{\tau ,0}{e}^{{\mathcal{A}}^{{\text{N}}_s}}{\mathcal{B}}^{\text{N}}\text{ds\hspace{0.17em}}\in \mathcal{L}\left(ℝ,{\mathcal{U}}^N\right)$, and ${\widehat{\mathcal{C}}}^N={\mathcal{C}}^{\text{N}}\in \mathcal{L}\left({\mathcal{U}}^N,ℝ\right)$. ∎

We can then prove the following convergence theorem (see [18,19]).

Theorem 4.1 Let assumptions (i)-(v) hold. Then for each N = 1,2,…., the problems $\left({\mathcal{P}}_N\right)$ given above admit a solution ${\widehat{\rho }}^N=\left({\overrightarrow{a}}^{\text{N}*},{\overrightarrow{b}}^{\text{N}*},{\theta }^{\text{N}*}\right)$. Suppose further that

• vi${\left|{\mathcal{P}}^{\text{N}}{\text{v}}^N-{\text{v}}^N\right|}_{{\mathcal{V}}^N}\to 0$ as N → ∞, ${\text{v}}^N\in {\mathcal{V}}^N$.

Then there exists a subsequence, ${\left\{{\widehat{\rho }}^{\text{N}j}\right\}}_{j=1}^{\infty }$, with ${\widehat{\rho }}^{{\text{N}}_j}=\left({\overrightarrow{a}}^{{\text{N}}_j*},{\overrightarrow{b}}^{{\text{N}}_j^{*}},{\theta }^{{\text{N}}_j^{*}}\right)\to \left({\overrightarrow{a}}^{*},{\overrightarrow{b}}^{*},{\theta }^{*}\right)=\widehat{\rho }$ as j → ∞, and $\widehat{\rho }=\left({\overrightarrow{a}}^{*},{\overrightarrow{b}}^{*},{\theta }^{*}\right)$ a solution to problem $(\mathcal{P})$.

The optimization problems $\left({\mathcal{P}}_{\mathit{N}}\right)$ are solved numerically, typically via an iterative gradient-based scheme. Once a basis for the space ${\mathcal{U}}^N$ is chosen, the operators in (4.1) can be represented as matrices and the value of the cost functional J and its gradient can then be computed. If for N = 1, 2, …, ${\mathcal{U}}^N=\text{\hspace{0.17em}span}{\left\{{\psi }_j^N\right\}}_{j=1}^{K^N}\subset {\mathcal{U}}^N$, then the matrix representation for ${\mathcal{A}}^{\text{N}}\in \mathcal{L}\left({\mathcal{U}}^N,{\mathcal{U}}^N\right)$ is given by ${\left[{\mathcal{A}}^{\text{N}}\right]}_{ij}=-{\left[{\langle {\psi }_i^N,{\psi }_j^N\rangle }_{{\mathcal{H}}^N}\right]}^{-1}\left[\mathcal{a}\left({\psi }_i^N,{\psi }_j^N\right)\right]$, for i, j = 1,2,…, K^N. Matrix representations for the operators ${\mathcal{B}}^{\text{N}}$ and ${\mathcal{C}}^{\text{N}}$ are computed analogously. The matrix representations for ${\mathcal{A}}^{\text{N}}$, ${\mathcal{B}}^{\text{N}}$, and ${\mathcal{C}}^{\text{N}}$ can then be used in a straight forward manner to compute the matrix representations for the operators ${\widehat{\mathcal{A}}}^{\text{N}}$, ${\widehat{\mathcal{B}}}^{\text{N}}$, and ${\widehat{\mathcal{C}}}^{\text{N}}$ appearing in (4.1).

We compute $\overrightarrow{\nabla }{J}^N$ using the adjoint [12]. For each i = 1,2, …, ν, set $v_{i,j}^N={\left[2\left({\widehat{C}}^N{x}_{i,j}^N-{\tilde{y}}_{i,j}\right),0,\dots ,0\right]}^T\in {ℝ}^{K^N}$, j = 0,1,2, …, μ_i and define the adjoint systems

$$Z_{i,j-1}^N={\left[{\widehat{\mathcal{A}}}^{\text{N}}\right]}^T{Z}_{i,j}^N+v_{i,j-1}^N.$$ (4.2)

Then $\overrightarrow{\nabla }{J}^N$ at $(\overrightarrow{a},\overrightarrow{b},\theta )$ can then be computed as

$$\overrightarrow{\nabla }{J}^N\left(\rho \right)=\sum _{i=1}^v\sum _{j=1}^{{\mu }_i}{\left[Z_{i,j}^N\right]}^T\left\{\frac{\partial {\widehat{\mathcal{A}}}^{\text{N}}}{\partial \rho }{x}_{i,j-1}^N-{\left({\mathcal{A}}^{\text{N}}\right)}^{-1}\left\{\frac{\partial {\mathcal{A}}^{\text{N}}}{\partial \rho }{\left({\mathcal{A}}^{\text{N}}\right)}^{-1}\left({\widehat{\mathcal{A}}}^{\text{N}}-I\right)\frac{\partial {\widehat{\mathcal{B}}}^{\text{N}}}{\partial \rho }{\tilde{u}}_{i,j-1}-\frac{\partial {\widehat{\mathcal{A}}}^{\text{N}}}{\partial \rho }{\widehat{\mathcal{B}}}^{\text{N}}{\tilde{u}}_{i,j-1}-\left({\widehat{\mathcal{A}}}^{\text{N}}-I\right)\frac{\partial {\widehat{\mathcal{B}}}^{\text{N}}}{\partial \rho }{\tilde{u}}_{i,j-1}\right\}\right\}+{\sum }_{i=1}^v{\sum }_{j=0}^{{\mu }_i}{\left({\mathcal{y}}_j^N-{\tilde{y}}_{i,j}\right)}^T\frac{\partial {\widehat{\mathcal{C}}}^{\text{N}}}{\partial \rho }{x}_{i,j}^N,$$ (4.3)

where $\rho =(\overrightarrow{a},\overrightarrow{b},\theta )$.

The tensor $\frac{\partial {\widehat{\mathcal{A}}}^{\text{N}}}{\partial q}$ can be computed at the same time as the matrix ${\widehat{\mathcal{A}}}^{\text{N}}$ is computed using the sensitivity equations. For t ≥ 0 set ${\text{Φ}}^N(t)=e^{{\mathcal{A}}^{\text{N}}t}$. Then Φ^N is the unique principal fundamental matrix solution to the initial value problem

$${\dot{\Phi }}^N={\mathcal{A}}^{\text{N}}{\text{Φ}}^N,{\text{Φ}}^N\left(0\right)=I.$$ (4.4)

Setting Ψ^N = ∂Φ^N/∂ρ, differentiating (4.4) with respect to ρ, interchanging the order of differentiation, and using the product rule, we obtain

$${\dot{\Psi }}^N={\mathcal{A}}^{\text{N}}{\text{Ψ}}^n+\left(\partial {\mathcal{A}}^{\text{N}}/\partial \rho \right){\text{Φ}}^N,{\text{Ψ}}^N\left(0\right)=0,$$ (4.5)

Combining the two initial value problems given in (4.4) and (4.5), and then solving we obtain

$$\left[\begin{array}{c}\frac{\partial {\widehat{\mathcal{A}}}^{\text{N}}}{\partial \rho }\\ {\widehat{\mathcal{A}}}^{\text{N}}\end{array}\right]=\left[\begin{array}{c}{\text{Ψ}}^N(\tau )\\ {\text{Φ}}^N(\tau )\end{array}\right]=\text{\hspace{0.17em}exp}\left(\left[\begin{array}{cc}{\mathcal{A}}^{\text{N}}& \left(\partial {\mathcal{A}}^{\text{N}}/\partial \rho \right)\\ 0& {\mathcal{A}}^{\text{N}}\end{array}\right]\tau \right)\left[\begin{array}{l}0\hfill \\ I\hfill \end{array}\right].$$ (4.6)

5. Consistency of the Estimator

In the context of the alcohol biosensor problem of interest to us here, the estimator, $\widehat{\rho }$ defined in (1.6) is given by, $\widehat{\rho }=\left({\overrightarrow{a}}^{*},{\overrightarrow{b}}^{*},{\theta }^{*}\right)$, where ${\overrightarrow{a}}^{*}=\left[a_i^{*}\right]$, ${\overrightarrow{b}}^{*}=\left[b_i^{*}\right]$ and θ* ∈ Θ are a solution to problem $(\mathcal{P})$ in Section 4.1. Under the following assumptions, using Theorem 4.2 in [4], it is possible to establish a consistency result for the estimator $\widehat{\rho }$.

1. The measurement noise {ε_i,j} in (1.5) is i.i.d. with respect to a probability space {Ω, Σ, P} with E_P [ε_i,j] = 0 and Var[ε_i,j] = σ².

2. The feasible set of parameters $\mathcal{R}$ is compact (i.e. closed and bounded since it is finite dimensional) and has nonempty interior.

3. For = 1,2, …,ν, μ_i = μ, and μτ = T, for some positive integer μ and some T > 0, where τ is the sampling time defined in Section 3.

4. Let V = {V_i,j} be as is given in (1.5) for some ρ₀ ∈ int $\mathcal{R}$ with ${\tilde{y}}_{i,j}\left({\tilde{u}}_i,{\rho }_0\right)$ as given in the definition of problem $(\mathcal{P})$.

5. For each i = 1,2,…, ν, and $\mathcal{y}\left(t;{\tilde{u}}_i,\rho \right)=\mathcal{y}\left(t;{\tilde{u}}_i,\overrightarrow{a},\overrightarrow{b},\theta \right)=\mathcal{y}(t)$ with $\mathcal{y}(t)$ given by (3.5), ρ₀ is the unique minimizer of J_i,0 in $\mathcal{R}$, where

$$J_{i,0}(\rho )={\sigma }^2+{\int }_0^t{\left(\mathcal{y}\left(t;{\tilde{u}}_i,{\rho }_0\right)-\mathcal{y}\left(t;{\tilde{u}}_i,\rho \right)\right)}^{2}dt.$$

A straight forward application of Theorem 4.2 in [4] can then be used to establish the following lemma.

Lemma 5.1 Assume that Assumptions (i)-(v) and (a) – (e) hold. Then there exists an A ∈ Σ with P(A) = 1 such that for all ω ∈ A and J_i,μ(ρ; V) as given in (1.6) with α_i,j = 1, we have

$$\frac{1}{v}\sum _{i=1}^v\left\{\frac{1}{\mu }{J}_{i,\mu }\left(\rho ;V(\omega )\right)-J_{i,0}(\rho )\right\}\to 0$$

as ν, μ → ∞, τ → 0, with μτ = T, uniformly in ρ, for $\rho \in \mathcal{R}$.

Theorem 5. 1 (Consistency of the estimator $\widehat{\rho }$) Let $\widehat{\rho }\in \mathcal{R}$ be as defined in (1.6) together with problem $(\mathcal{P})$. Then under the assumptions of Lemma 5.1, the estimator $\widehat{\rho }=\left({\overrightarrow{a}}^{*},{\overrightarrow{b}}^{*},{\theta }^{*}\right)$ is consistent for ρ₀. That is $\widehat{\rho }\stackrel{P}{\to }{\rho }_0$, as ν, μ → ∞, τ → 0, with μτ = T.

Proof The proof is quite similar to the proof of Theorem 4.3 in [4]. For ν = 1,2,…., let $J_0(\rho )=\frac{1}{v}{\sum }_{i=1}^v{J}_{i,0}(\rho )$, let A ∈ Σ be as in the statement of Lemma 5.1, let ω ∈ A be fixed, and let δ > 0 be arbitrary. Then Lemma 5.1 implies that there exists an open local neighborhood of ρ₀ of radius δ, N_δ(ρ₀), such that by Assumption (e) there exists an ε > 0 for which J₀(ρ) − J₀(ρ₀) > ε, for all $\rho \in {\mathcal{R}}_{\delta }$, where ${\mathcal{R}}_{\delta }$ is the compact (i.e. closed and bounded) set given by $\mathcal{R}\cap N_{\delta }{\left({\rho }_0\right)}^c$. Now once again by Lemma 5.1, there exist ν₀, μ₀, τ₀, such that for all ν > ν₀, μ > μ₀, τ < τ₀ with μτ = T, $\left|\frac{1}{\nu \mu }J(\rho ,V(\omega ))-J_0(\rho )\right|<\epsilon /4$, $\rho \in \mathcal{R}$, where J is as given in (1.6) or problem $(\mathcal{P})$. Then with ν > ν₀, μ > μ₀, τ < τ₀, μτ = T and $\rho \in {\mathcal{R}}_{\delta }$,

$$\frac{1}{v\mu }\left(J(\rho ,V(\omega ))-J\left({\rho }_0,V(\omega )\right)\right)=\frac{1}{v\mu }J(\rho ,V(\omega ))-J_0(\rho )+J_0(\rho )-J_0\left({\rho }_0\right)+J_0\left({\rho }_0\right)-\frac{1}{v\mu }J\left({\rho }_0,V(\omega )\right)\ge -\frac{\epsilon }{4}+\epsilon -\frac{\epsilon }{4}>0.$$

But $J(\widehat{\rho },V(\omega ))\le J\left({\rho }_0,V(\omega )\right)$. It follows that $\widehat{\rho }\in N_{\delta }\left({\rho }_0\right)$ if ν > ν₀, μ > μ₀, τ < τ₀, with μτ = T. Since δ > 0 was arbitrary and P (A) = 1, we have that $\widehat{\rho }\stackrel{P}{\to }{\rho }_0$, as ν, μ → ∞, τ → 0, with μτ = T.

6. Numerical Results

The approximating finite dimensional subspaces ${\mathcal{U}}^N$ were constructed as follows based on the discretization of (η, q₁, q₂)-space. For each n = 1,2,…., let ${\left\{{\phi }_j^n\right\}}_{j=0}^n$ denote the set of standard linear B-splines on the interval [0,1] defined with respect to the usual uniform mesh, ${\left\{j/n\right\}}_{j=0}^n$, and set $H^n=\text{\hspace{0.17em}span}{\left\{{\phi }_j^n\right\}}_{j=0}^n\subset V$ (note the ${\phi }_j^n$ are the usual “pup tent” or “chapeau” functions of height one and support of width $2/n,\left[\frac{j-1}{n},\frac{j+1}{n}\right]\cap [0,1]$). If Pⁿ:H → Hⁿ denotes the orthogonal projection of H = L₂ (0,1) onto Hⁿ, it is well known (see for example, (Schultz, [21]) that lim_n→∞ Pⁿ φ = φ in H for φ ∈ H and in V for φ ∈ V. Then for i =1,2, and each m_i = 1,2,…. let ${\left\{{\chi }_{i,j}^{m_i}\right\}}_{j=1}^{m_i}$ denote the set of standard 0^th order B-splines (i.e. piecewise constant functions) on the interval [a_i, b_i] defined with respect to the usual uniform mesh, ${\left\{a_i+\left(b_i-a_i\right)j/m_i\right\}}_{j=0}^{m_i}$. If $P_i^{m_i}$ denotes the orthogonal projection of L₂(a_i, b_i), it is not difficult to show [1,3] that ${\text{lim}}_{m_i\to \infty }{P}_i^{m_i}\zeta =\zeta$ in L₂(a_i, b_i) for every ζ ∈ L₂ (a_i, b_i). Then let N denote the triple (n, m₁, m₂), and L the multi-index L = (j, j₁, j₂), where j ∈ {0,1,2, …, n}, j₁ ∈ {1,2, …, m₁}, and, j₂ ∈ {1,2, …, m₂}. We then use tensor products to define ${\left\{{\psi }_L^N\right\}}_L^N$ as ${\psi }_L^N={\phi }_j^n{\chi }_{1,j_1}^{m_1}{\chi }_{2,j_2}^{m_2}$ and set ${\mathcal{U}}^N=\text{\hspace{0.17em}span}{\left\{{\psi }_L^N\right\}}_L^N$. It is then not difficult to argue that Assumption (vi) holds.

In both of the examples to follow we fit a truncated bivariate normal. Let $\overrightarrow{q}=\left(q_1,q_2\right)$, $\overrightarrow{a}=\left(a_1,a_2\right)$, and $\overrightarrow{b}=\left(b_1,b_2\right)$, and let $\varphi (\cdot ;\overrightarrow{\mu },\Sigma )$ denote the joint density for the bivariate normal with mean $\overrightarrow{\mu }$ and covariance matrix Σ:

$$\varphi \left(\overrightarrow{q};\overrightarrow{\mu },\Sigma \right)=\frac{1}{2\pi | \text{det}\Sigma {|}^{1/2}}\text{exp}\left(\frac{1}{2}(\overrightarrow{q}-\overrightarrow{\mu }){\Sigma }^{-1}{(\overrightarrow{q}-\overrightarrow{\mu })}^T\right).$$

Let $\Phi (\cdot ;\overrightarrow{\mu },\Sigma )$ denote the corresponding cumulative distribution function. We then set

$$f(\overrightarrow{q};\overrightarrow{a},\overrightarrow{b},\overrightarrow{\mu },\Sigma )=\frac{\varphi {\left(\overrightarrow{q};\overrightarrow{\mu },\Sigma \right)}_{{\chi }_{\left[a_1,b_1\right]\times \left[a_2,b_2\right]}}\left(\overrightarrow{q}\right)}{\text{Φ}\left(\overrightarrow{b};\overrightarrow{\mu },\Sigma \right)-\text{Φ}\left(\left(a_1,b_2\right);\overrightarrow{\mu },\Sigma \right)-\text{Φ}\left(\left(b_1,a_2\right);\overrightarrow{\mu },\Sigma \right)+\text{Φ}(\overrightarrow{a};\overrightarrow{\mu },\Sigma )}.$$

In order to guarantee that we only search over positive definite symmetric matrices Σ, we parameterize Σ as Σ = LL^T, where

$$L=\left[\begin{array}{cc}{L}_{11}& 0\\ L_{21}& L_{22}\end{array}\right].$$

It then follows that

$$\Sigma =L{L}^T=\left[\begin{array}{cc}{L}_{11}^2& L_{11}{L}_{21}\\ L_{11}{L}_{21}& L_{21}^2+L_{22}^2\end{array}\right]>0,$$

so long as L₁₁ and L₂₂ are both nonzero. Thus the optimization is over a feasible (e.g., since our model is diffusion based, we would want a₁, a₂ > 0 or ᾱ > 0) subset of ${ℝ}^9$ with ρ = (a₁, b₁, a₂, b₂, μ₁, μ₂, L₁₁, L₂₁, L₂₂).

All computations were carried out in Matlab on either MAC or PC laptops or desktops. For higher dimensional problems with high resolution discretization, faster platforms such as a cluster may be required. The optimization problems (${\mathcal{P}}_{\mathit{N}}$) were solved iteratively using the Matlab Optimization Toolbox routine FMINCON. We computed the requisite gradients using the adjoint as shown in (4.2) – (4.6) above and we also let FMINCON compute them using finite differences. Both yielded the same results. The finite difference calculations were faster, but the adjoint would likely be preferable for problems involving a higher dimensional parameter space such as would be encountered in the non-parametric case. This is because the required number of integrations of the state equation when using the adjoint method does not increase with the number of parameters to be estimated as it does with a finite difference scheme for computing the gradient of the cost functional. Initial estimates for the parameters were obtained by first fitting each dataset deterministically via nonlinear least squares to obtain estimates for q₁ and q₂. Then sample means, standard deviations, and covariances were used to compute initial estimates for a₁, b₁, a₂, b₂, μ₁, μ₂. The two random variables ${\mathcal{q}}_1$ and ${\mathcal{q}}_2$ were initially assumed to be independent, each with standard deviation one sixth of the length of the corresponding boundary of the initial domain. Some care must be exercised in choosing these initial guesses. Because of the nature of the approximation scheme we are using, if in any iteration the pdf becomes too flat, our Galerkin scheme’s mass and stiffness matrices can become singular or close to singular.

A WrisTAS™ 7 alcohol biosensor (Fig. 1.1) was worn for 18 days by one of the co-authors (S.E.L.) and was set to measure the local ethanol vapor concentration over the skin surface at 5-minute intervals. In addition, she contemporaneously collected breath measurements.

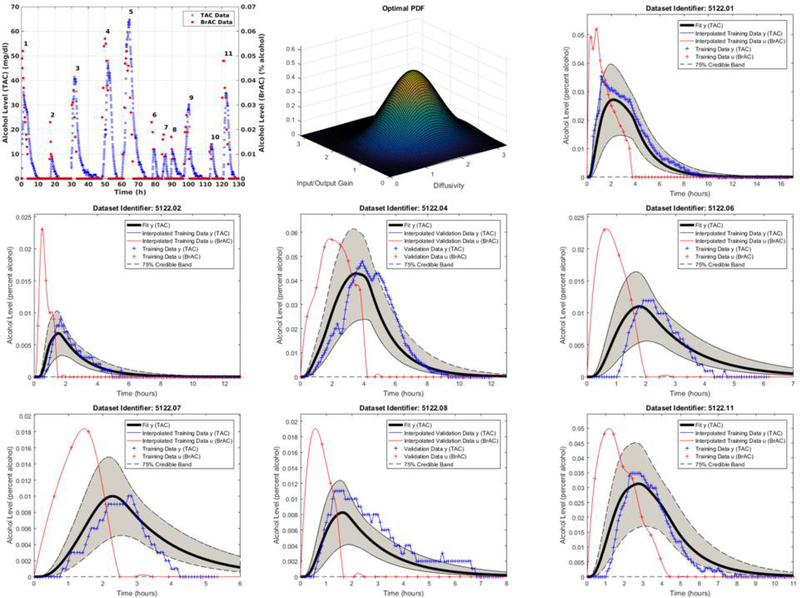
The first drinking episode was conducted in the laboratory with BrAC measured and recorded every 15 minutes from the start of the drinking session until BrAC returned to 0.000. She then wore the TAC device in the field and consumed alcohol ad libitum for the following 17 days. For each drinking episode, BrAC readings were taken every 30 minutes until the BrAC returned to 0.000. Figure 6.1.a shows the entire 18 day TAC signal along with the contemporaneous BrAC measurements. The 11 individual drinking episodes are marked. The TAC measurements provided by the sensor are in units of milligrams per deciliter (mg/dl), and the BrAC measurements are in units of percent alcohol.

Figure 2.1.

Row-wise from the top left: Panel (a) BrAC and TAC data for the 11 drinking episodes, Panel (b) the optimal pdf, Panels (c), (d), (f), (g), and (i) are the plots of training BrAC and corresponding TAC, resulting fit population model estimated TAC, and 75% credible band; Panels (e) and (h) are the cross validation results.

We fit the population consisting of all eleven drinking episodes, but we also visually stratified the population into two groups, one containing the seven episodes in which the peak BrAC was higher than the (bench calibrated) peak TAC (episodes 1,2,4,6,7,8, and 11), and a second containing the remaining four drinking episodes in which the reverse was true (episodes 3, 5, 9, and 10). Our results for the first stratified group are shown in Figure 6.1.b – 6.1.i. In Figures 6.1.c,d,f,g, and i we plotted the training BrAC and TAC data for each of the episodes 1, 2, 6, 7, and 11 along with resulting fit population model estimated TAC and the 75% credible band. In Figures 2.1.e and 6.1.h we plotted the results of a cross validation on episodes 4 and 8. In Figure 6.1.b we plotted the optimal fit population truncated bivariate normal pdf. The converged values for the parameters were $a_1^{*}=\text{\hspace{0.17em}0.0000}$, $b_1^{*}=1.4850$, $a_2^{*}=0.0000$, $b_2^{*}=2.0363$, ${\mu }_1^{*}=\text{\hspace{0.17em}\hspace{0.17em}0.6318}$, ${\mu }_2^{*}=1.0295$, and ${\Sigma }^{*}=\left[\begin{array}{ll}0.0259\hfill & 0.0077\hfill \\ 0.0077\hfill & 0.1232\hfill \end{array}\right]$.

The credible bands were computed directly from samples, $\overrightarrow{q}=\left(q_1,q_2\right)$ of $\overrightarrow{\mathcal{q}}=\left({\mathcal{q}}_1,{\mathcal{q}}_2\right)$, obtained from the optimal distribution for $\overrightarrow{\mathcal{q}}$ using importance sampling and the state as ${\langle c(\overrightarrow{\mathcal{q}}),{\mathcal{x}}_{i,j+1}^N\rangle }_{{\text{V}}^{*},\text{V}}={\mathcal{x}}_{i,j+1}^N(0,\overrightarrow{\mathcal{q}})$, where ${\mathcal{x}}_{i,j+1}^N={\mathcal{x}}_{i,j+1}^N(\eta ,\overrightarrow{\mathcal{q}})$ is given by (4.1). We note that, strictly speaking, this is not valid since our theory yields only that ${\mathcal{x}}_{i,j+1}^N\in \mathcal{V}=L_{\pi }^2(Q;V)$, and thus that pointwise evaluation in $\overrightarrow{q}$ is undefined. However, the results seem quite reasonable and are extremely useful and consequently we have included them. Our results for the full un-stratified data set and for the second stratified group were similar. We also applied our scheme to a population consisting of multiple subjects each with a single drinking episode with the results being quite similar to those presented above [20].

7. Discussion and Concluding Remarks

We note that our theory and general approach also applies to hyperbolic systems with either H-semicoercive or V-coercive damping [2] such as the telegraph equation which can be used to model diffusion with finite speed of propagation. We are investigating elimination of the requirement that the measures π be defined in terms of a density. We believe that it is possible to directly apply the Prohorov metric based framework developed in [4] by using a different version of the Trotter Kato-like semigroup approximation result in Section 4. We also believe that results for the estimation of functional parameters in parabolic systems could be used to estimate the pdfs non-parametrically. Indeed, in the system (3.2), (3.3), the pdf effectively plays the role of a non-constant coefficient in an abstract parabolic system. Thus, we should be able to estimate both the support and the shape of the density by parameterizing the pdf as a linear combination of basis elements (e.g. splines, orthogonal polynomials, etc.) and then estimating the coefficients in the expansion. We are also looking at polynomial chaos expansions for $\overrightarrow{\mathcal{q}}$, and then estimating the coefficients.

Of primary interest to us is the estimation of the input to the system u, or the BAC/BrAC, from the output y, or TAC. Once the distribution of the random parameters has been estimated, this takes the form of a deconvolution problem. In [20] we use the results presented here together with the framework in [9] and [17] to do just that. We obtain an estimate of the input along with error bars or credible bands. Finally, we are looking at using the approach in [9] and [17] to control random parabolic systems, in particular, the computation of the feedback solution to the LQR and LQG problems for random distributed parameter systems.