Abstract
Time-resolved frequency-domain fluorescence energy transfer measurements have been used to investigate the solution structure of a single-domain CCHH-type zinc finger peptide. These measurements reveal not only the range of accessible distances for a given donor–acceptor pair within the molecule but also the degree of conformational flexibility that occurs in solution. Two donor–acceptor (D–A)-pair zinc finger peptides have been synthesized. A single tryptophan residue located at the midpoint of the sequence was the energy donor for two different acceptors. One acceptor, attached at the amino terminus was a 5-(dimethylamino)-1-naphthalenesulfonyl (DNS) group; the second acceptor was a 7-amino-4-methylcoumarin-3-acetyl (AMCA) group, attached to the ϵ-amino function of a carboxy-terminal lysine residue. Distance distributions and the mutual site-to-site diffusion coefficients were determined for these two D–A-labeled peptides under zinc-bound, metal-free, and denatured conditions. The D–A distance distributions determined for these two peptides under metal-free and zinc-bound conditions indicated a shorter distance and a unique conformation (narrow distribution) when metal was bound and a longer distance with greater conformational flexibility when metal ion was absent. No site-to-site diffusion was detected for the zinc-bound peptide, whereas an appreciable amount of diffusion was measured for both metal-free and denatured peptide. Anisotropy measurements on the peptides indicated increased flexibility of all regions of the peptide chain in the absence of zinc and a more compact, less flexible structure when zinc was bound. It was concluded from these results that the metal-bound conformation represents a unique, well-defined structure. Comparison of distance distributions measured for metal-free and denatured peptide indicated that there is some residual structure present in the metal-free peptide.
The CCHH zinc finger motif (Miller et al., 1985; Brown et al., 1985) is a small protein domain which folds into a unique structural unit upon coordination of zinc ion via two cysteine (C) and two histidine (H) residues.1 Generally, multiple copies of this motif are present in nucleic acid-binding proteins, and these CCHH units site-specifically bind in the major groove of DNA (Pavletich & Pabo, 1991). Since the identification of this structural unit, hundreds of CCHH zinc finger sequences and/or proteins have been identified (Berg, 1990). The CCHH motif is frequently found in eukaryotic transcription factors (Johnson & McKnight, 1989); thus, zinc fingers are now classified as a major structural motif utilized by DNA-binding proteins. Many reviews on zinc finger proteins and their structures have appeared in the literature (Klug & Rhodes, 1987; Evans & Hollenberg, 1988; Struhl, 1989; Berg, 1989; Berg, 1990; Rhodes & Klug, 1993).
The consensus sequence of most CCHH zinc fingers is (Tyr, Phe)-Xaa-Cys-Xaa2,4-Cys-Xaa3-Phe-Xaa5-Leu-Xaa2-His-Xaa3,4-His, where Xaa represents a variable amino acid and the numerical subscript indicates the number of residues (Berg, 1990). After identification of the zinc finger motif and subsequent initial studies on single-domain zinc finger peptides (Frankel et al., 1987; Párraga et al., 1988), two structural models were predicted for the CCHH zinc finger (Berg, 1988; Gibson et al., 1988). The basic features of these models have since been confirmed with 2D NMR structures (Lee et al., 1989; Klevit et al., 1990; Omichinski et al., 1990; Kochoyan et al., 1991a,b,c) and an X-ray crystallographic structure (Pavletich & Pabo, 1991). The major secondary structural features of the CCHH zinc finger include a β-sheet in the amino-terminal half of the domain and a helical region (primarily α-helix) in the carboxy-terminal half. Three conserved hydrophobic residues form a pocket within the structure, and the zinc atom is tetrahedrally coordinated to the cysteine sulfhydryls and the histidine imidazole Nϵ atoms. Several groups have investigated single-domain zinc finger peptides with various spectroscopic methods (Frankel et al., 1987; Párraga et al., 1988; Lee et al., 1989; Klevit et al., 1990; Neuhaus et al., 1990; Omichinski et al., 1990; Párraga et al., 1990; Weiss et al., 1990; Weiss & Keutmann, 1990; Kochoyan et al., 1991a,b,c; Lee et al., 1991; Krizek et al., 1991; Michael et al., 1992). These studies have revealed that a single zinc finger is able to fold into a unique structure in the presence of metal ion. The metal-free zinc finger is thought to be relatively free of secondary structure, i.e., in a random coil conformation (Frankel et al., 1987; Párraga et al., 1988; Lee et al., 1991).
A limited number of fluorescence studies on zinc finger proteins have been reported (Hanas et al., 1989; Han et al., 1990). Both studies used steady-state fluorescence methods to examine fluorescently labeled Xenopus laevis TFIIIA protein under various conditions. Time-resolved fluorescence energy transfer measurements on a single-domain CCHH zinc finger have only recently appeared (Eis & Lakowicz, 1992; Eis et al., 1992). While fluorescence methods cannot be used to determine precise interatomic distances as can crystallographic or NMR methods, they are unique in that they can be used to reveal conformational distributions and internal site-to-site diffusion, as well as hydrodynamics and molecular interactions. Thus, in this report, time-resolved energy transfer measurements were used to determine the intramolecular distances and the degree of conformational flexibility in a CCHH zinc finger peptide under zinc-bound, metal-free, and denatured conditions via two different D–A pairs. The results of these measurements indicate that the CCHH zinc finger forms a unique and conformationally inflexible structure in the presence of zinc and that there is some residual structure in the metal-free peptide.
THEORY
Fluorescence Resonance Energy Transfer.
The usefulness of fluorescence resonance energy transfer in determining the distances between two sites in a molecule in solution was recognized by Stryer (1978). The theory for radiationless energy transfer from a donor to an acceptor chromophore was first developed by Förster (1948). Transfer of energy is due to the long-range dipole–dipole interactions between the donor and acceptor; thus energy transfer is a through-space interaction.
The rate of radiationless energy transfer (kT) between donor and acceptor molecules is given by
| (1) |
where τD is the donor-only lifetime, R0 is the Förster distance where 50% energy transfer occurs, and r is the distance between the donor and acceptor chromophores. The distance r is determined by measuring the transfer efficiency (E) and the Förster distance (R0) for a particular D–A pair. The R0 value is calculated from the spectral properties of the donor and acceptor chromophores as follows:
| (2) |
where κ2 is the orientation factor between the donor and acceptor dipole moments, ϕD0 is the quantum yield of the donor in the absence of acceptor, n is the refractive index of the solution, N is Avogadro’s number, FD(λ) are the donor emission spectra with the area normalized to 1, ϵA(λ) are the acceptor absorption spectra, and λ is the wavelength. The efficiency of energy transfer can be calculated from the steady-state intensities of the donor alone (ID) and D–A pair (IDA) molecules:
| (3) |
The experimentally measured values of E and R0 are used to calculate the distance r from
| (4) |
This expression is valid for a single donor and acceptor separated by a single distance.
Distance Distributions and Dynamics.
Many biological molecules are expected to be conformationally flexible in solution, in which case the distance r in eq 4 represents only the average D–A distance. Therefore, the ability to measure a range of D–A distances and the extent of flexibility within the molecule enables one to examine not only the molecule’s structure but also the internal dynamics. Distance distributions between donor and acceptor sites within a molecule can be measured with steady-state methods using multiple D–A pairs located at specific donor and acceptor sites (Wiczk et al., 1990; Wiczk et al., 1991) or more simply by generating multiple R0 values with the use of an external quencher (Gryczynski et al., 1988a,b).
The distance distributions and dynamics reported here were determined using the time-resolved fluorescence measurements of the donor decay in donor only and D–A molecules (Haas et al., 1978b; Haas & Steinberg, 1984; Haas et al., 1988; Lakowicz et al. 1990b; Lakowicz et al., 1991b,c,d). The tryptophan donor used in both zinc finger peptides (DNS-ZF28 and AMCA-ZF29) exhibits complex intensity decays in both the donor alone and D–A pair molecules, thus the donor lifetimes were recovered using a multiexponential description of the decay as follows:
| (5) |
where ID0 is the total donor intensity at t = 0, αDi are the preexponential factors representing the relative fractional intensities of the donor decay at t = 0, and τDi are the individual components of the donor decay. It is assumed that the R0 values are the same for each component in the intensity decay and that the transfer rates are inversely proportional to the decay time. Thus, eq 1 can be rewritten as follows:
| (6) |
where the subscript i represents each individual component of the decay.
The observed donor decay in the presence of acceptor, which contains contributions from all components with all allowable distances, will be multiexponential since particular molecular conformations cannot be uniquely examined in solution. The multiexponential donor decay in the presence of acceptor can then be defined in terms of the average of the individual decays, , which are weighted by their fractional intensity (αDi) and by the distance probability distribution, P(r), and the D–A pairs:
| (7) |
It should be noted for eq 7 that the initial (t = 0) donor intensity in the presence of acceptor is equivalent to the initial donor only intensity (IDA0 = ID0). The individual decays of the ith component, , are defined as follows:
| (8) |
where represents the actual distribution of excited molecules over the distance r and Ni0*(r) is the initial distribution of excited molecules. The shape of the initial distribution is assumed to be the same for all donor fractions, i.e., where is the total initial number of molecules of the ith component and P(r) is the probability density function describing the distribution of D–A distances. The distribution, P(r), is assumed to be Gaussian and is defined as follows:
| (9) |
where Z is the normalization factor, Rav is the average distance (most probable distance), and σ is the standard deviation of the untruncated Gaussian function. The half-width of the distribution (hw, full width at half-maximum probability) is a relative measure of the conformational flexibility that exists between the donor and acceptor. In the Gaussian model, hw = 2.355σ.
We note that one could have selected functions other than a Gaussian to describe the D–A distance distribution. However, a Gaussian appears to be the most realistic assumption. A Lorentzian distribution is not reasonable because this function has significant probability far from the mean value. Since the donor and acceptor must be within some bounds, the use of a Lorentzian results in an artificially narrow half-width resulting from the need to suppress the extremes to fit the data. Square or triangular distributions could be used but are not expected for long polymers with many degrees of freedom. Statistical mechanical simulations have suggested Gaussian-like distributions for long polymers (Flory, 1969). While we have not conducted an exhaustive analysis, the present data were judged to be inadequate to resolve a skewed Gaussian function. In past studies, such resolution was found to require a number of D–A pairs with different R0 values (Wiczk et al., 1991).
When there is no site-to-site diffusion (D) between the donor and acceptor, the decay from eq 8 can be defined in terms of the distance-dependent donor decay times (τDi) as follows:
| (10) |
The distance distribution recovered for a given D–A pair may sometimes be inaccurate due to mutual site-to-site diffusion between the donor and acceptor during the excited-state lifetime of the donor. Since the distributions reported below were determined in solution at room temperature, it is expected that D–A diffusion will occur. Haas and co-workers (Haas et al., 1978b; Beechem & Haas, 1989) have addressed this problem and have shown that in the presence of energy transfer and site-to-site diffusion, the function satisfies the diffusion equation with the addition of a sink term that takes into account the processes of donor decay and energy transfer. In our case we assume that each component of the donor decay (τDi) is governed by the Haas equation and is given by
| (11) |
A more detailed description of this theory is reported elsewhere (Lakowicz et al., 1990b; Lakowicz et al., 1991b,c,d).
It seems valuable to summarize the assumptions used in the distance distribution analysis. We assume that: (a) radiative energy transfer to the acceptor is the only effect of the acceptor on the donor decay; (b) the orientation factor κ2 is assumed to equal ⅔ for all conformational states; (c) the values of R0 are the same for all components in the donor intensity decay; (d) the transfer rates are inversely proportional to the decay times; and (e) the distance distribution at t = 0 is assumed to be adequately described by a Gaussian.
Frequency-Domain Expressions.
In frequency-domain fluorometry the fluorophore is excited with sinusoidally modulated light (Lakowicz, 1983). The sinusoidal emission resulting from such excitation is phase-shifted and demodulated, thus the measured parameters of this method are the phase angle ϕ and the modulation m at various frequencies ω. For each assumed intensity decay model, the parameter values are obtained by comparing the experimental phase (ϕω) and modulation (mω) values with the calculated values (ϕcω, mcω). At each frequency the calculated values are obtained from
| (12) |
| (13) |
where
| (14) |
| (15) |
The parameter values of a given model are determined using the experimental and calculated phase and modulation values with the method of nonlinear least-squares (Bevington, 1969; Johnson & Frasier, 1985; Johnson & Faunt, 1992) as follows:
| (16) |
where χR2 is the goodness-of-fit parameter that is minimized during the fitting procedure, v is the number of degrees of freedom, and δϕ and δm are the experimental uncertainties in the measured phase and modulation values. The experimental uncertainties generally used are δϕ = 0.2° and δm = 0.005.
Time-Resolved Anisotropy Decays.
Anisotropy measurements of molecules in solution can yield essentially two types of information (Steiner, 1991). If the molecule and its attached fluorophore rotate as a unit in solution, then information can be obtained abouts its size and shape. Internal rotational motions of the probe can provide information about the flexibility within the molecule. Anisotropy decays [r(t)] can be described as a sum of exponentials (Lakowicz, 1983) as follows:
| (17) |
where r0gi are the amplitudes associated with each component of the decay and θi are the rotational correlation times. Generally, one observes two correlation times: the longer component is associated with the global overall motion of the molecule, and the shorter component is representative of the probe’s local motions.
Anisotropy decays are determined by measuring the parallel (∥) and perpendicular (⊥) components of the emission. In frequency-domain measurements the anisotropy decay is recovered from the phase angle difference (Δω) and/or the ratio of the modulated amplitudes (Λω) between the parallel and perpendicular components of the emission
| (18) |
| (19) |
Calculated values (c) of Δω, and Λω, are obtained using
| (20) |
| (21) |
where D∥ and D⊥ and N∥ and N⊥ are determined from eq 14 and 15 (D∥ = D⊥ − Dω; N∥ = N⊥ = Nω). The goodness-of-fit to the anisotropy decay model is estimated using the method of nonlinear least-squares (Bevington, 1969; Johnson & Frasier, 1985; Johnson & Faunt, 1992) as follows:
| (22) |
which is analogous to eq 16. The experimental uncertainties in the measured values are δΔ = 0.2° and δΛ= 0.008.
MATERIALS AND METHODS
The 28- (ZF28) and 29- (ZF29) residue CCHH zinc finger peptides were synthesized on a Milligen 9050 Pepsynthesizer using Fmoc (N-fluorenylmethoxycarbonyl) chemistry. Cleavage of ZF28 from the resin was performed using a mixture of trifluoroacetic acid (TFA), thioanisole, ethanedithiol, and anisole (90:5:3:2) and a cleavage time of 4 h (Milligen/Biosearch Chemistry Update, December 1989). The cleaved peptide solution was filtered through a medium-porosity funnel and reduced in volume with N2, and the peptide precipitated overnight with cold diethyl ether. Precipitated peptide was washed with cold diethyl ether, and residual ether was removed with N2. Disulfide bonds were reduced by dissolving the peptide in 0.05 M N-ethylmorpholine, pH 8.4, adding solid dithiothreitol (DTT) to give a final concentration of 0.05 M, and heating the solution in a 55 °C-water bath for 4 h. The reduced peptide solution was acidified with acetic acid, filtered, and then purified by HPLC on a Vydac C4 (Hesparia, CA) column (1 × 25 cm) using gradient elution and 0.1% TF A in water and 0.1% TFA in acetonitrile as eluents.
The amino terminus of ZF29 was acetylated while the peptide was still attached to the resin. Thus, after cleavage and deprotection of the side chain blocking groups there remains a single lysine residue which can be selectively modified at its side chain ϵ-amino group. Since ZF29 contains an extra arginine residue on the amino terminus, it was cleaved with an alternative method (Milligen Technical Support) which more easily removes arginine side chain protection groups. The cleavage reagent was TFA, thioanisole, ethanedithiol, and anisole (90:5:3:2) plus 3% methanesulfonic acid, and the cleavage reaction time was ~20 min. All other details of the cleavage procedure are the same as above. Cleaved ZF29 was dissolved in a minimal amount of water, and NH4OH was added until the solution was pH 10–11; this procedure exchanges the methanesulfonic acid ion. The solution was then diluted with 0.05 M N-ethylmorpholine to give a final concentration of 3–5 mg/mL, and this solution was treated with DTT as described above.
Labeling of the ZF28 peptide’s amino terminus with DNS-Cl was accomplished by dissolving the peptide in 0.1 M NaHC03, pH 8.5 (3–5 mg/mL), and adding a 2-fold molar excess of DNS-Cl, which was dissolved in a minimal amount of acetone, in four aliquots over a period of 40 min. The labeling reaction was performed at room temperature and was allowed to proceed 30 min past the last addition of DNS-Cl. The LYS29 ϵ-amino group of acetylated ZF29 was labeled with 7-amino-4-methylcoumarin-3-acetic acid succinimidyl ester (AMCA) (Molecular Probes, Eugene, OR) at room temperature. The peptide was dissolved in 0.2 M NaHC03 pH 8 (3–5 mg/mL). The AMCA label was dissolved in a minimal amount of dimethylformamide, and a 10-fold molar excess of this solution was added to the peptide solution over a period of 1 h in four aliquots. The reaction was continued for 30 min after the last aliquot of dye was added. After being labeled with DNS-Cl or AMCA, peptide–dye solutions were filtered and diluted 3× with 0.05 M N-ethylmorpholine, and solid DTT was added to give a final concentration of 25 mM. Solutions were heated for 1 h at 55 °C, acidified with acetic acid, and then purified by HPLC as described above.
Amino acid analysis was performed on the unlabeled peptides to confirm the sequence. Analytical HPLC was performed on unlabeled and acceptor-labeled peptides to confirm their purity; a Vydac C18 column (Hesparia, CA) was employed along with gradient elution using 0.1% TFA in water and 0.1% TFA in water and 0.1% TFA in acetonitrile. Mass spectrometry was performed to confirm the peptide sequences, the presence of the amino-terminal acetyl group in ZF29, and the acceptor in each peptide.
All absorption measurements were performed on a Perkin-Elmer Lambda 6 UV/vis spectrophotometer. Measurements were performed with a 1-nm slit width and a scan speed of 200 nm/min. Circular dichroism measurements were performed on an Aviv CD 60 spectropolarimeter in the laboratory of Professor David Shortle at the Johns Hopkins University. Measurements were performed at room temperature in a 0.2-mm-pathlength cuvette on ZF28. Peptides were dissolved in 50 mM HEPES, 50 mM NaCl, 10 mM DTT, pH 7 buffer at a concentration of 50–70 μM; the zinc sample contained a 4-fold molar excess of Zn2+ and the guanidine hydrochloride (GuHCl) sample contained ~4 M GuHCl. Each sample’s spectrum is an average of 4 scans at 1-nm resolution, 5 s/nm acquisition time. Steady-state emission spectra were measured on a SLM 8000 fluorometer with excitation at 295 nm and magic angle polarization.
The R0 values for DNS-ZF28 and AMCA-ZF29 peptides were calculated using eq 2. Quantum yields of the tryptophan donor were determined relative to the value of tryptophan in water (ϕD = 0.13) (Chen, 1967). Tryptophan donor quantum yields for both ZF28 and ZF29 peptides are 0.08 for zinc-bound, 0.11 for metal-free, and 0.14 for peptide plus 5 M GuHCl. Tryptophan donor steady-state emission spectra were measured using ZF28 and ZF29. Acceptor absorption spectra used to calculate the R0 values were the difference spectra of D–A-labeled peptide minus the donor-only peptide. The R0 values for DNS-ZF28 are 18.6 Å for zinc-bound, 19.5 Å for metal-free, and 19.9 Å for GuHCl treated. The R0 values for AMCA-ZF29 are 24.1 Å for zinc-bound, 25.2 Å for metal-free, and 25.8 Å for GuHCl treated.
Time-resolved frequency-domain measurements were performed on a 10-GHz frequency-domain fluorometer (Laczko et al., 1990). Modulated excitation was achieved using the harmonic content of a picosecond dye laser (Coherent Model 700) that was cavity dumped at 3.79 MHz. The dye laser was pumped with a mode-locked argon-ion laser (Coherent Innova 15, Model 468 mode locker). Ultraviolet excitation of tryptophan (295 nm) was achieved using the frequency-doubled (Spectra Physics Model 390 doubler) output of the dye laser operating with Rhodamine 6G (Exciton, Dayton, OH). The frequency-doubled output of the dye laser operating with Pyridine 1 (Exciton) was used to excite the DNA (345 nm) or AMCA acceptor (360 nm). The detector was a Hamamatsu Model R2566 MCP PMT. Zinc finger peptide tryptophan emission was isolated using a 360-nm interference filter for DNS-ZF28 or a 340-nm filter for AMCA-ZF29. Acceptor emission was isolated using a Corning 3–71 longpass filter for DNS and a 460-nm interference filter for AMCA. The phase and modulation measurements were obtained relative to a scattering solution of Ludox (DuPont) in water. Distance distribution analyses for zinc-bound DNS-ZF28 were performed with the fraction-labeling parameter set to 0.977 to compensate for background fluorescence in the sample (Lakowicz et al., 1991a). In this procedure the extent of labeling (fL) is varied to yield the minimum value of χR2 in a distance-distribution analysis. The value of fL is held constant in all subsequent analyses. Experience with this procedure has shown it to reliably report the extent of labeling.
RESULTS
Design and Synthesis of Donor-Only and D–A Zinc Finger Peptides.
Two single-domain zinc finger peptides, ZF28 and ZF29 (Figure 1), were designed on the basis of the consensus zinc finger peptide work of Berg and co-workers (Krizek et al., 1991). Their peptide sequence contains the most frequently occurring amino acid residue in each position of a single zinc finger domain based on the catalogued sequences of 131 zinc finger proteins. Since this consensus peptide was shown to exhibit the metal binding properties and structural behavior of native sequence single-domain zinc fingers (Krizek et al., 1991), this design method was employed to yield zinc finger sequences that contain a single energy transfer donor and that could be selectively modified with various energy transfer acceptors in different positions.
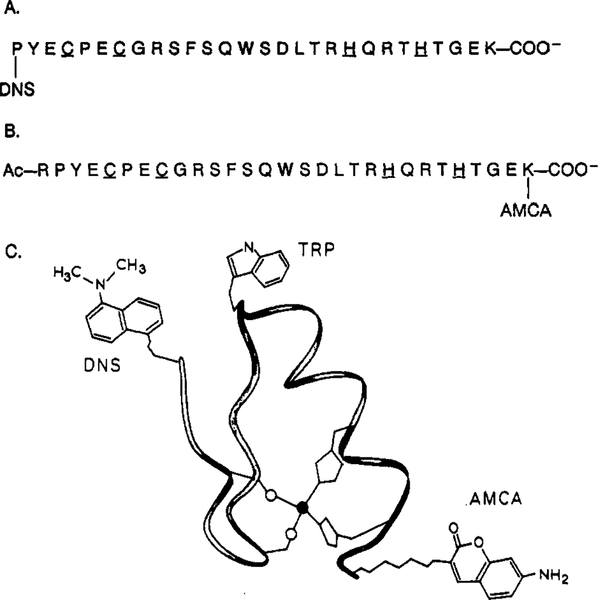
FIGURE 1:
Primary sequences and labeling sites of zinc finger peptides. The donor fluorophore for both ZF28 and ZF29 is a tryptophan residue (W) located at the midpoint of the sequence. Zinc-coordinating cysteine (C) and histidine (H) residues are underlined. Panel A: primary sequence of ZF28, DNS acceptor is attached to the amino terminus. Panel B: primary sequence of ZF29, AMCA acceptor is attached to the carboxy-terminal lysine’s ϵ-amino group. Panel C: schematic representation of the metal-bound zinc finger structure, relative positions of donor and acceptor labels are indicated.
A single tryptophan residue, which serves as the energy transfer donor to both the DNS and AMCA acceptors, was placed at a site (position 14) where tryptophan occurs with some regularity in native zinc finger sequences. The peptide sequences of ZF28 and ZF29 (Figures 1A and 1B, respectively) are very similar to Berg’s consensus peptide sequence; however, arginine residues were conservatively substituted for the multiple lysines within the sequence except for the carboxy-terminal lysine. Thus, the amino terminus and the ϵ-amino group of LYS29 both serve as potential sites for acceptor attachment. Selective labeling of ZF28’s amino terminus with a DNS group was accomplished by taking advantage of the pKa difference between the terminal α-amino group and the ϵ-amino group of LYS28 (Figure 1A). A second D–A pair was made by attaching an AMCA group to the single LYS29’s ϵ-amino group in amino-terminally acetylated ZF29. The location and structure of the donor and each acceptor is depicted in the schematic representation of the folded metal-bound zinc finger peptide shown in Figure 1C.
Cobalt absorption spectroscopy was used to ensure that the synthetic peptide ZF28 and ZF29 bound metal ion in the same manner as native-sequence zinc fingers (Bertini & Luchinat, 1984; Frankel et al., 1987; Krizek et al., 1991). It is known that the cobalt absorption spectrum is dependent on the types of coordinating atoms and the geometry of the coordination site (Bertini & Luchinat, 1984). The difference absorption spectra, cobalt-bound ZF28 or ZF29 minus zinc-bound peptide (data not shown), were nearly identical to the cobalt absorption spectrum obtained for other zinc finger peptides (Frankel et al., 1987; Berg & Merkle, 1989; Párraga et al., 1990; Krizek et al., 1991). Cysteinate ligand absorption maxima near 310 and 340 nm were obtained as well as the d–d transition absorption bands between 500 and 700 nm. Cobalt absorption spectroscopy was also used to insure that the metal-binding properties of the zinc finger peptides were not altered after labeling with acceptor. The difference in the absorption spectra obtained for the acceptor-labeled peptide also showed the characteristic absorption bands for a CCHH-type zinc finger peptide.
Circular dichroism (CD) measurements were performed on ZF28 (data not shown) to monitor the secondary structural changes under various conditions. The peptide was measured with and without zinc ion and with GuHCl. The zinc-bound spectrum is similar to that previously obtained for a native-sequence zinc finger peptide (Frankel et al., l987). No obvious secondary structure was present in the spectra, such as the double minima observed between 200 and 230 nm for the α-helix; however, the zinc-bound peptide’s spectrum does indicate a greater amount of secondary structure than that seen for either metal-free or denatured peptide. On the basis of the cobalt absorption spectroscopy and the CD measurements, it was concluded that these consensus zinc finger peptides tetrahedrally coordinated metal ions like the native-sequence single-domain zinc finger peptides.
Emission Spectra and Donor Decays of Donor-Only and D–A Peptides.
Steady-state fluorescence emission spectra were measured for both donor-only and D–A peptides under zinc-bound, metal-free, and GuHCl-treated conditions. Figure 2 shows the spectra obtained for ZF28 and DNS-ZF28. The tryptophan donor fluorescence in zinc-bound DNS-ZF28 is quenched to a significantly greater degree (Figure 2A) than for the metal-free (Figure 2B) or GuHCl-treated (Figure 2C) peptide. This high degree of donor quenching by the DNS acceptor indicates that TRP14 and the amino-terminal DNS group are nearest each other for the metal-bound case. Also, the difference in degree of donor quenching for the metal-free and GuHCl-treated peptide suggests that there are structural differences between these two cases.
FIGURE 2:
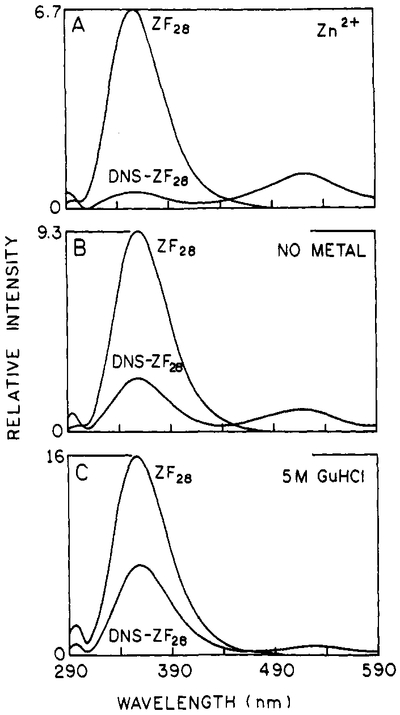
Steady-state emission spectra of ZF28 (donor alone) and DNS-ZF28 (donor-acceptor-labeled). Panel A: zinc-bound peptide. Panel B: metal-free peptide Panel C: peptide plus 5 M GuHCl.
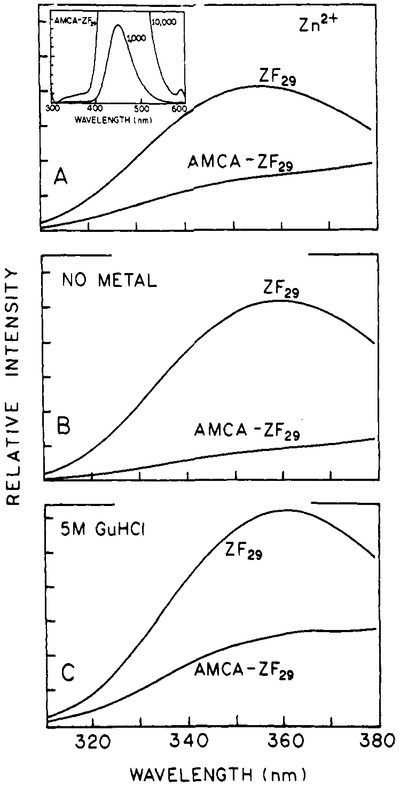
Steady-state spectra for ZF29 and AMCA-ZF29 are shown in Figure 3 for the zinc-bound (Panel A), metal-free (Panel B), and GuHCl-treated (Panel C) peptides. Only the tryptophan emission is shown for the donor and D–A peptides since the acceptor emission has a very high quantum yield relative to the tryptophan. A full D–A spectrum is shown in the inset in Figure 2A. The differences in transfer efficiencies observed for AMCA-ZF29 are less obvious than those seen for DNS-ZF28. The greatest degree of energy transfer for this D–A pair occurs for the metal-free peptide, which implies that unwinding of the α-helical portion of the peptide provides flexibility in the peptide chain and enables the donor and acceptor to come closer together.
FIGURE 3:
Steady-state emission spectra of ZF29 (donor alone) and AMCA-ZF29 (donor–acceptor-labeled). Due to the high quantum yield of AMCA, only the donor portions of the spectra are shown. The inset in panel A shows the full D–A spectrum scaled at 1000 and 10 000 to show the relative proportion of AMCA-to-TRP fluorescence. Panel A: zinc-bound peptide. Panel B: metal-free peptide. Panel C: peptide plus 5 M GuHCl.
Donor-only and D–A-pair tryptophan lifetimes were calculated from the measured time-resolved frequency responses for zinc-bound, metal-free, and GuHCl-treated ZF28 and DNS-ZF28 peptides (Figure 4). These were the same conditions used for the steady-state measurements. In each case the donor-only peptide’s frequency response, which includes measurement of the phase angle and the modulation, is on the left. When the tryptophan lifetime is quenched by the presence of the DNS acceptor, the frequency response curves shift to higher frequencies. As seen in the steady-state spectra (Figure 2), the binding of Zn2+ results in the highest degree of donor quenching, which is evident from the dramatic shift in the frequency response out to 4 GHz. Comparison of the metal-free and GuHCl donor-alone and D–A frequency-domain measurements also indicates that a different conformation is present in each of these cases (Figure 4).
FIGURE 4:
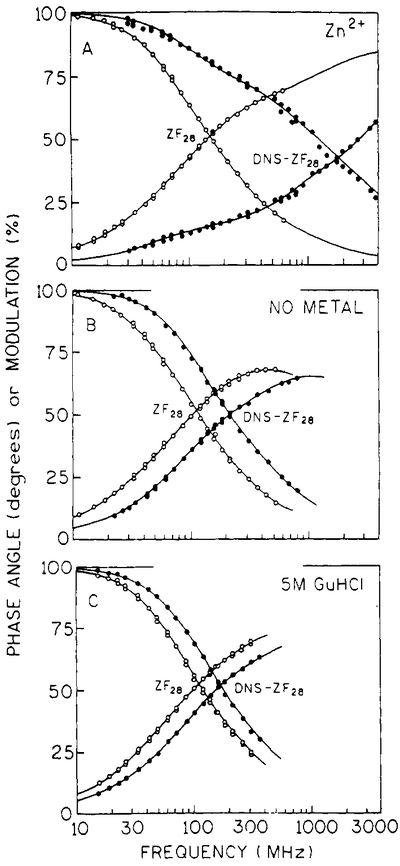
Multiexponential lifetime fits to the donor frequency response data for ZF28 and DNS-ZF28. In each case, donor-alone peptide data are the open circles (○) and D–A peptide data are the filled circles (●). Panel A: zinc-bound peptide. Panel B: metal-free peptide. Panel C: peptide plus 5 M GuHCl. Donor lifetime parameters are reported in Table I.
Both donor-alone (ZF28) and D–A data (DNS-ZF28) were fit with a three-component multiexponential intensity decay model; their lifetimes are reported in Table I. Observed differences in the donor-only decays (Table I) are indicative of structural differences between metal-bound and metal-free peptide. Binding of zinc shortens the average tryptophan lifetime (1.90 ns), whereas the average lifetime is nearly the same for the metal-free (2.47 ns) and GuHCl-treated (2.35 ns) peptides. Given what is known about the zinc finger structure (Lee et al., 1989; Klevit et al., 1990; Omichinski et al., 1990; Kochoyan et al., 1991a,b,c;Pavletich & Pabo, 1991), it is possible that the binding of metal ion results in a more solvent-exposed tryptophan residue which can then be more easily quenched by external quenchers. The average tryptophan lifetimes obtained for DNA-ZF28 (Table I) are, as expected, shorter than the donor-only lifetimes and indicate that the tryptophan donor is quenched by the presence of DNS acceptor.
Table I:
Donor Multiexponential Intensity Decay Analysis of ZF28 and DNS-ZF28
| samplea | 〈τ〉 (ns)b | τi (ns) | αi | fic | χR2 |
|---|---|---|---|---|---|
| ZF28 + Zn2+ | 1.90 | 0.214 | 0.361 | 0.067 | 1.99 |
| 1.31 | 0.504 | 0.569 | |||
| 3.12 | 0.135 | 0.363 | |||
| ZF28 + no metal | 2.47 | 0.040 | 0.662 | 0.035 | 4.84 |
| 1.60 | 0.260 | 0.558 | |||
| 3.90 | 0.078 | 0.407 | |||
| ZF28 + 5 M GuHCld | 2.35 | 0.315 | 0.265 | 0.049 | 2.11 |
| 1.58 | 0.427 | 0.368 | |||
| 3.07 | 0.308 | 0.555 | |||
| DNS-ZF28 + Zn2+ | 0.58 | 0.048 | 0.774 | 0.332 | 13.7 |
| 0.203 | 0.206 | 0.374 | |||
| 1.67 | 0.020 | 0.294 | |||
| DNS-ZF28 + no metal | 1.28 | 0.002 | 0.945 | 0.033 | 4.61 |
| 0.403 | 0.026 | 0.183 | |||
| 1.54 | 0.029 | 0.785 | |||
| DNS-ZF28 + 5 M GuHCl | 1.59 | 0.242 | 0.410 | 0.095 | 0.88 |
| 1.45 | 0.532 | 0.738 | |||
| 2.98 | 0.058 | 0.167 |
All samples were measured in 50 mM HEPES, 50 mM NaCl, 10 mM DTT pH 7 buffer at room temperature. The no metal and GuHCl samples also contained 1 mM EDTA.
Average lifetime, 〈τ〉 = Σiαiτi2/Σiαiτi.
Fractional intensity of each decay component, fi = αiτi/Σiαiτi.
These parameter values are the result of a global analysis of ZF28 and ZF29 measurements.
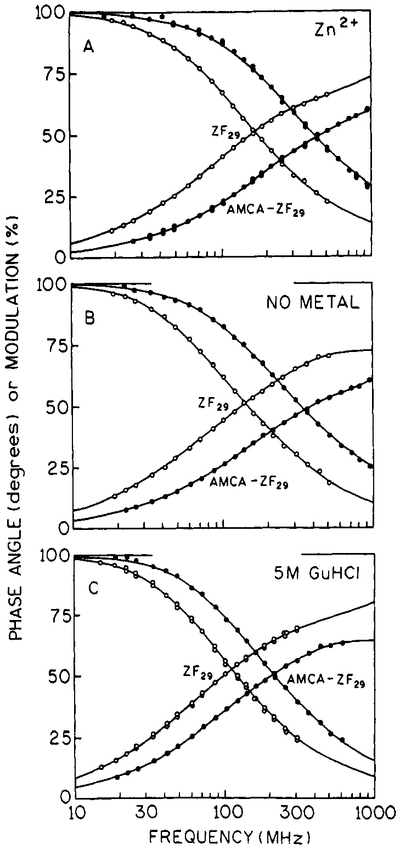
Figure 5 shows the frequency response data used to determine the tryptophan lifetimes for ZF29 and AMCA-ZF29. Differences between zinc-bound AMCA-ZF29 (Panel A) and metal-free AMCA-ZF29 (Panel B) frequency response curves are not as obvious as those seen for DNS-ZF28 (Figure 4). Lifetime data for ZF29 and AMCA-ZF29 are reported in Table II. As seen for ZF28, the average lifetime of zinc-bound ZF29 is shorter than the metal-free and GuHCl-treated peptide lifetimes. It should be noted that donor-only lifetime data for the GuHCl case were virtually identical for both ZF28 and ZF29; therefore, these data files were globally analyzed to generate the donor-alone GuHCl decay parameters given in Tables I and II. Although the steady-state emission spectra (Figure 3) for ZF29 and AMCA-ZF29 clearly show the greatest amount of transfer occurring for metal-free peptide, comparison of the donor-alone and D–A-pair frequency response curves indicates that the transfer rates for zinc-bound peptide (Figure 5A) and metal-free peptide (Figure 5B) are approximately the same.
FIGURE 5:
Multiexponential lifetime fits to the donor frequency response data for ZF29 and AMCA-ZF29. In each case, donor-alone peptide data are the open circles (○) and D–A peptide data are the filled circles (●). Panel A: zinc-bound peptide. Panel B: metal-free peptide. Panel C: peptide plus 5 M GnHCl. Donor lifetime parameters are reported in Table II.
Table II:
Donor Multiexponential Intensity Decay Analysis of ZF29 and AMCA-ZF29
| samplea | 〈τ〉 (ns)b | τi (ns) | αi | fic | χR2 |
|---|---|---|---|---|---|
| ZF29 + Zn2+ | 1.72 | 0.220 | 0.399 | 0.083 | 0.51 |
| 1.38 | 0.536 | 0.703 | |||
| 3.44 | 0.065 | 0.214 | |||
| ZF29 + no metal | 2.00 | 0.108 | 0.282 | 0.026 | 2.44 |
| 1.02 | 0.474 | 0.405 | |||
| 2.78 | 0.244 | 0.570 | |||
| ZF29 + 5 M GuHCld | 2.35 | 0.315 | 0.265 | 0.049 | 2.11 |
| 1.58 | 0.427 | 0.396 | |||
| 3.07 | 0.308 | 0.555 | |||
| AMCA-ZF29 + Zn2+ | 0.74 | 0.138 | 0.549 | 0.182 | 2.36 |
| 0.642 | 0.401 | 0.621 | |||
| 1.63 | 0.050 | 0.196 | |||
| AMCA-ZF29 + no metal | 0.95 | 0.125 | 0.550 | 0.147 | 1.36 |
| 0.697 | 0.379 | 0.566 | |||
| 1.86 | 0.071 | 0.285 | |||
| AMCA-ZF29 + 5 M GuHCl | 1.31 | 0.036 | 0.602 | 0.046 | 2.46 |
| 0.609 | 0.204 | 0.265 | |||
| 1.67 | 0.194 | 0.689 |
All samples were measured in 50 mM HEPES, 50 mM NaCl, 10 mM DTT pH 7 buffer at room temperature. The no metal and GuHCl samples also contained 1 mM EDTA.
Average lifetime, 〈τ〉 = Σiαiτi2/Σiαiτi.
Fractional intensity of each decay component, fi = αiτi/Σiαiτi.
These parameter values are the result of a global analysis of ZF28 and ZF29 measurements.
Anisotropy Measurements.
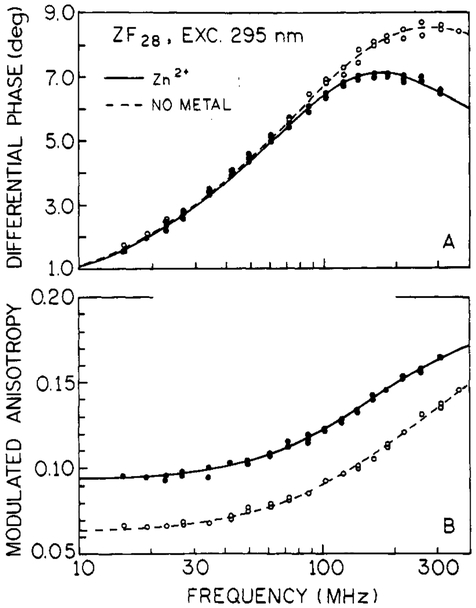
Frequency-domain anisotropy measurements of tryptophan were performed on both ZF28 and ZF29 donor peptides in the absence and presence of zinc. The ZF28 data are shown in Figure 6 (ZF29 data were nearly identical and are not shown), and the anisotropy values for both ZF28 and ZF29 are reported in Table III. Both the differential phase angles (Figure 6A) and the modulated anisotropy data (Figure 6B) are distinct for the metal-free and metal-bound conditions; similar results were observed for ZF29.
FIGURE 6:
Donor anisotropy data for ZF28. Panel A shows the differential phase data. Panel B shows the modulated anisotropy data. In each panel, zinc-bound peptide data are the filled circles (●) and solid lines and metal-free data are the open circles (○) and dashed lines. Anisotropy parameter values are reported in Table III.
Table III:
Tryptophan Anisotropy Decays for ZF28 and ZF29 and Acceptor Anisotropy Decays for DNS-ZF28 and AMCA-ZF29
| sample | θi (ns)a | r0gia | χR2 |
|---|---|---|---|
| Tryptophan Donor Anisotropy | |||
| ZF28b + Zn2+ | 1.91 | 0.173 | 0.49 |
| 0.227 | 0.035 | ||
| ZF28 + no metal | 2.09 | 0.095 | 0.42 |
| 0.463 | 0.101 | ||
| ZF29b + Zn2+ | 1.64 | 0.174 | 0.45 |
| 0.049 | 0.046 | ||
| ZF29 + no metal | 1.99 | 0.107 | 0.19 |
| 0.205 | 0.106 | ||
| Acceptor Anisotropy | |||
| DNS-ZF28c + Zn2+ | 2.48 | 0.176 | 3.60 |
| 0.295 | 0.165 | ||
| DNS-ZF28 + no metald | 1.05 | 0.119 | 0.41 |
| 0.389 | 0.093 | ||
| AMCA-ZF29e + Zn2+ | 1.48 | 0.071 | 4.86 |
| 0.288 | 0.218 | ||
| AMCA-ZF29 + no metal | 1.11 | 0.087 | 4.43 |
| 0.285 | 0.203 | ||
θi are the rotational correlation times, and r0gi are the amplitudes of each component.
Excitation at 295 nm.
Excitation at 345 nm.
Analysis performed with phase angle data only.
Excitation at 360 nm.
Tryptophan anisotropy data for both ZF28 and ZF29 under metal-free and zinc-bound conditions yield two rotational correlation times (θ) (Table III). The longer component (~2 ns) is associated with the global motion of the zinc finger molecule, and the shorter subnanosecond component is representative of the local motions of tryptophan. The presence of increased internal flexibility in the zinc-free peptide can be seen in Figure 6 by the larger differential phase angles at higher frequencies and the lower modulated anisotropies at all frequencies. For both zinc-bound donors ZF28 and ZF29, the amplitude (r0gi) of the longer component is 4–5-fold larger than the amplitude of the shorter component, which is consistent with the assumption that the metal-bound structure is compact and globular in nature. In the metal-free donors, the amplitudes of both components are nearly equal. These results are consistent with a less compact and relatively unfolded peptide structure.
Frequency-domain anisotropy measurements of the acceptors in DNS-ZF28 and AMCA-ZF29 were also performed in the absence and presence of zinc (data not shown). The anisotropy results for both acceptors are reported in Table III. The 2.48-ns DNS correlation time that is present under zinc-bound conditions is similar to the ~2-ns components observed for the tryptophan donors (Table III). The fact that it is slightly longer cound be partially explained by molecular weight differences between the donor alone and D–A molecules. Also, the longer lifetime of the DNS acceptor could be expected to result in longer apparent correlation times. Since the DNS acceptor is located at the end of the peptide chain, the shortening of its long component (2.4-fold decrease) under metal-free conditions is perhaps due to the increased flexibility in the N-terminal portion of the peptide chain under these conditions. Shortening of the long component does not occur for the tryptophan probably because it is located at the less flexible midpoint of the peptide chain (Hu et al., 1990).
The anisotropy results obtained for the AMCA acceptor in zinc-bound and metal-free peptide are very similar. In each case there is a long and short component, and the amplitude associated with the short component is 2–3-fold greater than that of the long component (Table III). Since the AMCA acceptor is attached to the four-carbon methylene side chain of LYS29, the subnanosecond component is expected to be the more dominant species due to the large degree of flexibility at this site. The long anisotropy component of AMCA is slightly shorter for the metal-free peptide (1.11 ns) than for the zinc-bound peptide (1.48 ns). This shortened long component is perhaps a result of the increased flexibility in the peptide chain that exists when the α-helix is unwound under metal-free conditions.
Energy-Transfer Distance Distributions.
Frequency-domain phase and modulation data measured for DNS-ZF28 (Figure 4) andAMCA-ZF29 (Figure 5) were used to calculate the D–A distance distributions. Since the peptides were measured at room temperature in buffer, a distance distribution model that includes the effects of mutual site-to-site donor–acceptor diffusion was also applied to the data. The two- (Rav and hw) and three- (Rav, hw, and D) parameter distance-distribution analyses for DNS-ZF28 and AMCA-ZF29 are reported in Tables IV and V, respectively. The data were fit with all three parameters (Rav, hw, and D) floated, except for the GuHCl case. A three-parameter fit to the GuHCl data was unstable; however, a good fit and reasonable result was obtained when hw was fixed at 30.0 Å.
Table IV:
Distance Distribution Parameters for DNS-ZF28
| sample | Rav (Å) | hw (Å) | D (Å2/ns)a | χRN2 b |
|---|---|---|---|---|
| Zn2+ | 11.2c,d (11.1–11.3)e | 2.96 (2.72–3.34) | 1.00 | |
| 11.2 (11.2–11.3) | 2.82 (2.75–3.00) | 0.001 (10−8–0.2) | 1.04 | |
| 11.2 | 2.94 | 〈0.2〉f | 1.03 | |
| 4.1 | 〈30.0〉 | 1000 | 3.11 | |
| no metal | 19.4c (19.2–19.5) | 7.71 (7.08–8.38) | 2.02 | |
| 20.1 (19.8–20.3) | 14.5 (12.5–16.3) | 12.3 (8.1–17.8) | 1.00 | |
| 19.2 | 〈3.0〉 | 10−5 | 7.90 | |
| 20.5 | 〈30.0〉 | 56.2 | 1.39 | |
| 5 M GuHCl | 22.2c (22.1–22.3) | 8.49 (7.65–9.34) | 2.48 | |
| 24.1g (23.5–24.7) | 〈30.0〉 | 36.3 [54]h (33.1–40.7) | 1.00 | |
| 24.5 | 〈3.0〉 | 10−7 | 120 | |
| 22.4 | 〈30.0〉 | 〈25.7〉 | 1.63 |
1 Å2/ns = 1 × 10−7 cm2/s.
χRN2 is the normalized χR2 value.
This analysis was performed without considering D-to-A diffusion.
Acceptor fraction labeling fixed at 0.977 to correct for background.
Values in parentheses are the 67% confidence limits.
Bracketed values indicate that this parameter was fixed during the analysis.
This analysis was not stable when floating all three parameters.
Number in brackets has been corrected for the increased viscosity of the GuHCl solution (CRC Handbook of Biochemistry (1978) (Sober, H. A., Ed.) 2nd ed., CRC Press, Cleveland, OH).
Table V:
Distance Distribution Parameters for AMCA-ZF29
| sample | Rav (Å) | hw (Å) | D (Å2/ns)a | χRN2 b |
|---|---|---|---|---|
| Zn2+ | 21.5c (21.4–21.5)d | 8.07 (7.86–8.29) | 1.27 | |
| 21.4 (21.3–21.5) | 9.90 (9.16–10.7) | 3.31 (2.24–5.13) | 1.00 | |
| no metal | 21.0c (20.7–21.3) | 13.2 (12.6–13.8) | 3.54 | |
| 14.6 (11.4–16.9) | 27.8 (24.3–32.7) | 20.4 (16.2–28.2) | 1.01 | |
| 16.3 (16.1–16.5) | 〈25.0〉e | 16.6 (15.8–17.8) | 1.00 | |
| 5 M GuHCl | 25.0c (24.8–25.3) | 13.4 (12.4–14.5) | 2.10 | |
| 22.5f (22.0–23.0) | 〈30.0〉 | 25.7 [39]g (22.9–28.8) | 1.00 | |
| 23.9 | 〈30.0〉 | 〈36.3〉 | 1.43 |
1 Å2/ns = 1 × 10−7 cm2/s.
χRN2 is the normalized χR2 value.
This analysis was performed without considering D-to-A diffusion.
Values in parentheses are the 67% confidence limits.
Bracketed values indicate that this parameter was fixed during the analysis.
This analysis was not stable when floating all three parameters.
Number in brackets has been corrected for the increased viscosity of the GuHCl solution (CRC Handbook of Biochemistry, (1978) (Sober, H. A., Ed.) 2nd ed., CRC Press, Cleveland, OH).
For zinc-bound DNS-ZF28; the best fit to the data yields a 3.0-Å hw, which indicates that the molecule exists primarily in a single conformation. Fixing the hw parameter at 30.0 Å yields a fit whose normalized χR2 value (χR2N) is 3-fold greater (Table IV) than that obtained when hw was floated; thus it can be concluded with a high degree of certainty that binding of zinc induces a fairly rigid and unique conformation in the peptide. An attempt was made to fit the metal-free and GuHCl-treated DNS-ZF28 data with the hw parameter fixed at the 3-Å zinc-bound peptide’s value. The elevated χR2N values (Table IV) obtained for these fits clearly indicate that the zinc finger peptide is a flexible molecule under these conditions.
Distance distributions determined with D–A diffusion for DNS-ZF28 are shown in Figure 7A. The 11.2-Å average D–A distance (Rav) for zinc-bound DNS-ZF28 is in good agreement with the distance determined from the 2D NMR structure of Wright and co-workers (Lee et al., 1989). Virtually no donor-to-acceptor diffusion is detected for zinc-bound peptide. This is apparent not only from the extremely low value of D (0.001 Å2/ns) but also from the relatively unchanged χR2N values obtained for distance distribution fits with (1.04) and without diffusion (1.00) (Table IV). Fixing D at the upper 67% confidence limit (0.2 Å2/ns) determined from the three-parameter fit (Table IV) yields virtually equivalent Rav and hw values, thereby indicating the validity of these measurements.
FIGURE 7:
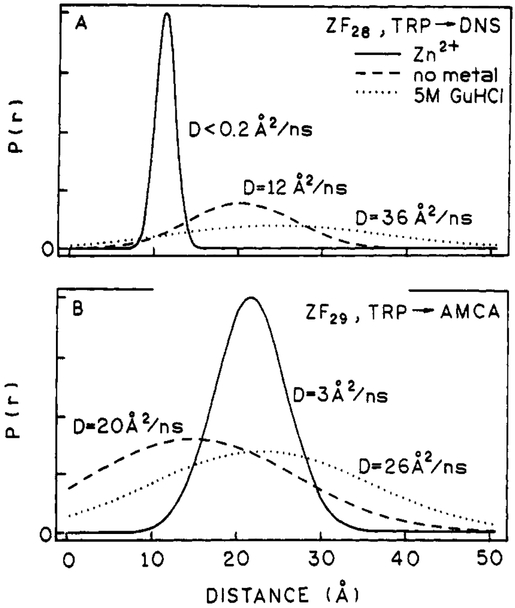
Zinc finger distance distributions calculated with diffusion. P(r) is the probability that a particular distance will occur. Panel A shows the DNS-ZF28 distance distributions. Panel B shows the AMCA-ZF29 distance distributions. In both panels the zinc-bound distribution is the solid line, metal-free is the dashed line, and GuHCl-treated is the dotted line. The calculated diffusion coefficient for each distribution is indicated. See Tables IV and V for distance-distribution parameter values.
It is obvious from Figure 7A that the metal-free and GuHCl-treated DNS-ZF28 distance distributions are very different from those of the zinc-bound peptide. The Rav values for both metal-free (20.1 Å) and GuHCl-treated peptide (24.1 Å) are approximately double that of the zinc-bound peptide (Table IV), which implies that the zinc finger structure is unfolded in the absence of metal ion, as others have concluded with other physical methods (Frankel et al., 1987; Párraga et al., 1988; Lee et al., 1991). However, the differences observed between the metal-free state and the assumed denatured state induced by GuHCl (Figure 7A, Table IV) indicate that there is probably some residual structure in metal-free peptide.
The larger degree of conformational flexibility observed for both metal-free (hw = 14.5 Å) and GuHCl-treated (hw = 30.0 Å) DNS-ZF28, as compared to the zinc-bound peptide (hw = 2.8 Å), also implies that alternate zinc finger conformational states exist. The values of D determined for the metal-free (12 Å2/ns) and GuHCl cases (36 Å2/ns) are consistent with the increased flexibility observed in the distributions. In both of these cases the distributions determined without diffusion yield at least 2-fold higher χR2N values (Table IV), thereby indicating that the more correct model is one that includes the effects of D–A diffusion. Since GuHCl significantly increases the viscosity of the solution, the value of D normalized to the viscosity of water at 25 °C is about 54 Å2/ns (Table IV). This large difference in mutual D–A diffusion (42 Å2/ns) between the metal-free and denatured peptide also suggests that metal-free peptide contains residual structure in the amino-terminal part of the peptide.
Distance distributions for AMCA-ZF29 are shown in Figure 7B and reported in Table V. As for DNS-ZF28, these distributions were determined for zinc-bound, metal-free, and GuHCl-treated peptide. Differences between the distributions for these three conditions are not as dramatic as those seen for DNS-ZF28 (Figure 7A). However, AMCA-ZF29 is most conformationally restricted when zinc is bound, which is consistent with the DNS-ZF28 results. The hw for zinc-bound AMCA-ZF29 is 8 Å as compared to only 3 Å for DNS-ZF28, but this increased conformational heterogeneity can be explained by the difference in point of attachment to the peptide for these two acceptors (Figure 1). The DNS acceptor is directly attached to the main chain of the peptide, whereas the AMCA acceptor is attached to the flexible side chain of lysine. The 21.5-Å Rav value obtained for zinc-bound AMCA-ZF29 is consistent with the NMR-determined structure (Lee et al., 1989) for this type of zinc finger.
When the AMCA-ZF29 distributions are analyzed with diffusion, the metal-free peptide’s hw value increases approximately 2-fold, but the zinc hw value is only slightly increased (Table V). As was the case for DNS-ZF28, the hw value for GuHCl-treated AMCA-ZF29 was fixed at 30 Å in order to resolve Rav and D. The AMCA-ZF29 distance distribution results are consistent with what was observed in the DNS-ZF28 distributions. In all cases, except for metal-free AMCA-ZF29, the Rav values are relatively unchanged when diffusion is added to the analysis. The Rav value for metal-free AMCA-ZF29 decreases from 21 to 15 Å. A decrease in Rav has previously been observed in distance distributions of a protein after unwinding of its α-helical segment (Lakowicz et al., 1990a; Lakowicz et al., 1992; Lakowicz et al., manuscript in preparation). The CD spectra for the ZF28 peptide do indicate the possible presence of an α-helix (data not shown) when zinc is bound and the 2D NMR structures obtained for CCHH-type peptides all contain a helical region (Lee et al., 1989; Klevit et al., 1990; Omichinski et al., 1990; Kochoyan et al., 1991 a,b,c). This helical segment in the zinc finger peptide chain appears to lock the TRP donor and AMCA acceptor into a relatively fixed position with respect to each other. However, when the helix is unwound in the absence of metal ion, the increased flexibility in the peptide chain then enables the donor and acceptor to come closer together in solution. The smaller difference in the value of D (19 Å2/ns) observed for metal-free and GuHCl-treated AMCA-ZF29, as compared to that observed for DNA-ZF28 (42 Å2/ns), suggests that the carboxy-terminal half of the peptide is less structured in the absence of metal ion as compared to the amino-terminal half.
The 67% confidence limits for the DNS-ZF28 and AMCA-ZR29 distance distribution parameters are reported in Tables IV and V, respectively (values in parentheses). Generally, the best resolution in distance distribution parameters is obtained for zinc-bound peptide. This level of resolution is achieved for both D–A pairs because the amount of D–A diffusion is very low (<0.2 Å2/ns for DNS-ZF28 and 3.3 Å2/ns for AMCA-ZF29). Metal-free AMCA-ZF29 distribution parameters are not well resolved when all three parameters are floated. For example, the 67% confidence limits for D are 16.2–28.2 Å2/ns. If the hw value is fixed at 25.0 Å, the level of resolution in Rav and D increases dramatically.
As previously mentioned, GuHCl-treated peptide distribution parameters could be resolved only if hw was fixed. One possible explanation for this inability to resolve the distance distribution parameters without fixing hw is that both D–A peptides could not be measured with background fluorescence values of less than 5% due to lower solubility of the D–A peptides and the amount of background that results from GuHCl alone. A second reason is that the level of D–A diffusion observed for GuHCl-treated peptide (26–36 Å2/ns) precludes the desired level of resolution with single-file analysis only. All three parameters could probably be resolved if global analysis (Beechem et al., 1991, and references cited therein) was used. For example, two-file analysis of the data reported here along with measurements of the peptides at low temperature in the viscous solvent propylene glycol should enable adequate resolution of all three parameters (Lakowicz et al., 1990b). Such measurements were not performed because a change in solvent could alter the conformation of the peptides. Quenching of the tryptophan donor with various amounts of an external quencher such as acrylamide might also enable resolution of all three distance-distribution parameters (Lakowicz et al., 1991b). However, the low quantum yield of the tryptophan in the zinc finger peptides precludes this type of measurement and analysis.
Theoretically, GuHCl-treated DNS-ZF28 and AMCA-ZF29 distance distributions should be very similar since both cases involve measuring from the midpoint (TRP14) of the peptide sequence to each end of the chain. When the data are analyzed with the three-parameter distance distribution model with the hw fixed at 30 Å, the Rav values obtained for DNS-ZF28 and AMCA-ZF29 are 24.1 and 22.5 Å, respectively. This Rav difference is negligible; however, the difference in diffusion observed for the D–A pairs (36.3 Å2/ns for DNS-ZF28 and 25.7 Å2/ns for AMCA-ZF29) is significant. Such a difference could be attributed to the lower level of resolution observed for both GuHCl-treated D–A pairs. However, an interesting result was obtained for both D–A pairs when not only hw was fixed (〈30.0 Å〉) but also D at the value obtained for the other D–A pair. For example, when the DNS-ZF28 data were analyzed with D fixed at 25.7 Å2/ns, the resultant Rav value was 22.4 Å, which is nearly equivalent to that obtained for AMCA-ZF29 (22.5 Å) when both Rav and D were floated during the analysis. Likewise, in the corresponding analysis of AMCA-ZF29, the calculated Rav value was 23.9 Å, which is very similar to the 24.1-Å value obtained for DNS-ZF28 when Rav and D were floated. These analyses suggest that the measured molecular conformations and dynamics for both GuHCl-treated D–A pairs are essentially the same.
Evaluation of the Energy Transfer Orientation Factor (κ2) Parameter.
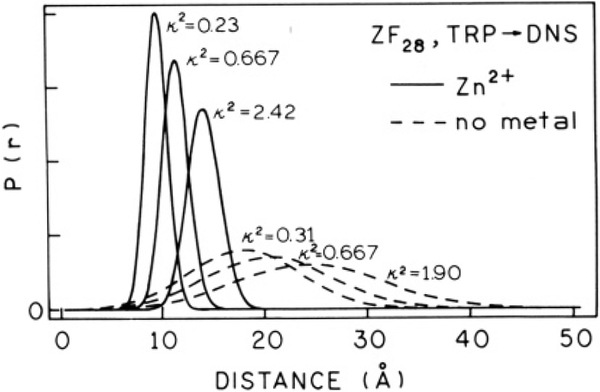
Ever since energy transfer measurements were recognized as a useful tool in determining molecular distances, questions have risen concerning the validity in using the random κ2 value of ⅔ in describing the orientation between the donor and acceptor dipole moments (Dale & Eisinger, 1974; Dale & Eisinger, 1976; Haas et al., 1978a,b; Dale et al., 1979). This average value was used in the results described above. However, in order to justify usage of this average value, one can use the anisotropy data of the fluorophores to set limits on the κ2 value (Dale et al., 1979; Cheung, 1991). This evaluation has previously been performed on distance distribution analyses of a protein (Lakowicz et al., 1988), and this same procedure has been applied to the data described above for DNS-ZF28.
Using the anisotropy data reported in Table III for ZF28 and DNS-ZF28, minimum and maximum values of κ2 were determined and used to recalculate the R0 values for zinc-bound and metal-free peptide (Cheung, 1991). The fundamental anisotropy (rf) was assumed to be 0.4 for both donor and acceptor (Dale et al., 1979). The calculated range of κ2 values of DNS-ZF28 was 0.23–2.42 and is the same range that was found for the acceptor-labeled protein Troponin I (Lakowicz et al., 1988), which also contains an intrinsic tryptophan donor. Figure 8 depicts the effect that κ2 has on the distance distributions. Variation in Rav for zinc-bound DNS-ZF28 was a modest 4.5 Å, and for hw it was only 1.2 Å. Similarly, the variations obtained for metal-free peptide was 2.3 Å for Rav and 2.4 Å for hw. Given the mixed polarization of the indole donor, it is possible that the actual effects of κ2 are less than those shown in Figure 8 (Haas et al., 1978a). It was therefore concluded that use of the dynamically averaged value of κ2 (⅔) did not dramatically affect determined values of Rav and hw and in any event does not affect the differences observed between the zinc-bound, metal-free, and denatured states.
FIGURE 8:
Effect of κ2 on the DNS-ZF28 distance distributions. A two-parameter model (no diffusion) was used to calculate the zinc-bound distributions (solid lines). A three-parameter model (with diffusion) was used to calculate the metal-free distributions (dashed lines). The κ2 value used to calculate each R0 is indicated next to each curve.
DISCUSSION
Fluorescence energy transfer distance distribution measurements are very useful in determining not only the range of accessible intramolecular distances for a given molecule but also the degree of conformational flexibility that exists within that molecule. The ability to assess varying degress of conformational flexibility with fluorescence energy transfer distance distribution methods has proven very useful in analyzing the zinc finger structure. All the experimental evidence reported here for the metal-bound zinc finger peptide are consistent with a compact, highly inflexible structure, whereas the metal-free and denatured peptides are relatively unfolded and very flexible. The anisotropy data indicate that a more compact structure is formed when zinc binds the peptide, but in the absence of metal more local motions are observed, indicating an increased flexibility in the peptide.
Both zinc-bound distance distributions indicate that the zinc finger peptide is rigid and adopts a unique conformation in the presence of zinc. The wider distribution obtained for metal-bound AMCA-ZF29, as compared to the metal-bound DNS-ZF28 distribution, is very likely due to the flexible lysine side chain where the AMCA acceptor is attached. The average energy transfer-determined distance between TRP14 and the amino-terminal DNS group in zinc-bound DNS-ZF28 is 11.2 Å, which is very close to the 10-Å value estimated from the NMR-determined zinc finger structure of Wright and co-workers (Lee et al., 1989). The crystallographic structure of a 3-zinc finger peptide bound to DNA has been reported (Pavletich & Pabo, 1991) and superimposition of finger 2 from this structure with the NMR-determined structure (Lee et al., 1989) gives a rms deviation of 0.74 Å. Thus, although a detailed structural comparison cannot be made between our measurements and the NMR-determined and crystallographic structures, it is reasonable to assume that our particular zinc finger typifies the CCHH-type structures reported by others.
A variety of zinc finger conformations exists in the absence of zinc. It appears that some residual structure is present in the amino-terminal half of the metal-free peptide. This conclusion is based on the approximately 2-fold lower half-width value obtained for DNS-ZF28 as compared to that of AMCA-ZF29. It is not known if this residual structure is important for metal binding and subsequent interaction of the zinc finger with DNA. Since the metal-free hw value obtained for AMCA-ZF29 is similar to that obtained for both GuHCl-treated peptide distributions, it is likely that in the absence of metal the carboxy-terminal half of the molecule is in a random coil conformation. It is interesting that the metal-free AMCA-ZF29 Rav value is 8–10 Å less than those obtained for both GuHCl-treated D–A pairs. Probably there are some attractive forces between individual amino acids within the sequence under metal-free conditions which are then abolished in the presence of GuHCl.
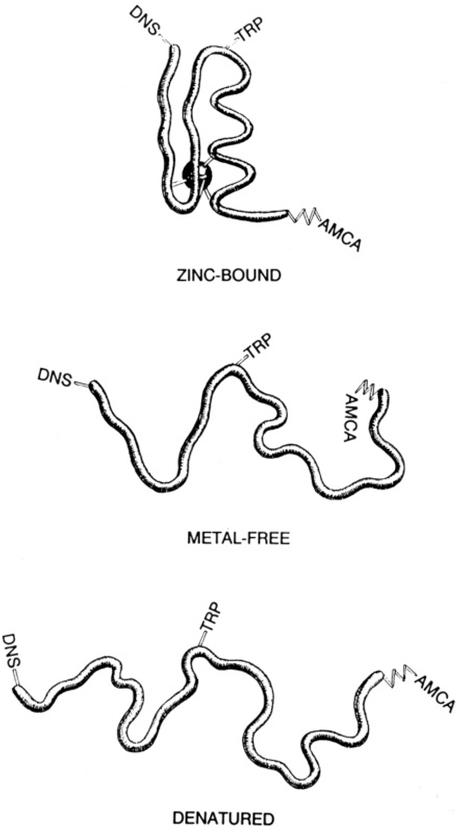
Figure 9 depicts a proposed structural model based on the distance distribution and anisotropy data. In the presence of metal ion, the zinc finger peptide adopts a compact and highly inflexible structure. All intramolecular motions are essentially frozen out after zinc coordination. In the absence of metal ion the zinc finger molecule retains some structure, which could be important in providing a high-affinity binding site (KD ≤ 10−9 M) for the zinc. This residual structure could be the result of association between the three conserved hydrophobic residues. It appears that the conserved hydrophobic residues of the CCHH-type zinc finger play some role in its structure on the basis of the metal binding studies of a zinc finger peptide which does not contain these hydrophobic residues (Michael et al., 1992). The implications for regulation are very interesting (Berg, 1989; Thiesen & Bach, 1991). It is not known if zinc levels fluctuate in the nucleus during transcription. If they do, it would be very important for the transcription factor zinc domains to be able to bind zinc in a highly efficient manner. Once metal is bound, the unique conformation of each individual finger enables binding of the transcription factor to the DNA. Any conformational flexibility within each zinc finger domain would probably preclude binding since each domain binds in the major groove of the DNA in a very modular fashion (Pavletich & Pabo, 1991).
FIGURE 9:
Proposed structural model for the zinc finger peptide under zinc-bound, metal-free, and denatured conditions. Energy transfer chromophores are indicated, TRP is the donor, and DNS and AMCA are the two acceptors.
Many additional fluorescence experiments could be devised for further examination of the zinc finger structure and its dynamic properties. For example, synthesis of a two- or three-finger native-sequence peptide as well as oligonucleotides corresponding to the peptide’s site-specific DNA-binding site might yield important information about the structure and dynamics of a zinc finger protein–DNA interaction. Additionally, such experiments could reveal if the peptide undergoes further changes in conformation upon interaction with DNA. It would also be interesting to examine the other types of zinc fingers such as the CCCC and CCHC motif to see if their structures are conformationally restricted as well when bound to zinc ion. In summary, the fluorescence energy transfer distance distribution results reported here suggest that this is a very useful biophysical method for examining the structural and dynamic properties of zinc finger peptides.
ACKNOWLEDGMENT
Mass spectral measurements were performed at the Structural Biochemistry Center at the University of Maryland Baltimore County, a NSF-supported Biological Instrumentation Center. P.E. thanks H. Szmacinski, I. Gryczynski, and H. Malak for their expert assistance with the frequency-domain measurements and J. Kuśba and M. L. Johnson (University of Virginia) for the data analysis software. P.E. and J.R.L. thank Prof. J. Collins and J. Theibert for the amino acid analysis, P. E. Wright and co-workers for the coordinates from their NMR-determined structure, and J. R. Lee for the illustration in Figure 9. P.E. also acknowledges J. M. Berg and co-workers at the Johns Hopkins University for their helpful suggestions concerning the design of the zinc finger peptide.
This work was supported by the National Institutes of Health (GM 35154); support for instrumentation is from the National Science Foundation (DIR-8710401) and the National Institutes of Health (RR 07510). P.E. was supported (in part) by a Graduate Research Assisstantship Award from the UMAB Designated Research Initiative Fund.
Abbreviations:
- A
energy transfer acceptor
- AMCA
7-amino-4-methylcoumarin-3-acetyl
- C
cysteine
- CD
circular dichroism
- D
energy transfer donor
- DNS
5-(dimethylamino)-1-naphthalenesulfonyl
- DTT
dithiothreitol
- EDTA
ethylenediaminetetraacetic acid
- GuHCl
guanidine hydrochloride
- H
histidine
- HEPES
4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid
- hw
full width of the distribution at half-maximum probability
- MCP PMT
microchannel plate photomultiplier tube
- Rav
average donor–acceptor distance
- TFA
trifluoroacetic acid
- ZF
zinc finger
REFERENCES
- Beechem JM, & Haas E (1989) Biophys. J 55, 1225–1236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beechem JM, Gratton E, Ameloot M, Knutson JR, & Brand L (1991) in Topics in Fluorescence Spectroscopy (Lakowicz JR, Ed.), Vol. 2, Principles, Chapter 5, Plenum Press, New York. [Google Scholar]
- Berg JM (1988) Proc. Natl. Acad. Sci. U.S.A. 85, 99–102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berg JM (1989) Prog. Inorg. Chem 37, 143–185. [Google Scholar]
- Berg JM (1990) Annu. Rev. Biophys. Chem 19, 405–421. [DOI] [PubMed] [Google Scholar]
- Berg JM, & Merkle DL (1989) J. Am. Chem. Soc 111, 3759–3761. [Google Scholar]
- Bertini I, & Luchinat C (1984) Adv. Inorg. Biochem 6, 71–111. [PubMed] [Google Scholar]
- Bevington PR (1969) in Data Reduction and Error Analysis for the Physical Sciences, McGraw-Hill, NY. [Google Scholar]
- Brown RS, Sander C, & Argos P (1985) FEBS Lett. 186, 271–274. [DOI] [PubMed] [Google Scholar]
- Chen RF (1967) Anal. Lett 1, 35–42. [Google Scholar]
- Cheung H (1991) in Topics in Fluorescence Spectroscopy (Lakowicz JR, Ed.), Vol. 2, Principles, Chapter 3, Plenum Press, New York. [Google Scholar]
- Dale RE, & Eisinger J (1974) Biopolymers 13, 1573–1605. [DOI] [PubMed] [Google Scholar]
- Dale RE, & Eisinger J (1976) Proc. Natl. Acad. Sci. U.S.A. 73, 271–273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dale RE, Eisinger J, & Blumberg WE (1979) Biophys. J 26, 161–194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eis PS, & Lakowicz JR (1992) Proc. SPIE–lnt. Soc. Opt. Eng 1640, 532–541. [Google Scholar]
- Eis PS, Kuśba J, Johnson ML, & Lakowicz JR (1993) J. Fluor (in press). [DOI] [PubMed] [Google Scholar]
- Evans RM, & Hollenberg SM (1988) Cell 52, 1–3. [DOI] [PubMed] [Google Scholar]
- Flory PL (1969) in Statistical Mechanics of Chain Molecules, Interscience Publishers (John Wiley & Sons, Inc.), New York. [Google Scholar]
- Förster Th. (1948) Ann. Phys. (Leipzig) 2, 55–75 (translated by R. S. Knox, University of Rochester). [Google Scholar]
- Frankel AD, Berg JM, & Pabo CO (1987) Proc. Natl. Acad. Sci. U.S.A. 84, 4841–4845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gibson TJ, Postma JPM, Brown RS, & Argos P (1988) Protein Eng. 2, 209–218. [DOI] [PubMed] [Google Scholar]
- Gryczynski I, Wiczk W, Johnson ML, & Lakowicz JR (1988a) Chern. Phys. Lett 145, 439–446. [Google Scholar]
- Gryczynski I, Wiczk W, Johnson ML, Cheung HC, Wang C-K, & Lakowicz JR (1988b) Biophys. J 54, 577–586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haas E, & Steinberg IZ (1984) Biophys. J 46, 429–437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haas E, Katchalski-Katzir E, & Steinberg IZ (1978a) Biochemistry 17, 5064–5070. [DOI] [PubMed] [Google Scholar]
- Haas E, Katchalski-Katzir E, & Steinberg IZ (1978b) Biopolymers 17, 11–31. [DOI] [PubMed] [Google Scholar]
- Haas E, McWherter CA, & Scheraga HA (1988) Biopolymers 27, 1–21. [DOI] [PubMed] [Google Scholar]
- Han MK, Cyran FP, Fisher MT, Kim SH, & Ginsberg A (1990) J. Biol. Chem 265, 13792–13799. [PubMed] [Google Scholar]
- Hanas JS, Duke AL, & Gaskins CJ (1989) Biochemistry 28, 4083–4088. [DOI] [PubMed] [Google Scholar]
- Hu Y, MacInnis JM, Cherayil BJ, Fleming GR, Freed KF, & Perico A (1990) Proc. SPIE–Int. Soc. Opt. Eng. 1204,425–447. [Google Scholar]
- Johnson ML, & Frasier SG (1985) Methods Enzymol. 117, 301–342. [Google Scholar]
- Johnson ML, & Faunt L,M (1992) Methods Enzymol. 210, 1–37. [DOI] [PubMed] [Google Scholar]
- Johnson PF, & McKnight SL (1989) Annu. Rev. Biochem 58, 799–839. [DOI] [PubMed] [Google Scholar]
- Klevit RE, Herriott JR, & Horvath SJ (1990) Proteins: Struct., Funct., Genet 7, 215–226. [DOI] [PubMed] [Google Scholar]
- Klug A, & Rhodes D (1987) Trends Biochem. Sci 12, 464–469. [Google Scholar]
- Kochoyan M, Havel TF, Nguyen D, Dahl CE, Keutmann HT, & Weiss MA (1991a) Biochemistry 30, 3371–3386. [DOI] [PubMed] [Google Scholar]
- Kochoyan M, Keutmann HT, & Weiss MA (1991b) Biochemistry 30, 7063–7072. [DOI] [PubMed] [Google Scholar]
- Kochoyan M, Keutmann HT, & Weiss MA (1991c) Biochemistry 30, 9396–9402. [DOI] [PubMed] [Google Scholar]
- Krizek BA, Amann BT, Kilfoil VJ, Merkle DL, & Berg JM 91991) J. Am. Chem. Soc 113, 4518–4523. [Google Scholar]
- Laczko G, Gryczynski I, Gryczynski Z, Wiczk W, Malak H, & Lakowicz JR (1990) Rev. Sci. Instrum 61, 2331–2337. [Google Scholar]
- Lakowicz JR (1983) in Principles of Fluorescence Spectroscopy, Plenum Press, New York. [Google Scholar]
- Lakowicz JR, Gryczynski I, Cheung HC, Wang C-K, Johnson ML, & Joshi N (1988) Biochemistry 27, 9149–9160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lakowicz JR, Gryczynski I, Wiczk W, Laczko G, Prendergast FC, & Johnson ML (1990a) Biophys. Chem 36, 99–115. [DOI] [PubMed] [Google Scholar]
- Lakowicz JR, Kuśba J, Wiczk W, Gryczynski I, & Johnson ML (1990b) Chem. Phys. Lett 173, 319–326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lakowicz JR, Gryczynski I, Wiczk W, Kuśba J, & Johnson ML (1991a) Anal. Biochem 195, 243–254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lakowicz JR, Kuśba J, Gryczynski I, Wiczk W, Szmacinski H, & Johnson ML (1991b) J. Phys. Chem 95, 9654–9660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lakowicz JR, Kuśba J, Szmacinski H, Gryczynski I, Eis PS, Wiczk W, & Johnson ML (1991c) Biopolymers 31, 1363–1378. [DOI] [PubMed] [Google Scholar]
- Lakowicz JR, Kuśba J, Wiczk W, Gryczynski I, Szmacinski H, & Johnson ML (1991d) Biophys. Chem 39, 79–84. [DOI] [PubMed] [Google Scholar]
- Lakowicz JR, Gryczynski I, Kuśba J, Wiczk W, Szmacinski H, & Johnson ML (1992) Proc. SPIE–Int. Soc. Opt. Eng 1640, 196–211. [Google Scholar]
- Lee MS, Gippert GP, Soman KV, Case DA, & Wright PE (1989) Science 245, 635–637. [DOI] [PubMed] [Google Scholar]
- Lee MS, Gottesfeld JM, & Wright PE (1991) FEBS Lett. 279, 289–294. [DOI] [PubMed] [Google Scholar]
- Michael SF, Kilfoil VJ, Schmidt MH, Amann BT, & Berg JM (1992) Proc. Nat/. Acad. Sci. U.S.A 89, 4796–4800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller J, McLachlan AD, & Klug A (1985) EMBO J. 4, 1609–1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neuhaus D, Nakaseko Y, Nagai K, & Klug A (1990) FEBS Lett. 262, 179–184. [DOI] [PubMed] [Google Scholar]
- Omichinski JG, Clore GM, Appella E, Sakaguchi K, & Gronenborn AM (1990) Biochemistry 29, 9324–9334. [DOI] [PubMed] [Google Scholar]
- Párraga G, Horvath SJ, Eisen A, Taylor WE, Hood L, Young ET, & Klevit RE (1988) Science 241, 1489–1492. [DOI] [PubMed] [Google Scholar]
- Párraga G, Horvath SJ, Hood L, Young ET, & Klevit RE (1990) Proc. Natl. Acad. Sci. U.S.A. 87, 137–141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pavletich NP, & Pabo CO (1991) Science 252, 809–817. [DOI] [PubMed] [Google Scholar]
- Rhodes D, & Klug A (1993) Sci. Am 268(2), 56–65. [DOI] [PubMed] [Google Scholar]
- Steiner RF (1991) in Topics in Fluorescence Spectroscopy (Lakowicz JR, Ed.), Vol. 2, Principles, Chapter 2, Plenum Press, New York. [Google Scholar]
- Struhl K (1989) Trends Biochem. Sci 14, 137–140. [DOI] [PubMed] [Google Scholar]
- Stryer L (1978) Annu. Rev. Biochem 47, 819–846. [DOI] [PubMed] [Google Scholar]
- Thiesen HJ, & Bach C (1991) Biochem. Biophys. Res. Commun 176, 551–557. [DOI] [PubMed] [Google Scholar]
- Weiss MA, & Keutmann HT (1990) Biochemistry 29, 9808–9813. [DOI] [PubMed] [Google Scholar]
- Weiss MA, Mason KA, Dahl CE, & Keutmann HT (1990) Biochemistry 29, 5660–5664. [DOI] [PubMed] [Google Scholar]
- Wiczk W, Eis PS, Fishman MN, Johnson ML, & Lakowicz JR (1990) Proc. SPIE–lnt. Soc. Opt. Eng 1204, 645–655. [Google Scholar]
- Wiczk W, Eis PS, Fishman MN, Johnson ML, & Lakowicz JR (1991) J. Fluor 1, 273–286. [DOI] [PubMed] [Google Scholar]