Blinded prediction of protein-ligand binding affinity using Amber thermodynamic integration for the 2018 D3R grand challenge 4

Abstract

In the framework of the 2018 Drug Design Data Resource (D3R) grand challenge 4, blinded predictions on relative binding free energy were performed for a set of 39 ligands of the Cathepsin S protein. We leveraged the GPU-accelerated thermodynamic integration (GTI) of Amber 18 to advance our computational prediction. When our entry was compared to experimental results, a good correlation was observed (Kendall’s τ: 0.62, Spearman’s ρ: 0.80 and Pearson’s R: 0.82). We designed a parallelized transformation map that placed ligands into several groups based on common alchemical substructures; TI transformations were carried out for each ligand to the relevant substructure, and between substructures. Our calculations were all conducted using the linear potential scaling scheme in Amber TI because we believe the softcore potential/dual-topology approach as implemented in current Amber TI is highly fault-prone for some transformations. The issue is illustrated by using two examples in which typical preparation for the dual-topology approach of Amber TI fails. Overall, the high accuracy of our prediction is a result of recent advances in force fields (ff14SB and GAFF), as well as rapid calculation of ensemble averages enabled by the GPU implementation of Amber. The success shown here in a blinded prediction strongly suggests that alchemical free energy calculation in Amber is a promising tool for future commercial drug design.

Introduction

Protein-ligand binding is central to both biological function and pharmaceutical activity. Some ligands simply inhibit protein function, while others induce protein conformational changes and hence modulate key cell-signaling pathways. In either case, achieving a desired therapeutic effect is often dependent upon the magnitude of the binding affinity of the ligand to its target receptor. Designing tight-binding ligands while maintaining the other ligand properties required for safety and biological efficacy is a primary objective of small-molecule drug discovery projects[1].

Binding affinity calculations in silico can significantly save cost and time invested in wet lab screening, if the accuracy of the binding affinity calculations can reach a certain threshold (root-mean-square errors under ^~2 kcal/mol)[2]. The ability to accurately predict modifications that lead to improved binding affinities can lead to a significant impact on lead-optimization campaigns. Virtual screening methods allow large numbers of binding affinity calculations to be done quickly. However, crucial statistical mechanical effects and other effects are often neglected in virtual screening including conformational entropy, averaging over multiple conformations or binding modes, the discrete nature of solvent, the tautomer distributions and their shifts upon binding[3]. A more rigorous computational approach is free-energy simulation. A variety of free-energy simulation methods, such as free-energy perturbation, thermodynamic integration (TI) and λ dynamics, employ an analysis of atomistic molecular dynamics (MD) or Monte Carlo simulations to determine the free-energy difference between two related ligands via an alchemical path[4–6,2].

Alchemical free energy calculations have been used for decades to study various free energy related problems for biomolecules and drug molecules. TI is one of the most fundamental methods for alchemical free energy calculation[7]. The statistical mechanics underlying the TI calculations follow this equation:

$$\mathrm{\Delta }G(A\to B)={\int }_0^1<\frac{\partial U(\lambda ,X)}{\partial \lambda }{>}_{\lambda }d\lambda$$ (1)

where λ represents the reaction coordinate between two chemical states A and B. X represents the spatial coordinates of the ligand and the target protein. <…>_λ is the ensemble averaged value at a particular λ value. U is the potential energy function defined by a force field. For the common case of linear scaling of the potential between two end states and potential energies A (U_A) and B (U_B), U can be expressed as:

$$U=\lambda U_B(X)+(1-\lambda )U_A(X)$$ (2)

and, the derivative of U with respect to λ is $U_B(X)-U_A(X)$ thus equation 1 can be expressed as:

$$\mathrm{\Delta }G(A\to B)={\int }_0^1<U_B(X)-U_A(X){>}_{\lambda }d\lambda$$ (3)

Methods like TI face several main challenges, including inaccuracy in the force fields and the high computational cost of obtaining the ensemble averages, both of which prevent the right side of equation 1 from being accurately estimated.

Moreover, these two issues are coupled since longer MD simulations with an inaccurate force field may cause the ensemble to deviate from the correct phase space. For example, a ligand with a correct initial pose may drift away from this binding mode if simulations are run long enough to obtain well converged ensemble averages, or the unbound states of ligands may sample erroneous conformations with a poor-quality ligand force field. Higher accuracy force fields allow prolonged MD simulations, which improve the convergence of the ensemble averages. Thus, a successful TI calculation requires both accurate force fields and sufficient computational power. Over the last ten years, both force fields and computing hardware have improved significantly, which allows the critical components on the right side of the equation to be calculated at high accuracy and low cost. These influence multiple aspects of equation 1, including X (the target protein can be stable near the experimentally determined structure during simulation as amino acids specific corrections on side-chain torsion angles were introduced to force fields[8–11]), U (potential energy surfaces of small compounds are modeled more accurately as the general force fields are becoming more and more versatile[12]) and <…> (the use of GPU brought MD simulations to a new level as it significantly speeds up and lowers cost of sampling ensemble averages [13–15]). In the specific case of TI, ensemble averaging in Amber is now more easily accessible via MD simulation due to implementation of TI on the CUDA GPU platform[16].

These improvements dramatically increase the feasibility of using alchemical free energy calculations in the lead-optimization process. In order to evaluate the accuracy, achievability and the cost of using alchemical free energy calculations in such practice, our group participated in the blind prediction of the binding free energy between Cathepsin S and the associated 39 ligands using an Amber TI-based protocol.

The Drug Design Data Resource (D3R) grand challenge[17–19] features blind prediction of protein-ligand binding pose, affinity ranking and binding free energy predictions. Submissions for the binding free energy predictions are scored by Kendall’s τ, Spearman’s ρ, Pearson’s R and centered root-mean-square error (RMSE). Protocols were categorized into ligand-based, structure-based and free energy-based methods. The challenge simulates a realistic drug discovery scenario in which binding affinity was not known a priori, thus allowing the community of computational chemists to better evaluate their methods and protocols without unconscious bias.

In D3R grand challenge 4, which took place from Sep to Dec in 2018, 39 ligands for Cathepsin S[20–23] and 38 ligands for beta-secretase 1 (BACE)[24–27] were selected for blind binding free energy predictions. In the Cathepsin S set, the ligands in the data set share the same scaffold which makes alchemical interconversion among these ligands easier. The time duration for the binding free energy predictions on this data set was 3 months. There is no structure of Cathepsin S with any of the 39 ligands available in the challenge set, but several other X-ray structures are available[19] for this target bound with some ligands sharing the same scaffold with these 39 ligands. All the ligands are expected to have a net charge of +2 in both free state and bound state, which was suggested by D3R.

Transitions between ligands in the BACE data set involve ring opening/closing and ring expansion/contraction, which are usually considered formidable in single-topology free energy calculations. The soft bond potential has been reported to successfully reproduce binding free energy changes involving ring opening/closing and ring expansion/contraction[28], and has been applied to macrocyclic ligands of BACE[29]. However, soft bond potential has not been implemented in Amber TI yet. Alternatively, it is possible to conduct such transitions using dual-topology approach. However, since we used the single-topology approach for reasons discussed below related to soft-core implementation, we opted not to test our protocol in the BACE challenge.

Methods

Ligand parameterization

Initial lead compound conformation was adopted from chain B of PDB ID 5qc6[30]. Atoms were added or removed from the initial lead compound to generate the 39 ligands in the binding affinity prediction data set for Cathepsin S. The structures of these ligands were energy minimized using the Maestro software[31]. AM1-BCC charges were assigned to the ligands using the ANTECHAMBER module in Amber v18 package[32]. Parameters for the bonded and Lennard-Jones (LJ) interactions of the ligands were adopted from GAFF2[12]. Modifications on F, Cl, Br and S were applied[33]. The lib files and frcmod files output by ANTECHAMBER can be found in the lib and frcmod folders in supporting information (SI).

Target protein preparation

The target protein structure was adopted from chain B of PDB ID 5qc6[30]. In chain A and chain B of PDB ID 5qc6, the BCJ ligands differ in the conformation of one of the piperidine groups which involves atom N70. They also differ in the direction of the charge carrying proton attached to N70. Since interchanges between the chair and boat conformation of the two piperidine groups are frequently observed during the simulations, we believe that the initial conformation of the piperidine groups is a less concern. However, protonation of the N70 atom in the ligand BCJ of chain A will result in the charge carrying proton facing the protein and being buried, which is energetically unfavorable. In chain B, the charge carrying proton attached to N70 will form a pi-cation interaction with Phe70, which is more energetically favorable.

Missing hydrogens of the protein were added by Molprobity[34]. The rotamer states of Asn/Gln/His were adjusted by following the suggestion of Molprobity. All acidic residues and the C-terminus were deprotonated. All basic residues and the N-terminus were protonated. All His residues were set to be neutral ε-His.

Thermodynamic integration calculations

1. Minimization and equilibration

The protein/ligands complexes were solvated in truncated octahedron boxes with a buffer distance of 8 Å. Waters observed in the X-ray structure (chain B of PDB ID 5qc6) were kept while all salt ions were deleted. Free energy calculations were performed using non-softcore TI implemented in Amber[32,7]. The Amber protein force field ff14SB and the TIP3P water model were used in the TI calculations[8,35]. Energy minimization and equilibration under constant pressure[36] were conducted to heat and relax the X-ray structures. The input files used for energy minimization and equilibration can be found in the input folder in the SI.

For the unbound state of ligands, the ligands were also solvated in truncated octahedron water boxes, but the buffer distance was set to 10 Å due to the higher mobility of an unbound small molecule. Protocols for the minimization and equilibration of the unbound state were the same as those used for the bound state.

2. Production runs

The production runs for the bound state and unbound state were conducted using the implementation of GPU-accelerated thermodynamic integration, pmemdGTI[16], under constant volume. Hydrogen atoms were constrained using the SHAKE algorithm[37]. No positional restraints were applied during the production runs. The temperature was set to 298K and no salt ions were included. Langevin dynamics was used to control temperature and the collision frequency was set to be 1.0 ps^-1. Particle mesh Ewald method was used to calculate electrostatic energies[38]. The cutoff of non-bonded interactions was set to 8 Å. A timestep of 2fs was used. The input files used for production runs can be found in the input folder of SI.

For transition steps involving changing the Lennard-Jones interactions, the λ values were set to 0.00922, 0.04794, 0.11505, 0.20634, 0.31608, 0.43738, 0.56262, 0.68392, 0.79366 0.88495, 0.95206, 0.99078, 0.995 and 0.999. These exponentially distributed λ values between 0.00922 and 0.99078 have more λ at regions where dU/dλ is expected to change more rapidly, as suggested in the Amber manual. Based on our experience, the two extra λ values, 0.995 and 0.999 can allow the scaled potential function to further approach the true end state. At λ value of 1.0, the VDW interactions of the disappearing atoms are completely turned off. This may cause these atoms to overlap with surrounding atoms and lead to infinite dU/dλ values in non-softcore TI, thus λ value of 1.0 was avoided here, as is a common practice. For transition steps only involving changing the partial charges, the λ values were set to 0.0, 0.04794, 0.11505, 0.20634, 0.31608, 0.43738, 0.56262, 0.68392, 0.79366 0.88495, 0.95206 and 1.0 as suggested by Amber manual as well. Here, λ=0.0 and λ=1.0 were included because changing partial charge only does not lead to singularities at end states.

3. Analysis

Trapezoidal integration was used to obtain the free energy changes in the bound state and unbound state. Three independent runs with different initial velocities and random seeds for Langevin dynamics were conducted to obtain better averages of free energy changes.

Parallelized transition mapping

Here, we designed a transition map (Fig. 1) which is highly parallelized in the sense of alchemical transitions between each ligand pair. Ligands were divided into four groups. Each ligand in the group was perturbed to the same common substructure (red circles in Fig. 1). The use of common substructures helps organize the transitions between ligands in a clear and concise fashion.

Fig. 1.

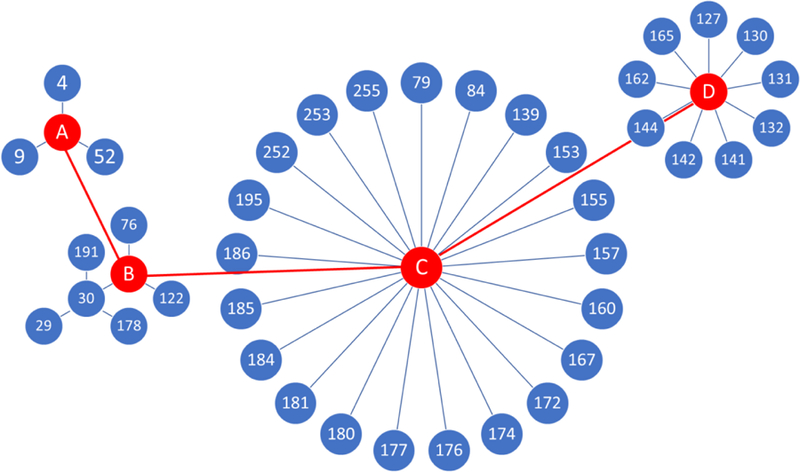
The transition map for the 39 ligands in the Cathepsin S free energy set. The numbers in the blue circles are the ligand indexes given in the D3R grand challenge 4. Each line indicates an alchemical free energy calculation carried out using TI. Red circles are the substructures designed to help the transitions between ligands.

Results

The design of substructures for each ligand groups

The rule of thumb for designing substructures is 1) to minimize the number of groups/substructures; 2) to have the least number of transition steps in the transition from ligands to substructures and the transitions between substructures. Since single-topology approach is used here, the substructure should always be “smaller” than the ligands in that group, which means the substructure can be obtained by merely (1) changing partial charges and (2) removing LJ interactions of any disappearing atoms of any ligand in that group without adding new interactions. The ligands included in each group are provided in the misc.ods file from SI.

The 2D sketch of the substructures designed for the 39 ligands in the Cathepsin S data set are shown in Fig. 2. Fig. 2A, 2B 2C and 2D correspond to the substructures A, B, C and D (red circles in Fig. 1), respectively. The substructures centered at each ligand group are not necessarily an actual ligand in the data set. In fact, substructure D is an alchemical compound designed on purpose to help construct a smooth transition pathway between each ligand pair. The substructure D was generated by replacing the CH₃O₂S-group in the substructure C with an alchemical atom D (Fig. 2D). The alchemical atom D has a gaff2 atom type of s6. The partial charges on substructure D were adopted from substructure C. The sum of all partial charges on the CH₃O₂S-was added to the nitrogen next to the alchemical atom D. The alchemical atom D has no charge. The smiles strings of substructures can be found in the smile4sub folder in the SI.

Fig. 2.

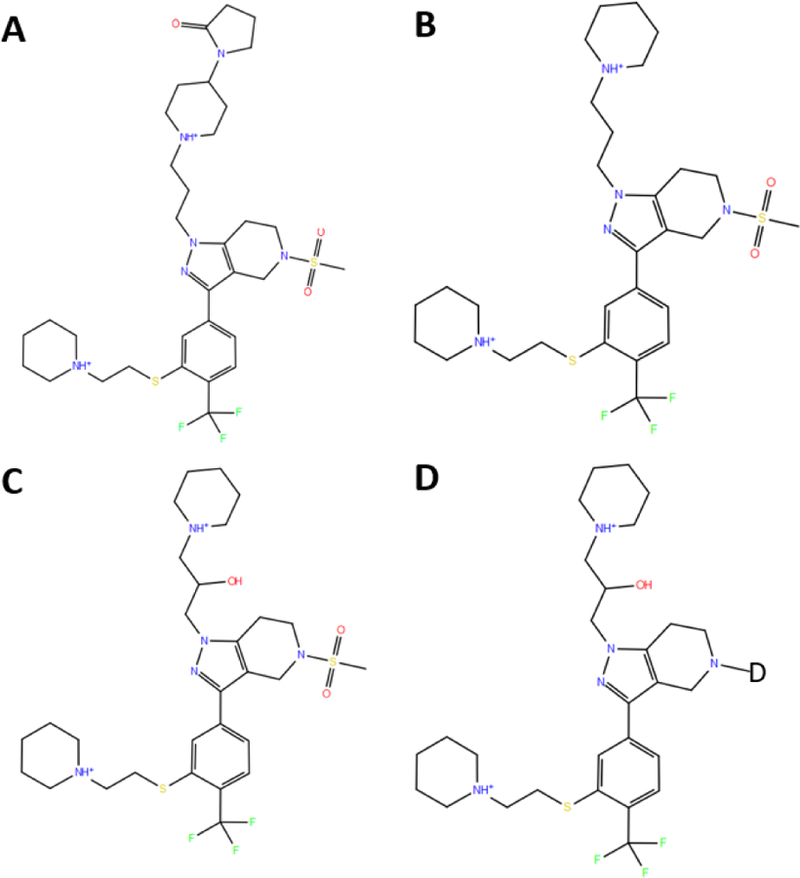
The substructures used in the parallel transition map shown in Figure 1. The atom D in substructure D is an alchemical atom with gaff2 atom type of s6.

Transitions from ligands to substructures and transitions between substructures

The first step in the transition from a ligand to its substructure involves the changing of partial charges. The partial charges of atoms in the ligand were changed to the partial charges of the corresponding atoms in the substructure and the partial charges on disappearing atoms were set to be zero. No charges were added as the substructure always has fewer atoms than the ligand.

The subsequent steps involved removing the LJ interactions of the disappearing atoms on the ligand to obtain the substructure. Based on our experience, if the absolute change of partial charge on the disappearing atom is less than 0.3 units of elementary charge, the removal of partial charges can be done with the removal of the LJ interactions on the atom in the same transition step. Otherwise, the removal of the LJ interaction must be done after the change of partial charges.

Since non-softcore TI was used in our calculations, for each transition from a ligand to its substructure, we designed multiple intermediates to minimize the perturbation caused by removing LJ interactions. For each transition, we trimmed off the heavy atoms furthest away from the substructures by removing the LJ interactions of the heavy atoms and the LJ interactions of any hydrogens attached to the heavy atoms. It is possible to trim multiple heavy atoms in a single transition step as long as the heavy atoms they attached to are not also disappearing in this step. For example, 1,1-dimethylcyclohexane can be transformed into cyclohexane in a single transition step instead of removing one methyl group at a time. The protocol for the transition between substructures is the same as the one used for transition from ligand to substructure. The initial substructures always have more atoms than the target substructures, so the transitions between substructures are A → B, C → B and C → D. The number of transition steps, the initial and end state for each transition can be found in misc.ods of SI. The parameter files associated with each transition step used for our calculations can be found in the prm7rst7 folder of SI.

Comparison between experimental and calculated ∆∆G values

We calculated the relative binding free energy (∆∆G) of ligands in the free energy set of Cathepsin S by following the transitions shown in Fig. 1. The relative binding free energies of ligands were all referenced to the ligand 4 as required by D3R. The centered RMSE of our predicted relative binding free energy, which is calculated after aligning the center of the predicted values to the center of the experimental values, is 0.49 kcal/mol. The Kendall’s τ, Spearman’s ρ and Pearson’s R of our predictions are 0.62, 0.80 and 0.82, respectively, which are the highest among all submissions in this dataset. The pairwise relative binding free energy difference for all pairs in the dataset was computed and compared to the experimental ∆∆G (Fig. 3A). The calculations seem to slightly overemphasize the differences between ligands by about 10%, with a best-fit slope of 1.12. All pairwise ∆∆G values are within 2 kcal/mol error. 83.8% of the pairwise ∆∆G values are within an error of 1 kcal/mol (Fig. 3B).

Figure 3.

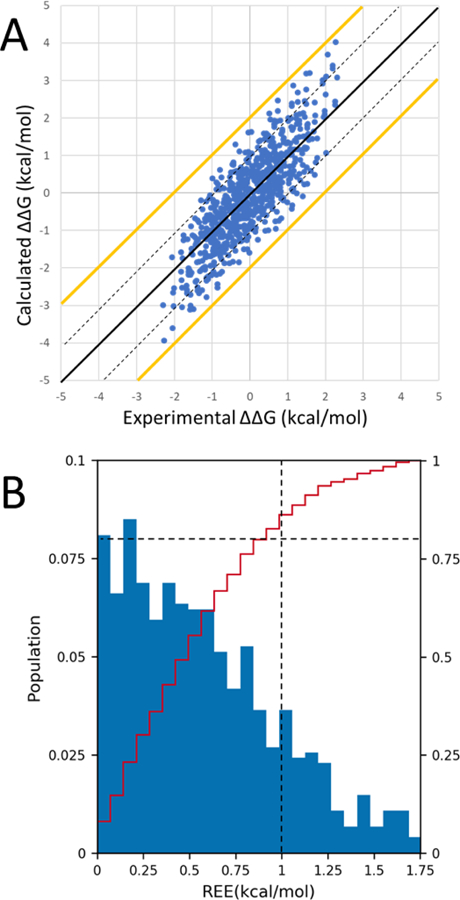
A) ∆∆G values for all 741 (39X38/2) pairs of ligands in the dataset. The black line represents y=x. The yellow lines represent a +/−2.0 kcal/mol error from the experimental ∆∆G. The dashed black lines represent a +/−1.0 kcal/mol error from the experimental ∆∆G. The data points fit a line of equation y=1.12x-0.06. B) Histogram (blue bars) and cumulative histogram (red line) of relative energy errors (REE) between calculated and experimental ∆∆G values. The horizontal dashed line indicates a cumulative population of 80% and the vertical dashed line indicates an REE of 1 kcal/mol.

In our transition map, instead of direct transition between ligands from different groups, the transition between ligands from different groups must go through the transition between their substructures. Thus, the ∆∆G between two substructures is shared by the ∆∆G between ligands from different groups. Poor accuracy in the ∆∆G values between substructures will be accumulated by the ∆∆G values between ligands from different groups. Moreover, on average, more transition steps are required for ligands from different groups. This could result in relatively higher accuracy for the ∆∆G values of ligands in the same group than the accuracy for the ∆∆G values of ligands from different groups. The errors between the calculated ∆∆G and the experimental ∆∆G for all ligand pairs were computed. We investigated the errors of ligands from the same group and ligands from different groups by plotting a heat map (Fig. 4) of pairwise ∆∆G values in group clusters. The heat map shows that the errors for ligands within the same group are comparable to the errors for ligands from a different group. Thus, we believe that the ∆∆G values between substructures have very little contribution to the discrepancy between the calculated values and the experimental values here.

Figure 4.

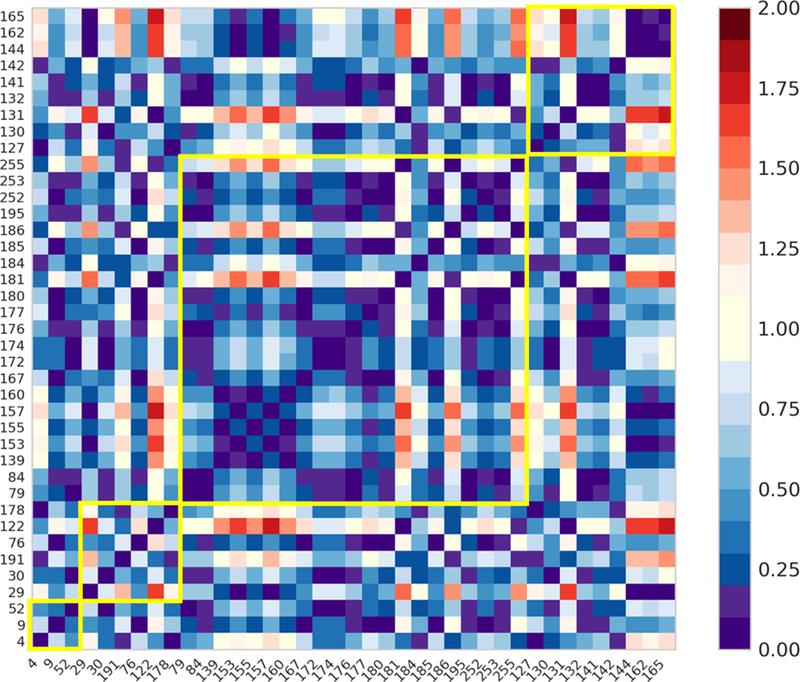
Heat map of absolute errors between the calculated and the experimental pairwise ∆∆G (unit in kcal/mol). Each yellow square indicates ∆∆G values of ligands from the same groups. The order of group A to D is from left to right.

Intuitively, predictions on similar ligands will usually be more accurate than the prediction on ligands with large differences. Since ligand pairs with larger chemical differences typically require more transition steps in the calculations, we use the number of transition steps as an indicator of the difference between ligands. The pairwise errors shown in Fig.4 were grouped into different number of transition steps. The median and mean values show a very mild increase in errors as the number of transition steps increases (Fig. 5).

Figure 5.

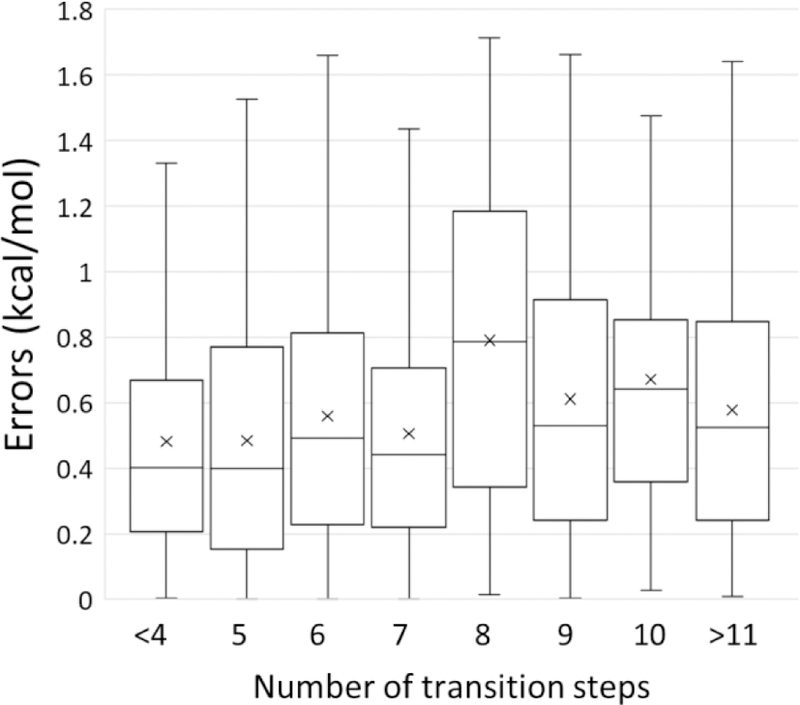
Box and whisker plot of errors between calculated and experimental ∆∆G values versus the number of transition steps. Boxes indicate the second and third quantiles of the data. Whisker indicates the first and fourth quantiles of the data. The mean values of errors are shown as crosses. The median values are shown as horizontal lines in the box.

The predictions with submission ID 3gjm2 and tkkqh are identical, as are submission ID 53cvi and szgth; duplicate submissions were made because JZ and CT have different affiliations. Submission 3gjm2 (or tkkqh) contains originally calculated values; these are the results discussed in this work. We found the calculations do not show any change of affinity when the hydrogen on atom C71 was changed to fluorine. However, in a previous publication[39], the IC50 of the compound 6 and 23 indicates a 0.2kcal/mol increase of affinity when the hydrogen on C71 was turned into fluorine. A robust examination of the discrepancy was not practical before the submission deadline, so an empirical correction was applied to the original results. In submission 53cvi (or szgth), empirical shifts of 0.2 kcal/mol were applied to ligands with 4-fluorine on atom C71, so they appear to be more favorable than the originally calculated values. However, the correlations and centered RMSE of the results for submissions 53cvi/szgth indicate that the empirical adjustment has a slightly negative effect on the accuracy of the predictions.

Discussion

The λ-dependent softcore potential[40] has been included in Amber v10. The softcore potential was implemented in AMBER TI in such a way that it allows the use of the dual-topology approach in TI. Since then the softcore potential/dual-topology approach has been used predominantly, as it provides a superior scaling scheme of chemical potential and eliminates the need of preparing dummy atoms when using single-topology approach. However, we found that the implementation of the dual-topology approach in AMBER v18 and earlier versions is highly fault-prone when calculating relative binding free energy changes. This issue arises from the fact that bond, angle, dihedral, 1–4 VDW and 1–4 electrostatic interactions involving atoms from both the softcore and non-softcore regions are λ-independent in AMBER v18 and earlier versions. The AmberTools19 update.8 (for sander) and Amber18 update.15 (for pmemd) allow the 1–4 VDW and 1–4 electrostatic interactions between softcore and non-softcore regions to be dependent on λ. However, these updates do not address the issue arise from λ-independent bond, angle, dihedral interactions between softcore and non-softcore regions. We discuss this issue in more detail, with examples, in the SI. We hope the examples can clarify possible problems for other researchers, as they led us to avoid the use of softcore in the results presented here.

Although GPU-accelerated TI allows hundreds of nanoseconds of MD simulations per day for a system with the size of Cathepsin S (51 kDa), long simulations can cause the protein target and the ligand to drift away from their correct conformations and binding pose due to inaccuracy in force fields. Thus, there is always a tradeoff between longer sampling which enables better ensemble averages, and shorter sampling which can help avoid the manifestation of force field errors. We believe that a smaller perturbation requires less sampling to get a converged dU/dλ, as the phase spaces at λ=0 and λ=1 better overlap if U_A and U_B are more similar. Thus, a small perturbation is more likely to ensure a converged dU/dλ before the accumulation of inaccuracy in force fields causes the system to drift away from its correct structure. Thus, even with fast MD using GPUs, it is worthwhile to design the transition map in a way that minimizes the need for an extended sampling of complex alchemical transitions.

In principle, relative binding affinity for any pair of ligands in the data set can be obtained by calculations through a serial and exhausted transition pathway: from 1^st ligand to 2^nd ligand, from 2^nd ligand to 3^rd ligand and so on. However, this approach will cause the errors from each transition of ligand pair to accumulate along the transition chain. We believe this could lead to a high RMSE of ∆∆G values. Moreover, the same functional groups may be repeatedly removed and added along the chain, which is very inefficient as calculations of the same change will be carried out multiple times. These issues can be avoided by designing a parallelized transition map between ligands in the data set because the calculated pairwise ∆∆G values will be independent of each other.

The success of using alchemical free energy calculations in a blinded prediction, which simulates the lead-optimization process in real applications, strongly indicates that alchemical free energy calculations can provide valuable guidance for commercial drug design. Moreover, we believe that the development of more accurate force fields, faster computing hardware and more efficient algorithms can further improve the accuracy and the achievability of alchemical free energy calculations.