RNA Dynamics by NMR Spectroscopy

Abstract

An ever‐increasing number of functional RNAs require a mechanistic understanding. RNA function relies on changes in its structure, so‐called dynamics. To reveal dynamic processes and higher energy structures, new NMR methods have been developed to elucidate these dynamics in RNA with atomic resolution. In this Review, we provide an introduction to dynamics novices and an overview of methods that access most dynamic timescales, from picoseconds to hours. Examples are provided as well as insight into theory, data acquisition and analysis for these different methods. Using this broad spectrum of methodology, unprecedented detail and invisible structures have been obtained and are reviewed here. RNA, though often more complicated and therefore neglected, also provides a great system to study structural changes, as these RNA structural changes are more easily defined—Lego like—than in proteins, hence the numerous revelations of RNA excited states.

RNA is a flexible molecule: This is what makes it functional, but also difficult to study, especially when the goal is to access those dynamic, often low‐populated and short‐lived conformers. Here the NMR methods and the structural insights, which have so far been obtained for RNAs and their picosecond‐to‐hour timescales are reviewed.

1. Introduction

Functions of molecules cannot be performed by static structures similar to rocks, as structures from X‐ray crystallography or high‐resolution NMR spectroscopy would make us believe. Flexibility and changes in structure are required to perform the desired functions, for example, the ribosome producing new proteins1 or the hepatitis B virus (HBV) replicating its genome.2 Changes in structure are referred to as dynamics, from Greek, meaning power/powerful, indicating that the structure of a molecule is in equilibrium and energy is required to move between different structural states. Historically, dynamics have been represented by a folding path, such as in the Fyn‐SH3‐domain, where a two‐state folding model was described between folded and unfolded states.3 Only when new methodology was sensitive enough to detect previously “invisible” intermediates, low populated, higher energy states, could be observed.4 Therefore structural equilibriums needed to include more complex models, where intermediates could be found in the transition from unfolded to folded proteins. This indicates that our current understanding of dynamics in folding and function is highly linked to the resolution of current methodology.

The lowest energy state (also called ground state; GS) is the most often observed structure (e.g., with X‐ray, Cryo‐EM and NMR spectroscopy), as it is usually the most stable state (Figure 1), but one can also imagine it as a resting state. Productive alternative states that for example, engage targets or transport single atoms for enzymatic reactions5 are often of somewhat higher energy. A functional molecule should be represented by an ensemble of structures, so‐called conformers, and a short‐lived state can be termed an excited state (ES in this review) but has also been called alternative conformer, invisible state or intermediate. It should be noted that in a dynamic system the ground state is in equilibrium with one or more excited states (GS⇄ES). Conformers of an ensemble can sometimes differ in only small changes in structure, for example, base‐pairing partner switches6 or rearrange complete structures (e.g., trapped conformers with drugs of the ribosome or riboswitches). These underlying structural changes are referred to as conformational exchange, which is not to be confused with chemical exchange, that can be measured by same or similar methodology and can also have similar data output, hence the type of exchange needs to be investigated. Chemical exchange is represented for example by ¹H with water of labile ¹H¹⁵N (imino)7 or keto‐enol tautomers.8

Figure 1.

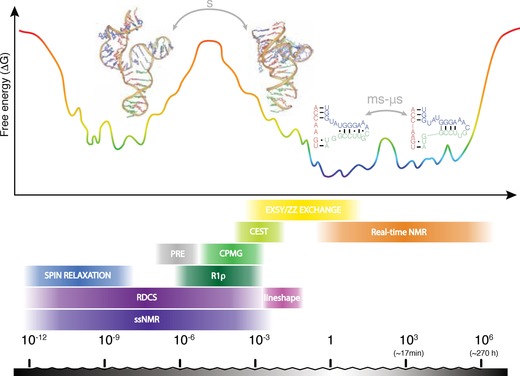
Energy landscape of RNA exemplified by tP5abc.15, 16, 17 Motions correspond to reorientation of bonds and molecular tumbling on ps–ns scale, base‐flipping on μs–ms scale and large structural reorientations, such as (re‐)folding on s scale. Several NMR methods access motions ranging from timescales of ps to days. RNA structures are reprinted with permission from refs. 15 and 16.

For these dynamic processes of structural or chemical nature, many different timescales exist (Figure 1) and different methodologies have been developed to observe some of the higher energy states (e.g., FRET1, 9, 10). However, these methods usually only give a single signal read‐out per molecule and not atomic resolution. Here we review how NMR spectroscopy can be used to study dynamics caused by structural and chemical changes and to identify and characterize higher energy structures in ribonucleic acids (RNA). A number of experiments were developed to cover different atom types (e.g., ¹H, ¹³C, ¹⁵N or ³¹P nuclei) and timescales (from ps to hours or longer). For slow and intermediate timescales NMR spectroscopy allows us to extract structural parameters (e.g., chemical shifts), which enables us to determine the structure of the excited, otherwise invisible conformer. ¹³C,¹⁵N isotope labeling is of advantage for most methods, either for improved resolution (e.g., fast dynamics or EXSY) or direct probing and increase in sensitivity (e.g., ¹³C CEST or ¹⁵N R _1ρ). Isotopically labeled RNAs are produced either by T7 in vitro transcription or solid‐phase synthesis with subsequent purification.11 Some exceptions exist to the typical ¹³C,¹⁵N labeling, such as: 1) no label is required for ¹H R _1ρ,12 off‐resonance ROESY2, 13 or ¹H,¹H EXSY, and 2) limitations of methods can require atom‐specific labeling (e.g., ¹³C CPMG) or deuteration (solid‐state NMR spectroscopy). Methodological breakthroughs in the last 10 years have led to the discovery of many RNA excited states6, 8, 14 and attempts have been made to investigate correlation to their function. Most methodology has been adapted from proteins, as these are significantly simpler to work with. However, the NMR methods need to be adapted with respect to nucleic acids (e.g., ¹³C−¹³C coupling in CPMG) or different structural behavior (e.g., base‐pair switches as local excited states) which are reviewed here.

1.1. Overall timescales

RNA is a dynamic molecule where different structures or conformers coexist and exchange into one another on various timescales. This leads to sometimes more, sometimes less observable changes in the NMR spectrum (Figure 2). Chemical and conformational exchange can influence the intensity, chemical shift, as well as the line width of the detected signal. The appearance in the NMR spectrum will mainly depend on two parameters: 1) The difference in resonance frequencies ΔΩ (chemical shift) of a certain nucleus in the two exchanging structures/chemical environments (Ω _A, Ω _B), with respect to 2) the exchange rate k _EX. For conformers of different energies, a third parameter comes into consideration, the different relative populations of the exchanging conformers. k _EX is the total exchange rate, k _EX=k _AB+k _BA, where p _A and p _B are the relative populations, which are linked to those exchange parameters through the following relationship: p _A=k _BA/k _EX and p _B=k _AB/k _EX=1−p _A. It should be noted that instead of calling the two exchanging environments/conformers A and B, they might also be referred to as GS (ground state) and ES (excited state), “low‐energy state” or “alternative state”. Figure 2 on the left shows simulated NMR spectra for such an asymmetric 2‐site exchange process, with populations p _A=0.9, p _B=0.1, and varying exchange rates. For comparison, the same simulations are also carried out with p _A=p _B=0.5, shown on the right in Figure 2.

Figure 2.

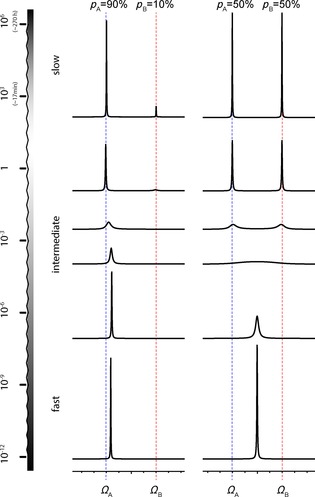
Effects of exchange occurring in different timescales on lineshapes in NMR spectra. The dashed blue line indicates the chemical shift of a ground state conformer (GS, A), while the alternative conformer (ES, B) has a chemical shift indicated by the dashed red line. From top to bottom, the exchange rate k _EX becomes faster with respect to the chemical shift difference ΔΩ between those two conformers. The effect of a population difference is compared (left: population ratio p _A /p _B=90:10, while on the right, the populations were set to 50:50). Spectra simulated with SpinDynamica.18

It is most straightforward to group exchange in three different regimes (slow, intermediate, fast) based on the relation between ΔΩ and k _EX. It should be noted that this approach does not result in a hard classification of processes as the three regimes rather blur into one another (Figure 1).

Slow regime (k _EX ≪ΔΩ , lifetime of alternative state is seconds or longer, typical on the timescale of T ₁ or slower): These are processes that are slower than the spectral timescale (usually on the order of seconds) and therefore hardly affect NMR line shapes (Figure 2, upper row). Slow exchange leads to two separate lines, each at the respective chemical shift, corresponding to one of the two chemical environments. The exchange process can be detected through the influence on longitudinal magnetization, as long as the timescale does not greatly exceed T ₁. For example, exchange spectroscopy (2D EXSY) allows the monitoring of the exchange of longitudinal magnetization as a cross‐peak between the two separate lines arising from the two conformers. Real‐time NMR experiments can be carried out to monitor even slower processes (multiple seconds/minutes), for example, hydrogen–deuterium (H‐D) exchange processes of labile ¹Hs. This regime can be identified by counting peaks in the NMR spectrum. More peaks than expected, provided that the sample is homogenous, indicate slow dynamics. Slow dynamics are discussed in detail in Section 2 of this review.

Intermediate regime (k _EX ≈ (comparable in size) to ΔΩ, lifetime of the alternative state of ≈ms–μs, typical on the timescale of T ₂ or slightly faster, often down to rotational tumbling, τ_C): Intermediate exchange processes happen on the spectral timescale (ms–μs) and the regime is therefore hallmarked by a strong influence of the dynamics on the NMR line shapes (Figure 2). Besides the direct analysis of the line shapes, typical NMR experiments for this regime include CPMG and R_1ρ relaxation dispersion. This regime is recognized in a spectrum by lines that are broader and therefore of lower intensity. The intermediate regime can be divided into two different subregimes:

Slow intermediate exchange regime (k_EX<ΔΩ/2, ≈ms): In this regime, the transitions between the conformational states do not happen very often, but when they occur, they still happen very fast. Due to the exchange process representing the change of the chemical environment, the precession frequency for the observed spin changes, jumping back and forth between GS and ES. While the precessing magnetization starts off in in‐phase, those jumps between different precession frequencies lead to enhanced dephasing of transverse magnetization and consequently lead to broader NMR peaks. This effect is called motional broadening. With increasing k _EX the effect becomes more apparent until the exchanging peaks “melt” into one broad line at the so‐called coalescence point (k _EX =ΔΩ/(2√2)). It should be noted that this point is close to, but not identical to the crossover point (k _EX=ΔΩ/2)19 between the slow intermediate regime and the fast intermediate regime.

Fast intermediate exchange regime (k_EX >ΔΩ/2, ≈μs): When the transitions between the conformational states happen more frequently, the spins do not have enough time to accumulate significant phase differences between those transitions. This effect is called motional narrowing and leads to a reduced line width compared to the coalescent peak (Figure 2, middle). The narrowing happens until in the limit of very fast transitions the spins experience the average precession frequency of the two chemical environments, leading to the fast regime. One, still broadened, signal is observed with a population‐weighted chemical shift and relaxation rate (Figure 2, 2nd line from the bottom). Dynamics observed in the intermediate timescale are discussed in Section 3 of this review.

Fast regime (k _EX ≫ΔΩ, lifetime of the alternative state is ≈ns–ps, ≈processes faster than rotational tumbling τ_c): Motions occurring at the Larmor timescale (corresponding to MHz frequencies) or faster, or in general, processes that are faster than the overall rotational tumbling of the molecule (τ _c), can directly influence relaxation. Motions within the molecule on the ns–ps timescale will due to the changes in bond lengths and intermolecular distances influence the CSA (chemical shift anisotropy) as well as DD (dipole–dipole coupling). These are both mechanisms stimulating and influencing nuclear relaxation. While it is not possible to measure those anistropic interactions and influences on them directly in solution‐state NMR spectroscopy, motions can be indirectly probed through site‐specific measurement of relaxation rates, R ₁ and R ₂, as well as the heteronuclear Overhauser effect. Dynamics observed in the fast timescale are discussed in Section 4 of this review. Another option is the introduction of a certain degree of alignment through sample preparation, which then allows the direct measurement of residual dipolar couplings (RDCs) or residual CSAs (RCSAs). This method can be applied for even broader timescales (ps–ms motions) and is typically used as complementary technique to spin relaxation and relaxation dispersion measurements (see Section 5).

1.2. Theoretical description of exchange

To describe slow to intermediate chemical exchange in NMR and in order to analyze data obtained by the above‐described experiments, a semi‐classical description in form of the Bloch–McConnell equations20 is usually used. These modified Bloch equations describe the time evolution of the transverse magnetization under exchange. To solve these equations means to solve at least two coupled first‐order differential equations. Besides looking for numerical solutions, many different analytical expressions have been derived and used for different exchange regimes. In contrast, in the case of fast exchange, it is not possible to obtain defined states interconverting in the exchange process. Instead, a Lipari–Szabo order parameter,21 S², is determined for each measured nucleus and used to describe the localized extent of internal motion. Data analysis is discussed separately for each timescale in the relevant sections.

1.3. Exchange processes detected in RNA

Figure 3 illustrates examples of exchange processes, which have been detected in various RNAs across all timescales using various NMR methods. It nicely illustrates how different NMR methods have to be applied to access information of exchange processes in different timescales. It can also be noted that within a single system, such as TAR, motions have been detected across a very broad range of timescales, illustrating the flexibility of RNA molecules and the importance of the study of these dynamics.

Figure 3.

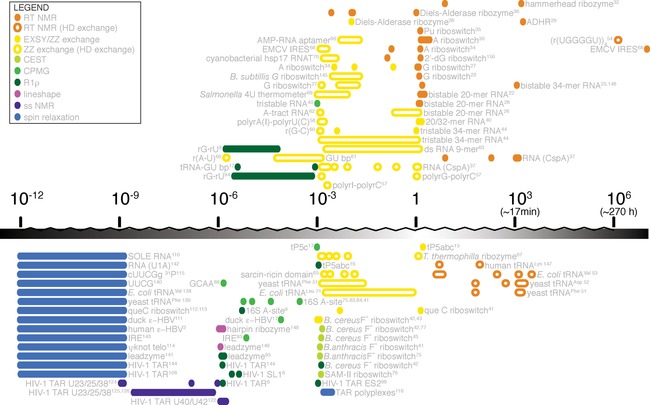
Non‐comprehensive overview over RNA systems that were studied with different NMR methods and approximate timescale of the dynamic process.

2. Slow Dynamics (Seconds and Slower)

Monitoring RNA dynamics in real‐time is perhaps the most intuitive of all NMR methods discussed here, as the changes that occur in a biological system can be directly associated with disappearance and appearance of signals. These changes are followed with series of spectra, recorded one after another, at certain time intervals. Example processes to be measured by real‐time NMR spectroscopy are RNA (re‐)folding by reshuffling of base‐paired nucleotides, or catalytic reactions of ribozymes. Slow base‐pair opening, resulting in exchange of labile‐bound protons with solvent can be followed with H‐D exchange experiments.

2.1. Real‐time (RT) NMR spectroscopy

Theory: In real time NMR spectroscopy, the exchange is so slow, that separate spectra are acquired showing the decay and build‐up of signals arising from different states. Chemical shifts of exchanging states are readily available and exchange rates can be extracted from build‐up and decay curves. An indication for a slowly exchanging system is typically the presence of a higher number of peaks in the NMR spectrum than anticipated. Recording a series of NMR spectra will result in a change of one set of resonances into another set, if the experiment starts with a system in non‐equilibrium conditions. Therefore, for consistency, the experiment needs to be designed with a clearly defined starting point. The exchange rates are usually seconds and longer, with typical processes that are slow enough for RNA folding or refolding and catalytic reactions. These processes are slow because they involve large structural rearrangements.

Examples: One of the challenges in measuring real‐time NMR is to follow the very early processes in a reaction or folding event. Before initiating the real‐time NMR measurement, the starting point of the process has to be synchronized with the start of the measurement. This is addressed differently for folding events or catalytic processes. The starting point of a catalytic process observed with real‐time NMR spectroscopy is typically the addition of either a cofactor or reactant that will start the reaction using fast mixing devices.24 For folding processes, RNAs with special photocleavable caged nucleotides have been designed that enable trapping of a higher energy structure.25 The caged nucleotide is designed to prevent formation of the more stable structure and results in exclusive formation of a less stable fold. The refolding event is in this case triggered with a laser beam delivered directly in the NMR tube,26 reducing dead times between reaction/folding and the beginning of acquisition and therefore conformational change can be followed with nucleotide precision. To monitor folding, ¹H‐¹⁵N iminos are very useful reporters, as they reflected changes in the base‐pairing pattern. To increase time resolution each spectrum is acquired with just one or two scans and then repeated and summed up to increase sensitivity (Figures 4 and 5). The measurements result in normalized signal intensity in relation to time, which can then be fitted to monoexponential decays/build‐ups. Information obtained from time‐resolved NMR studies may include both the overall kinetic behavior of the biological system and the residue‐specific kinetic characterization of the folding. Thermodynamic parameters and detailed analysis of the reaction mechanisms can be derived if the system is studied at different temperatures.25 Time‐resolved NMR data can be incorporated into experimentally restrained molecular dynamics simulations, which enables ligand‐induced conformational transition to be following.27

Figure 4.

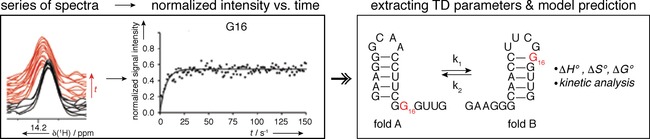
The concept of a real‐time NMR experiment. A series of spectra is recorded in short time‐intervals. Normalized signal intensity is plotted against time and fitted to an appropriate mono‐/bi‐exponential build‐up/decay equation. Extracted rate constants enable prediction of a folding model, while chemical shifts describing the states can be directly inferred from the spectra and population in steady‐state/equilibrium can be extracted from the maximum of the normalized intensity. Reprinted with permission from refs. 22, 23.

Figure 5.

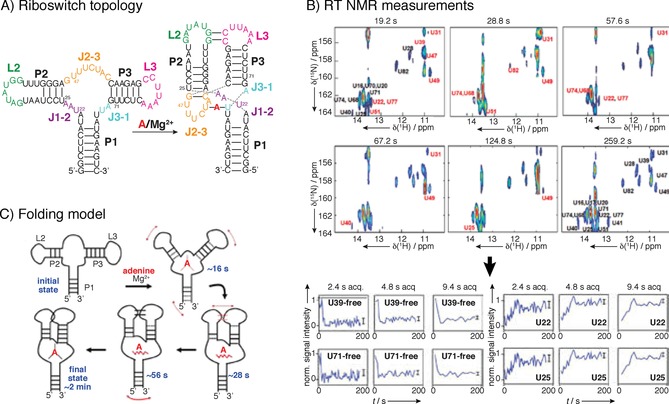
Example of real‐time NMR spectroscopy: adenine‐riboswitch folding and ligand binding. For assignment a 71‐mer RNA construct was perdeuterated at H5, H3′, H4′ and H5′/5′′ positions, which substantially reduced signal overlap. A) Initial structural characterization where done with adenine and Mg²⁺ as ligands, revealing differences in H1 and H3 protons of base‐paired guanine and uridine residues, which enables following of the signal using real‐time NMR spectroscopy. B) Series of UltraSOFAST ¹H,¹⁵N HMQCs of [¹⁵N‐G]‐ or [¹⁵N‐U]‐labeled riboswitches were recorded for RT NMR experiment at rates of approximately 0.5 Hz. At sample concentration of 1 mm, four single‐scan 2D acquisitions were needed to achieve good resolution, resulting in minimal acquisition time of 1.2 s per 2D spectrum. For residues that displayed slow folding kinetics, folding could be followed at a higher resolution by extended cycles of data averaging, as for certain fast folding parts of the structure 2.4 s acquisition time is too long, while for slow‐folding part′s build‐up curve can be resolved even at 9.4 s acquisition time. C) Proposed folding model based on the RT NMR data. Reprinted with permission from ref. 30.

Most experiments for slow folding or cleaving RNAs have been acquired with sets of 1D proton experiments, but the use of SOFAST methods, to add another dimension and help resolving overlapped signals, holds great potential.28 To monitor folding of large RNAs,29 several non‐overlapped reporter imino ¹H signals can monitor structural changes, eliminating the need for labeling.

Several studies have tested a setup with a laser beam releasing photocaged nucleotides26 and could thus follow the real‐time folding of bistable RNAs. This approach was later tested on larger systems, such as 73‐mer guanine sensing riboswitch, where caging was applied to the ligand and not the RNA itself.27 A similar approach of photocaging was used with a photoprotected 2′‐OH group at the scissile bond in combination with ¹³C labeling for characterization of a minimal hammerhead ribozyme cleavage reaction.32 A detailed study of 2′‐dG riboswitch from Mesoplasma florum monitored riboswitch folding in the presence and absence of ligands using BEST TROSY.14

A popular system for real‐time NMR are purine riboswitches, where the reaction is started with addition of the ligand.23, 33, 34, 35 Similarly, Lee et al. followed adenine‐induced folding of an adenine‐sensing riboswitch.30 They identified distinct steps associated with the ligand‐induced folding of the riboswitch: recognition of the ligand, formation of the long range loop–loop interactions followed by stabilization of long‐range interactions that result in a formation of a stable complex (Figure 5). Several ribozymes, such as adenine ribozyme29 and Diels–Alder ribozyme36 were studied by rapid addition of reactants. In an interesting setup of RT NMR experiment for RNA–protein system, refolding of two RNA hairpins into the heterodimer was followed in the presence of CspA of Escherichia coli. Changes in RNA refolding rates were detected for different protein mutants.37

Analysis: The measurements result in normalized signal intensity in relation to time, which can then be fitted to exponential decays/build‐ups. Information obtained from time‐resolved NMR studies may include both, the overall kinetic behavior of the biological system and the nucleotide‐specific kinetic characterization of the folding. Thermodynamic parameters and detailed analysis of the reaction mechanisms can be derived if the system is studied at different temperatures. Time‐resolved NMR data can be incorporated into experimentally restrained molecular dynamics simulations, which for example, enables following a ligand‐induced conformational transition.27 A detailed description of how to set up and analyze experiments can be found in refs. 29, 38, 39.

Advantages, limitations, challenges: For most real‐time examples the set‐up of experiments is straightforward from an NMR point‐of‐view, especially when 1D NMR is used to follow the exchange process. However, overlap can become a problem therefore 2D experiments, such as SOFAST experiments, have to be set up, which might be a bit more demanding. Another challenge is the set‐up of the experiment with a defined starting point. Often special equipment such as lasers or mixing devices are needed. Provided that those conditions are met, one can follow folding and catalytic events with nucleotide precision. Before the real‐time NMR experiment, it is necessary to identify and assign resonances of at least starting and ending conformation to be able to choose the most suitable reporter signal or design photocleavable constructs. Moreover, because imino protons can exchange with the solvent, it is important to identify any differences in the exchange rate. Any large differences in the solvent exchange rate influence the apparent rates of folding, which then cannot be interpreted in a straightforward manner.39

Labeling schemes for RT‐NMR spectroscopy: ¹⁵N‐labeled constructs for SOFAST methods, ¹⁵N,¹³C‐labeled constructs for assignment in case of large (>40‐mers) RNAs, site‐specific ¹³C labeling near the scissile bond of ribozymes as well as site‐specific introduction of caged nucleotides for refolding RNAs have been reported.

2.2. EXSY (EXchange SpectroscopY) and longitudinal exchange

Theory: Similar to intermediate exchange being measured as a contribution/effect on transverse relaxation rates, it is also possible to measure exchange on the timescale of longitudinal relaxation (T ₁). An example is EXSY (exchange spectroscopy), which is in principle a classical NOESY 2D experiment, where during the mixing period any exchange happening on the timescale of T ₁ can be detected as additional cross‐peaks to the usual NOESY cross‐peaks (Figure 6).

Figure 6.

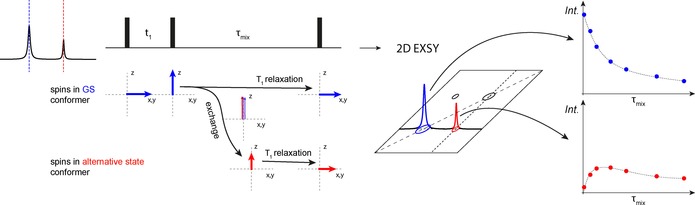
Theoretical scheme to explain the detection of exchange processes on the T ₁ timescale using EXSY. During the mixing time (besides magnetization transfer processes due to the NOE) magnetization is also transferred due to exchange. Limiting factor is the T ₁ relaxation, which will also occur during this period in the pulse sequence.

Care has to be taken to distinguish NOE from exchange cross‐peaks. For comparison a ROESY spectrum can be recorded where cross‐peaks arising due to cross relaxation have negative intensities for molecules in the size range of RNA. The EXSY experiment can be repeated with different mixing times/exchange durations and build‐up curves of magnetization on the minor state can be plotted and later fitted using Bloch–McConnell equations.

Examples: Most commonly ¹³C EXSY was used to assess exchange of several different bistable hairpin loops40 and Fsu preQ riboswitch system.41 In an interesting approach, ¹³C EXSY was used to determine fluoride binding for two conformers of a guanine nucleotide that displayed chemical shift changes upon fluoride addition while the overall structure remained unchanged.42, 43 ¹⁵N EXSY has been used to monitor labile N‐bound protons that directly report on base‐pairing changes, detecting two apo forms of adenine‐sensing riboswitch34 (Figure 7). Wenter et al.44 used a 34‐mer RNA that undergoes conformational exchange between three different hairpin loops and was designed to serve as a model for more complex RNA folding (Figure 8). ¹H‐¹H EXSY does not require a labeled sample and was applied to estimate rates of metal‐ion‐induced folding of the Diels–Alder ribozyme into a catalytically active form,36 to describe the equilibrium between extended and folded tP5abc ribozyme15 and to characterize binding of theophylline to the RNA aptamer.45 Especially ¹⁵N and ¹H EXSY often suffer from severe overlap in the imino region, where many signals are observed for large systems. Therefore, an elegant approach was demonstrated on a hairpin loop with ¹⁹F‐labeled nucleotide, where it was shown that ¹⁹F labeling minimally perturbs structure and that two conformations can be characterized with ¹⁹F EXSY. Advantage of ¹⁹F labeling is the large spectral dispersion and high sensitivity of ¹⁹F to the chemical environment.46, 47

Figure 7.

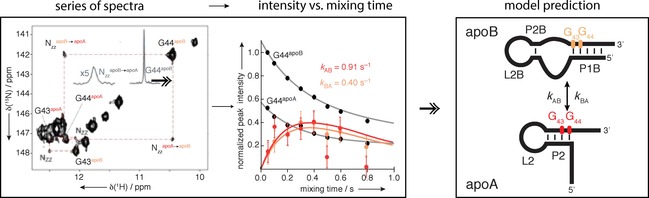
Concept of EXSY experiments. A series of EXSY spectra is recorded with increasing mixing times (ms). Transfer of magnetization is detected as a cross‐peak between the exchanging species, however, care must be taken to identify this correctly (use of ROESY). Normalized signal intensity of the cross‐peak is than plotted against the mixing time. The data are fitted to the Bloch–McConnell equation and exchange rates can be extracted. Populations of the two states can be extracted from the intensities of the diagonal peaks. Reprinted with permission from ref. 34.

Figure 8.

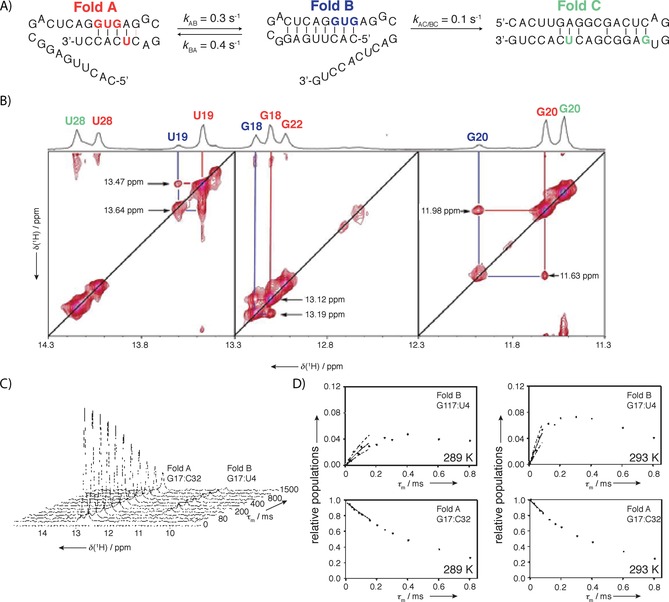
A) Example of EXSY measurements for a 34‐mer tristable RNA that was designed as model to estimate time requirements for more complex RNA folding. B) Combination of differently ¹⁵N‐labeled samples helped with resonance assignment and reduced signal overlap. 2D ¹H,¹⁵N EXSY experiment was used to detect cross‐peaks for different interchanging folds. 2D ¹⁵N EXSY spectrum recorded at mixing time of 400 ms showing exchange peaks between fold A and fold B, but not between fold C. C) Series of 1D ¹H detected ¹⁵N EXSY spectra showing decrease of intensity of H1 G17 of fold A and increase of intensity of H1 G17 of fold B as magnetization is transferred from fold A to fold B. D) Build‐up and decay of G17 signal at two different temperatures enabled determination of activation energy for the process. The refolding rates were strongly affected by an entropically favorable preorientation of the replacing strand. Two hairpins exchanged on the observable timescale, while the least‐stable fold was static on the timescale, leading to the conclusion that exchange of fold C with the other two folds was slower. Reprinted with permission from ref. 44.

Analysis: The chemical shifts of the exchanging states are readily readable from the NMR spectrum. To extract exchange rates, both build‐up curves of cross‐peaks as well as decay curves of diagonal peaks can be described and therefore fitted using a 2‐state Bloch–McConnell exchange matrix. A simplified method uses the first few points of the build‐up and decay curves and fits them to a linear function. A detailed description of how to set up and analyze experiments can be found in ref. 44.

Advantages, limitations, challenges: A clear limitation of this method is the relaxation time T ₁. It should be noted that through detecting exchange on different nuclei the available timescale might be changed slightly due to slightly different T ₁ relaxation times of different nuclei. An elegant solution was proposed to prolong the available timescale to detect exchange by using slowly relaxing states such as singlet states during the exchange period.48 Other challenges are overlap as well as cross‐peak sensitivity for lower populated alternative states.

2.3. Real‐time and longitudinal hydrogen–deuterium exchange

Theory of hydrogen exchange: Base‐pair opening in real time is usually monitored by dissolution of the lyophilized sample in D₂O which leads to gradual disappearance of the ¹H signals of hydrogen‐bonded imino protons as they exchange with deuterium.49 Information about life‐times of imino protons can be assessed qualitatively, for example, of imino protons resonances that were still observed 15 min after transfer into D₂O. The intensity of peaks in the imino region can be fitted to a simple exponential decay to extract exchange rates (Figure 9).

Figure 9.

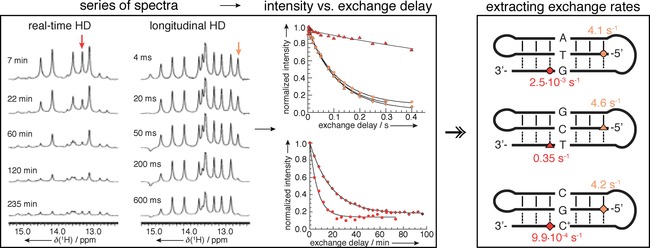
Concept of H‐D exchange experiments. A series of spectra are recorded after transfer of the sample in D₂O (left) or with different delay after magnetization transfer to water (middle). Normalized intensity of the signals in the imino region is plotted against the exchange delay and fitted to exponential decay to extract nucleotide‐specific exchange rates. Reprinted with permission from ref. 50.

Hydrogen exchange is a two‐step process: First, a closed base pair is opened and in this open state, a proton is accessible to proton acceptors and can in the second step exchange with the solvent. NMR spectroscopy only detects the second of the two steps [Eq. (1)]:

$${\displaystyle \mathrm{closed}\text{-}\mathrm{H}\underset{k{}_{\mathrm{cl}}}{\overset{k{}_{\mathrm{open}}}{\leftrightarrow }}\mathrm{open}\text{-}\mathrm{H}\underset{}{\overset{k{}_{\mathrm{ex},\mathrm{open}}}{\to }}\mathrm{open}+\mathrm{H}{}^{+}}$$ (1)

Forward and backward rates between closed and open state are k _open and k _cl, while the rate of exchange following the open state is k _ex,open. The experimentally observed exchange rate k _EX depends on k _open, k _cl and k _ex,open. The rates of opening and closing are related to the lifetimes of the base pair in the closed, paired state and in the open, solvent accessible state. The rate of exchange from the open state depends on the concentration of the proton acceptor. Two kinetic regimes for imino proton exchange can be distinguished depending on how the rate of exchange from the open state compares to the rate of closing. If proton exchange in the open state is faster than closing of the base‐pair (k _ex,open ≫ k _cl), then the measured exchange rate is equal to the base‐pair opening rate, k _EX = k _open. This kind of kinetic regime is called EX1 or fast. At low concentrations of proton acceptor, k _ex,open ≪ k _cl and the observed exchange rate k _EX is smaller than the base‐pair opening rate and is proportional to the concentration of proton acceptor. This regime is called EX2 or slow. The dependence of the exchange rate on the concentration of exchange catalyst provides a direct way to distinguish between EX1 and EX2 regimes. Adjusting the pH will mostly affect the rate of proton exchange, but will have little effect on the base‐pair opening rates. Hence if the observed exchange rate is independent of pH, the observed rate is the actual base‐pair opening rate and the observed regime is EX1. Conversely, for EX2, an increase in catalyst concentration will result in an enhancement of the exchange rate. Typically, exchange rates of imino protons are measured as a function of ammonia concentration, an example exchange catalyst. The base‐pair lifetime is obtained by extrapolation of the exchange time to infinite catalyst concentration. For real‐time NMR HD exchange intensities of signals in imino region are fitted against time and k _EX is obtained at certain catalyst concentration.

Examples: Base‐pair opening in real time is usually monitored by dissolution of the lyophilized sample in D₂O that leads to gradual disappearance of the ¹H signals of hydrogen‐bonded imino protons as they exchange with deuterium. The 1D proton spectra recorded in consequent fashion are used to monitor imino proton signal intensity (Figure 9). Exchange observed is on a timescale of a second or slower. Information about the life‐times of imino protons can be assessed qualitatively directly from the reduction of the intensity. As only Watson–Crick base pairs are somewhat stable, most imino protons in RNA motifs exchange too fast to be observed in real‐time and are unusual to have a lifetime of minutes. However, several very slow exchanging protons were observed in either tRNAs for so‐called D‐stem protons51, 52, 53 or in multi‐stranded RNA structures, where protons in extremely stable tetraplex structures exchanged after several days at 40 °C.54 Nozinovic et al.55 detected HD exchange on C8H8 protons of purines in an aged 14‐mer RNA on a very slow timescale and therefore demonstrated that HD exchange can be used on protons other than iminos for dynamic studies. For most other structures imino proton exchange is too fast to be observed in real time.

Imino proton exchange that can be accessed with longitudinal H‐D exchange is on a millisecond–second timescale. A selective pulse is used to invert water magnetization in a 1D spectrum and monitors which imino signals are inverted through exchange during mixing period, τ _m, and several spectra are recorded with increasing τ _m. As for EXSY, in principle any exchange on the timescale of T ₁ relaxation of water can be detected.49, 56 The measurement itself consists of four different experiments : 1) Determination of T ₁ relaxation of water, 2) measurement of inversion recovery rate for imino protons, 3) measurement of the exchange rate by selective inversion of water protons, and 4) measurement of water inversion efficiency factor.72 The same theory of water exchange that was discussed in the real‐time NMR section applies, with the difference that k _EX is calculated based on differential intensities of imino protons with mixing time (Figure 9).

For longitudinal H‐D exchange, several RNA–RNA, DNA–RNA and modified duplexes have been studied to offer deeper understanding on sequence‐dependent imino exchange rates.57, 58, 59, 60, 61, 62, 63, 64 Obtaining nucleotide‐resolution data on imino exchange rates was also used extensively to assess the effect of naturally occurring or artificially incorporated modifications on the stability of modified RNAs17 or the effect of protein binding on RNA stability.37 Several systems that were characterized with methods accessing a similar time‐scale of motion (EXSY or real‐time NMR) needed to take into an account contributions of imino exchange to the extracted dynamic parameters and complemented their study with measurements of imino exchange rates.26, 27, 37, 44 Interesting biological systems that have been studied include sarcin–ricin loop,65 AMP aptamer,66 Tetrahymena thermophila group I ribozyme,67 EMCV IRES,68 Salmonella RNA thermometer,69 hsp17 RNA thermometer70 and different tRNAs.51, 71

Analysis: The measurements result in normalized signal intensity in relation to time, which can then be fitted to an exponential decay. A detailed description of how to set up and analyze experiments can be found in refs. 49, 50, 72.

Advantages, limitations, challenges: One major challenge in this approach is that intermediates along the folding pathway need to be characterized, meaning somehow stabilized. The resolution of peaks, therefore to a certain extent the size of the molecule, is a limiting factor. Selective labeling is an option to circumvent this problem.

3. Intermediate Dynamics

3.1. CEST (chemical exchange saturation transfer)

Theory: The CEST experiment is mostly used in MRI and was introduced to measure slow‐intermediate to slow exchange (≈ms–s) in small molecules in 1963.73 Its application to biomolecules has been reviewed recently.74 The technique is especially useful if one of the two states’ populations is low and therefore its chemical shift cannot be observed directly. Figure 10 shows the simulated NMR spectrum with one major, observable ground state with a chemical shift indicated by the blue line giving rise to the peak shown in black, exchanging with a less populated “invisible” excited state with a chemical shift indicated by the red line. In this experiment, a low power spin lock (SL; typical on the length of seconds) is used to saturate different regions of a spectrum by varying its offset. In Figure 10 three representative cases of SL offset positions are displayed. 1) In case the spin lock offset matches the frequency of the detectable signal, for example, major/ground state (blue line), this signal is saturated and the intensity in the CEST NMR spectrum is close to zero (M _z ≈0). 2) In case the spin lock is applied to a region far off the chemical shifts of both, the ground state as well as the invisible, excited state, no saturation effect is visible and the detected signal in the CEST spectrum (M _z) is of the same intensity as the original signal (M ₀; M _z = M ₀). 3) The most interesting effect happens when the carrier frequency of the spin lock offset is on resonant with the chemical shift of the minor/excited state (red line). In this case, its magnetization will be saturated, leading to a reduced signal intensity, and due to exchange within the timescale of the applied spin lock, this will also reduce the amplitude of the observed, major state signal (M _z < M ₀). In practice, the carrier of the spin lock is shifted through the chemical shift region of interest and in a CEST curve, the intensity ratio M _z/M ₀ is plotted for each carrier position (see bottom of Figures 10 and 11).

Figure 10.

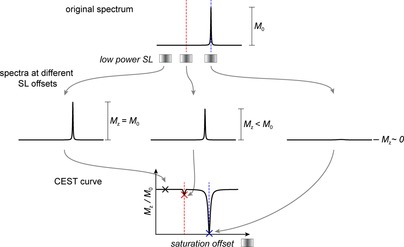
Acquisition of a CEST curve. Top: illustration of the appearance of the 1D spectrum representing a system of slow exchange with a small population of the alternative/excited conformer is shown. The observed line is mostly defined by the GS chemical shift. Middle: low‐power spin lock is chosen and multiple 1D spectra, each with the spin lock placed at a different offset, are recorded. The initial magnetization/intensity is obtained from a spectrum where the SL was far off‐resonant regarding the chemical shift of interest. This intensity is used as reference, M ₀ value and for each recorded 1D spectrum, the intensity is measured and the ratio in comparison with the reference intensity is displayed in the CEST curve (bottom).

Figure 11.

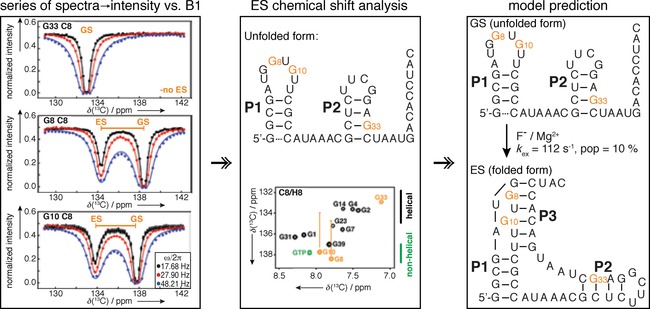
Concept of CEST experiments. Normalized intensities of peaks observed at different saturation offsets are fitted and k _EX, p _ES and the chemical shift of the excited stated is extracted. This chemical shift information of the excited state allows for the hypothesis of the excited state structure, and mutants stabilizing this state (mimics) need to be designed to make it the observable state for confirmation. If the mimic was chosen successfully, its CEST profile will show only one dip, as exchange will be suppressed at the chemical shift position where before the excited state chemical shift was found. Fitting CEST data to an appropriate exchange model will yield qualitative analysis of chemical shift difference and extraction of exchange rate and populations. Reprinted with permission from ref. 42.

From this curve, the exchange, including the chemical shift of the minor state is readily visible. The reduction of intensity on the major peak is much easier to detect than the minor exchanging peak in a conventional spectrum, therefore small populations can be detected. In practice, multiple CEST curves are acquired using different spin lock strengths. Exchange rate constants as well as populations can then be extracted by finding numerical solutions to the Bloch–McConnell equations when fitting the data.

Examples: ¹³C CEST was used for a dynamic study on a 47‐mer Bacillus cereus ligand‐free fluoride riboswitch and a 10 % populated excited state with a lifetime of 10 ms was detected. Analysis of the chemical shift of nucleotides in the non‐helical region of the GS suggests a helical environment in the ES, which was attributed to a putative pseudoknot structure that can be trapped by the binding of the ligand fluoride (Figure 11).42 Similar behavior was observed for the Bacillus anthracis fluoride riboswitch that accessed a 3 % populated pseudoknot ES with lifetime of 2 ms. Use of a ¹³C site‐specifically labeled sample on C1′/C6 or C1′/C8 simplified the analysis, as ¹³C,¹³C coupling contribution could be omitted from the analysis.41, 75 Site‐specific ¹³C C1′/C6 labeling of a single cytosine residue was used for characterization of dynamics of SAM II riboswitch, serving both assignment and dynamic measurement purposes. The apo form of the SAM II riboswitch reveals an equilibrium between an open (90 %) and a partially closed, sparsely populated (10 %) state with a lifetime of 31 ms, that was increased to 22 % by addition of Mg²⁺.76 An interesting approach was taken by the Zhang group, who used CEST for measuring RDCs, providing means for simultaneous measurements of RDCs of GS and ES of the ligand‐free fluoride riboswitch using a CEST‐TROSY approach.77 Expanding on the B. cereus F⁻ riboswitch studies, a short lived (3 ms), low populated (1 %) excited state of this riboswitch was detected with ¹³C CEST. Difficulties in confirming the proposed ES arose from the fact that mutants mimicking the ground state displayed substantially broadened NMR signals, preventing direct characterization. In a clever solution, CEST measurements were performed on a sample with intermediate Mg²⁺ concentration (Figure 12), where both the Mg²⁺‐bound and Mg²⁺‐free form coexist and can sample both Mg²⁺‐bound and ‐free excited states. CEST profiles showed coexistence of three forms in dynamic equilibrium: Mg²⁺ free, apo GS and apo ES. Therefore, CEST measurements of GS mutants were performed on the Mg²⁺ form, and confirmed that the A37–U45 base‐pair is absent in the ES.43

Figure 12.

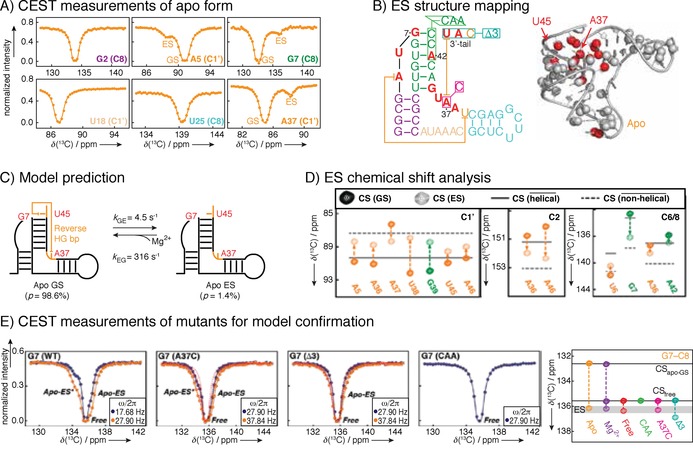
Example of a ¹³C CEST study performed on B. cereus fluoride binding aptamer with Mg²⁺. A) CEST profiles show a second intensity dip indicating an excited state. B) Schematic presentation of secondary structure of the fluoride‐binding aptamer and 3D structure with indication of conformational exchange clustering in one region. C) Global fit of the CEST data resulted in identification of a single excited state, and D) chemical shift analysis revealed model of apo ES with 3 ms lifetime and 1.4 % population. Subsequently, three different mutants were designed, abolishing the crucial linchpin base‐pair A37–U45. Without this base‐pair, the apo structure does not form a productive ligand binding form. E) CEST profiles of mutants to confirm proposed excited state and lack of dynamics towards previous GS. Reprinted with permission from ref. 43.

Analysis: Chemical shift of the ground state as well as the alternative state are readily available from the plotted CEST curves. CEST profiles can be fitted to a 2‐state exchange model described by the Bloch–McConnell equations and populations as well as exchange rates can be extracted through numerical fitting as described in ref. 42. CEST curves obtained using different spin lock strengths are usually fitted simultaneously to increase the number of available data points. A detailed description of how to set up and analyze experiments can be found in refs. 42, 43, 76, 77.

Advantages, limitations, challenges: Compared to other intermediate exchange NMR methods (CPMG, R _1ρ) the required measurement time is much shorter since for each point in the CEST curve only one NMR spectrum is required and not multiple spectra to fit an exponential decay. It is also advantageous to be able to directly read out the chemical shift of the “invisible” excited state. To confirm the nature of this excited state, mutant samples are usually designed and measured to confirm the structural hypothesis drawn from the chemical shift information. A major limitation of the CEST method is its relatively narrow window of accessible timescales, and that the excited state chemical shift must differ enough from the GS chemical shift to be visible (at least as a shoulder) in the CEST profile. Though CEST experiments are already short, there is an opportunity to reduce the measurement time still significantly, combining it with other newly developed NMR tools.

Labeling schemes for CEST: Reports41, 75 of selectively isotopically labeled [1′,6‐¹³C‐1,3‐¹⁵N‐5‐²H]UTP and 1′,6–¹³C CTP claim achieving both decrowding of the spectra and elimination of strong coupling between ribose carbons, resulting in a somewhat simplified data analysis. However, a specific labeling scheme is not necessary to study CEST of RNA as shown by different examples,42, 43 but ¹³C and ¹⁵N labels are required as natural abundance is currently of too low sensitivity.

3.2. CPMG

Theory: Figure 13 illustrates the behavior of two spins in different chemical environments, for example, with different resonance frequencies, during a Hahn echo78 pulse sequence. Coherent effects, such as chemical shift evolution, become refocused by the 180° pulse, while non‐refocusable dephasing occurs due to T ₂ relaxation. This dephasing effect (indicated by small arrows around the net magnetization vector in Figure 13) increases with longer echo evolution times, τ, and the detectable net magnetization decreases. By measuring the exponential decay of the signal with increasing echo times it is possible to determine T ₂ relaxation times. A more accurate way to determine transverse relaxation times can be obtained using a modified version of the Hahn echo, the Carr–Purcell–Meiboom–Gill spin echo (CPMG),79, 80 which is able to avoid errors arising from molecular diffusion processes during τ and slight miscalibrations of the 180° pulse. In this pulse sequence element, rather than increasing the length of τ, a train of spin echoes (τ _CPMG − 180° − τ _CPMG)_n is applied, with a certain repetition rate υ _CPMG sufficiently short before diffusion can lead to a shift in the precession frequency. In this case R ₂ can be determined by varying the number of echoes n in the train instead of increasing the delay τ.

Figure 13.

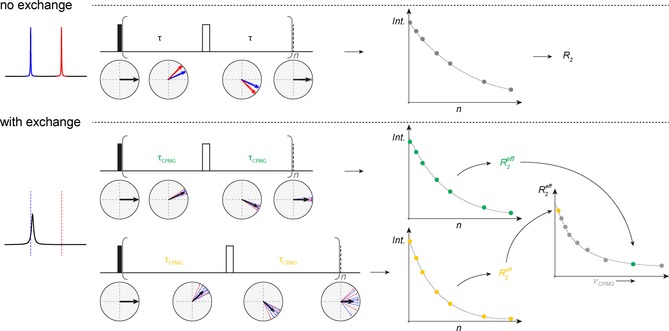
Illustration of CPMG. Upper panel: scheme of evolution of net magnetization in the x,y plane and refocusing of chemical shift during a spin echo for two non‐exchanging lines at two different resonance frequencies. The experiment is carried out with a different number of repetitions of this spin echo (n) and the intensity of the NMR signal is plotted against n, the total duration of the echo, to monitor the decay of net magnetization due to non‐refocusable dephasing of the signal. The obtained data points are fitted to an exponential decay in order to obtain the relaxation rate R ₂. Lower panel: same principle, but in this case including exchange contribution, R _EX. The spectrum is illustrated to appear as a broadened line with a chemical shift close to the ground state chemical shift (blue line), exchanging with a smaller populated excited state with invisible chemical shift (red line). The same echo sequence is carried out for different repetitions, n. In addition to the R ₂ dephasing, the signal's net magnetization now also decays due to the exchange process occurring during the spin‐echo time. An exponential fit now leads to the R _2,eff value. The measurement is then repeated with a different spin echo time and again multiple spectra are recorded for different repetitions (n) and R _2,eff value is extracted. This procedure is repeated for different spin‐echo times/CPMG frequencies and the CPMG dispersion curve is obtained.

While the determined relaxation rates R ₂ are independent of τ _CPMG or the repetition rate υ _CPMG, it was shown by Luz and Meiboom81 that exchange processes happening on the timescale of the CPMG pulsing rate would contribute to the dephasing of the net magnetization, and hence contribute to an “effective” relaxation rate R _2,eff. This effect is demonstrated in Figure 13. It illustrates a two‐site exchange between one mainly populated conformer (chemical shift indicated by the dotted blue line) and a lower populated alternative environment (chemical shift indicated by the red line). The detectable NMR signal is shown in black. During the evolution time of the CPMG, τ _CPMG, the observed nucleus fluctuates back and forth between those two chemical environments and therefore evolves with the respective frequencies for varying amounts of time. Because the fluctuations are stochastic these effects are not refocused by the echo and lead to an increased, observed effective relaxation rate R _2,eff = R ₂ + R _EX. This becomes even more apparent for longer echo delays (Figure 13, bottom), while for very short echo delays the contribution is suppressed. R _2,eff therefore can be measured as a function of τ _CPMG and depends on the exchange rate as well as the populations p _A and p _B and the chemical shift difference ΔΩ between the two states.

It should be noted that the CPMG element can be carried out on any NMR active nucleus (usually ¹H, ¹³C and ¹⁵N) and in practice is combined with other pulse sequence elements, such as insensitive nuclei enhanced by polarization transfer (INEPT) or selective Hartmann–Hahn transfers. To extract parameters of interest, for example, information about the exchange process, the data are usually acquired on at least two different fields and solutions to the Bloch–McConnell equations have to be found. As described above, a few different analytical expressions have been derived for different exchange regimes (slow‐intermediate and fast‐intermediate) and populations. The reader is referred to the original literature of the examples section to find out which simplifications and constraints were made and analytical expressions fitted in each specific case. A more concise description of the theory as well as the analysis of relaxation dispersion methods can be found in ref. 82.

Examples: Due to the problematic influence of ¹³C,¹³C couplings, specific single atom ¹³C labeling by chemoenzymatic synthesis has been extensively used for systems studied with CPMG. For example, 1,8′‐¹³C HCV SARS RNA and 2′,8‐¹³C‐labeled A‐site were produced and measured as a proof‐of‐principle and similar exchange parameters as with R _1ρ methods were detected, omitting problematic analysis due to the J‐coupled induced oscillations.41, 75 A combination of 8‐¹³C‐labeled A and G nucleotides and 6‐¹³C 5‐d‐2′ modifications was used for a 27‐mer A‐site mimic. In the absence of large homonuclear coupling between H5–H6, it was possible to apply a ¹H version of CPMG, enabling the characterization of a 4 % ES with a lifetime of 0.5 ms, where chemical shift analysis pointed towards a base‐pair reshuffling process.84 The 5‐¹³C uridine and 2,8‐¹³C adenine labels were used for studies of the 21‐mer T. thermophila group I ribozyme. The group detected a secondary structure switching event with a lifetime of 1 ms and a population of 9 %.

The 5‐¹³C uridine and 2,8‐¹³C adenine labels were subsequently used for studies of a 28‐mer epsilon RNA element of duck hepatitis B virus, detecting an unfolding event on a millisecond scale, in agreement with previous R _1ρ measurements.17 Chemical shifts of both protons and carbons for a bulge of A‐site ES were probed with combination of 2′,8‐¹³C‐ATP; 1′,6‐¹³C‐CTP; 1′,8‐¹³C‐GTP; 2′,6‐¹³C‐UTP labels and similar life times of ES were obtained with ¹³C and ¹H CPMG experiments.83 Experiments were expanded to include a methylene ¹H,¹³C TROSY‐detected CPMG pulse sequence that was successfully tested for iron responsive element83 (Figure 14). Another example investigated 96‐mer CCR5 pseudoknot RNA, which interacts with microRNA to stimulate −1 ribosomal frameshifting for virus HIV‐1. To better understand the CCR5 function and specifically miRNA binding, CPMG profiles were measured for eight of CCR5 8,1′‐¹³C‐labeled adenine nucleotides. A75, A76, A88, A90 and A95 displayed non‐flat CPMG profiles (Figure 15), while fits to a two‐state exchange model resulted in residue‐specific variations. At least two excited states were detected: in A76 samples a minor‐populated (30 %) state, while for nucleotides A75, A88, A90 and A95 sample an invisible, low‐populated (10 %) state. The exchange rate constants k _EX of A75, A88, and A90 were very close to one another within experimental error, whereas the rate parameters of A76 and A95 were roughly one magnitude higher. Titration with miR‐1224 resulted in similar chemical shift changes for A90 C1′ as determined ΔΩ for excited states, indicating miR‐1224 binding site at A88–A90 bulge.85

Figure 14.

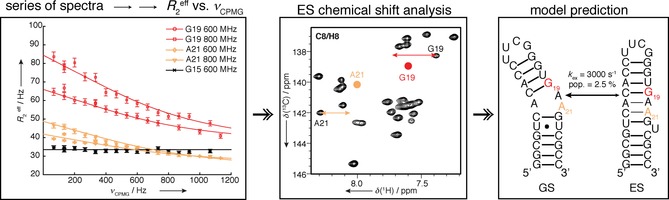
Concept of CPMG experiments. A series of spectra are recorded at different CPMG frequencies and extracted R _2,eff values are plotted. Measuring at different B ₀ fields enables extraction of ES chemical shifts that can be used to predict topology of ES. Reprinted with permission from ref. 83.

Figure 15.

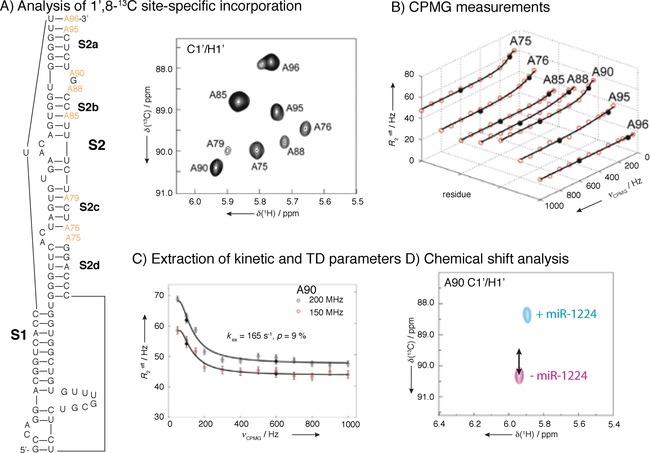
CPMG studies of CCR5 pseudoknot RNA. A) Design of site and atom‐specifically labeled construct and 2D HSQC showing assignment. Line‐broadening for certain nucleotides indicates exchange. B) ¹³C CPMG profiles of 8,1‐¹³C‐labeled adenine nucleotides. CPMG experiments were performed at 13 different CPMG frequencies at 600 and 800 MHz, yielding total experimental times of ≈70 h. C) ¹³C CPMG RD profiles of A90 ribose C1′ carbon of the CCR5 RNA at 150 (red dots) and 200 (blue) MHz ¹³C Larmor frequency. Black circles represent repeated experiments and solid lines are the best fits of the CPMG profiles. D) 2D HMQC spectrum of NMR titration of the ligated CCR5‐A90 RNA with miR‐1224. NMR chemical shift perturbation analysis of the CCR5‐RNA and microRNA 1224 complex indicated that A90 of CCR‐5 exhibit similar changes in chemical shift as observed in the excited state (black arrow) and identified an A88–A90 bulge as miRNA interaction site. Reprinted with permission from ref. 85.

Analysis: Bloch–McConnell equations can be used to describe evolution of magnetization in a two‐state intermediate exchange process and model relaxation rates can be obtained by numerical integration of the matrix and solutions. This procedure has been used for ¹H CPMG data of RNA.84 In addition different analytical solutions are available for different exchange regimes to fit CPMG data. However, care has to be taken to choose the right analytical expression for the investigated exchange process. In the intermediate exchange regime the so‐called Carver–Richards equation86 can be used. This approach was for example used in refs. 75, 85, 87 and is valid for exchange rates significantly faster than R ₂ and low populations of the excited state. For 2‐state processes in the fast‐intermediate exchange limit, Luz–Meiboom and Bloom equations81 can be used to fit the data. This has been shown for RNA and is described in ref. 88. This analytical expression is valid in the fast exchange limit (k _EX ≫ ΔΩ) and high field limit (ν_CPMG ≫ ΔΩ). Kloiber et al.40 have tested fitting their data to different analytical expressions, where besides using the Luz–Meiboom and Bloom equations for a 2‐state fast‐intermediate exchange process they have also used the Tollinger–Skrynnikov–Kay equation89 valid for the slow‐intermediate exchange limit and a numerical approach to fit a three‐state exchange process rather than two states. Care has to be taken to not “overfit” the data, especially in the case of including more states, and F‐tests should be carried out routinely to test if the data can be fitted with the analytical expressions used. A detailed description of how to set up and analyze experiments can be found in ref. 17.

Advantages, limitations, challenges: Even though CPMG measurements are very time consuming, they are often used since they provide good access to timescales and are straightforward to set up. A major challenge is to obtain enough data (at different magnetic fields) in order to be able to extract exchange rates as well as chemical shift information of the excited state. Due to the usage of 180° hard pulse trains, special care has to be taken for CPMG ¹H RD experiments or ¹³C/¹⁵N RD experiments in uniformly labeled samples, since magnetization transfer due to Overhauser effect or J‐couplings can easily occur.88 CPMG is therefore usually combined with extensive selective labeling schemes in order to obtain reliable exchange data. A reduction in experimental time and conquering ¹³C−¹³C couplings could make this experiment truly versatile.

Labeling schemes for CPMG: Numerous schemes exist, as this is essential for successful CPMG characterization and many have been developed by the Kreutz group.17, 40, 41, 75, 84, 85 Examples are C2′/C4′‐labeling of ribose,88 2′‐O‐¹³CH₃‐uridine, 6‐¹³C‐uridine and 6‐¹³C‐cytidine,41 8‐¹³C purines,75, 84 5‐¹³C‐uridine and a 2,8‐¹³C₂‐adenine.17

3.3. R _1ρ (relaxation in the rotating frame)

Theory: Similar to using CPMG in order to detect exchange contributions on top of R ₂ relaxation times, it is possible to replace the 180° train of hard pulses by a spin lock pulse and detect exchange as contribution to detected R _1ρ values. Before this idea was first used for RNA it was shown to measure exchange in the intermediate timescale for small molecules and proteins. Figure 16 (top) displays the effect of a spin lock on two lines with different chemical shifts. In this experiment the lines are prepared, for example, by a 90° pulse, to be aligned along the y axis, followed by a spin lock pulse applied with the same phase on‐resonant with one of the two lines (in the displayed case the blue one). If the radiofrequency field of the spin lock (SL) pulse is strong with respect to the chemical shift difference between the two lines, for example, the lines “are both in the SL” and experience the same field, then both magnetizations (red and blue) are spin locked along an effective field along the y axis and their magnetization during the spin lock decays, or relaxes (R _1ρ) with the same rate as R ₂. If the SL field which is applied is smaller (panel B), the on‐resonant blue line still experiences the same spin lock effect with an effective field along y and relaxes with R ₂, however, the red line experiences off‐resonance effects and a different field which leads to its effective field being no longer in the x,y plane anymore. The relaxation rate during the SL is then not pure R ₂ anymore, but a sum of R ₂ for the component of the product vector of magnetization present in x,y, and R ₁ for the component along z. Given that R ₁ and R ₂ relaxation rates are usually significantly different, also the measured R _1ρ relaxation rates, for example, decay of magnetization during the SL will be very different for the on‐resonant blue and off resonant red line.

Figure 16.

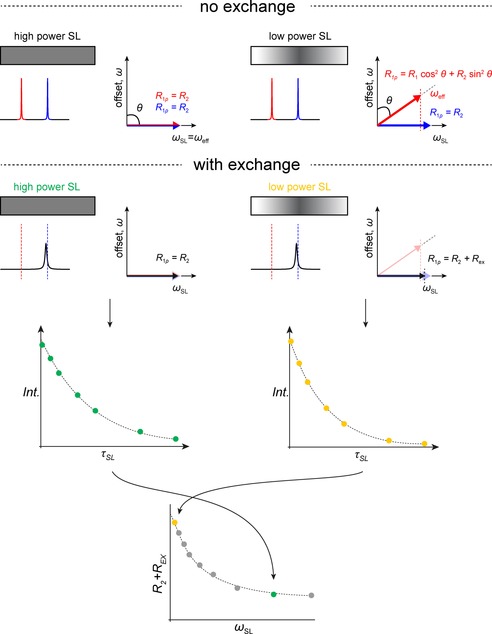
Illustration of R _1ρ. Upper panel: scheme of a spin lock applied to two non‐exchanging spins with two different chemical shifts. If the spin lock power is large, both lines are spin locked in the x,y plane, for example, the effective field is in the x,y plane, and for increasing duration of the spin lock, the signals will decay according to T ₂ relaxation (shown on the right). In the case on the left, the spin lock power is smaller and on‐resonant only with respect to the signal at the blue chemical shift, while the signal at the red chemical shift still experiences the spin lock, it experiences significant off‐resonance effects. This manifests itself as an effective field, which is no longer in the x,y plane, therefore the signal with the red chemical shift is no longer spin locked in the x,y plane but along an effective field and the net magnetization of the red line during the spin lock has a significant z‐component. Thus, the signal with the red chemical shift will not only decay according to T ₂ but also T ₁. The contributions of the different relaxation phenomena can be calculated from simple trigonometric functions from the angle between the effective field and the z axes. Lower panel: we illustrated for the two different spin locks, a scenario with exchange. Now only one (broadened) line is observable in the spectrum and a spin lock is applied on‐resonant with this line. For a high power spin lock covering both, the GS chemical shift as well as the excited chemical shift, even with exchange happening during the spin lock, the net magnetization decay rate will correspond to R ₂ since the magnetization of an exchanging spin is spin locked in the x,y plane, irrespective of whether it is in the GS conformer or the ES conformer. In practice, experiments with different spin lock durations are carried out and the decaying intensity of the observable signal is fitted to an exponential decay to obtain R _1ρ. In case of a weaker spin lock, which does not cover the ES chemical shift without any off‐resonance effects, for the duration that a spin is in the ES conformation during the spin lock, the magnetization will decay with a different decay rate due to the different effective field, compared to the GS. This manifests itself in a faster decay rate, an R _EX contribution, for the observed signal for weaker spin locks when fitted to an exponential. In practice the measurements are repeated for different spin lock durations for different spin lock strengths.

This effect is exactly what allows us to use this experiment to measure exchange. Figure 16 (bottom) shows the same scenario as before but with intermediate exchange. Again, the major state's chemical shift is indicated by the blue line, and the lower populated minor state's chemical shift is shown in red. The actual observed line is shown in black, with a chemical shift close to the blue line. The situation where the low power SL is applied on‐resonant with the detectable signal in the NMR spectrum, but off‐resonant with respect to the minor state's chemical shift, is indicated in yellow. During the spin lock, the majority of the magnetization is on‐resonant with the spin lock (blue line, major state), and therefore its effective field is along the y axis. However, if exchange happens on the timescale of the NMR experiment, meaning the applied spin lock, then a small part of the spins will have a different resonance frequency and therefore experience a different effective field (red line). This leads to an apparent faster decay of magnetization during the spin lock, R _1ρ = R ₂ + R _EX even though the SL was applied on‐resonant with the observable line. The exchange contribution depends on the exchange rate, the populations as well as the chemical shift difference between the two exchanging states. For higher power SLs (shown in green), where the effective field is the same for both the exchanging major and minor conformer's chemical shift, no exchange contribution on the measured R _1ρ rate is detectable.

In practice, R _1ρ decay rates are measured as exponential decays by using different SL lengths, for SLs of various strengths. This curve can then be fitted using the Bloch–McConnell equations or analytical expressions for simplified scenarios and specific exchange regimes.

The procedure described above leads to the so‐called on‐resonance R _1ρ curve (Figure 17). Similar to CEST, it is also possible to use a low‐power SL of a specific strength, where R _EX can be detected, and vary its offset with respect to the observable peak and measure the exponential decays. The measured decay rate is then a mixture of R ₁, R ₂ of the major state and R _EX, depending on the offset. Similar to CEST, when the SL happens to be on‐resonant with the chemical shift of the excited state, then the exchange contribution becomes more apparent. Therefore, those so‐called off‐resonance curves can give information on the chemical shift of the excited state as well as additional data to be fitted to extract other exchange parameters.90

Figure 17.

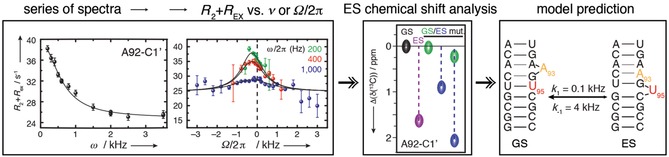
Concept of R _1ρ experiments. Series of spectra are recorded at different spin lock strengths (on resonance) or offsets (off resonance) of the ground state chemical shift, from which R _1ρ is determined. Chemical shift of the ES is extracted from off‐resonance curves and analyzed based on topological characteristics. Reprinted with permission from ref. 6.

In R _1ρ relaxation dispersion and CEST, it is possible to extract chemical shift information of otherwise non‐detectable states and therefore characterize these invisible structures. A suggestion for how to estimate and confirm the structure is the mutate‐and‐chemical‐shift‐fingerprint (MCSF) approach.6 In detail the process is the following. The chemical shift from relaxation experiments is compared with chemical shifts deposited in the BMRB database,91 taking into consideration corrections for wrong chemical shift referencing, and compared with secondary structure predictions for alternative states (e.g., from McFold92). Alternatively, LarmorD93 can be used to compare chemical shifts with simulated structures from an ensemble. As this is an indirect method to extract structural information, it is recommended to design mutations or modifications that stabilize the hypothesized structure, so‐called trapping, to be able to characterize the structure and chemical shifts of the trapped excited state with NMR spectroscopy and therefore confirm the correlation.

Examples: R _1ρ relaxation dispersion measurements have uncovered some of the basic principles of miss‐matches and rare tautomeric forms in RNA that are important for understanding of translation and replication errors.6, 8, 17, 94 Kimsey et al. have detected two excited states for GU base‐pairs in RNA and GT base pairs in DNA. Detailed dependence of populations and chemical shifts of excited states on pH and temperature combined with DFT calculations of chemical shifts led to the identification of excited states as enolic or anionic bases. Importantly, the probability of formation of these ES suggests that they are widespread in RNA and can affect mutation rates during translation (Figure 18).

Figure 18.

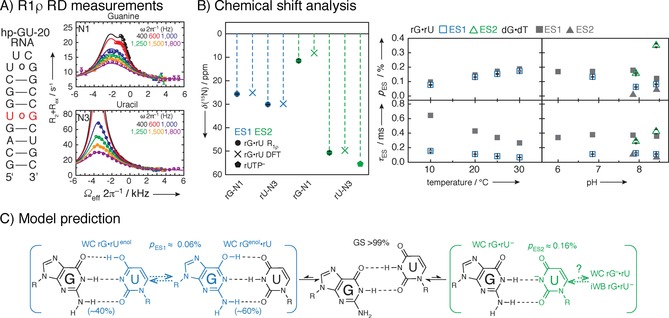
Example of an R _1ρ study of a 20‐mer RNA hairpin with GU base‐pair. A) Secondary structure of construct and ¹⁵N R _1ρ relaxation dispersion measurements with three‐state global fits of uracil N1 and guanine N3 of GU miss‐match base‐pair. Mono‐exponential decays with 4–20 points are recorded, and plotted against the offset referenced to the GS chemical shift, resulting in off‐resonance profiles. Fitting of >80 mono‐exponential and relaxation dispersion curves enables the detection of ES chemical shifts. B) Excited states can especially in the case of large chemical shift changes (>50 ppm) correspond to structures that have never been experimentally observed, as they are not a lowest energy structure. Therefore, methods other than structural database chemical shifts will have to be employed. In this case, to identify the underlying structures of the ES, structure‐based DFT prediction were employed. Population and lifetime of ESs as a function of temperature and pH was obtained to characterize the complex three‐state equilibrium. The chemical shift of ES1 and ES2 compared to structure‐based DFT prediction and rUTP ionization are shown in B. Population and lifetime of ES as a function of temperature at pH 6.9 and as function of pH at 20 °C indicated that detected ES1 represents rGNrU^enol/rG^enolNrU and ES2 ionized uridine, which was in agreement with excited states of GT base‐pair in DNA. C) Suggested exchange process depicts a multistate equilibrium between a GS wobble GU base‐pair and an ES Watson–Crick‐like GU base pair. Reprinted with permission from ref. 8.

R _1ρ RD was used to unravel conformational exchange at the active site of leadzyme. Active site adenine is involved in protonation/deprotonation equilibrium, while cytosine residue samples minor C2′‐endo state on a timescale of microseconds that is important for self‐cleavage activity.95, 96 In line with CEST measurements, unfolded F⁻ riboswitch was shown to sample an excited state that resembles folded riboswitch with k _EX 121 s⁻¹ and population of 10 %.42 A secondary structural switch was observed for group I intron ribozyme of T. thermophila with population of 3 % and k _EX of 423 s⁻¹, with structure resembling that of the native state. As rates of tertiary folding of the riboswitch are substantially slower, secondary structural switch was suggested to aid folding by adjusting the folding landscape.16 For the U6 RNA intramolecular stem–loop of the spliceosome, pH‐dependent excited state with life time of 84 ms was detected. The conformational change involves helical movement and base flipping of uracil residue and is important for the splicing activity of U6 RNA.97 Similarly, ribosomal A‐site mimic exhibits conformational equilibrium between ground state with flipped‐out adenine residue and 2.5 % populated excited state with flipped‐out uracil residue. ES was suggested to affect mRNA recognition and ribosomal subunit association (Figure 18).6 One of the systems that was studies in detail with R _1ρ and other methods is HIV‐1 TAR apical loop that represents flexible recognition site for binding of variety of proteins. The first excited state of HIV‐1 TAR with population of 15 % and lifetime of 45 ms sequesters most of the nucleotides in the loop, making them unavailable for biding of proteins. The second excited state with population of 0.4 % and lifetime of 2 ms exhibits remodeled stem, loop and bulge, even though these motifs are separated by several base pairs.6, 98

Analysis: Similar to all intermediate exchange processes, also R _1ρ data can be fitted numerically using the Bloch–McConnell equations. In practice (also in most of the examples presented above), an analytical expression, the Laguerre equation99 is usually used. The Laguerre approximation is valid in the intermediate‐fast exchange limit for excited states populations of up to ≈30 % and can be used to fit both, on‐ and off‐resonance relaxation dispersion data. If enough data points are available (which becomes especially feasible when off‐resonance curves are included), it is possible to extract chemical shift information as well as exchange rates and populations for two or even three state exchange processes. When slower processes are investigated by relaxation dispersion and low spin lock strengths are applied, this approximation cannot be reliably used, therefore exchange parameters as well as chemical shifts and populations are obtained from fits by solving the Bloch–McConnell equations for a two‐state exchange process (e.g., ref. 12). A detailed description of how to set up and analyze experiments can be found in ref. 100.

Advantages, limitations, challenges: R _1ρ measurements are also relatively time consuming and very similar to CPMG measurements with the difference that a continuous wave spin lock is used instead of a train of 180° pulses. This has the advantage that selective labeling is usually not necessary even when measuring ¹³C R _1ρ RD since the spin lock strength is not large enough to efficiently cover chemical shift regions of spatially close ¹³C nuclei. Special care has to be taken in case of ¹H RD where ROE and NOE artifacts can occur. Another advantage is the possibility to record off‐resonance data, which makes it possible to extract ES chemical shifts. The main challenge here is that due to homonuclear J‐couplings (¹³C,¹³C or ¹H,¹H) Hartmann–Hahn transfers can occur. Therefore, care has to be taken in the selection of SL strengths and offset values. Future improvements in faster data acquisition will allow for a more wide‐used applicability.

3.4. Cross‐correlated relaxation (CCR)

Most cross‐correlated relaxation studies to access dynamics data focus on proteins and to our knowledge only one example to use cross‐correlation rates to obtain information on dynamics in RNAs has been published.101 In their example they have investigated hydrogen bonds in a 22 nucleotide hairpin. Cross‐correlations between the fluctuations of DD interactions between nitrogen and protons, and CSA interactions of the nitrogen nuclei involved in Watson–Crick base pairs were measured and compared to calculated values. The systematically occurring difference between the measured and the calculated CCR rates was attributed to conformational exchange of Watson–Crick base pairs in the slow to intermediate range leading to a large chemical‐shift modulation rate contributing to the measured, apparent CCR values.101

4. Fast Dynamics (Below Tumbling)

4.1. R ₁, R ₂, HETNOE

Theory: Internal motions such as bond vibrations and librations, for example, changes in bond angles, angular orientation, as well as bond lengths, that are faster than the overall tumbling rate of the molecule directly influence local relaxation rates R ₁ and R ₂ as well as cross‐relaxation rates σ, for example, NOE σ _NOE and ROE σ _ROE (Figure 19). The observed relaxation rates at a specific site/nucleus are then not only a function of the overall molecular rotational correlation time, τ _c, but also of the local, effective correlation time, τ _e, and an order parameter S ² [Eq. (2)]:102

$${\displaystyle R=S{}^{2}R\left(\tau {}_{\mathrm{c}}\right)+(1-S{}^2)R\left(\tau {}_{\mathrm{e}}\right)}$$ (2)

Figure 19.

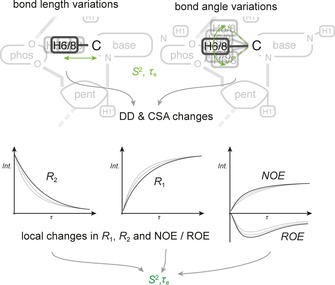
Principle of fast exchange. Geometrical changes within a molecule, such as bond length variations or bond angle variations, as illustrated in the top panel, lead to changes of DD and CSA interactions. Since these DD and CSA interactions are some of the most significant drivers for relaxation mechanisms, a change of these interactions faster than the tumbling rate of the molecule will lead to a direct influence of local relaxation rates. In practice, site specific R ₁, R ₂ and other geometry dependent observables such as NOE transfer rates are determined throughout the molecule.

where R is the observed rate constant based on R ₁, R ₂, σ _NOE or σ _ROE. It is usually assumed that the internal motions are faster than, and independent of, the overall tumbling of the molecule, and information about internal motions can thus be obtained via τ _e and S ². In the fast regime it is not possible to obtain information about defined states interconverting in the exchange process. Instead, for each site in the molecule, the time constant of the internal motion is determined through τ _e, while the order parameter describes the spatial restriction, for example, kind of the motion. If no internal motion is present, the order parameter is 1, while, if internal motion reorients the internal vector freely/randomly, S ²=0.

Depending on the investigated nucleus, the mechanisms driving transverse (R ₂) and longitudinal (R ₁) relaxation are mostly dipole–dipole (DD) interactions. The relaxation rates therefore both depend on spatial distances between the coupling nuclei (r) as well as the spectral density function J(ω), which in turn depends on the tumbling time (τ _c and τ _e). It is sometimes possible to remove the dependency on r, by looking at R ₂/R ₁ ratios instead, which then only depend on correlation times through J(ω).

For ³¹P and to a lesser extent aromatic ¹³C, chemical shift anisotropy (CSA) is an additional contribution to the observed relaxation rates. CSA arises from anisotropic shielding at the nucleus of interest due to a non‐spherically symmetric magnetic environment. Relaxation therefore depends on the apparent anisotropy parameter χ, which can be changed by internal motions changing the intramolecular geometry and, again, the spectral density function J(ω). It should be noted that R ₁, R ₂ (DD) as well as R ₁, R ₂ (CSA) have different strong dependencies on the magnetic field B ₀, thus at higher field strengths, the CSA mechanism eventually becomes dominant. The CSA accounts for >90 % of the relaxation at B ₀ > 9.4 T for ³¹P and 20 % at 9.4 T for aromatic ¹³C.

Similar to dipole–dipole relaxation mechanisms, ROE and NOE transfer rates also depend on internuclear distances r, and via the spectral density J(ω), on the orientation of the internuclear vector, for example, tumbling.

In practice, relaxation rates as well as cross‐relaxation, for example, NOE build‐up rates, are determined for various sites and nuclei, possibly at different field strengths, to obtain the order parameter S ² and the timescale (τ _e) of the underlying internal motion/conformational exchange process.

For ¹H relaxation and cross‐relaxation mainly depend on DD interactions. Effective cross relaxation rates can be determined from NOE build‐up curves for a single pair of protons with a well known and fixed distance between them (e.g., H5–H6). Through the measurement a cross‐relaxation rate constant can be determined. This value will be scaled for fast internal motions and lead to an apparent correlation time τ _e=S ²  τ _c. Estimates of correlation times from the ratio R ₂/R ₁ are not used very often mainly due to the non‐exponential behavior of R ₂ for the investigated protons.

For ³¹P at high magnetic field strengths, CSA is the main relaxation mechanism. Relaxation rates R ₁ and R ₂ can be combined to determine the anisotropy parameter χ, as well as correlation times τ _e and τ _c. {¹H}‐³¹P NOE is usually very small due to the large CSA and therefore not used.

For ¹³C, besides DD interactions, CSA might have a significant contribution to relaxation, especially for aromatic carbons. R ₁, R ₂ as well as heteronuclear NOE build‐up curves are measured for each site of the molecule. For sites with minimal NOEs, for example, minimal internal motions, the ratio R ₂/R ₁ can be used to determine an initial value for the rotational correlation time, τ _c, of the RNA molecule. The CSA component is usually not easily determined and therefore calculated for a determined correlation time. All relaxation rates are then used to fit the three parameters τ _c, τ _e and S ². The determination of separate, factorized contributions of τ _c and τ _e can only be used under the so‐called decoupling approximation, which holds true if internal and overall motions are not correlated and not of the same timescale. However, for globally flexible RNAs this approximation turns out to be violated and for example, helices can move collectively at timescales very similar to that of overall tumbling τ _c. A solution to manipulate overall tumbling times τ _c through a helix elongation strategy, and therefore decorrelate τ _c and τ _e, was proposed by Hansen et al.103

Examples: Due to the fact that current methodology does not allow single states to be discerned by NMR spectroscopy, which is possible only when coupled with simulations, as done for proteins,104 the measurement of fast dynamics has somewhat lost its appeal in recent years. Systems studied on fast timescale have been recently reviewed by Ban et al.,105 Bardon et al.106 and Rinnenthal et al.107

One of the latest examples where many timescales were covered, is the fluoride riboswitch (Figure 20), for which the ligand‐bound state and free state exhibit similar dynamic profiles.43 Recent studies with similar experimental setup, mostly probing ¹H,¹³C and sometimes ¹H,¹⁵N vectors have been published on TAR and modifications thereof,108, 109 SOLE RNA,110 apical loop HBV RNA,2, 111 single‐stranded RNA part of the prequeuosine riboswitch,112, 113 pseudoknot of the telomerase RNA114 and the well‐known UUCG tetraloop, where ³¹P dynamics were probed.115 An interesting application is the estimation of TAR RNA binding to dendrimers using ¹³C spin‐relaxation rates.116

Figure 20.

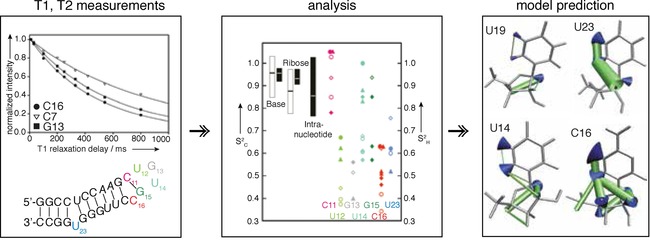
Concept and example of fast dynamics measured by spin relaxation and off‐resonance ROESY. Bottom left) Secondary structure of the apical loop of human HBV epsilon RNA, indicated are flexible nucleotides in color‐coding shown on the right. Top left) Representative T ₁ mono‐exponential decays including fitting, T ₁, T ₂ and HetNOE are recorded as a serious of 2D spectra with good (>10) S/N requiring approximately 5 days experimental time. Middle) Plot of S ² _C (open symbols), which are order parameter of ¹H−¹³C vectors measured by ¹³C spin‐relaxation, and S² _H (filled symbols), which are order parameter of ¹H−¹H through space distances, measured by off‐resonance ROESY. Right) Structural interpretation of S² _C using wobbling in a cone model and S² _H with increasing radii of distances reflecting increasing motion. Reprinted with permission from ref. 2.

Analysis: Two common methods exist: 1) R ₂/R ₁, and 2) model‐free formalism.21, 117 1) R ₂/R ₁, or variations thereof, for example, 2 R ₂−R ₂ = S ² _rel 103, 118 only provides a value to compare the extent of motion within the molecule, where one usually has to assume a rigid reference (e.g., present in an A‐form helical environment). However, it is a quick, more robust and less artifact prone analysis. Instead (2), usage of the model‐free formalism allows extraction of the order parameter S ² (S ² = 1 means completely rigid, S ² = 0 completely flexible). As S² is measured for X−H bond vectors (X = heteronucleus), the order parameter is often depicted as a wobbling in a cone.119 Though called ModelFree, it has nine models to be selected,117 requires input of the hydrodynamic radius or τ _c, and is sensitive to CSA of the atoms. Recently RotDiF has been developed, a convenient program with user interface that offers analysis of fast dynamics.120

Advantages, limitations, challenges: Currently it is not possible to describe the conformers involved in the motion, if simulation is not used. When measuring R ₂, care needs to be taken to suppress R _EX contribution. The timescale is limited by τ _c, however, τ _c can be shifted and the timescale extended by helical elongation.103 For fast dynamics measurements of RNA, development of experiments to discern single states or describe structures that are in fast exchange with each other, will help this area tremendously.

4.2. Off‐resonance ROESY

Theory: As discussed above, similar to dipole–dipole relaxation mechanisms, ROE and NOE transfer rates also depend on internuclear distances r, and with the spectral density J(ω) on the orientation of the internuclear vector, for example, tumbling. Similar to the ratio R ₂/R ₁, the ratio of homonuclear ¹H σ _NOE and σ _ROE can be used to obtain an experimental parameter, which then exclusively depends on correlation times τ _c and τ _e through J(ω). Instead of independently measuring NOESY and ROESY spectra, a more reliable way was proposed by Schleucher et al.13 In order to detect internal motions they propose an off‐resonance ROESY experiment, which allows direct measurement of the ratio of NOE and ROE rates. For large molecules σ _NOE and σ _ROE have opposite signs, therefore ROE and NOE contributions cancel out and the cross‐peak intensity becomes 0 at a certain angle θ  ⁰ of the effective spin lock field. Internal motions reduce both NOE and ROE rates, but the influence of the two is different (Figure 19). Therefore the exact angle θ  ⁰ where the two contributions cancel deviates for nucleotides, which undergo internal fast motions. In practice off‐resonance ROESY spectra with constant spin lock strengths but different offsets are recorded. Exact angles of the effective field θ  ⁱ can then be calculated for every investigated peak i, depending on the field strength, the offset and the chemical shift of the peak with respect to the offset of the spin lock. Cross‐peak intensities can then be plotted against the effective angle θ  ⁱ and the zero‐crossing including the corresponding angle θ  ⁰ can be determined for every peak/site. Differences in θ  ⁰ depend on internal motions and can then be used to extract τ _e and S ².13

Examples: Combined with motion from ¹³C spin relaxation experiments on the fast timescale, off‐resonance ROESY has been applied to the HBV apical loop.2 Off‐resonance ROESY is a complementary experiment to spin‐relaxation as it measures ¹H,¹H vectors through space (Figure 19) and aids in defining the underlying motion. In the future off‐resonance ROESY might aid to describe the participating states. It has the advantages, that no ¹³C/¹⁵N labeling is required, however, the sensitivity to motions is limited to a somewhat smaller timescale (100s of ps).

5. Independent of Tumbling Dynamics (Solid‐State/RDC)

5.1. Solid‐state NMR spectroscopy

Theory: As shown above, solution state NMR spectroscopy has enabled investigations of RNA dynamics in the ps–ns and microsecond–hour timescales. However, as can be seen from the example summary in Figure 3, motions occurring in the microsecond–nanosecond timescale are inaccessible to the presented methods, which is due to the averaging of interactions on the timescale of the overall tumbling of the molecule (τ _c). While RDC measurements can still cover this timescale (Figure 1) and probe the nature of motions, they cannot provide information about exchange rates. In solid‐state NMR spectroscopy this molecular tumbling, that is, stochastic averaging effect, is absent therefore motions can be studied over all timescales from picoseconds–seconds.121 Similar to solution‐state NMR spectroscopy, exchange regimes can be divided into slow (when the motion is slow compared to the observed NMR interaction), intermediate (when the timescale of the motion is comparable to the interaction strength), and fast (when the motion is so fast, that the observed interaction is averaged). While in solution‐state NMR spectroscopy, the observed interaction is usually the isotropic chemical shift, in solid‐state NMR spectroscopy these exchange regimes can be defined with respect to, now accessible, anisotropic interactions such as DD, CSA or quadrupolar interactions. Due to the nature of the strengths of these interactions (≈kHz or larger), line‐shape effects and averaging effects occur on different timescales compared to solution‐state NMR spectroscopy, and thus motions in different timescales become accessible.121

Examples: Drobny and Varani could show ns–ms motions in TAR RNA using deuterium solid‐state NMR line shapes and T1 relaxation experiments on deuterated solid‐state hairpin samples at different hydration levels.122, 123, 124, 125, 126 Motions such as unstacking or base flipping out of the helix on the order of 10⁷ s⁻¹ and fast local motions on the order of 10⁸ s⁻¹ were site‐specifically observed from relaxation data, as described in refs. 124, 126. Slower helical motions could be determined from deuterium solid‐state NMR line shapes for the upper and lower helix of TAR in the ranges of ≈10⁶ and ≈10⁵ s⁻¹, respectively.122 For analysis the two‐site jump model is used to analyze the NMR data and extract exchange rates from line shape analysis and relaxation data.124

Advantages, limitations, challenges: These results illustrate how solid‐state NMR spectroscopy can provide dynamics data complementary to solution‐state NMR experiments. Solid‐state NMR spectroscopy provides more observables, which are usually averaged out in solution‐state NMR spectroscopy, therefore a wider range of timescales of motions/exchange processes become accessible. However, measurement and interpretation can be challenging especially when carried out under magic angle spinning (MAS) conditions.121 It should be mentioned that the above‐shown examples of RNA dynamics measured in the solid‐state were acquired under static conditions. Special care has to be taken when comparing dynamics between solid‐state and solution‐state samples. Similar conditions can be achieved by controlling hydration levels of the lyophilized RNA samples before measuring them in the solid state.125

While first results illustrate how solid‐state NMR spectroscopy can provide dynamics data complementary to solution‐state NMR experiments, it has been shown in protein NMR spectroscopy that many more nuclei, spin–spin interactions as well as experiments could be explored to access dynamics using MAS NMR spectroscopy.121 Solid‐state NMR spectroscopy could also become especially interesting for accessing dynamics of RNAs embedded in larger systems/interacting with large proteins, which are outside the size limit of solution‐state NMR spectroscopy.

5.2. RDCs

Theory: Motions within the molecule will, due to the changes in bond‐lengths and intermolecular distances, for example, influence the CSA (chemical shift anisotropy) as well as DD (dipole–dipole coupling) interactions. As described above, it is not possible to measure those anisotropic interactions and influences on them directly in solution‐state NMR spectroscopy, since anisotropic interactions depend on the orientation relative to the magnetic field and are therefore averaged out in solution due to rotational molecular tumbling. However, through introduction of a certain degree of alignment of the sample in the magnetic field that is achieved through sample preparation, those interactions will not be fully averaged and small anisotropic residuals persist and allow the direct measurement of RDCs. For dynamic molecules or dynamic molecular regions, the observed RDC then arises from a weighted average over all molecular conformations, each of which align differently relative to the magnetic field.127 Therefore, molecular motion decreases the apparent RDC compared to a non‐dynamic RDC. This method can be applied for broad timescales (picosecond–millisecond motions) and is typically used as complementary technique to spin relaxation and relaxation dispersion measurements.

Examples: RDC dynamics is one of the few methods that allows the determination of larger scale motion, for example, the movement of helices and covers wide range of timescales and is also independent of τ _c. The methodology has been developed by the Al‐Hashimi laboratory128 and a protocol has been published.128 A highly investigated system is free HIV‐TAR RNA129, 130 or in complex with the Tat protein,131 or U1A.132 Furthermore, another HIV RNA that causes the ribosome to frameshift has been investigated and found to behave highly similarly.133

Elongation that has also been used for fast‐dynamic decoupling of τ _c, modulates alignment for RNA, as shown again on TAR134 and reviewed by Zhang et al.128 Instructions can be found in the published protocol from the Al‐Hashimi laboratory,135 which also provides analytical software like RAMAH (https://github.com/alhashimilab/RAMAH).

Advantages, limitations, challenges: It is not straightforward to assign a specific timescale and as RDCs span quite large timescales (though that can be an advantage), this can hamper comparison with other methods. It is a laborious method, but the dynamic analysis can be combined with the recording for RDCs for structure determination. It is one of the few methods that can be used to study helical dynamics.

6. Outlook

In summary, the measurement of dynamics in RNA has come a long way. Many issues are addressed with tweaking pulse sequences from protein dynamics,12, 103, 151, 152 selectively labeling atoms41 and carefully analyzing data. However, one needs to keep in mind that many more artifacts can occur in RNA than in proteins and much work is still to be done. This has allowed the research community to define experimentally structures that are in equilibrium with each other and that are higher in energy than the lowest energy state, and which are nonobservable using other methods,6, 8 These high‐energy, low‐populated structures can be defined using their chemical shift—an indicator of structural environment—population and life‐time from seconds up to the molecular tumbling boarder (lower‐microsecond and maybe soon higher‐nanosecond) by using a battery of different, complimentary methods that are reviewed here. Additionally, RNA is a rewarding molecule that enables interpretation of the gained chemical shifts in proper states with structures different from lowest energy, the ground state, which is not often the case for proteins. This structural interpretation of the exited state(s) is possible due to a quite clear chemical shift correlation with secondary structure elements.

Currently, although the methodology is improving continuously, the number of studies published is still small compared to the protein world. As is a trend in other areas, deposition of raw‐data, for example, spectra and statistics, will also help RNA dynamics, and NMR spectroscopy in general, to elucidate data and analytical quality as well as compare data with different methodologies. Increasing numbers of functional RNAs will require structural und dynamical characterization and the field is growing exponentially. Furthermore, methodological advance is needed to access structures experimentally with ever‐shorter life‐times, down to the ps. Advances in simplification of analysis as well as more robust NMR methodology will likely lead to an increased number of studied systems and expanded knowledge. Furthermore, a proper chemical shift database and de‐novo chemical shift prediction, for example, by using DFT, will simplify the elucidation of excited states, which is currently tedious and labor intensive. Additionally, few studies currently exist where systems have been compared across experiments and timescales, for example,43, 108, 136 which is an important part to expand on in the future.

Other methodology, such as for example, FRET, SAXS, XFEL, cryo‐EM, SHAPE137 or EPR have started to show their potential in elucidating dynamics in biomolecules and this will likely also expand in the near future. It will be interesting to see studies that combine different methodology to overcome current challenges, such as large size, complex systems etc., similar to development in RNA high‐resolution structural biology.

If you find yourself looking at a simple NMR spectrum of an RNA and see hallmarks of dynamics—the differences in peak intensity and line‐width—start studying the details. Altogether, RNA dynamics and the discovery of RNA excited states has just begun, methodology has been developed and we hope that this Review enables many more people to study the exquisite changes of RNA structure.

Conflict of interest

The authors declare no conflict of interest.

Biographical Information

Katja Petzold obtained her degree in biochemistry and biotechnology from Martin‐Luther University Halle, Germany (2005). She received her Ph.D. in Medical Biophysics from Umeå University, Sweden (2009), studying RNA dynamics and lipids with Prof. Jürgen Schleucher. She then completed a postdoctoral fellowship with Prof. Hashim M. Al‐Hashimi at the University of Michigan, Ann Arbor, USA, studying RNA dynamics and the structure of RNA excited states. In 2014, she moved to the Karolinska Institute, where she is currently an Associate Professor of Biophysics. Her group′s research focuses on RNA dynamics of disease related systems, such as ribosomes or microRNA, including viruses.

Biographical Information

Judith Schlagnitweit studied for a chemistry diploma at the Johannes Kepler University, Linz, Austria, and obtained her PhD in methods development for solution‐state NMR spectroscopy in the group of Prof. Norbert Müller. She then switched to solid‐state NMR spectroscopy as a postdoctoral fellow in the group of Prof. Lyndon Emsley at the CRMN in Lyon, France (2012–2015), and continued working in the field of solid‐state NMR spectroscopy during her employment as Senior Scientist at GlaxoSmithKline R&D in Stevenage, UK. In 2016 she joined the Petzold lab as a postdoctoral fellow, focusing on NMR methods development for studying RNAs.

Biographical Information

Maja Marušič studied for a diploma in biochemistry at the University of Ljubljana, Slovenia. She obtained her PhD in structural characterization of G‐quadruplexes from genomes of human papillomaviruses in the group of Prof. Janez Plavec at National Institute of Chemistry, Slovenia. For her postdoctoral studies she joined the Petzold lab at the Karolinska Institute, where she is investigating dynamics of ribosomal RNA.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

M. Marušič, J. Schlagnitweit, K. Petzold, ChemBioChem 2019, 20, 2685.