Abstract
The relative influence of niche vs. neutral processes in ecosystem dynamics is an on‐going debate, but the extent to which they structured the earliest animal communities is unknown. Some of the oldest known metazoan‐dominated paleocommunities occur in Ediacaran age (~ 565 million years old) strata in Newfoundland, Canada and Charnwood Forest, UK. These comprise large and diverse populations of sessile organisms that are amenable to spatial point process analyses, enabling inference of the most likely underlying niche or neutral processes governing community structure. We mapped seven Ediacaran paleocommunities using LiDAR, photogrammetry and a laser line probe. We found that neutral processes dominate these paleocommunities, with niche processes exerting limited influence, in contrast with the niche‐dominated dynamics of modern marine ecosystems. The dominance of neutral processes suggests that early metazoan diversification may not have been driven by systematic adaptations to the local environment, but instead may have resulted from stochastic demographic differences.
Keywords: Ecology, Ediacaran, neutral theory, paleoecology, paleontology, spatial point process analysis
Introduction
Two opposing theories lie at the heart of the debate regarding the fundamental mechanisms that govern ecosystem structure and biodiversity: niche and neutral. Niche theory is a central tenet of classical ecological theory, whereby species avoid competitive exclusion by occupying different niches within the ecosystem (MacArthur 1984). Smaller niche overlaps result in less competition between taxa, permitting numerous taxa to co‐exist in an area without excluding each other. Species are able to coexist because they have different requirements. Niche models describe selection‐dominated ecosystems, whereby species dynamics operate deterministically as a series of interspecific interactions, which act as stabilising mechanisms for the ecosystem (Adler et al. 2007). In contrast, for neutral processes, species similarities drive high diversity rather than species differences, enabling co‐existence (Hubbell 2001). Within neutral models, species fitness is similar across a community, and so different taxa can co‐exist because no single taxon has a substantial competitive advantage over any other. Despite this seemingly unrealistic assumption, neutral theories have been able to accurately reproduce certain species–area distributions (Hubbell 2001) and beta diversity patterns (Condit et al. 2002; Chisholm & Pacala 2010), sometimes better than niche theories (Rosindell et al. 2011). In recent years, unified or continuous theories have emerged, whereby niche and neutral processes are combined to enable species coexistence (Gravel et al. 2006; Comdit et al. 2007). In these combined models, species can exhibit strong differences and strong stabilisations (niche‐type), or similar fitness and weak stabilisations (neutral‐type), with the classic niche and neutral models forming the extreme end‐members of such continuum models.
The evolution of macroscopic metazoans was coupled with a transformation in ecosystem dynamics, with paleocommunities emerging from pre‐Ediacaran microbial populations with assumed simple community structure (Butterfield 2007), via late Ediacaran (~ 571–540 Ma) paleocommunities that exhibited both simple and complex community structures (Darroch et al. 2018), into Cambrian ‘modern’ metazoan ecosystems with comparable ecosystem structures to the present day (Dunne et al. 2008). In order to investigate how niche and neutral processes contributed to community dynamics in deep time, we focus on some of the oldest macroscopic paleocommunities that are currently known: those comprising the Avalonian Assemblage of the Ediacaran macrobiota (Waggoner 2003; Boag et al. 2016).
The Avalonian Assemblage is known primarily from Newfoundland, Canada and Leicestershire, UK (Fig. 1) and is comprised entirely of soft‐bodied sessile organisms that are preserved in situ beneath volcanogenic/volcaniclastic event beds. These event beds have deep‐water depositional settings (Wood et al. 2003; Narbonne 2005) that are dated to ~ 571–560 Ma (Noble et al. 2015; Pu et al. 2016), and are considered to represent early animals (Budd & Jensen 2017; Dunn et al. 2018; Wood et al. 2019). As such, bedding plane surfaces are interpreted to preserve near‐complete census paleocommunities (Clapham et al. 2003; Wood et al. 2003), although the impact of modern erosion needs to be considered (Matthews et al. 2017; cf. Mitchell et al. 2015). Unlike hard parts, which can accumulate for thousands of years (Kidwell & Bosence 1991; Kowalewski & Bambach 2008), there was no potential for these soft‐bodied Ediacaran organisms to accumulate over such a large temporal extent. Avalonian ecosystems pre‐date macro‐predation and vertical burrowing, and so also remained undisturbed post‐mortem (Liu et al. 2011; Wilby et al. 2015; Mitchell & Butterfield 2018). Consequently, the size and position of each specimen can be considered an accurate record of the organism’s life history, including its dispersal/reproduction (Seidler & Plotkin 2006), and the habitat (Wiegand et al. 2006) and community interactions it was subject to (Getzin et al. 2006; Lingua et al. 2008; Getzin et al. 2008). Consideration of these fossil assemblages as census communities permits their investigation using the Spatial Point Process Analyses (SPPA) that are used in modern ecological studies (Illian et al. 2008; Wiegand & Moloney 2013). While interpreting processes from these spatial point patterns is imprecise (Law et al. 2009; McIntire and Fajardo, 2009), the use of several complementary SPPA, combined with the fitting of multiple different types of models, enables the most‐likely underlying processes to be inferred (Levin 1995; Waagepetersen and Guan 2009; Wiegand & Moloney 2013; Jalilian et al. 2013, McFadden et al. 2019).
Figure 1.
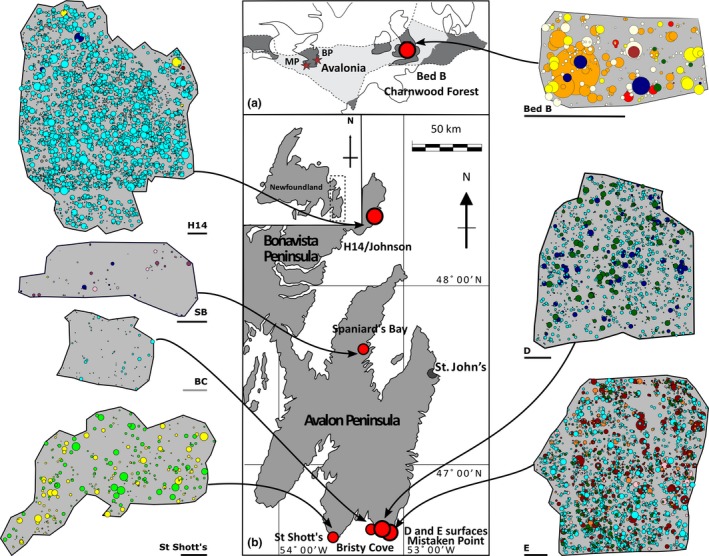
Locality map of study sites, showing: (a) the relative palaeogeographical locations of sites relative to the micro‐continent of Avalonia (grey shading), highlighting the Mistaken Point Ecological Reserve (MP) and the Bonavista Peninsula (BP) in Newfoundland, and Charnwood Forest, UK. (b) the Newfoundland sites of the ‘D’, ‘E’ and Bristy Cove (X‐Ray) surfaces, all in the Mistaken Point Ecological Reserve; the St. Shott’s (Sword Point) surface; the Spaniard’s Bay surface; and the H14/Johnson surface, Bonavista Peninsula (modified from Liu 2016). Associated spatial maps for each locality show the positions of the fossil specimens, where the size of the circle indicates the inferred in vivo vertical height of the organism. Black scale bar = 1 m, grey scale bar = 0.1 m. Different colours indicate different taxa as follows: Thectardis navy; Fractofusus light blue; Charnia bright yellow; Charniodiscus dark red; Aspidella light green; Bradgatia dark green; Feather Dusters light orange; Primocandelabrum dark orange; Trepassia dark purple; Beothukis bright pink; Pectinifrons dark blue; ‘Brushes’ brown; Avalofractus dark blue (Spaniard’s Bay only); Hylaecullulus light yellow.
SPPA can be used to investigate the underlying processes of community assembly because different types of spatial point models can be classified as either niche or neutral models (Harms et al. 2000; Seidler & Plotkin 2006; Lin et al. 2011; McFadden et al. 2019). Neutral processes are identified where intraspecific (univariate) distributions exhibit complete spatial randomness (CSR), or where dispersal processes acted independent of local environment (i.e. habitat heterogeneities; Diggle et al. 2005; Comita et al. 2007; Wiegand et al. 2007a, 2007b; Law et al. 2009). CSR indicates neutral processes because there are no biologically or ecologically significant intrinsic or extrinsic influences on the spatial distribution. Dispersal processes are also considered neutral since they describe cases where aggregations arise from propagules only travelling a limited distance, thus being unable to reach all suitable substrates regardless of underlying habitat heterogeneities or species requirements (Gunatilleke et al. 2006, Seider & Plotkin 2006). Niche processes are identified as intraspecific habitat associations, and/or non‐independent interspecific distributions (Lin et al. 2011; McFadden et al. 2019). Density‐dependent competition, as indicated by spatial segregation (Kenkel 1988), indicates a lack of sufficient resources, and is therefore a niche‐based process. For interspecific (bivariate) distributions, spatially independent patterns reflect neutral processes (McGill 2010), while non‐independent patterns result from niche processes such as resource competition, facilitation and/or habitat filtering (Wiegand et al. 2007b; Wiegand et al. 2009; McFadden et al. 2019).
Methods
Data collection and extraction
In this study, we assessed the univariate and bivariate spatial distributions of taxa from seven Avalonian bedding plane assemblages: the ‘D’, ‘E’, and Bristy Cove (X‐Ray) surfaces in the Mistaken Point Ecological Reserve (Clapham et al. 2003); the St. Shott’s surface at Sword Point; the H14 (Johnson) surface at Little Catalina (Hofmann et al. 2008); and the Spaniard’s Bay surface (Narbonne et al. 2009), all in Newfoundland, Canada; and Bed B in Charnwood Forest, UK (Wilby et al. 2011, Fig. 1 and Table 1). The spatial analyses require the mapping of large areas (up to 115 m2) at sufficient resolution to permit taxonomic identification of the specimens from the resulting digital data set. The method of mapping employed varied according to the nature of the bedding plane, in particular its dip and the fidelity of fossil preservation. We used LiDAR to scan all studied surfaces using a Faro Focus 330x, creating a 3D surface mesh (with a mean resolution of 1 mm) against which we referenced all subsequent data. The Spaniard’s Bay and Mistaken Point ‘D’ and ‘E’ surfaces were laser scanned using a Faro Scan Arm Laser Line Probe, generating surface meshes with a mean resolution of 0.050 mm. We scanned the areas in grids of 1 m × 1 m, incorporating control points common to the LiDAR scan to enable accurate alignment of the two data sets (performed using Geomagic 2015.1.1, Rock Hill, SC, USA). Fossil identification, position and dimensions (disc width, disc length, stem length, stem width, frond length and frond width) were digitized in Inkscape 0.92.3 on a 2D projection of the combined data set, resulting in a 2D vector map for each paleocommunity.
Table 1.
Summary data for studied surfaces. Area is total area mapped. Total number of specimens includes non‐abundant taxa and taphomorphs. Density is of abundant taxa (i.e. those with > 30 individuals) only. Minimum size consistently preserved is the modal height of small specimens; specimens beneath this threshold are more prone to being overlooked and/or misidentified
| Surface | Area mapped (m2) | Total number of specimens | Density (ind per m2) | Number of abundant (> 30) taxa | Minimum size of consistently preserved features (cm) |
|---|---|---|---|---|---|
| Bed B | 115.16 | 761 | 6.61 | 3 | 1.20 |
| MP E | 85.42 | 2977 | 36.83 | 6 | 0.70 |
| MP D | 70.89 | 1402 | 22.29 | 3 | 1.20 |
| H14 | 82.4 | 4235 | 52.55 | 1 | 1.50 |
| BC | 0.81 | 120 | 97.2 | 1 | 0.70 |
| St. Shott’s | 50.93 | 480 | 7.20 | 2 | 1.20 |
| Spaniard’s Bay * | 16.40 | 68 | 2.61 | 3 | 0.20 |
Note, due to low specimen numbers, we included taxa with > 15 specimens as abundant on this surface (see SI discussion)
Fossil relief was not sufficiently high on the H14, Bristy Cove and St. Shott’s surfaces to permit accurate capture of all morphological details using the laser line probe. However, the fossils are readily discernible based on colour, allowing us to create a photomap using Agisoft Photoscan software v1.3.5 by combining a grid of overlapping images. Reference to the LiDAR scan allowed an orthomosaic with sub‐millimeter resolution to be generated, and the fossils were digitised as vectors as above.
Bed B has a dip of ~ 45° and so is not suitable for in situ high‐resolution scanning using our equipment. Instead, we generated a vector map of its fossils from Reflectance Transformation Images (RTIs) of casts of the surface, using RTI Builder from Cultural Heritage Imaging (Wilby et al. 2011, Kenchington et al. 2018; Mitchell et al. 2018). The LiDAR scan enabled the detection of mould deformation and, where necessary, was used to retrodeform the vector map.
We processed all complete vector maps using a custom script in Haskell (Jones 2003), which output specimen identification number, taxonomic identification and specimen dimensions for the subsequent spatial analyses.
Taxonomic identification
Macrofossils present were assigned to one of twenty genera/morphogroups. These comprise thirteen taxonomically described groups and four forms that are widely recognised but remain to be formally described. Specimens that did not fit within these groups were assigned to one of two ‘bin’ groups (Shen et al. 2008), or to the taphomorph group (the decayed remains of already dead organisms, such as ivesheadiomorphs; Liu et al. 2011). Low abundance taxa (taken as < 30 specimens), organ taxa such as Hiemalora, and taphomorphs were excluded from analyses, leaving 12 abundant taxa: (1) Avalofractus, (2) Beothukis, (3) Bradgatia, (4) Charnia, (5) Charniodiscus, (6) Disc A (discs on the St. Shott’s surface with multiple concentric circles); (7) ‘Feather Dusters’, which includes Plumeropriscum and some Primocandlebrum specimens in Newfoundland; (8) Fractofusus, including both F. andersoni and F. misrai; (9) Pectinifrons, (10) Primocandelabrum, (11) Thectardis and (12) Trepassia.
Five of the identified taxa were not sufficiently abundant for use in our analyses: (13) Arborea, (14) “Brushes”, (15) Hylaecullulus, (16) “Ostrich Feathers” and (17) Vinlandia. The remaining specimens were classified as follows: (18) Ivesheadiomorphs (taphomorphs); (19) ‘Holdfast Discs’, which comprises of discoidal specimens of uncertain affinity, with or without associated stems, which lack sufficient detail to identify the parent taxon; and (20) ‘Other Species’, which describes rare forms that do not fall into any of the other groups (e.g. Hapsidophyllas). Three taxa (Charniodiscus, Charnia, Bradgatia) occurred abundantly on two bedding planes, and one (Fractofusus) on four bedding planes, enabling comparison among sites (cf. Mitchell & Butterfield 2018).
Bias analyses
Tectonic deformation and differential erosion of the surfaces can distort spatial analyses (Narbonne 2005; Matthews et al. 2017). Hence, the impact of such deformation and erosion was tested and corrections were applied to surfaces if they significantly affected specimen density distributions (Fig. S1 and Table S1). We modelled differential erosion (cf. Mitchell et al. 2015) by fitting at least three heterogeneous Poisson models to the data, with the models dependent on x (parallel to strike), y (parallel to dip) and a point where erosion was considered most likely (e.g. nearest to the sea), and selected the best fit model by AIC score comparison. The St. Shott’s, Bed B and H14 surfaces all showed significant fossil density changes depending on these physical characters, implying that the observed surface specimen density has been significantly influenced by modern erosion. Such heterogeneous erosional processes were incorporated into subsequent analyses so that the underlying biological and ecological processes could be investigated. Tectonically distorted data were retrodeformed by restoring elongated holdfast discs to a circular outline (Wood et al. 2003).
Spatial analyses
We performed initial data exploration, inhomogeneous Poisson modelling and segregation tests in R (R Core Team 2013) using the package spatstat (Berman 1986; Baddeley & Turner 2005). Programita was used to calculate distance measures and to perform aggregation model fitting (described in detail in Wiegand et al. 1999, 2006; Wiegand & Moloney 2004).
The univariate spatial distribution of each taxon on each bedding plane was described using the spatial summary statistic pair correlation functions (PCFs). PCFs describe how the (normalised) density of points (i.e. fossil specimens) at distance r from a typical point change as a function of distance (Illian et al. 2008; Wiegand & Moloney 2013; Baddeley et al. 2016). A PCF = 1 indicates complete spatial randomness (CSR); that is the point density is the same as the overall density. A PCF > 1 indicates aggregation, so a greater point density of points per area than the overall density; and PCF < 1 indicates segregation, so a smaller density of points per area than the overall density (Diggle 2003; Diggle et al. 2005; Illian et al. 2008). Univariate and bivariate PCFs were estimated from the population density using a bandwidth of 10 cm on all surfaces except Bristy Cove, where 1 cm bandwidth was used. To minimise noise, a smoothing was applied to the PCF that depended on specimen density. This smoothing was over three bandwidths for all bedding plane surfaces except Bristy Cove, which had a five bandwidth smoothing due to its much smaller area (< 1 m2). To test whether the PCF exhibited complete spatial randomness (CSR), 999 simulations were run for each univariate and bivariate distribution, with the 5% highest and lowest simulations used to define the simulation envelope (Levin 1992). CSR was modelled by a homogeneous Poisson model with a constant intensity function (homogeneous background) where the PCF = 1, and the fit of the fossil data to CSR was assessed using Diggle’s goodness‐of‐fit test (Diggle 2003; Diggle et al. 2005; Baddeley et al. 2016). Due to non‐independence of spatial data, Monte‐Carlo generated simulation envelopes cannot be interpreted as confidence intervals. If the observed data fell below the Monte‐Carlo simulations, the univariate or bivariate distribution was interpreted to be segregated, whereas the spatial distribution was interpreted to be aggregated if above the Monte‐Carlo simulations.
Where a taxon was not randomly distributed on a homogeneous background and was aggregated, its spatial distribution was fitted to a random model on a heterogeneous background (HP model, McFadden et al. 2019). Heterogeneous backgrounds are created by modifying the intensity function of the Poisson model to include a changing variable, which changes in proportion to the density of the taxon under consideration, being defined by a circle of radius R over which the density is averaged throughout the sample area. Heterogeneous Poisson models were formed using estimators within the range of 0.1 m < R < 1 m, with R corresponding to the best‐fit model used.
Thomas cluster models were fitted into the data where excursions outside the simulation envelopes for both homogeneous and heterogeneous Poisson models remained. Thomas cluster models are a type of parametric point process model that describe aggregation or a cluster process in which points are normally distributed about the centre point of the cluster – the parent point (Thomas 1949; Wiegand et al. 2007b). For a homogeneous Thomas cluster model, the parent points follow a homogeneous Poisson distribution, and for a homogeneous double cluster Thomas process (DTC), the parent points follow a Thomas cluster model that follows a homogeneous Poisson distribution. Inhomogeneous Thomas cluster models (ITC) result from realisations of a homogeneous Thomas cluster model that has been randomly thinned with the intensity function, thus resembling an additional action of habitat filtering (ITC) (Wiegand et al. 2007a; McFadden et al. 2019). Thomas cluster models were fit to the data as follows (c.f. Mitchell et al. 2015):
The PCF of the observed data and another distance measure, the L function (Thomas 1949; Besag 1974; Turkington & Harper 1979; Mahdi & Law 1987), were found. Both measures were calculated to ensure that the best‐fit model is not optimised towards only one distance measure, and thus encapsulate all spatial characteristics.
Best‐fit Thomas cluster processes (Wiegand et al. 2007b) were fitted to the two functions where PCF > 1. The best‐fit lines were not fitted to fluctuations around the random line of PCF = 1 in order to aid good fit about the actual aggregations, and to limit fitting of the model about random fluctuations. Programita used the minimal contrast method (Diggle 2003; Diggle et al. 2005) to find the best‐fit model.
Upon visual inspection, if the model did not describe the observed data well, the lines were refitted using just the PCF. If that fit was also poor, then only the L‐function was used.
999 simulations of this model were generated, and the top and bottom 5% of simulations were used to create simulation envelopes. The fit was checked using the O‐ring statistic and the nearest neighbour function (Wiegand & Moloney 2004).
The P‐value from Diggle’s goodness‐of‐fit test (pd) was calculated over the model range using both the PCF summary function and the nearest neighbour function to check model fit. Very small‐scale segregations (under 2 cm) were not included in the model fitting since they likely represent the finite size of the specimens (Illian et al. 2008; Mitchell et al. 2015), and a lack of specimen overlap.
A univariate homogeneous Thomas cluster model was interpreted as the best model if there were no excursions outside the simulation envelope and the pd value was high.
If a univariate homogeneous Thomas cluster model was found not to be a good fit to the data, then an inhomogeneous Thomas cluster model (ITC) was fitted, whereby the background intensity varied according to heterogeneous Poisson models instead of a homogenous Poisson process (c.f. Fig. S2).
If two univariate homogeneous Thomas cluster models were found to be a good fit to the data at different spatial scales, then a double Thomas cluster model was fit to the data (DTC).
Bivariate distributions
Spatial independence was tested using a toroidal shift model (Lotwick & Silverman 1982), whereby one pattern is fixed while the other is moved in its entirety. This analysis necessitated sub‐sampling of the mapped areas (to rectangular areas, Figs S3 and S4 and Table S2). Monte Carlo simulations of these toroidal shift models were run as detailed above and the bivariate distribution was taken to be non‐independent if there were excursions outside the simulation envelope.
Assignment of niche or neutral processes to models
Categories of spatial models were assigned following McFadden et al. (2019). The null model (CSR) was tested via goodness‐of‐fit tests and Monte Carlo simulations, and if there were significant departures from CSR, the distributions were tested for HP, then TC and ITC. CSR and dispersal limitation patterns are neutral processes, with homogeneous Poisson models describing CSR processes, and Thomas cluster (TC) or Double Thomas cluster (DTC) models (Wiegand et al. 2007b) indicating dispersal limitation processes (Wiegand et al. 2007a; Lin et al. 2011). More generally, neutral processes can be indicated if there are significant aggregations that are independent of the environment (McFadden et al. 2019). Intraspecific habitat associations are best modelled by a heterogeneous Poisson model (HP) or, when combined with dispersal limitations, an inhomogeneous Thomas cluster model (ITC), (Lin et al. 2011; Harms et al. 2001; McFadden et al. 2019). Therefore, for univariate distributions, neutral processes are indicated by CSR, TC or DTC models, whereas niche processes are indicated by segregation, HP, and ITC models, as well as non‐independent bivariate distributions.
Results
The univariate and bivariate analyses combine to provide strong evidence that neutral processes dominated Avalonian Assemblage paleocommunities, with only limited niche‐based influence. Across the seven surfaces and the 18 univariate distributions examined, nine taxon distributions were assigned to CSR (Fig. 2 and Table 2). Most of the non‐CSR taxon distributions were best modelled by TC (or DTC). Only Trepassia on the Spaniard’s Bay surface was best modelled by an ITC model (Fig. 2g and Table 2). The only taxon to exhibit univariate spatial distribution with an HP best‐fit model was Beothukis on the ‘E’ and Spaniard’s Bay surfaces (Fig. 2g). These three instances of HP and ITC all had strong goodness‐of‐fit pd values compared to other models (Table 2). These results suggest that dispersal limitation processes structured the majority of spatial distributions of Avalonian communities.
Figure 2.
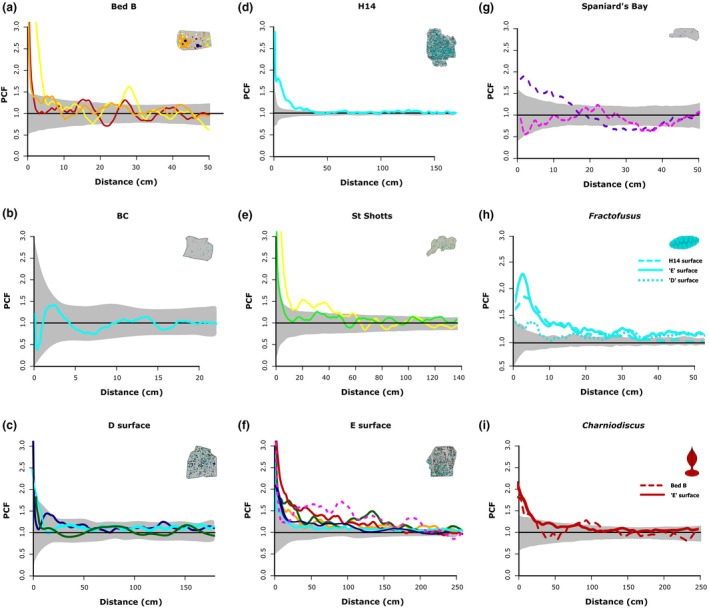
Univariate PCF analyses for the seven Ediacaran fossil surfaces (a–g) and for Fractofusus and Charniodiscus from multiple surfaces (h–i). (a) Bed B, Charnwood Forest, (b) Bristy Cove/X‐Ray surface, (c) ‘D’ surface, (d) H14/Johnson surface (e) St. Shott’s surface, (f) ‘E’ surface, and (g) Spaniard’s Bay surface. The univariate PCFs of (h) Fractofusus and (i) Charniodiscus demonstrating the consistency of their respective spatial distributions between localities. Where the best‐fit model for the distribution represents a niche process (Table 2), it is drawn as a dashed line. Models indicating neutral processes are drawn as solid lines. Black line represents the random model. The grey area is the simulation envelope for 999 Monte Carlo simulations of complete spatial randomness. The x‐axis is the inter‐point distance between organisms in metres. On the y‐axis PCF = 1 indicates complete spatial randomness (CSR), < 1 indicates segregation, and > 1 indicates aggregation. Different colours indicate different taxa as follows: Thectardis navy; Fractofusus light blue; Charnia bright yellow; Charniodiscus dark red; Aspidella light green; Bradgatia dark green; ‘Feather Duster’, light orange; Primocandelabrum dark orange; Trepassia dark purple; Beothukis bright pink; Pectinifrons dark blue; ‘Brushes’ brown; Avalofractus dark blue (Spaniard’s Bay surface only); Hylaecullulus light yellow. This figure shows that neutral processes (solid lines) dominated these Avalonian communities, and that Fractofusus and Charniodiscus show the same distributions across multiple surfaces.
Table 2.
Summary table of univariate PCF analyses. For the inhomogeneous point processes (HP and ITC), the moving window radius is 0.5 m, using the same taxon density as the taxon being modelled
| Surface | Taxon | n | Model fit | pd values PCF | pd values NN | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 100 | Mean number in cluster | CSR | HP | TC | ITC | CSR | HP | TC | ITC | ||||
| Bed B | Charniodiscus | 48 | 2.906 | 0.001 | 0.001 | 0.001 | 0.002 | 0.892 | 0.005 | 0.190 | 0.117 | 0.596 | 0.553 |
| Primocandelabrum | 106 | 21.47 | 0.124 | 0.124 | 0.124 | 0.002 | 0.647 | 0.137 | 0.251 | 0.268 | 0.981 | 0.255 | |
| Charnia | 69 | 12.027 | 0.294 | 0.294 | 0.294 | 0.266 | 0.972 | 0.272 | 0.020 | 0.020 | 0.923 | 0.071 | |
| Bristy Cove | Fractofusus | 76 | NA | 0.523 | 0.523 | 0.523 | 0.182 | 0.173 | 0.183 | 0.410 | 0.396 | 0.368 | 0.389 |
| Mistaken Point D | Fractofusus | 1067 | 4.312 | 0.001 | 0.001 | 0.001 | 0.512 | 0.767 | 0.021 | 0.001 | 0.005 | 0.168 | 0.001 |
| Pectinifrons | 108 | NA | 0.575 | 0.575 | 0.575 | 0.325 | 0.911 | 0.357 | 0.041 | 0.030 | 0.302 | 0.039 | |
| Bradgatia | 140 | NA | 0.664 | 0.664 | 0.664 | 0.425 | 0.466 | 0.397 | 0.544 | 0.482 | 0.505 | 0.512 | |
| Mistaken Point E | Bradgatia | 34 | NA | 0.44 | 0.44 | 0.540 | 0.001 | 0.445 | 0.002 | 0.001 | 0.003 | 0.323 | 0.001 |
| Charniodiscus | 326 | 2.133 | 0.01 | 0.01 | 0.001 | 0.132 | 0.451 | 0.142 | 0.001 | 0.001 | 0.074 | 0.001 | |
| Beothukis | 76 | 6.841 | 0.01 | 0.01 | 0.001 | 0.963 | 0.609 | 0.11 | 0.201 | 0.967 | 0.180 | 0.199 | |
| Feather Dusters | 272 | 5.616 | 0.01 | 0.01 | 0.001 | 0.019 | 0.282 | 0.183 | 0.002 | 0.001 | 0.206 | 0.001 | |
| Thectardis | 39 | 1.835 | 0.02 | 0.02 | 0.002 | 0.443 | 0.911 | 0.073 | 0.479 | 0.479 | 0.657 | 0.458 | |
| Fractofusus | 1137 | 11.842 | 0.01 | 0.01 | 0.001 | 0.031 | 0.325 | 0.35 | 0.001 | 0.001 | 0.971 | 0.001 | |
| H14 | Fractofusus | 3886 | 7.906 | 0.001 | 0.001 | 0.001 | 0.003 | 0.560 | 0.004 | 0.001 | 0.001 | 0.225 | 0.001 |
| St. Shott’s | Aspidella | 170 | 9.226 | 0.011 | 0.011 | 0.257 | 0.225 | 0.331 | 0.271 | 0.572 | 0.589 | 0.629 | 0.583 |
| Charnia | 54 | 10.97 | 0.257 | 0.257 | 0.011 | 0.016 | 0.963 | 0.015 | 0.45 | 0.491 | 0.985 | NA | |
| Spaniard’s Bay | Beothukis | 18 | 36.70 | 0.401 | 0.401 | 0.401 | 0.810 | 0.530 | 0.308 | 0.196 | 0.194 | 0.227 | 0.181 |
| Trepassia | 33 | 7.148 | 0.005 | 0.005 | 0.005 | 0.022 | 0.980 | 0.850 | 0.576 | 0.570 | 0.572 | 0.574 | |
pd = 1 corresponds to a perfect fit of the model to the data, while pd = 0 corresponds to no fit. Where observed data did not fall outside CSR Monte‐Carlo simulation envelopes, no further analyses were performed, which is indicated by NA. σ: cluster radius, ρ: density of specimens, CSR: Complete spatial randomness, HP: Heterogeneous Poisson model, TC: Thomas cluster model and ITC: inhomogeneous Thomas cluster model. Mean number in cluster refers to the mean the mean number of individuals in a cluster estimated as λ/ρ. Note that if the cluster model is not a good fit, the mean number in cluster will not necessarily be appropriate. Note that three taxa (Charniodiscus, Feather Dusters and Fractofusus) on Mistaken Point E surface and Fractofusus on H14 are not well described by a best‐fit single Thomas cluster model because they are best described by a double Thomas cluster model (see Mitchell et al. 2015 for details).
A direct analysis of spatial scale could not be performed on our data because the palaeocommunities are limited in spatial scale, with the largest surfaces enabling spatial analyses of only up to 2.5 m. Instead, to gain some indication of whether taxa behave differently over broad spatial scales, we compared the univariate spatial distributions of individual taxa across different sites, thereby representing paleocommunities separated by broad spatial and temporal scales. Bradgatia, Charnia, Charniodiscus and Fractofusus all exhibit a consistent best‐fit model (CSR, TC, TC and TC/DTC, respectively) across all the surfaces on which they were observed (Fig. 2 and Table 2). Previous work has demonstrated that Fractofusus consistently shows the same spatial distributions across multiple surfaces (Mitchell et al. 2015) in different geological units (cf. H14 and ‘E’ surface, Fig. 2h). Charniodiscus also shows consistent spatial distributions (Fig. 2i), even between paleocommunities that are temporally and geographically separate (e.g. Charniodiscus from the ‘E’ surface and from Bed B). The consistency of univariate spatial distributions across multiple sites suggests that the small‐spatial‐scale ecological behaviour of these taxa is constant over broad spatial and temporal scales, providing further evidence of the importance of neutral processes to these communities.
Three of the five studied paleocommunities contained more than one abundant taxon, thus enabling bivariate distribution analyses (‘E’, Spaniard’s Bay and Bed B surfaces; Mitchell & Butterfield 2018; Mitchell & Kenchington 2018). Non‐independent bivariate distributions were rare, with only 4 out of a possible 24 bivariate distributions showing non‐independence, revealing that neutral processes also dominate bivariate taxa distributions (Fig. 4 and Table S3). Furthermore, even when present, these non‐independent bivariate distributions are weaker in PCF magnitude than univariate distributions (Figs 1 and 3). Significant bivariate aggregations increased specimen density by up to 56% (50% for Spaniard’s Bay Beothukis – Trepassia specimens; 34% for ‘E’ surface Fractofusus – Feather Dusters specimens; and 56% for ‘E’ surface Feather Dusters – Charniodiscus specimens respectively; Fig. 4a), while significant bivariate segregations reduced specimen density by up to 39% (39% for Spaniard’s Bay Beothukis – Trepassia, specimens; 7% for Bed B Charnia – Primocandelabrum; 10% for ‘E’ surface Fractofusus – Feather Dusters; and 10% for ‘E’ surface Feather Dusters – Charniodiscus respectively; Fig. 4). In contrast, the univariate dispersal‐generated aggregations increased taxon density by 180–300% (Fig. 2), indicating that bivariate processes had less impact on spatial distributions than univariate processes. Non‐independent bivariate distributions reflect interactions with local resources, so these spatial distributions suggest that influence from local resources was rare, and where present was relatively weak in magnitude (Fig. 4; cf. Mitchell & Butterfield 2018; Mitchell & Kenchington 2018).
Figure 4.
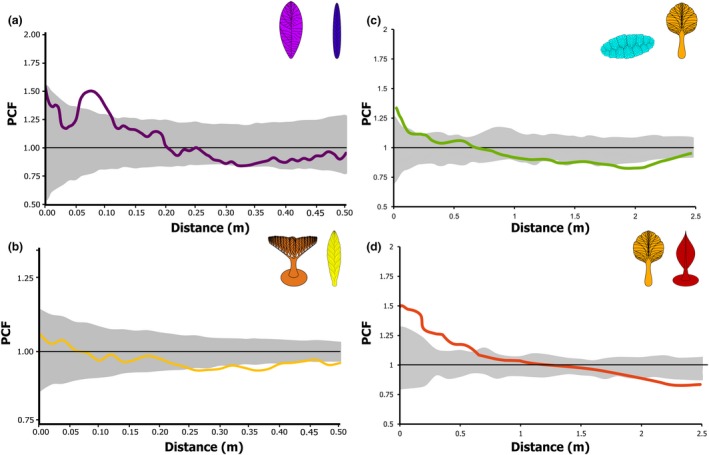
Bivariate PCF analyses for the taxa with non‐independent spatial distributions. The grey area is the simulation envelope of complete spatial randomness (CSR) for 999 Monte Carlo simulations CSR. The x‐axis is the interpoint distance between organisms in metres. On the y‐axis, PCF = 1 indicates CSR and is indicated by a black line, < 1 indicates segregation, and > 1 indicates aggregation. (a) Trepassia and Beothukis from Spaniard’s Bay. (b) Charnia and Primocandelabrum from Bed B, Charnwood Forest. (c) Feather Dusters and Fractofusus, and (d) Feather Dusters and Charniodiscus from Mistaken Point ‘E’ Surface. C and D reproduced from Mitchell and Butterfield (2018), with 99 Monte Carlo simulations of CSR.
Figure 3.
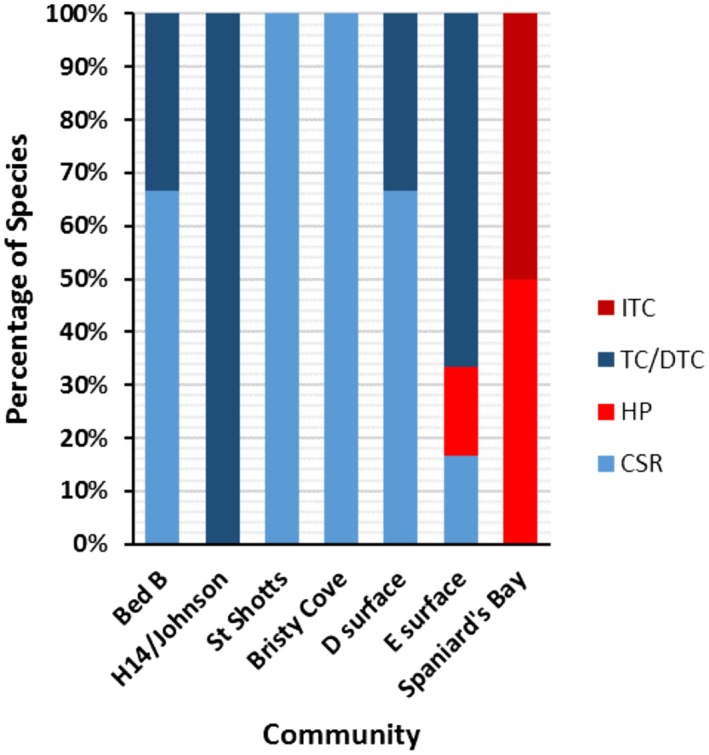
Proportion of best‐fit univariate models by surface. The percentage of taxa with univariate spatial distributions that are best described by CSR, HP, TC (or DTC) and ITC models. CSR and TC are considered neutral models and are shown in blue. HP and ITC are niche models, shown in red.
Discussion
This study provides strong evidence that neutral processes structured Avalonian Assemblage paleocommunities, with neutral best‐fit models dominating the univariate distributions, repetition of best‐fit univariate models across different paleocommunities, and weak and rare bivariate niche best‐fit models. These neutral‐process‐dominated community dynamics contrast with those observed in the modern marine realm, where neutral processes are typically rare across multiple spatial scales, from individual sites to regional scales (Dornelas et al. 2006; Connolly et al. 2014). This stark difference raises the question of whether Ediacaran early animal paleocommunities had fundamentally different community dynamics was to those of the present day. To our knowledge, the only other work investigating niche‐neutral influences in the geological record is from the Quaternary (2.58–0.01 Ma), where strong model and empirical support was found for environment‐led (niche) models of assembly (Jackson & Blois 2015), as in extant terrestrial systems. There are some important differences between Avalonian Assemblage paleocommunities and extant marine communities. Most notable is that Avalonian paleocommunities appear to differ from the majority of modern marine systems in the extent of their ecological maturity, generally preserving no more than three generations (Mitchell et al. 2015), though there is evidence for rare ‘survivors’ from earlier generations (Wilby et al. 2015), and for secondary community succession (Liu et al. 2012). These characteristics suggest that Avalonian communities are not always mature, and were perhaps curtailed by high frequency incursions of sediment, which acted to limit their maturity (Wilby et al. 2015). Recent simulations show that community dynamics in small populations living in fluctuating environments are dominated by neutral processes, implying a lack of small‐spatial scale environmental control on ecological dynamics in such systems (Fisher & Mehta 2014).
The relative influence of niche vs. neutral processes is affected by taxon dispersal ranges (Ron et al. 2018). Wide dispersal ranges increase the connectivity between populations, and so expand effective community size, with the net result of enhancing ecological selection (competition) and thereby increasing the relative importance of niche processes (Ron et al. 2018). The opposite is true when dispersal is limited, making such communities more likely to be dominated by neutral processes (Ron et al. 2018). The widespread distributions of certain Avalonian taxa (e.g. Charnia) provide evidence that these, at least, were capable of wide spatial dispersal (Darroch et al. 2013; Boag et al. 2016). The CSR and HP distributions of Beothukis and Bradgatia (Table 2) similarly suggest wide dispersal. In contrast, six of the seven studied paleocommunities were dominated by taxa which predominantly exhibit limited local dispersal (Fig 2a, h and i; Mitchell & Butterfield 2018, Mitchell & Kenchington 2018), with the PCF plots for Fractofusus, Charniodiscus and Primocandelabrum (Fig. 2a, h and i), suggesting typical dispersal ranges of < 20 cm. However, Fractofusus was also capable of a wide‐reaching waterborne propagule stage, although these only make a minor contribution to the population (Mitchell et al. 2015), and the global distribution of Charniodiscus suggests that it may have been similarly capable. The studied Ediacaran paleocommunities have comparatively small populations, experienced frequent disturbance events, and include many taxa with short dispersal ranges, so within this framework we would expect neutral processes to dominate. While the dominance of neutral processes within these paleocommunities differs substantively from the majority of the modern marine realm, the underlying dynamics are entirely consistent with models of assembly that include both niche and neutral processes, and are similar to those of modern communities subject to the same conditions. Thus, it is therefore likely that the fundamental mechanisms of metazoan community assembly were already in place in the Ediacaran Period, and so may have existed unchanged for ~ 570 million years.
Resource limitation and spatial scales
The relative importance of niche and neutral processes to community assembly generally changes with spatial scale in modern communities (Garzon‐Lopez et al. 2014; Chase 2014). SPPA analyses of modern deep‐sea benthic systems have yet to be performed over a range of spatial scales, so direct comparison with the Avalonian Assemblage palaeocommunities is not possible. Instead, we rely on analyses of terrestrial forests. In extant forests, larger spatial scales (~ 1000 m2) show strong habitat associations, whereas smaller spatial scales (~ 1 m2) show stronger neutral processes (Garzon‐Lopez et al. 2014). This pattern is unlikely to be repeated in extant deep‐sea communities because limited resources in such environments lead to clear niche‐processes (spatial segregation) at the small (~ 1 m2) spatial scales (Gage & Tyler 1991; Tecchio et al. 2011). Hence, it is unlikely that spatial scale alone can explain the dominance of neutral processes in Ediacaran communities at the metre scale.
In contrast to modern deep‐sea benthic communities, which are highly resource‐limited (Gage & Tyler 1991; Tecchio et al. 2011), the Avalonian communities do not appear to have been restricted by lack of resources, as demonstrated by the rarity of competition for resources (Mitchell & Kenchington 2018) and dominance of neutral processes. We would expect to see evidence of niche processes at the spatial scales presented here because the environment of the Ediacaran seafloor may have differed at the meter scale because microbial mats (which are interpreted to have covered the Ediacaran seafloor) can show variability in composition and structure even over distances of just a few centimetres (e.g. McKay et al. 2012). Even if Ediacaran substrates were homogeneous, sub meter‐scale environmental filtering is still possible: the highly limited resources of the modern deep‐sea environment lead to spatial segregation at sub‐meter scale (Tecchio et al. 2011). As such, the lack of evidence for environmental influence in these communities suggests that the dynamics found in these communities are characterised by environments that are not resource limited, enhancing the importance of stochastic processes for Avalonian community assembly.
Evolutionary context
In a similar manner to ecological processes, evolutionary processes can be categorised as niche (selection) or neutral (drift) processes (Chave 2004). Selection (niche) processes are considered deterministic because external factors, such as limited resources, lead to competition in a predictable way: given a set of initial conditions, the organisms/communities will always respond to these conditions (environment) in the same way (Chave 2004). By contrast, drift (neutral) processes are considered stochastic because they result from random fluctuations in population demography, so given a set of the same initial conditions, different populations/communities may emerge. Hence, the observed dominance of neutral ecological processes in the Ediacaran Avalonian paleocommunities establishes that they are inherently stochastic/probabilistic, with the possible implication that early metazoan diversification was not a systematic adaption to optimise survival under prevailing environmental conditions (which would be niche processes, and so deterministic). Instead, the existence of Avalonian organisms under a stochastic regime favours a scenario in which diversification was driven by demographic differences resulting from random within‐population differences. If this hypothesis is correct and early metazoan evolution was stochastic, then this stochasticity may help to explain why neutral models of evolution can reproduce substantial macro‐evolutionary trends such as the Cambrian Explosion (cf. Budd & Mann 2018), despite the known importance of niche processes in shaping evolution more broadly (e.g. Hutchinson 1957).
Conclusions
We have shown that paleocommunities of early macroscopic metazoans were overwhelmingly dominated by neutral ecological processes, with only limited and weak evidence for niche processes. Our results strongly contrast with modern marine systems. Since the studied Ediacaran paleocommunities have traits (short dispersal ranges, small populations and frequent disturbances) that are associated with extant communities governed by neutral processes, our results suggest that the fundamental mechanisms of community assembly may have been in place since the early stages of metazoan evolution. The dominance of neutral processes in these paleocommunities suggests that systematic adaptation of the Ediacaran organisms to their local environment may not have been the underlying driver of early metazoan diversification. Instead, late Neoproterozoic metazoan diversification may have resulted from stochastic demographic differences, with only limited environmental influence.
Conflict of Interest
The authors declare no competing interests.
Authorship
EGM conceived the project, designed the research, ran the analyses and wrote the first draft of the paper. SH developed the data post‐processing protocol. SH and EGM processed field data. All authors contributed to field data collection and were involved in writing the final manuscript.
Supporting information
Acknowledgements
The Parks and Natural Areas Division (PNAD), Department of Environment and Conservation, Government of Newfoundland and Labrador, provided permits to conduct research within the Mistaken Point Ecological Reserve (MPER) in 2010, 2016 and 2017. Readers are advised that access to MPER is by scientific research permit only. Bed B forms part of a designated Site of Special Scientific Interest (SSSI), protected in law and administered by Natural England. Access to Bed B was kindly facilitated by Natural England and the landowner. This work has been supported by the Natural Environment Research Council [grant numbers NE/P002412/1 to EGM; NE/1005927/1 to CGK and PRW; and Independent Research Fellowship NE/L011409/2 to AGL], a Gibbs Travelling Fellowship from Newnham College, Cambridge and a Henslow Research Fellowship from Cambridge Philosophical Society to EGM. CGK also acknowledges a Research Studentship funded by the Cambridge Philosophical Society.
Data availability statement
The data supporting the results are archived in Figshare in https://doi.org/10.6084/m9.figshare.9576863. Due to geoconservation concerns, only a subset of data from Bed B will be made publicly available, with the full set available to researchers on request from the corresponding author.
References
- Adler, P.B. , Hille, R. , Lambers, J. & Levine, J.M. (2007). A niche for neutrality. Ecol. Lett., 10, 95–104. [DOI] [PubMed] [Google Scholar]
- Baddeley, A. & Turner, R. (2005). Spatstat: an R package for analyzing spatial point patterns. J. Stat. Softw., 12, 1–42. [Google Scholar]
- Baddeley, A. , Turner, R. & Rubak, E. (2016). Adjusted composite likelihood ratio test for spatial Gibbs point processes. J Stat Comput Simul., 86(5), 922–941. [Google Scholar]
- Berman, M. (1986). Testing for spatial association between a point process and another stochastic process. Appl. Stat., 35, 54–62. [Google Scholar]
- Besag, J. (1974). Spatial interaction and the statistical analysis of lattice systems. J. R. Stat. Soc.: Ser. B (Methodological), 36, 192–236. [Google Scholar]
- Boag, T.H. , Darroch, S.A. & Laflamme, M. (2016). Ediacaran distributions in space and time: testing assemblage concepts of earliest macroscopic body fossils. Paleobiology, 42, 574–594. [Google Scholar]
- Budd, G.E. & Jensen, S. (2017). The origin of the animals and a ‘Savannah’ hypothesis for early bilaterian evolution. Biol. Rev., 92, 446–473. [DOI] [PubMed] [Google Scholar]
- Budd, G.E. & Mann, R.P. (2018). History is written by the victors: the effect of the push of the past on the fossil record. Evolution, 72, 2276–2291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butterfield, N.J. (2007). Macroevolution and macroecology through deep time. Palaeontology, 50, 41–55. [Google Scholar]
- Chase, J.M. (2014). Spatial scale resolves the niche versus neutral theory debate. J. Veg. Sci., 25(2), 319–322. [Google Scholar]
- Chave, J. (2004). Neutral theory and community ecology. Ecol. Lett., 7, 241–253. [Google Scholar]
- Chisholm, R.A. & Pacala, S.W. (2010). Niche and neutral models predict asymptotically equivalent species abundance distributions in high‐diversity ecological communities. Proc. Natl Acad. Sci., 107, 15821–15825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clapham, M.E. , Narbonne, G.M. & Gehling, J.G. (2003). Paleoecology of the oldest known animal communities: Ediacaran assemblages at Mistaken Point, Newfoundland. Paleobiology, 29, 527–544. [Google Scholar]
- Comita, L.S. , Condit, R. & Hubbell, S.P. (2007). Developmental changes in habitat associations of tropical trees. J. Ecol., 95, 482–492. [Google Scholar]
- Condit, R. , Pitman, N. , Leigh, E.G. , Chave, J. , Terborgh, J. , Foster, R.B. et al (2002). Beta‐diversity in tropical forest trees. Science, 295, 666–669. [DOI] [PubMed] [Google Scholar]
- Connolly, S.R. , MacNeil, M.A. , Caley, M.J. , Knowlton, N. , Cripps, E. , Hisano, M. et al (2014). Commonness and rarity in the marine biosphere. Proc. Natl Acad. Sci., 111, 8524–8529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darroch, S.A. , Laflamme, M. & Clapham, M.E. (2013). Population structure of the oldest known macroscopic communities from Mistaken Point, Newfoundland. Paleobiology, 39, 591–608. [Google Scholar]
- Darroch, S.A. , Laflamme, M. & Wagner, P.J. (2018). High ecological complexity in benthic Ediacaran communities. Nat. Ecol. Evol., 2, 1541. [DOI] [PubMed] [Google Scholar]
- Diggle, P. (2003). Statistical Analysis of Spatial Point Patterns, 2nd edn Arnold, London. [Google Scholar]
- Diggle, P. , Zheng, P. & Durr, P. (2005). Nonparametric estimation of spatial segregation in a multivariate point process: Bovine tuberculosis in Cornwall, UK. J. R. Stat. Soc. Ser. C (Appl. Stat.), 54, 645–658. [Google Scholar]
- Dornelas, M. , Connolly, S.R. & Hughes, T.P. (2006). Coral reef diversity refutes the neutral theory of biodiversity. Nature, 440, 80–82. [DOI] [PubMed] [Google Scholar]
- Dunn, F.S. , Liu, A.G. & Donoghue, P.C. (2018). Ediacaran developmental biology. Biol. Rev., 93(2), 914–932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunne, J.A. , Williams, R.J. , Martinez, N.D. , Wood, R.A. & Erwin, D.H. (2008). Compilation and network analyses of Cambrian food webs. PLoS Biol., 6, e102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher, C.K. & Mehta, P. (2014). The transition between the niche and neutral regimes in ecology. Proc. Natl Acad. Sci., 111, 13111–13116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gage, J.D. & Tyler, P.A. (1991). Deep‐Sea Biology: A Natural History of Organisms at the Deep Sea Floor. Cambridge University Press, Cambridge. [Google Scholar]
- Garzon‐Lopez, C.X. , Jansen, P.A. , Bohlman, S.A. , Ordonez, A. & Olff, H. (2014). Effects of sampling scale on patterns of habitat association in tropical trees. J. Veg. Sci., 25(2), 349–362. [Google Scholar]
- Getzin, S. , Dean, C. , He, F. , Trofymow, J.A. , Wiegand, K. & Wiegand, T. (2006). Spatial patterns and competition of tree species in a Douglas fir chronosequence on Vancouver Island. Ecography, 29, 671–682. [Google Scholar]
- Getzin, S. , Wiegand, T. , Wiegand, K. & He, F. (2008). Heterogeneity influences spatial patterns and demographics in forest stands. J. Ecol., 96, 807–820. [Google Scholar]
- Gravel, D. , Canham, C.D. , Beaudet, M. & Messier, C. (2006). Reconciling niche and neutrality: the continuum hypothesis. Ecol. Lett., 9, 399–409. [DOI] [PubMed] [Google Scholar]
- Gunatilleke, C.V.S. , Gunatilleke, I.A.U.N. , Esufali, S. , Harms, K.E. , Ashton, P.M.S. , Burslem, D.F. , et al. (2006). Species–habitat associations in a Sri Lankan dipterocarp forest. Trop. Ecol., 22(4), 371–384. [Google Scholar]
- Harms, K.E. , Condit, R. , Hubbell, S.P. & Foster, R.B. (2001). Habitat associations of trees and shrubs in a 50-ha neotropical forest plot. J. Ecol., 89(6), 947–959. [Google Scholar]
- Harms, K.E. , Wright, S.J. , Calderón, O. , Hernandez, A. & Herre, E.A. (2000). Pervasive density‐dependent recruitment enhances seedling diversity in a tropicalforest. Nature, 404, 493–495. [DOI] [PubMed] [Google Scholar]
- Hofmann, H.J. , O'brien, S. J. , & King, A. F. (2008). Ediacaran biota on bonavista peninsula, Newfoundland. Canada. J. Paleontol., 82(1), 1–36. [Google Scholar]
- Hubbell, S.P. (2001). The unified neutral theory of biodiversity and biogeography (MPB‐32) (monographs in population biology). Princeton University Press, Princeton, NJ. [Google Scholar]
- Hutchinson, G.E. (1957). A Treatise on Limnology. Wiley and Sons, London. [Google Scholar]
- Illian, J. , Penttinen, A. , Stoyan, H. & Stoyan, D. (2008). Statistical Analysis and Modelling of Spatial Point Patterns Vol 7. John Wiley, Chichester. [Google Scholar]
- Jackson, S.T. & Blois, J.L. (2015). Community ecology in a changing environment: perspectives from the Quaternary. Proc. Natl Acad. Sci., 112, 4915–4921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jalilian, A. , Guan, Y. & Waagepetersen, R. (2013). Decomposition of variance for spatial Cox processes. Scand. J. Stat., 40(1), 119–137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones, S.P. (Ed.). (2003). Haskell 98 Language and Libraries: The Revised Report. Cambridge University Press, Cambridge. [Google Scholar]
- Kenchington, C.G. , Harris, S.J. , Vixseboxse, P.B. , Pickup, C. & Wilby, P.R. (2018). The Ediacaran fossils of Charnwood Forest: shining new light on a major biological revolution. Proc. Geol. Assoc., 129, 264–277. [Google Scholar]
- Kenkel, N.C. (1988). Pattern of self thinning in Jack pine: testing the random mortality hypothesis. Ecology, 69, 1017–1024. [Google Scholar]
- Kidwell, S. & Bosence, D. (1991). Taphonomy and Time‐Averaging of Marine Shelly Faunas. Taphonomy: Releasing the Data Locked in the Fossil Record. Plenum; , New York, pp. 115–209. [Google Scholar]
- Kowalewski, M. & Bambach, K. (2008). The Limits of Paleontological Resolution. Springer, Tampa, FL. [Google Scholar]
- Law, R. , Illian, J. , Burslem, D.F. , Gratzer, G. , Gunatilleke, C.V.S. & Gunatilleke, I.A.U.N. (2009). Ecological information from spatial patterns of plants: insights from point process theory. J. Ecol., 97, 616–628. [Google Scholar]
- Levin, S.A. (1992). The problem of pattern and scale in ecology: the Robert H. MacArthur award lecture. Ecology, 73, 1943–1967. [Google Scholar]
- Levin, S.A. (1995). In Ecological Time Series Vol. 2 (eds Powell T.M., Steele J.H.). Springer, Boston, MA, pp. 277–326. [Google Scholar]
- Lin, Y.C. , Chang, L.W. , Yang, K.C. , Wang, H.H. & Sun, I.F. (2011). Point patterns of tree distribution determined by habitat heterogeneity and dispersal limitation. Oecologia, 165, 175–184. [DOI] [PubMed] [Google Scholar]
- Lingua, E. , Cherubini, P. , Motta, R. & Nola, P. (2008). Spatial structure along an altitudinal gradient in the Italian central Alps suggests competition and facilitation among coniferous species. J. Veg. Sci., 19, 425–436. [Google Scholar]
- Liu, A.G. (2016). Framboidal pyrite shroud confirms the ‘death mask' model for moldic preservation of Ediacaran soft‐bodied organisms. Palaios, 31, 259–274. [Google Scholar]
- Liu, A.G. , McIlroy, D. , Antcliffe, J.B. & Brasier, M.D. (2011). Effaced preservation in the Ediacara biota and its implications for the early macrofossil record. Paleontology, 54, 607–630. [Google Scholar]
- Liu, A.G. , McIlroy, D. , Matthews, J.J. & Brasier, M.D. (2012). A new assemblage of juvenile Ediacaran fronds from the Drook Formation, Newfoundland. J. Geol. Soc., 169, 395–403. [Google Scholar]
- Lotwick, H.W. & Silverman, B.W. (1982). Methods for analysing spatial processes of several types of points. J. R. Stat. Soc. Ser. B (Methodological), 44(3), 406–413. [Google Scholar]
- MacArthur, R.H. (1984). Geographical Ecology: Patterns in the Distribution of Species. Princeton University Press, Princeton, NJ. [Google Scholar]
- Mahdi, A. & Law, R. (1987). On the spatial organization of plant species in a limestone grassland community. J. Ecol., 75, 459–476. [Google Scholar]
- Matthews, J.J. , Liu, A.G. & McIlroy, D. (2017). Post‐fossilization processes and their implications for understanding Ediacaran macrofossil assemblages. Geological Society, London, Special Publications, 448, 251–269. [Google Scholar]
- McFadden, I.R. , Bartlett, M.K. , Wiegand, T. , Turner, B.L. , Sack, L. , Valencia, R. et al (2019). Disentangling the functional trait correlates of spatial aggregation in tropical forest trees. Ecology, 100, e02591. [DOI] [PubMed] [Google Scholar]
- McGill, B.J. (2010). Towards a unification of unified theories of biodiversity. Ecol. Lett., 13, 627–642. [DOI] [PubMed] [Google Scholar]
- McIntire, E.J. & Fajardo, A. (2009). Beyond description: the active and effective way to infer processes from spatial patterns. Ecology, 90, 46–56. [DOI] [PubMed] [Google Scholar]
- McKay, L.J. , MacGregor, B.J. , Biddle, J.F. , Albert, D.B. , Mendlovitz, H.P. , Hoer, D.R. et al (2012). Spatial heterogeneity and underlying geochemistry of phylogenetically diverse orange and white Beggiatoa mats in Guaymas Basin hydrothermal sediments. Deep Sea Res. Part I, 67, 21–31. [Google Scholar]
- Mitchell, E.G. & Butterfield, N.J. (2018). Spatial analyses of Ediacaran communities at Mistaken Point. Paleobiology, 44, 40–57. [Google Scholar]
- Mitchell, E.G. & Kenchington, C.G. (2018). The utility of height for the Ediacaran organisms of Mistaken Point. Nat. Ecol. Evol., 2, 1218–1222. [DOI] [PubMed] [Google Scholar]
- Mitchell, E.G. , Kenchington, C.G. , Liu, A.G. , Matthews, J.J. & Butterfield, N.J. (2015). Reconstructing the reproductive mode of an Ediacaran macro‐organism. Nature, 524, 343–346. [DOI] [PubMed] [Google Scholar]
- Mitchell, E.G. , Kenchington, C.G. , Harris, S. & Wilby, P.R. (2018). Revealing rangeomorph species characters using spatial analyses. Can. J. Earth Sci., 55(11), 1262–1270. [Google Scholar]
- Narbonne, G.M. (2005). The Ediacara biota: neoproterozoic origin of animals and their ecosystems. Annu. Rev. Earth Planet. Sci., 33, 421–442. [Google Scholar]
- Narbonne, G.M. , Laflamme, M. , Greentree, C. & Trusler, P. (2009). Reconstructing a lost world: ediacaran rangeomorphs from Spaniard's Bay. Newfoundland. J. Paleontol., 83(4), 503–523. [Google Scholar]
- Noble, S.R. , Condon, D.J. , Carney, J.N. , Wilby, P.R. , Pharaoh, T.C. & Ford, T.D. (2015). U‐Pb geochronology and global context of the Charnian Supergroup, UK: constraints on the age of key Ediacaran fossil assemblages. GSA Bulletin, 127, 250–265. [Google Scholar]
- Pu, J.P. , Bowring, S.A. , Ramezani, J. , Myrow, P. , Raub, T.D. , Landing, E. et al (2016). Dodging snowballs: Geochronology of the Gaskiers glaciation and the first appearance of the Ediacaran biota. Geology, 44, 955–958. [Google Scholar]
- R Core Team (2013). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. [Google Scholar]
- Ron, R. , Fragman‐Sapir, O. & Kadmon, R. (2018). Dispersal increases ecological selection by increasing effective community size. Proc. Natl Acad. Sci., 115, 11280–11285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosindell, J. , Hubbell, S.P. & Etienne, R.S. (2011). The unified neutral theory of biodiversity and biogeography at age ten. Trends Ecol. Evol., 26, 340–348. [DOI] [PubMed] [Google Scholar]
- Seidler, T.G. & Plotkin, J.B. (2006). Seed dispersal and spatial pattern in tropical trees. PLoS Biol., 4, e344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen, B. , Dong, L. , Xiao, S. & Kowalewski, M. (2008). The Avalon explosion: evolution of Ediacara morphospace . Science, 319, 81–84. [DOI] [PubMed] [Google Scholar]
- Tecchio, S. , Ramírez‐Llodra, E. & Sardà, F. (2011). Biodiversity of deep‐sea demersal megafauna in western and central Mediterranean basins. Sci. Marina, 75(2), 341–350. [Google Scholar]
- Thomas, M. (1949). A generalization of Poisson’s binomial limit for use in ecology. Biometrika, 36, 18–25. [PubMed] [Google Scholar]
- Turkington, R. & Harper, J.L. (1979). The growth, distribution and neighbour relationships of Trifolium repens in a permanent pasture. I ordination, pattern and contact. J. Ecol., 67, 201–218. [Google Scholar]
- Waagepetersen, R. , & Guan, Y. (2009). Two-step estimation for inhomogeneous spatial point processes. J. R. Stat. Soc: Ser. B (Statistical Methodology), 71(3), 685–702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waggoner, B. (2003). The Ediacaran biotas in space and time. Integr. Comp. Biol., 43, 104–113. [DOI] [PubMed] [Google Scholar]
- Wilby, P.R. , Carney, J.N. & Howe, M.P. (2011). A rich Ediacaran assemblage from eastern Avalonia: evidence of early widespread diversity in the deep ocean. Geology, 39(7), 655–658. [Google Scholar]
- Wiegand, T. & Moloney, K. (2004). Rings, circles, and null‐models for point pattern analysis in ecology. Oikos, 104, 209–229. [Google Scholar]
- Wiegand, T. & Moloney, K.A. (2013). Handbook of Spatial Point‐Pattern Analysis in Ecology. CRC Press, Boca Raton, FL. [Google Scholar]
- Wiegand, T. , Moloney, K. , Naves, J. & Knauer, F. (1999). Finding the missing link between landscape structure and population dynamics: a spatially explicit perspective. Am. Nat., 154, 605–627. [DOI] [PubMed] [Google Scholar]
- Wiegand, T. , Kissling, W. , Cipriotti, P. & Aguiar, M. (2006). Extending point pattern analysis for objects of finite size and irregular shape. J. Ecol., 94, 825–837. [Google Scholar]
- Wiegand, T. , Gunatilleke, S. & Gunatilleke, N. (2007a). Species associations in a heterogeneous Sri Lankan dipterocarp forest. Am. Nat., 170, E77–E95. [DOI] [PubMed] [Google Scholar]
- Wiegand, T. , Gunatilleke, S. , Gunatilleke, N. & Okuda, T. (2007b). Analyzing the spatial structure of a Sri Lankan tree species with multiple scales of clustering. Ecology, 88, 3088–3102. [DOI] [PubMed] [Google Scholar]
- Wiegand, T. , Huth, A. & Martínez, I. (2009). Recruitment in tropical tree species: revealing complex spatial patterns. Am. Nat., 174, E106–E140. [DOI] [PubMed] [Google Scholar]
- Wilby, P.R. , Kenchington, C.G. & Wilby, R.L. (2015). Role of low intensity environmental disturbance in structuring the earliest (Ediacaran) macrobenthic tiered communities. Paleogeogr. Paleoclimatol. Paleoecol., 434, 14–27. [Google Scholar]
- Wood, D.A. , Dalrymple, R.W. , Narbonne, G.M. , Gehling, J.G. & Clapham, M.E. (2003). Paleoenvironmental analysis of the late Neoproterozoic Mistaken Point and Trepassey formations, southeastern Newfoundland. Can. J. Earth Sci., 40, 1375–1391. [Google Scholar]
- Wood, R. , Liu, A.G. , Bowyer, F. , Wilby, P.R. , Dunn, F.S. , Kenchington, C.G. et al (2019). Integrated records of environmental change and evolution challenge the Cambrian Explosion. Nat. Ecol. Evol., 3, 528–538. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data supporting the results are archived in Figshare in https://doi.org/10.6084/m9.figshare.9576863. Due to geoconservation concerns, only a subset of data from Bed B will be made publicly available, with the full set available to researchers on request from the corresponding author.


