Abstract
Purpose
Positron emission tomography (PET) is an important tool for nuclear medical imaging. It has been widely used in clinical diagnosis, scientific research, and drug testing. PET is a kind of emission computed tomography. Its basic imaging principle is to use the positron annihilation radiation generated by radionuclide decay to generate gamma photon images. However, in practical applications, due to the low gamma photon counting rate, limited acquisition time, inconsistent detector characteristics, and electronic noise, measured PET projection data often contain considerable noise, which results in ill‐conditioned PET images. Therefore, determining how to obtain high‐quality reconstructed PET images suitable for clinical applications is a valuable research topic. In this context, this paper presents an image reconstruction algorithm based on patch‐based regularization and dictionary learning (DL) called the patch‐DL algorithm. Compared to other algorithms, the proposed algorithm can retain more image details while suppressing noise.
Methods
Expectation‐maximization (EM)‐like image updating, image smoothing, pixel‐by‐pixel image fusion, and DL are the four steps of the proposed reconstruction algorithm. We used a two‐dimensional (2D) brain phantom to evaluate the proposed algorithm by simulating sinograms that contained random Poisson noise. We also quantitatively compared the patch‐DL algorithm with a pixel‐based algorithm, a patch‐based algorithm, and an adaptive dictionary learning (AD) algorithm.
Results
Through computer simulations, we demonstrated the advantages of the patch‐DL method over the pixel‐, patch‐, and AD‐based methods in terms of the tradeoff between noise suppression and detail retention in reconstructed images. Quantitative analysis shows that the proposed method results in a better performance statistically [according to the mean absolute error (MAE), correlation coefficient (CORR), and root mean square error (RMSE)] in considered region of interests (ROI) with two simulated count levels. Additionally, to analyze whether the results among these methods have significant differences, we used one‐way analysis of variance (ANOVA) to calculate the corresponding P values. The results show that most of the P < 0.01; some P> 0.01 < 0.05. Therefore, our method can achieve a better quantitative performance than those of traditional methods.
Conclusions
The results show that the proposed algorithm has the potential to improve the quality of PET image reconstruction. Since the proposed algorithm was validated only with simulated 2D data, it still needs to be further validated with real three‐dimensional data. In the future, we intend to explore GPU parallelization technology to further improve the computational efficiency and shorten the computation time.
Keywords: dictionary learning, image reconstruction, patch regularization, positron emission tomography
1. Introduction
Positron emission tomography (PET) imaging is performed by injecting radioactive tracers into a patient's body and then measuring the distribution of radioisotopes. PET reconstruction algorithms can be divided into two main categories: analytical reconstruction algorithms and iterative reconstruction algorithms. The filtered back‐projection (FBP) method is based on the Radon transform, but it does not consider the spatial and temporal heterogeneity of the system response and does not take into account the measurement noise of the instrument; therefore, the reconstructed images contain considerable noise.1 Maximum‐likelihood expectation‐maximization (ML‐EM) is widely used for statistical reconstruction in clinical practice; however, as the number of iterations increases, the image quality deteriorates, and “checkerboard artifacts” are produced.1, 2 Early iteration termination and the incorporation of penalty terms or some prior knowledge of the likelihood function can help overcome the problems with the ML‐EM method to a certain extent.1 Here, we focus on the latter approach.
Most regularization methods discussed in the PET image reconstruction literature focus on the design of appropriate a priori functions for use in the maximum a posteriori (MAP) framework.2, 3 Many MAP‐based methods benefit from boundary information obtained from magnetic resonance imaging (MRI) and computed tomography (CT). Compared with PET images, CT and MRI images have higher resolutions and signal‐to‐noise ratios (SNRs) and can provide more abundant boundary information.
Patch‐based methods can obtain more image features than pixel‐based methods; consequently, they have been widely used in image denoising, restoration and reconstruction in the last decade.4, 5, 6 Kervrann et al. proposed a novel adaptive patch‐based approach for image denoising and representation.7 Cheng‐Liao and Qi developed a patch‐based regularization method for iterative image reconstruction by using neighborhood patches instead of individual pixels to compute a nonquadratic penalty. This reconstruction approach is also more robust to hyperparameter selection than conventional pixel‐based nonquadratic regularization is Ref. [2].
According to the standard image reconstruction theory applied in medical imaging, to avoid view aliasing artifacts, the sampling rate of the view angles must satisfy the Shannon/Nyquist sampling theorem. However, the Shannon/Nyquist sampling theorem does not assume any a priori image information, whereas in practice, some prior information about the image is typically available.8, 9 Candès et al. introduced a novel sampling theory called compressed sensing, also known as compressive sampling (CS). This theory asserts that one can recover signals and images from far fewer samples or measurements as long as one adheres to two basic principles: sparsity and incoherence or sparsity and restricted isometry.10, 11, 12, 13 The theory of CS asserts that one can combine “low‐rate sampling” with computational power for efficient and accurate signal acquisition. CS data acquisition systems directly translate analog data into a compressed digital form so that one can, at least in principle, obtain superresolved signals from just a few measurements. After the acquisition step, we need only to “decompress’’ the measured data through optimization.14 Recently, CS has become popular in image reconstruction and recovery applications.13, 15 CS is used to reconstruct images using only a small number of observations obtained via projection using prior knowledge of a sparse image representation. For the sparse transformation of images, the discrete cosine transform (DCT), the wavelet transform and the finite difference method are commonly used. When sparse transformation is performed with the finite difference method, the total variation (TV) is used as a metric. Sidky et al. proposed the adaptive‐steepest‐descent‐projection onto convex sets (ASD‐POCS) algorithm, which aims to achieve the constrained minimization of the estimated image TV. The constraints are enforced by means of projection onto convex sets (POCS), and the TV objective is minimized via steepest descent with an adaptive step size.16 Block et al. developed an iterative reconstruction method for undersampled radial MRI. The procedure relies on a two‐step mechanism in which the coil profiles are first estimated and a final image that complies with the actual observations is then rendered. Prior knowledge is introduced by penalizing edges in the coil profiles and by means of a TV constraint for the final image.17 Cone‐beam CT (CBCT) reconstruction is achieved by minimizing the energy function consisting of a data fidelity term and a TV regularization term.18
However, for undersampled and noisy images, the images reconstructed using TV constraints may not include some fine features and may have a blocky appearance. Compared to the discrete gradient transform used in the TV method, dictionary learning (DL) has been proven to be an effective approach for sparse representation.18, 19 In DL, the optimal representation is learned from the data such that the atomic scale and characteristics of the dictionary are as close as possible to those of the image signal that needs to be represented. At present, there are many DL algorithms, most of which are based on the ML and the MAP probability of a Bayesian framework. By acquiring prior information on the image signal, one can select more suitable atoms with which to form an adaptive dictionary. Among methods of this type, the method of optimal directions (MOD),20, 21 the family of iterative least‐squares‐based dictionary learning algorithms (ILS‐DLA),22 the recursive least squares dictionary learning algorithm (RLS‐DLA)23 and the singular value decomposition (K‐SVD) algorithm24 are widely used, and a multiscale version of the K‐SVD algorithm has also been developed.1 Numerous applied experiments have shown that compared to other algorithms, the K‐SVD algorithm yields superior results for various image processing tasks.1, 3, 23, 25 Aharon et al. proposed a novel algorithm for adapting dictionaries to achieve sparse signal representations.26 These authors showed that images can be sparsely represented by learned elements. Therefore, the method of sparse representation can be used to reduce the noise in reconstructed images.
Recently, sparse representation and DL have been applied to medical images, mainly for classification, denoising, and image reconstruction/restoration.15, 27, 28, 29, 30, 31 Valiollahzadeh et al. proposed a method that uses DL in a sparse domain to reconstruct PET images from partially sampled data.15 Tang et al. proposed the use of a DL‐based sparse signal representation in the formulation of the prior information for MAP PET image reconstruction.32 Xu et al. developed a low‐dose x‐ray CT image reconstruction method based on DL, and the results showed that this method can be used to generate images with less noise and more structural detail.20 C. Shuhang et al. developed a reconstruction framework that integrates a sparsity penalty on a dictionary into a ML estimator.1 However, these methods are most effective when the tissue function is uniform and the noise is low.
In this paper, we propose an image reconstruction algorithm based on patch‐based regularization and DL known as patch‐DL method. For the reconstruction of undersampled and noisy images, compared to other methods, the proposed method can preserve more details while removing noise and artifacts. The proposed algorithm has two obvious advantages. First, the degree of coincidence between anatomical structures and functional information has little effect on the reconstructed images. Second, regardless of whether there is noise interference along the edges of an image, this method can accurately distinguish the edges. We used a two‐dimensional (2D) brain phantom to evaluate the proposed algorithm by simulating sinograms that contained random Poisson noise.
This paper is organized as follows. We introduce the background on DL and describe the proposed algorithm in detail in Section 2. The design of the simulation experiments and the evaluation indexes used are presented in Section 3. The performance of the proposed algorithm is demonstrated in Section 4. Discussions on convergence and parameter optimization are presented in Section 5. Conclusions and future work are discussed in Section 6.
2. Materials and Methods
2.A. Problem formulation
2.A.1. Maximum‐likelihood estimation
The measured PET data, also called the sonogram y, can be assumed to be a collection of independent Poisson random variables. The measurement y is related to the unknown image x by a projective transform1:
| (1) |
| (2) |
where P is the system matrix, with pij denoting the probability of the detection of an event originating at pixel j by detector pair i; r accounts for background events, such as random noise and scattering; ni is the total number of detector pairs; and nj is the total number of pixels in the image. Based on the independent Poisson assumption, we can write the likelihood function as2:
| (3) |
In penalized likelihood (PL) reconstruction (or, equivalently, MAP reconstruction), an unknown image is estimated by maximizing a PL function:
| (4) |
where L(y/x) is the likelihood function, is a regularization parameter, and U(x) is an image roughness penalty. When goes to zero, the reconstructed image approaches the ML estimate.
2.A.2. Dictionary learning
Given an image x with dimensions of , suppose that the image is decomposed into many overlapping blocks with dimensions of . Each image patch Rv , w is uniquely indexed by the location of its top‐left corner pixel (v, w) in x. The dictionary is a matrix , and each column is called an atom. Thus, the dictionary contains m rows and s atoms. The number of rows in the dictionary corresponds to the patch size, and the number of atoms is an integer multiple of the number of rows. It is assumed that each patch Rv , w can be approximated by a linear combination of dictionary atoms. Accordingly, is the sparse representation of Rv , w with respect to the dictionary D.
DL is mainly applied to solve the following problem in image reconstruction:
| (5) |
| (6) |
where x is the given image, Rv , w is a patch obtained from x, D is a patch‐based dictionary, is the sparse representation of Rv , w with respect to the dictionary D, T 0 is the level of sparsity and is the reconstruction error threshold. The above equation can be rewritten in the following unconstrained form by the Lagrange method:
| (7) |
where μ denotes the Lagrange multiplier. The value of μ can be obtained by calculating the partial derivative of the objective function for each unknown number.
Next, we will solve the above optimization problems in two steps:
| (8) |
| (9) |
In other words, the algorithm alternates between finding the best dictionary using the K‐SVD algorithm when the coefficients () are fixed [Eq. (8)] and finding the sparse coefficients using the orthogonal matching pursuit (OMP) algorithm when the dictionary (D) is fixed [Eq. (9)].26, 33
Next, we discuss the convergence of the K‐SVD algorithm. Let us first assume that the result of the sparse coding is completely correct. In this case, the sparse coding will reduce the residual norm of the signal reconstruction. Furthermore, since the K‐SVD algorithm does not compute a list of elements in the dictionary, the residual will be further reduced, and the sparse constraints will continue to be maintained. Therefore, the calculation of K‐SVD must reduce the objective function. However, in practice, the current sparse coding methods are all approximate algorithms, which cannot guarantee the results, so K‐SVD cannot always guarantee convergence.26
2.B. Proposed algorithm
In PL reconstruction (or, equivalently, MAP reconstruction), an unknown image is estimated by maximizing a penalized likelihood function:
| (10) |
here, U(x) is a patch‐based roughness function:
| (11) |
| (12) |
where fj(x) and fk(x) are the values of each pixel in the patches centered at pixels j and k, respectively, and Nj is a neighborhood patch centered at pixel j. The Lagrange function is used here as a penalty function and is called the hyperparameter.2
When the penalty function satisfies the following three conditions, a convex PL function can be obtained. In this paper, given in Eq. (11) satisfies the following conditions. Therefore, the patch‐based algorithm is convergent.2
The function is symmetric and differentiable everywhere.
- The first‐order derivative
is nondecreasing (hence, is convex).(13) - The curvature
is nonincreasing for t ≥ 0, and .(14)
We use a surrogate function to solve the above objective function.2, 34 This optimization algorithm can guarantee global convergence. The function needs to satisfy the following two conditions2:
| (15) |
| (16) |
where denotes the gradient with respect to x.
The optimization of the original objective function is now transformed into the optimization of the combined surrogate function. Therefore, the new objective function is
| (17) |
where is a surrogate likelihood function2, 34, 35:
| (18) |
where
| (19) |
| (20) |
where the expected projection in iteration n is:
| (21) |
The surrogate likelihood function must satisfy the following two conditions:
| (22) |
| (23) |
here, is a surrogate penalty function2, 36:
| (24) |
where the pixelwise weights are
| (25) |
and the intermediate image is calculated as
| (26) |
where
| (27) |
| (28) |
Here, jl denotes the lth pixel in the patch fj(x), kl denotes the lth pixel in the patch fk(x), nl is the total number of pixels in a patch, and hl is a positive weighting factor equal to the normalized inverse spatial distance between pixel jl and pixel j.
By solving the quadratic equation derived from the Karush–Kuhn–Tucker (KKT) conditions, we obtain the PL image estimate in iteration (n + 1):
| (29) |
when , the above update equation is equivalent to the ML‐EM formula.
In this paper, we use an adaptive dictionary that is learned from the current estimate xn in each iteration using the K‐SVD algorithm to find the sparse coefficients using the OMP algorithm. The overall iteration scheme stops when the maximum number of iterations is reached. The algorithm is summarized in Algorithm 1.

3. Experiments and Evaluation
To study the proposed patch‐DL algorithm and evaluate its performance, we simulated a PET emission image. We compared the images reconstructed with various reconstruction algorithms through visual judgment and quantitative comparisons.
Figure 1(a) shows the 2D brain phantom that was used to simulate the PET emission image, and Fig. 1(b) shows the real CT image that was used to generate the attenuation factors. The activity phantom was forward‐projected to generate a noise‐free sinogram. In the simulations, independent Poisson noise was introduced to generate 20 realizations for a total number of events of 20 M (2e 7) and 10 M (1e 7), conforming to clinical use. A uniform background of 20% was added to simulate random noise and the scatter fraction in 2D.
Figure 1.
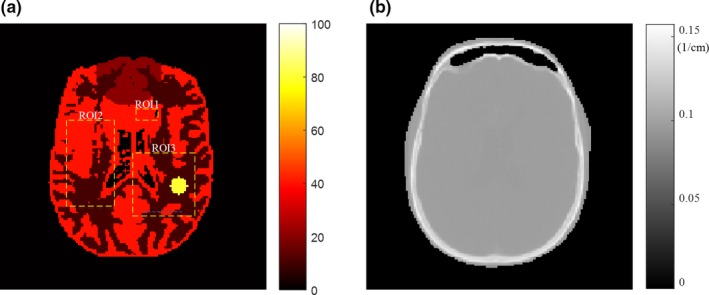
(a) Simulated positron emission tomography emission image and (b) attenuation map from a real computed tomography image. [Color figure can be viewed at http://wileyonlinelibrary.com]
The proposed patch‐DL algorithm has several parameters that need to be set: the regularization parameter was set to , and the hyperparameter value was set to . Both the patch size and the neighborhood size were set to 3 × 3 pixels. For DL, the patch size was set to 6 × 6 pixels, and the overlap stride was one pixel. The sparsity level T0 was set to 5. The local reconstruction error threshold was set to 0.00025. In general, the algorithm parameters followed the settings of Refs. [1, 2, 9, 15] with the best performance.
Several metrics were utilized in this paper for quantitative analysis of the reconstructed images.
The MAE and RMSE can be calculated as follows:
| (30) |
| (31) |
where xz and are the pixel values in the reconstructed image and the original image, respectively; Z is the total number of pixels in the reconstructed image; and q is the number of noise realizations.
The quality of the image reconstruction can also be measured in terms of the normalized mean square error (NMSE) and CORR, which can be calculated as
| (32) |
| (33) |
where xz, , t, q and Z have the same definitions as in (30) and (31); and are the mean values for the reconstructed image and the original image, respectively; and e is the number of regions of interest (ROIs).
To make the calculation more accurate, we calculated the standard deviation. The standard deviation (SD) can be calculated as follows:
| (34) |
where t and q have the same definitions as in (30) and (31); valuet represents the value of the tth noise realization of MAE, RMSE, NMSE, and CORR; and represents the average value of the q noise realization of MAE, RMSE, NMSE, and CORR.
In addition, the absolute difference between the reconstructed image and the ground truth image [Fig. 1(a)] is presented for visual judgment. The proposed patch‐DL methods were compared with the pixel‐based algorithm, patch‐based algorithm and adaptive dictionary learning (AD) algorithm. The AD algorithm was developed by Shuhang et al.1
4. Results
To evaluate the performance of the proposed patch‐DL method, several algorithms, including a pixel‐based algorithm, a patch‐based algorithm and an AD algorithm, were chosen for comparative experiments on a simulated PET emission image. To further optimize the pixel‐based algorithm and patch‐based algorithm, we added a post‐reconstruction smoothing operation (Gaussian filtering). We also optimized the AD algorithm to the optimal result. The optimal reconstruction results are obtained by adjusting the parameters, as shown in Fig. 2. The 2D brain phantom, as indicated in Fig. 1(a), has three ROIs.
Figure 2.
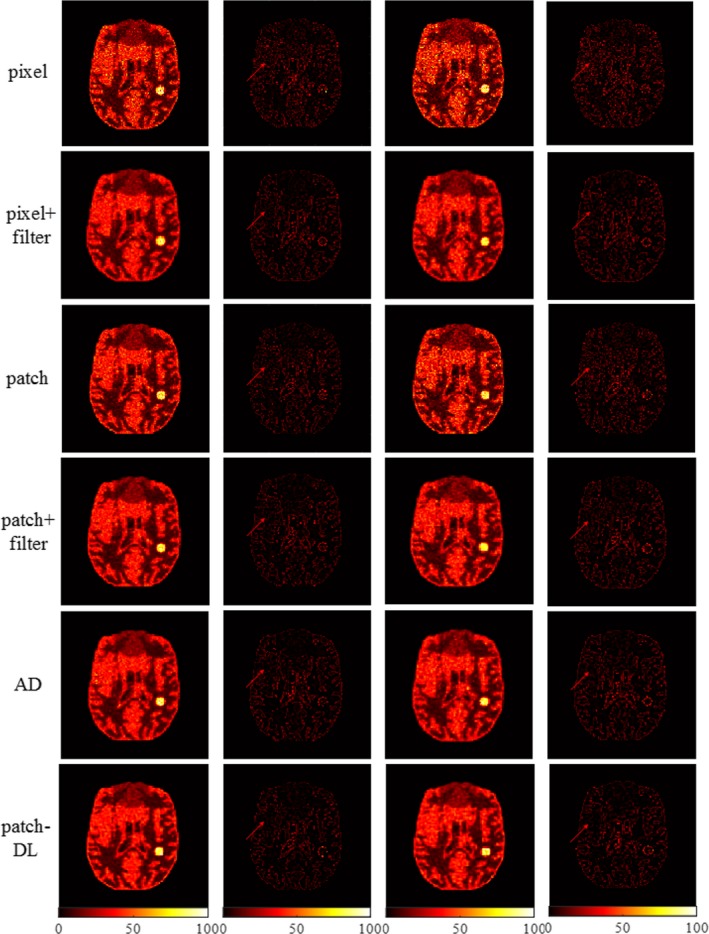
Reconstructed images of the two‐dimensional brain phantom using different algorithms. The two columns on the left correspond to the reconstructed images and subtraction images under one noise realization and the 2e 7 count level, and the two columns on the right correspond to the reconstructed images and subtraction images under one noise realization and the 1e 7 count level. [Color figure can be viewed at http://wileyonlinelibrary.com]
Figure 2 demonstrates the reconstruction results for the 2D brain phantom data under one noise realization. In Fig. 2, the first and third rows show the images reconstructed using the pixel‐based Lagrange regularization algorithm37, 38 and the patch‐based Lagrange regularization algorithm, respectively. The second and fourth rows show the images reconstructed using the pixel‐based algorithm plus a post‐reconstruction smoothing operation and the patch‐based algorithm plus a post‐reconstruction smoothing operation, respectively. Comparing the optimized reconstructed image with the unoptimized reconstructed image shows that the quality of the optimized reconstructed image is improved overall. The edges of the images and the tumor are preserved in the reconstructions. However, the reconstructed image still contains a large amount of noise, and the tumor region contains some residual artifacts. The fifth row shows the image reconstructed using the AD algorithm1; some artifacts and noise are still present. The sixth row shows the image reconstructed using the proposed method. By encouraging sparsity, the patch‐DL method can considerably suppress noise while preserving image detail, and the edges of the tumor are also well recovered. Figure 2 (the second and fourth columns) presents the corresponding subtraction images. The first row to the fifth row show that there are some differences between the images reconstructed by the pixel‐, patch‐, and AD‐based methods and the original phantom image. By contrast, the sixth row shows that there is little difference between the patch‐DL‐reconstructed image and the original phantom image. To further compare the performance of the pixel‐, pixel + filter‐, patch‐, patch + filter‐, AD‐based, and proposed methods, zoomed‐in views of the local ROIs marked with yellow squares in Fig. 1(a) are shown in Fig. 3. The results show that the patch‐DL method can suppress image noise more effectively while preserving subtle structures. At the same time, the results show that the image reconstructed with the patch‐DL method is closer to the reference image.
Figure 3.
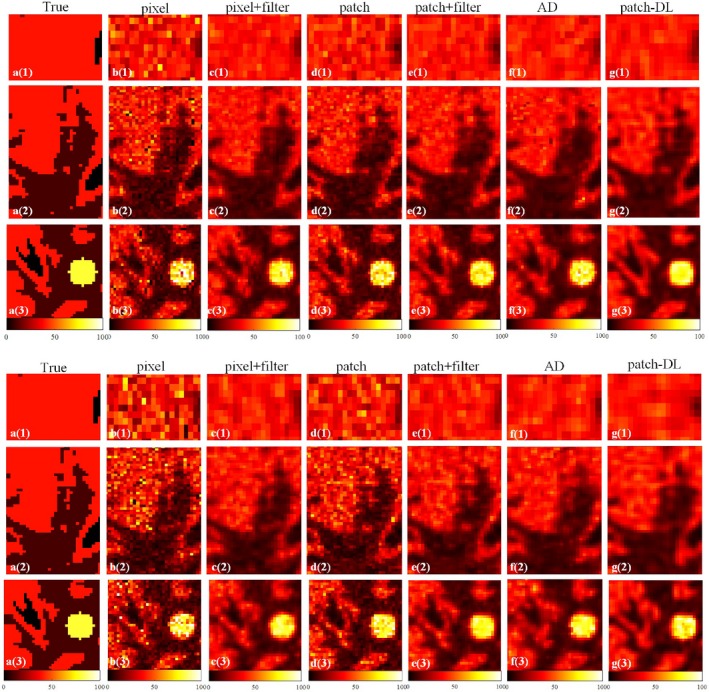
Zoomed‐in views of the ROIs marked with yellow squares in Fig. 1. (a). The zoomed‐in images in the first column were cropped from Fig. 1(a). The zoomed‐in images (b)–(g) in the first three rows were cropped from those in the first column (2e 7 count level) in Fig. 2, and the zoomed‐in images (b)–(g) in the last three rows were cropped from those in the third column (1e 7 count level) in Fig. 2. [Color figure can be viewed at http://wileyonlinelibrary.com]
Tables 1 and 2 show the MAE, CORR, and RMSE values of the whole image and the three ROIs (marked with yellow squares in Fig. 1 (a)) for the images processed with the pixel‐, pixel + filter‐, patch‐, patch + filter‐, AD‐based, and patch‐DL methods. Among these methods, the patch‐DL method has the highest CORR and the lowest MAE and RMSE. It is well known that a higher CORR value and lower MAE and RMSE values indicate a higher quality reconstructed image. Therefore, Tables 1 and 2 confirm that the proposed method results in a better MAE, CORR, and RMSE performance in each ROI under both count levels. At the same time, to analyze whether the results in Tables 1 and 2 have significant differences among the different methods, we used one‐way analysis of variance (ANOVA) to calculate P values. Five comparison algorithms are given in our paper. We calculated the P values by ANOVA between the five comparison algorithms and the proposed patch‐DL algorithm. The results show that all P < 0.05. Therefore, to simplify, only the P values between the AD and patch‐DL algorithms are given in the table because the performance of the AD algorithm is the best among the five comparison algorithms. From the results, we know that most of the P < 0.01; some P > 0.01 < 0.05. When a P < 0.01, there is a very significant difference; when a P value is between 0.01 and 0.05, there is a significant difference. Therefore, our method can achieve a better quantitative performance than those of the traditional methods.
Table 1.
Statistical analysis of the reconstructed two‐dimensional brain phantom with the 2e 7 count level and 20 noise realizations.
| Whole | ROI 1 | ROI 2 | ROI 3 | |
|---|---|---|---|---|
| MAE | ||||
| Pixel | 5.7059 ± 0.0449 | 8.3931 ± 0.6415 | 6.9348 ± 0.1660 | 7.3641 ± 0.1989 |
| Pixel + filter | 4.8590 ± 0.0349 | 4.7517 ± 0.2398 | 5.3207 ± 0.0877 | 6.2350 ± 0.0940 |
| Patch | 4.7213 ± 0.0365 | 5.7831 ± 0.2989 | 5.5695 ± 0.1070 | 6.0904 ± 0.1195 |
| Patch + filter | 4.5758 ± 0.0230 | 4.5750 ± 0.1807 | 5.0902 ± 0.0639 | 5.9397 ± 0.0787 |
| AD | 4.4745 ± 0.0495 | 5.1743 ± 0.8326 | 5.0584 ± 0.1535 | 5.7824 ± 0.1685 |
| Patch‐DL | 4.3283 ± 0.0333 | 3.8760 ± 0.1928 | 4.8036 ± 0.0504 | 5.5881 ± 0.1121 |
| P value (patch‐DL vs AD) | <0.01 | <0.01 | <0.01 | <0.01 |
| CORR | ||||
| Pixel | 0.8771 ± 0.0024 | 0.3587 ± 0.0288 | 0.8905 ± 0.0096 | 0.8624 ± 0.0101 |
| Pixel + filter | 0.9137 ± 8.5902e‐04 | 0.5499 ± 0.0343 | 0.8818 ± 0.0035 | 0.9051 ± 0.0026 |
| Patch | 0.9180 ± 0.0011 | 0.5430 ± 0.0278 | 0.8760 ± 0.0040 | 0.9108 ± 0.0031 |
| Patch + filter | 0.9234 ± 5.6424e‐04 | 0.5957 ± 0.0254 | 0.8933 ± 0.0028 | 0.9163 ± 0.0017 |
| AD | 0.9211 ± 0.0019 | 0.5399 ± 0.0625 | 0.8869 ± 0.0075 | 0.9099 ± 0.0062 |
| Patch‐DL | 0.9262 ± 8.1519e‐04 | 0.6647 ± 0.0269 | 0.8989 ± 0.0020 | 0.9184 ± 0.0024 |
| P value (patch‐DL vs AD) | <0.01 | <0.01 | <0.01 | <0.01 |
| RMSE | ||||
| Pixel | 8.4625 ± 0.0883 | 10.9409 ± 0.7150 | 9.3839 ± 0.2651 | 10.4620 ± 0.4015 |
| Pixel + filter | 7.1074 ± 0.0332 | 6.5841 ± 0.2558 | 7.2368 ± 0.0978 | 8.7842 ± 0.1059 |
| Patch | 6.8801 ± 0.0432 | 7.3881 ± 0.3222 | 7.3992 ± 0.1168 | 8.4226 ± 0.1366 |
| Patch + filter | 6.7115 ± 0.0231 | 6.2350 ± 0.1842 | 6.9040 ± 0.0813 | 8.2760 ± 0.0758 |
| AD | 6.7541 ± 0.0772 | 7.3017 ± 1.0949 | 7.0761 ± 0.2260 | 8.4625 ± 0.2855 |
| Patch‐DL | 6.5836 ± 0.0345 | 5.5962 ± 0.1987 | 6.7406 ± 0.0565 | 8.1558 ± 0.1020 |
| P value (patch‐DL vs AD) | <0.01 | <0.01 | <0.01 | <0.01 |
Table 2.
Statistical analysis of the reconstructed two‐dimensional brain phantom with the 1e 7 count level and 20 noise realizations.
| Whole | ROI 1 | ROI 2 | ROI3 | |
|---|---|---|---|---|
| MAE | ||||
| Pixel | 6.5879 ± 0.0666 | 10.0655 ± 0.4699 | 8.0939 ± 0.1515 | 8.3682 ± 0.2000 |
| Pixel + filter | 5.3071 ± 0.0416 | 5.8211 ± 0.3516 | 6.0035 ± 0.1226 | 6.7635 ± 0.1538 |
| Patch | 5.6771 ± 0.0479 | 7.9392 ± 0.3491 | 6.8066 ± 0.1202 | 7.1509 ± 0.1446 |
| Patch + filter | 5.1812 ± 0.0254 | 5.9834 ± 0.4583 | 5.9141 ± 0.1140 | 6.6174 ± 0.1339 |
| AD | 5.1189 ± 0.0401 | 5.3851 ± 0.8024 | 5.6096 ± 0.2895 | 6.6777 ± 0.2898 |
| Patch‐DL | 4.8585 ± 0.0322 | 5.0618 ± 0.3798 | 5.5494 ± 0.1014 | 6.3046 ± 0.163 |
| P value (patch‐DL vs AD) | <0.01 | 0.012 | 0.039 | <0.01 |
| CORR | ||||
| Pixel | 0.8417 ± 0.0030 | 0.3132 ± 0.0280 | 0.7583 ± 0.0072 | 0.8295 ± 0.0102 |
| Pixel + filter | 0.8987 ± 0.0015 | 0.4616 ± 0.0473 | 0.8544 ± 0.0052 | 0.8907 ± 0.0050 |
| Patch | 0.8832 ± 0.0019 | 0.4009 ± 0.0303 | 0.8212 ± 0.0057 | 0.8780 ± 0.0052 |
| Patch + filter | 0.9034 ± 9.3789e‐04 | 0.4832 ± 0.0493 | 0.8601 ± 0.0044 | 0.8948 ± 0.0046 |
| AD | 0.8986 ± 0.0028 | 0.4956 ± 0.0764 | 0.8628 ± 0.0107 | 0.8795 ± 0.0145 |
| Patch‐DL | 0.9110 ± 0.0011 | 0.5599 ± 0.0429 | 0.8725 ± 0.0047 | 0.8997 ± 0.0045 |
| P value (patch‐DL vs AD) | <0.01 | <0.01 | <0.01 | <0.01 |
| RMSE | ||||
| Pixel | 9.7647 ± 0.1091 | 13.0997 ± 0.5814 | 10.9506 ± 0.1934 | 11.8082 ± 0.4140 |
| Pixel + filter | 7.6190 ± 0.0511 | 7.7020 ± 0.3856 | 7.9594 ± 0.1331 | 9.3125 ± 0.1839 |
| Patch | 8.2298 ± 0.071 | 9.9147 ± 0.3798 | 9.0197 ± 0.1636 | 9.8332 ± 0.2088 |
| Patch + filter | 7.4423 ± 0.0343 | 7.7446 ± 0.4965 | 7.8198 ± 0.1153 | 9.1242 ± 0.1853 |
| AD | 7.6125 ± 0.0986 | 7.8617 ± 1.2873 | 7.7440 ± 0.2843 | 9.7183 ± 0.5794 |
| Patch‐DL | 7.1589 ± 0.0425 | 6.7084 ± 0.3901 | 7.4811 ± 0.1279 | 8.9203 ± 0.1823 |
| P value (patch‐DL vs AD) < 0.01 | <0.01 | <0.01 | <0.01 | |
For this simulation study, the CORR values are plotted vs the NMSE values in Fig. 4 for various numbers of iterations of the pixel‐, pixel + filter‐, patch‐, patch + filter‐, AD‐based, and patch‐DL algorithms. Figure 4 provides further evidence that the proposed method offers a better performance than those of the other methods. Moreover, the corresponding intensity profiles along the horizontal line (blue) through the tumor that is indicated in Fig. 1(a) are shown in Fig. 5. The profile obtained with the proposed patch‐DL algorithm best matches that of the original phantom.
Figure 4.
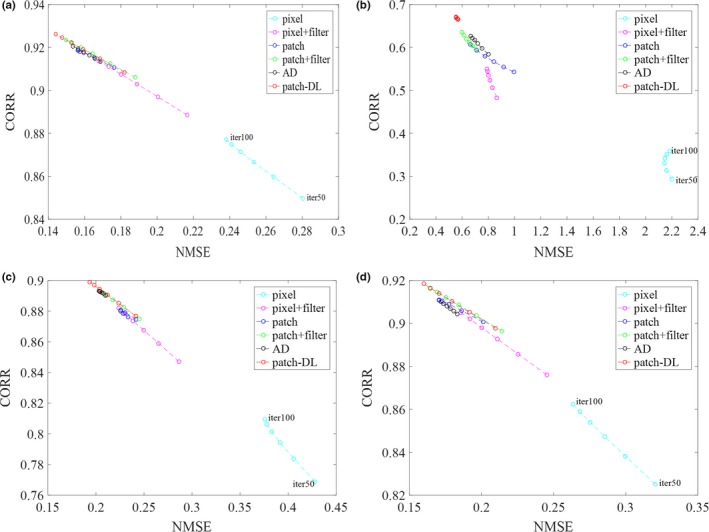
Correlation coefficient (CORR) and normalized mean square error (NMSE) plots comparing the proposed patch‐DL method with the pixel‐, pixel + filter‐, patch‐, patch + filter, and adaptive dictionary learning (AD)‐based methods based on the CORR and NMSE values for the whole image and three region of interests (ROIs) [marked with yellow squares in Fig. 1(a)] with the 2e 7 count level and 20 noise realizations. Values calculated for (a) the whole image, (b) ROI 1, (c) ROI 2, and (d) ROI 3. [Color figure can be viewed at http://wileyonlinelibrary.com]
Figure 5.
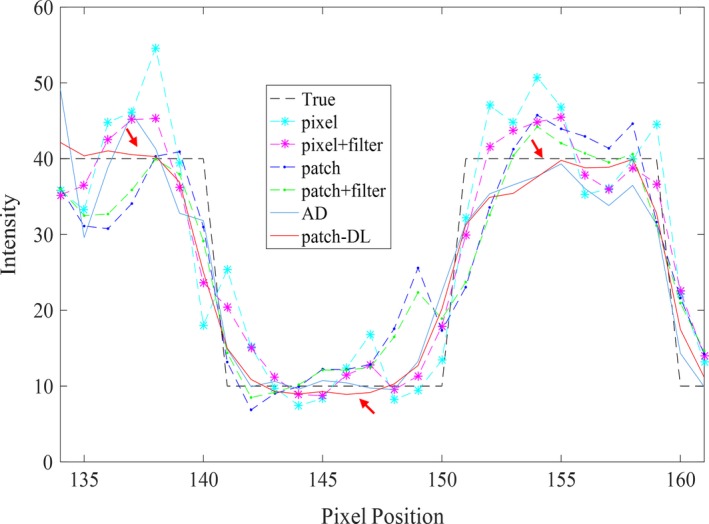
Intensity profiles along the horizontal line (blue) through the tumor indicated in Fig. 1(a) with the 2e 7 count level. [Color figure can be viewed at http://wileyonlinelibrary.com]
5. Discussion
5.A. The convergence of the algorithm
We analyze the convergence of the proposed patch‐DL algorithm in this section. We analyze whether the patch‐based regularization and DL methods converge in theory. Because our proposed algorithm uses a combination of patch‐based regularization and DL, we analyze the convergence of the patch‐based regularization and DL algorithms. First, the patch‐based regularization algorithm has proven to be convergent in the other literature.2 As discussed in part 2.B, the penalty functions used to achieve convergence need to satisfy three conditions: (a) The function is symmetric and differentiable everywhere. (b) The function has a first‐order derivative that is nondecreasing (hence, is convex). 3) The function curvature is nonincreasing for t ≥ 0, and . The patch‐based penalty given in Eq. (11) is convex for any that satisfies the above three conditions. Therefore, the patch‐based algorithm is convergent.2
Second, the DL algorithm has also been proven to be convergent in the literature.1, 15 With respect to the convergence of the DL algorithm, optimization techniques and Bayesian techniques are two general classes of DL from an algorithmic point of view. With respect to the optimization techniques, a dictionary is found by optimizing an objective function that includes parameters such as the patch size, dictionary size, sliding distance and sparsity level. The Bayesian techniques use a simulative statistical model to represent the data, and all the parameters of this model can be directly inferred from the data. In general, optimization techniques have several parameters that need to be justified, but such techniques can converge more quickly. In contrast, Bayesian techniques do not have any predetermined parameters but converge more slowly.15 In this paper, the proposed DL algorithm is an optimization technique, and we chose the adaptive DL method. Once the dictionary is learned, it is applied to reconstruct the noisy sinogram data; the dictionary is adaptively updated based on patches that are derived from the updated reconstructed image, and the process continues until convergence.
Through the above analysis, we know that the patch‐based regularization algorithm and DL algorithm are convergent in theory, but this does not guarantee that the patch‐DL algorithm is also convergent. It is difficult to prove the convergence of patch‐DL in mathematics, so we did not provide proof of the convergence of patch‐DL. However, to monitor the convergence of the proposed patch‐DL method, we performed many experiments. All the experimental results show that the patch‐DL algorithm is convergent. A representative result is given in this paper, as shown in Fig. 6. Figure 6 shows the RMSE value vs iteration number. This curve is obtained by the patch‐DL algorithm (2e 7 count level) in Fig. 2. From Fig. 6, we can see that after ~100 iterations, the RMSE changed little with further iterations, and at ~200 iterations, the algorithm reached convergence. Therefore, the patch‐DL algorithm proposed in this paper is convergent.
Figure 6.
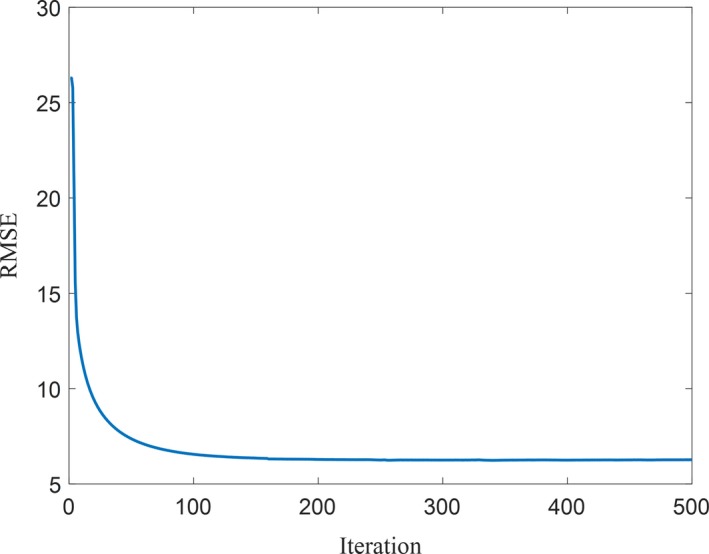
Root mean square error value vs iteration number for the patch‐DL algorithm (2e 7 count level) in Fig. 2. [Color figure can be viewed at http://wileyonlinelibrary.com]
5.B. Parameter optimization
In this section, we mainly studied the parameter optimization of the proposed patch‐DL algorithm. We discussed parameter selection and optimization based on patch‐based regularization and DL, respectively. For patch‐based regularization, there are four parameters in the presented algorithm that need to be manually tuned. The first parameter is , a regularization parameter in Eq. (4). is used to balance the prior information terms and data fidelity. It depends on the noise level, and it should be increased when the noise level increases, and vice versa. Therefore, choosing an optimal value is an interesting problem. Generally, it is difficult to find simple methods to determine an appropriate value for , and it is usually empirically selected in practice.39 In all of our experiments, we empirically found that it provided the best reconstructed images near 2−7. The second parameter is , the hyperparameter in Eq. (12). The experimental results show that the optimal range of is . When is , it has little effect on the quality of the reconstructed images, so in all our experiments, we chose a value of of . The third one is the patch size in Eq. (28), and the fourth one is the neighborhood size in Eq. (11). A smaller patch and neighborhood can lead to a slower computation, and vice versa. In addition, large patches may not be able to identify small image features and thus cannot preserve the corresponding edges. For our experiments, we selected different patch sizes of 1 × 1, 3 × 3, 5 × 5, and 7 × 7, and found that there was little difference in the computation and image quality performance among the patch sizes except for those of 1 × 1. We also selected different neighborhood sizes of 3 × 3, 5 × 5, 7 × 7, 9 × 9, 11 × 11, and 13 × 13, and found that a neighborhood size of 3 × 3 provided the best performance. Therefore, in our experiments, we set both the patch size and the neighborhood size to 3 × 3 pixels.
For DL, there are also four parameters in the presented algorithm that need to be manually tuned. To examine the robustness of the four tuning parameters within the range, we calculate the relative RMSE based on different choices of m, T 0, and r, and the results are shown in Fig. 7. Our results show that the proposed method is robust to the investigated parameters. The first parameter is m, the patch size in DL. Both adaptive and global dictionaries are trained from the extracted image patches by the K‐SVD algorithm. A large element size may not be able to identify small image features, while more computational time would be needed if we choose a small size. In the literature, the size of the dictionary element ranges from 2 × 2 to 10 × 10, which has the best performance.9, 15 Considering the options comprehensively, in our experiments, we set the patch size to 6 × 6, and the size of the dictionary was 36 × 1152. Thus, the number of rows in the dictionary corresponded to the patch size, and the number of columns was 32 times larger than the number of rows. The second parameter is T 0, the sparsity level in Eq. (5). The sparsity level is the number of atoms involved in representing a patch, which is empirically determined according to the complexity of the image to be reconstructed and the properties of the dictionary. In the literature, the sparsity level is selected as 5–10 atoms20 to achieve the best performance. Considering the options comprehensively, in our experiments, we set the sparsity level to 5. The third parameter is , the reconstruction error threshold in Eq. (6). The reconstruction error threshold represents the tolerance of the difference between the original and reconstructed images. This value is related to the property of the dictionary and noise level. In the literature, the value of the reconstruction error threshold is generally less than 1, and in all our experiments, we found that when the reconstruction error threshold is 0.00025, the best performance is achieved. The fourth parameter is r, the patch overlap stride. The larger the overlap stride is, the faster the speed, but some details may be missed. In all our experiments, we analyzed the results of varying the overlap stride in the range of 1 to 5. Considering the options comprehensively, in our experiments, we set the patch overlap stride to one pixel. Based on the above discussion, we summarized the selection of the parameters in Table 3.
Figure 7.
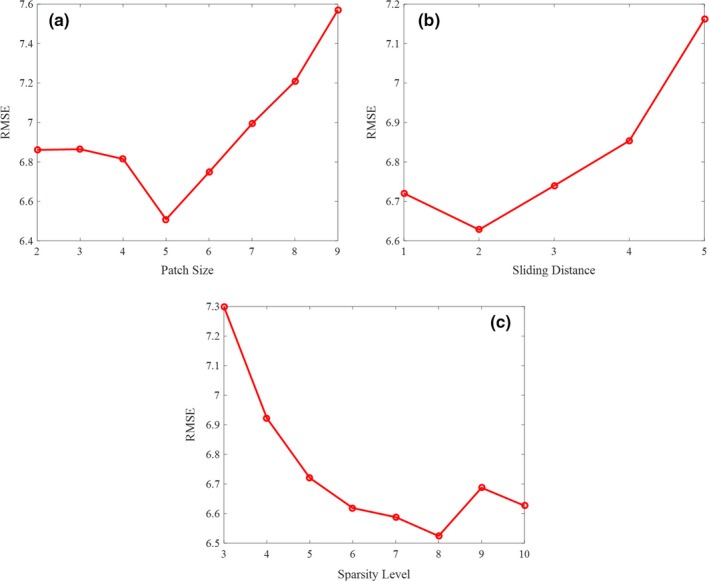
Parameter evaluations with 2e 7 count level. (a) root mean square error (RMSE) vs patch size. (b) RMSE vs sliding distance. (c) RMSE vs sparsity level. [Color figure can be viewed at http://wileyonlinelibrary.com]
Table 3.
Summary of the parameter selection guidelines.
| No. | Variable | Meaning | Criterion/range | |
|---|---|---|---|---|
|
|
Parameter to balance the prior information terms and data fidelity | It is related to the noise level and is usually empirically selected in practice | ||
| 2 |
|
Hyperparameter in Eq. (12) | The experimental results show that the optimal range of is | |
| 3 | Nj | Neighborhood size in Eq. (11) | It is selected as 3 × 3 in the image processing field and has the best performance in our study | |
| 4 | nl | Total number of pixels in a patch | The experimental results show that the optimal range of nl is 3 × 3–7 × 7 | |
| 5 | m | Patch size in dictionary learning | The experimental results show that the optimal range of m is 2 × 2–10 × 10 | |
| 6 | T0 | Sparsity level in Eq. (5) | The experimental results show that the optimal range of T 0 is 5–10 atoms | |
| 7 |
|
Tolerance of the difference between the original and reconstructed images | This value is related to property of the noise level and is generally less than 1 | |
| 8 | Patch overlap stride | In our experiments, we set the patch overlap stride to one pixel, which results in the best performance |
6. Conclusions
We have proposed a framework for PET image reconstruction based on patch‐based regularization and DL. This framework has been validated by computer simulations. The simulation results show that the proposed patch‐DL method outperforms the pixel‐, pixel + filter‐, patch‐, AD‐, and patch + filter‐based methods.
Traditional CS reconstruction techniques usually rely on TV regularization. Because of the piecewise constant image model, massive blocky regions are produced in the results obtained in practical applications. In contrast, the purpose of DL is to learn local patches and structural image patches while suppressing noise, leading to a reduction in artifacts. In addition, DL adapts to the acquired data, thus providing a sparse representation and better restoration quality. As to whether the algorithm converges, usually, the number of iterations required for the algorithm to converge depends on the complexity of the image and noise. In this paper, our experiments show that our proposed algorithm is convergent. To make the comparison more meaningful, we optimize the parameters of our algorithm separately. We refer to the literature and to our own experimental data to conduct a considerable experimental analysis and comparison and finally summarize the optimal parameters suitable for our data and algorithm. The experimental results show that the proposed method is robust to some investigated parameters.
Regarding the computation, because of the time consumed for sparse coding, patch extraction, and DL, the patch‐DL method takes longer to run than the pixel‐ and patch‐based methods. We can further improve the computing speed and reduce the reconstruction time by optimizing the DL algorithm and by implementing the algorithm in C++ and with GPUs.
However, due to the low SNR nature of PET measurements, controlling this tradeoff between noise and image details has proven to be technically difficult. Therefore, it has been verified that the proposed method has outperformed other algorithms, but it cannot be guaranteed that every detail in the reconstructed image outperforms that provided by other algorithms. Because the proposed algorithm was validated with only simulated 2D data, it still needs to be validated with real three‐dimensional data. In the future, we intend to explore GPU parallelization technology to further improve the computational efficiency and shorten the computing time. We conclude that the patch‐DL algorithm has the potential to improve quantitative PET imaging.
Acknowledgments
The authors thank the editor and anonymous reviewers for their constructive comments and suggestions. This work was supported by the National Natural Science Foundation of China (81871441), the Guangdong International Science and Technology Cooperation Project of China (2018A050506064), the Natural Science Foundation of Guangdong Province in China (2017A030313743) and the Guangdong Special Support Program (2017TQ04R395) of China. The authors thank Prof. Guobao Wang and Prof. Jinyi Qi at the University of California (Davis) for providing us with some program code.
References
- 1. Shuhang C, Huafeng L, Pengcheng S, Yunmei C. Sparse representation and dictionary learning penalized image reconstruction for positron emission tomography. Phys Med Biol. 2015;60:807–823. [DOI] [PubMed] [Google Scholar]
- 2. Wang G, Qi J. Penalized likelihood PET image reconstruction using patch‐based edge‐preserving regularization. IEEE Trans Med Imaging. 2012;31:2194–2204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Cheng‐Liao J, Qi J. PET image reconstruction with anatomical edge guided level set prior. Phys Med Biol. 2011;56:6899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Tahaei MS, Reader AJ. Patch‐based image reconstruction for PET using prior‐image derived dictionaries. Phys Med Biol. 2016;61:6833. [DOI] [PubMed] [Google Scholar]
- 5. Gilboa G, Osher S. Nonlocal linear image regularization and supervised segmentation. Multiscale Model Simul. 2007;6:595–630. [Google Scholar]
- 6. Kindermann S, Osher S, Jones PW. Deblurring and denoising of images by nonlocal functionals. Multiscale Model Simul. 2005;4:1091–1115. [Google Scholar]
- 7. Kervrann C, Boulanger J. Optimal spatial adaptation for patch‐based image denoising. IEEE Trans Image Process. 2006;15:2866–2878. [DOI] [PubMed] [Google Scholar]
- 8. Chen G‐H, Tang J, Leng S. Presented at the Photons Plus Ultrasound: Imaging and Sensing 2008: The Ninth Conference on Biomedical Thermoacoustics, Optoacoustics, and Acousto‐optics2008 (unpublished).
- 9. Hu Z, Liang D, Xia D, Zheng H. Compressive sampling in computed tomography: method and application. Nucl Instrum Methods Phys Res, Sect A. 2014;748:26–32. [Google Scholar]
- 10. Candès EJ, Romberg J, Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information. IEEE Trans Inf Theory. 2006;52:489–509. [Google Scholar]
- 11. Candes EJ, Romberg J. Quantitative robust uncertainty principles and optimally sparse decompositions. Found Comput Math. 2006;6:227–254. [Google Scholar]
- 12. Donoho DL. Compressed sensing. IEEE Trans Inf Theory. 2006;52:1289–1306. [Google Scholar]
- 13. Candes EJ, Tao T. Near‐optimal signal recovery from random projections: universal encoding strategies? IEEE Trans Inf Theory. 2006;52:5406–5425. [Google Scholar]
- 14. Baraniuk RG, Candes E, Nowak R, Vetterli M. Compressive sampling [from the guest editors]. Signal Processing Magazine IEEE. 2008;25:12–13. [Google Scholar]
- 15. Valiollahzadeh S, Clark JW Jr, Mawlawi O. Dictionary learning for data recovery in positron emission tomography. Phys Med Biol. 2015;60:5853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Sidky EY, Pan X. Image reconstruction in circular cone‐beam computed tomography by constrained, total‐variation minimization. Phys Med Biol. 2008;53:4777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Block KT, Uecker M, Frahm J. Undersampled radial MRI with multiple coils. Iterative image reconstruction using a total variation constraint. Magn Reson Med. 2007;57:1086–1098. [DOI] [PubMed] [Google Scholar]
- 18. Jia X, Lou Y, Li R, Song WY, Jiang SB. GPU‐based fast cone beam CT reconstruction from undersampled and noisy projection data via total variation. Med Phys. 2010;37:1757–1760. [DOI] [PubMed] [Google Scholar]
- 19. Chen Y, Shi L, Feng Q, et al. Artifact suppressed dictionary learning for low‐dose CT image processing. IEEE Trans Med Imaging. 2014;33:2271–2292. [DOI] [PubMed] [Google Scholar]
- 20. Xu Q, Yu H, Mou X, Zhang L, Hsieh J, Wang G. Low‐dose X‐ray CT reconstruction via dictionary learning. IEEE Trans Med Imaging. 2012;31:1682–1697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Elad M, Aharon M. Image denoising via sparse and redundant representations over learned dictionaries. IEEE Trans Image Process. 2006;15:3736–3745. [DOI] [PubMed] [Google Scholar]
- 22. Engan K, Aase SO, Husøy JH. Multi‐frame compression: theory and design. Sign Process. 2000;80:2121–2140. [Google Scholar]
- 23. Engan K, Skretting K, Husøy JH. Family of iterative LS‐based dictionary learning algorithms, ILS‐DLA, for sparse signal representation. Dig Sign Process. 2007;17:32–49. [Google Scholar]
- 24. Skretting K, Engan K. Recursive least squares dictionary learning algorithm. IEEE Trans Sign Process. 2010;58:2121–2130. [Google Scholar]
- 25. Bao C, Ji H, Quan Y, Shen Z. Dictionary learning for sparse coding: algorithms and convergence analysis. IEEE Trans Pattern Anal Mach Intell. 2016;38:1356–1369. [DOI] [PubMed] [Google Scholar]
- 26. Aharon M, Elad M, Bruckstein A. K‐SVD: an algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans Sign Process. 2006;54:4311. [Google Scholar]
- 27. Yang M, Zhang L, Feng X, Zhang D. Sparse representation based fisher discrimination dictionary learning for image classification. Int J Comput Vision. 2014;109:209–232. [Google Scholar]
- 28. Chen Y, Nasrabadi NM, Tran TD. Hyperspectral image classification using dictionary‐based sparse representation. IEEE Trans Geosci Remote Sens. 2011;49:3973–3985. [Google Scholar]
- 29. Li S, Yin H, Fang L. Group‐sparse representation with dictionary learning for medical image denoising and fusion. IEEE Trans Biomed Eng. 2012;59:3450–3459. [DOI] [PubMed] [Google Scholar]
- 30. Ravishankar S, Bresler Y. MR image reconstruction from highly undersampled k‐space data by dictionary learning. IEEE Trans Med Imaging. 2011;30:1028. [DOI] [PubMed] [Google Scholar]
- 31. Li T, Jiang C, Gao J, et al. Low‐count PET image restoration using sparse representation. Nucl Instrum Methods Phys Res, Sect A. 2018;888:222–227. [Google Scholar]
- 32. Tang J, Yang B, Wang Y, Ying L. Sparsity‐constrained PET image reconstruction with learned dictionaries. Phys Med Biol. 2016;61:6347. [DOI] [PubMed] [Google Scholar]
- 33. Tropp JA, Gilbert AC. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans Inf Theory. 2007;53:4655–4666. [Google Scholar]
- 34. Lange K, Hunter DR, Yang I. Optimization transfer using surrogate objective functions. J Comput Graph Stat. 2000;9:1–20. [Google Scholar]
- 35. Dempster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via the EM algorithm. J R Stat Soc Series B (methodological). 1977;1–38. [Google Scholar]
- 36. De Pierro AR. A modified expectation maximization algorithm for penalized likelihood estimation in emission tomography. IEEE Trans Med Imaging. 1995;14:132–137. [DOI] [PubMed] [Google Scholar]
- 37. Levitan E, Herman GT. A maximum a posteriori probability expectation maximization algorithm for image reconstruction in emission tomography. IEEE Trans Med Imaging. 1987;6:185–192. [DOI] [PubMed] [Google Scholar]
- 38. Panin V, Zeng G, Gullberg G. Presented at the 1998 IEEE Nuclear Science Symposium Conference Record. 1998 IEEE Nuclear Science Symposium and Medical Imaging Conference (Cat. No. 98CH36255)1998 (unpublished).
- 39. Zhang M, Zhou J, Niu X, Asma E, Wang W, Qi J. Regularization parameter selection for penalized‐likelihood list‐mode image reconstruction in PET. Phys Med Biol. 2017;62:5114–5130. [DOI] [PMC free article] [PubMed] [Google Scholar]


