Empirical evaluation of the implementation of the EMA guideline on missing data in confirmatory clinical trials: Specification of mixed models for longitudinal data in study protocols

Summary

In confirmatory clinical trials, the prespecification of the primary analysis model is a universally accepted scientific principle to allow strict control of the type I error. Consequently, both the ICH E9 guideline and the European Medicines Agency (EMA) guideline on missing data in confirmatory clinical trials require that the primary analysis model is defined unambiguously. This requirement applies to mixed models for longitudinal data handling missing data implicitly. To evaluate the compliance with the EMA guideline, we evaluated the model specifications in those clinical study protocols from development phases II and III submitted between 2015 and 2018 to the Ethics Committee at Hannover Medical School under the German Medicinal Products Act, which planned to use a mixed model for longitudinal data in the confirmatory testing strategy. Overall, 39 trials from different types of sponsors and a wide range of therapeutic areas were evaluated. While nearly all protocols specify the fixed and random effects of the analysis model (95%), only 77% give the structure of the covariance matrix used for modeling the repeated measurements. Moreover, the testing method (36%), the estimation method (28%), the computation method (3%), and the fallback strategy (18%) are given by less than half the study protocols. Subgroup analyses indicate that these findings are universal and not specific to clinical trial phases or size of company. Altogether, our results show that guideline compliance is to various degrees poor and consequently, strict type I error rate control at the intended level is not guaranteed.

Abbreviations

EMA

European Medicines Agency

KR

Kenward‐Rogers

ML

maximum likelihood

MMRM

mixed model for repeated measures

REML

restricted maximum likelihood

SAP

statistical analysis plan

1. INTRODUCTION

The prespecification of the primary analysis model is a universally accepted scientific principle in confirmatory clinical trials, which not only ensures thorough planning but also is necessary for strict control of the type I error at the intended significance level1 and increases confidence in the results. According to the ICH E9 Addendum (R1) on estimands,2 an analysis model is chosen as an estimator based on the chosen estimand. While the ICH E9 guideline requires the prespecification of the principal features in general,1 the EMA specified this requirement explicitly in the light of missing data problem in the “Guideline on missing data in confirmatory clinical trials.”3 Whenever statistical approaches are used, which handle missing data (explicitly or implicitly), the precise model settings are to be fully prespecified to such an extent that the analysis is replicable by an external data analyst.3 Thereby, it is aimed to prevent (unnoticed) selection options caused by imprecise model specifications, which would result in a multiplicity problem.

Mixed models for longitudinal data are commonly used to (implicitly) handle missing values taking into account the modeled covariance structure between the repeated measurements.4, 5, 6 While Carpenter et al7, 8 show that mixed models can be used as an estimator for a de jure estimand, Mehrotra et al9 caution that the estimate for an estimand of a between‐treatment difference that is free from the confounding effects of “rescue” medication can be exaggerated. In any case, the results do depend not only on the fixed and repeated/random effects specified in the model but also on the structure of the covariance matrix, modeling the correlation between the measurements of the same patient, and on the estimation, computation, and testing method.4, 5, 6 While the requirement of prespecification equally applies to all primary analysis models independently of the complexity, in this article, we focus on mixed model for longitudinal data for three reasons: (a) we need to focus on one model to allow detailed assessment of specification parameters (which would differ for different kinds of models), (b) in longitudinal studies missing data are a common and relevant problem, and (c) mixed models are commonly used for handling missing data.10

Especially in scenarios, where complex covariance structures (eg, an unstructured covariance matrix modeling several visits or multiple nested random effects) are modeled and the sample size is small, the mixed‐effects model for longitudinal data is known to be sensitive regarding the estimation method, and universal guidance is lacking.11, 12, 13, 14 For example, Gosho et al showed a substantial type I error rate inflation associated with the commonly used restricted maximum likelihood (REML) estimation in combination with the updated Kenward‐Rogers method for estimating the denominator degrees of freedom in comparison with the sandwich covariance estimator with the small‐sample correction by Mancl and DeRouen.15 Alternatively, Skene and Kenward16 show that in this situation, also the empirical sandwich estimator with the combined small‐sample adjustments of Mancl and DeRouen15 and Pan and Wall17 on the one hand holds the nominal significance level but on the other hand only has a low power for the detection of true effects. For hypothesis testing in situations with fairly complicated covariance structures and small to moderate sample sizes, however, Schaalje et al12, 13 recommend REML estimation in combination with the classical Kenward‐Rogers method for approximating the degrees of freedom18 rather than the Satterthwaite approximation method developed by Fai and Cornelius19 based on the idea of Satterthwaite.20 This heterogeneity in recommendations underlines the setting sensitivity of results generated by mixed models for longitudinal data (and strict type I error rate control) in some situations. Additionally, it is known that computational problems like convergence problems of the computational method11, 13, 14 or estimation of not positive‐definite matrices5 can occur, resulting in the need to abandon the primarily planned model and adjust settings. Options for fallback strategies range from minor adjustments to the starting value of the computational methods to major changes like modeling a different covariance matrix or removing random effects.5

Because of this known sensitivity regarding the exact model specifications generated by mixed models for longitudinal data, the requirement of unambiguous specification of model options was established in the EMA guideline on missing data in confirmatory trials.3 However, the compliance with this guideline, which came into effect 2011, has not been evaluated yet.

On the basis of the clinical trial applications submitted to the Ethics Committee at the Hannover Medical School between 1 November 2015 and 31 October 2018, this empirical study evaluated the compliance in accordance to the EMA guideline on missing data in confirmatory trials3 regarding the specifications of the mixed models for longitudinal data used in primary analyses. This time frame was chosen to assess only the most recent studies and to allow for an implementation period since the publication of the EMA guideline on missing data in confirmatory trials in 2011.3 Since the ICH‐E4 guideline on dose‐response studies recommends that a “well‐controlled dose‐response study is also a study that can serve as primary evidence of effectiveness”21 and also phase II trials are occasionally used in the drug approval for demonstrating the efficacy,22, 23, 24 strict type I error rate control is necessary for these trials. Therefore, we not only take into account phase III clinical trials but also include phase II clinical trials in the evaluation.

2. METHODS

2.1. Sampling of study protocols

The Ethics Committee of the Hannover Medical School, Germany, which is responsible for reviewing all clinical trials conducted at this site, granted full access to all the study protocols of clinical trials submitted for approval between November 2015 and October 2018.

2.2. Data protection

Results of the study protocol evaluation are reported aggregately and do not allow the identification of sponsors, investigational products, investigators, or other (commercially) sensitive information. All members of the research team handling the study protocols signed confidentiality agreements.

2.3. Selection and evaluation

For the selection of relevant studies, we applied the following inclusion criteria: the clinical trial (a) was submitted under the German Medicinal Products Act (AMG), (b) included a part assigned to development phase II or III, and (c) planned to use a mixed model for longitudinal data in the confirmatory testing strategy. In case a clinical trial contained separate parts of testing for development phases II and III, only the phase III part was included in the evaluation.

For all selected studies, we evaluated the mixed models by checking the specification of the following model characteristics: (a) the fixed and repeated/random effects, (b) the covariance matrix, (c) the testing method (eg, type III F test with the Kenward‐Rogers estimation method for the denominator degrees of freedom or a likelihood ratio test), (d) the computation method (eg, expectation‐maximization algorithm, Newton‐Raphson algorithm, and Fisher scoring algorithm), (e) the estimation method (eg, maximum likelihood, restricted maximum likelihood, estimation or minimum variance quadratic unbiased estimation, and empirical sandwich estimation), and (f) the fallback strategy defining the handling of computation or convergence problems. Since a study protocol might only include an outline of the primary analysis model and refers to an SAP that is not a substantial requirement for submission to the ethics committee, we also documented whether a reference to an SAP regarding the details of the primary analysis model was made. Additionally, the development phase, the sponsor, the planned sample size, and the medical indication of the studies were documented. On the basis of the medical indication, the studies were categorized using the 20 main therapeutic areas related to the International Classification of Diseases, 11th Revision (ICD‐11) classification of World Health Organization (WHO).25

The known ambiguity regarding the specification of the same statistical model by different descriptions was taken into account in the evaluation. For example, measuring the patient's blood pressure on two consecutive visits can be equivalently modeled by a linear mixed model including the patient as a random effect or by a covariance pattern model including the visit as a repeated factor within the patient in combination with a compound symmetry covariance matrix.4 In the former case, the sufficient specification of fixed and random effects implies the covariance structure, which does not have to be specified separately. In the latter case, the specification of the fixed and repeated effects would not suffice without the explicit specification of the covariance structure.

All study protocols fulfilling the inclusion criteria were evaluated independently by F.L. and S.H. All discordances were discussed and could be resolved.

The evaluation results were analyzed using descriptive statistics for the overall sample and stratified by clinical development phase. Additionally, the included clinical trials are analyzed stratified by sponsor (sponsored by one of the top 21 pharmaceutical industries determined by global sales26 in 2017 or not). Therefore, chi‐squared test or Fisher's exact test has been applied for exploratory hypothesis testing.

3. RESULTS

3.1. Characterization of study protocols

Between November 2015 and November 2018, 1098 applications were submitted to the Ethics Committee at Hannover Medical School, from which 469 trials were submitted according to the AMG. Out of these, 39 trials could be obtained, which used a mixed model for longitudinal data in the primary testing strategy and were assigned to development phase II (n = 15) or phase III (n = 24) (see Figure 1).

Figure 1.

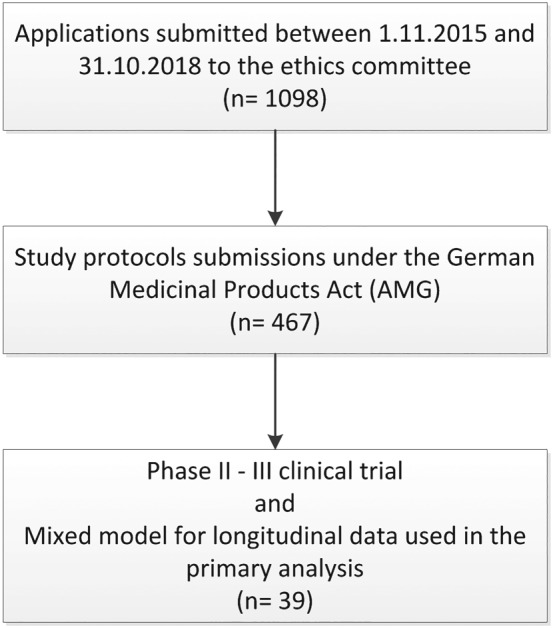
Flowchart for the retrieval of clinical trial protocols

Of these trials, 4/39 (10%) were sponsored by universities, while 35/39 (90%) of all trials were sponsored by pharmaceutical companies, including 17/39 (44%) sponsors from the top 21 pharmaceutical companies by global sales26 in 2017. The study protocols25 covered 13 out of 20 main therapeutic areas distinguished by ICD‐11. The planned sample sizes of all analyzed trials varied between 15 and 4126 patients with mean (±standard deviation) planned sample size of 454.9 (±814.82) and median planned sample size of 180 (Table 1).

Table 1.

Characteristics of included study protocols

Trial Characteristic	Phase II (n = 15)	Phase III (n = 24)	All Trials (n = 39)
Sponsor
Pharmaceutical companyb	12 (80%)	23 (96%)	35 (90%)
Top 21 pharmaceutical company	9 (60%)	13 (54%)	22 (56%)
Planned sample size
Mean (±standard deviation)	141 (±125)	651 (±992)	455 (±815)
Median (minimum, maximum)	99 (30, 500)	232 (15, 4126)	180 (15, 4126)
Therapeutic areaa
Blood or blood‐forming organs	0 (0.0%)	3 (12.5%)	3 (7.7%)
Endocrine, nutritional, or metabolic diseases	0 (0.0%)	2 (8.3%)	2 (5.1%)
Mental, behavioral, or neurodevelopmental disorders	0 (0.0%)	2 (8.3%)	2 (5.1%)
Nervous system	0 (0.0%)	3 (12.5%)	3 (7.7%)
Visual system	1 (6.7%)	2 (8.3%)	3 (7.7%)
Ear or mastoid process	1 (6.7%)	0 (0.0%)	1 (2.6%)
Circulatory/cardiovascular system	0 (0.0%)	2 (8.3%)	2 (5.1%)
Respiratory system	6 (40.0%)	6 (25.0%)	12 (30.8%)
Digestive System	3 (20.0%)	1 (4.2%)	4 (10.3%)
Skin	1 (6.7%)	1 (4.2%)	2 (5.1%)
Immune system	2 (13.3%)	1 (4.2%)	3 (7.7%)
Genitourinary system	1 (6.7%)	0 (0.0%)	1 (2.6%)
Developmental abnomalies	0 (0.0%)	1 (4.2%)	1 (2.6%)

^aOnly ICD‐11 (20) superior categories 01 to 20 are considered since categories 21 to 26 do not represent therapeutic areas.

^bIncluding the top 21 pharmaceutical companies.

3.2. Evaluation of mixed model reporting

The descriptive analysis of the reporting quality of mixed models for longitudinal data in phases II and III clinical trials is presented in Table 2. Nearly all protocols specify the fixed and random effects of the analysis model (95%), and most trial protocols report on the structure of the covariance matrix used for modeling the repeated measurements (77%). On the other hand, the testing method (36%) and the estimation method (28%) are given by less than half the study protocols. Even worse, only 18% of the protocols specified a fallback strategy, and only a single protocol specified the computation method (3%).

Table 2.

Reporting of primary mixed model analyses by clinical development phase

Evaluation Item	Development Phase		P Value	All Studies (n = 39)
	II (n = 15)	III (n = 24)
Fixed and random effects	15/15 (100.0%)	22/24 (91.7%)	.51**	37/39 (94.9%)
Covariance structure	13/15 (86.7%)	17/24 (70.8%)	.44**	30/39 (76.9%)
Testing method	5/15 (33.3%)	9/24 (37.5%)	.79*	14/39 (35.9%)
Estimation method	4/15 (26.7%)	7/24 (29.2%)	1.00**	11/39 (28.2%)
Computation method	0/15 (0.0%)	1/24 (4.2%)	1.00**	1/39 (2.6%)
Fallback strategy	1/15 (6.7%)	6/24 (25.0%)	.22**	7/39 (17.9%)
SAP reference	3/15 (20.0%)	9/24 (37.5%)	.31**	12/39 (30.8%)
All items specifieda	0/15 (0.0%)	0/24 (0.0%)	‐	0/39 (0.0%)
Main items specifiedb	5/15 (33.3%)	7/24 (29.2%)	.78*	12/39 (30.8%)
Main items specifiedb or SAP reference	7/15 (46.7%)	14/24 (58.3%)	.48*	21/39 (53.8%)

^aExcluding reference to SAP.

^bMain items are fixed/random effects, covariance structure, and testing method.

^* P value derived from chi‐squared test comparing proportions between study phases.

^** P value derived from Fisher's exact test comparing proportions between study phases.

Additionally, to the individual evaluation items, we clustered the main items and analyzed the number of protocols specifying the fixed and random effects, the covariance structure, and the testing method. Altogether, only 31% of the study protocols specified all main items, and only 54% of the study protocols specified all main items or had a reference to a supplementary SAP. Consequently, almost half of the analyzed protocols (46%) neither specified all main items nor planned to do so by an additional SAP. In particular, not a single study specified all evaluation items.

Between development phases II and III, no consistent difference could be observed regarding the specification of individual evaluation items (see Table 2). While the proportion of protocols specifying the fixed and random effects (100% vs 92%) and the covariance structure (87% vs 71%) is higher in phase II trials than in phase III trials, the testing method is less often specified in phase II trials compared with phase III trials (33% vs 38%). Surprisingly, the proportion of protocols specifying the main items (33% vs 29%) is higher in phase II compared with phase III. However, it is important to note that this analysis is merely descriptive and no comparison of the proportions of phases II and III reached statistical significance (see Table 2). In addition to the comparison between the study phases, we also grouped the study protocols by their type of sponsor, comparing study protocols submitted by a sponsor from the top 21 pharmaceutical companies in 2017 as determined by global sales (major sponsors)26 and protocols submitted by a sponsor not from the top 21 pharmaceutical companies (minor sponsors) (see Table 3). While no significant difference could be observed in the protocol specifications of single items between major and minor sponsors, the subgroup analysis indicates that major pharmaceutical companies specify the three main items more often (53% vs 14%; P < .05). This discrepancy can consistently be found in both phase II and phase III trials (see Data S1). However, in phase III clinical trials, the difference between major and minor sponsors is slightly less distinctive (46% vs 15%; P = .18) than in phase II (67% vs 11%; P = .09), as can be seen in Table 3.

Table 3.

Reporting of primary mixed model analyses by sponsor type

Evaluation Item	Sponsor Type		P Value*
	Minor (n = 22)	Major (n = 17)
Fixed and random effects	20/22 (90.9%)	17/17 (100.0%)	.50**
Covariance structure	15/22 (68.2%)	15/17 (88.2%)	.25**
Testing method	5/22 (22.7%)	9/17 (52.9%)	.05*
Estimation method	3/22 (13.6%)	8/17 (47.1%)	.03**
Computation method	0/22 (0.0%)	1/17 (5.9%)	.44**
Fallback strategy	2/22 (9.1%)	5/17 (29.4%)	.21*
SAP reference	9/22 (40.9%)	3/17 (17.6%)	.17**
All items specifieda	0/22 (0.0%)	0/17 (0.0%)	‐
Main items specifiedb	3/22 (13.6%)	9/17 (52.9%)	.01**
Main items specifiedb or SAP reference	11/22 (50.0%)	10/17 (58.8%)	.58*

^aExcluding reference to SAP.

^bMain items are fixed/random effects, covariance structure, and testing method.

^* P value derived from chi‐squared test comparing proportions between sponsor types.

^** P value derived from Fisher's exact test comparing proportions between sponsor types.

Summarizing, in all analyzed subgroups, the guideline compliance is to various degrees poor. This indicates that the identified problem of insufficient specification of mixed models for longitudinal data as the primary analysis method is universal and not specific to clinical trial phases or size of company.

4. DISCUSSION

Our analysis of the compliance with the EMA guideline on missing data in confirmatory clinical trials3 based on 39 clinical trials submitted to the Ethics Committee of the Hannover Medical School between 2015 and 2018 showed a substantial lack of statistical rigor in explicitly defining the characteristics of the primary analysis model when mixed models for longitudinal data are used. While typically the fixed and random effects are specified, even basic parameters like the used covariance matrix or testing method are often not or ambiguously specified. Particularly, the proportion of study protocols sufficiently determining the main model specifications is only 31%, showing that more than two thirds of the evaluated trials did not specify at least one of the main items. Because of this ambiguity in model definition, the type I error rate control at the intended level is not guaranteed. Subgroup analyses comparing the clinical development phases and trial sponsors indicate that these findings are universal and not specific to clinical trial phases or the size of the company. However, some differences could be observed between major and minor trial sponsors. Exploratory subgroup analyses indicate better guideline compliance for major pharmaceutical companies in comparison with minor trial sponsors. Especially, in the specification of the main model items, which are assumed to have the largest influence on model results, there is a marked difference. This difference was consistently observed in phase II and phase III clinical trials. However, it is important to note that although major sponsors on average give a more detailed model description, half of the major sponsors do not specify the main model items sufficiently and thus do not control the type I error rate at the intended level.

4.1. Limitations

It is important to note that the study protocols analyzed in this study are not a random sample but sampled from a pre‐defined period from a single ethics committee in Germany. Consequently, the generalizability of the evaluation results is not given per se. However, the wide range of covered therapeutic areas and most importantly the balanced proportions of major and minor trial sponsors and phase II and phase III clinical trials substantiate our findings.

Second, the transfer of the description of the primary model to an SAP, which typically was not finished at the time of application, accounts for some uncertainty in the evaluation. If an SAP was referenced in the study protocol, all missing specifications might be given in the nonavailable SAP. On the other hand, the mere existence of an SAP does not ensure that the missing information will be entirely and correctly specified within the SAP. However, for at least 69% of all evaluated trials, a definite evaluation of the compliance with the EMA guideline was possible. This outsourcing of information not only did hinder our evaluation but also did not allow the ethics committee to fully evaluate the application, which is a finding on its own.

Third, the inferential subgroup analyses comparing the model specifications between clinical development phases II and III and between major and minor trial sponsors were conducted explanatorily without correcting the significance level for multiple testing. On the other hand, this study was not powered to show differences between groups regarding the evaluation items. Consequently, both analysis results indicating a difference between subgroups (differences significant to the uncorrected significance level of 5%) and analysis results not indicating a difference (eg, a difference significant to the uncorrected significance level of 5%) should be interpreted with caution. On the basis of this first data on the compliance with the EMA guideline on missing data in confirmatory clinical trials,3 a follow‐up study needs to be conducted to confirm the hypothesis generated in this study.

Fourth, this study builds on previous work showing the potential influence of each individual evaluated item on the inference of the mixed model for longitudinal data. These works concentrated on comparing different choices for a single evaluation item (eg, comparing different methods for approximating the denominator degrees of freedom for an F test12, 13). To exactly determine the magnitude of type I error rate inflation caused by the simultaneous choice in multiple nuisance/technical parameters required for model specification, additional simulation studies are required. Because of the combinatorial explosion, the overall inflation might be markedly larger than the inflation associated with a single method.

4.2. Recommendations

In accordance with the ICH E9 Addendum (R1),2 it is important to first specify the estimand of interest. On the basis of this estimand, a corresponding primary analysis model for estimation needs to be chosen specified in sufficient detail to allow independent replication of the results.3 A practical way of sufficiently specifying the primary mixed model analysis in the study protocol is the definition of the statistical software and its version used for analysis together with the provision of the exact software code used. However, this should rather be done in addition than in substitution of the justification of the primary analysis model and the (implicit) assumptions on missing values as required by the EMA guideline on missing data in confirmatory trials.3

Additionally, a fallback strategy has to be specified for the scenario that convergence or estimation problems occur. While in some of the evaluated study protocols, vague alternatives to the primary analysis model were given (eg, the covariance matrix was to be simplified, without exactly specifying the intended simplification), the fallback strategies were rarely thought through to the end. For example, if convergence problems occur for the primary analysis model, a sole simplification of the covariance matrix does not guarantee model convergence. Instead, a confirmatory testing strategy including a step‐down fallback strategy, which simplifies the structure of the covariance matrix and the modeled random effects until a fixed‐effects analysis is reached, or a definite decision mechanism guarantees the formal type I error rate control. Nevertheless, sensitivity analyses should be conducted to investigate the discrepancy between the planning assumptions on the one hand, which justified the conduct of a complex model, and the resulting data on the other hand. In any case, the evidentiary weight of the analysis should be questioned, and the results should be interpreted with caution.

By slightly complementing the specification provided by Mallinckrodt et al27 (additions cursive), the following example specification assures that an independent data analyst could recreate the analysis results of a parallel‐group trial with repeated measures:

Mean changes from baseline will be analysed using a restricted maximum likelihood (REML)‐based repeated measures approach in combination with the Newton Raphson Algorithm. Analyses will include the fixed, categorical effects of treatment, investigative site, visit, and treatment‐by‐visit interaction, as well as the continuous, fixed covariates of baseline score and baseline score‐by‐visit interaction. A(n) common unstructured (co)variance structure will be used to model the within‐patient errors. If this analysis fails to converge, the following structures will be tested in a subsequent order until model‐convergence is achieved: (insert a list of structures appropriate for the specific application). (…) The Kenward‐Roger approximation will be used to estimate denominator degrees of freedom. Significance tests will be based on least‐squares means using a two‐sided α = .05 (two‐sided 95% confidence intervals). Analyses will be implemented using (insert software package and analysis procedure). The primary treatment comparisons will be the contrast between treatments at the endpoint visit.27

Corresponding code for the analysis software SAS 9.4 is provided in the 5 in the supplementary material. In the light of the type I error rate control and the prevention of data‐driven model selection, the EMA guideline allows the prespecification of the primary analysis in an SAP,3 which does not affect the type I error rate in blinded trials. However, this information transfer from the study protocol to the supplementing SAP constitutes a problem for ethics committees. In this study, none of the sponsors referencing to an SAP in the study protocol submitted the respective SAP to the ethics committee. Therefore, a thorough evaluation of the adequateness of the primary analysis model as an important part of the study concept was impeded or—depending on the information available in the study protocol—rendered impossible. While there is no issue in modifying the statistical analysis plan for the exploratory endpoints just shortly before the blind is broken at the end of a trial, postponing a detailed definition of the primary analysis is problematic from an ethics committee's point of view. As designated in the Declaration of Helsinki,28 to allow an informed approval of the planned clinical trial, “the design and performance of each research study involving human subjects must be clearly described and justified in a research protocol.”28 This underlines the importance of a full specification of the confirmatory analyses of clinical trials in the study protocol.

Supporting information

Data S1 Supporting information

Häckl S, Koch A, Lasch F. Empirical evaluation of the implementation of the EMA guideline on missing data in confirmatory clinical trials: Specification of mixed models for longitudinal data in study protocols. Pharmaceutical Statistics. 2019;18:636–644. 10.1002/pst.1964

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are not publicly available due to privacy restrictions.