Skip to main content
PMC home page
Wiley Open Access Collection logoLink to Wiley Open Access Collection
. 2019 Apr 29;94(6):1011–1018. doi: 10.1111/jfb.13967

What is multispecies MSY? A worked example from the North Sea

Robert B Thorpe 1,✉
PMCID: PMC6900025  PMID: 30883746

Abstract

The concept of an optimum yield at intermediate levels of fishing (the so called maximum sustainable yield or MSY) has been with us since the 1930s and is now enshrined in legislation as a key objective of fisheries management. The concept seems intuitively reasonable and is readily applicable to a single stock treated in isolation and assuming a constant environment. However, translating this concept into a mixed and multispecies fishery, where there are complex trade‐offs between fleets and stocks and in general no simple optimum solution, has been problematic. Here I introduce a framework for thinking about multispecies MSY in terms of an integrated risk of stock depletion and expected long‐term yield. Within this framework I consider the performance of a set of simple harvest control rules based upon a single‐limit fishing mortality rate (F) which is common to all stocks and a target biomass which is a set fraction of a stock's virgin biomass. Using a multispecies management strategy evaluation, I compare expected outcomes for a set of these harvest control rules with alternative scenarios, in which each stock has its own F based on the assessment process. I find that the simple framework can produce outcomes that are similar to those from the more sophisticated estimates of F. I therefore conclude that achieving multispecies MSY may depend more upon setting reasonable biomass targets and faithfully applying a harvest control rule approach rather than determining the best possible Fs for each stock.

Keywords: harvest control rules, maximum sustainable yield, multispecies, risk, North Sea, virgin biomass

1. INTRODUCTION

The notion of an optimum yield at intermediate levels of fishing arose in the 1930s (Russell, 1931), although the term maximum sustainable yield (MSY) appears to have been coined later (Mesnil, 2012). It can be defined as the maximum yield that can be taken indefinitely from a stock; that is, the maximum harvest that is sustainable in the long term. As a concept it has the advantages of being simple and transparent to understand and being intuitively reasonable. Consequently, managing fish stocks in accordance with obtaining MSY has been widely advocated by international bodies. From early on, FAO was a strong champion of this MSY‐based fisheries management (FAO, 1966) and this was later taken up by the International Whaling Commission (Allen & Kirkwood, 1988) and enshrined in the 1982 UN Convention on the Law of the Sea, where it is the only reference point explicitly referred to (Caddy, 1999). Subsequently the World Summit on Sustainable Development at Johannesburg in 2002 declared that fish stocks should be fished at MSY where possible by 2015 (UN, 2002).

Whilst MSY is easy to determine for a single stock in isolation, however, it is much more problematic for a multispecies community (Guillen et al., 2013), where it is not in general possible to maximise the yield of all stocks simultaneously (FAO, 2001; Voss et al., 2014; Farcas & Rossberg, 2016; Ulrich et al., 2016; Norrstrom et al., 2017, Pope et al., 2019), whilst maximising the total yield may place the most vulnerable stocks at unacceptable risk (Matsuda & Abrams, 2006). This tension can be seen in Figure 1, which is adapted from Worm et al. (2009) and represents the effect of progressively increasing a fixed pattern of fishing mortality across a fish community. For the figure, a multispecies MSY is defined as being the maximum yield that can be taken from the modelled community in the long run. There are three major issues with such a definition. Firstly, the total yield is a function of the relative exploitation pattern across stocks, which is in general not fixed and will affect the nature of the trade‐off between risk and reward. Secondly, it does not take account of the precautionary principle (Serchuk et al., 1999, p. 105); there is no guidance concerning the number of collapsed species that might be acceptable. Thirdly, it is not easy for a decision‐maker to visualise the trade‐off between risk and reward, as both are expressed relative to a third variable, the level of the fishing mortality rate F.

Figure 1.

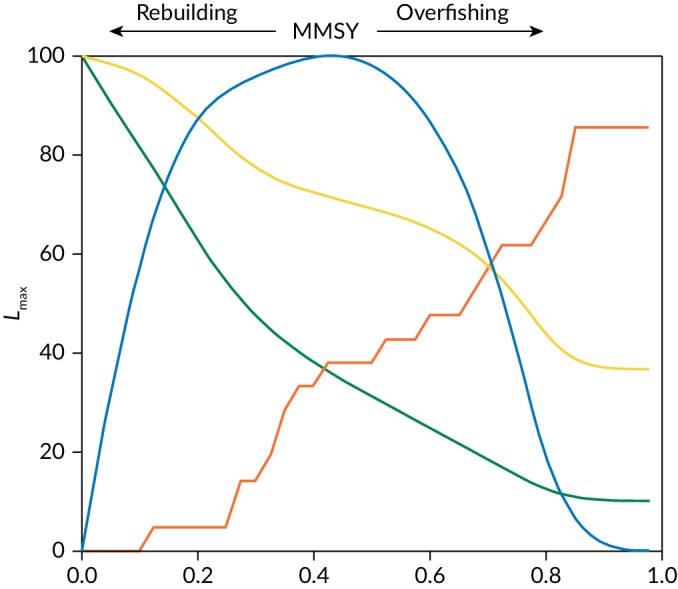
Figure 1

Open in a new tab

Schematic illustration of the effects of increasing exploitation across a fish community (reproduced from Worm et al., 2009). Here MMSY is defined as the maximum yield that can be extracted from the community in the long term, even though this is associated with a significant number of collapsed species. L max, Maximum fish length. (Inline graphic) Total catch, (Inline graphic) Total biomass, (Inline graphic) Mean Lmax and (Inline graphic) Collapsed species

In this study I propose an alternative framework for understanding and visualising a multispecies MSY, here termed a fish community (FC)MSY, which addresses these issues. I illustrate its use with an example taken from the North Sea in which I evaluate the performance of simple harvest control rules (Kvamsdal et al., 2016) which apply the same F LIMIT and B TARGET to each of the 21 stocks in the model community (Figure 2) using a management strategy evaluation (MSE; Sainsbury et al., 2000; Punt et al., 2016). These simple harvest control rules are used to manage towards the MSY objective and I evaluate the long‐term outcomes as a function of expected gross economic yields (catch × gross revenue per unit catch), catch variability, total effort (as a proxy for employment generated in the fishery), net profit and the risks of stock depletion summed across the multispecies community. I illustrate the utility of this framework by comparing the performance of these simple harvest control rules against harvest strategies that are informed by ICES single‐species assessments and multispecies modelling, which allow for different Fs to be tailored to each stock, based on the evidence of the stock assessment process. In this way I can estimate the long‐term value that is added by the stock‐specific Fs.

Figure 2.

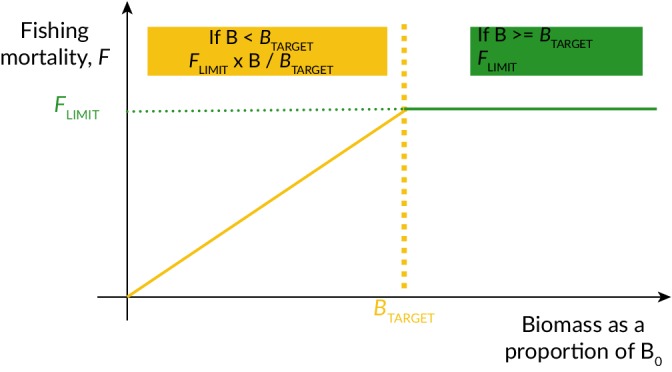
Figure 2

Open in a new tab

Schematic of the simple harvest control rules. Seventeen different FLIMIT (F = 0.05, 0.10, 0.15, 0.20, 0.25, 0.30, 0.35, 0.40, 0.45, 0.50, 0.55, 0.60, 0.80, 1.00, 1.20, 1.50, 2.00, 2.50) and fourteen different BTARGET thresholds (10%, 15%, 20%, 25%, 30%, 35%, 40%, 45%, 50%, 60%, 70%, 80%, 90% and 100% of B0) were considered, making 238 different harvest control rules in total. The HCR has the same form as the first type considered by Mackinson et al. (2018) and Froese et al. (2011)

2. MATERIALS AND METHODS

2.1. A new conceptual framework for multispecies MSY

Considering the bigger picture, the fisheries manager will want to extract as much yield from the system as he or she can without damaging the stock structure in such a way as to reduce overall returns in the long term or reduce the options of future policy‐makers. This implies a tension between yield today and risk (as a measure of the potential damage to the stock structure and yield or options for management flexibility that may be foregone tomorrow), so any estimate of MSY needs to take account of both. In the case of a single stock, this is straightforward and involves maximising the yield (tonnage or gross value), without violating the precautionary principle (for example, avoiding the stock dropping below the limit biomass; that is, becoming depleted with 95% confidence).

By analogy, in order to construct a multispecies MSY, I need a way of expressing the overall risk and reward across the community associated with any given fishing strategy. In the case of reward, this is relatively simple, being the sum of the catches (tonnage) or the gross revenue associated with the catch [tonnage caught × species specific value (price per tonne)] summed across all stocks (Srinivasan et al., 2010). In the case of risk, a simple average will not suffice. For example, if there were 21 stocks in the fish community (Thorpe et al., 2015; Thorpe et al., 2016; Thorpe et al., 2017), it would be possible to deplete one stock with 100% probability whilst the overall risk across the community could remain compliant with the precautionary principle (< 5%) if there was no risk to any of the other 20 stocks. This scenario might seem extreme but would be possible with a highly species‐selective pelagic fishery and would of course not be acceptable. So we need a risk metric which: (a) increases with the overall risk to stocks across the community; (b) approximates the individual risk to a stock in the case where all stocks are subject to the same risk; (c) heavily penalises outcomes where the risk is loaded disproportionately onto a small number of stocks; (d) assigns a certain risk of depletion to the community if any stock in the community is depleted with certainty.

I propose a simple fish community risk metric (FCRM) which has these properties and is related to the individual risk of depletion of stock i (R i) as follows: FRCM = ΣYi(Σ Y i + n)−1, where Y i = R i (1 − R i)−1. Here n is the number of stocks in the community, R i varies between 0 (no risk of stock depletion) and 1 (100% probability of stock depletion) for stock i of n and Y i is the ratio of instances of the stock being at risk to the instances of the stock not being at risk. The behaviour of this metric for a few simple examples is presented in Table 1, showing that it has the required properties. In the limit that the risk is spread evenly across the community, the community risk (CR) defaults to the mean risk (first scenario). In the limit that one stock is depleted with certainty, the community risk defaults to 1 (second scenario). In other cases, the community risk is always higher than the mean risk, lower than the highest individual risk and increases with unevenness of risk loading across the community. In this way it penalises outcomes that focus the risk on a small number of stocks.

Table 1.

Comparison of the community risk with the mean risk to stocks for some simple examples. Precautionary is taken to mean that the risk metric is < 0.05, to be consistent with the single species approach

Scenario risk profile
n = 21 5% risk of depletion across the community All stocks R = 0.05 n = 21 One stock depleted, others untouched. One stock has R = 1.0 All other stocks R = 0 n = 21 Two stocks have R = 0.5 19 stocks have R = 0 n = 21 5 stocks have R = 0.2 17 stocks have R = 0 n = 21 10 stocks have R = 0.1 11 stocks have R = 0
Mean risk to stocks 0.05 0.0476 0.0476 0.0476 0.0476
Fish community risk metric 0.05 1.00 0.0869 0.0562 0.0502
Open in a new tab

Cell colours illustrate the overall risk. Green = precautionary (<0.05), yellow = 0.05, the limit of precautionarity, and shades of orange and red are progressively less precautionary, with dark red = certainty of stock depletion.

Having defined acceptable measures of risk and reward across the fish community, I can then express management outcomes in terms of their position in the two‐dimensional risk–reward space. The maximum potential yield is estimated from considering a large number of potential strategies whilst any outcome with a community risk of < 5% is precautionary in the ICES sense. Therefore, any outcome providing close to the maximum yield across the community, with a CR < 5% can be said to be consistent with multispecies MSY. This is shown schematically in Figure 3.

Figure 3.

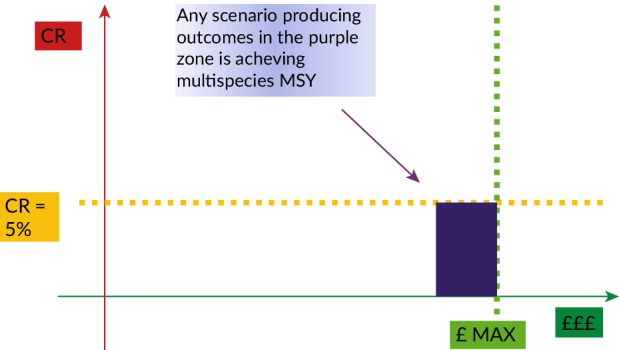
Figure 3

Open in a new tab

Schematic showing multispecies MSY in terms of community risk (CR) and reward. The maximum yield is estimated by simulation from a large number of potential strategies

2.2. Methodology of the management strategy evaluation

I investigated the outcomes of managing with different harvest control rules using a length‐based multispecies model as the operating model in a management strategy evaluation (MSE). The operating model is the same model as used in Thorpe et al. (2017). It is based upon the framework developed by Hall et al. (2006) and subsequently adapted for use in the North Sea by Rochet et al. (2011) and by Thorpe et al. (2015) to allow for increased interactions between stocks and improve model run time. The operating model is described in detail in Thorpe et al. (2017) and further details on parameter settings are provided in Thorpe et al. (2015). In brief, a total of 21 fish species is represented in 32 equal length classes. These are common across stocks and span the full range of sizes in the fish community. Thus, the longest fish, cod Gadus morhua L. 1758, may be present in all length classes, while smaller species such as sprat Sprattus sprattus (L. 1758) may only be present in, say, five. Individuals progress through length classes as they grow and mature at a threshold length at maturity. Reproduction is described with a hockey‐stick spawner‐recruit relationship (Barrowman & Myers, 2000), which determines the number of recruits entering the smallest size class as a function of the biomass of mature individuals. Species’ dynamics are linked via predation mortality (M 2) which is an emergent property depending upon predator and prey abundance as determined by a diet matrix and the preferred predator–prey mass ratio. Individuals are also susceptible to residual natural mortality (M 1) and F. Parameterisation and validation of the model are described in Thorpe et al. (2015).

The consequences of parameter uncertainty were assessed by developing 78,125 models [5 variants for each of 7 key parameters covering: (a) diet matrix, (b) predator size‐preference, (c) non‐predation natural mortality, (d) spawner‐recruit initial steepness, (e) efficiency of growth, (f) asymptotic length and (g) maximum recruitment], with parameters drawn from ranges that spanned literature estimates. Details of the parameter choices and their underlying rationale can be found in Thorpe et al. (2015) and Supporting Information Table S1 in Appendix S1. Models in the unfiltered ensemble were screened against stock assessment estimates of SSB to identify plausible models. The screening criteria were all species should persist in the absence of fishing and the mean predicted SSB of assessed species after 30 years simulated fishing at average 1990–2010 rates (ICES, 2012), should be within a factor of two of the SSB estimated in ICES (2012). Stochastic recruitment around the deterministic hockey‐stick spawner‐recruit relationship was simulated using a lognormal distribution scaled so as to both preserve mean recruitment levels and reproduce variability of similar magnitude to that found in the ICES stock‐recruit database (Thorpe et al., 2017 and Supporting Information Appendix S1). Each parameter combination was tested three times and accepted if all three stochastic simulations using this parameter set produced biomasses within a factor of two of the 1990–2010 averages for each of the 10 fully assessed stocks, giving rise to a filtered ensemble (FE) of 63 members. I used a factor of two because biomass estimates from assessments are uncertain and because a range of processes including environmental factors influence abundance in the real world. However, a previous analysis suggests that changing this factor, which affects the FE size, has only modest influence on predictions made by the filtered ensemble for FE sizes between 50 and 1000 (Thorpe et al., 2015, Supporting Information Appendix S1).

In Thorpe et al. (2017), we assumed constant fishing mortality in accordance with management targeting a specific point within the pretty good yield ranges (Hilborn, 2010; Rindorf et al., 2017a, 2017b), with the resulting yields and risks being long‐term averages. In practice, however, a target F would also depend on the stock abundances and would be reduced if the stock status was outside safe biological limit (ICES, 2016). In the current study I take account of this by performing an MSE (ICES, 2013; Kell et al., 2007; Mackinson et al., 2018; Punt et al., 2016), using pre‐agreed sets of rules that determine the level of F to apply across the community for any particular year, given estimates of the stock abundances at that time. Here, following Mackinson et al. (2018), I use HCRs of hockey‐stick form (Figure 2), designed to deliver MSY during times of high stock abundance, with pre‐specified reductions if stock abundance (biomass) falls below a certain limit (here termed B TARGET and equivalent to MSY B trigger in standard ICES terminology; ICES, 2016). Limits for management action (reducing F) were set with reference to the estimated stock abundance as a fraction of the unfished abundance (B 0).

Within the MSE framework, stock status was determined annually. Wiedenmann et al. (2015) found that there were typically high levels of autocorrelation in the stock assessment process of order 0.7–0.9 (stock assessment biases tend to persist through time rather than being white noise). Therefore, within the MSE I took the modelled spawning stock biomass (SSB) for each stock from the last but one year and applied a measurement–assessment error as follows: assessed biomass / true biomass (t) = exp {log[ assessed biomass / true biomass (t − 1)] × 0.8 + normal(0,0.5) × 0.2}. This generated a timeseries of estimates with autocorrelation of 0.8 and residuals of a magnitude consistent with the 2018 cod assessment for the North Sea (Supporting Information Appendix S1; http://www.stockassessment.org; accessed 04/02/2019). Fishing mortality for the following year was then assigned using the agreed HCR and applied subject to the same bias as the assessment (i.e., if the assessed biomass was a factor of 2 too high, then the applied F would also be a factor of 2 too high to reflect our lack of awareness of the state of the stock) and a lognormally distributed error term to reflect uncertainty in implementation of an agreed fishing strategy. Thus: F applied = F desired (assessed biomass/true biomass) lognormal (0, 0.3); for comparison an example discussed in ICES (2013) assumes an implementation error of 10% whilst Wiedenmann et al. (2015) suggest typical errors in the catch of 15%.

The 2 year lag reflects time delays associated with the current assessment framework, but the process could be readily adapted to consider other time lags (and hence the value of having more information) or indeed other levels of uncertainty.

The MSE simulations were run for 50 years and management outcomes were defined in terms of an average of the last 30 years of the simulation. I focussed on the expected outcomes for risk and reward and present results showing the gross economic yield (expected catch x value) and risk of stock depletion adjusted to reflect the need to avoid concentrating risk on a few stocks in the community to an unacceptable degree. The way in which I define and evaluate the risks and rewards associated with each strategy is detailed below. By defining a community risk in the manner described, one can be sure it meets the ICES definition of precautionary (i.e., if any single stock has a high chance of depletion, the community risk will also be high, irrespective of the risks to the other twenty stocks). I defined stocks to be depleted when their biomass was below a certain fraction of the estimated unfished biomass (B 0). In previous work we defined a stock to be at risk when its biomass falls below 10% of B 0 (Thorpe et al., 2016, 2017; Worm et al., 2009), but other definitions have been suggested (Smith et al., 2009). In Thorpe and De Oliveira (2019) we also looked at risk thresholds of 15% and 20% of B 0, but the results were qualitatively similar, so I just focus on the 10% threshold here. Results were expressed as the ensemble mean (across 63 ensemble members). Each calculation was repeated 100 times to take account of stochastic recruitment variation (Thorpe et al., 2017).

2.3. Candidate simple approaches for achieving FCMSY

This study looks at outcomes from managing the North Sea fish community in accordance with harvest control rules based upon a simple approach which is common to all stocks. Seventeen possible choices for F LIMIT and fourteen for B TARGET (Figure 2) were considered independently, giving 238 harvest control rule variants. Outcomes were then compared with five strategies for achieving FCMSY based only a tailored F for each stock which makes use of information from the stock assessment process. These were (a) applying Fs based on 10 single species assessments, (b) calculating a 21 stock multispecies Nash equilibrium (Thorpe et al., 2017) to provide a true multispecies reference point and estimating Fs based on targeting the (c) top, (d) middle and (e) bottom of the pretty‐good‐yield (PGY) ranges based on ICES assessments (Rindorf et al., 2017a, 2017b; Thorpe et al., 2017). For a) Fs for the non‐assessed stocks were estimated by relating them to the most similar assessed stocks (details in Thorpe et al., 2015), whilst for (3)–(5) these Fs emerge from maximising fishing across the community without violating any of the seven PGY ranges (Thorpe & De Oliveira, 2019).

3. RESULTS

The expected risk and reward outcomes for the 238 simple harvest control rule variants as compared with the tailored approaches, single species assessments, Nash equilibrium and top, middle and bottom of the ICES PGY ranges, are shown in Figure 4. The best combinations of F LIMIT and B TARGET produce overall yields that are extremely competitive with the tailored F approaches, being comparable with the Nash equilibrium and clearly superior to use of the single species assessments and the ICES PGY ranges.

Figure 4.

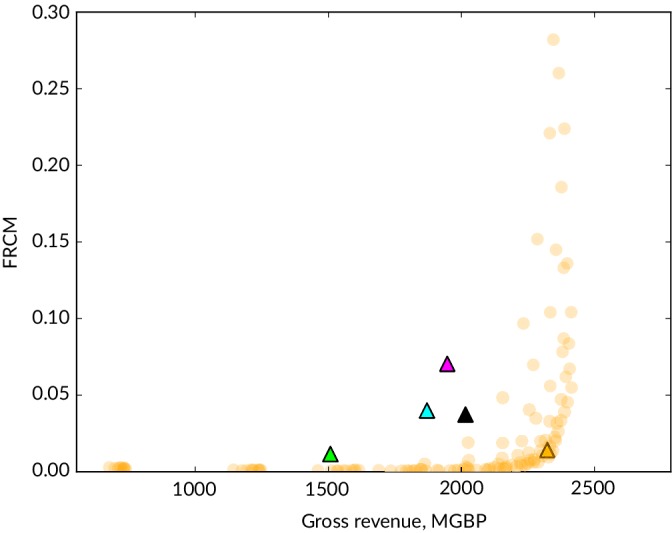
Figure 4

Open in a new tab

Expected outcomes for gross catch revenue and risk of stock depletion (FRCM) for the 120 simple harvest control rule variants (Inline graphic) as compared with assessment‐based single species fishing mortality rate (Inline graphic),multispecies Nash Equilibrium (Inline graphic),upper pretty good yield (PGY) ranges (Inline graphic),mid PGY ranges (Inline graphic) and lower PGY ranges (Inline graphic)

Having established the utility of the simple framework, the (a) yield, (b) risk of stock depletion, (c) variability of income and (d) estimated net profits vary as a function of F LIMIT and B TARGET are shown in Figure 5. The overall yield is very flat‐topped and a wide variety of choices are consistent with high yield. The best precautionary yield is delivered by a combination of F LIMIT = 0.8 and B TARGET = 0.90, but a number of other choices produce similar outcomes. Many choices are also precautionary showing the efficacy of the HCR approach of cutting F as stock status declines, the exception being combinations of high F LIMIT and low B TARGET, where there is not enough of a buffer against poor stock status. Income variability is lowest for low F LIMIT and low B TARGET, which is not surprising because this approximates a fixed F strategy and is highest for high F LIMIT and high B TARGET, which more closely approximates a boom–bust approach. Income variability is generally greater than for the tailored F approaches and is about 40% higher for the highest precautionary yields. The most profitable HCRs are associated with slightly lower yields and lower Fs for a given B TARGET. High and low F LIMITs are generally unprofitable, whilst good profits are obtained when F LIMIT is c. 0.3–0.4 for all B TARGET. The most profitable HCR is F LIMIT = 0.35, B TARGET = 0.40, which delivers about 90% of the maximum precautionary yield. Thus, there is a slight tension between yield and profits, whilst there is a much greater one between profits and jobs (effort), which is maximised at high F LIMIT and low B TARGET.

Figure 5.

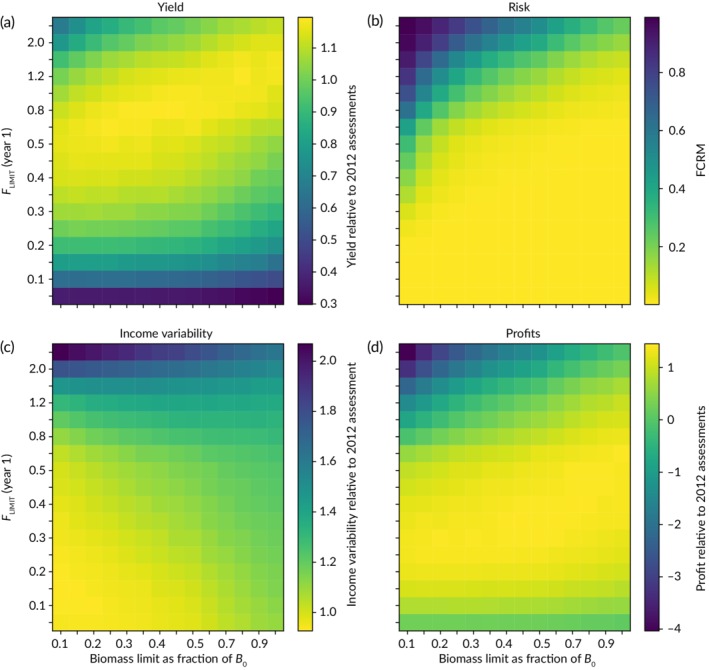
Figure 5

Open in a new tab

Expected outcomes for (a) gross economic yield, (b) fish community risk metric (FCRM, (c) income variability and (d) estimated net profits. (a) and (c) are expressed relative to expected outcomes for fish community (FC)MSY based on single species assessments; (b) is precautionary where FCRM is < 0.05

4. DISCUSSION

The North Sea fixed and multispecies fishery has been intensively studied and being relatively data rich provides an opportunity to examine the performance of simple strategies for managing a multispecies fish community as opposed to more complex ones with specific Fs for each stock. In this study, I have adapted a published modelling framework to perform a multispecies management strategy evaluation with an ensemble of related models (common structure but different parameterisations), thereby taking into account model parameter uncertainty alongside recruitment uncertainty. Using a novel framework for conceptualising multispecies MSY in terms of community risk and reward, I have been able to evaluate the performance of a suite of 238 generic harvest control rules and compare them with the expected outcomes from (a) single species assessments, (b) a true multispecies reference point based upon a 21 stock Nash equilibrium (Farcas & Rossberg, 2016; Norrstrom et al., 2017, Thorpe et al., 2017) and (c) approaches based on a mixed‐fishery implementation of the ICES PGY range concept. My main finding is that it is possible to achieve precautionary yields that are higher than those from assessment‐based F approaches and comparable with a true multispecies reference point, albeit at the cost of greater income variability.

Farcas and Rossberg (2016) have previously argued that using management targets based upon system state (biomass) rather than pressure (fishing mortality) are theoretically superior and will generate increased yield. Our results are consistent with this assertion because the suggest that specifying individual Fs per stock is less important in driving yield than knowing the biomass status of the stock and applying an appropriate harvest control rule. The main benefit of the tailored F approach is reduced variability of income, as the high‐yielding outcomes here all have more variable income streams than the tailored F approaches. If steady income is vital, then I may need to give more consideration as to how I can exploit biomass‐based management to maximise yield whilst minimising income variability before this approach becomes fully practical.

This study supports the widely held view that multispecies management involves the need to make trade‐offs. Because the overall yield is very flat‐topped, it is possible to achieve high levels of precautionary yield, so in practice there is modest tension between yield and risk. There is also little tension between profits and risk, as a number of harvest control rules support both. The more significant tensions are between profits and yield (10% of yield must be sacrificed to achieve maximum profits) and particularly effort (jobs) and profit, where no single approach delivers both.

These results reflect the model framework used and thus come with the caveats discussed previously (Thorpe et al., 2015; Thorpe et al., 2016; Thorpe et al., 2017). The uncertainty estimates are likely to be too low, as they do not reflect structural uncertainty (Spence et al., 2018). I assume that recruitment functions for all stocks can be approximated by the hockey‐stick form, that differences in stock productivity are governed primarily by basic life‐history characteristics such as the asymptotic length and that there are no depensatory stock dynamics. Whilst these assumptions seen reasonable for this set of 21 stocks in the North Sea, they might not translate well into other ecosystems where there may be less size‐structuring (e.g., the Antarctic), greater differences in stock productivity across the fish community (e.g., North Pacific Ocean), or stronger environmental forcing (e.g., Baltic Sea). One key assumption is that of food‐independent growth. Whilst this may be a reasonable simplification for the North Sea, it would be instructive to compare it with alternative model frameworks that do not make this assumption (Blanchard et al., 2014; Spence et al., 2016). The study also assumes a constant environment, whereas in practice overall productivity and hence MSY changes with time (Capuzzo et al., 2017; Larkin, 1977).

This management strategy evaluation makes two further key assumptions, which could be relaxed in future studies. Firstly, I have assumed that measurement errors can be approximated by a timeseries of uncertainties in B (and hence estimates of F) that is 80% autocorrelated with typical SD| of c. 0.19, with an additional lognormally distributed uncertainty of 30% in the implementation of the estimated F TARGET. This is consistent with the North Sea G. morhua assessment (Supporting Information Appendix S1), provided that I assume that there is no systematic long‐term bias. Secondly, I have further assumed that it is possible to determine the appropriate virgin or unfished biomass B 0, associated with the assumed constant environment (which in this study is done by averaging 30 years of no fishing in the operating model and averaging the biomass timeseries, with measurement error, that results). Whilst this is reasonable for ecosystems with a short history of fishing, for others (in practice, including the North Sea) that have long been subject to exploitation, this assumption is more problematic. I have made this assumption because it provides a clear baseline for stock abundance independent of our thinking on what constitutes FCMSY (and hence B MSY‐based proxies), but the methods could easily be adapted for other methods of determining stock reference points; for example, the biomasses at the Nash equilibrium could be used to generate B TARGET.

I have assumed in my evaluation, that the key risk of interest to society can be captured by our risk of stock depletion and the key reward is the gross expected revenue, whereas communities may have other priorities such as sustainable sources of income (even if lower), levels of profitability in the fishery, jobs provided, or preservation of a way of life. Nevertheless, the methods used here could be applied to other relevant metrics, provided they can be identified and quantified in some way and it illustrates the trade‐offs that are often involved in fisheries management.

I have also assumed stochastic (white‐noise) recruitment about a mean dependent on SSB, so there is no serial correlation in the recruitment variability beyond that caused by autocorrelation in SSB. In reality, if the recruitment variability was partly forced by environmental processes, there would probably be some additional autocorrelation, which would tend to reduce the performance of the HCRs below what is simulated here.

In conclusion, I have developed a way of characterising multispecies MSY in terms of expected risk and reward, using a novel risk metric to ensure that no single stock can become severely depleted in a precautionary scenario. With the aid of a length‐structured fish community model I then evaluate a variety of simple harvest control rule strategies for achieving MSY across the North Sea fish community (FCMSY) and compare them with tailored‐F alternatives. I find that simple generic harvest control rules can generate precautionary levels of yield that are competitive with the best multispecies outcomes, albeit at the potentially significant cost of higher income variability. Whilst the model is specific to this fish community in the North Sea, the results may be applicable to other fish communities that are size‐structured, provided that there is no strong evidence for depensatory dynamics, their constituent stocks have productivities that vary in a simple and well understood manner with life‐history traits, stocks are not short‐lived relative to management timescales and changes in environmental forcing applied to the community are modest.

Supporting information

Appendix S1 XXXX

Click here for additional data file. (86.9KB, docx)

ACKNOWLEDGMENTS

Supercomputing support was provided by high performance computing (HPC) at the University of East Anglia.

Thorpe RB. What is multispecies MSY? A worked example from the North Sea. J Fish Biol. 2019;94:1011–1018. 10.1111/jfb.13967

Funding information Funding for this work was provided by the Department for Environment, Food and Rural Affairs (Project MA016), the NERC MERP project and the EU H2020 project PANDORA.

REFERENCES

  1. Allen, K. R. , & Kirkwood, G. P. (1988). Marine mammals In Gulland J. A. (Ed.), Fish population dynamics: The implications for management (pp. 251–269). Chichester, UK: John Wiley and Sons Ltd.. [Google Scholar]
  2. Barrowman, N. J. , & Myers, R. A. (2000). Still more spawner‐recruit curves: The hockey stick and its generalisations. Canadian Journal of Fisheries and Aquatic Sciences, 57, 665–676. [Google Scholar]
  3. Blanchard, J. L. , Andersen, K. H. , Scott, F. , Hintzen, N. T. , Piet, G. , & Jennings, S. (2014). Evaluating targets and trade‐offs among fisheries and conservation objectives using a multispecies size spectrum model. Journal of Applied Ecology, 51(3), 612–622. [Google Scholar]
  4. Caddy, J. F. (1999). Fisheries management in the twenty‐first century. Will new paradigms apply? Reviews in Fish Biology and Fisheries, 9, 1–43. [Google Scholar]
  5. Capuzzo, E. , Lynam, C. P. , Barry, J. , Stephens, D. , Foster, R. M. , Greenwood, N. , … Engelhard, G. H. (2017). A decline in primary production in the North Sea over twenty‐five years, associated with reductions in zooplankton abundance and fish stock recruitment. Global Change Biology, 24, e352–e364. [DOI] [PubMed] [Google Scholar]
  6. FAO . (1966). Department of Fisheries and Department of Public Relations and Legal Affairs, International Fisheries Bodies. Papers presented at the first session of the Committee on Fisheries, 13‐18th June 1966. FAO Fisheries Technical Paper 64, Rome, pp. 41.
  7. FAO . (2001). A fishery manager's guidebook: Management measures and their application FAO Fisheries Technical Paper, 424. Retrieved from http://www.fao.org/docrep/005/y3427e/y3427e00.pdf
  8. Farcas, A. , & Rossberg, A. G. (2016). Maximum sustainable yield from interacting fish stocks in an uncertain world: Two policy choices and underlying trade‐offs. ICES Journal of Marine Science, 73, 2499–2508. [Google Scholar]
  9. Froese, R. , Branch, T. A. , Proelss, A. , Quaas, M. , Sainsbury, K. , & Zimmermann, C. (2011). Generic harvest control rules for European fisheries. Fish and Fisheries, 12(3), 340–351. [Google Scholar]
  10. Guillen, J. , Macher, C. , Merzeraud, M. , Bertignac, M. , Fifas, S. , & Guyader, O. (2013). Estimating MSY and MEY in multi‐species and multi‐fleet fisheries, consequences and limits: An application to the Bay of Biscay mixed fishery. Marine Policy, 40, 64–74. [Google Scholar]
  11. Hall, S. J. , Collie, J. S. , Duplisea, D. E. , Jennings, S. , Bravington, M. , & Link, J. (2006). A length‐based multispecies model for evaluating community responses to fishing. Canadian Journal of Fisheries and Aquatic Sciences, 63, 1344–1359. [Google Scholar]
  12. Hilborn, R. (2010). Pretty Good Yield and exploited fisheries. Marine Policy, 34, 193–196. [Google Scholar]
  13. ICES . (2012). Report of the ICES Advisory Committee 2012, Book 6: North Sea. Copenhagen, Denmark: ICES. [Google Scholar]
  14. ICES . (2013). Report of the Workshop on Guidelines for Management Strategy Evaluations (WKGMSE). 21–23 January 2013, ICES HQ, Copenhagen, Denmark.
  15. ICES . (2016). Advice Basis February 2016. ICES Advice, 2016. Book 1, Section 1.2, pp. 15. Retrieved from http://www.ices.dk/sites/pub/Publication%20Reports/Advice/2016/2016/Introduction_to_advice_2016.pdf
  16. Kell, L. T. , Mosqueiria, I. , Grosjean, P. , Fromentin, J.‐M. , Garcia, D. , Hillary, R. , … Scott, R. D. (2007). FLR: An open‐source framework for the evaluation and development of management strategies. ICES Journal of Marine Science, 64, 640–646. [Google Scholar]
  17. Kvamsdal, S. F. , Eide, A. , Ekerhovd, N.‐A. , Enberg, K. , Gudmundsdottir, A. , Hoel, A. H. , … Vestergaard, N. (2016). Harvest control rules in modern fisheries management. Elementa: Science of the Anthropocene, https://www.elementascience.org/articles/10.12952/journal.elementa.000114/. [Google Scholar]
  18. Larkin, P. A. (1977). An epitaph for the concept of maximum sustainable yield. Transactions of the American Fisheries Society, 106, 1–11. [Google Scholar]
  19. Mackinson, S. , Platts, M. , Garcia, C. , & Lynam, C. (2018). Evaluating the fishery and ecological consequences of the proposed North Sea multi‐annual plan. PLoS One, 13(1), e0190015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Matsuda, H. , & Abrams, P. A. (2006). Maximal yields from multispecies fisheries systems: Rules for systems with multiple trophic levels. Ecological Applications, 16(1), 225–237. [DOI] [PubMed] [Google Scholar]
  21. Mesnil, B. (2012). The hesitant emergence of maximum sustainable yield (MSY) in fisheries policies in Europe. Marine Policy, 36, 473–480. [Google Scholar]
  22. Norrstrom, N. , Casini, M. , & Holmgren, N. M. A. (2017). Nash equilibrium can resolve conflicting maximum sustainable yields in multispecies fisheries management. ICES Journal of Marine Science, 74, 78–90. [Google Scholar]
  23. Pope, J. G. , Bartolino, V. , Kulatska, N. , Bauer, B. , Horbowy, J. , Ribeiro, J. P. C. , … Thorpe, R. (2019). Comparing the steady state results of a range of multispecies models between and across geographical areas by the use of the Jacobian matrix of yield on fishing mortality rate. Fisheries Research, 209, 259–270. [Google Scholar]
  24. Punt, A. E. , Butterworth, D. S. , de Moor, C. L. , De Oliveira, J. A. A. , & Haddon, M. (2016). Management strategy evaluation: Best practices. Fish and Fisheries, 17, 303–334. [Google Scholar]
  25. Rindorf, A. , Cardinale, M. , Shephard, S. , De Oliveira, J. A. A. , Hjorleifsson, E. , Kempf, A. , … Vinther, M. (2017a). Fishing for MSY: Using "pretty good yield" ranges without impairing recruitment. ICES Journal of Marine Science, 74, 525–534. [Google Scholar]
  26. Rindorf, A. , Dichmont, C. M. , Levin, P. S. , Mace, P. , Pascoe, S. , Prellezo, R. , … Clausen, L. W. (2017b). Food for thought: Pretty good multispecies yield. ICES Journal of Marine Science, 74(2), 475–486. [Google Scholar]
  27. Rochet, M. J. , Collie, J. S. , Jennings, S. , & Hall, S. J. (2011). Does selective fishing conserve community biodiversity? Predictions from a length‐based multispecies model. Canadian Journal of Fisheries and Aquatic Sciences, 68, 469–486. [Google Scholar]
  28. Russell, E. S. (1931). Some theoretical considerations on the overfishing problem. Journal Conseil international pour l'exploration de la Mer, 6, 3–20. [Google Scholar]
  29. Sainsbury, K. J. , Punt, A. E. , & Smith, A. D. M. (2000). Design of operational management strategies for achieving fishery ecosystem objectives. ICES Journal of Marine Science, 57, 731–741. [Google Scholar]
  30. Serchuk, F.M. , Rivard, D. , Casey, J. and Mayo R.K. (1999) A conceptual framework for the implementation of the precautionary approach to fisheries management within the Northwest Atlantic Fisheries Organization (NAFO). Proceedings, 5th NMFS NSAW, 1999. NOAA Technical Memorandum. NMFS‐F/SPO‐40.
  31. Smith, D. , Punt, A. , Dowling, N. , Smith, A. , Tuck, G. , & Knuckey, I. (2009). Reconciling approaches to the assessment and management of data‐poor species and fisheries with Australia's Harvest Strategy Policy. Marine and Coastal Fisheries: Dynamics, Management and Ecosystem Science, 1, 244–254. [Google Scholar]
  32. Spence, M. A. , Blackwell, P. G. , & Blanchard, J. (2016). Parameter uncertainty of a dynamic multispecies size spectrum model. Canadian Journal of Fisheries and Aquatic Sciences, 73(4), 589–597. [Google Scholar]
  33. Spence, M. A. , Blanchard, J. L. , Rossberg, A. G. , Heath, M. R. , Heymans, J. J. , Mackinson, S. , … Blackwell, P. G. (2018). A general framework for combining ecosystem models. Fish and Fisheries, 19(6), 1031–1042. [Google Scholar]
  34. Srinivasan, U. T. , Cheung, W. W. L. , Watson, R. , & Sumaila, U. R. (2010). Food security implications of global marine catch losses due to overfishing. Journal of Bioeconomics, 12, 183–200. [Google Scholar]
  35. Thorpe, R. B. , & De Oliveira, J. A. A. (2019). Comparing conceptual frameworks for a fish community MSY (FCMSY) using management strategy evaluation – an example from the North Sea. ICES Journal of Marine Science. 10.1093/icesjms/fsz015. [DOI] [Google Scholar]
  36. Thorpe, R. B. , Dolder, P. J. , Reeves, S. , Robinson, P. , & Jennings, S. (2016). Assessing fishery and ecological consequences of alternate management options for multispecies fisheries. ICES Journal of Marine Science, 73(6), 1503–1512. 10.1093/icesjms/fsw028. [DOI] [Google Scholar]
  37. Thorpe, R. B. , Jennings, S. , & Dolder, P. J. (2017). Risks and benefits of catching pretty good yield in multispecies mixed fisheries. ICES Journal of Marine Science, 74(8), 2097–2106. 10.1093/icesjms/fsx062. [DOI] [Google Scholar]
  38. Thorpe, R. B. , Le Quesne, W. J. F. , Luxford, F. , Collie, J. S. , & Jennings, S. (2015). Evaluation and management implications of uncertainty in a multispecies size‐structured model of population and community responses to fishing. Methods in Ecology and Evolution, 6, 49–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Ulrich, C. , Vermard, Y. , Dolder, P. J. , Brunel, T. , Jardim, E. , Holmes, S. J. , … Rindorf, A. (2016). Achieving maximum sustainable yield in mixed fisheries: A management approach for the North Sea demersal fisheries. ICES Journal of Marine Science, 74(2), 566–575. 10.1093/icesjms/fsw126. [DOI] [Google Scholar]
  40. UN . (2002). Plan of implementation of the World Summit on Sustainable Development – A/CONF 199/20 – Chapter 1 Retrieved from http://www.un-documents.net/jburgptn.htm
  41. Voss, R. , Quaas, M. F. , Schmidt, J. O. , & Hoffmann, J. (2014). Regional trade‐offs from multispecies maximum sustainable yield (MMSY) management options. Marine Ecology Progress Series, 498, 1–12. [Google Scholar]
  42. Wiedenmann, J. , Wilberg, M. J. , Sylvia, A. , & Miller, T. J. (2015). Autocorrelated error in stock assessment estimates: Implications for management strategy evaluation. Fisheries Research, 172, 325–334. [Google Scholar]
  43. Worm, B. , Hilborn, R. , Baum, J. K. , Branch, T. A. , Collie, J. S. , Costello, C. , & Fogarty, M. J. (2009). Rebuilding global fisheries. Science, 31, 578–585. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Appendix S1 XXXX

Click here for additional data file. (86.9KB, docx)

Articles from Journal of Fish Biology are provided here courtesy of Wiley

RESOURCES