CAGI5: Objective performance assessments of predictions based on the Evolutionary Action equation

Abstract

Many computational approaches estimate the effect of coding variants, but their predictions often disagree with each other. These contradictions confound users and raise questions regarding reliability. Performance assessments can indicate the expected accuracy for each method and highlight advantages and limitations. The Critical Assessment of Genome Interpretation (CAGI) community aims to organize objective and systematic assessments: They challenge predictors on unpublished experimental and clinical data and assign independent assessors to evaluate the submissions. We participated in CAGI experiments as predictors, using the Evolutionary Action (EA) method to estimate the fitness effect of coding mutations. EA is untrained, uses homology information, and relies on a formal equation: The fitness effect equals the functional sensitivity to residue changes multiplied by the magnitude of the substitution. In previous CAGI experiments (between 2011 and 2016), our submissions aimed to predict the protein activity of single mutants. In 2018 (CAGI5), we also submitted predictions regarding clinical associations, folding stability, and matching genomic data with phenotype. For all these diverse challenges, we used EA to predict the fitness effect of variants, adjusted to specifically address each question. Our submissions had consistently good performance, suggesting that EA predicts reliably the effects of genetic variants.

1. INTRODUCTION

A major bottleneck towards the interpretation of genomic data is in estimating the fitness effect of individual variants. Most intronic and silent variants tend to have small effects, while most nonsense and frameshift indels tend to have large effects on gene function, but missense variants cannot be classified as a whole. Therefore, many computational approaches aim to predict the impact of missense variants (Cardoso, Andersen, Herrgård, & Sonnenschein, 2015; Ghosh, Oak, & Plon, 2017; Jordan, Ramensky, & Sunyaev, 2010; Katsonis et al., 2014). Some methods rely on structure to predict protein stability effects (Schymkowitz et al., 2005; Worth, Preissner, & Blundell, 2011), since the majority of disease drivers are linked to improper protein folding (Wang & Moult, 2001). Other methods rely on protein homology to find whether a similar substitution is observed in other species (Choi, Sims, Murphy, Miller, & Chan, 2012; Ng & Henikoff, 2001; Reva, Antipin, & Sander, 2007; Stone & Sidow, 2005). However, the vast majority of the methods use machine learning, trained over large data sets to integrate numerous variant features related to structure, homology, function annotation, and population frequency, amongst others (Adzhubei et al., 2010; Bromberg & Rost, 2007; Capriotti et al., 2013; Carter, Douville, Stenson, Cooper, & Karchin, 2013; Fariselli, Martelli, Savojardo, & Casadio, 2015; Karchin et al., 2005; Li et al., 2009; Liu, Jian, & Boerwinkle, 2011; Niroula, Urolagin, & Vihinen, 2015; Schwarz, Cooper, Schuelke, & Seelow, 2014; Wei, Xu, & Dunbrack, 2013; Yue & Moult, 2010). Other machine learning predictors, often called ensemble methods, combine the prediction scores of multiple available predictors (Gonzalez‐Perez & Lopez‐Bigas, 2011; Ioannidis et al., 2016; Ionita‐Laza, McCallum, Xu, & Buxbaum, 2016; Kircher et al., 2014), which may also include pre‐existing ensemble methods (Jagadeesh et al., 2016).

In contrast to these methods that rely on statistics or on machine learning, the Evolutionary Action (EA) approach relies on a formal equation of the genotype‐phenotype relationship and therefore it does not involve any training (Katsonis & Lichtarge, 2014). The required input of EA is sequence homology data, while accounting for protein structure features (solvent accessibility and secondary structure) may slightly improve performance. Briefly, the EA equation states that the fitness effect of a mutation equals the product of the sensitivity of the position with the magnitude of the change. The sensitivity of the position is calculated by quantifying the correlation of the variations in a residue with phylogenetic branching for an alignment of homologous sequences (Lichtarge, Bourne, & Cohen, 1996; Lichtarge & Wilkins, 2010; Mihalek, Res, & Lichtarge, 2004). The magnitude of the change is calculated from substitution likelihood throughout numerous alignments of homologous sequences for the given sensitivity of the position (and structural features, optionally). The calculated product is then normalized to represent the percentile rank of each variant within the protein. This approach has been applied broadly, such as to identify driver genes in liver cancer (Cancer Genome Atlas Research Network, 2017) and parathyroid cancer (Clarke et al., 2018), to interpret the effect of STAT3 variants (Bocchini et al., 2016) and the clinical significance of FARS2 variants (Almannai et al., 2018), to stratify patient survival in head and neck cancer (Neskey et al., 2015) and in colorectal liver metastases (Chun et al., 2017), and to assess the quality of exome sequencing data (Huang et al., 2018; Koire, Katsonis, & Lichtarge, 2016).

Given the plethora and diversity of available computational methods, the potential users become overwhelmed and reluctant to use them without performance assurance. Ideally, the performance of all these methods should be evaluated with objective, systematic, noncircular, and universal assessments. In practice this is impossible, because some methods are not readily available, the performance varies depending on the input data (Hicks, Wheeler, Plon, & Kimmel, 2011), the aim of each method differs, and the test data might have been used in training some of the methods. With these limitations, several assessments have been performed (Ghosh et al., 2017; Mahmood et al., 2017; Miosge et al., 2015). Most often, assessments are performed by the developers to benchmark their method, but they may not be objective when the developers: (a) Use test data that conceptually fit better to their method (e.g., the method was trained on similar data or its features are relevant to the data set), (b) exclude methods that perform better (perhaps because they focus on similar predictor types), (c) use options that increase the performance of their method in a data set (e.g., by choosing sequence alignment or training data) while keeping the default or the same options for the competitive methods, since the same input may work well with one method and poorly with another one (Hicks et al., 2011), and (d) use evaluation metrics that favor their method. Independent users may be objective in assessing the performance of existing methods, but may not be systematic. To avoid misinterpretation, they should use (a) standard assessment metrics, such as the balanced accuracy instead of the overall accuracy when the data is imbalanced (Brodersen, Ong, Stephan, & Buhmann, 2010; Xu et al., 2017), (b) multiple assessment metrics on prioritization, correlation, and proximity of predictions to true values (Vihinen, 2012; Zhang et al., 2017), and (c) identical test data in case some methods do not provide predictions for part of the data set, since some variants may be easy to predict while others may be difficult (Zhang et al., 2017). In either case, the assessor should know the underlying details of each method to avoid circularity, which happens when (a) methods use existing functional or clinical annotation on the same data they make predictions for, (b) methods were trained on annotations of variants that are present in the test data (Grimm et al., 2015; Mahmood et al., 2017), and (c) ensemble methods use as features the predictions of methods that are circular. However, even when an assessment is objective, systematic, and noncircular, good performance in one data set does not necessarily imply good performance in a different set. This is because the input data (e.g., homologous sequences alignment) may be more or less informative for different genes. Therefore, the assessment findings should not be generalized.

The community of Critical Assessment of Genome Interpretation (CAGI) aims to minimize the above biases and produce reliable assessments of the performance of computational approaches that interpret genome data (Hoskins et al., 2017). They organize experiments of multiple challenges that ask predictors to blindly submit answers on new unpublished genome data interpretation. After the prediction deadline passes, CAGI assigns independent assessors to each challenge (they cannot be predictors in the same challenge) to evaluate the anonymized submissions for agreement with the unpublished data. When the evaluations are done, the predictor identity is revealed and the results are presented in a dedicated conference.

We participated in several CAGI challenges as predictors, where we estimated the fitness effect of variants with the Evolutionary Action (EA) method. In older CAGI experiments (CAGI2 to CAGI4) we only submitted predictions on challenges that asked for the impact of individual variants (most often on enzymatic function), where EA was consistently one of the top methods (Katsonis & Lichtarge, 2017). In the CAGI5 experiment we participated in ten diverse challenges, which also included predictions of protein stability and matching exomes to phenotype. To properly address these aims, we complemented EA with simple frameworks that we describe later, in detail. Again, our submissions were consistently amongst the best on each challenge. This suggests that EA can be a reliable predictor of the fitness effect of variants and we may use simple frameworks together with EA to provide answers for a variety of genome interpretation questions.

2. EVOLUTIONARY ACTION THEORY

Let genotype (γ) be the sequence space (Smith, 1970) and phenotype (ϕ) be the fitness landscape (Wright, 1932). Then, each species reaches an optimum in fitness (equilibrium position) that corresponds to their reference genome. Polymorphisms correspond to small displacements away from the equilibrium position and they may accumulate, while deleterious mutations are big steps and they are selected against. Our hypothesis is that γ and ϕ are coupled to each other by a continuous and differentiable function f, and this function also holds across species. Then, a small genotype perturbation dγ will change the fitness phenotype by dϕ, which will be given by:

$$\mathrm{d}\mathrm{\varphi }=\nabla f•\mathrm{d}\mathbf{\gamma }$$ (1)

where ∇f is the gradient of f and • denotes the scalar product. Neglecting the higher order (epistatic) terms, a single amino acid change at sequence position i, from X to Y, will drive a phenotype change Δϕ that equals:

$$\mathrm{\Delta }\mathrm{\varphi }\approx \frac{\partial f}{\partial r_i}·\mathrm{\Delta }{r}_{i,X\to Y}$$ (2)

This action equation states that the fitness effect of a single mutation is proportional to the sensitivity of the phenotype to changes at the position i and the magnitude of the genotype change. Although the function f is unknown, the terms of expression (2) can be approximated from empirical data on protein evolution.

We approximated the gradient ∂f/∂r _i with Evolutionary Trace (ET) scores (Lichtarge et al., 1996; Lichtarge & Wilkins, 2010; Mihalek et al., 2004), because they represent the phylogenetic distance (~Δf) that corresponds to a mutation at each residue i (Δr _i = 1). To measure the magnitude of a substitution (Δr _i,X→Y), we used substitution odds (Henikoff & Henikoff, 1992; Overington, Donnelly, Johnson, Å ali, & Blundell, 1992) calculated for strata of ET scores and structural features (Overington et al., 1992).

3. METHODS

3.1. Calculation of evolutionary action (EA)

The action Δϕ was calculated by Equation (2) and normalized to represent the percentile rank of each variant within the protein in the scale of 0 (benign) to 100 (pathogenic). For example, an EA score of 73 suggests that the variant has larger fitness effect than 73% of random amino acid changes in the protein. Pre‐calculated EA scores are available for all human variants at: http://mammoth.bcm.tmc.edu/EvolutionaryAction. However, for the genes CALM1, GAA, PTEN, and TPMT, we calculated the EA scores after generating new multiple sequence alignments based on the most recent UniRef sequence databases (Suzek et al., 2015). These new alignments rather helped the EA predictions compared with the pre‐calculated ones, since the Pearson's correlation coefficient was higher by 0.04 for GAA, by 0.01 for TPMT, 0.006 for PTEN, and lower by 0.0002 for CALM1.

3.1.1. Multiple sequences alignment

We retrieved the homologous sequences of each protein from three databases, the NCBI nr, the UniRef100, and the UniRef90 (Suzek et al., 2015) with the blastall 2.2.15 software (Altschul et al., 1997). We set a maximum e‐value cutoff of 10⁻⁵ and a minimum sequence identity cutoff of 30% to obtain up to 5,000 homologous sequences with top e‐values. These sequences were compared to the query sequence and they were selected to represent different sequence identity. Typically, up to 160 homologous sequences per protein were selected and aligned with MUSCLE (Edgar, 2004) or ClustalW (Thompson, Gibson, & Higgins, 2002).

3.2. Performance assessment

The performance of the prediction submissions to CAGI5 were assessed by the independent CAGI assessors assigned to each challenge. Here, we summarize the assessments as accurately as possible, according to the CAGI assessor slides presented at the CAGI conference, which are available at: https://genomeinterpretation.org. Typically, assessors used multiple evaluation metrics. Some assessors integrated these metrics to a final score (e.g., CALM1), others presented them in parallel (e.g., TPMT and PTEN), while in other challenges the result was given as a table (e.g., SickKids5). To be brief and informative, we only presented the final score, the central metrics, or representative summary scores for each challenge, respectively. The reader may find further detail, additional metrics, or updated assessments at articles that present the assessment of each CAGI5 challenge, published in the same special issue of Human Mutation.

3.3. Statistical tests

3.3.1. Pearson's correlation coefficient (PCC)

We calculated PCC using the built‐in function of Microsoft Office Excel.

3.3.2. AUC of ROC

The area under the curve (AUC) of the receiver operating characteristic (ROC) was calculated using our own algorithm, written in Perl. The experimental values were transformed to binary values (0 or 1), using as cutoff value 50% of the wild‐type protein function.

3.3.3. Overall and balanced accuracy

The Overall Accuracy (OACC) was measured as OACC = (TP + TN)/(P + N) and the Balanced Accuracy (BACC) was measured as BACC = (TP/P + TN/N)/2, where TP = True positive; TN = True negative; P = Positive; N = Negative.

4. RESULTS

The CAGI5 experiment included 14 challenges that represent various genotype–phenotype association problems. We used the EA method to submit predictions in 10 challenges. We did not participate in the "Regulation Saturation," "MaPSy", and "Vex‐seq" challenges because they did not involve missense variants, nor in the "Annotate all missense" challenge because it did not involve performance assessment. Our predictions to the Intellectual Disability panel challenge were largely incomplete and therefore, we focus on the remaining nine challenges. These may be classified into predictions of: (a) The effect of variants on protein function (CALM1, GAA, and PCM1); (b) the effect of variants on protein stability (PTEN and TPMT, Frataxin); (c) the clinical effect of variants (ENIGMA and CHEK2); and (d) the aggregated effect of germline variants on disease (SickKids5, Clotting Disease). Below, we present each of the nine challenges with brief descriptions of the data sets, our submissions, and the performance evaluations of the CAGI assessors. We also added a paragraph with the title of “other considerations,” where we provide complementary analysis (we performed) and clarifications that may help to better understand the assessments.

4.1. Effect of variants on protein function

Three challenges asked for predictions of a variant's effect on protein function, which was measured with: (a) A high‐throughput yeast complementation assay (CALM1), (b) an enzymatic activity assay (GAA), or (c) phenotype features (brain ventricle pictures) in a zebrafish model (PCM1).

4.1.1. Challenge 1 – CALM1

Predict the fitness effect of 1,813 variants of the human calmodulin.

4.1.1.1. Challenge description

Mutations in calmodulin are causally associated with two cardiac arrhythmias: Catecholaminergic ventricular tachycardia (Nyegaard et al., 2012) and long QT syndrome (Crotti et al., 2013). The laboratory of Fritz Roth assessed a large library of calmodulin variants using a high‐throughput yeast complementation assay. They used random codon replacement to generate variants on human CALM1 and they assessed the ability of each variant to rescue a yeast strain carrying a temperature‐sensitive allele of the yeast calmodulin orthologue CMD1 (Sun et al., 2016). The assay output was scaled between 0 (no growth) and 1 (wild‐type‐like growth) and that score was able to separate pathogenic from nonpathogenic variants (Weile et al., 2017). Two replicates for each measurement were used to estimate the experimental standard deviation (SD).

4.1.1.2. EA approach

We used EA to address this challenge, assuming that each mutation reduces the calmodulin function proportionally to its EA score (we used the NP_008819 sequence of CALM1). Since the distribution of experimental values was given, we matched the EA scores with values that followed the given distribution by sorting them from highest to lowest impact (e.g., large EA values match small experimental values, because they both suggest high impact). In our first submission (EA1) we used the distribution as is, while in our second submission (EA2) we moved all counts with a negative value into the first positive interval (0–0.05) because there is no interpretation for negative experimental values.

4.1.1.3. CAGI assessment (Zhang et al., 2019)

There were seven submissions from four research groups. The CAGI assessor used 16 different measures of evaluation, which they divided into three categories (rank, original value, and rescaled value). They averaged the z‐scores within each category and then summed those averages to assess performance. To ensure fair evaluation, the CAGI assessors scaled the prediction scores of each submission to fit the distribution of experimental values, therefore, upon this scaling our two submissions look almost identical. The performance evaluation is given in Figure 1a. The assessor also used 5,000 simulated replicates of each submission to find that the EA predictions were consistently better than all submissions from the other research teams.

Figure 1.

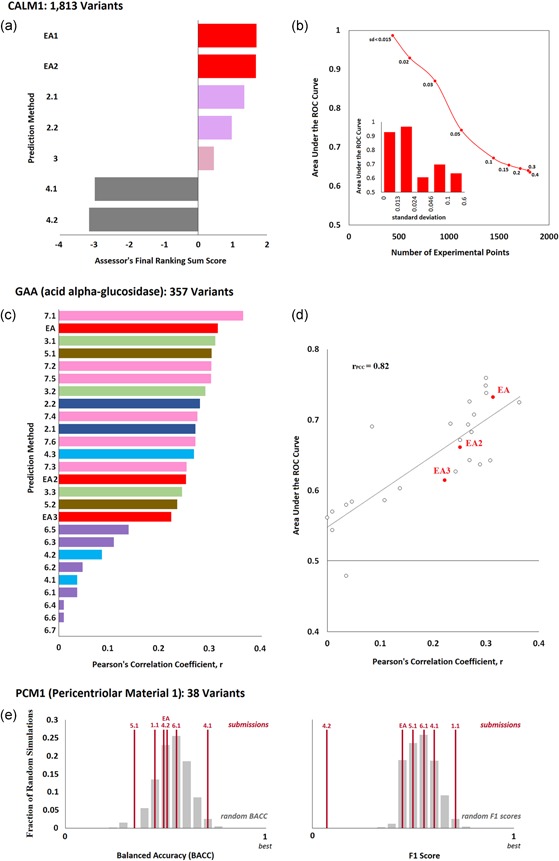
Effect of variants on protein function. (a) CALM1 challenge: Seven submissions aimed to predict the fitness effect of 1,813 variants of the human calmodulin measured with a competitive growth assay in yeast. The bar plot shows the final ranking sum scores for each submission, as calculated by the CAGI assessor. This score was derived from 16 different evaluation measures that represent three types of agreement (rank, original value, and rescaled value), and it is the sum of the average z‐scores of each type of agreement. Submissions from the same research team appear with the same color. (b) The area under the ROC curve (AUC) that corresponds to the Evolutionary Action submission (EA1) for data subsets defined by the experimental standard deviation values (SD). In the main panel, AUC was plotted as a function of the number of variants that have smaller SD than a maximum cutoff. The values next to each data point show the maximum standard deviation. In the insert bar plot, AUC was computed for five bins of variants that were created by sorting the variants according to their SD values and splitting them into nearly‐equal data point sets. (c) GAA challenge: 26 submissions aimed to predict the enzymatic activity of 357 variants of the human acid alpha‐glucosidase. The CAGI assessors used the Pearson's correlation coefficient (PCC) to assess the performance of the submissions. The bar plot presents the PCC for each method as calculated by the authors. (d) The area under the ROC curve versus the PCC values. The EA submissions are shown with red color. (e) PCM1 Challenge: Six submissions aimed to predict the effect of 38 human PCM1 variants on zebrafish brain development. The balanced accuracy (left plot) and F1 scores (right plot) of each submission are shown as vertical red lines, while the gray bars represent the corresponding distributions of 10,000 randomly generated predictions (calculated by the CAGI assessor). ROC, receiver operating characteristic

4.1.1.4. Other considerations

Although EA was the best submission of the CALM1 challenge, the agreement with the experimental data is not optimal, with an area under the ROC curve (AUC) of 0.63. Typically, the AUC of EA is above 0.8 for other data sets (Katsonis & Lichtarge, 2014). To find whether this discrepancy is related to the accuracy of the experimental values, we considered their standard deviations (SD). Since larger SD values indicate larger experimental errors, we sorted the variants by their SD values, divided them into five bins with nearly equal number of variants in each bin, and calculated the AUC for each bin (Figure 1b insert panel). Bins with low SD values (<0.024) yield AUC above 0.9, while bins with higher SD values yield AUC between 0.6 and 0.7. As a result, the agreement between predictions and experimental values improves dramatically when the experimental data are restricted to a certain SD value cutoff (Figure 1b), reaching 0.87 for 861 variants with S < 0.03 and 0.99 for 439 variants with SD < 0.015. Similar improvement was also seen for the submissions from the group 2 and the group 3, all of which yield indistinguishable performance to EA for SD < 0.02, indicating that selecting which experimental data to be used to assess the performance of computational methods requires caution.

4.1.2. Challenge 2 ‐ GAA

Predict the enzymatic activity of 357 variants of the human GAA gene.

4.1.2.1. Challenge description

Mutations in the GAA gene (acid alpha‐glucosidase) may cause Pompe disease (glycogen storage disease II) due to accumulation of lysosomal glycogen in multiple tissues (Kroos, Hoogeveen‐Westerveld, van der Ploeg, & Reuser, 2012). BioMarin Pharmaceutical measured the enzymatic activity of 357 missense mutations found in the ExAC data set (Lek et al., 2016) using an immortalized Pompe patient fibroblast cell line that has no GAA activity. The GAA activity was measured with a fluorogenic substrate (4‐methylumbelliferyl α‐D‐glucoside) and it was normalized to be the percentage of wild‐type GAA activity in at least three independent experiments. Participants were asked to submit predictions on the effect of the variants on GAA enzymatic activity as a numeric value ranging from 0 (no activity) to 1 (wild‐type level of activity), or > 1 if the predicted activity is greater than wild‐type activity.

4.1.2.2. EA approach

We used EA as our primary method to address this challenge, assuming that all mutations reduce the GAA function and that EA scores represent the percentage of function loss. Since EA scores vary between 0 (wild‐type) and 100 (loss of function), the activity of each GAA mutant was estimated as 1‐EA/100. In addition to the primary submission that used the default EA pipeline, we also submitted two alternatives. In the first alternative, EA2, we only used sequences with up to 50% sequence identity with each other (UniRef50), because when we did so, the most important residues clustered better in the structure of the GAA protein. In the second alternative, EA3, instead of the default Evolutionary Trace algorithm we used the pair‐interaction ET, a version that accounts for the structural neighbors of the protein residues (Wilkins et al., 2013). Both these alternatives performed worse than EA, indicating that they resulted in the loss of valuable input data and the alteration of critical data analysis, respectively.

4.1.2.3. CAGI assessment

There were 26 submissions from seven research groups and the CAGI assessors used the Pearson's correlation coefficient (PCC) as criterion of evaluation. Because the assessors acknowledged errors in the assessment calculations presented at the conference, we independently calculated PCC (Figure 1c) for all submissions. The EA submission had the second‐best PCC for predicting the GAA function amongst the 26 submissions, according to this calculation.

4.1.2.4. Other considerations

The assessment of this challenge was based on a single evaluation metric, the PCC, rather that multiple metrics that represent different types of agreement. PCC is a standard metric that informs about the correlation of predictions to experimental data, however, it would be informative to also use metrics that test the ability to prioritize the variants and the proximity of predictions to experimental values. For example, using the ROC as the evaluation metric, although it correlates strongly to PCC, would find a different method at the top (Figure 1d). Moreover, using this data set of GAA variants may raise concerns regarding circularity. Although the challenge used unpublished experimental data, the facts that all these mutations were present in ExAC (Lek et al., 2016) and that 75 mutations had already been reported as disease associated in HGMD (Stenson et al., 2003) may play to the advantage of methods trained on clinical data overlapping with some of those variants and methods that use the population allele frequency as a prediction feature.

4.1.3. Challenge 3 – PCM1

Predict the effect of 38 human PCM1 variants on zebrafish brain development.

4.1.3.1. Challenge description

The Katsanis lab assayed 38 PCM1 variants implicated as a risk factor for schizophrenia in a zebrafish model with suppressed native PCM1 protein to determine their impact on the posterior ventricle area. For each mutation, the brain ventricle formation of zebrafish was compared with that with wild‐type human PCM1 and that with no PCM1 injection (Niederriter et al., 2013). Images were taken and their differences were estimated with automated image processing.

4.1.3.2. EA approach

Briefly, we used EA to classify the PCM1 variants as pathogenic (EA > 70), benign (EA < 30), and hypomorphic (30 ≤ EA ≤ 70). We also submitted p‐values that depend exponentially on EA such that p‐values of 0.05 correspond to our EA cutoffs of 30 for benign and 70 for pathogenic.

4.1.3.3. CAGI assessment (Monzon et al., 2019)

There were seven submissions from six research groups. The CAGI assessor used five measures of evaluation to rank the methods and summed the five ranks to calculate a final ranking score. The CAGI assessor also generated a set of 10,000 random predictions and plotted the distributions for select evaluation measures (Figure 1e). Although the 4.1 and 1.1 methods had p‐values <0.05 in BACC and F1, respectively, in both cases the p‐value in the other measure was above 0.05. This fact together with the borderline significance lead to the conclusion that there was no agreement between experimental data and predictions. In that limited context, the assessor ranked EA fourth amongst the seven submissions.

4.1.3.4. Other considerations

We were not able to find any significant agreement between predictions and experimental data (neither for EA, nor for the rest submissions) when we used ROC and BACC measures. The area under the ROC values we calculated for the different submissions ranged from 0.32 to 0.55, suggesting that all the predictions were random and that the final ranking is tentative and not informative. Unfortunately, we cannot provide any additional insight, since the experimental data do not come with confidence values (e.g., SD) and the assay is too complex to understand dependencies on the genetic context and other factors.

4.2. Effect of variants on protein stability

Two challenges asked for predictions of the effect of variants on protein stability, which was measured by: (a) The presence of EGFP fused to the mutated proteins (TPMT and PTEN), and (b) using circular dichroism and intrinsic fluorescence spectra to calculate a ΔΔG^H2O value of the unfolding free energy between the mutant and wild‐type protein (Frataxin).

4.2.1. Challenge 4 ‐ TPMT and PTEN

Predict the effect of 4,002 PTEN and 3,952 TPMT variants on protein stability.

4.2.1.1. Challenge description

The Fowler lab measured the steady state abundance of thousands protein variants of phosphatase and tensin homolog (PTEN) and thiopurine S‐methyltransferase (TPMT) in parallel (Matreyek et al., 2018). Mutants were barcoded and fused to EGFP (fluorescent reporter system). The variant stability dictated the abundance of the fusion protein and thus the cells were flow sorted into bins. Deep sequencing was used to quantify the frequency of each variant in each bin and calculate a stability score (0 meaning unstable, 1 meaning wild‐type stability, and > 1 meaning more stable than wild‐type).

4.2.1.2. EA approach

EA measures the fitness effect of each variant, which may be related to folding or to other functional factors required for proper protein activity. Thus, protein stability (what the challenge asks for) is just one of many components that govern the fitness effect (what EA scores represent). To account for this discrepancy and make proper prediction for this challenge, we assumed that the solvent accessibility of each protein residue can be used to de‐couple the effect on folding and on dynamics (protein stability) from the effect on more directly functional interactions (effect beyond folding). Therefore, we calculated for each residue the fraction of its solvent inaccessible area, w_fr (we used the DSSP software (Joosten et al., 2011) and the structures with PDB ID of 1d5r for PTEN and 2bzg for TPMT). To find whether this de‐coupling helps, we made a second submission to serve as a control, where w_fr was set to 1 for all residues. The predicted values were calculated as: 1−w_fr·EA/100 (it matches the experimental value range of 0 (unstable) to 1 (wt stability). Silent variants were assumed to be stable (EA = 0). Nonsense variants were annotated as unstable (EA = 100) or as stable (EA = 0), if they occurred inside or outside of the folded domains (according to the PDB structures we mentioned), respectively. To obtain the EA scores, we used the NP_000305 sequence of PTEN and the NP_000358 sequence of TPMT.

4.2.1.3. CAGI assessment (Pejaver et al., 2019)

There were 16 submissions from eight research groups in this challenge and the CAGI assessor evaluated them by using correlation and class prediction metrics. The correlations were assessed either by the Pearson's correlation coefficient (Figure 2a) or by the Spearman's rank correlation coefficient (there were only minor differences in the assessments of the two metrics), in both of which our primary submission was the best approach and our submission without solvent accessibility weighting placed third. The CAGI assessor noticed that the experimental values followed a smooth distribution with a shallow peak at wild‐type stability (consistent with the smooth distribution of EA values), which contradicts the bimodal distributions of common classifiers, such as SIFT (Ng & Henikoff, 2001), SNAP (Hecht, Bromberg, & Rost, 2015), and PolyPhen2 (Adzhubei et al., 2010). Therefore, they also tested the performance of the submissions when the experimental data were binned in classes (either tri‐class or bi‐class groups). They calculated the accuracy of each submission to predict these classes, but, surprisingly, these assessments did not correlate with the PCC ranking (see Figure 2b). Our primary submission accounting for solvent accessibility ranked 6th in the class‐based assessments. The methods that performed best in the class‐based assessments ranked 14th and 15th in PCC. Therefore, our primary, solvent accessibility‐adjusted EA submission had the best performance when the two assessments were combined. The control EA submission also did well, however, just only slightly less so.

Figure 2.

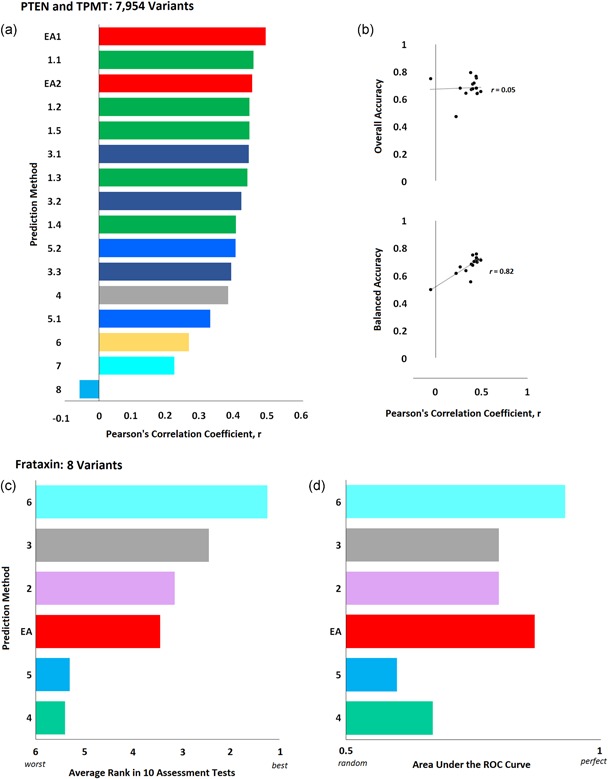
Effect of variants on protein stability. (a) PTEN and TPMT Challenge: Sixteen submissions aimed to predict the effect of 4,002 PTEN and 3,952 TPMT variants on protein stability measured with a fluorescent reporter system. The bars represent the Pearson's correlation coefficient of each submission (colors correspond to each research team) as calculated by the CAGI assessor. (b) The overall accuracy (upper plot) and the balanced accuracy (bottom plot) of each submission as a function of the Pearson's correlation coefficient (the accuracy was calculated by the authors). (c) Frataxin Challenge: Six submissions aimed to predict the difference in unfolding free energy of eight frataxin variants (ΔΔG^H2O). The CAGI assessor used the average rank of each submission according to 10 evaluation scores (including Pearson's, Matthew's, Spearman's rank, and Kendall tau rank correlation coefficients, root mean square error, mean absolute error, area under the ROC curve, and weighted accuracy). The bar plot shows the average rank (the actual values were calculated by the authors, since they were not available in the assessor slides). (d) The area under the ROC curve, as calculated by the assessor, for the different submissions. CAGI, Critical Assessment of Genome Interpretation; ROC, receiver operating characteristic

4.2.1.4. Other considerations

To find whether the performance of the EA submissions was robust for mutations with different solvent accessibility, we divided the data set into three parts: 924 completely buried mutations, 4,634 partially exposed mutations (solvent accessibility 1–99 Å), and 2,396 exposed mutations. The PCC we measured for EA1 and EA2, respectively, was 0.47 and 0.5 for buried mutations, 0.47 and 0.46 for partially exposed mutations, 0.32 and 0.26 for exposed mutations. The worse performance of the predictions in the exposed residues may be attributed to the fact that this group contains more stabilizing variants (37% had experimental score higher than 1, while this percentage was 20% for partially buried mutations and only 8% for buried mutations). We also compared the performance of our submissions in each protein separately. The two submissions had nearly identical performance on the TPTM variants and EA1 performed better than EA2 on the PTEN variants. The reasons for this difference may be related to features of the two structures, as PTEN variants had about 40% higher solvent accessibility than TPTM variants on average. The dramatic difference between the class‐based assessment and the correlation assessment is due to using the overall accuracy (rate of true calls) instead of the balanced accuracy (average rate of true positive calls and true negative calls) when the classes and the prediction calls have unbalanced numbers of variants. For example, a cutoff of 50% of the wild‐type experimental value classifies the experimental data into 6,000 benign variants and only 1,954 pathogenic variants. Then, a trivial predictor that assigns all variants as benign will have an overall accuracy of more than 0.75, although it would be random (0.5) for a cutoff of 80% of the wild‐type experimental value that yields equal numbers of pathogenic and benign variants. In contrast, the same trivial predictor will have balanced accuracy of 0.5, independently of the cutoff used. Therefore, the balanced accuracy is a reliable assessment metric and correlates with PCC, while the overall accuracy does not (Figure 2b). More metrics, such as the precision and recall values, the F‐measure, and the Matthews correlation coefficient may be also needed for better understanding of the performance. A concern for the tri‐class assessment is that the average standard deviation of the experimental values (0.22) is perhaps too large to separate wild‐type stability (1 ± 0.1) from the stabilizing variants (>1.2), so, in practice, these two classes are indistinguishable.

4.2.2. Challenge 5 ‐ frataxin

Predict the difference in unfolding free energy of eight frataxin variants compared with wild‐type.

4.2.2.1. Challenge description

The thermodynamic stability of the frataxin variants was measured by the group of Roberta Chiaraluce and Valerio Consalvi, by monitoring spectral changes (far‐UV circular dichroism and intrinsic fluorescence emission). The ΔΔG^H2O value was calculated between each variant and the wild‐type protein.

4.2.2.2. EA approach

We assumed that the difference in the unfolding free energy is proportional to the fitness effect of the variant and therefore we used the NP_000135 sequence of frataxin to calculate the EA scores. Since EA is not designed to predict folding stability and because we did not use any training data, we simply made a linear transformation to convert the EA scores to ΔΔG^H2O values wherein EA scores of 30 were set to 0 kcal/mol and EA scores of 100 were arbitrarily set to − 3 kcal/mol.

4.2.2.3. CAGI assessment (Savojardo et al., 2019)

There were 12 submissions from six research groups in this challenge. The CAGI assessor used the average rank of 10 scores to assess the performance of the predictions (five correlations scores and five difference‐based scores) considering the best submission of each group (we only had one submission). Overall, EA was ranked at the fourth place in this challenge (Figure 2c), although it was the second‐best submission according to the area under the ROC curve rank (Figure 2d) and to the mean absolute error rank.

4.2.2.4. Other considerations

The main concern on driving any conclusions based on this challenge is the small number of variants (only eight variants). When we did a leave one variant out Pearson's correlation analysis for our submission, it yield a standard deviation of 0.12, which is large (25%) compared with the computed PCC value. Therefore, the assessment results are indicative rather than robust. The PCC of 0.49 for our submission indicates a good correlation with the experimental data and the AUC of 0.87 suggests that EA can prioritize well the frataxin variants. Perhaps, using better scaling and separating the folding effect of EA from the effect on other interactions (like we did in the PTEN and TMTP challenge) may improve the performance, although one should guard against over‐interpretation given the small number of variants.

4.3. Clinical effect of variants

Two challenges asked for predictions on the clinical consequences of variants in (a) the BRCA1 and BRCA2 genes and (b) the CHEK2 gene. The BRCA1 and BRCA2 variants were annotated by experts and they represent confident associations, in contrast to the CHEK2 variants that were observations in cases and controls and their clinical significance is still unknown.

4.3.1. Challenge 6 ‐ ENIGMA

Predict the clinical effect of 146 BRCA1 and 178 BRCA2 variants.

4.3.1.1. Challenge description

Germline variants of unknown significance in BRCA1 and BRCA2 genes have been linked to breast cancer and are perplexing to clinicians and patients alike. The ENIGMA consortium (https://enigmaconsortium.org/) classified BRCA1 and BRCA2 variants according to the IARC 5‐tier classification scheme using multifactorial likelihood analysis. The procedure assesses clinically‐calibrated bioinformatics information and clinical information (pathology, segregation, co‐occurrence, family history, and case‐control) for each variant to produce a best guess for the likelihood of pathogenicity. Likelihood values were calibrated against the features of known high‐risk cancer‐causing variants in BRCA1/2 (Goldgar et al., 2008; Plon et al., 2008).

4.3.1.2. EA approach

We used EA scores as the probability of each variant to be pathogenic. In our first submission, we used the NP_009225 sequence of BRCA1 and the NP_000050 sequence for BRCA2. In our second submission, we used the same EA scores for BRCA2, but for BRCA1 we used four additional BRCA1 transcripts (NP_009228, NP_009229, NP_009230, and NP_009231) that differed between each other in alternative splicing. To account for the different BRCA1 transcripts, the EA scores were multiplied by the fraction of transcripts that had an amino acid present at each residue position, respectively.

4.3.1.3. CAGI assessment (Cline et al., 2019)

There were 14 submissions from six research groups in this challenge. The CAGI assessor used a multiclass ROC AUC to assess the performance of the predictions (Figure 3a). The performance of our two EA submissions was very similar to each other and ranked second compared with all other research groups. Interestingly, the top group was a genetic testing company that specializes on BRCA genes. Their four submissions relied on machine learning, trained on clinical data that combined BRCA variants annotations from the literature (HGMD database), population frequencies, splice impact, and six third‐party functional prediction algorithms, amongst others. The CAGI assessor noticed that the EA scores were higher for likely pathogenic variants than for strongly pathogenic variants (Figure 3b). This difference was attributed to the ENIGMA classification procedure that assessed variants that affect splicing only as strongly pathogenic (not as likely pathogenic variants) and to the fact that evolution‐based predictors, such as EA, do not account for splicing effects.

Figure 3.

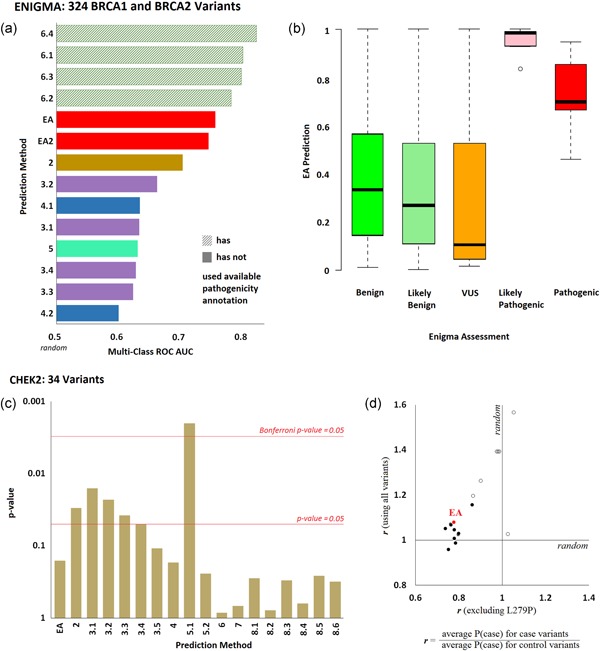
Effect of variants on clinical presentation. (a) ENIGMA Challenge: Fourteen submissions aimed to predict the clinical effect of 146 BRCA1 and 178 BRCA2 variants, which were classified using multifactorial likelihood analysis. The bars represent the multiclass area under the ROC curves of each submission, as calculated by the CAGI assessor (colors correspond to each research team; the pattern fill corresponds to submissions that used clinical annotation from other sources to predict the ENIGMA annotations). (b) The whisker diagram shows the EA prediction values for each pathogenicity class. (c) CHEK2 Challenge: Eighteen submissions aimed to predict the probability for each of 34 CHEK2 variants to occur in a case cohort rather than in a control cohort. The bar plot shows the p‐values for the agreement of predictions and observations, as calculated by the CAGI assessor. The red horizontal lines correspond to statistical significance levels and they were added by the authors. (d) The ratio of the average prediction P(case) for the variants seen in cases over the average prediction P(case) for the variants seen in controls, when the L279P variant was included (y‐axis) or excluded (x‐axis). Open circles represent submissions in the scale of 0–1, while the solid circles represent submissions in the scale of 0.5–1. The EA submission is shown with red color. CAGI, Critical Assessment of Genome Interpretation; EA, Evolutionary Action; ROC, receiver operating characteristic

4.3.1.4. Other considerations

The performance of EA in this challenge was remarkable. First, EA makes unbiased predictions that are untrained and that do not account for splicing effects. Yet, despite the fact that several of the pathogenic variants affected splicing, our submissions still performed better than machine learning approaches that used splicing information as prediction features. Second, closer examination provides a simple explanation for the reason that the genetic testing company achieved better predictions. Their submissions relied mostly on annotations already available in literature rather than on de novo predictions of the variant effects. This is because the variants in the challenge, although not annotated previously by the strict classification scheme of ENIGMA, had been flagged in public databases as being associated to disease, or not. To be clear, the HGMD database already listed 16 of the 17 pathogenic BRCA variants as cancer drivers and these associations were directly used in the submissions of the genetic testing company. Due to this circularity, we should be cautious with the interpretation of the assessment: Literature‐based methods will work well on variants with available annotations, but for rare variants of truly unknown significance their performance will be worse. At a lesser degree, circularity also happens when machine learning methods use some of these BRCA variants in training, resulting in slightly better performance. This discussion highlights important limitations due to the difficulty of separating training data from testing.

4.3.2. Challenge 7 – CHEK2

Predict the probability that each of 34 CHEK2 variants occurs in cases.

4.3.2.1. Challenge description

Germline variants in CHEK2 have been linked to breast cancer. About 1,000 Latina breast cancer cases and 1,000 ancestry matched controls were sequenced for CHEK2 variants. The predictors were asked to provide the probability that each variant was seen in cases rather than in controls.

4.3.2.2. EA approach

We used the EA scores to predict the fitness effect of missense variants. Then, we estimated the probability (p) that each variant is seen in cases with a linear transformation of the EA scores: p = 0.5 + EA/200. With this transformation, EA of 0 yields p = 0.5 (benign variants have even probability in cases and controls) and EA of 100 yields p = 1 (pathogenic variants only occur in cases).

4.3.2.3. CAGI assessment (Voskanian et al., 2019)

There were 18 submissions from eight research groups in this challenge. The CAGI assessor evaluated the performance by calculating p‐values using a generalized linear model. Five submissions achieved p‐values <0.05, with one of them <.005 (Figure 3c).

4.3.2.4. Other considerations

The interpretation of this challenge is problematic since the exact nature of the association between CHEK2 and breast cancer is debatable (Apostolou & Papasotiriou, 2017). Moreover, the frequency of the variants is too low to make pathogenicity annotations: Twenty‐four variants were seen once (either in a case or in a control), six variants two times, two variants three times, one variant four times, and one variant 17 times. Given this fact, the predictions cannot be assessed unless an erroneous hypothesis is assumed correct: Variants observed in cases are drivers and variants observed in controls are benign. The problem with this reasoning is that benign variants are expected to be evenly seen in cases and controls, while driver variants may also appear in controls with a lower frequency than in cases. For example, of the 24 variants only seen once, eight variants were present in controls, and 16 variants were present in cases. This means that approximately eight variants seen once in cases (50%) are expected to be benign, but they were incorrectly treated as pathogenic for the assessment. Perhaps, only one variant can be clearly associated with pathogenicity based on these clinical data: the L279P variant was seen in 14 cases and only in three controls. In our submission, L279P was given a probability of p = 0.9232, which was the second largest probability we predicted amongst the 34 variants. Besides our submission, 10 of the 17 other submissions scored L279P within the top five most pathogenic variants. To find whether the predictions for the rest variants agree with the clinical observations, we calculated for each submission the ratio of the average P(case) prediction of variants seen in cases over the average P(case) prediction of variants seen in controls, using all variants and excluding L279P (Figure 3d). While 16 of the 18 methods had ratio above 1 when L279P was included, only two methods had ratio above 1 when L279 was excluded. In summary, we should be cautious with the interpretation of this assessment, as the clinical observations may not indicate disease associations.

4.4. Aggregated effect of germline variants on disease

Two challenges provided exome sequencing data and asked predictors to assign phenotype to each exome. These challenges were to: (a) Identify the disease class associated with each of 24 exomes and match each exome to clinical descriptions (SickKids5), and (b) separate the patients with either of two distinct diseases (clotting disease). These challenges generally fall beyond the immediate current questions addressed by EA, but were seen as valuable learning opportunities.

4.4.1. Challenge 8 – SickKids5

Predict the disease class of each individual based on their genetic variants and match the sequencing data to the corresponding clinical description.

4.4.1.1. Challenge description

This challenge involved 24 children with either of three genetic disorder classes: Six eye disorders, seven neurogenetic diseases, and 11 connective tissue disorders. Predictors were given the unlinked genomes and phenotypic descriptions for 24 undiagnosed children from the SickKids Genome Clinic Panel Sequencing Cohort. The challenge was to predict what class of disease is associated with each genome, and which genome corresponds to which specific clinical description. The data were provided by the Hospital for Sick Children at Toronto.

4.4.1.2. EA approach

For each exome, we predicted the function loss of each gene due to genetic variants. Specifically, we assumed the EA score of each variant is the percentage of function loss in that gene. For genes with multiple mutations i, their loss of function LOF_g was calculated as: LOF_g = 1−∏(1−EA_i/100), where ∏ indicates product for all mutations in that gene. LOF_g was weighted for the ability of each gene to tolerate mutations (w_g), which we calculated as the percentile rank of the average EA score of mutations seen in the gnomAD data (Lek et al., 2016) for that gene. Then, the weighted LOF_g scores were used as starting values of the genes in a diffusion process (Lin et al., 2018) across an interaction network of genes and diseases (Davis et al., 2017; Gutierrez‐Sacristan et al., 2015; Mattingly, Colby, Forrest, & Boyer, 2003; Stark et al., 2006; Szklarczyk et al., 2015). After diffusion, we measured the signal on each disease class or on specific symptoms of the clinical descriptions. To estimate the probability that each individual belongs to each disorder class (eye disorder, neurogenetic disease, or connective tissue disorder), we sorted the individuals by their diffusion signal on the class and calculated the percentile rank (more signal yields higher probability). To link the exomes to phenotypic descriptions, first we narrowed down the possible links by using gender and ethnic information. To identify the gender, we used the concordance of reads (zygosity) in the X chromosome. To identify the ethnic background of each exome, we estimated its proximity, P, to the exomes of each ethnic group, e, available in the 1000 Genomes Project (The Genomes Project Consortium et al., 2015), as P_e = ∏(A_e/A_g)_i, where A_e and A_g are the ethnic and global allele frequencies, respectively, and ∏ indicates the product for all variants i with non‐zero ethnic allele frequencies. After we narrowed down the possible matches, we used the diffusion scores on select symptoms of the clinical report and we manually drew matches. Due to the lack of automation, by the closing time of the challenge, we had matches for only 12 of the 24 exomes.

4.4.1.3. CAGI assessment (Kasak et al., 2019)

There were nine submissions from eight research groups in this challenge. To assess the ability to predict the correct genetic disorder class (eye, neurogenetic, or connective tissue disorder), the CAGI assessor counted the number of individuals for whom the correct disorder class was given the highest (1st), intermediate (2nd), and lowest (3rd) probability. A perfect prediction would have 24 individuals in the 1st bin and a random prediction would have equal number of individuals in the three bins. The EA‐based submission had 11 individuals in the 1st bin, one individual shared in the 1st and 2nd bins, eight individuals in the 2nd bin, and four individuals in the 3rd bin and it was one of the three submissions with nonrandom performance (all three had 11 individuals in the 1st bin). To calculate a performance score for each method that reflects this table, we added 1 for each individual in the 1st bin and subtracted 1 for each individual in the third bin, such that random predictions will score 0 and perfect predictions will score 24 (Figure 4a). In the second part of this challenge, the CAGI assessor assessed the submissions by counting the number of correct matches, defined as individuals for whom the correct clinical description was given the highest probability (Figure 4b). Our submission was ranked the third best, with five correct matches, when the two better submissions had six correct matches each. However, while all other submissions predicted best matches for all 24 exomes, we only predicted matches for 12 exomes (for the rest 12 exomes we submitted a flat probability of 0.1).

Figure 4.

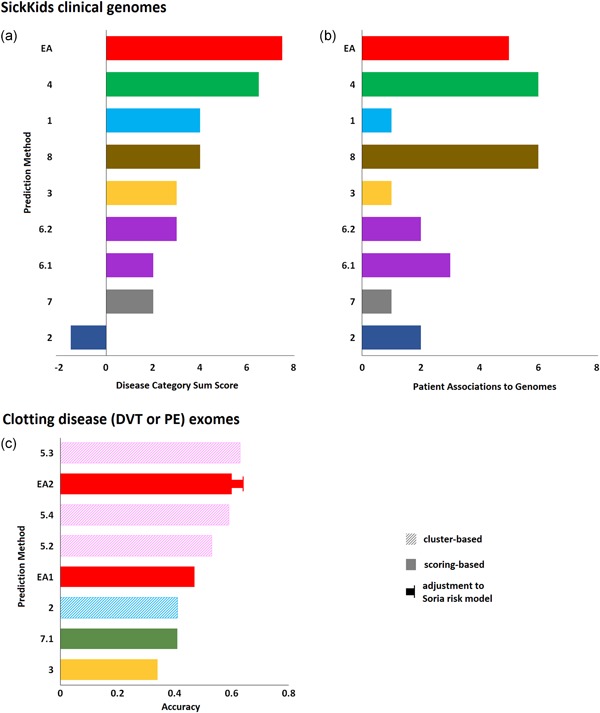
Exome sequencing data and phenotype matching. (a) Sick Kids5 Challenge: Nine submissions aimed to predict the disease category (eye, neurogenetic, or connective tissue disorders) of 24 children based on their exomic data and to match each exome to the corresponding clinical description. The CAGI assessor presented a table that listed the number of exomes for which the correct disease category was ranked first, second, or third, by each submission. Based on that table, we calculated a sum score for each method by adding 1, 0, or − 1 each time the correct phenotype was ranked first, second, or third, respectively. The bars represent that score (the colors correspond to research teams). (b) The number of individuals that were matched to the correct phenotypic description with the highest probability (than the rest phenotypic descriptions) by each submission. The EA submission was incomplete, providing matches for only 12 of the 24 individuals through human evaluation of predicted values for several clinical symptoms. (c) Clotting disease: Eight submissions aimed to separate patients with venous thromboembolism from atrial fibrillation patients based on their exome data. The bars represent the accuracy of the separation, as calculated by the CAGI assessor. Pattern fills represent cluster‐based methods that yield binary classifications and solid fills represent scoring‐based (impact burden) methods that yield continuous probabilities (colors correspond to research groups). The CAGI assessor used a probability cutoff of p = 0.5 to assess the methods, or they adjusted the cutoff (p = 0.4 for the EA submission) to match the specificity of a current genetic risk model. CAGI, Critical Assessment of Genome Interpretation; EA, Evolutionary Action

4.4.1.4. Other considerations

The first part of this challenge illustrates the ability of current approaches to link exomic data with phenotype. Our approach was partially automated and the assignment of disorder classes was purely based on genetic information. Although, the accuracy of the current approaches is still not satisfactory, these results suggest that our approach was very competitive and that EA can help in further advancing the current state‐of‐the‐art. On the second part of the challenge, narrowing down the possibilities was a critical step and therefore the outcome may not only represent the ability to identify specific clinical symptoms. We had five correct matches out of the 12 predictions, which is a higher rate compared with the six correct matches out of the 24 predictions made by the two top submissions. This high success rate of the EA‐based approach suggests that it can help in improving the interpretation of genomic data.

4.4.2. Challenge 9 – clotting disease

Separate patients with venous thromboembolism (VTE) from atrial fibrillation (AF) patients based on their exomic data.

4.4.2.1. Challenge description

A cohort of African Americans has been prescribed long term warfarin either because of venous thromboembolism (VTE) or atrial fibrillation (AF). The challenge was to separate those two groups based on their exome sequencing data.

4.4.2.2. EA approach

For each exome, we predicted the function loss of each gene due to genetic variants. Specifically, we assumed the EA score of each variant is the percentage of function loss in that gene. For genes with multiple mutations i, their loss of function LOF_g was calculated as: LOF_g = 1−∏(1−EA_i/100), where ∏ indicates product for all mutations in that gene. Then, we identified which genes predispose for VTE and which ones for AF, using the DisGeNET platform (Pinero et al., 2017). For each disease, DisGeNET provides a list of genes scored with an index that represents the confidence of association, which we term DGN score. To avoid false positive associations, we arbitrarily used genes with DGN scores of 0.1 or above. This yield eight genes associated to VTE (F5, F2, FGA, PROC, PLAT, SERPINC1, TNF, and SERPIND1) and 38 genes associated with AF (SCN5A, KCNE2, HCN4, NKX2–5, ACE, GJA5, KCNQ1, NOS3, KCNA5, LMNA, NPPA, ZFHX3, KCNN3, VWF, NPPB, PRKAG2, NUP155, SELE, CAV1, SCN10A, MYH7, ANK2, SOX5, HTR4, SYNE2, PLN, C9orf3, PRRX1, CAV2, CACNA1C, WNT8A, EDN1, CACNB2, SMAD3, TNNI3K, TAB2, DTNA, and DES). To account for the strength of the association of a gene to disease we calculated a weighting factor for each gene based on the DGN score, as: w_gene = w_GI·(DGN−0.1), where w_GI may represent the ability of the genes to tolerate variations. In our first submission w_GI was the percentile rank of the genes according to the average EA score of the variants seen in gnomAD (Lek et al., 2016), while in our second submission we assumed that DGN scores already account for this effect and we set w_GI = 1. Then, we calculated the fitness effect on VTE genes (EA_VTE) and on AT genes (EA_AF) as the sum of w_gene· LOF_g, respectively. To normalize the two fitness effect scores, we assumed that the number of patients with VTE is about equal to the number of AF patients and we calculated the ratio: r = ave(EA_VTE)/ave(EA_AF), where ave represents the average values for all individuals. The probability (p) of an individual to have VTE was finally calculated as: p = EA_VTE/(EA_VTE + r·EA_AF).

4.4.2.3. CAGI assessment (McInnes et al., 2019)

There were 14 submissions from seven research groups in this challenge, based either on clustering or on impact burden (such as the EA submission). Because the warfarin dose is a strong confounder, the CAGI assessors disqualified approaches that used dosage information. The assessors used the overall accuracy to assess the performance of the predictions (Figure 4c). Our second submission had the second‐best accuracy, while it was the best amongst the burden‐based methods. In contrast to cluster‐based methods that may provide binary classifications, our approach calculated probabilities (p) and the assessor used the cutoff of p = 0.5 to categorize the data. To compare the predictions with a published model of genetic risk for VTE (Soria et al., 2014), the assessor adjusted the cutoff of the EA‐based predictions to p = 0.4. For that cutoff, the EA‐based predictions yield almost identical sensitivity and specificity to the reported values for the published VTE risk model and the accuracy of our submission increased to 0.64 (Figure 4c).

4.4.2.4. Other considerations

The heritability of VTE has been estimated at about 60% (Souto et al., 2000) and GWAS studies have implicated several noncoding variants (Sabater‐Lleal et al., 2012; Tang et al., 2013). Therefore, it is not a surprise that the prediction accuracy is relatively low when only exome sequencing data were used for the predictions. As mentioned above (in the PTEN and TPMT challenge), the balanced accuracy should have been preferred instead of the overall accuracy. The fact that our approach, which is general and untrained, achieved similar performance to the current model of VTE risk is very encouraging.

5. DISCUSSION

So far, CAGI has run five experiments with a total of 50 challenges that aimed to objectively assess the performance of computational methods for predicting phenotypic impact. To make informative assessments, the data sets should be large, unpublished, highly reproducible, and readily interpretable. Challenges that meet these conditions should be appropriate for the assessment of predictions, otherwise they may be hard to interpret or even misleading. The CAGI experiments follow the highest standards and assure objectivity to the highest possible extent, although one should always be cautious with the assessment interpretation. The test data are properly described and any predictor is called to blindly submit answers. The participating predictors represent mostly state‐of‐the‐art and new untested methods, since older methods that had poor or modest performance in past CAGI experiments tend to abstain from future challenges. Independent scientists run the assessment (often the data providers) on the anonymized submissions and they evaluate them systematically using any metrics of their choice. Circularity in CAGI is rarely an issue, since the challenges consist of new and unpublished data sets. Also, because CAGI challenges are multiple and diverse, they offer insight on the consistency of methods that have been used in multiple challenges.

The CAGI assessments consistently found the Evolutionary Action submissions are amongst the best predictors of the fitness effect of variants. This was shown in older CAGI experiments (Katsonis & Lichtarge, 2017) and in the most recent one: Best assessor's score for CALM1, second best correlation for GAA, and best multiclass ROC in ENIGMA amongst submissions that did not rely on prior (circular) annotation data. This last challenge is clinically relevant as variants of unknown significance bedevil the results of BRCA1/2 sequencing in breast cancer clinics. Surprisingly, we found that EA also has strong correlation with protein stability data on PTEN and TPMT variants (better than state‐of‐the‐art stability predictors), which becomes even stronger when we distinguish between the folding and nonfolding components of the EA fitness effect. A further strikingly positive development was also the good performance of our submissions on exome interpretation: The best method in assigning disorder classes to exome data in SickKids5 and the second‐best method in accuracy (or best after adjusting the cutoff) in separating VTE from AF patients in the clotting disease challenge. The performance of EA is especially good when the challenges involve numerous data points. We speculate this is because EA is a scalable and untrained method, free of training biases. Training biases may help in matching better the fitness effect for few well‐studied variants, while they harm the predictions for the bulk of the variants. Also, in challenges with very few data points, such as Frataxin that included only eight variants, it might be hard to drive robust conclusions, but even in that challenge EA had a large AUC of 0.87. Using EA scores based on new multiple sequence alignments instead of the pre‐calculated values was beneficial for the GAA challenge, gave marginal improvement for the PTEN and TPMT challenge, and it was practically the same for the CALM1 challenge.

In the PCM1 and CHEK2 challenges nearly all computational approaches yield predictions that were indistinguishable from random. The fact none of the methods could make informative predictions suggests a fundamental mismatch between the test data and the predictions. Such a discrepancy was obvious in the CHEK2 challenge: All but one variant were sparsely seen in cases and controls, making impossible to assess this challenge without assuming that variants seen in cases are pathogenic and variants seen in controls are benign. This assumption is problematic, since benign variants are equally likely to be in cases or in controls and pathogenic variants may be found often in cases and rarer in controls. Due to this discrepancy, at least one‐third of the variants are expected to be used with wrong annotation in the assessment and therefore even the true annotation may appear insignificant in the assessment. For the PCM1 challenge, it was a surprise to see no correlation between predictions and experimental data. Given that each computational method uses a different input that informs the selection constraints during protein evolution, this discrepancy suggests a lack of connection between the experimental phenotype and PCM1 evolution. This disconnect calls for caution in evaluating the many factors that may affect a link between PCM1 variants and brain development in the posterior ventricle area in a zebrafish model of schizophrenia. Perhaps, the genetic context and molecular function differences between human and zebrafish can affect the observed impact of PCM1 variants. Multiple positive and negative controls could give insight on this (e.g., test known benign and loss‐of‐function human PCM1 variants with this assay). Also, we may need confidence values through experimental repeats to test whether stronger confidence leads to better performance (as smaller standard deviations dramatically increased agreement in the CALM1 challenge, see Figure 1b).

These results suggest that computational methods should be used cautiously and their predictions should be interpreted according to their principles, to avoid discrepancies. For example, EA has not been trained to match experimental data or clinical associations. Instead, EA uses a differential calculus framework to compute the principles that determine the selection or elimination of the numerous variations that spontaneously occurred and shaped the evolution of proteins (protein homology information). The same principles can inform us about the fitness of future mutational events (predictions). These predictions refer to the “evolutionary effect” of variants, which correlates imperfectly with their clinical and with their experimental effects. Such imperfections are apparent when experimental data disagree with the vast majority of independent predictors (Zhang et al., 2017). Since it is known that discrepancies between experimental and clinical data also exist (Bisio, Ciribilli, Fronza, Inga, & Monti, 2014), training may bias the prediction towards the type of the training data used. Such biases may improve the agreement with effects of the same type, but will worsen the agreement with the other types of effects because they have no evolutionary basis. Because EA is not trained and it does not contain any such biases, it can apply equally well on effects of different nature and we think this may explain the robust performance throughout the different challenges. Moreover, since protein evolution took place at various environmental conditions and genetic context, the evolutionary effect is expected to be broader than the context of any specific assay. Interestingly, when the variant impact represents combined evidence from multiple assays at multiple conditions the agreement with the EA scores becomes stronger (Gallion et al., 2017).

In summary, the challenges of the CAGI5 experiment offer objective and systematic assessments of the performance of computational methods, but they should be cautiously interpreted. The Evolutionary Action method, consistent with the previous CAGI experiments, was found to be one of the top methods across challenges in predicting the experimental and clinical effect of missense variants. EA was also used as the basis to predict protein stability and to match genome data to disease phenotype, where it was also found to be one of the top predictors. The performance of EA is particularly good in challenges that involve many variants (PTEN and TPMT had 7,954 variants and the CALM1 had 1,813 variants) compared with those with few (Frataxin had eight variants), suggesting that the performance holds well when applied large scale. The main advantage of EA is that it is an untrained model of protein evolution, therefore its predictions reflect evolution principles and are free of training data biases. As a result, EA is likely robust to differences between de novo mutations and well‐studied polymorphisms or between proteins of eukaryotic, prokaryotic, or viral origin. The robust performance of EA in various challenge types, suggests it is valuable for the interpretation of genetic variations.

6. CONFLICT OF INTERESTS

The authors declare no competing financial interests.

Katsonis P, Lichtarge O. CAGI5: Objective performance assessments of predictions based on the Evolutionary Action equation. Human Mutation. 2019;40:1436–1454. 10.1002/humu.23873