Tensor‐valued diffusion MRI in under 3 minutes: an initial survey of microscopic anisotropy and tissue heterogeneity in intracranial tumors

Abstract

Purpose

To evaluate the feasibility of a 3‐minutes protocol for assessment of the microscopic anisotropy and tissue heterogeneity based on tensor‐valued diffusion MRI in a wide range of intracranial tumors.

Methods

B‐tensor encoding was performed in 42 patients with intracranial tumors (gliomas, meningiomas, adenomas, and metastases). Microscopic anisotropy and tissue heterogeneity were evaluated by estimating the anisotropic kurtosis (MK_A) and isotropic kurtosis (MK_I), respectively. An extensive imaging protocol was compared with a 3‐minutes protocol.

Results

The fast imaging protocol yielded parameters with characteristics in terms of bias and precision similar to the full protocol. Glioblastomas had lower microscopic anisotropy than meningiomas (MK_A = 0.29 ± 0.06 vs. 0.45 ± 0.08, P = 0.003). Metastases had higher tissue heterogeneity (MK_I = 0.57 ± 0.07) than both the glioblastomas (0.44 ± 0.06, P < 0.001) and meningiomas (0.46 ± 0.06, P = 0.03).

Conclusion

Evaluation of the microscopic anisotropy and tissue heterogeneity in intracranial tumor patients is feasible in clinically relevant times frames.

1. INTRODUCTION

Diffusion MRI (dMRI) has long been recognized as useful for the characterization of tumor microstructure. Quantification of the apparent diffusion coefficient (ADC) yields an imaging biomarker linked with tumor cellularity,1, 2, 3 and monitoring the response of ADC to treatment can enable early prediction of therapy response.4, 5 However, the ADC is also sensitive to a number of mechanisms other than the cellularity,6, 7 such as aquaporin expression.8 Therefore several approaches have been proposed to improve the ability of dMRI to characterize tumor microstructure. Some rely on microstructure modeling, where assumptions on the microgeometry of tumors are translated into mathematic models that enable estimation of parameters with an assigned interpretation (e.g., the “intracellular volume fraction”). However, such approaches may lead to misleading results if the model assumptions are invalid.9, 10, 11, 12 Signal representations belong to another class of approaches that provide parameters without predetermined interpretations10 but can be associated with microscopic features of the tissue in a pathology‐by‐pathology basis. An example of the latter is diffusional kurtosis imaging (DKI),13 which demands imaging protocols with higher b‐values than what is required for ADC quantification alone, and provides parameters such as the mean kurtosis (MK). DKI has shown promise in enabling a higher sensitivity to changes in tumor microstructure and an improved ability to predict glioma grade.14, 15, 16 However, the biologic interpretation of the mean kurtosis is ambiguous in tumors, because it is sensitive to both microscopic diffusion anisotropy and intra‐voxel variation in isotropic diffusivity, also known as tissue heterogeneity,17 as well as intra‐compartmental kurtosis13, 18 and water exchange.19

Tensor‐valued diffusion encoding is a concept for dMRI that can be used to separate microscopic anisotropy from isotropic heterogeneity. Where conventional dMRI encodes for diffusion by a single pair of pulsed gradients,20 tensor‐valued encoding use gradients that encode for diffusion in more than one direction before the image readout.21, 22, 23 This enables control of the shape of the so‐called b‐tensor.21, 22, 23 Separation of microscopic anisotropy and heterogeneity is enabled by combining dMRI data acquired with more than one shape of the b‐tensor and is therefore not possible with just conventional dMRI because it can only generate linear b‐tensors.22, 24, 25, 26 Tensor encoding protocols that support separation of microscopic anisotropy and heterogeneity can be based on so‐called double diffusion encoding that permits linear and planar tensor encoding27, 28, 29 or continuous gradient waveforms that enables encoding with arbitrary b‐tensor shapes, for example, combinations of linear and spherical tensor encoding,25, 26, 30 or any combination of linear, prolate, spherical, and oblate encoding tensors.21, 22, 23 Here, we used continuous gradient waveforms to achieve linear and spherical encoding because these waveforms can be optimized for minimal TEs and therefore enhanced SNR,31, 32 while also (in contrast to spin echo double diffusion encoding) eliminating artefacts from concomitant fields.33

Data acquired with multiple b‐tensor shapes at moderate or high b‐values can be analyzed by the use of higher‐order tensors,22 microstructure models,9 or by using an approach similar to the inverse Laplace transform.34 Here, we chose to use a signal representation based on the cumulant expansion and high‐order tensors,21, 22 because it yields robust parameters and does not require explicit assumptions on the tumor microstructure. The analysis involves estimation of a fourth‐order tensor, similar to the kurtosis tensor in diffusional kurtosis imaging (DKI).13 It differs in that conventional diffusion encoding in DKI necessitates an assumption of full symmetry of this fourth‐order tensor, whereas the inclusion of tensor‐valued encoding can be used to relax this assumption to one of major and minor symmetry. This allows the separation of two invariant components of this fourth‐order tensor,22 which capture the information on the microscopic anisotropy and the heterogeneity of isotropic diffusivities, respectively.26 Note that this interpretation of the results assumes that data is acquired with different b‐tensor shapes while keeping other experimental features constant. Violating this assumption may result in a parameter bias, with a magnitude that depends on the protocol. This is obvious for relaxation weighting: echo and repetition times should be kept constant while varying the b‐tensor shape. It may be less obvious but, depending on the context, just as important for features such as diffusion times (spectral content)35, 36 or concomitant field gradients.33

Previous studies including tensor‐valued diffusion encoding were relatively lengthy that may hamper their clinical use. In this study, we used the insights from “fast DKI,”37, 38 showing that the relevant components of the fourth‐order tensor can be estimated with a parsimonious and rapid signal sampling scheme. The purpose of this study was to demonstrate that tensor‐valued diffusion encoding can be performed in just 3 minutes of scan time and to provide an initial survey of the microscopic anisotropy and tissue heterogeneity in various intracranial tumors.

2. THEORY

2.1. Signal expression

The magnetic‐resonance signal (S) becomes diffusion‐weighted by inducing a dispersion in the phase distribution (ϕ). In the absence of net flow, the signal can be approximated by the second and fourth cumulants of the phase distribution (c ₂ and c ₄)

$$\frac{S}{S_0}=〈\exp \left(-i\varphi \right)〉\approx \exp \left(-\frac{1}{2}{c}_2+\frac{1}{24}{c}_4\right),$$ (1)

where $〈·〉$ indicates averaging over all spin‐bearing particles in the voxel, $\varphi =\gamma \int \mathbf{g}\left(t\right)·\mathbf{r}\left(t\right)\mathrm{d}t$, γ is the gyromagnetic ratio, g(t) is the magnetic field gradient vector at time t, and r(t) is the position of the spin‐bearing particle.39 Assuming the voxel can be subdivided into multiple local and non‐exchanging microenvironments in which the diffusion is approximately Gaussian, so that effects of time‐dependent diffusion on the time‐scales of g(t) can be neglected, we express the second cumulant as

$$c_2=2\mathbf{B}:〈\mathbf{D}〉,$$

where B is the b‐tensor, $⟨\mathbf{D}⟩$ is the voxel‐average of local diffusion tensors, and ‘:’ denotes the double inner product between 2 tensors, so that $\mathbf{A}:\mathbf{B}={\sum }_{i=1..3,j=1..3}{a}_{\mathit{ij}}{b}_{\mathit{ij}}$. For completeness, we note that

$$\mathbf{B}=\underset{0}{\overset{\tau }{\int }}\mathbf{q}{\left(t\right)}^{\otimes 2}dt,$$

where τ is the echo time, $\otimes$ denotes the outer product so that ${\mathbf{x}}^{\otimes 2}=\mathbf{x}\otimes \mathbf{x}$, and

$$\mathbf{q}\left(t\right)=\gamma \underset{0}{\overset{t}{\int }}\mathbf{g}\left(t^{\prime }\right)d{t}^{\prime }.$$

The conventional b‐value is given by the trace of the b‐tensor:

$$b=\text{Tr}\left(\mathbf{B}\right).$$

The fourth cumulant is given by

$$c_4=⟨c_4^{\prime }⟩+3\left(⟨{c_2^{\prime }}^2⟩-{⟨c_2^{\prime }⟩}^2\right),$$

where $c_2^{\prime }$ and $c_4^{\prime }$ denotes the cumulants of the phase distribution in each local microenvironment, and $〈·〉$ averaging across those microenvironments. Assuming the phase distribution in each microenvironment is approximately Gaussian, $c_4^{\prime }$ is ~0, and therefore

$$c_4=12{\mathbf{B}}^{\otimes 2}:\mathbb{C},$$

where

$$\mathbb{C}=〈{\mathbf{D}}^{\otimes 2}〉-{〈\mathbf{D}〉}^{\otimes 2},$$

is the covariance between the diffusion tensors of the local microenvironments.22 Under these assumptions, the MR signal is given by

$$\frac{S}{S_0}\approx \exp \left(-\mathbf{B}:\mathbf{D}+\frac{1}{2}{\mathbf{B}}^{\otimes 2}:\mathbb{C}\right).$$ (2)

The voxel‐average diffusion tensor has six independent elements and the fourth‐order tensor has 21 independent parameters because it has major and minor symmetry.22 Methods that support calculations with fourth‐order tensors can be found in the multidimensional diffusion MRI framework (https://github.com/markus-nilsson/md-dmri/tree/master/tools/tensor_maths).40 Note that this approach includes only second‐order terms in b, which results in parameter bias when higher‐order terms have a relevant impact on the acquired signal.41

2.2. Powder averaging

To simplify estimation of the relevant properties of the tensor covariance, we can use so‐called powder averaging where the signal is averaged across a number of rotations of the b‐tensor to induce approximately complete orientation dispersion regardless of the actual orientational distribution within the voxel.26, 29, 42 In this section, we assume the b‐tensors to be cylinder symmetric. After averaging, the second and fourth cumulants are given by

$$c_2\approx 2〈\mathbf{B}〉:{〈\mathbf{D}〉}_{\mathrm{I}},$$

and

$$c_4\approx 12〈{\mathbf{B}}^{\otimes 2}〉:{\mathbb{C}}_{\mathrm{I}},$$

where $〈\mathbf{B}〉$ and $〈{\mathbf{B}}^{\otimes 2}〉$ are averages of $\mathbf{B}$ and ${\mathbf{B}}^{\otimes 2}$ across the b‐tensor rotations, and ${〈\mathbf{D}〉}_{\mathrm{I}}$ and ${\mathbb{C}}_{\mathrm{I}}$ are isotropic second and fourth‐order tensors. The goal is to include a sufficient number of rotations so that

$$〈\mathbf{B}〉\approx b·\frac{1}{3}\mathbf{I},$$ (3)

where I is the second order identity tensor (${\mathrm{\delta }}_{\mathit{ij}}$), and

$$〈{\mathbf{B}}^{\otimes 2}〉\approx b^2\left({\mathbb{I}}_{\mathrm{I}}+b_{\mathrm{\Delta }}^2·\frac{2}{5}{\mathbb{I}}_{\mathrm{A}}\right),$$ (4)

where and ${\mathbb{I}}_{\mathrm{I}}$ and ${\mathbb{I}}_{\mathrm{A}}$ are two isotropic but orthogonal fourth‐order tensors (${\mathbb{I}}_{\mathrm{I}}:{\mathbb{I}}_{\mathrm{A}}=0$). The parameter $b_{\mathrm{\Delta }}$ describes the shape of the b‐tensor, is unitless and has a value of –1/2 for planar b‐tensor encoding, 0 for spherical b‐tensor encoding, and 1 for linear tensor encoding.23 The isotropic tensors are given by ${\mathbb{I}}_{\mathrm{I}}={\left(\frac{1}{3}\mathbf{I}\right)}^{\otimes 2}=\frac{1}{9}{\delta }_{\mathit{ij}}{\delta }_{\mathit{kl}}$ and ${\mathbb{I}}_{\mathrm{A}}={\mathbb{I}}_{\mathrm{T}}-{\mathbb{I}}_{\mathrm{I}}$ where ${\mathbb{I}}_{\mathrm{T}}=\frac{1}{6}\left({\delta }_{\mathit{ik}}{\delta }_{\mathit{jl}}+{\delta }_{\mathit{il}}{\delta }_{\mathit{jk}}\right)$. In Westin et al.,22 ${\mathbb{I}}_{\mathrm{I}}$, ${\mathbb{I}}_{\mathrm{A}}$, and ${\mathbb{I}}_{\mathrm{T}}$ were denoted ${\mathbb{E}}_{\text{BULK}}$, ${\mathbb{E}}_{\text{SHEAR}}$, and ${\mathbb{E}}_{\text{ISO}}$, respectively.

Under these conditions, the logarithm of the powder averaged signal will be given by a linear equation

$$\ln S\approx \ln S_0-b\text{MD}+\frac{1}{2}{b}^2\left[V_I+b_{\mathrm{\Delta }}^2{V}_{\mathrm{A}}\right]=\mathbf{e}·\mathbf{m},$$ (5)

where $\mathbf{e}=\left[1-b\frac{1}{2}{b}^2\frac{1}{2}{b}^2{b}_{\mathrm{\Delta }}^2\right]$ describes the experiment and $\mathbf{m}={\left[\ln S_0\text{MD}{V}_{\mathrm{I}}{V}_{\mathrm{A}}\right]}^{\mathrm{T}}$ are the model parameters defined by

$$\text{MD}=〈d_I〉={〈\mathbf{D}〉}_{\mathrm{I}}:\frac{1}{3}\mathbf{I}$$

$$V_I={\mathbb{C}}_{\mathrm{I}}:{\mathbb{I}}_{\mathrm{I}}=〈d_I^2〉-{〈d_I〉}^2$$

$$V_A={\mathbb{C}}_{\mathrm{I}}:\frac{2}{5}{\mathbb{I}}_{\mathrm{A}},$$

where the first parameter $〈d_I〉$ is the voxel‐averaged isotropic diffusivity and referred to as the mean diffusivity (MD) in the context of DTI and DKI, and V _I and V _A are the intra‐voxel variances in apparent diffusivities because of isotropic heterogeneity and microscopic anisotropy, respectively.22, 26 Note that the average eigenvalue variance of local diffusion tensors, often denoted $〈V_{\lambda }〉$, is related to V _A according to $\frac{2}{5}〈V_{\lambda }〉=V_A$.17, 26 An estimate of the model parameters ($\widehat{\mathbf{m}}$) can now obtained from the linear least squares solution, just as for DTI,43 according to

$$\widehat{\mathbf{m}}={\left({\mathbf{E}}^{\mathrm{T}}·\mathbf{C}·\mathbf{E}\right)}^{-1}·{\mathbf{E}}^{\mathrm{T}}·\mathbf{C}·\ln \mathbf{S},$$ (6)

where ${\mathbf{E}}^{\mathrm{T}}=\left[{\mathit{e}}_1^{\mathbf{T}}{\mathit{e}}_2^{\mathbf{T}}\dots {\mathit{e}}_n^{\mathbf{T}}\right]$ is a 4 by n matrix describing an encoding protocol featuring n “shells,” meaning acquisitions with b‐tensors of identical size (b) and shape ($b_{\mathrm{\Delta }}$) but different orientations, S is an n by one vector of the acquired signal, and a C is a diagonal matrix correcting for the heteroscedasticity induced by the logarithm operation43 and the possibly different number of acquisition directions (m) in shell i by having diagonal elements given by $C_{\text{ii}}={\mathrm{S}}_i^2{m}_i$.

2.3. A minimal protocol

Our goal was to enable rapid estimation of the four unknowns in Equation 5: S ₀, MD, V _I, and V _A. With four unknowns and in the absence of voxel‐scale anisotropy, this requires at the very minimum four acquisitions of the signal S with different “shells.” It can be shown that four “shells” with $\left[b,b_{\mathrm{\Delta }}\right]$ = $\left[0,0\right]$, $\left[1,0\right]$, $\left[2,0\right]$, and $\left[2,1\right]$, with b in units of ms/µm², is sufficient for the matrix inversion in Equation 6 to be performed and could therefore enable estimation of the four parameters.

In the presence of voxel‐scale anisotropy, data for each shell would have to be acquired with a sufficient number of rotations of the b‐tensors (“directions”) to provide an accurate powder average. From theory, we know this number to increase with the b‐value.44 For low b‐values, rotation invariance is obtained by fulfilling Equation 3. This can be done with a single spherical b‐tensor or by averaging over three linear b‐tensors

$$〈\mathbf{B}〉=\frac{1}{3}\left[\begin{array}{ccc}b& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]+\frac{1}{3}\left[\begin{array}{ccc}0& 0& 0\\ 0& b& 0\\ 0& 0& 0\end{array}\right]+\frac{1}{3}\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& b\end{array}\right]=b\frac{1}{3}\mathbf{I}.$$

At higher b‐values, we need to fulfil Equation 4 to obtain rotation invariance. This can be obtained by averaging over the six directions defined by the icosahedral sampling scheme, because

$${\mathbb{I}}_{\mathrm{I}}+\frac{2}{5}{\mathbb{I}}_{\mathrm{A}}=\frac{1}{6}\sum _{i=1}^6{\mathit{n}}_i^{\otimes 4},$$

where ${\mathit{n}}_1=\left[\begin{array}{ccc}0& c_1& c_2\end{array}\right]$, ${\mathit{n}}_2=\left[\begin{array}{ccc}0& c_1& -c_2\end{array}\right]$, ${\mathit{n}}_3=\left[\begin{array}{ccc}{c}_1& c_2& 0\end{array}\right]$, ${\mathit{n}}_4=\left[\begin{array}{ccc}{c}_1& -c_2& 0\end{array}\right]$,${\mathit{n}}_5=\left[\begin{array}{ccc}{c}_2& 0& c_1\end{array}\right]$, and ${\mathit{n}}_6=\left[\begin{array}{ccc}-c_2& 0& c_1\end{array}\right]$, where $c_1=\sqrt{\left(5-5^{1/2}\right)/10}$, and $c_2=\sqrt{\left(5+5^{1/2}\right)/10}$.45 Previous studies have shown that a similar rotation invariance is possible also by averaging across nine custom directions.46 In practice, just six directions may not be sufficient because of the influence of higher‐order terms (e.g., b³ terms).41 For the purpose of rotation invariance, however, we have previously shown that six directions are sufficient for an accurate powder average up to moderate attenuation factors ($b·\text{MD}<2$) if the system of interest has a low voxel‐level anisotropy (FA < 0.5),32 which is likely the case for most tumors.

In summary, the theoretical analysis shows that rotation‐invariant estimates of the four model parameters of interest can be obtained in a voxel with low to moderate voxel‐level anisotropy with just nine measurements: three with spherical b‐tensors having b = 0, 1, and 2 ms/µm² and six with linear b‐tensors and b = 2 ms/µm² played out along the icosahedral sampling scheme. In practice, more measurements may be preferred to improve the precision of the estimated parameters.

2.4. Microstructure measures

From the parameters in Equation 5, we define the two microstructure measures that we will focus on in this study, which we refer to as the isotropic and anisotropic kurtosis (MK_I and MK_A, respectively), defined by

$${\text{MK}}_{\mathrm{I}}=3V_{\mathrm{I}}/{\text{MD}}^2$$

and

$${\text{MK}}_{\mathrm{A}}=3V_{\mathrm{A}}/{\text{MD}}^2.$$

The sum of these parameters yields the total mean kurtosis (MK_T = MK_I + MK_A), which is similar but not identical to the mean kurtosis (MK) obtained in diffusional kurtosis imaging. The dissimilarity stems from the powder averaging operation applied in the present analysis.

We have previously demonstrated that MK_A and MK_I capture microstructure features of tumors via quantitative histology.17 Results showed that the MK_I was associated with cell density heterogeneity within the voxel, whereas the MK_A was associated with what can informally be described as the average cell shape within the voxel and formally as the average anisotropy of the structure tensor, determined by image analysis of the histology images.47, 48, 49

3. METHODS

3.1. Acquisition protocol

Imaging was performed on a 3T MAGNETOM Prisma with a 20‐channel head coil array (Siemens Healthcare, Erlangen, Germany). Morphologic imaging was performed with a T₁‐weighted 3D‐MPRAGE sequence pre‐ and post‐intravenous gadolinium (Gd) administration and a FLAIR (fluid‐attenuated inversion recovery) sequence. Diffusion‐weighted images were acquired before the administration of Gd with a prototype spin‐echo sequence that enables diffusion encoding with arbitrarily shaped b‐tensors.32 Imaging was performed with TE = 80 ms, TR = 3.2 s, FOV = 230 × 230 mm², slices = 21, resolution = 2.3 × 2.3 × 2.3 mm³, iPAT = 2 (GRAPPA), and partial‐Fourier = 6/8. Tensor encoding was performed using asymmetric gradient waveforms that were optimized to minimize TE using a constrained optimization approach described in Sjölund et al31 and available at https://github.com/jsjol/NOW. The optimization used the following settings: “max norm,” heat dissipation factor 0.5, and a slew rate limit of 50 T/m/s. A short TR was enabled by limiting the number of slices. The resulting 5‐cm thick imaging volume was positioned across the lesion of interest by the radiographers based on images from previous examinations (CT or MRI).

3.2. Evaluating the rotation invariance of the tensor encoding protocol

The dMRI protocol comprised four b‐values (b = 0.1, 0.7, 1.4, and 2.0 ms/μm²) acquired in 3, 3, 6, and 6 directions for the linear tensor encoding, and with 6, 6, 10, and 16 averages of the spherical tensor encoding, respectively. This resulted in an acquisition time of 3 minutes. Previous b‐tensor encoding protocols has featured more than six directions at the maximum b‐value to ensure that a rotation‐invariant powder‐averaged signal could be obtained.17, 32 The accuracy of powder averaging with a limited number of directions was analyzed by acquiring extra data in a volunteer using three different diffusion protocols referred to as the “full,” “subsampled,” and “optimized” protocols. All protocols comprised the same four b‐values (b = 0.1, 0.7, 1.4, and 2.0 ms/μm²), but were applied in 6, 6, 10, and 16 directions for the full protocol and in 3, 3, 6, and 6 directions for the subsampled and optimized protocols. All protocols sampled STE signals with 6, 6, 10, and 16 averages for the different b‐values. The directions in the full protocol were obtained by the so‐called electrostatic repulsion algorithm.50, 51 The directions in the subsampled protocol were selected from the full protocol to be as spread out across the sphere as possible. The optimized protocol was the one used in the full study, and for that protocol, the 3 directions used for the lower b‐values were orthogonal, and the six directions used at higher b‐values were selected from an icosahedral sampling scheme (that intrinsically minimize the electrostatic repulsion). The accuracy of MD, MK_A, and MK_I was then assessed by investigating the difference between the two shorter protocols (subsampled and optimized) and the full protocol. The hypothesis was that the short optimized protocol would provide for rotationally invariant parameter estimates (high accuracy), whereas the subsampled protocol would exhibit a parameter bias dependent on the direction of anisotropic structures.

The rotation invariance were also investigated by simulations of a system comprised of cylinder‐symmetric diffusion tensors with an axial and radial diffusivity of 2.0 µm²/ms and 0.2 µm²/ms, respectively. The diffusion tensors were aligned along a given direction with a small orientation dispersion corresponding to an angular standard devaition (SD) of 15°. This represents a realistic scenario with highly anisotropic diffusion tensors and a sharp orientation distribution function, therefore serving as a worst‐case test of the ability of the protocols to produce accurate (rotation‐invariant) parameters. Noise was added to the simulated signal so that it followed a Rice distribution, with a noise‐free magnitude given by the true signal and a noise level corresponding to SNR = 40 at b = 0. The noisy signal was then powder‐averaged, and used to estimate MD, MK_A, and MK_I. The process was repeated for 1000 random rotations of the diffusion tensors and for each rotation, the mean and SD of the three parameters were computed for each of the three protocols. For a protocol with an accurately determined powder averaged signal, the SD ($\mathrm{\sigma }$) would represent only noise, whereas it would be higher for a protocol with suboptimal directions because of a variable rotation‐dependent bias. Assuming the two sources or error are uncorrelated, we can express this as ${\mathrm{\sigma }}^2={\mathrm{\sigma }}_{\text{rotation}}^2+{\mathrm{\sigma }}_{\text{noise}}^2$. Simulations performed without noise therefore allowed separate estimation of ${\mathrm{\sigma }}_{\text{rotation}}^2$, and therefore the two terms were reported separately.

3.3. Subjects

Patients were recruited from those scheduled for a clinical MRI because of a suspected or recurrent brain lesion and were enrolled after giving informed consent. The study was approved by the Ethical Review Board in Lund, Sweden. During the period between March 2017 and August 2018, 42 patients (24 female and 18 male) with intracranial tumors were enrolled with an average (SD) age of 56 (15) y. The analyzed material included 22 gliomas (13 glioblastoma, 4 astrocytoma, 2 oligoastrocytoma, 1 oligodendroglioma, 1 unclassified glioma, 1 brain stem glioma), 5 meningiomas, 1 hemangiopericytoma, 6 brain metastases (3 with primary breast tumors, 2 with primary lung tumors, and 1 with rectal cancer), and 1 pituitary adenoma. Of the gliomas, 12 had undergone surgery before imaging. Six patients were excluded because there were no lesions visible in the contrast‐enhanced T₁W images. One patient was excluded because the lesion was in the frontal lobe close to the petrous apex that led to strong susceptibility artefacts.

3.4. Image post processing

The diffusion‐weighted images were processed in three steps. The first step aimed at correction of motion and image distortions from eddy currents and included registration of the diffusion‐weighted volumes to extrapolated references using ElastiX.52, 53 The use of extrapolation‐based references has been shown to be necessary for accurate registration of high b‐value data.53 In the second step, all volumes were smoothed by a 3D Gaussian kernel with a SD of 0.4 voxels. In the third step, parameter maps were obtained by fitting S ₀, MD, V_I, and V _A to the data using Equation 6. The fitting was performed by linear least squares fitting of the log signal, while correcting for heteroscedasticity (see Theory section for details). Once these parameters were estimated, the isotropic and anisotropic kurtosis components were computed. In addition to these steps, the post‐Gd T₁W image volumes were registered to the diffusion‐weighted volumes to enable the tumor definition for the quantitative analysis. All post processing was performed using the multidimensional diffusion MRI toolbox,40 which is implemented in MATLAB (The MathWorks, Natick, MA) and available at https://github.com/markus-nilsson/md-dmri.

For one subject, perfusion maps of the relative cerebral blood volume (rCBV) were calculated using Nordic ICE (NordicNeuroLab, Bergen, Norway) from data acquired with dynamic susceptibility contrast (Gd) acquisition with a time resolution of 1.5 s using a single‐shot gradient echo EPI‐gradient sequence and a spatial resolution of 1.7 × 1.7 × 6.0 mm³ and an TE of 28 ms. The maps were computed using truncated singular value decomposition, leakage‐corrected with Boxerman and gamma fitting, and coregistered with the diffusion data.

3.5. Quantitative analysis

Regions of interest (ROIs) were drawn in the contrast‐enhancing regions on the post‐Gd T₁W images, excluding apparently necrotic parts where MD >2 μm²/ms. Parts of the images affected by image artefacts because of for example insufficient fat suppression were also excluded. ROIs were also drawn in normal‐appearing frontal white matter to characterize normal‐appearing white matter. The diffusion parameters were then obtained from all subjects except those with glioblastoma, extensive edema, or an imaging slab that did not cover frontal white matter. Average values of MD, MK_A, and MK_I were obtained for each ROI, and basic descriptive statistics were calculated.

4. RESULTS

Figure 1 shows a comparison of the three sampling protocols: the first was a full protocol (5‐minutes long) whereas the second and third were shorter and referred to as the subsampled and optimized protocols (both 3‐minutes long). Numeric simulations showed estimated values of MD close to the expected value of 0.8 µm²/ms for all three protocols, with average values (SD) of 0.78 (0.03), 0.78 (0.07), and 0.78 (0.04) µm²/ms, respectively. For MK_A, the expected value was 1.35 and there was a substantial bias for all three protocols, with average (SD) values of 1.10 (0.12), 1.14 (0.28), and 1.09 (0.15). A similar level of bias was found for MK_I, with values of –0.12 (0.18), –0.17 (0.42), and –0.09 (0.22), compared with the true value of zero. Bias of this magnitude is expected when using truncated cumulant expansions for the data analysis.41, 54 The parameter uncertainty, represented by SDs, has two origins: noise and incomplete rotation invariance that contributed to random errors because of the random rotation applied to the synthetic sample in the simulations. For both the full and the optimized protocols, the variation caused by rotation was substantially smaller than that because of noise, whereas for the subsampled protocol it was larger (Figure 1B). Corresponding results were found in the bias maps from the volunteer measurement (Figure 1D), where the subsampled protocol showed location‐dependent bias in all parameters, whereas the bias from the optimized protocol appeared negligible. In summary, the full and the short protocols exhibited similar characteristics, whereas the naively subsampled protocol suffered from high variance because of rotational variance.

Figure 1.

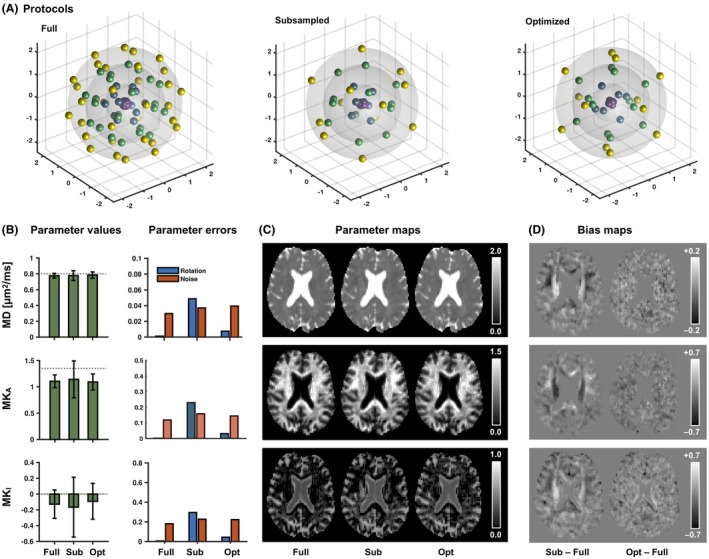
Accuracy and precision for the different imaging protocols. (A) Visualizes the diffusion encoding directions (with antipodal points) in each b‐shells of the linear tensor encoding part of the three protocols. The full protocol featured more directions than the subsampled (sub) and optimized (opt) protocols. (B) Average parameter values (error bars show SDs) from the numerical simulation with the different protocols. The dashed line represents the true values. The right‐hand plot shows parameter errors from the same simulation, separated into errors from rotation variance and noise. (C and D) Parameter and bias maps, respectively, from a healthy volunteer. The optimization yielded results similar to the full protocol, whereas the subsampled protocol exhibited location‐dependent bias likely caused by the suboptimal distribution of encoding directions

Figure 2 shows post‐Gd T₁W and FLAIR images and maps of the mean diffusivity, microscopic anisotropy, and tissue heterogeneity (columns) in four different types of brain tumors (rows). Data were obtained with the optimized protocol. Within the contrast enhancing parts of the glioma and the metastasis, we note a low but non‐zero microscopic anisotropy probably indicating the presence of some residual white matter. Parts of the enhancing lesions also displayed an elevated tissue heterogeneity. In the glioma and brain metastasis patients, edema surrounded the contrast enhancing lesions. This region exhibited elevated mean diffusivity, reduced microscopic anisotropy, and a moderately increased tissue heterogeneity. The pituitary adenoma and the meningioma both had higher microscopic anisotropy than what was observed in the glioma and the metastasis, indicating the presence of elongated cell structures within these tumors. The pituitary adenoma differed from the meningioma in terms of its tissue heterogeneity, which was clearly elevated.

Figure 2.

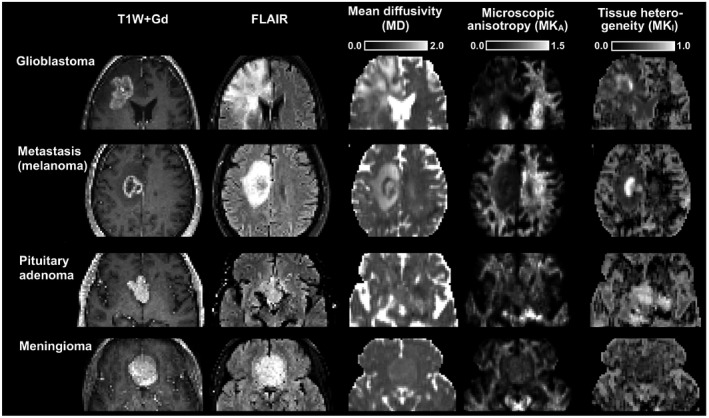
Morphology and microstructure parameter maps in 4 brain tumor types. Both the glioblastoma and brain metastasis cases exhibited low microscopic anisotropy, whereas the pituitary adenoma and the meningioma cases exhibited higher microscopic anisotropy. All tumors in this figure, except the meningioma, displayed regions with markedly elevated tissue heterogeneity (isotropic kurtosis)

In some patients, parts of the tumor edges showed exceptionally high tissue heterogeneity (Figure 3). This parameter depends on data acquired with isotropic diffusion weighting (spherical tensor encoding), and regions with high heterogeneity also had a conspicuous contrast in the raw signal data (Figure 4). The increase in image contrast with high b‐value spherical encoding compared to conventional linear tensor encoded data is particularly striking.

Figure 3.

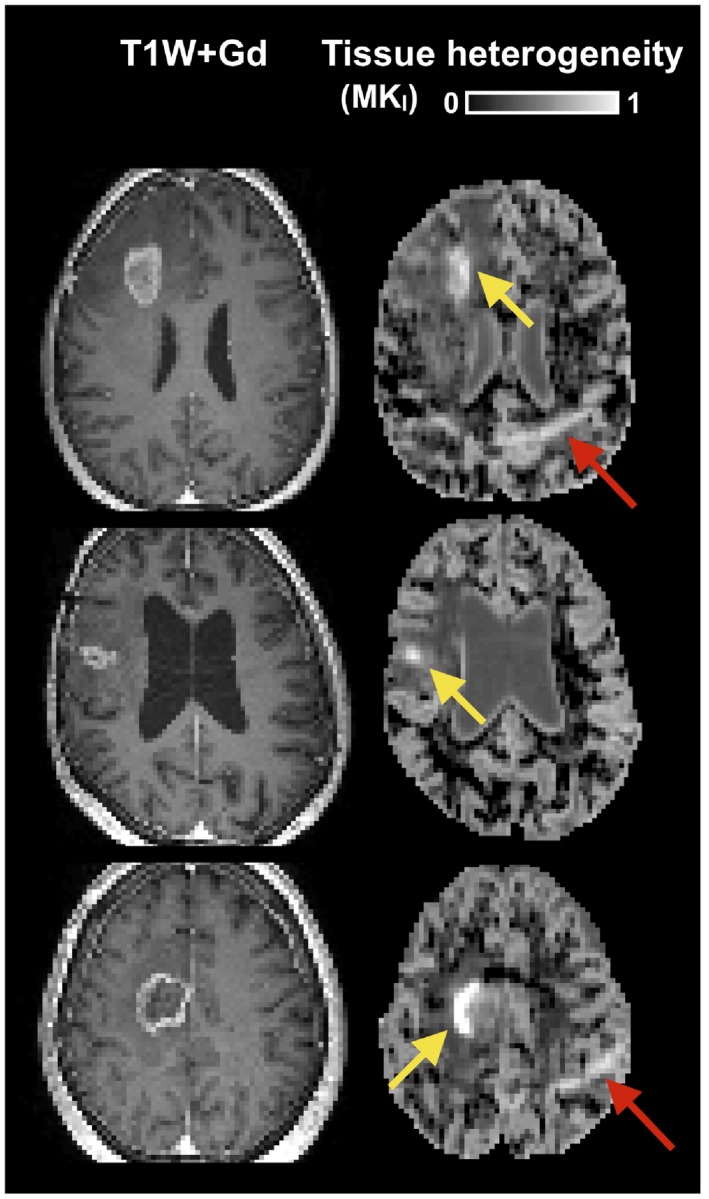
Examples of tumors with high tissue heterogeneity. Cases include two glioblastomas (top rows) and one brain metastasis (bottom row). The yellow arrows point to regions with exceptionally high tissue heterogeneity. The red arrow points to an artefact caused by insufficient fat suppression

Figure 4.

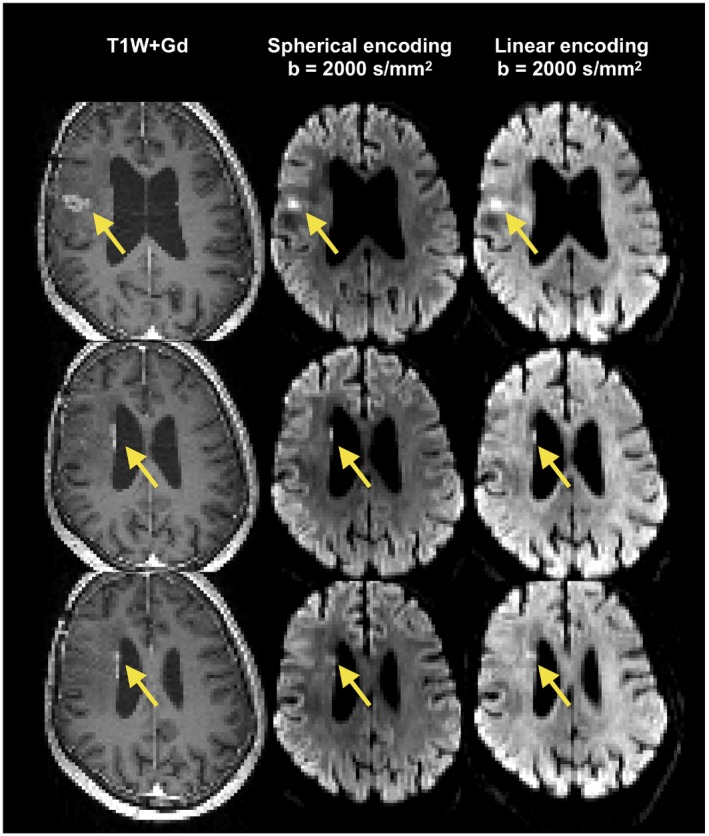
Illustration of stronger image contrast with spherical compared with linear tensor encoding. Yellow arrows point to the locations with high gadolinium load. These regions were associated with high contrast in the high b‐value image with spherical encoding (middle column), whereas a lower contrast was observed when using linear encoding (right column). Identical windowing was applied to the spherical and linear encoding data. Data represent consecutive slices from one patient. The images indicate that tissue anisotropy in surrounding tissue can obfuscate regions of dense tumor tissue, which can reduce detectability

Follow‐up examinations were available for one patient. Figure 5 shows morphologic images, a perfusion map (relative cerebral blood volume), and the diffusion parameter maps (columns) at the baseline and at 12 and 26 weeks post treatment (rows). All diffusion parameter maps were consistent across time on the side contralateral to the lesion, except for some image artefacts. Changes on the maps of the mean diffusivity and microscopic anisotropy on the side ipsilateral to the lesion were aligned with the changes of the edema. The tissue heterogeneity was elevated at baseline but was gradually reduced at later time points. Elevated tissue heterogeneity co‐occurred with low relative blood volumes.

Figure 5.

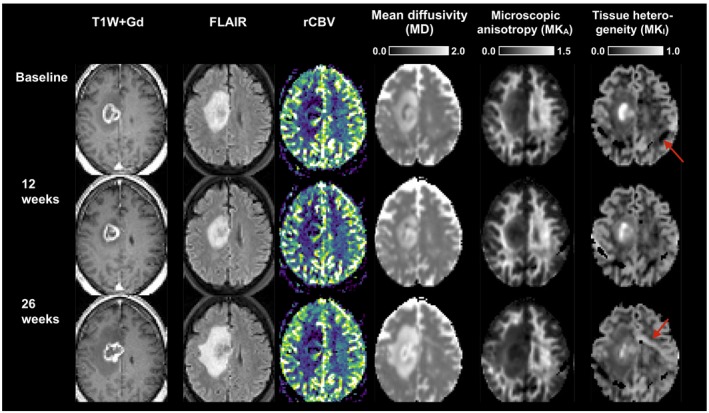
Temporal evolution of the morphological images, relative cerebral blood volume (rCBV), and the diffusion parameter maps in a brain metastasis patient. Contrast enhancement is seen on all of the T₁W + Gd images. The edema seen on the FLAIR image contracts at week 12 but expands at week 26. Parts of the tumor shows consistently elevated relative blood volume. All diffusion parameter maps were consistent across time on the side contralateral to the lesion, except for some image artefacts (red arrow). Changes on the maps of the mean diffusivity and microscopic anisotropy on the side ipsilateral to the lesion were aligned with the changes of the edema. The tissue heterogeneity was elevated at baseline but was gradually reduced at later time points

Finally, average parameter values across the tumors are displayed in Figure 6, categorized by tumor type (glioma, glioblastoma, metastasis, and meningioma) and compared with normal‐appearing white matter. The glioma group included a diverse set of tumors, which manifested as a high variability between the tumors in this group. Compared with normal‐appearing white matter, all tumors except two gliomas had higher mean diffusivity, lower microscopic anisotropy, higher tissue heterogeneity, and lower total kurtosis. Glioblastomas had lower average microscopic anisotropy than meningiomas (MK_A = 0.29 ± 0.06 vs. 0.45 ± 0.08, P = 0.003, rank‐sum test). Metastases had higher tissue heterogeneity (MK_I = 0.57 ± 0.07) than both the glioblastomas (0.44 ± 0.06 P < 0.001, rank‐sum test) and meningiomas (0.46 ± 0.06, P = 0.03, rank‐sum test).

Figure 6.

Overview of parameters in tumors and normal‐appearing white matter (WM). The tumors were categorized by type: glioma excluding glioblastoma (G*), glioblastoma (GB), metastasis (MET), and meningioma (MEN). Bars show average values, whereas black dots show values from individual patients (averaged across the ROIs)

5. DISCUSSION

In this study, we demonstrated that tensor‐valued diffusion encoding can be performed in just 3 minutes to quantify MK_A and MK_I as measures of microscopic anisotropy and tissue heterogeneity in brain tumors. In contrast to normal‐appearing white matter that exhibited high microscopic anisotropy and low tissue heterogeneity, the tumors exhibited low to intermediate microscopic anisotropy and low to high tissue heterogeneity, with the specific characteristics depending on tumor type. Considerable variation was also found within the tumors themselves. Differences in microscopic anisotropy between the glioma and meningioma groups were in line with previous investigations showing that meningiomas contain more microscopically anisotropic tissue.17 High microscopic anisotropy was also found in the pituitary tumor, suggesting that the tumor comprised elongated spindle cells common for e.g., pituicytomas,55 however, we reserve final interpretation until MK_A can be associated to structural anisotropy from histology in a larger sample of this type of tumor. Moreover, substantially elevated tissue heterogeneity were found in some tumors. The biologic interpretation of this is unclear but indicates a high variation of the diffusivity within the voxel. Although speculative, we hypothesize that this could be caused by partial necrosis within the voxel, meaning that some parts of the voxel feature high cell density and therefore low apparent diffusivity whereas others are necrotic with high diffusivity. The co‐occurrence of low relative blood volumes and high tissue heterogeneity could support this hypothesis (Figure 5). Note that high MK_I can also be the result of partial volume effects. This can be seen for example along the ventricle walls where there are voxels that contain both tissue and cerebrospinal fluid, which have substantially different isotropic diffusivities. Further investigations are therefore necessary to determine the association between these novel diffusion parameters and pathology.

Previous imaging protocols with b‐tensor encoding were longer than the one used in the present study. The acceleration relied on four factors: optimized gradient waveforms, limited number of directions, limited slice coverage, and sample balancing. Gradient waveforms were optimized to make use of all the encoding time available in a spin echo sequence.31 Therefore, the gradient waveforms were asymmetric in contrast to the symmetric approach taken in some previous papers.17, 22 The limited number of directions made it possible to reduce the total scan time, and by using a combination of directions that provide a balanced sample of the fourth‐order tensor, and was inspired by previous papers on “fast DKI.”37, 38 However, because of the limited number of directions (6), we expect a slight rotation‐dependent bias in white matter signal with high orientation coherence, however, in tumors, this bias should be negligible because of their low voxel‐level anisotropy (FA).32 The results in Figure 1 indicate that the orientation‐dependent bias in the short protocol is indeed small. The third factor contributing to a faster protocol was the use of a limited number of slices. This allowed a shorter repetition time and therefore a shorter total scan time. The shorter scan time also led to a lower total heat load on the gradient coils, which in turn could be used to shorten the repetition time further while still respecting duty cycle limits.56 Although using a limited number of slices also reduces the coverage, this limitation can be addressed by the use of simultaneous multislice acquisition.57 Finally, high quality maps were enabled by an adapted distribution of samples. In previous works,32 we observed that MK_I had a lower precision than MK_A when acquiring an equal number LTE and STE volumes. Therefore, this protocol featured a higher relative fraction of STE volumes. It should be noted, however, that the protocol design was the result of an experience‐based act of balancing a number of factors that influenced scan time and parameter precision. Future work could explore formal means of protocols optimization to improve parameter precision.58, 59 Such optimization does not generally address the parameter bias reported in Figure 1. This bias is expected when higher order terms affect the acquired data, but the analysis is truncated to second cumulant.41 Finding an optimal protocol requires balancing accuracy and precision,54 and here, we prioritized precision over accuracy (with the exception of minimizing rotation‐dependent bias by using an optimized protocol).

We acknowledge three main limitations of the current study. First, the presence of artefacts because of concomitant fields may have led to parameter bias because of the use of asymmetric waveforms.60 Waveforms can today be optimized to mitigate this effects,60 however, this project was initiated before such waveforms were available and may have resulted in a minor bias toward higher values of the microscopic anisotropy. This should be addressed in future studies. Second, the linear and spherical tensor encoding were performed using gradient waveforms with different timings, so the difference between the acquisitions was not only in the shape of the b‐tensor, but also in the effective diffusion time.35, 36, 41 In the protocol design process, we tried to minimize this difference by making the diffusion time of the linear tensor encoding as short as possible, but the remaining timing difference could have resulted in parameter bias. In healthy white and gray matter, the time‐dependence of the diffusion is negligible between ~10 and 250 ms,61, 62 but whether this is true in all of the tumors investigated remains to be tested. Third, some patients were investigated before surgery and others after. This may have affected the parameters. To test whether the novel diffusion parameters can contribute with diagnostically relevant information, future studies should do imaging before treatment.

Future work can use this short protocol to test clinically relevant questions, for example, whether separation of the 2 diffusional kurtosis components can increase the performance of glioma grade discrimination over the total kurtosis alone,63 enable mapping of meningioma consistency,64, 65 monitor or predict treatment response, or to correlate imaging and histologic analysis of biopsies to elucidate the microstructural underpinnings of the observed contrasts. The impact of the sampling protocol (e.g., b‐values and b‐tensor shapes) on the accuracy and precision of MD, MK_I, and MK_A also need to be investigated, and such work is ongoing.66

CONFLICTS OF INTEREST

M.N. declares research support from and ownership interests in Random Walk Imaging (formerly Colloidal Resource), and patent applications in Sweden (1250453‐6 and 1250452‐8), USA (61/642 594 and 61/642 589), and PCT (SE2013/050492 and SE2013/050493). F.S. has been employed at Random Walk Imaging.

Nilsson M, Szczepankiewicz F, Brabec J, et al. Tensor‐valued diffusion MRI in under 3 minutes: an initial survey of microscopic anisotropy and tissue heterogeneity in intracranial tumors. Magn Reson Med. 2020;83:608–620. 10.1002/mrm.27959